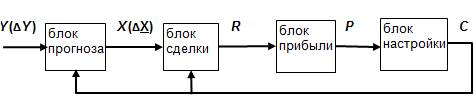
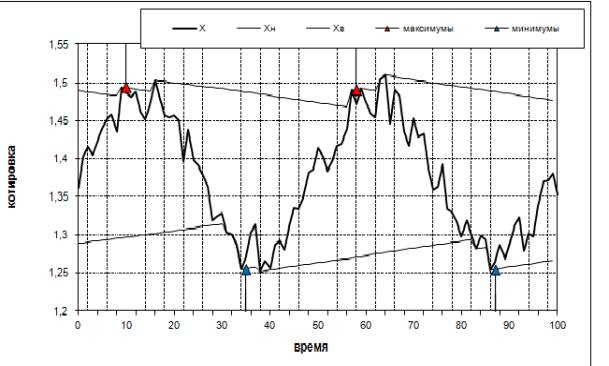
Для записи формул алгоритмов применим стандартный язык Microsoft Office Excel. Алгоритм прогноза цены по апериодическому звену имеет вид:

- прогноз цены X

(1а)…..X_t=X_t-1+(Y_t-X_t-1)/T;

- прогноз тренда цены ∆X

(1б)…..∆X_t=∆X_t-1+(∆Y_t-∆X_t-1)/T.

Здесь: T – временной параметр модели – константа алгоритма прогноза, нижний индекс t – дискретное время.

Алгоритм прогноза цены по колебательному звену имеет вид:

- прогноз цены X

(2а)…..X_t=X_t-1+(1-b)*(X_t-1-X_t-2)+(Y_t-X_t-1)/T,

- прогноз тренда цены ∆X

(2б)…..∆X_t=∆X_t-1+(1-b)*(∆X_t-1-∆X_t-2)+(∆Y_t-∆X_t-1)/T.

Здесь: b – коэффициент затухания колебательного звена - константа алгоритма прогноза. При b=1 колебательное звено превращается в апериодическое, а при 0≤b≤1 оно резонансно усиливает гармонические колебания. В каждой из приведенных формул последнее слагаемое (Y_t-X_t-1) или (∆Y_t-∆X_t-1) представляет собой невязку прогноза – отклонение факта от прогноза, сделанного на предыдущем шаге.

Как известно из теории колебательное звено, в отличие от апериодического, обладает свойством резонанса, что может искажать амплитуду естественных рыночных колебаний цены. Но зато прогноз по колебательному звену обладает меньшим запаздыванием. Здесь важно отметить, что торговые сделки наиболее эффективны (прибыльны) в моменты экстремумов рыночной цены. Естественно, что сделку покупки целесообразно производить на минимуме цены, когда по прогнозу ожидается ее рост, а сделку продажи целесообразно производить на максимуме цены, когда по прогнозу ожидается ее снижение. Такая стратегия торговли – сделки только в моменты экстремумов цены, названа нами релейной. Понятно, что для релейной стратегии искажение амплитуд прогнозируемых ценовых колебаний не влияет на эффективность системы.

Помимо описанных алгоритмов прогноза был разработан специфический алгоритм прогноза ценовых колебаний, специально предназначенный для прогноза экстремумов цены. Основанием для разработки такого алгоритма явилась то обстоятельство, что рыночные цены сильно зашумлены помехами типа белого шума. Конечно, алгоритм прогноза по формулам (1) или (2) фильтрует эти помехи, но для хорошей фильтрации приходится принимать достаточно большие значения временного параметра T. Результатом такой фильтрации измеряемой информации является неминуемое запаздывание прогнозов, а значит и запаздывание торговых сделок, что приводит к их убыточности. Новый алгоритм прогноза мы назвали прогнозом по модели ценового коридора. По такому алгоритму получаются верхняя и нижняя границы ценовых колебаний, т. е. уровни сопротивления и поддержки цены. Разница этих границ, т. е. высота коридора изменения цен дает дополнительную полезную информацию – оценку волатильности рыночной цены.

Математически данный алгоритм получается переходом от аддитивного учета невязки цены к учету ее наибольшего и наименьшего значений с помощью операторов max( ) и min( ). Алгоритм прогноза по ценовому коридору имеет вид:

- прогноз верхней границы коридора Xв

(3а)…..Xв_t=МАКС(Xв_t-1-A_t-1/T;Y_t),

- прогноз нижней границы коридора Xн

(3б)…..Xн_t=МИН(Xн_t-1-A_t-1/T;Y_t),

- высота коридора A

(3в)…..A_t=Xв_t-Xн_t.

На рисунке 2 показаны графики фактической цены Y – котировки валютной пары на рынке Форекс, границ коридора Xн и Xв и прогнозируемые моменты максимумов и минимумов цены.

Рис. 2. Графики фактической цены Y, границ коридора Xн и Xв и прогнозируемые моменты максимумов и минимумов цены.

Зубчатый характер на графике реальной котировки обусловлен рыночным шумом. Главное преимущество данного способа прогноза заключается в малой чувствительности к измерительному шуму: математические операторы max и min в формулах (3) большую часть времени не реагируют на шумы измеряемой величины Y. Реакция на эти шумы проявляется только вблизи экстремумов Y, т. е. вблизи гребней и впадин ценовых волн. Это хорошо видно на графиках рис. 2.

Для формирования торговых сделок необходимо по результатам прогноза сформировать бинарный критерий R, дающий сигнал +1 для сделки покупки или -1 для сделки продажи. Понятно, что для торговли на разнице цен достаточно прогнозировать только будущее направление изменения цены, независимо от величины этого изменения. Поэтому величина R определяется либо непосредственно по прогнозу тренда цены ∆X, либо по приращению прогнозов самой цены X_t-X_t-1. Первый вариант предпочтительнее, ибо непосредственный прогноз потенциально точнее любого косвенного прогноза. Алгоритм вычисления критерия R при прогнозе по формулам (1б) или (2б) имеет вид:

(4)…..R_t=ЗНАК(∆X_t).

В случае прогноза цены по модели ценового коридора необходимо анализировать на минимум три соседних по времени значения Xн и аналогично на максимум для значений Xв. Если соответствующий экстремум приходится на среднюю из трех сравниваемых величин, то на текущий момент t диагностируется данный экстремум цены. В противном случае значение критерия R_t сохраняется прежним R_t-1:

(5)….. R_t=ЕСЛИ(МИН(Xн_t-2:Xн_t)=Xн_t-1;1;ЕСЛИ(МАКС(Xв_t-2:Xв_t)=Xв_t-1;-1;R_t-1)).

Таким образом, и в этом случае критерий R сигнализирует знак тренда цены. Далее для торговли по релейной стратегии сигналом для сделки является момент смены знака R_t: переход с -1 на +1 это признак минимума цены и сигнал на покупку, а переход с +1 на -1 это признак максимума цены и сигнал на продажу. В соответствии с этой логикой формируется сделка с объемом Z. Тип сделки определяется знаком величины Z: знак «+» - сделка покупки, знак «-» - сделка продажи:

(6)…..Z_t=R_t*Zm.

Улучшить качество прогнозов рыночных цен можно путем рассмотрения поведения ценовых колебаний в двух разных временных масштабах. Об этом часто упоминается в исследованиях рынков. Объяснение этому феномену в том, что цены одновременно подвержены колебаниям разных периодов, т. е. образуют сумму разнопериодных гармонических колебаний. Поэтому появляется возможность полезного сочетания прогнозов для разных периодов T. При этом алгоритмы прогнозов по приведенным выше формулам производятся каждый со своей константой T1 или T2, а результаты прогнозов также различаются индексами 1 и 2. Комбинировать такие прогнозы можно двояко: путем комбинирования самих прогнозов (цен X или их трендов ∆X) или путем комбинирования полученных по ним бинарных критериев R. Соответственно следует различать раннее и позднее связывание прогнозов. Раннее связывание на уровне самих прогнозов организуется в виде простого суммирования: прогноз по медленной гармонике с константой T2 остается без изменения, а прогноз по быстрой гармонике с константой T1заменяется суммой обоих прогнозов X1+X2. Связывание на уровне бинарных критериев R производится путем логического умножения. Окончательный сигнал на сделку – результирующий критерий Rрез находится по формуле:

(7)…..Rрез_t=ЕСЛИ(R1_t=R2_t;R2_t;Rрез_t-1).

Таким образом, сигнал на сделку появляется только когда направления быстрого и медленного трендов цены совпадают. Практическое исследование торговых систем с обоими способами связывания прогнозов показало, что вариант связывания на уровне критериев заметно эффективнее.

Как уже говорилось, основой эффективности торговли на разнице цен является качество прогнозов колебаний рыночных цен. Но для маржинальной торговли при посредничестве брокерской компании и с залогом в виде депозита не менее важен контроль и поддержание подходящего уровня риска утери депозита при убыточной торговле. Эта сторона маржинальной торговли пока недостаточно изучена теоретически. В обучающих курсах предлагается удерживаться на фиксированной, но ничем не обоснованной стоимости сделки порядка 2- 5% от депозита и не поддаваться эйфории от череды прибыльных сделок. Под стоимостью сделки здесь понимается возможная прибыль или убыток. Организовать торговлю следует так, чтобы убыток одной неудачной сделки или непрерывной серии таких убыточных сделок не превысил заложенный депозит за вычетом дилерского залога. В связи с этим вводится понятие просадки торговой системы – это убытки, наблюдающиеся за выбранную историю системы. Но оперировать максимальной просадкой системы, определяемой на ее истории неудобно, так как эта величина по природе случайна и на другой истории может оказаться другой. Дальнейший ход рассуждений очевиден: следует статистическими приемами найти гарантированную просадку для данной системы и дальнейшие расчеты по уровню риска торговли производить с ней. Под гарантированной просадкой данной торговой системы понимается такая величина, что любая фактическая максимальная просадка не превысит эту величину. Разумеется, с учетом случайного характера максимальной просадки следует говорить «не превысит с заданной вероятностью». Эта пороговая вероятность очень круто приближается к 100% при увеличении величины гарантированной просадки. Это - замечательное свойство нормального распределения вероятностей большинства природных случайных процессов, к каковым относятся и рыночные цены. Обозначим текущую фактическую просадку через Pпр, гарантированную просадку через гарPпр, а депозит – через Dep. Кроме того, обозначим дилерский залог через B.

Допустим, что гарантированная просадка данной системы уже найдена. Тогда по ней можно найти максимальный объем торговли (объем склада) Zm из условия, чтобы гарантированная просадка не превысила величину депозита (за вычетом дилерского залога), т. е. из условия:

(8)…..гарPпр≤Dep-B.

Отсюда легко вычислить искомую величину Zm для случая торговли по одному рыночному инструменту. Действительно, просадка любой системы c одним торгуемым инструментом пропорциональна объему торговли Zm и этой же величине пропорционален дилерский залог. Следовательно, можем записать гарPпр=k1*Zm и B=k2*Zm, где k2 – известный коэффициент а k1 – пока неопределенный коэффициент. Тогда для искомого объема склада имеем неравенство Zm*(k1+k2)≤Dep. Из этого соотношения можно найти искомую величину Zm подбором ее на истории системы из условия приближения соотношения (8) к равенству. Но задача значительно усложняется для комбинированной торговли по нескольким инструментам, но с единым депозитом. В этом случае неравенство (8) включает несколько неизвестных Zmi, где i – номер торгуемого инструмента в их ассортименте. Сложность здесь в том, что гарантированная просадка такой комбинированной торговой системы не равна сумме просадок по каждому инструменту. Общая просадка оказывается не только меньше суммы просадок по всем инструментам, но зачастую даже меньше максимальной из них. Это обстоятельство объясняется тем, что некоторые убыточные сделки по какому-то инструменту перекрываются прибыльными сделками по другим инструментам. В этом проявляется известное свойство диверсификации портфеля с несколькими торгуемыми инструментами и обязано оно применением в комбинированной торговле единого депозита. Тем не менее, эта многомерная задача также решается численно подбором всех величин Zmi на истории системы. Эта задача формулируется как поиск условного максимума итогового показателя эффективности системы, получаемого на данной истории, при сформулированном выше ограничении (8). Для численного решения такой задачи в программном обеспечении Microsoft Office Excel любого персонального компьютера предусмотрена процедура «поиск решения». Эта процедура допускает еще одно ограничение в виде перебора только целочисленных значений Zmi, что актуально для условий торговли на валютных рынках.

Напомним теперь, что решение поставленной задачи приведено нами в предположении, что гарантированная просадка гарPпр для данной торговой системы уже известна. Покажем, как ее можно найти на истории системы. Для этого можно применить теорию проверки статистических гипотез. В данном случае проверяется гипотеза: «любая фактическая просадка Pпр на выбранной истории окажется меньше гарантированной просадки гарPпр c высокой вероятностью, скажем с вероятностью более 98%». Для этого на истории системы необходимо найти первые два статистических момента случайного процесса Pпр : его среднее значение срPпр и стандартное отклонение от среднего σPпр. Все значения текущей просадки в силу ее определения вычисляются по формуле:

(9)…..Pпр_t=МИН(0;P_t+Pпр_t-1).

Здесь P_t – текущая фиксируемая прибыль очередной сделки. По этой информации стандартными статистическими формулами находятся моменты срPпр и σPпр. Затем по этим моментам находится гарантированная просадка гарPпр по известной формуле статистики:

(10)…..гарPпр=-срPпр+γ*σPпр.

Здесь множитель γ принимается от 3 до 5. Значение 4 отвечает величине вероятности около 97%, т. е вероятности потери депозита 3%.

На этом исчерпана вся процедура отыскания объемов торгового склада Zmi. При таком выборе объемов торговли статистически обеспечивается риск потери депозита на заданном уровне 3%. При периодическом пересчете по формулам (9), (10) и повторении процедуры поиска величин Zmi данный уровень риска торговли сохраняется все время работы торговой системы. Интересно отметить, что по такой методике средняя прибыль одной сделки в комбинированной системе доходит до нескольких десятков % от депозита, в отличие от рекомендаций учителей трейдинга не более 5% от депозита.

Все теоретические результаты проверялись путем тестирования конкретных торговых систем на представительной истории. Эти результаты выложены на авторском сайте www.teoryforex.ucoz.ru. В данном докладе упоминается способ комбинированной торговли по нескольким рыночным инструментам с общим депозитом. Это сулит большой выигрыш и составляет целый пласт теории комбинированных торговых систем. Такая теория будет рассмотрена в следующих докладах.