| главная :: экономика :: право :: сертификация :: учебники :: поиск | ||||||||||
| Каталог статей | ||||||||||
|
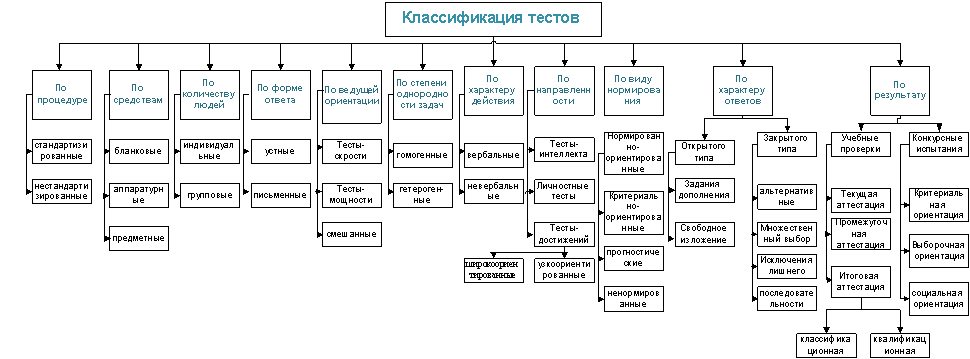
Жилина Е.В. Ростовский государственный экономический университет (РИНХ) Анализ применяемых моделей и методов тестирования для оценки знаний специалистаОсновные формы и виды тестов. В соответствии с ГОСТ 17369 – 85, классификация представляет собой разделение множества объектов на подмножества по их сходству или различию на основании принятых методов и правил. Однако в практической деятельности классификацию тестов учебных достижений часто подменяют перечислением некоторых видов тестов, не указывая основания классификации. Классификации тестов состоит в том, что она, с одной стороны, служит ориентиром для конструирования, выбора и оценки качества тестов, а с другой – облегчает их комплектование, сертификацию, применение, каталогизацию и хранение. Основанием для классификации форм тестов служит наличие у них внешних и внутренних признаков, таких как результат, содержание, форма и т.д. Поскольку каждый тест является носителем не одного, а нескольких признаков, то в зависимости от выбранного основания он может принадлежать к различным классам. Отсюда следует, что основная сложность в разработке корректного разделения тестов состоит в выявлении признаков, адекватных конкретной классификации. На основании анализа литературы [1, 2, 3] была получена классификация тестов, представленная на рисунке 1. Математические основы тестирования. Многие авторы выделяют две теории тестирования [4]: - классическая теория тестирования (Classical Test Theory – CTT); - современная теория тестирования (Item Response Theory – IRT). Классическая теория тестирования была разработана для анализа и построения тестов. Она рассматривает баллы обучаемых как постоянные числа и основывается на изучении статистик от начальных данных. Принципы ССТ: 1. одноразмерность: тест измеряет только одну черту или способность;
Рис. 1. Классификация тестов 2. вероятность получить тот или иной итоговый балл не зависит от того, какая подгруппа из всех обучаемых будет проходить тест; 3. задания тестов не зависят друг от друга; 4. ответы экзаменуемых не зависят друг от друга. В теории ССТ обычно используют следующие математические величины: - средний арифметический балл для всех испытуемых: x = 1/n ∑xi , (1) где xi - итоговый балл i-го испытуемого; - сумма квадратов отклонений результатов испытуемых от среднего: SSx = ∑(xi – x)2 , (2) - дисперсия результатов испытуемых: D = SSx/(n – 1), (3) - стандартное (среднеквадратичное) отклонение результатов испытуемых от среднего:Sx = √D, (4) при нормальном распределении результатов тестирования: x = 3Sx; - коэффициент корреляции Пирсона: rxy = SPx / √SSx*SSy, где SPx = ∑(xi – x)(yi – y), (5) - легкость задания: Fac(x) = x/xmax, (6) где x – средняя оценка всех отвечавших на задание, xmax – максимальная возможная оценка задания; - дискриминация задания: коэффициент корреляции Пирсона между заданием и итоговым баллом или между заданием и итоговым баллом минус это задание. Дискриминация равна +1, когда те, кто хорошо отвечают на это задание, хорошо пишут тест; и равна –1, когда те, кто хорошо отвечают на это задание, плохо пишут тест; - надежность (стабильность) теста: корреляция между баллами обучаемых по тесту в первый раз и во второй раз (test-retest); - надежность теста (R Бакхауза): R = (λ + 1)((1 - ∑njSj²)/nSx²) – λ((∑nj,tmj,tmt,j - nM²)/nSx²), (7) λ = (∑nj)/(∑nj,t), (8) где k – число заданий, n – число экзаменуемых, nj – число людей, отвечавших на задание j, nj,t – число людей, отвечавших на задания j и t, Sj – стандартное отклонение задания j, М – средний балл теста, mj – средний балл по заданию j, mj,t – средний балл по заданию j тех, кто ответил на вопрос t. - стандартная ошибка измерений: SE = Sx/√(1 – R), (9) где R – надежность теста. Баллы 95% экзаменуемых находятся внутри x ± 2SE; - индекс выбора (если анализируются вопросы по выбору): C = ni/n, (10) показывает, насколько эффективно вопросы привлекают экзаменуемых. Построение теста при помощи классической теории тестирования: 1. Исходя из теоретических предположений и при хорошем понимании того, что надо измерить, пишутся задания теста. Необходимо написать как минимум в два раза больше заданий, чем предполагается включить в окончательный вариант теста. 2. Калибровка: полученные задания нужно протестировать при помощи людей, близких к той группе, для которой предназначается тест. 3. Следует отбросить задания с низкой (<0,2) или отрицательной корреляцией задание-итоговый балл. 4. Если дискриминация отрицательна, то, возможно, нарушилось предположение об одноразмерности теста. 5. Выбирается нужное число заданий с самой высокой корреляцией задание-итоговый балл, так как они повышают надежность теста, снижая стандартную ошибку измерения. 6. Чтобы подобрать необходимую сложность теста, можно заменить часть заданий на более или менее сложные. Не желательно иметь легкость задания более 0,85 или менее 0,15. Чтобы обучающиеся всех уровней подготовки могли быть оценены, лучше иметь задания разного уровня легкости (сложности). 7. Таким образом, получается тест, который будет наиболее адекватным образом оценивать именно ту группу обучаемых, для которых он предназначался. Недостатки ССТ: 1. Способности обучаемых определяются сложностью теста: если тест сложный, то все обучаемые будут выглядеть так, как если они имеют низкую способность, а если легкий, то высокую. Сложно сравнить сходные способности обучаемых, проходивших разные тесты. 2. Свойства каждого задания определяются группой обучаемых, проходивших их: если обучаемые имеют высокую способность, то задания будут более легкими, чем для группы обучаемых с низкой способностью. Сложно оценить трудность заданий в независимости от уровня способности группы экзаменуемых. 3. Тестовые баллы по-разному достоверны для разных экзаменуемых: хотя предполагается, что SE одинакова для всех экзаменуемых, это не всегда так: в экстремальных случаях оценки способностей обучаемых менее надежны (достоверны), чем в середине распределения. Таким образом, сложно сравнить соответствующие способности обучаемых. Современная теория тестирования была разработана для решения первых двух проблем классической теории тестирования. IRT предполагает, что получаемые при тестировании баллы обучаемых определяются ненаблюдаемыми переменными – латентными параметрами. Достоинства IRT: - инвариантность заданий: характеристики заданий не зависят от группы экзаменуемых, при помощи которой они были получены; - инвариантность способностей: оценки способностей обучаемых не зависят от используемого теста; - в CCT каждая оценка “стоит” одинаково независимо от того, “сложная” или “простая”, то есть было ли задание, за которое получена эта оценка, сложным или простым. Благодаря итерационной процедуре нахождения оценок параметров IRT это учитывает. Принципы IRT: 1. Основное предположение IRT: Pij = f(θi – bj), (11) где Pij – вероятность, что i-й экзаменуемый выполнит j-е задание, θi – латентный параметр, определяющий уровень знаний i-го экзаменуемого, bj – латентный параметр, определяющий уровень трудности j-го задания теста. В зависимости от модели, точный вид зависимости может меняться; также могут появляться дополнительные параметры. 2. Одноразмерность: тест измеряет только одну черту или способность. Тем ни менее Lord (1968) предполагает, что предположение об одноразмерности не удовлетворяет большинству тестов. 3. Вероятность получить тот или иной итоговый балл не зависит от того, какая подгруппа из обучаемых будет проходить тест. 4. Задания тестов не зависят друг от друга. 5. Ответы экзаменуемых не зависят друг от друга. Модель Раша (1960, Rasch, 1PL) для дихотомических данных: Pij = exp(θi – bj)/(1 + exp(θi – bj)). (12) Вероятность успеха зависит только от разницы между уровнем способности и сложностью задания. Модель Раша не позволяет заданиям различаться по дискриминации: задания можно расположить только по уровню их сложности. Достоинства модели Раша по сравнению с другими моделями IRT: 1. Простота. 2. Для оценивания параметров не требуется никаких предположений и достаточно только сырых данных. В других моделях IRT необходимы дополнительные ограничения для контроля взаимодействия параметров. 3. Минимальные полезные данные: 4 задания для 10 человек. Для других моделей IRT необходимо не менее 1000 человек. 4. Данные для стабильных оценок: 20 заданий для 200 человек. Для других моделей IRT: не существует. Двухпараметрическая модель Бирбаума (Birbaum, 2PL) для дихотомических данных: Pij = exp(D*aj*(θi – bj))/(1 + D*aj*exp(θi – bj)), (13) где aj – различающая способность (дискриминация задания), D – константа шкалирования (обычно, 1.7), используемая для того, чтобы сделать распределение близким к нормальному. Трехпараметрическая модель Бирбаума (Birbaum, 3PL) для дихотомических данных: Pij = cj + (1 - cj)*exp(D*aj*(θi – bj))/(1 + D*aj*exp(θi – bj)), 14) где aj – различающая способность (дискриминация задания), cj – вероятность угадывания правильного ответа на j-е задание. Иногда также cj называют уровнем псевдо-успеха, то есть вероятностью ответить на задание правильно для экзаменуемых с минимальной способностью. Свойства моделей Раша и Бирбаума: - очевидно, что если с = 0, то получается двухпараметрическая модель Бирбаума; а если с = 0, а = 1, то модель Раша. - в тестах, где экзаменуемому предлагается выбрать правильный ответ из нескольких возможных, и где есть существенная вероятность случайного выбора правильного ответа, использование трех параметров может увеличить соответствие между данными и моделью. - чем выше b, тем сложнее задание. В идеале, среднее быть нулем, показывая, что кандидаты и вопросы примерно одной сложности/способности. - чем выше дискриминация, тем лучше задание (оно повышает надежность теста); значения ниже 0,3 следует считать подозрительными. - чем выше с, тем больше угадывание влияет на результат теста. Если в задании есть n возможных вариантов ответа, то c = 1/n. Оценка латентных параметров: 1. Используется метод максимального правдоподобия. Для теста из n заданий и N кандидатов, необходимо оценить 3n+N параметров для 3PL, 2n+N для 2PL и n+N параметров для 1PL. 2. Необходимо исключить экзаменуемых, которые ответили на все вопросы правильно или на все неправильно. 3. Начальное значение параметра способности устанавливаем как ноль, или как отношение правильных ответов по всем зданиям к неправильным, нормированное к среднему 0 и стандартному отклонению 1: Θi0 = k*ln(pi/(1 - pi)), i = 1,2, …N, (15) где N – число обучаемых, pi – число правильных ответов i-го обучаемого на все задания теста. 4. Начальное значение параметра сложности задания устанавливаем как ноль, или как отношение неправильных ответов всех экзаменуемых по этому зданию к правильным, нормированное к среднему 0 и стандартному отклонению 1: bj0 = k*ln((1 – pj)/pj), i = 1,2, …n, (16) где n – число заданий, pj – число правильных ответов всех обучаемого на j-ое задание теста. 5. Для нахождения оценок значений параметров используется итеративная процедура Ньютона-Ральфсона. Например, для модели Раша формулы имеют вид: Θi = Θi0 + 4*(xi - ∑x)/n, (17) bj = bj0 + 4*(rj - ∑r)/n, (18) где ∑x = ∑1/(1 + exp(θi0 – bj0)), ∑r = ∑1/(1 + exp(θi0 – bj0)), xi – балл i-го экзаменуемого, rj – сумма баллов всех экзаменуемых по j-му заданию. 6. Проверка достижения необходимой точности α: |Θi - Θi0 | < α, (19) | bj - bj0 | < α. (20) 7. Если требуемая точность не достигнута, то повторяем шаги 5 и 6, подставляя вместо Θi0 и bj0 значения полученные на предыдущем шаге, пока неравенства не будут выполнены. 8. Для экзаменуемых с экстремальным баллом 0 вычисляем Θ, используя шаги 5,6 и 7, с xi = 0,25. Для экзаменуемых с экстремальным баллом n вычисляем Θ, используя шаги 5,6 и 7, с xi = n - 0,25. 9. Для нормально распределенных данных: стандартные ошибки оценок персональной способности и сложности задания оцениваются соответственно (включая случаи xi = 0,25 и xi = n - 0,25): SEΘi ≈ 1/√(∑(1/(1 + exp(θi – bj)))(1 - 1/(1 + exp(θi – bj)))), (21) SEbj ≈ 1/√(∑(1/(1 + exp(θi – bj)))(1 - 1/(1 + exp(θi – bj)))). (22) 10. На практике мера способности не удобна, так как она может меняться между ±∞, что трудно сопоставить с тестовым баллом. Поэтому обычно используется ее линейная трансформация, которая дает значения между 0 и максимальной оценкой теста. Например: θi* = T*exp(θi)/(1 + exp(θi)), (23) где T – максимальный балл теста. В отличие от CCT, где используются описательные статистики, полезность моделей современной теории тестирования зависит от того, насколько они подходят к данным. Hambleton and Swaminathan (1985) предположили, что мера того, насколько модель подходит к данным, основывается на трех типах свидетельств: 1. Выполнение предположений для данных: - одноразмерность. Измеряется ковариация заданий и итогового балла теста. Если она отрицательна, то, вероятно, предположение нарушено (McDonald, 1981); - угадывание минимально (для 1PL и 2PL). Если наблюдаемый уровень правильных ответов экзаменуемых с самым низким уровнем способностей на наиболее сложных заданиях близок к нулю, то предположение верно; - все задания имеют одинаковую дискриминацию (для 2PL). Корреляция между заданиями и итоговым баллом должна быть однородной; - тест решался, то есть экзаменуемый не писал ответы наугад. Если отношение дисперсии числа пропущенных к заданий к дисперсии числа неверно отвеченных заданий близко к нулю, то предположение верно (Gulliksen, 1950); 2. Степень, в которой обнаружены ожидаемые свойства: - инвариантность оценок параметров заданий. Если разница между оценками параметров, полученными при использовании различных групп экзаменуемых, не превышает ошибок измерения, то предположение верно (Wright, 1968); - инвариантность оценок параметров способностей. Если разница между оценками параметров, полученными при использовании различных частей теста, не превышает ошибок измерения, то предположение верно (Wright, 1968); 3. Точность предсказаний модели. Проверка производится при помощи нормированных остатков: zij = (Pij – M(Pij))/√(M(Pij)*(1 – M(Pij))/Nj), (24) где i – номер задания, j – уровень способности, Nj – число экзаменуемых уровня спосбности j, Pij – наблюдаемая доля правильных ответов на задание i кандидатов уровня способности j, M(Pij) – его математическое ожидание. Если наблюдаемые данные соответствуют модели, то zij распределены более или менее случайно со средним 0 и дисперсией 1: Qi = ∑z²ij, Qi ~ χ² с m-k числом степеней свободы, (25) где m – число интервалов по уровням способности, k – число параметров в модели. В таблице 1 изложены основные возможности создания тестов в рамках классической и современной теории тестирования. Таблица 1 Основные возможности создания тестов в рамках теорий тестирования
Вывод: Рассмотрев возможности классической и современной теорий тестирования, можно сделать вывод о том, что каждая из теорий обладает своими достоинствами и недостатками, отбросить которые при построении компьютерной тестовой системы нельзя. Поэтому необходимо найти компромисс между теориями в виде интегральной системы тестирования, базируясь лишь на достоинствах рассматриваемых подходов. Литература: 1. Аванесов В.С. Композиция тестовых заданий. – М.: Из-во Центра тестирования Минобразования РФ, - 2002. - 239 c. 2. Переверзев В.Ю. Критериально-ориентированные педагогические тесты для итоговой аттестации студентов. - М.: НМЦ СПО Минобразования РФ, 1998. -152 с. 3. Тягунова Т.Н. Философия и концепция компьютерного тестирования. – М: МГУП, 2003. – 246 с. 4. [сылка более недоступна} | ||||||||||