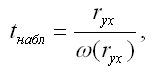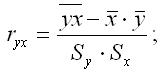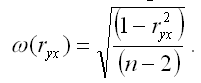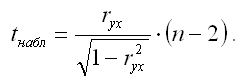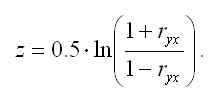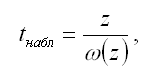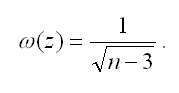Проверка гипотезы о значимости парного коэффициента корреляции

Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости парного коэффициента корреляции между результативной переменной у и факторной переменной х.

Основная гипотеза состоит в предположении о незначимости парного коэффициента корреляции, т. е.

Н₀:r_xy=0.

Обратная или конкурирующая гипотеза состоит в предположении о значимости парного коэффициента корреляции, т. е.

Н₁:r_xy0.

Данные гипотезы проверяются с помощью t-критерия Стьюдента.

Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.

При проверке значимости парного коэффициента корреляции критическое значение t-критерия определяется как tкрит(a;n-h), где а – уровень значимости, (n-h) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.

При проверке основной гипотезы вида Н₀:r_xy=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

где r_yx – выборочный парный коэффициент корреляции между результативной переменной у и факторной переменной х, который рассчитывается по формуле:

(r_yx) – величина стандартной ошибки парного выборочного коэффициента корреляции.

Показатель стандартной ошибки парного выборочного коэффициента корреляции для линейной модели парной регрессии рассчитывается по формуле:

Если данное выражение подставить в формулу для расчёта наблюдаемого значения t-критерия для проверки гипотезы вида Н₀:r_xy=0, то получим:

При проверке основной гипотезы возможны следующие ситуации:

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|>tкрит, то с вероятностью (1-а) или основная гипотеза о незначимости парного коэффициента корреляции отвергается.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|tкрит, то с вероятностью а или (1-) основная гипотеза о незначимости парного коэффициента корреляции принимается. В этом случае корреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.

Применение t-статистики Стьюдента для проверки гипотезы вида Н₀:r_xy=0 основано на выполнении двух условий:

1) если объём выборочной совокупности достаточно велик (n30);

2) коэффициент корреляции по модулю значительно меньше единицы:

0,45|r_yx|0.75.

В том случае, если модуль парного выборочного коэффициента корреляции близок к единице, то гипотеза вида Н₀:r_xy=0 также может быть проверена с помощью z-статистики. Данный метод оценки значимости парного коэффициента корреляции был предложен Р. Фишером.

Между величиной z и парным выборочным коэффициентом корреляции существует отношение вида:

В связи с тем, что величина z является нормально распределённой величиной, то проверка основной гипотезы о незначимости парного коэффициента корреляции сводится к провреке основной гипотезы о незначимости величины z:

Н₀:z=0.

Обратная или конкурирующая гипотеза состоит в предположении о значимости величины z, т. е.

Н₁:z0.

Данные гипотезы проверяются с помощью t-критерия Стьюдента.

Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.

Критическое значение критерия tкрит определяют по таблице нормального распределения (z-распределения) с доверительной вероятностью или (1-a).

При проверке основной гипотезы вида Н₀:z=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

где (z) – это величина стандартной ошибки величины z.

Показатель стандартной ошибки величины z для линейной модели парной регрессии рассчитывается по формуле:

При проверке основной гипотезы возможны следующие ситуации:

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|>tкрит, то с вероятностью (1-а) или основная гипотеза о незначимости парного коэффициента корреляции отвергается.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|tкрит, то с вероятностью а или (1-) основная гипотеза о незначимости парного коэффициента корреляции принимается. В этом случае корреляционная зависимость между исследуемыми переменными отсутствует, и продолжение регрессионного анализа считается нецелесообразным.