Ефремов А.А.

Прогнозирование структуры рыночного спроса на основе модели Брауна

В ходе разработки производственной программы применяют различные методики. В частности, можно сначала спрогнозировать совокупный объём рыночного спроса (пользуясь различными методами прогнозирования динамических рядов, например, спектральным анализом, методом Алмана, стандартным регрессионным анализом и др.)

Затем для получения прогноза объёма спроса на каждую ассортиментную позицию в отдельности следует умножить прогнозное значение совокупного объёма продаж на долю в нём конкретной ассортиментной позиции.

Таким образом, возникает необходимость предсказать, какой будет доля  -й ассортиментной позиции в общем объёме продаж. При этом должно выполняться условие:

                                                     .                                                        (1)

Здесь  - число ассортиментных позиций, по которым проводится анализ.

Поскольку большие социально-экономические системы, необратимо развиваясь во времени, адаптируются к различным внешним и внутренним факторам, модели, которые описывают закономерности этого развития, также должны учитывать это свойство, то есть – быть адаптивными. Иначе причинно-следственные связи будут не описаны и прогнозные модели будут не точны – Вот почему в данном случае мы отдали предпочтение адаптивному методу, который позволяет «уловить» последние по времени сиюминутные отклонения от сложившихся тенденций (т.е. отклонения, которые вызваны кратковременным действием некоторых факторов) – модели Брауна.

Предположим, что перед прогнозистом стоит задача изучить некоторый временной ряд , не имеющий какой-либо явно выраженной тенденции, и сделать прогноз в конце ряда на один шаг наблюдения:

                                          .                                       (2)

При этом должно выполняться условие:

                                                   .                                                         (3)

Естественное желание учесть текущую информацию в большей степени, чем прошлую, может быть математически выражено так:

                                                 .                                               (4)

Такая возможность имеется при показательном характере задания весов наблюдений:

                                  .                          (5)

Поскольку постоянная сглаживания определяет то, как описывает модель Брауна прогнозируемый ряд, а, значит, определяет и то, насколько точным может быть прогноз, выполненный с помощью этой модели, возникает необходимость выбора наилучшего значения величины постоянной сглаживания для каждого ряда. Для этого используют процедуру ретропрогноза. Исходный ряд данных  описывают с помощью модели Брауна, предварительно задав некоторое значение постоянной сглаживания , и вычисляют ошибку ретропрогноза на каждом наблюдении:

                                               .                                                      (6)

Рекомендуется поступать так. Изменяя величину постоянной сглаживания с шагом, равным 0,1, можно вычислить соответствующие дисперсии ретропрогноза. Анализ этих дисперсий позволяет определить окрестности оптимальной точки и уже в этой окрестности, используя любой известный прогнозисту численный метод, можно найти оптимальное значение постоянной сглаживания.

Целевая функция при этом имеет вид:

                                         .                                                  (7)

Используем приведённую выше методику для прогнозирования структуры рыночного спроса на продукцию Могилёвского автомобильного завода им. С.М. Кирова.

Проследим, каким образом в 2006–2011 гг. изменялась доля каждой из пяти анализируемых ассортиментной позиции в общем объёме продаж. Результаты вычислений занесём в таблицу 1.

Таблица 1 – Структура объёма продаж МоАЗ им. С.М. Кирова в 2006 – 2011 гг., %

Наименование продукции	2006 г.	2007 г.	2008 г.	2009 г.	2010 г.	2011 г.
А/поезд самосвальный МоАЗ-7405	19,7	15,9	10,1	15,8	18,9	31,1
А/погрузчик МоАЗ-4048	30,3	21,7	3,2	3,3	8,3	8,1
Скрепер самоходный МоАЗ-6014	22,1	25,5	21,8	2,6	10,6	29,7
Самосвал шахтный МоАЗ-7529	16,4	6,4	8,0	2,6	33,3	13,5
А/бетоносмеситель СМБ	11,5	30,6	56,9	75,7	28,8	17,6
Всего:	100	100	100	100	100	100

Для того, чтобы обеспечить максимальный учёт текущих значений, применим краткосрочное прогнозирование по модели Брауна. Рассчитаем среднее значение доли каждой ассортиментной позиции по формуле, изменяя значение постоянной сглаживания.

В качестве целевой функции рассмотрим сумму квадратов отклонений значений доли от соответствующих средних значений, рассчитанных по модели Брауна. Значения целевой функции при различных  представлены в таблице 2.

Таблица 2 – Подбор оптимального значения постоянной сглаживания

Значение постоянной сглаживания	Значение целевой функции
0,7	0,67103
0,8	0,746543
0,9	0,825857

Здесь рассматривались только три возможных значения коэффициента , поскольку при меньших значениях модель не удовлетворяет условию (3). Найденному оптимальному значению постоянной сглаживания (), которое удовлетворяет условию (1), соответствует предполагаемая структура объёма реализации автотехники в 2012 г., представленная на рисунке.

При этом прогноз производится по каждой ассортиментной позиции в отдельности согласно формуле (5).

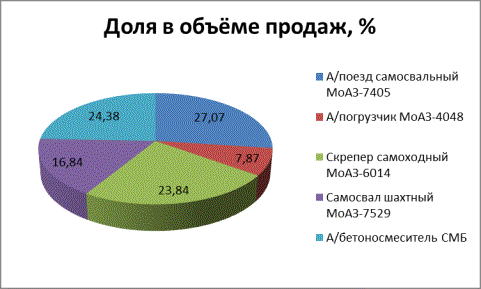
Рисунок – Структура объёма реализации МоАЗ им. С.М. Кирова в 2012 г.

Зная прогнозное значение совокупного объёма продаж и цену по каждой ассортиментной позиции, можно рассчитать, сколько единиц автотехники каждого вида нужно произвести в 2012 г. для удовлетворения запросов рынка. Производственная программа предприятия представлена в таблице 3.

Таблица 3 – Производственная программа МоАЗ им. Кирова на 2012 г.

Наименование продукции	Среднегодовая производственная мощность, шт.	Плановый объём выпуска, шт.	План. коэфф. использ. произв. мощности, %
А/поезд самосвальный МоАЗ-7405	210	95	45,2
А/погрузчик МоАЗ-4048	60	16	26,7
Скрепер самоходный МоАЗ-6014	40	80	200
Самосвал шахтный МоАЗ-7529	50	35	70
А/бетоносмеситель СМБ	180	105	58,3

Литература:

1. С.Г. Светуньков Адаптация и адаптивные методы краткосрочного прогнозирования. Модель Брауна. Режим доступа: [сылка более недоступна}

2. Данные статистической отчётности МоАЗ им. С.М. Кирова за 2006–2011 гг.