Каталог статей

Терелянский П.В., Костикова А.В.

Динамика нечетких чисел в принятии решений

Ряд проведенных авторами исследований показал, что описание эволюционирующих систем возможно с помощью динамических нечетких множеств. Динамическое нечеткое множество может быть представлено в декартовом пространстве (абсцисса – ось времени, ордината – степень принадлежности, аппликата – область определения нечеткого значения), что сопровождается сдвигом функции принадлежности относительно абсциссы и перерождением как самого исследуемого пространства из двумерного в трехмерное, так и самой функции принадлежности в поверхность. То есть всякое динамическое множество можно представить в виде поверхности, а график функции принадлежности нечеткому множеству – в трехмерной системе координат, где одна из осей на графике будет фиксировать его изменение во времени. Установленная динамика нечетких множеств приводит к возникновению проблемы получения актуального решения на определенный момент времени с соответствующими экспертными оценками. Основополагающей задачей становится получение степеней принадлежности на всем временном диапазоне анализа. Рассмотрим процесс принятия решения в нечетких моделях с учетом динамики функции принадлежности. Поведение системы в определенный момент времени можно описать некоторым набором точек на плоскости , отражающий степень принадлежности значения параметра множеству. Как правило, эксперт обладает информацией о некоторых опорных или, так называемых, реперных точках системы в строго определенные моменты времени [1-4]. Данных точек может оказаться недостаточно для построения максимально точной динамической функции принадлежности. Задача сводится к поиску значений функции в промежуточных точках и определению вида функции. Как правило, эксперт почти со 100 - процентной вероятностью может указать вид и значения функции принадлежности в начальный момент времени [1-4], несколько важных для эксперта точек на рассматриваемом интервале (обычно это бифуркационные точки системы), а также точка в конечный момент времени, если и в конечном моменте возможны бифуркации [1,2]. На основе указанных точек мы получаем  массивы экспериментальных данных,  описывающих степень принадлежности каждого исследуемого параметра заданному нечеткому множеству в разные моменты времени (рис.1). 

Рисунок 1. Массив экспериментальных данных, где - числовая величина, определяющая степень принадлежности конкретного значения критерия  заданному нечеткому множеству.

Применяя интерполяцию, мы прогнозируем значения принадлежности динамическому нечеткому множеству на какой-то момент времени  , А(t)=А{хn,хi,хe}, где хn – множество достоверно известных точек, zi – точки, полученные в результате интерполяции,  ze – экстраполируемые состояния, а Т - есть множество моментов времени существования исследуемой системы [1,2].

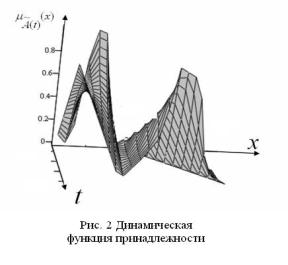
Множество реперных точек можно получить либо путем накопления информации о состоянии отдельных элементов системы в момент времени t с последующей их интеграцией, либо путем привлечения экспертных оценок. Если изменение данной метрической величины соответствует какой-либо закономерности, то для количественной оценки вполне можно подобрать функциональное представление этой закономерности и получить изменение вектора степени принадлежности во времени.

Таким образом, в данный определенный момент времени рассчитывается степень принадлежности искомого критерия множеству и определяется лучшая альтернатива. Аппроксимируя точки в полученном массиве данных можно получить функциональное представление динамики принадлежности. В результате можно получить несколько  функций принадлежности в разные моменты времени и совместить их в трехмерном пространстве (рис. 2), что и будет являться фазовым пространством решения данной задачи. Процедуру построения динамической функции принадлежности можно упростить, если воспользоваться двумерной интерполяцией, которая приводит к построению поверхности, проходящей через массив точек, описывающий сетку на координатной плоскости. Поверхность создается участками двумерных кубических сплайнов, являющихся функциями и имеющих непрерывные первые и вторые производные по обеим координатам. Для поиска конкретного значения функции принадлежности для выбранного критерия в искомый момент времени, необходимо опустить проецирующие лучи (перпендикуляры) из указанной точки до пересечения с плоскостями проекций m, x, t. Положение точки в евклидовом пространстве будет определяться с помощью трех чисел, выражающих расстояние от этой точки до координатных плоскостей проекций.

Предложенный авторами подход позволяет учитывать динамику нечетких множеств в процессе принятия экономических решений. Прогнозирование изменения функции принадлежности во времени позволит лицам, принимающим решения получать наиболее полную информацию  об экономических процессах и явлениях, расширить границы стратегического планирования, и тем самым, достигнуть максимально актуального решения на определенный момент времени.

Литература:

1. Непараметрическая экспертиза объектов сложной структуры: Монография / П.В. Терелянский. – М.: Издательско-торговая корпорация «Дашков и Ко», 2009. – 221 с.

2. Терелянский, П. В. Компьютерная система принятия решений с прогнозированием динамики предпочтений / П. В. Терелянский // Международная конференция по проблемам управления, Москва, 29 июня-2 июля 1999г. : тез. докл. – М., 1999. – Т. 2. – C. 342-344.

3. Терелянский, П. В. Анализ динамических систем экспертных предпочтений для принятия решений в экономике / П. В. Терелянский // Nauka i inowacja – 2008 : mater. IV miedzynar. nauk.-prakt. konf., 07-15 pazdziernika 2008 r. T. 3. Ekonomiczne nauki. – Przemysl, 2008. – C. 3-5.

4. Терелянский, П. В. Математические и инструментальные средства поддержки принятия решений в экономике / П. В. Терелянский // Аудит и финансовый анализ. – 2008. – №  6. – С. 461-471.