| Каталог статей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
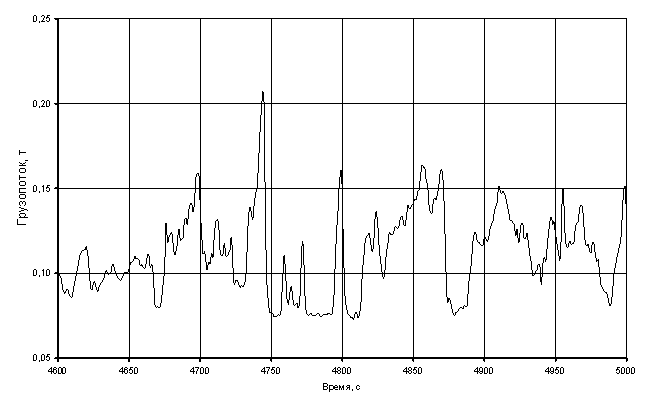
Огеенко В. В., Огеенко П.Ю. Автоматизация процессов управления грузопотоками конвейерного транспорта на основе нечетких децентрализованных моделейШахтные грузопотоки характеризуются крайней неравномерностью: в течение кратковременных периодов грузопотоки могут резко изменять свою величину. Угольный грузопоток формируется под влиянием множества горно-геологических, технических, технологических и организационных факторов, случайным образом влияющих на величину рассматриваемого грузопотока. Это определяет случайный характер его интенсивности - мгновенных значений грузопотока, приведенного на рисунке 1. Процесс выемки угля является циклическим, периоды непрерывного поступления угля из забоя чередуются с периодами отсутствия его поступления и длительность этих периодов носит также случайный характер. Это и является причинами неравномерности грузопотока, а также приводит к лишним затратам электроэнергии и времени, снижению производительности и т. п.В большинстве существующих на данный момент систем управления конвейерным транспортом возможность регулирования грузопотоком просто не заложена. В ходе проведенного анализа подходов при управлении грузопотоками предложено использовать для решения этой задачи децентрализованное управление на основе математической модели распределения ограниченного ресурса. Обеспечение заданного грузопотока на магистральной конвейерной линии в этом случае будет реализовываться посредством использования аккумулирующих бункеров.
Рисунок 1 - Грузопоток на конвейере 2ЛУ120 ОП «Шахта «Должанская-Капитальная»
В децентрализованных системах «центр», как таковой, отсутствует. Достижение отмеченных системных целей осуществляется в результате действий отдельных устройств управления – микропроцессорных контроллеров (МПК), направленных на достижение своих локальных целей (критериев) [1]. Такая децентрализованная система состоит из «коллектива» МПК, которые руководят отдельными машинами. Каждый МПК не имеет информации об общих целях системы. Он знает только свою локальную цель управления, локальный критерий, локальную функцию превращения энергии, сырья и т. д. Структура децентрализованной системы управления приведена на рисунке 2. Полная формулировка задачи выглядит так: необходимо распределить имеющийся ресурс входных влияний X между потребителями в части Xi так, чтобы обеспечить минимальное отклонение исходной величины конечного продукта Y от заданной величины Yз - это и является критерием управления. В соответствии с этим, правило формирования запроса на ресурс каждым контроллером представлено формулой 1.
где k - номер шага; C - коэффициент шага итерации (в дальнейшем коэффициент шага). Коэффициенты α1 и α2 в уравнении (1) вводятся для обеспечения безразмерности получаемого результата, что облегчит рассмотрение моделей объектов разной физической природы.
Рисунок 2 - Структура децентрализованной системы управления
Цель проведения исследований заключалась в разработке нечеткого метода реализации децентрализованного управления. Нечеткий подход отличается от детерминированного тем, что в его основу положены не численные величины. Входные и выходные данные называют лингвистическими переменными, каждая из которых может нести нечеткое значение – терм. Например, БЛИЖЕ, ДАЛЬШЕ. Для принятия решения по управлению, то есть формирования управляющего воздействия, на основе входных числовых значений нечеткая модель использует так называемый нечеткий вывод. В основу нечеткой модели распределения ограниченного ресурса положен нечеткий вывод согласно алгоритму Мамдани. Он включает 6 этапов: формирование базы правил, фаззификацию, агрегирование, активизацию, аккумуляцию и дефаззификацию [2]. В модели используются две входные и одна выходная лингвистические переменные: отклонение суммы запросов всех устройств от заданного значения (v), характер изменения отклонения (θ) и прирост значения запроса для i–го устройства на каждом шаге (Δ). Каждая переменная может принимать следующие значения: отрицательное большое (ОБ), отрицательное среднее (ОС), отрицательное малое (ОМ), близкое к нулю (БН), положительное малое (ПМ), положительное среднее (ПС) и положительное большое (ПБ). Степень принадлежности термов лингвистических переменных числовым множествам представлена в виде графиков на рисунках 3-5.
Рисунок 3 - Функции степеней принадлежности термов лингвистической переменной v множеству значений X
Рисунок 4 - Функции степеней принадлежности значений лингвистической переменной θ множеству Y
Рисунок 5 - Функции степеней принадлежности значений лингвистической переменной Δ множеству Z
В таблице 1 приведены сформированные правила поведения модели.
Таблица 1 – База правил системы нечеткого вывода
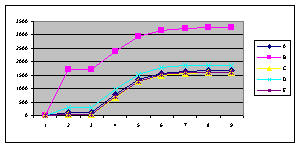
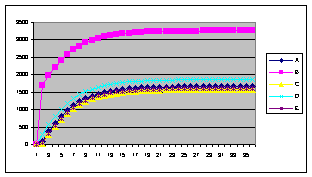
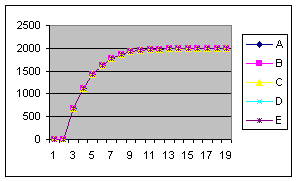
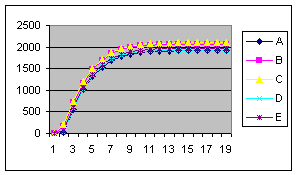
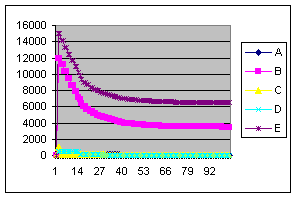
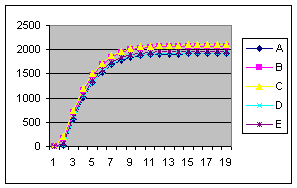
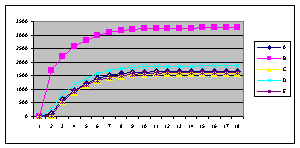
В ходе выполнения исследований проведены три эксперимента. В первом эксперименте исследовалось влияние значений начальных запросов устройств на количество шагов распределения. Графики зависимостей величин запросов от номера шага приведены на рисунке 6 (по оси абсцисс отложены значения шага распределения).
а) в) д) Рисунок 6 – Графики изменения величины запроса на k–ом шаге распределения (а-д – выходные кривые опытов 1-5)
По результатам анализа сделан вывод, что значения начальных запросов оказывают значительное влияние на длительность распределения. Во втором эксперименте проводилось исследование влияния коэффициента точности (ε) на количество шагов распределения. Кривые зависимостей приведены на рисунке 7 (по оси абсцисс отложены значения шага распределения).
а) в) Рисунок 7 – Графики изменения величины запроса на k–ом шаге распределения (а-в – выходные кривые опытов 1-3)
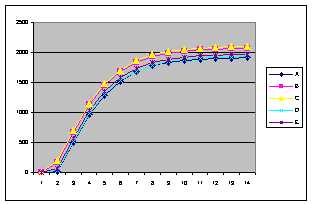
Результат анализа показал, что коэффициент точности также оказывает влияние на длительность распределения, однако его использование для уменьшения числа шагов может привести к нестабильности работы системы в целом. В третьем эксперименте исследовалось влияние границ диапазона при определении терма входной лингвистической переменной v на количество шагов распределения. Кривые зависимостей приведены на рисунке 8 (по оси абсцисс отложены значения шага распределения). Результаты анализа полученных данных показывают, что границы диапазона также оказывают влияние на скорость распределения.
а) в) Рисунок 8 – Графики изменения величины запроса на k–ом шаге распределения (а-в – выходные кривые опытов 1-3)
По результатам исследований были сделаны выводы: - процесс распределения ограниченного ресурса в задачах децентрализованного управления может быть реализован на основе разработанной нечеткой модели; - количество шагов нечеткого распределения ресурса зависит от начальных значений запросов устройств на ресурс и диапазонов определения термов лингвистических переменных на нечеткое множество значений.
Литература: 1. Децентрализованное управление: [Монография] / Г. Г. Пивняк, С. Н. Проценко, С. М. Стадник, В. В. Ткачев. – Д.: НГУ 2007. – 107 с.-Бібліогр.:с. 107.-ISBN 978-966-350-082-9 2. Нечеткое моделирование в среде MATLAB и fuzzyTECH./ А. В. Леоленков. – СПб.: БХВ-Петербург,2005. – 736 с.: ил.-ISBN 5-94157-087-2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
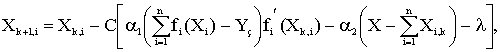 (1)
(1)




 б)
б)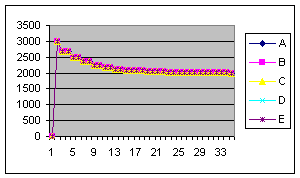
 г)
г)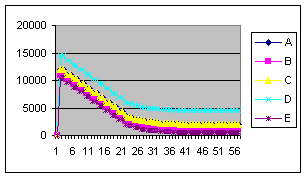
 б)
б)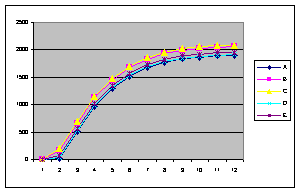
 б)
б)