| Каталог статей |
|
Плаксиенко Е.А. Использование модели Солоу для анализа управления производствомКак известно, производство может развиваться в плане повышения валового продукта, если часть средств, вырученных при реализации продуктов производства, расходуются на инвестиции в производство [1, 2]. Другая часть этих средств расходуется на непроизводственные нужды. Определение влияния изменений этой части валового продукта на производство является одним из важных элементов управления производством. Математическое выражение, описывающее зависимость управления от переменных производства называется законом управления [3].Менеджеру при выборе того или иного решения по изменению процесса производства целесообразно заранее предвидеть его последствия. Важно так же знать, когда можно оценивать эффект от принятого решения [2]. Как и в общем случае динамических систем управления, эти и другие количественные и качественные характеристики легко находятся по модели производства [3]. В работе [4] с использованием модели Солоу показано, что в зависимости от вида применяемого закона управления существенно изменяются динамические и статические (установившиеся) характеристики производства. В данной работе на основе результатов, полученных в [4], устанавливаются количественные соотношения между параметрами законов управления и характеристиками производств, которые описываются моделью Солоу, а так же получен ряд качественных выводов. Допустим, что производственная функция является функцией Кобба-Дугласа [1]
где K – производственные фонды, L – трудовые ресурсы (число занятых на производстве), А, α – некоторые коэффициенты. Тогда модель Солоу можно представить в виде следующей системы дифференциального уравнения первого порядка и функции , где
; k – удельные
производственные фонды (фонды на одного работающего – фондовооруженность), Линейный закон управления. В этом случае закон управления определяется равенством [3, 4] , где т.е. управление прямо пропорционально удельным производственным фондам (фондовооруженности). При этом изменение фондовооруженности и удельного валового продукта во времени описываются следующими выражениями: , Здесь
– постоянная
времени производства, Как видно, функция , описывающая изменения фондовооруженности, имеет две
составляющих: переходную Графики функции (3) при
Рис.1. Изменение фондовооруженности при линейном законе управления. Из выражения (3) и графиков на рис. 1 следует,
что начальное значение фондовооруженности
Если считать, что переходной процесс производства
заканчивается, когда значение меняющейся функции . (5) Из выражений (4) и (5) следует, что при линейном
законе управления (2) и установившиеся значение и длительность переходного
процесса зависят от коэффициента пропорциональности Согласно рис. 1 эффект влияния управления, очевидно, можно оценить лишь по окончании переходного процесса. Поэтому оценку влияния изменения параметра необходимо осуществлять в различные моменты времени. Это свойство является существенным недостатком линейного закона управления (2). Нелинейный закон управления. В связи с указанным недостатком линейного закона управления в работе [4] предложен нелинейный закон управления
при котором управление пропорционально фондовооружнности в степени α. В этом случае изменение удельной фондовооруженности описывается [4] выражением: , (7) где
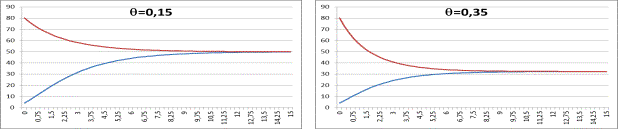
Рис.2 Изменение фондовооруженности при нелинейном законе управления. Из выражения (7) и графиков на рис. 2 следует,
что при нелинейном управлении (2) длительность переходной составляющей не
зависит от параметра этого закона.
Это очень важное свойство этого управления, так как эффект изменения Как и в случае закона управления (2), здесь
установившиеся значения фондовооруженности зависит от параметра Однако, если в случае закона (2) его параметр может принимать
значения не более Таким образом, возможности нелинейного закона
управления (6) значительно шире. В частности этот закон охватывает и
возможности линейного закона (2). Например, если , (9) то
согласно (8) установившиеся значение Действительно, подставляя (9) в равенство (8), получим:
Правая часть этого выражения, очевидно, совпадает с правой частью выражения (4). Полученное соотношение можно использовать, в частности, для решения следующих задач. Задача 1. Какое требуется управление производством (1), чтобы его
фондовооруженность изменилась на β% от имеющейся Решение. Так как
Отсюда с учетом равенства (6) выводим: , Задача 2. Какое требуется управление производством (1), что бы изменить удельный валовой продукт на g% от имеющегося при той же постоянной времени производства? Решение. Так как постоянная
времени производства не должна измениться, то применим нелинейный закон
управления с параметром (11) Решение этого уравнения приводит к следующему выражению для искомого параметра управления:
Заключение. В работе показано, что нелинейное управление производством, которое описывается моделью Солоу, является более эффективным и обладает более широкими возможностями по сравнению с линейным управлением. Оно не изменяет постоянной времени, но является менее быстродействующим. Постоянная времени производства при этом управлении в раз больше, чем при линейном управлении. Литература: 1. Колемаев В.А. Математическая экономика. Учебник для вузов. М.: Юнити-Дана, 2005. 2. Мескон М., Альберт М., Хедоури Ф. Основы менеджмента. М.: Дело, 1998. 3. Красовский А.А. Избранные труды. Теоретическая и практическая теория управления. Последние проекты и открытия. М.: Мысль, 2001. 4. Плаксиенко Е.А. Некоторые способы управления производством на основе модели Солоу. Таганрог: Изд-во ТИУиЭ, 2011.
|
 Графики переходных
процессов, соответствующие этому случаю приведены на рис. 2.
Графики переходных
процессов, соответствующие этому случаю приведены на рис. 2.
 . (8)
. (8)
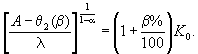
 .
(10)
.
(10)
