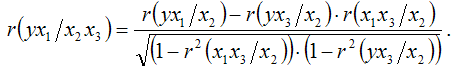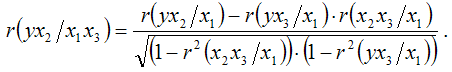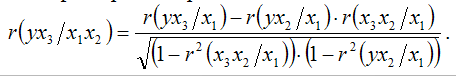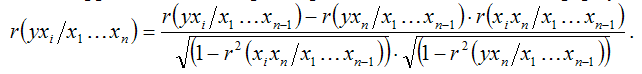Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными

Частные коэффициенты корреляции для модели множественной регрессии с тремя и более факторными переменными позволяют определить степень зависимости между результативной переменной и одной из факторных переменных при постоянстве остальных факторных переменных, включённых в модель.

Для модели множественной регрессии с тремя факторными переменными рассчитываются частные коэффициенты, как первого, так и второго порядка.

Общий вид модели трёхфакторной регрессии:

y_i=₀+₁x_1i+₂x_2i+₃x_3i+_i,

где y_i – результативная переменная, i=1,n;

x_1i – первая факторная переменная;

x_2i – второй факторная переменная;

x_3i – третья факторная переменная;

₀,₁,₂,₃ – неизвестные коэффициенты модели регрессии;

_i  – случайная ошибка модели регрессии.

Частные коэффициенты корреляции первого порядка для модели трёхфакторной регрессии строятся точно так же, как и для модели двухфакторной регрессии.

Частные коэффициенты корреляции второго порядка для модели трёхфакторной регрессии строятся следующим образом.

Частный коэффициент корреляции между результативной переменной у и факторной переменной х₁ при постоянстве факторных переменных х₂ и х₃:

Частный коэффициент корреляции между результативной переменной у и факторной переменной х₂ при постоянстве факторных переменных х₁ и х₃:

Частный коэффициент корреляции между результативной переменной у и факторной переменной х₃ при постоянстве факторных переменных х₁ и х₂:

Частные коэффициенты корреляции второго порядка построены с использованием частных коэффициентов корреляции первого порядка.

Следовательно, частный коэффициент корреляции порядка t может быть построен через частный коэффициент корреляции (t-1) порядка. Формулы, построенные через указанную взаимосвязь, называются рекуррентными.

При анализе модели множественной регрессии с n факторными переменными, частный коэффициент корреляции (n-1) порядка рассчитывается по общей формуле:

Частные коэффициенты корреляции, вычисленные по рекуррентным формулам, изменяются в пределах от минус единицы до плюс единицы.