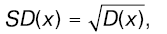Анализ и управление риском

Совокупный риск деятельности предприятий, связанный с производством товаров и услуг, включает два компонента — диверсифицируемый и недиверсифицируемый риск.

Диверсифицируемый риск, или несистематический риск, представляет собой часть риска, которая обусловлена неуправляемыми или случайными событиями и может быть устранена в результате диверсификации, т.е. путем такого сочетания производимых предприятием продуктов, которое снижает совокупный риск. Недиверсифицируемый риск, или систематический риск, — это риск, связанный с силами, воздействующими на все продукты предприятия, и не являющийся уникальным для какого-то товара или услуги.

Йота-коэффициент — это измеритель риска, равный коэффициенту вариации величины, в отношении которой делается оценка риска. Коэффициент вариации определяется по формуле

I = [SD(x)/M(x)] 100%,

где I — йота-коэффициент, коэффициент вариации случайной величины х; M(x) — математическое ожидание величины x; SD(x) — среднеквадратичное отклонение величины x.

Математическое ожидание дискретной случайной величины подсчитывается так:

M(x) = [x_j P(x_j)],

где M(x) — математическое ожидание случайной величины x; x_j — j-й вариант возможного значения величины x; P(x_j) — вероятность j-го варианта значения величины x; j — номер возможного варианта значения величины; — сумма по всем вариантам значений величины x.

По результатам большого числа измерений математическое ожидание определяется как среднее арифметическое полученных значений:

М(x) = x_ср = x_i/n,

где x_ср — среднее значение случайной величины x; x_i — значение случайной величины, полученное при i-м измерении; n — число измерений; — сумма по всем измерениям.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от математического ожидания. При заданном законе распределения дисперсия дискретной случайной величины определяется так:

D(x) = {[(x_j – М(х)]² P(x_j)},

где D(x) — дисперсия.

По результатам большого числа измерений дисперсия определяется так:

D(x) = {(x_i – x_ср)²}/n.

По результатам малого числа измерений дисперсия определяется так:

D(x) = {(x_i – x_ср)²}/(n – 1).

Среднее квадратичное отклонение — стандартное отклонение равно квадратному корню из дисперсии:

где SD(x) — стандартное отклонение.