| Микроэкономика (Вечканов Г.С.) |
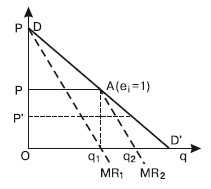
Модель дуополии КурноВпервые попытку создать теорию олигополии предпринял французский математик, философ и экономист Антуан Огюстен Курно еще в 1838 г. Однако его книга, в которой излагалась эта теория, осталась незамеченной современниками. В 1863 г. он выпустил новую работу «Принципы теории богатства», где изложил старые положения своей теории, но без математических доказательств. Лишь в 70-е гг. XIX в. последователи стали развивать его идеи. Модель Курно исходит из того, что на рынке действуют только две фирмы и каждая фирма принимает цену и объем производства конкурента неизменными, а затем принимает свое решение. Каждый из двух продавцов допускает, что его конкурент всегда будет удерживать свой выпуск стабильным. В модели предполагается, что продавцы не узнают о своих ошибках. Фактически же эти предположения продавцов о реакции конкурента, очевидно, изменятся, когда они узнают о своих предыдущих ошибках. Модель Курно представлена на рис. 34.1.
Рис. 34.1. Модель дуополии Курно
Предположим, что первым начинает производство дуополист 1, который в первое время оказывается монополистом. Его выпуск (рис. 34.1) составляет Q1; что при цене Р позволяет ему извлекать максимальную прибыль, ибо в этом случае MR = МС = 0. При данном объеме выпуска эластичность рыночного спроса равна единице, а общая выручка достигнет максимума. Затем производство начинает дуополист 2. В его представлении объем выпуска сдвинется вправо на величину OQ1 и совместится с линией AQ1. Сегмент AD' кривой рыночного спроса DD он воспринимает как кривую остаточного спроса, которой соответствует кривая его предельной выручки MR2. Выпуск дуополиста 2 будет равен половине неудовлетворенного дуополистом 1 спроса, т. е. сегмента Q1D', а величина его выпуска равна Q1Q2, что даст возможность получить максимум прибыли. Данный выпуск составит четверть всего рыночного объема спроса при нулевой цене,
На втором шаге дуополист 1, допуская, что выпуск дуополиста 2 сохранится стабильным, решит покрыть половину оставшегося все еще неудовлетворенным спроса. Исходя из того что дуополист 2 покрывает четверть рыночного спроса, выпуск дуополиста 1 на втором шаге составит
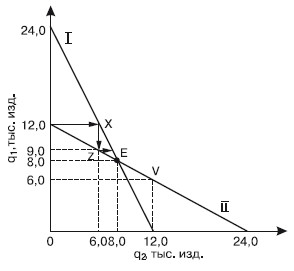
Модель Курно многие экономисты считали наивной по следующим основаниям. Модель допускает, что дуополисты не делают никаких выводов из ошибочности своих предположений относительно реакции конкурентов. Модель закрыта, т. е. число фирм ограничено и не меняется в процессе движения к равновесию. Модель ничего не говорит о возможной продолжительности этого движения. И наконец, нереальным представляется предположение о нулевых операционных издержках. Равновесие в модели Курно можно изобразить через кривые реагирования, показывающие максимизирующие прибыль объемы выпуска, который будет осуществляться одной фирмой, если даны объемы выпуска конкурента. На рис. 34.2 кривая реагирования I представляет максимизирующий прибыль выпуск первой фирмы как функцию от выпуска второй. Кривая реагирования II представляет максимизирующий прибыль выпуск второй фирмы как функцию от выпуска первой.
Рис. 34.2. Кривые реагирования
Кривые реагирования можно использовать для того, чтобы показать, как устанавливается равновесие. Если следовать стрелкам, нарисованным от одной кривой к другой, начиная с выпуска Q1 = 12 ООО, то это приведет к осуществлению равновесия Курно в точке Е, в которой каждая фирма производит 8000 изделий. В точке Е пересекаются две кривые реагирования. Это и есть равновесие Курно. КУРНО Антуан Огюстен (1801–1877), французский экономист, математик и философ, предшественник математической школы буржуазной политической экономии. В работе «Исследования математических принципов теории богатства» (1838) он предпринял попытку исследовать экономические явления с помощью математических методов. Им впервые была предложена формула D = F(P), где D – спрос; Р – цена, согласно которой спрос является функцией цены. Вечканов Г.С. Микроэкономика | Кушнир И.В. Микроэкономика | Левкина Е.В. Микроэкономика |
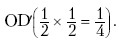
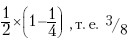 всего
рыночного спроса, и т. д. С каждым последующим шагом выпуск
дуополиста 1 будет уменьшаться, в то время как выпуск дуополиста 2 будет
увеличиваться. Такой процесс окончится уравновешиванием их выпуска, и
тогда дуополия достигнет состояния равновесия Курно.
всего
рыночного спроса, и т. д. С каждым последующим шагом выпуск
дуополиста 1 будет уменьшаться, в то время как выпуск дуополиста 2 будет
увеличиваться. Такой процесс окончится уравновешиванием их выпуска, и
тогда дуополия достигнет состояния равновесия Курно.