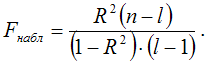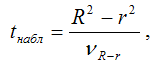| Эконометрика (Яковлева А.В.) |
Проверка гипотезы о значимости нелинейной модели регрессииНа нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все методы проверки гипотез, используемые для классических линейных моделей регрессии. Таким образом, если внутренне линейную модель регрессии можно свести к линейной модели парной регрессии, то на эту модель будут распространяться все методы проверки гипотез, используемые для парной линейной зависимости. Проверка гипотезы о значимости линейной модели множественной регрессии состоит в проверке гипотезы значимости индекса детерминации R2. Рассмотрим процесс проверки гипотезы о значимости индекса детерминации. Основная гипотеза состоит в предположении о незначимости индекса детерминации, т. е. Н0:R2=0. Обратная или конкурирующая гипотеза состоит в предположении о значимости индекса детерминации, т. е. Н1:R20. Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора. Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим. При проверке значимости индекса детерминации критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l-1 и k2=n-l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. При проверке основной гипотезы вида Н0:R2=0 наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:
При проверке основной гипотезы возможны следующие ситуации. Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то с вероятностью а основная гипотеза о незначимости индекса детерминации отвергается, и он признаётся значимым. Следовательно, полученная модель регрессии также признаётся значимой. Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл=Fкрит, то основная гипотеза о незначимости индекса детерминации принимается, и он признаётся незначимым. Полученная модель регрессии является незначимой и нуждается в дальнейшей доработке. Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей. Проверка предположения о возможной линейной зависимости между исследуемыми переменными осуществляется с помощью коэффициента детерминации r2 и индекса детерминации R2. Выдвигается основная гипотеза Н0о наличии линейной зависимости между переменными. Альтернативной является гипотеза Н1 о нелинейной зависимости между переменными. Данные гипотезы проверяются с помощью t-критерия Стьюдента. Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента. При проверке гипотезы о линейной зависимости между переменными критическое значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента. При проверке основной гипотезы Н0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:
где R-r – величина ошибки разности (R2-r2), которая определяется по формуле:
При проверке основной гипотезы возможны следующие ситуации. Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл›tкрит, то с вероятностью а основная гипотеза о линейной зависимости между переменными отвергается. В этом случае построение нелинейной модели регрессии считается целесообразным. Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнаблtкрит, то основная гипотеза о линейной зависимости между переменными принимается. Следовательно, взаимосвязь между данными переменными можно аппроксимировать простой линейной формой зависимости. Яковлева А.В. Эконометрика |