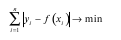Методы регрессионного анализа

Термин «регрессия» ввел английский психолог и антрополог Ф.Гальтон.

Для точного описания уравнения регрессии необходимо знать чакон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии ffc), так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.

Рассмотрим взаимоотношение между истинной f (х) = = М(у/х), модельной регрессией у и оценкой у регрессии. Пусть результативный показатель у связан с аргументом х соотношением:

у=2х 1,5+σ

где σ – случайная величина, имеющая нормальный закон распределения.

Причем M σ= 0 и d σ– σ ². Истинная функция регрессии в этом случае имеет вид:

f(х) = М(у/х) = 2х i 1,5+ σ?

Для наилучшего восстановления по исходным статистическим данным условного значения результативного показателя f(x) и неизвестной функции регрессии /(х) = М(у/х) наиболее часто используют следующие критерии адекватности (функции потерь).

Согласно методу наименьших квадратов минимизируется квадрат отклонения наблюдаемых значений результативного показателя y(i = 1, 2, ..., п)от модельных значений y i= f(х i),где х i– значение вектора аргументов в i-м наблюдении:

σ(y i– f(х i)² → min

Получаемая регрессия называется среднеквадратической.

Согласно методу наименьших модулей, минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений:

y i = f(x i)

И получаем среднеабсолютную медианную регрессию:

Регрессионный анализ – это метод статистического анализа зависимости случайной величины уот переменных х j(j=1,2, ..., k), рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения х j.