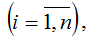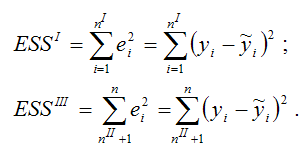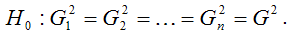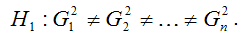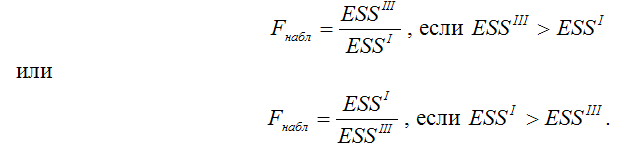Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии

Основным условием проведения теста Голдфелда-Квандта является предположение о нормальном законе распределения случайной ошибки _i модели регрессии.

Рассмотрим применение данного теста на примере линейной модели множественной регрессии.

Предположим, что на основе проведённого исследования зависимость между переменными можно аппроксимировать линейной моделью множественной регрессии.

В модели множественной регрессии выбирается независимая переменная x_ik, от которой наиболее вероятно могут зависеть остатки модели ei.

На следующем этапе значения независимой переменной x_ik ранжируются

располагаются по возрастанию и делятся на равные 3 части.

Для I и III частей строятся две независимые модели регрессии вида:

Для каждой из построенных моделей регрессий рассчитываются суммы квадратов остатков:

Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:

Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы: k1=nI–l и k2=nI–l,  где l – число оцениваемых по данной выборке параметров.

Наблюдаемое значение F-критерия находят по формуле:

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза отвергается, и, следовательно, в модели регрессии присутствует гетероскедастичность, зависящая от переменной x_ik.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл‹Fкрит, то основная гипотеза принимается, и гетероскедастичность в модели множественной регрессии не зависит от переменной x_ik.

На следующем этапе проверяются другие независимые переменные, если есть предположение об их тесной связи с G2(_i).

Если тест Голдфелда-Квандта проводился для линейной модели парной регрессии, то вывод о принятии основной гипотезы означает гомоскедастичность построенной модели регрессии.