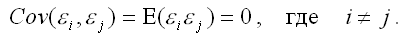Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция

Автокорреляцией называется корреляция, возникающая между уровнями изучаемой переменной. Это корреляция, проявляющаяся во времени. Наличие автокорреляции чаще всего характерно для данных, представленных в виде временных рядов.

Автокорреляцией остатков модели регрессии ei (или случайных ошибок регрессии модели _i) называется корреляционная зависимость между настоящими и прошлыми значениями остатков.

Временным лагом называется величина сдвига между рядами остатков модели регрессии.

Величина временного лага определяет порядок коэффициента автокорреляции. Например, если между остатками en и en-1 существует корреляционная зависимость, то временной лаг равен единице. Следовательно, данную корреляционную зависимость можно охарактеризовать с помощью коэффициента автокорреляции первого порядка между рядами остатков e1…en-1 и e2…en.

Одно из условий, которое учитывается при построении нормальной линейной модели регрессии, заключается в некоррелированности случайных ошибок модели регрессии, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:

Если в модели регрессии случайные ошибки коррелированны между собой, то данное условие нарушается.

Последствия, к которым может привести наличие в модели регрессии автокорреляции остатков, совпадают с последствиями, к которым может привести наличие в модели регрессии гетероскедастичности:

1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;

2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Наиболее наглядным способом обнаружения автокорреляции случайных остатков регрессионной модели является графический метод. При этом осуществляется построение графиков автокорреляционной и частной автокорреляционной функций.

Автокорреляционной функцией называется функция оценки коэффициента автокорреляции в зависимости от величины временного лага между исследуемыми рядами.

Графически автокорреляционная функция изображается с помощью коррелограммы. Коррелограмма отражает численно и графически коэффициенты автокорреляции и их стандартные ошибки для последовательности лагов из определённого диапазона (например, от 1 до 25). При этом по оси Х откладываются значения (тау) – величины сдвига между рядами остатков, которые совпадают с порядком автокорреляционного коэффициента. Также на коррелограмме отмечается диапазон в размере двух стандартных ошибок коэффициентов автокорреляции на каждом лаге.

Частная автокорреляционная функция является более углублённой версией обычной автокорреляционной функции. Её отличительной особенностью является исключение корреляционной зависимости между наблюдениями внутри лагов, т. е. частная автокорреляционная функция на каждом лаге отличается от обычной автокорреляционной функции на величину удалённых автокорреляций с меньшими временными лагами. Следовательно, частная автокорреляционная функция более точно характеризует автокорреляционные зависимости внутри временного ряда.