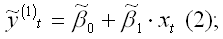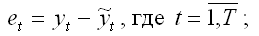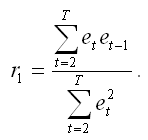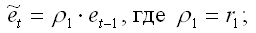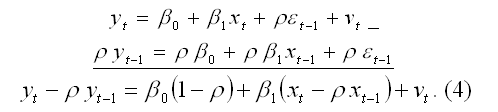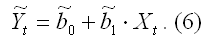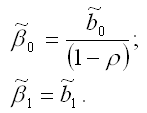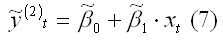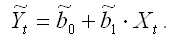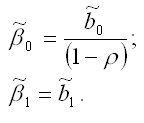Методы Кохрана-Оркутта и Хилдрета-Лу оценки коэффициента автокорреляции

Помимо вычисления выборочного коэффициента автокорреляции остатков оценку автокорреляционного коэффициента можно рассчитать методом Кохрана-Оркутта.

Предположим, что на основе собранных наблюдений была построена линейная парная модель регрессии:

y_t=₀+₁x_t+_t.(1)

Рассмотрим применение метода Кохрана-Оркутта оценки коэффициента автокорреляции на примере данной модели.

Осуществление метода Кохрана-Оркутта происходит в несколько этапов.

1) оценки неизвестных коэффициентов исходной модели регрессии определяются классическим методом наименьших квадратов. В результате мы получим оценённую модель регрессии вида:

2) на основании исходной (1) и оценённой (2) моделей регрессии рассчитываются остатки модели:

3) рассчитывается выборочный автокорреляционный коэффициент первого порядка по формуле:

С помощью данного коэффициента можно оценить авторегрессионную зависимость остатков:

4) строится преобразованная модель регрессии. Модель регрессии в момент времени (t-1) может быть представлена виде y_t-1=₀+₁x_t-1+_t-1.(3). Если модель регрессии в момент времени (t-1) умножить на величину коэффициента автокорреляции и вычесть её из исходной модели регрессии в момент времени t, то в результате мы получим преобразованную модель регрессии, учитывающую процесс автокорреляции первого порядка:

Для более наглядного представления преобразованной модели воспользуемся методом замен:

Y_t=y_t–y_t-1;

X_t=x_t–x_t-1;

Z_t=1– .

В результате преобразованная модель регрессии примет вид:

Y_t= Z_t* ₀+₁ X_t+ _t. (5)

5) оценки неизвестных коэффициентов преобразованной модели регрессии рассчитываются с помощью традиционного метода наименьших квадратов:

Далее рассчитываются оценки коэффициентов исходной модели регрессии по формулам:

В результате полученную модель регрессии можно представить в виде:

6) на заключительном этапе вновь вычисляются остатки e_t между исходной (1) и преобразованной оценённой (7) моделями регрессии, и процесс повторяется с третьего этапа.

Метод Кохрана-Оркутта является итеративным методом оценивания. Его основное отличие состоит в том, что процесс итеративного оценивания исходной модели регрессии сходится или останавливается при условии, если последнее вычисленное значение оценки коэффициента автокорреляции первого порядка ₁ почти не отличается от своего предыдущего значения.

Другим методом вычисления оценки коэффициента автокорреляции является метод Хилдрета-Лу.

В этом случае коэффициент автокорреляции задаётся двумя параметрами: диапазоном и величиной шага. Например, коэффициента автокорреляции 1 заключается в пределах [-1;+1], и его значения вычисляются с шагом 0,02.

Для каждого из значений коэффициента автокорреляции с помощью метода разностей строится преобразованная модель регрессии вида:

Y_t= Z_t* ₀+₁X_t+ _t,

где Y_t=y_t–ry_t-1;

X_t=x_t–rx_t-1;

Z_t=1–r.

Далее оценки неизвестных коэффициентов преобразованной модели регрессии рассчитываются с помощью классического метода наименьших квадратов:

Оценкой коэффициента автокорреляции первого порядка ₁ будет являться то значение коэффициента, с помощью которого вычисляется минимальная сумма квадратов отклонений теоретических значений от расчётных значений (на основе преобразованной модели регрессии).

Оценки неизвестных коэффициентов результативной модели регрессии рассчитываются по формулам: