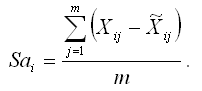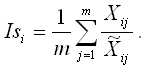| Эконометрика (Яковлева А.В.) |
Сезонные и циклические компоненты временного рядаДля построения адекватной модели временного ряда необходимо охарактеризовать сезонные и циклические компоненты временного ряда. К основным методам моделирования сезонных и циклических колебаний относятся:
В связи с тем, что моделирование сезонных и циклических колебаний происходит аналогично, применение данных методов мы будем рассматривать на примере моделирования сезонных колебаний. Аддитивная модель временного ряда стоится в том случае, если амплитуда сезонных колебаний не меняется во времени: yt=Tt+St+t, где T – это трендовая компонента; S – это сезонная компонента; – случайный шум. Мультипликативная модель временного ряда стоится в том случае, если амплитуда сезонных колебаний изменяется во времени: yt=Tt*St+t. Предположим, что задача состоит в исследовании временного ряда Xij, где i – это номер сезона (периода времени внутри года, например, месяца или квартала), i=1,L, L – число сезонов в году, j – номер года, j=1,m, m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m. Прежде чем рассчитывать сезонную компоненту, исходный временной ряд необходимо выровнять. Для этого применяются методы механического выравнивания, к которым относятся:
Результатом процедуры сглаживания будет временной ряд выровненных значений
Если временной ряд представлен аддитивной моделью, то в качестве сезонной компоненты используется показатель абсолютного отклонения – Sai. Сумма всех сезонных компонент, т.е. показателей абсолютных отклонений Sai. должна быть равна нулю. Если временной ряд представлен мультипликативной моделью, то в качестве сезонной компоненты используется индекс сезонности – Isi. Произведение всех сезонных компонент, т. е. индексов сезонности Isi, должно быть равно единице. Показатель абсолютного отклонения в i-том сезоне рассчитывается как среднее арифметическое из отклонений фактического и выровненного уровней временного ряда:
Индекс сезонности в i-том сезоне рассчитывается как среднее арифметическое из отношений фактического уровня временного ряда к выровненному:
Если при построении аддитивной модели временного ряда сумма всех абсолютных отклонений не равна нулю, то рассчитываются скорректированные значения сезонных компонент по формуле:
где L – общее количество сезонных компонент. На следующем этапе построения модели временного ряда осуществляется расчёт трендовой компоненты с помощью метода аналитического выравнивания функциями времени или кривыми роста. Данный метод выравнивания применяют не к исходному временному ряду, а к временному ряду с исключённой сезонной компонентой. При этом уровни исходного временного ряда корректируются на величину сезонной компоненты следующим образом:
Яковлева А.В. Эконометрика |
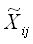 не содержащих сезонной компоненты.
не содержащих сезонной компоненты.