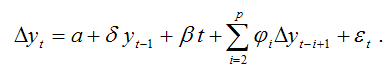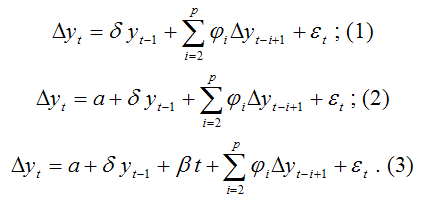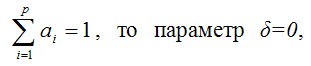| Эконометрика (Яковлева А.В.) |
Критерий Дикки-Фуллера проверки наличия единичных корнейПроверкой наличия единичных корней называется задача проверки основной гипотезы вида H0:=0 в модели авторегрессии первого порядка: yt=a+yt–1+t. Для данного ряда справедливы следующие предположения:
Таким образом, гипотеза о стационарности временного ряда yt состоит в проверке основной гипотезы вида H0:=1. Критерий Дикки-Фуллера используется при проверке гипотезы о наличия единичных корней. При этом выдвигается основная гипотеза вида H0:=1 для модели авторегрессии первого порядка: yt=a+yt–1+t. Однако на следующем этапе оценивается не эта модель авторегрессии, а модель, которая получается после перехода к первым разностям: yt=yt-1+t, где =–1. Проверка основной гипотезы вида H0:=1 для исходной модели авторегрессии первого порядка аналогична проверке гипотезы H0:=0 для полученной модели. Проверка данной гипотезы может осуществляться для трёх типов регрессионных уравнений: yt=yt-1+t;(1) yt=а+yt-1+t; (2) yt=а+yt-1+t+t. (3) Данные модели регрессии отличаются только наличием членов модели a и t. Первая модель является моделью случайного тренда, во вторую модель включается свободный член a, являющийся коэффициентом случайного тренда. В третью модель включены и коэффициент случайного тренда, и коэффициент линейного временного тренда t. Проверка основной гипотезы H0:=0 состоит в оценивании методом наименьших квадратов одной или нескольких из моделей регрессии 1, 2, 3 для получения оценки и её стандартной ошибки. Наблюдаемое значение t-критерия для проверки основной гипотезы вида H0:=0 состоит в оценивании методом наименьших квадратов одной или нескольких из моделей регрессии 1, 2, 3 для получения оценки
Наблюдаемое значение t-критерия для проверки основной гипотезы вида H0:=0 рассчитывают по формуле:
где
Однако критическое значение t-критерия в данном случае нельзя определить по таблице распределения Стьюдента. Дикки и Фуллер провели исследования, в результате которых определили критические значения t-критерия для проверки гипотезы H0:=0 в зависимости от вида модели регрессии и объёма выборочной совокупности. Данные статистики обозначаются как – для первой модели регрессии, – для второй модели регрессии, х – для третьей модели регрессии. Они приведены в таблице критических значений статистик Дикки-Фуллера для различных уровней значимости. При проверке гипотезы о наличии во временном ряду авторегрессии более чем первого порядка используется расширенный критерий Дикки-Фуллера (Augmented Dickey-Fuller Test – ADF). Процесс авторегрессии порядка р можно записать следующим образом:
Основная гипотеза формулируется как H0:=0. Если данная гипотеза верна, то данная модель авторегрессии имеет единичный корень, т. е. подчиняется процессу авторегрессии первого порядка. Проверка основной гипотезы H0:=0 осуществляется для различных типов регрессионных уравнений:
Справедливость основной гипотезы проверяется с помощью статистики для первой модели регрессии (при отсутствии свободного члена и временного тренда). Справедливость основной гипотезы проверяется с помощью статистики для второй модели регрессии, включающей свободный член. Справедливость основной гипотезы проверяется с помощью статистики х для третьей модели регрессии, включающей свободный член и временной линейный тренд. Если сумма коэффициентов модели регрессии вида
равна единице, т. е.
т. е. в данной модели имеется единичный корень. Яковлева А.В. Эконометрика |
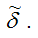 и её стандартной ошибки.
и её стандартной ошибки.

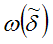 – стандартная ошибка оценки
– стандартная ошибка оценки