Контрольная работа: Интегралы, объем тела вращения, метод наименьших квадратов
Контрольная работа (вариант 8)
1. Найти неопределенные интегралы:
![]()
2. Интегрирование по частям

Вычислить определенные интегралы:
3.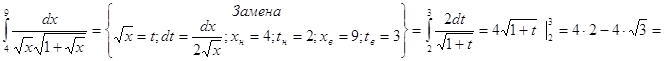
=8-6,92=1,08
Интегрирование по частям
4.![]()
5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями
![]() . Построить чертеж.
. Построить чертеж.
Решение.
В декартовой системе координат построим линии и найдем точки их пересечения.
Объем
тела вращения по формуле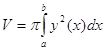
Точки пересечения линий
![]()
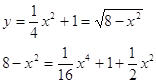
![]()
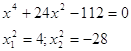
(второй вариант не подходит, т.к. отрицателен)
Отсюда
![]()
Границы фигуры:
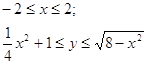
Фигура симметрична относительно оси ОУ, поэтому
Объем тела

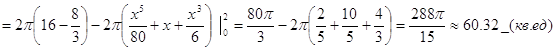
6. Методом наименьших квадратов найти эмпирическую формулу вида y=ax+b для функции, заданной следующей таблицей:
| X | 3.3 | 3.5 | 3.7 | 3.9 | 4.1 |
| Y | 13 | 13.5 | 11.4 | 11.2 | 9.7 |
Изобразить графически таблично заданную и соответствующую линейную функции. По эмпирической формуле вычислить значение переменной при х=4,0
Решение
Заполним таблицу
|
|
|
|
|
|
| 1 | 3,3 | 13 | 10,89 | 42,9 |
| 2 | 3,5 | 13,5 | 12,25 | 47,25 |
| 3 | 3,7 | 11,4 | 13,69 | 42,18 |
| 4 | 3,9 | 11,2 | 15,21 | 43,68 |
| 5 | 4,1 | 9,7 | 16,81 | 39,77 |
|
|
18,5 | 58,8 | 68,85 | 215,78 |
Составим для определения коэффициентов систему уравнений вида:
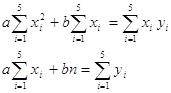
Получим
![]()
Решая систему методом исключения определяем:
![]()
Искомая эмпирическая формула y=28.23-4.45x
Значение переменной при x=4.0
y=28.23-4.45*4=10.43
7. Исследовать сходимость ряда.
![]()
Исследуем ряд сначала на абсолютную сходимость. Общий член ряда
![]()
В свою очередь ряд ![]() расходится
как гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем
на условную сходимость по признаку Лейбница.
расходится
как гармонический. Значит абсолютной сходимости у исходного ряда нет. Исследуем
на условную сходимость по признаку Лейбница.
1) ![]() при
при ![]()
2)

действительно для ![]()
По признаку Лейбница, исходный ряд сходится условно.
| Нахождение неопределенных интегралов | |
|
Контрольная работа (вариант 8) Найти неопределенные интегралы: 2. Интегрирование по частям Вычислить определенные интегралы: 3. =8-6,92=1,08 ... 5. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями Исследуем на условную сходимость по признаку Лейбница. |
Раздел: Рефераты по математике Тип: реферат |
| Вычислительная математика | |
|
Содержание Введение Тема 1. Решение задач вычислительными методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2 ... Далеко не все интегралы можно вычислить по известной из математического анализа формуле Ньютона - Лейбница: Суть численного интегрирования заключается в том, что подынтегральную функцию f(x) заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к f(x) и, во вторых ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Формирование познавательной потребности у учащихся средствами ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Поволжская государственная ... Формула Ньютона-Лейбница Площадь криволинейной трапеции и интеграл Этот подход предполагает введение операции интегрирования как независимой операции; при этом интеграл определяется как предел последовательности, составленной из интегральных сумм. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... Цель - ознакомить учащихся с интегрированием, как операцией обратной диф-ию, показать применение интеграла к решению геом задач. 3. площадь квадрата со стороной =ед.изм. =1ед. далее дается определение площади произвольной фигуры не являющейся простой: фигура имеет площадь, если существуют содержащие ее ... |
Раздел: Рефераты по математике Тип: реферат |
| Физические модели при изучении интеграла в курсе алгебры и начал ... | |
|
Содержание. Введение Глава1. Теоретические основы изучения темы "Интеграл" с помощью моделей 1.1. Модели и моделирование в обучении 1.2. Психолого ... При рассмотрении понятия интеграла в школах с углубленным изучением математики возможно также и обучение простейшим методам интегрирования (технике вычисления интеграла). Но на практике для вычисления интеграла используют формулу Ньютона - Лейбница, которую при данном подходе необходимо доказать. |
Раздел: Рефераты по педагогике Тип: дипломная работа |