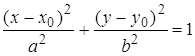Реферат: Кривые второго порядка
ВЫСШАЯ МАТЕМАТИКА
СОДЕРЖАНИЕ
1 Окружность. Эллипс
2 Гипербола
3 Парабола
4 Литература
1 Окружность. Эллипс
При
рассмотрении уравнений прямой на плоскости мы видели, что все они – уравнения
первой степени, т. е. переменные х и у входят в них
в первой степени. Рассмотрим основные виды так называемых кривых второго
порядка, т. е. кривых, в уравнениях которых переменная х или переменная у,
или обе переменные х и у, входят во второй степени, или же входит
произведение х·у (степени складываем – получаем
тоже вторую степень). Ранее вы уже знакомились с такими уравнениями: ![]() – урав-нение окружности с центром в
начале координат радиуса R;
– урав-нение окружности с центром в
начале координат радиуса R; ![]() – уравнение гиперболы,
– уравнение гиперболы, ![]() –
уравнение параболы. Получим так называемые
канонические (основные) уравнения некоторых кривых второго порядка.
–
уравнение параболы. Получим так называемые
канонические (основные) уравнения некоторых кривых второго порядка.
Окружностью называется
множество точек плоскости, равноудаленных от данной точки, называемой ее
центром. Пусть ![]() – центр
– центр
окружности. R – радиус
окружности. Пусть ![]() – произвольная точка окружности.
Следовательно,
– произвольная точка окружности.
Следовательно, ![]() = =
= = ![]()
![]()
![]() (1)
(1)
(1) – уравнение
окружности радиуса R c центром в точке с
координатами ![]()
Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек F1 и F2 этой плоскости, называемых фокусами эллипса, есть заданная постоянная величина, равная 2а, а > 0, большая, чем расстояние между фокусами 2с, с > 0.
Пусть фокусы эллипса
лежат на оси Х, причем ![]() т. е.
т. е. ![]() – межфокусное расстояние эллипса.
– межфокусное расстояние эллипса.
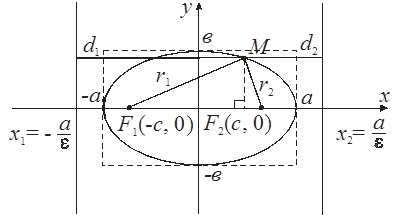
Пусть ![]() – произвольная точка эллипса. Величины
– произвольная точка эллипса. Величины ![]()
![]() называются фокальными
радиусами точки М эллипса.
называются фокальными
радиусами точки М эллипса.
По определению эллипса: r1 + r2 = 2a, а > c. Из прямоугольных треугольников, по теореме Пифагора, имеем:
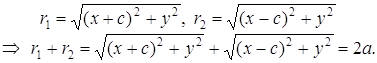 (2)
(2)
Умножим (2) на ![]()
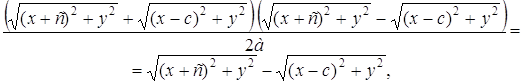
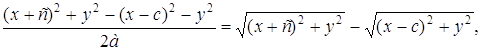
![]() (3)
(3)
Сложим уравнения (2) и (3):
![]()
![]() (4)
(4)
Возведем (4) в квадрат:
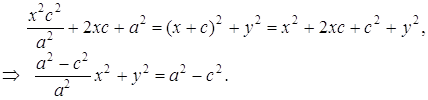
Пусть 
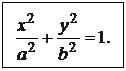
![]() (5)
(5)
(5) – каноническое уравнение эллипса с центром в начале координат. Соответственно, уравнение
– каноническое уравнение эллипса с центром в точке 
Числа а и ![]() называются соответственно большой и малой
полуосями эллипса. Заметим, что а >
называются соответственно большой и малой
полуосями эллипса. Заметим, что а > ![]() , если а
<
, если а
< ![]() , то фокусы эллипса будут на оси Оу,
если а =
, то фокусы эллипса будут на оси Оу,
если а = ![]() , то эллипс превращается в
окружность.
, то эллипс превращается в
окружность.
Точки ![]() ,
, ![]() называются вершинами
эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника:
называются вершинами
эллипса. Отметим, что эллипс целиком расположен внутри прямоугольника: ![]()
Так как ![]()
![]() (6)
(6)
Эксцентриситетом эллипса e называют отношение межфокусного расстояния 2с к длине большой оси 2а.
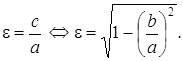 (7)
(7)
Следовательно, ![]() причем
причем ![]() когда
когда ![]() т. е. имеем окружность.
т. е. имеем окружность.
При ![]() стремящемся к 1 эллипс становится более
вытянутым вдоль оси Ох.
стремящемся к 1 эллипс становится более
вытянутым вдоль оси Ох.
Выразим фокальные радиусы
точки ![]() через эксцентриситет. Из (4):
через эксцентриситет. Из (4):
![]() (8)
(8)
Из (3): ![]()
Значит, подставив
координаты точки ![]() эллипса в уравнения (8), получаем
фокальные радиусы точки М.
эллипса в уравнения (8), получаем
фокальные радиусы точки М.
Прямые ![]() называются директрисами эллипса.
называются директрисами эллипса.
![]() –
левая директриса,
–
левая директриса,
![]() –
правая директриса.
–
правая директриса.
Заметим, что директрисы эллипса обладают следующим важным свойством:
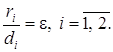 (9)
(9)
т. е. отношение расстояния ri от любой точки эллипса до фокуса к расстоянию di от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса.
2 Гипербола
Гиперболой называется множество точек
плоскости, для каждой из которых модуль разности расстояний от которых до двух
данных точек ![]() той же плоскости, называемых фокусами
гиперболы, есть заданная постоянная величина
той же плоскости, называемых фокусами
гиперболы, есть заданная постоянная величина ![]() меньшая,
чем расстояние между фокусами
меньшая,
чем расстояние между фокусами ![]()
Пусть
фокусы гиперболы лежат на оси Ох, причем ![]() т. е.
т. е. ![]() Заметим, что
Заметим, что ![]()
Пусть ![]() – произвольная точка гиперболы. Как и ранее,
– произвольная точка гиперболы. Как и ранее,
![]() – фокальные радиусы точки М.
– фокальные радиусы точки М.
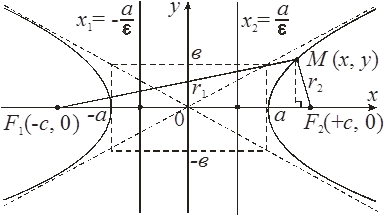
По определению гиперболы:
![]()
где ![]()
Следовательно,
![]() (10)
(10)
Умножим (10) на
![]()
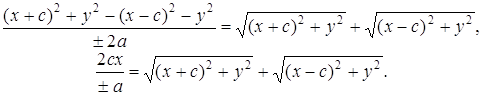 (11)
(11)
Сложим уравнения (10) и (11):
![]() (12)
(12)
Возведем (12) в квадрат:
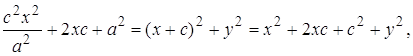
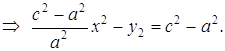
Пусть 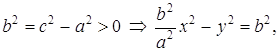
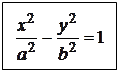 (13)
(13)
(13) – каноническое уравнение гиперболы с центром в начале координат. Соответственно, уравнение
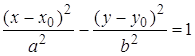
– каноническое уравнение
гиперболы с центром в точке ![]()
Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (a=b) называется равносторонней, ее каноническое уравнение имеет вид:
![]()
Точки ![]() называются вершинами гиперболы.
называются вершинами гиперболы.
Заметим, что если уравнение гиперболы имеет вид
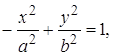 (14)
(14)
то фокусы гиперболы находятся на оси Оу, а ветви гиперболы будут направлены не влево и вправо, а вверх и вниз.
Так как ![]() , то
, то ![]() (15)
(15)
Как
и в случае с эллипсом, эксцентриситетом гиперболы ![]() называется отношение межфокусного расстояния
называется отношение межфокусного расстояния
![]() к длине действительной оси
к длине действительной оси ![]() :
:
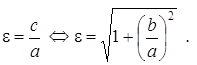 (16)
(16)
Следовательно, ![]()
Выразим фокальные радиусы
точки ![]() через эксцентриситет. Из (12)
через эксцентриситет. Из (12)
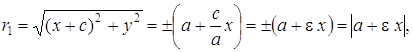
![]() (17)
(17)
Прямые 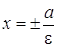 называются директрисами
гиперболы.
называются директрисами
гиперболы.
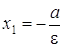 – левая
директриса,
– левая
директриса,
![]() –
правая директриса.
–
правая директриса.
Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса
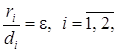 (18)
(18)
т. е. отношение
расстояния ![]() от любой точки гиперболы до фокуса к
расстоянию
от любой точки гиперболы до фокуса к
расстоянию ![]() от нее до соответствующей директрисы есть
величина постоянная, равная эксцентриситету гиперболы.
от нее до соответствующей директрисы есть
величина постоянная, равная эксцентриситету гиперболы.
Для гиперболы важную роль играют также прямые
![]() (19)
(19)
которые являются ее асимптотами,
т. е. прямыми к которым график гиперболы неограниченно близко приближается, но
не пересекает их. Заметим, что асимптоты гиперболы совпадают с диагоналями
прямоугольника (если их продолжить) ![]()
Следует отметить, что
если уравнение гиперболы имеет вид (14), т. е. ее фокусы находятся на оси Оу,
то изменятся формулы для вычисления фокальных радиусов, эксцентриситета,
директрис. Так ![]() – эксцентриситет,
– эксцентриситет, ![]() – уравнения директрис.
– уравнения директрис.
3 Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки F этой плоскости, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Построим уравнение параболы.
Пусть ось Оx проходит через фокус F параболы и перпендикулярен
директрисе, а ось Оу проходит посередине между фокусом и директрисой. Обозначим
через p – расстояние между фокусом и директрисой. Тогда 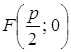 , а уравнение директрисы
, а уравнение директрисы ![]() .
.
Число p – называется фокальным параметром параболы.
Пусть
![]() – произвольная точка параболы. Пусть
– произвольная точка параболы. Пусть ![]() – фокальный радиус точки M. d – расстояние от
точки М до директрисы. Тогда
– фокальный радиус точки M. d – расстояние от
точки М до директрисы. Тогда ![]()
По
определению параболы ![]() . Следовательно
. Следовательно

Возведем это уравнение в квадрат
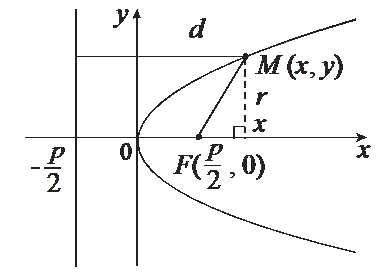
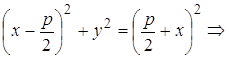
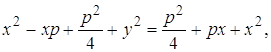
![]() (20)
(20)
– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.
Точка (0; 0) – вершина параболы.
Если р > 0 (р > 0 ), то парабола (20) расположена правее (левее) оси Оу.
Так как для параболы ![]() , а для эллипса и гиперболы
, а для эллипса и гиперболы ![]() , то, следовательно, эксцентриситет параболы
равен 1 (e = 1).
, то, следовательно, эксцентриситет параболы
равен 1 (e = 1).
Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением
х2 = 2q y (21)
Фокус этой параболы
находится в точке 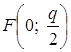 . Уравнение ее директрисы
. Уравнение ее директрисы ![]() . Фокальный радиус ее точки М(х,
у) выражается формулой
. Фокальный радиус ее точки М(х,
у) выражается формулой ![]() .
.
Если q > 0 (q < 0), то ветви параболы (21) расположены выше (ниже) оси Ох.
Рассмотрим примеры.
ПРИМЕР 1
Найти координаты центра и радиус окружности, определяемой уравнением
х2 + у2 – 4х + 6у – 3 = 0.
Решение.
Выделим полные квадраты в данном уравнении:
х2 + у2 – 4х + 6у – 3 = (х2 – 4х + 4) – 4 + (у2 + 6у + 9) – 9 – 3 = 0
Þ (х – 2)2 + (у + 3)2 = 16.
Учитывая уравнение окружности (1), имеем, что ее центр находится в точке с координатами (2; –3), а радиус равен 4.
ПРИМЕР 2
Эллипс, симметричный
относительно осей координат, фокусы которого находятся на оси Ох,
проходит через точку М(–4; ![]() ) и имеет эксцентриситет
) и имеет эксцентриситет ![]() . Написать уравнение эллипса и найти
фокальные радиусы точки М.
. Написать уравнение эллипса и найти
фокальные радиусы точки М.
Решение.
Каноническое уравнение
эллипса имеет вид ![]()
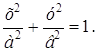
Так как эллипс проходит через точку М, то ее координаты должны удовлетворять этому уравнению
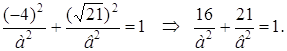
Фокусы находятся на оси Ох, следовательно
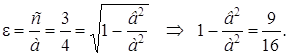
Объединив полученные два уравнения в систему, найдем а2 и в2:
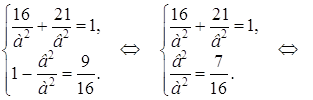
![]()
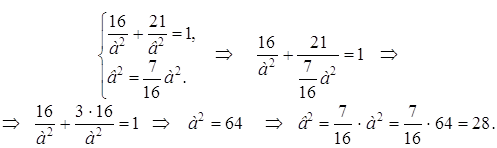
Следовательно, уравнение данного эллипса имеет вид:
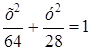
Фокальные радиусы точки М
определим по формулам (8): х = –4, ![]() ,
, ![]() .
.
Þ r1 = а + eх
= ![]() = 8 – 3 = 5,
= 8 – 3 = 5,
r2 = а – eх = ![]() = 8 + 3 = 11.
= 8 + 3 = 11.
ПРИМЕР 3
Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке F (–1; 0), чем к прямой х = –4.
Решение.
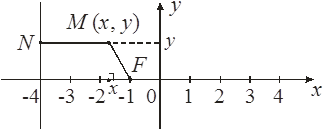
Пусть М (х,
у). Тогда çMNú = 2 çMFú , çMNú = ç–4 – xú , çMFú =
= ![]() , Þ ç– (4 + х)ú =
, Þ ç– (4 + х)ú = ![]() .
.
Возведем в квадрат: (4 + х)2 = 4 ((х + 1)2 + у2),
Þ 16 + 8х + х2 = (х2 + 2х + 1 + у2) · 4 = 4х2 + 8х + 4 + 4у2,
Þ
3х2
+ 4у2 = 12 Þ ![]() Þ
Þ 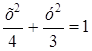 .
.
Таким образом, точка М (х, у) движется по эллипсу.
ПРИМЕР 4
Написать уравнение
гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса 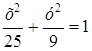 .
.
Решение.
Из уравнения данного эллипса имеем: а = 5; в = 3, а > в.
Следовательно, ![]() Поэтому, вершинами эллипса будут точки (±5; 0), (0; ±3), а фокусами точки F1(–с; 0) = (–4; 0), F2(4; 0).
Поэтому, вершинами эллипса будут точки (±5; 0), (0; ±3), а фокусами точки F1(–с; 0) = (–4; 0), F2(4; 0).
Так как фокусы эллипса находятся на оси Ох (а > в), то вершины (±5; 0) будут фокусами гиперболы. Каноническое уравнение гиперболы, имеющей фокусы на оси Ох, имеет вид (13)
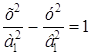 ,
,
причем F1(–5; 0), F2(5; 0) – фокусы данной гиперболы, т. е. с1 = 5. Найдем а1 и в1.
Так как вершины данной гиперболы находятся в фокусах эллипса, то а1 = с = 4. Следовательно:
![]() .
.
Таким образом, уравнение гиперболы имеет вид
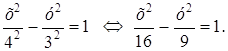
ПРИМЕР 5
Составить уравнение геометрического места точек, одинаково удаленных от точки F(2; 0) и от прямой у = 2. Найти вершину параболы, точки пересечения ее с осью Ох.
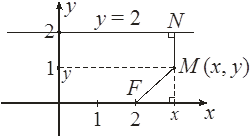
Решение.
Пусть точка М (х, у) – принадлежит данному множеству точек.
Следовательно çFMú = çNMú , çFMú = = ![]() , çNMú = 2 – у, Þ 2 – у =
, çNMú = 2 – у, Þ 2 – у = ![]() .
.
Возведем в квадрат:
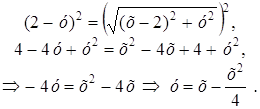
– парабола, ветви которой направлены вниз.
Найдем точки пересечения данной параболы с осью Ох.
у = 0 Þ ![]() Þ
Þ  Þ х1 = 0; х2
= 4.
Þ х1 = 0; х2
= 4.
Т. е. это будут точки (0; 0); (4; 0).
Þ Вершина параболы будет в точке с абсциссой х
= 2 Þ ![]() = = 2 – 1 = 1, т. е.
= = 2 – 1 = 1, т. е.
Вершиной параболы будет точка (2; 1).
ПРИМЕР 6
На параболе у2 = 6х найти точку, фокальный радиус которой равен 4,5.
Решение.
Так как у2
= 2рх Þ 2р = 6, р = 3. ![]() Þ
Þ ![]() =
=
=
= ![]() Значит у2 = 6 · 3 = 18 Þ у = ±
Значит у2 = 6 · 3 = 18 Þ у = ±![]() = ±
= ±![]() . Þ (3; ±
. Þ (3; ±![]() ) – две таких точки.
) – две таких точки.
ЛИТЕРАТУРА
1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.
2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.
| Большая коллекция шпор для МАТАНа (1 семестр 1 курс) | |
|
1. Векторы. Действия над векторами. Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n ... Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз ... Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса. |
Раздел: Рефераты по математике Тип: шпаргалка |
| Полный курс лекций по математике | |
|
МАТЕМАТИКА Тема 1. Роль математики в современном мире. Основные этапы становления математики. Тема 2. Аксиоматический метод построения научной теории ... К кривым второго порядка относят кривые, записанные уравнением Ах2 + Вху + Су2 + Ех + Ду + F = 0. В зависимости от значений коэффициентов (вещественные числа) это могут быть ... Гипербола, заданная уравнением симметрична относительно осей координат (Рис 2). Она пересекает ось ох в точках А1( -а, 0) и А2(+а, 0) - вершинах гиперболы и не пересекает ось оу. |
Раздел: Рефераты по математике Тип: реферат |
| Шпоры по математическому анализу | |
|
Производные и дифференциалы высших порядков Опр-ие: производной n-го порядка (n 2) функции у=f(х) называется производная (первого порядка) от ... Обозначим расстояние между фокусом и директрисой через р. Канонической уравнение параболы имеет вид: у2=2рх и получается, если фокус F поместить в точку (р 2, 0), а в качестве директрисы взять прямую х = - р 2. Число р называют параметром параболы, точку (0,0) - ее вершиной. |
Раздел: Рефераты по математике Тип: реферат |
| Геометрические построения на плоскости | |
|
Геометрические построения на плоскости Введение Вам, будущим учителям, в школьном курсе математики придется учить ребят решению задач на построение ... Геометрическое место центров всех окружностей, которые касаются окружности К1`` и проходят через точку Р, есть эллипс или гипербола, в зависимости от того, лежит ли Р внутри ... Геометрическое место центров окружностей, которые касаются прямой l и проходят через точку Р, есть парабола, имеющая прямую l своей директрисой, а фокус - в точке Р. |
Раздел: Рефераты по математике Тип: учебное пособие |
| Линии на плоскости | |
|
При чтении экономической литературы приходится иметь дело с большим количеством графиков. Укажем некоторые из них. Кривая безразличия - кривая ... ... экономистов умение строить графики и разбираться в свойствах простейших кривых, каковыми являются прямые линии и кривые второго порядка - окружность, эллипс, гипербола, парабола. Парабола y2 = 2рx имеет фокус F( р/2,0) и директрису x = - р/2, фокальный радиус-вектор точки M(x,y) на ней r = x+ р/2. |
Раздел: Рефераты по математике Тип: реферат |