Контрольная работа: Решение линейной системы уравнений с тремя неизвестными
Задача 1
Решить систему линейных уравнений двумя способами: по формулам Крамера и методом Гаусса
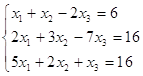
Решение:
1) решим неоднородную систему линейных алгебраических уравнений Ах = В методом Крамера
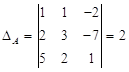
Определитель системы D не равен нулю. Найдем вспомогательные определители D1, D2, D3, если они не равны нулю, то решений нет, если равны, то решений бесконечное множество
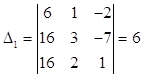
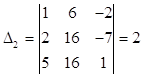
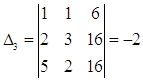
Система 3 линейных уравнений с 3 неизвестными, определитель которой отличен от нуля, всегда совместна и имеет единственное решение, вычисляемое по формулам:

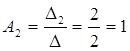
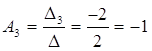
Ответ: получили решение: 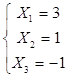
2) решим неоднородную систему линейных алгебраических уравнений Ах = В методом Гаусса
Составим расширенную матрицу системы
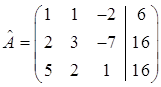
Примем первую строку за направляющую, а элемент а11 = 1 – за направляющий. С помощью направляющей строки получим нули в первом столбце.
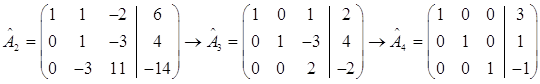
Матрице ![]() соответствует
множество решений системы линейных уравнений
соответствует
множество решений системы линейных уравнений 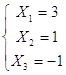
Ответ: получили решение: 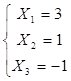
Задача 2
Даны координаты вершин треугольника АВС
Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
3) внутренний угол при вершине В в радианах с точностью до 0,01
4) уравнение медианы АЕ;
5) уравнение и длину высоты CD;
6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой CD;
7) уравнение окружности с центром в точке Е, проходящей через вершину В
Построить заданный треугольник и все линии в системе координат.
А(1; -1), В(4; 3). С(5; 1).
Решение
1) Расстояние между точками А(х1; у1) и В(х2; у2) определяется по формуле
![]()
воспользовавшись которой находим длину стороны АВ;
![]()
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
Уравнение прямой, проходящей через две заданные точки плоскости А(х1; у1) и В(х2; у2) имеет вид
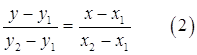
Подставляя в (2) координаты точек А и В, получаем уравнение стороны АВ:
![]()
Угловой коэффициент kАВ прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у = kx - b.
У нас ![]() , то
есть
, то
есть ![]() откуда
откуда ![]()
Аналогично получим уравнение прямой ВС и найдем ее угловой коэффициент.
Подставляя в (2) координаты точек В и С, получаем уравнение стороны ВС:
![]()
Угловой коэффициент kВС прямой ВС найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у = kx - b.
У нас ![]() , то
есть
, то
есть ![]()
3) внутренний угол при вершине В в радианах с точностью до 0,01
Для нахождения внутреннего угла нашего треугольника воспользуемся формулой:
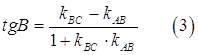
Отметим, что порядок вычисления разности угловых коэффициентов, стоящих в числителе этой дроби, зависит от взаимного расположения прямых АВ и ВС.
Подставив ранее вычисленные значения kВС и kАВ в (3), находим:
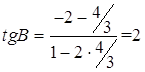
Теперь, воспользовавшись таблицами инженерным микрокалькулятором, получаем В » 1,11 рад.
4) уравнение медианы АЕ;
Для составления уравнения медианы АЕ найдем сначала координаты точки Е, которая лежит на середине отрезка ВС
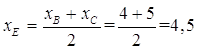
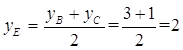
Подставив в уравнение (2) координаты точек А и Е, получаем уравнение медианы:
![]()
5) уравнение и длину высоты CD;
Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку М(х0; у0) с заданным угловым коэффициентом k, которое имеет вид
![]()
и условием перпендикулярности прямых АВ и CD, которое выражается соотношением kABkCD = -1, откуда kCD = -1/kAB = - 3/4
Подставив в (4) вместо k значение kСD = -3/4, а вместо x0, y0 ответствующие координаты точки С, получим уравнение высоты CD
![]()
Для вычисления длины высоты СD воспользуемся формулой отыскания расстояния d от заданной точки М(х0; у0) до заданной прямой с уравнением Ax + By + С = 0 , которая имеет вид:
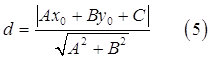
Подставив в (5) вместо х0; у0 координаты точки С, а вместо А, В, С коэффициенты уравнения прямой АВ, получаем
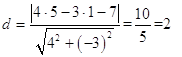
6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой CD;
Так как искомая прямая EF параллельна прямой АВ, то kEF = kAB = 4/3. Подставив в уравнение (4) вместо х0; у0 координаты точки Е, а вместо k значение kEF получаем уравнение прямой EF'.
![]()
Для отыскания координат точки М решаем совместно уравнения прямых EF и CD.
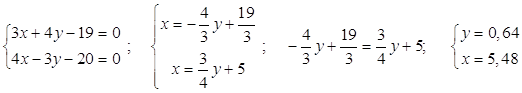
Таким образом, М(5,48; 0,64).
7) уравнение окружности с центром в точке Е, проходящей через вершину В
Поскольку окружность имеет центр в точке Е(4,5; 2) и проходит через вершину В(4; 3), то ее радиус
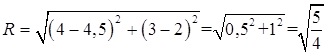
Каноническое уравнение окружности радиуса R с центром в точке М0(х0; у0) имеет вид
![]()
Имеем
![]()
Треугольник АВС, высота СD, медиана AE, прямая EF , точка M и окружность построенная в системе координат x0у на рис.1.

Рис. 1
Задача 3
Составить уравнение линии, для каждой точки которой ее расстояние до точки А (2; 5) равно расстоянию до прямой у = 1. Полученную кривую построить в системе координат
Решение
Пусть М (x, у) - текущая точка искомой кривой. Опустим из точки М перпендикуляр MB на прямую у = 1 (рис.2). Тогда В(х; 1). Так как МА = MB , то
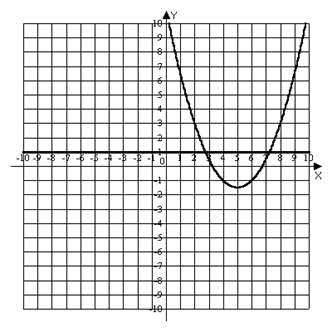
Pиc. 2
![]()
![]()
![]()
![]()
![]()
Полученное уравнение определяет параболу с вершиной в точке С(5; -1,5) и ветвями, направленными вверх (см. рис 2).
Задача 4
Найти указанные пределы:
а) 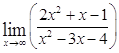
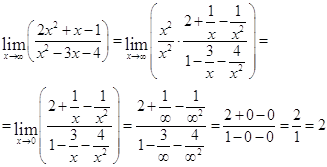
Ответ: 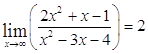
б)
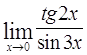
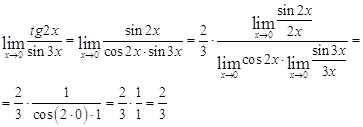
Ответ: 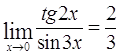
Задача 5
Найти производные dy/dx, пользуясь правилами и формулами дифференцирования
Решение:
а)
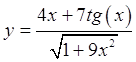
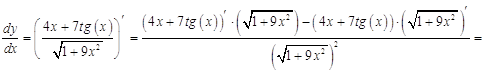
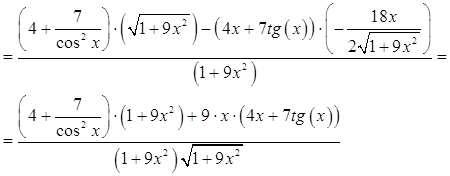
Ответ: 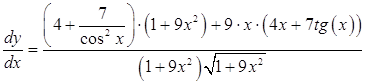
б)
![]()
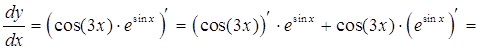
![]()
![]()
![]()
Ответ: 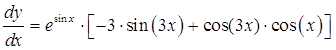
в) ![]()
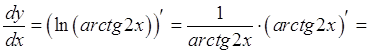
![]()
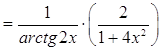
Ответ: 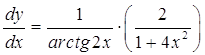
Задача 6
Исследовать заданные функции методами дифференциального исчисления, начертить их графики.
а) ![]() ; б)
; б) 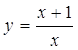
Решение
а) ![]()
1) Областью определения данной функции являются все действительные значения аргумента х, то есть D(y) = {х: хÎ(-¥, +¥)}, а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
2) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
![]()
![]()
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки первого рода х1 = 1, х2 = 2.
Разбиваем область определения этими точками на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:
| х | (-¥; 1) | 1 | (1; 2) | 2 | (2; ¥) |
| f ’(x) | + | 0 | - | 0 | + |
| f(x) |
|
max |
|
min |
|
![]()
![]()
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
![]()
![]()
Итак, функция имеет одну критическую точку второго рода х = -1,5. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
| х | (-¥; 1,5) | 1,5 | (1,5; ¥) |
| f ‘’(x) | - | 0 | + |
| f(x) | Ç | т. п. | È |
Значение х = 1,5 является абсциссой точки перегиба графика функции, а ордината этой точки:
![]()
4) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx – b воспользуемся формулами
![]()
![]()
Таким образом, у графика заданной функции наклонных асимптот нет.
5) построим график функции

б)
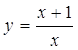
1) Областью определения данной функции являются значения аргумента х
D(y) = хÎ(-¥, 0) È (0, +¥).
2) Исследование на непрерывность и классификация точек разрыва
Заданная функция непрерывна всюду, кроме точки х = 0. Вычислим ее односторонние пределы в этой точке:
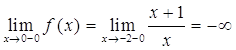
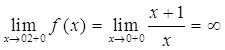
Итак точка х = 0 – точка разрыва второго рода, а прямая х = 0 – вертикальная асимптота.
3) Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
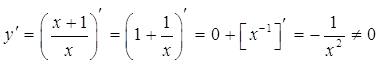
Следовательно, функция не имеет критических точек первого рода.
Так как y’ < 0 для всех х, то функция убывает во всей области определения
4) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
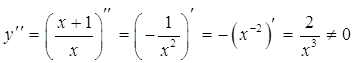
Итак функция не имеет точек перегиба. Разобьем область определения точкой х = 1 в каждой из которых установим знак второй производной:
| х | (-¥; 0) | 0 | (0; ¥) |
| f ‘’(x) | - | не существует | + |
| f(x) | Ç | не существует | È |
5) Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты y = kx + b воспользуемся формулами
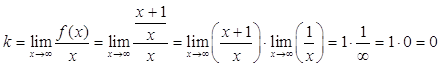
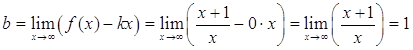
Таким образом, у графика заданной функции есть наклонная асимптота
y = 0*x + 1 = 1.
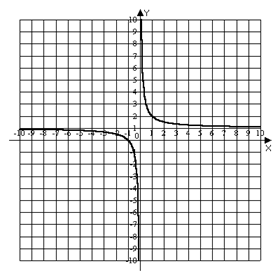
6) построим график функции
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... Пусть прямая задана направляющим вектором a"{m,n} и фикс. точкой M(x0,y0) Угловым кооф-ом прямой называется отношение второй координаты направляющего вектора к первой. k=n/m Если m ... Т: Всякая пряма может быть задана в афинной системе координат линейным уравнением. |
Раздел: Рефераты по математике Тип: реферат |
| Синхронные машины. Машины постоянного тока | |
|
Синхронные машины. Машины постоянного тока Учебное пособие 1. Синхронные машины 1.1 Принцип действия синхронной машины Статор 1 синхронной машины (рис ... При неизменном токе Iн катет АВ характеристического треугольника является постоянным; катет ВС зависит не только от тока Iн, но и от степени насыщения магнитной системы, т.е. от ... На этой прямой располагают вершину А характеристического треугольника; катет АВ должен быть параллелен оси ординат, а вершина С должна лежать на характеристике холостого хода 1 ... |
Раздел: Рефераты по физике Тип: учебное пособие |
| Дифференциальные уравнения | |
|
Задача №1 Даны вершины треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в ... 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение ... 6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая прямая ВС и содержит точку А, а третья ... |
Раздел: Рефераты по математике Тип: контрольная работа |
| Самостоятельная работа как средство обучения решению уравнений в 5-9 ... | |
|
... РФ Светлоградский педагогический колледж Дипломная работа Самостоятельная работа как средство обучения решению уравнений в 5 - 9 классах Выполнила: Первое из них описывает широкий класс уравнений (левая и правая части уравнения - нуль или многочлены не выше первой степени), а второе-более узкий (уравнение вида kx+b=0, k 0). Кроме того, требуется усвоить факт: график линейного уравнения ах + bу= с, где а 0 или b 0, есть прямая линия, а также научиться строить график конкретных линейных уравнений с ... |
Раздел: Рефераты по педагогике Тип: реферат |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Будем искать уравнение прямой в виде y=kx+b. Поскольку прямая проходит через точку A, то ее координаты удовлетворяют уравнению прямой, т.е. 1=3k+b, Ѭ b=1-3k. Поэтому если подставить в уравнение прямой вместо x и`y заданные величины xi и yi, то окажется, что левая часть уравнения равна какой-то малой величине ei=`yi -yi; а именно: для ... |
Раздел: Рефераты по математике Тип: дипломная работа |