Реферат: Финансовая рента
Финансовые операции часто носят продолжительный характер и состоят не из разового платежа, а из их последовательности, т.е. из потока платежей.
Поток платежей, все члены которого положительные величины, а временные интервалы постоянны, называют финансовой рентой или аннуитетом [5, с.46].
Основные правила процентных вычислений, рассмотренные нами ранее, остаются неизменными и для совокупности платежей, однако возникает необходимость ввести несколько дополнительных понятий. В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента.
Частным случаем ренты является финансовая рента или аннуитет - такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними.
Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет [7, с.28].
В буквальном переводе "аннуитет" подразумевает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат.
Очевидно, что рента - это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно [7, с.28].
Форму аннуитетов имеют многие финансовые потоки, например выплата доходов по облигациям или платежи по кредиту, страховые взносы. Можно сказать, что финансы тяготеют к упорядочению денежных потоков.
Принцип временной ценности денег делает невозможным прямое суммирование членов ренты. Для учета влияния фактора времени к каждому члену ренты применяются рассмотренные выше правила наращения и дисконтирования только сложных процентов, то есть предполагается, что получатель потока имеет возможность реинвестировать получаемые им суммы.
Если бы размеры рент всегда ограничивались двумя-тремя членами, то необходимость создания специальных способов расчета денежных потоков, возможно, и не возникла.
Ни в теории, ни на практике таких ограничений нет, наоборот, существуют большие, очень большие и даже бесконечные денежные потоки (вечные ренты), поэтому были разработаны специальные методы, позволяющие анализировать ренту не по каждому ее члену в отдельности, а как единую совокупность - рассчитывать ее будущую и приведенную величины, а также определять размеры других важных параметров ренты.
Финансовая рента имеет следующие параметры:
член ренты - величина каждого отдельного платежа;
период ренты - временной интервал между двумя соседними платежами, срок ренты - время, измеренное от начала финансовой ренты до конца ее последнего периода;
процентная ставка - ставка, используемая при наращении или дисконтировании платежей, образующих ренту, число платежей в году, число начислений процентов в году, моменты платежа внутри периода ренты [3, с.62].
Классификация рент может быть произведена по различным признаками.
В зависимости от продолжительности периода, ренты делят на годовые и p-срочные, где p - число выплат в году.
По числу начислений процентов различают ренты с начислением один в году, m раз или непрерывно. Моменты начисления процентов могут не совпадать с моментами рентных платежей [5, с.47].
По величине членов различают постоянные (с равными членами) и переменные ренты.
Если размеры платежей изменяются по какому - либо математическому закону, то часто появляется возможность вывести стандартные формулы, значительно упрощающие расчеты.
По вероятности выплаты членов различают ренты верные и условные.
Верные ренты подлежат безусловной выплате, например, при погашении кредита. Выплата условной ренты ставится в зависимость от наступления некоторого случайного события. Поэтому число ее членов заранее неизвестно. Например, число выплат пенсий зависит от продолжительности жизни пенсионера.
По числу членов различают ренты с конечным числом членов или ограниченные и бесконечные или вечные. В качестве вечной ренты можно рассматривать выплаты по облигационным займам с неограниченными или не фиксированными сроками.
В зависимости от наличия сдвига момента начала ренты по отношению к началу действия контракта или какому-либо другому моменту ренты подразделяются на немедленные и отложенные или отсроченные. Срок немедленных рент начинается сразу, а у отложенных запаздывает.
Ренты различают по моменту выплаты платежей.
Если платежи осуществляются в конце каждого периода, то такие ренты называются обычными или постнумерандо. Если же выплаты производятся в начале каждого периода, то ренты называются пренумерандо. Иногда предусматриваются платежи в середине каждого периода.
Анализ потоков платежей в большинстве случаев предполагает расчет наращенной суммы или современной величины ренты.
Рассмотрим расчет современной стоимости и наращенной суммы постоянной обычной (постнумерандо) p - срочной ренты [4, с.84].
Ежегодно сумма R вносится равными долями p раз
в году на банковский счет в течение n лет. Тогда имеем поток из np
платежей величиной ![]() каждый в моменты
каждый в моменты
![]() .
.
Примем за единицу измерения времени 1 год.
Пусть i - годовая эффективная процентная ставка начисления сложных процентов на поступающие платежи.
Согласно определению современной стоимости потока платежей, получаем
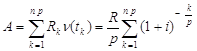 (1)
(1)
Вычисляя сумму np членов геометрической прогрессии,
знаменатель которой ![]() , получим:
, получим:
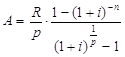 (2)
(2)
современная стоимость постоянной обычной p - срочной ренты при начислении процентов на члены ренты 1 раз в году в течение n лет.
Отсюда современная стоимость годовой обычной ренты (p = 1) при начислении процентов на члены ренты 1 раз в году:
![]() . (3)
. (3)
Используя соотношения эквивалентности для эффективной процентной ставки
![]() и
и ![]() ,
,
получим современную стоимость обычной p - срочной ренты при начислении на члены ренты сложных процентов m раз в году по номинальной процентной ставке i (m) и непрерывном начислении процентов при постоянной интенсивности процентов δ в год:
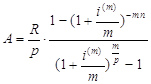 (4)
(4)
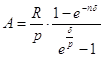 . (5)
. (5)
Формулы для наращенной суммы ренты можно получить непосредственно по определению согласно формуле (3).
Например, для постоянной обычной p - срочной ренты при начислении процентов на члены ренты 1 раз в году в течение n лет получаем:
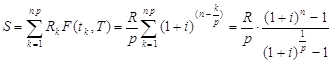 . (6)
. (6)
Наращенную сумму ренты можно рассчитать, используя формулу связи современной стоимости и наращенной суммы потока платежей.
Например, для годовой ренты при начислении процентов 1 раз в год:
S = A F (T) = A (1 + i) n
= ![]() (7)
(7)
Для других видов обычной ренты из (4) и (5), используя
множители наращения ![]() и
и ![]() соответственно, получим:
соответственно, получим:
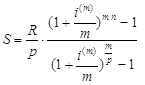 (8)
(8)
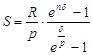 (9)
(9)
В частности, при m = p (период начисления процентов равен периоду ренты) из (4) и (8) получаем
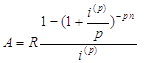 (10)
(10)
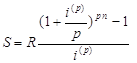 (11)
(11)
Если единицей измерения времени является 1 год, а R -
это выплата за год (единицу времени), то множитель в формулах современной
стоимости ренты, равный ![]() ,
называется коэффициентом дисконтирования ренты.
,
называется коэффициентом дисконтирования ренты.
Множитель в формулах наращенной суммы ренты, равный ![]() , называется коэффициентом
наращения ренты.
, называется коэффициентом
наращения ренты.
Из (1) - (11) можно получить коэффициенты наращения и дисконтирования всех рассмотренных видов обычной ренты.
Согласно (1) и (5), коэффициенты дисконтирования и наращения обычной p - срочной ренты с начислением процентов 1 раз в году в течение n лет равны соответственно:
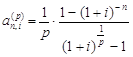 (12)
(12)
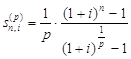 (13)
(13)
![]() и
и ![]() - это соответственно
современная стоимость и наращенная сумма постоянной обычной p - срочной
ренты с ежегодной выплатой 1 д. е. равными долями p раз в году в размере
- это соответственно
современная стоимость и наращенная сумма постоянной обычной p - срочной
ренты с ежегодной выплатой 1 д. е. равными долями p раз в году в размере
![]() в моменты времени
в моменты времени ![]() с начислением на члены
ренты процентов 1 раз в году.
с начислением на члены
ренты процентов 1 раз в году.
Следовательно, ![]() и
и ![]() связаны соотношением (14):
связаны соотношением (14):
![]() = (1 + i) n
= (1 + i) n![]() (14)
(14)
Аналогичный смысл имеют коэффициенты дисконтирования и наращения других рассмотренных видов обычной ренты.
Для этих рент имеем соотношения:
![]() - годовая рента
с начислением процентов 1 раз в год;
- годовая рента
с начислением процентов 1 раз в год;
![]() - p - срочная
рента с начислением процентов m раз в год;
- p - срочная
рента с начислением процентов m раз в год;
![]() - p - срочная
рента с непрерывным начислением процентов.
- p - срочная
рента с непрерывным начислением процентов.
Коэффициенты дисконтирования и наращения годовой ренты при начислении процентов 1 раз в год:
![]() и
и ![]() (15)
(15)
Если применяется p - срочная рента с начислением процентов
p раз в год (m = p) по годовой номинальной ставке i (p),
то за единицу измерения времени можно принять ![]() часть
года. Тогда
часть
года. Тогда ![]() - выплата за единицу
времени (постнумерандо),
- выплата за единицу
времени (постнумерандо), ![]() - процентная
ставка за 1 единицу времени,
- процентная
ставка за 1 единицу времени,
срок ренты - np единиц времени.
Коэффициенты дисконтирования и наращения такой ренты равны соответственно
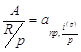 и
и 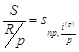 .
.
Из формул (10), (11) имеем
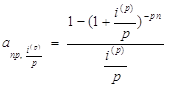 ,
, 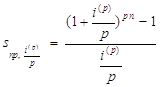 (16),
(16),
что позволяет для этой ренты использовать те же таблицы
коэффициентов. Заметим, что если единицей измерения времени является 1 год, то
коэффициенты дисконтирования и наращения этой ренты определяются как ![]() =
= ![]() и
и ![]() =
= ![]() и рассчитываются по
формулам, полученным из (10), (11):
и рассчитываются по
формулам, полученным из (10), (11):
 ,
,  (17). Тогда
(17). Тогда
![]() =
= ![]() и
и ![]() =
= ![]() (18)
(18)
Рассмотрим ренту пренумерандо.
Связь между коэффициентами дисконтирования и наращения рент
пренумерандо и постнумерандо следует из их определения. Срок дисконтирования
каждого платежа ренты пренумерандо уменьшается, а срок наращения увеличивается
на один период ренты по сравнению с обычной рентой. По - прежнему единицей
измерения времени считаем 1 год. Если ![]() и
и
![]() - коэффициенты
дисконтирования и наращения p - срочной ренты пренумерандо (платежи
поступают в начале каждого периода длиной
- коэффициенты
дисконтирования и наращения p - срочной ренты пренумерандо (платежи
поступают в начале каждого периода длиной ![]() )
при начислении на члены ренты процентов 1 раз в год, то справедливы соотношения:
)
при начислении на члены ренты процентов 1 раз в год, то справедливы соотношения:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() = (1 + i)
n
= (1 + i)
n ![]() .
.
Отсюда при p = 1 получаем соотношения для годовых рент:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() = (1 + i)
n
= (1 + i)
n ![]() .
.
При непрерывном начислении процентов для p - срочной ренты имеем соотношения:
![]() =
= ![]()
![]()
![]()
![]() .
.
Рассмотрим непрерывную ренту.
Коэффициенты дисконтирования и наращения постоянной
непрерывной ренты можно получить из формул для p - срочной ренты при ![]() или по определению для
непрерывного равномерно выплачиваемого потока платежей с постоянной годовой
интенсивностью f (t) = 1.
или по определению для
непрерывного равномерно выплачиваемого потока платежей с постоянной годовой
интенсивностью f (t) = 1.
Например, для постоянной непрерывной ренты при непрерывном
начислении процентов по постоянной силе роста ![]() получаем:
получаем:
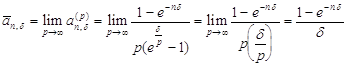 ,
,
где ![]() - коэффициент
дисконтирования обычной p - срочной ренты при непрерывном начислении
процентов.
- коэффициент
дисконтирования обычной p - срочной ренты при непрерывном начислении
процентов.
Заметим, что так как
![]() ,
,
где ![]() - коэффициент
дисконтирования p - срочной ренты пренумерандо при непрерывном
начислении процентов, то
- коэффициент
дисконтирования p - срочной ренты пренумерандо при непрерывном
начислении процентов, то
![]()
![]() .
.
Действительно, при непрерывно поступающих платежах различие между рентами пренумерандо и постнумерандо исчезает.
Коэффициент дисконтирования постоянной непрерывной ренты при начислении процентов 1 раз в год получим по определению:
![]() .
.
Коэффициенты наращения непрерывных рент можно найти из равенств вида:
![]() =
= ![]() ,
,
![]() =
= ![]() .
.
Соотношения между коэффициентами дисконтирования рассмотренных трех видов рент - обычной, пренумерандо и непрерывной - можно установить из следующих соображений.
Так как
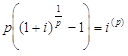 ,
,
где i (p) - эквивалентная годовая номинальная процентная ставка, то
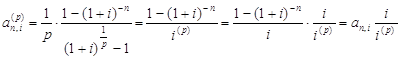 .
.
С другой стороны,
![]()
![]() .
.
Следовательно
![]()
![]() , (19)
, (19)
где ![]() ,
, ![]() - коэффициенты дисконтирования
обычной годовой ренты с начислением процентов 1 раз в год и постоянной
непрерывной ренты при непрерывном начислении процентов.
- коэффициенты дисконтирования
обычной годовой ренты с начислением процентов 1 раз в год и постоянной
непрерывной ренты при непрерывном начислении процентов.
Равенства (19) можно продолжить для ренты пренумерандо, если учесть соотношения коэффициентов дисконтирования обеих рент:
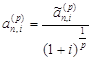 и
и ![]() .
.
Тогда
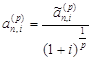 =
= ![]() =
= ![]() . (20)
. (20)
где ![]() - эквивалентная
учетная ставка.
- эквивалентная
учетная ставка.
Из (19), (20) получаем
![]() , (21)
, (21)
где 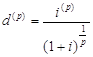 - эквивалентная
номинальная учетная ставка.
- эквивалентная
номинальная учетная ставка.
Каждое выражение в этом равенстве - современная стоимость процентов, выплачиваемых по займу 1 д. е. на протяжении n лет в соответствии с различными способами выплаты процентов.
Аналогичные соотношения можно получить и для коэффициентов наращения рент.
Если полагают, что срок ренты n = ∞, то ренту называют вечной. Наращенная сумма вечной ренты бесконечна. Однако современную величину такой ренты можно найти.
Для обычной вечной p - срочной ренты с начислением процентов 1 раз в год получаем при n → ∞:
![]() .
.
Для такой же ренты пренумерандо:
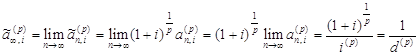 .
.
Кроме того, 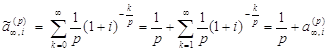 .
.
Таким образом, ![]() ,
, ![]() ,
, ![]() . (21)
. (21)
Если вечная рента является годовой (p = 1), то имеем:
![]() ,
, ![]() ,
, ![]() . (22)
. (22)
Если начало ренты, т.е. начало ее первого периода, переносится в будущее на t единиц времени относительно текущего момента t = 0, то такую ренту называют отсроченной. Современная стоимость отсроченной ренты At определяется следующим образом. Согласно определению современной стоимости потока платежей,
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() - дисконтные множители k
- го платежа на временных отрезках [0, tk], [t, tk],
[0, t] соответственно. Так как
- дисконтные множители k
- го платежа на временных отрезках [0, tk], [t, tk],
[0, t] соответственно. Так как ![]() , то A - стоимость
ренты, рассчитанная на момент начала ее первого периода, т.е. на момент начала
неотсроченной ренты.
, то A - стоимость
ренты, рассчитанная на момент начала ее первого периода, т.е. на момент начала
неотсроченной ренты.
Следовательно, A - это современная стоимость неотсроченной ренты.
Таким образом, современная стоимость отсроченной ренты определяется путем дисконтирования по процентной ставке ренты в течение времени t современной стоимости A неотсроченной ренты:
![]() , (23)
, (23)
Рассмотрим зависимость коэффициентов наращения ренты от срока ренты и процентной ставки.
Поскольку характер зависимости не должен зависеть от числа платежей в году, рассмотрим годовую обычную ренту с начислением процентов 1 раз в год.
Имеем ![]() ,
, ![]() .
.
Ситуацию можно рассматривать как беспроцентный долг, выданный в сумме n и возвращаемый равными долями в течение n лет.
Установим зависимость от i коэффициента наращения
ренты ![]() .
.
![]() .
.
Очевидно, ![]() - возрастающая
функция i, что следует из свойств наращенной суммы разового платежа. Действительно,
так как
- возрастающая
функция i, что следует из свойств наращенной суммы разового платежа. Действительно,
так как ![]() и
и ![]() , то
, то ![]() - возрастающая выпуклая
функция аргумента i (рис.1).
- возрастающая выпуклая
функция аргумента i (рис.1).
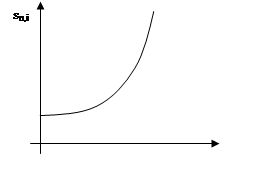 |
Рис.1.
3) Установим зависимость от i коэффициента
дисконтирования ренты ![]() .
.
![]() .
.
Очевидно, ![]() - убывающая
функция i, что следует из свойств современной стоимости разового платежа.
Действительно, так как
- убывающая
функция i, что следует из свойств современной стоимости разового платежа.
Действительно, так как ![]() и
и ![]() , то
, то ![]() - убывающая выпуклая
функция аргумента i (рис.2).
- убывающая выпуклая
функция аргумента i (рис.2).
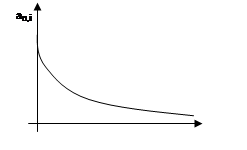
Рис. 2
Установим зависимость от n коэффициента наращения
ренты ![]() .
.
![]() , где
, где ![]() .
.
Так как ![]() и
и ![]() , то
, то ![]() - возрастающая выпуклая
функция аргумента n (рис.3).
- возрастающая выпуклая
функция аргумента n (рис.3).
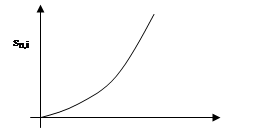
Рис. 3
Установим зависимость от n коэффициента
дисконтирования ренты ![]() .
.
![]() ,
,
где ![]() .
.
Так как ![]() и
и ![]() (вечная рента), то
(вечная рента), то ![]() - возрастающая вогнутая
функция аргумента n (рис.4).
- возрастающая вогнутая
функция аргумента n (рис.4).
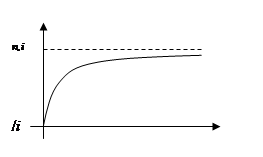
Рис.4
Эти свойства используются в задачах на определение параметров ренты.
Задача.
Раскрой материала.
На раскрой (распил) поступает материал нескольких видов в определенном количестве. Из этого материала необходимо изготовить различные изделия. Материал может быть раскроен разными способами. Каждый способ имеет свою себестоимость и позволяет получить разное количество изделий каждого вида. Определить способ раскроя, при котором суммарная себестоимость минимальна (построить математическую модель в общем виде).
Решение:
Пусть поступает в раскрой m различных материалов.
Требуется изготовить из них k разных комплектующих изделий (комплектов) в количествах, пропорциональных величинам b1, b2,., bk (условия комплектности).
Пусть каждую единицу j-го материала j=1,., m можно раскроить n различными способами, так что при использовании i-го способа раскроя, i=1,., n получим аij единиц k-го изделия.
Нужно определить такой план раскроя материалов, обеспечивающий максимальное количество комплектов, если имеющийся запас j-го материала составляет аj единиц.
Обозначим через xij количество единиц j-го материала, раскраиваемых i-м способом, а через x-общее количество изготавливаемых комплектов.
Математическая модель этой задачи имеет такой вид:
максимизировать x (1)
при условиях
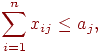
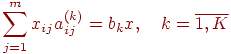
Условие 2 означает ограничение на запас j-го материала, а условие 3 - условие комплектности.
Список используемой литературы
1. Багриновский К. Матюшок В. Экономико-математические метода и модели: Учебник / К. Багриновский, В. Матюшок. - М.: Экономистъ, 1999. - 185с.
2. Бочаров П.П., Касимов Ю.Ф. Финансовая математика: Учебник / П.П. Бочаров, Ю.Ф. Касимов. - М.: Гардарики, 2002. - 624с.
3. Кузнецов Б.Т. Финансовая математика: Учебное пособие / Б.Т. Кузнецов. - М.: Экзамен, 2005. - 128с.
4. Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем. - М.: Дело, 1998. - 304с.
5. Лукашин Ю.П. Финансовая математика: Учебное пособие / Ю.П. Лукашин. - М.: МФПА, 2004. - 81с.
6. Малыхин В.И. Финансовая математика / В.И. Малыхин. - М.: Юнити - Дана, 2003. - 237с.
7. Меньшиков С. Рентабельность и рента / С. Меньшиков // Экономическое стратегии. - 2004. - №1. - с.28-31.
8. Четыркин Е.М. Финансовая математика / Е.М. Четыркин. - 4-е изд. - М.: Дело, 2004. - 400с.
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Ренты делятся на годовые и р-срочные, где р характеризует число выплат на протяжении года. Выше при анализе непрерывных потоков платежей предполагалось, что годовая сумма ренты R равномерно распределяется на протяжении года. |
Раздел: Рефераты по математике Тип: дипломная работа |
| Определение современной и будущей величины денежных потоков | |
|
Олег Лытнев Основные правила процентных вычислений, рассмотренные нами ранее, остаются неизменными и для совокупности платежей, однако возникает ... При заданных значениях R, n, i (j, d) наиболее высокий результат даст дисконтирование p-срочной ренты с 1 начислением процентов в год (m = 1). Самый низкий результат при этих же ... Причем изменение p дает относительно больший езультат, чем изменение m. То есть любая p-срочная рента даже с непрерывным начислением процентов (m = =) будет стоить дороже, чем ... |
Раздел: Рефераты по экономике Тип: реферат |
| Институт ренты в гражданском законодательстве | |
|
СОДЕРЖАНИЕ ВВЕДЕНИЕ 1. ОБЩАЯ ХАРАКТЕРИСТИКА ДОГОВОРА РЕНТЫ 1.1 Понятие и развитие рентных отношений 1.2 Понятие и правовая природа договора ренты 2 ... При отсутствии условия о выкупной цене в договоре постоянной ренты, по которому имущество передано за плату под выплату постоянной ренты, выкуп осуществляется по цене ... Этот вид договора ренты порождает срочные обязательства по выплате рентных платежей. |
Раздел: Рефераты по государству и праву Тип: дипломная работа |
| Финансовые расчеты | |
|
... htm Лекция 1 Базисные финансовые расчеты. Основная страница Лекция 1. Базисные финансовые расчеты. Начисление процентов по простой процентной ставке. Здесь R - член ренты, т.е. величина каждого годового платежа, p - число платежей в году, m - число начислений процентов в году, T - срок ренты в годах (время от начала ренты до ... При погашении долга равными срочными уплатами c платежами p раз в году с одновременной выплатой процентов параметры плана погашения определяются по формулам |
Раздел: Рефераты по финансам Тип: реферат |
| Договор ренты | |
|
Введение Договор ренты известен со средних веков. В литературе упоминаются две основные причины возникновения договора ренты в европейском ... При отсутствии условия о выкупной цене в договоре постоянной ренты, по которому имущество передано за плату под выплату постоянной ренты, выкуп осуществляется по цене ... Этот вид договора ренты порождает срочные обязательства по выплате, которые устанавливаются на период жизни получателя ренты. |
Раздел: Рефераты по теории государства и права Тип: реферат |