Курсовая работа: Методика вивчення логарифмічних рівнянь і нерівностей у старшій школі з використанням мультимедійних засобів навчання
ВІННИЦЬКИЙ ДЕРЖАВНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ
імені МИХАЙЛА КОЦЮБИНСЬКОГО
ІНСТИТУТ МАТЕМАТИКИ ФІЗИКИ І ТЕХНОЛОГІЧНОЇ ОСВІТИ
Кафедра алгебри і методики викладання математики
Курсова робота
Методика вивчення логарифмічних рівнянь і нерівностей у старшій школі з використанням мультимедійних засобів навчання
Студента Левковича
Миколи Олександровича
Науковий керівник
Михійленко Л.Ф.
Вінниця – 2010
Зміст
1. Вступ
2. Загальне використання мультимедійних засобів в навчальному процесі
3. Методика навчання розв'язання логарифмічних рівнянь та нерівностей
3.1 Логарифмічні рівняння
3.2 Логарифмічні нерівності
4. Фрагменти уроків з використанням мультимедійної дошки та проектора
Висновки
Список використаних джерел
1. Вступ
Ні в кого не виникає сумнівів, що інструментом створення якісно нової освіти є інноваційна діяльність. Чи варто використовувати мультимедійні засоби навчання в школі? Багато хто з педагогів відповідає на це запитання позитивно. У декого є заперечення філософського або чисто практичного характеру. Однак усі згодні з тим, що певна адаптація школи до комп'ютерного століття необхідна. Єдиної ж думки про те, якою вона повинна бути, на сьогодні не існує.
Тільки 45 хвилин проводиться урок, а вчителю треба зробити дуже багато: провести опитування, перевірити домашнє завдання, розібрати новий матеріал, закріпити його, розглянути приклади тощо. Так, при вивченні теми «Логарифмічні рівняння та нерівності», для забезпечення наочності, підтримки групових та індивідуальних форм в умовах класно-урочної системи, підвищення ефективності і динамічності уроку, активізації пізнавальної діяльності учнів незамінними помічниками вчителя стають мультимедійні засоби навчання.
Отже метою курсової роботи є розробка методики вивчення логарифмічних рівнянь та нерівностей в старшій школі з використанням мультимедійних засобів навчання.
Для досягнення мети було поставлено такі завдання:
опрацювати навчально-методичну літературу по даній темі;
підібрати теоретичний матеріал по темі «Логарифмічні рівняння та нерівності»;
з’ясувати за допомогою яких мультимедійних засобів можна покращити навчальний процес та охарактеризувати їх;
розробити уроки з використанням мультимедійних засобів навчання.
2. Загальне використання мультимедійних засобів в навчальному процесі
Мультимедіа – це спеціальна інтерактивна технологія, що забезпечує за допомогою технічних і програмних засобів роботу з анімованою комп’ютерною графікою і текстом, мовою, високоякісним звуком, нерухомими зображеннями і рухомим відео.
Найдоцільніше використовувати мультимедійні засоби навчання при виконанні таких педагогічних завдань: формування світогляду учнів, їх ідейних і моральних переконань; формування вмінь і навичок учнів, зокрема: виділяти головне, аналізувати, узагальнювати, порівнювати, класифікувати, конкретизувати, абстрагувати, систематизувати; формування спеціальних вмінь і навичок учнів в залежності від навчальних дисциплін; взаємозв’язок теорії і практики; засвоєння учнями складних тем.
Використання мультимеда в класно-урочній діяльності дозволяє педагогам зробити свої заняття емоційними та ефективними. Це дає можливість забезпечити заняття динамічною наочністю, збільшити кількість тренувальних завдань, збільшити темп виконання робіт учнями, диференціації їхньої діяльності, наявність зворотнього зв’язку, об’єктивність контролю, підвищення мотивації навчання.
Комп’ютер – це знаряддя, яке полегшує працю вчителя. Вчителеві необхідно творчо переглянути матеріали до уроків та методику їх викладу з точки зору насичення цих уроків мультимедійною інформацією, для того щоб зробити навчання не тільки динамічним, інформаційно насиченим, а й індивідуальним.
Найбільш ефективне використовування комп'ютера на уроках математики: при вивченні нового матеріалу (ілюстрація різноманітними наочними засобами; мотивація введення нового поняття; моделювання); при перевірці фронтальних самостійних робіт (швидкий контроль результатів); при рішенні задач повчального характеру (виконання малюнків, складання плану роботи; відробіток певних навиків і умінь); при організації дослідницької діяльності учнів; при інтеграції предметів природно-математичного циклу.
Вигідні особливості роботи з комп'ютерною підтримкою на уроці: учень стає суб'єктом навчання, бо програма вимагає від нього активного управління; легко досягається рівнева диференціація навчання; досягається оптимальний темп роботи учня, оскільки кожний учень виконує індивідуальне завдання, працюючи в своєму темпі; скорочується час при виробленні технічних навиків учнів; збільшується кількість тренувальних завдань; відстежуються помилки, допущені учнем, і повторно відпрацьовується недостатньо засвоєний матеріал; робота учня оцінюється відразу; при роботі з комп'ютером присутній елемент гри, у більшості дітей підвищується мотивація учбової діяльності.
На уроках математики в залежності від поставлених цілей використовують, як наприклад, такі програми:
Paint: побудова графіків функції, геометричних фігур їх дослідження; побудова у системі координат точок за їхніми координатами;
Test W: на початку вивчення теми для самоконтролю; для проведення контролю знань учнів; для самостійного створення учнями тестів до уроків в позаурочний час;
Microsoft Word: створення та використання математичних диктантів, блок – схем, таблиць, діаграм; використання редактора формул Microsoft Equation для запису математичних виразів.
Microsoft Exel: створення, форматування та друк таблиць даних; проведення розрахунків різної складності; побудова діаграм і графіків…
Однак для ефективного використання комп’ютера в класно – урочній системі навчання потрібно мати обладнаний комп’ютером спеціалізований кабінет, в якому є ще і спеціальні пристрої колективного призначення, наприклад мультимедійний проектор, інтерактивна дошка.
Інтерактивна дошка – сенсорний екран, приєднаний до комп’ютера. Зображення на дошку передається через проектор. Сучасні дошки для навчальних аудиторій: на них пишуть спеціальними маркерами, а написане зберігається в комп’ютерному файлі, який миттєво передається слухачам, записується на магнітні носії. Цими файлами можуть користуватися ті, хто не зміг бути присутнім на уроці.
Завдяки об’єднанню комп’ютера та інтерактивної дошки, викладачі отримали можливість об’єднати безумовні переваги комп’ютера з традиційними формами навчання. Викладач, проектуючи на інтерактивну дошку завдання, може викликати до неї одного чи навіть декількох учнів для публічного розв’язання задач; у випадку неправильної відповіді організувати дискусію або (якщо робота ведеться у складі локальної мережі) продемонструвати результати індивідуальної роботи учнів, доповнюючи їх своїми рукописними і графічними коментарями.
Види навчальної діяльності, котрі доступні при використанні електронної інтерактивної дошки: робота з текстом і зображеннями; створення приміток за допомогою електронних маркерів; збереження створених приміток для передачі їх засобами електронної пошти, разміщення в Internet; колективний перегляд Web-сайтів; вільне переміщення по класу під час демонстрації з використанням відповідного програмного забезпечення; демонстрація і нанесення приміток поверх навчальних відеокліпів; використання вбудованого в програмне забезпечення інтерактивної дошки презентаційного інструментарію для збагачення дидактичного матеріалу; демонстрація презентацій, створених учнями.
Інтерактивні дошки бувають прямої та оберненої проекцій. При прямій – проектор розміщують перед дошкою на підставці або на стільці. При оберненій – проектор встановлюють за дошкою.
Сенсорні технології в інтерактивних дошках реалізуються двома способами. Сенсорна резистивна інтерактивна дошка складається із двох прошарків тонких провідників, які реагують на дотик до поверхні екрану. Використовуючи разом з інтерактивною дошкою інші засоби інтерактивних технологій, наприклад, графічний планшет, викладач може одночасно залучити до активної роботи кількох учнів. При наявності локальної мережі та налагодженій роботі електронної пошти чи FTP можна інтенсивно використовувати графічні планшети для підготовки ескізів малюнків до пояснення нового матеріалу чи перевірити виконання домашнього завдання, пов’язаного з побудовою графіків, створенням креслень, схем, ескізів, зображень тощо.
Перед освітою стоїть проблема підготувати сучасної людини до життя у швидко мінливому інформаційному суспільстві. В умовах інформаційно-комунікаційних та мультимедійних технологій результатом навчання є нова якість особистості інформаційно-комунікативна компетентність (ІКК), яка має стати потребою, природним стереотипом поведінки сучасної людини.
Виникає необхідність використання освітніх, розвиваючих можливостей інформаційно-комунікаційних технологій, можливості їх інтеграції з основним освітнім процесом. Інформаційно-методичні вміння педагога повинні відображати нерозривна єдність ефективної методичної діяльності з використанням інформаційно-комунікаційних технологій (ІКТ) в предметній методикою. Освітній процес, що інтегрує комп'ютерні та педагогічні технології, забезпечує формування ІКК тих, хто навчається, сприяє розкриттю можливостей мультимедіа технологій для викладання навчальних предметів, забезпечує не лише навчання, а самостійну діяльність з оволодіння знаннями; формування усвідомлених мотивів навчання.
У той же час відзначений низький рівень мотивації багатьох педагогів шкіл до використання різних видів інформаційної діяльності в предметних методиках навчання, що пов'язано, зокрема, з відсутністю позитивного суб'єктивного досвіду в проектуванні та використання засобів ІКТ, у тому числі мультимедіа технологій.
Слід зазначити, що використання мультимедійних технологій на уроках математики дозволяє зробити процес навчання цікавим, наочним, розвиває творчу діяльність учнів, їх абстрактне та аналітичне мислення; дозволяє здійснювати пошук інформації на електронних носіях та в мережі Інтернет, проходити on-line тестування, що є ефективним засобом формування інформаційно-комунікативних компетенцій учнів. Використання комп'ютерних технологій у курсі алгебри дає можливість проводити дослідницькі роботи на з'ясування і встановлення різних закономірностей, взаємозв'язків об'єктів (наприклад, при дослідженні властивостей функцій). Сучасний вчитель повинен не тільки володіти знаннями в галузі ІКТ, а й бути фахівцем із застосування нових технологій у своїй професійній діяльності. Сьогодні основою організації самостійної роботи учнів є не тільки традиційна навчальна література, але всі можливі види електронних баз знань: навчальні та тестуючі програмні комплекси на CD-RAM і DVD-RAM, розроблені вченими-фахівцями, вчителями-предметниками.
ІКТ виступають тут як інструмент дослідження, як джерело додаткової інформації, як спосіб самоосвіти.
У навчанні особливий акцент ставиться сьогодні на власну діяльність учня з пошуку, усвідомлення й переробці нових знань. Вчитель виступає як організатор процесу навчання, керівник самодіяльності учнів, що надає їм потрібну допомогу і підтримку. Як стверджували відомі філософи «Поганий учитель підносить істину, хороший вчить її знаходити» (А. Дістервега), завдання вчителя - «навчити вчитися», «не наповнити посудину», а «запалити факел» (Сократ).
3. Методика навчання розв’язання логарифмічних рівнянь та нерівностей
3.1 Логарифмічні рівняння
При введенні поняття логарифму і властивостей логарифмічної функції необхідно значну увагу приділити вмінню застосовувати основну логарифмічну тотожність, а також формулу переходу від однієї основи логарифма до іншої.
Приступаючи до розв’язування логарифмічних рівнянь, треба враховувати, що всі властивості логарифмічної функції були доведені за умови, що вирази, які стоять під знаком логарифма, додатні.
Наприклад,
![]()
тільки при
![]() і
і ![]() .
.
Якщо ж у рівнянні
або нерівності знаходиться вираз-добуток ![]() , то він буде додатнім не тільки
тоді, коли
, то він буде додатнім не тільки
тоді, коли ![]() і
і
![]() додатні,
але й тоді,, коли
додатні,
але й тоді,, коли ![]() та
та ![]() будуть одночасно від’ємні. У
цьому випадку формулу «логарифм добутку» не використовують, бо можлива втрата
коренів.
будуть одночасно від’ємні. У
цьому випадку формулу «логарифм добутку» не використовують, бо можлива втрата
коренів.
Структура рівносильних перетворень рівнянь.
Область визначення.
Обмеження, які необхідні для гарантування прямих і обернених перетворень.
Відповідні властивості числових рівностей або властивості відповідних функцій.
Як бачимо, щоб виконувані перетворення були рівносильні, необхідно, щоб виконувалися і обернені перетворення на області визначення даного рівняння.
Бажано по можливості не використовувати формули логарифмування добутку, частки, і парного степеня, якщо це призводить до звуження області визначення рівняння, а користуватися цими формулами тільки справа наліво, що приводить до розширення області визначення (в цьому випадку можлива хіба що поява сторонніх коренів, але їх можна відсіяти перевіркою).
Приклад: Розв’язати рівняння
![]() (1).
(1).
Розв’язання: На
області визначення рівняння 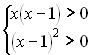 це рівняння рівносильне рівнянню
це рівняння рівносильне рівнянню
![]() (2)
(2)
яке в свою чергу рівносильне рівнянню
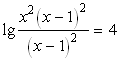 (3)
(3)
Усі перетворення
рівносильні, бо на області визначення даного рівняння можна виконувати
перетворення (1) - (2) - (3) і обернені перетворення (3) - (2) - (1).
Скоротивши в рівнянні (3) дріб на ![]() (
(![]() на області визначення), дістанемо
рівносильне рівняння:
на області визначення), дістанемо
рівносильне рівняння:
![]() (4).
(4).
Це рівняння за означенням логарифма рівносильне рівнянню
![]() (5).
(5).
Звідси ![]() . Оскільки ці
значення входять в область визначення рівняння і ніяких додаткових обмежень у
нас не було, то
. Оскільки ці
значення входять в область визначення рівняння і ніяких додаткових обмежень у
нас не було, то ![]() - корені даного рівняння.
- корені даного рівняння.
Слід звернути увагу учнів на те, що при розв’язуванні логарифмічних рівнянь можна користуватися не тільки рівносильними перетвореннями, але й діставати рівняння-наслідки (коли ми гарантуємо тільки прямі перетворення і не гарантуємо обернені). Учні повинні розуміти, що при використанні рівнянь-наслідків можлива поява стороніх коренівь і тому в цьому випадку перевірка є складовою частиною розв’язування рівняння.
Слід звернути увагу учнів на те, що певної акуратності потребує використання формули переходу від однієї основи до іншої:
![]()
де ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Якщо ![]() і
і ![]() -числа, що
недорівнюють одиниці, то цю формулу можна застосовувати і зліва направо і
справа наліво (при
-числа, що
недорівнюють одиниці, то цю формулу можна застосовувати і зліва направо і
справа наліво (при ![]() ), тобто використання цієї формули
при розв’язуванні рівнянь або нерівностей приводить до рівняння (нерівності),
рівносильного даному. Якщо ж новою основою логарифма є вираз із змінною, то
може виявитися, що цей вираз на області визначення початкового рівняння
дорівнюватиме одиниці, а після застосування формули переходу від однієї основи
до іншої вираз, що стоїть в основі логарифма, вже не дорівнюватиме одиниці. В
цьому випадку застосування формули переходу від однієї основи до іншої може
привести до втрати тих коренів початкового рівняння, для яких нова основа логарифма
дорівнює одиниці.
), тобто використання цієї формули
при розв’язуванні рівнянь або нерівностей приводить до рівняння (нерівності),
рівносильного даному. Якщо ж новою основою логарифма є вираз із змінною, то
може виявитися, що цей вираз на області визначення початкового рівняння
дорівнюватиме одиниці, а після застосування формули переходу від однієї основи
до іншої вираз, що стоїть в основі логарифма, вже не дорівнюватиме одиниці. В
цьому випадку застосування формули переходу від однієї основи до іншої може
привести до втрати тих коренів початкового рівняння, для яких нова основа логарифма
дорівнює одиниці.
Підсумовуючи ці міркування, робимо висновки: якщо при переході від однієї основи логарифмів до іншої нова основа - число (звичайно більше від нуля і не дорівнює одиниці), то дістанемо рівняння, рівносильне даному на його області визначення.
Якщо доводиться використовувати вираз із змінною як нову основу логарифма, то щоб не втратити корені рівняння, необхідно розглядати два випадки:
вираз, який береться як нова основа, дорівнює одиниці (якщо це можливо на області визначення розглядуваного рівняння), і перевіряємо, чи будуть ці значення змінної, при яких вираз дорівнює одиниці, коренями даного рівняння;
нова основа не дорівнює одиниці - в цьому випадку користаємося формулою переходу від однієї основи логарифма до іншої.
Бажано звернути
увагу учнів на те, що деякі логарифмічні рівняння, які зведені до вигляду ![]() можна
розв’язати за допомогою розкладання лівої частини рівняння на множники.
можна
розв’язати за допомогою розкладання лівої частини рівняння на множники.
Досить часто зустрічаються рівняння, члени яких є степенями, в яких основа і показник степеня - функції від змінної величини.
Приклад: Розв’язати рівняння
![]() .
.
Розв’язання:
Область визначення: ![]() . Тоді ліва і права частини цього
рівняння додатні на області визначення. Прологарифмуємо обидві частини за
основою 4:
. Тоді ліва і права частини цього
рівняння додатні на області визначення. Прологарифмуємо обидві частини за
основою 4:
![]() .
.
Дістаємо рівняння, рівносильне даному на області визначення:
![]() .
.
Позначимо ![]() і, врахувавши,
що
і, врахувавши,
що ![]() ,
маємо:
,
маємо:
![]()
Звідки ![]() або
або ![]() .
.
Тоді ![]() або
або ![]() . Отже,
. Отже,
![]() або
або ![]() .
.
Оскільки ці
значення входять до області визначення, то ![]() і
і ![]() - корені даного рівняння.
- корені даного рівняння.
Підводячи підсумки розв’язування цього рівняння, бажано звернути увагу учнів на те, що в цьому рівнянні (в його лівій частині) змінна входить і в основу, і в показник степеня. Доцільно зафіксувати в зошитах учнів, що рівняння, в якому змінна входить і в основу, і в показник степеня, найчастіше розв’язується логарифмуванням обох частин рівняння.
Слово «найчастіше» присутнє в наведеному правилі в зв’язку з рівняннями типу:
![]() .
.
На його області
визначення ![]() це
рівняння рівносильне рівнянню:
це
рівняння рівносильне рівнянню:
![]() ,
,
яке за основною логарифмічною тотожністю рівносильне (на області визначення) рівнянню
![]() .
.
Звідси ![]() (не входить до
області визначення) або
(не входить до
області визначення) або ![]() (входить до області визначення і
є коренем).
(входить до області визначення і
є коренем).
Після
відпрацювання цього правилу на прикладах доцільно запропонувати учням більш
загальний підхід (він, як правило, використовується тоді, коли немає можливості
взяти логарифм від обох частин рівняння) - перехід від степеня, в основі якого
стоїть вираз із змінною, до степеня з числовою основою ![]() за формулою
за формулою
![]() , де
, де ![]() ,
, ![]() .
.
Зауваження.
Очевидно, що при ![]() цю формулу можна застосовувати як
зліва направо, так справа наліво. Якщо ми використаємо цю формулу при
розв’язуванні рівняння, на області визначення якого
цю формулу можна застосовувати як
зліва направо, так справа наліво. Якщо ми використаємо цю формулу при
розв’язуванні рівняння, на області визначення якого ![]() , то ми гарантуємо і прямі, і
обернені перетворення, тобто гарантуємо рівносильність утвореного рівняння на
області визначення даного.
, то ми гарантуємо і прямі, і
обернені перетворення, тобто гарантуємо рівносильність утвореного рівняння на
області визначення даного.
Необхідно
звернути увагу учнів на те, що ідея логарифмування обох частин рівняння (або
нерівності) є досить плідною і може використовуватись для розв’язування різних
типів рівнянь (нерівностей), починаючи з найпростіших показникових типу ![]() (за означенням
логарифма або прологарифмувавши обидві частини за основою 2, маємо:
(за означенням
логарифма або прологарифмувавши обидві частини за основою 2, маємо:
![]() , тобто
, тобто ![]() ).
).
Враховуючи те, що в останні 40-50 років у старших класах середньої школи реалізується функціональний підхід до рівняння, будемо вважати, що степені, в яких і основа, і показник степеня є функціями від змінної величини, означені тільки для тих значень змінних, при яких їх основи додатні (якщо в самій умові задачі не сказано протилежне).
3.2 Логарифмічні нерівності
Розв’язуючи логарифмічні нерівності, доцільно використати загальну схему рівносильних перетворень нерівностей. Ця схема іноді дає надмірну систему обмежень, яку можна суттєво спростити. Для рівносильності рівнянь надмірність системи обмежень майже не впливає на об’єм роботи щодо розв’язування цих рівнянь - можна не знаходити відповідні значення змінної з цих обмежень, а тільки перевіряти для кожного знайденого кореня. Розв’язком нерівності, як правило, є інтервал (або кілька інтервалів), які містять нескінчену множину чисел, а всі їх перевірити неможливо. Отже для розв’язування нерівності доведеться знаходити відповідні значення змінної з усіх записаних обмежень, і тому чим менше залишиться цих обмежень, тим краще. Бажано запропонувати учням не знаходити окремо область визначення нерівності, а спочатку записувати повну систему обмежень і рівносильну нерівність, а потім намагатися спростити утворену систему.
Приклад: Розв’язати нерівність
![]()
Розв’язання:
Оскільки ![]() ,
то
,
то ![]() . Тоді
функція
. Тоді
функція ![]() -
спадна, і наша нерівність рівносильна системі:
-
спадна, і наша нерівність рівносильна системі:
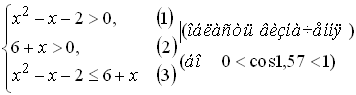
Нерівність (2) є
наслідком нерівностей (3) і (1) ![]() . Отже, ця система рівносильна
системі, що складається тільки з нерівностей (1) і (3), тобто
. Отже, ця система рівносильна
системі, що складається тільки з нерівностей (1) і (3), тобто
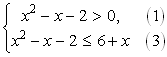
Розв’язуючи окремо нерівності (1) і (3), дістаємо: для
(1) - ![]() ;
;
для (3) - ![]() .
.
Тоді загальним розв’язком системи буде
![]() .
.
Слід звернути увагу учнів на те, що при розв’язуванні логарифмічних нерівностей можна використовувати всі ті прийоми, які використовувалися при розв’язуванні логарифмічних рівнянь.
Розв’язування деяких нерівностей за допомогою рівносильних перетворень досить громіздке, і тому використовуємо для розв’язування деяких нерівностей узагальнений метод інтервалів.
Приклад: Розв’язати нерівність.
![]()
Розв’язання: Методом інтервалів.
Область визначення.
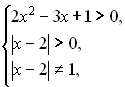 тобто
тобто 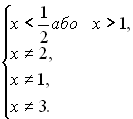
Корені
![]() .
.
Це рівняння на області визначення рівносильне рівнянню
![]() .
.
Звідки ![]() або
або ![]() (входять до
області визначення).
(входять до
області визначення).
Позначимо корені на області визначення (на малюнку) і знайдемо знак у кожному інтервалі, на які розбивається область визначення.
+ - + - - +
0 ![]() 1
1 ![]() 2 3
2 3
Відповідь: ![]()
4. Фрагменти уроків з використанням мультимедійної дошки та проектора.
1.Запускаємо слайд, на якому учням повідомляється тема і мета заняття.

2. математичний диктант (показуємо слайд, а учні самостійно записують відповіді на листочках)

3. наступний слайд учні та вчитель розглядають усно

4. далі вчитель пропонує учням по черзі виходити і на мультимедійній дошці розв’язувати завдання.

5. далі хтось один розв’язує рівняння біля дошки а всі інші – в зошитах




Бачимо що в даному фрагменті значно економиться час на диктовку завдань учням – вони розв’язують вже записані завдання.
При перевірці домашнього завдання можна використовувати Графопроектор (кодоскоп). На приклад, домашнім завданням було розв’язати нерівність:
![]() .
.
Одразу показуємо розв’язання і учні звіряють чи правильно вони розв’язали дану нерівність.

При поясненні нового матеріалу (приклад слайду):

Сьогодні нові інформаційні технології міцно увійшли в усі сфери життєдіяльності нашого суспільства. Інформатизація освіти є одним із пріоритетних напрямків програми розвитку освіти. При цьому очевидно, що завдання інформатизації освіти не можна звести тільки до завдання наповнення шкільних класів сучасною обчислювальною технікою. Поява в ліцеї комп'ютерного та математичного класів має вплинути на весь процес навчання. Використання комп'ютерної техніки та інформаційних технологій значно підвищує ефективність процесу навчання завдяки його індивідуалізації, зворотному зв'язку, розширенню наочності. Сьогодні інформаційні технології розкривають матеріал так, як це неможливо зробити за допомогою традиційних технологій. Існують різні форми використання новітніх інформаційних технологій, але найпростішою з них є презентація, коли комп'ютер відіграє роль і дошки, і підручника, і дидактичного посібника. Використання цієї форми дає низку переваг:
можливість забезпечити учневі індивідуальний режим роботи;
можливість представити різну інформацію кожному учневі в різному вигляді;
великі можливості оформлення інформації: використання широкої кольорової гами при оформленні слайдів, різноманітних шрифтів і, звичайно, ефекти анімації; ,..
оптимізація роботи вчителя при підготовці уроку (організація уроків, які потребують великої кількості дидактичного матеріалу — ілюстрацій, схем, діаграм), при проведенні контролю знань (одночасно дозволяє використовувати різні види контролю і перевірки знань: тести, завдання знайти помилку у тексті, продовжити речення тощо).
Висновки
Отже використання комп'ютерних технологій на уроках математики дозволяє зробити процес навчання цікавим, наочним, дозволяє здійснити індивідуальний і диференційований підхід з боку вчителя.
У курсі алгебри використання комп'ютерних технологій (КТ) дає можливість проводити дослідницькі роботи на з'ясування і встановлення різних закономірностей. Високий рівень наочності забезпечує більшу успішність при поясненні нового матеріалу. Використання КТ дозволяє підвищити ефективність навчання, раціонально використовувати навчальний час, з'являється можливість по-новому реалізовувати міжпредметні зв'язки.
При проведені дослідження були виконані такі завдання:
1. Була опрацьована навчально–методична література по даній темі;
2. Підібраний теоретичний матеріал по темі «Логарифмічні рівняння та нерівності»;
3. Розглянуті основні методи та прийоми викладу матеріалу;
4. Досліджено доцільність та необхідність використання мультимедійних засобів навчання та їх вплив на навчальний процес;
5. Були розроблені фрагменти уроків по даній темі з використанням мультимедійних засобів навчання.
Список використаних джерел
1. Слєпкань З.І. Методика навчання математики. – К.,: «Зодіак-ЕКО», 2000.
2. Інтерактивні технології на уроках математики: Навч. - метод. Посібник / Упоряд. І.С. Маркова – Х.: Вид. група «Основа». 2007 – 126с.
3. Урок математики в сучасних технологіях: теорія і практика: Метод проектів. Комп’ютерні технології. Розвивальне навчання / Упоряд. І.С. Маркова – Х.: Вид. група «Тріада». 2007 – 171с.
4. Урок математики в сучасних технологіях: теорія і практика: Розвиток критичного мислення: Навч. – метод. посібник / Упоряд. І.С. Маркова – Х.: Вид. група «Основа». 2007 – 125с
5. Капіносов А.М. Основи технології навчання. Проектуємо урок математики – Х.: Вид. група «Основа». 2006.–140с.
6. Кларин М.В. Интерактивное обучение – инструмент освоения нового опыта // Педагогика. – 2000. – № 7. – с. 12–18.
7. Пометун О.І, Пироженко Л.В. Інтерактивні технології навчання: теорія, практика, досвід. – К., 2002.
8. Пометун О.І., Пироженко Л.В. Сучасний урок. Інтерактивні технології навчання: Наук.-метод. пос. – К.: Вид-во А.С.К., 2003. – 192 с.
9. Систематизація методів розв’язування показникових і логарифмічних рівнянь і нерівностей/ Т.І. Іванко // Математика в школах України.- 2007. – березень (№ 7). С. 16-21.
10. Логарифмічні рівняння // Математика. – 2004. – квітень (№ 14). с 7-10.
11. Логарифмічні та показникові нерівності // Математика в школі. – 2004. - № 1. с.20-22.
12. Розв’язування логарифмічних нерівностей / Н.М. Повзло // Математика в школах України. – 2006. – квітень (№ 11). с. 7-17.
| Формування у другокласників умінь розв"язувати складені задачі | |
|
... національний педагогічний університет імені Володимира Гнатюка Кафедра природничих і математичних дисциплін та методики їх викладання ДИПЛОМНА РОБОТА Так, "під час розв'язування будь-якої задачі учень виконує аналіз: відокремлює запитання від умови, виділяє дані і шукані числа; складаючи план розв'язання, він виконує синтез ... Враховуючи вимоги, які ставляться щодо проблемного навчання, вчитель має спрямовувати учнів на самостійне розв'язування задач за допомогою відповідних підготовчих вправ чи засобів ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Теоретичні основи та актуальні проблеми сучасної дидактики | |
|
В.О. ВИХРУЩ ТЕОРЕТИЧНІ ОСНОВИ ТА АКТУАЛЬНІ ПРОБЛЕМИ СУЧАСНОЇ ДИДАКТИКИ Тернопіль 1997 Рекомендовано Вченою Радою Тернопільського експериментального ... Використання проблемних ситуацій пов"язано з різними ступенями активності вчителя і учня залежно від змісту пропонованої проблеми та методики її розв"язання. Організаційна цілісність і завершеність уроку полягає в тому, що він починається і закінчується в чітко визначений час; учні і вчителі готуються до у року; роботу учнів вміло ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Формування в учнів умінь розв"язувати задачі на рух | |
|
Зміст Вступ 1. Теоретичні основи розв"язування задач на рух 1.1 Роль задач у початковому курсі математики 1.2 Місце задач на рух у системі складених ... А тому "важливе значення для розв'язування текстових задач у навчальному процесі має ретельний добір навчальних завдань, які мають відповідати певним загально-методичним вимогам ... Звичайно, вчитель рекомендує дітям працювати самостійно, але учень у будь-який час може побачити запис розв'язання чи почути пояснення ходу розв'язування і звірити його зі своїм ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Методика роботи над простими задачами, що розкривають конкретний зміст ... | |
|
Зміст Вступ Розділ 1. Теоретичні основи дослідження процесу опрацювання простих арифметичних задач 1.1 Сутність і особливості процесу розв"язування ... Найпростіша символіка вводиться в початковій школі (знаки дій, рівності та нерівності, дужки, знаки кута, паралельності і т.д.). Правильному використанню символів слід вчити ... Важливе значення для розв'язування простих задач, що розкривають конкретний зміст арифметичних дій, має ретельний добір навчальних завдань, які мають відповідати певним загально ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| ... пізнавальної діяльності учнів в процесі навчання математики | |
|
ЗМІСТ Вступ Розділ 1. Теоретичні основи активізації пізнавальної діяльності учнів 9 класу основної школи в процесі навчання математики 1.1 Зміст та ... Евристична самостійна робота спрямована на навчання учнів пошуковій діяльності, виявленню залежностей між знаннями, пошуку нового способу розв"язування задач та розв"язанню ... В ході експерименту здійснювалась цілеспрямована робота з активізації пізнавальної діяльності учнів при розв"язуванні математичних задач фінансового змісту на уроках математики. |
Раздел: Рефераты по педагогике Тип: дипломная работа |