Курсовая работа: Механизм поперечно-строгального станка
Кафедра «Основы проектирования машин»
Тема
Механизм поперечно-строгального станка
Содержание
1 СИНТЕЗ РЫЧАЖНОГО МЕХАНИЗМА
1.1 Структурный анализ механизма
1.2 Определение недостающих размеров
1.3 Определение скоростей точек механизма
1.4Определение ускорений точек механизма
1.5 Диаграмма движения выходного звена
1.6 Определение угловых скоростей и ускорений
1.7 Определение ускорений центров масс звеньев механизма
1.8 Аналитический метод расчёта
2 СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА
2.1 Определение сил инерции
2.2 Расчёт диады 4-5
2.3 Расчёт диады 2-3
2.4 Расчет кривошипа
2.5 Определение уравновешенной силы методом Жуковского
2.6 Определение мощностей
2.7 Определение кинетической энергии и приведённого момента инерции механизма
3 ГЕОМЕТРИЧЕСКИЙ РАСЧЁТ ЗУБЧАТОЙ ПЕРЕДАЧИ, ПРОЕКТИРОВАНИЕ ПЛАНЕТАРНОГО МЕХАНИЗМА
3.1 Геометрический расчёт зубчатой передачи
3.2 Определение передаточного отношения планетарной ступени и подбор чисел зубьев колёс
3.3 Определение частот вращения зубчатых колёс аналитическим методом
4 СИНТЕЗ И АНАЛИЗ КУЛАЧКОВОГО МЕХАНИЗМА
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
4.2 Построение профиля кулачка
4.3 Определение максимальной линейной скорости и ускорения толкателя
5 СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Введение
Поперечно-строгальный станок предназначен для строгания плоских поверхностей.
Привод станка состоит из простой зубчатой передачи и планетарной передачи, который соединен с электромотором.
Резание металла осуществляется резцом, установленным в резцовой головке, закреплённой на ползунке, при рабочем ходе ползунка.
Кривошип жёстко соединен с зубчатым колесом. Во время перебега в конце холостого хода осуществляется перемещение стола с заготовкой на величину подачи с помощью храпового механизма и кулачкового механизма, кулачёк которого жестко соединен с зубчатым колесом.
При проектировании профиля кулачка необходимо обеспечить заданный закон движения толкателя.
1 Синтез и анализ рычажного механизма

Исходные данные: lo1o2=460мм ; H=460мм ; nкр=70 мин-1 ; К=1,5;
1.1. Структурный анализ механизма :
Степень подвижности механизма:
![]() ;
;
где к=5 – число подвижных звеньев,
p1=7 – число одноподвижных кинематических пар,
p2=0 – число двухподвижных кинематических пар.
![]()
![]()
Разложение механизма на структурные группы Асура
Формула строения механизма:
I(0;1)→ II2(2;3)→II2(4;5)
Механизм II класса , второго порядка.
1.2. Определение недостающих размеров:
Угол размаха кулисы:
![]()
![]()
Длина кривошипа:
![]()
![]()
Длина кулисы:
![]()
![]()
![]()
![]()
Масштабный коэффициент построения схемы :
![]()
![]()
Строим 12 планов механизма , приняв за начало отсчета крайнее положение, соответствующее началу рабочего хода механизма.
1.3 Определение скоростей точек механизма.
Скорость точки А кривошипа определяем по формуле :
![]() ,
,
где ![]() , где nкр=70мин-1
, где nкр=70мин-1
![]()
![]()
Планы скоростей строим в масштабе :
![]()
![]()
Скорость точки А’ находим графически , решая совместно систему :

На плане Рvа’=30мм . Абсолютная величина скорости точки А’ :
![]()
![]()
![]()
![]()
Скорость точки В находим из соотношения :
![]() , откуда
, откуда ![]()
![]()
![]()
Абсолютная величина скорости точки В :
![]()
![]()
Скорость точки С определим, решая совместно систему :

На плане Рvс=34мм. Абсолютная величина скорости точки С :
![]()
![]()
![]() , на плане
, на плане ![]() =14мм
=14мм
![]()
Для всех остальных положений скорости определяем аналогично.
Полученные результаты сводим в таблицу 1.1
Таблица 1.1.- Значения скоростей
| Скоростим/с | Положения механизма | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|
va |
1.03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 | 1,03 |
|
va’ |
0,6 | 1,02 | 1,2 | 1,26 | 1,1 | 0,7 | 0.16 | 0,56 | 1.1 | 1,24 | 0,64 | 1,32 |
|
vb |
0,88 | 1,32 | 1,5 | 1,6 | 1,43 | 0,92 | 0,26 | 1,18 | 2,5 | 2,8 | 1,3 | 0 |
|
vc |
0,68 | 1,24 | 1,5 | 1,6 | 1,48 | 0,92 | 0,32 | 1,4 | 2,54 | 2,8 | 1 | 0 |
1.4 Определение ускорений точек механизма.
Пересчетный коэффициент С :
![]()
![]()
Ускорение точки А конца кривошипа определяем по формуле:
![]()
![]()
Ускорение аа направлено по кривошипу к центру вращения О1.
Выбираем масштабный коэффициент ускорений:
![]()
![]()
На плане ускорений изображаем ускорение точки А отрезком Раа=55мм
Ускорение точки А’ определяем, решая совместно систему:

Кориолисово ускорение:
![]()
![]()
![]()
 ;
; ![]()
![]()
![]()
![]()
По свойству подобия определяем ускорение точки В :
![]() ;
; ![]()
![]()
![]()
![]()
Система уравнений для определения ускорений точки С:

![]() , откуда
, откуда ![]()
![]()
![]()
![]()
![]()
![]()
Ускорения всех точек найдены. Ускорения для остальных положений механизма находим аналогично . Значения ускорений сводим в таблицу
Таблица 1.2. – Значения ускорений
|
Ускорения м/с2 |
Положения механизма | ||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 12 | |
|
аа |
7,5 | 7,5 | 7,5 | 7,5 | 7,5 | 7,5 | 7,5 |
|
аА’ |
3,8 | 2,5 | 2,6 | 6,4 | 8,5 | 10,3 | 7,5 |
|
ab |
5,7 | 3,4 | 3,8 | 10,5 | 19,3 | 21,4 | 11 |
|
ac |
5,8 | 2,1 | 1,7 | 10,5 | 16,1 | 20,8 | 11,7 |
1.5 Диаграммы движения выходного звена.
Диаграмму перемещения строим , используя полученную из S-t плана механизма траекторию движения точки С.
Диаграммы скорости V-t и ускорений A-t строим из полученных 12 планов скоростей и 7 планов ускорений.
Масштабные коэффициенты диаграмм:
![]()
![]()
![]()
![]() ,
,
где хt=180 мм
![]()
![]()
![]()
1.6 Определение угловых скоростей и ускорений
Угловые скорости и ускорения звеньев механизма определяются для первого положения
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
1.7. Определение ускорений центров масс звеньев механизма
Ускорение центров масс звеньев определяем из планов ускорений:
![]()
![]()
![]()
![]()
1.8 Аналитический метод расчета

![]()
1. Расчет ведется для первого положения кулисы:
![]()
![]()
2. В проекциях на координатные оси:
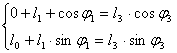
![]()
3. Поделим второе уравнение на первое:
![]()
![]()
![]()
![]()
4. Передаточное отношение U31:
![]()
![]()
5. Передаточная функция ускорений U’31:
![]()
![]()
6. Угловая скорость кулисы:
![]()
7. Угловое ускорение кулисы:
![]()
8. Уравнение замкнутости верхнего контура в проекциях на оси:
![]()
 (1)
(1)
9. Решая совместно два уравнения находим sinφ4:
![]()
![]()
10 . Дифференцируем уравнения (1) по параметру φ1:
 (2)
(2)
где ![]() и
и ![]() - соответствующие передаточные
отношения.
- соответствующие передаточные
отношения.
11. Передаточное отношение U43 и угловая скорость ω4:
![]()
![]()
12. Передаточное отношение U53:
![]()
13. Дифференцируем уравнение по параметру φ3:
 (3)
(3)
где ![]() и
и ![]()
14. Из второго уравнения системы (3) определяем U’43:
![]()
15. Из первого уравнения системы (3) находим U’53:
![]()
![]()
16. Скорость и ускорение точки С выходного звена:
![]()
![]()
![]()
1.9 Расчет на ЭВМ
Program kulise1;
User crt;
Const
h=0.;
l0=0.456;
l1=0.143;
shag=30;
w1=7.33;
a=0.270;
var
f1, w3, e3, vb, ab, u53, u53_, u31_:real;
cosf3, tgf3, sinf3: real;
begin
write (`,Введите угол в градусах`);
read(f1);
repeat
w3:=w1*((sqr(l1)+l0*l1*sin(f1))/(sqr(l1)+sqr(l0)+2*l0*l1-*sin(f1)));
u31_;=l0*l1*cos(n)*(sqr(l0)-sqr(l1))/(sqr(sqr(l1)+sqr(l0)+2*l0*l1*sin(f1)));
E3:=sqr(w1)*u31_;
cosf3:=sqrt((sqr(l1)*sqr(cos(f1)))/(sqr(l1)+sqr(l0)+2*l0*l1*sin(f1)));
tgf3:=(l0+l1*sin(f1))/(l1*cos(f1));
sinf3:=tgf3/sqrt(1+sqr(tgf3));
u53:=-(a/(sqr(sinf3)));
u53_:=(2*a*cosf3)/(sqr(sinf3)*sinf3);
Ab:=sqr(w3)*u53_+E3*u53;
Writeln(`’Скорость Vb=`, Vb=`,Vb:3:4);
Writeln(`’Ускорение Ab=`, Ab=`,Vb:3:4);
Decay(10000)
Writein;
F1:=F1+Shag;
Until F1>=
End.
| Положения | Скорости | Ускорения |
| 0 | 0 | 76,6 |
| 1 | 35,963 | 49,8936 |
| 2 | 63,5161 | 30,9 |
| 3 | 80,1509 | 18,5649 |
| 4 | 86,5 | 0 |
| 5 | 85,3494 | -7,3299 |
| 6 | 77,2378 | -14,32 |
| 7 | 56,7787 | -63,818 |
| 8 | 0 | 200,7 |
| 9 | -132,198 | -273,396 |
| 10 | -260 | 0 |
| 11 | -94,5398 | 272,2544 |
Планы скоростей и ускорений:

Рис. 3 – Диаграмма скоростей

Рис. 4 – Диаграмма ускорений
2 Силовой анализ механизма
Исходные данные:
вес кулисы ![]() кг;
кг;
вес шатуна ![]() кг;
кг;
вес ползуна ![]() кг.
кг.
2.1 Силы тяжести и силы инерции
Силы тяжести:
![]() Н
Н
![]() Н
Н
![]() Н
Н
Силы инерции:
![]() Н
Н
![]() Н
Н
![]() Н
Н
![]()
![]()
![]() Н м
Н м
![]() мм
мм
2.2 Расчет диады 4-5
Для расчета этой диады изобразим ее со всеми приложенными к ней силами: силами тяжести, полезного сопротивления и реакциями.
Эти реакции в поступательных парах известны по направлению, но неизвестны по модулю. Определяем с помощью плана сил. Составим уравнение равновесия диады 4-5.

Строим план сил диады в масштабе сил
![]()
Уравнение содержит три неизвестных, поэтому составляем дополнительное уравнение равновесия в форме моментов сил относительно точки С.

Рассчитаем вектора сил

Строим план сил по уравнению сил, в том порядке как силы стояли в уравнении.
Значения сил из плана сил
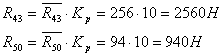
Для рассмотрения внутренних реакций в диаде 4-5 необходимо рассмотреть равновесие одного звена, звена 4.
![]()
2.3 Расчет диады 2-3
Изобразим диаду со всеми приложенными к ней
силами. В точках А и О2 взамен отброшенных связей прикладываем
реакции ![]() и
и ![]() . В точке В
прикладываем ранее найденную реакцию
. В точке В
прикладываем ранее найденную реакцию![]() . Составляем уравнение равновесия
диады 2-3.
. Составляем уравнение равновесия
диады 2-3.

Плечи измеряем на плане. Теперь в уравнении сил
две неизвестных, поэтому строим план сил и определяем реакцию![]() , как замыкающий вектор.
, как замыкающий вектор.
Строим план диады в масштабе сил ![]() . Значения сил из плана
сил.
. Значения сил из плана
сил.
![]()
![]()
2.4 Расчет кривошипа
Изобразим кривошип с приложенными к нему силами и
уравновешивающей силой ![]() , эквивалентной силе действия на
кривошип со стороны двигателя. Действие отброшенных связей учитываем вводя
реакции
, эквивалентной силе действия на
кривошип со стороны двигателя. Действие отброшенных связей учитываем вводя
реакции ![]() и
и
![]() .
Определяем уравновешивающую силу, считая, что она приложена в точке А
кривошипа, перпендикулярно ему. Составляем уравнение равновесия кривошипа.
.
Определяем уравновешивающую силу, считая, что она приложена в точке А
кривошипа, перпендикулярно ему. Составляем уравнение равновесия кривошипа.

Значение силы определяем из плана сил.

2.5 Определение уравновешивающей силы методом Жуковского
Строим повернутый на 900 план скоростей
и в соответствующих точках прикладываем все внешние силы, включая![]() и силы инерции.
Составим уравнение моментов относительно точки
и силы инерции.
Составим уравнение моментов относительно точки ![]() , считая
, считая ![]() неизвестной:
неизвестной:

Подлинность графического метода:
![]()
2.6. Определение мощностей
Потери мощности в кинематических парах:
![]()
Потери мощности на трение во вращательных парах:
![]()
где ![]() - коэффициент
- коэффициент
![]() - реакция во вращательной паре,
- реакция во вращательной паре,
![]() - радиус цапф.
- радиус цапф.

Суммарная мощность трения
![]()

Мгновенно потребляемая мощность

Мощность привода, затрачиваемая на преодоление полезной нагрузки.
![]()
2.7 Определение кинетической энергии механизма
Кинетическая энергия механизма равна сумме кинетических энергий входящих в него массивных звеньев.

Приведенный момент инерции
![]()
3 Геометрический расчёт эвольвентного зубчатого зацепления. Синтез планетарного редуктора
3.1 Геометрический расчёт равносмещённого эвольвентного зубчатого зацепления
Исходные данные:
число зубьев
шестерни: Z![]() =14
=14
число зубьев
колеса: Z![]() =28
=28
модуль зубчатых колёс: m=4мм
Нарезание зубчатых колес производится инструментом реечного типа, имеющего параметры:
![]() - коэффициент высоты
головки зуба
- коэффициент высоты
головки зуба
![]() - коэффициент
радиального зазора
- коэффициент
радиального зазора
![]() - угол профиля зуба
рейки
- угол профиля зуба
рейки
Суммарное число зубьев колёс:
![]()
![]() поэтому проектирую
равносмещённое зацепление.
поэтому проектирую
равносмещённое зацепление.
Делительно-межосевое расстояние:
![]() мм
мм
Начальное межосевое
расстояние: ![]() мм
мм
Угол зацепления: ![]()
Высота зуба:
![]() мм
мм
Коэффициент смещения:
![]()
![]()
Высота головки зуба:
![]() мм
мм
![]() мм
мм
Высота ножки зуба:
![]() мм
мм
![]() мм
мм
Делительный диаметр:
![]() мм
мм
![]() мм
мм
Основной диаметр:
![]() мм
мм
![]() мм
мм
Диаметры вершин:
![]() мм
мм
![]() мм
мм
Диаметр впадин:
![]() мм
мм
![]() мм
мм
Толщина зуба:
![]() мм
мм
![]() мм
мм
Делительный шаг:
![]() мм
мм
Основной шаг:
![]() мм
мм
Радиус галтели:
![]() мм
мм
Коэффициент перекрытия:

Коэффициент перекрытия, полученный аналитически:
![]()

Масштабный коэффициент построения зацепления:
![]()
3.1.1 Расчёт равносмещённого эвольвентного зубчатого зацепления на ЭВМ
Public Sub programma()
m = 4
Z1 = 14
Z2 = 28
ha = 1
c = 0.25
N = (20 * 3.14159) / 180
a = 0.5 * m * (Z1 + Z2)
h = 2.25 * m
x1 = (17 - Z1) / 17: x2 = -x1
ha1 = m * (ha + x1): ha2 = m * (ha + x2)
hf1 = m * (ha + c - x1): hf2 = m * (ha + c - x2)
d1 = m * Z1: d2 = m * Z2
db1 = d1 * Cos(N): db2 = d2 * Cos(N)
da1 = d1 + 2 * ha1: da2 = d2 + 2 * ha2
df1 = d1 - 2 * hf1: df2 = d2 - 2 * hf2
S1 = 0.5 * 3.14159 * m + 2 * x1 * m * Tan(N): S2 = 0.5 * 3.14159 * m + 2 * x2 * m * Tan(N)
P = 3.14149 * m
Pb = P * Cos(N)
Rf = 0.38 * m
Worksheets(2).Cells(10, 2) = a
Worksheets(2).Cells(11, 2) = h
Worksheets(2).Cells(12, 2) = x1
Worksheets(2).Cells(12, 3) = x2
Worksheets(2).Cells(13, 2) = ha1
Worksheets(2).Cells(13, 3) = ha2
Worksheets(2).Cells(14, 2) = hf1
Worksheets(2).Cells(14, 3) = hf2
Worksheets(2).Cells(15, 2) = d1
Worksheets(2).Cells(15, 3) = d2
Worksheets(2).Cells(16, 2) = db1
Worksheets(2).Cells(16, 3) = db2
Worksheets(2).Cells(17, 2) = da1
Worksheets(2).Cells(17, 3) = da2
Worksheets(2).Cells(18, 2) = df1
Worksheets(2).Cells(18, 3) = df2
Worksheets(2).Cells(19, 2) = S1
Worksheets(2).Cells(19, 3) = S2
Worksheets(2).Cells(20, 2) = P
Worksheets(2).Cells(21, 2) = Pb
Worksheets(2).Cells(22, 2) = Rf
End Sub
Таблица 3.1 – Параметры зубчатой передачи на ЭВМ
| Исходные данные: | |||
| Число зубьев шестерни: | Z1=14 | ||
| Число зубьев колеса: | Z2=28 | ||
| Модуль: | m=4 | ||
| Коэффициент головки зуба: | ha=1 | ||
| Коэффициент радиального зазора: | C=0,25 | ||
| Угол профиля зуба рейки: | α=20° | ||
| Результаты счёта: | |||
| Колесо | Шестерня | ||
| Межосевое расстояние: | 84,000 | ||
| Высота зуба: | 13,500 | ||
| Коэффициент смещения: | 0,176 | -0,176 | |
| Высота головки зуба: | 3,312 | 4,688 | |
| Высота ножки зуба: | 4,288 | 5,712 | |
| Делительный диаметр: | 78,000 | 174,000 | |
| Основной диаметр: | 52,636 | 105,267 | |
| Диаметр вершин: | 65,424 | 118,576 | |
| Диаметр впадин: | 47,324 | 100,676 | |
| Делительная толщина зуба: | 10,452 | 8,397 | |
| Делительный шаг: | 12,564 | ||
| Основной шаг: | 11,788 | ||
| Радиус кривизны галтели: | 1,521 | ||
3.2 Синтез планетарного редуктора
Исходные данные:
Частота вращения двигателя nдв=840 мин-1;
Частота вращения кривошипа nкр=70 мин-1;
Число зубьев шестерни z5=14;
Число зубьев колеса z6=28;
Знак передаточного отношения «- ;
Общее передаточное отношение редуктора:
![]()
Передаточное отношение простой передачи z5-z6:
![]()
Передаточное отношение планетарной передачи:
![]()
Передаточное отношение обращённого планетарного механизма – простого зубчатого ряда:

Формула Виллиса. Передаточное отношение обращённого механизма:
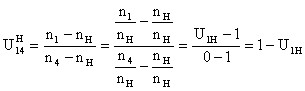
![]()
Подбор чисел зубьев планетарной передачи:
![]()
Условие соосности для данной передачи:
![]()
![]()
![]()
Принимаем числа зубьев колёс, равных: z1=24; z2=24; z3=48; z4=60.
По принятым числам зубьев определяем диаметры колёс:
![]()
![]()
![]()
![]()
![]()
![]()
Принимаем масштабный коэффициент построения кинематической схемы редуктора:
![]()
Скорость точки А зубчатого колеса 1:
![]()
Строим планы скоростей. Масштабный коэффициент плана скоростей:
![]()
Строим план частот вращения звеньев редуктора. Масштабный коэффициент плана частот вращения звеньев редуктора:
![]()
3.3 Определение частот вращения зубчатых колёс аналитическим и графическим методом
Значения частот, полученные аналитическим методом:
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Значения частот, полученных графическим методом:
![]()
![]()
![]()
![]()
Определяем погрешность расчётов:
![]()
4 Синтез и анализ кулачкового механизма
Исходные данные:
Максимальный подъём толкателя h=20мм;
Рабочий угол кулачка φр=280°;
Смещение оси толкателя е=0;
Угол давления α=0;
Частота вращения кривошипа nкр=70 мин-1;
число зубьев
шестерни:![]()
число зубьев
колеса: ![]()
4.1 Диаграмма движения толкателя
По заданному графику скорости толкателя v(t) графическим диффириенцированием по методу хорд получаем ускорение толкателя а=f(t), а графическим интегрированием по методу хорд получаем перемещения толкателя s=f(t).
Базы интегрирования Н1=20мм; Н2=30 мм.
Графики υ(s), a(s), a(υ) получаю методом исключения общего переменного параметра t.
Масштабные коэффициенты диаграмм:
Масштабный коэффициент перемещения:
![]()
Масштабный коэффициент времени:
![]()
![]()
![]()
Масштабный коэффициент скоростей:
![]()
Масштабный коэффициент ускорений:
![]()
4.2 Выбор минимального радиуса кулачка
Минимальный радиус кулачка выбираю из условия выпуклости кулачка. Для этого необходимо, чтобы минимальный радиус был больше ил равен максимальному значению аналога ускорения в отрицательной части графика:
![]()
Где ![]() считаем:
считаем:
![]()
![]()
![]()
![]()
4.3 Построение профиля кулачка
Построение профиля кулачка произвожу методом обращённого движения.
Масштабный коэффициент построения:
![]()
В выбранном
масштабе строю окружность радиуса ![]() . Откладываю фазовый рабочий угол
. Откладываю фазовый рабочий угол ![]() . Делю этот
угол на 13 частей. Через точки деления провожу оси толкателя в обращённом
движении. Для этого соединяю точку деления с центром вращения кулачка. Вдоль
осей толкателя от окружности минимального радиуса откладываю текущие
перемещения толкателя в выбранном масштабе. Через полученные точки провожу
тарелки перпендикулярные осям толкателя. Кривая, огибающая все положения
тарелок, является профилем кулачка.
. Делю этот
угол на 13 частей. Через точки деления провожу оси толкателя в обращённом
движении. Для этого соединяю точку деления с центром вращения кулачка. Вдоль
осей толкателя от окружности минимального радиуса откладываю текущие
перемещения толкателя в выбранном масштабе. Через полученные точки провожу
тарелки перпендикулярные осям толкателя. Кривая, огибающая все положения
тарелок, является профилем кулачка.
4.4 Максимальное значение скорости и ускорения толкателя
![]()
![]()
4.4.1 Расчёт кулачка на ЭВМ
Public Sub kul()
Dim I As Integer
Dim dis1, dis2, R, a1, a2, arksin1, arksin2, BETTA, BET As Single
Dim R0, FIR, FI0, FII, SHAG, E As Single
Dim S(1 To 36) As Single
R0 = InputBox("ВВЕДИТЕ МИНИМАЛЬНЫЙ РАДИУС КУЛАЧКА RO")
FIR = InputBox("ВВЕДИТЕ РАБОЧИЙ УГОЛ КУЛАЧКА FIR")
FI0 = InputBox("ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ УГЛА ПОВОРОТА КУЛАЧКА FI0")
E = InputBox("ВВЕДИТЕ ДЕЗАКСИАЛ E")
For I = 1 To 36
S(I) = InputBox("ВВЕДИТЕ СТРОКУ ПЕРЕМЕЩЕНИЙ S(" & I & ")")
Next I
FIR = FIR * 0.0174532
SHAG = FIR / 13
FI0 = FI0 * 0.0174532
FII = FI0
For I = 1 To 36
dis1 = (R0 ^ 2 - E ^ 2) ^ (1 / 2)
dis2 = S(I) ^ 2 + R0 ^ 2 + 2 * S(I) * dis1
R = dis2 ^ (1 / 2)
a1 = E / R
a2 = E / R0
arksin1 = Atn(a1 / (1 - a1 ^ 2) ^ (1 / 2))
arksin2 = Atn(a1 / (1 - a2 ^ 2) ^ (1 / 2))
BETTA = FII + arksin1 - arksin2
BETTA = BETTA * 180 / 3.1415
Worksheets(1).Cells(I, 1) = R
Worksheets(1).Cells(I, 2) = BETTA
FII = FII + SHAG
Next I
End Sub
Таблица- Результаты расчета
| 52 | 20,00048 |
| 60 | 40,00097 |
| 73 | 60,00145 |
| 86 | 80,00194 |
| 94 | 100,0024 |
| 98 | 120,0029 |
| 94 | 140,0034 |
| 86 | 160,0039 |
| 73 | 180,0044 |
| 60 | 200,0048 |
| 52 | 220,0053 |
| 48 | 240,0058 |
| 48 | 260,0063 |
| 48 | 280,0068 |
| 48 | 300,0073 |
| 48 | 320,0077 |
| 48 | 340,0082 |
| 48 | 360,0087 |
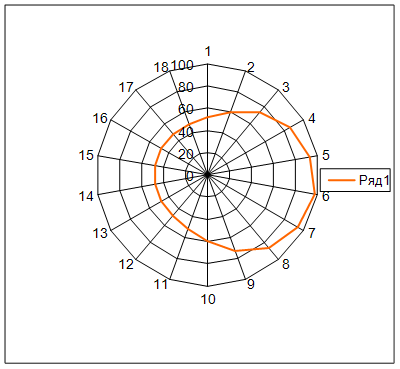
Рис.8 – График построения кулачка
Список используемых источников
1 А. А. Машков, Теория механизмов и машин. – Машиностроение, г. Москва, 1969г. – 583.
2 С. Н. Кожевников, Теория механизмов и машин. – Машиностроение, г. Москва, 1969г. – 583с.
3 А. С. Кореняко, Курсовое проектирование по теории механизмов и машин. Высшая школа, Киев, 1970г. – 330с.
4 И. П. Филонов, Теория механизмов и машин и манипуляторов. – Дизайн ПРО, г. Минск, 1998г. – 428с.
5 И. И. Артоболевский, Теория механизмов и машин. – Наука, г. Москва, 1998г. – 720с.
6 К. В. Фролов, Теория механизмов и машин. – Высшая школа, г. Москва, 1998г. – 494с.
| Привод конвейера ПК-19 | |
|
Введение Конвейер типа ПК-19 предназначен для перемещения сыпучих материалов в горизонтальном направлении. Строгание осуществляется резцом ... sinf3 = (l0 + l1 * Sin(f1)) / (Sqr(l1 ^ 2 + l0 ^ 2 + 2 * l0 * l1 * Sin(f1)) Worksheets(1).Cells(3, h) = Vc |
Раздел: Промышленность, производство Тип: курсовая работа |
| Расчет поворотного крана на неподвижной колонне | |
|
Министерство образования Российской Федерации Санкт-Петербургская Государственная лесотехническая академия им. С.М. Кирова Кафедра "Техническая ... Составление кинематической схемы.583.5.1. Определение общего передаточного числа механизма.583.5.2. Расчет эквивалентных моментов на валан.583.5.3. Выбор червячного редуктора.603.5 ... Определяем ширину зубчатого венца колеса по формуле /8/: |
Раздел: Остальные рефераты Тип: реферат |
| Расчёт на прочность закрытой цилиндрической одноступенчатой передачи и ... | |
|
Министерство образования Российской Федерации Санкт-Петербургский государственный горный институт им. Г. В. Плеханова (технический университет ... Согласно рекомендациям [3, с.108], вычисляем делительные диаметры, диаметры вершин зубьев и диаметры впадин зубчатого колеса и шестерни. Зубчатое зацепление смазывается окунанием зубчатого колеса в масло, заливаемое внутрь корпуса до уровня, обеспечивающего погружение колеса приблизительно на 11 мм, но не менее чем ... |
Раздел: Промышленность, производство Тип: дипломная работа |
| Проектирование механического привода с цилиндрическим соосным ... | |
|
Министерство транспорта Российской федерации Федеральное агентство железнодорожного транспорта Государственное образовательное учреждение высшего ... Окружная скорость зубчатых колёс, м/с: Где - угол наклона зубьев ѭ косозубых зубчатых колёс выбирается из условия получения коэффициента торцового перекрытия ѭѭ более 1,1, которому соответствуют значения ѭ = (8 = 18)0 ... |
Раздел: Промышленность, производство Тип: курсовая работа |
| Расчет и проектирование привода для пластинчатого конвейера | |
|
Содержание Введение. 4 Техническая характеристика изделия. 5 Обоснование выбора конструкции. 6 1.1 Задача. 8 1.2 Расчетная схема. 8 1.3 Данные для ... Редуктор состоит из корпуса (литого чугунного или сварного стального), в котором помещают элементы передачи - зубчатые колеса, валы, подшипники и т. д. В отдельных случаях в ... В качестве максимальных передаточных чисел можно принимать: при прямозубых конических колесах Umax == 22; при конических колесах с круговыми зубьями Umax = 34 (в отдельных случаях ... |
Раздел: Промышленность, производство Тип: курсовая работа |