Реферат: Геометрические векторы
Дисциплина: Высшая математика
Тема: Геометрические векторы
1. Геометрические векторы. Основные определения
В математике, физике, теоретической механике приходится иметь дело с величинами двух типов: одни имеют чисто числовой характер; другие же имеют не только числовую характеристику, но и связаны с понятием о направлении в пространстве. Рассмотрим, например, температуру, массу, энергию, скорость, ускорение, силу. Отличие последних трех величин от первых трех состоит в том, что с ними должно быть связано понятие о направлении. Первые три величины, не связанные с понятием о направлении, называются скалярами. Остальные три величины, имеющие определенное направление, называются векторами.
Так, при измерении температуры, мы получим положительное или отрицательное число, характеризующее ее величину в градусах. Точно так же можно измерить массу, энергию.
Определение 1. Скаляром называется величина, характеризующаяся только числом.
Следовательно, скаляры - это обычные числа, и различие между двумя одинаковыми числами может заключаться лишь в их размерности (м и см, м и кг).
Если необходимо измерить такую величину, как скорость точки, то для этого знать два числа (путь и время) недостаточно. Необходимо еще знать, куда двигается точка, то есть ее направление движения.
Определение 2. Вектором называется величина, характеризующаяся не только численным значением, но и направлением в пространстве.
Следовательно, утверждать, что если обе точки движутся со
скоростью 2 ![]() , то их скорости равны, нет
никакого основания. Необходимо знать в какие стороны они двигаются.
, то их скорости равны, нет
никакого основания. Необходимо знать в какие стороны они двигаются.
Из сказанного следует, что для описания скаляра достаточно написать число и указать его размерность. Для описания векторной величины используют направленные отрезки, длина которых при выбранном масштабе соответствует величине вектора, а направление - совпадает с направлением векторной величины. В дальнейшем эти отрезки и будем называть геометрическими векторами.
При изображении вектора одна точка, ограничивающая вектор,
называется началом, а вторая - концом вектора. В конце вектора ставится стрелка.
Для краткой записи вектор можно обозначить с помощью двух букв ![]() (первая соответствует
началу, вторая - концу) или же одной буквы
(первая соответствует
началу, вторая - концу) или же одной буквы ![]() (здесь
начало и конец не обозначены).
(здесь
начало и конец не обозначены).

Определение 3. Расстояние между началом и концом вектора
называется его длиной или модулем и обозначается ![]() или
или
![]() .
.
Определение 4. Вектор, у которого конец совпадает с началом,
называется ноль вектором и обозначается ![]() .
.
Определение 5. Векторы называются коллинеарными, если они расположены на одной прямой или параллельных прямых. Векторы называются коллинеарными, если они расположены в одной плоскости или в параллельных плоскостях.
Определение 6. Два вектора ![]() и
и
![]() называются равными, если
они коллинеарные, одинаково направлены и равны по длине.
называются равными, если
они коллинеарные, одинаково направлены и равны по длине.
Записывается это так ![]() .
.
Из определения 6 следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства. При этом каждый новый вектор будет равен исходному.
Однако следует отметить, что все сказанное выше связано с так называемыми свободными векторами. Кроме них существуют еще передвижные и определенные векторы. У свободных векторов точку приложения можно выбирать где угодно. У передвижных - точку приложения можно перемещать вдоль самого вектора (например, сила, приложенная к твердому телу). У определенных векторов точка приложения должна быть зафиксирована (например, сила, действующая на жидкость). Но изучение всех векторов можно, в конечном счете, свести к изучению свободных векторов, поэтому в дальнейшем мы будем заниматься только ими.
2. Простейшие операции над векторами
К простейшим операциям над векторами относится сложение и вычитание векторов и умножение вектора на скаляр. Все эти операции называются линейными.
1) Сложение векторов.
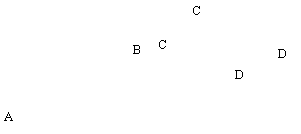
Определение 1. Чтобы найти сумму двух векторов ![]() и
и ![]() , необходимо конец вектора
, необходимо конец вектора ![]() совместить с началом
совместить с началом ![]() . Вектор
. Вектор ![]() , соединяющий точки
, соединяющий точки ![]() и
и ![]() , будет их суммой.
, будет их суммой.
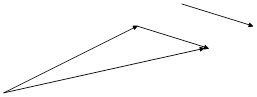
Обозначается сума следующим образом: ![]() . Величину ее можно найти и
другим способом. Начала векторов
. Величину ее можно найти и
другим способом. Начала векторов ![]() и
и ![]() совмещаются и на них как
на сторонах строится параллелограмм. Диагональ параллелограмма и будет суммой
векторов.
совмещаются и на них как
на сторонах строится параллелограмм. Диагональ параллелограмма и будет суммой
векторов.


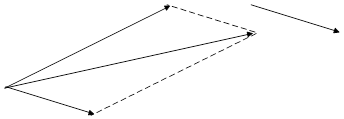
Из правила параллелограмма видно, что сумма векторов обладает переместительным свойством
![]() .
.
Если слагаемых больше, например, три: ![]() , поступают следующим
образом. Строят вначале сумму
, поступают следующим
образом. Строят вначале сумму ![]() , а
затем, прибавляя
, а
затем, прибавляя ![]() , получают вектор
, получают вектор
![]() .
.


Из рисунка видно, что тот же результат будет, если сложить
вначале ![]() , а затем прибавить
, а затем прибавить ![]() , то есть сумма векторов
обладает сочетательным свойством:
, то есть сумма векторов
обладает сочетательным свойством:
![]() .
.
Если при сложении нескольких векторов конец последнего
совпадает с началом первого, то сумма равна ноль вектору ![]() . Очевидно,
. Очевидно, ![]() .
.
2) Разность векторов.
Определение 2. Разностью двух векторов ![]() и
и ![]() называется такой вектор
называется такой вектор ![]() , сумма которого с
вычитаемым
, сумма которого с
вычитаемым ![]() дает вектор
дает вектор ![]() .
.
Значит, если ![]() , то
, то ![]() .
.
Из определения суммы двух векторов вытекает правило
построения разности. Откладываем из общей точки векторы ![]() и
и ![]() . Вектор
. Вектор ![]() соединяет концы векторов
соединяет концы векторов ![]() и
и ![]() и направлен от вычитаемого
к уменьшаемому.
и направлен от вычитаемого
к уменьшаемому.


Видно, что если на векторах ![]() и
и
![]() построить параллелограмм,
то одна его диагональ соответствует их сумме, а вторая - разности.
построить параллелограмм,
то одна его диагональ соответствует их сумме, а вторая - разности.
3) Умножение вектора на число.
Определение 3. Произведением вектора ![]() на число
на число ![]() называется вектор
называется вектор ![]() , определенный следующими
условиями:
, определенный следующими
условиями:
1) ![]() ;
;
2) вектор ![]() коллинеарен
вектору
коллинеарен
вектору ![]() ;
;
3) векторы ![]() и
и ![]() направлены одинаково, если
направлены одинаково, если
![]() , и противоположно, если
, и противоположно, если ![]() .
.
Очевидно, что операция умножения вектора на число приводит к
его растяжению или сжатию. Противоположный вектор ![]() можно
рассматривать как результат умножения вектора
можно
рассматривать как результат умножения вектора ![]() на
на
![]() . Отсюда,
. Отсюда,
![]() .
.
Из определения 3 следует, что если ![]() , то векторы
, то векторы ![]() и
и ![]() коллинеарны. Отсюда
вытекает определение коллинеарности векторов.
коллинеарны. Отсюда
вытекает определение коллинеарности векторов.
Определение 4. Любые два вектора ![]() и
и
![]() коллинеарны, если связаны
соотношением
коллинеарны, если связаны
соотношением ![]() , где
, где ![]() - некоторое число.
- некоторое число.
Величину ![]() можно
определить из отношения
можно
определить из отношения ![]() . Оно
положительно, если векторы направлены в одну сторону, и наоборот отрицательно,
если направление векторов противоположно.
. Оно
положительно, если векторы направлены в одну сторону, и наоборот отрицательно,
если направление векторов противоположно.
Из построения параллелограмма легко убедиться, что умножение вектора на число обладает распределительным свойством:
![]() ;
; ![]()
и сочетательным свойством
![]() .
.
Определение 5. Вектор, длина которого равна единице, называется единичным вектором или ортом.
Обозначаются единичные векторы символами ![]() или
или ![]() .
.
Используя понятие единичного вектора, любой вектор можно
представить следующим образом: ![]() .
.
3. Проекция вектора на ось
В процессе выполнения простейших операций иногда приходится сталкиваться с таким понятием, как проекция вектора на какую-либо ось. Введем вначале понятие угла между векторами.
Определение 1. Углом между векторами ![]() и
и ![]() называется наименьший угол
называется наименьший угол
![]() , на который надо повернуть
один из векторов до совмещения со вторым.
, на который надо повернуть
один из векторов до совмещения со вторым.


Положительным считается отсчет угла против часовой стрелки.
Пусть необходимо найти проекцию вектора ![]() на ось
на ось ![]() . Выберем на оси начало
отсчета 0 и масштаб. Совместим с началом отсчета единичный вектор
. Выберем на оси начало
отсчета 0 и масштаб. Совместим с началом отсчета единичный вектор ![]() . Тогда угол между
. Тогда угол между ![]() и осью
и осью ![]() будет равен углу
будет равен углу ![]() между
между ![]() и
и ![]() . Спроецируем начало и
конец вектора на ось
. Спроецируем начало и
конец вектора на ось ![]() . Тогда длина
отрезка
. Тогда длина
отрезка ![]() , а
, а ![]() . Длина же проекции вектора
. Длина же проекции вектора
![]() :
:
![]() .
.
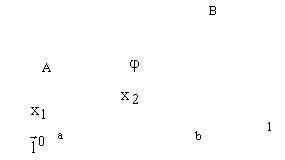
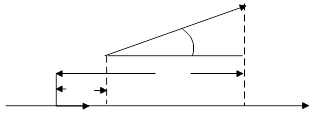
Рис. 1
Определение 2. Проекцией вектора ![]() на
ось
на
ось ![]() называется разность между
координатами проекций конца и начала вектора
называется разность между
координатами проекций конца и начала вектора ![]() на
ось
на
ось ![]() .
.
Очевидно, что если ![]() -
острый угол, проекция положительна; если
-
острый угол, проекция положительна; если ![]() -
тупой угол, то отрицательна; если
-
тупой угол, то отрицательна; если ![]() , то
проекция равна нулю.
, то
проекция равна нулю.
Теорема 1. Проекция вектора ![]() на
ось
на
ось ![]() равна произведению модуля
этого вектора на косинус угла между ними:
равна произведению модуля
этого вектора на косинус угла между ними:
![]() .
.
Доказательство теоремы вытекает из Рис. 1.
Теорема 2. Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось.
Доказательство. Пусть ![]() .
Обозначим проекцию точки
.
Обозначим проекцию точки ![]() через
через ![]() , точки
, точки ![]() - через
- через ![]() , точки
, точки ![]() - через
- через ![]() .
.

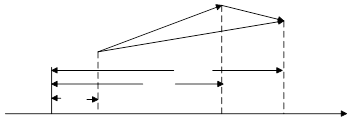
Тогда
![]() ;
; ![]() ;
; ![]() .
.
Но
![]() .
.
Теорема 3. Если вектор ![]() умножить
на число
умножить
на число ![]() , то его проекция на ось
умножится на то же число.
, то его проекция на ось
умножится на то же число.
Докажем для случая ![]() :
:
![]() .
.
Если ![]() , то
, то
![]() .
.
Литература
1. Артамонов Вячеслав Введение в высшую алгебру и аналитическую геометрию. Изд-во: Факториал, Факториал Пресс, 2007. - 128с.
2. Ефимов Н.В. Высшая геометрия. Издательство: ФИЗМАТЛИТ®, 2003. - 584c.
3. Клейн Ф. Высшая геометрия. изд. - 2. Издательство: Едиториал УРСС, 2004. - 400c.
4. Клейн Ф., Феликс Христиан Клейн Высшая геометрия: Пер. с нем. Изд.3. ЛИБРОКОМ, 2009. - 400c.
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... Тогда вектор суммы будет вектор соединяющий начало первого с концом последнего слагаемого вектора. (если начало первого и конец последнего слагаемых векторов совпали то сумма равно ... Операции над векторами вводятся в координатной форме; геометрический смысл действий над векторами раскрывается в соответствующих теоремах и задачах. |
Раздел: Рефераты по математике Тип: реферат |
| Геометрии Галилея и Минковского как описания пространства-времени | |
|
Дипломная работа "Геометрии Галилея и Минковского как описания пространства-времени" (факультатив для старших школьников) Введение В ... Если вектор имеет отрицательную проекцию на ось OY' (как на рис. 3), то мировая точка В является более ранней в системе OX'Y', чем точка А. При этом проекция вектора на ось OY ... Таким образом, геометрическое место точек в четырехмерном пространстве, описываемое уравнением (2.39), представляет собой трехмерное пространство, а так как любой принадлежащий ему ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Лекции по Физической оптике | |
|
я2Московский Физико-Технический Институт я2Факультет Физической и Квантовой Электроники я_я3Л. Н. КУРБАТОВ. я_я3КВАНТОВАЯ ЭЛЕКТРОНИКА. я_я2Москва ... Объясним на его примере, как найтия2оптическую ось и направления,по которым колеблются векторы лу-я2чей "o" и "e" (рис.4). Форма кристалла,полученная скалываниемя2по плоскости ... Когда E падающего пучка образует ся2главными направлениями угол 45 , тогда амплитуды обоих лучейя2одинаковы и разность фаз равная2где и - показатели преломления для главных ... |
Раздел: Рефераты по физике Тип: реферат |
| Измерения геометрических величин в курсе геометрии 7-9 классов | |
|
Оглавление Введение Глава 1. Психолого-педагогические и научно-методические основы изучения измерений геометрических величин в школе §1. Практическая ... В результате проведенного сравнительного анализа школьных учебников по геометрии мы можем сделать вывод: в школьном курсе геометрии основное внимание уделяется вычислению ... Оборудование: картонные геометрические фигуры: треугольники, квадрат, прямоугольник, трапеции, параллелограмм, учебник Геометрия 7 - 9, Л.С. Атанасян и др. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Развитие понятия "Пространство" и неевклидова геометрия | |
|
Оглавление Введение Глава I. Развитие геометрии 1.1 История геометрии 1.2 Постулаты Евклида 1.3 Аксиоматика Гильберта 1.4 Другие системы аксиом ... Из школьного курса геометрии известно, что в трехгранном угле любой его плоский угол меньше суммы двух других плоских углов и больше их разности. 13 окружности нулевого радиуса изображаются с точки зрения евклидовой геометрии биссектрисами координатных углов, окружности вещественного радиуса - гиперболами, пересекающими ось ... |
Раздел: Рефераты по математике Тип: дипломная работа |