Контрольная работа: Формула Лапласа. Математическое ожидание
Контрольная работа № 3
1. Вероятность попадания в цель при залпе из двух орудий равна 0,35. Найти вероятность попадания при одном выстреле первым орудием, если для второго орудия эта вероятность 0,75.
Решение:
Вероятность попадания в цель при залпе из двух орудий равна
![]() .
.
Вероятность попадания при одном выстреле вторым орудием
![]() .
.
Вероятность попадания при одном выстреле первым орудием
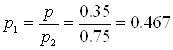
Ответ: ![]()
2. Что вероятнее: выиграть у равносильного противника (ничейный результат исключается)
а) 3 партии из 4 или 5 из 8
б) не менее 3 партии из 4 или не менее 5 из 8
Решение:
Вероятность выиграть
![]() .
.
Вероятность проиграть
![]() .
.
а) Что вероятнее: выиграть у равносильного противника (ничейный результат исключается) 3 партии из 4 или 5 из 8:
![]()
![]()
Вероятнее выиграть 3 партии из 4, чем 5 из 8
б) Что вероятнее: выиграть у равносильного противника (ничейный результат исключается) не менее 3 партии из 4 или не менее 5 из 8:
![]()
![]()
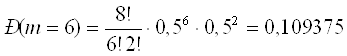
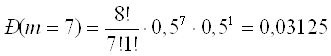
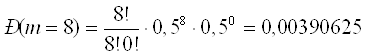
![]()
0,3125 < 0,36328125
Вероятнее выиграть не менее 5 партии из 8, чем не менее 3 из 4.
3. При установившемся технологическом процессе в день в среднем происходит 10 обрывов нити на 100 веретенах. Определить вероятность того, что на 800 веретенах произойдет:
а) ровно 78 обрывов нити;
б) обрыв нити произойдет не более чем на 100 веретенах.
Решение:
р = 0,1, тогда q = 1 – p = 1 – 0,1 = 0,9
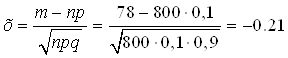
![]()
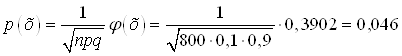
б) По интегральной формуле Лапласа
![]()
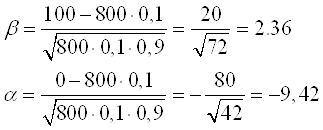
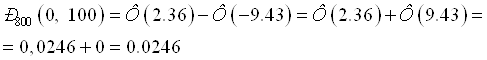
4. Участник олимпиады отвечает на 3 вопроса с вероятностью ответа на каждый соответственно 0,6, 0,7, 0,4.
За каждый верный ответ ему начисляется 5 баллов, за неверный списывается 5 балов. Составить закон распределения числа баллов, полученных участником олимпиады. Найти мат. ожидание этой случайной величины.
Решение:
Ряд распределения случайной величин X (числа баллов, полученных участником олимпиады)
|
xi |
-15 | -5 | 5 | 15 |
|
pi |
0,4*0,3*0,6 = = 0,072 |
0,6*0,3*0,6+0,4*0,7*0,6+0,4*0,3*0,6=0,312 | 0,6*0,7*0,6+0,4*0,7*0,4+0,6*0,3*0,4=0,436 | 0,6*0,7*0,4=0,168 |
![]()
5. Случайная величина Х подчинена нормальному закону распределения с нулевым математическим ожиданием. Вероятность попадания этой CD в интервал [-2, 2] равна 0,5705. Найти среднее квадратическое отклонение и плотность вероятности этой СВ.
Решение:
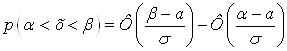
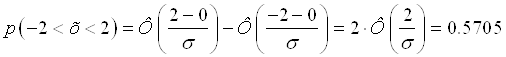
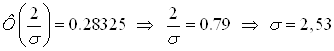
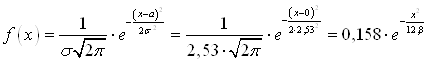
| Методика обучения элементам теории вероятностей на факультативных ... | |
|
Введение Глава I. Вероятностно - статистическая линия в базовом школьном курсе математики 1.1 Статистическое мышление и школьное математическое ... Т. о. геометрические вероятности-вероятности попадания точки в область (отрезок, часть плоскости и т. д.) Для случая, когда первый игрок выиграл одну партию, а второй - ни одной, Паскаль приводит формулу W=A+A*(1*3*5*...*(2n-1))/(2*4*6*...2n), где А - ставка каждого игрока, а W ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Участие политических партий в формировании органов государственной ... | |
|
УЧАСТИЕ ПОЛИТИЧЕСКИХ ПАРТИЙ В ФОРМИРОВАНИИ ОРГАНОВ ГОСУДАРСТВЕННОЙ ВЛАСТИ Студентки Курса ГМУ-33, группы ГМУ-331 Специальность: "Государственное и ... Но всегда ясно, кто больше выиграл от сотрудничества -партия или кандидат. Вероятность попадания в "лист ожидания" связана с номером в партийном списке)-составило около половины от числа переизбранных. |
Раздел: Рефераты по политологии Тип: курсовая работа |
| Серьёзные лекции по высшей экономической математике | |
|
Комбинаторные задачи. 1.Сколькими способами колода в 52 карты может быть роздана 13-ти игрокам так, чтобы каждый игрок получил по одной карте каждой ... Найти вероятность того, что определённый игрок выиграет ровно m партий, 0 m n. Пусть имеется нормально распределённая случайная величина с математическим ожиданием, равным а и дисперсией 2. Определим вероятность попадания в интервал (а - 3 ; а + 3 ), то есть ... |
Раздел: Рефераты по математике Тип: реферат |
| Теория вероятностей. От Паскаля до Колмогорова | |
|
Теория вероятностей. От Паскаля до Колмогорова Санкт-Петербург 2010 Введение Сейчас уже трудно установить, кто впервые поставил вопрос, пусть и в ... Кто первым достигнет 6 лучших попаданий, тот выигрывает. Ему же удалось найти вероятности , что игрок выиграет игру за партий (соответственно выиграет за партий игрок ) |
Раздел: Рефераты по математике Тип: курсовая работа |
|
Содержание 1. Основные понятия 2. Предвидение случайных событий 3. Примеры расчетов на будущее 4. Методы прогнозирования Библиографический список 1 ... Доля, которую это число составит от общего числа выстрелов, и есть частота попаданий. "Вероятность попадания 70 процентов" - значит предположить, что при очередной стрельбе 70 пуль из ста попадут в мишень. |
Раздел: Рефераты по социологии Тип: курсовая работа |