Контрольная работа: Экономико-математические методы и прикладные модели
Министерство образования РФ
Всероссийский заочный финансово-экономический институт
Факультет учетно-статистический
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Экономико-математические методы и прикладные модели»
Вариант № 5
Исполнитель:
Специальность: БУАиА
Группа:
№ зачетной книжки:
Преподаватель: Орлова И.В.
Москва 2007
Задача 1
Решить графическим методом типовую задачу оптимизации
Продукция двух видов (краска для внутренних (I) и наружных (E) работ) поступает в оптовую продажу. Для производства красок используется два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов составляют 6 8 тонн соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице.
| Исходный продукт | Расход исходных продуктов на тонну краски, т | Максимально возможный запас, т | |
| Краска Е | Краска I | ||
| А | 1 | 2 | 6 |
| В | 2 | 1 | 8 |
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1т. Кроме того, установлено, что спрос на краску I не превышает 2 т в сутки. Оптовые цены одной тонны красок равны 3000 ден.ед. для краски Е и 2000 ден.ед. для краски I. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
Решение
Введем следующие переменные:
Х1 – количество краски Е (т);
Х2 – количество краски I (т).
Цена краски Е составляет 3000 (ден. ед.), а цена краски I –2000 (ден. ед.). Необходимо максимизировать целевую функцию:
![]()
Введены следующие ограничения:
Х1+2Х2≤6;
2Х1+Х2≤8;
Х2≤2;
Х2-Х1≤1.
Первое ограничение по продукту А Х1+2Х2≤6. Прямая Х1+2Х2=6 проходит через точки (0;3) и (6;0).
Второе ограничение по продукту В 2Х1+Х2≤8. Прямая 2Х1+Х2=8 проходит через точки (0;8) и (4;0).
Третье ограничение Х2≤2. Прямая Х2=2 проходит параллельно оси Х1 через точку Х2=2.
Четвертое ограничение Х2-Х1≤1. Прямая Х2-Х1=1 проходит через точки (0;1) и (-1;0).
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений.
Решением неравенств будет являться полуплоскость, лежащая ниже пересекающихся прямых Х1+2Х2=6, 2Х1+Х2=8, Х2=2, Х2-Х1=1.
При максимизации функции линия уровня перемещается по направлению вектору – градиенту.
После решения системы уравнений
Х1+2Х2=6
2Х1+Х2=8
Находим, что Х1=3,33, Х2 = 1,33
![]() (ден.
ед.)
(ден.
ед.)
Ответ:
Прибыль фирмы будет максимальной, т.е. 12650 ден. ед., если ежедневно будет производиться 3,33 т краски Е и 1,33 т краски I.
При решении задачи на минимум – решений не будет.
Задача 2
Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования
На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
| Вид ресурсов | Нормы расхода ресурсов на ед. продукции | Запасы ресурсов | ||
| I вид | II вид | III вид | ||
| Труд | 1 | 4 | 3 | 200 |
| Сырье | 1 | 1 | 2 | 80 |
| Оборудование | 1 | 1 | 2 | 140 |
| Цена изделия | 40 | 60 | 80 |
Требуется:
1. Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3. Пояснить нулевые значения переменных в оптимальном плане.
4. На основе свойств двойственных оценок и теорем двойственности:
· проанализировать использование ресурсов в оптимальном плане исходной задачи;
· определить, как изменяется выручка от реализации продукции и план ее выпуска при увеличении запасов сырья на 18 единиц;
· оценить целесообразность включения в план изделия четвертого вида ценой 70 единиц, на изготовление которого расходуется по две единицы каждого вида ресурсов.
Решение
1) Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Х1- норма расхода ресурса первого вида
Х2 - норма расхода ресурса второго вида
Х3 - норма расхода ресурса третьего вида.
Целевая функция имеет вид
![]() ,
где
,
где ![]()
Ограничения:
1) по труду
![]()
2) по сырью
![]()
3) по оборудованию
![]()
![]()
Оптимальный план найдем через Поиск решений в надстройках Excel (рис. 2.1) и (рис. 2.2).
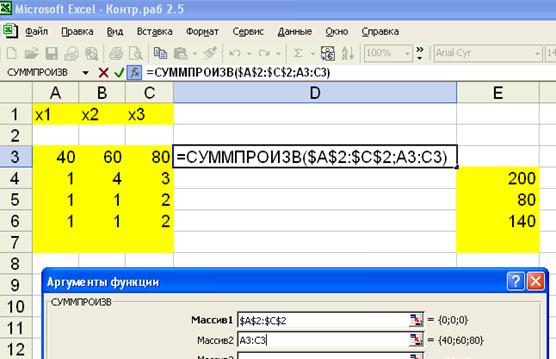 Рис. 2.1
Рис. 2.1
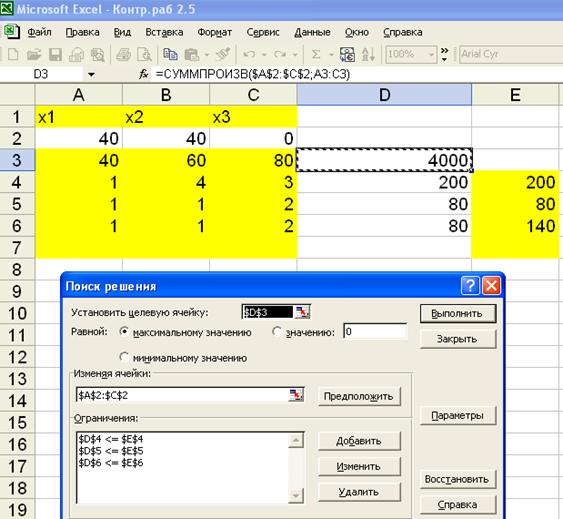
Рис. 2.2
Полученное решение означает, что максимальную выручку от реализации готовой продукции (4000 ед.) предприятие может получить при выпуске 40 единиц изделия 1 вида и 40 единиц изделия 2 вида. При этом ресурс «труд» и «сырье» будут использованы полностью, из 140 единиц оборудования будет использовано только 80 единиц.
Excel позволяет представить результаты поиска решения в форме отчета рис. 2.3
|
Microsoft Excel 10.0 Отчет по результатам |
||||||
|
Рабочий лист: [Контр.раб 2.5.xls]кр 2.5 |
||||||
|
Отчет создан: 06.12.2007 18:42:36 |
||||||
| Целевая ячейка (Максимум) | ||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
| $D$3 | 4000 | 4000 | ||||
| Изменяемые ячейки | ||||||
|
Ячейка |
Имя |
Исходное значение |
Результат |
|||
| $A$2 | х1 | 40 | 40 | |||
| $B$2 | х2 | 40 | 40 | |||
| $C$2 | х3 | 0 | 0 | |||
| Ограничения | ||||||
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
| $D$4 | 200 | $D$4<=$E$4 | связанное | 0 | ||
| $D$5 | 80 | $D$5<=$E$5 | связанное | 0 | ||
| $D$6 | 80 | $D$6<=$E$6 | не связан. | 60 | ||
| Рис.2.3 |
В
отчете по результатам содержатся оптимальные значения переменных ![]() , которые
соответственно равны 40; 40; 0; значение целевой функции – 4000, а также недоиспользованный
ресурс «оборудование» в размере 60 единиц.
, которые
соответственно равны 40; 40; 0; значение целевой функции – 4000, а также недоиспользованный
ресурс «оборудование» в размере 60 единиц.
Оптимальный
план ![]()
2) Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Число неизвестных в двойственной задаче равно числу функциональных ограничений в исходной задаче. Исходная задача содержит 3 ограничения: труд, сырье и оборудование. Следовательно, в двойственной задаче 3 неизвестных:
![]() двойственная оценка ресурса труд
двойственная оценка ресурса труд
![]() двойственная
оценка ресурса сырья
двойственная
оценка ресурса сырья
![]() двойственная
оценка ресурса оборудования
двойственная
оценка ресурса оборудования
Целевая функция двойственной задачи формулируется на минимум. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи:
![]()
Необходимо найти такие
«цены» на типы сырья![]() ,чтобы общая стоимость используемых типов сырья была
минимальной.
,чтобы общая стоимость используемых типов сырья была
минимальной.
Ограничения. Число ограничений в системе двойственной задачи равно числу переменных в исходной задаче. В исходной задаче 3 переменных, следовательно, в двойственной задаче 3 ограничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть определяет стоимость типа сырья, затраченного на производство единицы продукции.
Каждое ограничение соответствует определенной норме расхода сырья на единицу продукции:
![]()
![]()
![]()
![]()
Найдем оптимальный план двойственной задачи, используя теоремы двойственности.
Воспользуемся первым соотношением второй теоремы двойственности
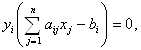 тогда
тогда
![]()
![]()
![]()
![]()
Подставим оптимальные значения вектора ![]() в полученные выражения
в полученные выражения
![]()
![]()
![]()
И получим
![]() ,
,
![]() ,
,
![]() , так как 80
< 140, то
, так как 80
< 140, то ![]()
В задаче ![]() и
и ![]() , поэтому первое и второе
ограничения двойственной задачи обращаются в равенства
, поэтому первое и второе
ограничения двойственной задачи обращаются в равенства
![]()
![]()
![]()
Решая систему уравнений получим, y1 = 6,67, y2 = 33,33, y3 = 0.
Проверяем выполнение первой теоремы двойственности
![]()
![]()
Это означает, что оптимальный план двойственной задачи определен, верно.
Решение двойственной задачи можно найти, выбрав команду Поиск решений – Отчет по устойчивости (рис.2.4).
|
Microsoft Excel 10.0 Отчет по устойчивости |
|||||||
|
Рабочий лист: [Контр.раб 2.5.xls]кр 2.5 |
|||||||
|
Отчет создан: 06.12.2007 19:04:27 |
|||||||
| Изменяемые ячейки | |||||||
|
|
|
Результ. |
Нормир. |
Целевой |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
стоимость |
Коэффициент |
Увеличение |
Уменьшение |
|
| $A$2 | х1 | 40 | 0 | 40 | 20 | 4.000000003 | |
| $B$2 | х2 | 40 | 0 | 60 | 100 | 20 | |
| $C$2 | х3 | 0 | -6.666666672 | 80 | 6.666666672 | 1E+30 | |
| Ограничения | |||||||
|
|
|
Результ. |
Теневая |
Ограничение |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
Цена |
Правая часть |
Увеличение |
Уменьшение |
|
| $D$4 | 200 | 6.666666667 | 200 | 120 | 120 | ||
| $D$5 | 80 | 33.33333333 | 80 | 60 | 30 | ||
| $D$6 | 80 | 0 | 140 | 1E+30 | 60 |
Рис 2.4
3) Пояснить нулевые значения переменных в оптимальном плане.
Подставим в ограничения двойственной задачи
оптимальные значения вектора ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Затраты на 3 изделия превышают цену (![]() ). Это же видно и в отчете
по устойчивости (рис. 2.4) значения
). Это же видно и в отчете
по устойчивости (рис. 2.4) значения ![]() (нормир.
стоимость) равно -6.67. Т.е. стоимость нормы расходов на единицу изделия больше
чем цена изделия. Эти изделия не войдут в оптимальный план из-за их
убыточности.
(нормир.
стоимость) равно -6.67. Т.е. стоимость нормы расходов на единицу изделия больше
чем цена изделия. Эти изделия не войдут в оптимальный план из-за их
убыточности.
4) На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка от реализации продукции и план ее выпуска при увеличении запасов сырья на 18 единиц;
- оценить целесообразность включения в план изделия четвертого вида ценой 70 единиц, на изготовление которого расходуется по две единицы каждого вида ресурсов.
Проанализировать использование ресурсов в оптимальном плане исходной задачи;
|
|
Запасы сырья по первому и второму виду были использованы полностью, а по третьему виду – оборудование - было недоиспользовано 60.
Определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья на 18 единиц
Из теоремы об оценках известно, что колебание
величины ![]() приводит к увеличению или
уменьшению
приводит к увеличению или
уменьшению ![]() . Оно определяется:
. Оно определяется:
![]()
|
|
|
|
|
Из расчетов видно, если мы увеличим запасы сырья на 18 единицы, то выручка возрастет на 600 единиц, т. е общая выручка составит после изменения запасов 4600 единиц.
![]() При этом структура плана не изменилась
– изделия, которые были убыточны, не вошли и в новый план выпуска, так как цены
на них не изменились.
При этом структура плана не изменилась
– изделия, которые были убыточны, не вошли и в новый план выпуска, так как цены
на них не изменились.
|
|
|
|
|
|
|
|
|
Решим систему уравнений:
![]()
![]()
И получим
![]()
![]()
Новый оптимальный план ![]()
Изменение общей стоимости продукции на 600 ед. получено за счет увеличения плана выпуска 1 вида продукции на 24 ед по цене 40 ед (40*(64-40)=960 ед.) и уменьшения на 6 ед. плана выпуска продукции 2 вида по цене 60 (60*(34-40)=-360 ед.)
Оценить целесообразность включения в план изделия четвертого вида ценой 70 единиц, на изготовление которого расходуется по две единицы каждого вида ресурсов.
Для оценки целесообразности включения в план изделия четвертого вида воспользуемся вторым свойством двойственной оценки.
![]() ,
подставим
,
подставим ![]() ,
, ![]() ,
, ![]()
![]()
т.к. 80>70, то включение в план изделия четвертого вида невыгодно.
Задача 3
Используя балансовый метод планирования и модель Леонтьева, построить баланс производства и распределения продукции предприятий.
Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске одного вида: первое предприятие специализируется на выпуске продукции первого вида; второе предприятие – продукции второго вида; третье предприятие – продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутренне потребление), остальная часть поставляется за его пределы (внешним потребителям, является конечным продуктом). Специалистами управляющей компании получены экономические оценки aij (i=1,2,3; j=1,2,3) элементов технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов yi вектора конечной продукции Y.
Требуется:
1. Проверить продуктивность технологической матрицы А=( aij) (матрицы коэффициентов прямых материальных затрат).
2. Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
| Предприятие (виды продукции) | Коэффициенты прямых затрат aij | Конечный продукт Y | ||
| 1 | 2 | 3 | ||
| 1 | 0,2 | 0,3 | 0 | 120 |
| 2 | 0,3 | 0,1 | 0,2 | 250 |
| 3 | 0,1 | 0 | 0,3 | 180 |
Решение
1) Проверить продуктивность технологической матрицы A=(аij) (матрицы коэффициентов прямых материальных затрат).
1.1. Для решения данной экономической задачи будет выбрана среда табличного процессора MS Excel. (рис. 3.1)
Рис. 3.1
Исходные данные
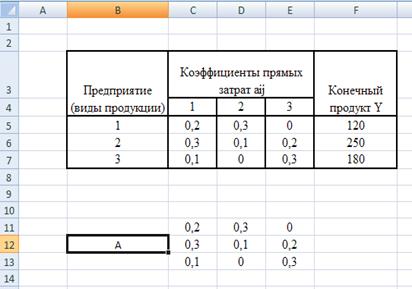
1.2. Найдем разность между единичной матрицей Е и матрицей А.
Для этого воспользуемся правилом вычитания матриц
одинаковой размерности. ![]() (рис.
3.2)
(рис.
3.2)
![]()
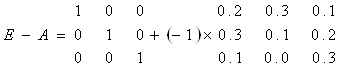
| 0,8 | -0,3 | -0,1 | |
| E-A | -0,3 | 0,9 | -0,2 |
| -0,1 | 0 | 0,7 |
1.3. Найдем обратную
матрицу ![]() . Воспользуемся встроенными
функциями MS Excel (математические,
обратная матрица) (рис. 3.2).
. Воспользуемся встроенными
функциями MS Excel (математические,
обратная матрица) (рис. 3.2).
Рис 3.2
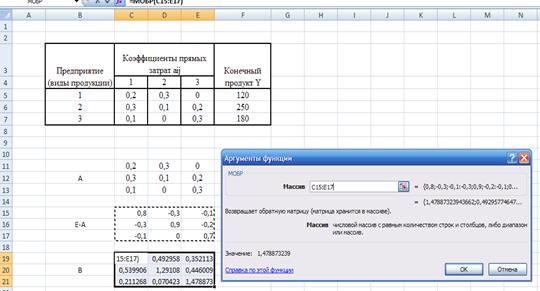
1.4. Чтобы определить
Валовую продукцию (матрицу![]() ), надо
матрицу
), надо
матрицу ![]() =
=![]() умножить на Конечный
продукт (матрицу
умножить на Конечный
продукт (матрицу ![]() ). Воспользуемся
опять встроенными функциями MS Excel
(математические, умножение матриц) (рис. 3.3).
). Воспользуемся
опять встроенными функциями MS Excel
(математические, умножение матриц) (рис. 3.3).
Рис. 3.3
Определение валовой продукции (матрица![]() )
)
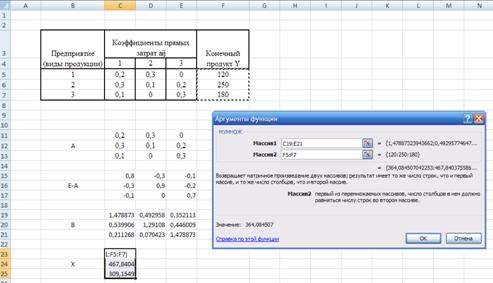
1.5. Матрица ![]() (матрица коэффициентов
прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор
(матрица коэффициентов
прямых материальных затрат) продуктивна, т.к. существует неотрицательный вектор
![]() .
.
2) Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
2.1. Для распределения
продукции предприятий холдинга необходимо найти ![]() (рис. 3.4)
(рис. 3.4)
Рис. 3.4
Распределение продукции предприятий холдинга
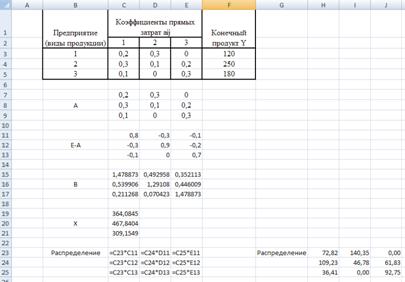
2.2. Построим межотраслевой баланс производства (рис. 3.5)
Рис 3.5
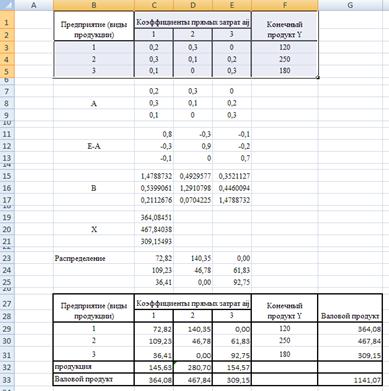
Условно чистая продукция – это разность между валовым продуктом и суммой продуктов, которые потребляет каждая отрасль.
Ответ:
1) Матрица ![]() (матрица
коэффициентов прямых материальных затрат) продуктивна, т.к. существует
неотрицательный вектор
(матрица
коэффициентов прямых материальных затрат) продуктивна, т.к. существует
неотрицательный вектор ![]() .
.
2)
| Межотраслевой баланс | |||||
| Предприятие (виды продукции) | Коэффициенты прямых затрат aij | Конечный продукт Y | Валовой продукт | ||
| 1 | 2 | 3 | |||
| 1 | 72,82 | 140,35 | 0,00 | 120 | 364,08 |
| 2 | 109,23 | 46,78 | 61,83 | 250 | 467,84 |
| 3 | 36,41 | 0,00 | 92,75 | 180 | 309,15 |
| Условно чистая продукция | 145,63 | 280,70 | 154,57 | ||
| Валовой продукт | 364,08 | 467,84 | 309,15 | 1141,07 |
Задача 4
Исследовать динамику экономического показателя на основе анализа одномерного временного ряда.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен в таблице.
| Номер наблюдения ( t = 1,2,…,9) | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 5 | 7 | 10 | 12 | 15 | 18 | 20 | 23 | 26 |
Требуется:
1. Проверить наличие аномальных наблюдений.
2. Построить линейную модель Y(t) = a0 + a1t, параметры которой оценить МНК (Y(t)) – расчетные, смоделированные значения временного ряда).
3. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S–критерия взять табулированные границы 2,7-3,7).
4. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
5. По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности p = 70%)
6. Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Решение
1). Наличие аномальных наблюдений приводит к
искажению результатов моделирования, поэтому необходимо убедиться в отсутствии
аномальных данных. Для этого воспользуемся методом Ирвина и найдем
характеристическое число (![]() ) (таблица
4.1).
) (таблица
4.1).
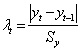 ;
; 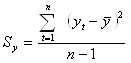 ,
, ![]()
Расчетные значения сравниваются с табличными
значениями критерия Ирвина, и если они оказываются больше табличных, то
соответствующее значение ![]() уровня
ряда считается аномальным.
уровня
ряда считается аномальным.
Таблица 4.1
| t | Y |
|
|
|
|
|
|
|
| 1 | 5 | -4 | 16 | -10,11 | 102,23 | - | - | |
| 2 | 7 | -3 | 9 | -8,11 | 65,79 | 2 | 0,28 | |
| 3 | 10 | -2 | 4 | -5,11 | 26,12 | 3 | 0,42 | |
| 4 | 12 | -1 | 1 | -3,11 | 9,68 | 2 | 0,28 | |
| 5 | 15 | 0 | 0 | -0,11 | 0,01 | 3 | 0,42 | |
| 6 | 18 | 1 | 1 | 2,89 | 8,35 | 3 | 0,42 | |
| 7 | 20 | 2 | 4 | 4,89 | 23,90 | 2 | 0,28 | |
| 8 | 23 | 3 | 9 | 7,89 | 62,23 | 3 | 0,42 | |
| 9 | 26 | 4 | 16 | 10,89 | 118,57 | 3 | 0,42 | |
| Сумма | 45 | 136 | 0 | 60 | 0 | 416,89 | ||
| Среднее | 5 | 15,11 |
![]()
![]() Все
полученные значения сравнили с табличными значениями,
Все
полученные значения сравнили с табличными значениями, ![]() не превышает их, то есть,
аномальных наблюдений нет.
не превышает их, то есть,
аномальных наблюдений нет.
2) Построить линейную модель ![]() , параметры которой
оценить МНК (
, параметры которой
оценить МНК (![]() - расчетные,
смоделированные значения временного ряда).
- расчетные,
смоделированные значения временного ряда).
Для этого воспользуемся Анализом данных в Excel (рис. 4.2).
Рис 4.1
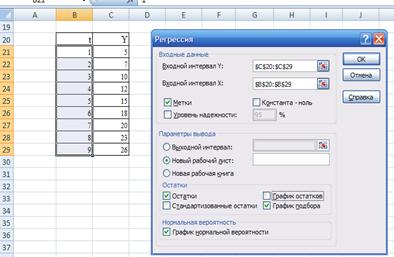
Результат регрессионного анализа содержится в таблице 4.2 и 4.3.
Таблица 4.2
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
|
Y-пересечение а0 |
1,944 | 0,249 | 7,810 |
|
t a1 |
2,633 | 0,044 | 59,516 |
Во втором столбце табл. 4.3 содержатся коэффициенты уравнения регрессии а0, а1, в третьем столбце – стандартные ошибки коэффициентов уравнения регрессии, а в четвертом – t – статистика, используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости ![]() (спрос на кредитные
ресурсы) от
(спрос на кредитные
ресурсы) от ![]() (время) имеет вид
(время) имеет вид ![]() (рис. 4.5).
(рис. 4.5).
Таблица 4.3
Вывод остатков
| ВЫВОД ОСТАТКА | ||
|
Наблюдение |
Предсказанное Y |
Остатки |
| 1 | 4,58 | 0,42 |
| 2 | 7,21 | -0,21 |
| 3 | 9,84 | 0,16 |
| 4 | 12,48 | -0,48 |
| 5 | 15,11 | -0,11 |
| 6 | 17,74 | 0,26 |
| 7 | 20,38 | -0,38 |
| 8 | 23,01 | -0,01 |
| 9 | 25,64 | 0,36 |
Рис. 4.4
3) Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7—3,7).
Модель является адекватной, если математическое ожидание значений остаточного ряда случайны, независимы и подчинены нормальному закону распределения.
3.1. Проверим независимость (отсутствие автокорреляции) с помощью d – критерия Дарбина – Уотсона по формуле:

Таблица 4.2
|
Наблюдение |
|
|
|
|
|
| 1 | 0,42 | 0,18 | - | - | - |
| 2 | -0,21 | 0,04 | -0,63 | 0,42 | 0,18 |
| 3 | 0,16 | 0,02 | 0,37 | -0,21 | 0,04 |
| 4 | -0,48 | 0,23 | -0,63 | 0,16 | 0,02 |
| 5 | -0,11 | 0,01 | 0,37 | -0,48 | 0,23 |
| 6 | 0,26 | 0,07 | 0,37 | -0,11 | 0,01 |
| 7 | -0,38 | 0,14 | -0,63 | 0,26 | 0,07 |
| 8 | -0,01 | 0,00 | 0,37 | -0,38 | 0,14 |
| 9 | 0,36 | 0,13 | 0,37 | -0,01 | 0,00 |
|
Сумма |
0,00 | 0,82 | 0,70 |
![]() ,
,
![]()
Т.к. расчетное значение d попадает в интервал от 0 до d1, т.е. в интервал от 0 до 1,08, то свойство независимости не выполняется, уровни ряда остатков содержат автокорреляцию. Следовательно, модель по этому критерию неадекватна.
3.2. Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. P > [2/3(n-2) – 1, 96 √ (16n-29)/90]
Количество поворотных точек равно 6 (рис.4.5).
Рис. 4.5

Неравенство выполняется (6 > 2). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
3.3. Соответствие ряда остатков нормальному закону распределения определим при помощи RS – критерия:
![]() , где
, где
![]() - максимальный уровень ряда
остатков,
- максимальный уровень ряда
остатков, ![]()
![]() - минимальный уровень ряда
остатков,
- минимальный уровень ряда
остатков, ![]()
![]() - среднеквадратическое
отклонение,
- среднеквадратическое
отклонение,
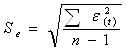 ,
, ![]()
![]()
Расчетное значение попадает в интервал (2,7-3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.
3.4. Проверка равенства нулю математического ожидания уровней ряда остатков.
В нашем случае ![]() , поэтому гипотеза о равенстве
математического ожидания значений остаточного ряда нулю выполняется.
, поэтому гипотеза о равенстве
математического ожидания значений остаточного ряда нулю выполняется.
В таблице 4.3 собраны данные анализа ряда остатков.
Таблица 4.3
| Проверяемое свойство | Используемые статистики | Граница | Вывод | ||
| наименование | значение | нижняя | верхняя | ||
| Независимость | d-критерий | 0,85 | 1,08 | 1,36 | неадекватна |
| Случайность | Критерий поворотных точек | 6>2 | 2 | адекватна | |
| Нормальность | RS-критерий | 2,81 | 2,7 | 3,7 | адекватна |
| Среднее=0? | t-статистика Стьюдента | 0 | -2,179 | 2,179 | адекватна |
| Вывод: модель статистики неадекватна |
4) Оценить точность модели на основе использования средней относительной ошибки аппроксимации.
Для оценки точности полученной модели будем использовать показатель относительной ошибки аппроксимации, который вычисляется по формуле:
![]() ,
где
,
где ![]()
Расчет относительной ошибки аппроксимации
Таблица 4.4
| t | Y | Предсказанное Y |
|
|
|
| 1 | 5 | 4,58 | 0,42 | 0,08 | |
| 2 | 7 | 7,21 | -0,21 | 0,03 | |
| 3 | 10 | 9,84 | 0,16 | 0,02 | |
| 4 | 12 | 12,48 | -0,48 | 0,04 | |
| 5 | 15 | 15,11 | -0,11 | 0,01 | |
| 6 | 18 | 17,74 | 0,26 | 0,01 | |
| 7 | 20 | 20,38 | -0,38 | 0,02 | |
| 8 | 23 | 23,01 | -0,01 | 0,00 | |
| 9 | 26 | 25,64 | 0,36 | 0,01 | |
| Сумма | 45 | 136 | 0,00 | 0,23 | |
| Среднее | 5 | 15,11 |
![]()
Если ошибка, вычисленная по формуле, не превосходит 15%, точность модели считается приемлемой.
5) По построенной модели осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
![]()
![]()
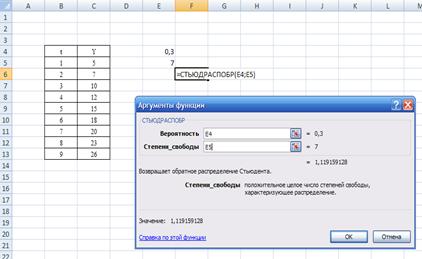
Воспользуемся функцией Excel СТЬЮДРАСПОБР. (рис. 4.10)
t = 1,12
Рис. 4.6
Для построения интервального прогноза
рассчитаем доверительный интервал. Примем значение уровня значимости ![]() , следовательно,
доверительная вероятность равна 70 %, а критерий Стьюдента при
, следовательно,
доверительная вероятность равна 70 %, а критерий Стьюдента при ![]() равен 1,12.
равен 1,12.
Ширину доверительного интервала вычислим по формуле:
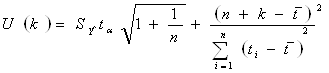 ,
где
,
где
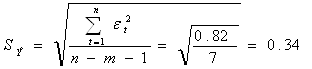
![]()
![]()
![]() (находим из таблицы 4.1)
(находим из таблицы 4.1)
![]() ,
,
![]() .
.
Вычисляем верхнюю и нижнюю границы прогноза (таб. 4.11).
Таблица 4.5
Таблица прогноза
| n +k | U (k) | Прогноз | Формула | Верхняя граница | Нижняя граница |
| 10 | U(1) =0.84 | 28.24 | Прогноз + U(1) | 29.сен | 27.40 |
| 11 | U(2) =1.02 | 30.87 | Прогноз - U(2) | 31.89 | 29.85 |
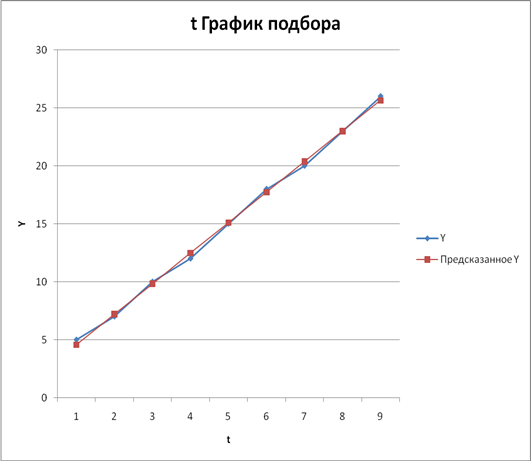
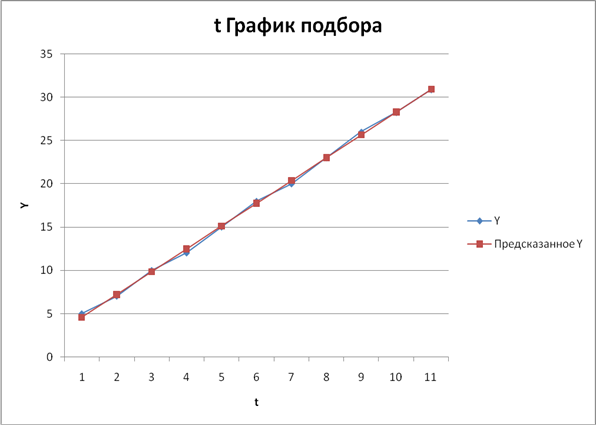
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Преобразуем график подбора (рис. 4.5), дополнив его данными прогноза.
Рис. 4.7
| ... транспортной задачи линейного программирования в среде MS Excel | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН КАЗАХСКИЙ ГОСУДАРСТВЕННЫЙ ЖЕНСКИЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ИНФОРМАТИКИ Дипломная работа ... А именно, если одна из задач (1.6) и (1.7) или (3.1) и (3.2) имеет оптимальное решение, то и двойственная ей задача линейного программирования имеет оптимальное решение, при этом ... Напомним, что исходная постановка задачи о красках сформулирована в форме (3.1) и (3.2). двойственная к ней задача линейного программирования после выполнения простейших ... |
Раздел: Рефераты по информатике, программированию Тип: дипломная работа |
| Билеты на государственный аттестационный экзамен по специальности ... | |
|
1 Кибернетический подход к информационной системе как системе управления. Понятие кибернетической системы связано с процессами управления и ... 2) Матрица коэффициентов системы ограничений будет представлять собой транспонированную матрицу соответствующих коэффициентов исходной задачи. 3) Число переменных в двойственной задаче равно числу ограничений в исходной задаче, и наоборот, число ограничений в двойственной задаче равно числу переменных в исходной. |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Матричные антагонистические игры с нулевой суммой в чистых стратегиях | |
|
Введение Реальные конфликтные ситуации приводят к различным видам игр. Игры различаются по целому ряду признаков: по количеству участвующих в них ... Общая задача линейного программирования заключается в отыскании вектора (х1, х2,..., хn) максимизирующего (минимизирующего) критерий оптимальности (функцию цели задачи) Фирме требуется определить объемы производства (в тоннах) каждой из красок, который максимизирует доход (в тысячах долларов) от реализации продукции, с учетом ограничений на спрос ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Некоторые задачи оптимизации в экономике | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Вятский государственный ... Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находятся с помощью теорем двойственности ... Оптимальный набор потребителя составляет 6 ед. продукта х1 и 8 ед. продукта х2. |
Раздел: Рефераты по экономико-математическому моделированию Тип: дипломная работа |
| ... задачи в матричной форме. Задача оптимального распределения ресурсов | |
|
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ Факультет "Экономический" Кафедра "Экономика, финансы и управление на ... -х1 - х2 = -1 Выразим х2 из второго ограничения и подставим его выражение в первое и третье ограничения, а также в выражение для целевой функции: |
Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа |