Курсовая работа: Матричные антагонистические игры с нулевой суммой в чистых стратегиях
Введение
Реальные конфликтные ситуации приводят к различным видам игр. Игры различаются по целому ряду признаков: по количеству участвующих в них игроков, по количеству возможных игроков, по количеству возможных стратегий, по характеру взаимоотношений между игроками, по характеру выигрышей, по виду функций выигрышей, по количеству ходов, по характеру информационной обеспеченности игроков и т.д. Рассмотрим виды игр в зависимости от их разбиения:
· По количеству стратегий игры делятся на конечные (каждый из игроков имеет конечное число возможных стратегий) и бесконечные (где хотя бы один из игроков имеет бесконечное число возможных стратегий).
· По характеру выигрышей различают игры с нулевой суммой (общий капитал игроков не изменяется, а перераспределяется между игроками в зависимости от получающихся исходов) и игры с ненулевой суммой.
· По виду функций выигрыши игры делятся на матричные (это конечная игра двух игроков с нулевой суммой, в которой задается выигрыш игрока А в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока В, столбец – номеру применяемой стратегии игрока В; на пересечении строки и столбца матрицы находится выигрыш игрока А, соответствующий применяемым стратегиям.
Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования), биматричные игры (это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока А, столбец – стратегии игрока В, на пересечении строки и столбца в первой матрице находится выигрыш игрока А, во второй матрице – выигрыш игрока В.
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные непрерывные игры (Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения), и т.д.
Возможны также и другие подходы к разбиению игр. Теперь вернёмся непосредственно к теме исследования, а именно к Теории игр. Для начала дадим определение этому понятию.
Теория игр - раздел математики, изучающий формальные модели принятия оптимальных решений в условиях конфликта. При этом под конфликтом понимается явление, в котором участвуют различные стороны, наделённые различными интересами и возможностями выбирать доступные для них действия в соответствии с этими интересами. В условиях конфликта стремление противника скрыть свои предстоящие действия порождает неопределённость. Наоборот, неопределённость при принятии решений (например, на основе недостаточных данных) можно интерпретировать как конфликт принимающего решения субъекта с природой. Поэтому теория игр рассматривается также, как теория принятия оптимальных решений в условиях неопределённости. Она позволяет систематизировать некоторые важные аспекты принятия решений в технике, сельском хозяйстве, медицине и социологии и других науках. Участвующие в конфликте стороны называются коалициями действия; доступные для них действия - их стратегиями; возможные исходы конфликта – ситуациями.
Задача теории состоит в том, что является:
1) оптимальным поведением в игре.
2) исследование свойств оптимального поведения
3) определение условий, при которых его использование осмысленно (вопросы существования, единственности, а для динамических игр и вопросы именной состоятельности).
4) построение численных методов нахождения оптимального поведения.
Теория игр, созданная для математического решения задач экономического и социального происхождения, не может в целом сводиться к классическим математическим теориям, созданным для решения физических и технических задач. Однако в различных конкретных вопросах теория игр широко используются весьма разнообразные классические математические методы.
Кроме этого, теория игр связана с рядом математических дисциплин внутренним образом. В теории игр систематически и по существу употребляются понятия теории вероятностей. На языке теории игр можно сформулировать большинство задач математической статистики, и так как теория игр, связана с теорией принятия решений, то она рассматривается как существенная составная часть математического аппарата исследования операций.
Математическое понятие игры необычайно широко. Оно включает в себя так называемые салонные игры (в том числе шахматы, шашки, игра ГО, карточные игры, домино), но может использоваться и для описания моделей экономической системы с многочисленными конкурирующими друг с другом покупателями и продавцами. Не вдаваясь в детали, игру в общих чертах можно определить как ситуацию, в которой одно или несколько лиц («игроков») совместно управляют некоторым множеством переменных и каждый игрок, принимая решение, должен учитывать действия всей группы. «Платеж», приходящийся на долю каждого игрока, определяется не только его собственными действиями, но и действиями других членов группы. Некоторые из «ходов» (индивидуальных действий) в ходе игры могут носить случайный характер. Наглядной иллюстрацией может служить известная игра в покер: начальная сдача карт представляет собой случайный ход. Последовательность ставок и контрставок, предшествующая финальному сравнению взяток, образована остальными ходами в игре.
Математическая ТЕОРИЯ ИГР началась с анализа спортивных, карточных и других игр. Рассказывают, что первооткрыватель теории игр, выдающийся американский математик XX в. Джон фон Нейман пришел к идеям своей теории, наблюдая за игрой в покер. Отсюда и произошло название «теория игр».
Начнем исследование данной темы с ретроспективного анализа развития теории игр. Рассмотрим историю и развитие вопроса теории игр. Обычно «генеалогическое дерево» представляется в виде дерева в смысле теории графов, в которых разветвление происходит от некоторого единого «корня». Родословная теории игр - книга Дж. фон Неймана и О. Моргенштерна. Поэтому исторический ход развития теории игр как математической дисциплины, естественным образом расчленяется на три этапа:
Первый этап - до выхода в свет монографии Дж. фон Неймана и О. Моргенштерна. Его можно назвать «до монографическим». На этом этапе игра выступает пока еще как конкретное состязание, описываемое своими правилами в содержательных терминах. Лишь в конце его Дж. фон Нейман вырабатывает представление об игре как об общей модели абстрактного конфликта. Итогом этого этапа явилось накопление ряда конкретных математических результатов и даже отдельных принципов будущей теории игр.
Второй этап составляет сама монография Дж. фон Неймана и
О. Моргенштерна «Теория игр и экономическое поведение» (1944), объединившая в себе большинство ранее полученных (впрочем, по современным математическим масштабам довольно немногочисленных) результатов. Она впервые представила математический подход к играм (как в конкретном, так и в абстрактном понимании этого слова) в виде систематической теории.
Наконец, на третьем этапе теория игр в своем подходе к изучаемым объектам мало, чем отличается от других разделов математики и развивается в значительной мере по общим с ними закономерностям. При этом, разумеется, существенное влияние на формирование направлений теории игр оказывает специфика ее практических приложений, как фактических, так и возможных.
Однако даже математическая теория игр не способна стопроцентно предопределить исход некоторых конфликтов. Представляется возможным выделить три основные причины неопределенности исхода игры (конфликта).
Во-первых, это игры, в которых имеется реальная возможность исследования всех или, по крайней мере, большинства вариантов игрового поведения из них одного наиболее истинного, ведущего к выигрышу. Неопределенность вызвана значительным числом вариантов, поэтому не всегда представляется возможным исследовать абсолютно все варианты (к примеру, японская игра ГО, русские и международные шашки, британские реверси).
Во-вторых, непрогнозируемое игроками, случайное влияние факторов на игру. Эти факторы оказывают решающее воздействие на исход игры и лишь в малой степени могут быть или вообще не могут быть контролируемыми и определяемыми играющими. Окончательный исход игры лишь в малой, крайне незначительной степени определяется самими действиями игроков. Игры, исход которых оказывается неопределенным в силу случайных причин, называются азартными. Исход игры всегда носит вероятностный либо предположительный характер (рулетка, игра в кости, игра в «орлянку»).
В-третьих, неопределенность вызвана отсутствием информации о том, какой именно стратегии придерживается играющий противник. Неведение игроков о поведении соперника носит принципиальный характер и определяется самим правилами игры. Такие игры именуются стратегическими.
Теория игр является одним из важных разделов «Исследования операций» и представляет собой теоретические основы математических моделей принятия оптимальных решений в конфликтных ситуациях рыночных отношений, носящих характер конкурентной борьбы, в которых одна противоборствующая сторона выигрывает у другой за счет проигрыша другой. Наряду с такой ситуацией в рамках науки «Исследование операций», которая предоставляет математическое описание постановок различных задач по принятию решений, рассматриваются ситуации риска и неопределенности. В ситуации неопределенности вероятности условий неизвестны и нет никакой возможности получить о них дополнительную статистическую информацию. Окружающая решение задачи среда, которая проявляется в тех или иных условиях, называется «природой», а соответствующие математические модели называются «играми с природой» или «теорией статистических игр». Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявление для каждого из них «оптимальной стратегии».
Теория игр является нормативной теорией, то есть предметом её изучения являются не столько сами модели конфликтов (игры), сколько содержание принимаемых в играх принципов оптимальности, существования ситуаций, на которых эти принципы оптимальности реализуются (такие ситуации или множества ситуаций называются решениями в смысле соответствующего принципа оптимальности), и, наконец, способы разрешения таких ситуаций. Рассматриваемые в теории игр объекты (игры), весьма разнообразны. Практически это означает, что единого для всех игр истолкования понятия оптимальности ещё не выработано. Поэтому прежде чем говорить, например, о наивыгоднейшем поведении игрока в игре, необходимо установить, в каком смысле эта выгодность понимается. Все применяемые в теории игр принципы оптимальности при всём их внешнем разнообразии отражают прямо или косвенно идею устойчивости ситуаций или множеств ситуаций, составляющих решения. В бескоалиционных играх основным принципом оптимальности считается принцип осуществимости цели, приводящий к ситуациям равновесия. Эти ситуации характеризуются тем свойством, что любой игрок, который отклонится от ситуации равновесия (при условии, что остальные игроки не изменят своих стратегий), не увеличит этим своего выигрыша.
Теория игр, созданная для математического решения задач экономического и социального происхождения, не может в целом сводиться к классическим математическим теориям, созданным для решения физических и технических задач. Однако в различных конкретных вопросах теория игр широко используются весьма разнообразные классические математические методы. В теории игр систематически и по существу употребляются понятия теории вероятностей. Кроме того, теория игр, будучи теорией принятия решений, может рассматриваться как существенная составная часть математического аппарата исследования операций. Теория игр рассматривает задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого из субъектов зависит и от решений, принимаемых всеми остальными участниками. Предметом исследования теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия. Примерами игр являются обычные игры: салонные спортивные, карточные игры. Именно с анализа подобных игр начиналась математическая теория игр, которые служат прекрасным материалом для иллюстрации положений и выводов этой теории. В итоге, всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, т.е. описывать:
а) множество заинтересованных сторон (мы будем называть их игроками; в литературе по теории игр они именуются также субъектами, лицами, сторонами, участниками). В случае если число игроков, конечно, они различаются по своим номерам (1-й игрок и 2-й игрок в игре в орлянку или в случае дуополии) или по присваиваемым им именам (например, продавец и покупатель в ситуации монополия-монопсония);
б) возможные действия каждой из сторон, именуемые также стратегиями или ходами;
в) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.
В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общеизвестны, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функции выигрыша и стратегии всех остальных игроков, и в соответствии с этой информацией организует свое поведение.
Теория игр впервые была систематически изложена Дж. фон Нейманом и О. Монгерштерном в 1944 г., хотя отдельные результаты были опубликованы еще в 20-х годах. Нейман и Моргенштерн написали оригинальную книгу, которая содержала главным образом экономические примеры, поскольку экономическому конфликту легче всего придать численную форму. Во время второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. Затем главное внимание снова стало уделяться экономическим проблемам.
ГЛАВА 1. МАТРИЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ
1.1 Принятие решений
Принятие решений – каждодневная деятельность человека, часть его повседневной жизни. Простые решения принимаются легко, часто автоматически; в сложных и ответственных случаях человек обращается за помощью к друзьям, родственникам, опытным людям, книгам для подтверждения своего решения, несогласия с ним или советом. Решения разрабатываются и реализуются с разной степенью профессионализма, поэтому их диапазон практически неограничен – от необдуманных до детально разработанных.
Что же такое «наилучшее» решение? В исследованиях операций «наилучшим» считается решение, доставляющее оптимум функции, выражающей цель системы. Более общее определение «правильного» или «наилучшего» решения в смысле принятия решений будем считать выбор такой альтернативы из числа возможных, в которой с учетом всех разнообразных факторов и противоречивых требований будет оптимизирована общая ценность, то есть она будет в максимальной степени соответствовать достижению поставленной цели. Отметим, что в отличии от исследования операций, в теории принятия решений не существует абсолютно лучшего решения. Решение является лучшим лишь для конкретного лица принимающего решение, в отношении поставленных им целей, при заданных условиях. Эта субъективная оценка оказывается в настоящее время единственно возможной основой объединения разнородных физических параметров решаемой проблемы в единую модель, позволяющую оценивать варианты решений.
Альтернативы.
Альтернатива – это один из возможных способов достижения цели или один из конечных вариантов решений. Альтернативы отличаются друг от друга последовательностью и приемами использования активных ресурсов. Для любой задачи принятия решений должна существовать тройка: цель, критерии, альтернативы. Если отсутствует один из компонентов, то проблема не поставлена. При наличии менее двух альтернатив, отсутствует выбор.
Альтернативы могут быть зависимыми и независимыми. Если действие над какой-либо альтернативой не влияет на качество других, то такая альтернатива является независимой. При зависимых альтернативах оценки одних из них оказывают влияние на качество других.
Задачи принятия решений существенно различаются в зависимости от наличия альтернатив на момент выработки политики и принятия решений. В некоторых задачах все возможные альтернативы известны и из них производится выбор наилучшей. Например, можно выбирать лучший университет, наиболее надежный банк или же банк с оптимальным соотношением «выгода-риск», наиболее благоприятный район для покупки квартиры и т.д. Существует множество задач, в которых все альтернативы или их часть появляются после принятия решений. Например, требуется разработать правила отбора лиц на предоставление грантов на конкурсной основе. Альтернативы в такой задаче появляются после разработки и декларации правил отбора.
Также существуют задачи, когда на основе рассмотрения имеющихся альтернатив возникают новые альтернативы. Первичные альтернативы не всегда удовлетворяют участников процесса выбора. Рассматривая их, участники понимают, чего же все-таки не хватает, что реализуемо при данной ситуации, а что нет. Этот класс задач можно назвать задачами с конструируемыми альтернативами.
Критерии
В современной науке о принятии решений считается, что варианты решений (альтернативы) характеризуются различными показателями их привлекательности для ЛПР (лицо, принимающее решение). Эти показатели называют признаками, факторами, атрибутами, критериями.
Пусть задано некоторое конечное множество
альтернатив![]() . Из множества
. Из множества ![]() или любого его подмножества
или любого его подмножества
![]() необходимо выделить одно или
несколько вариантов решений в некотором смысле лучших или более соответствующих
каким-либо заранее оговоренным условиям. Для решения этой задачи обычно используется
следующий подход:
необходимо выделить одно или
несколько вариантов решений в некотором смысле лучших или более соответствующих
каким-либо заранее оговоренным условиям. Для решения этой задачи обычно используется
следующий подход:
Множество вариантов ![]() проецируется на числовую ось,
так что каждому варианту соответствует конкретная точка числовой оси. В одну и ту
же точку может либо не может проецироваться более одного варианта. Числовая ось,
на которую спроецировано множество вариантов
проецируется на числовую ось,
так что каждому варианту соответствует конкретная точка числовой оси. В одну и ту
же точку может либо не может проецироваться более одного варианта. Числовая ось,
на которую спроецировано множество вариантов ![]() ,
называется шкалой. Сам процесс проецирования, то есть приписывания элементам из
,
называется шкалой. Сам процесс проецирования, то есть приписывания элементам из
![]() числовых значений, соответствующих
точкам числовой оси, в которые они проецируются – шкалированием. Если после такого
проецирования упорядочить все варианты из
числовых значений, соответствующих
точкам числовой оси, в которые они проецируются – шкалированием. Если после такого
проецирования упорядочить все варианты из ![]() по
величине приписанных им числовых оценок и сохранить за вариантами лишь их порядковый
номер, то образованная таким образом шкала называется порядковой или ранговой.
по
величине приписанных им числовых оценок и сохранить за вариантами лишь их порядковый
номер, то образованная таким образом шкала называется порядковой или ранговой.
Если вариант считается тем «лучше» или тем более соответствующим заранее фиксированной цели выбора, чем большая (или меньшая) числовая или ранговая оценка приписывается варианту, то шкала называется критерием для выбора или критериальной шкалой.
Рассмотрим вариант ![]() и выразим его критериальную
оценку, т.е. числовое значение той точки шкалы, в которую вариант спроецирован через
и выразим его критериальную
оценку, т.е. числовое значение той точки шкалы, в которую вариант спроецирован через
![]() . Обозначим через
. Обозначим через ![]() функцию, заданную на всех вариантах
функцию, заданную на всех вариантах
![]() из
из ![]() и имеющую числовые значения,
определяемые критериальной шкалой. Такая функция и называется критерием.
и имеющую числовые значения,
определяемые критериальной шкалой. Такая функция и называется критерием.
Критерий – это способ выражения различий в оценке альтернативных вариантов с точки зрения участников процесса выбора, т.е. показатель привлекательности вариантов решений. Именно с помощью критерия ЛПР будет судить о предпочтительности исходов, а значит, и способов проведения операции по решению проблемы. Значимость того или иного из выбранных критериев определяется именно тем, что ЛПР не считает возможным выносить суждения о предпочтительности исхода операции, если именно того или иного критерия оценки недостает.
В профессиональной деятельности выбор критериев часто определяется многолетней практикой, опытом. В подавляющем большинстве задач выбора имеется достаточно много критериев оценок вариантов решений. Существует ряд свойств или требований, которым должен (по возможности) удовлетворять набор критериев. Набор критериев должен быть: полным, действенным, разложимым, неизбыточным и минимальным.
Полнота набора означает, что он должен охватывать
все важные аспекты проблемы. Набор критериев является полным, если с его помощью
можно показать степень достижения общей цели, то есть набор из ![]() критериев полон, если, зная
значения n-мерного критерия, связанного с общей
целью, ЛПР имеет полное представление о степени достижения общей цели.
критериев полон, если, зная
значения n-мерного критерия, связанного с общей
целью, ЛПР имеет полное представление о степени достижения общей цели.
Действенность критериев. ЛПР должно понимать смысл критериев и влияние их действий на обсуждаемую проблему. Критерии должны быть такими, чтобы их можно было объяснять другим, особенно в тех случаях, когда важнейшей целью работы является выработка и защита определенной позиции. Поскольку смысл анализа решений помочь ЛПР выбрать лучший курс действий, то и критерии должны служить этой цели.
Разложимость. При использовании n критериев необходимо построить n-мерную функцию предпочтений. Для задач с большим числом критериев полезно произвести декомпозицию задачи и разложить ее на подзадачи, каждая из которых содержит меньшее число критериев. То есть желательно, чтобы набор критериев был разложим.
Неизбыточность. Критерии должны быть определены так, чтобы не дублировался учет одних и тех же аспектов решаемой проблемы.
Минимальная размерность. Желательно, чтобы набор критериев оставался настолько малым, насколько это возможно. Увеличение числа критериев приводит, с одной стороны, к анализу решаемой задачи в более широком плане, с другой стороны, может сильно усложнить и запутать анализ, что приведет к ошибочности результатов.
Формальные методы формирования набора критериев предложить трудно. Они очень сильно зависят от опыта и способности экспертов и, что крайне важно, характера лица, принимающего решения.
Схема процесса принятия решений
В классической книге лауреата нобелевской премии профессора Г. Саймона «The New Science of Management Decision», 1960 процесс принятия решений разбит на четыре фазы: сбор информации (intelligence); поиск и построение альтернатив (design); выбор альтернатив (choice); оценка результатов (review). Первая фаза – сбор информации, сконцентрирована на идентификации проблемы принятия решения и сборе всей доступной информации о ней. При поиске и построении альтернатив (вторая фаза) центральным вопросом становится определение относительно небольшого числа альтернатив, которые следует изучить в деталях. На третьей фазе происходит выбор одного из вариантов решений из множества альтернатив, подготовленных на второй фазе. Последний шаг в процессе принятия решений – это реализация выбранной альтернативы и обобщение опыта, полученного в процессе решения проблемы.
Таким образом, само решение принимается в рамках второй и третьей фаз:
· конструирование относительно небольшого множества альтернатив;
· окончательный выбор варианта решения из сформированного множества.
Схематически две эти фазы представлены на рисунке 1. Фазы существенным образом различаются как целями и информацией, так и методами. На фазе, в которой одним из вопросов является выбор относительно небольшого числа альтернатив (эту фазу часто называют early screening). ЛПР должно принять во внимание все возможные пути достижения цели. В процессе же детального анализа и окончательного выбора альтернативы, ЛПР ограничивает себя малым числом подготовленных вариантов решений. Выбору альтернативы из этого числа предшествует их детальное изучение.
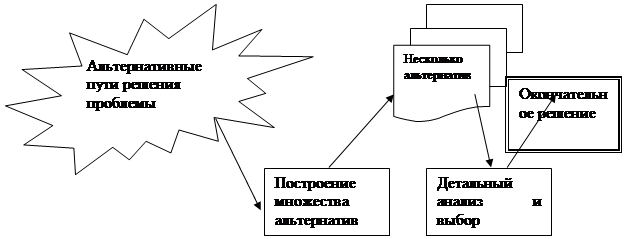
Рис. 1 - Фазы процесса принятия решений
Классификация задач принятия решений
Задачи принятия решений отличаются большим многообразием, классифицировать их можно по различным признакам, характеризующим количество и качество доступной информации. В общем случае задачи принятия решений можно представить следующим набором информации:
![]()
где ![]() – постановка задачи;
– постановка задачи;
![]() – множество допустимых альтернативных вариантов;
– множество допустимых альтернативных вариантов;
![]() – множество методов измерения предпочтений;
– множество методов измерения предпочтений;
![]() – множество методов измерения предпочтений (например,
использование различных шкал);
– множество методов измерения предпочтений (например,
использование различных шкал);
![]() – отображение множества допустимых альтернатив в множество
критериальных оценок;
– отображение множества допустимых альтернатив в множество
критериальных оценок;
![]() – системы предпочтений эксперта;
– системы предпочтений эксперта;
![]() - решающее правило, отражающее систему предпочтений.
- решающее правило, отражающее систему предпочтений.
Любой из элементов этого набора может служить классификационным признаком принятия решений.
По виду отображения F. Попытки применения исследования операций для решения различного класса задач выявили большие различия в природе изучаемых систем. В связи с этим Г. Саймоном и А. Ньюэллом была предложена следующая классификация:
1 Хорошо структурированные или количественно сформулированные проблемы, в которых существенные зависимости выяснены настолько хорошо, что они могут быть выражены в числах или символах, принимающих, в конце концов, численные оценки.
2 Слабоструктурированные или смешанные проблемы, которые содержат как качественные, так и количественные элементы, причем качественные, малоизвестные и неопределенные стороны имеют тенденцию доминировать.
3 Неструктурированные или качественно выраженные проблемы, содержащие лишь описание важнейших ресурсов, признаков и характеристик, количественные зависимости между которыми совершенно неизвестны.
Согласно этой классификации проблемы исследования операций можно назвать хорошо структурированными. В типичных задачах исследования операций объективно существует реальность, допускающая строгое количественное описание и определяющая существование единственного очевидного критерия качества. Этот класс задач широко применяется при оценке и выборе элементов технических устройств, например: оптимизация форм корпуса самолетов или кораблей, управление электростанцией, расчет радиоактивного заражения местности, минимизация затрат на перевозки и т.д. Для этих задач существуют адекватные математические модели процессов и/или устройств, и существуют данные, позволяющие априорно определить параметры моделей.
Характерными особенностями проблем третьего класса являются:
1 уникальность выбора в том смысле, что каждый раз проблема является новой для ЛПР;
2 неопределенность в оценках альтернативных вариантов решений проблемы;
3 качественный характер оценки вариантов решения проблемы, чаще всего формулируемой в словесной форме;
4 оценка альтернатив может быть получена лишь на основе субъективных предпочтений ЛПР или ГПР;
5 критериальные оценки могут быть получены только от экспертов.
К этому классу проблем относятся, например, проблемы планирования научных исследований, конкурсного отбора проектов, планирования развития города и т.д.
Ко второму классу проблем относят многие смешанные задачи, использующие как эвристические предпочтения, так и аналитические модели. Сюда относятся многие проблемы, связанные с экономическими и политическими решениями, проблемы медицинской диагностики и т.п.
По постановке задачи Т. Задачи принятия решений можно разбить на две группы:
Задачи первой группы:
Дано: группа из ![]() альтернатив-вариантов решения
проблемы и
альтернатив-вариантов решения
проблемы и ![]() критериев, предназначенных
для оценки альтернатив; каждая из альтернатив имеет оценку по каждому из критериев.
Требуется: построить решающие правила на основе предпочтений ЛПР, позволяющие:
выделить лучшую альтернативу; упорядочить альтернативы по качеству; отнести альтернативы
к упорядоченным по качеству классам решений.
критериев, предназначенных
для оценки альтернатив; каждая из альтернатив имеет оценку по каждому из критериев.
Требуется: построить решающие правила на основе предпочтений ЛПР, позволяющие:
выделить лучшую альтернативу; упорядочить альтернативы по качеству; отнести альтернативы
к упорядоченным по качеству классам решений.
Задачи второй группы:
Дано: группа из ![]() критериев, предназначенных
для оценки любых возможных альтернатив; альтернативы либо заданы частично, либо
появляются после построения решающего правила.
критериев, предназначенных
для оценки любых возможных альтернатив; альтернативы либо заданы частично, либо
появляются после построения решающего правила.
Требуется: на основании предпочтений ЛПР построить решающие правила, позволяющие: упорядочить по качеству все возможные альтернативы; отнести все возможные альтернативы к одному из нескольких (указанных ЛПР) классов решений.
А теперь от теории принятия решений перейдём к матричным играм.
Матричная игра игроков с нулевой суммой может рассматриваться, как следующая абстрактная игра двух игроков.
Игрок А имеет m стратегий i = 1, 2,
…, m. Игрок В имеет n стратегий j = 1, 2,
…, n. Каждой паре стратегий (i, j) поставлено в соответствие число а![]() , выражающее выигрыш игрока
А за счет игрока В, если первый игрок примет свою i-ю стратегию, а второй – свою j-ю стратегию.
, выражающее выигрыш игрока
А за счет игрока В, если первый игрок примет свою i-ю стратегию, а второй – свою j-ю стратегию.
Каждый из игроков делает один ход: игрок
А выбирает свою i-ю
стратегию (i = ![]() ), В – свою j-ю стратегию (j =
), В – свою j-ю стратегию (j = ![]() ), после чего игрок
А получает выигрыш а
), после чего игрок
А получает выигрыш а![]() за счет
игрока А (если а
за счет
игрока А (если а![]() < 0, то это значит,
что игрок В платит второму сумму |а
< 0, то это значит,
что игрок В платит второму сумму |а![]() |).
На этом игра заканчивается.
|).
На этом игра заканчивается.
Каждая стратегия игрока i = ![]() или j =
или j = ![]() часто называется
чистой стратегией.
часто называется
чистой стратегией.
Если рассмотреть матрицу А:
|
а |
а |
… |
а |
… |
а |
| … | … | … | … | … | … |
|
а |
а |
… |
а |
… |
а |
| … | … | … | … | … | … |
|
а |
а |
… |
а |
… |
а |
то проведение каждой партии матричной
игры с матрицей сводится к выбору игроком А i-й строки, а игроком В j-го столбца и получения игроком А
(за счет игрока В) выигрыша а![]() .
.
Как было сказано выше, главным в теории игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока.
Исходя из этих позиций, игрок А
исследует матрицу выигрышей следующим образом: для каждого значения i (i = ![]() ) определяется минимальное значение выигрыша в зависимости
от применяемых стратегий игрока В
) определяется минимальное значение выигрыша в зависимости
от применяемых стратегий игрока В
![]() а
а![]() (i =
(i = ![]() )
)
т.е. определяется минимальный выигрыш
для игрока А при условии, что он примет свою i-ю чистую стратегию, затем из этих минимальных выигрышей
отыскивается такая стратегия i = i![]() , при которой этот минимальный выигрыш
будет максимальным, т.е. находится
, при которой этот минимальный выигрыш
будет максимальным, т.е. находится
![]()
![]() а
а![]() =
а
=
а![]() = α
= α
1.2 Определение игры
Дадим определение понятию «Игра». Игрой называется набор
![]() ,
,
где N – произвольное множество
игроков; S – произвольное множество всех исходов
игры; XK - произвольное множество
стратегий коалиции K![]() N; S(XK)
N; S(XK) ![]() S – множество возможных
исходов, если коалиция K применяет стратегию
хK
S – множество возможных
исходов, если коалиция K применяет стратегию
хK![]() ХK;
ХK; ![]() - транзитивное отношение предпочтения
коалиции K
- транзитивное отношение предпочтения
коалиции K![]() N на S. При математической
формализации игра, должна проходить по определенным правилам, которые представляют
следующую систему условий:
N на S. При математической
формализации игра, должна проходить по определенным правилам, которые представляют
следующую систему условий:
- возможные действия каждого из игроков;
- объем информации, которую может получить каждая сторона о действиях другой;
- исход игры в результате каждой совокупности ходов противников.
Игроки: Считается заданным
список игроков. Если игроков различать по номерам, то их список сводится к множеству
![]() , где
, где ![]() -
число игроков. Считается, что игроки осведомлены о наличии каждого из своих партнеров.
-
число игроков. Считается, что игроки осведомлены о наличии каждого из своих партнеров.
Действия: Каждый игрок ![]() имеет в своём
распоряжении некоторый набор стратегий
имеет в своём
распоряжении некоторый набор стратегий ![]() .
Множества
.
Множества ![]() могут быть как конечными, так
и бесконечными. В основе рационального поведения участников игры лежит так называемый
постулат «общего знания»: каждый полностью информирован о своих стратегических возможностях
и о стратегических возможностях своих партнёров. Процесс игры состоит в выборе каждым
из игроков своей стратегии:
могут быть как конечными, так
и бесконечными. В основе рационального поведения участников игры лежит так называемый
постулат «общего знания»: каждый полностью информирован о своих стратегических возможностях
и о стратегических возможностях своих партнёров. Процесс игры состоит в выборе каждым
из игроков своей стратегии: ![]() . В результате
складывается игровая ситуация
. В результате
складывается игровая ситуация ![]() . Множество
Ω всех возможных игровых ситуаций образует ситуационное пространство игры,
обозначаемое
. Множество
Ω всех возможных игровых ситуаций образует ситуационное пространство игры,
обозначаемое ![]() .
.
Интересы: Степень заинтересованности игрока k в той или иной ситуации s определяется размером выигрыша ![]() ,
который в этой ситуации он может получить. Таким образом, правила игры получаются
заданием так называемых, функций выигрыша
,
который в этой ситуации он может получить. Таким образом, правила игры получаются
заданием так называемых, функций выигрыша ![]() .
Эти функции принимают числовые значения и имеют общую область определения
.
Эти функции принимают числовые значения и имеют общую область определения ![]() . Каждая из таких функций есть
функция «n-переменных»:
. Каждая из таких функций есть
функция «n-переменных»: ![]() .
.
Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, то есть выявление для каждого из них «оптимальной стратегии». Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимально возможный средний проигрыш).
Опишем некоторые основные понятия, используемые в теории игр. Заинтересованные стороны называются игроками. Любое возможное действие для игрока называется его стратегией. В условиях конфликта каждый игрок придерживается выбранной им стратегии, в результате появляется набор стратегий, называемый ситуацией. Заинтересованность игроков в каждой конкретной ситуации, проявляется в том, что каждому игроку в данной ситуации приписывается число, выражающее степень удовлетворённости его интересов. Такое число называется выигрышем.
Игра начинается с некоторого положения и состоит из последовательности личных ходов, при каждом из которых один из игроков совершает выбор среди нескольких возможностей. Некоторые ходы могут быть случайными (таковы, например, бросание кости или тасование колоды карт).
Примерами игр такого типа являются шахматы, в которых нет случайных ходов (кроме разыгрывания того, кто будет играть белыми), бридж, в котором случай играет большую роль.
На примере бриджа и шахмат можно показать другой важный элемент игры. Именно, в шахматной игре каждый игрок знает любой ход, который был сделан до этого момента, в то время как в бридже это знание игрока обычно неполно. Таким образом, в некоторых играх игрок не в состоянии определить, какой из нескольких возможных ходов был фактически сделан, будь то ход одного из его противников или случайный ход. На практике это означает, что, когда игрок делает свой ход, он не знает точной позиции игры и должен делать ход с учетом того, что имеется несколько возможных позиций.
В конце игры игроки обычно получают какой-либо выигрыш, (может быть в форме денег, престижа или иного удовлетворения), который зависит от протекания игры. В общее представление об игре входят 3 элемента:
1 чередование ходов, которые могут быть как личными, так и случайными
2 возможная недостаточность информации
3 функция выигрыша
Запишем теперь основные этапы поиска решения игры:
1 проверка наличия (или отсутствия) равновесия в чистых стратегиях (к этому вопросу вернёмся чуть позже). При наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры.
2 поиск доминирующих стратегий (в случае успеха этого поиска – отбрасывание доминирующих строк и столбцов в исходной матрице игры).
3 замена игры на её смешанное расширение и отыскание оптимальных смешанных стратегий и цены игры.
| Игрок 2 стратегия 1 | Игрок 2 стратегия 2 | |
| Игрок 1 стратегия 1 |
4, 3 |
–1, –1 |
| Игрок 1 стратегия 2 |
0, 0 |
3, 4 |
|
Нормальная форма для игры с 2 игроками, у каждого из которых по 2 стратегии. |
Отметим, что нормальная форма антагонистической игры сводится к некоторой
матрице А с числом строк равным числу стратегий игрока 1 и с числом столбцов,
равным числу стратегий игрока 2. Выигрыш – если игрок 1 выбирает i-ю стратегию, а игрок 2 j-ю стратегию – представляет собой элемент
![]() в i-ой строке и в j-ом столбце
данной матрицы.
в i-ой строке и в j-ом столбце
данной матрицы.
Игроков, как участников игры, интересует, какие из стратегий являются выигрышными
с точки зрения максимизации доли каждого игрока в выигрыше. Однако, результаты случайных
ходов, известны только в вероятностном смысле, поэтому лучше рассматривать математическое
ожидание функции выигрыша, определённое в случае, когда игроки используют n-набор стратегий. Поэтому для описания
математического ожидания функции выигрыша, при условии, что игрок i применяет стратегию ![]() ,
можно употребить следующее обозначение
,
можно употребить следующее обозначение ![]() Исходя
из этого функцию
Исходя
из этого функцию ![]() на множестве всех
возможных значений переменных
на множестве всех
возможных значений переменных ![]() можно выразить
либо в форме соотношения, либо в виде n-мерной матрицы n-векторов. Такая n-мерная таблица называется нормальной формой игры
Г. В нормальной (стратегической) форме игра описывается платёжной матрицей.
Каждая сторона матрицы – это игрок, строки определяют стратегии первого игрока,
а столбцы – второго. На пересечении двух стратегий можно увидеть выигрыши, которые
получат игроки. На примере, если игрок 1 выбирает первую стратегию, а второй игрок
– вторую, то на пересечении получится (1,-1). Это значит, что в результате хода
игроки потеряли по одному очку.
можно выразить
либо в форме соотношения, либо в виде n-мерной матрицы n-векторов. Такая n-мерная таблица называется нормальной формой игры
Г. В нормальной (стратегической) форме игра описывается платёжной матрицей.
Каждая сторона матрицы – это игрок, строки определяют стратегии первого игрока,
а столбцы – второго. На пересечении двух стратегий можно увидеть выигрыши, которые
получат игроки. На примере, если игрок 1 выбирает первую стратегию, а второй игрок
– вторую, то на пересечении получится (1,-1). Это значит, что в результате хода
игроки потеряли по одному очку.
Пример 1: игра «Орлянка».
|
X \ Y |
Орел |
Решка |
|
Орел |
-1, 1 | 1, -1 |
|
Решка |
1, -1 | -1, 1 |
Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает – платит первому одну денежную единицу, если угадывает – первый платит ему одну денежную единицу. В данной игре каждый игрок имеет две стратегии: «орёл» и «решка». Множество ситуаций в игре состоит из 4 элементов. В строках таблицы указаны стратегии первого игрока Х, в столбцах – стратегии второго игрока Y. Для каждой из ситуаций указаны выигрыши первого и второго игроков.
Рассмотрим основную теорему матричных игр.
Основная теорема теории матричных игр (по Дж. фон Нейману).
Для матричной игры с любой матрицей А величины ![]() и
и ![]() равны между собой, т.е.
равны между собой, т.е.
![]()
Более того, существует хотя бы одна ситуация в смешанных стратегиях ![]() , для которой выполняется соотношение
, для которой выполняется соотношение
![]()
Иными словами, любая матричная игра имеет решение в смешанных стратегиях. Поиск этого решения опирается на установленные факты.
Приведём доказательство данной теоремы (автор: Дж. Б. Данциг, 1951г.)
Теорема. Каждая матричная игра с нулевой суммой всегда имеет решение в смешанных
стратегиях, т.е. существуют такое число ![]() и
такие стратегии
и
такие стратегии ![]() и
и ![]() игроков 1 и 2 соответственно,
выполняются неравенства:
игроков 1 и 2 соответственно,
выполняются неравенства:
![]() .(*)
.(*)
Комментарий. Формула (*) означает, что: если игрок 1 отклоняется от своей оптимальной стратегии, то его выигрыш не увеличивается по сравнению с ценой игры; если от своей оптимальной стратегии отклоняется игрок 2, то по сравнению с ценой игры его проигрыш не уменьшается.
Доказательство.
Пусть матрица игры равна ![]() . Всегда
можно считать, что все коэффициенты
. Всегда
можно считать, что все коэффициенты ![]() . Если это
не так, то предположим, что наименьший из всех отрицательных коэффициентов есть
. Если это
не так, то предположим, что наименьший из всех отрицательных коэффициентов есть
![]() . Тогда увеличим все элементы
платёжной матрицы на произвольное положительной число
. Тогда увеличим все элементы
платёжной матрицы на произвольное положительной число ![]() . Функция выигрыша при этом
окажется равной
. Функция выигрыша при этом
окажется равной
![]() .
.
Из этого следует, что от увеличения всех элементов матрицы ![]() на величину
на величину ![]() цена игры увеличивается на
эту величину, причём оптимальные смешанные стратегии не изменяются.
цена игры увеличивается на
эту величину, причём оптимальные смешанные стратегии не изменяются.
Для определения среднего оптимального выигрыша игрока 1, соответствующего
первоначальной платёжной матрице, необходимо из найденной цены игры вычесть величину
![]() .
.
1.3 Классификация игр
Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков, по числу стратегий, по свойствам функций выигрыша, по возможности предварительных переговоров и взаимодействия между игроками в ходе игры. В зависимости от числа игроков различают игры с двумя, тремя и более участниками. Согласно другому принципу классификации (по количеству стратегий) различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий (например, в игре в орлянку игроки имеют по два возможных хода - они могут выбрать "орел" или "решку"). Сами стратегии в конечных играх нередко называются чистыми стратегиями (смысл этого названия будет ясен далее).
Соответственно, в бесконечных играх игроки имеют бесконечное число возможных стратегий. Так в ситуации «Продавец-Покупатель» каждый из игроков может назвать любую устраивающую его цену и количество продаваемого (покупаемого) товара. Третий способ классификации игр-по свойствам функции выигрыша (платежных функций). Важным случаем в теории игр является ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Игры в орлянку или в шахматы - типичные примеры антагонистических игр. Прямой противоположностью играм такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков. Можно также выделить 2 способа задания игры.
1 так называемая позиционная форма. При этом определяются:
· порядок ходов
· альтернативы (возможные ходы), доступные каждому из игроков на момент наступления его хода
· информация, которой владеет каждый из игроков на момент очередного хода
· выигрыши (для каждого игрока) как функции от выбранных ходов
· вероятностные распределения на множестве возможных состояний внешней среды
2.
нормальная или стратегическая форма. Каждый
участник (игрок) k, где![]() ,
характеризуется наличием индивидуальной системы целевых установок и множеством стратегий
,
характеризуется наличием индивидуальной системы целевых установок и множеством стратегий
![]() , т.е. возможных вариантов действий
в игре.
, т.е. возможных вариантов действий
в игре.
Ранее упоминалось о таком понятии, как «антагонистическая игра». Примером такой игры может служить игра «Орлянка». Дадим определение антагонистической игре.
Антагонистическая игра - игра, в которой участвуют два игрока (обычно обозначаемые I и II) с противоположными интересами. Для антагонистической игры характерно, что выигрыш одного игрока равен проигрышу другого и наоборот, поэтому совместные действия игроков, их переговоры и соглашения лишены смысла.. Определяются антагонистические игры заданием множеств стратегий игроков и выигрышей игрока I в каждой ситуации, состоящей в выборе игроками своих стратегий. Таким образом, формально антагонистическая игра есть тройка ‹А, В, Н›, в которой А и В - множества стратегий игроков, а Н (а, b) - вещественная функция (функция выигрыша) от пар (а, b), где а A, b В. Игрок I, выбирая а, стремится максимизировать Н(а, b), а игрок II, выбирая b, - минимизировать Н (а, b).
Пример 2:
Рассмотрим игру G (4х5) в матричной форме.
|
|
|
|
|
|
|
|
|
3 | 4 | 5 | 2 | 3 |
|
|
1 | 8 | 4 | 3 | 4 |
|
|
10 | 3 | 1 | 7 | 6 |
|
|
4 | 5 | 3 | 4 | 8 |
Очевидно надо выбирать ту стратегию, при которой выигрыш
максимален. (Это так называемый принцип минимакса. О нём чуть позже). В правом добавочном
столбце запишем минимальное значение выигрыша в каждой строке; обозначим его для
i-ой строки ![]() .
.
|
|
|
|
|
|
|
|
|
|
3 | 4 | 5 | 2 | 3 | 2 |
|
|
1 | 8 | 4 | 3 | 4 | 1 |
|
|
10 | 3 | 1 | 7 | 6 | 1 |
|
|
4 | 5 | 3 | 4 | 8 |
3 |
|
|
10 | 8 |
5 |
7 | 8 |
Из всех значений ![]() выделено
наибольшее (3). Ему соответствует величина
выделено
наибольшее (3). Ему соответствует величина ![]() -
гарантированный выигрыш, который называется нижней ценой игры. Исходя из
принципа осторожности, надо выбрать стратегию
-
гарантированный выигрыш, который называется нижней ценой игры. Исходя из
принципа осторожности, надо выбрать стратегию ![]() ,
а противник должен выбрать стратегию
,
а противник должен выбрать стратегию ![]() . Такая стратегия
называется «минимаксной». Выше было упомянуто о принципе минимакса. Рассмотрим далее
соответствующую терему.
. Такая стратегия
называется «минимаксной». Выше было упомянуто о принципе минимакса. Рассмотрим далее
соответствующую терему.
Теорема о минимаксе.
Можно доказать, что для любой функции F(x,y) определённой на
произвольном декартовом произведении X ×
Y имеет место неравенство ![]() . Отсюда следует, что
. Отсюда следует, что ![]()
Запишем 2 утверждения:
Утверждение 1. Точка 0 (в m-мерном пространстве) содержится в выпуклой оболочке m+n точек
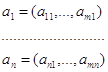 и
и 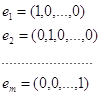
Утверждение 2. Существуют числа ![]() удовлетворяющие условиям
удовлетворяющие условиям ![]()
Доказательство: Пусть А – матричная игра. Имеет место либо утверждение 1, либо утверждение 2. Если верно утверждение 1 то 0 является выпуклой линейной комбинацией m+n векторов. Поэтому существуют такие
![]() что
что 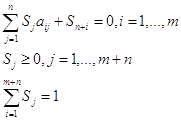
Если бы все числа ![]() были
бы равны нулю, то 0 оказывался бы выпуклой линейной комбинацией m единичных векторов
были
бы равны нулю, то 0 оказывался бы выпуклой линейной комбинацией m единичных векторов ![]() , что невозможно,
т.к. они линейно независимы. Следовательно, по крайней мере одно из чисел
, что невозможно,
т.к. они линейно независимы. Следовательно, по крайней мере одно из чисел ![]() положительно и
положительно и
![]()
тогда можно положить
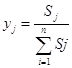 и получится
и получится 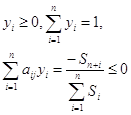 для всех i
для всех i
Значит ![]() и
и ![]()
Предположим, что верно утверждение 2. Тогда ![]() , так что
, так что ![]() . Следовательно, неравенство
. Следовательно, неравенство
![]() не имеет смысла. Предположим,
что игра А изменена на игру
не имеет смысла. Предположим,
что игра А изменена на игру ![]() , где
, где ![]() . Для любых х и y
. Для любых х и y ![]() , поэтому
, поэтому ![]() . Так как неравенство
. Так как неравенство ![]() не имеет смысла, то неравенство
не имеет смысла, то неравенство
![]() также не выполняется. Но k произвольно. Значит неравенство
также не выполняется. Но k произвольно. Значит неравенство ![]() невозможно.
Т.к.
невозможно.
Т.к. ![]() то
то ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Принцип минимакса.
Рассмотрим игру ![]() с
платежной матрицей
с
платежной матрицей ![]() Следует определить наилучшую стратегию
игрока I среди стратегий
Следует определить наилучшую стратегию
игрока I среди стратегий ![]() ,
, ![]() и игрока II среди стратегий
и игрока II среди стратегий ![]() ,
, ![]() . Определение наилучших
стратегий игроков основано на принципе, который предполагает, что противники, участвующие
в игре, одинаково разумны и каждый из них делает все для того, чтобы добиться своей
цели. Найдем наилучшую стратегию игрока I. Допустим, что он выбрал i-ю стратегию
(i –ю строку матрицы (1)). Тогда он получит меньше, чем
. Определение наилучших
стратегий игроков основано на принципе, который предполагает, что противники, участвующие
в игре, одинаково разумны и каждый из них делает все для того, чтобы добиться своей
цели. Найдем наилучшую стратегию игрока I. Допустим, что он выбрал i-ю стратегию
(i –ю строку матрицы (1)). Тогда он получит меньше, чем ![]() – наименьшее число в этой
строке. Причем это будет в том случае, если игрок II каким-то образом раскроет стратегию
игрока I. Из сказанного следует, что I игрок, если он не желает рисковать, т.е.
играть не оптимально, должен действовать следующим образом – определить наименьшие
элементы всех строк и выбрать ту из них, в которой это число наибольшее. В этом
случае он гарантирует себе выигрыш равный наибольшему из меньших чисел всех строк.
Этот выигрыш равен
– наименьшее число в этой
строке. Причем это будет в том случае, если игрок II каким-то образом раскроет стратегию
игрока I. Из сказанного следует, что I игрок, если он не желает рисковать, т.е.
играть не оптимально, должен действовать следующим образом – определить наименьшие
элементы всех строк и выбрать ту из них, в которой это число наибольшее. В этом
случае он гарантирует себе выигрыш равный наибольшему из меньших чисел всех строк.
Этот выигрыш равен ![]() Число
Число ![]() это “низкий выигрыш” игрока I и его
называют нижним значением или нижней ценой игры. Как же рассуждает
второй игрок? “Если я выберу j-ую стратегию (j-ый столбец), то самый лучший выигрыш
у игрока I будет
это “низкий выигрыш” игрока I и его
называют нижним значением или нижней ценой игры. Как же рассуждает
второй игрок? “Если я выберу j-ую стратегию (j-ый столбец), то самый лучший выигрыш
у игрока I будет ![]() наибольшее число
этого столбца. Чтобы рисковать, я должен выбрать столбец, в котором это число наименьшее.
В результате I игрок не сможет получить больше, чем
наибольшее число
этого столбца. Чтобы рисковать, я должен выбрать столбец, в котором это число наименьшее.
В результате I игрок не сможет получить больше, чем ![]() Число
Число ![]() представляет собой ”верхний выигрыш”
игрока I и называется верхним значение или верхней ценой игры. Можно
показать, что для всякой матричной игры выполняется условие
представляет собой ”верхний выигрыш”
игрока I и называется верхним значение или верхней ценой игры. Можно
показать, что для всякой матричной игры выполняется условие ![]() . Если
. Если ![]() , то такие игры называются
играми с седловой точкой. Из неравенства
, то такие игры называются
играми с седловой точкой. Из неравенства ![]() следует, что
следует, что ![]() . Это фактически означает,
игрок I мог бы рассчитывать на выигрыш
. Это фактически означает,
игрок I мог бы рассчитывать на выигрыш ![]() .
.
1.4 Матричные игры
В этом параграфе будет рассказано о принципе максимина, рациональном представлении матрицы игры, о решении игры при помощи фиктивного разыгрывания.
| н/ч | ч | |
| н/ч | 1 | -1 |
| ч | -1 | 1 |
Начнём непосредственно с матричных игр. Тройка ![]() (где x и y – множества, H – функция от двух переменных
(где x и y – множества, H – функция от двух переменных ![]() )
называется антагонистической игрой. Процесс разыгрывания конечной антагонистической
игры (игра называется конечной, если тройка
)
называется антагонистической игрой. Процесс разыгрывания конечной антагонистической
игры (игра называется конечной, если тройка ![]() конечна)
состоит в том, что игроки 1 и 2 независимо друг от друга выбирают соответственно
некоторые чистые стратегии x и y, в результате чего складывается ситуация
(x,y).
конечна)
состоит в том, что игроки 1 и 2 независимо друг от друга выбирают соответственно
некоторые чистые стратегии x и y, в результате чего складывается ситуация
(x,y).
Мы знаем, что антагонистическую игру двух участников с
нулевой суммой (напомним, что нулевая сумма – это когда выигрыш одного игрока равен
проигрышу другого) удобно задавать с помощью, так называемой платёжной матрицы.
Каждый элемент такой матрицы ![]() содержит
числовое значение выигрыша игрока 1 (или проигрыша игрока 2) в ситуации, когда первый
игрок применяет стратегию i,
а второй – стратегию j.
Классическим примером антагонистической игры является игра с двумя участниками,
которые независимо друг от друга загадывают числа. Предполагается, что если сумма
оказывается чётной, то выигрыш равный 1, достаётся первому игроку, а если нечётной,
то второму. Если предположить, что загадывание нечётного числа – стратегия первого
игрока, а загадывание чётного числа – стратегия второго игрока, то платёжная матрица
выглядит следующим образом:
содержит
числовое значение выигрыша игрока 1 (или проигрыша игрока 2) в ситуации, когда первый
игрок применяет стратегию i,
а второй – стратегию j.
Классическим примером антагонистической игры является игра с двумя участниками,
которые независимо друг от друга загадывают числа. Предполагается, что если сумма
оказывается чётной, то выигрыш равный 1, достаётся первому игроку, а если нечётной,
то второму. Если предположить, что загадывание нечётного числа – стратегия первого
игрока, а загадывание чётного числа – стратегия второго игрока, то платёжная матрица
выглядит следующим образом:
Строки матрицы соответствуют стратегиям игрока 1, столбцы
– стратегиям игрока 2, а её элементы – результатам (т.е. выигрышам) первого. Если
взять элементы матрицы с обратным знаком, то это будут выигрыши второго игрока.
Здесь надо отметить, что вопрос о выборе стратегии является основным в теории игр.
Для примера проанализируем произвольную игру ![]() .
При выборе игроком 1 стратегии i, его выигрыш в независимости от игрока 2 составит
.
При выборе игроком 1 стратегии i, его выигрыш в независимости от игрока 2 составит ![]() . Стратегия I произвольно, поэтому главная цель игрока
1 максимизировать величину полученного выигрыша, т.е. получить
. Стратегия I произвольно, поэтому главная цель игрока
1 максимизировать величину полученного выигрыша, т.е. получить ![]() . Такой принцип получил название
принципа максимина. Напомним, что максимин – это выигрыш максимальный из
минимальных. Надо также отметить, что принцип максимина обеспечивает игрокам гарантированный
«выигрыш» при любых стратегиях противников.
. Такой принцип получил название
принципа максимина. Напомним, что максимин – это выигрыш максимальный из
минимальных. Надо также отметить, что принцип максимина обеспечивает игрокам гарантированный
«выигрыш» при любых стратегиях противников.
Теорема о принципе максимина.
Для ![]() с
с ![]() (где
(где ![]() - множества чистых стратегий
игроков, (х, у) – ситуация игры
- множества чистых стратегий
игроков, (х, у) – ситуация игры ![]() - функции
полезности игроков, заданные на множестве ситуаций
- функции
полезности игроков, заданные на множестве ситуаций ![]() игры
аналитически
игры
аналитически ![]() ) общего вида
) общего вида
![]() .
.
Доказательство.
Для
![]()
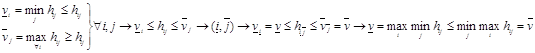
Для игры, заданной матрицей выигрышей ![]() можно записать следующее равенство
можно записать следующее равенство
![]() .
.
Скажем ещё несколько слов о матричных играх. Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования.
Матричная игра игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.
Первый игрок имеет m страте6гий i = 1,2,...m, второй
имеет n стратегий j=1,2,...n. Каждой
паре стратегий (i, j) поставлено в соответствии число a![]() , выражающее выигрыш игрока 1 за счет
игрока 2, если первый игрок примет свою i-ю стратегию, а 2-ю j-ю стратегию.
, выражающее выигрыш игрока 1 за счет
игрока 2, если первый игрок примет свою i-ю стратегию, а 2-ю j-ю стратегию.
Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (i=![]() ), 2- свою j-ю стратегию (j=
), 2- свою j-ю стратегию (j=![]() ) после чего игрок 1 получает выигрыш
a
) после чего игрок 1 получает выигрыш
a![]() за счет игрока 2 ( если a
за счет игрока 2 ( если a![]() <0, то это значит, что игрок 1 платит
второму сумму
<0, то это значит, что игрок 1 платит
второму сумму ![]() a
a![]()
![]() ). На этом игра заканчивается.
). На этом игра заканчивается.
Каждая стратегия игрока i=![]() ; j=
; j=![]() часто называется чистой стратегией.
часто называется чистой стратегией.
Если рассмотреть матрицу
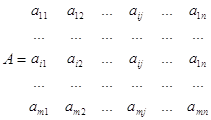
то проведение каждой партии матричной игры с матрицей А сводится к выбору
игроком 1 i- строки, а игроком 2 j-го столбца и получения игроком 1 (за
счет игрока 2) выигрыша a![]() .
.
Главным в исследовании игр является понятие оптимальных стратегий игроков.
В это понятие вкладывается следующий смысл: обеспечивается наибольший гарантированный
выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок
1 исследует матрицу выигрышей А следующим образом: для каждого значения i (i=![]() ) определяется минимальное значение
выигрыша в зависимости от применяемых стратегий игрока 2
) определяется минимальное значение
выигрыша в зависимости от применяемых стратегий игрока 2
min a![]() (i=
(i=![]() )
)
j
т.е определяется минимальный выигрыш для игрока 1 при условии, что он примет
свою i-ю чистую стратегию, затем из этих минимальных
выигрышей отыскивается такая стратегия i=i![]() , при которой этот минимальный выигрыш
будет максимальным, т.е. находится
, при которой этот минимальный выигрыш
будет максимальным, т.е. находится
max min a![]() = a
= a ![]()
![]() =
= ![]() (1)
(1)
Определение: Число ![]() , определенное
по формуле (1) называется чистой нижней ценой игры показывает,
какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые
стратегии при всевозможных действиях игрока 2.
, определенное
по формуле (1) называется чистой нижней ценой игры показывает,
какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые
стратегии при всевозможных действиях игрока 2.
Игрок 2 при оптимальном своем поведении должен стремиться по возможности за счет своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается
max a![]()
i
т.е. определяется max выигрыш
игрока 1, при условии, что игрок 2 применит свою j-ю чистую стратегию, затем игрок 2 отыскивает свою j=j![]() стратегию, при которой игрок 1 получит
min выигрыш, т.е. находит
стратегию, при которой игрок 1 получит
min выигрыш, т.е. находит
min max a![]() =a
=a![]()
![]() =
= ![]() (2)
(2)
j i
Определение. Число ![]() , определяемое
по формуле (2), называется чистой верхней ценой игры и показывает, какой
максимальный выигрыш за счет своих стратегий может себе гарантировать игрок 1.
, определяемое
по формуле (2), называется чистой верхней ценой игры и показывает, какой
максимальный выигрыш за счет своих стратегий может себе гарантировать игрок 1.
Другими словами, применяя свои чистые стратегии, игрок 1 может обеспечить
себе выигрыш не меньше ![]() , а игрок 2 за счет
применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем
, а игрок 2 за счет
применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем
![]() .
.
Переходя к рациональному представлению матрицы игры, отметим, что стратегии двух игроков сводятся в таблицу, а непосредственно само представление упрощает поиск решения матричных игр.
ПРИМЕР 3: Провести SP-разбиение матрицы игры (Н)
| X1 | 2 | 3 | 4 | 5 |
| X2 | 1 | 4 | 0 | 5 |
| X3 | 1 | 0 | 6 | 7 |
| X4 | 1 | 2 | 3 | 4 |
| Y1 | Y2 | Y3 | Y4 |
![]()
|
|
|
|
|
|
|
|
|
2 |
3 | 4 | 5 |
2 |
|
|
1 | 4 | 0 | 5 | 0 |
|
|
1 | 0 | 6 | 7 | 0 |
|
|
1 | 2 | 3 | 4 | 1 |
|
|
2 |
4 | 6 | 7 |
|
Решение: вычисляем верхнюю и нижнюю цену игры
Исходная игра имеет SP ![]() (x1,y1) в чистых стратегиях. Существование
SP в чистых стратегиях матричной игры с полной
информацией позволяет провести SP-разбиение
(Н) исходной игры:
(x1,y1) в чистых стратегиях. Существование
SP в чистых стратегиях матричной игры с полной
информацией позволяет провести SP-разбиение
(Н) исходной игры:
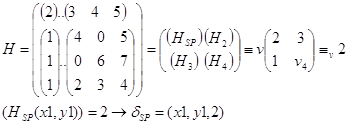 .
.
Формирование SP- разбиения матричной игры с SP по существу и является рациональным представлением исходной матрицы (Н) игры. Значит, понятие рациональности представления матрицы игры преследует цель сформулировать методы рационального преобразования платёжной матрицы с целью вычисления цены игры v или упрощения построения подыгры-решения.
Далее рассмотрим такое понятие, как решение, при помощи
фиктивного разыгрывания. Есть 2 игрока, которые без теории игр, хотят сделать
игру несколько раз, причём каждый из них склонен к статистике и оценивает стратегию
своего противника. При каждом разыгрывании противоборствующие стороны стремятся
максимизировать свой ожидаемый выигрыш против наблюдаемого вероятностного распределения
противника: если игрок 2 использует j-ю стратегию ![]() раз, то игрок 1 выберет
i-ю стратегию, чтобы максимизировать
раз, то игрок 1 выберет
i-ю стратегию, чтобы максимизировать ![]() . Аналогично, если игрок 1 использует
i-ю стратегию
. Аналогично, если игрок 1 использует
i-ю стратегию ![]() раз, то игрок 2 выберет j-ю стратегию, чтобы минимизировать
раз, то игрок 2 выберет j-ю стратегию, чтобы минимизировать ![]() . Условно эмпирические распределения
сходятся к оптимальным стратегиям. Точнее, пусть
. Условно эмпирические распределения
сходятся к оптимальным стратегиям. Точнее, пусть ![]() -
число использований первым игроком i-ой стратегии в течение первых N розыгрышей.
Пусть
-
число использований первым игроком i-ой стратегии в течение первых N розыгрышей.
Пусть ![]() , то тогда
, то тогда ![]() является смешанной стратегией.
Здесь справедливо утверждение о том, что предел любой сходящейся подпоследовательности
является оптимальной стратегией, т.е. если
является смешанной стратегией.
Здесь справедливо утверждение о том, что предел любой сходящейся подпоследовательности
является оптимальной стратегией, т.е. если ![]() и
и
![]() полученные стратегии игроков
1 и 2, то выполняется равенство
полученные стратегии игроков
1 и 2, то выполняется равенство ![]() . Такой
метод полезен в случае игры с большим числом стратегий.
. Такой
метод полезен в случае игры с большим числом стратегий.
Опишем некоторые свойства решений матричных игр. Пусть
G(X,Y,A) – игра двух лиц с нулевой суммой, в
которой игрок 1 выбирает стратегию ![]() , а игрок
2 -
, а игрок
2 - ![]() , после чего игрок 1 получает
выигрыш A=A(x,y) за счёт игрока 2.
, после чего игрок 1 получает
выигрыш A=A(x,y) за счёт игрока 2.
Свойство 1: Если чистая стратегия одного из игроков содержится в спектре (спектр – множество чистых стратегий, вероятность которых положительна) некоторой его оптимальной стратегии, то выигрыш этого игрока в ситуации, образованной данной стратегией и любой оптимальной стратегией другого игрока, равен значению конечной антагонистической игры.
Свойство 2: Ни одна доминируемая чистая стратегия игрока не содержится в спектре его оптимальной стратегии.
Свойство 3: Если ![]() – конечная антагонистическая
игра, а
– конечная антагонистическая
игра, а ![]() , подыгра игры G причём
, подыгра игры G причём ![]() - чистая
стратегия игрока 1 в игре G, доминируемая
над некоторой стратегией
- чистая
стратегия игрока 1 в игре G, доминируемая
над некоторой стратегией ![]() , спектр
которой не содержит
, спектр
которой не содержит ![]() . Тогда всякое решение
. Тогда всякое решение
![]() игры
игры ![]() является решением игры G.
является решением игры G.
Свойство 4: Тройка ![]() является
решением игры
является
решением игры ![]() <=>, когда
<=>, когда
![]() является решением игры
является решением игры ![]() , где а – любое вещественное
число, к>0
, где а – любое вещественное
число, к>0
ГЛАВА 2. Игры с нулевой суммой в чистых стратегиях
2.1 Вычисление оптимальных стратегий на примере решения задач
Используя теорему о минимаксе, можно утверждать, что каждая антагонистическая игра имеет оптимальные стратегии.
Теорема: пусть А – матричная игра и строки ![]() данной матрицы являются доминирующими.
Тогда игрок 1 имеет такую оптимальную стратегию х, что
данной матрицы являются доминирующими.
Тогда игрок 1 имеет такую оптимальную стратегию х, что ![]() ; кроме того, любая оптимальная
стратегия для игры, получающаяся в результате удаления доминирующих строк, будет
также оптимальной для первоначальной игры.
; кроме того, любая оптимальная
стратегия для игры, получающаяся в результате удаления доминирующих строк, будет
также оптимальной для первоначальной игры.
Пример 1. Игра доминирования
Рассмотрим игру с матрицей 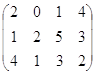 .
Здесь второй столбец доминирует 4 и игрок 2 соответственно не будет использовать
4 стратегию. Поэтому можно рассмотреть матрицу следующего вида
.
Здесь второй столбец доминирует 4 и игрок 2 соответственно не будет использовать
4 стратегию. Поэтому можно рассмотреть матрицу следующего вида 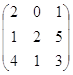 . В этой матрице третья строка
доминирует первую. При удалении получается матрица
. В этой матрице третья строка
доминирует первую. При удалении получается матрица ![]() .
А в этой матрице третий столбец доминируется вторым. Следовательно, исходная матрица
сводится к следующей матрице
.
А в этой матрице третий столбец доминируется вторым. Следовательно, исходная матрица
сводится к следующей матрице ![]() .
.
Пример 2. Игра на уклонение.
Предполагается, что игроки выбирают целые числа i и j между 1 и n, а игрок 1 выигрывает величину ![]() ,
т.е. расстояние между i и
j. Пусть первый игрок придерживается стратегии
,
т.е. расстояние между i и
j. Пусть первый игрок придерживается стратегии
![]() , тогда
, тогда ![]() для всех
для всех ![]() ((
((![]() - значение игры).
- значение игры).
·
Пусть ![]() нечётно, тогда игрок 2 имеет
чистую стратегию
нечётно, тогда игрок 2 имеет
чистую стратегию ![]() для всех
для всех ![]()
·
Предположим, что ![]() чётно, тогда игрок 2 имеет
такую стратегию
чётно, тогда игрок 2 имеет
такую стратегию ![]() где
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для всех
для всех ![]() . Теперь используя теорему можно
убедиться, что значение игры
. Теперь используя теорему можно
убедиться, что значение игры ![]() . Игрок 1
имеет оптимальную стратегию
. Игрок 1
имеет оптимальную стратегию ![]() , а оптимальная
стратегия игрока 2 равна
, а оптимальная
стратегия игрока 2 равна ![]() , если
, если ![]() и
и ![]() если
если ![]()
Приведём теорему, по которой решалась эта игра. Теорема:
для того, чтобы ситуация ![]() была равновесной
в игре
была равновесной
в игре ![]() , а число
, а число ![]() - значение игры
- значение игры ![]() , необходимо и достаточно выполнение
следующего неравенства. Для всех
, необходимо и достаточно выполнение
следующего неравенства. Для всех ![]() и
и ![]() :
: ![]() ).
).
Ситуация ![]() называется
ситуацией равновесия в чистых стратегиях, если для любых
называется
ситуацией равновесия в чистых стратегиях, если для любых ![]() выполнено двойное неравенство
выполнено двойное неравенство
![]() (*). Если каждый из игроков
стремится достичь ситуации равновесия, то принцип, которому они следуют, называют
принципом равновесия. Для игры, заданной матрицей
(*). Если каждый из игроков
стремится достичь ситуации равновесия, то принцип, которому они следуют, называют
принципом равновесия. Для игры, заданной матрицей ![]() равенство
равенство
![]() (т.е. верхнее значение игры
равно нижнему значению) записывается в виде
(т.е. верхнее значение игры
равно нижнему значению) записывается в виде ![]() , а неравенство (*) – в виде
, а неравенство (*) – в виде
![]() , где
, где ![]() чистые максиминная и минимаксная
стратегии соответственно игроков I и I I.
чистые максиминная и минимаксная
стратегии соответственно игроков I и I I.
Пример 3. Игра «Дуэль».
Два дуэлянта (игроки А и В) начинают сходиться в момент времени
t=0. Встреча произойдёт в момент времени
t=1. У каждого есть возможность выстрелить
в любой момент времени. Если одному из них удастся выстрелить раньше соперника,
то он становится победителем. Если же оба выстрелят одновременно, то дуэль закончится
вничью. Если игрок А произведёт выстрел в момент времени x (![]() ) то его выстрел будет успешным с вероятностью р(x). Подобным образом будет вероятным выстрел игрока В
в момент времени y (
) то его выстрел будет успешным с вероятностью р(x). Подобным образом будет вероятным выстрел игрока В
в момент времени y (![]() )
c вероятностью q(y). При условии
)
c вероятностью q(y). При условии ![]() игрок А
выиграет с вероятностью р(x), а проиграет с вероятностью (1- р(x)) q(y). Тем самым его средний выигрыш при
игрок А
выиграет с вероятностью р(x), а проиграет с вероятностью (1- р(x)) q(y). Тем самым его средний выигрыш при ![]() будет равен
будет равен ![]() . С другой стороны, если x> y, то его средний выигрыш будет равен
. С другой стороны, если x> y, то его средний выигрыш будет равен ![]() . При x= y средний выигрыш
. При x= y средний выигрыш ![]() .
Таким образом, функция H(x,y) игрока А имеет вид
.
Таким образом, функция H(x,y) игрока А имеет вид
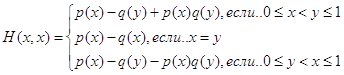
и антагонистическая игра задана. В частности, если игроки стреляют без промаха,
![]() ,
, 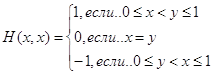
2.2 Примеры матричных игр в чистой и смешанной стратегиях Уменьшение порядка платёжной матрицы
Порядок платёжной матрицы (количество строк и столбцов) может быть уменьшен за счёт исключения доминируемых и дублирующих стратегий.
Стратегия K* называется доминируемой стратегией K**, если при любом варианте поведения противодействующего игрока выполняется соотношение
![]() <
< ![]() ,,
,,
где ![]() и
и ![]() - значения выигрышей при выборе
игроком, соответственно, стратегий K* и K**.
- значения выигрышей при выборе
игроком, соответственно, стратегий K* и K**.
В случае, если выполняется соотношение
![]() =
= ![]() ,
,
стратегия K* называется дублирующей по отношению к стратегии K**.
Например, в матрице
| B1 | B2 | B3 | B4 | B5 | B6 | |
| A1 | 1 | 2 | 3 | 4 | 4 | 7 |
| A2 | 7 | 6 | 5 | 4 | 4 | 8 |
| A3 | 1 | 8 | 2 | 3 | 3 | 6 |
| A4 | 8 | 1 | 3 | 2 | 2 | 5 |
Платёжная матрица с доминируемыми и дублирующими стратегиями. Стратегия A1 является доминируемой по отношению к стратегии A2, стратегия B6 является доминируемой по отношению к стратегиям B3, B4 и B5, а стратегия B5 является дублирующей по отношению к стратегии B4. Данные стратегии не будут выбраны игроками, так как являются заведомо проигрышными и удаление этих стратегий из платёжной матрицы не повлияет на определение нижней и верхней цены игры, описанной данной матрицей.
Множество недоминируемых стратегий, полученных после уменьшения размерности платёжной матрицы, называется ещё множеством Парето (по имени итальянского экономиста Вильфредо Парето, занимавшегося исследованиями в данной области)
Пример решения матричной игры в чистых стратегиях
Рассмотрим пример решения матричной игры в чистых стратегиях, в условиях реальной экономики, в ситуации борьбы двух предприятий за рынок продукции региона.
Задача
Два предприятия производят продукцию и поставляют её на рынок региона. Они являются единственными поставщиками продукции в регион, поэтому полностью определяют рынок данной продукции в регионе.
Каждое из предприятий имеет возможность производить продукцию с применением одной из трёх различных технологий. В зависимости от качества продукции, произведённой по каждой технологии, предприятия могут установить цену единицы продукции на уровне 10, 6 и 2 денежных единиц соответственно. При этом предприятия имеют различные затраты на производство единицы продукции.
Затраты на единицу продукции, произведенной на предприятиях региона (д.е.).
| Технология | Цена реализации единицы продукции, д.е. | Полная себестоимость единицы продукции, д.е. | |
| Предприятие 1 | Предприятие 2 | ||
| I | 10 | 5 | 8 |
| II | 6 | 3 | 4 |
| III | 2 | 1.5 | 1 |
В результате маркетингового исследования рынка продукции региона была определена функция спроса на продукцию:
Y = 6 – 0.5×X,
где Y – количество продукции, которое приобретёт население региона (тыс. ед.), а X – средняя цена продукции предприятий, д.е.
Данные о спросе на продукцию в зависимости от цен реализации приведены в таблице.
Спрос на продукцию в регионе, тыс. ед.
| Цена реализации 1 ед. продукции, д.е. | Средняя цена реализации 1 ед. продукции, д.е. | Спрос на продукцию, тыс. ед. | |
| Предприятие 1 | Предприятие 2 | ||
| 10 | 10 | 10 | 1 |
| 10 | 6 | 8 | 2 |
| 10 | 2 | 6 | 3 |
| 6 | 10 | 8 | 2 |
| 6 | 6 | 6 | 3 |
| 6 | 2 | 4 | 4 |
| 2 | 10 | 6 | 3 |
| 2 | 6 | 4 | 4 |
| 2 | 2 | 2 | 5 |
Значения долей продукции предприятия 1, приобретенной населением, зависят от соотношения цен на продукцию предприятия 1 и предприятия 2. В результате маркетингового исследования эта зависимость установлена и значения вычислены.
Доля продукции предприятия 1, приобретаемой населением в зависимости от соотношения цен на продукцию (табл. 1.1)
| Цена реализации 1 ед. продукции, д.е. | Доля продукции предприятия 1, купленной населением | |
| Предприятие 1 | Предприятие 2 | |
| 10 | 10 | 0,31 |
| 10 | 6 | 0,33 |
| 10 | 2 | 0,18 |
| 6 | 10 | 0,7 |
| 6 | 6 | 0,3 |
| 6 | 2 | 0,2 |
| 2 | 10 | 0,92 |
| 2 | 6 | 0,85 |
| 2 | 2 | 0,72 |
По условию задачи на рынке региона действует только 2 предприятия. Поэтому долю продукции второго предприятия, приобретённой населением, в зависимости от соотношения цен на продукцию можно определить как единица минус доля первого предприятия.
Стратегиями предприятий в данной задаче являются их решения относительно технологий производства продукции. Эти решения определяют себестоимость и цену реализации единицы продукции. В задаче необходимо определить:
1. Существует ли в данной задаче ситуация равновесия при выборе технологий производства продукции обоими предприятиями?
2. Существуют ли технологии, которые предприятия заведомо не будут выбирать вследствие невыгодности?
3. Сколько продукции будет реализовано в ситуации равновесия? Какое предприятие окажется в выигрышном положении?
Решение задачи
1. Определим экономический смысл коэффициентов выигрышей в платёжной матрице задачи. Каждое предприятие стремится к максимизации прибыли от производства продукции. Но кроме того, в данном случае предприятия ведут борьбу за рынок продукции в регионе. При этом выигрыш одного предприятия означает проигрыш другого. Такая задача может быть сведена к матричной игре с нулевой суммой. При этом коэффициентами выигрышей будут значения разницы прибыли предприятия 1 и предприятия 2 от производства продукции. В случае, если эта разница положительна, выигрывает предприятие 1, а в случае, если она отрицательна – предприятие2.
2. Рассчитаем коэффициенты выигрышей платёжной матрицы. Для этого необходимо определить значения прибыли предприятия 1 и предприятия 2 от производства продукции. Прибыль предприятия в данной задаче зависит:
- от цены и себестоимости продукции;
- от количества продукции, приобретаемой населением региона;
- от доли продукции, приобретённой населением у предприятия.
Таким образом, значения разницы прибыли предприятий, соответствующие коэффициентам платёжной матрицы, необходимо определить по формуле (1):
D = p×(S×R1-S×C1) – (1-p) ×(S×R2-S×C2) (1),
где D – значение разницы прибыли от производства продукции предприятия 1 и предприятия 2;
p - доля продукции предприятия 1, приобретаемой населением региона;
S – количество продукции, приобретаемой населением региона;
R1 и R2 - цены реализации единицы продукции предприятиями 1 и 2;
C1 и C2 – полная себестоимость единицы продукции, произведённой на предприятиях 1 и 2.
Вычислим один из коэффициентов платёжной матрицы.
Пусть, например, предприятие 1 принимает решение о производстве продукции в соответствии с технологией III, а предприятие 2 – в соответствии с технологией II. Тогда цена реализации единицы. продукции для предприятия 1 составит 2 д.е. при себестоимости единицы. продукции 1,5 д.е. Для предприятия 2 цена реализации единицы. продукции составит 6 д.е. при себестоимости 4 д.е. (табл. 1.1).
Количество продукции, которое население региона приобретёт при средней цене 4 д.е., равно 4 тыс. ед. (таблица 1.2). Доля продукции, которую население приобретёт у предприятия 1, составит 0,85, а у предприятия 2 – 0,15 (табл. 1.3). Вычислим коэффициент платёжной матрицы a32 по формуле (1): a32 = 0,85×(4×2-4×1,5) – 0,15×(4×6-4×4) = 0,5 тыс. ед.
где i=3 – номер технологии первого предприятия, а j=2 – номер технологии второго предприятия.
Аналогично вычислим все коэффициенты платёжной матрицы. В платёжной матрице стратегии A1 – A3 – представляют собой решения о технологиях производства продукции предприятием 1, стратегии B1 – B3 – решения о технологиях производства продукции предприятием 2, коэффициенты выигрышей – разницу прибыли предприятия 1 и предприятия 2. Платёжная матрица в игре «Борьба двух предприятий за рынок продукции региона».
| B1 | B2 | B3 |
Minj |
|
| A1 | 0,17 | 0,62 | 0,24 | 0.17 |
| A2 | 3 | -1,5 | -0,8 | -1.5 |
| A3 | 0,9 | 0,5 | 0,4 | 0.4 |
|
Maxi |
3 | 0.62 | 0.4 |
В данной матрице нет ни доминируемых, ни дублирующих стратегий. Это значит, что для обоих предприятий нет заведомо невыгодных технологий производства продукции. Определим минимальные элементы строк матрицы. Для предприятия 1 каждый из этих элементов имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Минимальные элементы матрицы по строкам имеют значения: 0,17, -1,5, 0,4.
Определим максимальные элементы столбцов матрицы. Для предприятия 2 каждый из этих элементов также имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Максимальные элементы матрицы по столбцам имеют значения: 3, 0,62, 0,4.
Нижняя цена игры в матрице равна 0,4. Верхняя цена игры также равна 0,4. Таким образом, нижняя и верхняя цена игры в матрице совпадают. Это значит, что имеется технология производства продукции, которая является оптимальной для обоих предприятий в условиях данной задачи. Эта технология III, которая соответствует стратегиям A3 предприятия 1 и B3 предприятия 2. Стратегии A3 и B3 – чистые оптимальные стратегии в данной задаче.
Значение разницы прибыли предприятия 1 и предприятия 2 при выборе чистой оптимальной стратегии положительно. Это означает, что предприятие 1 выиграет в данной игре. Выигрыш предприятия 1 составит 0,4 тыс. д.е. При этом на рынке будет реализовано 5 тыс. ед. продукции (реализация равна спросу на продукцию, таблица 1.2).. Оба предприятия установят цену за единицу продукции в 2 д.е. При этом для первого предприятия полная себестоимость единицы продукции составит 1,5 д.е., а для второго – 1 д.е (таблица 1.1). Предприятие 1 окажется в выигрыше лишь за счёт высокой доли продукции, которую приобретёт у него население.
Смешанные стратегии в матричных играх
Понятие о матричных играх со смешанным расширением
Исследование в матричных играх начинается с нахождения её чистой цены. Если матричная игра имеет решение в чистых стратегиях, то нахождением чистой цены заканчивается исследование игры. Если же в игре нет решения в чистых стратегиях, то можно найти нижнюю и верхнюю цены этой игры, которые указывают, что игрок 1 не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры. Улучшение решений матричных игр следует искать в использовании секретности применения чистых стратегий и возможности многократного повторения игр в виде партии. Этот результат достигается путём применения чистых стратегий случайно, с определённой вероятностью.
Определение. Смешанной стратегией игрока называется полный набор чистых стратегий, применённых в соответствии с установленным распределением вероятностей. Матричная игра, решаемая с использованием смешанных стратегий, называется игрой со смешанным расширением.
Стратегии, применённые с вероятностью, отличной от нуля, называются активными стратегиями.
Доказано, что для всех игр со смешанным расширением существует оптимальная смешанная стратегия, значение выигрыша при выборе которой находится в интервале между нижней и верхней ценой игры:
Vн £ V £ Vв.
При этом условии величина V называется ценой игры.
Кроме того, доказано, что, если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры V, независимо от того, каких стратегий придерживается другой игрок, если только он не выходит за пределы своих активных стратегий. Поэтому, для достижения наибольшего гарантированного выигрыша второму игроку также необходимо придерживаться своей оптимальной смешанной стратегии.
Решение матричных игр со смешанным расширением методами линейного программирования
Решение матричной игры со смешанным расширением – это определение оптимальных смешанных стратегий, то есть нахождение таких значений вероятностей выбора чистых стратегий для обоих игроков, при которых они достигают наибольшего выигрыша.
Для матричной игры, платёжная матрица которой показана на рис. 1.1, Vн ¹ Vв, определим такие значения вероятностей выбора стратегий для игрока 1 (p1, p2,…, pm) и для игрока 2 (q1, q2,…, qn), при которых игроки достигали бы своего максимально гарантированного выигрыша.
Если один из игроков придерживается своей оптимальной стратегии, то, по условию задачи, его выигрыш не может быть меньше цены игры V. Поэтому данная задача может быть представлена для игроков в виде следующих систем линейных неравенств:
Для первого игрока:
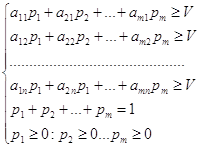
Для второго игрока:
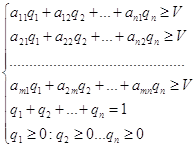
Чтобы определить значение V, разделим обе части каждого из уравнений на V. Величину pi/V обозначим через xi, а qj/V – через yj.
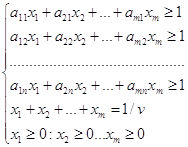
Для игрока 1 получим следующую систему неравенств, из которой найдём значение 1/v:
Для игрока 1 необходимо найти максимальную цену игры (V). Следовательно, значение 1/V должно стремиться к минимуму.
Целевая функция задачи будет иметь следующий вид:
min Z = min 1/V = min (x1 + x2 + … + xm)
Для игрока 2 получим следующую систему неравенств, из которой найдём значение 1/v:
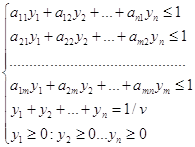
Для игрока 2 необходимо найти минимальную цену игры (V). Следовательно, значение 1/V должно стремиться к максимуму.
Целевая функция задачи будет иметь следующий вид:
![]()
Все переменные в данных системах линейных неравенств должны быть неотрицательными: xi = pi/V, а yi = qj/V. Значения pi и qj не могут быть отрицательными, так как являются значениями вероятностей выбора стратегий игроков. Поэтому необходимо, чтобы значение цены игры V не было отрицательным. Цена игры вычисляется на основе коэффициентов выигрышей платёжной матрицы. Поэтому, для того, чтобы гарантировать условие неотрицательности для всех переменных, необходимо, чтобы все коэффициенты матрицы были неотрицательными. Этого можно добиться, прибавив перед началом решения задачи к каждому коэффициенту матрицы число K, соответствующее модулю наименьшего отрицательного коэффициента матрицы. Тогда в ходе решения задачи будет определена не цена игры, а величина
V* = V + K
Для решения задач линейного программирования используется симплекс-метод. [1, 5].
В результате решения определяются значения целевых функций (для обоих игроков эти значения совпадают), а также значения переменных xi и yj.
Величина V* определяется по формуле: V* = 1/z
Значения вероятностей выбора стратегий определяются: для игрока 1: Pi = xi×V*: для игрока 2: qi = yi×V*.
Для определения цены игры V из величины V* необходимо вычесть число K.
Пример решения матричной игры со смешанным расширением
Рассмотрим пример решения матричной игры со смешанным расширением. Платёжную матрицу игры составим на основе исходных данных, заменив лишь значения долей продукции предприятия 1, приобретаемой населением в зависимости от соотношений цен (табл. 2.1).
Таблица 2.1 - Доля продукции предприятия 1, приобретаемой населением в зависимости от соотношения цен на продукцию
| Цена реализации 1 ед. продукции, д.е. | Доля продукции предприятия 1, купленной населением | |
| Предп. 1 | Предп. 2 | |
| 10 | 10 | 0,31 |
| 10 | 6 | 0,33 |
| 10 | 2 | 0,18 |
| 6 | 10 | 0,7 |
| 6 | 6 | 0,3 |
| 6 | 2 | 0,2 |
| 2 | 10 | 0,9 |
| 2 | 6 | 0,85 |
| 2 | 2 | 0,69 |
Применив к исходным данным задачи формулу (1) определения разницы прибыли от производства продукции, получим следующую платёжную матрицу
Платёжная матрица в игре «Борьба двух предприятий за рынок продукции региона»
| B1 | B2 | B3 |
minj |
|
| A1 | 0,17 | 0,62 | 0,24 | 0.17 |
| A2 | 3 | -1,5 | -0,8 | -1.5 |
| A3 | 0,75 | 0,5 | 0,175 | 0,175 |
|
maxi |
3 | 0.62 | 0.24 |
В данной матрице нет доминируемых или дублирующих стратегий. Нижняя цена игры равна 0,175, а верхняя цена игры равна 0,24. Нижняя цена игры не равна верхней. Поэтому решения в чистых стратегиях не существует и для каждого из игроков необходимо найти оптимальную смешанную стратегию.
Решение задачи
1. В данной матрице имеются отрицательные коэффициенты. Для соблюдения условия неотрицательности в задачах линейного программирования прибавим к каждому коэффициенту матрицы модуль минимального отрицательного коэффициента. В данной задаче к каждому коэффициенту матрицы необходимо прибавить число 1,5 – значение модуля наименьшего отрицательного элемента матрицы. Получим платёжную матрицу, преобразованную для выполнения условия неотрицательности
Платёжная матрица, преобразованная для выполнения условия неотрицательности
| B1 | B2 | B3 | |
| A1 | 1,67 | 2,12 | 1,74 |
| A2 | 4,5 | 0 | 0,7 |
| A3 | 2,25 | 2 | 1,675 |
2. Опишем задачу линейного программирования для каждого игрока в виде системы линейных неравенств:
Для игрока 1:
1,67×x1 + 4,5×x2 + 2,25×x3 ³ 1
2,12×x1 + 0×x2 + 2×x3 ³ 1
1,74×x1 + 0,7×x2 + 1,675×x3 ³ 1
x1³ 0; x2³ 0; x3³ 0
min Z = x1 + x2 + x3
Для игрока 2:
1,67×y1 + 2,12×y2 + 1,74×y3 £ 1
4,5×y1 + 0×y2 + 0,7×y3 £ 1
2,25×y1 + 2×y2 + 1,675×y3 £ 1
y1³ 0; y2³ 0; y3³ 0
max Z = y1 + y2 + y3
3. Решим обе задачи с использованием симплекс-метода, применяя программный комплекс "Линейная оптимизация".
В результате решения задачи получим следующие значения целевой функции и переменных:
Z = 0,5771
V* = 1/0,5771 = 1,7328
x1 = 0,5144; x2 = 0; x3 = 0,0626
y1 = 0,0582; y3 = 0,5189
4. Для определения значений вероятностей выбора стратегий игроков 1 и 2 умножим значения переменных на V*. P1 = x1×V* = 0,8914, p2 =0, p3 = x3×V* = 0,1083: q1 = y1×V* = 0,1008, q2 = 0, q3 = y3×V* = 0,8991.
5. Определим значение цены игры. Для этого из величины V* вычтем 1,5 (значение модуля наименьшего отрицательного элемента).
V = 1,7328 - 1,5 = 0,2328
Таким образом, в данной игре выиграет предприятие 1 (значение V > 0). Для достижения своей оптимальной стратегии (получения максимального математического ожидания гарантированного выигрыша) предприятие 1 должно выбирать технологию 1 с вероятностью 0,8914, а технологию 3 – с вероятностью 0,1083. Предприятие 2, соответственно, должно выбирать технологию 1 с вероятностью 0,1008, а технологию 3 – с вероятностью 0,8991. Значение математического ожидания выигрыша предприятия 1 составит 0,2328 тыс. д.е.
2.3 Исследование операций
Скажем несколько слов об основных методологических принципах Исследования операций:
· Системный подход. Его суть состоит в систематическом поиске существенных взаимодействий при оценке деятельности или стратегии любой части организации
· Комплексный научный коллектив. Необходимость привлечения к решению практических задач разных специалистов связана с требованием всестороннего подхода к проблеме
· Научный метод. Так как эксперимент в узком смысле этого слова невозможен, нужно заменить реальную действительность её научной моделью. Поэтому решение задач исследования операций при научном подходе сводится на практике к решению уравнений или систем уравнений при условии выполнения различных заданных критериев.
Назовём теперь основные этапы исследования операций:
· Содержательная постановка задачи
· Построение математической модели
· Решение задачи на модели
· Проверка адекватности модели
· Построение конкурирующего алгоритма
· Реализация решения
Несмотря на различное содержание задач, их физическую суть, математические постановки этих задач имеют много общего. В каждой из них требуется максимизировать или минимизировать некоторую линейную функцию нескольких переменных, ограничения, положенные на совокупность этих переменных являются либо линейными уравнениями, либо линейными неравенствами. Поэтому далее рассмотрим только математическую постановку задачи линейного программирования. К настоящему времени в литературе выделяют следующую классификацию ЗЛП (общая задача линейного программирования; каноническая целевая функция задачи линейного программирования; основная задача линейного программирования; основная задача линейного программирования с ограничениями – неравенствами) и их решений (допустимое решение; допустимое базисное решение; оптимальное решение).
Общая задача линейного программирования заключается в отыскании вектора (х1, х2,..., хn) максимизирующего (минимизирующего) критерий оптимальности (функцию цели задачи)
![]()
при ограничениях линейного типа в виде равенств:
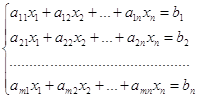
в виде неравенств:
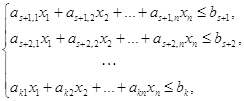
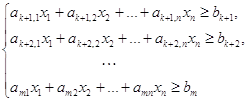
и ограничениях на переменные состояния:
![]()
Эта задача при наличии двух (или трех) переменных имеет наглядное геометрическое представление.
Пусть целевая функция имеет вид ![]() . Если на плоскости переменных
. Если на плоскости переменных
![]() и
и ![]()
![]() принимает некоторое постоянное
значение
принимает некоторое постоянное
значение ![]() то определяемое последним соотношением
множество точек плоскости (
то определяемое последним соотношением
множество точек плоскости (![]() ,
,![]() ) является линией равного значения
уровня (линией уровня) целевой функции. Причем, при
) является линией равного значения
уровня (линией уровня) целевой функции. Причем, при ![]() =
=
![]() = 0 эта линия «сжимается»
в точку (рис. 1), при имеем
= 0 эта линия «сжимается»
в точку (рис. 1), при имеем ![]() и линия
равного уровня является прямой линией, проходящей через точки
и линия
равного уровня является прямой линией, проходящей через точки 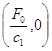 и
и 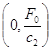
Рис. 1 - Геометрическое представление целевой функции
Операцией – называется всякое мероприятие (или система действий), объединенное единым замыслом, и направленное к достижению какой-то определённой цели. Операция всегда есть управляемое мероприятие, т.е. наблюдается зависимость, каким способом выбрать параметры, характеризующие её организацию. Всякий определённый выбор параметров называется решением. Оптимальными называются решения по тем или другим признакам предпочтительные перед другими.
В исследовании операций используется научный метод для изучения и объяснения явлений, связанных с функциональными системами, так как в рамках данной дисциплины изучается определенный круг явлений реальной действительности. Такие системы нередко включают людей и механизмы, которые действуют в условиях реального мира, причем слову «механизм» мы придаем достаточно общее значение, охватывающее все случаи – от механических устройств, обычно определяемых их названиями, до сложных социальных структур, функционирующих в соответствии с установленными правилами.
Научная дисциплина, называемая исследованием операций, наблюдает реальные явления, связанные с функциональными системами, разрабатывает теории (которые многие исследователи называют моделями), предназначенные для объяснения данных явлений, использует эти теории для описания того, что произойдет при изменении условий, и проверяет предсказания новыми наблюдениями.
Таким образом, исследование операций – наука, так как эта дисциплина использует научный метод для получения соответствующих знаний и отличается от других наук предметом исследований. Она изучает явления, связанные с функциональными системами, в том аспекте, который почти не рассматривается другими науками.
Учитывая этапы реализации научного метода, для любой научной дисциплины можно ожидать систематических публикаций четырех категорий, в которых соответственно приводятся результаты, получаемые при наблюдении явлений, и специальные способы проведения таких наблюдений. Даются построения математических моделей; описывается применение этих моделей для составления прогноза на основе полученных результатов; проводится проверка прогнозов путем сравнения с результатами новых наблюдений.
Во всяком случае, на протяжении всей истории развития методов исследования операций научные работники следовали рекомендациям Блеккета согласно которым, исследование операций, как и любая другая наука, не базируется на использовании точных копий аналитических методов какой-либо другой науки, а требует разработки своего собственного математического аппарата – методов исследований операций, ориентированного на специфику, присущую этой области и задачам исследования. Этот аппарат не должен оставаться неизменным; наоборот, он должен меняться в соответствии с характером исследуемых задач.
Довольно часто отправным моментом построения моделей служило сходство с моделями, используемыми другими науками. Таким образом, новые теоретические направления были развиты в основном в послевоенное время. Основы теории ведения боевых действий заложены Ланчестером в 1916г., и, хотя во время войны математические аспекты этой теории исследовались достаточно интенсивно, непосредственного применения при разработке операций военного времени она не нашла; действительно, вплоть до 1954г. Эта теория не была достаточно проверена.
Зарождение исследования операций как научной дисциплины было обусловлено неотложным требованием решения важных практических проблем. Поэтому в процессе становления исследования операции научные работники, которые занимались соответствующими исследованиями, не только заложили фундамент некоторого нового научного направления, но и использовали полученные знания для практического решения проблем. В течение второго и третьего десятилетий существования группы по исследованию операций значительно выросли и стали достаточно отличаться друг от друга по направлениям. Однако тесная связь между исследовательскими и практическими аспектами разработок оставалась характерной особенностью данной дисциплины: термин «исследование операций» как раз и подчеркивает их неразрывность. Итак, исследование операций включает как научное исследование систем, так и соответствующие виды технической деятельности, направленной на практическую реализацию результатов таких исследований.
Однако эти прикладные аспекты исследования операций предполагают не только простое применение знаний, полученных в результате использования теории, но требуют и наличие творческого начала (ориентации работы в желаемых направлениях), а также профессионального умения и навыков практического проектирования (направленных на выполнение требуемых задач или решение важных проблем). Кроме того, важно обеспечить внедрение результатов работ.
В исследовании операций немаловажную роль играют задачи, которые непосредственно вносят вклад в рациональное использование имеющихся в наличии ресурсов. Для примера рассмотрим подробное решение одной из задач.
Пример задачи о производстве красок Задача фирмы Reddy Mikks Небольшая фабрика фирмы Reddy Mikks изготовляет два вида красок: для внутренних (I) и наружных (E) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта-А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1 т соответствующих красок и максимально возможный запас приведены в таблице.

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме этого установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. долл. для краски Е 2 тыс. долл. для краски I.
Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Построение математической модели
Процесс построения математической модели для решения поставленной задачи можно начать с ответов на три следующие вопроса:
1. Для определения, каких величин должна быть построена модель?
2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, для моделируемой системы?
3. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному (наилучшему) решению задачи?
Отвечая на поставленные вопросы, сформулируем суть проблемы. Фирме требуется определить объемы производства (в тоннах) каждой из красок, который максимизирует доход (в тысячах долларов) от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов.
Введем переменные: так как нужно определить объемы производства каждого вида краски, то переменными в модели являются
· xE - суточный объем производства краски Е (в тоннах)
· xI - суточный объем производства краски I (в тоннах).
Так как стоимость 1 т краски Е равна 3 тыс. долл., суточный доход от ее продажи
составит 3 xE тыс. долл. Аналогично доход от реализации xI тонн краски I составит
2 xI тыс. долл. в сутки. При допущении независимости объемов сбыта каждой из красок
можно дать следующую математическую формулировку целевой функции: определить (допустимые)
значения xЕ и xI, максимизирующие величину общего дохода ![]() Ограничения: При
решении рассматриваемой задачи должны быть учтены ограничения на расход исходных
продуктов и спрос на изготовляемые краски. Ограничение на расход исходных продуктов
можно записать следующим образом:
Ограничения: При
решении рассматриваемой задачи должны быть учтены ограничения на расход исходных
продуктов и спрос на изготовляемые краски. Ограничение на расход исходных продуктов
можно записать следующим образом:
Это приводит к следующим двум ограничениям: ![]() (для А)
(для А) ![]() (для В) Ограничения на величину спроса
красок имеют вид
(для В) Ограничения на величину спроса
красок имеют вид
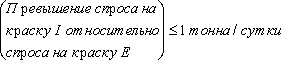
![]()
Эти ограничения имеют вид: ![]() (соотношение величин спроса на краску I и краску Е),
(соотношение величин спроса на краску I и краску Е), ![]() (максимальная величина спроса на краску
I). Переменные xI и xE не могут принимать отрицательных значений:
(максимальная величина спроса на краску
I). Переменные xI и xE не могут принимать отрицательных значений: ![]() (объем производства краски I),
(объем производства краски I), ![]() (объем производства краски Е). Итак,
математическую модель можно записать следующим образом. Определить суточные объемы
производства (xI и xE ) краски I и краски Е (в тоннах), при которых достигается
(объем производства краски Е). Итак,
математическую модель можно записать следующим образом. Определить суточные объемы
производства (xI и xE ) краски I и краски Е (в тоннах), при которых достигается
![]() (целевая функция) при ограничениях:
(целевая функция) при ограничениях:
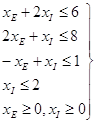
Что определяет линейный характер построенной модели? С формальных позиций данная модель является линейной потому, что все входящие в нее функции (ограничения и целевая функция) линейны. Линейность предполагает наличие двух свойств - пропорциональности и аддитивности.
1 Пропорциональность означает, что вклад каждой переменной хЕ и хI в целевую функцию прямо пропорционален этим переменным.
2 Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Однако если фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
Задача о пищевом рационе.
Пусть имеется 4 вида продуктов: ![]() . Стоимость единицы каждого продукта
. Стоимость единицы каждого продукта ![]() . Согласно этим условиям, требуется
составить пищевой рацион, в котором должны содержаться белки, в количестве не менее
. Согласно этим условиям, требуется
составить пищевой рацион, в котором должны содержаться белки, в количестве не менее![]() единиц, углеводов – не менее
единиц, углеводов – не менее
![]() единиц, жиров – не менее
единиц, жиров – не менее ![]() единиц.
единиц.
Составим таблицу.
| продукт | элементы | продукт | элементы | ||||
| Белки | углеводы | Жиры | Белки | углеводы | Жиры | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() (
(![]() ) – какие
то определённые числа. Первый индекс указывает номер продукта, второй – номер элемента
(белки, жиры углеводы). Требуется составить пищевой рацион таким образом, чтобы
условия по белкам, жирам и углеводам были выполнены. Математическая модель будет
выглядеть следующим образом:
) – какие
то определённые числа. Первый индекс указывает номер продукта, второй – номер элемента
(белки, жиры углеводы). Требуется составить пищевой рацион таким образом, чтобы
условия по белкам, жирам и углеводам были выполнены. Математическая модель будет
выглядеть следующим образом: ![]() - количества
продукции
- количества
продукции ![]() входящих в рацион. Показатель
эффективности L – стоимость рациона (эту величину требуется
минимизировать). Запишем линейную зависимость
входящих в рацион. Показатель
эффективности L – стоимость рациона (эту величину требуется
минимизировать). Запишем линейную зависимость ![]() .
Учитывая, что в одной единице продукта
.
Учитывая, что в одной единице продукта ![]() содержится
содержится
![]() единиц белка, в
единиц белка, в ![]() единицах -
единицах - ![]()
![]() единиц белка, в
единиц белка, в ![]() единицах продукта
единицах продукта ![]() содержится
содержится ![]()
![]() единиц белка и т.д. получим
три неравенства:
единиц белка и т.д. получим
три неравенства: 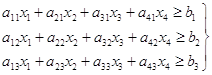 эти линейные неравенства
представляют собой ограничения, накладываемые на элементы решения
эти линейные неравенства
представляют собой ограничения, накладываемые на элементы решения ![]() . Таким образом задача сводится
к следующей: найти такие неотрицательные значения переменных
. Таким образом задача сводится
к следующей: найти такие неотрицательные значения переменных ![]() , чтобы они удовлетворяли ограничениям
– неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
, чтобы они удовлетворяли ограничениям
– неравенствам и одновременно обращали в минимум линейную функцию этих переменных:
![]()
2.4 Математический аппарат теории игр и его применение к решению прикладных задач
Транспортная задача. Подобная задача возникает в своем простейшем варианте, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителю. Поэтому здесь естественно возникает задача о наиболее рациональном прикреплении транспорта, правильном направлении перевозок груза, при котором полностью удовлетворяются потребности при минимальных затратах на транспортировку. Итак, задача формулируется следующим образом.
Имеется m пунктов производства
с объемами производства в единицу времени аi,
i= ![]() и
n пунктов потребления bi,
i=
и
n пунктов потребления bi,
i= ![]() ,
естественно, что потребление не должно превышать возможностей производства
,
естественно, что потребление не должно превышать возможностей производства ![]() ai
ai
![]()
![]() bi,
затраты на перевозку единицы продукции из i-го
пункта производства в j-й пункт потребления составляют Сij,
а количество перевезенного продукта xij.
bi,
затраты на перевозку единицы продукции из i-го
пункта производства в j-й пункт потребления составляют Сij,
а количество перевезенного продукта xij.
Требуется составить такой план перевозок,
при котором суммарные затраты на них были бы минимальны min ![]()
![]() Cij
xij
при условиях, что в каждый пункт потребления завозится требуемое количество продукта
Cij
xij
при условиях, что в каждый пункт потребления завозится требуемое количество продукта
![]() xij
xij
![]() bj, j =
bj, j = ![]() ,
из каждого пункта производства вывозится не более произведенного количества продукта
,
из каждого пункта производства вывозится не более произведенного количества продукта
![]() xij
xij
![]() ai,
=
ai,
= ![]() и
перевозимый объем продукта не может быть отрицательным xij
и
перевозимый объем продукта не может быть отрицательным xij
![]() 0,
i
=
0,
i
=
![]() , j
=
, j
=
![]() .
.
Рассмотрим далее транспортную задачу в частной постановке.
На двух станциях отправления ![]() и
и ![]() сосредоточено соответственно
сосредоточено соответственно ![]() и
и ![]() единиц некоторого однородного груза. Этот
груз следует доставить в три пункта назначения
единиц некоторого однородного груза. Этот
груз следует доставить в три пункта назначения ![]() ,
, ![]() ,
, ![]() , причём в каждый из них должно быть завезено
соответственно
, причём в каждый из них должно быть завезено
соответственно ![]() ,
, ![]() ,
, ![]() единиц этого груза. Стоимость перевозки единицы груза из пункта
единиц этого груза. Стоимость перевозки единицы груза из пункта
![]() в пункт
в пункт ![]() (равную
(равную ![]() ), считаем заданной. Все данные полезно
представить в виде таблицы 2.2.
), считаем заданной. Все данные полезно
представить в виде таблицы 2.2.
Таблица 2.2
|
Пункты назначения Пункты отправления |
Пункты назначения | Запасы груза | ||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
| Потребность в грузе |
|
|
|
|
Естественно считать, что общий запас грузов на станциях отправления равен суммарной потребности в этом грузе всех станций назначения. Следовательно
![]() (1)
(1)
Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.
Обозначим через ![]() количество единиц груза, предназначенного к отправке из пункта
количество единиц груза, предназначенного к отправке из пункта
![]() в пункт
в пункт ![]() . Тогда количество груза, который планируется
к доставке в пункт
. Тогда количество груза, который планируется
к доставке в пункт ![]() из пунктов
из пунктов ![]() и
и ![]() составит
составит
![]() .
.
Но так как потребность в грузе в пункте ![]() равна
равна ![]() , то должно выполняться равенство
, то должно выполняться равенство ![]() .
.
Аналогичные рассуждения приводят к равенствам
![]() ,
, ![]() .
.
С другой стороны, общее количество груза, отправленного со станции ![]() , выражается суммой
, выражается суммой ![]() , которая, очевидно, обязана совпадать
с запасом груза
, которая, очевидно, обязана совпадать
с запасом груза ![]() , сосредоточенным на этой станции, т.е.
, сосредоточенным на этой станции, т.е.
![]() .
.
Подобно этому ![]() .
.
Полученные соотношения легче запомнить, если все величины свести в таблицу
2 (матрицу перевозок). Тогда легко проверить, что сумма всех ![]() , расположенных в
, расположенных в ![]() -ой строке, равна запасу
-ой строке, равна запасу ![]() в пункте назначения
в пункте назначения ![]() . Сумма же всех
. Сумма же всех ![]() из столбца
из столбца ![]() равна потребности
равна потребности ![]() пункта назначения
пункта назначения ![]() .
.
Таблица 2.3
|
Пункты назначения Пункты отправления |
Пункты назначения | Запасы груза | ||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
| Потребности |
|
|
|
Из условий задачи с очевидностью вытекает, что общая стоимость ![]() всех перевозок
всех перевозок
![]()
Таким образом, математическая формулировка транспортной задачи (по критерию стоимости перевозок) такова.
Задана система
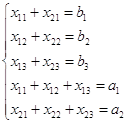 (2)
(2)
пяти линейных алгебраических уравнений с шестью переменными и линейная целевая функция
![]() (3)
(3)
Требуется среди всех неотрицательных решений ![]() системы (2) выбрать такое, при котором
целевая функция
системы (2) выбрать такое, при котором
целевая функция ![]() минимизируется (достигает наименьшего значения).
минимизируется (достигает наименьшего значения).
Необходимо отметить, что при решении транспортной задачи следует учитывать важное соотношение
![]() (4)
(4)
вытекающего из самого условия задачи.
Впрочем, возможны и иные постановки транспортной задачи, когда условие (1а) не выполнено.
Задача о выборе производственной программы. Эта задача была одной из первых практических задач линейного программирования, решенная в 1939 году известным русским математиком Л.В.Канторовичем.
На m предприятиях нужно произвести
n продуктов в заданном ассортименте l1, l2,...,
ln. Если xij,
i
=
![]() , j
=
, j
=
![]() –
рабочее время i-го предприятия,
отводимое под j-й продукт, аij – производительность i-го
предприятия в единицу времени по выпуску j-го продукта, то задача о выборе
производственной программы для случая, когда продукция дефицитна, производственные
мощности ограничены и должны использоваться максимально полно, ставится следующим
образом.
–
рабочее время i-го предприятия,
отводимое под j-й продукт, аij – производительность i-го
предприятия в единицу времени по выпуску j-го продукта, то задача о выборе
производственной программы для случая, когда продукция дефицитна, производственные
мощности ограничены и должны использоваться максимально полно, ставится следующим
образом.
Требуется составить программу работы
предприятий – указать время хij,
отведенное на производство каждого вида продукции на данном предприятии таким образом,
чтобы получить максимальный суммарный объем продукции в заданном ассортименте в
единицу времени, т.е. необходимо найти xij
из условий, что время не может быть отрицательным xij
>
0,
сумма всех временных долей не превосходит полного времени работы предприятия ![]() xij
xij
![]() 1,
количество ассортиментных наборов продуктов максимально.
1,
количество ассортиментных наборов продуктов максимально.
Задача об использовании
сырья. Предположим, что изготовление продукции двух видов ![]() и
и
![]() требует
использования четырех видов сырья
требует
использования четырех видов сырья ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Запасы сырья каждого
вида ограничены и составляют соответственно
. Запасы сырья каждого
вида ограничены и составляют соответственно ![]() ,
, ![]() ,
, ![]() ,
, ![]() условных
единиц. Количество единиц сырья, необходимое для изготовления единицы каждого из
видов продукции, известно и задаётся таблицей 2.4.
условных
единиц. Количество единиц сырья, необходимое для изготовления единицы каждого из
видов продукции, известно и задаётся таблицей 2.4.
Таблица 2.4
| Виды сырья | Запасы сырья | Виды продукции | |
|
|
|
||
|
|
|
|
|
| Доход |
|
|
В этой экономической ситуации ![]()
![]() означает количество единиц сырья вида
означает количество единиц сырья вида
![]() , необходимое для изготовления
продукции вида
, необходимое для изготовления
продукции вида ![]() . В последней строке таблицы указан доход, получаемый предприятием
от реализации одной единицы каждого вида продукции.
. В последней строке таблицы указан доход, получаемый предприятием
от реализации одной единицы каждого вида продукции.
Нужно определить такой план выпуска продукции видов![]() и
и ![]() , при котором доход предприятия от реализации
всей продукции оказался бы максимальным.
, при котором доход предприятия от реализации
всей продукции оказался бы максимальным.
Математическую форму поставленной задачи изучим на следующем числовом примере (см. таблицу 2.5).
Таблица 2.5
| Виды сырья | Запасы сырья | Виды продукции | |
|
|
|
||
|
|
19 | 2 | 3 |
|
|
13 | 2 | 1 |
|
|
15 | 0 | 3 |
|
|
18 | 3 | 0 |
| Доход | 7 | 5 |
Допустим, что предприятие выпускает ![]() единиц продукции вида
единиц продукции вида ![]() и
и ![]() единиц продукции вида
единиц продукции вида ![]() . Для этого потребуется
. Для этого потребуется ![]() единиц сырья
единиц сырья ![]() (на основании таблицы 2.5). Так как в
наличии имеется всего 19 единиц сырья
(на основании таблицы 2.5). Так как в
наличии имеется всего 19 единиц сырья ![]() , то должно выполняться неравенство
, то должно выполняться неравенство ![]() . Неравенство, а не точное равенство появляется
в связи с тем, что максимальный доход может быть достигнут предприятием и в том
случае, когда запасы сырья вида
. Неравенство, а не точное равенство появляется
в связи с тем, что максимальный доход может быть достигнут предприятием и в том
случае, когда запасы сырья вида ![]() используются не полностью.
используются не полностью.
Аналогичные рассуждения, проведённые для остальных видов сырья, позволяют записать следующие неравенства:
![]() (сырьё
(сырьё ![]() )
)
![]() (сырьё
(сырьё ![]() )
)
![]() (сырьё
(сырьё ![]() ).
).
При этих условиях доход ![]() , получаемый предприятием, составит
, получаемый предприятием, составит ![]() .
.
Таким образом, математически рассматриваемую экономическую ситуацию можно сформулировать так.
Дана система
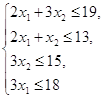
четырёх линейных неравенств и линейная целевая функция
![]() .
.
Требуется среди неотрицательных решений системы (4) выбрать
такое, при котором целевая функция ![]() принимает наибольшее значение (максимизировать).
принимает наибольшее значение (максимизировать).
Рассмотрим на примере ещё несколько игр.
Игра Морро. Игроки показывают одновременно 1 или 2 пальца и в тоже время называют число. Если число, названное одним игроком, совпадает с общим числом пальцев, то игрок получит от своего противника выигрыш, равный этому числу. Если оба угадают верно, то чистый платёж будет равен нулю.
|
|
|
|
|
|
|
|
0 | 2 | -3 | 0 |
|
|
-2 | 0 | 0 | 3 |
|
|
3 | 0 | 0 | -4 |
|
|
0 | -3 | 4 | 0 |
Оборона города («Игра полковника Блотто»)
Полковник Блотто имеет m полков, а его противник – n полков. Противник защищает 2 позиции. Позиция будет защищена полковником, если на ней наступающие полки окажутся в численном превосходстве. Противоборствующим сторонам тре6уется распределить полки между двумя позициями. Если игрок 1 (полковник) имеет на позиции больше полков, то выигрыш равен числу полков противника плюс один (занимаемая позиция равносильна захвату одного полка). Если у противника (игрока 2) больше полков на позиции, то игрок 1 таким образом теряет свои полки на этой позиции и ещё единицу. Если обе стороны имеют одинаковое количество полков на позиции, то имеет место ничья. Посмотрим на стратегии игроков.
Игрок 1 имеет следующие стратегии:
![]() - послать все полки на первую позицию
- послать все полки на первую позицию
![]() - послать
- послать ![]() полков на
первую позицию, а
полков на
первую позицию, а ![]() полков – на вторую
позицию и т.д.
полков – на вторую
позицию и т.д.
![]() - послать все полки на вторую позицию
- послать все полки на вторую позицию
Игрок 2 имеет такие стратегии:
![]() - послать все полки на первую позицию
- послать все полки на первую позицию
![]() - послать
- послать ![]() полков на
первую позицию, а
полков на
первую позицию, а ![]() полков – на вторую
позицию и т.д.
полков – на вторую
позицию и т.д.
![]() - послать все полки на вторую позицию
- послать все полки на вторую позицию
Пусть m=4, n=3. Тогда рассмотрев всевозможные ситуации, получим матрицу выигрышей, для этой игры
|
Игрок 1 Игрок 2 |
|
|
|
|
|
|
4 | 2 | 1 | 0 |
|
|
1 | 3 | 0 | -1 |
|
|
-2 | 2 | 2 | -2 |
|
|
-1 | 0 | 3 | 1 |
|
|
0 | 1 | 2 | 4 |
Основная задача линейного программирования.
Любую задачу линейного программирования можно свести к
ОЗЛП (основной задаче линейного программирования). Основной принцип данной задачи
таков: найти такие неотрицательные значения переменных ![]() , которые удовлетворяли условиям
– равенствам
, которые удовлетворяли условиям
– равенствам

и обращали бы в максимум линейную функцию этих переменных:
![]() . Если функцию L требуется обратить в минимум, то для этого нужно изменить знак
этой функции (т.е. максимизировать не L, а
. Если функцию L требуется обратить в минимум, то для этого нужно изменить знак
этой функции (т.е. максимизировать не L, а ![]() ). Рассмотрим конкретный пример,
объясняющий эту позицию.
). Рассмотрим конкретный пример,
объясняющий эту позицию.
Пример. Пусть требуется найти неотрицательные
значения переменных ![]() , удовлетворяющих
ограничениям – неравенствам
, удовлетворяющих
ограничениям – неравенствам 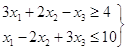 и обращающие
в максимум линейную функцию
и обращающие
в максимум линейную функцию ![]() . Приведём
условия в фигурной скобке к стандартному виду. Получим
. Приведём
условия в фигурной скобке к стандартному виду. Получим 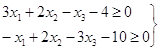 (1). А теперь обозначим левые
части неравенств через y1 и y2 =>
(1). А теперь обозначим левые
части неравенств через y1 и y2 => 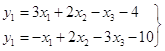 (2). Из условий (1) и (2) следует
что переменные y1 и y2 тоже должны быть неотрицательными.
(2). Из условий (1) и (2) следует
что переменные y1 и y2 тоже должны быть неотрицательными.
Выводы
1 Представлены основные понятия теории игр и исследования операций.
2 Приведены примеры игр в чистой и смешанной стратегиях (задача Борьба двух предприятий за рынок продукции региона»).
3 Представлена основная теорема Теории игр (с доказательством) и использован принцип сведения теоретико-игровой модели к ЗЛП (задаче линейного программирования)
4 В работе приведена серия задач, связанных с теорией игр и исследованием операций (в частности – основная задача линейного программирования).
5 Раскрыто современное понятие «Принятие решений» на основе математических методов и моделей Теории игр
ЛИТЕРАТУРА
1. Борисова С.П., Власова И.А., Коваленко А.Г. Теория игр и исследование операций – Издательство «Самарский университет», 2006.
2. Берж Л. Общая теория игр нескольких лиц – М.: ГИФМЛ, 1961. 327.стр.
3. Барсов А.С. Линейное программирование в технико-экономических задачах. М.: Наука, 1964. – 278 с.
4. Воробьёв Н.Н. Матричные игры – М.: Физматгиз, 1961.
5. Власов Д.А., Монахов Н.В., Монахов В.М. Математические модели и методы внутримодельных исследований – Издательство «Альфа», 2007.
6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология – М.: Дрофа, 2006. 208 страниц.
7. Гасс С. Линейное программирование (методы и приложения) – М., 1961.
8. Гамецкий А.Ф., Слободенюк В.А., Спиридонова Г.В. Теория игр, исследование операций – Издательство КГУ, 1987.
9. Громенко Г.Н. Теория игр – М.: Издательство МГОУ, 2005. 198 стр.
10. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр – М.: Наука, 1989. 310 стр.
12. Давыдов Э.Г. Исследование операций: учебное пособие – М., 1990.
13. Зайченко Ю.П. Исследование операций – Киев, 1979. 278 стр.
14. Краснов М.Л., Киселёв А.И. Высшая математика, том 5 – М.: Издательство ЛКИ, 2007. 300 стр.
15. Конюховский П.В. Математические методы исследования операций в экономике - СПб.: Издательство СПбГУ. 394 стр.
16. Карлин С. Математические методы в теории игр, программировании и экономике – М., 1964. 400 стр.
17. Льюис Р.Д., Райфа Г. Игры и решения. – М.: ИЛ, 1961 285 стр.
18. Лагунов В.Н. Игры преследования и введение в теорию игр. Т., 1993
19. Мак-Кинси Дж. Введение в теорию игр. – М.: Физматгиз, 1960.
20. Малыхин В.И.. Статкус А.В. Теория принятия решений. МИУ, М., 1989. 382 стр.
21. Мулен Э Теория игр с примерами из математической экономики - М.: Мир 1985.
22. Нейман Дж. Фон, Моргенштерн О. Теория игр и экономическое поведение – М.: Издательство «Наука», 2007. 420 стр.
23. Нестеров Е.П. Транспортные задачи линейного программирования – М.: Транспорт 1971. 216 стр.
24. Оуэн Г. Теория игр - М.: Издательство ЛКИ, 2007. 232 стр.
25. Петросян Л.А. Теория игр – М.: Издательство «Высшая школа», 1998.
26. Протасов И.Д. Теория игр и исследование операций – М.: Издательство «Гелиос» АРВ, 2006. 368 страниц.
27. Парфёнов Г.Н. Принципы теории игр – Издательство СПбГУ, 2001.
28. Секацкий В.В., Худякова Г.И. Элементы теории матричных игр в курсе математики.// Ярославский педагогический вестник. 2000, №1(23).
29. Терехов Л.Л. Применение математических методов в экономике – М.: Статистика, 1968. 188 стр.
30. Таха Х. Введение в исследование операций – М.: издательство «Вильямс», 2001.
31. Фатхутдинов Р.А. Управленческие решения – М.: нфра 2007.
32. Хорн Р., Джонсон Ч. Матричный анализ – М.: Мир, 1989. 427 стр.
33. Хазанова Л.Э. Математические методы в экономике – М.: издательство БЕК, 2002. 144 стр.
34. Шикин Е.В. От игр к играм – М.: УРСС, 1997. 149 стр.
35. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория, методы, приложения – М.: «Наука», 1969. 364 стр.
36. Яновская Е.Б. Антагонистические игры // Проблемы кибернетики. – М.: Наука, 1978. С. 221 – 246.
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... Линейная алгебра и теория матриц определяют множество операций над матрицами, которые непо-средственно поддерживаются (т.е. выполняются как стандартные операции) в MATLAB-е. В ... Функции, действующие над плоскостями или матрицами, такие как функции линейной алге-бры или матричные функции в директории matfun , не принимают в качестве аргументов многомерные ... |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... Любая неособенная матрица, которая удовлетворяет матричному дифференциальному уравнению (12), называется фундаментальной матрицей системы (11). Из неравенства (28) следует, что если существует интеграл, то математическое ожидание интеграла от случайной функции Х(t) равно интегралу от математического ожидания этой случайной ... |
Раздел: Рефераты по математике Тип: реферат |
| Теория принятий решений | |
|
ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ Курс лекций. Урицкая О.Ю. ВВЕДЕНИЕ Искусство принятия наилучших решений, основанное на опыте и интуиции, является сущностью ... В матричных играх ситуация i*, j* называется приемлемой для первого игрока, если a ij* Ѭ ai*j* и приемлемой для второго игрока , если ai*j* Ѭ a i*j. Если же человек - первый игрок - будет продолжать играть оптимально, то его выигрыш составит v(x*) = - 150 0,3 - 160 0,4 - 170 0,2 - 180 0,1 = - 161 , а если применит первую ... |
Раздел: Рефераты по теории организации Тип: реферат |
| Линейное программирование | |
|
Содержание Содержание 1. Пояснительная записка 1.1.Введение 2. Теоретическая часть 2.1 Элементы теории матричных игр 2.2 Решение матричных игр в ... то проведение каждой партии матричной игры с матрицей А сводится к выбору игроком 1 i-й строки, а игроком 2 j-го столбца и получения игроком 1 (за счёт игрока 2) выигрыша аij. Средний выигрыш игрока 1 в матричной игре с матрицей А выражается в виде математического ожидания его выигрышей |
Раздел: Рефераты по информатике, программированию Тип: курсовая работа |
| Теория информации | |
|
Лекции по Теории информации Подготовил В.С. Прохоров Содержание Введение 1. Понятие информации. Задачи и постулаты прикладной теории информации 1.1 ... 4.8.4. Матричное представление линейных кодов Основой математического описания линейных кодов является линейная алгебра (теория векторных пространств, теория матриц, теория групп). |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |