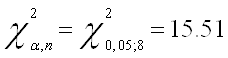Курсовая работа: Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка
Министерство образования Республики Беларусь
Белорусский Государственный Университет
Экономический факультет
Кафедра Экономической и институциональной экономики
Курсовой проект
По дисциплине «Эконометрика и прогнозирование»
На тему
«Построение эконометрической модели и исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка»
Выполнила
Студентка третьего курса
Отделения «Экономическая теория»
Волкова Ольга Александровна
Научный руководитель:
Абакумова Юлия Георгиевна
Минск, 2008 г.
Содержание
Введение
Теоретический раздел
Аналитический раздел
Построение базовой регрессионной модели и оценка её качества
Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка
Устранение гетероскедастичности в модели
Заключение
Список использованных источников
Введение
Вся история развития человечества неразрывно связана с изменениями динамики численности и воспроизводства населения. Современные очень высокие темпы роста численности населения мира в решающей степени определяются темпами его увеличения в развивающихся странах.
Современный «взрыв» населения в развивающихся странах имеет существенные особенности. Главная особенность заключается в том, что если в Европе быстрый рост населения был обусловлен в первую очередь социально-экономическими изменениями, т.е. следовал за экономическим ростом и изменениями в социальной сфере, то в развивающихся странах мы наблюдаем прямо противоположную картину: быстрый рост населения значительно опережает их экономическое и социальное развитие, усугубляя тем самым и без того ложные проблемы занятости, социальной сферы, обеспечения продовольствием, экологии.
Наряду с наблюдаемым во второй половине XX века демографическим взрывом проявился и демографический кризис, затронувший в первую очередь развитые страны мира.
Суть современного демографического кризиса заключается не только в резком ухудшении развития народонаселения, что выражается в резком уменьшении темпов роста численности населения в развитых странах, а в некоторых из них и снижении этого показателя за нулевую отметку, но и в определенном кризисе института семьи, в некотором ухудшении качества развития населения, в демографическом старении.
Наблюдаемая в развитых странах мира тенденция к резкому падению рождаемости значительно ниже уровня, обеспечивающего простое воспроизводств населения, ведет к значительному демографическому старению, сокращению трудовых ресурсов и увеличению «экономической нагрузки» на экономически активное население, на старение населения или увеличение доли пожилых и старых людей.
Итак, изменение показателя общей численности населения происходит под воздействием целого ряда прямых и косвенных факторов. В своей работе я бы хотела рассмотреть влияние показателей рождаемости, смертности и численности пожилого населения в разных странах мира на общую численность населения этих стран.
Такой выбор обусловлен, в первую очередь, целью моей работы – проверка регрессионной модели на гетероскедастичность (т.к. эта проблема в большей степени присуща пространственным данным и редко встречается во временных рядах).
Таким образом построенная мною модедь содержит следующие объясняющие переменные:
X1 – численность рожденных детей за 2007г. (чел.),
X2 – численность умерших за 2007г. (чел),
Х3 – численность населения в возрасте от 65 лет и старше (чел.), и объясняемую переменную:
Y – общая численность населения на начало 2008г. (чел.).
Статистические данные по странам взяты за период 2007г, влияющие на общую численность населения начала 2008г. (Таблица 1)
| Страны | Общая численность населения на начало года | X1- численность рожненных детей за 2007г. | X2 - смертность за 2007г. | X3 - численность населения старше 65 лет за 2007г. |
| Бельгия | 10666866 | 120663 | 374.0553 | 1824034.086 |
| Болгария | 7640238 | 75349 | 693.2108 | 1321761.174 |
| Чехия | 10381130 | 114632 | 355.3592 | 1484501.59 |
| Дания | 5475791 | 64082 | 256.328 | 837796.023 |
| Германия | 82221808 | 682700 | 2594.26 | 16279917.98 |
| Эстония | 1340935 | 15775 | 78.875 | 229299.885 |
| Ирландия | 4419859 | 70623 | 261.3051 | 490604.349 |
| Греция | 11214992 | 110048 | 418.1824 | 2085988.512 |
| Испания | 45283259 | 488335 | 1806.8395 | 7562304.253 |
| Франция | 63753140 | 816500 | 3102.7 | 10328008.68 |
| Италия | 59618114 | 563236 | 2140.2968 | 11864004.69 |
| Кипр | 794580 | 8529 | 52.8798 | 97733.34 |
| Латвия | 2270894 | 23273 | 202.4751 | 388322.874 |
| Литва | 3366357 | 32346 | 190.8414 | 525151.692 |
| Люксембург | 483799 | 5477 | 9.8586 | 67731.86 |
| Венгрия | 10045000 | 97600 | 575.84 | 1597155 |
| Мальта | 410584 | 3871 | 25.1615 | 56660.592 |
| Нидерланды | 16404282 | 180882 | 741.6162 | 2378620.89 |
| Австрия | 8331930 | 76250 | 282.125 | 1408096.17 |
| Польша | 38115641 | 387873 | 2327.238 | 5107495.894 |
| Португалия | 10617575 | 102492 | 348.4728 | 1836840.475 |
| Румыния | 21528627 | 214728 | 2576.736 | 3207765.423 |
| Словения | 2025866 | 19636 | 60.8716 | 322112.694 |
| Словакия | 5400998 | 54424 | 331.9864 | 642718.762 |
| Финляндия | 5300484 | 58729 | 158.5683 | 874579.86 |
| Швеция | 9182927 | 103421 | 258.5525 | 1597829.298 |
| Великобритания | 61185981 | 770651 | 3467.9295 | 9789756.96 |
| Турция | 70586256 | 1361000 | 29533.7 | 4658692.896 |
| Исландия | 314321 | 4508 | 6.3112 | 36775.557 |
| Норвегия | 4737171 | 58459 | 181.2229 | 691626.966 |
| Швейцария | 7591414 | 74440 | 290.316 | 1229809.068 |
Табл. 1
Теоретический раздел
При практическом проведении регрессионного анализ модели с помощью МНК необходимо обращать внимание на проблемы, связанные с выполнимостью свойств случайных отклонений модели, т.к. свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса-Маркова), т.к. при их нарушении МНК может давать оценки с плохими статистическими свойствами.
Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: т.е. D( εi ) = D( εj ) = σ2 для любых наблюдений i и j. Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
Наличие гетероскедастичности может привести к снижению эффективности оценок, полученных по МНК, к смещению дисперсий, к ненадежности интервальных оценок, получаемых на основе соответствующих t- и F-статистик. Таким образом, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключения по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно можно признать статистически значимыми коэффициенты, которые таковыми не являются. Причиной гетероскедастичности могут быть выбросы (резко выделяющиеся наблюдения), ошибки спецификации модели, ошибки в преобразовании данных, ассиметрия распределения какой-либо из объясняющих переменных. Чаще всего, появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако обычно приходиться решать эту проблему уже после построения уравнения регрессии. Не существует какого-либо однозначного метода определения гетероскедастичности. Существует довольно большое количество тестов и критериев, наиболее популярными и наглядными из которых являются: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Голдфельда-Квандта и тест Уайта. Моя работа посвящена исследованию поледних двух тестов.
Тест Уайта
Алгоритм этого теста заключается в том, что сперва оценивается исходная модель и определяются остатки εi , затем строится вспомогательно уравнение регрессии и определяется его коэффициент детерминации, произведение n*R^2 сравнивается со значением χ^2- распределения и делается вывод о наличии или об отсутствии гетероскедастичности.
Тест Парка
Парк в свою очередь предложил следующую функциональную зависимость:
![]()
Алгоритм теста:
1) Оцениваем исходное уравнение и определяем ei.
2) Оцениваем уравнение
![]()
Проверяем статистическую значимость коэффициента β уравнения на основе статистики
![]()
Если β значим, то гетероскедастичность. Если нет, то гомоскедастичность.
Тест Бреуша-Пагана-Годфри
1) Оценивается исходная модель и определяются остатки
![]()
Строится оценка:
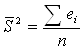
2) Оценивается регрессия
![]()
![]()
![]()
Если ![]()
При установлении присутствия гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Сначала можно попробовать устранить возможную причину гетероскедастичности, скорректировав исходные данные, затем попробовать изменить спецификацию модели, а в случае, если не помогут эти меры, использовать метод взвешенных наименьших квадратов.
Далее в работе проведем довольно полный анализ базовой модели, включая непосредственно тесты на обнаружение гетероскедастичности.
Аналитический раздел
1. Построение базовой регрессионной модели и оценка её качества
По данным Таблицы 1 построим исходную модель с помощью пакета Eviews3.1. Получим следующее уравнение построенной модели:

Где:
Population – общая численность населения на начало 2008г. (чел.),
Birth – численность рожденных детей за 2007г. (чел.),
Mortality – численность умерших за 2007г. (чел),
Old – численность населения в возрасте от 65 лет и старше (чел.).
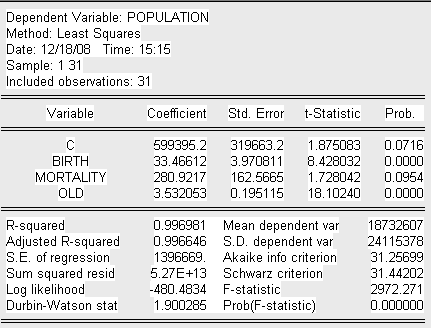
Проверим на значимость коэффициенты уравнения регрессии. Для этого оценим t-статистику:

![]()
Используем в данном
случае уровень значимости ![]() . Тогда критическое значение t-статистики соответственно:
. Тогда критическое значение t-статистики соответственно:
![]()
Значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.
Продолжая оценивать общее качество модели, используем критерий Фишера:
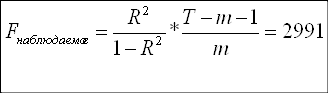
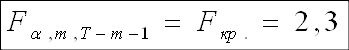
Н0: R-квадрат=0
Н1: R-квадрат>0
Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна. Поскольку значение F-наблюдаемого велико, можно сделать предположение о наличии мультиколлинеарности, что будет проверено мною в дальнейшем.
Оценим также распределение остатков в модели:
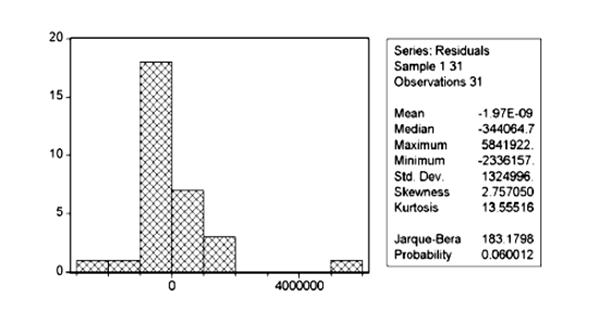
P (J-B) = 0,06, следовательно присутствует нормальное распределение остатков.
Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.
1) Первоначально воспользуемся тестом Бреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:
Запишем значение ![]() распределения
для последующего сравнения с Obs* R-squared:
распределения
для последующего сравнения с Obs* R-squared:
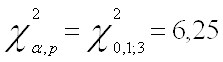
Приведем результаты теста с lag = 1:
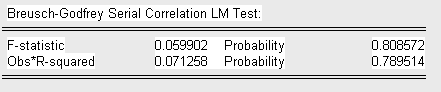
с lag = 2:

с lag = 3:

Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше
![]()
а P-вероятность статистики Бреуша-Годфри больше уровня значимости
(![]() )
)
2) Воспользуемся также тестом Дарбина-Уотсона:
Приведем значение статистики:
![]()
Значения критических точек
![]() при уровне значимости
при уровне значимости ![]() :
:
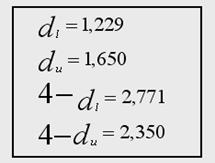
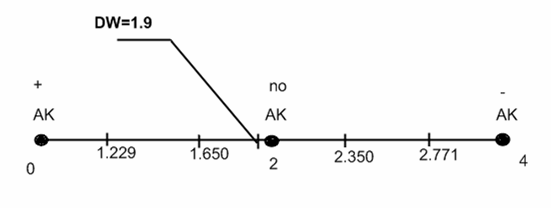
Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-W в данном случае близко к 2.
Выполним проверку регрессионной модели на мультиколлинеарность.
Построим корреляционную матрицу коэффициентов:
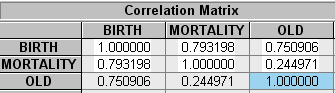
Найдем частные коэффициенты корреляции:
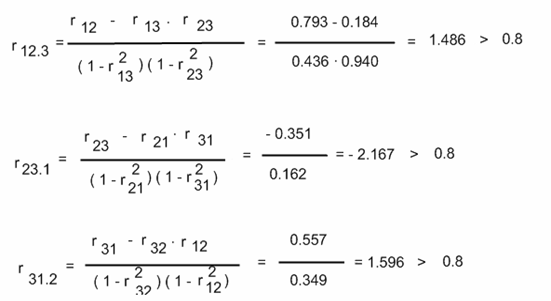
Делаем вывод о наличии высокой зависимости (коллинеарности) между переменными в каждом из трех случаев. Следовательно в модели присутствует мультиколлинеарность. Эта проблема оказывает определенное влияние на качество модели, однако ее устранение не является обязательным этапом, поэтому перейдем к дальнейшему исследованию качества регрессионной модели.
2. Исследование проблемы гетероскедастичности с помощью тестов Вайта, Бреуша-Пагана-Годфри и Парка
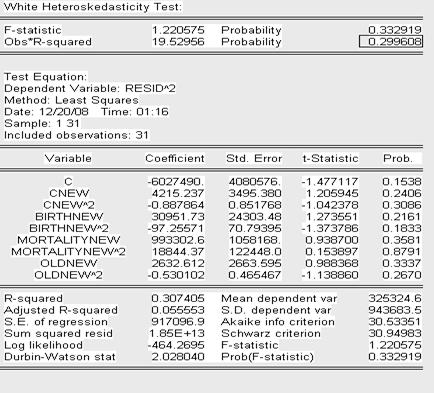
Переходим непосредственно к основной теме курсвой - проверяем модель на наличие гетероскедастичности. Для этого первоначально проведем тест Вайта и оценим его результаты:
![]()
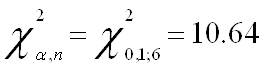

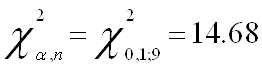

Т.к. значение P- вероятности в обоих случаях теста Уайта (no cross terms/ cross terms) меньше уровня значимости
(![]() ) и Obs*
) и Obs*
R-squared превышает
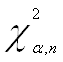
то принимаем гипотезу о наличии гетероскедастичности в модели.
Дополнительно можно использовать графический анализ ряда остатков, который подтверждает вывод о наличии гетероскедастичности, т.к. график имеет выбросы и не укладывается в полосу постоянной ширины, параллельную оси ОХ (-1000000,1000000).
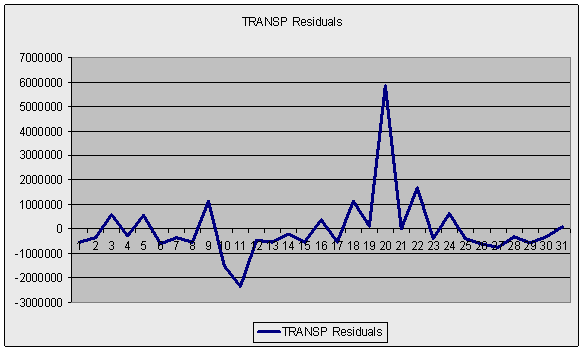
Таким образом, в этой модели мы имеем две проблемы – мультиколлинеарность и гетероскедастичность, в связи с чем нельзя доверять статистическим выводам и оценкам качества регрессионной модели. Продолжим дальнейший анализ модели с помощью теста Парка. Данный тест не предполагает особой свободы выбора и мы строим три регрессионные модели натуральных логарифмов остатков базовой модели на натуральные логарифмы каждой объясняющей переменной отдельно.
Представим вспомогательную модель 1 теста Парка:
Запишем уравнение вспомогательной модели 1:
![]()
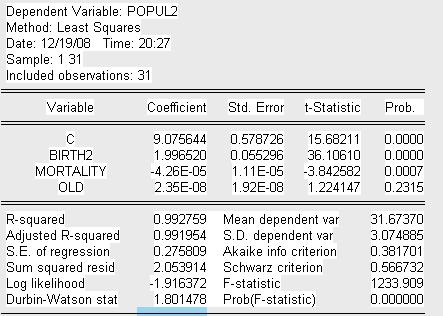
Где:
POPUL2=ln (population^2)
BIRTH2=ln(birth).
Оценим значимость коэффициентов уравнения регрессии. Для этого оценим t-статистику:

Найдем критическое значение t-статистики на уровне значимости
(![]() )
)
![]()

После
проведенного теста можно сделать вывод о наличии гетероскедастичности по
переменной Birth в следствие того, что коэффициент ![]() при данной
переменной является значимым.
при данной
переменной является значимым.
Представим вспомогательную модель 2 теста Парка:
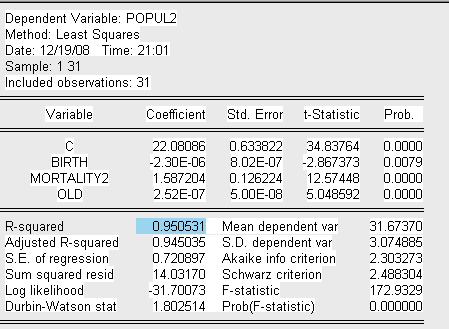
Где:
POPUL2=ln (population^2)
MORTALITY2=ln(mortality).
Запишем уравнение вспомогательной модели 2:

Оценим значимость коэффициентов уравнения
регрессии. Для этого оценим t-статистику.
Найдем
критическое значение t-статистики
на уровне значимости (![]() )
)
![]()
![]()
После
проведенного теста можно сделать вывод о наличии гетероскедастичности по
переменной Mortality в следствие того, что коэффициент ![]() при данной
переменной является значимым.
при данной
переменной является значимым.
Представим вспомогательную модель 3 теста Парка:
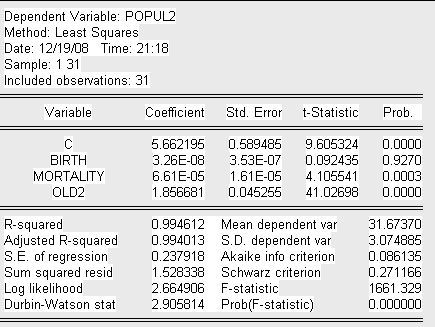
Где:
POPUL2=ln (population^2)
OLD2=ln(old).
Запишем уравнение вспомогательной модели 2:

Оценим значимость коэффициентов уравнения
регрессии. Для этого оценим t-статистику.
Найдем
критическое значение t-статистики
на уровне значимости (![]() )
)
![]()
После
проведенного теста можно сделать вывод о наличии гетероскедастичности по
переменной Old в следствие того, что коэффициент ![]() при данной
переменной является значимым.
при данной
переменной является значимым.
Оценив каждую переменную по тесту парка в отдельности подтверждаем выводы сделанные ранее по тесту Вайта о гетероскедастичности исходной модели.
Теперь используем тест Бреуша-Пагана для окончательного подтвержения гетероскедастичности. Для начала строим временной ряд квадратов остатков, деленных на величину
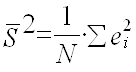
а затем строим для него саму регрессионную модель.
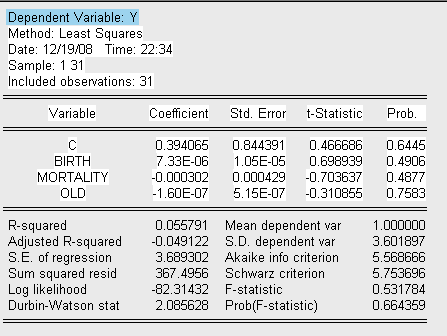
Находим необходимые для анализа параметры вспомогательной регрессии:
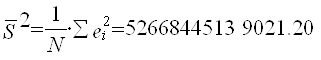
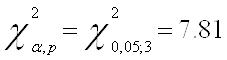
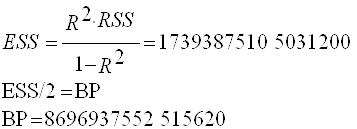
Делаем вывод об очевидном присутствии в модели гетероскедастичности, так как
![]() >>
>>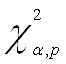
Устранение гетероскедастичности в модели
После проведения тестов Вайта, Бреуша-Пагана-Годфри и Парка было выявлено очевидное наличие проблемы гетероскедастичности остатков в базовой модели регрессии. Приступим к ее устранению при помощи веса, выбранного соответственно тесту Бреуша-Пагана. Предпологаем форму выявленной гетероскедастичности:
![]()
Вес: 
Оцененная с помощью метода взвешанных наименьших квадратов базовая регрессия выглядит следующим образом:
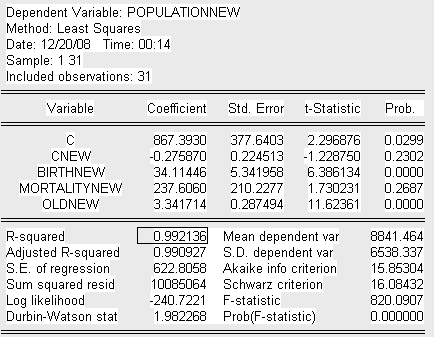
Получим следующее уравнение построенной модели-NEW:

Где переменные, скорректированные на вес:
PopulationNEW – общая численность населения на начало 2008г. (чел.),
cNEW – константа базовой модели, деленная на вес,
BirthNEW – численность рожденных детей за 2007г. (чел.),
MortalityNEW – численность умерших за 2007г. (чел),
OldNEW – численность населения в возрасте от 65 лет и старше (чел.).
Проверим на значимость
коэффициенты уравнения регрессии. Для этого оценим t-статистику. Используем в данном случае уровень значимости ![]() . Тогда
критическое значение t-статистики
соответственно:
. Тогда
критическое значение t-статистики
соответственно:
![]()
Если значения t-статистик рассматриваемых переменных больше критического значения (критерий Стьюдента), следовательно делаем вывод о их значимости. Лишь одна переменная, являющаяся в прошлой базовой модели константой в данном случае незначима, что логично, ведь она не имеет реального смысла, т.е. не описывает реальным образом объясняемую переменную. По анализу исследованных t-статистик и коэффициента детерминации R-квадрат делаем предварительный вывод об адекватности построенной модели.
Продолжая оценивать общее качество модели, используем критерий Фишера:
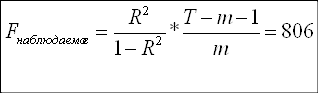
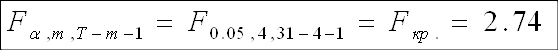
Н0: R-квадрат=0
Н1: R-квадрат>0
Так как F-наблюдаемое больше F-критического, принимаем гипотезу Н1, согласно которой модель адекватна.
Проверим модель на присутствие автокорреляции. Для этого будем использовать тесты Бреуша-Годфри и Дарбина-Уотсона.
1) Первоначально воспользуемся тестом Бреуша-Годфри и оценим модель на присутствие автокорреляции по трем лагам:
Запишем значение ![]() распределения
для последующего сравнения с Obs* R-squared:
распределения
для последующего сравнения с Obs* R-squared:
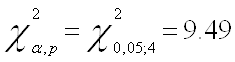
Приведем результаты теста с lag = 1:

с lag = 2:

с lag = 3:

Сделаем выводы об отсутствии серийной корреляции, так как во всех трех случаях Obs* R-squared меньше
![]()
а P-вероятность статистики Бреуша-Годфри больше уровня значимости
(![]() )
)
2) Воспользуемся также тестом Дарбина-Уотсона:
Приведем значение статистики:
![]()
Значения критических точек
![]() при уровне значимости
при уровне значимости ![]() :
:
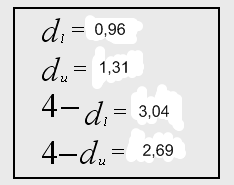
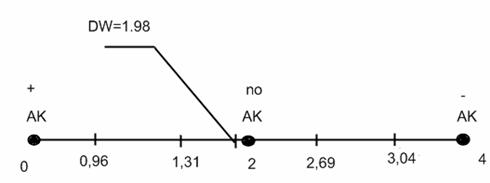
Делаем вывод об отсутствии автокорреляции, т.к. значение статистики D-W в данном случае близко к 2.
Проверим скорректированную модель на наличие гетероскедастичности с помощью теста Вайта
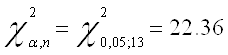
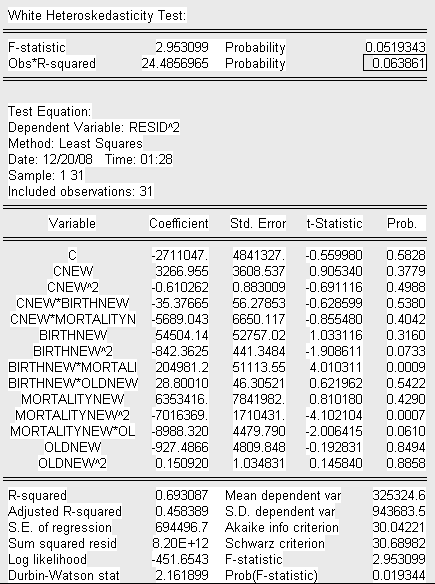
Т.к. значение P- вероятности в обоих случаях теста Уайта (no cross terms/ cross terms) больше уровня значимости
(![]() )
)
и Obs* R-squared превышает
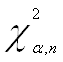
то принимаем гипотезу об отсутствии гетероскедастичности в модели (гомоскедастичность).
Заключение
В моей курсовой работе я построила регрессионную модель по реальным данным. Я разбиралась с моделью зависимости общей численности населения от показателей рождаемости, смертности и численности пожилого населения, их влиянием друг на друга и на объясняемую переменную. Так как целью моей работы являлось проверить, как работают на практике тесты Уайта и Бреуша-Пагана-Годфри и Парка, то я использовала пространственные данные, которые позволяют наиболее наглядно проиллюстрировать проблему гетероскедастичности и способы ее устранения.
В работе достаточно наглядно продемонстрирована работа тестов для выявления гетероскедастичности, также удалось решить задачу с выбором веса для ВНК.
В ходе курсовой работы мне удалось скорректировать модель с помощью метода взвешенных наименьших квадратов, правильно подобрав вес при помощи теста Бреуша-Пагана, поскольку тест Вайта, к примеру, не дает нам точного ответа на вопрос о весе для ВНК. Построенная в конце моего исследования модель-NEW значима и является качественной, остатки ее в свою очередь гомоскедастичны.
Список использованных источников:
1. Бородич С.А. Вводный курс эконометрики: Учеб. пособие. – Мн.; БГУ, 2000. – 209, 227, 245 с.
2. Бородич С.А. Эконометрика: Учеб. пособие. – Мн.; Новое знание, 2006. – 237, 238 с.
3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.; ИНФРА-М, 1997.
4. Данные Eurostat http://epp.eurostat.ec.europa.eu/potal.
| Решение уравнений и неравенств с использованием свойств функций на ... | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Вятский государственный ... Существует стандартный прием решения: возведение в квадрат (при условии 0). Мы рассмотрим решение данного неравенства с использованием свойства монотонности. (Множество всех значений переменной, при которых уравнение (неравенства) имеет смысл, или ОДЗ). |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Статистика | |
|
Казань 2000 год Оглавление Введение 4 1. Источники статистической информации 7 2. Сводка и группировка материалов статистического наблюдения. 15 3 ... Самый распространенный способ определения параметров уравнения - это метод наименьших квадратов. (смотри решение тренировочных заданий, дискета №1 PR-2 задание 17). Статистика численности и состава рабочей силы. |
Раздел: Рефераты по статистике Тип: реферат |
| Теория экономического анализа | |
|
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования "Красноярский государственный ... Уравнение регрессии показывает, как в среднем изменяется результативный признак (Y) при изменении любой из переменных (Хi) и имеет вид: Сущность решения уравнений регрессии заключается в нахождении параметров регрессии (а и b). Это осуществляется по способу наименьших квадратов с использованием системы нормальных ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Составление и решение уравнений линейной регрессии | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ... 4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента Для обнаружения гетероскедастичности используем тест Голдфельда - Квандта: |
Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа |
| Статистика | |
|
Предмет и метод статистической науки. Предмет статистики. Актуальность и место этой науки в современных условиях. Основные категории статистики. Метод ... Данное свойство средней, гласящее, что сумма квадратов отклонений всех вариантов ряда от средней арифметической меньше суммы квадратов их отклонений от любого другого числа ... Параметры уравнения регрессии оцениваются на вероятностную надежность. После подстановки факторов в уравнение, проводятся расчеты его параметров по методу наименьших квадратов, и полученные результаты оцениваются на вероятностную надежность, путем ... |
Раздел: Рефераты по статистике Тип: реферат |