Реферат: Моделирование ситуаций и выработка управленческих решений
Содержание
1. Основные понятия. Классификация. Методы
2. Моделирование ситуаций
3. Процесс подготовки и принятия решений
4. Примеры применения количественных методов выработки решений
Библиографический список
1. Основные понятия. Классификация. Методы
Решение – один из необходимых моментов волевого действия и способов его выполнения. Волевое действие предполагает предварительное осознание цели и средств действия, мысленное обсуждение оснований, говорящих за или против его выполнения и т. п. Этот процесс заканчивается принятием решения.
Решение не есть доказательство математической теоремы или получение ответа математической задачи, ибо здесь нет волевого момента – ответ однозначен (в этом смысле выражение «решить арифметическую задачу» неточно). С другой стороны, решение не есть и чистый волевой акт: волевым усилием завершается обоснованный выбор, расчет. Как правило, решение предполагает выбор с участием воли одного из нескольких возможных вариантов действий.
Нас будут интересовать так называемые управленческие решения. Под управленческими решениями понимаются такие, которые принимаются и реализуются в процессе управления (в отличие, например, от инженерных, конструкторских или технологических решений).
Управленческие решения классифицируются по ряду признаков (рис. 1).
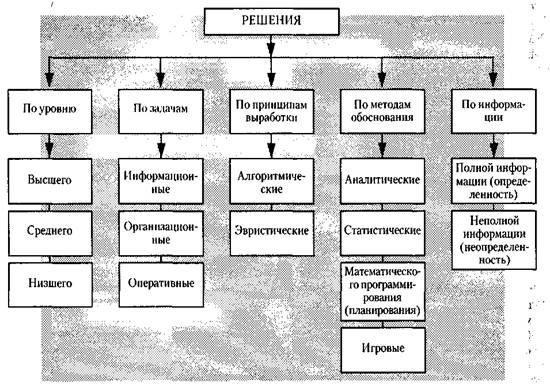
Рис. 1. Классификация решений
В зависимости от того, в какой руководящей инстанции принимается решение, оно бывает высшего, среднего или низшего уровня.
По решаемым задачам различают информационные, организационные и оперативные решения. Информационные решения имеют целью оценить получаемую информацию, ответить на вопрос: «Что правда?» Организационные решения призваны установить необходимую структуру управления, ответить на вопрос: «Каким быть?» Оперативные решения есть решения на действия: «Как действовать?»
Решения по принципам их выработки делятся на алгоритмические и эвристические. Алгоритмические решения – такие, выполнение которых производится по определенным правилам – алгоритмам. Эти решения допускают строгую формализацию. Эвристические решения – такие, которые выполняются неформальным, творческим путем, без каких-либо строгих правил.
По методам обоснования решения бывают аналитические, статистические, математического программирования и игровые, а по характеру исходной информации – в условиях определенности (полной информации) или в условиях неопределенности (неполной информации).
Средством, инструментом для выработки решений является исследование операций. Под исследованием операций понимают комплекс научных математических методов, применяемых для обоснования наилучших, правильных решений в любой области человеческой деятельности. Под операцией при этом понимается любое целенаправленное действие.
Исследование операций широко применяет такие разделы современной математики, как теория вероятностей, теория массового обслуживания, математическое программирование (линейное, нелинейное, динамическое), метод динамики средних, сетевое планирование, теория игр, теория статистических решений. Оснащение теории решений математическим аппаратом свидетельствует о становлении этой теории как науки.
Термин «исследование операций» появился в годы Второй мировой войны применительно к операциям военного характера. В послевоенные годы исследование операций получило широчайшее распространение не только в военной, но и в мирной области человеческой деятельности. С его помощью сегодня вырабатываются решения в промышленности, на транспорте, в городском хозяйстве и т. п.
Методы исследования операций не представляют собой единого универсального аппарата, пригодного для выработки решений на все случаи жизни. Исследование операций – это набор различных математических методов, объединенных общей задачей обоснования наилучших решений. Каждый из этих методов имеет свою область применения.
Методы исследования операций могут быть отнесены к четырем основным группам: аналитические, статистические, математического программирования, теоретико-игровые.
Аналитические методы характерны тем, что устанавливаются аналитические, формульные зависимости между условиями решаемой задачи и ее результатами. К этим методам относятся теория вероятностей, теория марковских процессов, теория массового обслуживания, динамика средних.
Теория вероятностей – наука о закономерностях в случайных явлениях. С ее помощью вырабатываются решения, зависящие от условий случайного характера.
Теория марковских случайных процессов разработана для описания операций, развивающихся случайным образом во времени.
Теория массового обслуживания рассматривает массовые повторяющиеся процессы.
Метод динамики средних применяется в тех случаях, когда можно составить зависимости между условиями операции и ее результатом исходя из средних характеристик указанных условий.
Статистические методы основаны на сборе, обработке и анализе статистических материалов, полученных как в результате фактически действий, так и выработанных искусственно путем статистического моделирования на ЭВМ. К этим методам относятся последовательный анализ и метод статистических испытаний.
Последовательный анализ дает возможность принимать решения на основе ряда гипотез, каждая из которых сразу же последовательно проверяется, например при проверке качества партии изделий.
Метод статистических испытаний (Монте-Карло) заключается в том, что ход операций проигрывается, как бы копируется на ЭВМ, со всеми присущими операции случайностями.
Математическое программирование представляет собой ряд методов, предназначенных для наилучшего распределения имеющихся в наличии ограниченных ресурсов, а также для составления рационального плана операции. Математическое программирование подразделяется на линейное, нелинейное и динамическое. Сюда же обычно относят и методы сетевого планирования.
Линейное программирование применяется в тех случаях, когда условия ведения операций описываются системой линейных (1-й степени) уравнений или неравенств. В случае, если указанные зависимости носят нелинейный характер (2-й и более степени), применяется метод нелинейного программирования.
Динамическое программирование служит для выбора наилучшего плана выполнения многоэтапных действий, когда результат каждого последующего этапа зависит от предыдущего.
Сетевое планирование, предназначено для составления и реализации рационального плана ведения операции, предусматривающего решение задачи в кратчайший срок и с наилучшими результатами.
предназначены для обоснования решений в условиях неопределенности (неполноты, неясности) данных обстановки. К теоретико-игровым методам относятся теория игр и теория статистических решений.
Теория игр применяется в тех случаях, когда неопределенность обстановки вызвана сознательными, злонамеренными действиями конфликтующей стороны.
Теория статистических решений применяется тогда, когда неопределенность обстановки вызвана объективными обстоятельствами, которые либо неизвестны, либо носят случайный характер.
Принципиально важной особенностью применения методов исследования операций является то, что выработка и реализация решений, как правило, не мыслятся без применения электронно-вычислительной техники. С другой стороны, и ЭВМ не могут функционировать без исследования операций. Причем ЭВМ не только, как это иногда считают, облегчает проведение расчетов и освобождает от сложных вычислений. Главное в том, что исследование операций и электронно-вычислительные машины придают выработанным решениям новое качество. Они способны производить такие расчеты и в такой срок, которые без них оказываются принципиально невыполненными.
Наряду с количественными методами современная наука, как это делалось и в прошлом, прибегает также к обоснованию решений исходя из факторов, пока не поддающихся точному количественному учету. Имеется в виду моральный фактор, общая ситуация, психологические моменты и т. п. При этом сохраняют свое значение традиционные методы обоснования решений на основе изучения опыта прошлых действий, обобщения результатов производства, а также просто по интуиции. Однако и к этим методам обоснования решений, относящимся к области искусства, следует подходить с позиции современной науки – психологии, эвристики (наука о творческом мышлении) и др.
Таким образом, современная теория обоснования решений включает: количественные методы обоснования решений, основанные на математическом аппарате исследования операций (теории вероятностей, теории игр, математическом программировании и др.); описательные методы обоснования и принятия решений, относящихся к области искусства (психология принятия решений, эвристика и др.).
Исследование операций, ориентированное на решение экономико-производственных задач, является базой для экономико-математических методов моделирования производственных процессов.
2. Моделирование ситуаций
стратегический решение модель система
Моделирование является основным методом исследования производственно-экономических систем. Под моделированием понимается такой способ отображения объективной реальности, при котором для изучения оригинала применяется специально построенная модель, воспроизводящая определенные (как правило, лишь существенные) свойства исследуемого реального явления (процесса).
Модель – это объект любой природы, который способен замещать исследуемый объект так, что его изучение дает новую информацию об исследуемом объекте.
В соответствии с этими определениями в понятие моделирования входит построение модели (квазиобъекта) и операции над ней для получения новой информации об исследуемом объекте. С позиций использования под моделью можно понимать удобное для анализа и синтеза отображение системы. Между системой и ее моделью существует отношение соответствия, которое и позволяет исследовать систему посредством исследования модели.
Тип модели определяется в первую очередь вопросами, на которые желательно получить ответ при помощи модели. Возможна различная степень соответствия модели и моделируемой системы.
Часто модель отображает только функцию системы, а структура модели (и ее адекватность системе) не играет роли, она рассматривается как черный ящик.
Имитационная модель включает уже единое отображение и функции системы, и существа происходящих в ней процессов.
Моделирование как метод познания основано на том, что все модели так или иначе отображают действительность. В зависимости оттого, как и какими средствами, при каких условиях, по отношению к каким объектам познания реализуется это их свойство, возникает большое разнообразие моделей. Существует ряд принципов классификации моделей разной природы, из которых наиболее существенными представляются следующие:
– по способу отображения действительности, а следовательно, и по аппарату построения (форма);
– по характеру моделируемых объектов содержание).
По способу отображения или аппарату построения различают два вида моделей (рис. 2): материальные и мысленные, или идеальные.
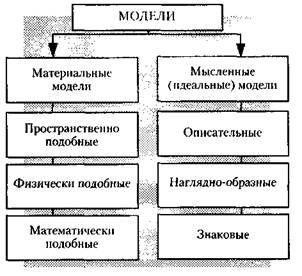
Рис. 2. Классификация моделей
Материальные модели – это модели, которые построены или отобраны человеком, существуют объективно, будучи воплощены в металле, дереве, стекле, электрических элементах биологических организациях и других материальных структурах.
Материальные модели делятся на три подвида.
Пространственно подобные модели – сооружения, предназначенные для отображения пространственных свойств или отношений объекта (макеты домов, заводов, районов города, транспортной сети, расположения оборудования в цехе и т. д.). Обязательным условием таких моделей является геометрическое подобие.
Физически подобные модели – материальные модели, имеющие целью воспроизвести разного рода физические связи и зависимости изучаемого объекта (модели плотин электростанций кораблей и самолетов). Основой построения таких моделей является физическое подобие – одинаковость физической природы и тождественность законов движения.
Математически подобные модели - модели обладающие в той или иной степени одинаковым математическим формализмом, описывающим поведение объекта и модели (аналог ЭВМ, кибернетические функциональные модели). Математически подобные материальные модели – это вещественные или физические оболочки некоторых математических отношений, но не сами отношения.
Мысленные (или идеальные) модели делятся на три подвида:
– описательные (концептуальные) модели, в которых отношения выражены в образах языка;
– наглядно-образные модели, образы которых в сознании построены из чувственно-наглядных элементов;
– знаковые (в том числе математические модели, в которых элементы объекта и их соотношения выражены при помощи знаков (в том числе математических символов и формул).
Классификацию моделей по характеру моделируемых объектов вследствие их чрезвычайного разнообразия приводить здесь не представляется целесообразным.
Конечной целью моделирования является изучение не модели как таковой, а некоторого отличного от нее, но воспроизводимого ею подлинного объекта изучения.
Очевидно, никакие модели не могут и не должны полностью воспроизводить все стороны и детали изучаемых явлений: предприятие может быть охарактеризовано с различных точек зрения – директора или главного инженера, бухгалтера, снабженца или энергетика. В соответствии с этим и характер, и построение модели будут различны.
Моделирование, как способ научного познания, основано на способности человека абстрагировать исходные признаки или свойства различных явлений (процессов) и устанавливать определенное соотношение между ними. Благодаря этому создается возможность исследовать явления или процессы косвенным путем, а именно изучением моделей, аналогичных им в некотором строго определенном отношении.
В общем случае целесообразна следующая последовательность моделирования систем: концептуальное описание (исследование) системы, ее формализация и, наконец, если это необходимо, алгоритмизация и квантификация системы.
При моделировании производственно-экономических систем наряду с формализованными, математическими методами анализа, используемыми для отдельных подсистем или частных процессов, приходится использовать также и эвристические методы анализа производства в тех его элементах и связях, которые не поддаются формализации. А при использовании математических методов вследствие множества переменных приходится зачастую прибегать к упрощениям, использовать методы декомпозиции и агрегирования переменных. В результате решения приобретают приближенный, качественный характер.
Вследствие наличия в больших сложных системах организационно-производственного управления звеньев и связей, которые трудно или вообще не формализуются, для их исследования приходится использовать в основном описательные модели, подвергая систему декомпозиции на отдельные функциональные подсистемы; затем искать те подсистемы, которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса.
Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения.
Модели производственно-экономических систем можно различать по следующим признакам:
– по целям моделирования;
– по задачам (функциям) управления;
– по этапам (процедурам) управления;
– по математическим методам моделирования.
В зависимости от целей моделирования различают модели, предназначенные для:
– проектирования систем управления;
– оценки эффективности;
– анализа возможностей предприятия в различных условиях его деятельности;
– выработки оптимальных решений в различных производственных ситуациях;
– расчета организационных структур системы управления;
– расчета информационного обеспечения и т. д.
Специфика моделей этого классификационного подразделения выражается в первую очередь в выборе соответствующих критериев эффективности, а также в процедуре реализации результатов моделирования.
В зависимости от задач (функций) управления различают модели календарного планирования, управления развитием предприятия, контроля качества продукции и т. д. Модели этого подразделения ориентированы на конкретные производственно-экономические задачи и, как правило, должны обеспечивать получение результатов в численном виде.
В зависимости от этапа (процедуры) автоматизации управления модели могут быть информационными, математическими, программными. Модели этого подразделения нацелены на соответствующие этапы движения и переработки информации.
В зависимости от применяемого математического аппарата модели можно разбить на пять больших групп: экстремальные, математического программирования (планирования), вероятностные, статистические и теоретико-игровые.
К экстремальным моделям относятся модели, дающие возможность отыскания экстремума функции или функционала. Сюда относятся модели, построенные с помощью графических методов, метода Ньютона и его модификаций, методов вариационного исчисления, принципа максимума Понтрягина и др. Исходя из возможностей этих методов они применяются в первую очередь для решения задач оперативного регулирования.
Модели математического программирования (планирования) включают модели линейного программирования, нелинейного программирования, динамического программирования. Сюда же обычно относят и модели сетевого планирования.
Математическое программирование объединяет ряд математических методов, предназначенных для наилучшего распределения имеющихся в наличии ограниченных ресурсов – сырья, топлива, рабочей силы, времени, а также для составления соответствующих наилучших (оптимальных) планов действий.
К вероятностным моделям относятся модели, построенные с помощью аппарата теории вероятностей, модели случайных процессов марковского типа (марковские цепи), модели теории массового обслуживания и др.
Вероятностные модели описывают явления и процессы случайного характера, например связанные со всевозможными несистематическими отклонениями и ошибками (производственный брак и др.), влиянием стихийных явлений природы, возможными неисправностями оборудования и т. п.
К статистическим моделям относятся модели последовательного анализа, метода статистических испытаний (Монте-Карло) и др. Сюда же можно отнести и методы случайного поиска.
Метод статистических испытаний заключается в том, что ход той или иной операции проигрывается, как бы копируется с помощью ЭВМ, со всеми присущими данной операции случайностями, например при моделировании организационных задач, сложных форм кооперации различных предприятий и т.п. Применение данного метода называют имитационным моделированием.
Методы случайного поиска применяются для нахождения экстремальных значений сложных функций, зависящих от большого числа аргументов. В основе этих методов лежит использование механизма случайного выбора аргументов, по которым осуществляется минимизация. Методы случайного поиска находят применение, например, при моделировании организационных структур управления.
Теоретико-игровые модели предназначены для обоснования решений в условиях неопределенности, неясности (неполноты информации) обстановки и связанного с этим риска. К теоретико-игровым методам относятся теория игр и теория статистических решений.
Теория игр – это теория конфликтных ситуаций. Она применяется в тех случаях, когда неопределенность обстановки вызывается возможными действиями конфликтующих сторон.
Теоретико-игровые модели могут найти применение при обосновании управленческих решений в условиях производственных, трудовых конфликтов, при выборе правильной линии поведения по отношению к заказчикам, поставщикам, контрагентам и т. п.
Теория статистических решений применяется тогда, когда неопределенность обстановки вызывается объективными обстоятельствами, которые либо неизвестны (например, некоторые характеристики новых материалов, качества новой техники и т. п.), либо носят случайный характер (состояние погоды, возможное время выхода отдельных узлов изделия из строя и т. п.).
Теоретико-игровые модели целесообразно использовать при подготовке, проведении и оценке результатов деловых игр.
Все математические модели могут быть подразделены также на модели оценки эффективности и модели оптимизации.
Модели оценки эффективности предназначены для выработки характеристик производства и управления. К этой группе относятся все вероятностные модели. Модели оценки эффективности являются «входными» по отношению к моделям оптимизации.
Модели оптимизации предназначены для выбора наилучших в данных условиях способов действий или линии поведения. К этой группе относятся экстремальные и статистические модели, модели математического программирования, а также теоретико-игровые модели.
Ниже будут рассмотрены некоторые наиболее распространенные модели, применяемые при решении производственных задач, а также для формирования организационных структур управления производством.
Основным направлением моделирования управления производственно-экономическими системами является создание моделей управления производством.
В настоящее время разработаны и находят применение модели следующих функций управления производством:
– планирования производственно-экономической деятельности предприятия;
– оперативного управления;
– оперативного регулирования;
– управления материально-техническим снабжением производства;
– управления сбытом готовой продукции;
– управления технической подготовкой производства.
Разработана также система взаимосвязанных моделей производства и управления.
Модели планирования производственно -экономической деятельности предприятия. Целевая функция моделей этой группы предусматривает:
– максимизацию критерия эффективности производственной деятельности предприятия исходя из наличных мощностей и отпускаемых ресурсов;
– минимизацию расхода ресурсов в рамках заданного критерия эффективности.
Модели планирования производственной деятельности предприятия подразделяются на: модели прогнозирования, модели технико-экономического планирования, модели оперативно-производственного планирования.
Модели прогнозирования представляют собой модели, либо основанные на математических методах (наименьших квадратов, пороговых значений, экспоненциального сглаживания), либо на методах экспертных оценок.
Модели технико-экономического планирования базируются на методах математического программирования (планирования). В качестве основного критерия эффективности (целевой функции) при выработке оптимального плана обычно избираются конечные результаты производства, например величина прибыли. В качестве ограничений берутся ограничения по сложности выпускаемой продукции, времени работы оборудования, ресурсам и т.д. Поскольку величина некоторых из указанных ограничений носит случайный характер (например, время работы оборудования), при решении таких задач оптимизации применяется вероятностный подход. Типовыми оптимизационными моделями технико-экономического планирования являются модели для расчета оптимального плана, распределения производственной программы по календарным периодам, оптимальной загрузки оборудования. Эти модели строятся с помощью математических методов оптимизации.
Модели оперативно-производственною планирования обычно совмещаются с моделями оперативного управления.
Модели оперативного управления. Основными задачами оперативного управления являются оперативно-календарное планирование производства, систематический учет и контроль за выполнением календарных планов, а также оперативное регулирование хода производства.
Типовыми моделями оперативного управления являются модели для расчета оптимального размера партий изделий и расчета оптимального графика запуска-выпуска партий деталей (календарное планирование).
Модели для расчета оптимального размера партий изделий могут быть созданы применительно как к простой, так и полной постановке задачи. В простой постановке определение размера производства или закупки партии деталей, при котором годовые затраты оказываются минимальными, сводится к обычной задаче на отыскание минимума функции. В полной постановке отыскивается такая совокупность размеров партий, которой соответствуют минимальные суммарные затраты на переналадку оборудования и отчисления на незавершенное производство при ограничениях по длительности переналадок, ресурсам оборудования, взаимозависимости размеров партий на смежных операциях и обеспечению занятости рабочего. Решение этой задачи достигается с помощью математических методов оптимизации.
Модели для расчетов календарного планирования могут быть:
– статистические с оптимизацией методом случайного поиска;
– имитационные с набором правил предпочтения;
– эвристические, применяемые в тех случаях, когда невозможно создание строгих алгоритмов, но есть необходимость использовать информацию и оценить факты, не имеющие количественного выражения.
Модели оперативного регулирования. Эти модели имеют целью обеспечить удержание отклонения результатов производственной деятельности от плановых показателей в заданных пределах. В этом случае применяются модели двух типов: модели регулирования по критерию оптимальности, модели регулирования по отклонению.
Модели регулирования по критерию оптимальности основываются на том, что после конкретного замера фактического состояния процесса производства составляется план, оптимальным образом приводящий процесс к заранее намеченному состоянию на момент окончания периода планирования.
Модели регулирования по отклонению базируются на том, что после конкретного замера производственный процесс в кратчайший срок выводят на первоначально составленный план-график.
Построение обеих моделей осуществляется с помощью математического аппарата оптимизации, применяемого в теории автоматического регулирования.
Модели управления материально-техническим снабжением производства. В качестве центральной проблемы управления материально-техническим снабжением производства выступает задача определения необходимого объема запасов всех видов снабжения. При этом могут быть построены две принципиально отличающиеся модели управления запасами – с фиксированным размером заказа и с фиксированным уровнем запасов. Существует также промежуточная модель, в которой фиксируется как верхний уровень запасов, так и нижний уровень заказа.
Построение моделей управления материально-техническим снабжением осуществляется с помощью специальных математических методов оптимизации, которые получили название «теория управления запасами».
Модели управления сбытом готовой продукции. Главной проблемой управления сбытом готовой продукции является задача расчета годового плана поставок готовой продукции. Для решения этой задачи с помощью математических методов оптимизации строится оптимизационная модель годового плана поставок готовой продукции. В качестве целевой функции при этом выступает стоимость реализованной продукции, в качестве ограничений – требование, чтобы суммарный объем продукции, отгруженной в определенный интервал времени всем потребителям, не превышал объема выпуска продукции за то же время, а суммарный объем поставок потребителю за все временные интервалы не превышал месячной заявки.
Модели управления технической подготовкой производства. Техническая подготовка производства включает стадии конструкторской и технологической подготовки.
С помощью математического моделирования могут быть решены три основные задачи управления технической подготовкой производства:
– определение минимального срока выполнения комплекса мероприятий технической подготовки производства при ограничениях на уровень наличных ресурсов;
– определение минимальной стоимости выполнения комплекса мероприятий технической подготовки производства при ограничениях на сроки его выполнения и на уровень наличия ресурсов;
– определение минимального уровня потребления дефицитных ресурсов при ограничении на стоимость и на сроки выполнения мероприятий технической подготовки производства.
Процесс технической подготовки производства наиболее полно и удобно воспроизводит сетевая модель. Сетевая модель дает возможность учесть вероятностный характер таких основных параметров операций технической подготовки производства, как длительность выполнения работ и интенсивность потребления ресурсов.
Оптимизация достигается применением методов математического программирования (в частности, симплекс-метода) и случайного (статистического) поиска.
Наряду с рассмотренными отдельными моделями, реализующими основные функции управления процессом производства, существует и система взаимосвязанных моделей производства и управления. Сущность этой системы моделей, построенной с помощью математического аппарата теории множеств, теории графов и повторного исчисления, заключается в следующем. В качестве множеств рассматриваются множество изделий, выпускаемых предприятием, и множество используемых при этом ресурсов. Производственный процесс, обеспечивающий выпуск множества изделий, описывается совокупным графом, а технологический процесс производства отдельного изделия – его конструкторско-технологическим графом. Множество ресурсов, обеспечивающих производство, состоит из подмножеств ресурсов рабочей силы, оборудования и дефицитных комплектующих изделий и материалов. Состояние производства на любой момент времени может при этом быть описано вектором, представляющим собой совокупность готовых изделий, полуфабрикатов и деталесборочных единиц, выпущенных к этому моменту. Аналогично с помощью вектора определяется и состояние ресурсов на любой момент времени. Плановая траектория производственного процесса при этом будет описываться вектор-функцией.
При такой постановке задачи оптимальное управление предприятием в плановый период может быть найдено исходя из следующего требования: на множестве допустимых планов, определяемых вектор-функцией, найти такой план, который максимизирует прибыль при условии, что вероятность его выполнения и получения прибыли установленного уровня будет не меньше заданного уровня, а затрачиваемые ресурсы не превысят имеющихся в наличии.
Моделирование организационных структур управления имеет целью совершенствование, оптимизацию системы управления предприятием. Оно является необходимым предварительным шагом автоматизации управления производственно-экономическими системами, которая требует серьезной подготовительной работы.
В качестве математического аппарата моделирования организационных структур управления применяется теория массового обслуживания. При этом элементы системы массового обслуживания принимаются как элементы системы управления, каждый из которых предназначен для решения определенной управленческой задачи. Для всех задач – элементов предусматривается система приоритетов в очередности решения. Для каждой задачи известны также и характеристики входящих потоков требований на обслуживание – решение соответствующих задач управления.
Элемент системы управления, решающий ту или иную задачу, располагает одним или несколькими преобразователями информации, в качестве которых выступают либо специалисты определенной квалификации, либо технические средства.
Эффективность работы системы управления оценивается по качеству и длительности обслуживания решения задач управления, с учетом их приоритетов и сложности.
Моделирование систем массового обслуживания может выполняться как аналитическими, так и статистическими методами. Наибольшее применение при моделировании организационных структур управления получил статистический метод, так называемый метод статистических испытаний (метод Монте-Карло). Этому методу отдается предпочтение на том основании, что он позволяет решать задачи большой сложности, для которых не существует аналитического (формульного) описания или последнее обладает чрезвычайной сложностью.
Статистическая модель позволяет поставить математический эксперимент, аналогичный натурному, произвести имитацию организационной структуры управления наиболее дешевым способом и в приемлемое время. Вместе с тем необходимо учитывать и специфические недостатки метода статистических испытаний, из которых главными являются относительно большое время моделирования и частный характер получаемых решений, определяемый фиксированными значениями параметров системы массового обслуживания.
При моделировании с помощью математического аппарата теории массового обслуживания структура системы управления предприятием рассматривается как совокупность взаимосвязанно функционирующих элементов. Такими элементами в реальной системе являются дирекция и функциональные отделы управления: производственно-технический, плановый, снабжения и др.
В результате совместного функционирования указанных элементов в системе управления осуществляется преобразование информации состояния в командную информацию, являющуюся основой управления предприятием.
Упомянутые элементы – подразделения системы управления предприятием составляют цепь, анализ функционирования которой может быть достаточно формализован с целью оптимизации процесса управления. Простейшей цепью, дающей хорошее приближение к реальности, является строго последовательная цепь элементов. При моделировании такой цепи возможны два похода: квазирегулярное и случайное представление. В квазирегулярной модели моделирование осуществляется по каждому элементу отдельно по усредненным показателям.
В случайной модели рассчитываются статистические оценки для каждого запроса на обслуживание, проходящего не по отдельным элементам, а по системе в целом.
Наряду с моделированием организационных структур управления с помощью цепей элементов существует способ математического описания оргструктуры системы управления с помощью линейных стохастических сетей, являющихся одним из классов многофазных систем массового обслуживания. В данной модели информация также проходит последовательно через ряд элементов системы управления, каждый из которых описывается с помощью математического аппарата теории массового обслуживания. При последовательном прохождении информации через элементы сети имеют место переходы марковского типа. Структура такой сети с соответствующими переходами представляется определенным графом. Составляется стохастическая матрица переходов.
Поскольку целевая функция (критерий эффективности) при математическом моделировании организационных структур управления, как правило, может быть описана лишь статистически, оптимизация производится в основном численными методами, из которых наибольшее применение получили методы динамического программирования и статистического поиска.
Решение задачи оптимизации методом динамического программирования реализуется путем составления для каждого шага процесса управления функционального рекуррентного уравнения (уравнения Беллмана).
Оптимизация организационных структур управления с помощью метода статистического поиска, несмотря на менее жесткие ограничения, накладываемые на критерии эффективности и допущения, описывающие физику явления при данном методе, пока не получила, применительно к рассматриваемой задаче, достаточно широкого распространения.
Игровое моделирование занимает особое место в ряду методов, применяемых для автоматизации управления производственно-экономическими системами. Отличительная черта этого метода – привлечение для моделирования процесса управления людей, участвующих в разработке и проведении деловой игры. Под деловой игрой при этом понимается имитация группой лиц решения отдельных задач хозяйственной или организационной деятельности предприятия, выполняемая на модели объекта в обстановке, максимально приближенной к реальной.
Введение в модель человека как элемента организации управления дает возможно учесть его поведение в тех случаях, когда оно не может быть адекватно описано с помощью известных сегодня математических моделей; позволяет решать такие управленческие задачи, которые не укладываются в рамки существующих формализованных методов.
Деловая игра вводит в процесс подготовки и принятия управленческих решений психологические и эмоциональные моменты, поощряя использование в этом процессе прошлого опыта руководителей, их интуиции, развивая способность к эвристическим решениям. Деловая игра проводится применительно к определенной управленческой задаче по заранее тщательно разработанному сценарию. Общая игровая модель формируется как совокупность частных моделей, создаваемых участниками – лицами, готовящими и принимающими управленческие решения.
Модель деловой игры включает как формализованную, так и неформализованную часть. Участники игры действуют по определенным правилам. Они руководствуются специально разработанными инструкциями по ведению игры, а также поступающими в их распоряжение данными обстановки.
В соответствии со сценарием игры участники периодически получают вводные об изменении обстановки. Готовя свои решения, участники деловой игры оценивают обстановку и производят необходимые расчеты вручную или с помощью ЭВМ. При этом используются формализованные, заготовленные заранее элементы игровой модели, соответствующие современным методам исследования операций.
Осуществляя управление ходом деловой игры, ее руководитель оценивает решения участников, устанавливает результаты их действий и доводит последние до играющих. При необходимости руководитель игры может менять установку, доводя эти изменения до участников в виде вводных. Оценка действий участников игры производится путем расчетов, экспертными методами, а также исходя из опыта руководителя, его интуиции и здравого смысла.
Основным видом игрового моделирования, проводимого на предприятиях, является производственная деловая игра. Ее цель – совершенствование существующих и выработка новых форм организации управления производством, отработка руководящих документов, перестройка производства и т. д.
В качестве моделей при проведении деловых игр широко применяются методы сетевого планирования и управления (СПУ), построенные на основе сетевых графиков. При решении задач планирования находят применение методы динамического программирования, а при решении задач распределения ресурсов – линейного программирования.
Для обучения управленческого персонала производственная деловая игра может проводиться в учебном варианте, т. е. учебная деловая игра. Ее главной задачей является обучение работников, совершенствование их навыков в управлении. При необходимости учебная деловая игра используется и для аттестования руководящих работников предприятий в выполнении ими своих должностных обязанностей, а также при выдвижении их на высшую должность.
3. Процесс подготовки и принятия решений
Подготовка и принятие решения представляют собой процесс содержательного преобразования информации состояния в управляющую информацию. Подготовка и принятие решения в целом являются не формальным, а творческим процессом, хотя и включают в себя определенные элементы, поддающиеся формализации. Совокупность этих элементов называется формализованной частью процесса содержательного преобразования информации.
Эта часть процесса представляет собой формальное преобразование информации состояния в управляющую в соответствии с какой-либо математической моделью, описывающей интересующую нас производственно-экономическую ситуацию. Поскольку модель, как правило, не может учесть всех факторов, влияющих на решение задачи, то информация, полученная на выходе модели, должна подвергаться творческому анализу со стороны человека и лишь после этого принимается решение, т. е. вырабатывается управляющая информация.
Здесь под словом «человек» понимается человек или группа людей в органе управления, ответственных за принятие решения. Фактически решение может принимать не всегда один человек, но также объединение или группа людей, вырабатывающих единую линию поведения, даже в том случае, если некоторые из членов объединения имеют отличную от предполагаемой точку зрения.
Процесс принятия решения можно представить в виде этапов, составляющих модель переработки информации состояния в информацию управления или модель процесса принятия решения:
– анализ проблемной ситуации и постановка задачи;
– определение параметров операции и выбор показателей ее успешности;
– построение описательной (концептуальной) модели выбора решения;
– построение математической модели функционирования системы;
– формирование решения.
Вместе с тем это деление принято лишь для удобства рассмотрения процесса подготовки и принятия решения и является условным. Между указанными этапами этого единого процесса имеются как прямые, так и обратные связи. Рассмотрим в общих чертах содержание каждого из названных этапов.
Анализ проблемной ситуации и постановка задачи. Постановка задачи заключается в том, что принимающий решение устанавливает самостоятельно или получает от вышестоящей инстанции определенную цель (задачу).
Пути достижения указанной цели в этот период еще не ясны. Наличие цели при неясности путей ее достижения рождает проблему. Появление проблемы приводит к сознательному поиску действия, пригодного для достижения цели. Найти такое действие – означает решить проблему. В общем случае решение проблемы должно удовлетворять основным требованиям:
– его осуществление (воплощение на практике) должно иметь своим результатом достижение желаемого состояния (цели);
– оно должно быть таким, чтобы исходя из данного состояния его можно было осуществить путем некоторого действия или набора действий.
Совокупность проблемы, человека, призванного ее решить, и комплекса условий, в которых он столкнулся с этой проблемой, определяет так называемую проблемную ситуацию. Одним из основных моментов анализа ситуации является уяснение (уточнение) целей.
Обычно человеку, принимающему решение в сложной ситуации, трудно выявить одну-единственную цель, которую он бы преследовал на протяжении всего процесса принятия решения. Поскольку цели, несомненно, связаны между собой, определить глубину этих связей удается редко. Одни цели могут дополнять друг друга, а другие – противоречить друг другу. Поэтому при анализе проблемной ситуации первостепенную важность имеет выявление по крайней мере некоторых основных целей.
Цели, которые стремится достичь человек, не являются неизвестными. В некоторых случаях изменение целей происходит постепенно и не отражается заметным образом на процессе принятия решения. Иногда же замена целей приводит к существенным изменениям в принятом решении.
Следовательно, в процессе уяснения проблемной ситуации совершенно необходима максимально возможная определенность цели или целей. Этот момент является главенствующим в принятии правильного решения. Поэтому он требует пристального внимания и специального рассмотрения со стороны принимающего решение. В дальнейшем полагаем, что уточненная и доопределенная цель остается неизменной, пока она не будет достигнута.
Не менее важным моментом является сбор и обработка данных о признаках и элементах проблемной ситуации, т. е. получение информации о состоянии управляемых объектов и о состоянии среды.
Для принятия решения необходимы в первую очередь различные директивные и нормативные данные, статистические материалы. Кроме того, необходима та или иная информация о параметрах объектов управления и среды, об их взаимосвязях. Организуя поиск и добывание информации, следует всегда сопоставлять полноту и достоверность сведений с затратами их получение. Важное значение имеет своевременность получения информации. Как затрат на получение информации, так и ее своевременность следует оценивать с точки зрения достижения поставленной цели.
Анализ информации представляет собой весьма сложный и в первую очередь целевой процесс. Технически он включает оценку достоверности информации, выявление возможных ошибок, учет недостаточной представительности выработки, несовершенства источников информации. Вследствие этого возникает необходимость фильтрации данных и связанного с ней обобщения информации. В основу фильтрации могут быть положены операции: отсечка информации, ее агрегация, типологическая выборка информации.
При отсечке множество информации разбивается на два класса: протекаемой и отсекаемой с помощью различных пороговых величин, шкал важности и т. д.
При агрегации сведения укрупняются, отдельные данные объединяются в подмножества на основе избранных признаков агрегации. При этом, конечно, теряется определенная информация о микросвязях, но возникают обобщенные характеристики макросвязей. Здесь самое важное сохранить интересующие нас целевые характеристики и связи в удобном для последующего использования виде.
При типологической выборке производится разделение исходного множества на классы и отбор элементов, представляющих эти классы.
Определение параметров операции и выбор показателей ее успешности. На этом этапе предусматривается установление тех величин (параметров), которые наиболее существенным образом влияют на исход действий и путем изменения которых можно добиться наилучшего конечного результата. Выбор наилучшего варианта решения задачи сводится к установлению тех наивыгоднейших параметров, приемов и способов действий, которые приводят к наилучшему в данных условиях (оптимальному) результату.
Показатели успешности (эффективности) операции – количественные критерии (числа), характеризующие ожидаемый результат операции. В качестве показателей должны выбираться такие величины, которые позволяют:
– прогнозировать ожидаемый исход действий;
– сравнивать различные приемы и способы действий между собой для выбора наилучшего;
– оценивать степень соответствия полученного результата действий требуемому.
Для того чтобы показатели успешности операции отвечали указанным требованиям, они должны вскрывать самую суть процессов операции, определять главные, решающие связи и показывать пути необходимых изменений параметров для повышения эффективности операции. Показатели успешности должны быть достаточно просты, наглядны и доступны для получения на практике.
Основной принцип выбора показателя успешности обоснован еще в 1945 году академиком А. Н. Колмогоровым и состоит в установлении строгого соответствия между целью, которая может быть достигнута в результате действий, и избранным показателем успешности. В этом смысле показатель успешности операции иногда называют целевой функцией.
Выбор наилучшего (оптимального) варианта решения задачи в самом общем виде можно представить как отыскание максимума целевой функции (показателя успешности операции W).
Выбор наилучшего варианта решения задачи можно сформулировать следующим образом: найти такие значения управляемых параметров b1, b2, ..., которые при заданных параметрах a1, a2,..., с учетом неизвестных параметров x1, x2, ..., обеспечивают максимум целевой функции – показателя успешности W. Столь простой на первый взгляд путь выбора наилучшего варианта решения задачи наталкивается, однако, на практике на ряд существенных трудностей.
Прежде всего, выбор одного из многих вариантов может потребовать огромного перебора параметров, недоступного даже для самой быстродействующей ЭВМ. Подсчитано, например, что при решении задачи распределения 20 средств по 10 объектам число возможных вариантов составит 108. Даже если расчет каждого варианта потребует всего 10 арифметических операций, то и тогда общее число расчетных операций достигнет миллиарда, что не может быть выполнено ЭВМ в приемлемые сроки. Поэтому для решения подобных задач исследование операции применяет вместо «слепого» перебора специальные методы так называемого направленного перебора. Эти методы составляют, например, содержание линейного и нелинейного программирования.
Зачастую искомое решение задачи должно не только обеспечить максимум избранного показателя успешности, но и удовлетворять ряду дополнительных требований, например ограничениям по материальным средствам, времени решения задачи и т. п. Исследование операций располагает специальными методами, позволяющими учесть эти ограничения и выбрать из множества возможных решений именно то (или те), которое им полностью удовлетворяет.
Для ряда производственных задач характерно отсутствие или неполнота информации. В этих случаях приходится принимать решения в условиях неопределенности. Для выработки наилучших решений в условиях неопределенности создан специальный математический аппарат (например, методы теории игр и статистических решений), который широко применяется в исследовании операций.
Выбор оптимального способа ведения действий на научной основе и с использованием вычислительной техники порой приводит к результатам, значительно отличающимся от тех, которые могут быть получены на основе так называемого здравого смысла с помощью современных научных методов.
Следует отметить, что анализ проблемной ситуации продолжается на протяжении всего процесса принятия решения. После этого проблемная ситуация переходит в ситуацию принятия решения, в основе которой лежит проблемная ситуация, подлежащая всестороннему исследованию и анализу, так как только на этой основе и возможно принятие наиболее целесообразного решения.
Вообще изучение любой деятельности можно проводить как изучение ситуаций, в которых приходится принимать решения, т. е. таких ситуаций, когда человек сталкивается с необходимостью выбора какого-нибудь одного действия из нескольких. Решение может состоять из числа или из сложного множества правил, которым нужно следовать в течение длительного промежутка времени.
Элементами ситуации принятия решения являются:
– множество мотивирующих целей; _
– множество допустимых стратегий (Ui);
– множество состояний обстановки, среды (Zj) – параметры состояний;
– множество следствий (исходов).
Рассмотрим более подробно каждый из названных элементов. Множество мотивирующих целей представляет собой систему подцелей, возникшую в результате уяснения и разработки основной (главной) цели.
Допустим, что цели лица, принимающего решение (ЛПР), выявлены и имеют достаточную ясность. Возможные способы достижения этих целей принято называть стратегиями. Стратегия – это план или программа действий, которая может быть выбрана ЛПР и осуществлена им или другими лицами, ответственными перед ним.
Все стратегии, которые могут быть полностью осуществлены, по мнению ЛПР, который вырабатывает свое суждение на основании опыта и имеющейся информации, составляют в совокупности множество возможных стратегий.
Возможные стратегии могут быть двух разновидностей: множество допустимых стратегий и множество недопустимых стратегий. Возможная стратегия допустима тогда и только тогда, когда ЛПР считает ее достойной рассмотрения и дальнейшей оценки, когда он чувствует, что есть вероятность того, что он осуществит ее. В противном случае стратегия считается недопустимой.
В различных ситуациях процесс выявления допустимых стратегий может потребовать не только таланта, присущего ЛПР, но также и использования специалистов различных профессий. Обычно этот процесс сопровождается большой исследовательской работой. Усилия, затраченные на поиски допустимых стратегий, зависят в том числе и от изобретательности ЛПР, ответственности, которую он несет, а также и от значения, которое придается рассматриваемой ситуации принятия решения.
Некоторые возможные стратегии могут оцениваться как недопустимые на основании различных доводов – правовых, социальных, моральных, материальных, отдельно или в любой их совокупности. Не исключена вероятность, что некоторые из возможных стратегий, первоначально оцененные как допустимые, могут быть с течением времени отнесены к недопустимым на основании дополнительной информации, полученной в процессе принятия решения.
Множество допустимых стратегий ограничивается и такими условиями, как состояние техники и знание исследуемой области. Существенное влияние на выявление номинального множества допустимых стратегий оказывает также выбор правильного направление оценки эффективности функционирования системы.
Состояния обстановки реализации решений представляют собой обстоятельства, которых могут произойти и которые не поддаются полному контролю со стороны ЛПР. Указанные состояния существенным образом связаны с состоянием среды исследуемой системы (явления): они могут повлиять на ход принятия решения, а также на конечный результат, т. е. выбор соответствующей стратегии.
В большинстве ситуаций принятия решений приходится сталкиваться с неопределенностью, особенно в сложных условиях. Ошибки в выработке решений часто заключаются в том, что недостаточно учитываются факторы, не зависящие непосредственно от ЛПР.
Анализ проблемной ситуации является сложным процессом, основанным на четком уяснении поставленной задачи, личном знании обстановки, правильной оценке состояния возможностей системы, а также на всестороннем изучении условий, в которых будет выполняться задача. Важным моментом здесь является определение возможности формализации всей задачи или части ее, выделение той части задачи, которая поддается формализации, и выбор показателя эффективности.
Построение описательной (концептуальной) модели выбора решения. Эта модель строится на основе определения ситуации принятия решения.
После определения показателя эффективности устанавливается возможность формализованного представления данной ситуации и степень влияния формализованного представления на решение задачи. При этом нужно установить, что в данной ситуации не поддается формализации и должно быть решено в процессе творческой деятельности человека, в том числе с помощью игровых моделей, описанных выше.
При оценке возможности формализации ситуации следует обязательно учесть время, которым располагает орган управления, и наличие тех или иных математических моделей, имеющихся в его распоряжении.
Построение математической модели функционирования системы. Этап формализации задачи в принципе может иметь два крайних случая. В первом случае в распоряжении органа управления к моменту получения задачи имеется формальная модель, подходящая для описания возникшей ситуации; во втором случае такой готовой модели нет, но время позволяет ее составить. На практике же, как правило, возникают случаи, когда есть модели, частично пригодные для формализации возникшей ситуации. Но, сузив или расширив область решения, описываемого математической моделью, их всегда важно отнести к одному из крайних случаев.
Если допустить, что в органе управления имеются достаточно квалифицированные специалисты, то решающим фактором для оценки возможности формализовать ситуацию при отсутствии готовой модели является наличие времени, имеющегося в распоряжении органа управления. Однако при составлении новой модели, а также при анализе моделей, имеющихся в наличии, органу управления необходимо обратить внимание на:
– уяснение характера и внутренней структуры исследуемого явления;
– выбор математического аппарата для формализации;
– установление ограничении и допущений, принятых при составлении формальной модели, и сравнение модели с реальной ситуацией.
Последний момент весьма важен, поскольку позволяет получить обоснованное суждение о ценности формализованной модели и уточнить формальную и творческую составляющие решения.
Группа параметров, обозначенная символами U = U1, U2,..., U, представляет собой те параметры, изменение которых находится во власти органа управления. К числу параметров решения относятся также и параметры системы управления. Изменение значений каждого из параметров этой группы влечет за собой изменение достигнутого значения избранного показателя эффективности, т. е. влияет на степень решения поставленной задачи. Выбор совокупности параметров вида U = U1, U2,..., U*, и представляет собой с формализованной точки зрения выбор решения. Поэтому эта группа параметров, выбор значений которых находится во власти органа управления, как сказано выше, получила название параметров решения.
Однако на результат действий оказывают влияние не только те факторы, изменение которых находится во власти органа управления, но и такие факторы, изменить которые он не может, – состояние среды, взаимозависимость предприятий и т. д. (Эту группу факторов или параметров будем называть параметрами среды.)
После того как формальная модель, описывающая данную ситуацию составлена, нужно найти такое сочетание параметров решения, которое приводило бы к экстремальному значению показателя эффективности.
Поскольку, однако, экстремальное значение показателя эффективности связано не только со значениями параметров решения, но и со значениями параметров среды, задача принятия решения осложняется необходимостью учета факторов, не зависящих от органа управления и часто даже ему неизвестных или известных плохо.
Для решения этой задачи с учетом параметров среды составляется матрица решений. Приведем в качестве примера матрицу (см. табл. 1).
Таблица 1
Матрица решений I

Здесь U носит условное наименование параметра решения, a Z – параметра среды.
При этом считаем, что параметры среды есть сочетание определенных значений всех параметров обстановки, дающих определенный столбец матрицы, а параметр решения – сочетание соответствующих значений всех параметров решения, дающих в совокупности определенную строку матрицы. Строки матрицы соответствуют определенному сочетанию параметров решения, т. е. определенному варианту решения органа управления, а столбцы – определенному сочетанию параметров среды.
Элементами матрицы являются значения показателя эффективности, рассчитанные для сочетания параметра решения и параметра среды соответственно данной клетке матрицы. Так, элемент, записанный на пересечении j-го столбца и i-й строки матрицы, соответствует значению показателя эффективности, рассчитанному для значений параметров Ui и Zj.
При составлении матрицы следует стремиться к ее сжатию, для чего нужно выбирать такие шаги значений параметра решения и параметра среды, которые давали бы достаточно существенные изменения значения показателя эффективности.
Если бы органу управления удалось точно установить значение параметра среды Z** = Zj , то матрица решений сузилась бы до одного столбца, и задача оптимизации решения заключала в выборе из элементов этого столбца такой клетки, в которой значение показателя Wij** экстремальное. Этим было бы выбрано значение i = i**, т. е. предложена наивыгоднейшая комбинация параметров решения или, что то же самое, предложено лучшее решение данной математической задачи. Однако мы не всегда можно знать точно значение параметра среды. В связи с этим следует проводить оптимизацию не только по параметру решения, но и по параметру среды.
Формальная оптимизация заканчивается выработкой количественных оснований для принятия решений по результатам анализа конкретной математической модели.
Формирование решения. На последнем этапе процесса принятия решения – этапе формирования решения – производится сопоставление значения эффективности оптимальной стратегии с требующимся уровнем эффективности. Если результаты сопоставления окажутся удовлетворительными, то тогда эта стратегия подвергается соответствующим модификациям с целью учета неподдающихся формализации факторов (психологических, моральных, экономических т. п.), а также допущенных при формализации ограничений. Такая модифицированная формализованная стратегия и будет решением.
Если же результаты сопоставления окажутся неудовлетворительными, то производится так называемая внутренняя корректировка решения, т. е. возвращение к одному из описанных выше этапов с целью выявления возможности доопределения решения.
Поскольку любая формальная модель не учитывает ряда факторов в силу абстракций и допущений, а также вследствие неумения (а иногда и отсутствия целесообразности) формализовать ряд вопросов, связанных с психологическими, правовыми и другими моментами, окончательное решение – выработку командной информации в процессе управления – производит человек. При этом он, учитывая результат формальной оптимизации, стремится учесть и ряд других факторов.
Поскольку объектом управления является коллектив людей, деятельность их совершается в большой степени по законам психологии. Целевая функция социально-психологических методов состоит в том, чтобы, воздействуя определенным образом на работника, создать ситуацию, ориентирующую его на максимальную реализацию своих потенциальных способностей при выполнении поставленных задач.
Поэтому, принимая решение, следует учитывать следующие моменты психологического характера:
– социально-психологический уровень развития коллектива;
– способность коллектива к восприятию предстоящих целей и задач;
– индивидуальные качества исполнителей;
– желание людей выполнять задачи;
– степень самоорганизации коллектива;
– административно-правовое положение руководителя;
– личные качества работника, принимающего решения.
В силу творческого субъективного характера акта принятия решения невозможно установить какие-нибудь строгие единые правила. Основную роль здесь играет практический опыт, способность к предвидению хода событий. Вместе с тем следует учитывать возможность использования дополнительных (по сравнению с принятыми в формальной модели) показателей эффективности, а также дополнительную оценку качества информации состояния и всех допущений, принятых в формальной модели.
Процесс принятия решения завершается реализацией решения, анализом полученных результатов и корректировкой решения.
4. Примеры применения количественных методов выработки решений
Станковая задача
Современные методы управления тесно связаны с количественными обоснованиями принимаемых решений, с широким использованием экономико-математических методов и моделей управления производством.
Представим себе, например, группу из трех станков, каждый из которых может производить два типа деталей, назовем их условно деталями А и Б. Производительность каждого из станков по разным типам деталей, как правило, различна:
станок № 1 производит в одну минуту 5 деталей А или 5 деталей Б,
станок № 2 производит в одну минуту 6 деталей А или 2 детали Б,
станок № 3 производит в одну минуту 5 деталей А или 3 детали Б.
Задача осложняется тем, что требуется выполнить два важных условия или, как говорят в математике, учесть два ограничения:
– ни один из станков не должен простаивать;
– продукция должна быть комплектна, т. е. количество произведенных деталей А должно равняться количеству деталей Б (это, например, могут быть гайки и болты).
Несмотря на кажущуюся простоту задачи, ни одним из существовавших ранее методов она не решалась. Попробуем и мы, опуская некоторые несущественные подробности, решить столь поучительную задачу. Прежде всего, попытаемся, как, наверное, сделали и те, кто впервые столкнулся с этой задачей, получить ее глазомерное решение.
Все расчеты будем производить исходя из общей продолжительности времени работы в 6 часов = 360 минут (одна смена). Попробуем на все это время загрузить станок № 1 деталями А. Станки № 2 и № 3 также загрузим на все время работы, но деталями Б. Результат такого глазомерного решения изобразим следующим образом: слева от вертикальной черты покажем время загрузки станков по различным деталям, а справа – соответствующее количество произведенной продукции (произведение времени работы на минутную производительность).
Итак, глазомерное решение см. в табл. 2.
Таблица 2
| Станок | Продолжительность работы станка, мин | Производительность станка (количество деталей за время работы) | ||||||||
|
А | Б | А | Б |
|
|||||
| №1 | 360 | 0 | 1800 | 0 | ||||||
| №2 | 0 | 360 | 0 | 720 | ||||||
| №3 | 0 | 360 | 0 | 1080 | ||||||
|
Общее количество 1800 + 1800 = выпущенной продукции = 3600 деталей |
||||||||||
Глазомерное решение полностью отвечает поставленным условиям: во-первых, все станки полностью загружены в течение рабочего времени; во-вторых, количество произведенных деталей А равно количеству деталей Б. Остается, однако, открытым главный вопрос планирования: является ли наше глазомерное решение наилучшим в данных условиях? Нельзя ли составить другой план распределения станков, который отличался бы от глазомерного наибольшей производительностью?
Обоснованием такого оптимального решения занимается математическое программирование. Суть метода удобнее всего выразить с помощью наглядного геометрического представления, графика (рис. 3). Здесь показан построенный по правилам математического программирования многоугольник OABCD (он заштрихован). Многоугольник соответствует условиям нашей задачи и представляет собой область допустимых планов распределения времени работы станков № 2 и № 3 над деталью А. По соответствующим осям графика отмечена продолжительность работы этих станков. (В своих расчетах мы вполне можем обойтись двумя станками и одной деталью, так как по этим данным нетрудно рассчитать и все остальные.)
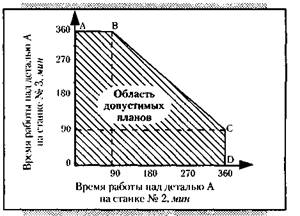
Рис. 3. График решения станковой задачи
Любая точка заштрихованной области допустимых планов, как видно из ее названия, даст нам какой-либо один возможный план, отвечающий обоим принятым условиям – ограничениям. Так, например, точка О соответствует нашему глазомерному плану: время работы над деталью А на станках № 2 и № 3 равно нулю.
В поисках наилучшего плана посмотрим, какой план распределения станков дает другие точки области. Вот, скажем, точка В. Как видно из графика, этой точке соответствует время работы над деталью А станка № 2, равное 90 минутам, станка № 3 – 360 минутам. По этим данным нетрудно составить второй план распределения станков, причем время, отводимое на производство детали Б станками № 2 и № 3, получится как дополнение до 360 минут времени, снятого с графика,– станки не должны простаивать. Что касается станка № 1, то его время работы подбирается таким, чтобы общее количество деталей А и Б совпадало.
Второе решение, следовательно, будет выглядеть так (табл. 3).
Таблица 3
| Станок | Продолжительность работы станка, мин | Производительность станка (количество деталей за время работы) |
|
||||||
|
А | Б | А | Б | |||||
| №1 | 0 | 360 | 0 | 1800 |
|
||||
| №2 | 90 | 270 | 540 | 540 |
|
||||
| №3 | 360 | 0 | 1800 | 0 |
|
||||
|
Общее количество 2340 + 2340 = выпущенной продукции = 4680 деталей |
|
||||||||
Вот так результат! Мы сразу же, можно сказать бесплатно, на том же оборудовании увеличили производительность на 1080 деталей, т. е. на целых 30 %.
Нас, однако, продолжает мучить законный вопрос – добились ли мы уже самого лучшего, оптимального решения, или нет? Стоит ли дальше пытаться улучшить план?
В теории математического программирования убедительно показывается, что оптимальному решению соответствует одна из вершин многоугольника допустимых планов, а именно та, для которой общая производительность окажется максимальной. В нашем случае это вершина С.
Действительно, рассчитывая известным уже нам путем план распределения станков для этой точки, получим следующее решение (табл. 4).
Таблица 4
| Станок | Продолжительность работы станка, мин | Производительность станка (количество деталей за время работы) |
|
|||||||
|
А | Б | А | Б | ||||||
| №1 | 0 | 360 | 0 | 1800 |
|
|||||
| №2 | 360 | 0 | 2160 | 0 |
|
|||||
| №3 | 90 | 270 | 450 | 810 |
|
|||||
|
Общее количество 2610 + 2610 = выпущенной = 5220 деталей продукции |
|
|||||||||
Мы получили план почти наполовину (на 45 %) лучше, чем глазомерный. И этот существенный прирост, подобно и предыдущему улучшению, ничего (если не считать умственных усилий на планирование) не стоит. Никакого дополнительного расхода каких-либо ресурсов не потребовалось. Те же станки, те же детали, те же станочники работают то же время. Не меняются и производительности станков. Эффект здесь чисто интеллектуальный, «умственный», – за счет рационального распределения ресурсов оборудования (кстати, латинское слово «рационалист» означает «разумный»). Умное, обоснованное решение сделало чудо, в которое даже трудно поверить. Подобный «чудесный» результат, как мы уже понимаем, характерен для всех решений, принимаемых с помощью научных методов.
Может возникнуть, правда, вопрос: а нельзя ли обойтись в подобных задачах без какого-либо специального математического аппарата, идя путем простого перебора всех возможных вариантов решения? Этот соблазн следует тут же отмести. Расчет показывает, что перебор всех возможных вариантов решений подобных задач не под силу даже самому большому коллективу вычислителей.
Уместно отметить еще несколько интересных моментов, связанных с решением данной задачи. Полученный нами оптимальный план – это не просто правильный, допустимый план распределения оборудования, по которому можно работать, – такими были и оба предыдущих. Они обеспечивали как беспростойность оборудования, так и комплектность продукции. Оптимальный план помимо того, что он должен отвечать этим требованиям, должен быть еще обязательно самым эффективным. В данном случае это означает требование максимума деталей. Действительно, как уже отмечалось, оптимизация обязательно должна предусматривать обращение одного из показателей в максимум (или минимум). Но только одного показателя. Нельзя вести оптимизацию по нескольким показателям одновременно. Между тем мы часто слышим: «максимум продукции при минимуме издержек». А правильно будет: «максимум продукции при данном уровне издержек» или «минимум издержек при данном уровне продукции».
И еще один важный вывод, к которому подводит станковая задача: оптимизация возможна лишь по верхнему уровню управления, для всей производственной системы в целом. В данном случае это означает, что мы получили оптимальный план лишь для всех трех станков вместе. А для каждого в отдельности? Тут оптимальности может и не быть. В нашей задаче оптимальный план явно не понравится станочнику, работающему на станке № 3: при большей производительности – 5 деталей в минуту – план предлагает ему работать всего 90 минут, а при меньшей – 3 детали в минуту – целых 270 минут. Но тут уже ничего не поделаешь: чтобы получить оптимальный, сбалансированный план предприятия, кому-то на нижнем уровне приходится работать в неоптимальном режиме. И значительно дешевле компенсировать издержки «внизу», чем лишиться огромного эффекта оптимизации работы целого предприятия.
Несколько слов о существе решения станковой задачи. Идея математического программирования заключается в том, чтобы вместо сплошного (иногда говорят – слепого или дурного) перебора всех возможных вариантов вести перебор выборочный, направленный на скорейшее последовательное улучшение результата. Поэтому в нашей задаче мы и рассматривали не все точки области допустимых планов (их бесчисленное множество), а только вершины многоугольника, одна из которых и дала нам наилучшее решение.
Методы математического программирования находят широкое применение для обоснования оптимальных решений в самых различных областях человеческой деятельности: при планировании перевозок и в торговле, для правильной организации труда, в управлении городским транспортом и строительством.
Рассмотрим, как вырабатываются правила решения еще одной важной производственной задачи.
Резервы раскроя
Изготовление многих видов современной промышленной продукции начинается с раскроя материала. Выкраивают не только одежду и обувь, но и детали корпуса корабля, кузова автомобиля, фюзеляжа самолета. Раскраивают ткани и кожу, бумагу и стекло, металл и пластмассу. Кроить можно по-разному...
Перед нами листы дефицитного материала размером 6 х 13 метров (рис. 4). Из каждого такого листа необходимо выкроить по несколько заготовок двух видов: заготовки А – размером 5x4 метра и заготовки Б – размером 2x3 метра. Задача заключается в том, чтобы получить как можно больше заготовок обоих видов с наименьшим количеством отходов. Кроме того, как и в задаче со станками, необходимо обеспечить комплектность заготовок: на 1 заготовку А должно приходиться 5 заготовок Б.
Как вести раскрой? Какое решение принять?
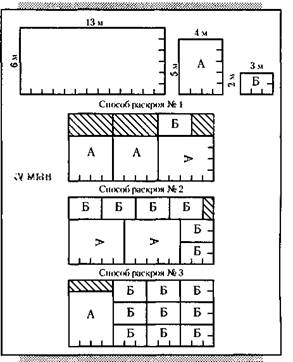
Рис. 4. Способы раскроя материала
Прежде всего, нужно установить все возможные способы раскроя наших листов по требуемым заготовкам. Начнем с того, что постараемся получить с одного листа как можно больше заготовок А – они крупнее, чем Б, и для них труднее подыскать место на листе. Оказывается, однако, что более трех заготовок А с листа выкроить невозможно. Исходя из этого предусмотрим способы раскроя для получения трех, двух и одной заготовки А и наибольшего возможного количества заготовок Б с листа. Каждому способу дадим номер:
способ № 1:3 заготовки А и 1 заготовка Б;
способ № 2: 2 заготовки А и 6 заготовок Б;
способ № 3: 1 заготовка А и 9 заготовок Б.
Заметим, что при всех способах раскроя часть площади листа остается неиспользованной и идет в отходы. На рис. 4 эта площадь заштрихована.
Для составления оптимального плана раскроя материала построим график, подобный тому, который мы рисовали в задаче со станками. На рис. 5 по оси X отложено количество заготовок А, а по оси Y – число заготовок Б. При этом каждому способу раскроя соответствует своя точка на графике. Так, точка «способ № 2» стоит на пересечении двух заготовок А и шести заготовок Б. Точки – способы раскроя – указывают границы области допустимых планов.
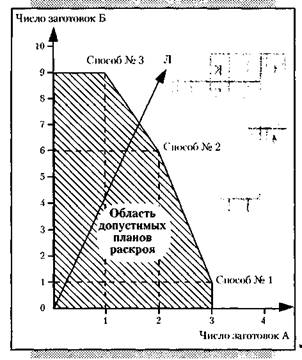
Рис. 5. График раскроя материала
Для того чтобы обеспечить комплектность заготовок, необходимо ограничиваться лишь теми точками области допустимых планов, которые лежат на луче ОЛ. Он построен таким образом, что все его точки соответствуют требуемому отношению заготовок А и Б:
![]()
Какой же план раскроя наиболее рационален?
Очевидно, тот, которому соответствует точка, наиболее отдаленная от начала координат, – ведь при этом число заготовок будет наибольшим. Этот план дает точка, лежащая на пересечении луча ОЛ с границей области допустимых планов – линией, соединяющей способы № 2 и № 3. Она находится как раз посередине между упомянутыми способами. Итак, оптимальный план раскроя заключается в том, что половина листов кроится способом № 2, а половина – способом № 3.
Проверим теперь наш оптимальный план на партии в 200 листов. Половину – 100 листов раскроим по способу № 2 и получим 100 х 2 = 200 заготовок Б. Всего же получилось 300 заготовок А и 1500 заготовок Б – комплектность 1 к 5 соблюдена. А чем этот план лучше других? На этот вопрос ответят следующие любопытные цифры.
Предположим, что тот, кто ведет раскрой, не знает современных методов обоснования решений и действует без расчета, «на глазок». Не исключено, что он станет раскраивать наши 200 листов способами № 1 и № 3. Для того чтобы иметь возможность сравнивать глазомерный план с оптимальным, примем, что способом № 1 раскраивалось 50, а способом № 3–15 листов. Вот что при этом получается.
50 листов, раскроенные по способу № 1, дают:
50 х 3 = 150 заготовок А и 50 х 1 = 50 заготовок Б;
150 листов, раскроенных по способу № 3, дают:
150 х 1 = 150 заготовок А и 150 х 9 = 1350 заготовок Б.
Всего получается 300 заготовок А и 1400 заготовок Б.
А куда же исчезло 100 заготовок Б? Ведь при оптимальном раскрое их было 1500. Их «съел» плохой план. Все они ушли в отходы. Дефицитный материал остался неиспользованным.
Таким образом, рациональный раскрой даже в такой скромной задаче, как наша,– разрезается всего 200 листов – экономит 600 квадратных метров дефицитного материала: 100 заготовок Б х 2 метра х 3 метра = 600 квадратных метров.
Еще одной важной областью выработки решений производственных задач является составление всевозможных расписаний. С помощью расписаний определяется порядок действий персонала предприятий, устанавливается последовательность выполнения операций обработки материалов и сборки сложных изделий, назначается очередность при распределении различных материальных благ и т. д. Как же строятся наилучшие расписания?
Управление очередями
Простейшее решение по составлению расписаний имеет так называемая задача директора. Сущность этой задачи заключается в следующем.
На прием к директору записалось несколько посетителей. Секретарь директора составил список в алфавитном порядке, указав для каждого требующуюся ему ориентировочную продолжительность приема. Фамилии записавшихся обозначены в списке их заглавными буквами (табл. 5).
На весь прием директор, как видно из таблицы, отвел 2 часа =120 минут, поэтому пришлось ограничиваться всего шестью посетителями. Является ли составленное расписание наилучшим?
Таблица 5
| № п/п | Фамилия (начальная буква) | Продолжительность приема, мин | Время ожидания, мин |
| 1 | Б | 25 | 0 |
| 2 | Д | 15 | 25 |
| 3 | Е | 10 | 40 |
| 4 | К | 5 | 50 |
| 5 | С | 35 | 55 |
| 6 | Т | 30 | 90 |
|
Суммарное время 120 мин = 260 мин = = 2 часа = 4 часа 20 мин |
С точки зрения общей продолжительности приема любая очередность посетителей равнозначна: суммарное время приема не меняется при любой его последовательности. А с точки зрения ожидания в очереди? Подсчитаем общее время ожидания как сумму времени ожидания всех посетителей. В нашем алфавитном списке оно составляет 260 минут = 4 часа 20 минут. Понятно, что это время желательно было бы уменьшить: ведь время ожидания – зря потраченное время. Но вот можно ли это сделать? Приведет ли расписание с другой последовательностью приема к экономии общего времени ожидания при сохранении намеченного суммарного времени приема?
Оказывается, получение такого расписания возможно. В одном из методов исследования операций – так называемой теории расписаний – доказывается, что наименьшее суммарное время ожидания получается при составлении расписания в порядке нарастания продолжительности приема. Составим такое расписание (табл. 6).
|
№ п/п | Фамилия (начальная буква) | Продолжительность приема, мин | Время ожидания, мин |
|
||
| 1 | К | 5 | 0 | ||||
| 2 | Е | 10 | 5 | ||||
| 3 | Д | 15 | 15 | ||||
| 4 | Б | 25 | 30 | ||||
| 5 | Т | 30 | 55 | ||||
| 6 | С | 35 | 85 | ||||
|
Суммарное время 120 мин = 190 мин = = 2 часа = 3 часа 10 мин |
|||||||
Таблица 6
Полученное оптимальное расписание позволяет уменьшить суммарное время ожидания на 1 час 10 минут. Это значительное сэкономленное время можно использовать на полезные дела.
Задача директора находит применение не только в приемной руководителя. Ведь таким же образом можно составить и расписание очередности работы станка или другого оборудования над различными деталями. Продолжительность обработки при этом бывает различной, и нужно составить расписание таким образом, чтобы суммарное время обработки оказалось наименьшим. Это, как мы видели, дает существенный временной, а значит, и экономический эффект.
Задачу директора иногда называют задачей одного станка. Ее дальнейшим развитием является задача двух станков. В чем ее суть?
Детали обрабатываются последовательно на двух станках. В табл. 7 показана продолжительность этой обработки для каждой из 10 деталей на двух станках. Нумерация деталей и последовательность их обработки взяты при этом произвольно.
Таблица 7
| Номера деталей и последовательность их обработки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Продолжительность обработки на станке № 1 , мин | 7 | 3 | 12 | 14 | 20 | 4 | 2 | 9 | 19 | 6 |
| Продолжительность обработки на станке № 2, мин | 18 | 13 | 9 | 5 | 8 | 16 | 20 | 15 | 1 | 13 |
Расчет показывает, что суммарное время обработки всех деталей составляет 118 минут. Кроме того, существует время ожидания обработки первой поданной детали на станке № 2, равное 7 минутам, и время ожидания, пока освободится станок № 2 для обработки детали № 5, равное 11 минутам. Итого – обработка всех деталей на двух станках с учетом времени ожидания продолжается 136 минут.
В теории расписаний доказывается, что в задаче двух станков для обеспечения оптимальной последовательности обработки с наименьшим временем ожидания необходимо составлять расписание, руководствуясь следующими правилами:
1) выбирается деталь с наименьшей продолжительностью обработки на одном из станков; в нашем примере это № 9;
2) выбранная деталь помещается в начало очереди, если наименьшая продолжительность обработки соответствует станку № 1, или в конец очереди, если – станку № 2; в нашем примере деталь № 9 помещается в конец очереди;
3) столбец таблицы 7.7, ранее занятый выбранной деталью, вычеркивается;
4) выбирается деталь среди оставшихся со следующей наименьшей продолжительностью обработки на одном из станков; в нашем примере – деталь № 7;
5) выбранная деталь помещается в начало или конец очереди по указанному в пункте 2 правилу; в нашем примере деталь № 7 помещается в начало очереди;
6) вычеркивается соответствующий столбец таблицы.
И так далее.
В итоге можно получить оптимальное расписание работы двух станков (табл. 8).
Таблица 8
| Последовательность обработки (порядковый номер очереди) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Номер детали | 7 | 2 | 6 | 10 | 1 | 8 | 3 | 5 | 4 | 9 |
| Продолжительность обработки на станке № 1 , мин | 2 | 3 | 4 | 6 | 7 | 9 | 12 | 20 | 14 | 19 |
| Продолжительность обработки на станке № 2, мин | 20 | 13 | 16 | 13 | 18 | 15 | 9 | 8 | 5 | 1 |
Полученное оптимальное расписание уменьшает время ожидания обработки до 2 минут (станок № 2 ждет в самом начале, пока станок № 1 обработает деталь № 7). Общее время обработки с учетом времени ожидания тем самым сокращается до 120 минут- на 12 %.
Заметим, что, не зная описанного простого правила, эту задачу не решить и опытному специалисту. Ведь чтобы выйти на оптимальное расписание, необходимо перебрать несколько миллионов вариантов очередности.
Данное решение, так же как и предыдущее, применяется не только для станков. Оно может быть использовано для составления расписаний очередности любых работ, последовательности процедуры применения, функционирования различных технических или организационных производственных систем.
Говоря о составлении наилучших расписаний, нельзя обойти еще один важный для практики тип задач. Речь пойдет о так называемой задаче о назначениях.
Задача о назначениях
На предприятии подготовлен резерв для замещения однородных должностей начальников производства (скажем, начальников производственных участков). Руководители предприятия, кадровая служба составили список резерва (в алфавитном порядке) и путем экспертного опроса установили, приблизительно конечно, степень соответствия каждого кандидата каждой из возможных вакансий. Например, установлено, что кандидат А для замещения должности IV подходит примерно в два раза лучше, чем для должности II, для замещения должности I кандидат Б в два раза хуже, чем В, и т. д. Придавая таким характеристикам численную форму, можно составить таблицу соответствия кандидатов различным должностям (табл. 9).
Таблица 9
|
Кандидат | Должность | |||||||||
| I | II | III | IV | V |
|
||||||
|
А | 10 | 20 | 50 | 40 | 60* | |||||
|
Б | 40* | 20 | 30 | 10 | 80 | |||||
|
В | 80 | 50* | 30 | 30 | 70 | |||||
|
Г | 60 | 70 | 20* | 10 | 40 | |||||
|
Д | 50 | 70 | 60 | 10* | 40 | |||||
Как будет проходить подбор кандидатов на должность? Решим эту задачу сначала глазомерно.
Первый по алфавиту кандидат А лучше всего отвечает должности V. Закрепим за ним эту должность, поставив в правом верхнем углу соответствующей клетки звездочку.
Следующего кандидата – Б лучше всего было бы назначить на должность V, но она уже занята. Поэтому направим его на наиболее подходящую из оставшихся – должность I. И так далее.
Оценку полученного штатного расписания произведем так, как мы это делали в задачах математического программирования – суммируя оценки соответствующих назначений:
60 + 40 + 50 + 20 + 10 = 180.
Хорошее ли это расписание? Ответить на такой вопрос можно, лишь зная оптимальный вариант. Получить его путем сплошного перебора всех возможных расписаний, как мы уже знаем, практически нельзя: при распределении всего 10 кандидатов по 10 должностям число возможных вариантов измеряется миллионами.
Существуют, к счастью, приемы направленного перебора вариантов, построенные на основе методов исследования операций. Применение этих приемов выводит на следующее оптимальное штатное расписание (табл. 10).
Таблица 10
|
Кандидат | Должность | |||||||||
| I | II | III | IV | V | |||||||
|
А | * | |||||||||
|
Б | * | |||||||||
|
В | * | |||||||||
|
Г | * | |||||||||
|
Д | * | |||||||||
Оценка качества данного расписания:
40 + 80 + 80 + 70 + 60 = 330.
Оценка показывает, что оптимальное расписание почти в два раза лучше, чем глазомерное.
Еще один полезный метод выработки управленческих решений – сетевое планирование.
Управление временем
Сетевое планирование служит для составления рационального плана решения производственной задачи, предусматривающего осуществление его в кратчайший срок и с минимальными затратами.
Методы сетевого планирования дают возможность оценивать «узкие» места выполняемой задачи и вносить необходимые коррективы в организацию решения.
Сетевое планирование рассмотрим на следующем примере. Производственная задача решается в три этапа (I, II и III). Исходным моментом является получение директором предприятия задания (заказа). Далее на основании этого задания под руководством заместителя директора по производству разрабатываются задания подразделениям № 1 и № 2. После этого подразделения одновременно приступают к I этапу работы. Для того чтобы начать II этап работы, подразделение № 2 должно получить комплект изделий, изготовленных подразделением № 1 в ходе I этапа. Поэтому подразделение № 1 начинает II этап работы сразу же после окончания I этапа, а подразделение № 2– лишь после получения комплектующих из подразделения № 1. Далее роли подразделений меняются: для того чтобы начать III этап, теперь уже подразделение № 1 должно ожидать комплектующих от подразделения № 2. С окончанием III этапа работы обоими подразделениями изделие считается готовым. Транспортная служба доставляет его потребителю.
Все мероприятия решаемой задачи в их взаимосвязи представляются в виде наглядной схемы – сетевого графика (рис. 6), состоящего из двух типов элементов – работ и событий.
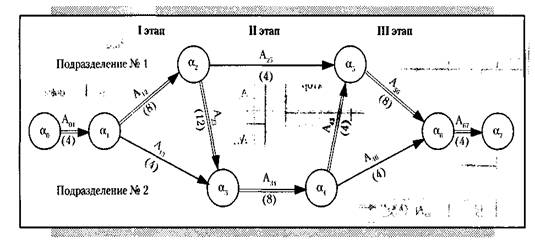
Рис. 6. Схема сетевого графика
Работа представляет собой выполнение некоторого мероприятия, например выполнение определенной технологической, транспортной или складской операции. Работа связана с затратой времени и расходом ресурсов, она должна иметь начало и конец. Работа обозначается на графике стрелкой, над которой проставлен номер работы (большая буква с индексом), а под ней – продолжительность работы (в скобках).
Событиями называются начальные и конечные точки работы, например начало или окончание производственной операции. Событие не является процессом и поэтому не сопровождается затратами времени или ресурсов. Событие обозначается кружком с буквенным обозначением внутри (маленькая буква с индексом).
Относительно данной работы события могут быть предшествующими (непосредственно перед ней) и последующими (непосредственно за ней). Относительно данной работы другие работы могут быть предшествующими и последующими. Каждая входящая в данное событие работа является предшествующей каждой выходящей работе; каждая выходящая работа является последующей для каждой входящей.
Основные свойства сетевого графика:
ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы;
ни одна работа, выходящая из данного события, не может начаться до тех пор, пока не произойдет данное событие;
ни одна последующая работа не может начаться раньше, чем будут закончены все предшествующие ей работы.
Приступая к построению сетевого графика, разрабатывают перечень событий, определяющих планируемый процесс – производственную задачу, без которых она не может состояться (табл. 11). Затем предусматриваются работы, в результате которых все необходимые события должны произойти (табл. 12).
Таблица 11
| Обозначение события | Наименование события | Ответственное лицо |
| a0 | Получено задание предприятием | Директор |
| a1 | Разработаны задания подразделениям № 1 и № 2 | Заместитель директора по производству |
| a2 | Выполнена работа I этапа в подразделении № 1 | Начальник подразделения № 1 |
| a3 | Выполнена работа I этапа в подразделении № 2. Подразделением № 2 получены комплектующие из подразделения № 1 | Начальник подразделения № 2 |
| a4 | Выполнена работа II этапа в подразделении № 2 | Начальник подразделения № 2 |
| a5 | Выполнена работа II этапа в подразделении № 1. Подразделением № 1 получены комплектующие из подразделения № 2 | Начальник подразделения № 1 |
| a6 | Выполнены работы III этапа в подразделениях № 1 и № 2. Заказ готов. | Начальники подразделений № 1и № 2 |
| a7 | Изделие доставлено потребителю | Начальник транспортной службы |
Таблица 12
| Обозначение работы | Наименование работы | Продолжительность выполнения работы, ч |
| А01 | Разработка заданий подразделениям № 1 и № 2 | 4 |
| А12 | Выполнение работ I этапа в подразделении № 1 | 8 |
| А13 | Выполнение работ I этапа в подразделении № 2 | 4 |
| А23 | Передача комплектующих из подразделения № 1 в подразделение № 2 | 12 |
| А25 | Выполнение работ II этапа в подразделении № 1 | 4 |
| А34 | Выполнение работ II этапа в подразделении № 2 | 8 |
| А45 | Передача комплектующих из подразделения № 2 в подразделение № 1 | 4 |
| А46 | Выполнение работ III этапа в подразделении № 1 | 4 |
| А56 | Выполнение работ III этана в подразделении № 2 | 8 |
| А67 | Доставка заказа потребителю | 4 |
Исходя из перечня событий и работ составляется сетевой график (см. рис. 6). Вначале это можно сделать схематично, без учета масштаба времени. Сетевой график строится от исходного события к завершающему, слева направо. Исходному событию присваивается нулевой номер, завершающему событию – последний номер. Остальные события нумеруются так, чтобы номер предыдущего события был меньше номера последующего события.
Работа кодируется индексом, содержащим номера событий, между которыми она заключена. Совершение события зависит от окончания самой длительной из всех входящих в него работ. Последовательные работы и события формируют пути (цепочки), которые ведут от исходного к завершающему событию.
Далее сетевой график строится в масштабе времени (рис. 7).
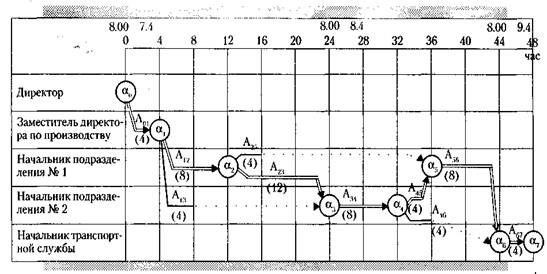
Рис. 7. Сетевой график в масштабе времени
Сетевой график дает возможность оценить количество и качество мероприятий планируемой производственной задачи. Он позволяет установить, от каких из них и в какой степени зависит достижение конечной цели действий. Так, ранг события показывает, какое количество работ необходимо выполнить, чтобы данное событие состоялось. Сетевой график также показывает, какое мероприятие следует выполнять в первую очередь, какие можно выполнять параллельно. Так, в нашем примере видно, что ни одна последующая работа не может выполняться раньше, чем закончатся все предшествующие. Видно также, что работы А25 и A23 могут выполняться параллельно.
После построения сетевого графика производится его анализ. Для этого строится так называемый критический путь. Это полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение задачи в целом, поэтому любая задержка на работах критического пути увеличивает время всего процесса. На рис. 6 и 7 критический путь обозначен двойной линией.
Сущность анализа сетевого графика заключается в том, что выявляются резервы времени работ, лежащих вне критического пути, и направляются на работы, лежащие на критическом пути, который лимитирует срок завершения работы в целом. В нашем примере продолжительность работ, лежащих на критическом пути, равна 4 + 8 + 12 + 8 + 4 + 8 + 4 = 48 часов.
Это и есть общее время решения всей производственной задачи.
На рис. 7 видно, что в подразделениях № 1 и № 2 появляются отрезки времени, на которых эти подразделения остаются без работы (волнистые линии). В этих случаях целесообразно снять отсюда часть трудовых и технических ресурсов и передать их тому подразделению, работа которого лежит в это время на критическом пути и лимитирует тем самым конечный результат. Так, например, после того как подразделение № 2 в момент, соответствующий 8-му часу работы, выполнит этап I, ему целесообразно передать часть своих ресурсов подразделению № 1 с расчетом, чтобы к событию a3 подразделения № 1 и № 2 подошли одновременно. Для этого нужно передать из подразделения № 2 в подразделение № 1 ровно столько ресурсов, чтобы сократить сумму работ А12 и А23, в подразделении № 1 на 8 часов, то есть до 12 часов. При этом подразделение № 2, лишенное части ресурсов, увеличит время своей работы на эти же 8 часов (работа А13, станет равна 12 часам) и критический путь между событиями a3 и a2 будет равен 12 часам. Это сокращение общего времени критического пути означает и сокращение на то же время – на 8 часов – продолжительности решения всей производственной задачи.
Библиографический список
1. Предприимчивость и риск. – СПб.: ИПК РП, 2008. - 64 с.
2. Задачник по экономике. – СПб.: Специальная литература, 2008. - 191 с.
3. Азбука менеджмента. - СПб.: Союз, 2009. - 269 с.
4. Курс предпринимательства. – М.: Альфа, 2007.- 543 с.
| Исследования в современном управлении | |
|
СОДЕРЖАНИЕ 1. ИССЛЕДОВАНИЯ В СОВРЕМЕННОМ УПРАВЛЕНИИ.. 5 1.1 Предпосылки исследования систем управления.. 5 1.2 Системный анализ как средство ... Поступление материалов или деталей на центральный склад и выдача их на участки являются случайными процессами по своей природе, но в то же время они полностью поддаются ... Мы вначале рассмотрим графическое представление в виде классических сетевых графиков (опираясь на упоминавшуюся выше теорию графов), а в конце главы продемонстрируем представление ... |
Раздел: Рефераты по менеджменту Тип: учебное пособие |
| Экзамен 3 курс | |
|
Билет 1. Роль управления в развитии экономики, предпринимательства и общества Управление (менеджмент) - процесс сочетания ресурсов для достижения ... ... системный подход к решению проблем, а также применение таких методов как моделирование, экспериментирование, экономико-математические и социологические измерения и др. ... и помогает расположенным на более низкой иерархической ступени подразделениям разрабатывать цели и стратегии, наилучшим образом согласующиеся с целью и стратегией организации. |
Раздел: Рефераты по менеджменту Тип: реферат |
| Автоматизация работы экономических служб на ОАО "ВСЗ" | |
|
Содержание ВВЕДЕНИЕ.. 6 1. ВОПРОСЫ НАУЧНО-ТЕХНИЧЕСКОГО ПРОГРЕССА В ЭКОНОМИЧЕСКОМ РАЗВИТИИ ПРЕДПРИЯТИЯ.. Под экономико-математическими методами принято понимать комплекс формализованных математических методов, позволяющих находить оптимальные или близкие к ним решения экономических ... В универсальных токарных и токарно-револьверных станках, предназначенных для обработки заготовок диаметром до 500 мм, время остановки шпинделя с патроном (без закрепленной ... |
Раздел: Рефераты по экономике Тип: дипломная работа |
| Организация, планирование и управление производственным предприятием | |
|
НОО ВПО НП "Тульский институт экономики и информатики" Кафедра "ЭКОНОМИКИ И МЕНЕДЖМЕНТА" КОНСПЕКТ ЛЕКЦИЙ по курсу "Организация, планирование и ... ... осуществляются разработка и оценка альтернативных решений и курсов действий, проводимых на основе многовариантны расчетов; отбор критериев выбора оптимального решения; выбор и ... События (1 - получено задание на планирование с финансированием; 2 - выполнен анализ методических документов по планированию, моделированию, оптимизации; 3 - уточнены нормативы ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Курс лекции по компьютерным сетям | |
|
Министерство транспорта России Дальневосточная государственная морская академия имени адмирала Г.И. Невельского Н. Н. Жеретинцева Курс лекции по ... Прокладка наилучшего пути для передачи данных называется маршрутизацией, и ее решение является главной задачей сетевого уровня. Различные типы сетевых адаптеров отличаются не только методами доступа к каналу связи и протоколами, но еще и следующими параметрами: |
Раздел: Рефераты по информатике, программированию Тип: реферат |