Лабораторная работа: Паралельні проекції
Лабораторна №3
Паралельні проекції
Метою разділу є ознайомлення з елементарним математичним апаратом плоских геометричних проекцій. Для простоти будемо вважати, що при центральному проектуванні картинна площина перпендикулярна осі z і збігається з площиною z = d, а при паралельному збігається з площиною z = 0. Проекції розглядаються в системі координат спостерігача, що є лівосторонньою. Система координат, в якій вісь х спрямована вправо, вісь у - вгору, а вісь z - усередину екрана, природньо погоджується з екраном дисплея.
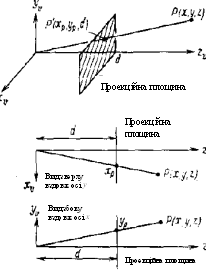
Рис.1 Центральна проекція
Кожну з проекцій можна описати матрицею розміром 4х4. Цей спосіб виявляється зручним, оскільки з'являється можливість об'єднати матрицю проектування з матрицею перетворення, представивши в результаті дві операції (перетворення і проектування) у виді однієї матриці. У цьому розділі ми одержимо матриці розміром 4х4 для декількох проекцій і насамперед для центральної. На рис.1 наведені три зображення лівосторонньої системи координат, у яких точка P проектується на проекційну площину, розташовану на відстані d від початку координат. Для обчислення координат Xр і Yp проекції точки (x, у, z) напишемо співвідношения, отримані з подібності трикутників (рис.1):
![]()
Перемножуючи обидві сторони кожного співвідношення на d, одержимо
![]()
Відстань d є в даному випадку масштабним множником, застосованим до координат Xp і Yp. Фактором, що приводить до того, що на центральній проекції більш віддалені об'єкти виглядають дрібніше, ніж ближчі, є ділення на z. Відзначимо, що допустимі всі значення z, крім z = 0. Точки можуть розташовуватися як за центром проекції на від’ємній частині осі z, так і між центром проекції і проекційною площиною.
Ці перетворення можна представити у вигляді матриці розміром 4х4:

Множачи точку ![]() на матрицю
на матрицю ![]() . отримаємо загальний вираз для точки
в однорідних координатах
. отримаємо загальний вираз для точки
в однорідних координатах ![]() :
:
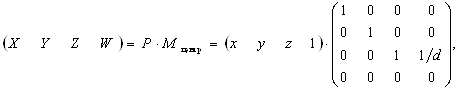
![]()
геометричний проекція косокутний матриця
Тепер, поділивши на W (що дорівнює z/d) для зворотнього переходу до трьох вимірів, отримаємо
![]()
Цей результат є коректним, оскільки містить перетворену z - координату з 1, що відповідає положенню проекційної ПЛОЩИНИ ВЗДОВЖ ОСІ 2.
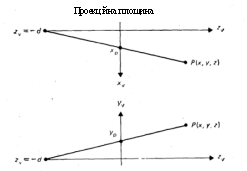
Рис. 2 Інша схема побудови центральної проекції
При іншому представленні центрального проектування, застосовуваному в деяких роботах, проекційна площина сполучається з площиною 2 = 0, а центр проекції розташовується в точці 2 = - с (рис. 2). З подібності трикутників випливає
![]()
Звідси одержуємо
![]()
Матриця записується у виді
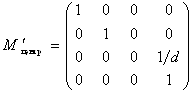
Цю матрицю можна одержати з матриці ![]() шляхом переносу центра проекції в
початок координат, застосування
шляхом переносу центра проекції в
початок координат, застосування ![]() і зворотнього переносу:
і зворотнього переносу:
![]()
Ортографічне проектування на площину z = 0 очевидне. Напрямок проектування збігається з нормаллю до площини проекції, тобто в нашому випадку з віссю z. Таким чином, точка Р має координати:
![]()
Ця проекція описується матрицею
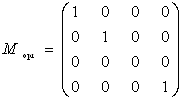
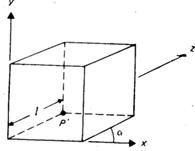
Рис. 3 Косокутна рівнобіжна проекція одиничного куба.
Точка Р' є проекцією точки P (0, 0, 1)
Розглянемо тепер косокутну проекцію, матриця якої може бути записана виходячи зі значень a і l (рис. 3). На рис. 3 зображений одиничний куб, спроектований на xy-площину. З малюнка видно, що проекцією точки P (0, 0, 1), що знаходиться на задній стороні' одиничного куба, є точка Р'(l соsа, l sіnа, 0), що належить площині ху. По визначенню це означає, що напрям проектування збігається з відрізком РР', що проходить через ці дві точки (рис. 4). Цей напрям є Р'-Р= (l соsа, l sina, -1). Напрям проектування складає кут р із площиною ху.
Тепер розглянемо довільну точку x, у, z і визначимо її косокутну проекцію (Хр,Ур) на площину ху. На рис. 5 показані два зображення точки і проектор, що рівнобіжний проектору, приведеному на рис.4. Рівняння для x- і y-координат проектора як функцій z мають вид у=mz+b. Вирішуючи два рівняння относительно Хр і Yр, відзначених на рис.5, одержуємо
![]()
Матриця розміром 4х4, що виконує ці дії і, отже, описує косокутну проекцію, має вигляд

Застосування матриці ![]() приведе до зсуву і наступного
проектування об'єкта: площини з постійною координатою z = z1 переносяться в
напрямку х на z1*l соsa в напрямку y на z1*l sina і потім проектуються на
площину z = 0. Зсув зберігає паралельність прямих, а також кути і відстані в
площинах, паралельних осі z.
приведе до зсуву і наступного
проектування об'єкта: площини з постійною координатою z = z1 переносяться в
напрямку х на z1*l соsa в напрямку y на z1*l sina і потім проектуються на
площину z = 0. Зсув зберігає паралельність прямих, а також кути і відстані в
площинах, паралельних осі z.
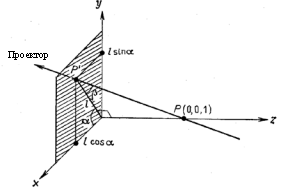
Рис. 4. Косокутна паралельна проекція Р'(l соsа, l sinа, 0) проекцією точки P (0, 0, 1).
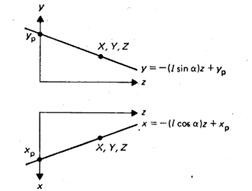
Рис. 5 Косокутна паралельна проекція (Xp, Yp, 0) точки (x, y, z).
Для проекції кавальє l=1, тому кут р, показаний на рис.4.17,
складає 45°. Для проекції кабіні l=1/2, а b=агtg (2) =63,4°. У випадку
ортографічної проекції l = 0 і b = 90°, тому ![]() є окремим випадком
є окремим випадком ![]() .
.
| Застосування нарисної геометрії у геодезії | |
|
Розділ. І . Метод проекцій з числовими відмітками, проекції точки 1.1 Суть та область застосування метода проекцій з числовими відмітками Метод ... Враховуючи, що в проекціях з числовими відмітками об'єкт проектується тільки на одну площину проекцій, а одна проекція на визначає положення об'єкта в просторі, другу фронтальну ... 4.1. земляні укоси задані на плані прямолінійними горизонтальними бровками 7.0 та 9.0 і лініями найбільшого скату k, l , які мають нахили i = 1:2. Задані укоси паралельні, тому що ... |
Раздел: Рефераты по геологии Тип: учебное пособие |
| Фізика напівпровідників | |
|
Міністерство освіти і науки України Український державний університет водного господарства і природокористування Кафедра фізики 073-90 В.О.Дубчак, М.О ... З мал 5.13 видно, що різниця ходу для хвиль, які відбились від сусідніх атомних площин, дорівнює 2dsin, де d - період кристалічної решітки, - кут ковзання падаючих променів. Зокрема, для електрона в ямі шириною l, яка співмірна з розміром атома, отримаємо В цей же час для макрооб"єктів, коли m i l - дуже великі, відстань між рівнями стає зникаюче малою ... |
Раздел: Рефераты по физике Тип: учебное пособие |
| Нарисна геометрія | |
|
Нарисна геометрія Вступ Засновником "Нарисної геометрії" є видатний французький геометр кінця VXIII - початку XIX століття Гаспар Монж. У своєму ... П1 - горизонтальна площина проекцій; П2 - фронтальна площина проекцій; О - початок координат; Х, У, Z - осі координат; А - точка у просторі; А1 та А2 - відповідно горизонтальна та ... Усі точки геометричного об"єкта обертаються у площинах, паралельних тій площині проекцій, відносно якої вісь обертання перпендикулярна. |
Раздел: Рефераты по математике Тип: курсовая работа |
| Вивчення елементів стереометрії у курсі геометрії 9 класу | |
|
ДИПЛОМНА РОБОТА "Вивчення елементів стереометрії у курсі геометрії 9 класу" Вступ Дитина дуже рано починає орієнтуватися в оточуючому її реальному, а ... Можна дати означення паралельних прямої та площини: пряму та площину називають паралельними, якщо вони не мають спільних точок. 40.Діагональ осьового перерізу циліндра дорівнює і утворює з площиною основи кут 45°. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Опір матеріалів: інженерні методи розрахунків | |
|
1. Предмет і завдання опору матеріалів Інженерам будь якої спеціальності необхідно створювати надійні споруди, машини і прилади. Надійними прийнято ... Повернемо вправо Декартову сис-му координат в додатному напрямі на деякий кут ѭ. В новій сис-мі координат z1 i y1. Головна площина зорієнтована під кутом 90o до напряму ѭ1. |
Раздел: Промышленность, производство Тип: изложение |