Контрольная работа: Потрійний інтеграл
ПОТРІЙНИЙ ІНТЕГРАЛ
1. Поняття потрійного інтеграла. Умови його існування та властивості
Схема побудови потрійного інтеграла така сама, як і звичайного визначеного інтеграла та подвійного інтеграла.
Нехай функція ![]() визначена в
обмеженій замкненій області
визначена в
обмеженій замкненій області ![]() . Розіб'ємо область
. Розіб'ємо область ![]() сіткою поверхонь на
сіткою поверхонь на ![]() частин
частин ![]() , які не мають спільних внутрішніх точок
і об'єми яких дорівнюють
, які не мають спільних внутрішніх точок
і об'єми яких дорівнюють ![]() . У кожній частині
. У кожній частині ![]() візьмемо довільну точку
візьмемо довільну точку
![]() і
утворимо суму
і
утворимо суму
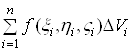 ,(1)
,(1)
яка називається інтегральною
сумою для функції ![]() за областю
за областю ![]() . Нехай
. Нехай ![]() – найбільший з діаметрів областей
– найбільший з діаметрів областей ![]() .
.
Якщо інтегральна
сума (1) при ![]() має скінченну границю, яка не
залежить ні від способу розбиття області
має скінченну границю, яка не
залежить ні від способу розбиття області ![]() на частини
на частини ![]() , ні від вибору в них
точок
, ні від вибору в них
точок ![]() , то
ця границя називається потрійним інтегралом і позначається одним із таких
символів:
, то
ця границя називається потрійним інтегралом і позначається одним із таких
символів:
![]() або
або ![]() .
.
Таким чином, за означенням
 ,(2)
,(2)
де ![]() – функція, інтегровна в
області
– функція, інтегровна в
області ![]() ;
; ![]() – область
інтегрування;
– область
інтегрування; ![]() і
і ![]() – змінні інтегрування;
– змінні інтегрування; ![]() (або
(або ![]() ) – елемент
об'єму.
) – елемент
об'єму.
Якщо по тілу ![]() розподілено
масу з об'ємною густиною
розподілено
масу з об'ємною густиною ![]() в точці
в точці ![]() , то маса
, то маса ![]() цього тіла знаходиться за
формулою
цього тіла знаходиться за
формулою
![]() . (3)
. (3)
Формула (3)
аналогічна формулі (1.8) і може розглядатися як механічний зміст потрійного
інтеграла, коли підінтегральна функція невід'ємна в області ![]() . Якщо всюди в області
покласти
. Якщо всюди в області
покласти ![]() ,
то з формули (2) випливає формула для обчислення об'єму
,
то з формули (2) випливає формула для обчислення об'єму ![]() тіла
тіла ![]() :
:
![]() .(4)
.(4)
Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.
Теорема (достатня умова інтегровності
функції). Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
то вона в цій області інтегрована.
,
то вона в цій області інтегрована.
Властивості потрійних інтегралів.
1. Сталий множник можна винести за знак потрійного інтеграла:
![]() .
.
Потрійний інтеграл від суми кількох інтегровних функцій дорівнює сумі потрійних інтегралів від доданків:
![]() .
.
3. Якщо в області
інтегрування ![]() , то
, то
![]() .
.
4. Якщо функції ![]() та
та ![]() визначені в
одній і тій самій області
визначені в
одній і тій самій області ![]() і
і ![]() , то
, то
![]() .
.
5. (Адитивність
потрійного інтеграла.) Якщо область інтегрування ![]() функції
функції ![]() розбити на частини
розбити на частини ![]() і
і ![]() , які не мають спільних
внутрішніх точок, то
, які не мають спільних
внутрішніх точок, то
![]() .
.
6. (Оцінка
потрійного інтеграла.) Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
яка має об'єм
,
яка має об'єм ![]() , то
, то
![]() ,
,
де ![]() і
і ![]() відповідно найменше і
найбільше значення функції
відповідно найменше і
найбільше значення функції ![]() в області
в області ![]() .
.
7. (Середнє
значення функції.) Якщо функція ![]() неперервна в обмеженій замкненій
області
неперервна в обмеженій замкненій
області ![]() ,
яка має об'єм
,
яка має об'єм ![]() , то в цій області існує така
точка
, то в цій області існує така
точка ![]() , що
, що
![]() .
.
Величина
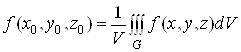
називається середнім
значенням функції ![]() в області
в області ![]() .
.
2. Обчислення потрійного інтеграла
Обчислення потрійного інтеграла зводять до обчислення повторних, тобто до інтегрування за кожною змінній окремо.
Нехай область ![]() обмежена знизу
і зверху поверхнями
обмежена знизу
і зверху поверхнями ![]() і
і ![]() , а з боків циліндричною
поверхнею, твірні якої паралельні осі
, а з боків циліндричною
поверхнею, твірні якої паралельні осі ![]() . Позначимо проекцію області
. Позначимо проекцію області ![]() на площину
на площину ![]() через
через ![]() (рис. 1) і
вважатимемо, що функції
(рис. 1) і
вважатимемо, що функції ![]() і
і ![]() неперервні в
неперервні в ![]() .
.
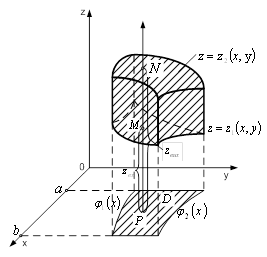
Рисунок 1 – Область ![]()
Якщо при цьому
область ![]() є
правильною, то область
є
правильною, то область ![]() називається правильною у напрямі
осі
називається правильною у напрямі
осі ![]() . Припустимо,
що кожна пряма, яка проходить через кожну внутрішню точку
. Припустимо,
що кожна пряма, яка проходить через кожну внутрішню точку ![]() паралельно осі
паралельно осі ![]() , перетинає
межу області
, перетинає
межу області ![]() у точках
у точках ![]() і
і ![]() . Точку
. Точку ![]() назвемо точкою входу в область
назвемо точкою входу в область ![]()
![]() , а точку
, а точку ![]() – точкою виходу з
області
– точкою виходу з
області ![]() ,
а їхні аплікати позначимо відповідно через
,
а їхні аплікати позначимо відповідно через ![]() і
і ![]() . Тоді
. Тоді ![]() ,
, ![]() і для будь-якої неперервної в
області
і для будь-якої неперервної в
області ![]() функції
функції
![]() має місце
формула
має місце
формула
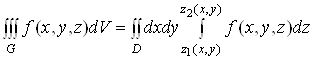 .(5)
.(5)
Зміст формули (5)
такий. Щоб обчислити потрійний інтеграл, потрібно спочатку обчислити інтеграл 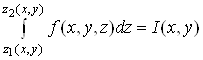 за змінною
за змінною ![]() , вважаючи
, вважаючи ![]() та
та ![]() сталими.
Нижньою межею цього інтеграла є апліката точки
сталими.
Нижньою межею цього інтеграла є апліката точки ![]() входу
входу ![]() , а верхньою – апліката
, а верхньою – апліката ![]() точки виходу
точки виходу ![]() . Внаслідок
інтегрування отримаємо функцію
. Внаслідок
інтегрування отримаємо функцію ![]() від змінних
від змінних ![]() та
та ![]() .
.
Якщо область ![]() , наприклад,
обмежена кривими
, наприклад,
обмежена кривими ![]() і
і ![]()
![]() , де
, де ![]() і
і ![]() – неперервні функції, тобто
– неперервні функції, тобто
![]() , то, переходячи від
подвійного інтеграла
, то, переходячи від
подвійного інтеграла ![]() до повторного (п. 1.3), отримаємо
формулу
до повторного (п. 1.3), отримаємо
формулу
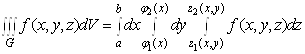 ,(6)
,(6)
яка зводить
обчислення потрійного інтеграла до послідовного обчислення трьох визначених
інтегралів. Порядок інтегрування може бути й іншим, тобто змінні ![]() і
і ![]() у правій частині
формули (6) за певних умов можна міняти місцями.
у правій частині
формули (6) за певних умов можна міняти місцями.
Якщо, наприклад,
область ![]() правильна
в напрямі осі
правильна
в напрямі осі ![]() :
:
![]() ,
,
де ![]() – неперервні функції, то
– неперервні функції, то
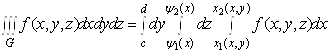 .
.
Зокрема, якщо областю інтегрування є паралелепіпед:
![]() ,
,
то
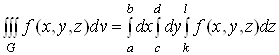 . (7)
. (7)
У цьому разі
інтегрування виконується в будь-якому порядку, оскільки область ![]() правильна у напрямі
всіх трьох координатних осей
правильна у напрямі
всіх трьох координатних осей ![]() .
.
3. Заміна змінних в потрійному інтегралі
Заміну змінної в
потрійному інтегралі виконують за таким правилом: якщо обмежена замкнена
область ![]() взаємно
однозначно відображується на область
взаємно
однозначно відображується на область ![]() за допомогою неперервно
диференційовних функцій
за допомогою неперервно
диференційовних функцій ![]() ,
, ![]() ,
, ![]() , якобіан
, якобіан ![]() в області
в області ![]() не дорівнює нулю:
не дорівнює нулю:

і ![]() – неперервна в
– неперервна в ![]() , то справедлива формула
, то справедлива формула
![]() . (8)
. (8)
На практиці
найуживанішими є циліндричні та сферичні координати. При переході від
прямокутних координат ![]() до циліндричних
до циліндричних ![]() (рис.4, а), пов'язаних
з
(рис.4, а), пов'язаних
з ![]() співвідношеннями
співвідношеннями
![]() ;
;
![]() ,
,
якобіан перетворення
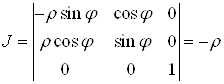 .
.
З формули (8) отримуємо потрійний інтеграл у циліндричних координатах:
![]() .(9)
.(9)
Назва
«циліндричні координати» пов'язана з тим, що координатна поверхня ![]() є циліндром,
прямолінійні твірні якого паралельні осі
є циліндром,
прямолінійні твірні якого паралельні осі ![]() .
.
При переході від
прямокутних координат ![]() до сферичних
до сферичних ![]()
(рис. 4, б), які
пов'язані з ![]() формулами
формулами
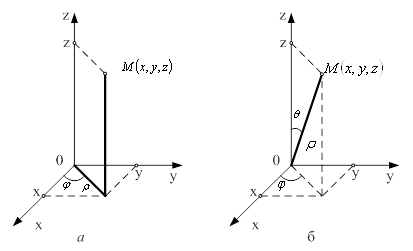
Рисунок 4 – Координати: а) циліндричні; б) сферичні
![]() ;
;
![]() ,
,
якобіан перетворення
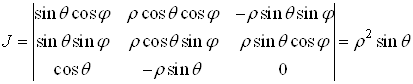 .
.
З формули (8) знаходимо потрійний інтеграл у сферичних координатах:
![]() . (10)
. (10)
Назва «сферичні
координати» пов'язана з тим, що координатна поверхня ![]() є сферою. При обчисленні
потрійного інтеграла в циліндричних чи сферичних координатах область
є сферою. При обчисленні
потрійного інтеграла в циліндричних чи сферичних координатах область ![]() , як правило,
не будують, а межі інтегрування знаходять безпосередньо за областю
, як правило,
не будують, а межі інтегрування знаходять безпосередньо за областю ![]() , користуючись
геометричним змістом нових координат. При цьому рівняння поверхонь
, користуючись
геометричним змістом нових координат. При цьому рівняння поверхонь ![]() та
та ![]() , які обмежують
область
, які обмежують
область ![]() ,
записують у нових координатах.
,
записують у нових координатах.
Зокрема, якщо
область ![]() обмежена
циліндричною поверхнею
обмежена
циліндричною поверхнею ![]() та площинами
та площинами ![]() , то всі межі
інтегрування в циліндричній системі координат сталі:
, то всі межі
інтегрування в циліндричній системі координат сталі:
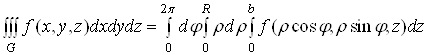
і не змінюються
при зміні порядку інтегрування. Те саме буде у сферичних координатах у випадку,
коли ![]() –
куля:
–
куля: ![]() або
кульове кільце. Наприклад, якщо
або
кульове кільце. Наприклад, якщо ![]() – кульове кільце з внутрішньою
сферою
– кульове кільце з внутрішньою
сферою ![]() , то
рівняння цієї сфери в сферичних координатах має вигляд
, то
рівняння цієї сфери в сферичних координатах має вигляд
![]()
або
![]() ,
,
звідки ![]() . Аналогічно
. Аналогічно ![]() – рівняння
зовнішньої сфери, тому
– рівняння
зовнішньої сфери, тому
![]() .
.
У випадку, коли ![]() – куля
– куля ![]() , у цій
формулі слід покласти
, у цій
формулі слід покласти ![]() . Інших будь-яких загальних
рекомендацій, коли необхідно переходити до тієї чи іншої системи координат,
дати неможливо. Це залежить і від області інтегрування, і від підінтегральної
функції. Іноді потрібно написати інтеграл у різних системах координат і лише
після цього вирішити, в якій з них обчислення буде найпростішим.
. Інших будь-яких загальних
рекомендацій, коли необхідно переходити до тієї чи іншої системи координат,
дати неможливо. Це залежить і від області інтегрування, і від підінтегральної
функції. Іноді потрібно написати інтеграл у різних системах координат і лише
після цього вирішити, в якій з них обчислення буде найпростішим.
Приклад
1. Обчислити
інтеграл ![]() ,
якщо область
,
якщо область ![]() обмежена поверхнями
обмежена поверхнями ![]() і
і ![]() .
.
Розв’язання
Область ![]() є конусом
(рис. 5).
є конусом
(рис. 5).
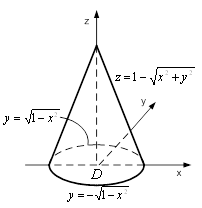
Рисунок 5 – Область ![]()
Рівняння конічної
поверхні, яка обмежує область ![]() , можна записати у вигляді
, можна записати у вигляді ![]() , а саму
область
, а саму
область ![]() подати
таким чином:
подати
таким чином: ![]() , де
, де ![]() – круг радіуса
– круг радіуса ![]() з центром
з центром ![]() . Тому даний
потрійний інтеграл можна звести до послідовного обчислення трьох визначених
інтегралів у прямокутних координатах:
. Тому даний
потрійний інтеграл можна звести до послідовного обчислення трьох визначених
інтегралів у прямокутних координатах:
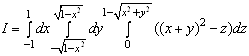 .
.
Проте зручніше
перейти до циліндричних координат ![]() . Тоді прообраз круга
. Тоді прообраз круга ![]() є прямокутник
є прямокутник ![]() , прообраз
конічної поверхні – плоска поверхня
, прообраз
конічної поверхні – плоска поверхня ![]() , а прообраз області
, а прообраз області ![]() – область
– область ![]() . Якобіан
переходу до циліндричних координат дорівнює
. Якобіан
переходу до циліндричних координат дорівнює ![]() , підінтегральна функція в
циліндричних координатах дорівнює
, підінтегральна функція в
циліндричних координатах дорівнює![]() . Зводячи потрійний інтеграл за
областю
. Зводячи потрійний інтеграл за
областю ![]() до
послідовного обчислення трьох визначних інтегралів, отримаємо
до
послідовного обчислення трьох визначних інтегралів, отримаємо
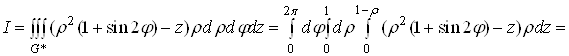
![]()
Зазначимо, що
розставлення меж інтегрування в циліндричних координатах, як правило, виконують,
розглядаючи не область ![]() , а зміну циліндричних координат в
області
, а зміну циліндричних координат в
області ![]() . Наочно видно, що в області
. Наочно видно, що в області ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , при кожному значенні
, при кожному значенні ![]() змінна
змінна ![]() змінюється від
змінюється від ![]() до
до ![]() , а для кожної точки
, а для кожної точки ![]() області
області ![]() змінна
змінна ![]() змінюється в області
змінюється в області ![]() від
від ![]() (значення
(значення ![]() в області
в області ![]() ) до
) до ![]() (значення
(значення ![]() на конічній
поверхні).
на конічній
поверхні).
4. Деякі застосування потрійного інтеграла
інтеграл потрійний обчислення змінний
1. Обчислення об'ємів. Якщо деяке тіло є обмеженою і замкненою
областю ![]() , що має об'єм
, що має об'єм ![]() , то згідно з
формулою (4)
, то згідно з
формулою (4)
![]() .(11)
.(11)
Застосування у
механіці. Нехай ![]() – обмежена
замкнена область простору
– обмежена
замкнена область простору ![]() , яку займає деяке матеріальне
тіло з густиною
, яку займає деяке матеріальне
тіло з густиною ![]() , де
, де ![]() – неперервна функція в області
– неперервна функція в області ![]() , тоді:
, тоді:
а)маса цього тіла
![]() ;(12)
;(12)
б)моменти інерції
![]() тіла
відносно координатних осей
тіла
відносно координатних осей ![]() відповідно дорівнюють
відповідно дорівнюють
![]() . (13)
. (13)
Моменти інерції ![]() тіла відносно
координатних площин
тіла відносно
координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() .(14)
.(14)
Момент інерції тіла відносно початку координат
![]()
![]() (15)
(15)
в) статичні
моменти ![]() тіла
відносно координатних площин
тіла
відносно координатних площин ![]() обчислюються за формулами
обчислюються за формулами
![]() ;(16)
;(16)
г) координати ![]() центра маси
тіла визначаються за формулами
центра маси
тіла визначаються за формулами
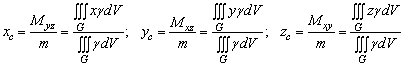 . (17)
. (17)
Доведення формули (11), як уже зазначалося, випливає з означення потрійного інтеграла:
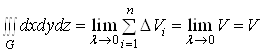 .
.
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... угловыми положениями (координатами) ЛА и равления ЛА неестественным для летчика, что сильно снижает ка- |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Экономическая система | |
|
1. Эк-я с-ма - ед-во ч-ка и общ-го пр-ва В любой ЭС существует 2 вида отношений: 1-отношение людей к природе; 2. отношение людей друг к другу. В ... 1-При выпуске готовой пр-ции исп-ся метод прямого счёта(норма расхода на 1 изд-е * кол-во изд-й.2-При выпуске новой пр-ции потребность мат-ла рассч-ся по методу аналогии(норма ... Зп = Зм / t'раб * tраб, где Зм - месячная повременная ЗП работника, руб.; tраб - число рабочих часов по графику в данном месяце; t'раб - количество часов, фактически отраб-х ... |
Раздел: Рефераты по экономике Тип: шпаргалка |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... И наоборот, каждая матрица n-го пор-ка явл-ся матрицей некот-го вполне опред-го лин-го опре-ра ѭ прост-ва vn в базисе e1,e2,.en. В начале детьми движут безусловные рефлексы, инстинкты, естеств потр-ти. |
Раздел: Рефераты по математике Тип: реферат |
| Вопросы и ответы к экзамену по курсу "История экономических учений" | |
|
Для студентов 2 курса специальности 061100 - "Менеджмент организации" Составитель: к.и.н., доцент кафедры международного маркетинга Ешкилев Ю.Б. 1 ... М. глубоко исследов. функц. денег, отверг сведение их к сред-ву обращен., ввел понятия денег как реал-х д-г. Проблема денег решалась на почве новой теории стоим-ти. Маржин-зм - это экономич. школа, к-рая использ-ла предельн. анализ, заним-сь изучен. предельн. величин. |
Раздел: Рефераты по экономике Тип: шпаргалка |
| Политология | |
|
19. Пол сис: суть. Всякое класс общ-во политически оформлено, им механизм вл, обеспечивающ его норм функциониров в кач единого соц орг-ма. Эт механизм ... Т пол сис и их элемент-исслед проб созд и функц госуд, парт, общ-пол организ чер анал конст-х, адм-прав, эконх и соц функ управ на основ сравнит анал полит инстит, отнош м/д суб ... 1с т зр зон и област их проявлен. Но подоб изложен мат-ла не прием-мо если кан-т предст в роли "символа партии", ч-ка идей, дел акцент на концептуал наработках. |
Раздел: Рефераты по политологии Тип: реферат |