Реферат: Исследование методов вычисления определенных интегралов
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФИЛИАЛ В ГОРОДЕ СТЕРЛИТАМАК
КАФЕДРА ЕСТЕСТВЕННО-НАУЧНЫХ И ОБЩЕПРОФЕССИОНАЛЬНЫХ ДИСЦИПЛИН
ИССЛЕДОВАНИЕ МЕТОДОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по ИНФОРМАТИКЕ
2403.302413.000ПЗ
(обозначение документа)
| Группа ВТС-109 | Фамилия, и. о. | Подпись | Дата | Оценка |
| Студент | Терещук А.И. | |||
| Консультант | Карасев Е.М. | |||
| Проверил |
Стерлитамак 2011г.
Содержание
Введение
Теоретическая часть
Метод Симпсона (парабол)
Пример применения
Практическая часть
Программное вычисление
Визуализация методов
Заключение
Список литературы
Введение
При решении ряда актуальных физических и технических задач встречаются определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определенными интегралами, сами подынтегральные функции которых не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.
Мне была поставлена задача исследовать два метода вычисления определенных интегралов: метод трапеций и метод Симпсона (парабол)
метод трапеция симпсон интеграл
Теоретическая часть
Метод трапеций
Пусть требуется вычислить интеграл 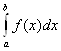 . Разобьем сегмент
. Разобьем сегмент ![]() на n равных частей при помощи точек
на n равных частей при помощи точек ![]() . Метод трапеций заключается в замене
интеграла
. Метод трапеций заключается в замене
интеграла 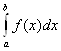 суммой
суммой
![]() площадей трапеций с основаниями, соответственно
равными
площадей трапеций с основаниями, соответственно
равными ![]() и
и ![]() , и с высотами,
равными
, и с высотами,
равными ![]() .
.
Таким образом, справедлива формула:
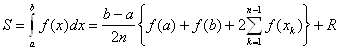 ,
,
Где R - остаточный член. Это формула называется формулой трапеций.
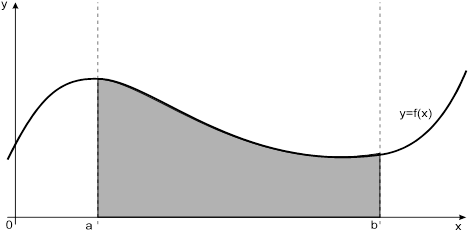
Рисунок 1 - Криволинейная трапеция
По методу трапеций интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине.
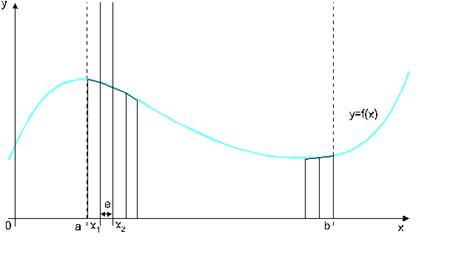
Рисунок 2 - Метод трапеций
Метод Симпсона (парабол)
Для вычисления интеграла 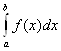 снова разобьем сегмент
снова разобьем сегмент ![]() на n равных частей при помощи точек
на n равных частей при помощи точек ![]() и обозначим через
и обозначим через
![]() середину сегмента
середину сегмента
![]() . Метод парабол
заключается в замене интеграла
. Метод парабол
заключается в замене интеграла 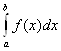 суммой
суммой
 площадей фигур и представляющий собой
трапеции, лежащие под параболами, проходящими через три точки графика функции f (x) c абсциссами
площадей фигур и представляющий собой
трапеции, лежащие под параболами, проходящими через три точки графика функции f (x) c абсциссами ![]() .
.
Таким образом, справедлива формула:
![]()
 ,
,
Где R - остаточный член. Это формула называется формулой Симпсона.
Пример применения
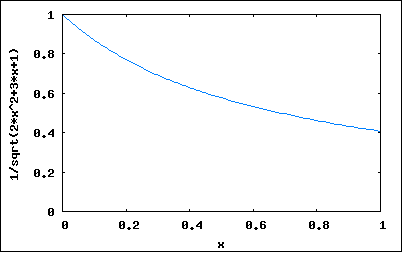
Рисунок 3 - График функции
|
|
y0 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
| x | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| y | 1 | 0,86 | 0,76 | 0,68 | 0,6 | 0,55 | 0,5 | 0,47 | 0,46 | 0,43 | 0,41 |
![]()
Найдем площадь криволинейной трапеции методом трапеций:
S=0,1* ( (1+0,41) /2+0,86+0,76+0,68+0,6+0,55+0,5+0,47+0,46+0,43) =0,6025 кв. ед
Найдем площадь криволинейной трапеции методом Симпсона:
S=0,0017*2* (1+0,41+2* (0,76+0,6+0,5+0,46) +4* (0,86+0,68+0,55+0,47+0,43)) =
=0,6123 кв. ед
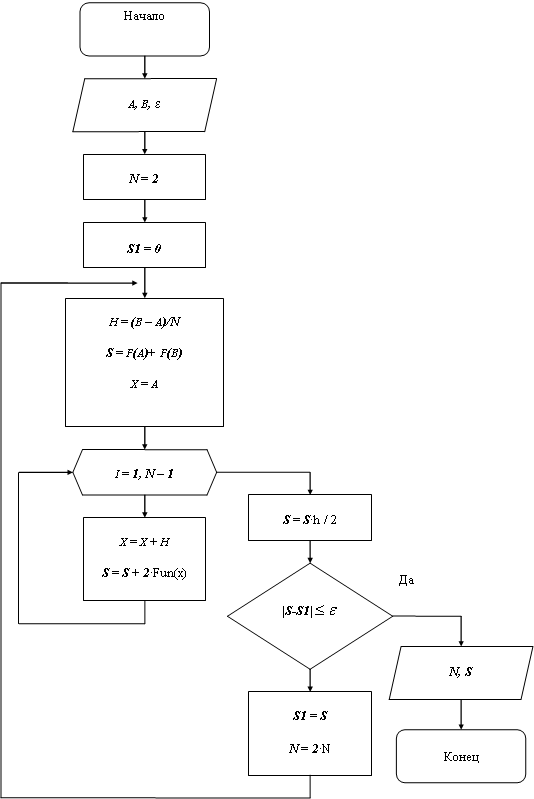
Блок-схема метода трапеций
 |
Блок-схема метода Симпсона
Практическая часть
Конструирование интерфейса
Программа разрабатывается в объектно-ориентированной среде программирования Lazarus.
Перед началом программирования, была создана форма Заставка.
Рисунок 4 - Заставка
В этом окне расположены:
· Кнопка "Запуск", позволяющая приступить к началу программы;
· Компоненты Label;
Затем была создана основная форма Меню, позволяющая выбирать операции.

Рисунок 5 - Основная форма
Данное окно представляет главное окно программы.
В этом окне расположены:
· Компоненты Label для подписи компонентов Edit;
· Компонент MainMenu для выбора операции;
Далее была создана форма Параметры, предназначенная для введения данных.
Рисунок 6 - Параметры
В этом окне расположены:
· Компоненты Label для подписи компонентов Edit;
· Две кнопки: "OK" - принимает данные и возвращается на главное меню; "Отмена" - позволяет вернуться к главному окну, не принимая данных;
Затем была создана форма Решение, на которой будет показана площадь по разным методам вычислений и визуализироваться один из методов.

Рисунок 7 - Решение
В этом окне расположены:
· Компонент Label для подписи компонента Edit;
· Две кнопки: "График" - визуализирует метод трапеций; "OK" - принимает данные и возвращается на главное меню;
· Компонент Chart для отображения графика;
Следующая форма была создана сравнение методов, то есть для исследования методов на погрешность с заданной точностью.
Рисунок 8 - Исследование на погрешность
В этом окне расположены:
· Три кнопки: Кнопка "График погрешности" визуализирует сравнение методов; Кнопка "Сохранить" сохраняет результаты сравнения в текстовый файл; Кнопка "OK" - принимает данные и возвращается на главное меню;
· Компонент Chart для отображения графика;
Программное вычисление
По блок-схеме была создана программа для вычисления интеграла методами Симпсона и трапеций:
// Вводим переменные:
var
Form2: TForm2;
a,b,E,h,S,S1,x: real; n, i: integer;
implementation
{ TForm2 }
uses unit1,unit3,unit4,unit5;
// Описываем функцию:
function f (x: real): real;
begin
f: =1/Sqrt (1+3*x+2*x*x);
end;
// В соответствие с блок-схемой напишем программу на языке высокого уровня:
procedure TForm2. MenuItem4Click (Sender: TObject);
begin
// найдем площадь интеграла по методу трапеций
S: =0; // изначально обнуляем значение площади интеграла
n: =1; // начальное значение количества разбиений
Repeat // начало цикла
S1: =S; // предыдущее значение площади изначально равно значению площади с количеством разбиений равным 1
n: =2*n; // увеличиваем количество разбиений в два раза
h: = (b-a) /n; // формула вычисления шага
S: =f (a) +f (b); // значение функции в нижнем пределе + значение функции в верхнем пределе определенного интеграла
x: =a; // значению x присвоим значение нижнего предела
for i: =1 to n-1 do // для i-того элемента, изменяющегося от 1 до n-1
begin
x: =x+h; // х увеличиваем на шаг
S: =S+2*f (x) // сумма площадей трапеций
end;
S: =S*h/2; // вычислим площадь по формуле
Until abs (S-S1) <=E; // если разность значения площади и предыдущего значения площади меньше или равна заданной точности Е, то
Form4. Edit1. Text: =FloatToStr (S); // выводим значение на экран
Form4. Caption: ='Вычисление методом трапеций';
Form4. Button2. visible: =True;
Form4. Chart1. Visible: =True;
Form4. ShowModal;
end;
procedure TForm2. MenuItem8Click (Sender: TObject);
begin
// найдем площадь интеграла по методу Симпсона (парабол)
S: =0; // начальное значение количества разбиений
n: =1; // изначально обнуляем значение площади интеграла
Repeat // начало цикла
S1: =S; // предыдущее значение площади изначально равно значению площади с количеством разбиений равным 1
n: =2*n; // увеличиваем количество разбиений в два раза
h: = (b-a) /n; // формула вычисления шага
S: =f (a) +f (b); // значение функции в нижнем пределе + значение функции в верхнем пределе определенного интеграла
x: =a; // значению x присвоим значение нижнего предела
for i: =0 to n do // для i-того элемента, изменяющегося от 1 до n-1
begin
x: =a+i*h; // х увеличиваем
if x=a then s: =s+f (x) else
if x=b then s: =s+f (x) else
if i mod 2 = 0 then s: =s+2*f (x) else s: =s+4*f (x); // если число четное, то вычисляется по формуле s: =s+2*f (x), а если нечетное, то по s: =s+4*f (x)
end;
S: =S*h/3; // вычислим площадь по формуле
Until abs (S-S1) <=E; // если разность значения площади и предыдущего значения площади меньше или равна заданной точности Е, то
Form4. Edit1. Text: =FloatToStr (S); // выводим значение на экран
Form4. Caption: ='Вычисление методом парабол';
Form4. Button2. visible: =False;
Form4. Chart1. Visible: =False;
Form4. ShowModal;
end;
Визуализация методов
Для открытия программы необходимо запустить project1. exe. После запуска откроется окно программы (рис.4). Предварительно создаем текстовый файл integral. txt в том же каталоге, где расположена программа (рис.9) в этом файле должны сохраниться результаты сравнения.
Запускаем программу. С помощью компонента MainMenu выберем вкладки "Ввод", "Решение", "Исследование" и "Заставка".
Выбираем вкладку "Ввод - Параметры" открывается Form 2 и вводим параметры (рис.10):

Рисунок 9 – Меню
Рисунок 10 - Параметры
Нажимаем на кнопку "OK" и возвращаемся к основной форме. Выбираем методы решения:
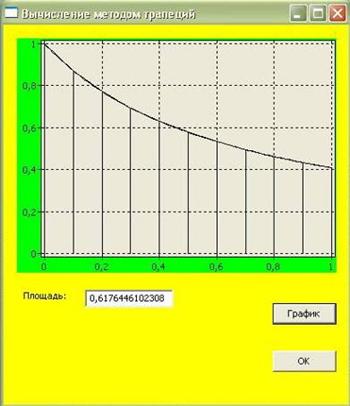
Рисунок 12 - Вычисление методов трапеций
Аналогично выглядит форма, когда вычисляем площадь по методу Симпсона (парабол). Далее выбираем вкладку "Исследование на погрешность" открывается Form 5, нажимаем на кнопку "График", затем на кнопку "Сохранить"
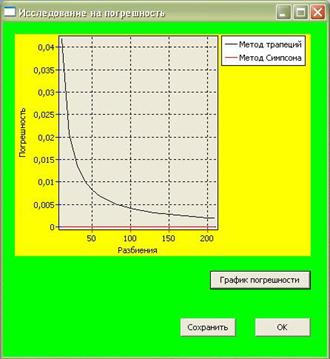
Рисунок 14 - Исследование на погрешность
Из графика видно, что метод Симпсона (парабол) намного точнее, почти совпадает с точным значением, вычисленным в пакете Maxima.
Затем на кнопку "Сохранить". Откроем каталог, где расположена программа и откроем текстовый файл integral. Txt
Рисунок 15 - Сохранение результатов сравнения
Нажмем на кнопку "OK" и вернемся в основной форме, чтобы завершить исследование вычислительных методов для нахождения интеграла.
Заключение
В процессе разработки курсовой работы были проработаны следующие методы вычисления определенных интегралов - метод трапеций и метод Симпсона (парабол). Был визуализирован ход вычисления интеграла в виде графика. На графике была представлена зависимость разбиений от заданной точности.
В процессе выполнения курсовой работы были закреплены практические навыки по разработке пользовательских приложений при помощи объектно-ориентированного языка программирования Lazarus и современных компьютерных технологий обработки информации, а также навыки в составлении текстовой документации.
Список литературы
1. Намиот Д.Е. Основные особенности языка программирования Delphi 7. - М.: ‘Память ’, 1999.
2. Пильщиков В.Н. Программирование на языке Delphi 7. - М.: Диалог--Мифи, 1999.
3. Михеева Е.В. Информационные технологии в профессиональной деятельности: Учебное пособие для сред. проф. образования. - 2-е издание, стер. - М.: Издательский центр "Академия", 2005. - 384 с.
4. Румянцева Е.Л., Слюсарь В.В. Информационные технологии: учеб. пособие / Под. ред. проф. Л.Г. Гагариной. - М.: ИД "ФОРУМ": ИНФРА - М, 2007. - 256 с.: ил.
5. Ильин В.А., Поздняк Э.Г. - Основы математического анализа. Часть 1 - М.: Физматлит, 2008 - 648 с.
| Вычислительная математика | |
|
Содержание Введение Тема 1. Решение задач вычислительными методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2 ... Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции y = f(x), осью абсцисс и прямыми x = a и x = b (рис. Заменим график функции y = f(x) на отрезке [xi, xi+1], i = 0, 2, . , n - 1, параболой, проведенной через точки (xi, f(xi)), (x,f(x)), (xi+1, f(xi+1)), где x - середина отрезка [xi ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Основные понятия дифференциального исчисления и история их развития ... | |
|
Министерство общего и профессионального образования Астраханский Государственный Педагогический Университет Бакалаврская работа Студентки IV курса ... Таким образом, в случае, когда f(х) 0, то есть, когда график функции у = f(х) располагается над осью Ох, определённый интеграл численно равен площади S криволинейной трапеции. Вычислением интегралов от степеней хr, или, как говорили в то время, квадратурой "парабол" у = хr, где r - рациональное число, П.Ферма занимался ещё в 1644 г. позже Ферма изложил ... |
Раздел: Рефераты по математике Тип: реферат |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... Для вычисления выделенных выражений в командном окне следует нажать правую кнопку мыши и выбрать в контекстном меню опцию Evaluate Selection. Если матрица A является квадратной и несингулярной, то, пренебрегая ошибками округле-ния, выражение X = inv(A)*B теоретически означает то же, что и X = A\B , а Y = B*inv(A ... |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Полный курс лекций по математике | |
|
МАТЕМАТИКА Тема 1. Роль математики в современном мире. Основные этапы становления математики. Тема 2. Аксиоматический метод построения научной теории ... Совокупность всех первообразных для функции f(x) на интервале Х называется неопределенным интегралом от функции f(x) и обозначается f(x)dx, где - знак интеграла, f(x ... Эту сумму будем называть интегральной суммой для функции у=f(x) на отрезке [а, в]. Интегральная сумма зависит как от способа разбиения отрезка [a, в] на п частей так и от выбора ... |
Раздел: Рефераты по математике Тип: реферат |
| Hpor | |
|
Билет№1 1)Функция y=F(x) называется периодической, если существует такое число Т, не равное нулю, что для любых значений аргумента из области ... 1)Функция y=F(x) называется периодической, если существует такое число Т, не равное нулю, что для любых значений аргумента из области определения функции выполняются равенства f(x ... Для вычисления площади S разобьём отрезок [a;b] на n равных отрезков, длинна каждого отрезка [Xj;Xj+1] равна b-a / n; на каждом из отрезков построим прямоугольник, высота которого ... мало отличатся" от криволинейной трапеции, и если Sn-сумма площадей всех прямоугольников, то Sn~=S. В курсе математического анализа показывается, что для любой непрерывной на ... |
Раздел: Рефераты по математике Тип: реферат |