Реферат: Похідні та диференціали функції багатьох змінних
ПОХІДНІ ТА ДИФЕРЕНЦІАЛИ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
1 Частинні похідні
Нехай функція ![]() визначена в
деякому околі точки
визначена в
деякому околі точки ![]() .
.
Надамо змінній x приросту![]() , залишаючи
змінну
, залишаючи
змінну ![]() незмінною,
так, щоб точка
незмінною,
так, щоб точка ![]() належала заданому околу.
належала заданому околу.
Величина
![]()
називається
частинним приростом функції ![]() за змінною x.
за змінною x.
Аналогічно
вводиться частинний приріст ![]() функції за змінною
функції за змінною![]() :
:
![]() .
.
Якщо існує границя
![]() ,
,
то вона
називається частинною похідною функції ![]() в точці
в точці ![]() за змінною x і позначається одним
із таких символів:
за змінною x і позначається одним
із таких символів:
![]() .
.
Аналогічно
частинна похідна функції ![]() за
за ![]() визначається як границя
визначається як границя
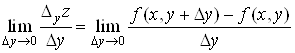
і позначається одним із символів:
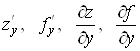 .
.
Згідно з
означенням при знаходженні частинної похідної ![]() обчислюють звичайну похідну
функції однієї змінної x, вважаючи змінну
обчислюють звичайну похідну
функції однієї змінної x, вважаючи змінну ![]() сталою, а при знаходженні
похідної
сталою, а при знаходженні
похідної ![]() сталою
вважається змінна x. Тому частинні похідні знаходять за формулами і правилами
обчислення похідних функцій однієї змінної.
сталою
вважається змінна x. Тому частинні похідні знаходять за формулами і правилами
обчислення похідних функцій однієї змінної.
Частинна похідна ![]() (або
(або![]() ) характеризує
швидкість зміни функції в напрямі осі
) характеризує
швидкість зміни функції в напрямі осі ![]() (або
(або![]() ).
).
З’ясуємо
геометричний зміст частинних похідних функції двох змінних. Графіком функції ![]() є деяка
поверхня (рис 1). Графіком функції
є деяка
поверхня (рис 1). Графіком функції ![]() є лінія перетину цієї поверхні з
площиною
є лінія перетину цієї поверхні з
площиною![]() .
Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо,
що
.
Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо,
що![]() , де
, де![]() – кут між віссю
– кут між віссю
![]() і
дотичною, проведеною до кривої
і
дотичною, проведеною до кривої ![]() в точці
в точці![]() . Аналогічно
. Аналогічно![]() .
.
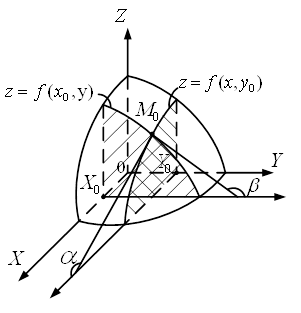
Рисунок 1 – Геометричний зміст частинних похідних
Для функції ![]() n змінних
можна знайти n частинних похідних:
n змінних
можна знайти n частинних похідних:
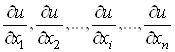 ,
,
де
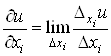 ,
,
![]() .
.
Щоб знайти
частинну похідну![]() , необхідно взяти звичайну похідну
функції
, необхідно взяти звичайну похідну
функції ![]() за
змінною
за
змінною![]() , вважаючи
решту змінних сталими.
, вважаючи
решту змінних сталими.
Якщо функція ![]() задана в
області
задана в
області ![]() і
має частинні похідні
і
має частинні похідні ![]() в усіх точках
в усіх точках![]() , то ці похідні можна
розглядати як нові функції, задані в області
, то ці похідні можна
розглядати як нові функції, задані в області![]() .
.
Якщо існує
частинна похідна за x від функції![]() , то її називають частинною
похідною другого порядку від функції
, то її називають частинною
похідною другого порядку від функції ![]() за змінною x і позначають
за змінною x і позначають ![]() або
або ![]() .
.
Таким чином, за означенням
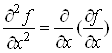 або
або![]() .
.
Якщо існує
частинна похідна від функції ![]() за змінною
за змінною![]() , то цю похідну
називають мішаною частинною похідною другого порядку від функції
, то цю похідну
називають мішаною частинною похідною другого порядку від функції ![]() і позначають
і позначають![]() , або
, або![]() .
.
Отже, за означенням
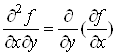 або
або ![]() .
.
Для функції двох
змінних ![]() можна
розглядати чотири похідні другого порядку:
можна
розглядати чотири похідні другого порядку:
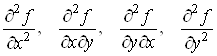 .
.
Якщо існують
частинні похідні від частинних похідних другого порядку, то їх називають
частинними похідними третього порядку функції![]() , їх вісім:
, їх вісім:
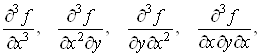
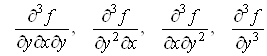 .
.
Виникає запитання: чи залежить результат диференціювання від порядку диференціювання? Інакше кажучи, чи будуть рівними між собою мішані похідні, якщо вони взяті за одними і тими самими змінними, одне й те саме число разів, але в різному порядку? Наприклад, чи дорівнюють одна одній похідні
![]() і
і ![]() або
або 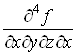 і
і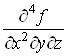 ?
?
У загальному випадку відповідь на це запитання негативна.
Проте справедлива теорема, яку вперше довів К.Г.Шварц.
Теорема (про мішані похідні). Якщо
функція ![]() визначена
разом із своїми похідними
визначена
разом із своїми похідними ![]() в деякому околі точки
в деякому околі точки ![]() , причому
похідні
, причому
похідні ![]() та
та
![]() неперервні
в точці
неперервні
в точці![]() ,
то в цій точці
,
то в цій точці
![]() .
.
Аналогічна теорема справедлива для будь-яких неперервних мішаних похідних, які відрізняються між собою лише порядком диференціювання.
2 Диференційованість функції
похідна диференціал функція змінна
Нехай функція ![]() визначена в
деякому околі точки
визначена в
деякому околі точки![]() . Виберемо прирости
. Виберемо прирости ![]() і
і ![]() так, щоб точка
так, щоб точка ![]() належала
розглядуваному околу і знайдемо повний приріст функції в точці
належала
розглядуваному околу і знайдемо повний приріст функції в точці![]() :
:
![]() .
.
Функція ![]() називається
диференційовною в точці М, якщо її повний приріст в цій точці можна подати у
вигляді
називається
диференційовною в точці М, якщо її повний приріст в цій точці можна подати у
вигляді
![]() , (1)
, (1)
де ![]() та
та ![]() – дійсні числа, які не
залежать від
– дійсні числа, які не
залежать від ![]() та
та ![]() ,
, ![]() – нескінченно малі при
– нескінченно малі при ![]() і
і ![]() функції.
функції.
Відомо, що коли функція однієї змінної диференційовна в деякій точці, то вона в цій точці неперервна і має похідну. Перенесемо ці властивості на функції двох змінних.
Теорема 1 (неперервність диференційовної функції).
Якщо функція ![]() диференційовна
в точці М, то вона неперервна в цій точці.
диференційовна
в точці М, то вона неперервна в цій точці.
Доведення
Якщо функція
диференційовна в точці М, то з рівності (1) випливає, що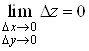 . Це означає, що функція
неперервна в точці М.
. Це означає, що функція
неперервна в точці М.
Теорема 2 (існування частинних похідних
диференційовної функції). Якщо функція ![]() диференційовна в точці
диференційовна в точці ![]() , то вона має в
цій точці похідні
, то вона має в
цій точці похідні ![]() та
та ![]() і
і![]() .
.
Доведення
Оскільки ![]() диференційовна
в точці
диференційовна
в точці![]() ,
то справджується рівність (1). Поклавши в ній
,
то справджується рівність (1). Поклавши в ній![]() , отримаємо,
, отримаємо,
![]() .
.
Поділимо обидві
частини цієї рівності на ![]() і перейдемо до границі при
і перейдемо до границі при![]() :
:
![]() .
.
Отже, в точці ![]() існує частинна
похідна
існує частинна
похідна![]() .
Аналогічно доводиться, що в точці
.
Аналогічно доводиться, що в точці ![]() існує частинна похідна
існує частинна похідна![]() .
.
Твердження,
обернені до теорем 1 і 2, взагалі кажучи, неправильні, тобто із неперервності
функції ![]() або
існування її частинних похідних ще не випливає диференційовність. Наприклад,
функція
або
існування її частинних похідних ще не випливає диференційовність. Наприклад,
функція ![]() неперервна
в точці
неперервна
в точці![]() ,
але не диференційовна в цій точці. Справді, границі
,
але не диференційовна в цій точці. Справді, границі

не існує, тому не
існує й похідної![]() . Аналогічно впевнюємося, що не
існує також похідної
. Аналогічно впевнюємося, що не
існує також похідної![]() . Оскільки задана функція в точці
. Оскільки задана функція в точці ![]() не має частинних
похідних, то вона в цій точці не диференційовна.
не має частинних
похідних, то вона в цій точці не диференційовна.
Більш того, відомо приклади функцій, які є неперервними в деяких точках і мають в них частинні похідні, але не є в цих точках диференційовними.
Теорема 3 (достатні умови диференційовності ).
Якщо функція ![]() має частинні
похідні в деякому околі точки
має частинні
похідні в деякому околі точки ![]() і ці похідні неперервні в точці М,
то функція
і ці похідні неперервні в точці М,
то функція ![]() диференційовна
в точці М.
диференційовна
в точці М.
Доведення
Надамо змінним x
і ![]() приростів
приростів
![]() , таких,
щоб точка
, таких,
щоб точка ![]() належала
даному околу точки
належала
даному околу точки ![]() . Повний приріст функції
. Повний приріст функції ![]() запишемо у
вигляді
запишемо у
вигляді
![]() . (2)
. (2)
Вираз у перших
квадратних дужках рівності (2) можна розглядати як приріст функції однієї
змінної x, а в других – як приріст функції змінної ![]() . Оскільки дана функція має
частинні похідні, то за теоремою Лагранжа отримаємо:
. Оскільки дана функція має
частинні похідні, то за теоремою Лагранжа отримаємо:
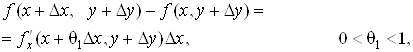
![]() .
.
Похідні ![]() та
та ![]() неперервні в
точці М, тому
неперервні в
точці М, тому
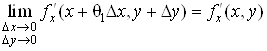 ,
,
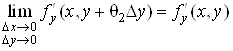 .
.
Звідси випливає, що
![]() ,
,
![]() ,
,
де![]() ,
, ![]() – нескінченно малі
функції при
– нескінченно малі
функції при ![]() і
і![]() .
.
Підставляючи ці вирази у рівність (2), знаходимо
![]() , а це й означає, що функція
, а це й означає, що функція
![]() диференційовна
в точці
диференційовна
в точці![]() .
.
З теорем 2 і 3
випливає такий наслідок: щоб функція ![]() була диференційовною в точці,
необхідно, щоб вона мала в цій точці частинні похідні, і достатньо, щоб вона
мала в цій точці неперервні частинні похідні.
була диференційовною в точці,
необхідно, щоб вона мала в цій точці частинні похідні, і достатньо, щоб вона
мала в цій точці неперервні частинні похідні.
Зазначимо, що для
функції ![]() однієї
змінної існування похідної
однієї
змінної існування похідної ![]() в точці
в точці ![]() є необхідною і достатньою умовою
її диференційовності в цій точці.
є необхідною і достатньою умовою
її диференційовності в цій точці.
3 Повний диференціал функції та його застосування до обчислення функцій і похибок. Диференціали вищих порядків
Нагадаємо, що
коли функція ![]() диференційовна в точці
диференційовна в точці![]() , то її повний
приріст у цій точці можна подати у вигляді
, то її повний
приріст у цій точці можна подати у вигляді
![]() ,
,
де ![]() і
і ![]() при
при![]() .
.
Повним
диференціалом ![]() диференційовної в точці
диференційовної в точці ![]() функції
функції ![]() називається
лінійна відносно
називається
лінійна відносно ![]() та
та ![]() частина повного приросту цієї
функції в точці M, тобто
частина повного приросту цієї
функції в точці M, тобто
![]() . (3)
. (3)
Диференціалами
незалежних змінних x та ![]() назвемо прирости цих змінних
назвемо прирости цих змінних![]() . Тоді з
урахуванням теореми 2 рівність (3) можна записати так:
. Тоді з
урахуванням теореми 2 рівність (3) можна записати так:
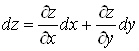 . (4)
. (4)
Аналогічна
формула має місце для диференційовної функції трьох змінних![]() :
:
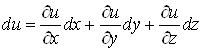 . (5)
. (5)
З формул (4) і
(5) може здатися, що повний диференціал ![]() існуватиме у кожній точці, в якій
існують частинні похідні. Але це не так. Згідно з означенням, повний
диференціал можна розглядати лише стосовно диференційовної функції.
існуватиме у кожній точці, в якій
існують частинні похідні. Але це не так. Згідно з означенням, повний
диференціал можна розглядати лише стосовно диференційовної функції.
Теореми та
формули для диференціалів функції однієї змінної повністю зберігаються і для
диференціалів функцій двох, трьох і т.д. змінних . Так, незалежно від того, від
яких аргументів залежать функції u і ![]() , завжди справедливі рівності
, завжди справедливі рівності
![]()
![]()
![]()
![]()
Покажемо, що
різниця між повним приростом ![]() і диференціалом
і диференціалом ![]() при
при ![]() і
і ![]() є нескінченно мала
величина вищого порядку, ніж величина
є нескінченно мала
величина вищого порядку, ніж величина![]() .
.
Дійсно, з формул (1) і (3) маємо
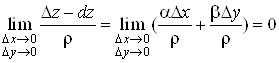 ,
,
оскільки функції ![]() – нескінченно
малі при
– нескінченно
малі при![]() ,
, ![]() , а
, а ![]() та
та ![]() – обмежені
функції:
– обмежені
функції:
 .
.
Отже, різниця ![]() – нескінченно
мала величина вищого порядку, ніж
– нескінченно
мала величина вищого порядку, ніж![]() . Тому повний диференціал
називають також головною частиною повного приросту диференційовної функції. При
цьому виконується наближена рівність
. Тому повний диференціал
називають також головною частиною повного приросту диференційовної функції. При
цьому виконується наближена рівність ![]() або
або
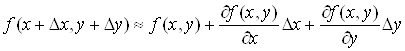 . (6)
. (6)
Ця рівність тим
точніша, чим менша величина![]() . Рівність (6) широко
використовується у наближених обчисленнях, оскільки диференціал функції
обчислюється простіше, ніж повний приріст.
. Рівність (6) широко
використовується у наближених обчисленнях, оскільки диференціал функції
обчислюється простіше, ніж повний приріст.
Покажемо, як за допомогою диференціала можна оцінити похибку в обчисленнях.
Нехай задана
диференційовна функція![]() , незалежні змінні якої виміряні з
точністю
, незалежні змінні якої виміряні з
точністю![]() .
Потрібно знайти похибку, з якою обчислюється u.
.
Потрібно знайти похибку, з якою обчислюється u.
Природно вважати, що ця похибка дорівнює величині
![]() .
.
Для малих значень
![]() маємо
маємо
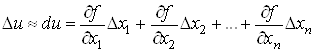 ,
,
звідки
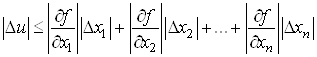 .
.
Якщо через ![]() позначити
максимальну абсолютну похибку змінної
позначити
максимальну абсолютну похибку змінної ![]() , то можна отримати значення
максимальної абсолютної похибки
, то можна отримати значення
максимальної абсолютної похибки ![]() функції
функції ![]() :
:
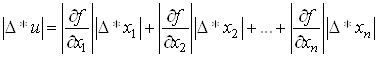 . (7)
. (7)
Щоб оцінити
максимальну відносну похибку функції u, поділимо обидві частини рівності (7) на![]() :
:
 .
.
Оскільки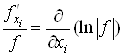 , то
, то
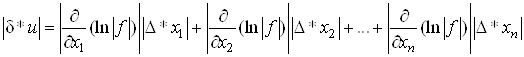 ,
,
або
![]() ,
,
тобто максимальна відносна похибка функції дорівнює максимальній абсолютній похибці її логарифма.
Введемо поняття диференціала вищого порядку.
Нехай ![]() функція
незалежних змінних
функція
незалежних змінних ![]() ,
,![]() . Повний диференціал цієї функції,
знайдений за формулою (3), називають ще диференціалом
. Повний диференціал цієї функції,
знайдений за формулою (3), називають ще диференціалом
першого порядку. Диференціал другого порядку визначають за формулою
![]() .
.
Тоді, якщо
функція ![]() має
неперервні частинні похідні, то
має
неперервні частинні похідні, то
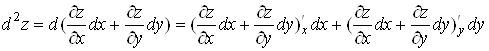 ,
,
звідки
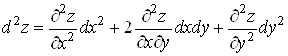 . (8)
. (8)
Символічно це записують так:
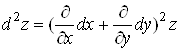 .
.
Аналогічно можна отримати формулу для диференціала третього порядку:
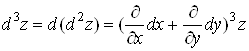 .
.
Застосовуючи метод математичної індукції, можна отримати формулу для диференціала n-го порядку:
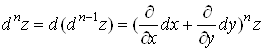 . (9)
. (9)
Зазначимо, що
формула (9) справедлива лише для випадку, коли змінні x і ![]() функції
функції ![]() є незалежними змінними.
є незалежними змінними.
4 Похідна складеної функції. Повна похідна. Інваріантність форми повного диференціала
Нехай ![]() – функція двох
змінних
– функція двох
змінних ![]() та
та
![]() , кожна з
яких, у свою чергу, є функцією незалежної змінної
, кожна з
яких, у свою чергу, є функцією незалежної змінної ![]() :
:
![]()
тоді функція ![]() є складеною
функцією змінної
є складеною
функцією змінної ![]() .
.
Теорема. Якщо функції ![]() диференційовні в точці
диференційовні в точці ![]() , а функція
, а функція ![]() диференційовна в точці
диференційовна в точці ![]() , то складена функція
, то складена функція ![]() також
диференційовна в точці
також
диференційовна в точці ![]() . Похідну цієї
функції знаходять за формулою
. Похідну цієї
функції знаходять за формулою
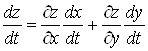 . (10)
. (10)
Доведення
За умовою теореми
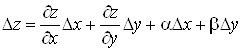 ,
,
де ![]() та
та ![]() при
при![]() ,
,![]() .
.
Поділимо ![]() на
на ![]() і перейдемо до
границі при
і перейдемо до
границі при![]() :
:

Аналогічно
знаходять похідну, якщо число проміжних змінних більше двох. Наприклад, якщо ![]() , де
, де ![]() , то
, то
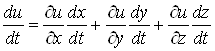 . (11)
. (11)
Зокрема, якщо![]() , а
, а![]() , то
, то
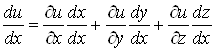 ,
,
а оскільки ![]() , то
, то
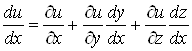 . (12)
. (12)
Цю формулу
називають формулою для обчислення повної похідної
(на відміну від частинної похідної![]() ).
).
Розглянемо
загальніший випадок. Нехай ![]() – функція двох змінних
– функція двох змінних ![]() та
та![]() , які, в свою
чергу, залежать від змінних
, які, в свою
чергу, залежать від змінних ![]() :
:![]() ,
, ![]() , тоді функція
, тоді функція ![]() є складеною функцією
незалежних змінних
є складеною функцією
незалежних змінних ![]() та
та![]() , а змінні
, а змінні ![]() та
та ![]() – проміжні.
– проміжні.
Аналогічно попередній теоремі доводиться таке твердження.
Якщо функції ![]() та
та ![]() диференційовні
в точці
диференційовні
в точці ![]() ,
а функція
,
а функція ![]() диференційовна
в точці
диференційовна
в точці ![]() ,
то складена функція
,
то складена функція ![]() диференційовна в точці
диференційовна в точці ![]() і її частинні
похідні знаходяться за формулами:
і її частинні
похідні знаходяться за формулами:
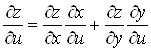 ;
; 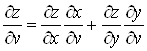 . (13)
. (13)
Формули (13)
можна узагальнити на випадок більшого числа змінних. Якщо![]() , де
, де![]() , то
, то
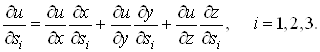
Знайдемо диференціал складеної функції. Скориставшись формулами (13), отримаємо
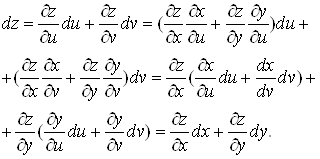
Отже, диференціал
функції![]() ,
де
,
де ![]() ,
, ![]() , визначається
формулою
, визначається
формулою
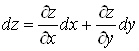 ,
(14)
,
(14)
де
![]() .
.
Порівнявши
формули (14) і (4) дійдемо висновку, що повний диференціал функції ![]() має
інваріантну (незмінну) форму незалежно від того, чи є x та
має
інваріантну (незмінну) форму незалежно від того, чи є x та ![]() незалежними змінними,
чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові
лише за формою, а по суті різні, бо у формулі (4)
незалежними змінними,
чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові
лише за формою, а по суті різні, бо у формулі (4) ![]() і
і![]() – диференціали незалежних змінних,
а у формулі (14)
– диференціали незалежних змінних,
а у формулі (14) ![]() і
і![]() – повні диференціали функцій
– повні диференціали функцій ![]() та
та ![]() .
.
Диференціали
вищих порядків властивості інваріантності не мають. Наприклад, якщо![]() , де
, де ![]() ,
, ![]() , то
, то
 (15)
(15)
Формула (15)
відрізняється від формули (8), оскільки для складеної функції диференціали ![]() та
та ![]() можуть і не
дорівнювати нулю. Отже, для складеної функції
можуть і не
дорівнювати нулю. Отже, для складеної функції![]() , де
, де ![]() ,
, ![]() , формула (8) неправильна.
, формула (8) неправильна.
5 Диференціювання неявної функції
Нехай задано рівняння
![]() , (16)
, (16)
де ![]() – функція двох змінних.
– функція двох змінних.
Нагадаємо, що
коли кожному значенню x з деякої множини ![]() відповідає єдине значення
відповідає єдине значення![]() , яке разом з x
задовольняє рівняння (16), то кажуть, що це рівняння задає на множині
, яке разом з x
задовольняє рівняння (16), то кажуть, що це рівняння задає на множині ![]() неявну функцію
неявну функцію![]() .
.
Таким чином, для
неявної функції![]() , заданої рівнянням (16), має
місце тотожність
, заданої рівнянням (16), має
місце тотожність
![]() .
.
Які ж умови має
задовольняти функція ![]() щоб рівняння (16) визначало
неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема
існування неявної функції [8].
щоб рівняння (16) визначало
неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема
існування неявної функції [8].
Теорема. Нехай функція ![]() і її похідні
і її похідні ![]() та
та ![]() визначені та
неперервні у будь-якому околі точки
визначені та
неперервні у будь-якому околі точки ![]() і
і ![]() , а
, а![]() ; тоді існує окіл точки
; тоді існує окіл точки ![]() , в якому
рівняння
, в якому
рівняння ![]() визначає
єдину неявну функцію
визначає
єдину неявну функцію![]() , неперервну та диференційовну в
околі точки
, неперервну та диференційовну в
околі точки ![]() і
таку, що
і
таку, що ![]() .
.
Знайдемо похідну
неявної функції. Нехай ліва частина рівняння (16) задовольняє зазначені в
теоремі умови, тоді це рівняння задає неявну функцію![]() , для якої на деякій множині точок
x має місце тотожність
, для якої на деякій множині точок
x має місце тотожність![]() . Оскільки похідна функції, що
тотожно дорівнює нулю, також дорівнює нулю, то повна похідна
. Оскільки похідна функції, що
тотожно дорівнює нулю, також дорівнює нулю, то повна похідна![]() . Але за формулою (12)
маємо
. Але за формулою (12)
маємо 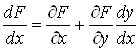 ,
тому
,
тому 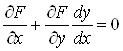 ,
звідки
,
звідки
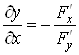 .
(17)
.
(17)
За цією формулою знаходять похідну неявної функції однієї змінної.
| Экономическая система | |
|
1. Эк-я с-ма - ед-во ч-ка и общ-го пр-ва В любой ЭС существует 2 вида отношений: 1-отношение людей к природе; 2. отношение людей друг к другу. В ... Зп = Зм / t'раб * tраб, где Зм - месячная повременная ЗП работника, руб.; tраб - число рабочих часов по графику в данном месяце; t'раб - количество часов, фактически отраб-х ... Преим-ва: созд-ся благопр-е усл-я для внедр-я новой техники, поточного метода орг-ции пр-ва, механизации и автом-ции, сокращ-ся дл-сть цикла. |
Раздел: Рефераты по экономике Тип: шпаргалка |
| Шпоры по предпринимательскому праву | |
|
4. Принципы и система РПП. Принципы ПП - это основополагающие начала, пронизывающие весь массив правовоых норм. Осн. принципы: Принцип свободы ... Принцип признания многообразия форм собс-сти - зак-вом не м.б. устан-ны какие-либо привилегии или ограничения для S2, ведущих предприн. деят-сть 1) это необходимое юр. ср-во ограничения, устанав-щее доп. прав. гарантии нормального функц-ния рыночной экономики и конкуренции 2) оберегает экономику о возможных деформаций ... |
Раздел: Рефераты по праву Тип: реферат |
| Административное право (шпаргалка) | |
|
1. ГОСУДАРСТВЕННОЕ УПР-ИЕ, ПОНЯТИЕ И ОСОБЕННОСТИ Понятие и особ-ти соцупр-ия. Определение упр-ия: 1. Это целенапр-ое орг-щее возд-ие человека на соотв ... ОИВ - это структурное подразделение гос.- властного мех-ма (госаппарата), создаваемое специально для повседневного функц-ия в системе разделения властей с целью проведения в жизнь ... Адм. право и деесп-сть ОИВ возникает одновременно с их образованием и определением компетенции, прекращается в связи с их упразднением. |
Раздел: Рефераты по административному праву Тип: шпаргалка |
| Экзаменационные вопросы по экономике | |
|
1.1. Сферы и подразделения экономики. Сферы экономики Общественное производство подразделяется на две сферы: 1. материальное производство 2 ... АО образ. на основе устава, уставом опред. макс. сумма на кот. м.б. выпущены акции, именуемая УК. и их номин. ст-сть. Рук-во объявл. общую миссию О, цели и страт-кие задачи каждого СХП и функц. подразд. |
Раздел: Рефераты по экономике Тип: шпаргалка |
| Вопросы,ответы и шпоры по специальным дисциплинам | |
|
1.Современные представления о сущности, функциях и роли денег. Современные экономические теории не определяют строго сущность денег. Согласно ... Фин/ мех-зм дел. на:- фин/мех-зм орг-ций; - страх. мех-зм; - мех-зм функци-ния гос/органов;- кредит. политику. ... спец.уполномоч-х на это орг-й.Акционер-е страх-е - негос.орг-я форма, где в качестве страх-ка выступ. частн. кап-ал в виде акц-го общ-ва,уставн/фонд кот.форм-тся из акций (обл.) и ... |
Раздел: Рефераты по экономике Тип: шпаргалка |