Курсовая работа: Определение мольной теплоемкости методом интерполяции
Федеральное агентство по образованию
Федеральное государственное образовательное учреждение
Высшего профессионального образования
"СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ"
Институт космических и информационных технологий
Кафедра системы искусственного интеллекта
КУРСОВАЯ РАБОТА
Тема: ОПРЕДЕЛЕНИЕ МОЛЬНОЙ ТЕПЛОЕМКОСТИ МЕТОДОМ ИНТЕРПОЛЯЦИИ
Красноярск, 2009
Содержание
1. Цели и задачи курсовой работы
2. Теоретические основы курсовой работы
3. Массив исходных данных
4. Математические модели, применяемые для расчетов
5. Результаты расчетов, представляющиеся в виде таблиц и графиков
6. Текст программы
Вывод
Список литературы
1. Цели и задачи курсовой работы
Цель курсовой работы: закрепление навыков работы с языком высокого уровня Си, умение писать на этом языке программы решения технических задач (определение мольной теплоемкости кислорода, c помощью метода интерполяции).
Задача: определение приблизительных значений теплоемкости при температурах от 0 0 С до 1500 0С с шагом Dt=10 0 C, методами интерполяции, позволяющими узнать приблизительные значения функции в промежуточных точках.
2. Теоретические основы курсовой работы
Результаты экспериментов зачастую представляют собой таблицу следующего вида:
| X |
|
|
… |
|
|
|
|
|
… |
|
где Х - это может быть, например, время, а f(X) скорость или, как в нашем примере Х – это температура, а f(X) это теплоемкость.
Из этой таблицы, например, известны значения функции f(X) в
точках х0 и х1, но мы ничего не знаем о ее
значении, например, в точке ![]() ,
однако, существуют методы, позволяющие узнать приблизительные значения функции
в промежуточных точках. К таким методам относятся методы интерполяции.
,
однако, существуют методы, позволяющие узнать приблизительные значения функции
в промежуточных точках. К таким методам относятся методы интерполяции.
Определение 1: Интерполяцией называется отыскание приближенной функции F(X), такой что F(xi)=f(xi), где i=0,1…n, a f(xi) известные значения функции F(X) на отрезке[x0, xn]. Точки, в которых F(xi)=f(xi) называются узлами интерполяции.
Определение 2: Если найденная интерполяционная функция F(X) для отрезка [x0, xn] имеет область определения вне этого отрезка, тогда она будет называться экстраполяцией функции f(x).
Одним из методов интерполяции является метод Интерполяции степенным многочленом
Будем искать интерполяционную функцию F(X) в виде многочлена степени n:
![]() (*)
(*)
Многочлен Pn(x) имеет n+1 коэффициент, следовательно, n+1 условие, наложенное на многочлен однозначно определит его коэффициенты, которые могут быть получены их условия:
![]()
или
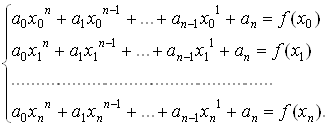
Разрешив эту систему относительно ai (i=0,1…,n), получим аналитическое выражение для полинома (*).
3. Массив исходных данных
Опытным путем найдены данные истинной мольной теплоемкости кислорода m ср при постоянном давлении P=const, при температуре t=0 0 C, t=500 0 C, и t=1000 0 C, представленные таблицей 1.
Таблица 1.
| № варианта |
|
|
|
| 1 | 29.2741 | 33.5488 | 35.9144 |
| 2 | 29.2801 | 33.5501 | 35.9201 |
| 3 | 29.2729 | 33.5493 | 35.9167 |
| 4 | 29.30 | 33.5479 | 35.9251 |
| 5 | 29.2752 | 33.5485 | 35.9109 |
| 6 | 29.2748 | 33.5397 | 35.8999 |
| 7 | 29.2752 | 33.5501 | 35.9123 |
| 8 | 29.2744 | 33.5486 | 35.9128 |
| 9 | 29.2699 | 33.5484 | 35.9251 |
| 10 | 29.2742 | 33.5481 | 35.9109 |
| 11 | 29.2753 | 33.5399 | 35.9201 |
| 12 | 29.2748 | 33.5501 | 35.9167 |
| 13 | 29.2801 | 33.5493 | 35.9144 |
| 14 | 29.2729 | 33.5479 | 35.9201 |
| 15 | 29.2744 | 33.5485 | 35.9123 |
| 16 | 29.2699 | 33.5493 | 35.9128 |
| 17 | 29.2742 | 33.5479 | 35.9251 |
| 18 | 29.2753 | 33.5485 | 35.9109 |
| 19 | 29.2748 | 33.5397 | 35.9128 |
| 20 | 29.2752 | 33.5501 | 35.9251 |
| 21 | 29.2744 | 33.5486 | 35.9201 |
| 22 | 29.2741 | 33.5484 | 35.9167 |
| 23 | 29.2801 | 33.5481 | 35.9144 |
| 24 | 29.2753 | 33.5486 | 35.9201 |
мольный теплоемкость интерполяция программа
В нашем случае рассматриваются данные варианта №5.
№ варианта |
|
|
|
| 5 | 29.2752 | 33.5485 | 35.9109 |
4. Математические модели, применяемые для расчетов
Интерполяционный многочлен m ср=f(t0), будет иметь следующий вид:
![]() ,
,
на основе него составляется система линейных уравнений, разрешив которую относительно коэффициентов a, b, d, получим интерполяционную функцию. Составим для этих данных интерполяционные уравнения:
1.
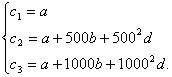
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.![]()
![]()
![]()
y=29,2752+0,0104575*t-0,0000038218*t2
5. Результаты расчетов
| t°,C |
m ср |
t°,C |
m ср |
| 0 | 29.2752 | 400 | 32.8467 |
| 10 | 29.3794 | 410 | 32.9203 |
| 20 | 29.4828 | 420 | 32.9932 |
| 30 | 29.5855 | 430 | 33.0653 |
| 40 | 29.6874 | 440 | 33.1366 |
| 50 | 29.7885 | 450 | 33.2072 |
| 60 | 29.8889 | 460 | 33.2770 |
| 70 | 29.9885 | 470 | 33.3460 |
| 80 | 30.0873 | 480 | 33.4143 |
| 90 | 30.1854 | 490 | 33.4818 |
| 100 | 30.2827 | 500 | 33.5485 |
| 110 | 30.3793 | 510 | 33.6145 |
| 120 | 30.4551 | 520 | 33.6797 |
| 130 | 30.5701 | 530 | 33.7441 |
| 140 | 30.6643 | 540 | 33.8078 |
| 150 | 30.7578 | 550 | 33.8707 |
| 160 | 30.8506 | 560 | 33.9329 |
| 170 | 30.9425 | 570 | 33.9943 |
| 180 | 31.0337 | 580 | 34.0549 |
| 190 | 31.1242 | 590 | 33.1148 |
| 200 | 31.2138 | 600 | 34.1739 |
| 210 | 31.3027 | 610 | 34.2322 |
| 220 | 31.3909 | 620 | 34.2897 |
| 230 | 31.4783 | 630 | 34.3466 |
| 240 | 31.5649 | 640 | 34.4026 |
| 250 | 31.6507 | 650 | 34.4579 |
| 260 | 31.7358 | 660 | 34.5124 |
| 270 | 31.8201 | 670 | 34.5661 |
| 280 | 31.9037 | 680 | 34.6191 |
| 290 | 31.9865 | 690 | 34.6713 |
| 300 | 32.0685 | 700 | 34.7228 |
| 310 | 32.1497 | 710 | 34.7735 |
| 320 | 32.2302 | 720 | 34.8234 |
| 330 | 32.3100 | 730 | 34.8725 |
| 340 | 32.3890 | 740 | 34.9209 |
| t°,C |
m ср |
t°,C |
m ср |
| 750 | 34.9686 | 1150 | 36.2470 |
| 760 | 35.0154 | 1160 | 36.2633 |
| 770 | 35.0615 | 1170 | 36.2788 |
| 780 | 35.1069 | 1180 | 36.2936 |
| 790 | 35.1514 | 1190 | 36.3076 |
| 800 | 35.1952 | 1200 | 36.3208 |
| 810 | 35.2383 | 1210 | 36.3333 |
| 820 | 35.2806 | 1220 | 36.3450 |
| 830 | 35.3221 | 1230 | 36.3559 |
| 840 | 35.3628 | 1240 | 36.3661 |
| 850 | 35.4028 | 1250 | 36.3755 |
| 860 | 35.4420 | 1260 | 36.3842 |
| 870 | 35.4805 | 1270 | 36.3920 |
| 880 | 35.5185 | 1280 | 36.3992 |
| 890 | 35.5551 | 1290 | 36.4055 |
| 900 | 35.5913 | 1300 | 36.4111 |
| 910 | 35.6267 | 1310 | 36.4159 |
| 920 | 35.6613 | 1320 | 36.4200 |
| 930 | 35.6952 | 1330 | 36.4233 |
| 940 | 35.7283 | 1340 | 36.4258 |
| 950 | 35.7607 | 1350 | 36.4276 |
| 960 | 35.7922 | 1360 | 36.4286 |
| 970 | 35.8230 | 1370 | 36.4288 |
| 980 | 35.8531 | 1380 | 36.4283 |
| 990 | 35.8824 | 1390 | 36.4270 |
| 1000 | 35.9109 | 1400 | 36.4250 |
| 1010 | 35.9387 | 1410 | 36.4222 |
| 1020 | 35.9656 | 1420 | 36.4186 |
| 1030 | 35.9919 | 1430 | 36.4142 |
| 1040 | 36.0173 | 1440 | 36.4091 |
| 1050 | 36.0420 | 1450 | 36.4032 |
| 1060 | 36.0660 | 1460 | 36.3966 |
| 1070 | 36.0891 | 1470 | 36.3892 |
| 1080 | 36.1116 | 1480 | 36.3810 |
| 1090 | 36.1332 | 1490 | 36.3721 |
| 1100 | 36.1541 | 1500 | 36.3624 |
| 1110 | 36.1742 | ||
| 1120 | 36.1935 | ||
| 1130 | 36.2121 | ||
| 1140 | 36.2299 |
График:
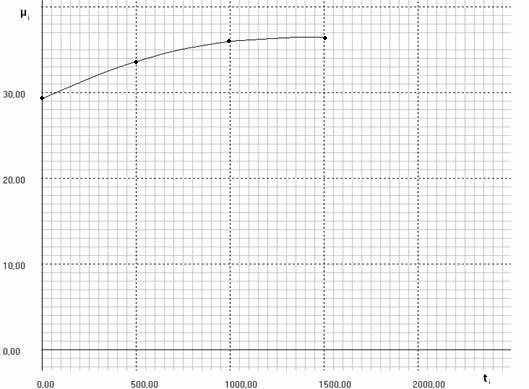
6. Текст программы
#include<stdio.h>
#include<conio.h>
#include<math.h>
float andrey (float c1, float c2, float m);
void main()
{clrscr();
float p1,p2,b,d;
int t1=500,i;
float k1=29.2752,k2=33.5485,k3=35.9109;
p1=(k2-k1)/t1;
p2=(k3-k1)/(2*t1);
d=-(p1-p2)/t1;
b=p1-t1*d;
printf ("\n b=%f",b);
printf ("\n d=%f",d);
andrey (b,d,k1);}
float andrey (float c1,float c2,float m)
{clrscr();
float t[1000];
float y[1000];
int h=10,i;
for (t[0]=0,i=0;i<=150;i++)
{t[i]=t[0]+i*h;
y[i]=m+c1*t[i]+c2*t[i]*t[i];
printf ("\n t[%i]=%7.2f y[%i]=%7.2f",i,t[i],i,y[i]);}
getch();}
Вывод
Данные истинной мольной теплоемкости кислорода m ср ,найденные опытным путем при постоянном давлении P=const, при температуре t=0 0 C, t=500 0 C, и t=1000 0 C, совпали с m ср, найденные мной с помощью языка Си. Значит, метод интерполяции сработал.
Список литературы:
1. Паппас Крис Мюрей. Программирование на языке С++:-К.: Издательская группа BHV, 2000. - 320с.
2. Крячков А.В., Сухинина И.В., Томшин В.К. Программирование на С и С++. Практикум: Учеб. пособие для вузов/ Крячков А.В., Сухинина И.В., Томшин В.К.: Под ред. Томшина – 2-е изд. испр. – М.: Горячая линия – Телеком. 2000 – 344 с.: ил.
3. Подбельский В.В., Фомин С.С. Программирование на языке Си: Учеб. пособие – 2-е доп. изд. – М.: Финансы и статистика, 2000 – 600 с.: ил.
4. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. – 2-е изд., перераб. – М.: Наука, 1970, 432 с.
5. Волков Е.А. Численные методы. – 2-е изд. испр. – М.: Наука, 1987, 248 с.
6. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль – Томск: "РАСКО", 1991, - 272 с.: ил.
7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике.: Учеб. пособ. для втузов. . – 2-е изд., перераб. и доп. – М.: Высш. шк., 1994. – 416 с.
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... (19) K= ...................... =M[X°(X°)T]=[M[Xi°Xj°] Если известны математическое ожидание m(t) и корреляционная функция К(t1,t2) случайной функции Х(t), то всегда можно построить n-мерный вектор математического ожидания многомерной ... |
Раздел: Рефераты по математике Тип: реферат |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... где y есть вектор, содержащий значения функции; x - вектор такой же длины, содержащий те точки (значения аргумента), в которых заданы значения y; вектор xi содержит те точки, в ко ... Find Y = f(X) - Данная панель дает возможность произвести интерполяцию или экстраполя-цию текущей подгонки. |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Matlab | |
|
Министерство образования Республики Беларусь Учреждение образования "Гомельский государственный университет им. Ф. Скорины" Математический факультет ... 1;tic, x=0:1/200:1; [X,Y]=meshgrid(x); M=abs(X+i*Y-.5-i*.5)<1/2; s=sum(M(:)), t1=toc 1;x=1:.1:5; m=length(x); A=toeplitz(exp(x)); ut=sin(x)'; f=A*ut; u=A\f; |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Вычислительная математика | |
|
Содержание Введение Тема 1. Решение задач вычислительными методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2 ... Обозначим эти значения следующим образом: yi = f(xi), i = 0, 1, . , n. Требуется найти такой многочлен P(x) степени m, Пусть функция f(x) дифференцируема n +1 раз на отрезке [a, b], содержащем узлы интерполяции xi I [a, b], i = 0, 1, . , n. Тогда для погрешности интерполяции в точке x I [a, b ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Приложения производной | |
|
Лицей информационных технологий Реферат Производная и ее приложения Выполнил: ученик 11А класса Новиков А. Проверила: Шекера Г.В. г.Хабаровск 2004 ... Из определения выпуклости вверх (вниз) кривой y = f(x) в точке x0 следует, что для любой точки x из интервала (x0 - h, x0 + h), не совпадающей с точкой x0, имеет место неравенство ... 2). Проведем касательные t1 и t2 соответствено в точках A и B к кривой y = f(x). Пусть a и j - углы наклона касательных t1 и t2. |
Раздел: Рефераты по математике Тип: реферат |