Курсовая работа: Задача о коммивояжере и ее обобщения
Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
(ГОУВПО «АмГУ»)
Факультет математики и информатики
Кафедра математического анализа и моделирования
КУРСОВАЯ РАБОТА
на тему: «Задача о коммивояжере и ее обобщения»
по дисциплине «Вариационное исчисление и методы оптимизации»
СОДЕРЖАНИЕ
Введение
1 Постановка задачи
2 Эвристические методы
2.1 Алгоритм Борувки
2.2 Алгоритм Крускала
2.3 Алгоритм Прима
2.4 Вывод
3 Генетический алгоритм
4 NP-полная задача
5 Метод ветвей и границ
6 Практическое применение задачи коммивояжер
Заключение
Библиографический список
ВВЕДЕНИЕ
В 1859 г. Сэр Вильям Гамильтон, знаменитый математик, давший миру теорию комплексного числа и кватерниона, предложил детскую головоломку, в которой предлагалось совершить «круговое путешествие» по 20 городам, расположенных в различных частях земного шара.
Гамильтонова задача о путешественнике нередко преобразуется в задачу о коммивояжере. Коммивояжер – не свободно путешествующий турист, а деловой человек, ограниченный временными, денежными или какими-либо другими ресурсами. Гамильтонова задача может стать задачей о коммивояжере, если каждое из ребер снабдить числовой характеристикой. Это может быть километраж, время на дорогу, стоимость билета, расход горючего и т.д. Таким образом, условные характеристики дадут числовой ряд, элементы которого могут быть распределены между ребрами как угодно.
Задача о коммивояжере относится к классу NP-трудных задач. Методы решения задачи о коммивояжере различны. В данной курсовой кратко рассказывается только о некоторых наиболее известных.
К эвристическим методам решения задачи коммивояжёра следует отнести «жадный» алгоритм, на каждом шаге выбирающий ребро наименьшей стоимости из множества рёбер, не нарушающих корректности решения. Эти методы имеют большую погрешность. Хорошо исследована область генетических алгоритмов, показавших свою эффективность для данной задачи, но они довольно громоздки. Метод перебора прост, но только лишь при небольшом количестве итераций.
И наиболее удобным мне кажется метод ветвей и границ. Его можно применять и при большом количестве городов.
1. ПОСТАНОВКА ЗАДАЧИ
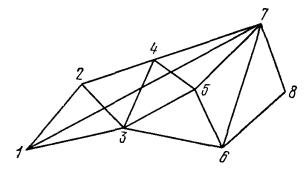
Рис.1
Предположим, что бродячий торговец должен, покинув город, которому присвоим номер 1, объехать еще N – 1 городов и вернутся снова в город номер 1. В его распоряжении есть дороги, соединяющие эти города. Он должен выбрать свой маршрут – порядок посещения городов так, чтобы путь, который ему придется пройти, был как можно короче. Основное условие этой задачи состоит в том, что коммивояжер не имеет права возвращаться снова в этот город, в котором он однажды уже побывал. Это условие будем называть условием (α). Мы считаем, что расстояние между двумя городами – функция f(xi, xj) – определено. Разумеется, функция f(xi, xj) может означать не только расстояние, но, например, время или издержки в пути и т.д. поэтому в общем случае
f(xi, xj) ≠ f(xj, xi),
а функции f(xi, xi) естественно приписать значение ∞. Длина l пути S определяется формулой
![]() (1.1)
(1.1)
Сумма в выражении (1) распространена по всем индексам i и j, удовлетворяющим условию (α), т.е. условию, что каждый из индексов i и j входит в выражение (1) один и только один раз. Функция l = l(x1, …, xN) является, таким образом, аддитивной – она представима в виде суммы слагаемых, однако сама задача – задача отыскания минимума l – в силу ограничения (α) не является аддитивной и не удовлетворяет принципу оптимальности.
Рассмотрим снова плоскость t, x, где t – дискретный аргумент, принимающий значения 0,1, 2, …, N, соответствующие этапам путешествия торговца. Значит t = 0 соответствует его начальному положению в городе номер 1, t = 1 – переходу из города номер 1 в город, который он выбрал первым для посещения, и т.д., t = N означает последний этап его путешествия – возвращение в город номер 1. Аргумент x теперь также принимает дискретные значения 1,2, …, N (Рисунок 1.1). Соединим точку (0, 1) с точками (1,1), (1, 2), …(1, N) и длинам отрезков, соединяющих эти точки, припишем значения f(x1,xj). Далее точки (1, s) – узлы, лежащие на первой вертикали, мы соединим со всеми уздами второй вертикали, длинам отрезков мы припишем значения f(xs, xk) и т.д. точки (N-1, s) соединим с точкой (N,1).
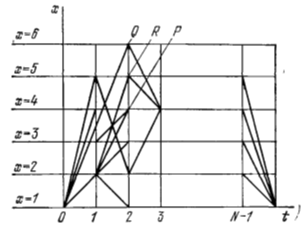
В результате мы построили некоторый граф, каждая ломанная которого, соединяющая точку (0,1) сточкой (N,1), описывает путь коммивояжера. Нашу задачу мы можем теперь сформулировать следующим образом. Среди всех ломанных, принадлежащих этому графу и соединяющих точки (0,1) и (N,1) и удовлетворяющих условию (α), найти ломанную кратчайшей длины. Условие (α) состоит теперь в том, что искомая ломанная пересекает (в узле) каждую из прямых x = i один и только один раз. Таким образом, задача о коммивояжере формулируется более привычным для нас языком.
Рассмотрим узел P, лежащий на третьей вертикали (Рисунок 1.2). Если бы условие (α) отсутствовало, то выбор траектории, которая соединяет точку P с точкой (N, 1), не зависел бы от того пути, который привел нас в точку P. В данном случае ситуация иная, и если два коммивояжера находятся в точке P, но один из них пришел в это состояние, двигаясь вдоль траектории, проходящей через точку Q, а второй через точку R, то их состояния существенно отличаются друг от друга.
Коммивояжер, который двигался по второй траектории , уже побывал в городах номер 2 и номер 5 и в будущем он уже не имеет права снова заезжать в эти города. Что касается коммивояжера, который двигался вдоль первой траектории, то он побывал в городах номер 3 и номер 6; он не имеет права возвращаться в эти города, но зато он еще обязан посетить города номер 2 и номер 5 и т. Д.
Поскольку функция f(xi, xj) определена на конечном множестве точек, то и функция l(х1,…,xN) также определена на конечном множестве точек.
Следовательно, задача определения минимума функции l сводится к перебору некоторого конечного множества значений этой функции, и проблема носит чисто вычислительный характер. Однако именно вычислительные трудности здесь огромны.
Легко подсчитать, что число возможных вариантов (число значений функции l) равно (N — 1)!. Таким образом, непосредственно перебрать и сравнить между собой все возможные пути, по которым может следовать бродячий торговец, для достаточно большого количества городов практически невозможно.
Возникает проблема построения такого метода последовательного анализа вариантов, который выделял бы по возможности большое количество неперспективных вариантов и сводил задачу к перебору относительно небольшого количества «подозрительных» вариантов.
2. ЭВРИСТИЧЕСКИЕ МЕТОДЫ
Решить задачу коммивояжера можно с помощью алгоритма Крускала. Также нам могут помочь алгоритмы Борувки и Прима, так называемые «жадные алгоритмы» Эти методы ускоряют разработку алгоритма по сравнению с методом полного перебора, однако не всегда дают оптимальное решение. Но немного расскажем о них.
Итак, имеется n городов, которые нужно обойти. Для этого достаточно проложить (n-1) путей между городами. Как соединить города так, чтобы суммарная стоимость путешествия была минимальна?
В общем случае, задачу можно сформулировать так. Пусть дан связный, неориентированный граф с весами на ребрах G(V, E), в котором V — множество вершин (городов), а E — множество их возможных попарных соединений (дороги). Пусть для каждого ребра (u,v) однозначно определено некоторое вещественное число w(u,v) — его вес (длина или стоимость пути). W(u,v) называется весовой функцией. Задача состоит в нахождении такого связного ациклического подграфа T ⊂ G, содержащего все вершины, что суммарный вес его ребер будет минимален.
Так как T связен и не содержит циклов, он является деревом и называется остовным или покрывающим деревом. Остовное дерево T, у которого суммарный вес его ребер w(T) = ∑(u,v)∈T w(u,v) минимален, называется минимальным остовным или минимальным покрывающим деревом.
Так как рассматриваются только деревья, можно считать все ребра положительными (достаточно добавить к весу всех ребер некоторую относительно большую положительную константу). В противном случае, если стоимость соединения между двумя вершинами равна отрицательному числу, можно несколько раз параллельно соединить их для уменьшения суммарного веса остовного подграфа.
Также считаем, что для любой пары ребер их весовые характеристики будут различны. Это гарантирует уникальность построенного минимального остовного дерева. Для примера, если все ребра имеют единичный вес, то любое остовное дерево будет минимальным (с суммарным весом v-1, где v – количество вершин в графе).
Искомый остов строится постепенно. Алгоритм использует некоторый ациклический подграф А исходного графа G, который называется промежуточным остовным лесом. Изначально G состоит из n вершин-компонент, не соединенных друг с другом (n деревьев из одной вершины). На каждом шаге в A добавляется одно новое ребро. Граф A всегда является подграфом некоторого минимального остова. Очередное добавляемое ребро e=(u,v) выбирается так, чтобы не нарушить этого свойства: A ∪ {e} тоже должно быть подграфом минимального. Такое ребро называется безопасным.
По определению A, он должен оставаться подграфом некоторого минимального остова после любого числа итераций. Конечно, главный вопрос состоит в том, как искать безопасное ребро. Понятно, что такое ребро всегда существует, если A еще не является минимальным остовом (любое ребро остова, не входящее в A). Заметим, что так как A не может содержать циклов, то на каждом шаге ребром соединяются различные компоненты связности (изначально все вершины в отдельных компонентах, в конце A – одна компонента). Таким образом анализ графа выполняется (n-1) раз.
Далее приводится общее правило отыскания безопасных ребер. Для этого есть теорема, которая поможет находить безопасные ребра.
Теорема: Пусть G(V;E) – связный неориентированный граф и на множестве Е определена весовая функция w. Пусть А – некоторый подграф G, являющийся в то же время подграфом некоторого минимального остовного дерева T. Рассмотрим компоненту связности К из А. Рассмотрим множество E(K) ребер графа G, только один конец которых лежит в К. Тогда ребро минимального веса из E(K) будет безопасным.
В связи с приведенной теоремой введем следующее: безопасным ребром e относительно некоторой компоненты связности К из А назовем ребро с минимальным весом, ровно один конец которого лежит в К.
2.1 АЛГОРИТМ БОРУВКИ
На первом шаге A состоит из всех вершин G и пустого множества ребер. В начале очередной фазы алгоритма Борувки, для каждой компоненты связности промежуточного остовного леса выбирается лидер или корень – вершина, сопоставляемая каждой компоненте. Сделать это можно в простейшем случае с помощью обхода A в глубину: вершина, с которой начинается обход очередной компоненты, и будет ее лидером.
После того, как лидеры выбраны, для каждой компоненты связности находится безопасное для нее ребро, по существу методом грубой силы. Как только все такие ребра отобраны, они добавляются к A. Процесс продолжается до тех пор, пока в A присутствует больше одной компоненты связности.
2.2 АЛГОРИТМ КРУСКАЛА
Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех ребер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Безопасность ребра гарантируется ранее показанной теоремой о безопасных ребрах. Так как ребро является самым легким из всех ребер, выходящих из данной компоненты, оно будет безопасным.
Остается понять, как реализовать выбор безопасного ребра на каждом шаге. Для этого в алгоритме Крускала все ребра графа G перебираются по возрастанию веса. Для очередного ребра проверяется, не лежат ли концы ребра в разных компонентах связности, и если это так, ребро добавляется, и компоненты объединяются.
Удобно использовать для хранения компонент структуры данных для непересекающихся множеств, как, например, списки или, что лучше, лес непересекающихся множеств со сжатием путей и объединением по рангу (один из самых быстрых известных методов). Элементами множеств являются вершины графа, каждое множество содержит вершины одной связной компоненты.
2.3 АЛГОРИТМ ПРИМА
Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгоритма построения минимального остовного дерева: на каждом шаге мы добавляем к строящемуся остову безопасное ребро. Алгоритм Прима относится к группе алгоритмов наращивания минимального остова: на каждом шаге существует не более одной нетривиальной (не состоящей из одной вершины) компоненты связности, и каждый к ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами. По теореме такое ребро является безопасным.
При
реализации надо уметь на каждом шаге быстро выбирать безопасное ребро. Для
этого удобно воспользоваться очередью с приоритетами (кучей). Алгоритм получает
на вход граф G и его корень r – вершина, на которой будет
наращиваться минимальный остов. Все вершины G, еще не попавшие в
дерево, хранятся в очереди с приоритетом Ω. Приоритет вершины v
определяется значением key[v],
которое равно минимальному весу ребер, соединяющих v с вершинами
минимального остова. Поле p[v]
для вершин дерева указывает на родителя, а для вершин из очереди, указывает на
остов дерева, в которою ведет ребро с весом key[v]
(одно из таких ребер, если их несколько).
2.4 ВЫВОД
В завершение рассказа о жадных алгоритмах приведу пример. Рассмотрим небольшую «детскую» задачу. Допустим, что у нас есть монеты достоинством 25, 10, 5 копеек и 1 копейка и нужно вернуть сдачу 63 копейки. Почти не раздумывая, мы преобразуем эту величину в две монеты по 25 копеек, одну монету в 10 копеек и три монеты по одной копейке. Нам не только удалось быстро определить перечень монет нуясного достоинства, но и, по сути, мы составили самый короткий список монет требуемого достоинства.
Алгоритм, которым мы в этом случае воспользовались, заключался в выборе монеты самого большого достоинства (25 копеек), но не больще 63 копеек, добавлению ее в список сдачи и вычитанию ее стоимости из 63 (получается 38 копеек). Затем снова выбираем монету самого больщого достоинства, но не больще остатка (38 копеек): этой монетой опять оказывается монета в 25 копеек. Эту монету мы опять добавляем в список сдачи, вычитаем ее стоимость из остатка и т.д.
Этот метод внесения изменений называется «жадным» алгоритмом. На каждой отдельной стадии «жадный» алгоритм выбирает тот вариант, который является локально оптимальным в том или ином смысле. Обратите внимание, что алгоритм для определения сдачи обеспечивает в целом оптимальное рещение лищь вследствие особых свойств монет. Если бы у нас были монеты достоинством 1 копейка, 5 и 11 копеек и нужно было бы дать сдачу 15 копеек, то «жадный» алгоритм выбрал бы сначала монету достоинством 11 копеек, а затем четыре монеты по одной копейке, т.е. всего пять монет. Однако в данном случае можно было бы обойтись тремя монетами по 5 копеек.
И все приведенные выше алгоритмы являются «жадными».
Следует подчеркнуть, что не каждый «жадный» алгоритм позволяет получить оптимальный результат в целом. Как нередко бывает в жизни, «жадная стратегия» подчас обеспечивает лишь сиюминутную выгоду, в то время как в целом результат может оказаться неблагоприятным.
Существуют задачи, для которых ни один из известных «жадных» алгоритмов не позволяет получить оптимального решения; тем не менее имеются «жадные» алгоритмы, которые с большой вероятностью позволяют получать «хорошие» решения. Нередко вполне удовлетворительным можно считать «почти оптимальное» решение.
3. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ
Генетический алгоритм — это алгоритм, который позволяет найти удовлетворительное решение к аналитически неразрешимым проблемам через последовательный подбор и комбинирование искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «кроссовера», который производит операцию, роль которой аналогична роли скрещивания в живой природе. «Отцом-основателем» генетических алгоритмов считается Джон Холланд, книга которого «Адаптация в естественных и искусственных системах» является основополагающим трудом в этой области исследований.
Задача кодируется таким образом, чтобы её решение могло быть представлено в виде вектора («хромосома»). Случайным образом создаётся некоторое количество начальных векторов («начальная популяция»). Они оцениваются с использованием «функции приспособленности», в результате чего каждому вектору присваивается определённое значение («приспособленность»), которое определяет вероятность выживания организма, представленного данным вектором. После этого с использованием полученных значений приспособленности выбираются вектора (селекция), допущенные к «скрещиванию». К этим векторам применяются «генетические операторы» (в большинстве случаев «скрещивание» - crossover и «мутация» - mutation), создавая таким образом следующее «поколение». Особи следующего поколения также оцениваются, затем производится селекция, применяются генетические операторы и т. Д. Так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий останова алгоритма. Таким критерием может быть: нахождение глобального, либо субоптимального решения; исчерпание числа поколений, отпущенных на эволюцию; исчерпание времени, отпущенного на эволюцию. Генетические алгоритмы служат, главным образом, для поиска решений в очень больших, сложных пространствах поиска.
Таким образом, можно выделить следующие этапы генетического алгоритма:
создание начальной популяции;
вычисление функций полезности для особей популяции (оценивание);
выбор индивидов из текущей популяции (селекция);
скрещивание и\или мутация;
вычисление функций полезности для всех особей;
формирование нового поколения;
если условия совпали, то решение найдено (конец цикла), если нет, то цикл повторяется.
Применяются генетические алгоритмы для решения следующих задач:
оптимизация функций, разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний), настройка и обучение искусственной нейронной сети, задачи компоновки, составление расписаний, игровые стратегии, аппроксимация функций, искусственная жизнь, биоинформатика (свёртывание белков).
4. NP-ПОЛНАЯ ЗАДАЧА
Все эффективные (сокращающие полный перебор) методы решения задачи коммивояжёра — методы эвристические («жадные алгоритмы»). В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы так называемые any-time алгоритмы, то есть постепенно улучшающие некоторое текущее приближенное решение.
Задача коммивояжёра есть NP-полная задача. Часто на ней проводят обкатку новых подходов к эвристическому сокращению полного перебора.
В теории алгоритмов NP-полные задачи — это класс задач, лежащих в классе NP (то есть для которых пока не найдено быстрых алгоритмов решения, но проверка того, является ли данное решение правильным, проходит быстро), к которым сводятся все задачи класса NP.
Назовём языком множество слов над алфавитом Σ. Задачей здесь является определение того, принадлежит данное слово языку или нет. Язык L1 называется сводимым (по Карпу) к языку L2, если существует функция, вычислимая за полиномиальное время, обладающая следующим свойством: f(x) принадлежит L2 тогда и только тогда, когда x принадлежит L1. Язык L2 называется NP-трудным, если любой язык из класса NP сводится к нему. Язык называют NP-полным, если он NP-труден и при этом сам лежит в классе NP. Таким образом, если будет найден алгоритм, решающий хоть одну NP-полную задачу за полиномиальное время, все NP-задачи будут лежать в классе P.
Равенство классов P и NP уже более 30 лет является открытой проблемой. Научное сообщество склоняется к отрицательному решению этого вопроса — в этом случае за полиномиальное время решать NP-полные задачи не удастся.
5. МЕТОД ВЕТВЕЙ И ГРАНИЦ
Существует метод решения задачи коммивояжера, который дает оптимальное решение. Этот метод называется методом ветвей и границ.
Основа этого, ныне широко распространенного метода состоит в построении нижних оценок решения, которые затем используются для отбраковки неконкурентоспособных вариантов.
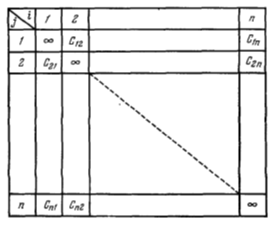
Функция f(xi, xj) принимает конечное число значений сij, которые мы можем представить в виде таблицы (Рисунок 5.1). Предположим, что мы выбрали некоторый путь Ss. Его длина будет равна
![]() (5.1)
(5.1)
причем сумма (5.1) распространена по i, j так, что каждый из индексов встречается в ней один и только один раз. Величины сij с двумя одинаковыми индексами мы приняли равными ∞.
Так как в каждый из вариантов s входит только один элемент из каждой строки и столбца, то мы можем проделать следующую операцию, которая здесь называется приведением матрицы. Обозначим через hi наименьший элемент из строки номера i и построим новую матрицу С(1) с элементами
![]()
Матрица С(1) определяет новую задачу коммивояжера, которая, однако, в качестве оптимальной будет иметь ту же последовательность городов. Между величинами ls и ls(1) будет существовать, очевидно, следующая связь:
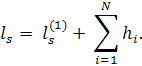
Заметим, что в каждой из строк матрицы С(1) будет теперь, по крайней мере, один нулевой элемент. Далее обозначим через gj наименьший элемент матрицы С(1), лежащий в столбце номера j, и построим новую матрицу С(2) с элементами
![]()
Величины hi и gj называются константами приведения. Оптимальная последовательность городов для задачи коммивояжера с матрицей С(2) будет, очевидно, такой же, как и для исходной задачи, а длины пути для варианта номера s в обоих задачах будут связаны между собой равенством
![]() (5.2)
(5.2)
где
![]() (5. 3)
(5. 3)
т. Е. d0 равна сумме констант приведения.
Обозначим через l* решение задачи коммивояжера, т.е.
![]()
где минимум берется по всем вариантам s, удовлетворяющим условию (α) Тогда величина d0 будет простейшей нижней оценкой решения:
![]() (5.4)
(5.4)
Будем рассматривать теперь задачу коммивояжера с матрицей С(2) которую мы будем называть приведенной матрицей.
Рассмотрим путь, содержащий непосредственный переход из города номера i в город номера j, тогда для пути s, содержащего этот переход, мы будем иметь, очевидно, следующую нижнюю оценку:
![]()
Следовательно, для тех переходов, для которых ![]() = 0, мы будем иметь снова оценку (5.4). Естественно ожидать, что
кратчайший путь содержит один из таких переходов — примем это соображение в
качестве рабочей гипотезы. Рассмотрим один из переходов, для которого
= 0, мы будем иметь снова оценку (5.4). Естественно ожидать, что
кратчайший путь содержит один из таких переходов — примем это соображение в
качестве рабочей гипотезы. Рассмотрим один из переходов, для которого ![]() =0, и обозначим через
=0, и обозначим через ![]() множество всех тех путей, которые не содержат перехода из i в j.
множество всех тех путей, которые не содержат перехода из i в j.
Так как из города i мы должны куда-то выйти, то
множество ![]() содержит один из переходов i→k, где k ≠ j; так как в город номера j мы должны прийти, то
множество
содержит один из переходов i→k, где k ≠ j; так как в город номера j мы должны прийти, то
множество ![]() содержит переход m→j, где т ≠ i.
содержит переход m→j, где т ≠ i.
Следовательно, некоторый путь ls из множества (ij), содержащий переходы i→k и m→j, будет иметь следующую нижнюю оценку:
![]()
Обозначим через
![]()
Тогда очевидно, что для
любого ls из множества путей ![]() мы будем иметь оценку
мы будем иметь оценку
![]() (5.5)
(5.5)
Мы предполагаем исключить некоторое множество вариантов ![]() ,
поэтому мы заинтересованы выбрать такой переход i → j, для которого оценка (5.5) была бы самой высокой. Другими
словами, среди нулевых элементов матрицы С(2) выберем
тот, для которого
,
поэтому мы заинтересованы выбрать такой переход i → j, для которого оценка (5.5) была бы самой высокой. Другими
словами, среди нулевых элементов матрицы С(2) выберем
тот, для которого ![]() максимально.
Это число обозначим через
максимально.
Это число обозначим через ![]() Таким
образом, все множество возможных вариантов мы разбили на два множества I1 и I2. Для путей из множества I1, мы имеем оценку (5.4). Для
путей из множества I2 оценка будет следующей:
Таким
образом, все множество возможных вариантов мы разбили на два множества I1 и I2. Для путей из множества I1, мы имеем оценку (5.4). Для
путей из множества I2 оценка будет следующей:
![]() (5.6)
(5.6)
Рассмотрим теперь множество I1 и матрицу С(2). Так как все пути, принадлежащие этому множеству, содержат переход i → j , то для его исследования нам достаточно рассмотреть задачу коммивояжера, в которой города номеров i и j совпадают. Размерность этой задачи будет уже равна N – 1, а ее матрица получится из матрицы С(2) вычеркиванием столбца номера j и строки но мера i.
Поскольку i → j невозможен, то элемент ![]() принимаем равным бесконечности.
принимаем равным бесконечности.
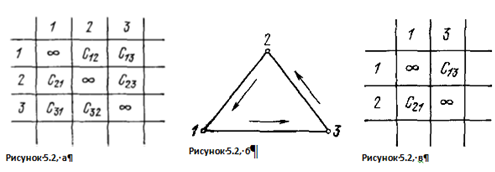
Рассмотрим случай N=3 (Рисунок 5.2, а), и предположим, что мы рассматриваем тот вариант, который содержит переход 3 → 2. Тогда задача коммивояжера после вычеркивания третьей строки и второго столбца вырождается в тривиальную. Ее матрица изображена на рисунке 5.2, в. В этом случае мы имеем единственный путь, и его длина будет, очевидно, равна сумме
![]()
Итак, если в результате вычеркивания строки номера i и столбца номера j мы получим матрицу второго порядка, то задачу можно считать решенной.
Пусть теперь N >3. После вычеркивания мы получим матрицу порядок
N -1 > 2.
С этой матрицей (N — 1)-го порядка совершим процеурру
приведения. Матрицу, которую таким образом получим, обозначим через С(3),
а через d(1) – сумму ее констант
приведения. Тогда для ls ![]() I1, мы будем иметь оценку
I1, мы будем иметь оценку
![]() (5.7)
(5.7)
На этом первый шаг алгоритма закончен. В результате одного шага мы разбили множество всех возможных вариантов на два множества I1 и I2 и для путей, принадлежащих этим множествам, мы получили оценки (5.7) и (5.6) (Рисунок 5.3)
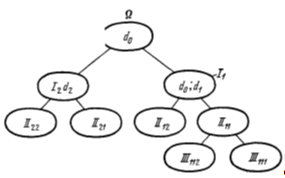
Рис.5.3
Введем понятие стандартной операции, которую мы будем обозначать
символом ![]() Этим
термином мы назовем процедуру разбиения произвольного множества вариантов Ω
с приведенной матрицей N – п-го порядка С(n + 2) и оценкой dω на два множества. Одно из
этих множеств состоит из всех тех путей, которые содержат переход из города
номер s в город номер l и имеют нижнюю оценку d . Другое множество состоит из всех путей, не содержащих этого
перехода и имеющих в качестве нижней оценки число dk. Стандартную операцию можно представить в форме следующей
блок-схемы (см. Рисунок 5.4).
Этим
термином мы назовем процедуру разбиения произвольного множества вариантов Ω
с приведенной матрицей N – п-го порядка С(n + 2) и оценкой dω на два множества. Одно из
этих множеств состоит из всех тех путей, которые содержат переход из города
номер s в город номер l и имеют нижнюю оценку d . Другое множество состоит из всех путей, не содержащих этого
перехода и имеющих в качестве нижней оценки число dk. Стандартную операцию можно представить в форме следующей
блок-схемы (см. Рисунок 5.4).
задача коммивояжер решение алгоритм обобщение
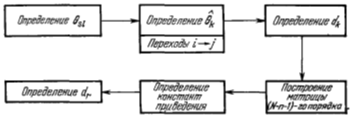
Рисунок 5.4
Итак, первый шаг метода ветвей и границ состоит в проведении стандартной операции над исходным множеством Ω. На следующем шаге мы продолжаем развивать дерево возможных вариантов. Сначала мы сравниваем две оценки d1 и d2 и для последующего анализа выбираем то из множеств I1 или I2, для которого соответствующая оценка меньше.
Предположим, что
d1 < d2;
тогда над множеством I1 с матрицей С(3) мы совершим стандартную операцию. В результате мы разобьем множество возможных вариантов I1 на два подмножества II11 и II12, первое из которых содержит некоторый переход i1 → j1 а другое содержит все пути, не имеющие непосредственною перехода из города i1 в город j1. Еще раз повторим рассмотренную выше процедуру: для каждого из нулевых элементов матрицы С(3) построим число
![]()
Определим значение
![]()
и элемент матрицы С(3),
для которого достигается это значение. Если ls ![]() II12, то
II12, то
![]() (5.8)
(5.8)
Затем в матрице С(3) вычеркиваем строку номера i1 и столбец номера j1, полагаем ![]() и
над полученной матрицей совершаем операцию приведения. В результате мы найдем
новые константы приведения. Их сумму обозначим через d(II) и в заключение находим
оценку d11 для элементов множества II11.
и
над полученной матрицей совершаем операцию приведения. В результате мы найдем
новые константы приведения. Их сумму обозначим через d(II) и в заключение находим
оценку d11 для элементов множества II11.
Если ls ![]() II11, то
II11, то
![]() (5.9)
(5.9)
На этом второй шаг алгоритма ветвей и границ закончен. Мы разбили множество вариантов I1 на два множества, II11 и II12, и для элементов этих множеств получили нижние оценки (5.9) и (5.8), соответственно.
Теперь мы должны сравнить оценку (5.9) с оценкой (5.6) для элементов множества I2, которое мы исключили из рассмотрения на предыдущем шаге. Если окажется, что d2 > d11,
то мы переходим к третьему шагу, который состоит в применении стандартной операции к множествуII11. (Если размерность матрицы при этом равна двум, то, как мы видели выше, процесс заканчивается.)
Если окажется, что d11 > d2, то множеством вариантов с
оптимальной нижней оценкой будет множество I2. Другими словами, теперь будем предполагать, что наиболее
короткий путь содержится среди элементов множества I2 — множества всех вариантов, не содержащих перехода i → j. Следовательно, матрица,
характеризующая это множество, получается из матрицы С(2)
заменой величины ![]() на ∞.
Над этим множеством мы производим стандартную операцию и разбиваем его на два
множества II21 и II22 с оценками d21 и d22, соответственно. Одновременно мы выделяем переход k→l, который содержит все варианты множества II21. Затем мы снова сравниваем все оценки d11, d12, d21 и d22 и выбираем то из множеств, для которого оценка будет наименьшей.
Над выбранным множеством совершаем стандартную операцию и т. Д. Так мы
продолжаем до тех пор, пока очередная матрица не будет иметь порядок (2x2). В
этом случае, как мы видели, расчет заканчивается — мы получаем задачу
коммивояжера для двух городов (Рисунок 5.5), и длина единственного маршрута
будет
на ∞.
Над этим множеством мы производим стандартную операцию и разбиваем его на два
множества II21 и II22 с оценками d21 и d22, соответственно. Одновременно мы выделяем переход k→l, который содержит все варианты множества II21. Затем мы снова сравниваем все оценки d11, d12, d21 и d22 и выбираем то из множеств, для которого оценка будет наименьшей.
Над выбранным множеством совершаем стандартную операцию и т. Д. Так мы
продолжаем до тех пор, пока очередная матрица не будет иметь порядок (2x2). В
этом случае, как мы видели, расчет заканчивается — мы получаем задачу
коммивояжера для двух городов (Рисунок 5.5), и длина единственного маршрута
будет ![]()
Итак, мы получили некоторую цепочку (ветвь) переходов, длину которой мы вычислили. Сам порядок построения этой цепочки показывает, что ее длина — наименьшая среди всех ветвей дерева, изображенного на рисунке 5.3.
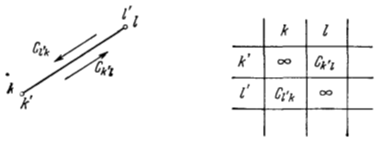
Рисунок 5.5
6. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ЗАДАЧИ КОММИВОЯЖЕРА
Задача коммивояжера имеет ряд практических применений. Как следует из самого названия задачи, ее можно использовать для составления маршрута человека, который должен посетить ряд пунктов и, в конце концов, вернуться в исходный пункт. Например, задача коммивояжера использовалась для составления маршрутов лиц, занимающихся выемкой монет из таксофонов. В этом случае вершинами являются места установки таксофонов и "базовый пункт". Стоимостью каждого ребра (отрезка маршрута) является время в пути между двумя точками (вершинами) на маршруте.
Задача о производстве красок. Имеется производственная линия для производства n красок разного цвета; обозначим эти краски номерами 1,2… n. Всю производственную линию будем считать одним процессором.. Будем считать также, что единовременно процессор производит только одну краску, поэтому краски нужно производить в некотором порядке. Поскольку производство циклическое, то краски надо производить в циклическом порядке (j1,j2,..,jn,j1). После окончания производства краски i и перед началом производства краски j надо отмыть оборудование от краски i. Для этого требуется время C[i,j]. Очевидно, что C[i,j] зависит как от i, так и от j, и что, вообще говоря,C[i,j] ≠ C[j,i]. При некотором выбранном порядке придется на цикл производства красок потратить время, где tk - чистое время производства k-ой краски (не считая переналадок). Однако вторая сумма в правой части постоянна, поэтому полное время на цикл производства минимизируется вместе с общим временем на переналадку.
Таким образом, задачи коммивояжера и задача о минимизации времени переналадки – это просто одна задача, только варианты ее описаны разными словами.
Задача о дыропробивном прессе. Дыропробивной пресс производит большое число одинаковых панелей – металлических листов, в которых последовательно по одному пробиваются отверстия разной формы и величины. Схематически пресс можно представить в виде стола, двигающегося независимо по координатам x, y, и вращающегося над столом диска, по периметру которого расположены дыропробивные инструменты разной формы и величины. Каждый инструмент присутствует в одном экземпляре. Диск может вращаться одинаково в двух направлениях (координата вращения z). Имеется собственно пресс, который надавливает на подвешенный под него инструмент тогда, когда под инструмент подведена нужная точка листа. Операция пробивки j-того отверстия характеризуется четверкой чисел (xj,yj,zj,tj),, где xj,yj- координаты нужного положения стола, zj - координата нужного положения диска и tj -время пробивки j-того отверстия.
Производство панелей носит циклический характер: в начале и конце обработки каждого листа стол должен находиться в положениях (x0, y0) диск положении z0 причем в этом положении отверстие не пробивается. Это начальное состояние системы можно считать пробивкой фиктивного нулевого отверстия. С параметрами (x0,y0,z0,0). Чтобы пробить j-тое отверстие непосредственно после i-того необходимо произвести следующие действия:
1. Переместить стол по оси x из положения xi в положение xj, затрачивая при этом время t(x)(|xi-xj|)=ti,j(x);
2. Проделать то же самое по оси y, затратив время ti,j(y);
3. Повернуть головку по кратчайшей из двух дуг из положения zi в положение zj, затратив время ti,j(z);
4. Пробить j-тое отверстие, затратив время tj.
Конкретный вид функций t(x), t(y), t(z) зависит от механических свойств пресса и достаточно громоздок. Явно выписывать эти функции нет необходимости. Действия 1-3 (переналадка с i-того отверстия j-тое) происходит одновременно, и пробивка происходит немедленно после завершения самого длительного из этих действий. Поэтому С[i,j] = max(t(x), t(y), t(z)). Теперь, как и в предыдущем случае, задача составления оптимальной программы для дыропробивного пресса сводится к задачи коммивояжера (здесь - симметричной).
Еще одним применением задачи коммивояжера является задача обхода доски шахматным конем: надо найти последовательность ходов, которые позволят коню обойти все поля шахматной доски, попадая на каждое поле лишь один раз, и вернуться, в конце концов, на исходное поле. В этом случае роль вершин графа выполняют поля шахматной доски. Предполагается также, что ребра между двумя полями, которые являются "составными частями" хода коня, имеют нулевой вес; все остальные ребра имеют вес, равный бесконечности. Оптимальный маршрут имеет нулевой вес и должен быть маршрутом коня. Читатель, возможно, удивится, узнав, что поиск маршрутов коня с помощью хороших эвристических алгоритмов для задачи коммивояжера вообще не составляет проблемы, в то время как поиск "вручную" является весьма непростой задачей.
ЗАКЛЮЧЕНИЕ
Задача коммивояжера является частичным случаем гамильтоновой задачи о путешественнике. Суть задачи коммивояжера состоит в нахождении суммарной минимальной характеристики (расстояния, стоимости проезда и т.д.), при этом коммивояжер должен пройти все n городов по одному разу, вернувшись в тот город, с которого начал.
Существуют несколько методов решения задачи коммивояжера: метод полного перебора, «жадные» методы (Крускала, Прима, и т.п.), генетические алгоритмы и еще множество их обобщений. Однако только метод ветвей и границ дает нам в итоге самое оптимальное решение.
В основе метода ветвей и границ лежит следующая идея если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева).
Задача о коммивояжере имеет множество обобщений и методы её решения в различных проявлениях используются на практике.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 Моисеев Н.Н. Методы оптимизации: Моисеев Н.Н., Иванилова Ю.П., Столярова Е.М.-М., 1978, 352 с;
2 Черноусько Ф.Л. Вариационные задачи механики и управления: Численные методы/ Черноусько Ф.Л., Баничук Н.В.-М.,1973;
3 http://dic.academic.ru/;
4 http://www.lobanov-logist.ru/index.php?newsid=470;
5 http://swsys.ru/index.php?page=article&id=827;
6 http://e-maxx.ru/algo/mst_prim;
7 http://www.dissercat.com/content/nekotorye-zadachi-marshrutizatsii-i-raspredeleniya-zadanii-metod-dinamicheskogo-programmirov;
8 www.vecon.ru.
| Эйлеровы и гамильтоновы графы | |
|
Министерство народного образования Республики Дагестан Дагестанский Государственный Университет Курсовая работа Программирование задач на графах ... Пусть [cij] - матрица весов ребер G. Используя алгоритм нахождения кратчайшей цепи, образуем |X-|*|X-| - матрицу D=[dij], где dij - вес цепи наименьшего веса, идущей из некоторой ... Возьмём произвольную пару вершин j,k. Исключим непосредственное ребро D[j,k]. С помощью алгоритма Дейкстры найдём кратчайшее расстояние между городами j,.,k. Пусть это расстояние ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Нахождение кратчайшего пути | |
|
... заочного и послевузовского обучения Курсовой проект По дисциплине: "Технология программирования" Тема: "Определение кратчайшего пути в графе" Воронеж ... Для конечных графов, т. е. для графов с конечным множеством вершин и ребер, как правило, проблема существования алгоритма решения задач, в том числе экстремальных, решается ... Расстояния D[v] от фиксированной вершины s до всех остальных вершин v V, фиксированная вершина t, матрица весов ребер, A[u, v], u, v V. |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Алгоритм раскраски графа (точный) | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра САПР Пояснительная записка к курсовому проекту по ... Наибольшему полному подграфу графа G=(Х,U) соответствует наибольшее ВУП в графе G=(Х,U), где Uполн\U, Uполн - множество ребер полного графа, построенного на n вершинах. К приближенный алгоритмам раскраски относятся алгоритмы, основанные на упорядочивании множества вершин графов , последовательном удалении из графа вершин, имеющих максимальную ... |
Раздел: Рефераты по математике Тип: курсовая работа |
| Разработка системы задач (алгоритмы-программы) по дискретной ... | |
|
... прикладной математики Курсовая работа по информатике Тема: Разработка системы упражнений и задач (алгоритмы-программы) по дискретной математике Определим граф как конечное множество вершин V и набор Е неупорядоченных и упорядоченных пар вершин и обозначим G=(V,E). Мощности множеств V и Е будем обозначать буквами N и М ... Пусть мы находим кратчайший путь из i в j с промежуточными вершинами из множества [1..(m+1)]. Если этот путь не содержит вершину (m+1), то D(m+1)[i,j]=Dm[i,j]. Если же он содержит ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Нечеткие множества в системах управления | |
|
В. Я. Пивкин, Е. П. Бакулин, Д. И. Кореньков Нечеткие множества в системах управления Под редакцией доктора технических наук, профессора Ю.Н ... Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с получаемыми при общепринятых алгоритмах управления. В случае конечных или счетных универсальных множеств очевидна интерпретация нечеткого отношения в виде нечеткого графа, в котором пара вершин (xi,xj) в случае XRX соединяется ... |
Раздел: Рефераты по логике Тип: реферат |