Реферат: Определение параметров материалов по данным рентгенографии
Лабораторная работа “”
Цель работы: ознакомление с методами исследования материалов электроники и идентификации кристаллических веществ по рентгенограммам.
МЕТОДЫ ИССЛЕДОВАНИЯ МОНОКРИСТАЛЛОВ
Метод неподвижного кристалла. Основы метода. В этом методе неподвижный кристалл освещается неоднородным пучком рентгеновских лучей (лучами со сплошным спектров). Если кристалл имеет явно выраженные грани, пучок лучей пропускают в направлении какой-нибудь из кристаллографических осей или осей симметрии кристалла.
Получающаяся дифракционная картина регистрируется на фотопластинке, помещенной перпендикулярно к направлению первичного луча на расстоянии 30—50 мм от кристалла.
|
|
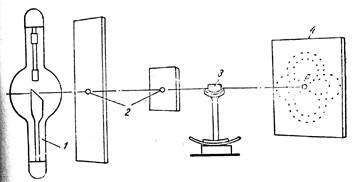
Принципиальная схема метода дана на рисунке слева; 1- рентгеновская трубка, 2 - диафрагма, 3 - кристалл, 4 - фотопластинка. Когда пучок неоднородных лучей падает на кристалл, каждая атомная плоскость отражает лучи соответствующей длины волны (согласно уравнению Вульфа-Брегга). В результате такого селективного (выборочного) отражения рентгеновских лучей отдельными плоскостями на фотопластинке получается .ряд интерференционных пятен различной интенсивности. Происхождение этих пятен для одного из семейств плоскостей иллюстрируется на рис.1.
Расположение интерференционных пятен на рентгенограмме зависит от размеров и формы элементарной ячейки, от симметрии кристалла и его ориентировки относительно первичного пучка лучей. Так как во время съемки кристалл остается неподвижным, то элементы симметрии (плоскости), параллельные направлению первичного пучка, непосредственно проектируются на рентгенограмму, иными словами, симметрия в расположении пятен рентгенограммы отражает симметрию кристалла в направлении просвечивания.
Это обстоятельство не нуждается в особом пояснении, так как совершенно очевидно, что симметричному расположению атомных плоскостей соответствует симметричное расположение отраженных лучей, а следовательно, и интерференционных пятен на рентгенограмме.
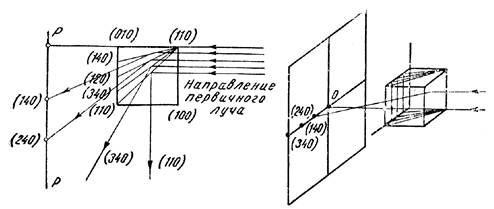
Рис. 1. Схема, поясняющая происхождение пятен на рентгенограмме, полученной по методу неподвижного кристалла
Иллюстрацией может служить рентгенограмма, приведенная на рис. 2, полученная с кристалла гексагональной системы при просвечивании в направлении гексагональной оси . На рисунке видим, что .в расположении пятен наблюдается симметрия шестого порядка относительно центрального пятна, что отвечает симметрии гексагонального кристалла в направлении оси С6. Таким образом, рентгенограмма, полученная по методу неподвижного кристалла, выявляет прежде всего симметрию кристалла.
Всякое изменение в ориентировке кристалла сказывается на изменении соответствующей дифракционной картины. Таким образом, несколько рентгенограмм, полученных в разных направлениях, позволяют сделать суждение о симметрии' кристалла.
|
|
Рис. 2. Рентгенограмма гексагонального кpисталла, полученная при просвечивании в направлении оси шестого порядка.
Каждому интерференционному пятну на рентгенограмме отвечает определенное положение отражающей плоскости с соответствующими индексами. Установление этих индексов позволяет в ряде случаев судить о кристаллической структуре исследуемого вещества, так как для каждого-типа кристаллической структуры существует своя система индексов.
Применение метода. В настоящее время метод неподвижного кристалла применяют главным - образом для определения ориентировки кристаллов и их симметрии. Кроме того, этот .метод используют для определения дефектов кристаллической структуры, возникающих в процессе роста или деформации кристаллов при исследования процессов рекристаллизации и старения металлов.
МЕТОДЫ ИССЛЕДОВАНИЯ ПОЛИКРИСТАЛЛИЧЕСКИХ МАТЕРИАЛОВ
а) Обычный метод исследования поликристаллического вещества (метод порошка)
1. Общие основы метода. При обычном методе исследования поликристаллических материалов тонкий столбик из измельченного порошка или другого мелкозернистого материала освещается узким пучком рентгеновских лучей с определенной длиной волны. Картина дифракции лучей фиксируется на узкую полоску фотопленки, свернутую в виде цилиндра, по оси которого располагается исследуемый образец. Сравнительно реже применяется съемка на плоскую фотографическую пленку.
|
|
|
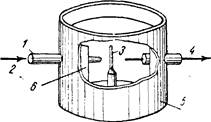
Рис. 3 Принципиальная схема съемки по методу порошка: / — диафрагма: 2 — место входа лучей; 3 — образец: 4 — место выхода лучей; 5 — корпус камеры; б — (фотопленка) |
Принципиальная схема метода дана на рис. 3. Когда пучок .монохроматических лучей падает на образец, состоящий из множества мелких кристалликов с разнообразной ориентировкой, то в образце всегда найдется известное количество кристалликов, которые будут расположены таким образом, что некоторые группы плоскостей будут образовывать с падающим лучом угол Q, удовлетворяющий условиям отражения.
Однако в различных кристалликах рассматриваемые плоскости отражения, составляя один и тот же угол Q с направлением первичного луча, могут быть по-разному повернуты относительно этого луча, в результате чего отраженные лучи, составляя с первичным лучом один и тот же угол 2 Q, будут лежать в различных плоскостях. Поскольку все виды ориентации кристалликов одинаково вероятны, то отраженные лучи образуют конус, ось которого совпадает с направлением первичного луча.
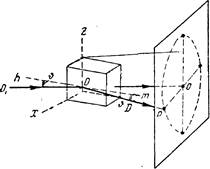
Для того чтобы более детально разобраться в возникновении конусов дифракционных лучей и в образовании соответствующей дифракционной картины, обратимся к следующей модели. Выделим из большого количества кристалликов исследуемого образца один хорошо образованный кристалл. Пусть грань (100) этого кристалла (рис. 4) образует с направлением первичного луча как раз требуемый угол скольжения Q. В этих условиях от плоскости произойдет отражение, и отклоненный луч даст на фотопластинке, помещенной перпендикулярно направлению первичного луча, почернение в некоторой точке Р. Будем далее поворачивать кристалл вокруг направления первичного луча (O1O) таким образом, чтобы падающий луч все время составлял с плоскостью отражения (100) угол Q (это может быть достигнуто, если линию тп, лежащую в плоскости отражения, поворачивать так вокруг направления O1O, чтобы она описывал конус, образуя все время с направлением угол Q). Тогда отраженный луч опишет конус, осью которого является первичный луч (O1O), и угол при вершине равен 4 Q. При непрерывном вращении кристалла след отраженного луча на фотопластинке опишет непрерывную кривую в виде окружности (кольца).
Если в кристалле имеется другое семейство плоскостей с соответствующим межплоскостным расстоянием d1, составляющих с первичным лучом необходимый угол отражения Q1, то при повороте кристалла на фотопластинке получится новое кольцо и т. д. Таким образом, при соответствующем поворачивании кристаллика вокруг направления первичного луча на фотопластинке получается система концентрических кругов (колец), с центром в точке выхода первичного луча.
Каждое такое кольцо в общем случае является отражением лучей с определенной длиной волны l от системы плоскостей с индексами (hkl). Если падающий пучок лучей не строго монохроматичен (что обычно всегда имеет место, так как используются характеристические лучи К-серии) и содержит в своем составе несколько длин волн, то для одного и того же семейства параллельных плоскостей на рентгенограмме получится соответствующее число близлежащих колец. Будем ли мы поворачивать один кристалл вокруг направления первичного луча или расположим вокруг этого луча множество мелких, различно ориентированных кристалликов, картина отражения будет совершенно одинаковой. В этом случае различные положения кристалликов пол и кристаллического образца будут как бы соответствовать определенным положениям поворачиваемого нами кристалла — эта идея и положена в основу метода порошков.
|
|
Рис. 4. Схема, поясняющая образование конусов дифракции
Стремление зафиксировать отражения от плоскостей под различными углами привело к применению вместо плоской фотопластинки, позволяющей улавливать отражения в очень ограниченном диапазоне углов, узкой полоски фотопленки, свернутой в в виде цилиндра и почти целиком окружающей образец. При съемке на такую пленку при пересечении конусов дифракционных лучей на пленке получаются неполные кольца (рис. 5), т. е. ряд дуг, расположенных симметрично относительно центра.
![]()
Рис. 5. Рентгенограмма порошка
При малых углах Q получающиеся линии близки к кругам, а для конуса с углом 4 Q =180° они становятся прямыми. Для углов Q, больших 45°, линии меняют направление радиуса кривизны. Число линий, получающихся на рентгенограмме, зависит от структуры кристаллического вещества и длины волны применяемых лучей. В случае сложной структуры и коротковолнового излучения число линий может быть очень велико.
Линии рентгенограммы имеют различную интенсивность и ширину. Интенсивность этих линий определяется числом и расположением атомов в элементарной ячейке и их рассеивающей способностью, а распределение интенсивности вдоль самих линий, т. е. структура линий (точечная, сплошная — равномерное и неравномерное почернение вдоль линий) зависит от размеров отдельных кристалликов и их ориентировки. Если кристаллики расположены беспорядочно, а их размеры (линейные) меньше 0,01—0,002 мм, линии на рентгенограмме получаются сплошными. Кристаллики большого размера дают на рентгенограмме линии, состоящие из отдельных точек, так как в этом случае число различных положений плоскостей при той же величине освещаемого участка недостаточно для образования непрерывно зачерненной линии.
Если отдельные кристаллы, образующие поликристаллы, имеют преимущественную ориентировку (холоднотянутая проволока, прокатанная полоса и т д.), то на линиях вдоль кольца обнаруживаются характерные максимумы почернения. Часто анализ расположения этих максимумов позволяет выявлять соответствующие закономерности в ориентировке кристалликов поликристаллического вещества. Ширина линий рентгенограммы зависит от размеров отдельных кристалликов, диаметра образца и поглощения в нем рентгеновских лучей. При очень малых размерах кристалликов от 10-6 см. и меньше линии расширяются, причем чем меньше размеры кристалликов, тем больше расширение линий. Основываясь на этой зависимости, по ширине интерференционных линий можно определить средние размеры отдельных кристалликов.
Расстояние между соответствующими симметричными, линиями на рентгенограмме определяется углом при вершине конуса дифракционных лучей и положением пленки относительна исследуемого образца. Эти величины связаны следующим простым соотношением:
| 2L = 4R • Q . |
( Расстояние между симметричными линиями на рентгенограмме, как дуга окружности, равно радиусу окружности R, умноженному на соответствующий центральный угол 4 Q, т. е. угол при вершине конуса дифракционных лучей.) 2L—расстояние между симметричными линиями, измеренное по' экваториальной лилии рентгенограммы; R—радиус цилиндрической фотопленки; Q —угол скольжения (в радианах).
Выражая угол в градусах, получим:
Q0=2L.57,4/4R (#)
Формула (#) является одной из основных расчетных формул, применяемых при расчете рентгенограмм порошков. По этой формуле, зная радиус цилиндрической пленки и расстояние между линиями на рентгенограмме, можно определить угол скольжения, а по нему, используя уравнение Вульфа-Брэгга, соответствующее расстояние между плоскостями и периоды кристаллической решетки исследуемого вещества.
Для вычисления периодов решетки удобно пользоваться преобразованной формой уравнения Вульфа-Брэгга, заменяя в уравнении межплоскостное расстояние d, выраженное через соответствующие значения периодов решетки и индексы плоскостей. В результате получим следующие расчетные уравнения :
1) для кубических кристаллов: sin2 Q=(h2+k2+l2)l2/(4a2);
2) для тетрагональных кристаллов: sin2 Q=((h2+k2)/a2+l2/c2)l2/4;
3) для гексагональных кристаллов: sin2 Q=(4(h2+hk+k2)/(3a2)+l2/c2)l2/4;
4) для кристаллов ромбической системы: sin2 Q=(h2/a2+k2/b2+l2/c2)l2/4;
Для отражений первого порядка (при n=1) числа hkl в указанных уравнениях соответствуют индексам отражающей плоскости. Для отражений высших порядков эти числа будут отличаться от индексов плоскости на некоторый общий множитель, равный порядку отражения, т. е. получаются путем умножения индексов отражающей плоскости на порядок отражения.
Элементарный анализ приведенных формул .позволяет сделать ряд весьма важных практических выводов.
1. Чем больше длина волны применяемых лучей, тем дальше от центра располагаются линии, соответствующие отражениям. от одних и тех же плоскостей одного и того же кристалла. Правильность такого утверждения вытекает из того факта, что большим длинам волн будут соответствовать большие углы скольжения,. а при увеличении последних, согласно уравнению (#), увеличивается расстояние между линиями на рентгенограмме. Таким образом, длина волны применяемых лучей является весьма важным фактором, определяющим построение самой рентгенограммы. Снимая рентгенограммы с одного и того же вещества на разных. излучениях, мы никогда не получим тождественной картины. Полученные рентгенограммы будут отличаться одна от другой и по положению линий и по числу их. На рентгенограммах, полученных на излучении с большими длинами волн, число этих линий будет меньше, и, наоборот, при съемке рентгенограмм на коротковолновом излучении число линий возрастает.
2. С увеличением индексов плоскостей отражения соответствующие им линии будут располагаться дальше от центра рентгенограммы, так как с увеличением индексов увеличивается угол отражения, а следовательно, и расстояние между линиями на рентгенограмме.
3. Чем менее симметрична кристаллическая решетка, тем больше линий получается на рентгенограмме. Если взять, например, высокосимметричную простую кубическую решетку, то для всех шести граней куба, имеющих индексы (100), (010), (001) и симметрично расположенные плоскости с отрицательными индексами, на .рентгенограмме получится одно кольцо (определяемое парой симметричных дуг), т.к. всем этим значениям индексов для одного порядка отражения будет соответствовать одно значение угла Q, а следовательно, и одно определенное значение 2L. В этом случае говорят, что такие плоскости структурно равноценны (эквивалентны). Число структурно эквивалентных плоскостей называется множителем повторяемости.
Совершенно очевидно, что чем больше множитель повторяемости для плоскостей определенного типа, тем интенсивнее соответствующие линии на рентгенограмме.
Таким образом, на рентгенограмме поликристаллического образца с кубической решеткой, вследствие совпадения отражений от нескольких структурно эквивалентных плоскостей, получаются сравнительно малочисленные, но зато очень интенсивные линии. Чем ниже симметрия кристалла, тем на его рентгенограмме больше линий, интенсивность же этих линий будет меньше.
Только что рассмотренные закономерности в построении рентгенограмм относятся к простым решеткам.
Если решетка кристалла сложная (объемноцентрированная - ОЦК или гранецентрированная - ГЦК), то в ней появляется ряд промежуточных плоскостей, причем отражения от этих плоскостей могут гасить отражения от основных плоскостей кристалла. Так, в ОЦК решетке будут давать отражения только те плоскости, для которых сумма индексов - четна. Для ГЦК решетки отражения возможны лишь тогда, когда индексы интерференции или все четные или все нечетные. Из этого следует, что для ОЦК решетки квадраты синусов углов относятся как простые четные числа: 2:4:6:8....., а для ГЦК: 3:4:8:11:12:16:19:20..., в последнем случае линии располагаются неравномерно и часто группируются парами. В примитивной решетке это отношение представляет собой натуральный ряд чисел.
Расчет и расшифровка рентгенограмм.
Конечной целью работы по структурному рентгеноанализу является определение формы и размеров элементарной кристаллической ячейки исследуемого вещества и размещения атомов внутри этой ячейки.
Однако непосредственно по рентгенограмме порошков эти вопросы можно достаточно успешно решить только для кристаллов, принадлежащих к кубической системе, и с некоторым трудом и не всегда достоверно—для кристаллов тетрагональной и гексагональной систем. Для кристаллов низших сингоний эти задачи нельзя разрешить при помощи метода порошков.
Расшифровку и расчет рентгенограммы вещества с известной структурою обычно ведут в такой последовательности:
1. Нумеруют все линии рентгенограммы, начиная от центра рентгенограммы, причем симметричные дуги одного и того же интерференционного кольца обозначаются одним тем же номером.
2. Оценивают интенсивность линии; оценивают интенсивность на глаз, по степени их почернения: очень сильная, сильная, средняя, слабая и очень слабая.
3. Масштабной линейкой измеряют расстояния между симметричными линиями рентгенограммы. Промеряют линии вдоль экваториальной линии рентгенограммы, за которую условно принимается прямая, разделяющая пополам (по ширине) экспонированную часть рентгенограммы.
4. Вычисляют интерференционные углы Q для всех линий рентгенограммы по формуле (#). При съемке в стандартной камере (2R=57,4 мм) выраженный в градусах искомый угол численно равен половине измеренного в миллиметрах расстояния между линиями на рентгенограмме. Для найденных углов Q вычисляют sin Q.
7. Находят квадраты синусов этих углов.
8. Индицируют рентгенограмму.
При индицировании необходимо иметь в виду, что при применении нефильтрованного излучения К-серии характеристических лучей на рентгенограммах для одной и той же плоскости всегда будут появляться две группы линий: сильные линии, отвечающие Ka -излучению, и более слабые (приблизительно в 5— 6 раз) —Кb.
Индицирование рентгенограмм кристаллов кубической системы. Одновременно с индицированием рентгенограммы устанавливается тип кристаллической ячейки кубическое кристалла (простая, ОЦК, или ГЦК). Для этого следует рассмотреть отношения sin2 Q для линий одного и того же излучения. (см. пред. Раздел.)
Отличать эти ячейки друг от друга можно следующим образом: для ОЦК ячейки , отношение sinQ2 к sinQ1 равно 2, а для ГЦК - 4/3.
Для получения этого соотношения необходимо взять отношение sin2 Q, вычисленное по квадратичным формулам для соответствующих длин волн для индексов hkl.
После того как тип решетки установлен, всем линиям можно приписать индексы, используя известное правило, что индексы интерференции (точнее, сумма квадратов и.ндексов h2 + k2 +l2) увеличиваются от линии к линии по мере их удаления от центра, причем для решетки ОЦК возможны отражения с индексами, сумма которых есть число четное; для ГЦК—все три индекса одновременно четные или нечетные числа.
Таким образом, например, для кристаллов с ГЦК решеткой первая Ка. линия на рентгенограмме имеет индексы (111), следующая (200) и т. д. Следует, однако, иметь в виду, что в некоторых сложных решетках, построенных из неидентичных атомов (например, решетки химических соединений, упорядоченных твердых растворов), могут появляться дополнительные линии, отвечающие другим индексам отражения.
Индицирование рентгенограмм кристаллов гексагональной и тетрагональной систем. Для гексагональных и тетрагональных кристаллов при расшифровке рентгенограмм пользуются главным образом графическим методом индицирования, основанным на использовании специальных графиков номограмм.
Ниже в качестве примера приводится расчет рентгенограммы, данный на рис. 5, полученной с порошка алюминия в стандартной камере с диаметром 2R=57,4 мм на медном излучении:
lKa =1,539нм; lKb=l,389 Диаметр образца 2r= 0,5 мм.
В соответствии с изложенным ранее порядком расчета нумеруем линии, оцениваем их интенсивность (на глаз) и измеряем расстояния между линиями. Результаты промера рентгенограммы и данные об интенсивности соответствующих линий заносим в графы 2 и 3 табл. 1. В данном случае промер рентгенограммы производился масштабной линейкой по наружным краям линий.
По этим данным вычисляем по формуле (#) углы скольжения Q0, а затем и sin Q и sin Q. Эти величины для каждой линии занесены в графах 4, 5, 6. Получив таким образом значения синусов для различных линий рентгенограммы и учитывая их интенсивность и взаимное расположение, можно далее разделить линии, принадлежащие Кa и Кb -излучениям. Известно, что отношение квадратов синусов для любой пары линий, соответствующих Кa и Кb -излучению для одних и тех же индексов интерференции., равно отношению квадратов соответствующих длин волн, т. е., в данном случае 1,23. Если взять первую пару линий, лежащих вблизи от центра, и подсчитать отношение квадратов синусов, получится:
sin2 Q2: sin2 Q1 =0,112: 0,092 =1,22 ( Некоторое несоответствие теоретическому значению отношения объясняется ошибками при промере рентгенограмм).
Таким образом, первые две линии рентгенограммы; соответствуют отражениям Кa. и Kb—лучей от одной и той же плоскости (пока с неизвестными индексами), причем ближайшая к центру линия отвечает Kb-излучению, более дальняя—Ka. Правильность такого заключения подтверждается также данными об интенсивности линий (линия Кb имеет меньшую интенсивность). Испытывая таким образом вторую и третью пару линий, получим: sin2 Q4: sin2 Q3 =1,22, sin2 Q6: sin2 Q5 = 1,21
Следовательно, линии 4 и 6 отвечают Кa, -излучению, линии 3 и 5 — Кb .
Однако далее такая закономерность в чередовании линий нарушается. Так, например, для линий 7 и 8 это отношение будет равно: sin2 Q8: sin2 Q7 = 1,10, т. е. линии не являются отражениями от одной плоскости.
Для комбинации линий 7 и 9 это условие вновь выполняется: sin2 Q9: sin2 Q7 = 1,24.
Следовательно, линия 7 отвечает Кb -излучению, линия 9 — Ka -излучению и т.д. В графе 7 табл. 1 линии, отвечающие различным излучениям, отмечены соответствующими значками.
Рассматривая далее отношение квадратов синусов для одного и того же излучения, можно определить в простейших случаях тип кристаллической структуры исследуемого вещества.
Составляя такое отношение для линий Кa, получим:
sin2 Q2: sin2 Q4 :sin2 Q6: sin2 Q9 =0,112:0,144:0,292:0,399. . .=3:4:8:11. . . .
Следовательно, алюминий имеет решетку ГЦК. Воспользовавшись табл.2, не трудно далее расставить и индексы линий.
Начнем индицирование с линий Кa. В ГЦК решетке ближайшая к центру рентгенограммы линия 2 будет иметь индексы (111), следующая за ней линия 4— (002) и т. д., в порядке возрастания индексов по мере удаления линий от центра. Соответствующие им линии Кb имеют одинаковые индексы. Индексы всех линий рентгенограммы даны в графе табл. 2.
После указанных выше операций промера и расшифровки рентгенограммы переходим непосредственно к вычислению периода решетки. Проведем в качестве образца подобный расчет на примере некоторых линий рентгенограммы.
Линия 2. Из расчетной формулы следует, что
a=lKa(h2+k2+l2)1/2/(2sin Q)=3,98 ![]()
Таблица 1
К расчету рентгенограммы алюминия
| N | Интенсивность | 2L, мм |
Q0 |
sin Q |
sin2 Q |
hkl |
период решетки, |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
1 2 3 4 5 6 7 8 9 10 11 |
слабая сильная слабая сильная слабая сильная слабая очень слабая сильная средняя очень слабая |
35,5 38,5 40,5 45 59,0 65,5 70 73,5 78,5 82,5 88 |
17045` 19042` 20012` 22024` 29030` 32042` 34050` 36036` 39012` 41012` 43048` |
0,304 0,336 0,345 0,380 0,492 0,540 0,566 0,595 0,632 0,658 0,693 |
0,092 0,112 0,119 0,144 0,242 0,292 0,320 0,354 0,399 0,438 0,480 |
111b 111a 002b 002a 022b 022a 113b 222b 113a 222a 004b |
3,98 4,05 4,02 4,04 4,05 |

Рис. 5. Рентгенограмма алюминия:
а — излучение меди; 6 — излучение железа
Задание: по рентгенограмме определить тип кристаллической решетки исследуемого образца, параметры элементарной ячейки, материал образца. Обосновать результаты.
Литература
1.Б.Н. Арзамасов, А.И. Крашенников, Ж.П. Пастухова, А.Г. Рахштадт. Научные основы материаловедения. -М., МВТУ, 1994
2. М.П. Шаскольская. Кристаллография. - М., Высшая школа, 1984
3. И.И. Новиков, Г.Б Строганов, А.И. Новиков. Металловедение, термообработка и рентгенография. - М., МИСиС, 1994
Табл.2
Возможные индексы интерференции для кристаллов кубической системы
__________________________________________________________________
|
Индексы интерференции |
h2+k2+l2 |
Возможные индексы интерференции | ||
| hkl | примитивная | ОЦК | ГЦК | |
|
_____________ 001 011 111 002 012 112 022 122, 003 013 113 222 023 213 004 |
_____________________ 1 2 3 3 5 6 8 9 10 11 12 13 14 16 |
_____________________ 001 011 111 002 012 112 022 122, 033 013 113 222 023 213 004 |
_____________________ - 011 - 002 - 112 022 - 013 - 222 - 213 004 |
_____________________ - - 111 002 - - 022 - - 113 222 - - 004 |
Табл.3
Длины волн К-серии излучения для некоторых металлов, применяемых в
качестве анодов в рентгеновских трубках.
| Анод | Длины волн, нм | |
| (материал) | Кa-средняя | Kb-средняя |
|
хром железо кобальт никель медь молибден вольфрам |
0,22909 0,19373 0,17902 0,16568 0,15418 0,07107 0,02114 |
0,2081 0,1754 0,1618 0,1498 0,1391 0,0631 0,0185 |
| Структурный анализ системы | |
|
Министерство образования Республики Беларусь Учреждение образования "Брестский государственный университет имени А.С. Пушкина" Физический факультет ... Микроскопически - кристалл может быть описан как кристаллическая решетка, т.е. правильно периодически повторяющаяся система точек (центров тяжести частиц, слагающих кристалл ... В этих условиях от плоскости произойдет отражение, и отклоненный луч даст на фотопластинке, помещенной перпендикулярно направлению первичного луча, почернение в некоторой точке Р ... |
Раздел: Рефераты по физике Тип: курсовая работа |
| Твердые кристаллы | |
|
... И УПРАВЛЕНИЯ ПЕРСОНАЛОМ СПЕЦИАЛЬНОСТЬ: МЕНЕДЖМЕНТ СПЕЦИАЛИЗАЦИЯ: УПРАВЛЕНИЕ ПЕРСОНАЛОМ К У Р С О В А Я Р А Б О Т А НА ТЕМУ: ТВЕРДЫЕ КРИСТАЛЛЫ Гениально предвычислив все законы симметрии структуры кристаллов задолго до того, как существование атомных решеток в кристаллах было доказано на опыте, Федоров считал несомненным ... Рентгенограммы кристаллических веществ и их расшифровка на основе федоровских законов построения пространственной решетки позволяют судить о симметрии кристаллических структур. |
Раздел: Рефераты по геологии Тип: реферат |
| Кристаллы в природе | |
|
Содержание ВВЕДЕНИЕ 3 Тепловые и механические свойства твёрдых тел I. Симметрия кристаллов 1.1 Как растут кристаллы 5 1.2 Идеальная форма кристаллов 7 ... В кристаллах можно найти различные элементы симметрии: плоскость симметрии, ось симметрии, центр симметрии. Специалист по этой рентгенограмме легко определит порядок симметрии той оси в кристалле, которая расположена параллельно рентгеновским лучам, и рассчитает ряд параметров ... |
Раздел: Рефераты по физике Тип: реферат |
| Использование компьютерных технологий в изучении наглядной геометрии | |
|
Введение Преподавание геометрии не может обойтись без наглядности. В тесной связи с наглядностью обучения находится и его практичность. Ведь именно из ... уметь применять свойства движений для распознавания фигур, в которые переходят данные фигуры при движении, строить точки и простейшие фигуры, симметричные данным относительно ... Отметьте на плоскости точку О. Постройте фигуру центрально-симметричную данной, взяв за центр симметрии отмеченную точку О. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Симметрия в неживой природе | |
|
ВВЕДЕНИЕ 1 1. ЗАГЛЯНЕМ В СЛОВАРЬ 3 2. ВИДЫ СИММЕТРИЙ 4 3. АСИММЕТРИЯ ВНУТРИ СИММЕТРИИ 7 4. СИММЕТРИЯ В ГЕОЛОГИИ 8 4.1. ЛЕГЕНДЫ РУДОКОПОВ 9 4.2 ... Рассматривая решетки Браве внимательней и пробуя мысленно построить из них кристаллы, мы, вероятно, увидим, как можно провести в них плоскости и оси симметрии. Анализ элементов симметрии в каждой из осевых систем кристаллических решеток приводит к возникновению 32 классов симметрии. |
Раздел: Рефераты по геологии Тип: реферат |