Реферат: Задача остовных деревьев в k–связном графе
begin
s_1[v]:=i2;inc(v);
end;
if v=3 then
begin
a2:=data[s_1[1]].x1;d2:=data[s_1[1]].y1;
a1:=data[s_1[2]].x1;d1:=data[s_1[2]].y1;
a:=round((sqr(a1)+sqr(d1)-sqr(a2)-sqr(d2))/(2*(a1+d1-a2-d2)));
b:=a;
R:=sqrt(sqr(a2-a)+sqr(d2-b));
image2.canvas.pen.color:=clblue;
image2.Canvas.arc(round(a-R),round(a-R),round(a+R),round(a+R),a1,d1,a2,d2);
v:=1;
end;
end;end;
//*******vybor vershin************************************
procedure TForm1.ComboBox1Change(Sender: TObject);
begin
if combobox1.ItemIndex = 0 then
Graph
else
begin
newselect(combobox1.ItemIndex);
duga(combobox1.ItemIndex); end;
end;
end.
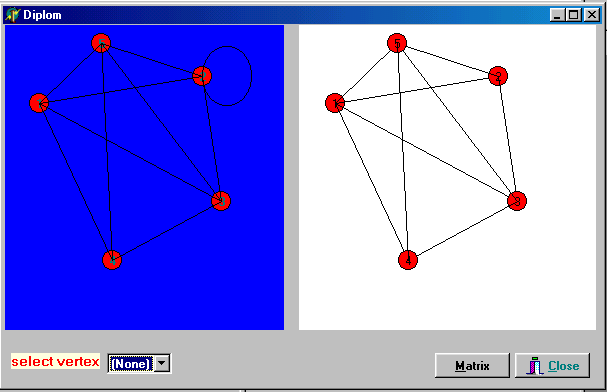
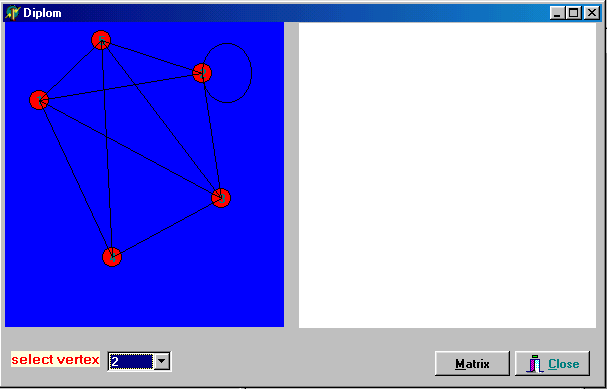
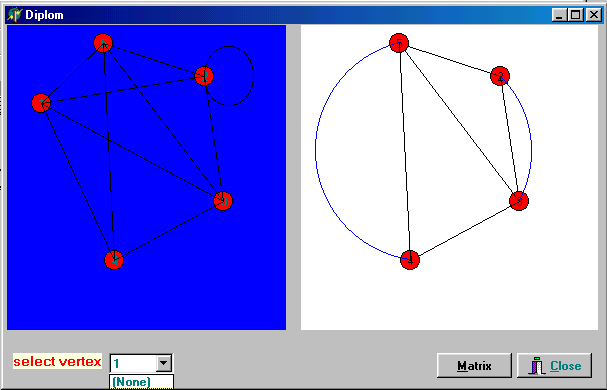
Вывод Целью моей дипломной работы была исследовать задачу на построение разреза в графе по вершине z. Был разработан алгоритм, который строит разрез по заданому графу. По данному алгоритму была написанна программа. Алгортм заключался в следующем: задается граф, по нем строится матрица смежности. В матрице суммируется строка и если при делении на два остаток от деления равен нулю, тогда данную вершину удаляют, а те вершины которые были смежные с ней соединяются между собой.
| Графы. Решение практических задач с использованием графов (С++ | |
|
Курсовая работа Выполнил: студент 1-го курса факультета КНиИТ, группа № 121, Жучков Андрей Сергеевич Саратовский государственный университет им. Н.Г ... Эксцентриситетом вершины v в связном графе G(V,E) называется максимальное расстояние от вершины v до других вершин графа G. Теорема 8. Если данный граф является связным и имеет 2k вершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному ... |
Раздел: Рефераты по математике Тип: реферат |
| Основы дискретной математики | |
|
Федеральное агентство по образованию Новомосковский институт (филиал) Государственного образовательного учреждения высшего профессионального ... у вершины v два сына; в этом случае находим в левом поддереве вершины v наибольший элемент b, рекурсивно удаляем из этого поддерева вершину, содержащую b, и присваиваем вершине v ... Для графа это означает, что если существует ребро (a, b) и ребро (b, c), то существует ребро (a, c). Такой граф называется связным. |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Исследования в современном управлении | |
|
СОДЕРЖАНИЕ 1. ИССЛЕДОВАНИЯ В СОВРЕМЕННОМ УПРАВЛЕНИИ.. 5 1.1 Предпосылки исследования систем управления.. 5 1.2 Системный анализ как средство ... В дальнейшем под деревом взаимосвязей будем понимать связный, неориентированный граф, вершины которого интерпретируются как элементы дерева, а ребра - как связи между ними. Множество ребер R={rjiz} графа G обозначают взаимосвязи между элементами, из которых выходит ребро, и элементами, в которые оно входит. j - номер элемента i-го уровня, из которого ... |
Раздел: Рефераты по менеджменту Тип: учебное пособие |
| Эйлеровы и гамильтоновы графы | |
|
Министерство народного образования Республики Дагестан Дагестанский Государственный Университет Курсовая работа Программирование задач на графах ... Пусть мы достигли некоторой вершины v, начав с вершины u, v = u. Удалив ребра пути из v в u, видим, что оставшийся граф G1 связен и содержит ровно две нечетных вершины v и u ... Если вершина xѭ сочетается с другой вершиной xѭ, то определим цепь ѭѭѭ наименьшего веса (из xѭ в xѭ), соответствующую весу dѭѭ, делая шаг 1. Добавим искусственные ребра в G ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Орграфы, теория и применение | |
|
Федеральное агентство по образованию РФ Государственное образовательное учреждение высшего профессионального образования "Санкт-Петербургский ... Граф G=(V,E) связен тогда и только тогда, когда множество го вершин нельзя разбить на два непустых подмножества V1 и V2 так, чтобы бе граничные точки каждого ребра находились в ... Орграф, называемый конъюнкцией D=Dl/\D2 двух орграфов Z)j и D2, имеет в качестве множества вершин K=V1XV2, и вершина u=(u1, ы2) смежна к вершине v=(v-L,v2) тогда и только тогда ... |
Раздел: Рефераты по математике Тип: реферат |