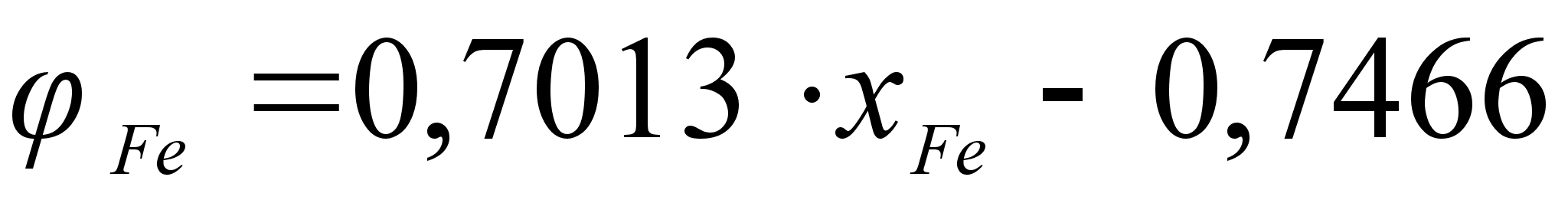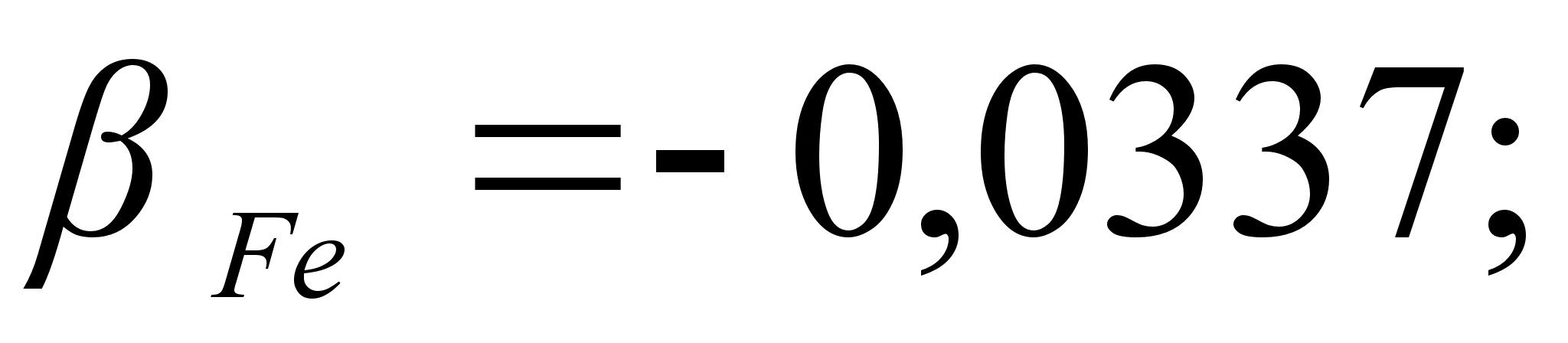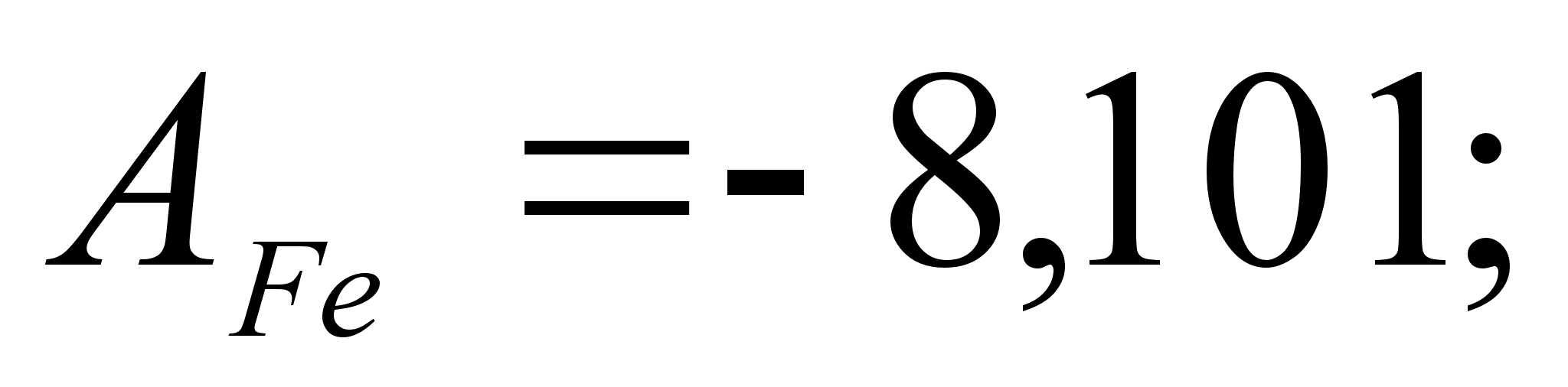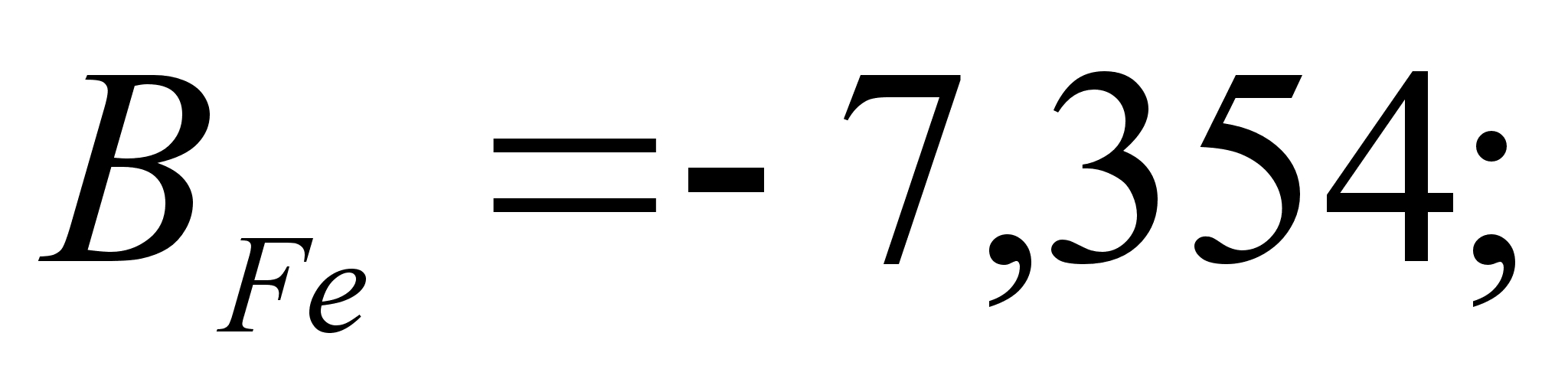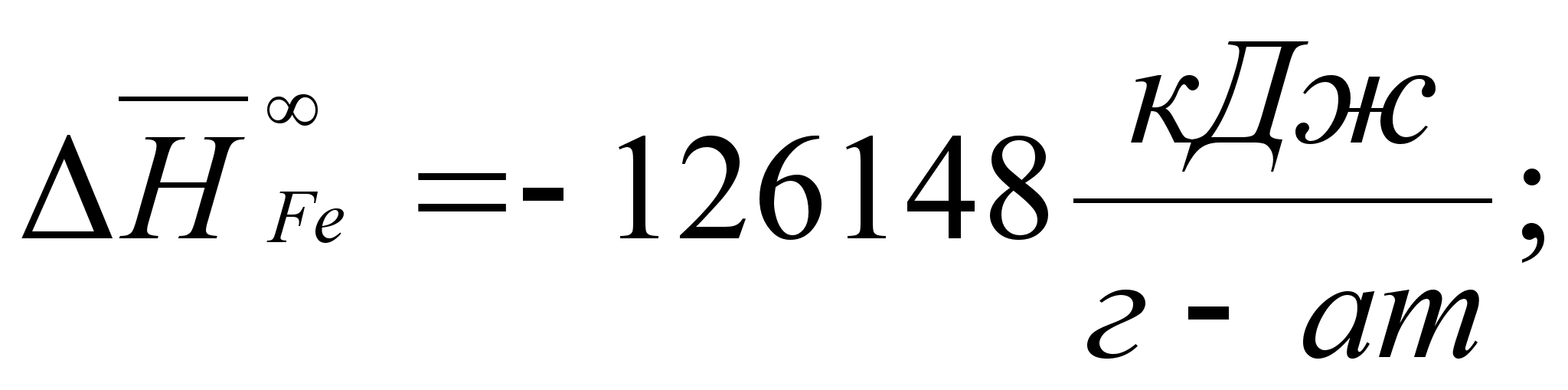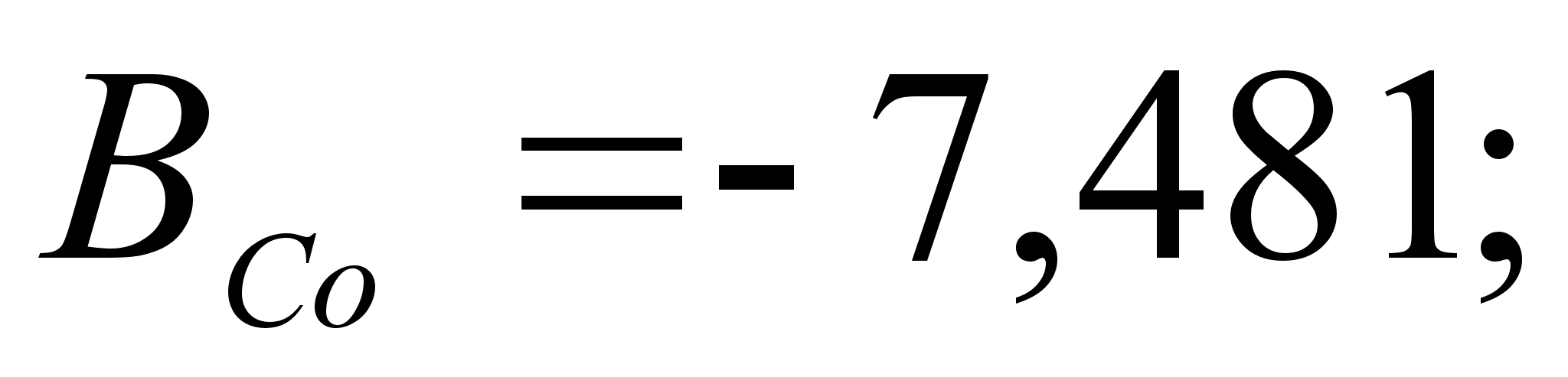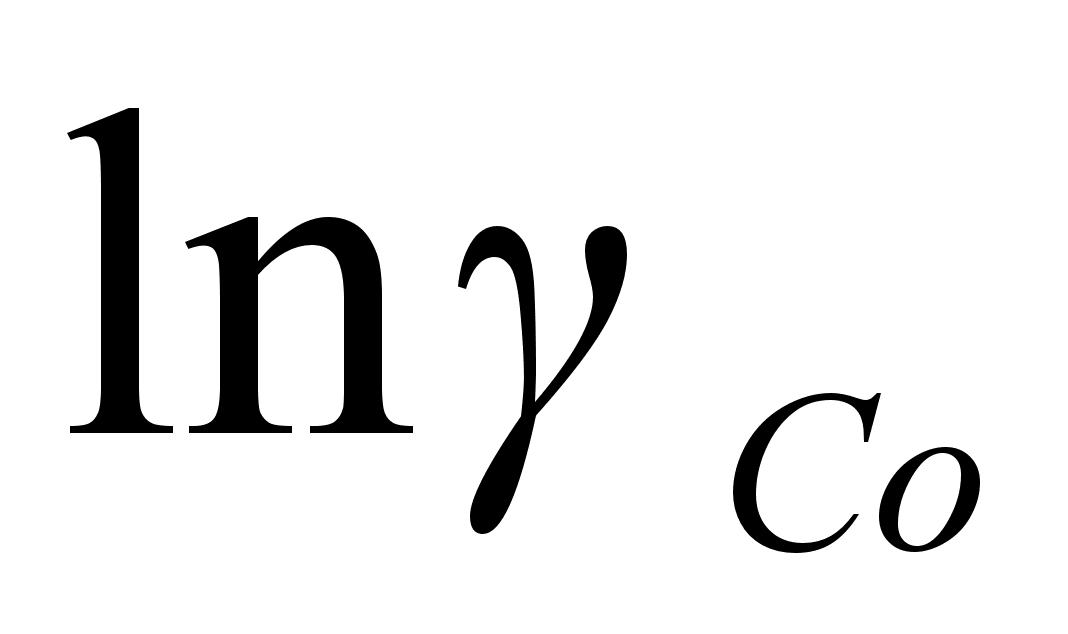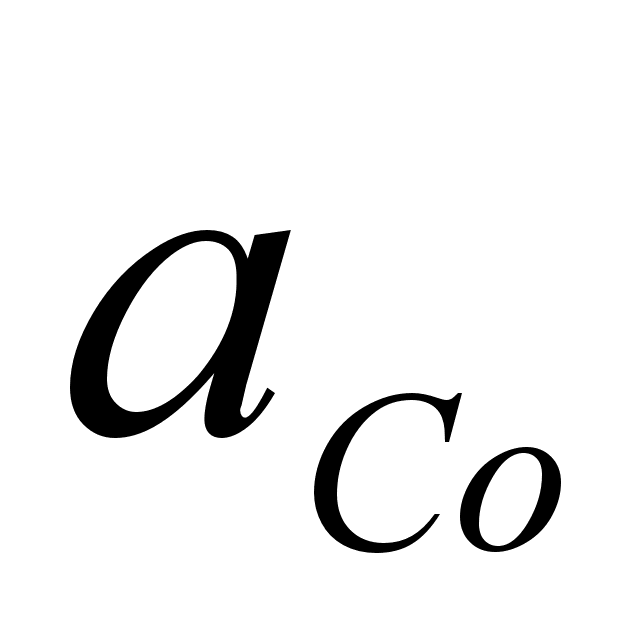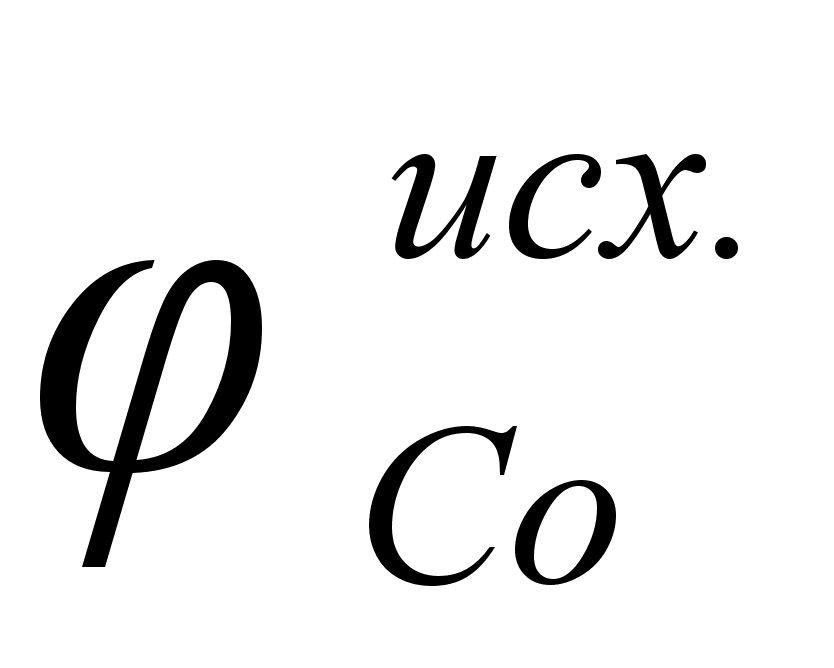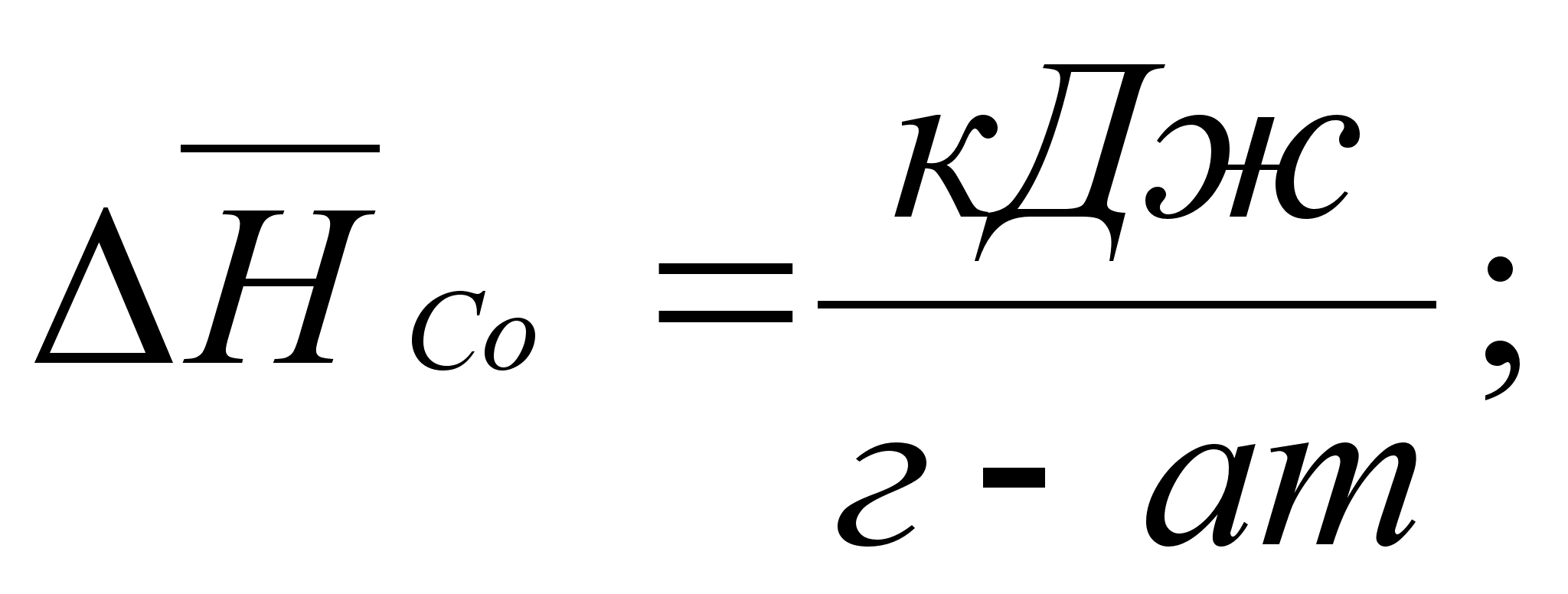Реферат: Термодинамические характеристики расплавов на основе железа
1 ТЕРМОДИНАМИКА РАСТВОРОВ
1.1 Основные понятия
1.1.1 Энтальпия.
Величина равная (E+PV) , часто встречается в термодинамических расчетах процессов, происходящих в системах при постоянном давлении; её обозначают через Н и называют энтальпией и иногда теплосодержанием.
Т
(1)
аким образом,
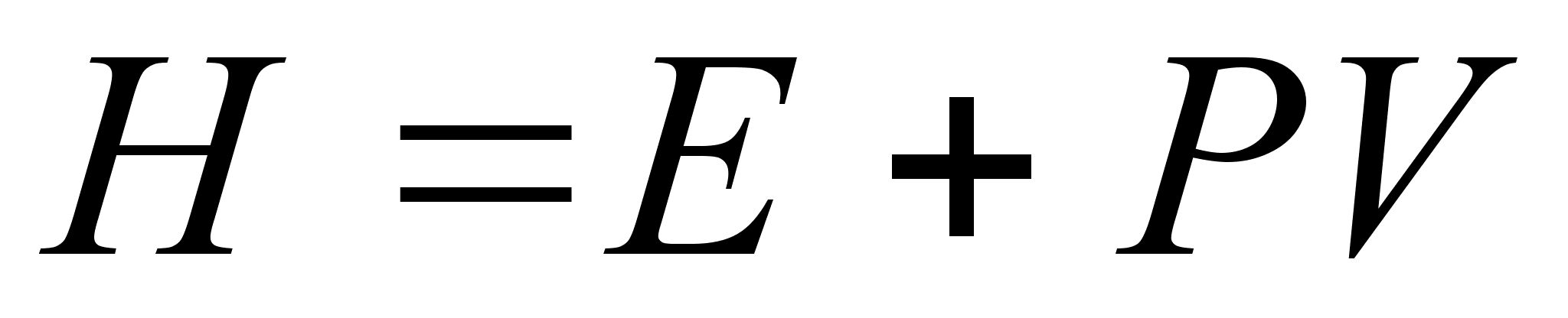 ,
,
где Е – внутренняя энергия системы;
Р – давление в системе;
V – объем.
Из определения энтальпии следует, что она, подобно энергии, является функцией состояния системы, так как она выражена через энергию (функцию состояния) и переменные состояния P и V. Следовательно, изменение энтальпии для любого термодинамического цикла (циклического процесса) равно нулю.
Если процесс не циклический, то при постоянном давлении изменение энтальпии системы равно полученной ею (системой) теплоте:
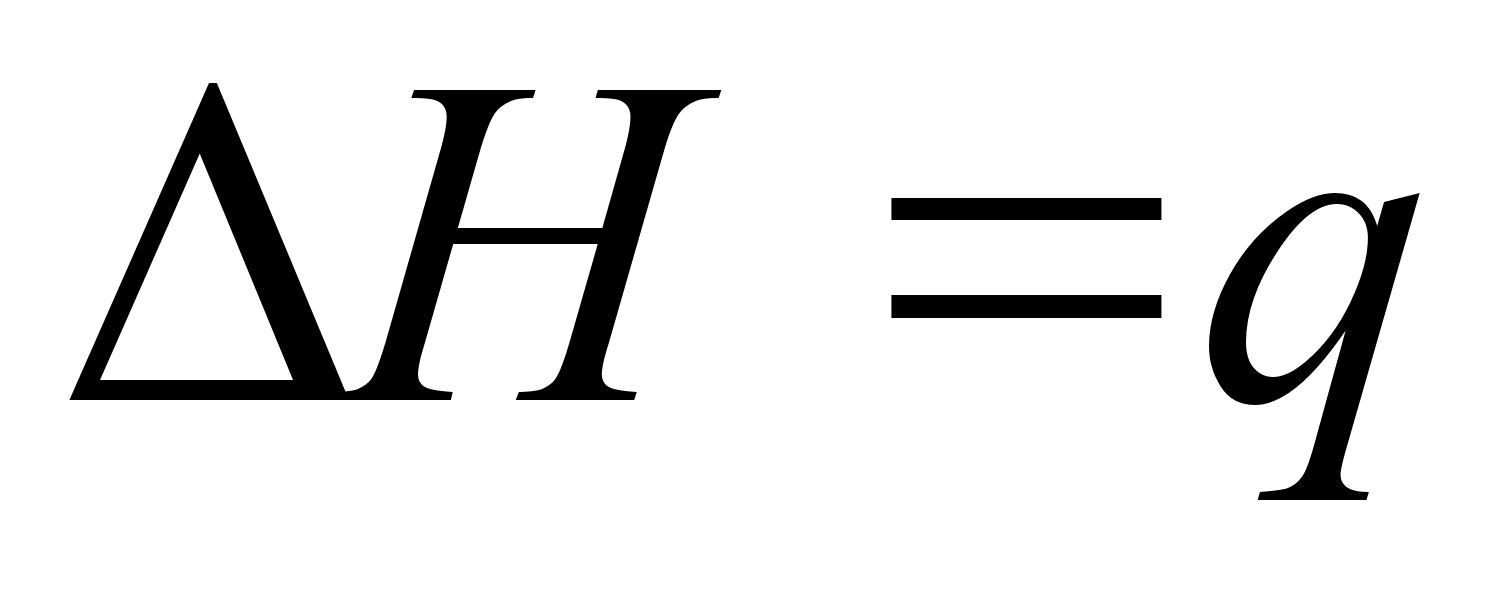
(2)
.Таким образом, для изобарического процесса обмениваемая между системой и внешней средой теплота представляет разность между начальной и конечной энтальпией самой системы и не зависим от пути достижения конечного состояния системы. Этот вывод следует из уравнения (2) и первоначально установленного факта, что энтальпия системы является функцией только её состояния. Следует подчеркнуть, что уравнение (2) применимо только к системе при постоянном давлении, так как теплота q вообще является не только функцией начального и конечного состояний, но зависит также от пути процесса. [2]
1.1.2 Энтропия.
Пусть две системы с термодинамическими вероятностями W1 и W2 образуют одну сложную систему, для которой термодинамическая вероятность W1+2. Так как каждый способ, которым осуществляется состояние первой системы, может сочетаться со всеми способами осуществления второй системы, то общее число способов, которыми может быть осуществлена сложная система, составляет:

(3)
Это свойство мультипликативности делает функцию W неудобной для непосредственных расчетов. [1]
Х
(4)
арактеризовать в этом смысле состояние системы оказалось удобнее не самой вероятностью осуществления данного макросостояния, а величиной, пропорциональной её логарифму. Эта величина называется энтропией. Энтропия (S) связана с числом (W) равновероятных микроскопических состояний, которыми можно реализовать данное макроскопическое состояние системы, уравнением:
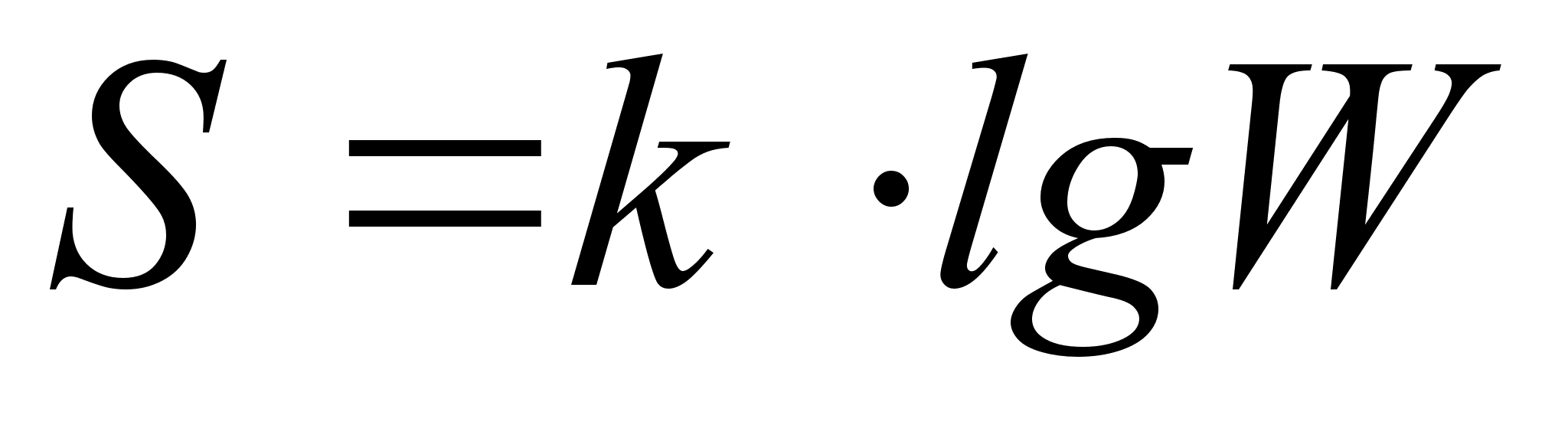
где k – коэффициент пропорциональности
Наименьшую энтропию имеют идеально правильно построенные кристаллы при абсолютном нуле. Энтропия кристалла, в структуре которого имеются какие-либо неправильности, уже при абсолютном нуле в несколько раз больше, так как нарушения идеальности могут реализоваться не единственным способом. С повышением температуры энтропия всегда возрастает, так как возрастет число способов их расположения. Возрастает она также при превращении вещества из кристаллического состояния в жидкое и, в особенности, при переходе из жидкого состояния в газообразное. Изменяется энтропия и при протекании химических процессов. Эти изменения обычно особенно велики в случае реакций, приводящих к изменению числа молекул газов: увеличение числа газовых молекул приводит к возрастанию энтропии, уменьшение – к её понижению. [4]
Изменение
энтропии при
различных
процессах.
Энтропия это
функция, дифференциал
которой равен
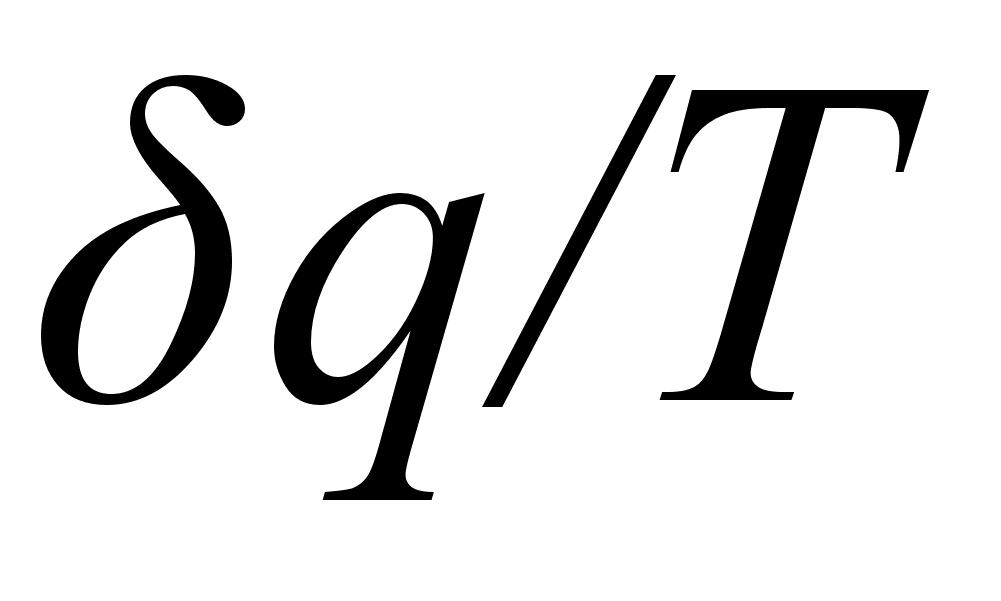 .
Из определительного
соотношения:
.
Из определительного
соотношения:
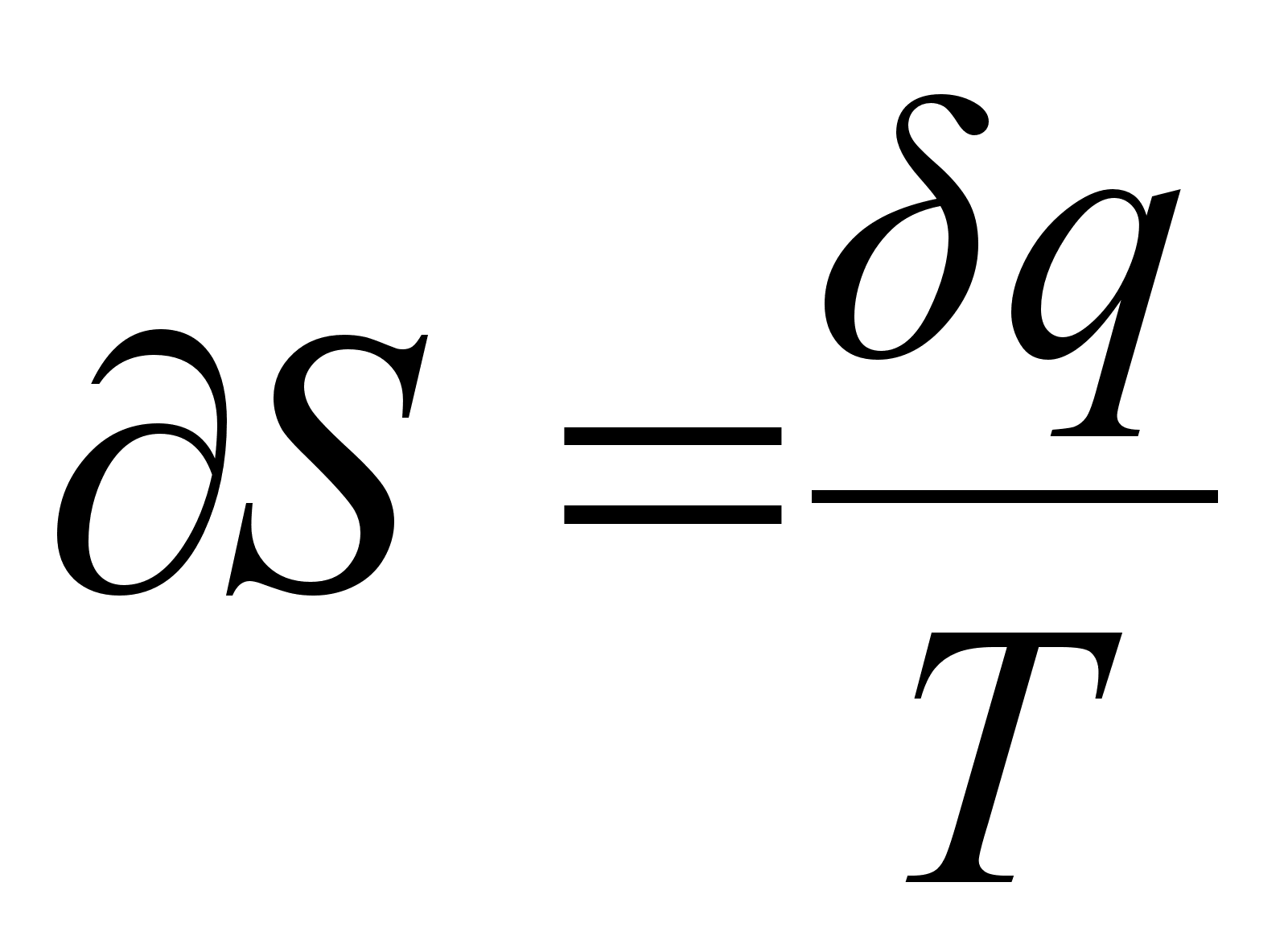
(5)
,
где
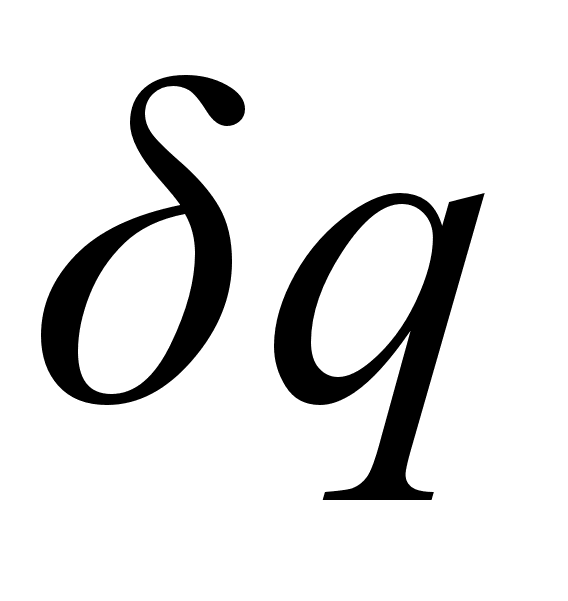 - приращение
теплоты, следует,
что для любого
обратимого
процесса,
протекающего
при постоянной
температуре,
изменение
энтропии системы:
- приращение
теплоты, следует,
что для любого
обратимого
процесса,
протекающего
при постоянной
температуре,
изменение
энтропии системы:
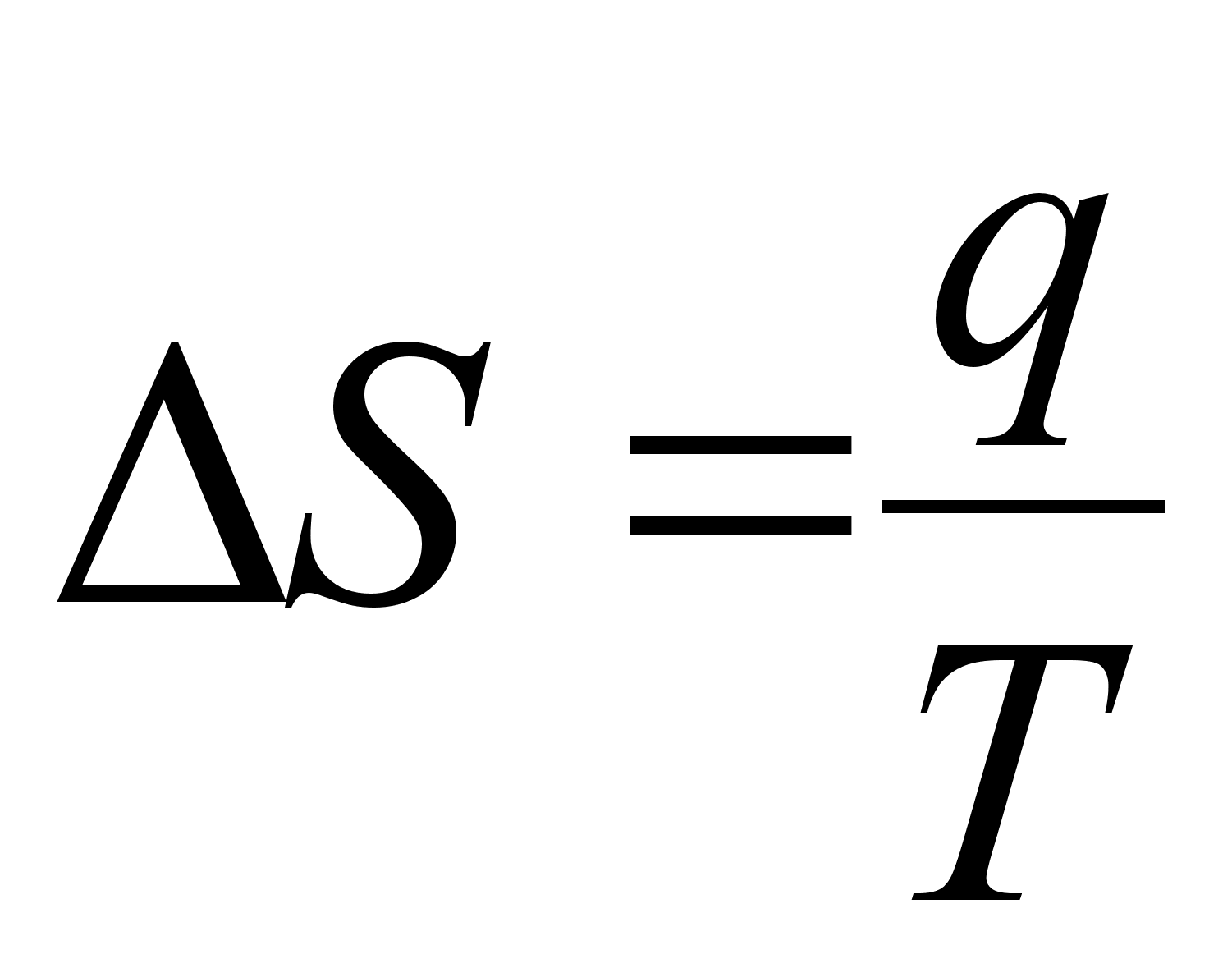
(6)
.Для процессов, протекающих при постоянных давлении и температуре, имеем:
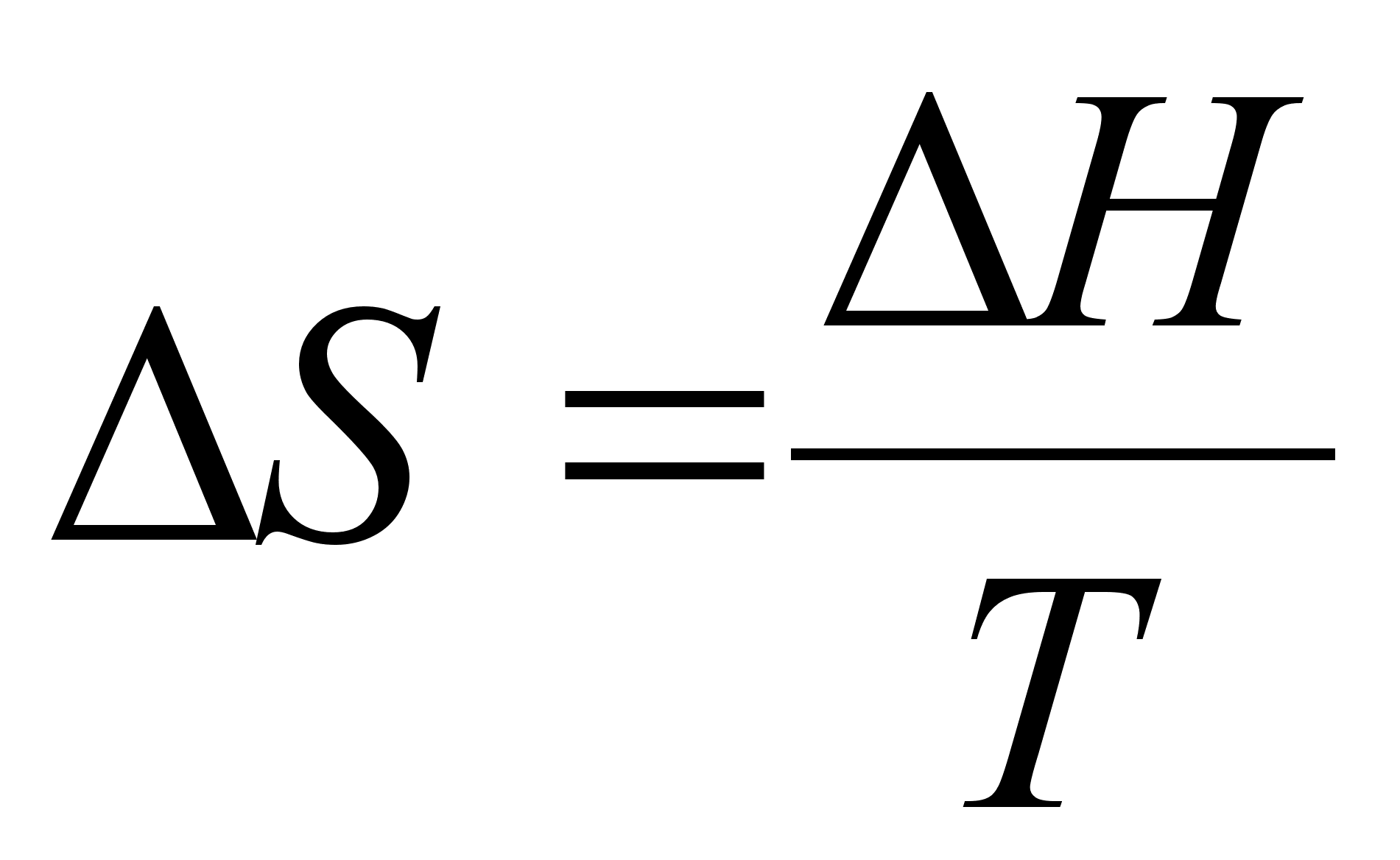
(7)
.Для термодинамического вещества, нагретого и охлажденного при постоянном давлении,
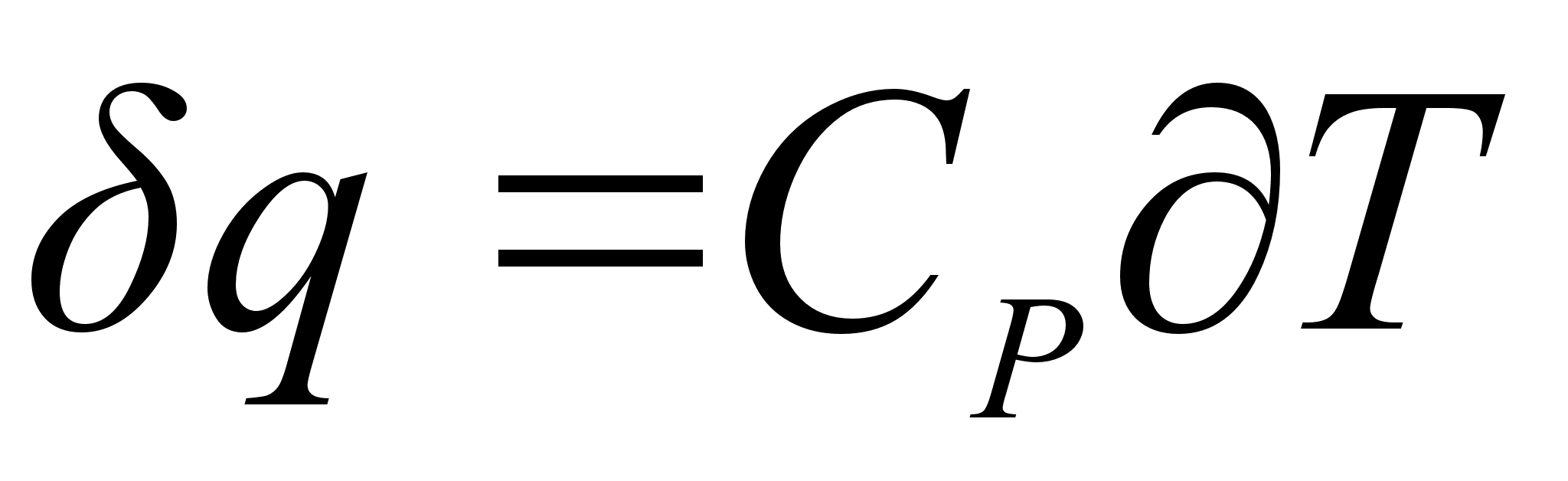 ,
,
где СР - теплоемкость вещества при постоянном давлении; и, следовательно,
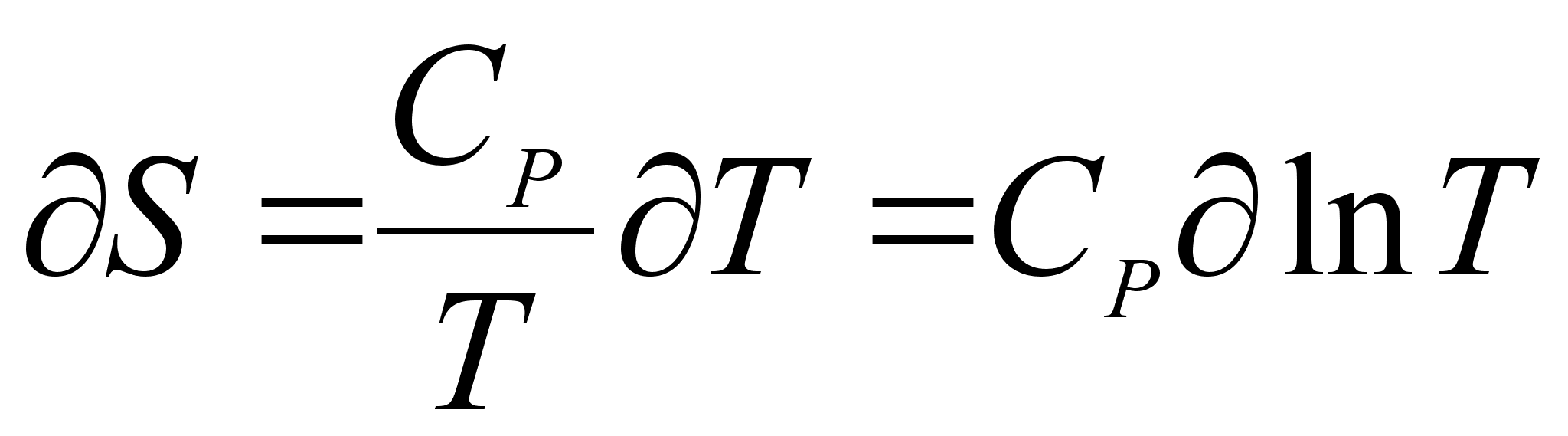
(8)
Точно также при нагреве и охлаждении вещества при постоянном объеме имеем: [2]
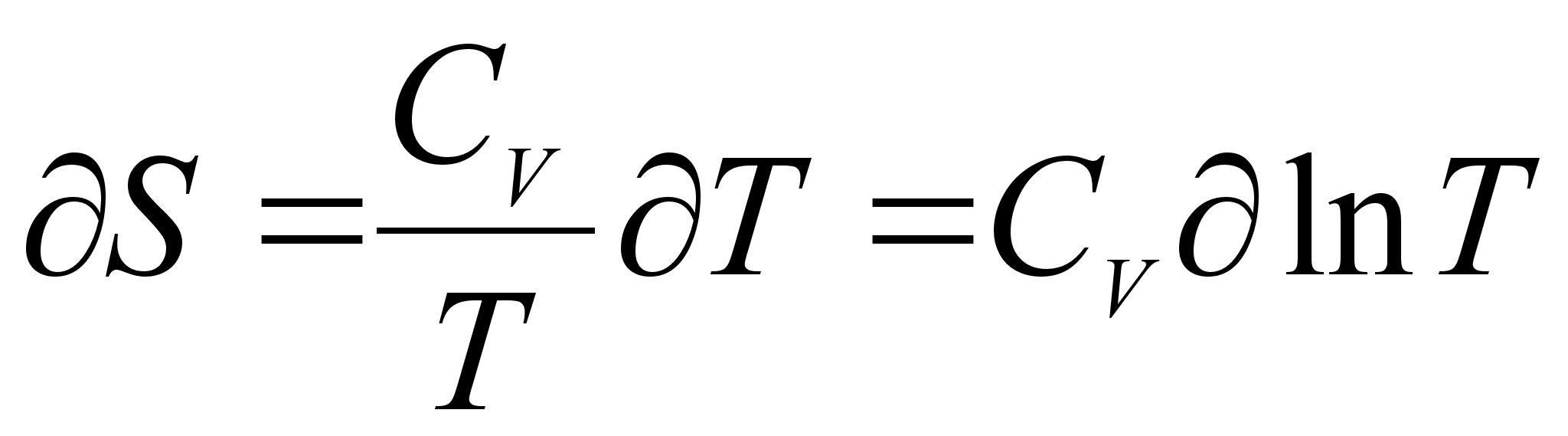
(9)
Если система
изолирована
от окружающей
среды, то
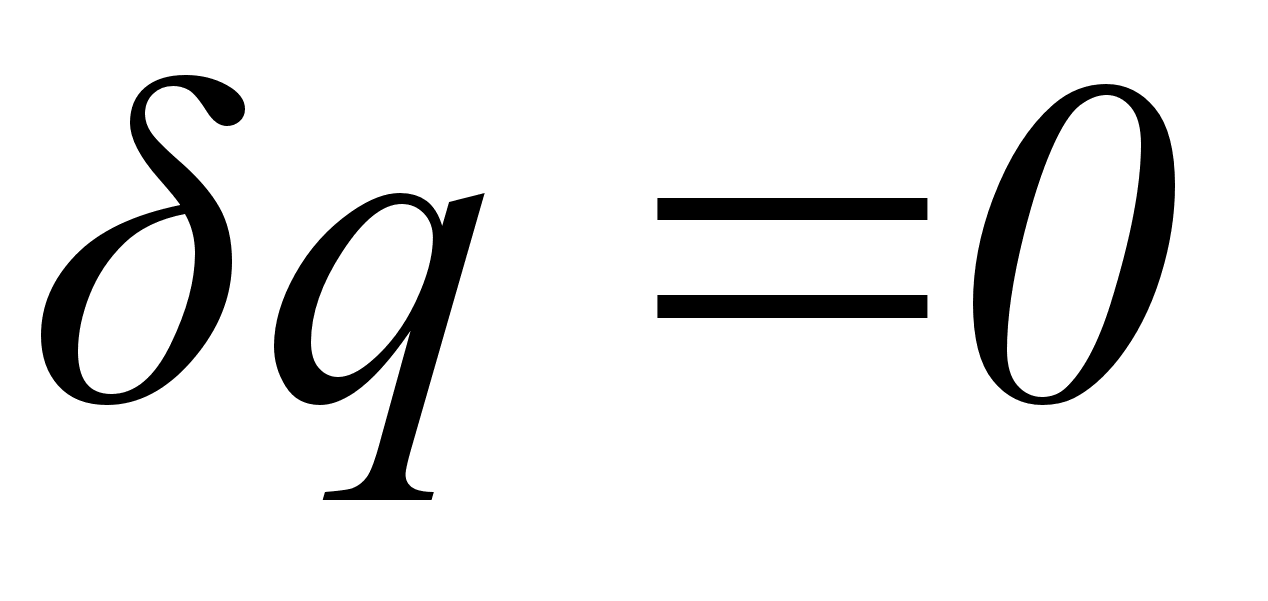 и, следовательно,
и, следовательно,
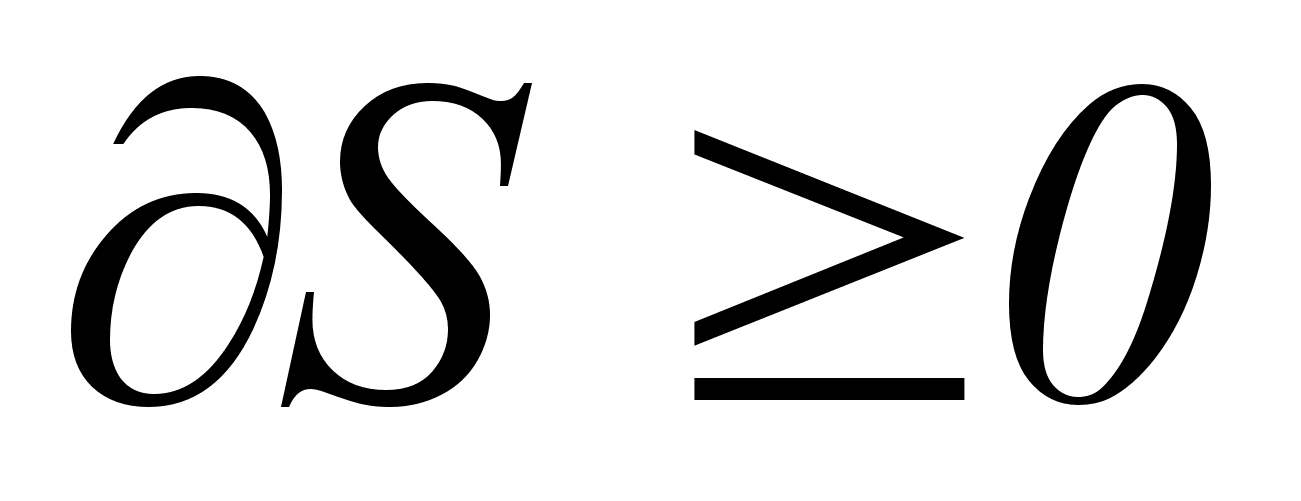 .
Протекание
любого самопроизвольного
процесса
характеризуется
неравенством:
.
Протекание
любого самопроизвольного
процесса
характеризуется
неравенством:
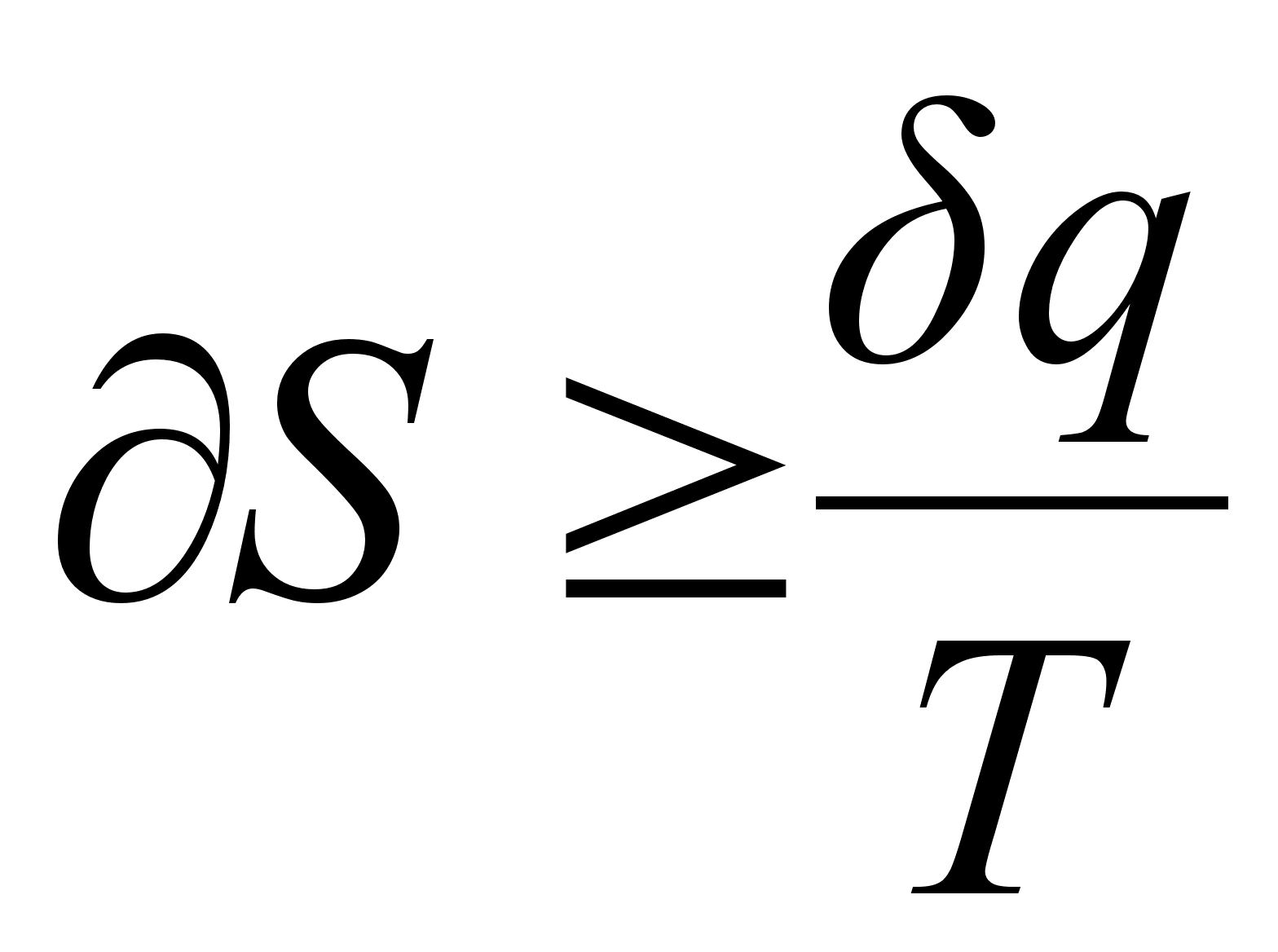
(10)
.Следовательно, в замкнутой системе такие процессы сопровождаются увеличением энтропии. При равновесии энтропия замкнутой системы остается постоянной. [1]
1.1.3 Энергия Гиббса.
Термодинамические
характеристики
реакций включают
значения тепловых
эффектов и
величины
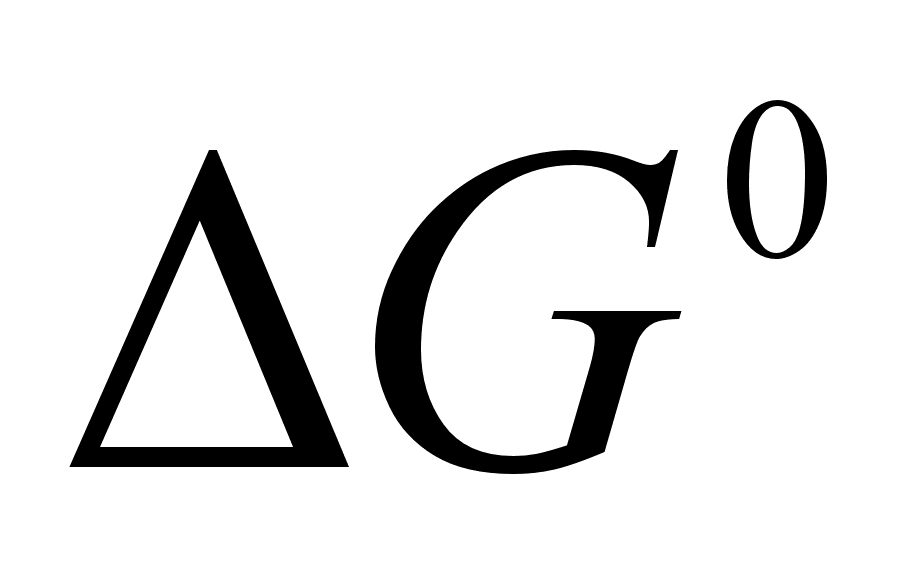 -
стандартного
изменения
свободной
энергии для
соответствующих
реакций. [5]
-
стандартного
изменения
свободной
энергии для
соответствующих
реакций. [5]
Изменение
энергии Гиббса
системы является
основной
термодинамической
характеристикой
химической
реакции. Для
определенности
исходные вещества
и продукты
реакции принимают
обычно находящимися
в их стандартных
состояниях.
Соответствующую
величину и
называют стандартной
энергией Гиббса
химической
реакции
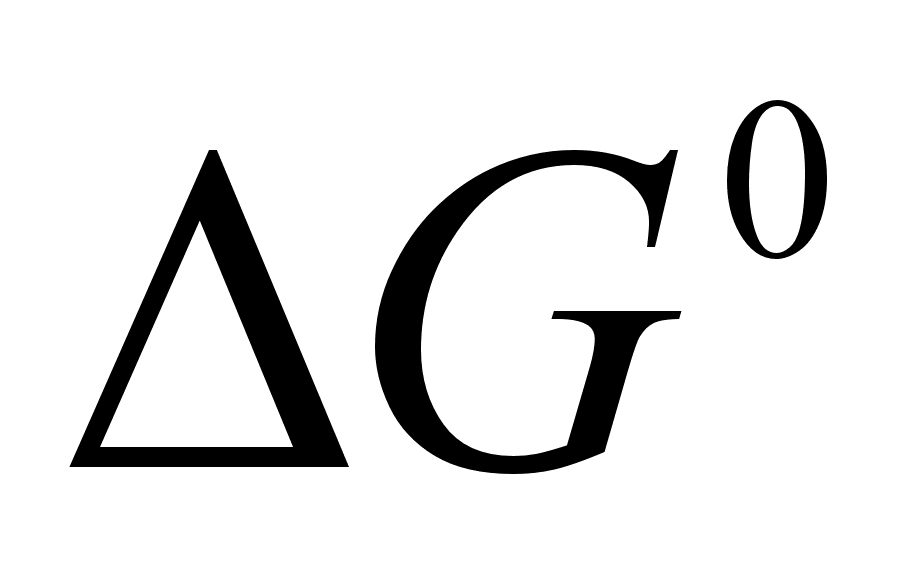 .
[6]
.
[6]
З
(11)
ависимость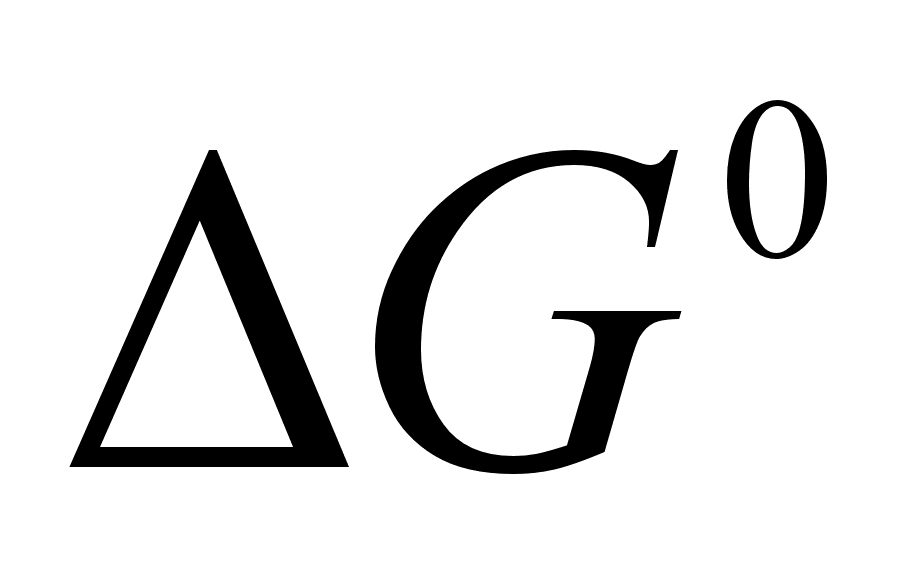 от различных
реакций от
температуры
с достаточной
точностью
выражается
формулой:
от различных
реакций от
температуры
с достаточной
точностью
выражается
формулой:
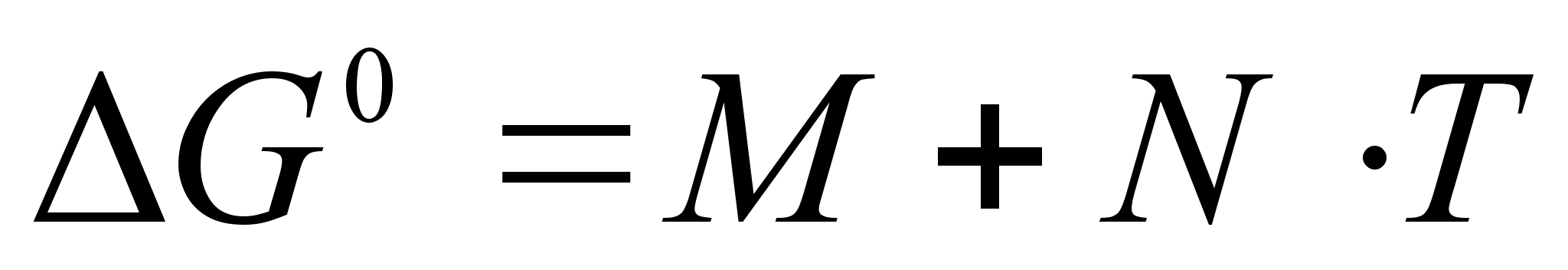
К
(12)
оэффициенты М и N для различных реакций приведены в справочной литературе. Эти коэффициенты определяются на основе обобщения экспериментальных данных по равновесиям различных реакций. Величины M и N близки к средним значениям тепловых эффектов ( )
и изменения
энтропии (
)
и изменения
энтропии (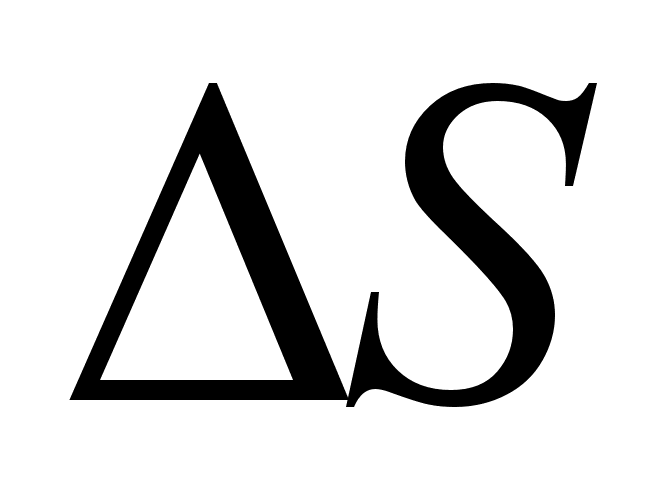 )
для соответствующих
реакций: [5]
)
для соответствующих
реакций: [5]
 .
.
(13)
В некоторых справочных изданиях приведены не энергии Гиббса веществ GT , а приведенные энергии Гиббса ФТ , которые связаны с GT соотношением: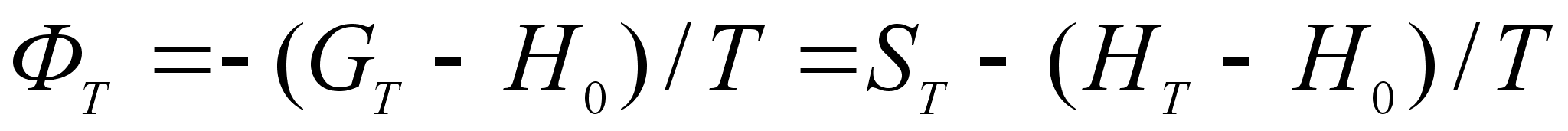 .
.Д
(14)
ля энергии Гиббса реакции aA+bB=cC+dD , как и для некоторых других величин, применимо выражение:
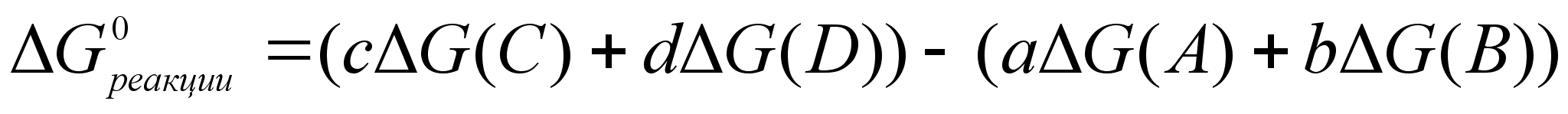
Согласно
второму закону
термодинамики,
энергия Гиббса
при необратимых
процессах может
только убывать.
Отсюда следует,
что
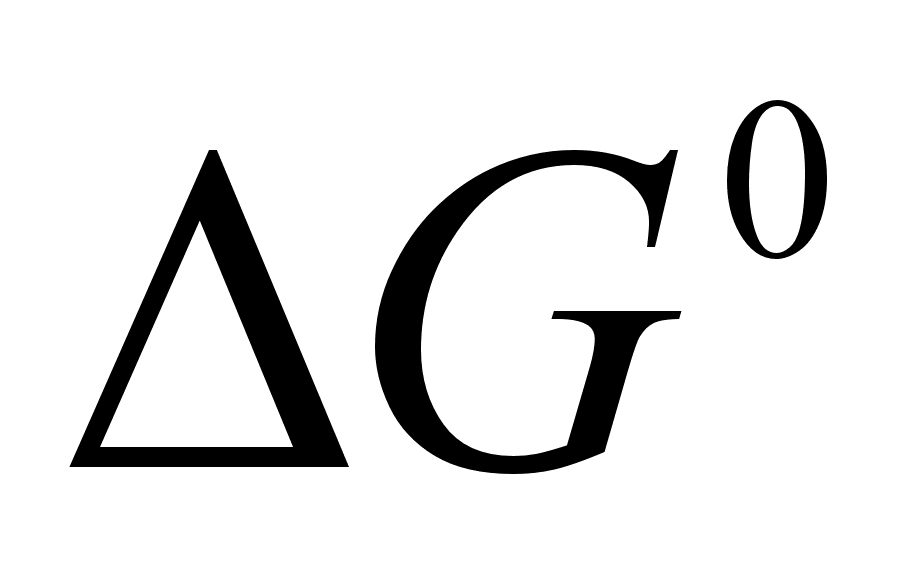 является критерием
направления
и полноты протекания
реакции между
веществами,
взятыми в стандартном
состоянии.
Реакция может
протекать
только в том
направлении,
которое характеризуется
отрицательным
значением
является критерием
направления
и полноты протекания
реакции между
веществами,
взятыми в стандартном
состоянии.
Реакция может
протекать
только в том
направлении,
которое характеризуется
отрицательным
значением
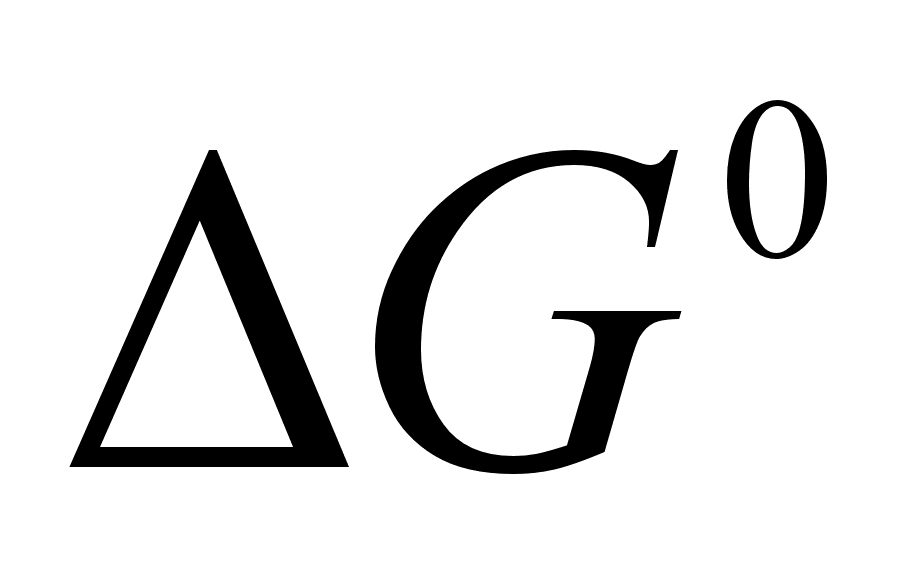 , т.е. реакция
всегда идет
в направлении
снижения энергии
Гиббса системы.
Если
, т.е. реакция
всегда идет
в направлении
снижения энергии
Гиббса системы.
Если
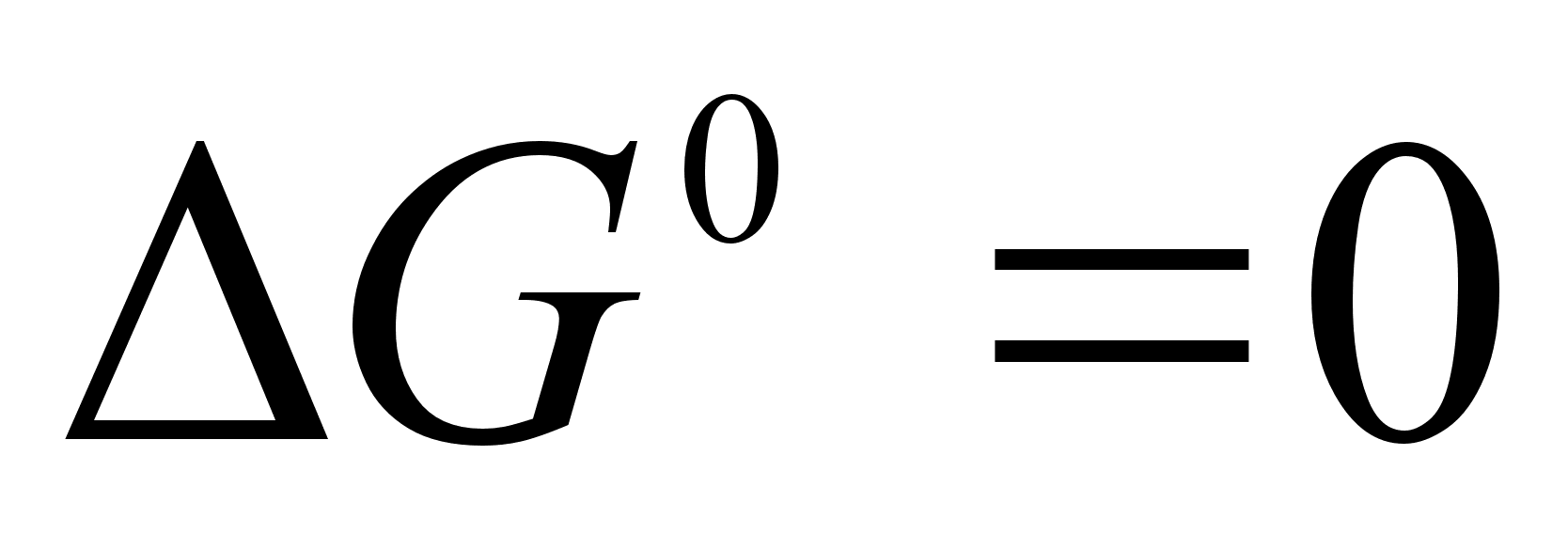 ,
то это указывает
на равновесие
между реагентами
в их стандартных
состояниях
(реакция не
идет). Полнота
протекания
реакции характеризуется
константой
равновесия
К, связанной
с
,
то это указывает
на равновесие
между реагентами
в их стандартных
состояниях
(реакция не
идет). Полнота
протекания
реакции характеризуется
константой
равновесия
К, связанной
с
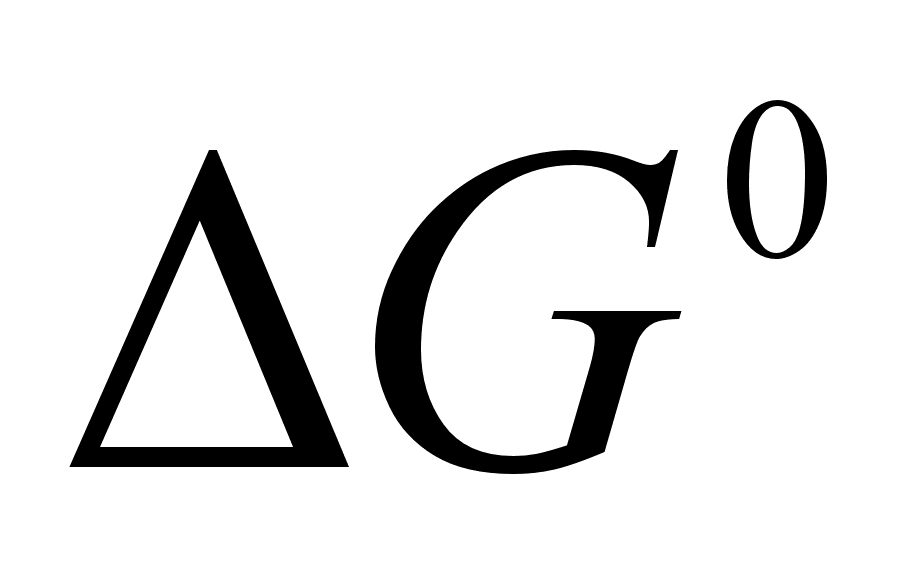 уравнением
изотермы:
уравнением
изотермы:
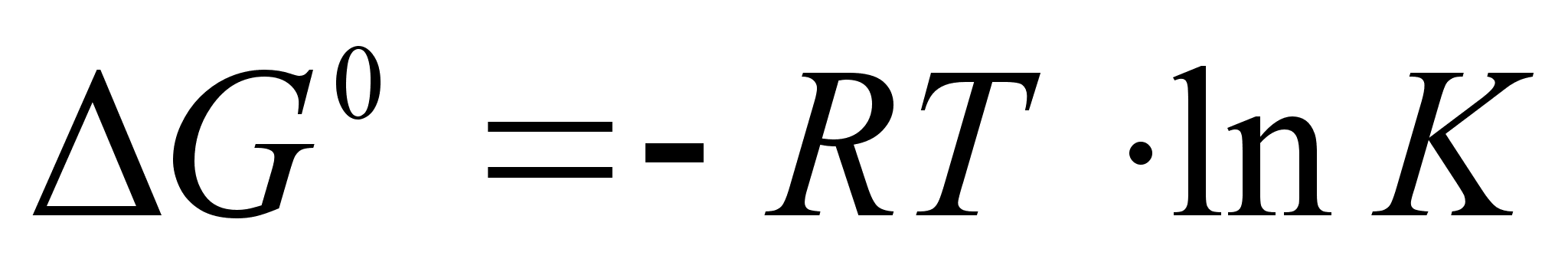 .
.
Поскольку
R=8,3192 Дж/(моль*К):
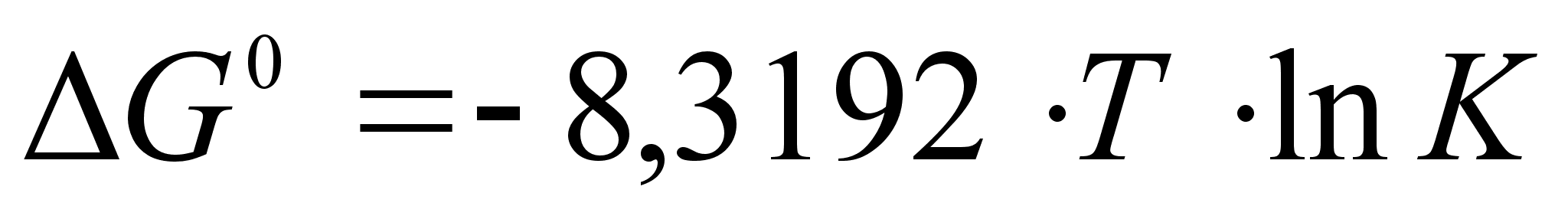 .
.
При переходе
к десятичным
логарифмам
получаем:
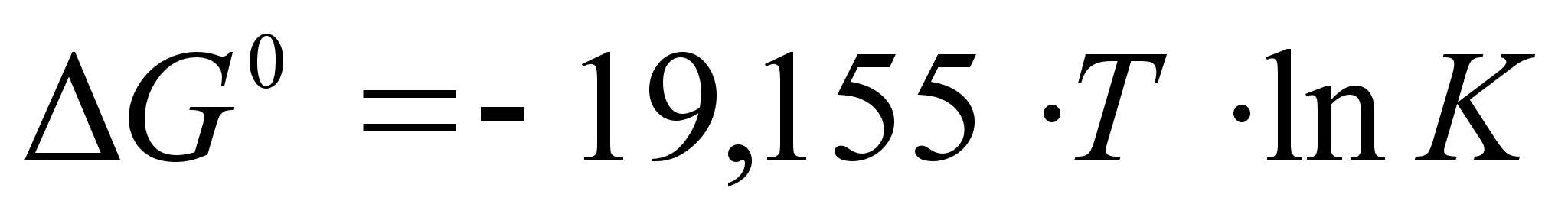 .
.
Пользуясь
этим уравнением,
можно по известному
значению
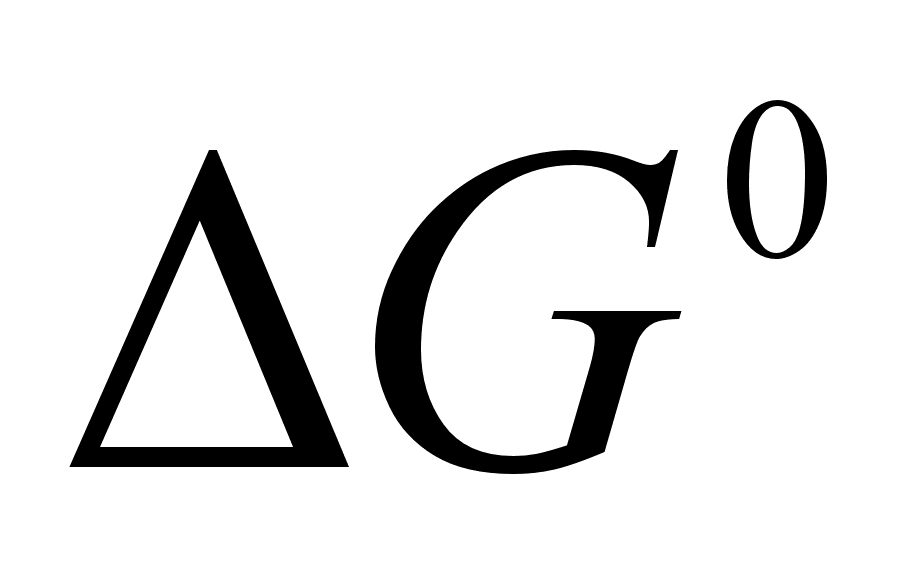 определить
константу
равновесия
реакции, и найти
необходимые
для практики
равновесные
концентрации
и другие характеристики.
Например, для
реакции получения
TiC (
определить
константу
равновесия
реакции, и найти
необходимые
для практики
равновесные
концентрации
и другие характеристики.
Например, для
реакции получения
TiC (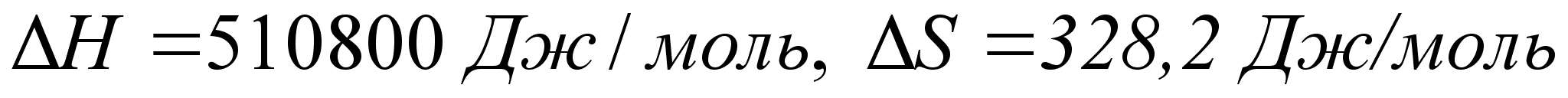 ),
исходя из последнего
уравнения и
температурной
зависимости
),
исходя из последнего
уравнения и
температурной
зависимости
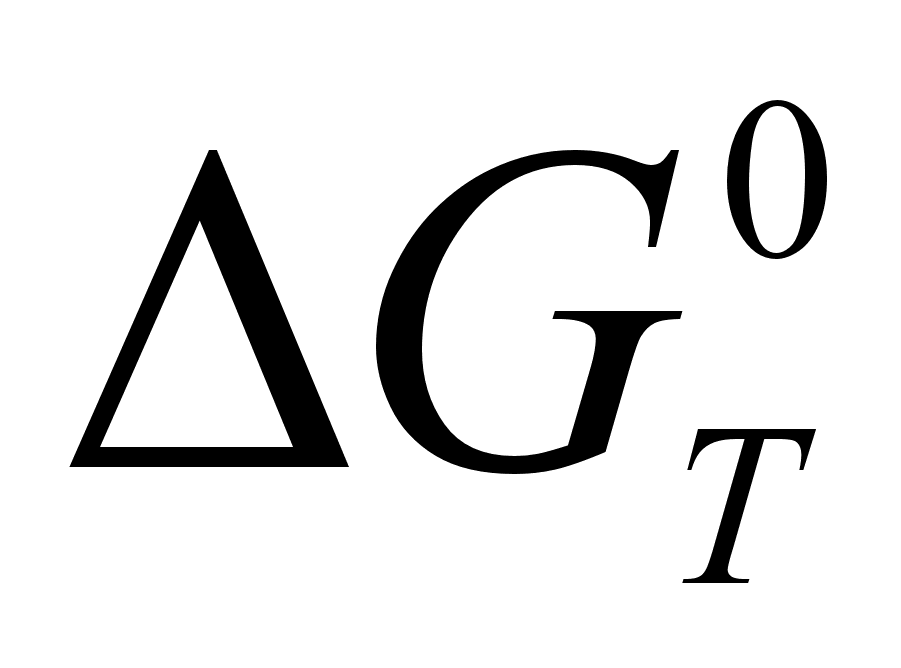 ,
можно получить
следующее
выражение для
константы
равновесия:
,
можно получить
следующее
выражение для
константы
равновесия:
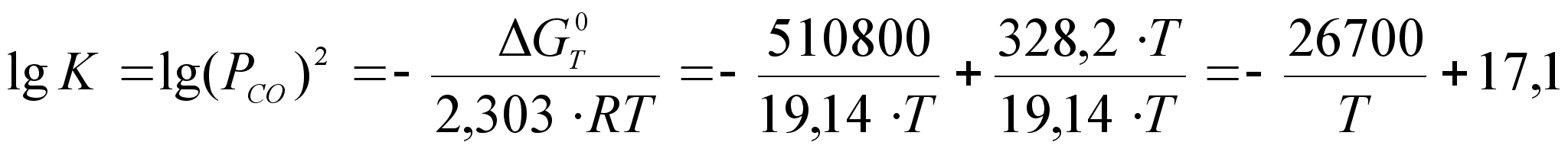
(15)
1.1.4 Экстенсивные, интенсивные свойства; парциальные величины.
Э
(16)
кстенсивными называют свойства, которые зависят от количества вещества : V, H, S, G и т.д. Для определения экстенсивного свойства g раствора необходимо просуммировать интенсивные (парциальные мольные) характеристики компонентов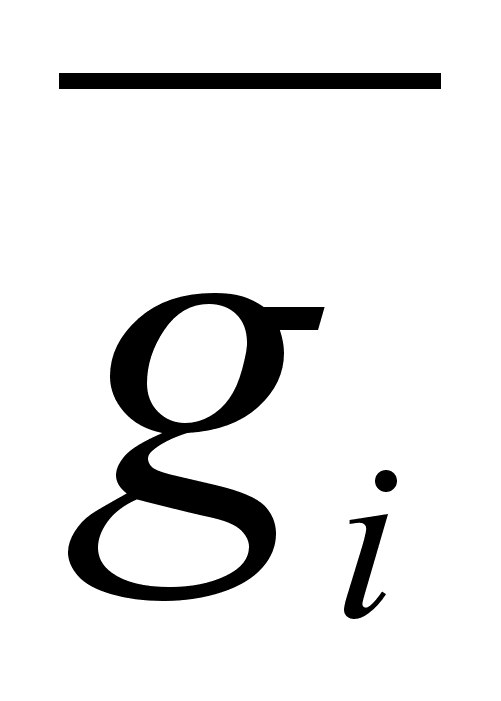 ,
умноженные
на соответствующие
числа молей
ni.
Например, для
энтальпии
раствора имеем
,
умноженные
на соответствующие
числа молей
ni.
Например, для
энтальпии
раствора имеем
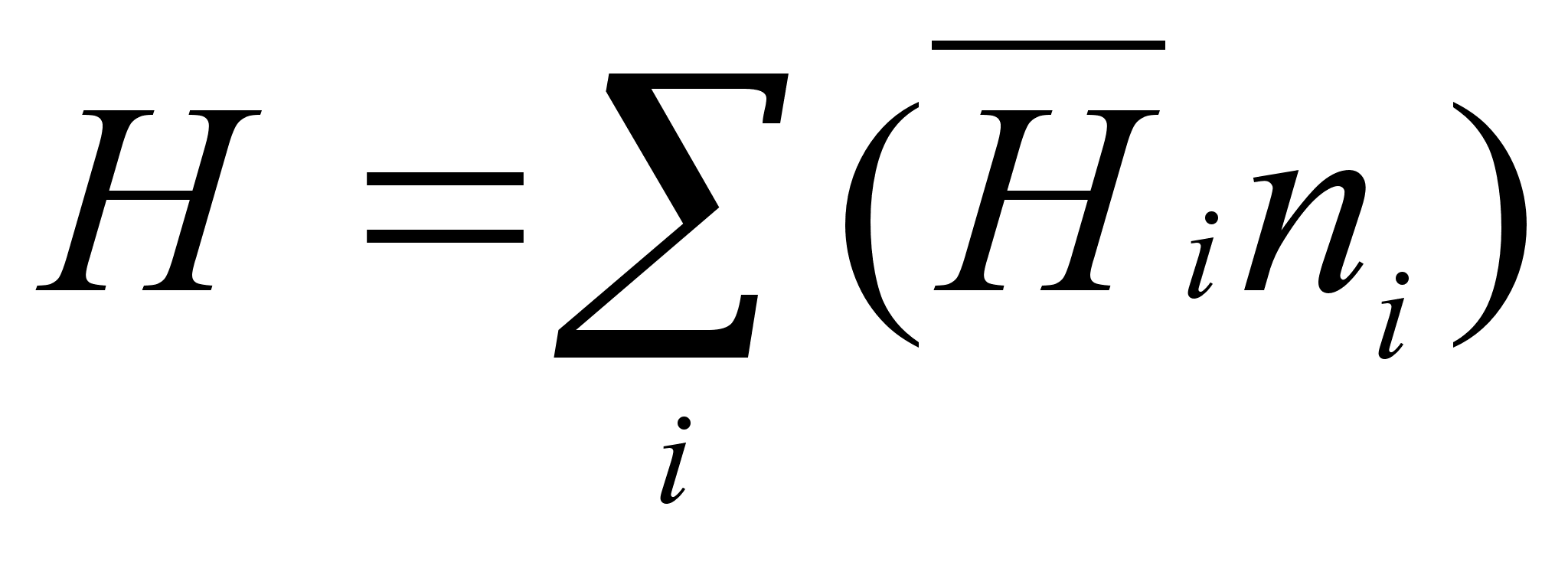 ,
или для 1 моля
раствора:
,
или для 1 моля
раствора: 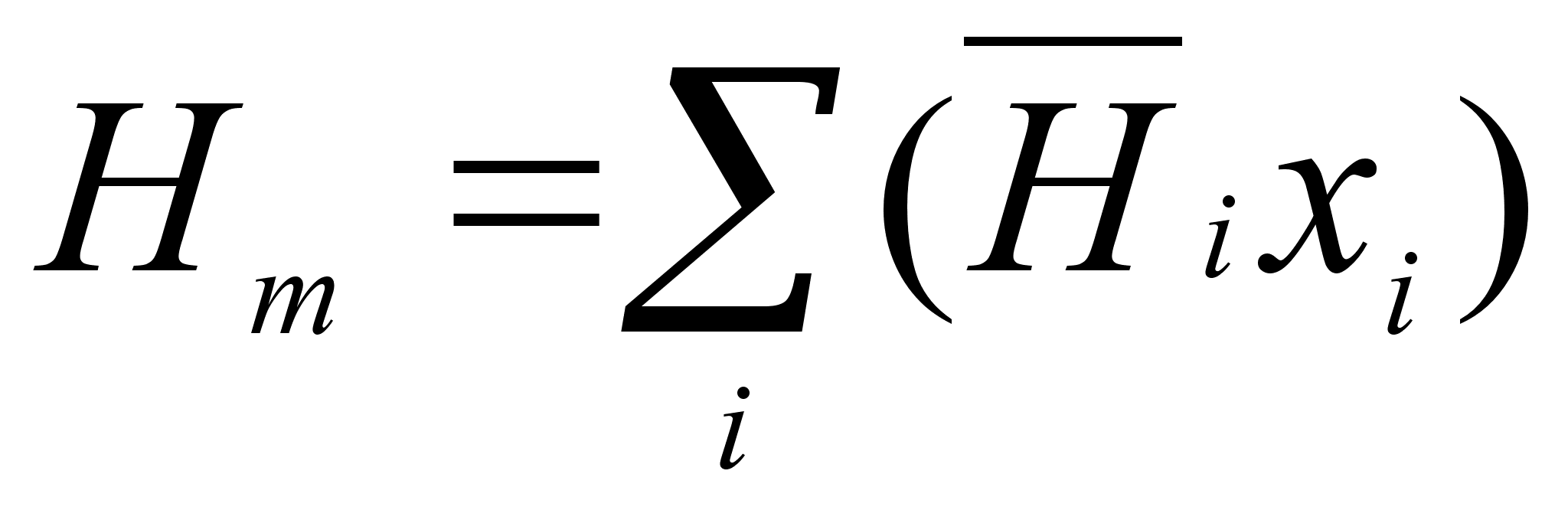 .
.
Интенсивные
свойства раствора
– свойства, не
зависящие от
количества
вещества, такие,
например, как
температура,
давление. К
числу интенсивных
принадлежат
и парциальные
мольные характеристики
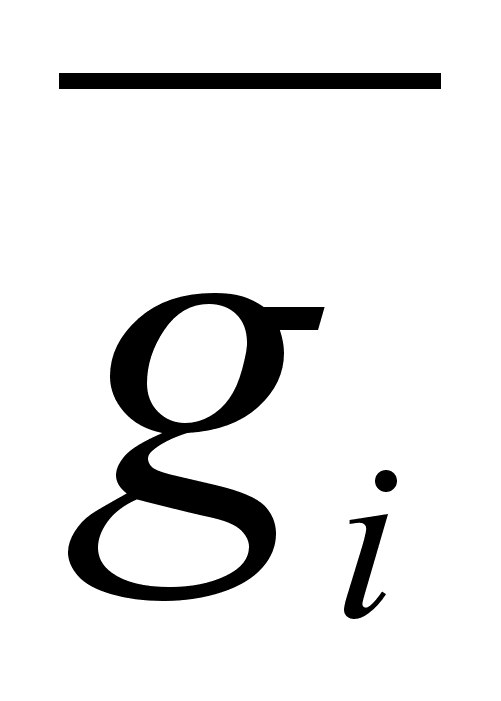 .
Интенсивные
свойства представляют
собой частные
производные
от соответствующих
экстенсивных
свойств раствора
по числу молей
данного компонента
при постоянных
температуре,
давлении и
числах молей
других компонентов:
.
Интенсивные
свойства представляют
собой частные
производные
от соответствующих
экстенсивных
свойств раствора
по числу молей
данного компонента
при постоянных
температуре,
давлении и
числах молей
других компонентов:
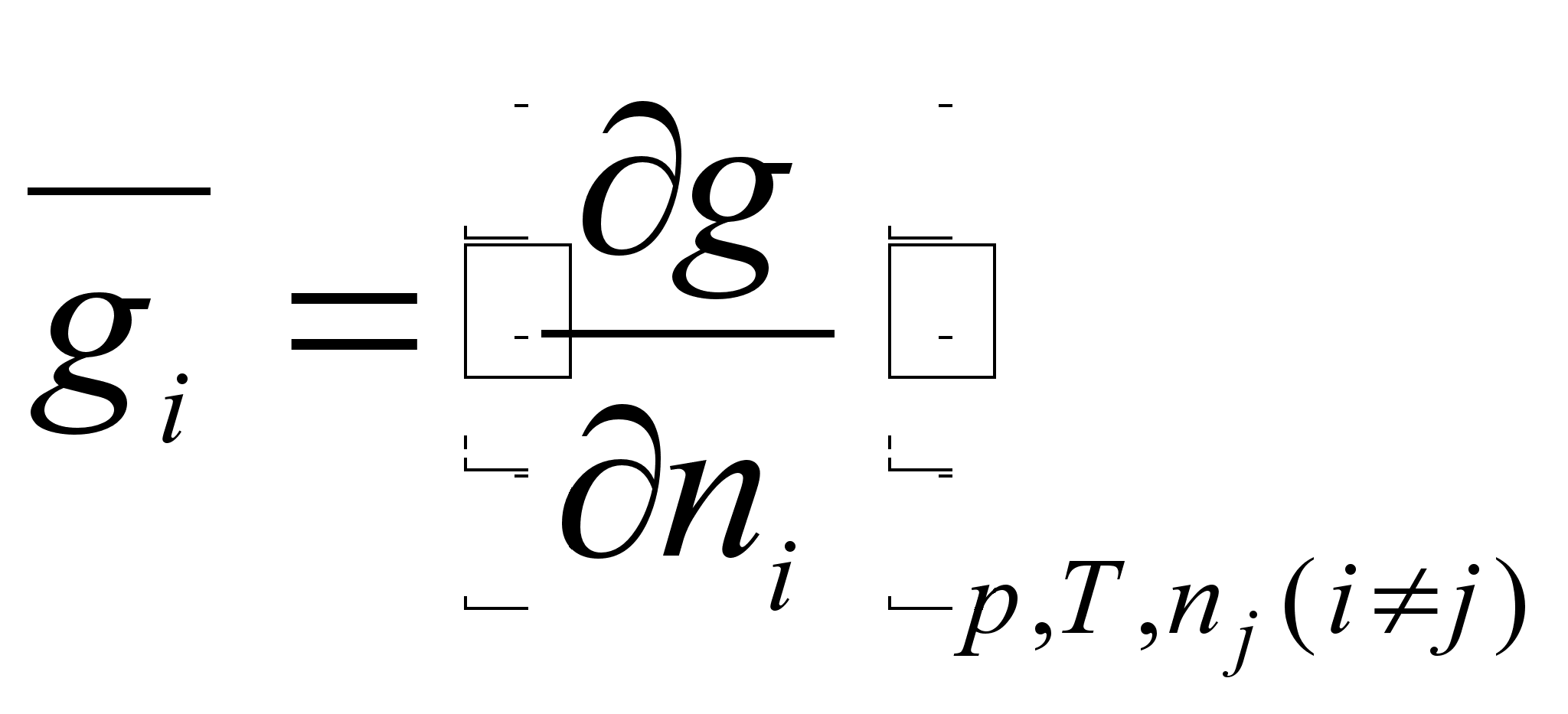
(17)
.
Таким образом,
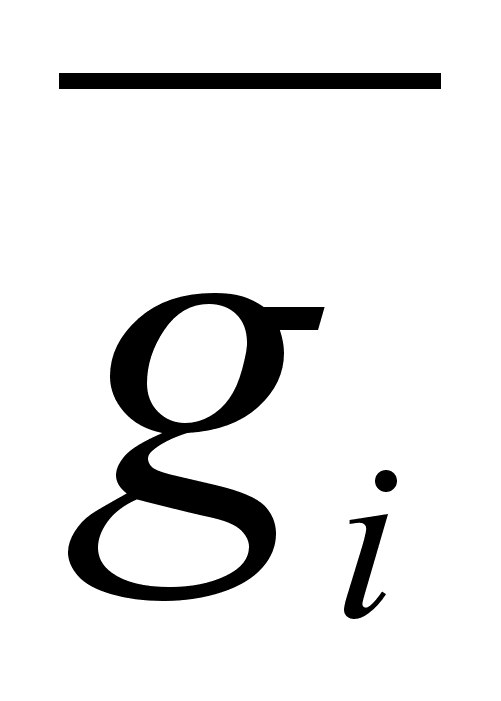 представляет
собой приращение
свойства бесконечно
большого количества
раствора при
добавлении
1 моля i-того
компонента.
Например, парциальный
мольный объём
компонента
в растворе
заданного
состава показывает,
на какую величину
изменится объём
этого раствора
(взятого в бесконечно
большом количестве)
при добавлении
1 моля данного
компонента.
[6]
представляет
собой приращение
свойства бесконечно
большого количества
раствора при
добавлении
1 моля i-того
компонента.
Например, парциальный
мольный объём
компонента
в растворе
заданного
состава показывает,
на какую величину
изменится объём
этого раствора
(взятого в бесконечно
большом количестве)
при добавлении
1 моля данного
компонента.
[6]
1.2 Растворы
Раствором называется однородная смесь, состоящая из двух или большего числа веществ, состав которой в известных пределах может непрерывно изменяться.
Однородными являются и химические соединения, однако их состав не может изменяться непрерывно, так как они подчиняются законам постоянства состава и кратных отношений.
1.2.1 Идеальные растворы
Цель термодинамической теории расплавов состоит в том, чтобы связать различные свойства растворов и найти способы предсказания свойств растворов, исходя из свойств чистых компонентов. Ввиду очень сложного характера взаимодействия компонентов в растворах решение этой задачи в общем виде невозможно. Поэтому целесообразно сначала рассмотреть идеализированные случаи, в которых можно отделить главные черты явления от второстепенных. [1]
Раствор называется идеальным, если :
а) теплота
смешения равна
нулю
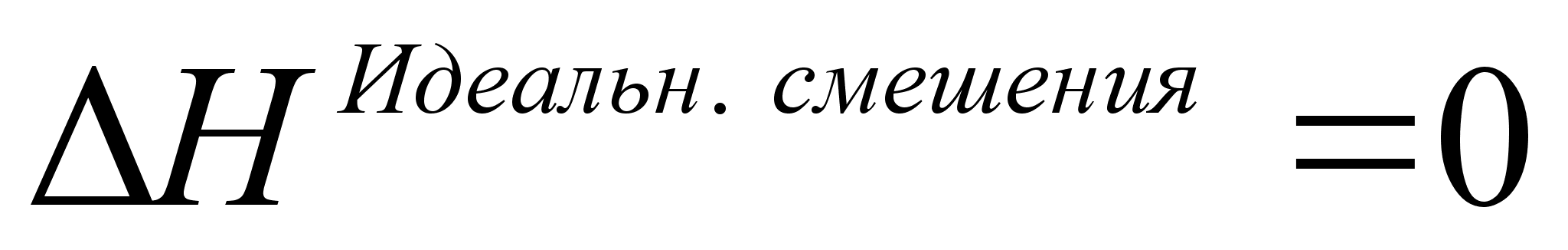 ,
,
б) изменение объема при смешении чистых компонентов равно нулю
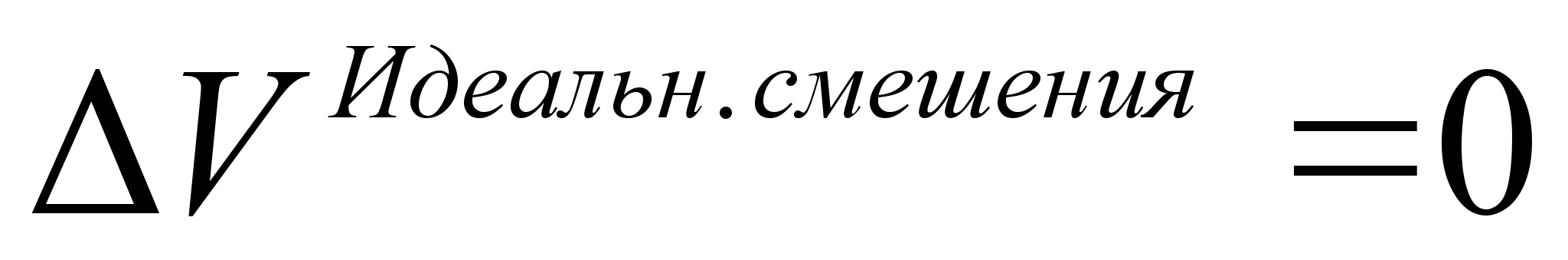 ,
,
в) парциальное давление пара каждого компонента пропорционально его молярной доле. Это означает, при всех концентрациях соблюдается закон Рауля при условии, что пары следуют законам идеальных газов и, следовательно, парциальные давления равны летучим. [7]
Идеальным
называется
раствор, в котором
соблюдается
закон Рауля
при температурах
и давлениях,
при которых
возможно его
существование.
Закон Рауля
гласит, что для
ограниченного
числа растворов
парциальное
давление каждого
компонента
pi
равно произведению
молярной доли
компонента
xi
на упругость
пара в его чистом
виде (давление
пара чистого
компонента)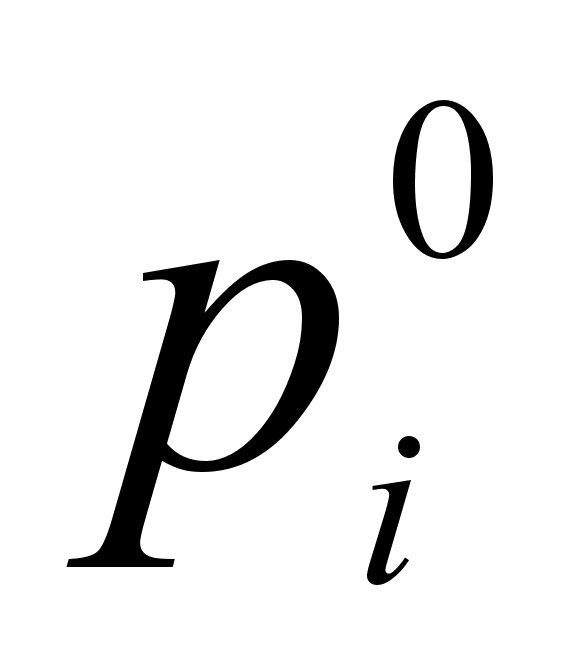 :
[2]
:
[2]
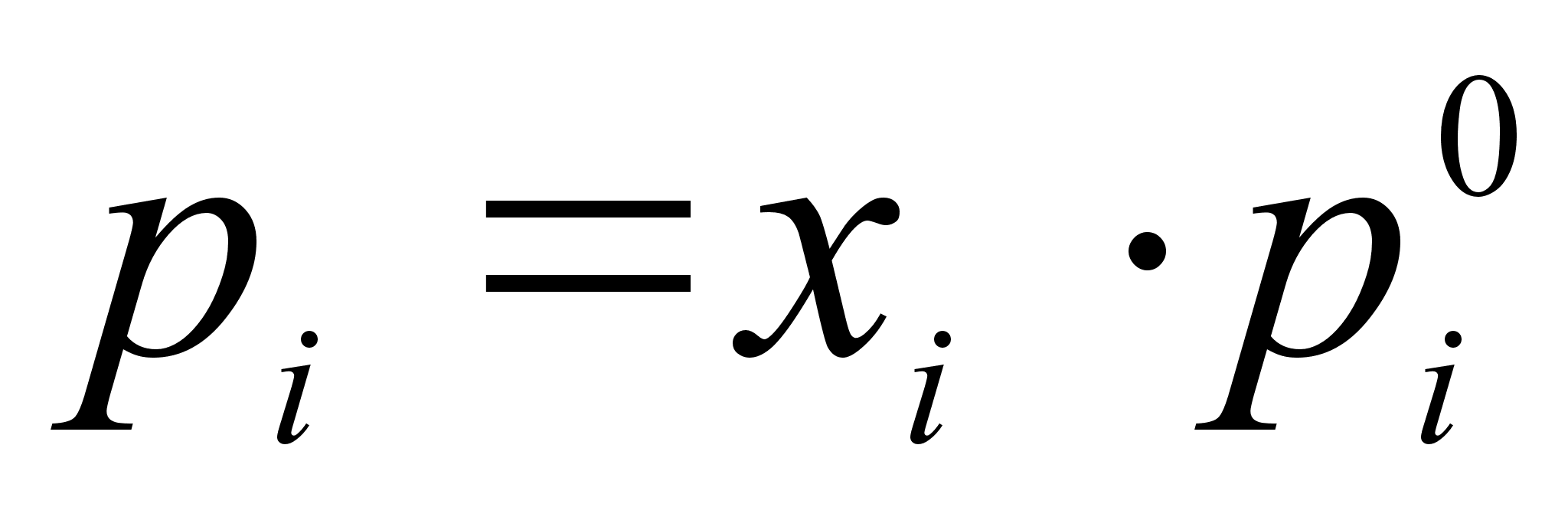
(18)
Теплота
образования
идеального
раствора. Поскольку,
суммарная
энергия взаимодействия
частиц при
образовании
идеального
раствора из
чистых компонентов
не изменяется
(такие растворы
называют
совершенными),
парциальные
объемы компонентов
и их парциальные
энтальпии будут
равны соответствующим
мольным характеристикам:
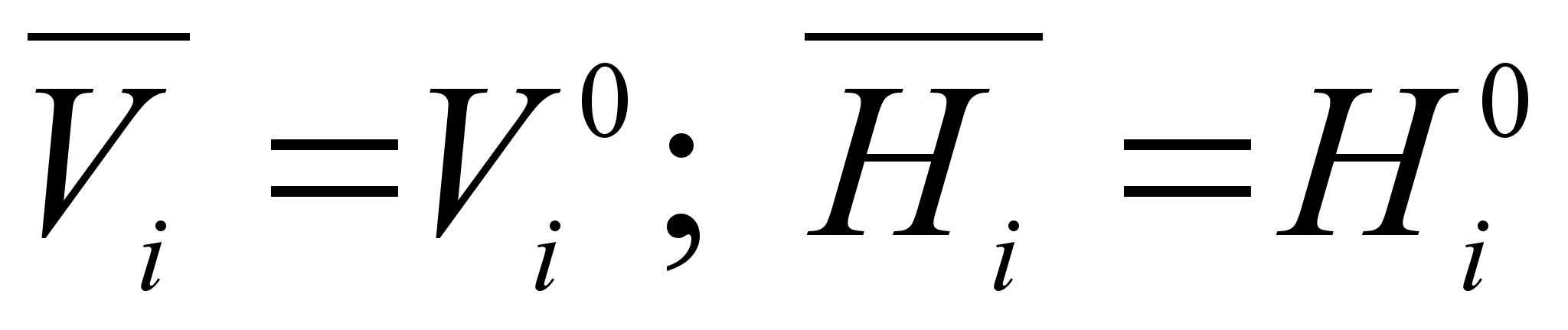 .
[6] Таким образом,
теплота испарения
компонента
в идеальном
растворе равна
теплоте испарения
его в чистом
виде. [2] В этом
случае энтальпия
раствора аддитивно
складываются
из мольных
величин:
.
[6] Таким образом,
теплота испарения
компонента
в идеальном
растворе равна
теплоте испарения
его в чистом
виде. [2] В этом
случае энтальпия
раствора аддитивно
складываются
из мольных
величин:
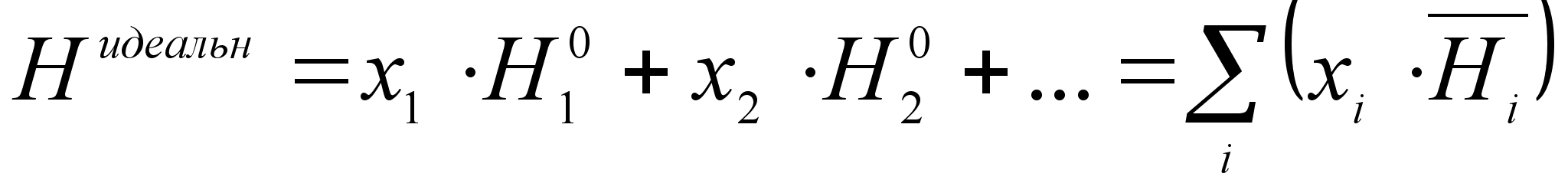
(19)
где Нидеальн - энтальпия 1 моля идеального раствора;
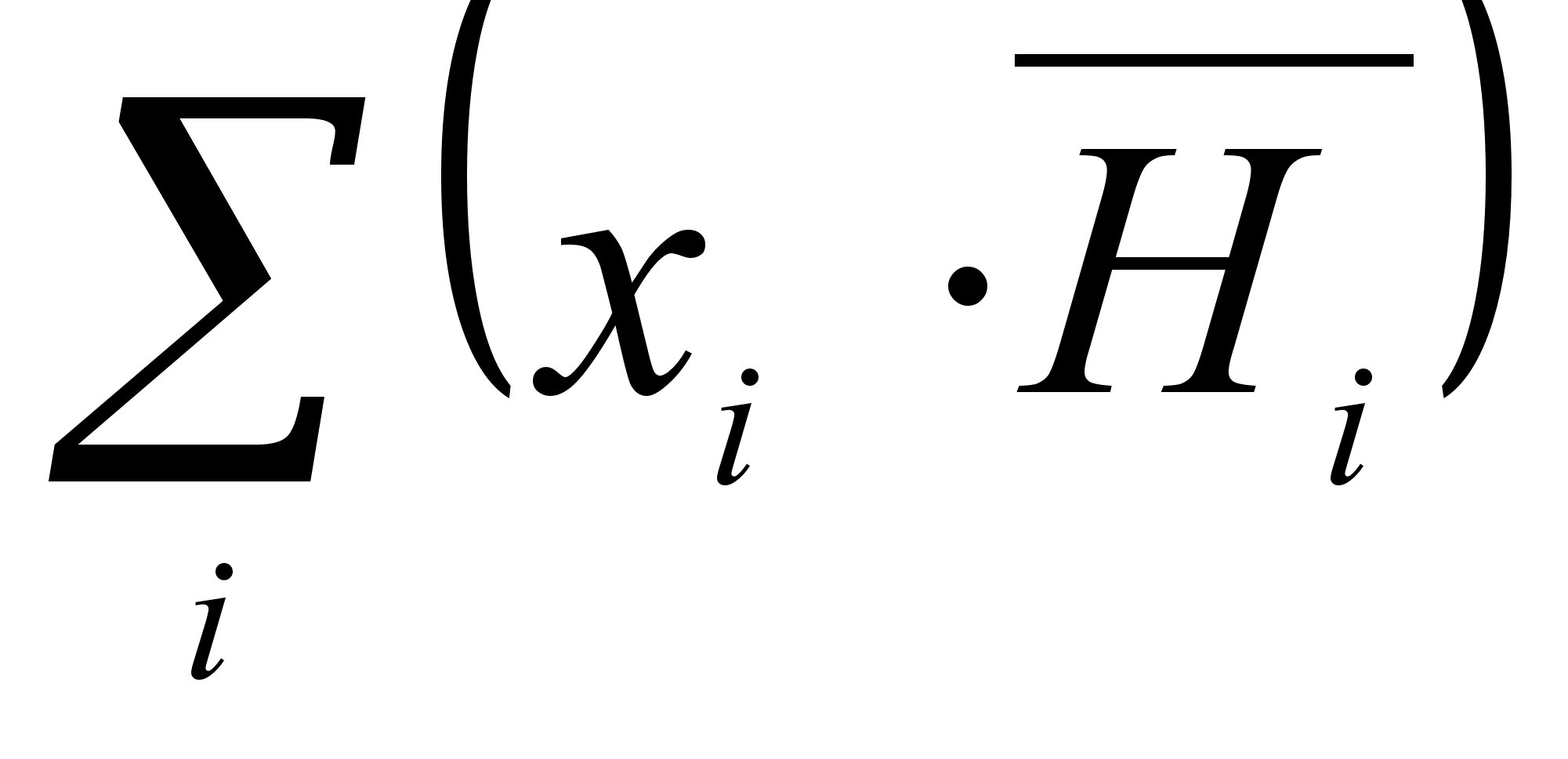 - энтальпия
всех компонентов
раствора до
смешения.
- энтальпия
всех компонентов
раствора до
смешения.
Из этого
следует, что
энтальпия, или
теплота смешения
для идеального
раствора
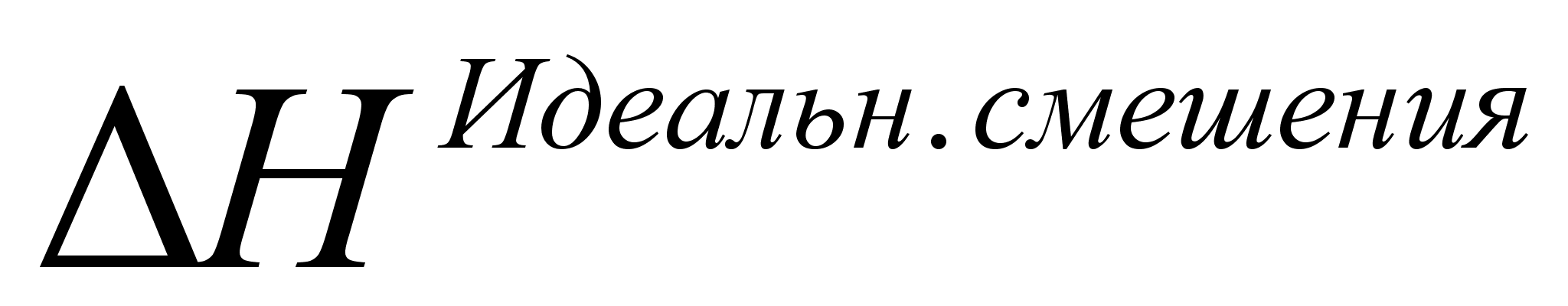 ,
равна нулю,
т.е. [2]
,
равна нулю,
т.е. [2]
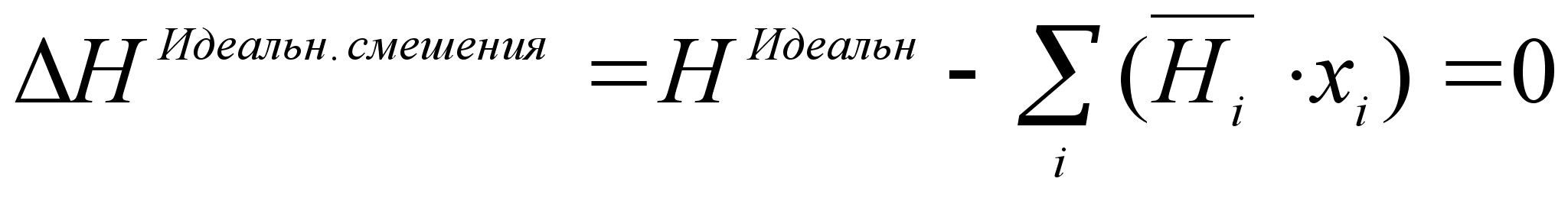
(20)
.Изменение объема при образовании идеального раствора. Можно показать таким же образом, как это было сделано выше, что изменение объема при образовании идеального раствора по отношению к аддитивному равно нулю.
Как
было сказано
ранее,
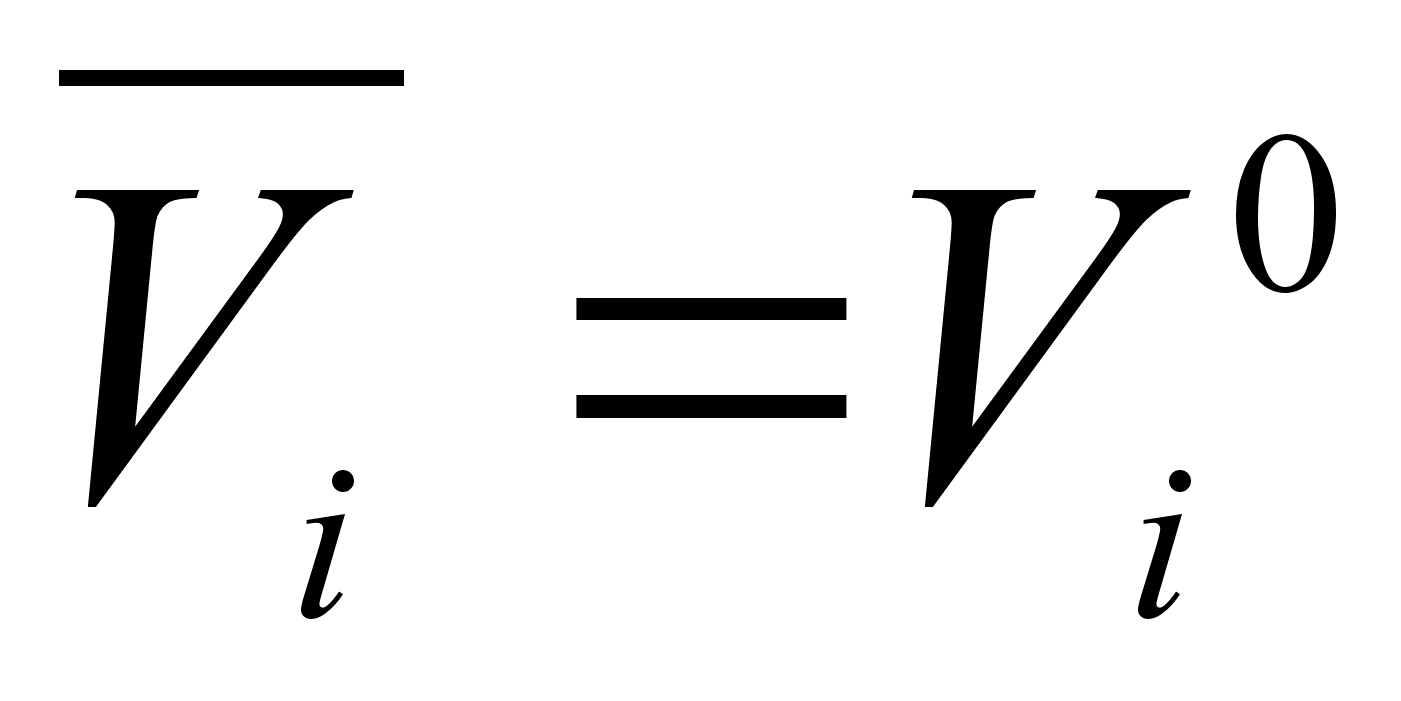 ,
т.е. парциальный
объем компонента
идеального
раствора равен
молярному
объему чистого
компонента.
Подставляя
значение
,
т.е. парциальный
объем компонента
идеального
раствора равен
молярному
объему чистого
компонента.
Подставляя
значение
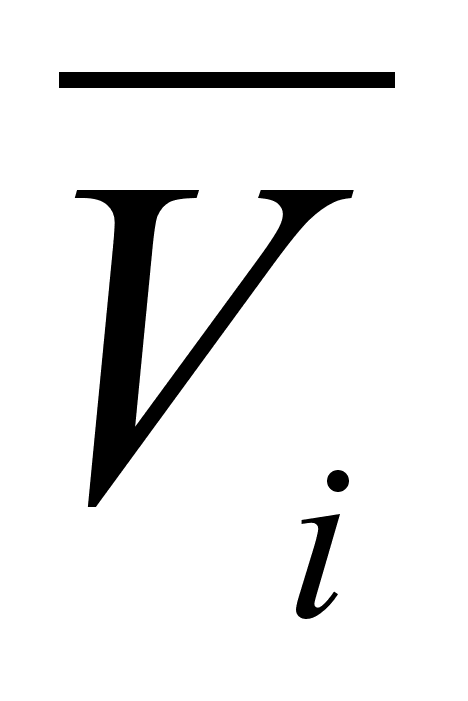 для каждого
компонента
в уравнение
аддитивного
сложения
характеристик
раствора, получим:
для каждого
компонента
в уравнение
аддитивного
сложения
характеристик
раствора, получим:
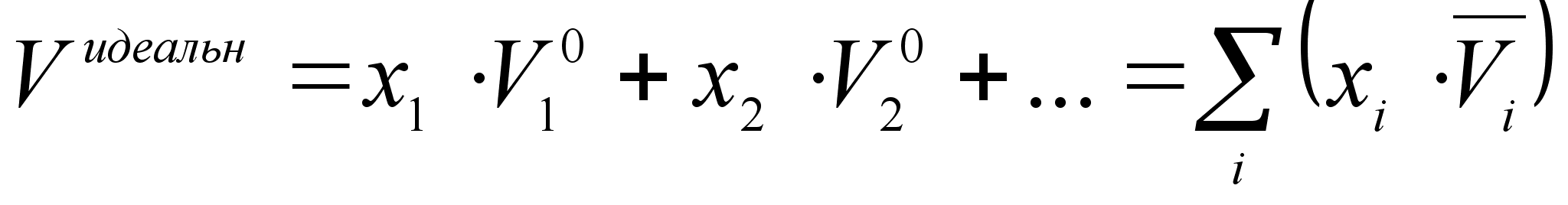
(21)
где Vидеальн - объем 1 моля идеального раствора;
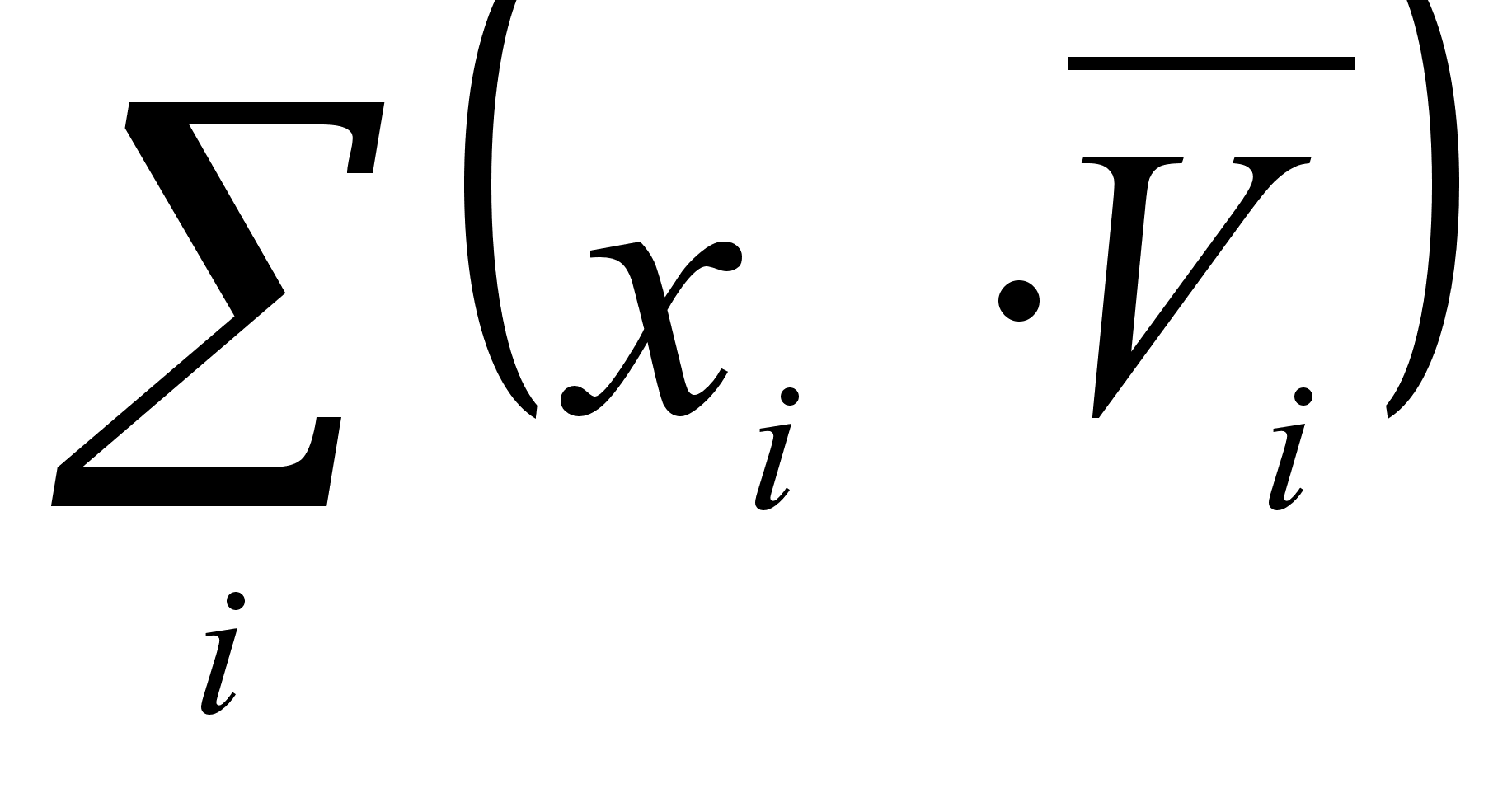 - объем
всех компонентов
раствора до
смешения.
- объем
всех компонентов
раствора до
смешения.
1.2.1.1 Совершенные растворы.
Как уже говорилось, идеальный совершенный раствор представляет такую модель, в которой закон Рауля выполняется с абсолютной точностью во всем интервале составов. Суммарная энергия взаимодействия частиц при образовании такого раствора из чистых компонентов не изменяется. [6] Такие растворы характеризуется благодаря близости свойств компонентов тем, что они образуются без теплового эффекта и без изменения объема. [1]
Фактором, который вызывает самопроизвольное образование совершенного раствора из чистых компонентов, является изменение энтропии. Оно обусловлено тем, что термодинамическая вероятность раствора (в котором каждая из молекул может находиться в любой части занимаемого им объема) выше, чем вероятность системы, где каждый из компонентов занимает только свой объем, составляющий лишь часть общего объема. Никакого дополнительного изменения энтропии, связанного с упорядочением хаотичного движением молекул, при образовании совершенного раствора не происходит. [6]
Таким образом, в отличие от величин H и V свободная энергия и энтропия при образовании совершенного раствора неаддитивны. Очевидно, энтропия раствора определяется уравнением: [1]
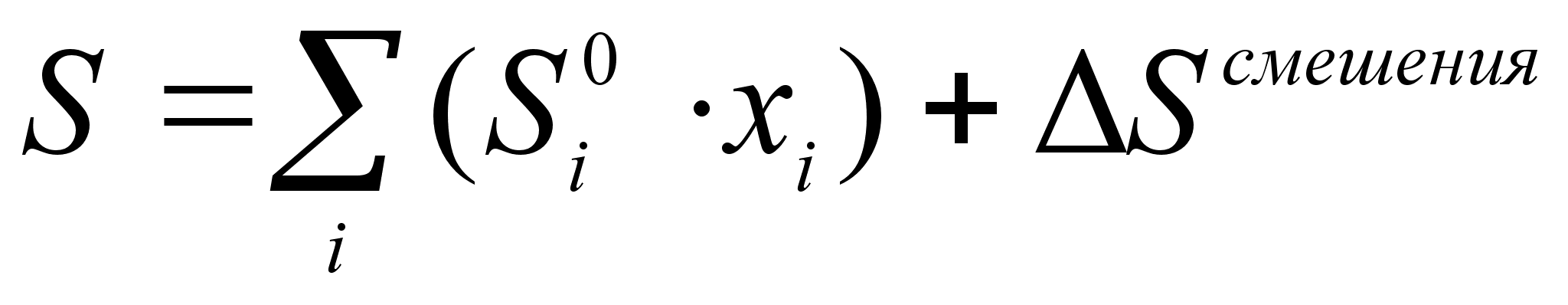
(22)
О
(23)
пределение энтропии образования совершенного раствора с использованием формул молекулярной статистики дает следующие выражения: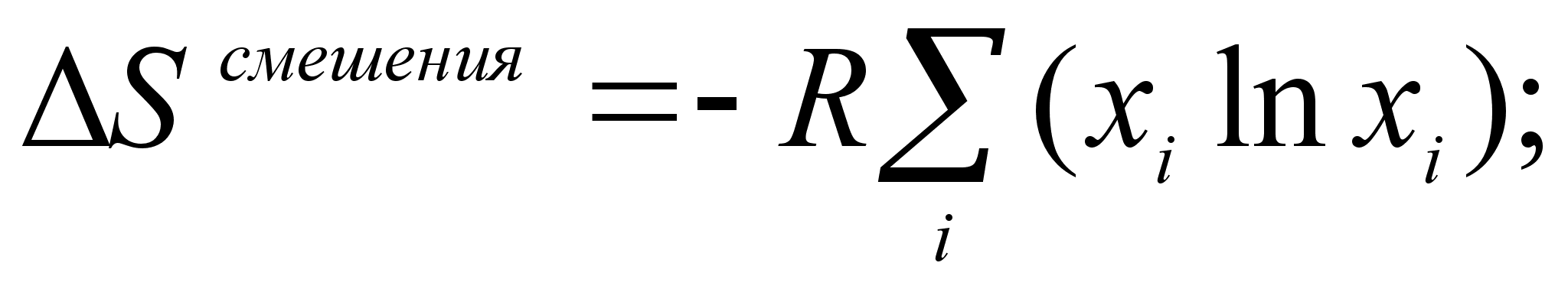
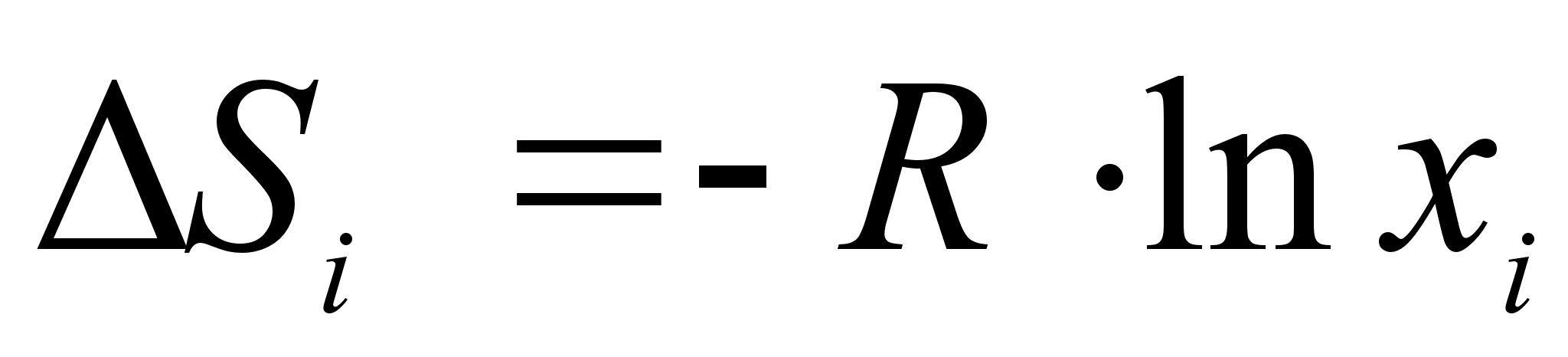
(24)
.Отсюда следует:
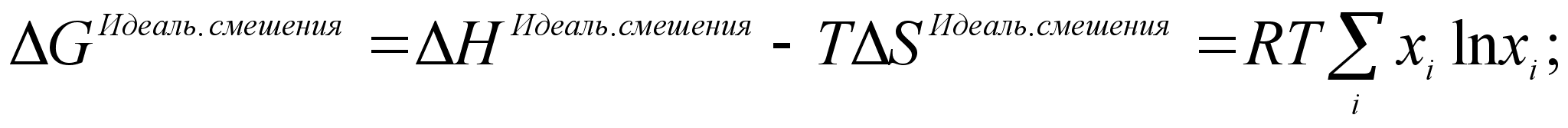
(25)

(26)
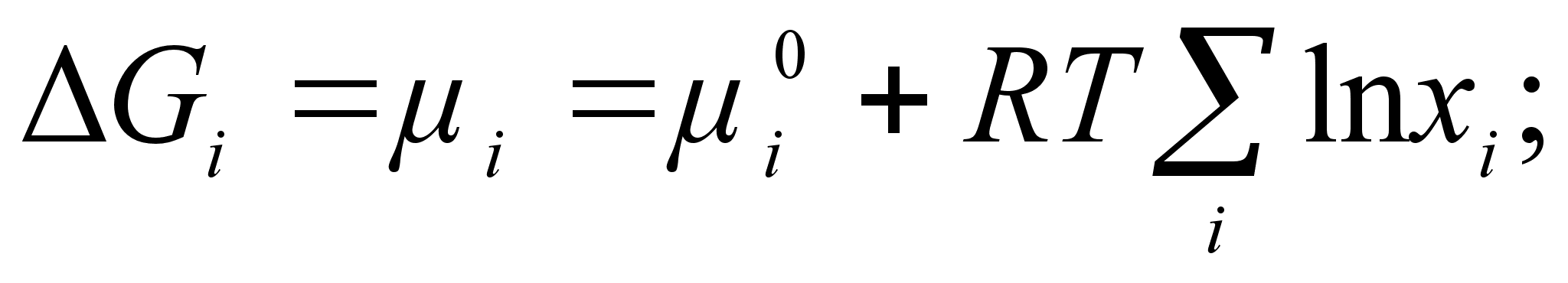
(27)
где
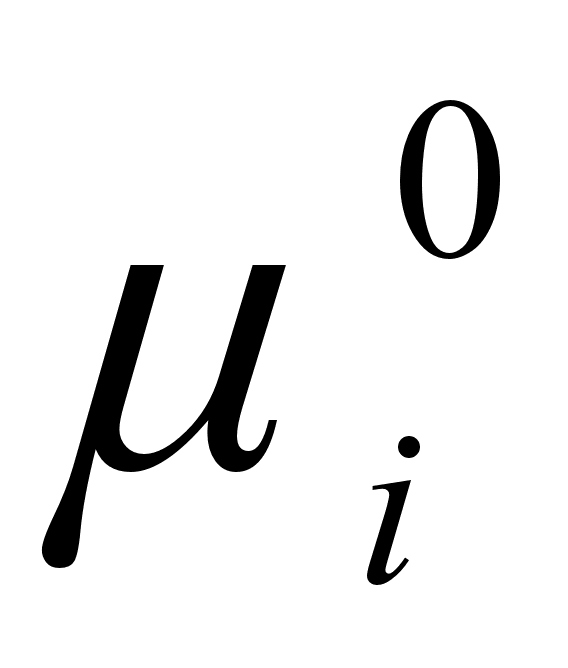 - химический
потенциал
компонента
в стандартном
состоянии (при
xi=1).
Из приведенных
выражений (с
учетом xi
- химический
потенциал
компонента
в стандартном
состоянии (при
xi=1).
Из приведенных
выражений (с
учетом xi характеризуется
симметричной
кривой (см. рисунок
1) с максимумом
в точке х1=х2=0,5
, для которой
характеризуется
симметричной
кривой (см. рисунок
1) с максимумом
в точке х1=х2=0,5
, для которой
 =5,77
Дж/(моль*К).
=5,77
Дж/(моль*К).
П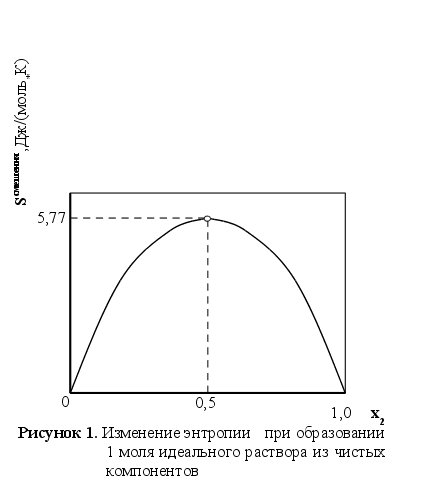 од
активностью
компонента
в растворе
понимают отношение
давления насыщенного
пара компонента
над раствором
к аналогичной
величине для
компонента
в стандартном
состоянии:
од
активностью
компонента
в растворе
понимают отношение
давления насыщенного
пара компонента
над раствором
к аналогичной
величине для
компонента
в стандартном
состоянии:
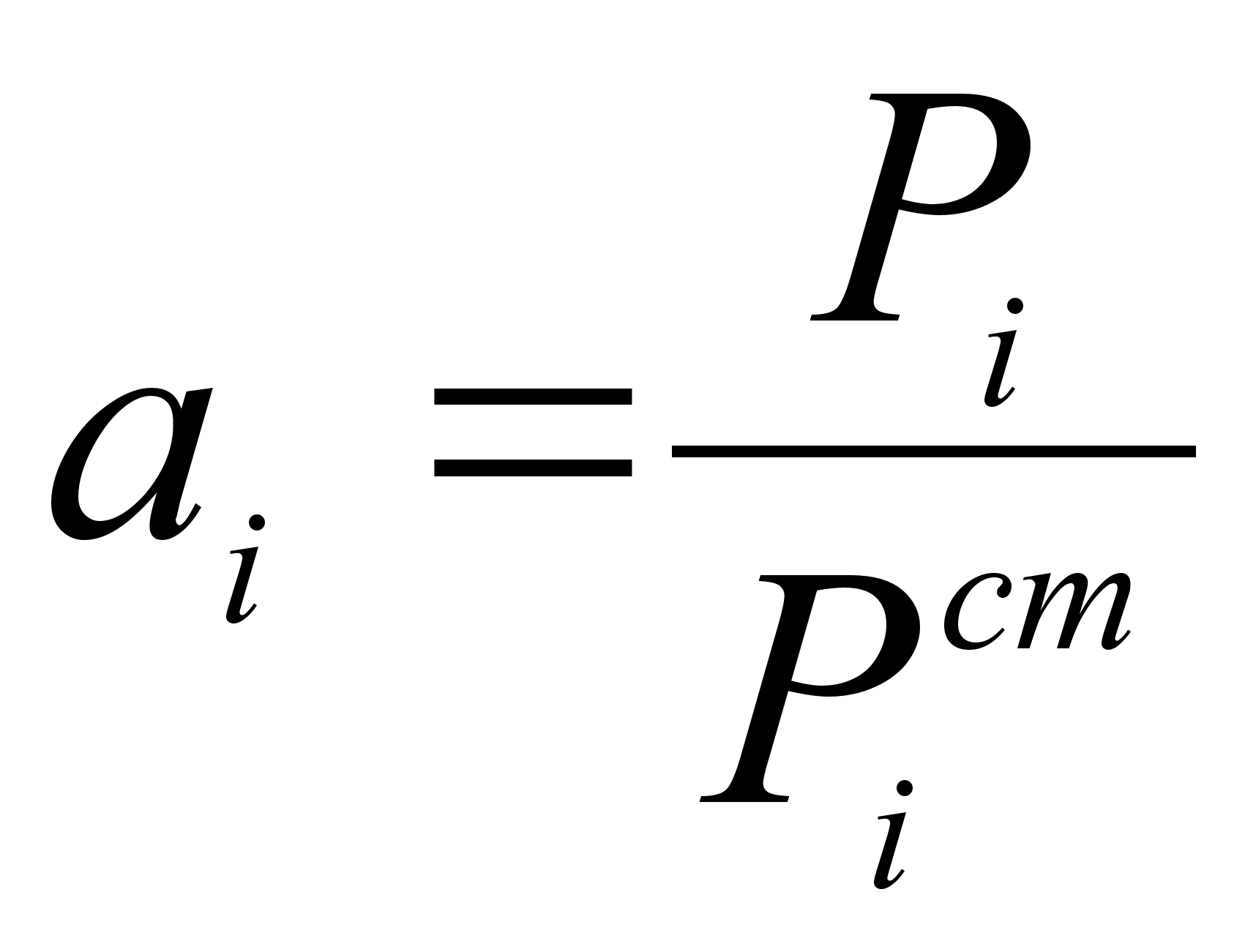
(28)
,где ai – активность компонента i в растворе;
Pi – давление насыщенного пара компонента i над раствором;
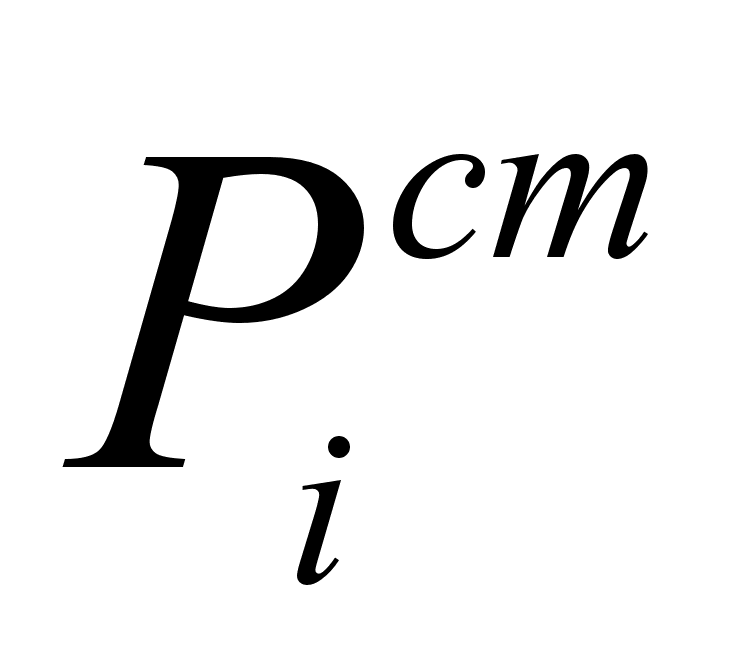 -
давление насыщенного
пара компонента
в стандартном
состоянии.
-
давление насыщенного
пара компонента
в стандартном
состоянии.
В бинарном растворе 1-2 (рисунок 1) активность компонента 2 при его молярной доле х2:
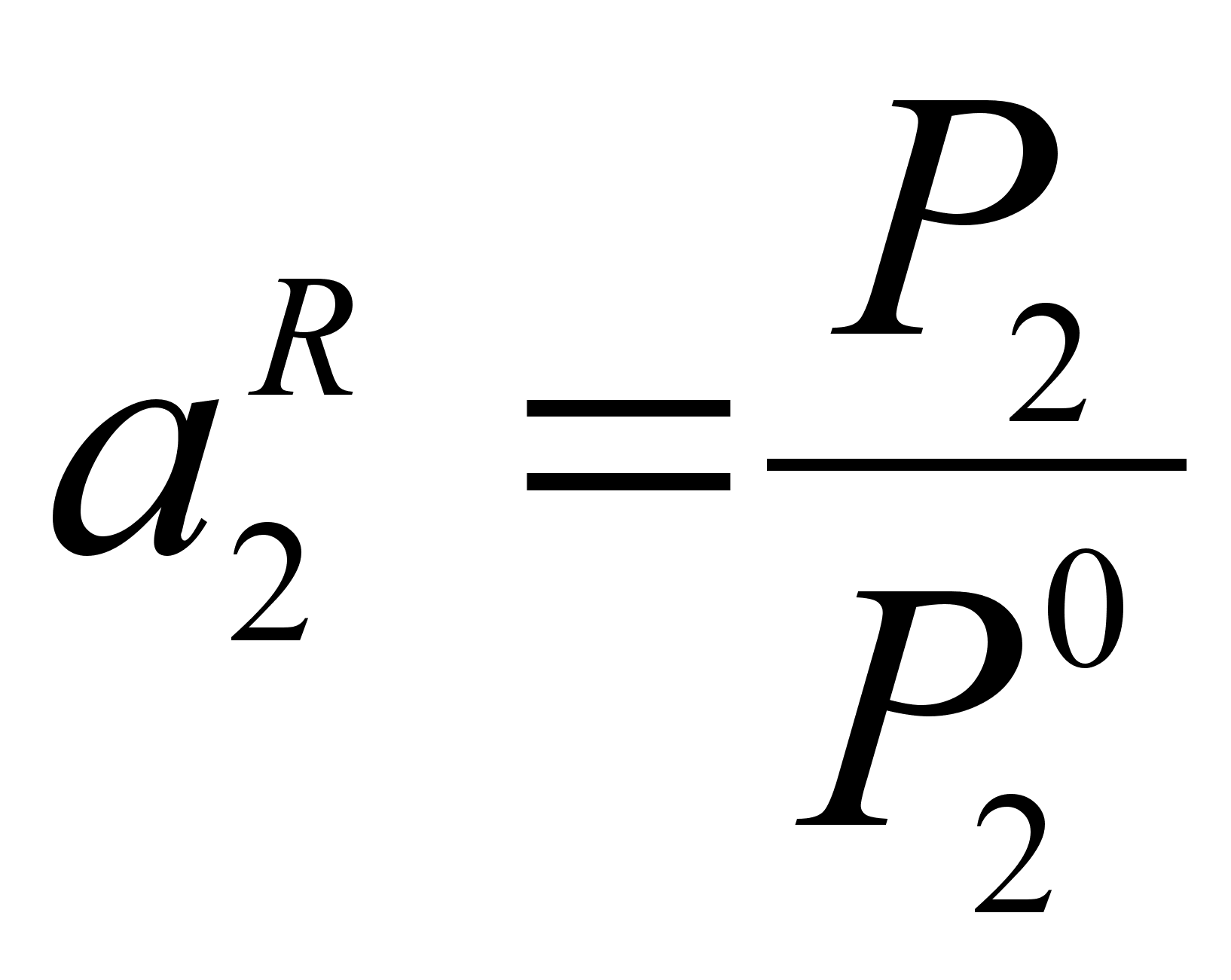
(29)
,где Р2 – давление насыщенного пара компонента 2 над раствором с концентрацией 2, равной х2;
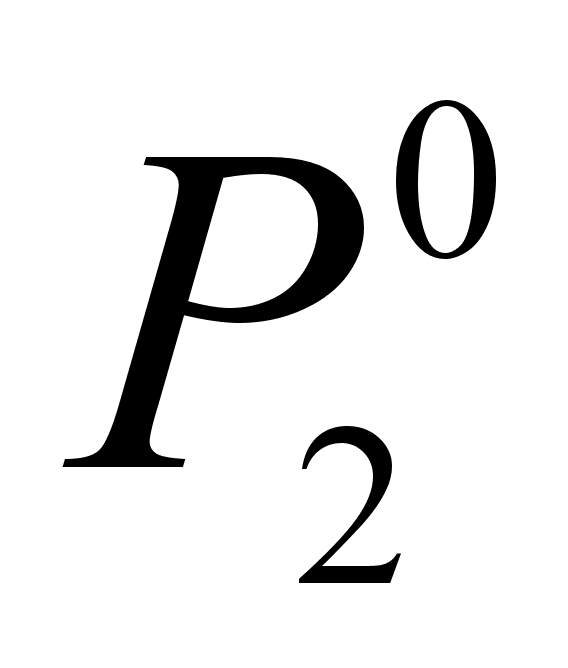 - давление
насыщенного
пара компонента
2 над чистым
веществом 2 при
той же температуре.
- давление
насыщенного
пара компонента
2 над чистым
веществом 2 при
той же температуре.
Из закона Рауля при той же концентрации х2 (см. рисунок 1) имеем:
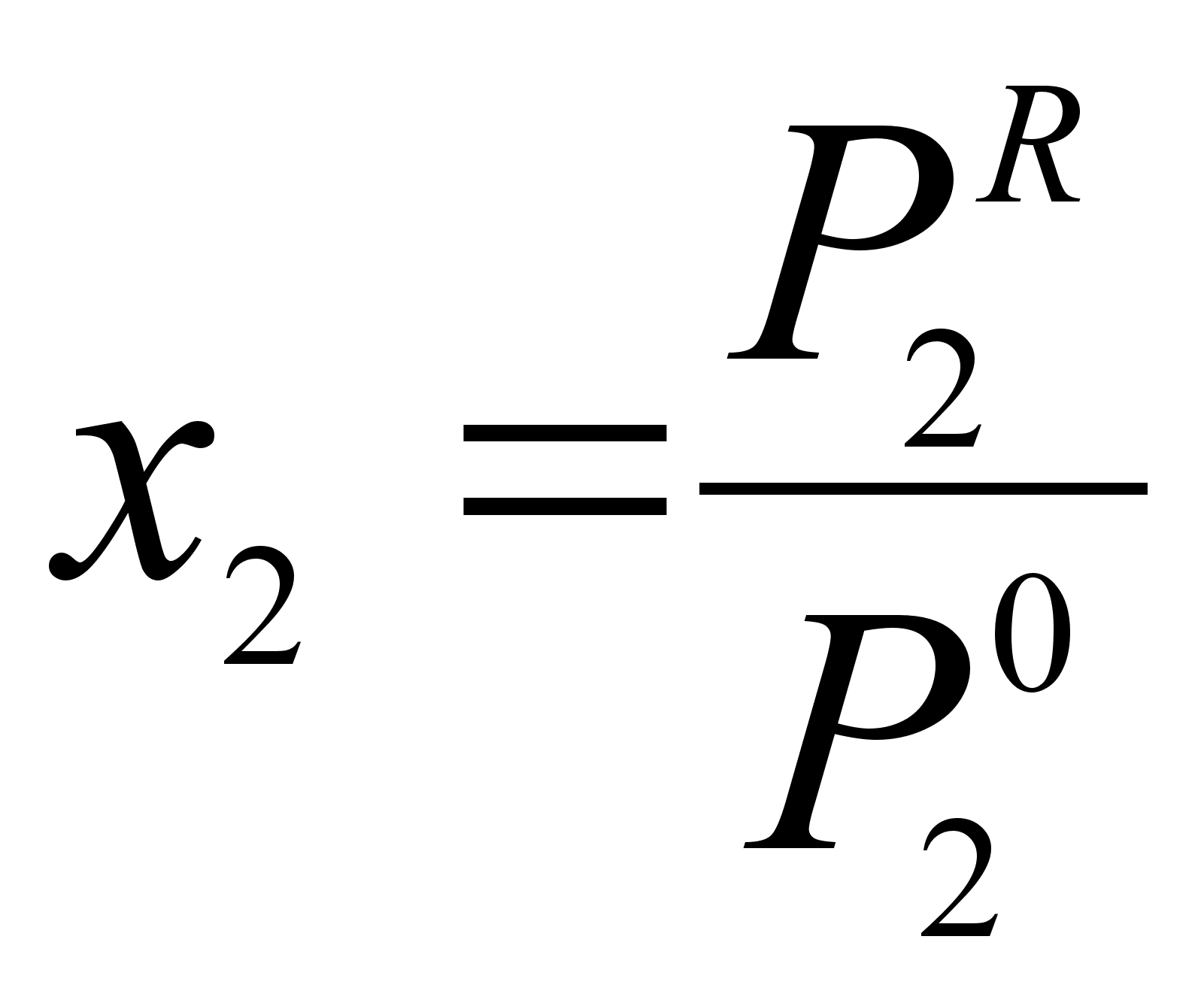
(30)
,
где
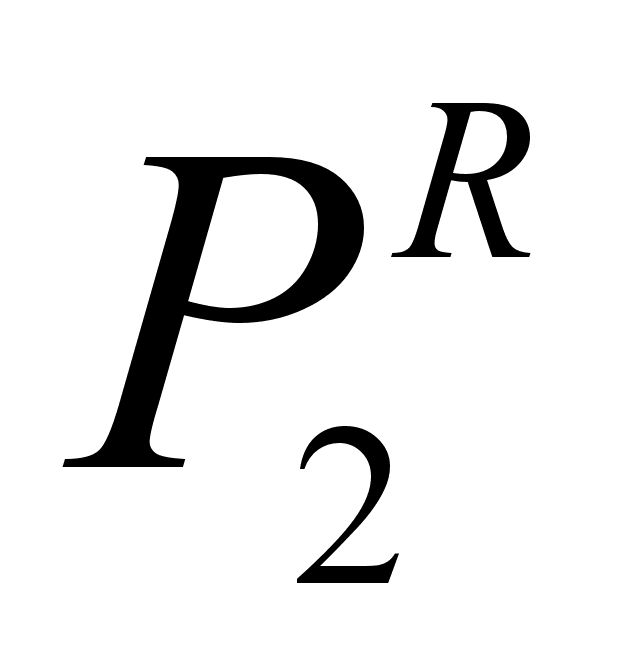 -
давление насыщенного
пара компонента
2, полученное
расчетом по
закону Рауля
для концентрации
х2.
-
давление насыщенного
пара компонента
2, полученное
расчетом по
закону Рауля
для концентрации
х2.
Для количественной
оценки отклонения
от закона Рауля
вводится коэффициент
активности
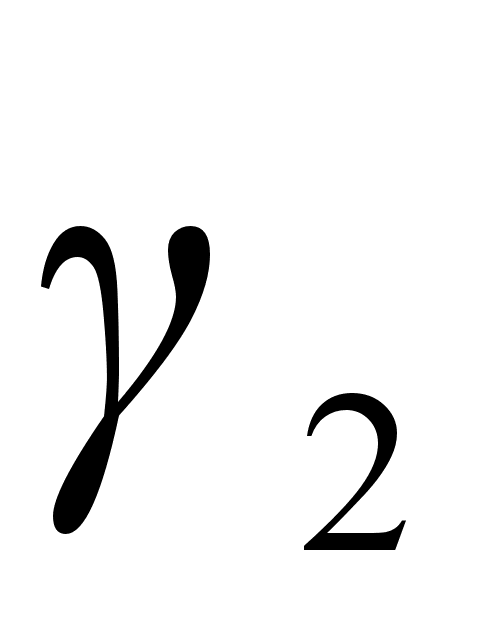 ,
который устанавливает
связь между
активностью
и концентрацией:
,
который устанавливает
связь между
активностью
и концентрацией:
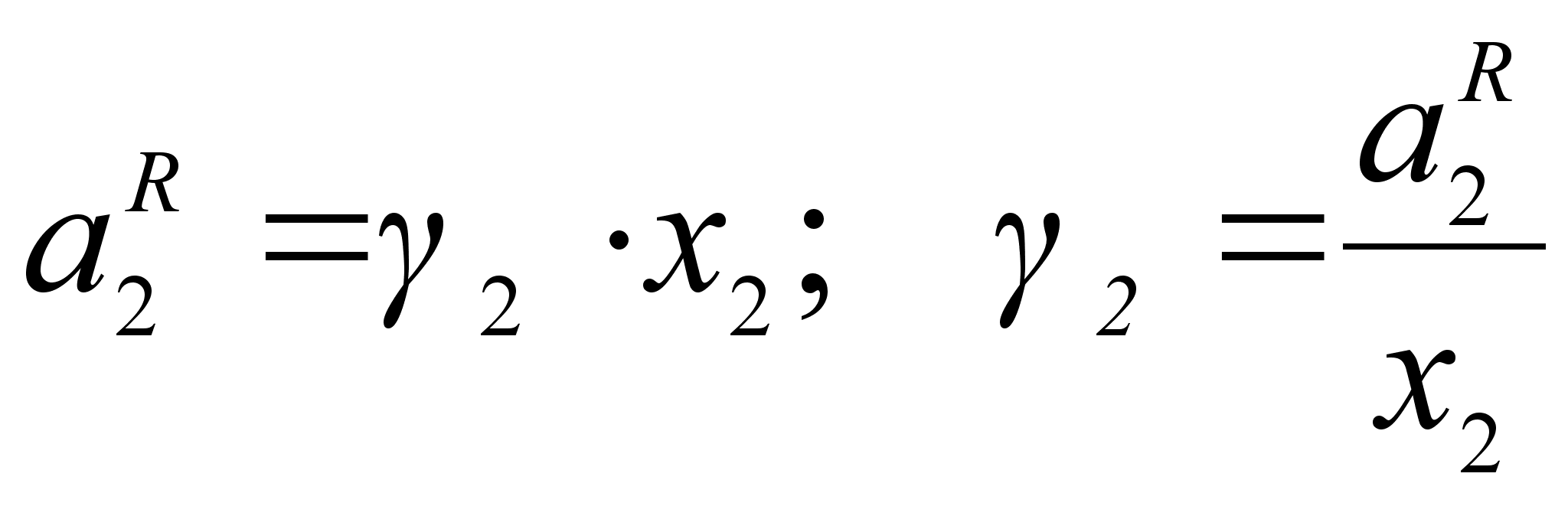
(31)
.И
(32)
з рисунка 1 следует также, что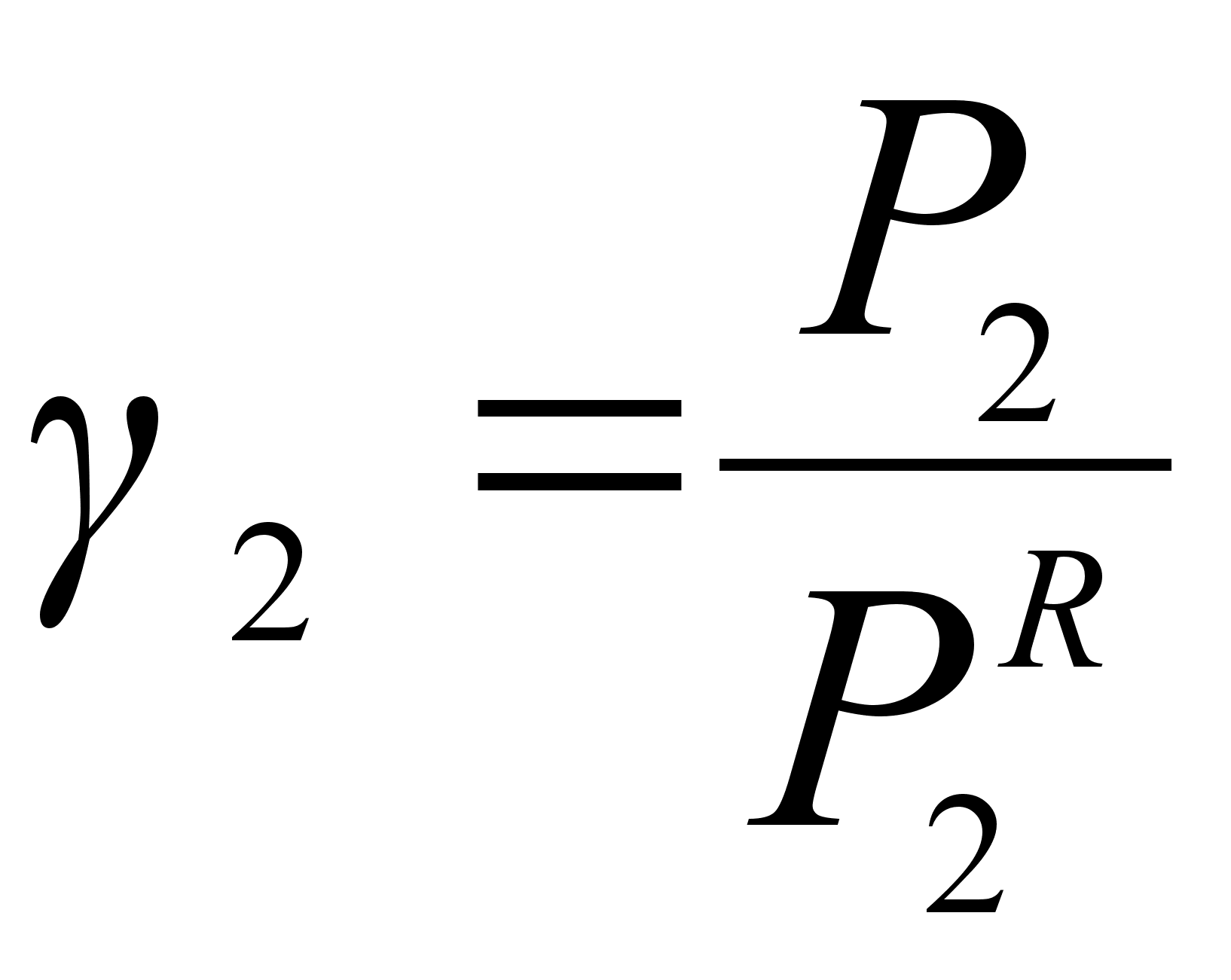
Для идеальных
растворов
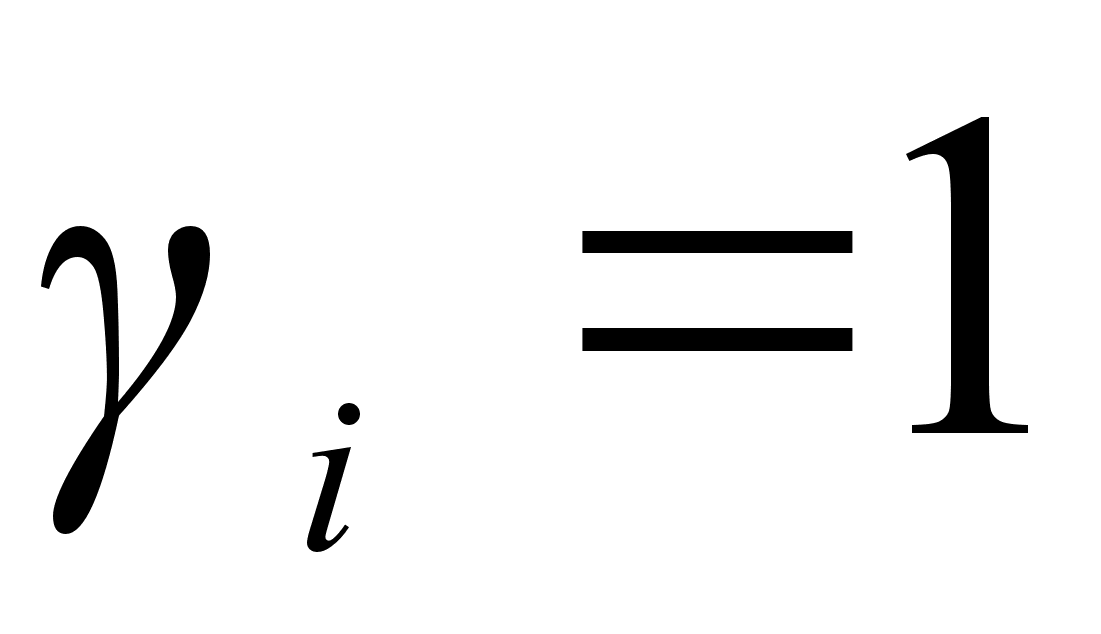 и
и
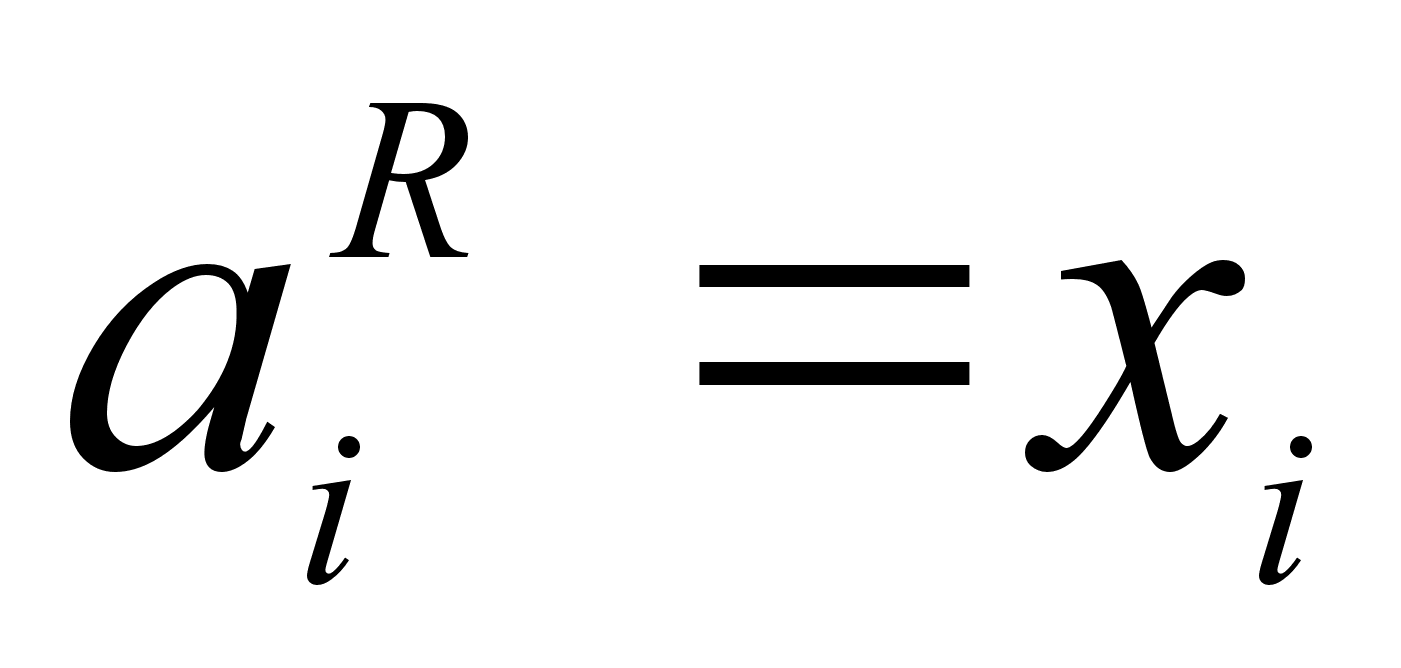 .
В случае отрицательных
отклонений
от закона Рауля
.
В случае отрицательных
отклонений
от закона Рауля
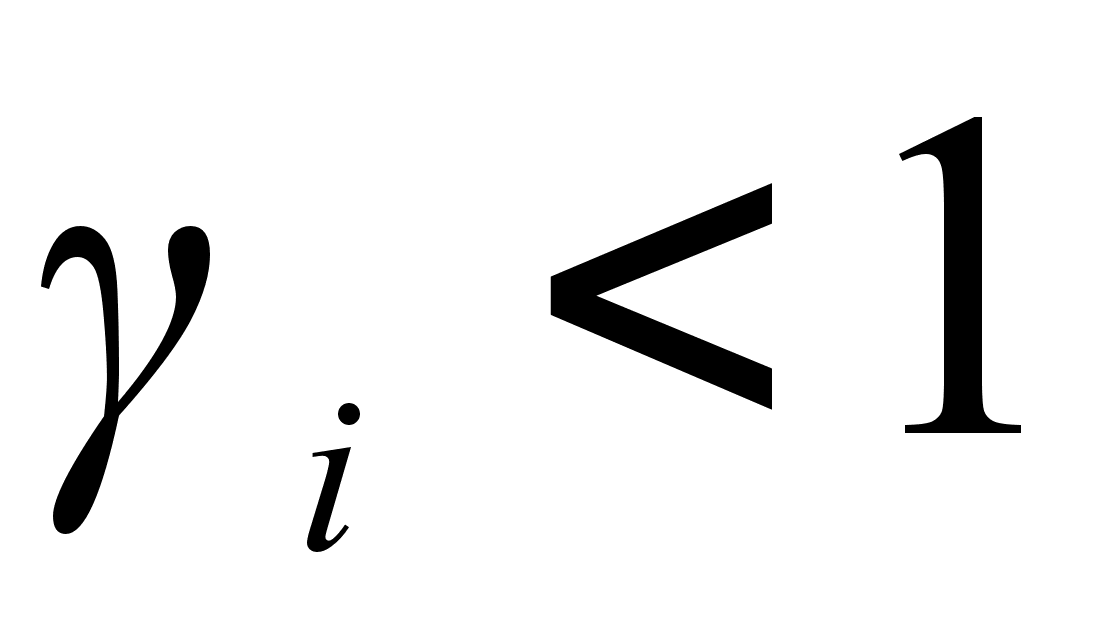 .
При положительных
отклонений
от закона Рауля
.
При положительных
отклонений
от закона Рауля
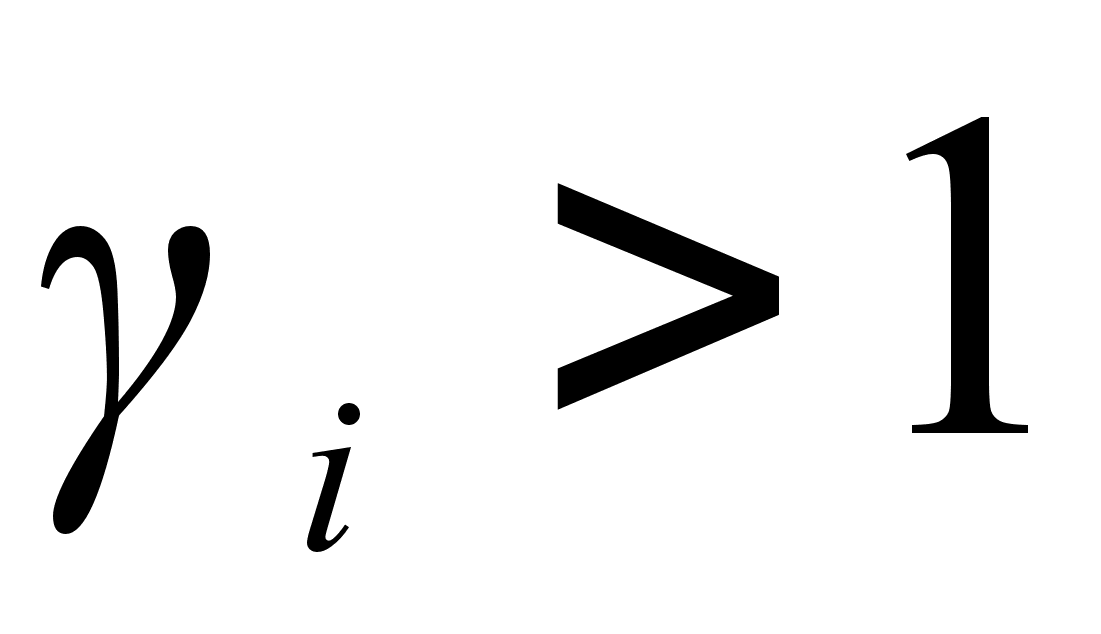 .
[6]
.
[6]
1.2.1.2 Совершенные растворы
Применительно к растворам различных компонентов в металлах, мы обычно имеем дело с разбавленными растворами этих компонентов. Термин «разбавленный раствор» применяют к системам, в жидкой фазе которых содержание одного элемента значительно превышает содержание других компонентов. В количественном отношении этот термин является довольно неопределенным, так как нельзя указать какие-то концентрационные границы, в пределах которых раствор следует считать разбавленным. В каждом отдельном случае представление о степени разбавленности раствора связано с тем, какие свойства его и с какой точностью исследуют. [3]
В таких разбавленных растворах термодинамические характеристики растворенного вещества пропорциональны его концентрации, несмотря на значительные отклонения от закона Рауля. Такое поведение растворенного вещества в разбавленном растворе соответствует закону Генри. [5]
С
(33)
огласно закону Генри, при малых концентрациях растворенного вещества его парциальное давление (давление насыщенного пара над раствором) прямо пропорционально мольной доле этого компонента:Рi=ki ci
(при условии, что вещество i - не растворитель),
где ki – коэффициент (константа) Генри, зависящий от химической природы компонентов, а также от выбранных единиц измерения концентрации.
Особенность
модели разбавленного
раствора заключается
в том, что она
(в отличие от
модели совершенного
раствора) не
определяет
величину энергии
взаимодействия
растворенного
вещества с
растворителем.
Для упрощения
(необходимого
в любой модели)
не учитывается
взаимодействие
молекул растворенного
вещества друг
с другом (в связи
с их малой
концентрацией),
они реагируют
лишь с молекулами
растворителя.
Таким образом,
добавление
растворенного
вещества в
разбавленный
раствор вызывает
такое же изменение
внутренней
энергии и энтальпии
системы, как
добавление
его в чистый
растворитель
(при условии,
что раствор
и после добавления
останется
разбавленным),
т.е. парциальная
мольная энтальпия
растворенного
вещества в
разбавленном
растворе
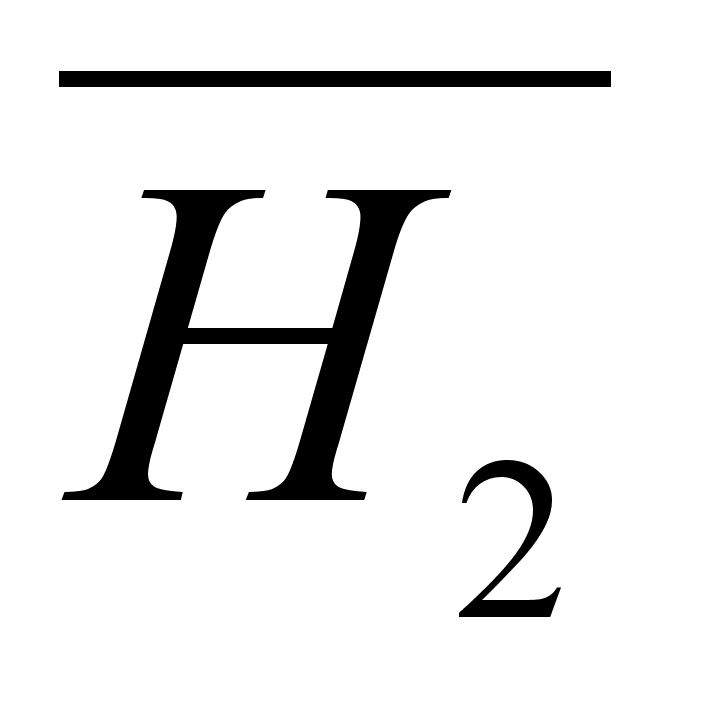 не зависит от
концентрации:
не зависит от
концентрации:

(34)
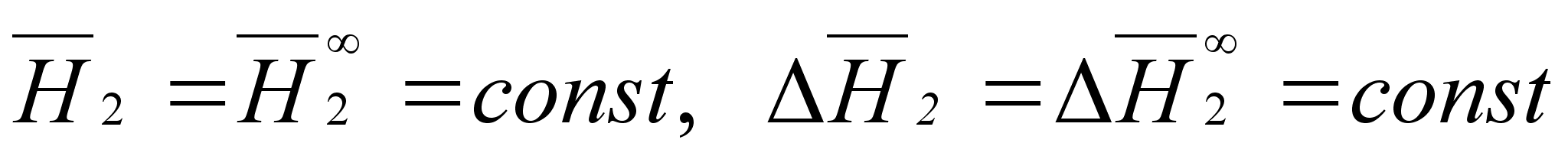 .
.
Знак
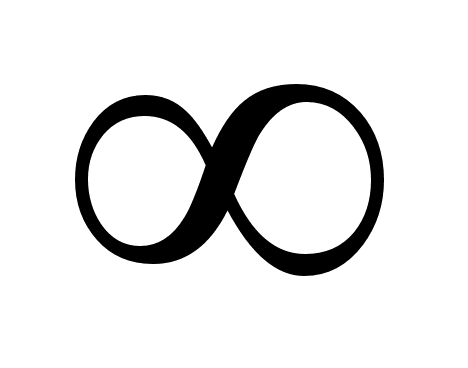 означает, что
величина относится
к начальной
области концентраций
и имеет такое
же значение,
как в бесконечно
разбавленном
растворе. [6]
означает, что
величина относится
к начальной
области концентраций
и имеет такое
же значение,
как в бесконечно
разбавленном
растворе. [6]
Гипотетическое
стандартное
состояние
вещества (Генриево
гипотетическое
состояние)
получают путем
экстраполяции
закона Генри
от крайне низких
концентраций
 до значения
до значения
 .
Это состояние
(точка h
на рисунке 2)
представляет
собой чистое
вещество 2
в гипотетическом,
нереальном
состоянии, в
котором оно
существовало
как чистый
компонент, если
бы подчинялось
закону Генри
во всем интервале
концентраций,
вплоть до чистого
вещества. Иными
словами, если
бы вещество
в чистом виде
характеризовалось
теми же свойствами,
что и в бесконечно
разбавленном
растворе. [5]
.
Это состояние
(точка h
на рисунке 2)
представляет
собой чистое
вещество 2
в гипотетическом,
нереальном
состоянии, в
котором оно
существовало
как чистый
компонент, если
бы подчинялось
закону Генри
во всем интервале
концентраций,
вплоть до чистого
вещества. Иными
словами, если
бы вещество
в чистом виде
характеризовалось
теми же свойствами,
что и в бесконечно
разбавленном
растворе. [5]
И
(35)
зменение энтропии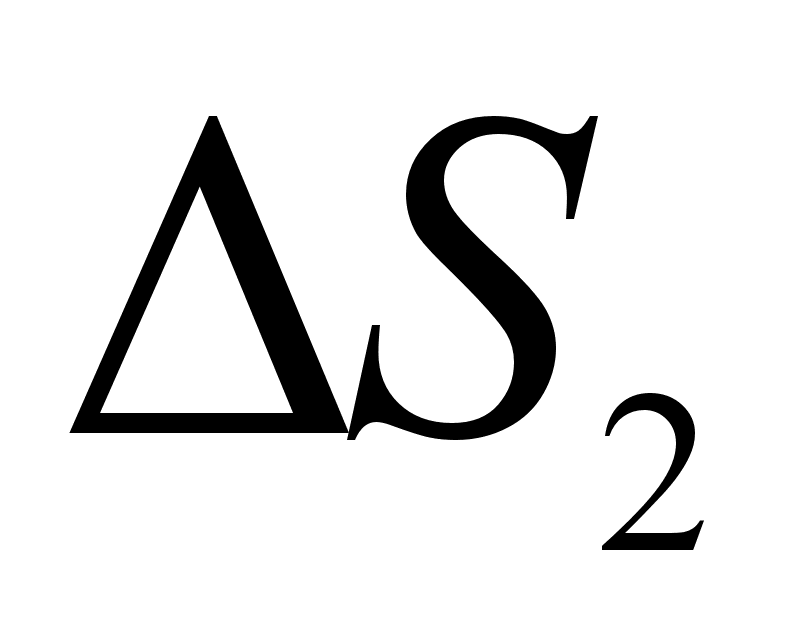 при образовании
разбавленного
раствора представляет
собой сумму
двух величин.
Первая величина
связана с изменением
состояния
молекул и,
следовательно,
в области
разбавленных
растворов не
зависит от
состава. Вторая
величина, как
и в случае
совершенных
растворов,
обусловлена
увеличением
объема, предоставленного
молекулам
растворенного
вещества при
переходе их
из индивидуального
компонента
в раствор. Эта
величина
пропорциональна
логарифму
объема раствора,
приходящегося
на единицу
количества
компонента
2, т.е.
обратно пропорциональна
логарифму
концентрации
с2,
выраженной
в любых единицах.
Таким образом:
при образовании
разбавленного
раствора представляет
собой сумму
двух величин.
Первая величина
связана с изменением
состояния
молекул и,
следовательно,
в области
разбавленных
растворов не
зависит от
состава. Вторая
величина, как
и в случае
совершенных
растворов,
обусловлена
увеличением
объема, предоставленного
молекулам
растворенного
вещества при
переходе их
из индивидуального
компонента
в раствор. Эта
величина
пропорциональна
логарифму
объема раствора,
приходящегося
на единицу
количества
компонента
2, т.е.
обратно пропорциональна
логарифму
концентрации
с2,
выраженной
в любых единицах.
Таким образом:
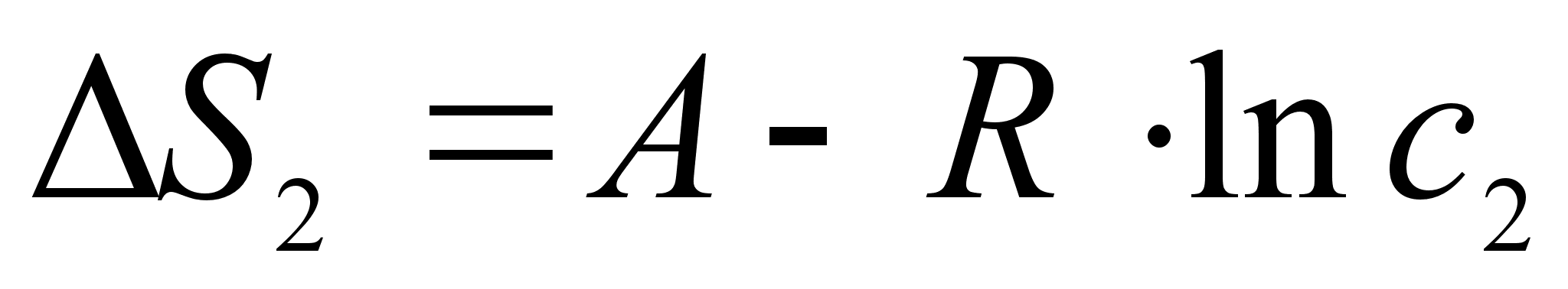
где А - постоянная величина, не зависящая от состава раствора, но зависящая от выбора единиц измерения с2. [6]
О
(36)
(37)
тсюда: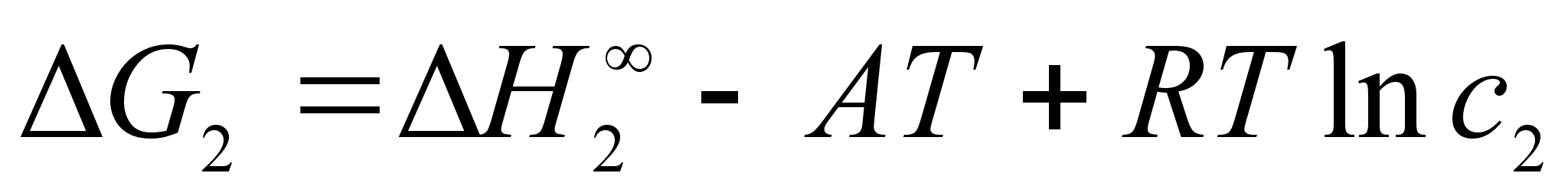
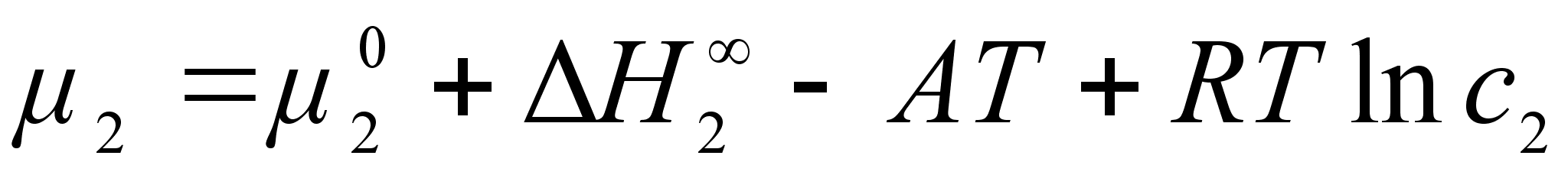
Активность компонента 2 при его концентрации х2 по отношению к гипотетическому стандартному состоянию (см. рисунок 2):
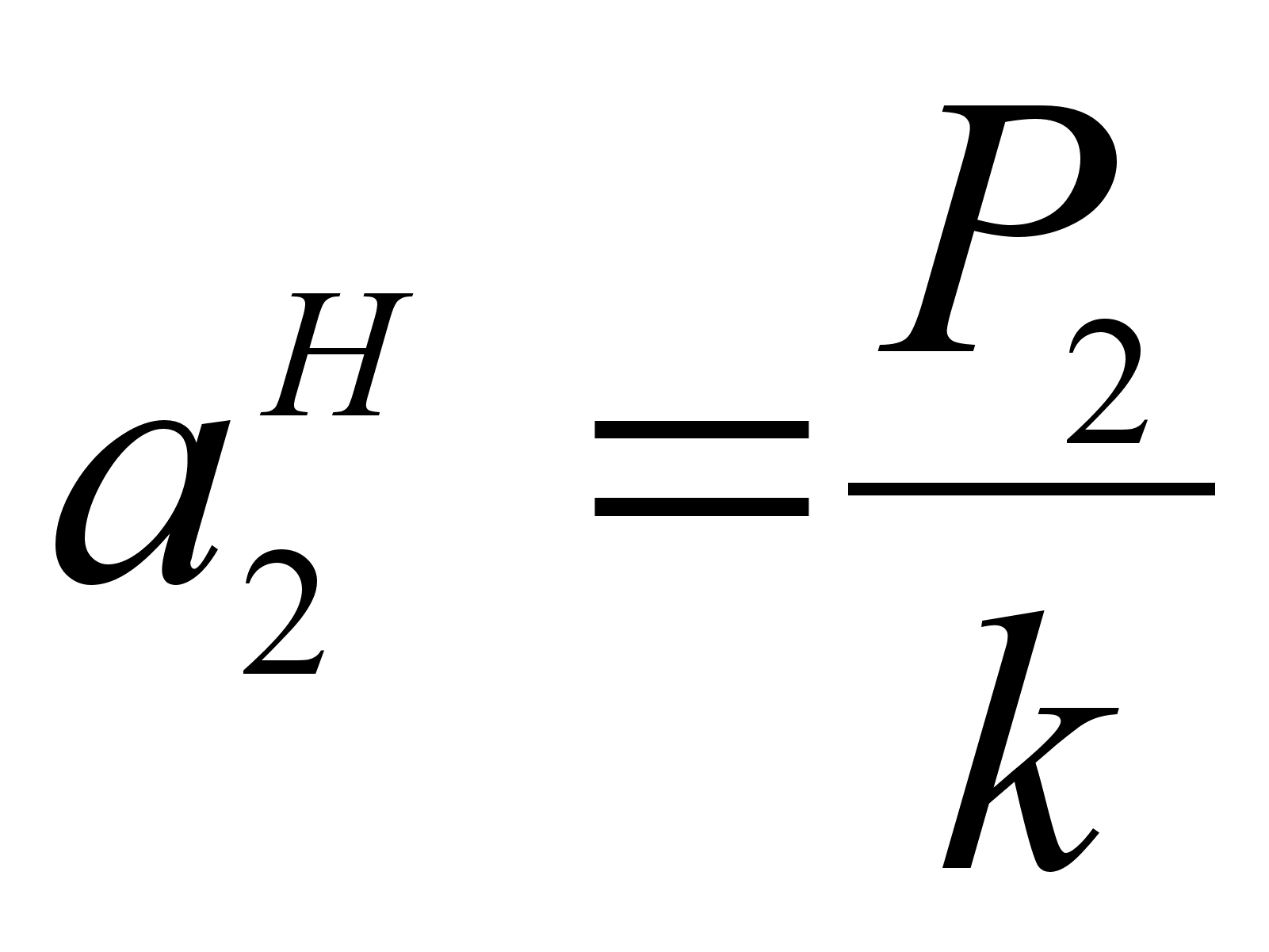
(38)
Т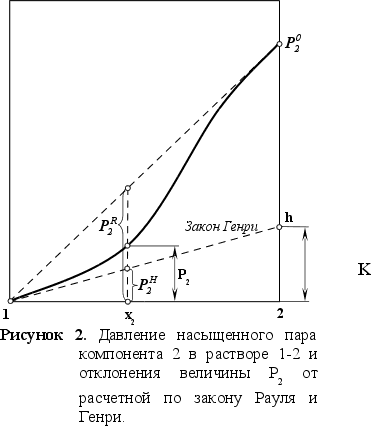 акое
же выражение
получается
из закона Генри
путем замены
концентрации
на активность:
акое
же выражение
получается
из закона Генри
путем замены
концентрации
на активность:
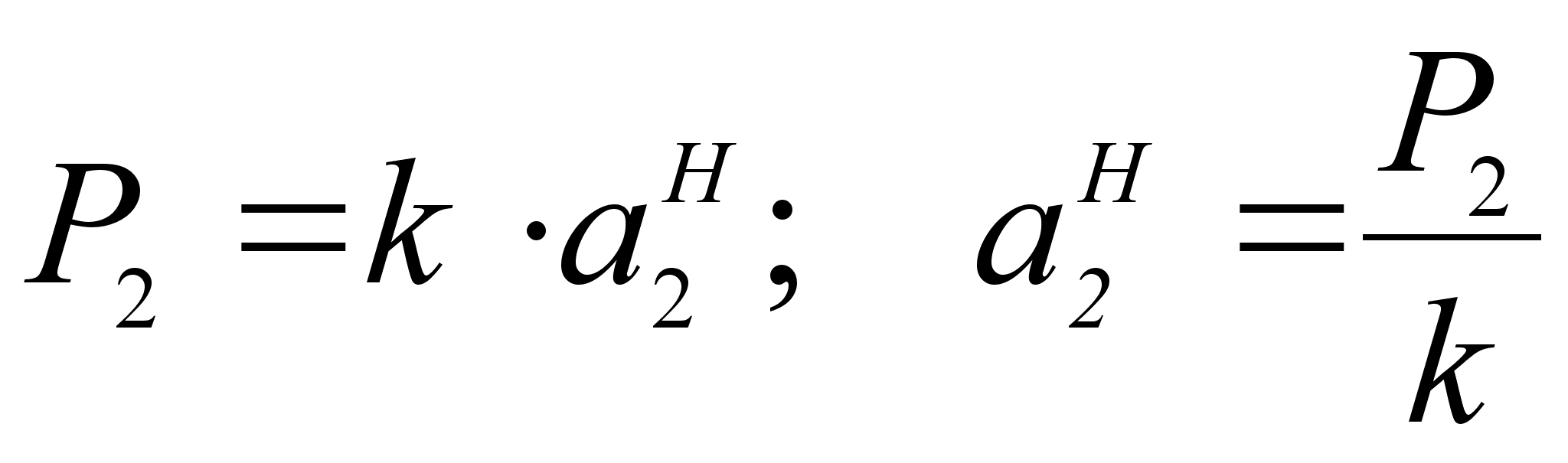 .
.
Отклонение
от закона Генри
характеризуется
коэффициентом
активности
f2.
Такое обозначение
для коэффициента
активности
веществ в
разбавленных
растворах
введено для
того, чтобы
отличить этот
коэффициент
активности,
показывающий
отклонения
от закона Генри
от коэффициента
активности
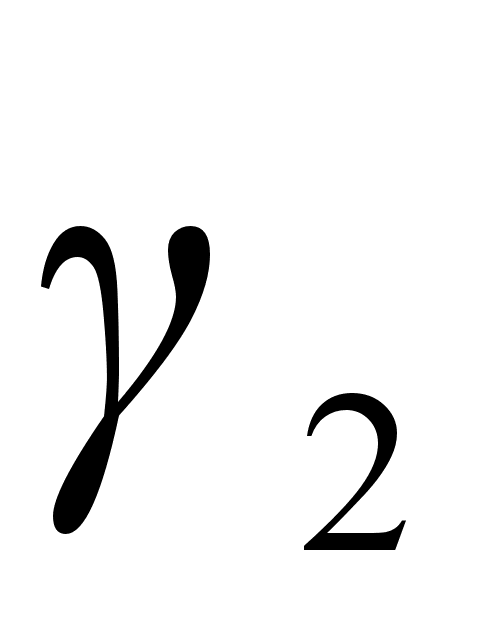 ,
показывающего
отклонения
от закона Рауля.
,
показывающего
отклонения
от закона Рауля.
Коэффициент активности f2 связывает концентрацию компонента х2 с его активностью в разбавленном растворе по отношению к гипотетическому стандартному состоянию в виде следующего выражения:
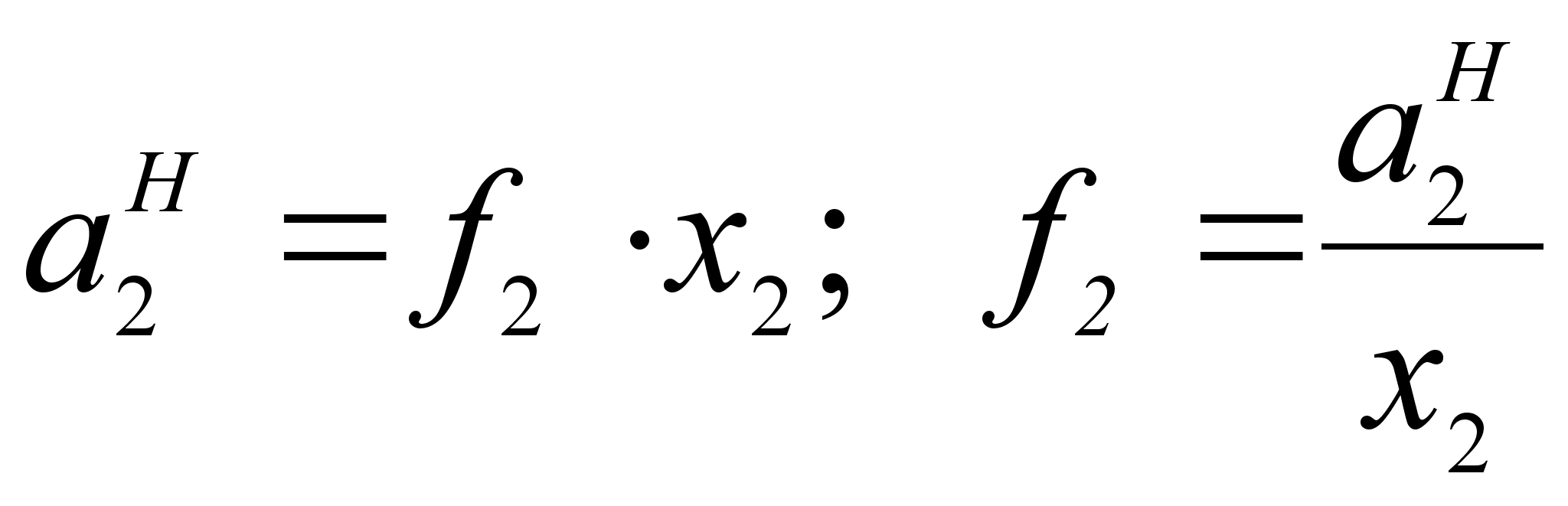
(39)
.Из закона Генри следует, что :
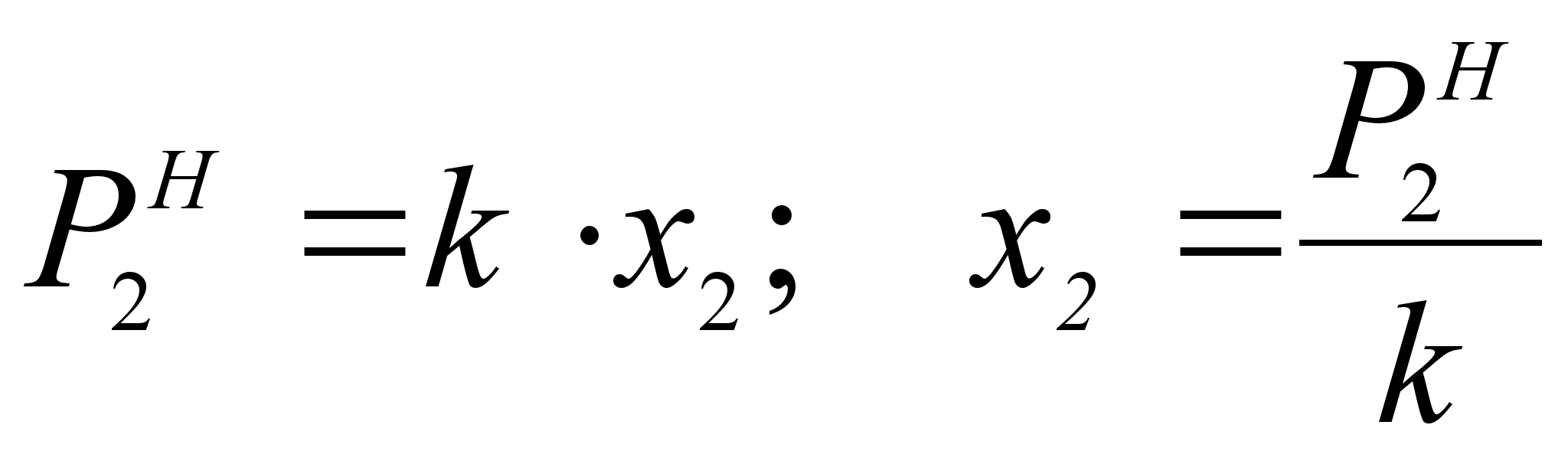
(40)
.Поэтому коэффициент активности можно определить по соотношению (см. рисунок 2):
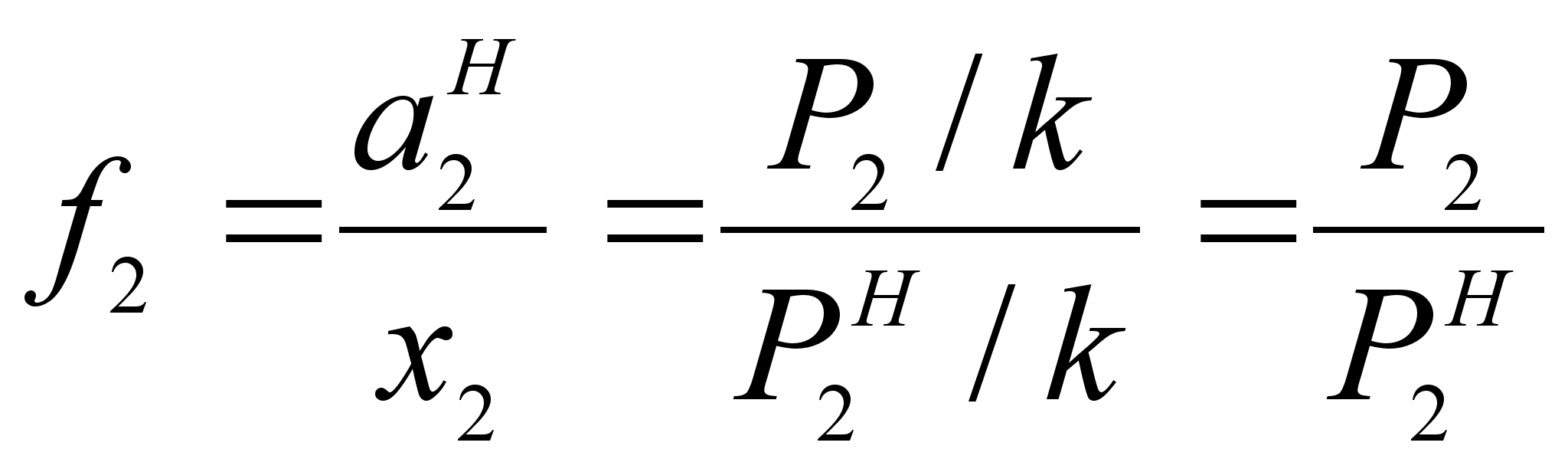
(41)
.
В области
разбавленных
растворов
разница между
Р2
и
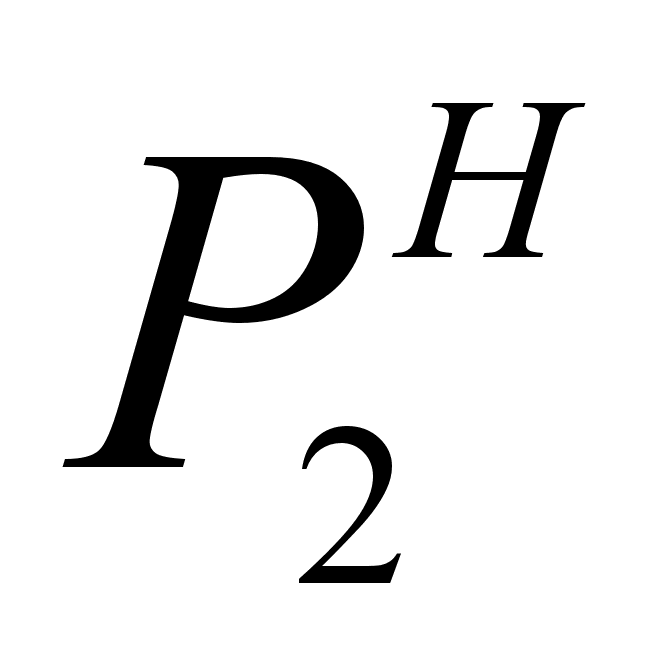 обычно мала,
поэтому для
области низких
концентраций
растворенного
вещества
обычно мала,
поэтому для
области низких
концентраций
растворенного
вещества
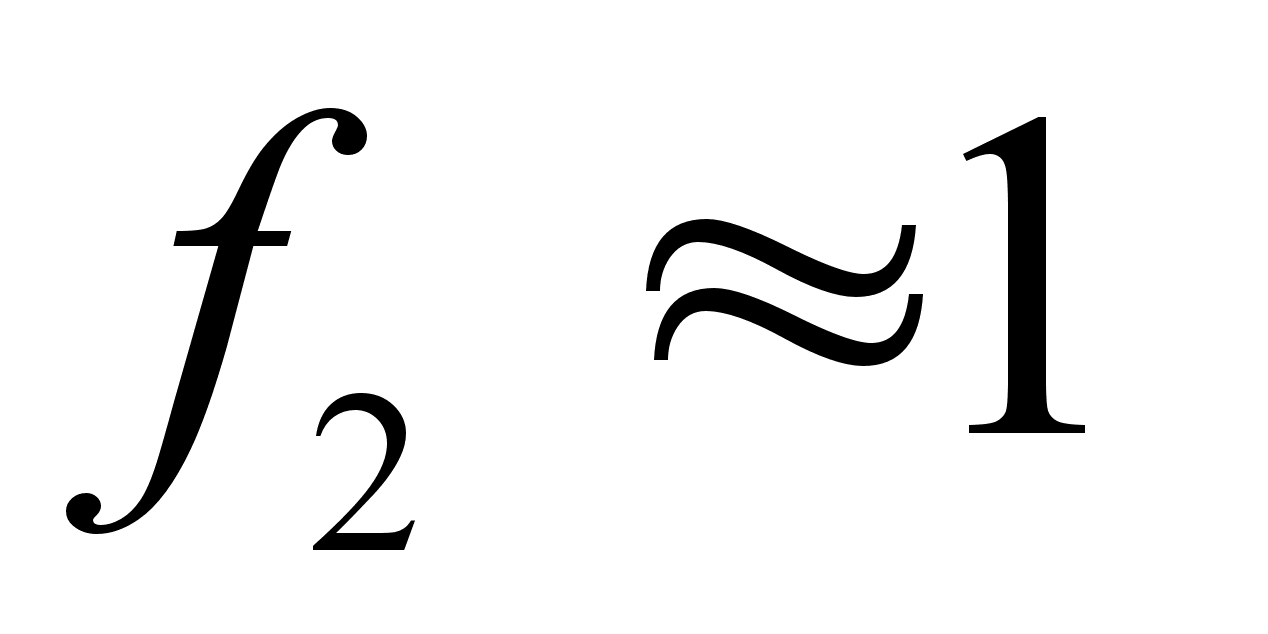 и
и
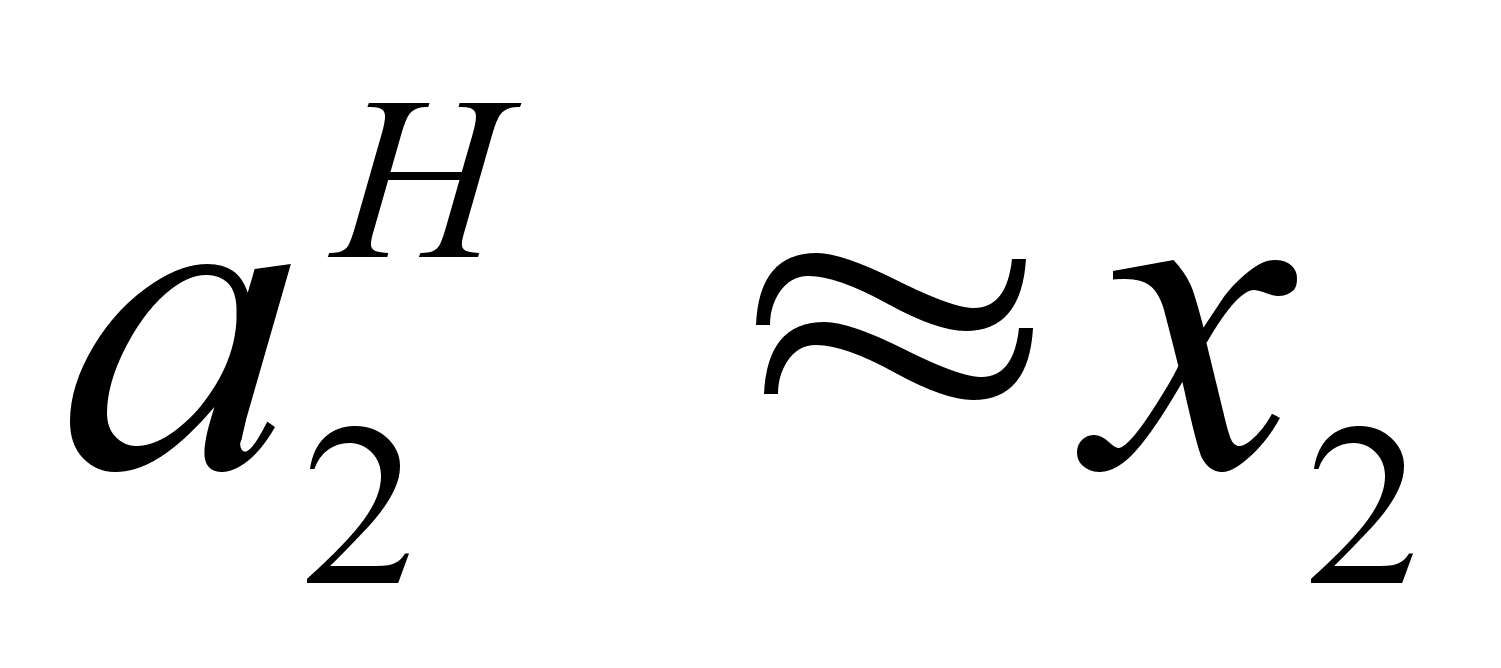 .
.
П
(42)
оскольку в разбавленном растворе молярная доля растворенного компонента пропорциональна его массовому проценту, очень удобным для практических расчетов является использование 1% стандартного состояния, поскольку это устраняет необходимость перевода процентов по массе, которыми обычно выражают состав раствора, в молярные доли. В разбавленных растворах активность растворенного компонента по отношению к этому стандартному состоянию становится равной концентрации, выраженной в процентах по массе. Активность растворенного компонента по отношению к 1%-му стандартному состоянию:
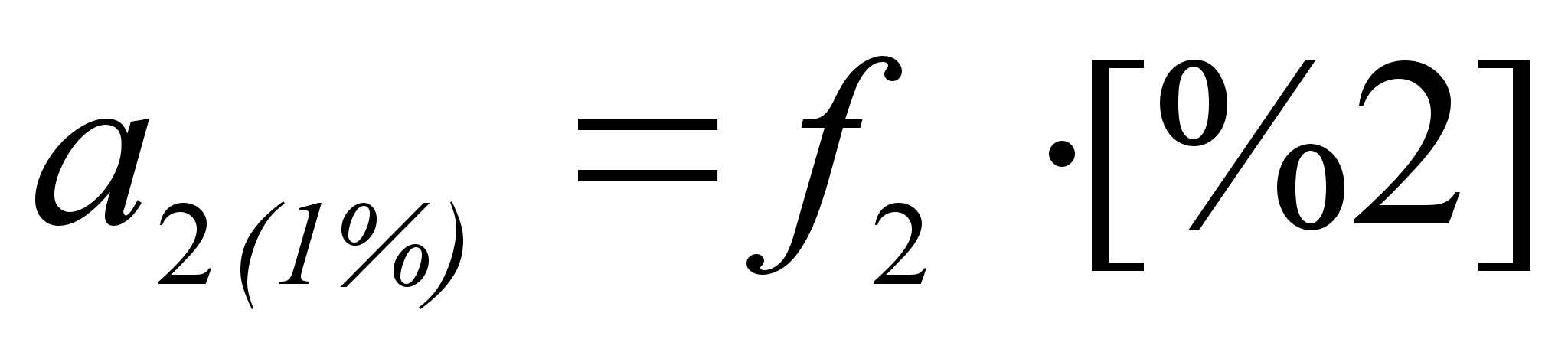
где f2 – коэффициент активности для этого стандартного состояния.
[%2] – концентрация компонента 2 в растворе. [5]
1.2.2 Реальные растворы
Как отмечалось,
совершенные
растворы
характеризуются
следующими
свойствами:
образование
раствора не
сопровождается
тепловым эффектом
(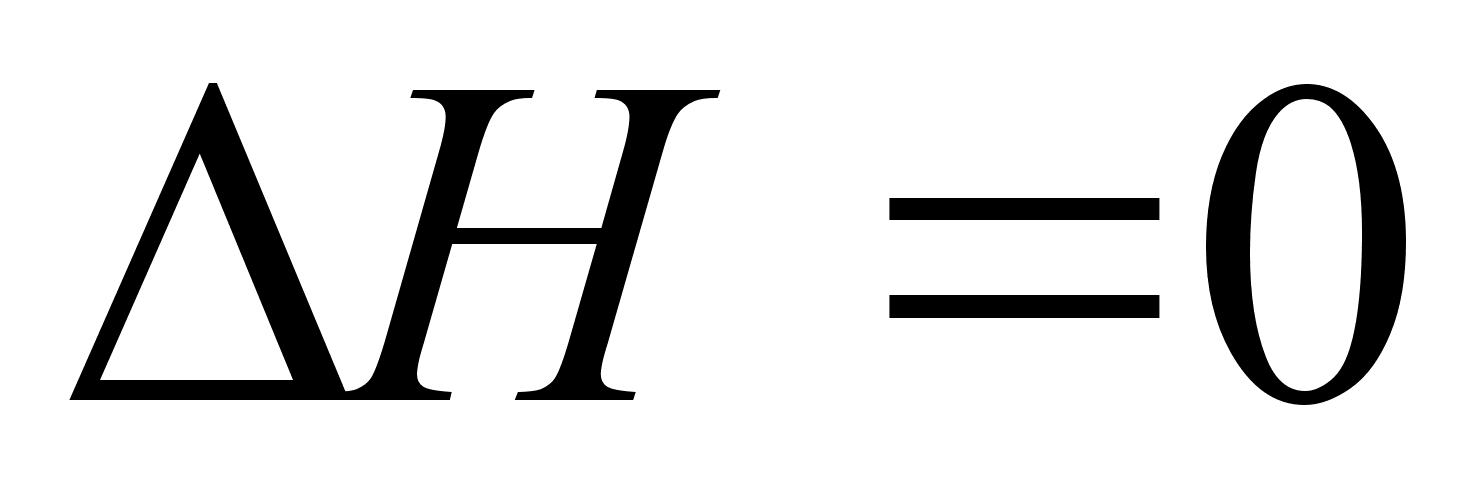 ),
а изменение
энтропии определяется
уравнением:
),
а изменение
энтропии определяется
уравнением:
(43)
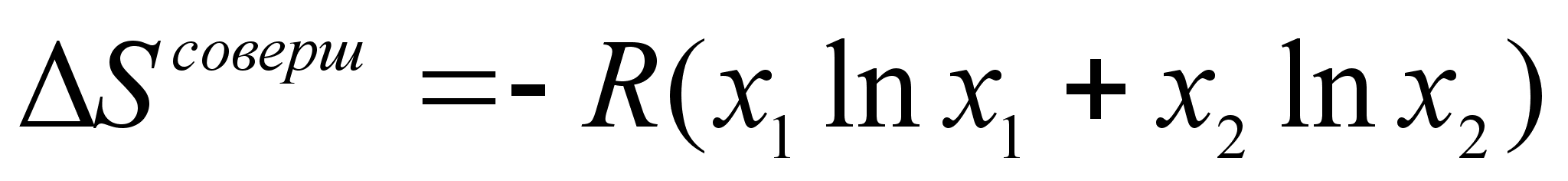 .
.
Р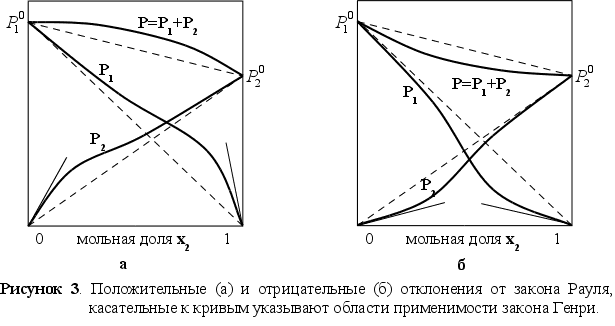
еальные
растворы, вообще
говоря, не обладают
этими свойствами
и для них не
соблюдается
законы Рауля
и Генри. На рисунке
3 представлены
зависимости
давления пара
от состава для
двух реальных
растворов.
Прямые штриховые линии соответствуют давлению пара, которое наблюдалось, если бы растворы были совершенными. На рисунке 3-а показаны положительные отклонения, при которых давление пара выше, чем для совершенного раствора такой же концентрации, а на рисунке 3-б – отрицательные отклонения, где давление пара меньше, чем для совершенного раствора.
Наличие положительных отклонений показывает, что образование раствора затруднено (из-за стремления каждого типа атомов группироваться с одноименными атомами) по сравнению с совершенным. При больших отклонениях жидкости расслаиваются. Отрицательные отклонения указывают на более сильную тенденцию к образованию раствора (тенденцией атомов одного типа образовывать группы с атомами других типов), чем в случае совершенного раствора. Это означает, что есть дополнительные причины для образования раствора. [1]
И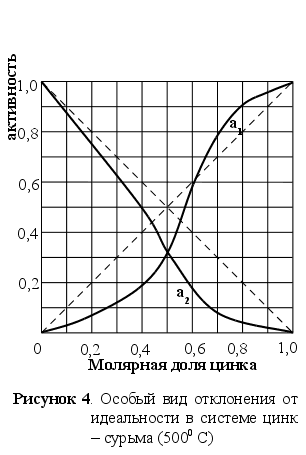 ногда
в одной и той
же системе
встречаются
и положительные
и отрицательные
отклонения
от закона Рауля.
В качестве
характерного
примера можно
привести бинарную
систему цинк
– сурьма, представленную
на рисунке 4.
Активность
цинка меньше
его атомной
доли при малых
концентрациях
и больше при
высоких содержаниях.
Коэффициент
активности
вначале меньше
единицы, непрерывно
возрастает
и становится
больше единицы,
а затем вблизи
чистого цинка
вновь понижается
до единицы.
Наличие обоих
видов отклонений
– положительного
и отрицательного
не требует
объяснений
с точки зрения
термодинамики,
просто тенденция
атомов обособляться
в группы должна
сильно изменяться
с изменением
состава раствора.
[2]
ногда
в одной и той
же системе
встречаются
и положительные
и отрицательные
отклонения
от закона Рауля.
В качестве
характерного
примера можно
привести бинарную
систему цинк
– сурьма, представленную
на рисунке 4.
Активность
цинка меньше
его атомной
доли при малых
концентрациях
и больше при
высоких содержаниях.
Коэффициент
активности
вначале меньше
единицы, непрерывно
возрастает
и становится
больше единицы,
а затем вблизи
чистого цинка
вновь понижается
до единицы.
Наличие обоих
видов отклонений
– положительного
и отрицательного
не требует
объяснений
с точки зрения
термодинамики,
просто тенденция
атомов обособляться
в группы должна
сильно изменяться
с изменением
состава раствора.
[2]
Так как
изменение
свободной
энергии (энергии
Гиббса)
выражается
уравнением
(26), то отклонения
в поведении
реальных растворов
от совершенных
могут определяться
как тем, что
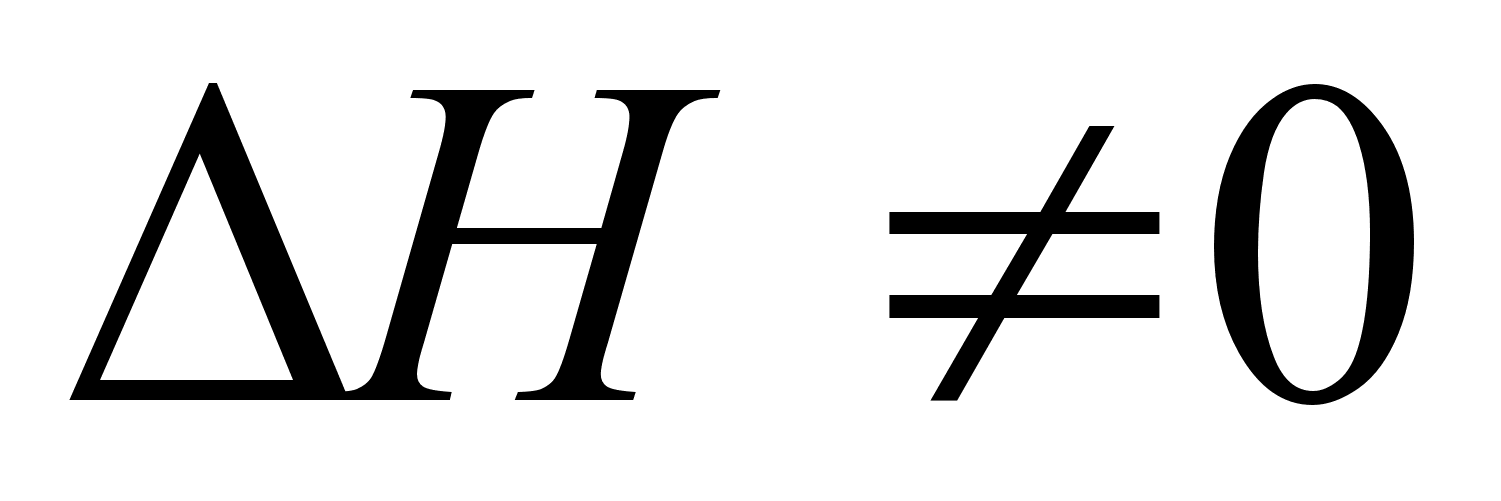 ,
так и тем, что
изменение
энтропии при
смешении не
подчиняется
уравнению (43).
[1]
,
так и тем, что
изменение
энтропии при
смешении не
подчиняется
уравнению (43).
[1]
Д
(44)
ля характеристики отклонения реальных систем от идеальных целесообразно ввести понятие об избыточных термодинамических функциях смешения. Так, для энергии Гиббса можно записать:

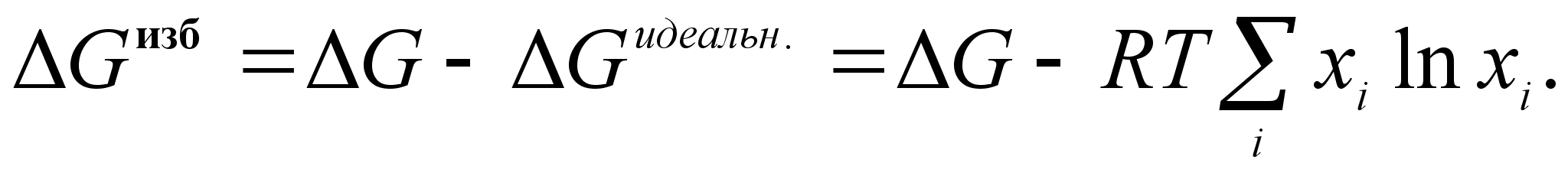
(45)
Для двухкомпонентной системы:
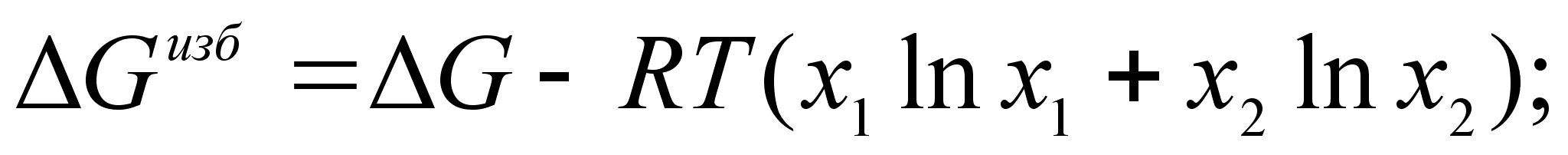
(46)
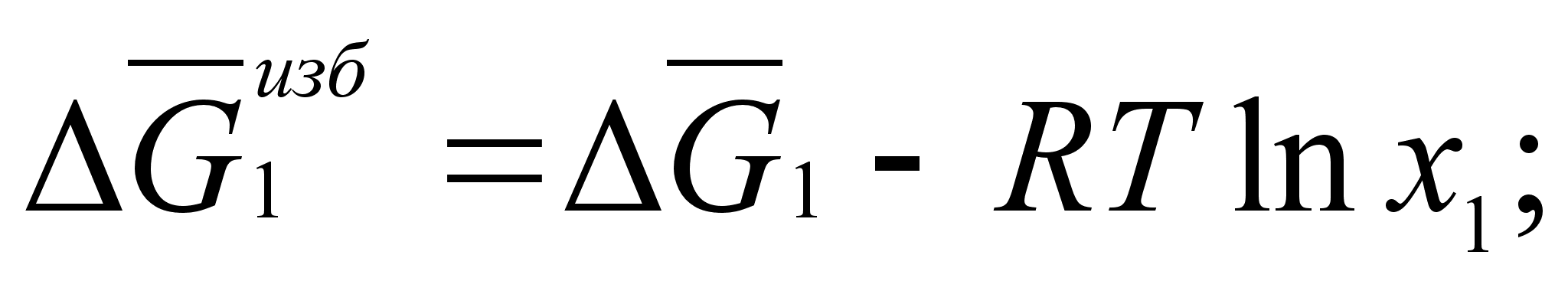
(47)
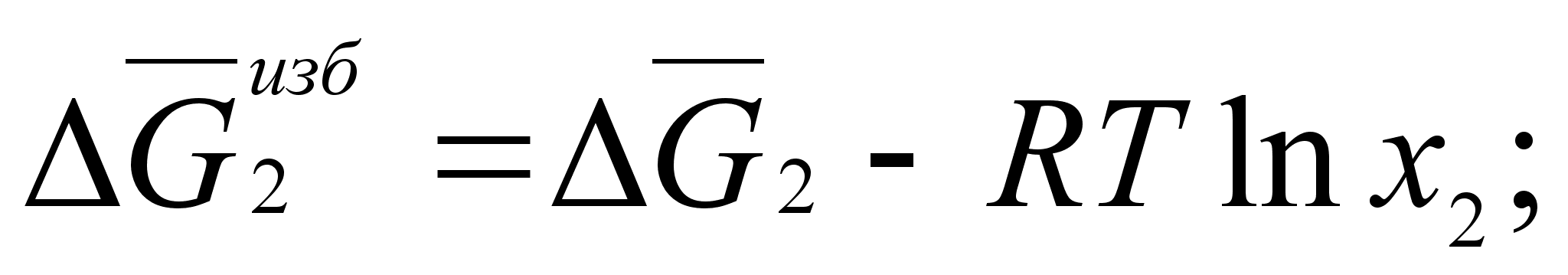
(48)
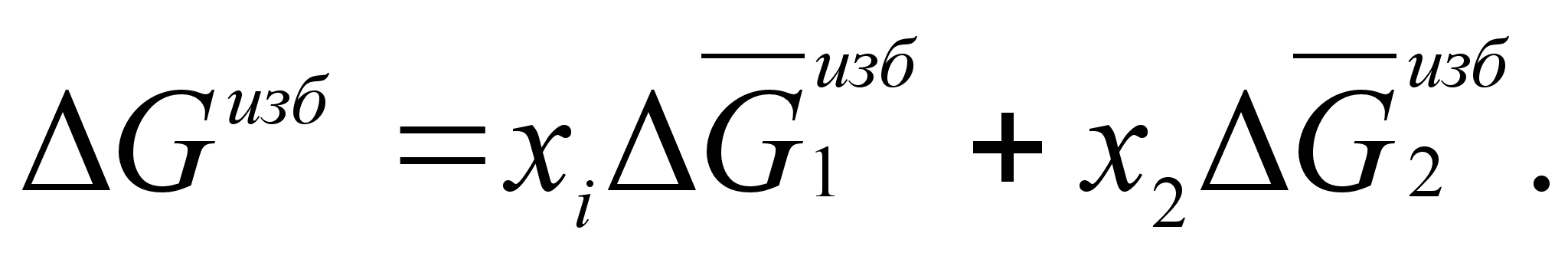
(49)
Энтропия:
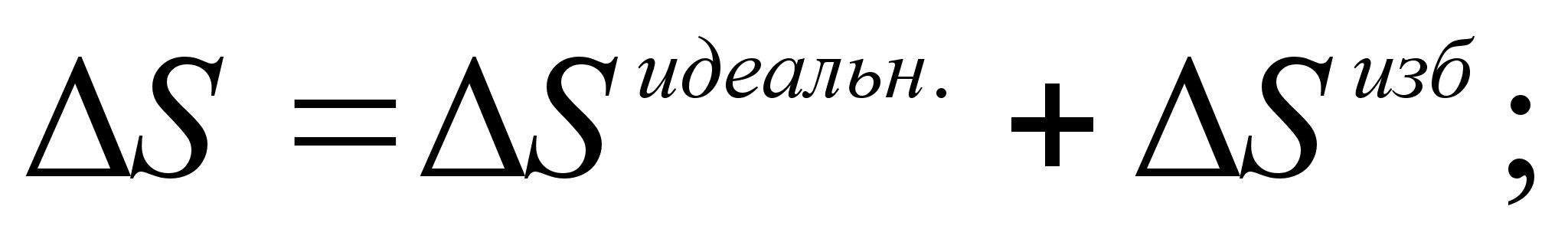
(50)
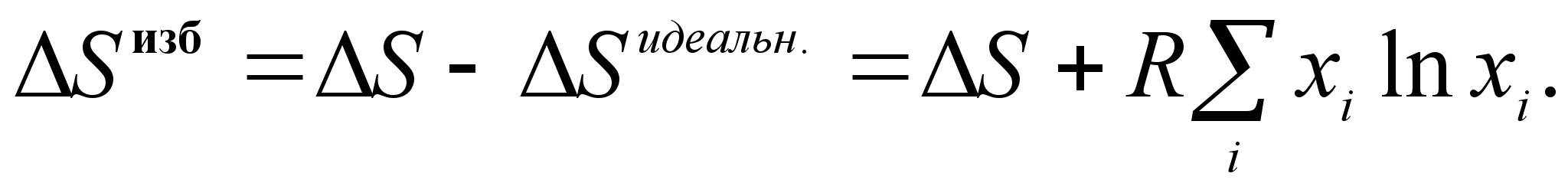
(51)
Для двухкомпонентной системы:
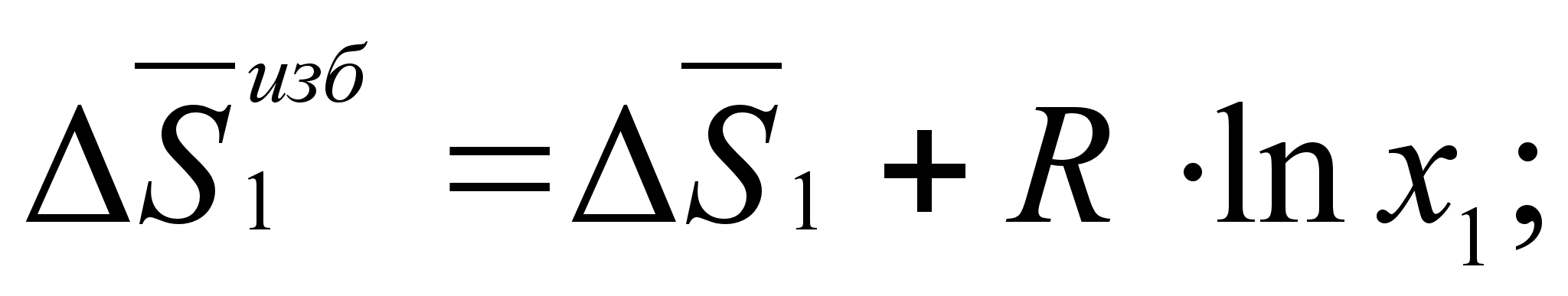
(52)
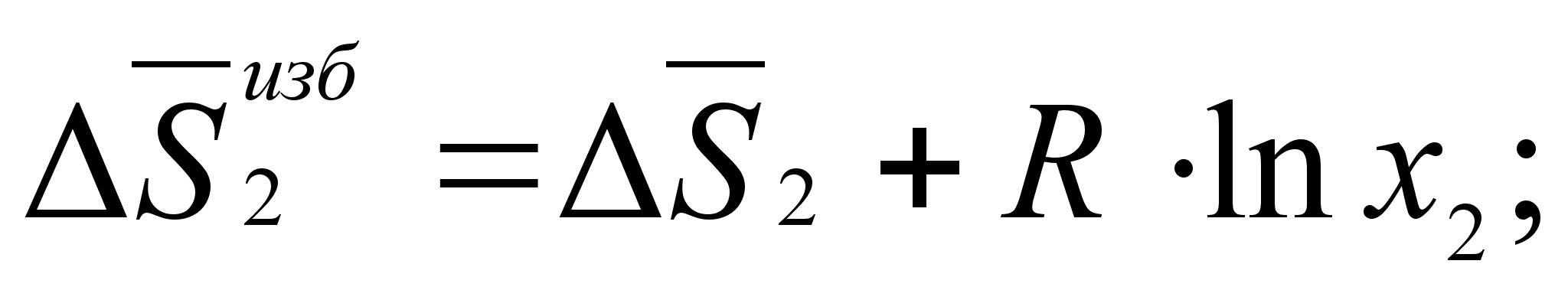
(53)
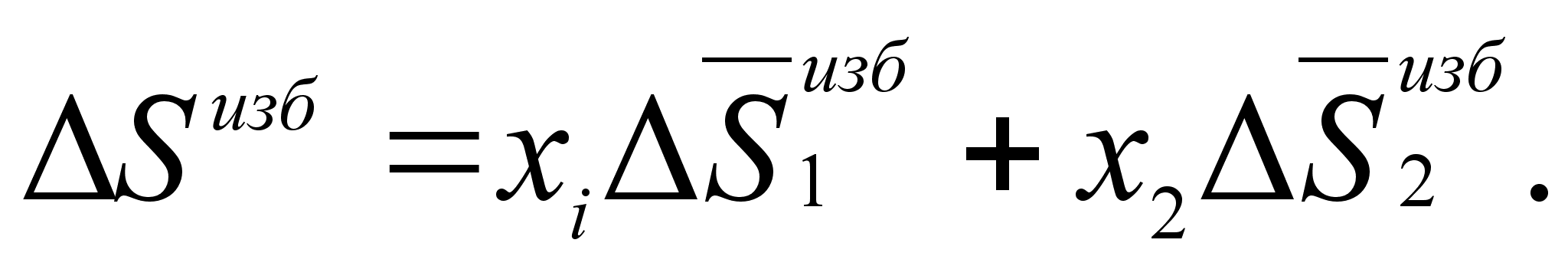
(54)
Поскольку
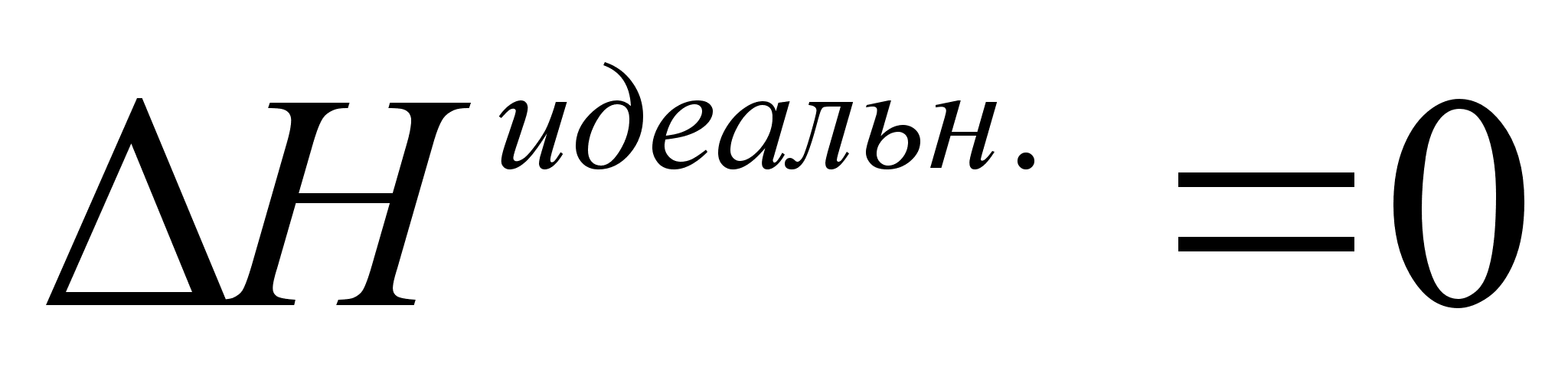 и
и
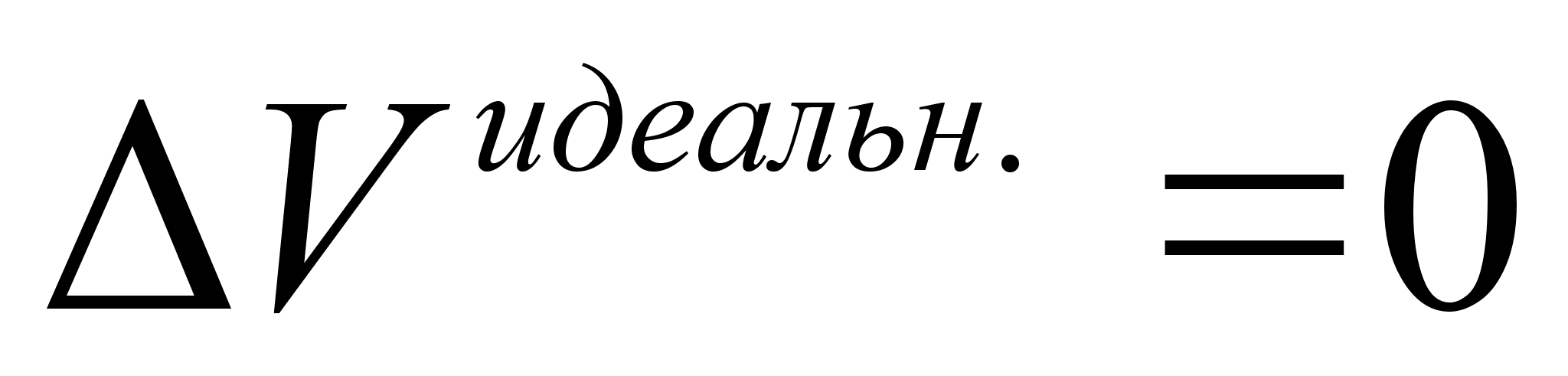 ,
применение
термина «избыточные
функции» для
энтальпии и
объёма не имеют
смысла.
,
применение
термина «избыточные
функции» для
энтальпии и
объёма не имеют
смысла.
Для избыточных функций справедливы все общие соотношения между интегральными и парциальными величинами.
Величина
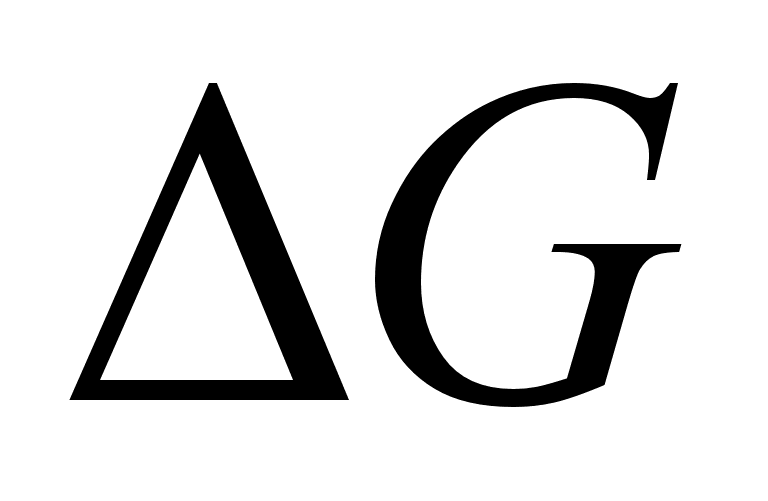 для равновесных
систем всегда
отрицательна.
Это вытекает
из общего положения,
что при постоянных
давлении и
температуре
все самопроизвольно
протекающие
сопровождаются
убылью энергии
Гиббса. Тогда:
для равновесных
систем всегда
отрицательна.
Это вытекает
из общего положения,
что при постоянных
давлении и
температуре
все самопроизвольно
протекающие
сопровождаются
убылью энергии
Гиббса. Тогда:
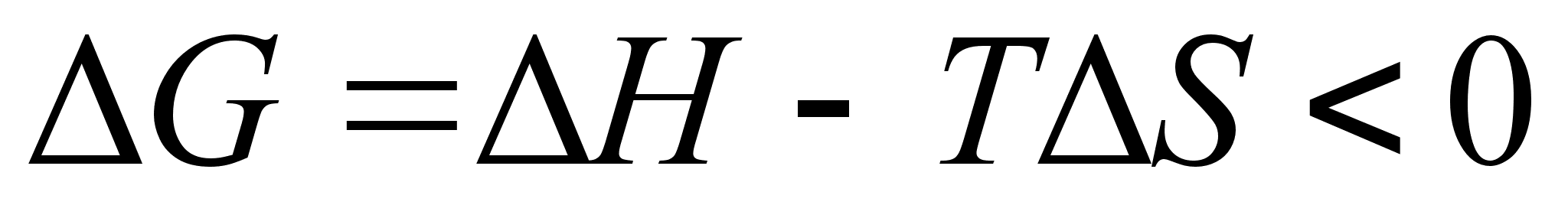 .
.
Каких-либо
ограничений
для знаков
 и
и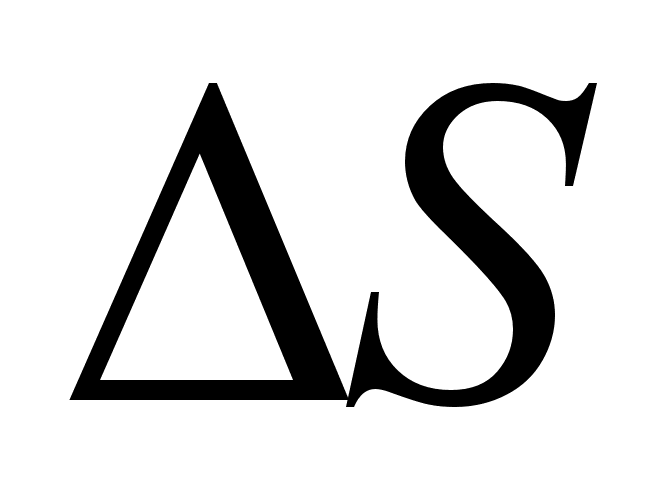 нет. Если
нет. Если
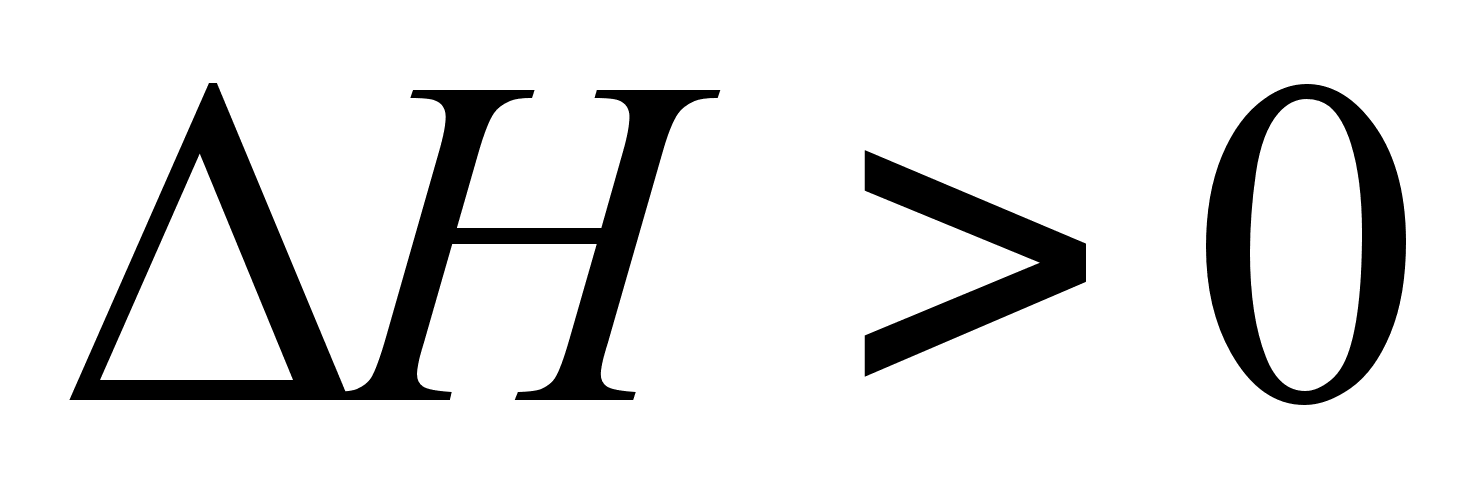 ,
то
,
то
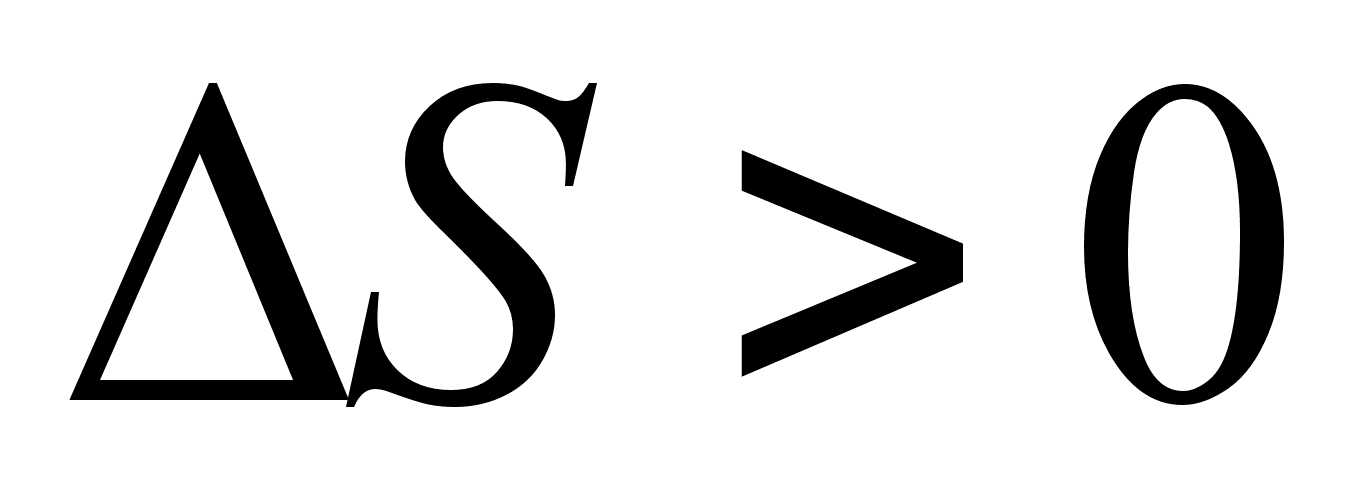 и
и
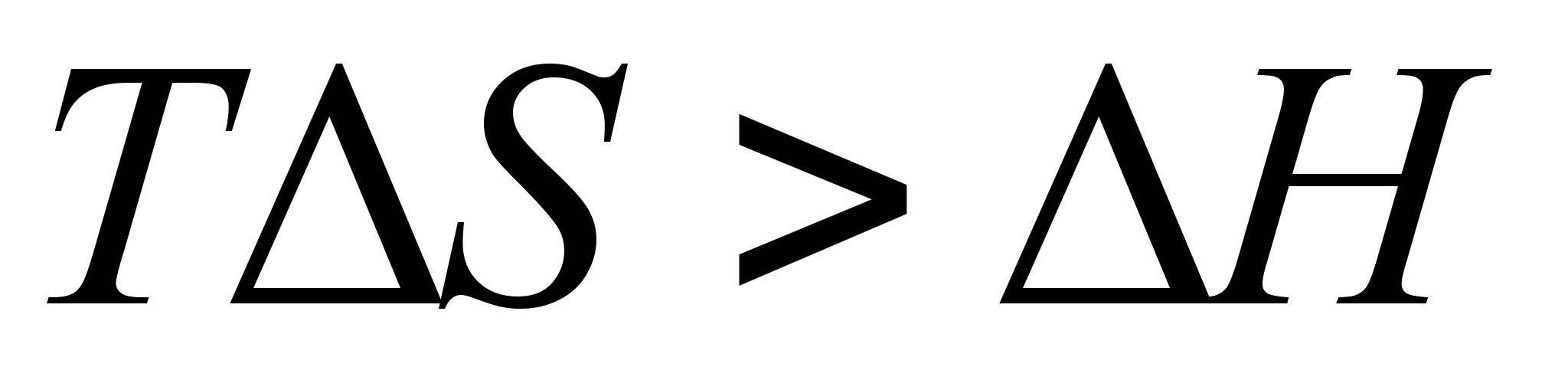 ;
если
;
если
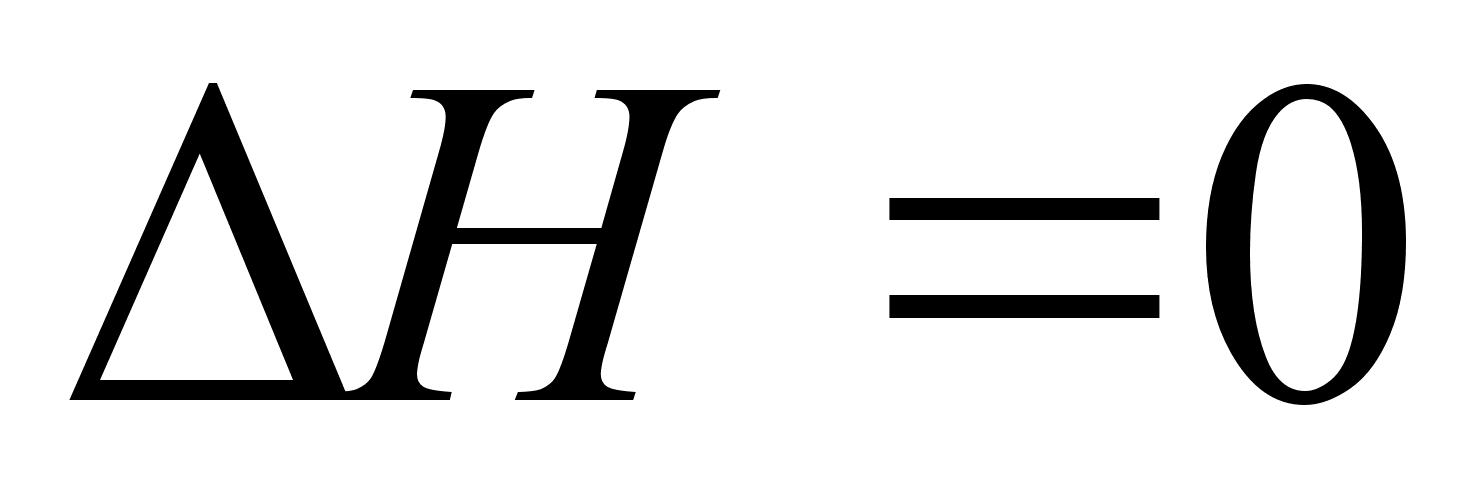 ,
то
,
то
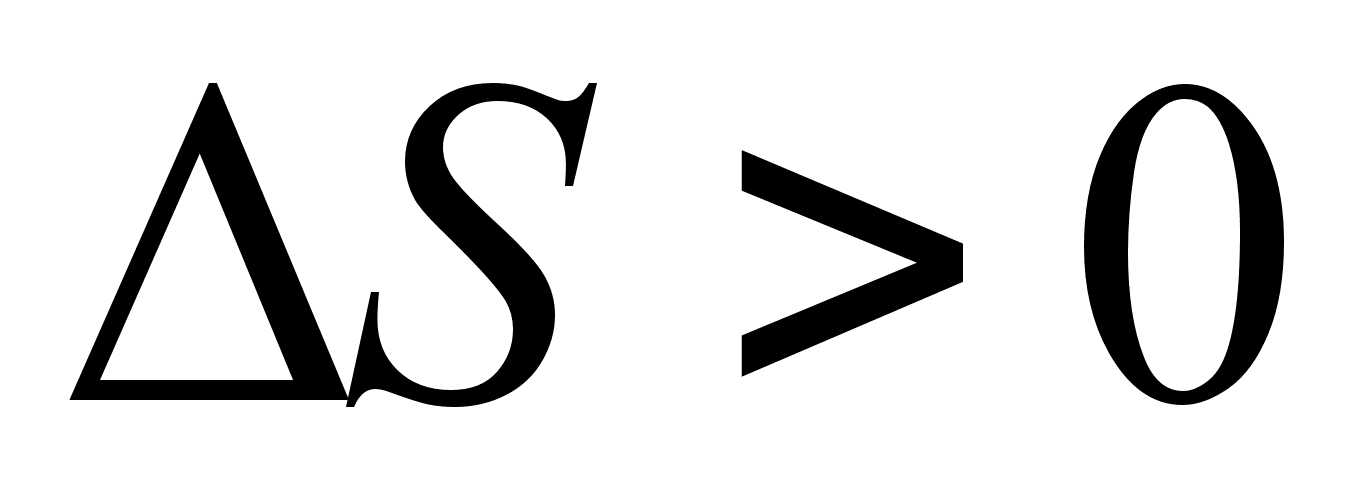 ;
если
;
если
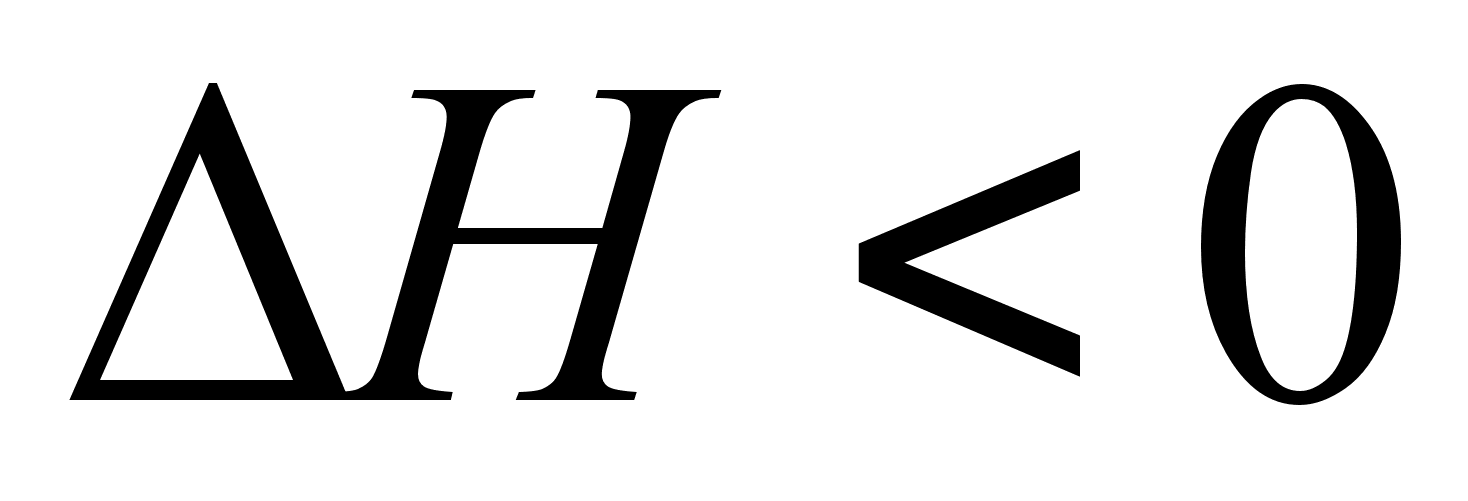 ,
то
,
то
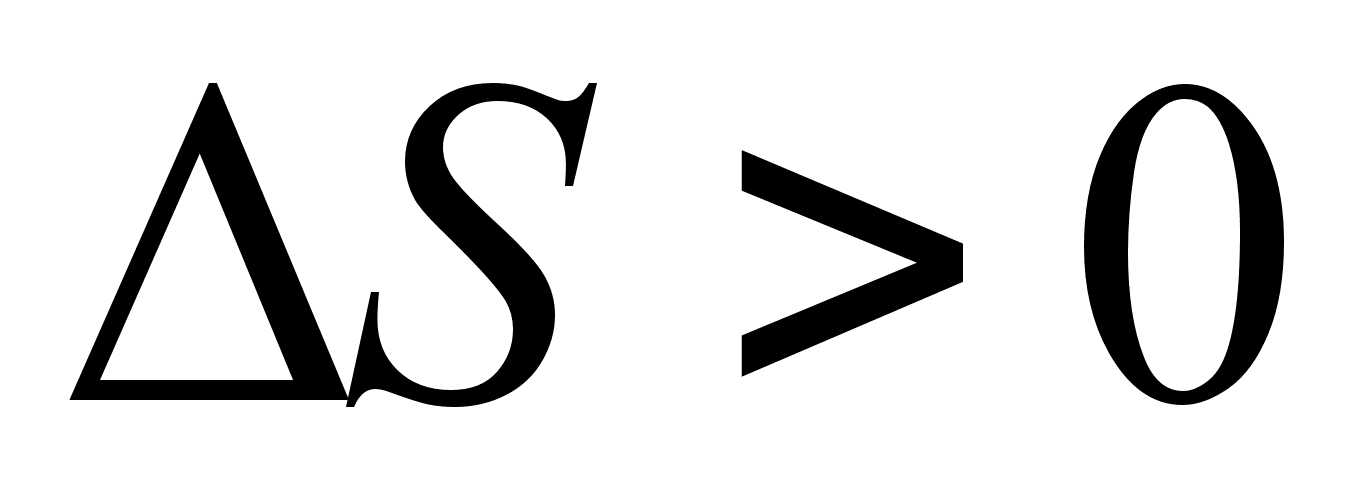 или
или
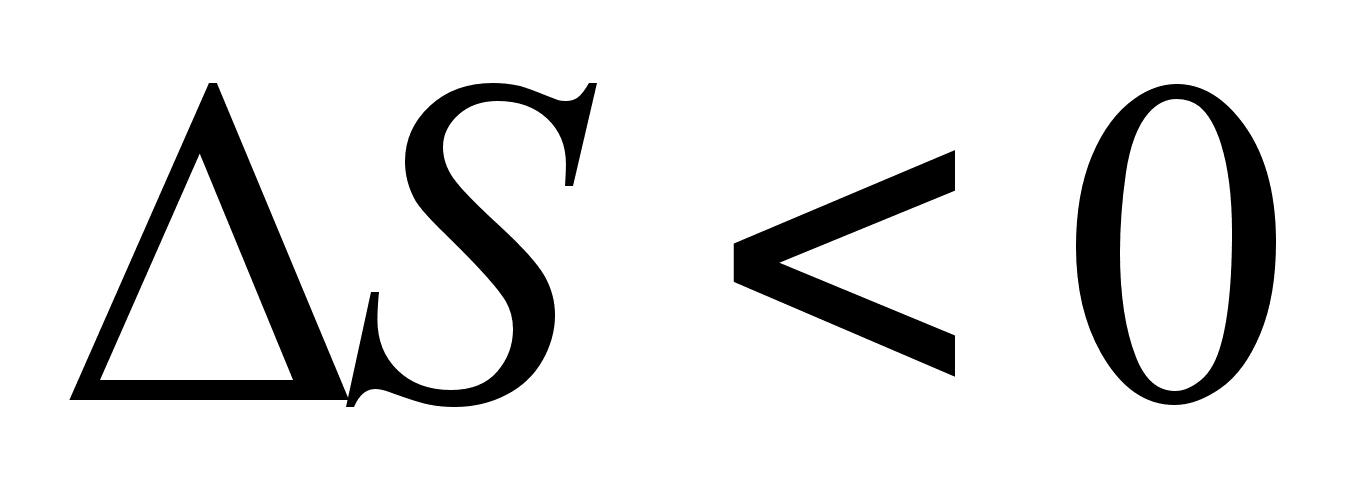 .
.
В последнем
случае по абсолютной
величине
 должно превышать
произведение
должно превышать
произведение
 .
Аналогичные
соотношения
распространяются
и на парциальные
мольные энтальпию
и энтропию.
[3]
.
Аналогичные
соотношения
распространяются
и на парциальные
мольные энтальпию
и энтропию.
[3]
1.2.2.1 Регулярные растворы
Р
(55)
егулярными называются растворы, образование которых сопровождается тепловым эффектом, а величина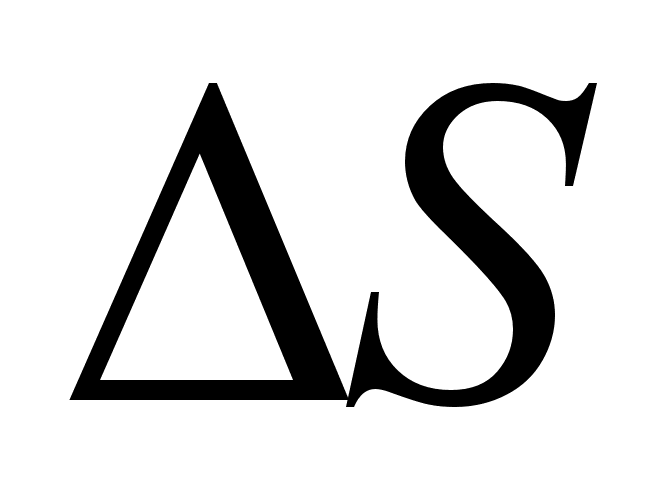 такая же, как
для совершенных.
[1] Таким образом,
отклонение
регулярного
раствора от
совершенного,
т.е. появление
избыточной
энергии Гиббса
обусловлено
только энтальпийным
членом:
такая же, как
для совершенных.
[1] Таким образом,
отклонение
регулярного
раствора от
совершенного,
т.е. появление
избыточной
энергии Гиббса
обусловлено
только энтальпийным
членом:
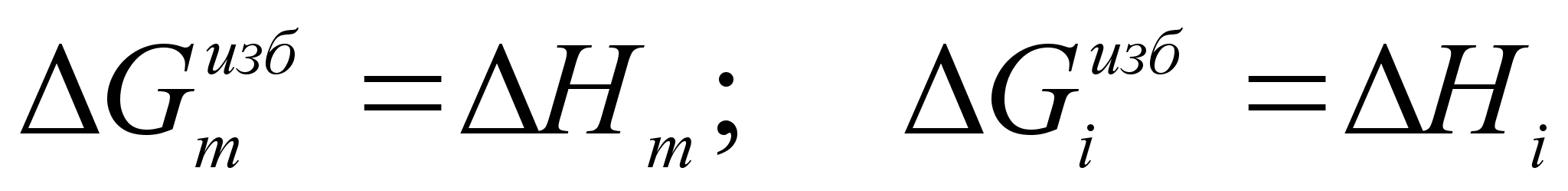
И
(56)
з этого выражения можно вывести важное для практических расчетов соотношение:
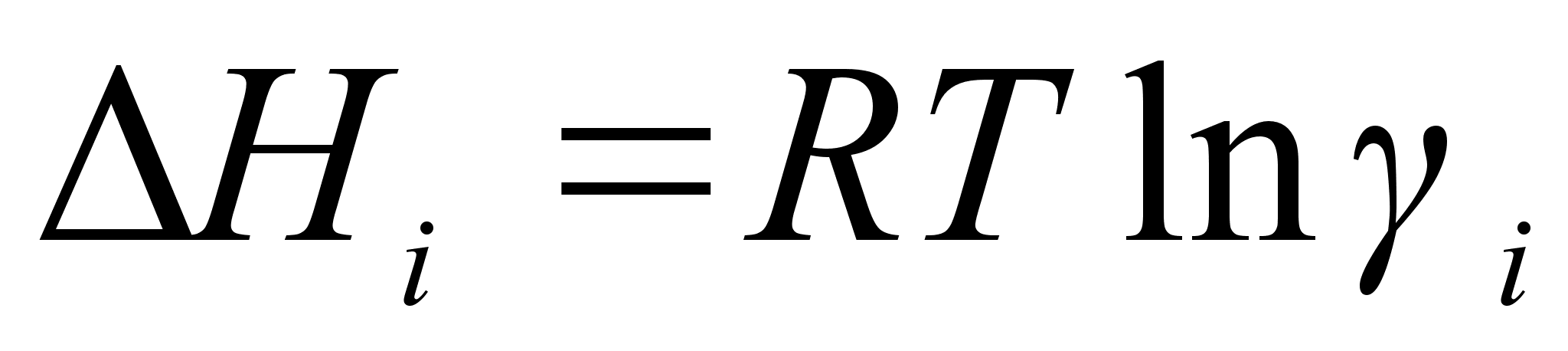 ,
,
которое
позволяет
оценить температурную
зависимость
коэффициента
активности,
если известно
хотя бы одно
его значение.
Принимая, что
 не зависит от
температуры,
данное выражение
можно записать,
например:
не зависит от
температуры,
данное выражение
можно записать,
например:
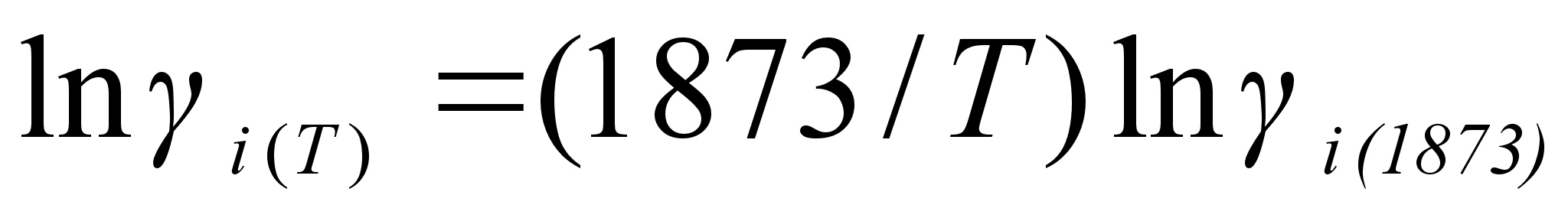
(57)
.Предполагается, что энтропийная составляющая энергии Гиббса в регулярном растворе такая же, как в совершенном, и может быть рассчитана исходя из допущения о полной хаотичности в расположении атомов. Таким образом, энергия Гиббса в регулярном растворе определяется следующими выражениями:
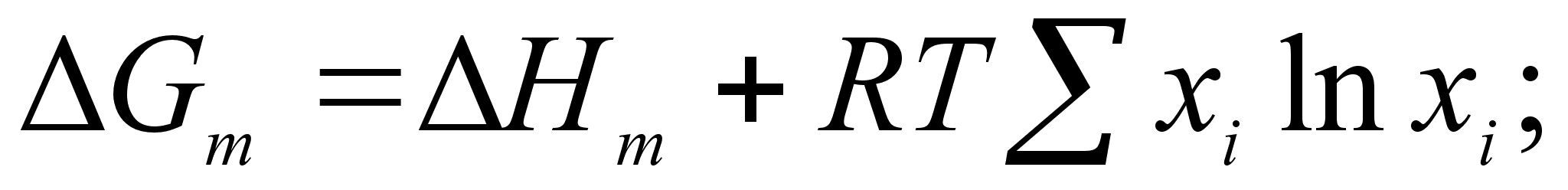
(58)
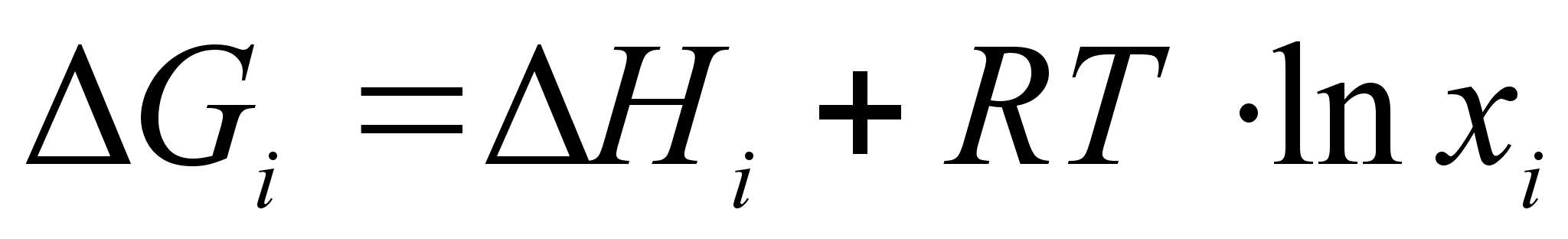
(59)
.
Допущение
о хаотичности
расположения
атомов при
определенном
взаимодействии
между ними
является главным
противоречием
модели регулярного
раствора,
ограничивающим
область её
применения.
Очевидно, что
наилучшие
результаты
модель регулярных
растворов может
дать для систем
с относительно
слабым взаимодействием.
В таких системах
величина
 ,
характеризующая
тенденцию к
упорядочению
(к определенной
группировке
атомов), должна
быть не больше
(или не на много
больше), чем
энергия теплового
движения атомов
RT,
определяющая
тенденцию к
разупорядочению.
С повышением
температуры
область возможного
применения
теории регулярных
растворов
увеличивается.
,
характеризующая
тенденцию к
упорядочению
(к определенной
группировке
атомов), должна
быть не больше
(или не на много
больше), чем
энергия теплового
движения атомов
RT,
определяющая
тенденцию к
разупорядочению.
С повышением
температуры
область возможного
применения
теории регулярных
растворов
увеличивается.
Р
(60)
яд полезных соотношений теории регулярных растворов может быть получен из статистического анализа модели, предполагающей хаотическое расположение атомов по узлам некоторой решетки, существование которой допускается как в твердом теле, так и в жидкости. Одним из результатов такого анализа является следующее выражение для избыточной энергии Гиббса образования одного моля регулярного раствора из чистых компонентов 1 и 2:
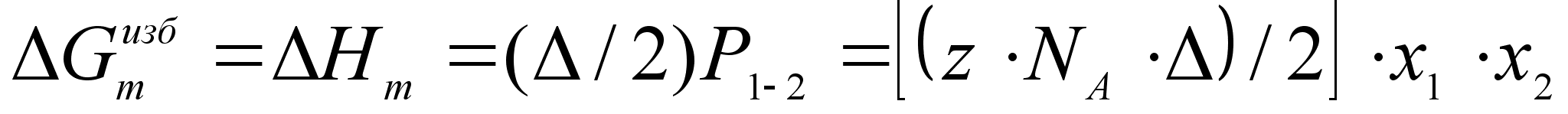 ,
,
где z – число ближайших соседей атома;
NA – число Авогадро;
 -
энергия образования
двух связей
между разноименными
атомами:
-
энергия образования
двух связей
между разноименными
атомами:
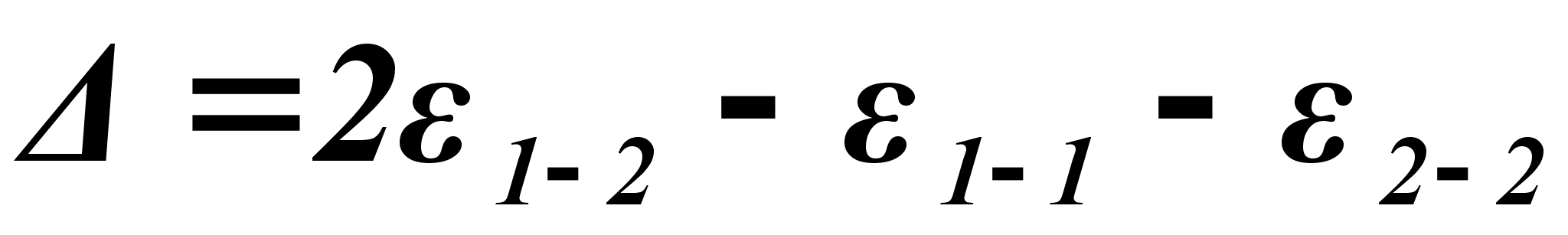
(61)
Р
(62)
1-2 – число связей 1-2; при хаотическом расположении атомов:Р1-2=z NA x1x2 .
Р
(63)
ассмотрим концентрационную зависимость величины ,
следующую из
данного уравнения.
Величину
,
следующую из
данного уравнения.
Величину
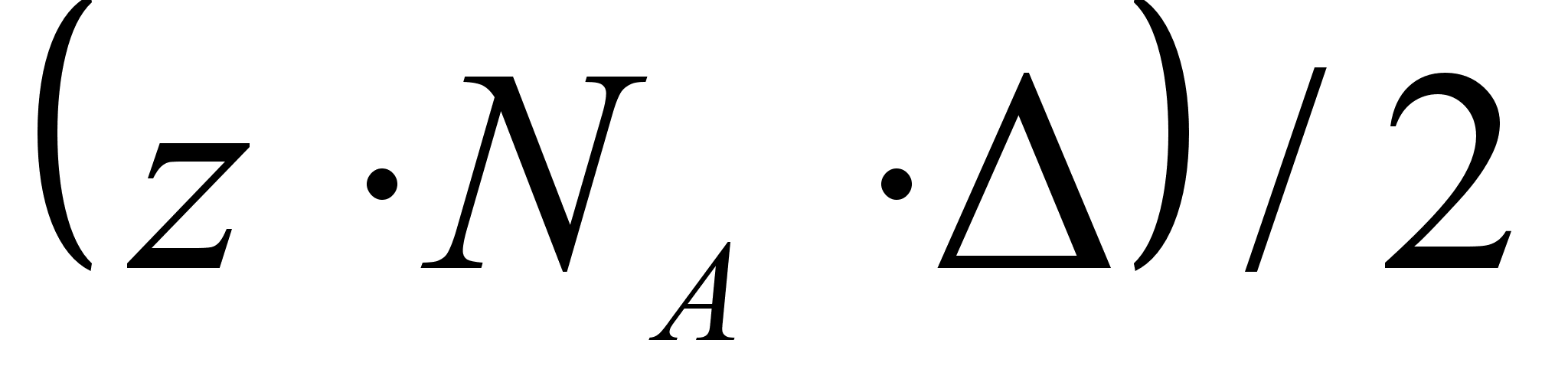 ,
не зависящую
от состава,
обозначим
,
не зависящую
от состава,
обозначим
 (энергия смешения).
Подставляя,
получим:
(энергия смешения).
Подставляя,
получим:
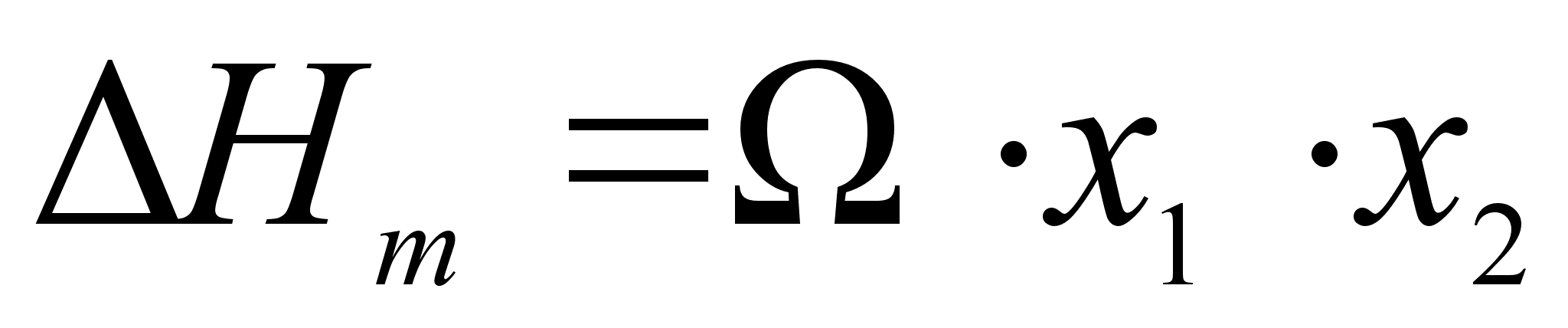 ,
,
что соответствует
параболе с
экстремумом
в точке х1=х2=0,5.
Экспериментальное
значение
 в этой точке
равно
в этой точке
равно
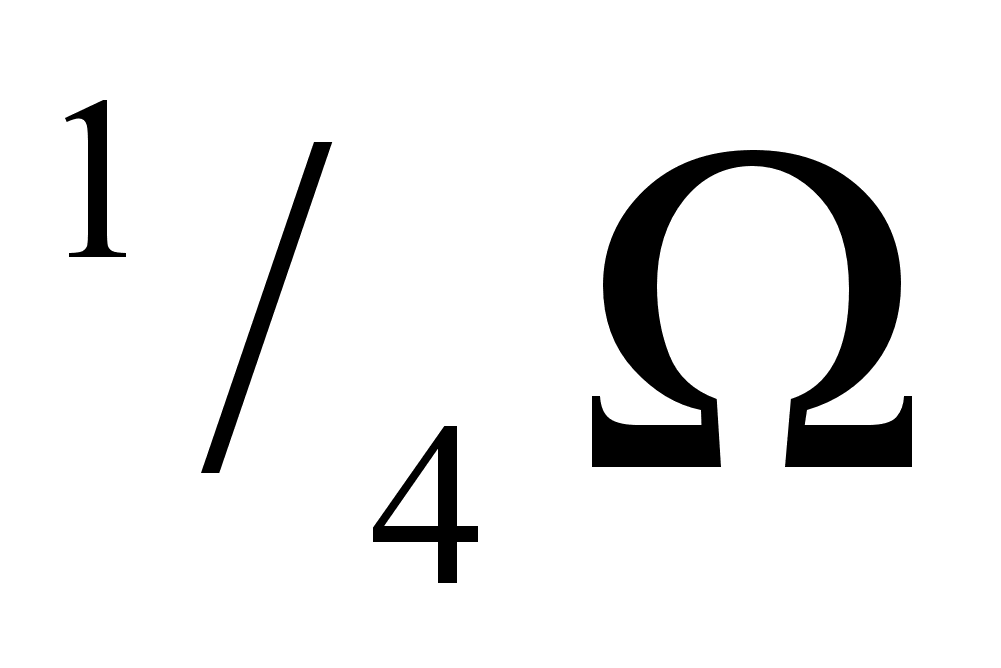 .
Для определения
парциальных
энтальпий
компонентов
.
Для определения
парциальных
энтальпий
компонентов
 и
и
 необходимо
продифференцировать
данное уравнение,
переписав его
для раствора,
содержащего
n1+
n2
молей компонентов,
следующим
образом:
необходимо
продифференцировать
данное уравнение,
переписав его
для раствора,
содержащего
n1+
n2
молей компонентов,
следующим
образом:
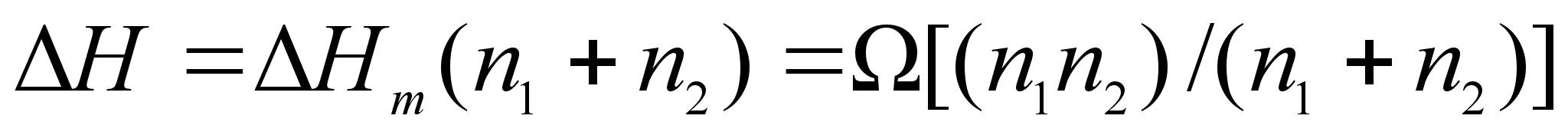
(64)
.Отсюда получим:
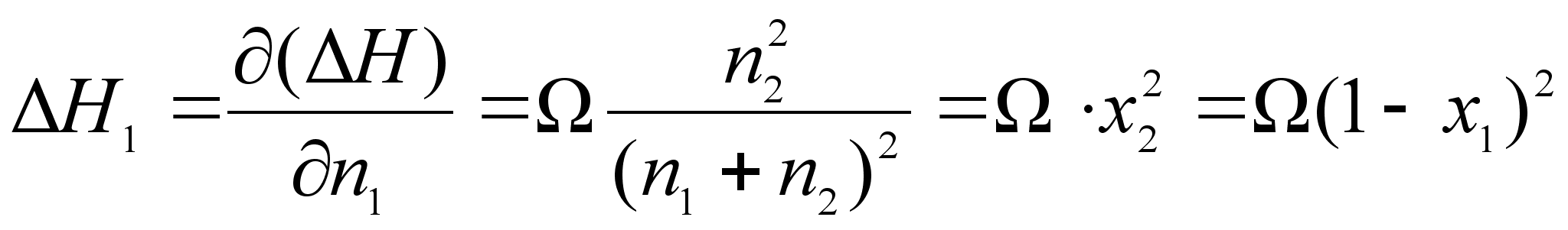
(65)
(66)
,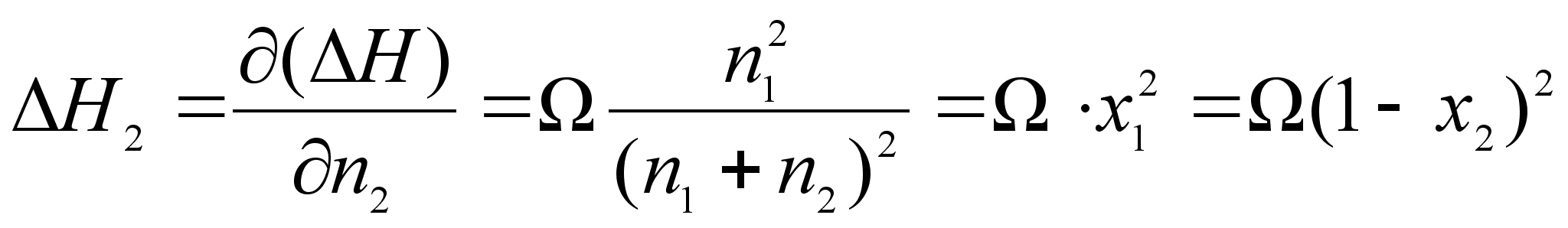 .
.
Как
видно из уравнений,
энергия смешения
 равна предельному
значению
равна предельному
значению
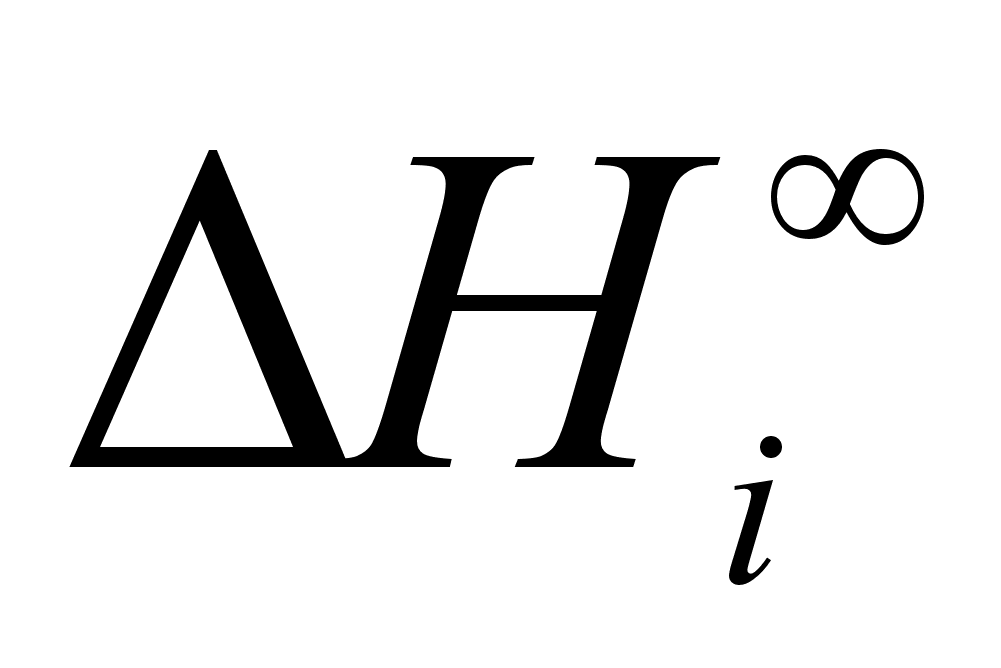 (при
(при
 ).
Учитывая связь
между теплотой
растворения
и коэффициентом
активности,
можно получить
следующее
выражение для
зависимости
коэффициентов
активности
от концентрации:
).
Учитывая связь
между теплотой
растворения
и коэффициентом
активности,
можно получить
следующее
выражение для
зависимости
коэффициентов
активности
от концентрации:
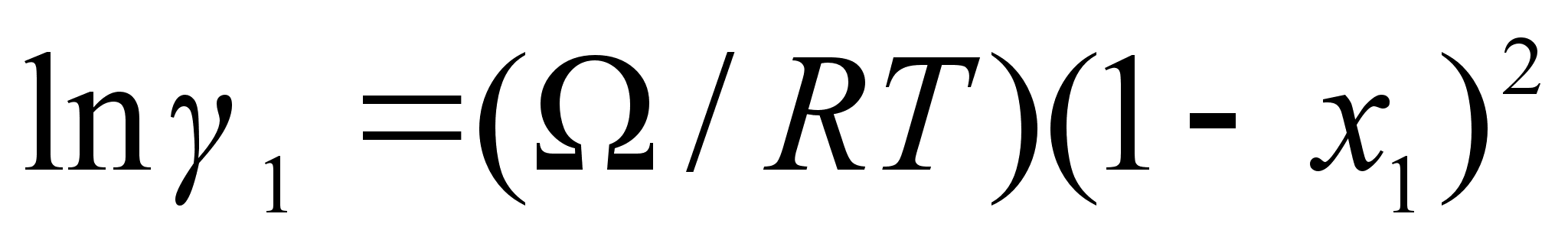
(67)
;
(68)
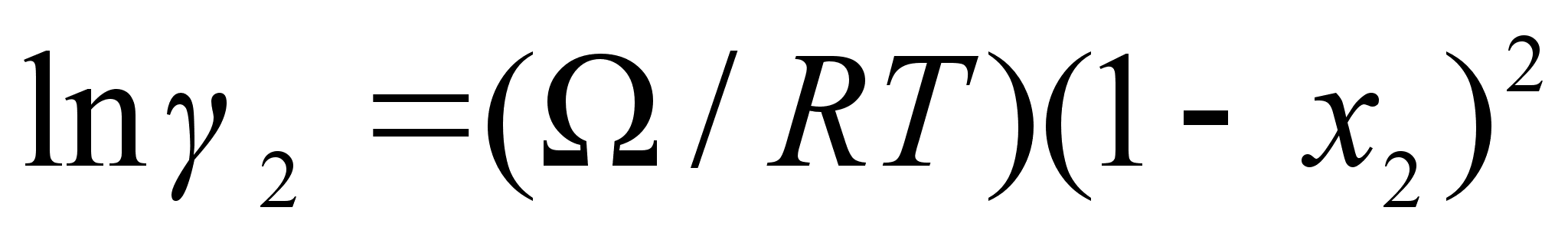 .
.
Из данных
уравнений
следует, что
при
 коэффициент
коэффициент
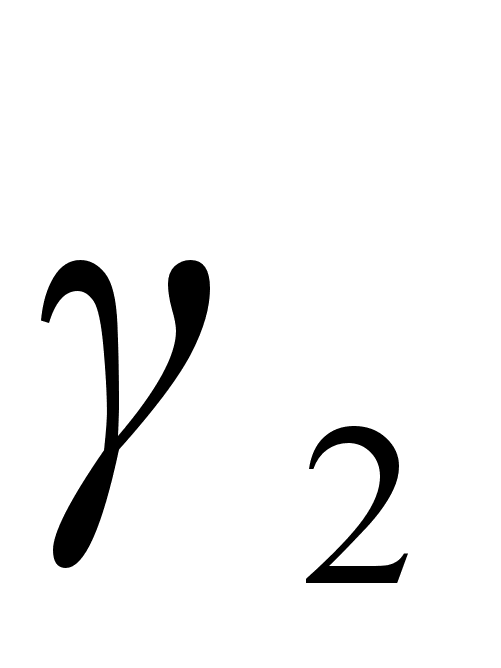 стремится к
стремится к
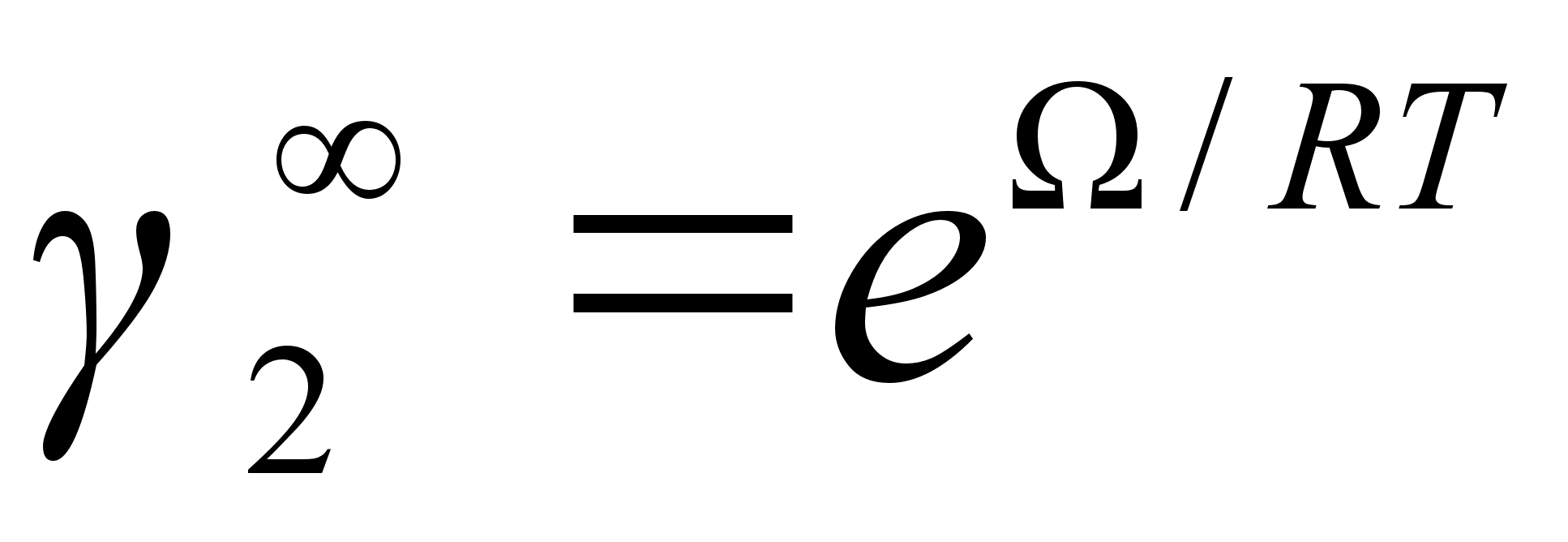 ,
а
,
а
 .
Таким образом,
в теории регулярных
растворов
возможно только
приближенное
выполнение
законов Генри
(
.
Таким образом,
в теории регулярных
растворов
возможно только
приближенное
выполнение
законов Генри
(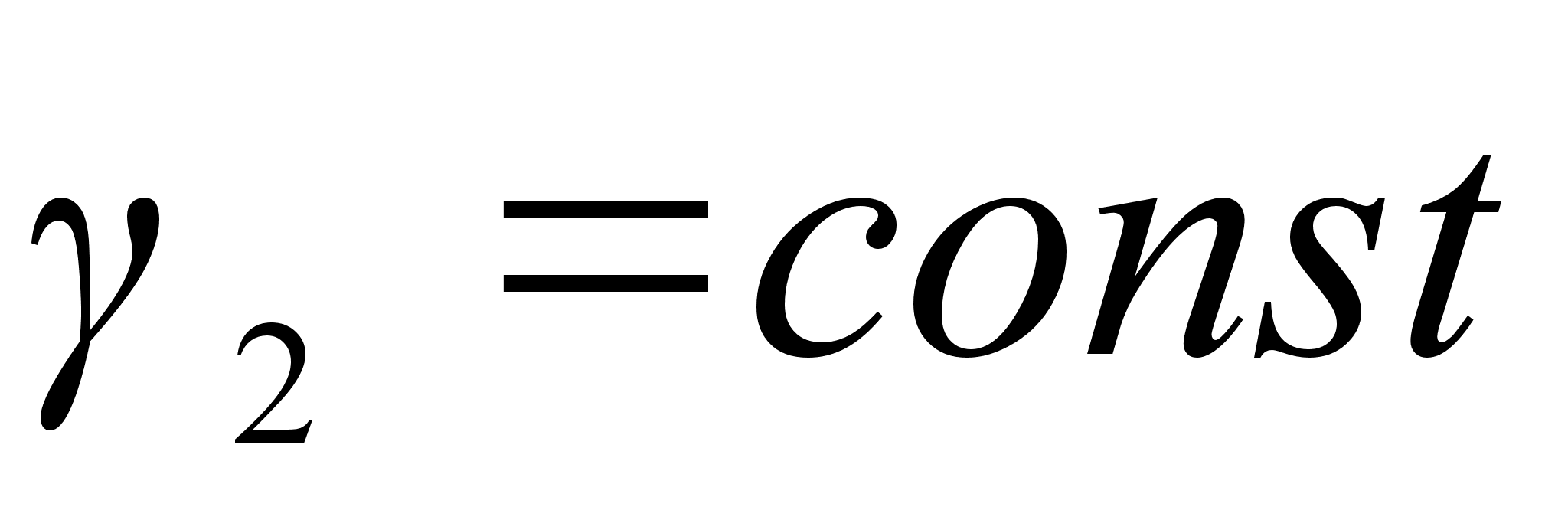 )
и Рауля(
)
и Рауля(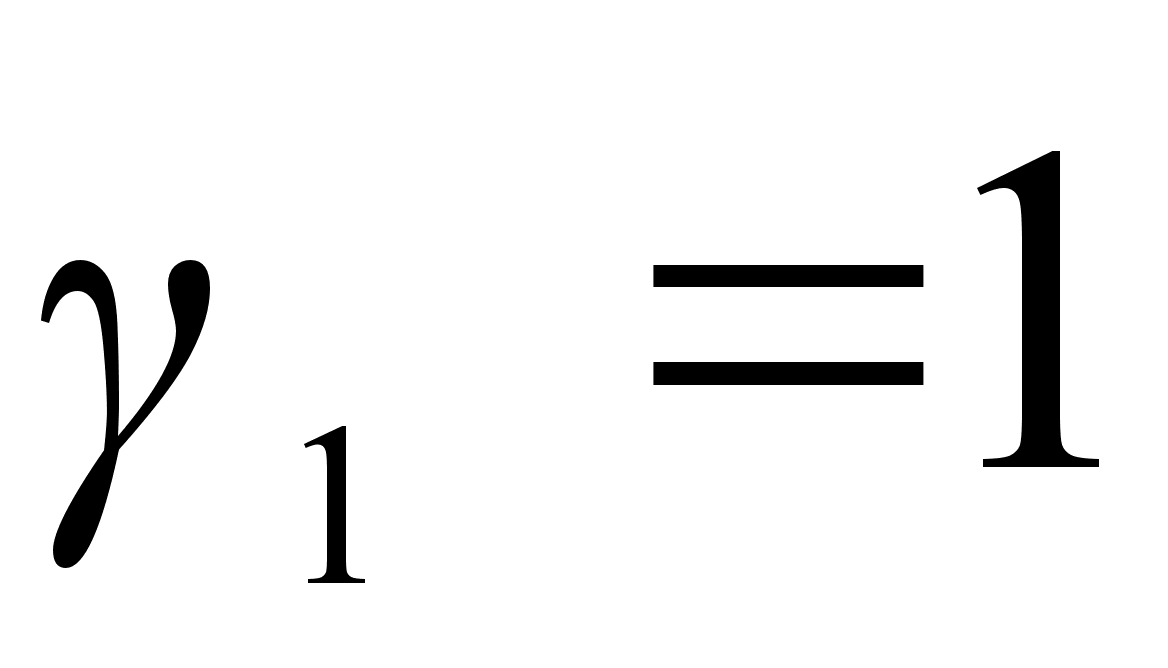 )
в области малых
значений х2
отличных от
нуля.
)
в области малых
значений х2
отличных от
нуля.
Таким образом, энергия Гиббса (для бинарного раствора):
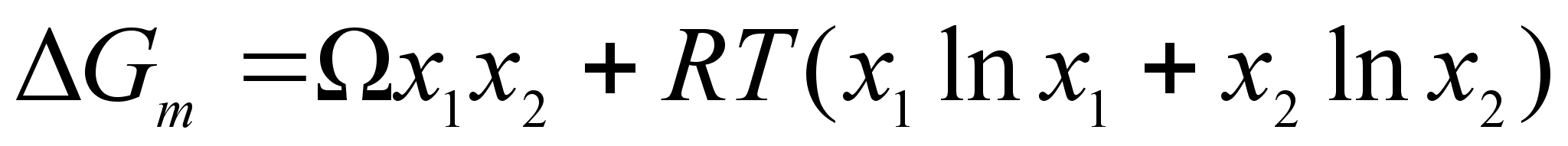
(68)
;
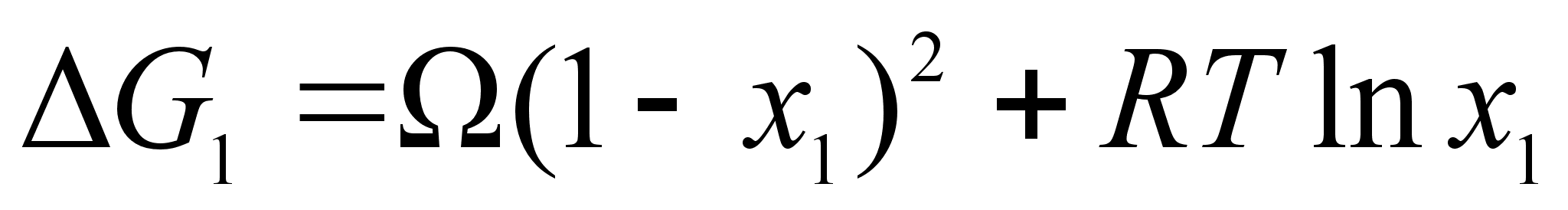
(68)
;
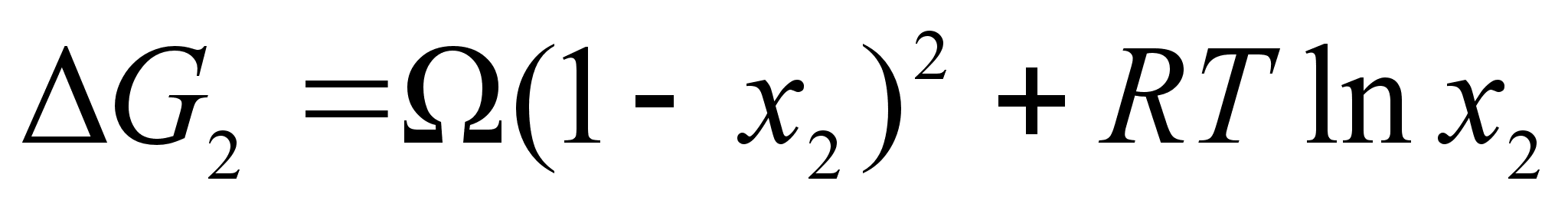
(68)
.
Как видно,
все основные
термодинамические
характеристики
регулярного
раствора, включая
температурную
и концентрационную
зависимость
активности,
могут быть
рассчитаны,
если известен
один параметр
– энергия смешения
 .
Величину
.
Величину
 ,
принимаемую
в простейшем
случае не зависящей
от температуры
и концентрации,
можно рассчитать
по данным одного
эксперимента.
Такой расчет
может быть
выполнен при
помощи уравнений
(65), (66) по известной
величине
,
принимаемую
в простейшем
случае не зависящей
от температуры
и концентрации,
можно рассчитать
по данным одного
эксперимента.
Такой расчет
может быть
выполнен при
помощи уравнений
(65), (66) по известной
величине
 или по уравнениям
(67), (68) если известно
одно значение
коэффициента
активности
или по уравнениям
(67), (68) если известно
одно значение
коэффициента
активности
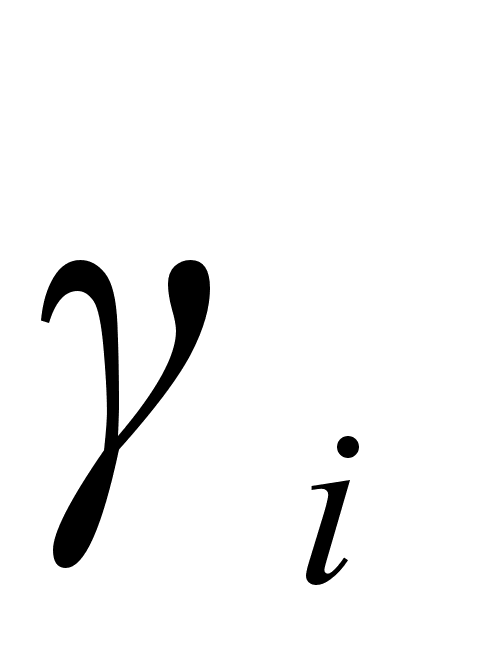 (при заданных
концентрации
и температуре).
Отметим для
сравнения, что
в теории идеальных
разбавленных
растворов для
вычисления
(при заданных
концентрации
и температуре).
Отметим для
сравнения, что
в теории идеальных
разбавленных
растворов для
вычисления
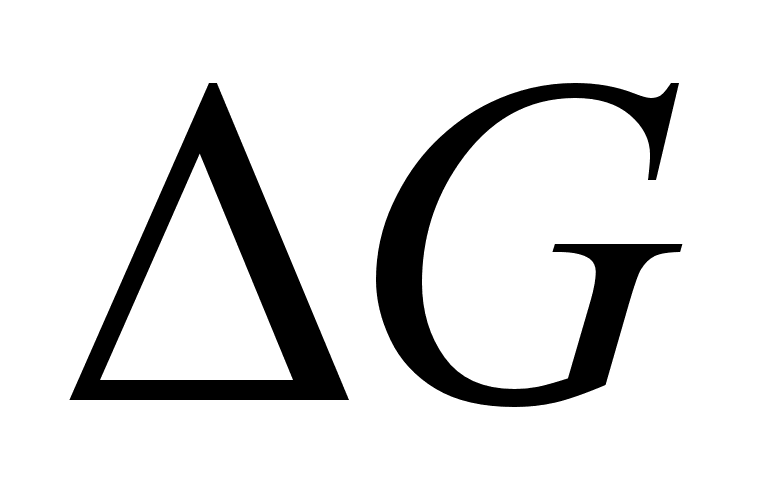 как функции
температуры
требуется не
менее двух
значений
как функции
температуры
требуется не
менее двух
значений
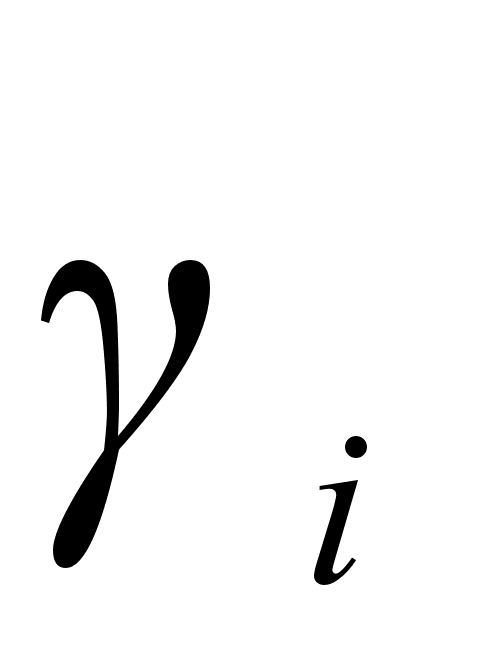 при
разных Т
(см. уравнение
(36)).
при
разных Т
(см. уравнение
(36)).
Таким образом,
теория регулярных
растворов
предоставляет
довольно широкие
возможности
для расчета
термодинамических
характеристик.
Однако довольно
ограничен круг
расплавов,
которые могут
быть описаны
этой теорией
с удовлетворительной
степенью точности
и в широком
диапазоне
температур
и концентраций.
Проведенный
анализ имеющихся
экспериментальных
данных о 175 бинарных
металлических
системах показал,
что только
восемь из них
можно удовлетворительно
описать теорией
регулярных
растворов в
простейшем
её варианте.
На практике
эти уравнения
часто используют
в качестве
интерполяционных
формул в ограниченном
интервале
температур
или концентраций.
При этом величину
 подбирают таким
образом (например,
при помощи
метода наименьших
квадратов),
чтобы уравнения
соответствовали
всей данной
совокупности
экспериментальных
значений. Далекая
экстраполяция
найденных таким
способом зависимостей
в область
неисследованных
температур
и концентраций,
как правило,
недопустима.
Тем не менее,
во многих случаях
теория регулярных
растворов может
быть использована
для обработки
экспериментальных
данных и практических
расчетов. Наилучшие
результаты
эта теория дает
при высоких
температурах
и в применении
к системам с
относительно
слабым взаимодействием
(с малым различием
свойств компонентов).
[6]
подбирают таким
образом (например,
при помощи
метода наименьших
квадратов),
чтобы уравнения
соответствовали
всей данной
совокупности
экспериментальных
значений. Далекая
экстраполяция
найденных таким
способом зависимостей
в область
неисследованных
температур
и концентраций,
как правило,
недопустима.
Тем не менее,
во многих случаях
теория регулярных
растворов может
быть использована
для обработки
экспериментальных
данных и практических
расчетов. Наилучшие
результаты
эта теория дает
при высоких
температурах
и в применении
к системам с
относительно
слабым взаимодействием
(с малым различием
свойств компонентов).
[6]
1.2.2.2 Субрегулярные растворы
Одно из наиболее
часто встречающихся
противоречий
заключатся
в том, что реальные
системы характеризуются
обычно несимметричными
зависимостями
термодинамических
характеристик
от состава, а
теория регулярных
растворов
предсказывает
их симметрию.
Чтобы устранить
это расхождение
теории с экспериментом
был предложен
один из усложненных
вариантов
модели, которых
получил название
субрегулярного
раствора. Отличие
этого раствора
от регулярного
заключается
в том, что его
энергия смешения
 не является
константой,
а изменяется
в зависимости
от состава и
принимает
значения от
не является
константой,
а изменяется
в зависимости
от состава и
принимает
значения от
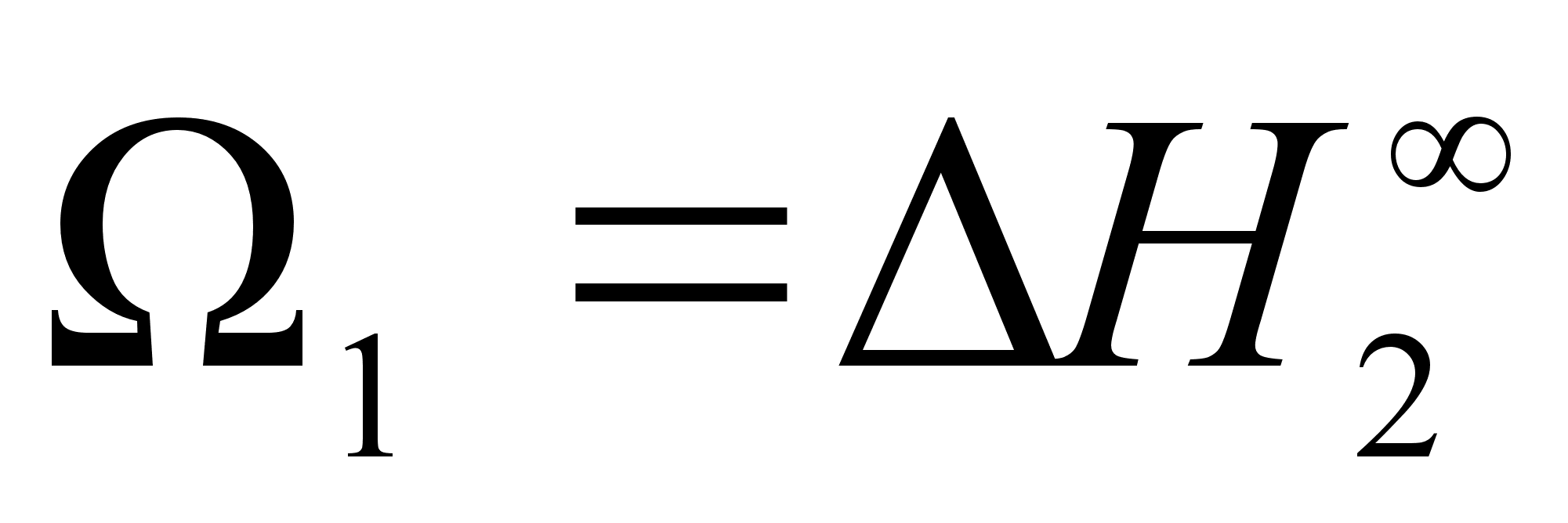 в чистом компоненте
1 до
в чистом компоненте
1 до
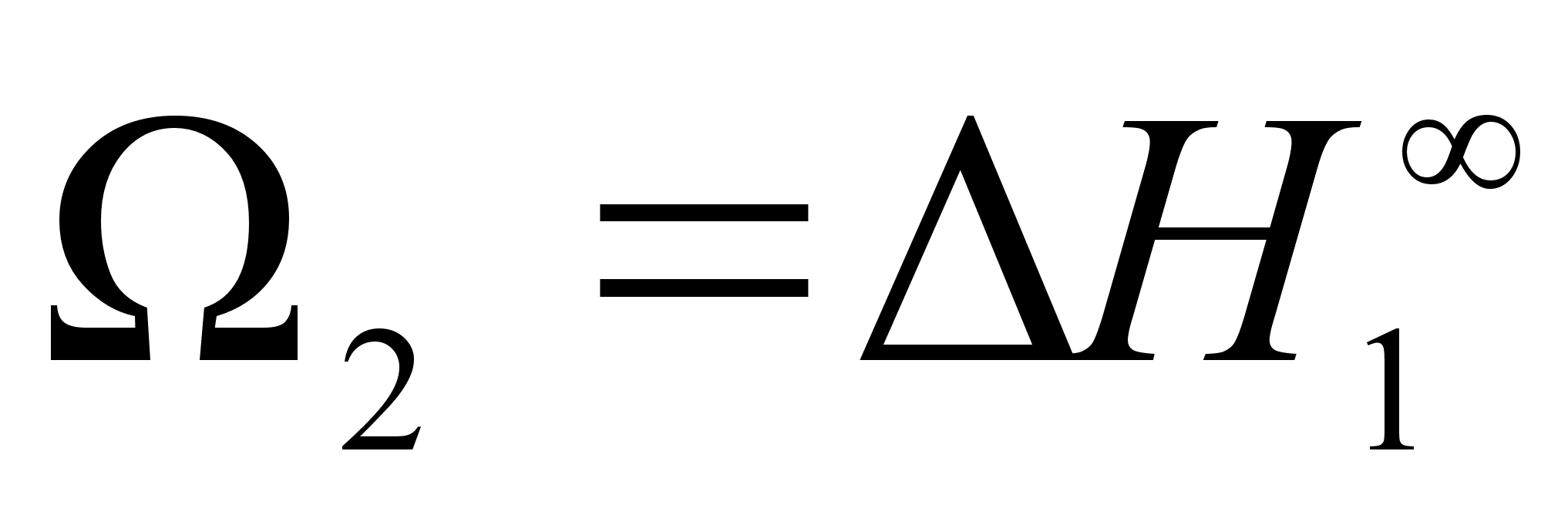 в компоненте
2. Это
можно записать
в виде уравнения:
в компоненте
2. Это
можно записать
в виде уравнения:
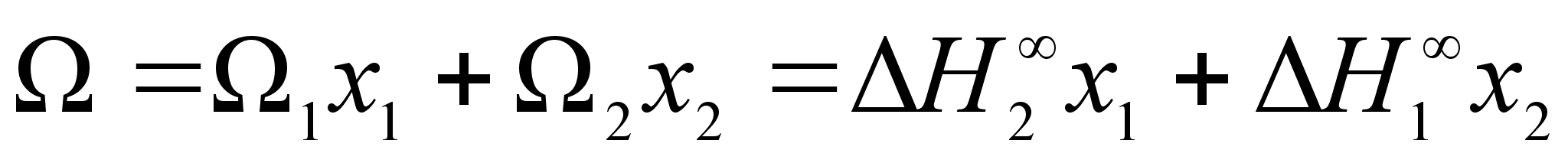
(69)
.
Так как
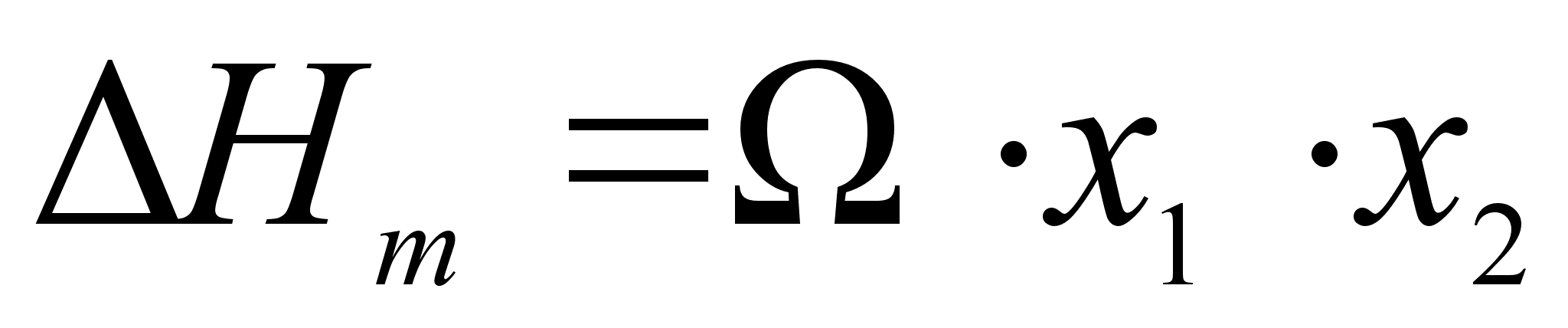 ,
получим:
,
получим:
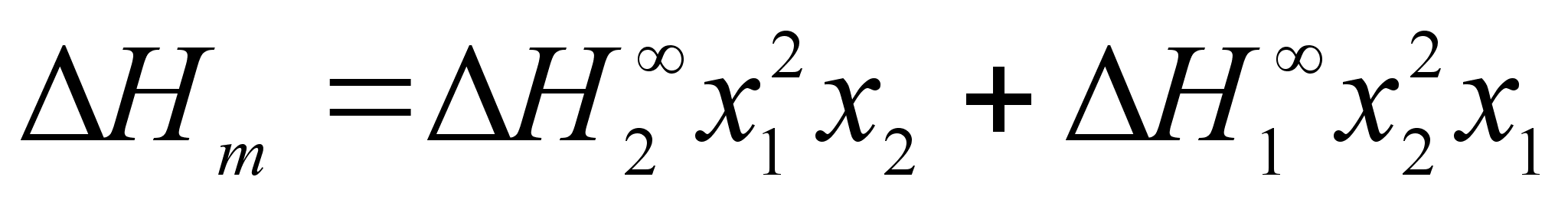
(70)
.Для определения парциальных теплот растворения воспользуемся формулой:
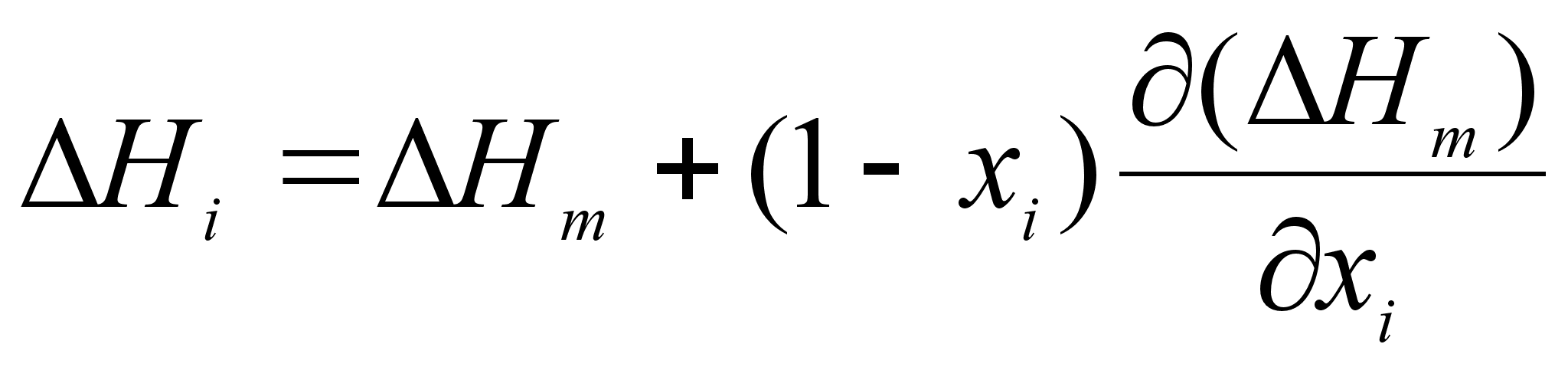
(71)
.В результате получим:
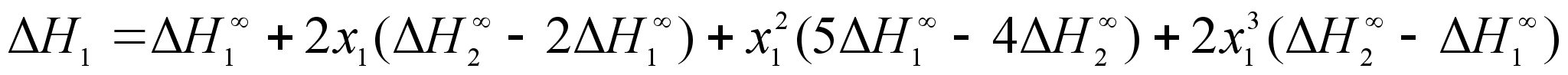
(72)
;
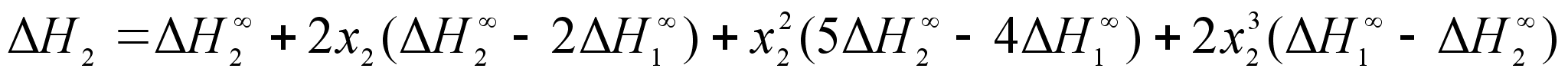
(73)
.Остальные формулы теории субрегулярных бинарных растворов следуют из соответствующих формул для регулярных систем:
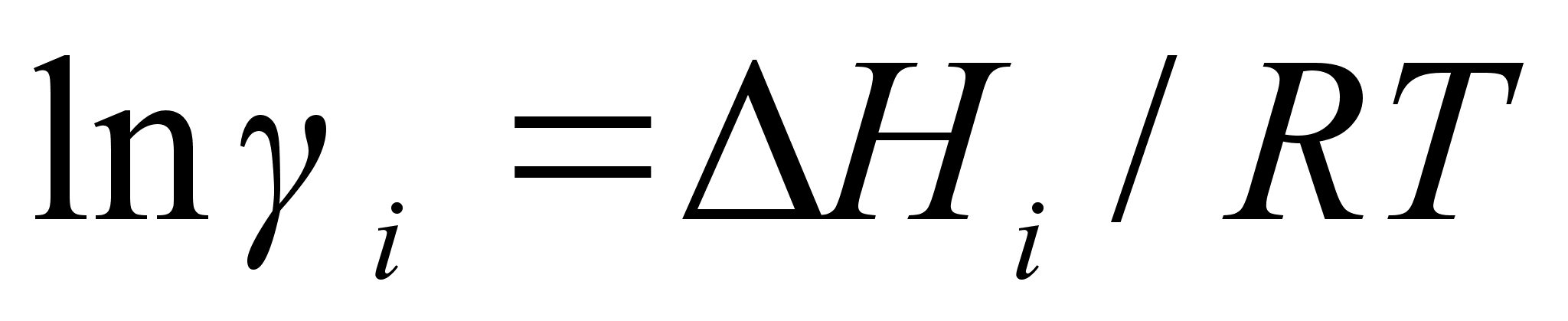
(74)
;
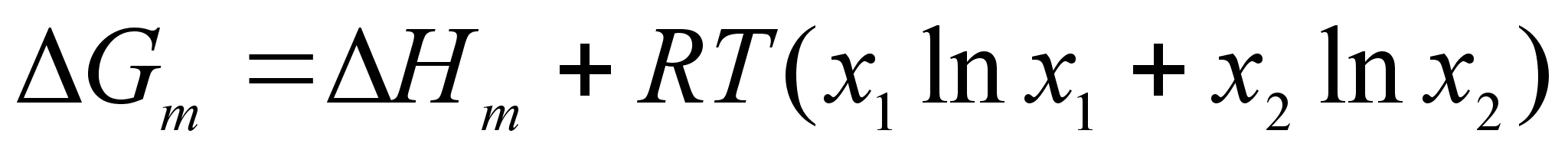
(75)
;
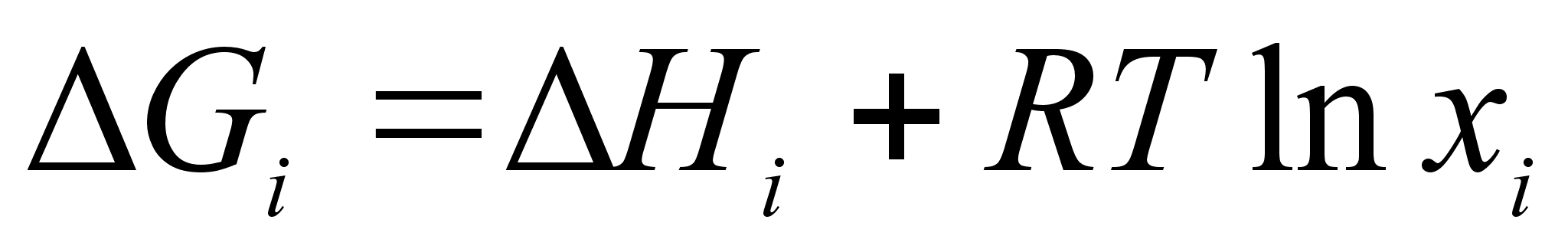
(76)
.
Как видно
из полученных
уравнений,
усложнение
модели привело
к тому, что в
расчетные
формулы входит
теперь не один
параметр (как
в теории регулярных
растворов), а
два:
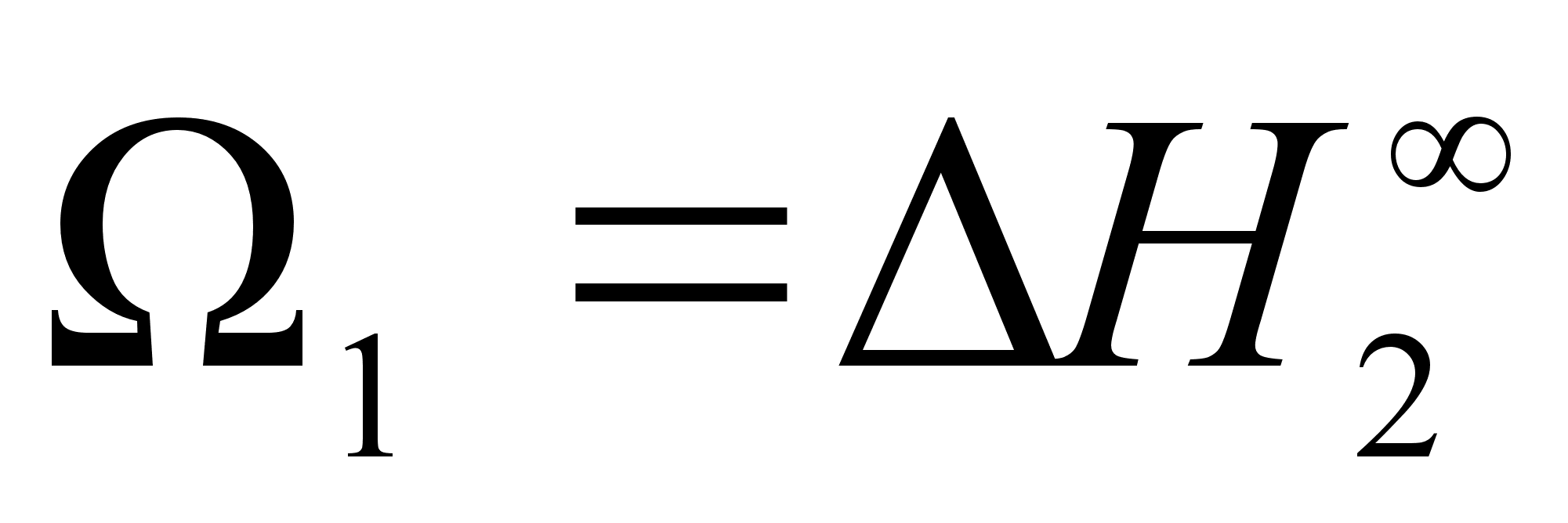 и
и
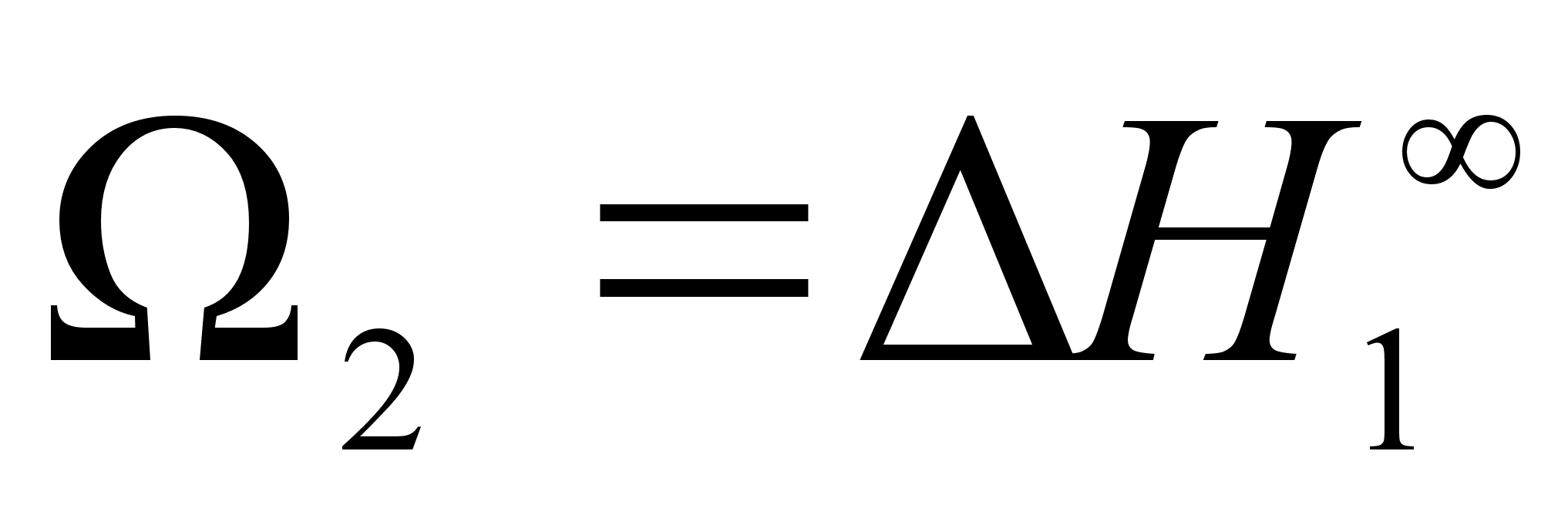 .
Таким образом,
повышение
точности расчетов
достигается
в этом случае
в результате
увеличения
количества
исходной информации
об объекте. Во
многих случаях
это не только
приемлемо, но
и необходимо
для лучшего
согласования
расчетных
данных с практическими.
Чтобы найти
необходимые
для расчетов
два параметра
.
Таким образом,
повышение
точности расчетов
достигается
в этом случае
в результате
увеличения
количества
исходной информации
об объекте. Во
многих случаях
это не только
приемлемо, но
и необходимо
для лучшего
согласования
расчетных
данных с практическими.
Чтобы найти
необходимые
для расчетов
два параметра
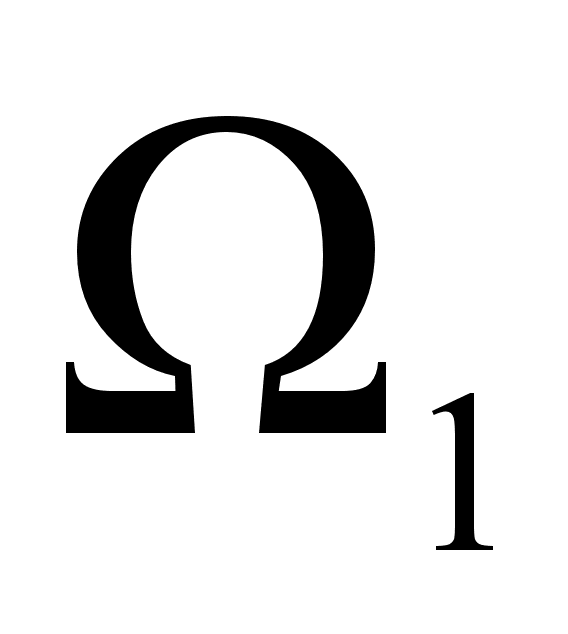 и
и
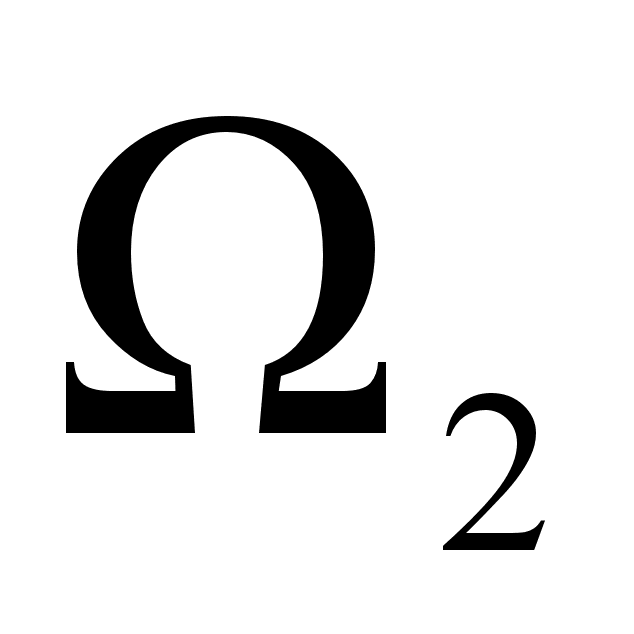 в случае, когда
неизвестны
значения
в случае, когда
неизвестны
значения
 и
и
 ,
можно воспользоваться
любыми двумя
известными
характеристиками:
,
можно воспользоваться
любыми двумя
известными
характеристиками:
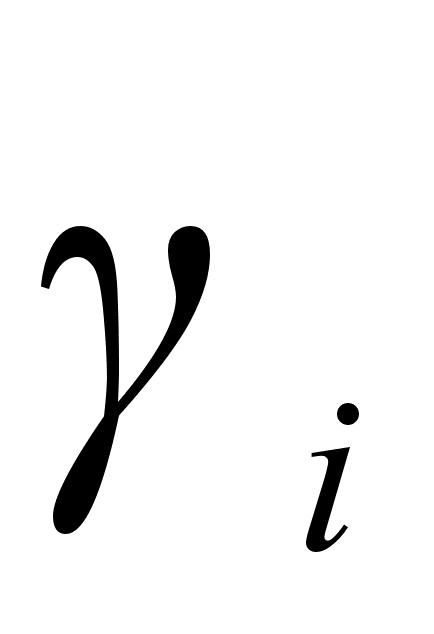 ,
,
 ,
,
 ,
,
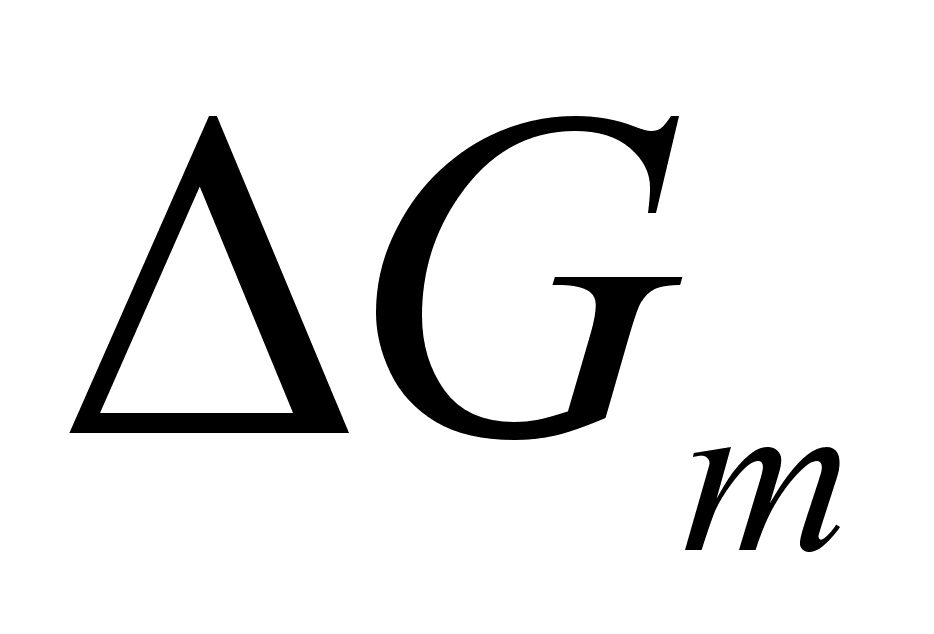 или
или
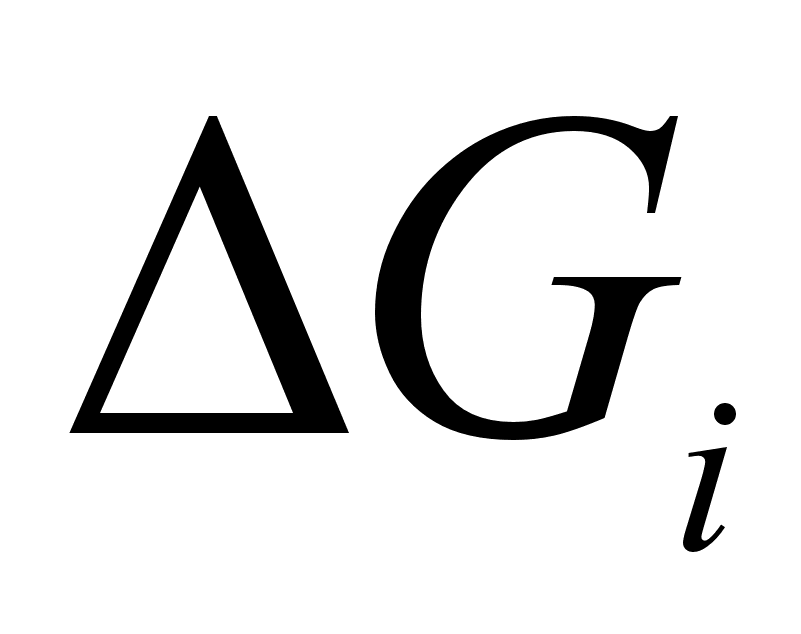 .
Усложнение
расчета сводится
при этом к
необходимости
решения системы
двух линейных
уравнений типа
рассмотренных
выше. [6]
.
Усложнение
расчета сводится
при этом к
необходимости
решения системы
двух линейных
уравнений типа
рассмотренных
выше. [6]
1.2.2.3 Квазирегулярные растворы
В случае квазирегулярного раствора поправка вводится как избыточная энтропия, связанная с теплотой образования раствора простым соотношением:
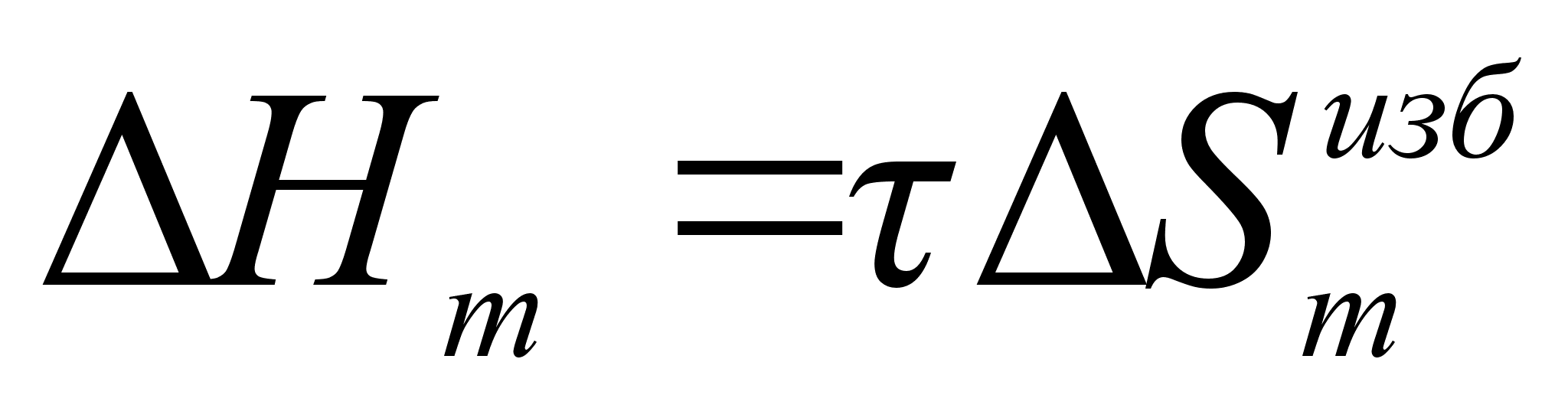
(77)
,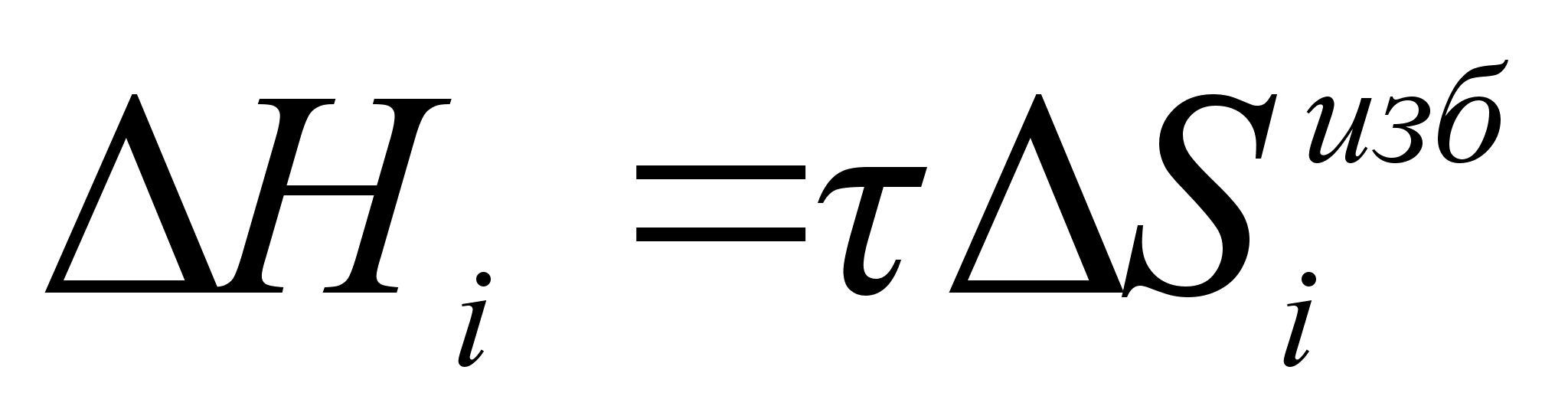 .
.
Из этого следуют важные расчетные формулы:
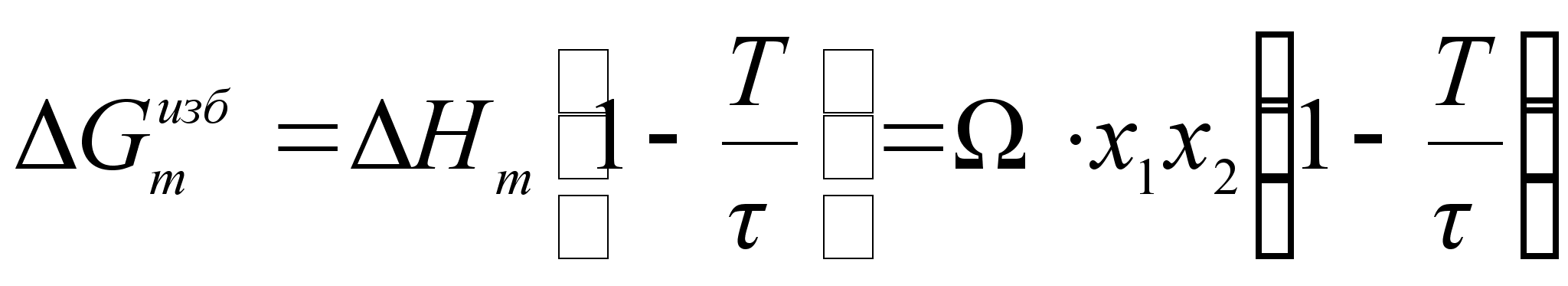
(78)
;
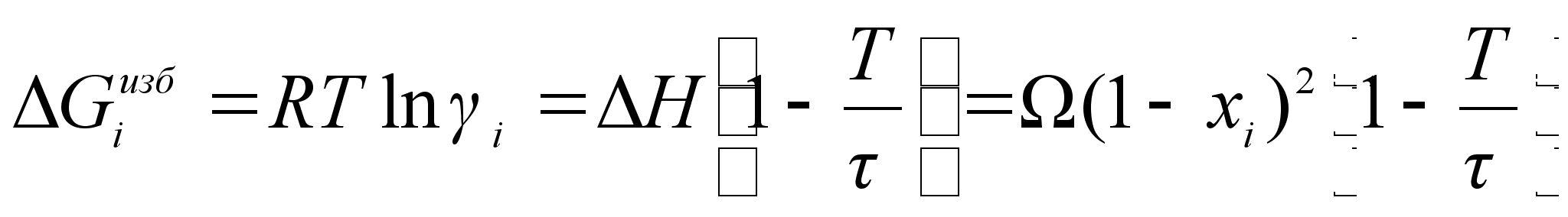
(79)
.
Из данного
выражения можно
вывести формулу
для расчета
температурной
зависимости
коэффициента
активности
по его значению
при одной
температуре.
При обычном
допущении
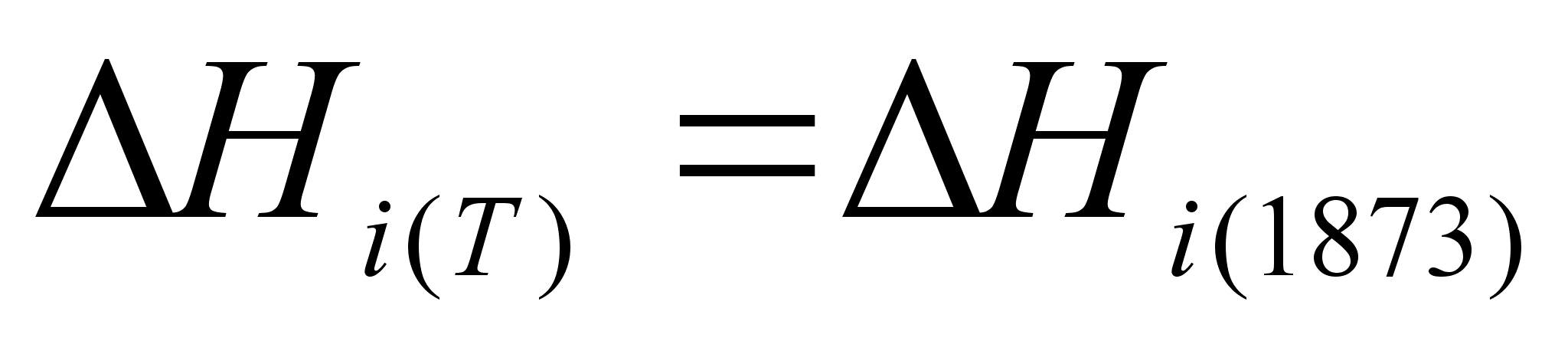 имеем:
имеем:
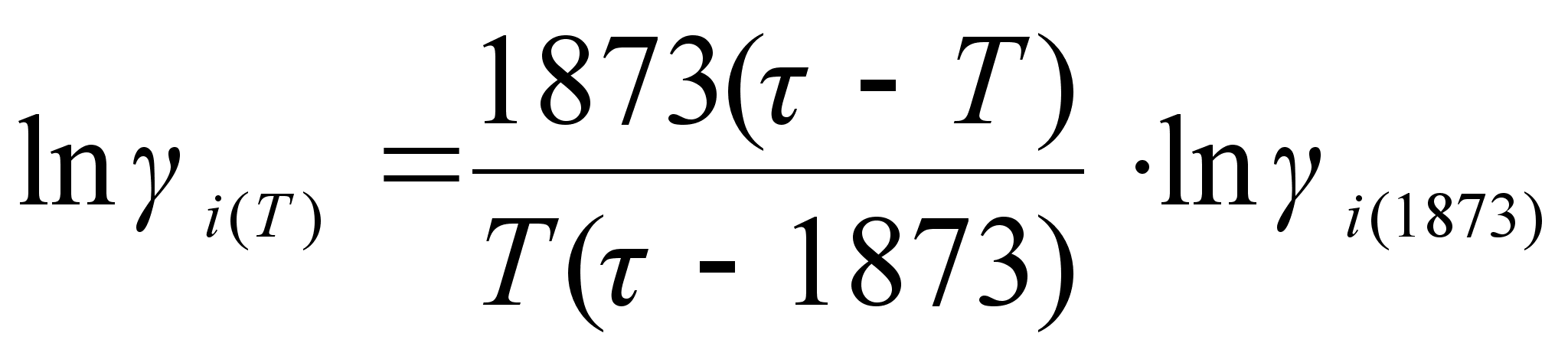
(80)
.
Сопоставляя
это выражение
с выражением
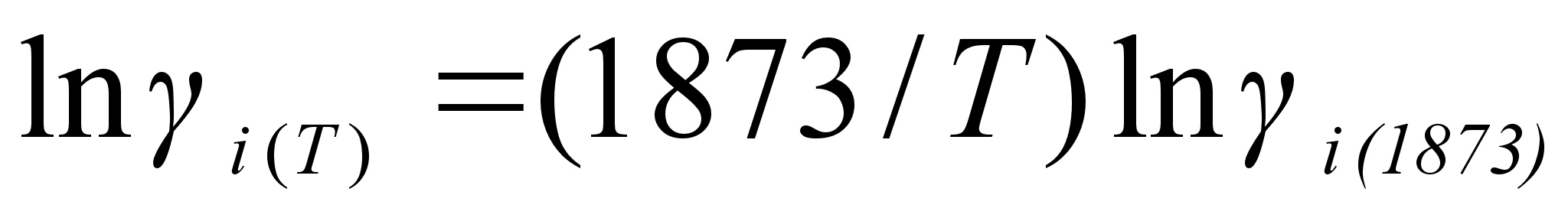 для регулярных
растворов,
видно, что при
очень больших
значениях
для регулярных
растворов,
видно, что при
очень больших
значениях
 (по сравнению
с Т и
1873 К) формулы
теории квазирегулярного
раствора и
регулярного
раствора
эквивалентны.
(по сравнению
с Т и
1873 К) формулы
теории квазирегулярного
раствора и
регулярного
раствора
эквивалентны.
Как и для
субрегулярных
растворов, в
формулы (78), (79) входят
два параметра,
в данном случае
 и
и
 ,
для определения
которых необходимо
не менее двух
экспериментально
полученных
значений
,
для определения
которых необходимо
не менее двух
экспериментально
полученных
значений
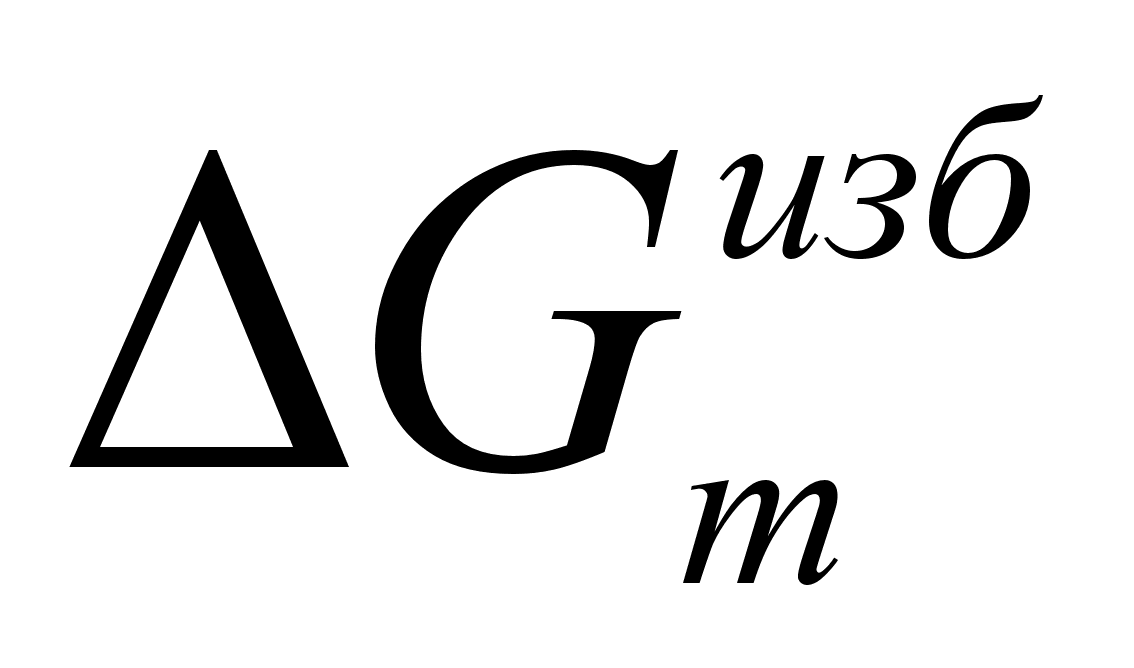 ,
,
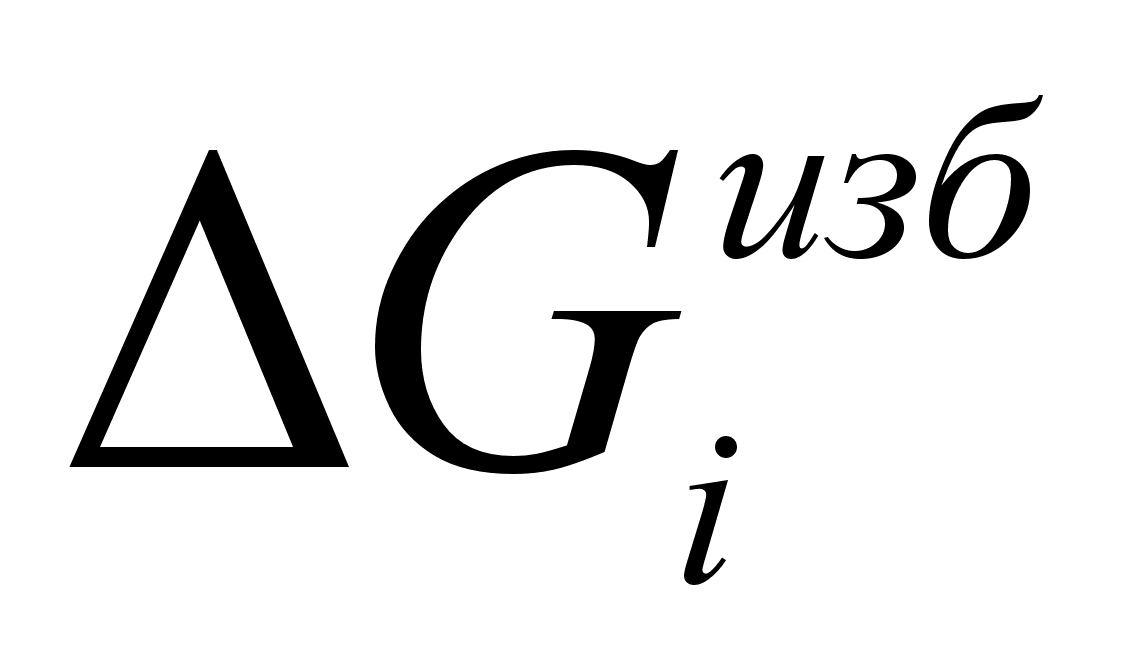 или
или
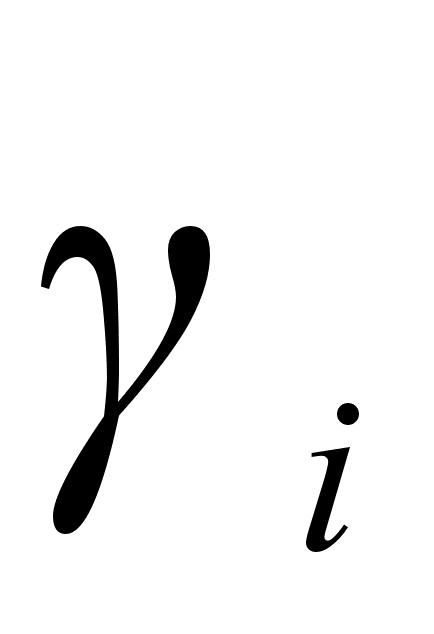 .
Чтобы определить
параметры, как
и в предыдущем
случае, необходимо
решить систему
двух линейных
уравнений типа
(78), (79). Указанное
минимально
необходимое
количество
исходных данных
достаточно
для выполнения
расчета, но,
как правило,
не обеспечивает
высокой точности
получаемых
результатов.
В связи с этим
для определения
параметров
используют
обычно максимальное
количество
экспериментальных
данных. Вычисления
при этом выполняют
методом наименьших
квадратов.
.
Чтобы определить
параметры, как
и в предыдущем
случае, необходимо
решить систему
двух линейных
уравнений типа
(78), (79). Указанное
минимально
необходимое
количество
исходных данных
достаточно
для выполнения
расчета, но,
как правило,
не обеспечивает
высокой точности
получаемых
результатов.
В связи с этим
для определения
параметров
используют
обычно максимальное
количество
экспериментальных
данных. Вычисления
при этом выполняют
методом наименьших
квадратов.
Важным
моментом в
теории квазирегулярных
растворов
является то,
обстоятельство,
что параметр
 в первом приближении
можно считать
независящим
от индивидуальных
свойств компонентов
раствора. Его
можно заранее
определить
для широкого
круга систем
по имеющимся
данным о теплотах
и энтропиях
образования
некоторых из
них. Формально
в первом приближении
можно считать
независящим
от индивидуальных
свойств компонентов
раствора. Его
можно заранее
определить
для широкого
круга систем
по имеющимся
данным о теплотах
и энтропиях
образования
некоторых из
них. Формально
 представляет
собой температуру,
при нагреве
до которой
раствор приобретает
свойства идеального.
Это следует
из того, что
при
представляет
собой температуру,
при нагреве
до которой
раствор приобретает
свойства идеального.
Это следует
из того, что
при
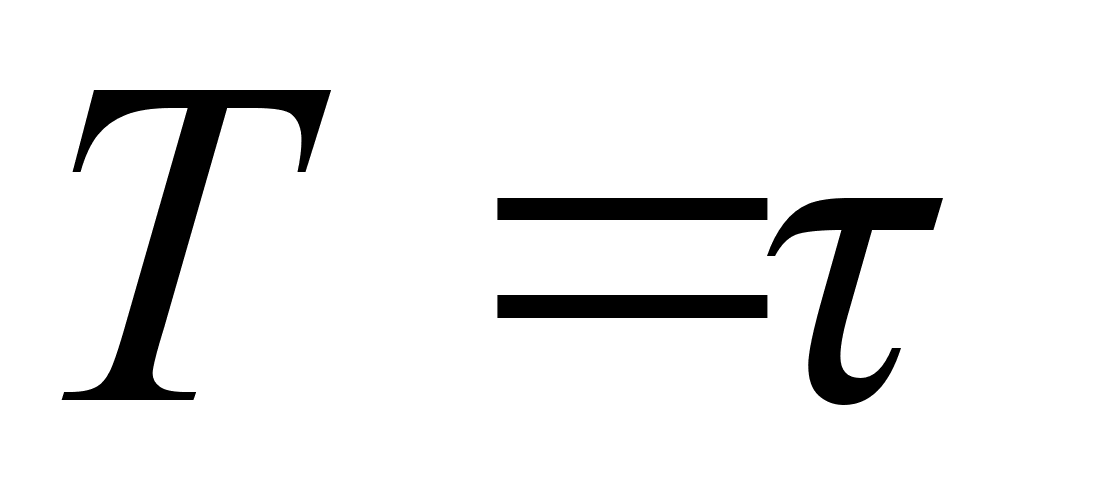 формулы теории
квазирегулярных
растворов (78),
(79) переходят
в выражения
для совершенного
раствора. Расчеты
показали, например,
что корреляция
между
формулы теории
квазирегулярных
растворов (78),
(79) переходят
в выражения
для совершенного
раствора. Расчеты
показали, например,
что корреляция
между
 и
и
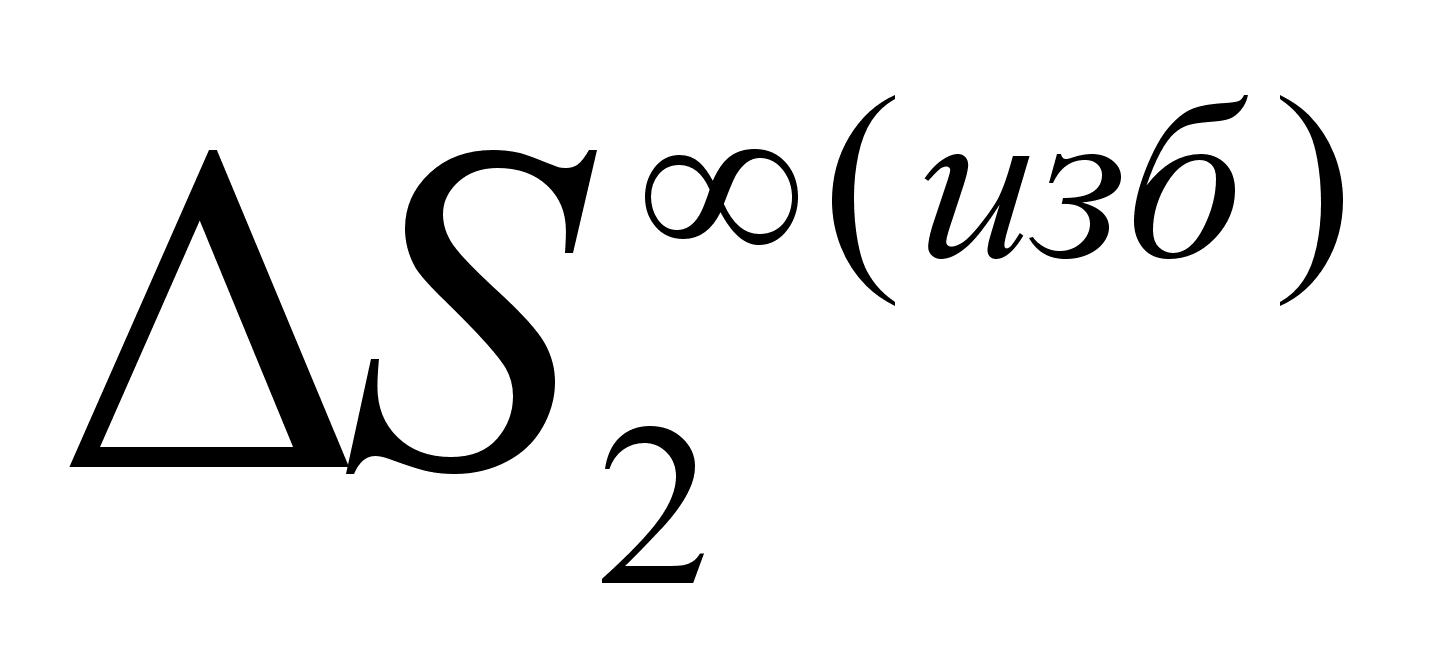 в 90 растворах
(жидких и твердых)
на основе целого
ряда растворителей
при температуре
от 293 до 1426 К удовлетворительно
характеризуется
одним значением
параметра
в 90 растворах
(жидких и твердых)
на основе целого
ряда растворителей
при температуре
от 293 до 1426 К удовлетворительно
характеризуется
одним значением
параметра
 ,
равным 3000 К. Далекая
экстраполяция
зависимостей,
полученных
на основе модельных
представлений,
обычно не дает
хороших результатов,
поэтому не
рекомендуется.
[6]
,
равным 3000 К. Далекая
экстраполяция
зависимостей,
полученных
на основе модельных
представлений,
обычно не дает
хороших результатов,
поэтому не
рекомендуется.
[6]
2 Концентрационные уравнения для бинарных растворов с полной взаимной растворимостью
До недавнего времени в качестве математических моделей при исследовании термодинамических характеристик растворов применялись только интерполяционные уравнения:
«…пока не удается вывести в общем виде теоретически обоснованную формулу концентрационной зависимости термодинамических функций для реальных систем. В связи с этим при обработке экспериментальных данных применяются различные интерполяционные формулы [8] ».
Как известно, таким методом невозможно описать всего многообразия реально существующих металлических расплавов. Поэтому, в работе [9] впервые были выведены аналитические уравнения, связывающие термодинамические функции бинарного расплава с концентрацией его компонентов. Далее приведено краткое описание вывода.
2.1 Вывод концентрационных уравнений.
При образовании
раствора
относительная
парциальная
молярная энергия
Гиббса
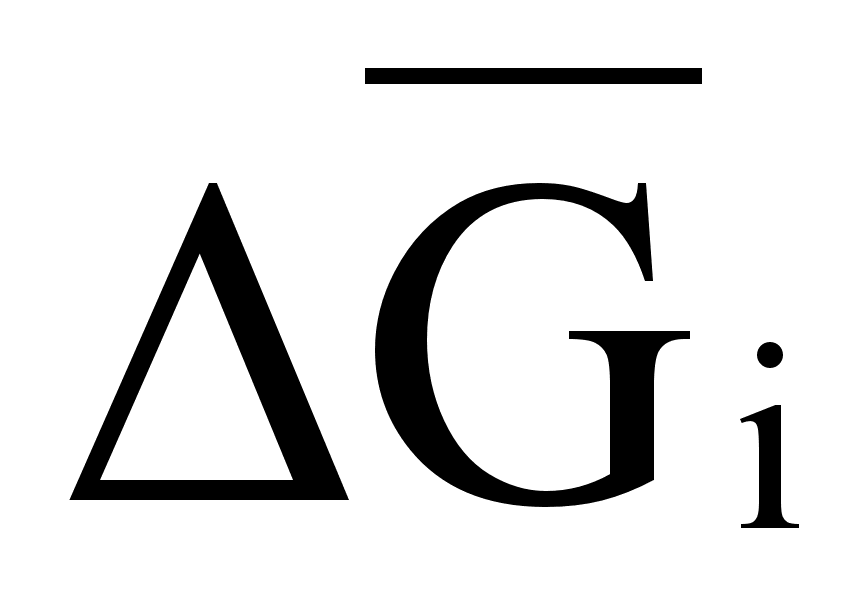 одного из компонентов
описывается
уравнением:
одного из компонентов
описывается
уравнением:
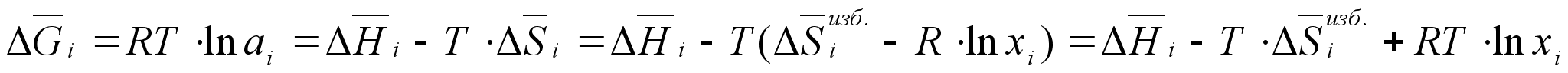
(81)
;из данного уравнения активность компонента можно выразить следующим образом:
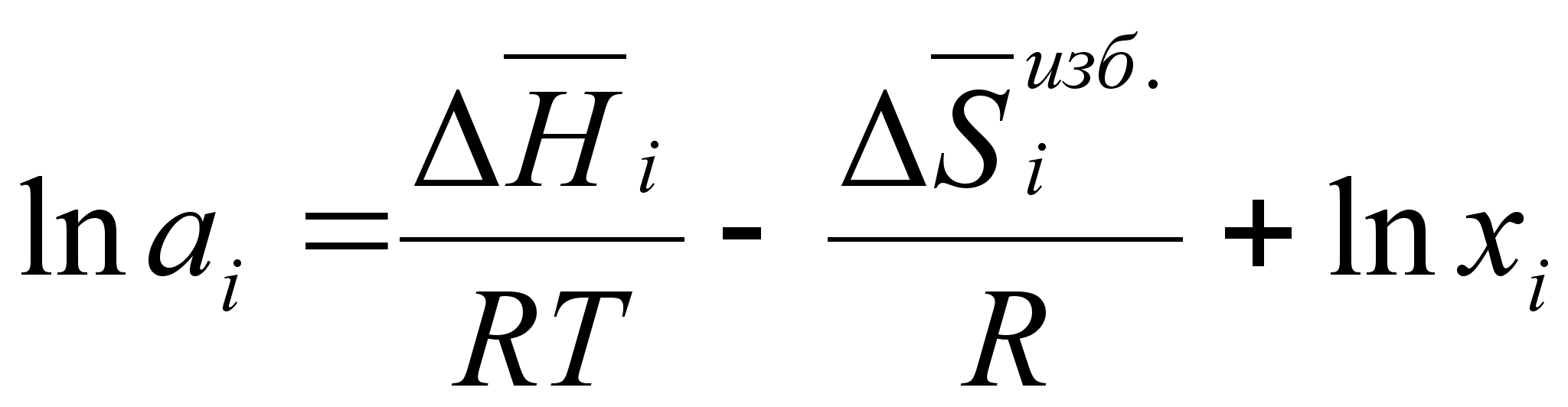
(82)
.
Поскольку
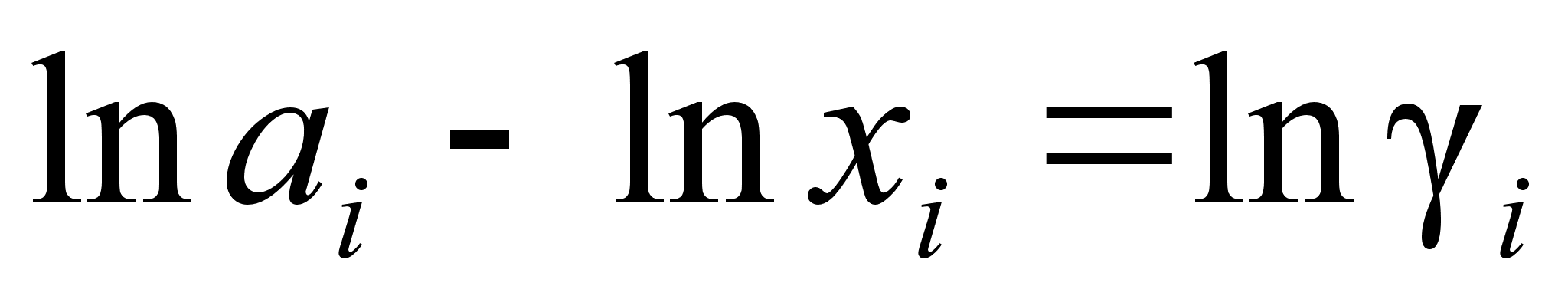 ,
то коэффициент
активности:
,
то коэффициент
активности:
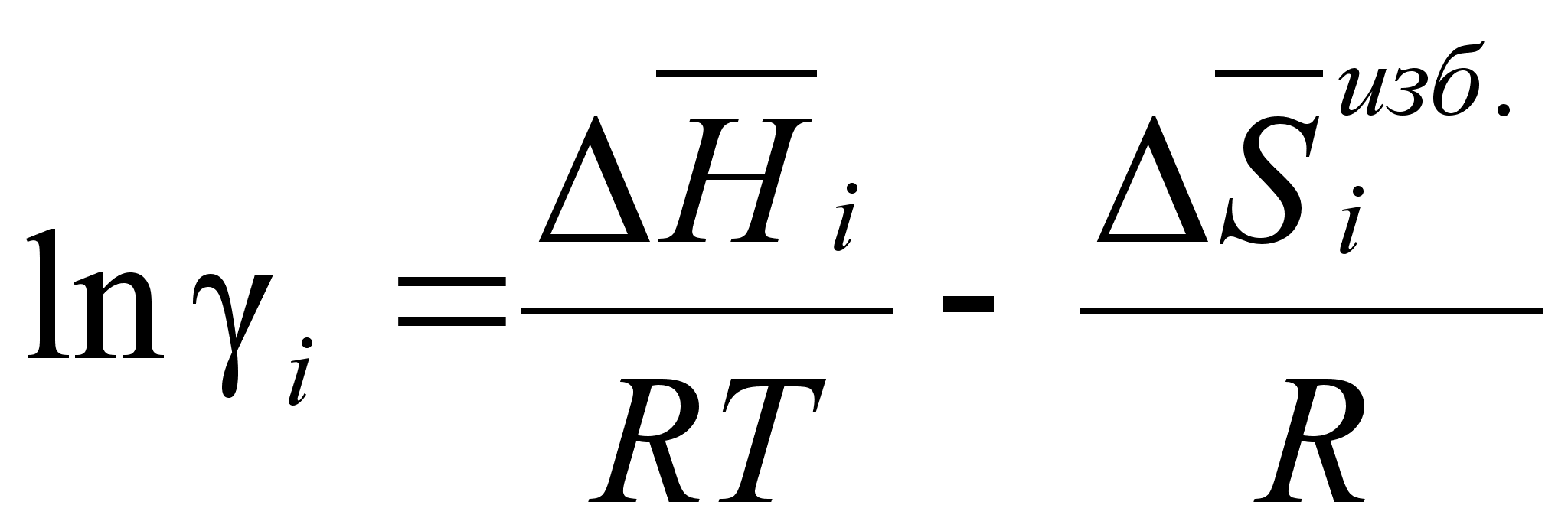
(83)
.
Задача
заключается
в том, чтобы
величины
 ,
,
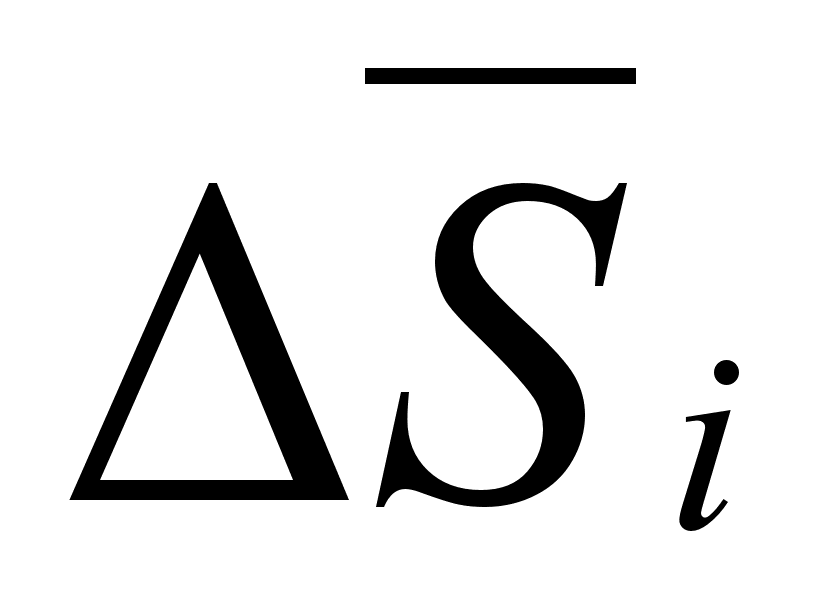 ,
а следовательно
и
,
а следовательно
и
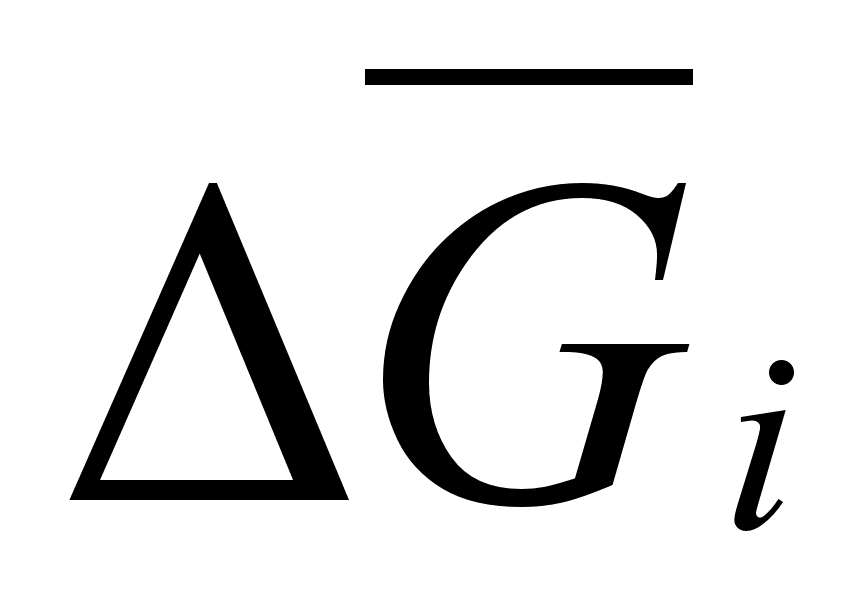 представить
как соответствующие
концентрационные
функции в компактной
форме без каких–либо
ограничений.
представить
как соответствующие
концентрационные
функции в компактной
форме без каких–либо
ограничений.
Рассмотрим
парциальные
молярные энтальпии
компонентов
бинарного
раствора
 и
и
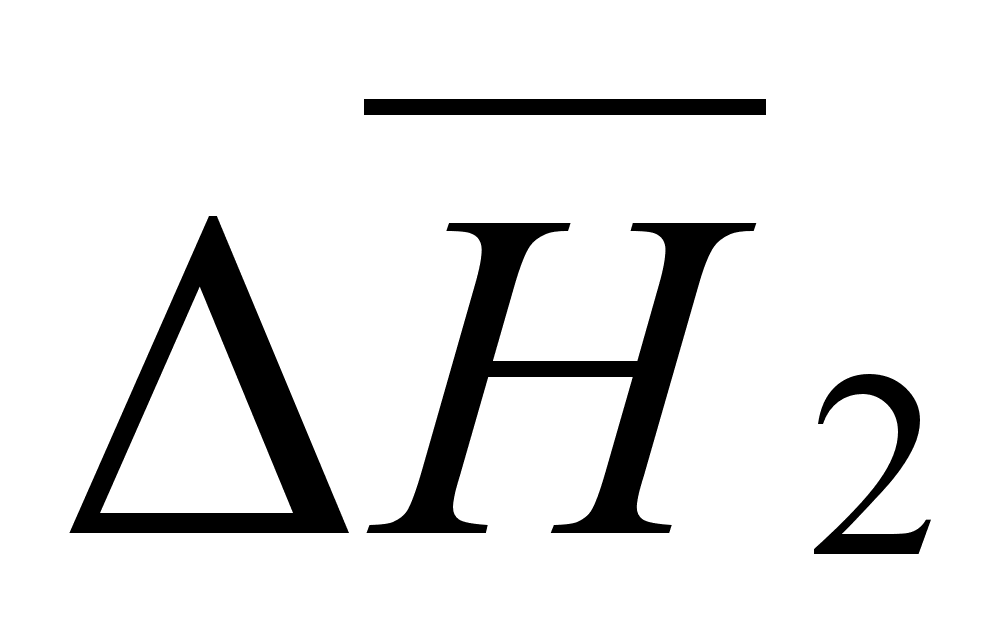 ,
которые связаны
между собой
соотношением
Гиббса – Дюгема:
,
которые связаны
между собой
соотношением
Гиббса – Дюгема:
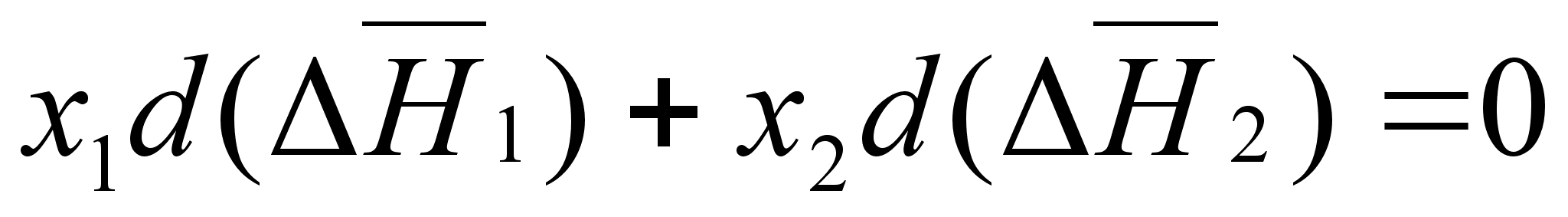
(84)
;которое можно записать в следующей форме:
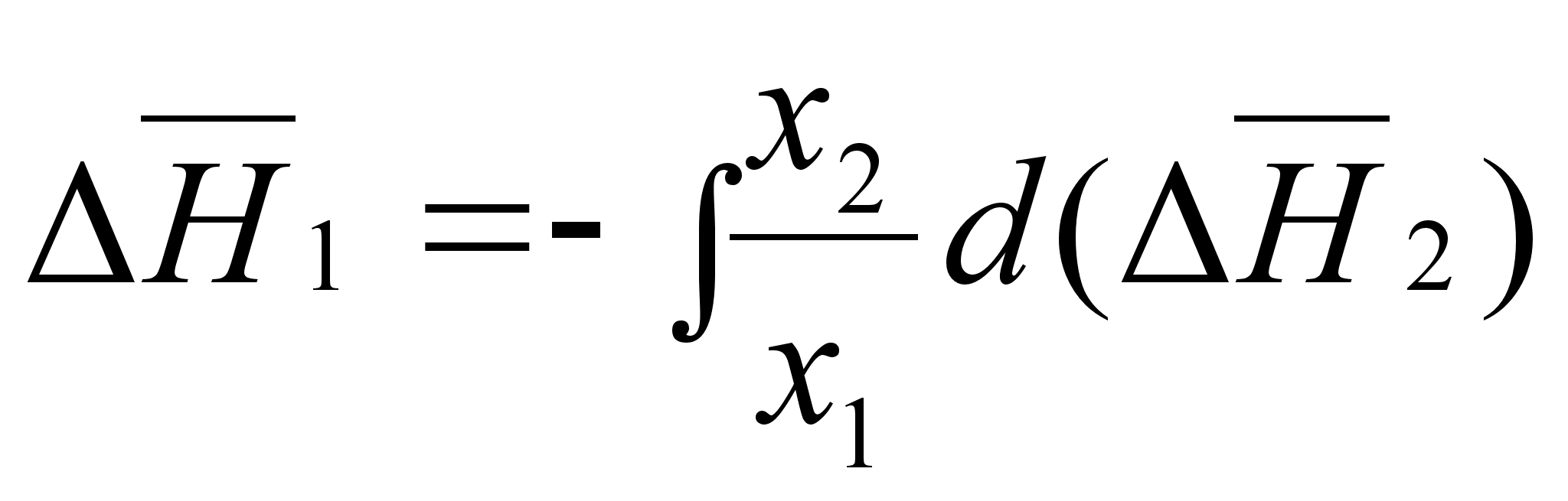
(84’)
.В результате определенных преобразований, аналитически получены концентрационные уравнения для парциальной молярной энтальпии компонентов в бинарном растворе с неограниченной растворимостью:
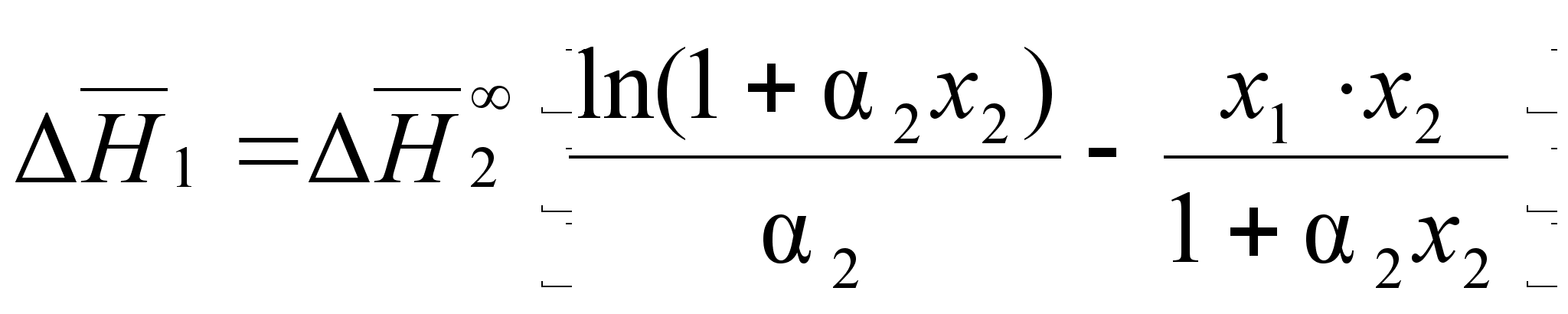
(85)
,
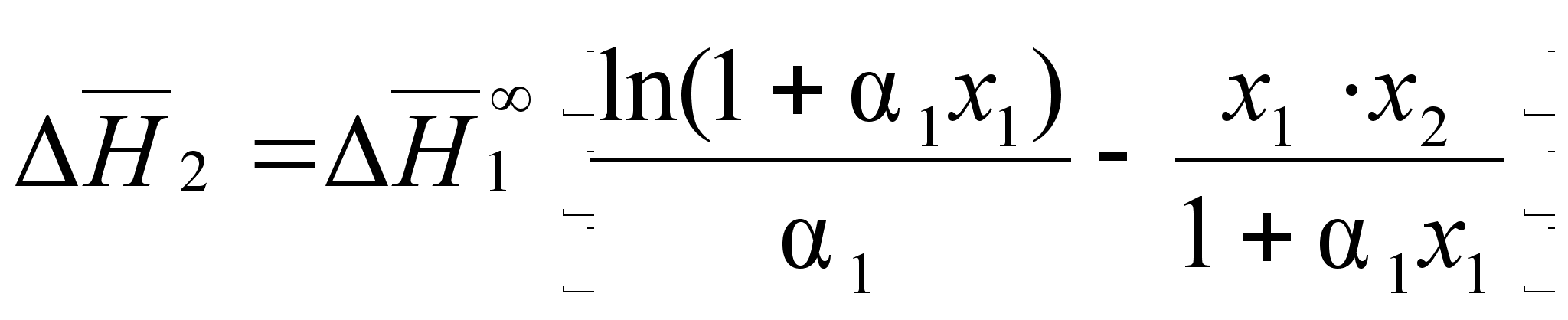
(86)
.
В этих
уравнениях
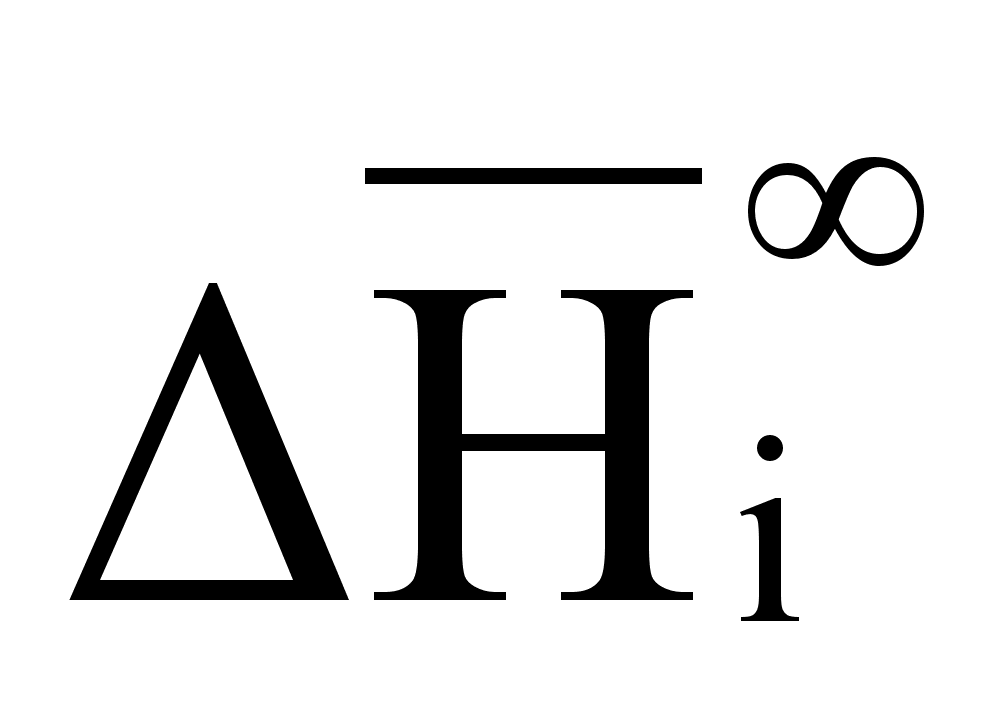 - парциальная
молярная энтальпия
при образовании
бесконечно
разбавленного
раствора:
- парциальная
молярная энтальпия
при образовании
бесконечно
разбавленного
раствора:
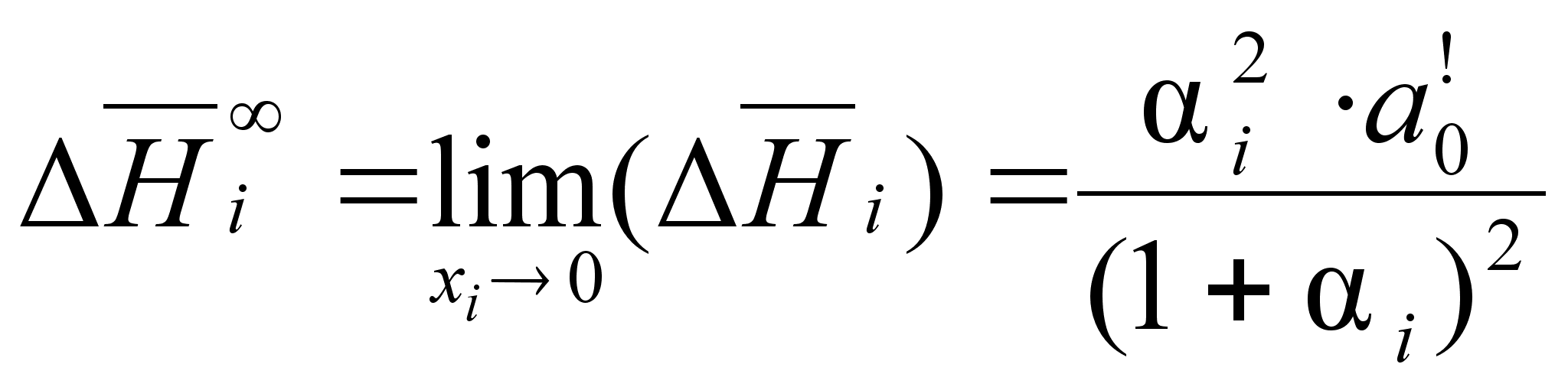
(87)
.
Однако,
в уравнениях
(85) и (86) функции
 и
и
 выражены через
«чужие» коэффициенты;
т.е. парциальная
молярная энтальпия
первого компонента
выражена через
термодинамические
характеристики
второго и наоборот.
Чтобы получить
функции
выражены через
«чужие» коэффициенты;
т.е. парциальная
молярная энтальпия
первого компонента
выражена через
термодинамические
характеристики
второго и наоборот.
Чтобы получить
функции
 и
и
 через «свои»
коэффициенты,
обратимся к
уравнению
(84’). Подставляя
в него выражение
для
через «свои»
коэффициенты,
обратимся к
уравнению
(84’). Подставляя
в него выражение
для
 из уравнения
(86) и производя
интегрирование,
получим:
из уравнения
(86) и производя
интегрирование,
получим:
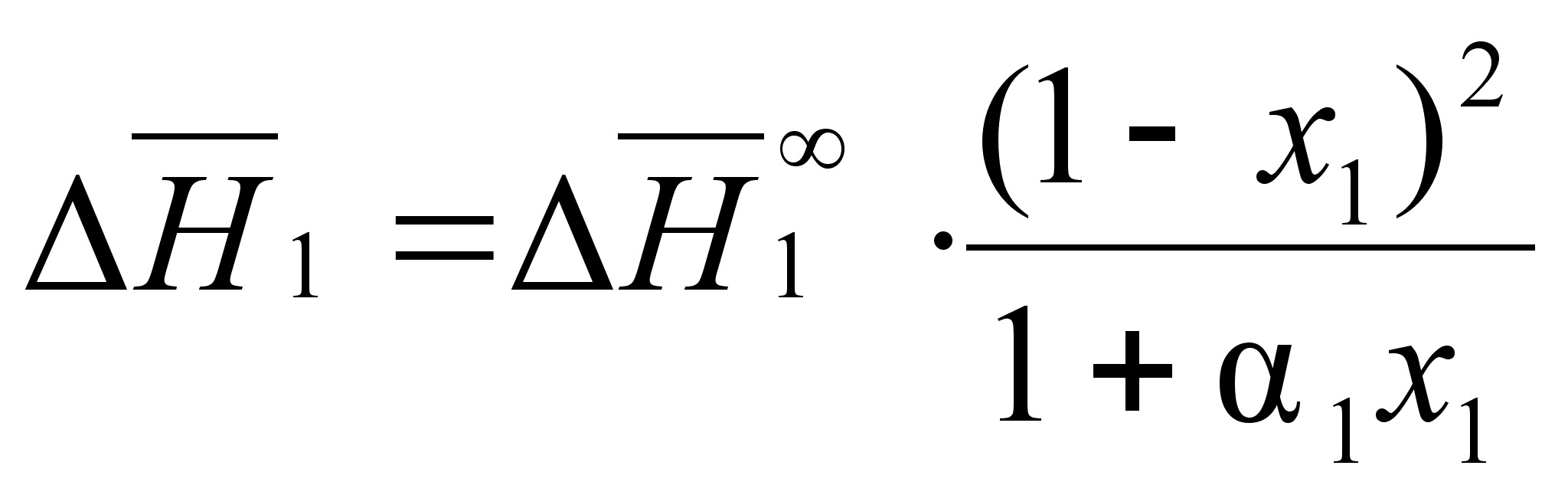
(88)
.
Аналогичное
выражение
запишем и для
 :
:
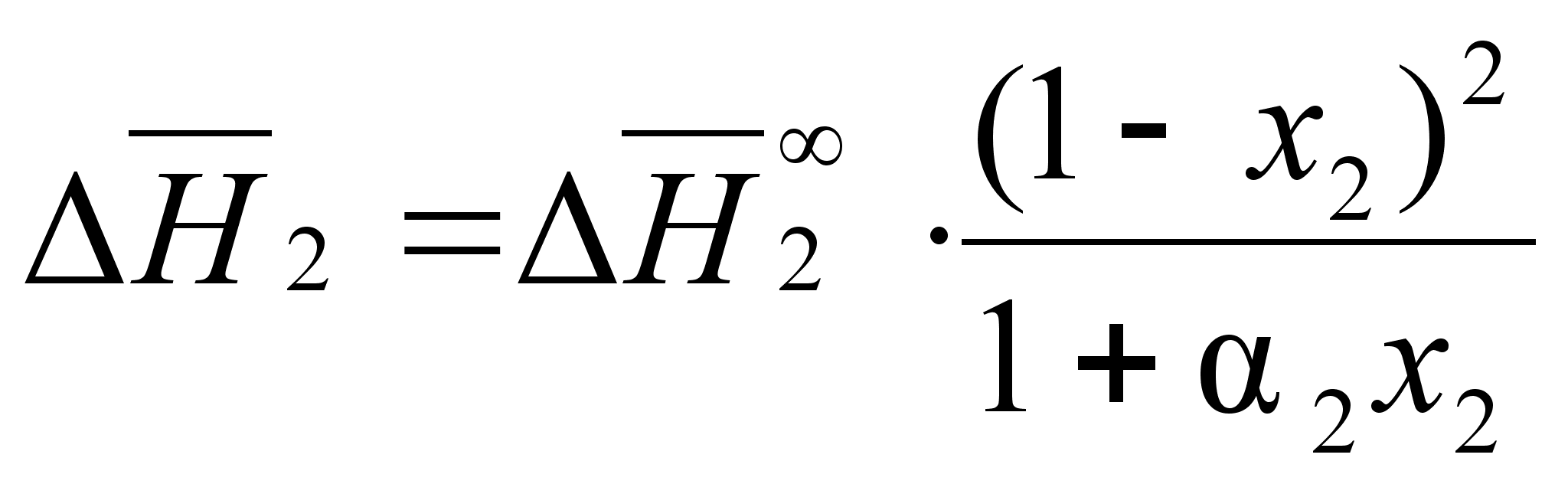
(89)
.Теперь парциальная молярная энтальпия выражена как концентрационная зависимость через величины, характеризующие природу соответствующего компонента.
С учетом соотношения (87) уравнения (85) и (86) будут иметь вид:
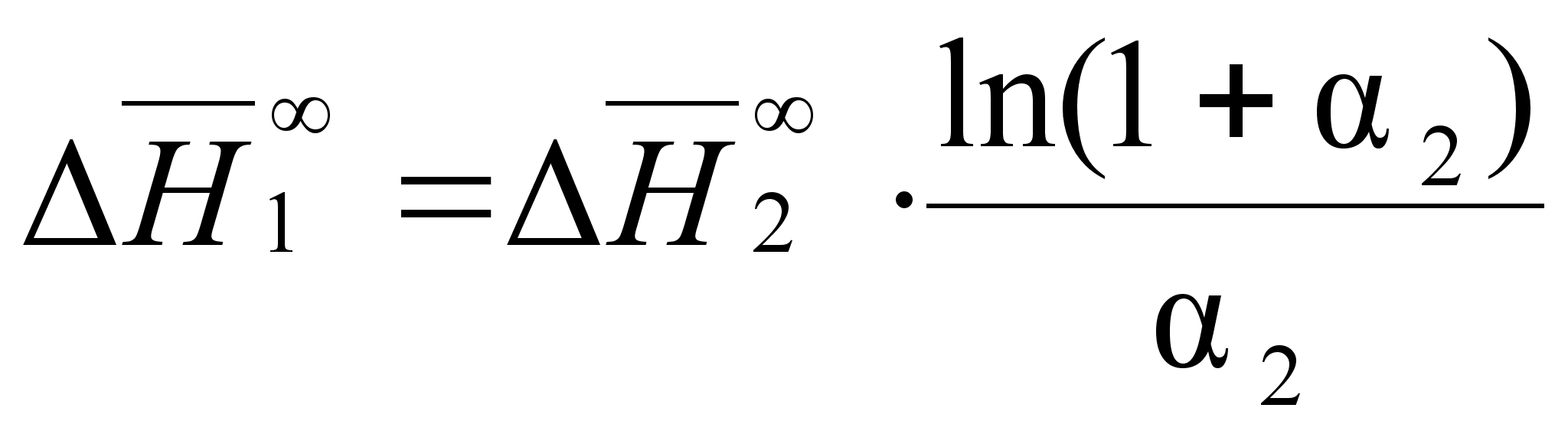
(90)
;
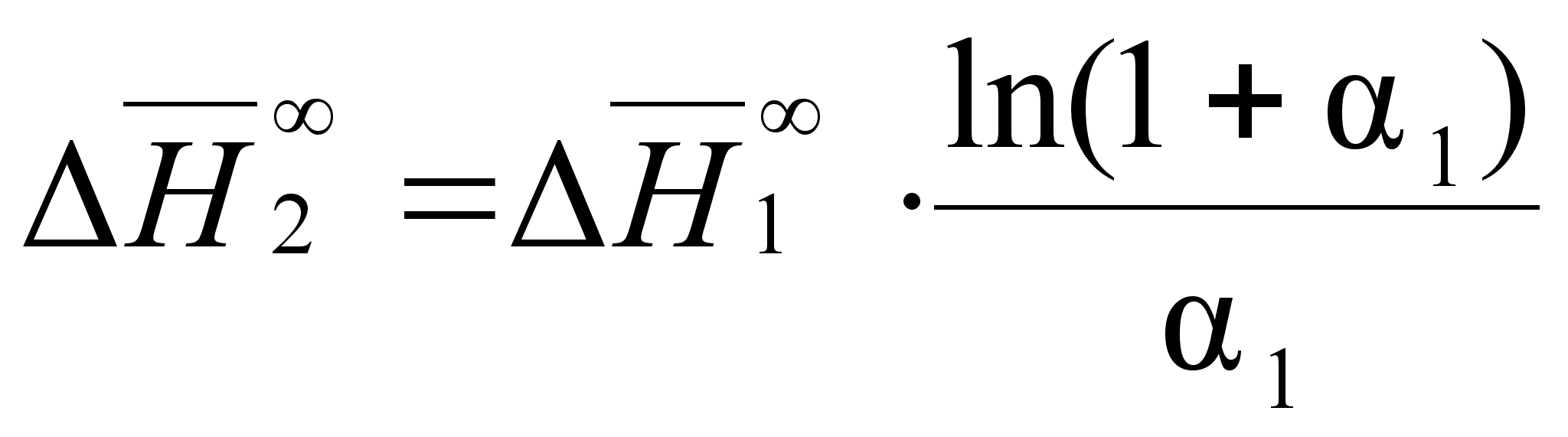
(91)
.Из этих уравнений следует равенство:
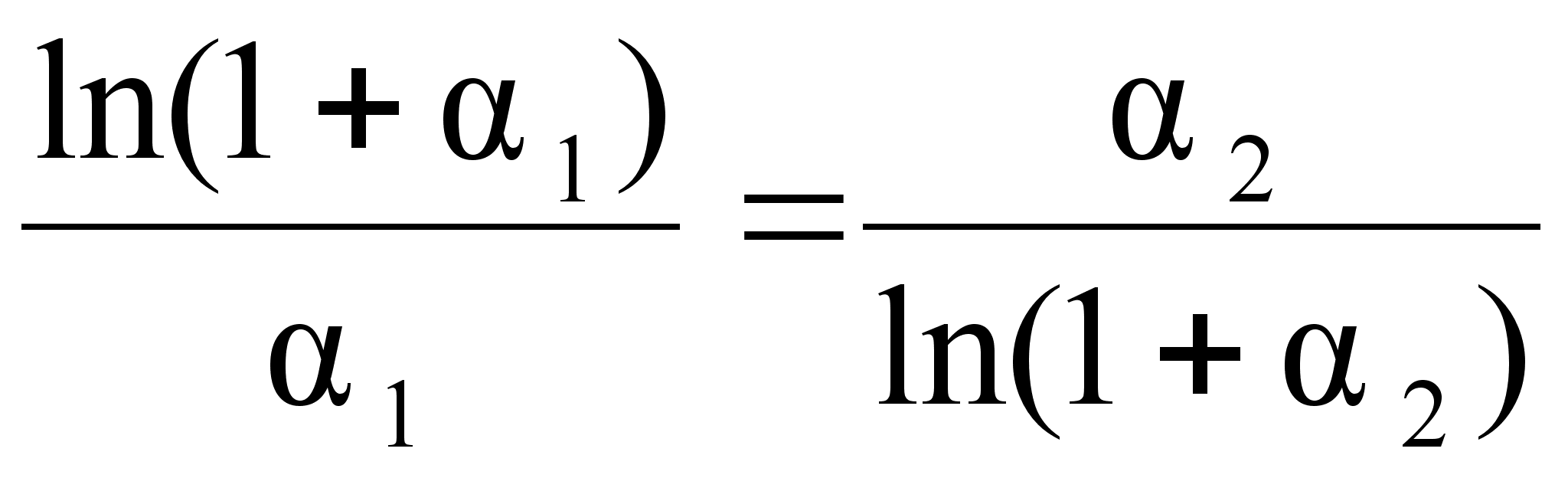
(92)
,
связывающее
между собой
коэффициенты
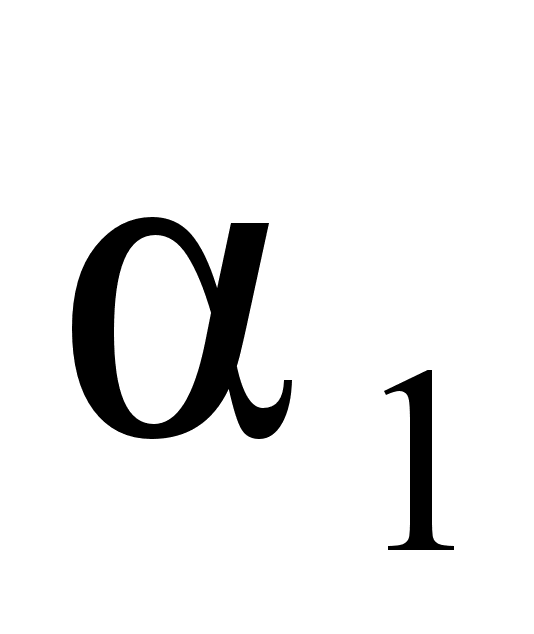 и
и
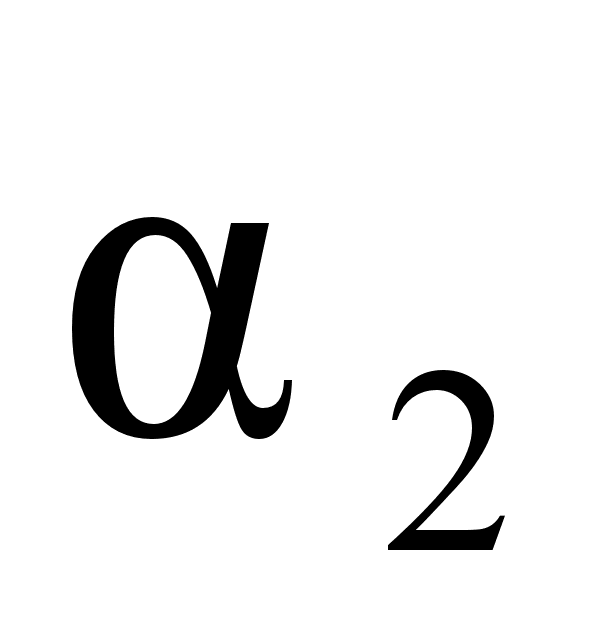 .
И вообще, уравнения
(90)–(92) позволяют
находить
соответствующие
постоянные
величины для
одного компонента,
если они известны
для другого.
.
И вообще, уравнения
(90)–(92) позволяют
находить
соответствующие
постоянные
величины для
одного компонента,
если они известны
для другого.
Все приведенные
выше рассуждения
справедливы
и для другой
термодинамической
функции
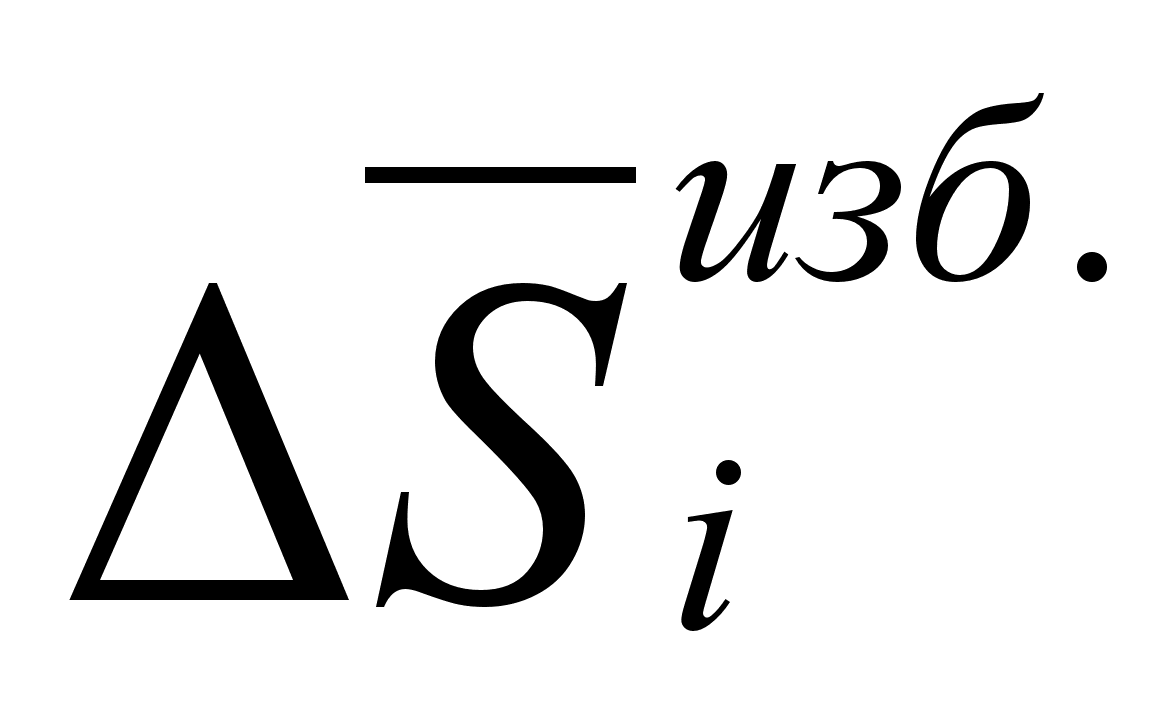 .
Поэтому, сразу
запишем для
нее конечное
выражение:
.
Поэтому, сразу
запишем для
нее конечное
выражение:
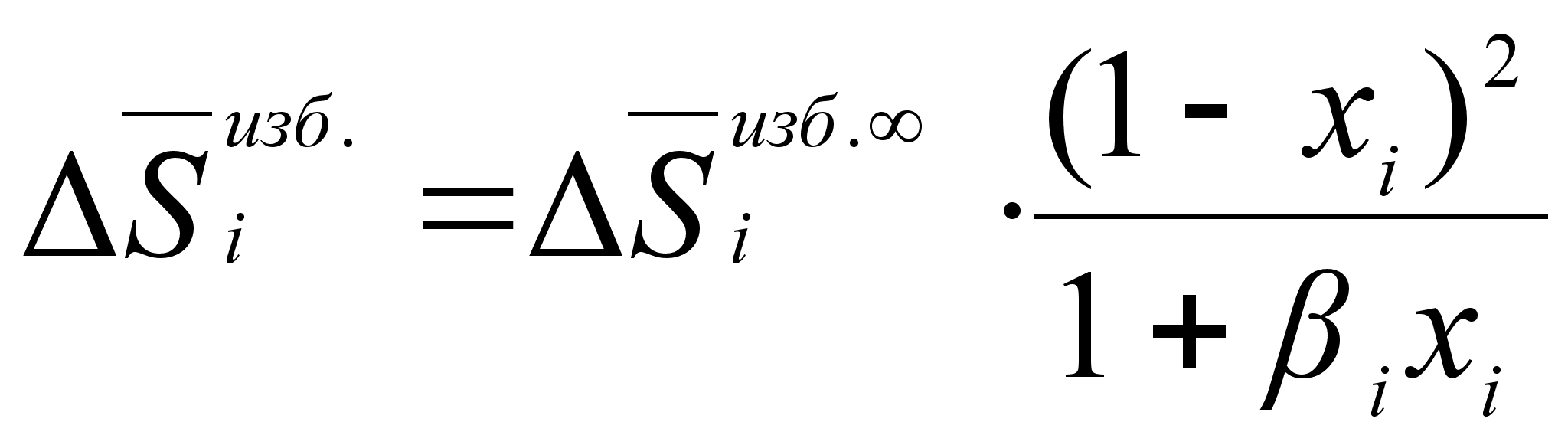
(93)
.
Зная
концентрационные
выражения для
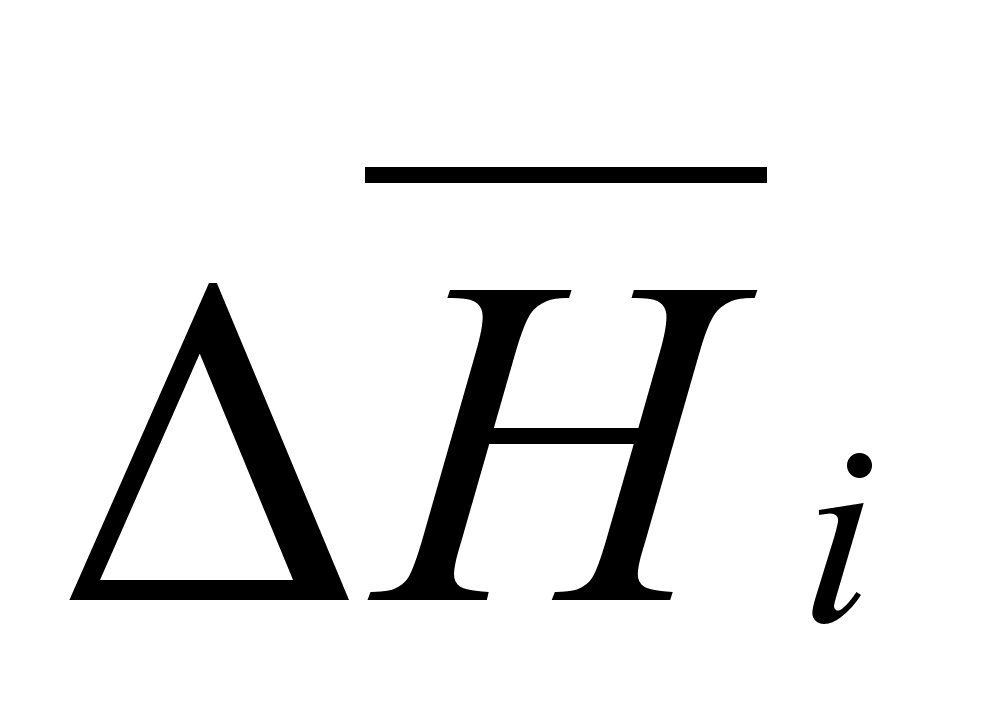 и
и
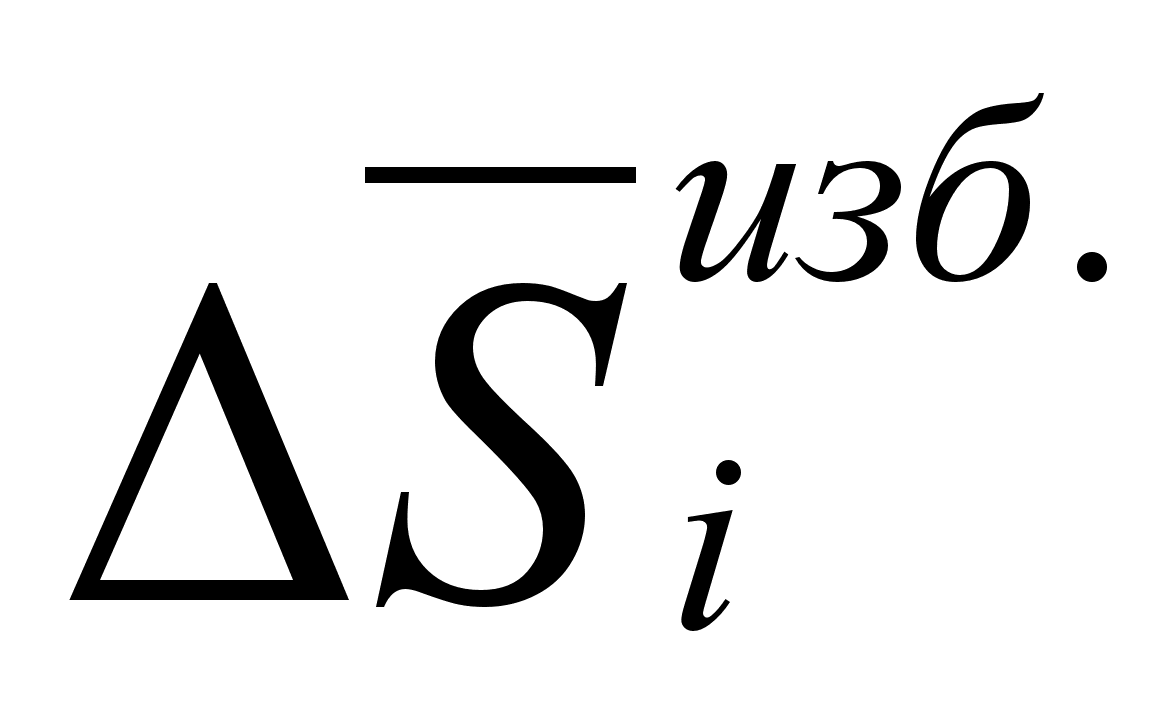 ,
можно написать
соответствующее
уравнение для
парциальной
молярной свободной
энергии Гиббса:
,
можно написать
соответствующее
уравнение для
парциальной
молярной свободной
энергии Гиббса:
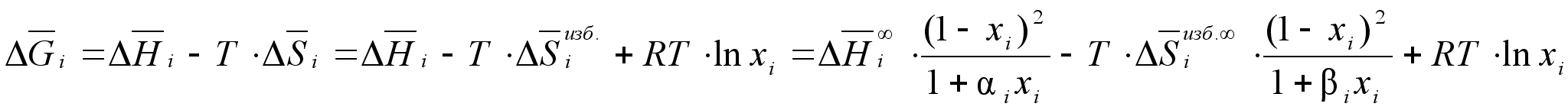
(94)
.Для активности компонента в растворе данное уравнение перепишется так:
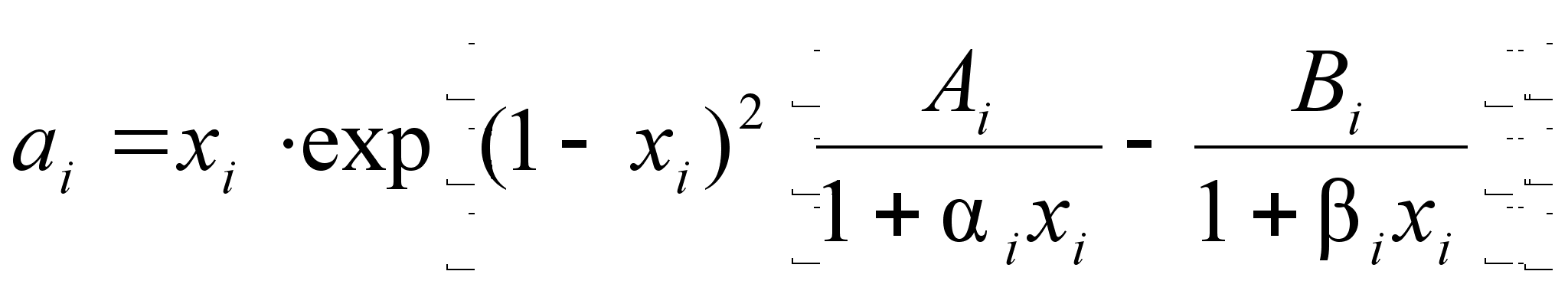
(95)
,г
(96)
де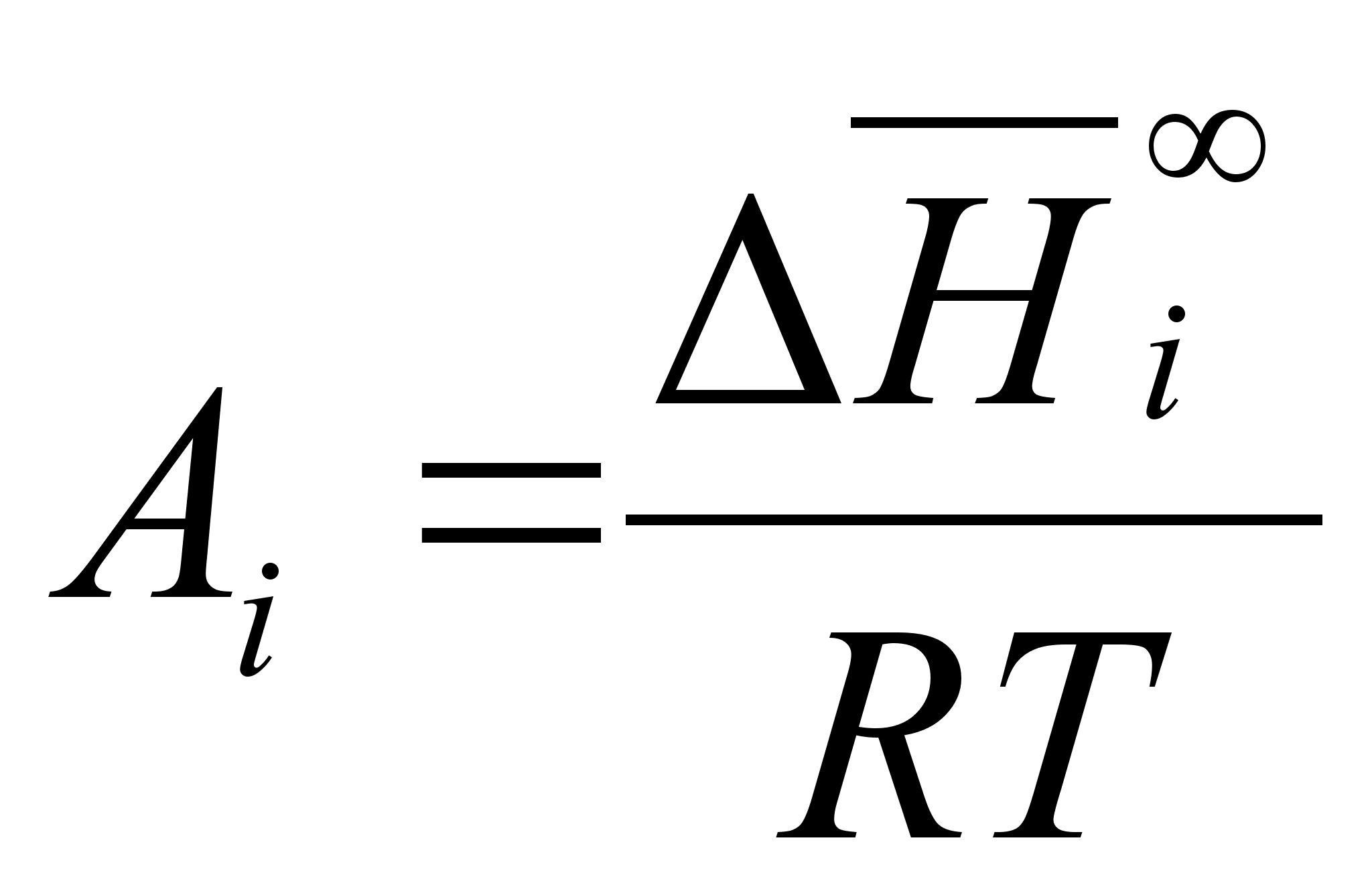 ;
;
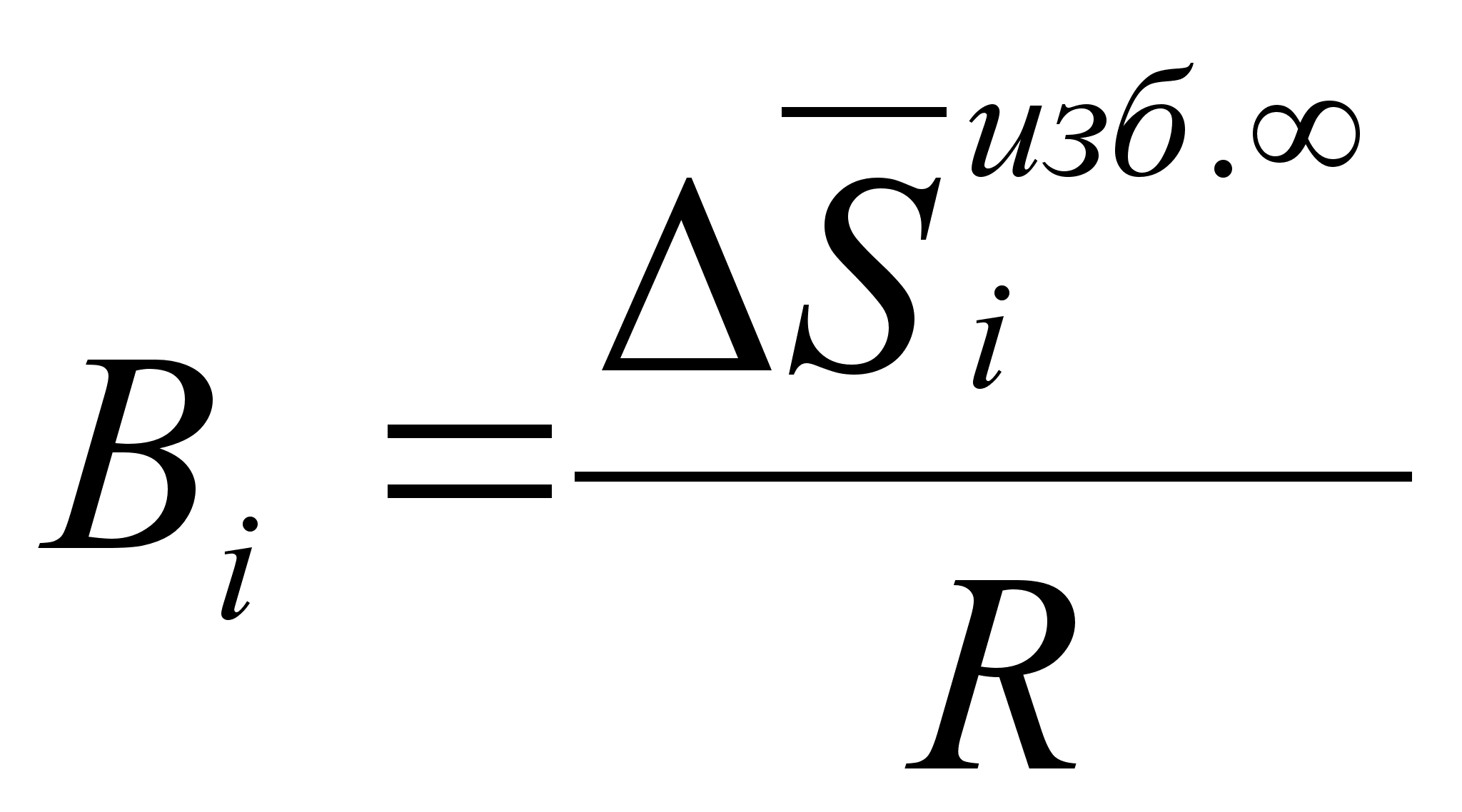 .
.
Выражение (95) позволяет описать экспериментальные данные зависимости активности компонента от состава бинарного раствора. Перепишем его следующим образом:
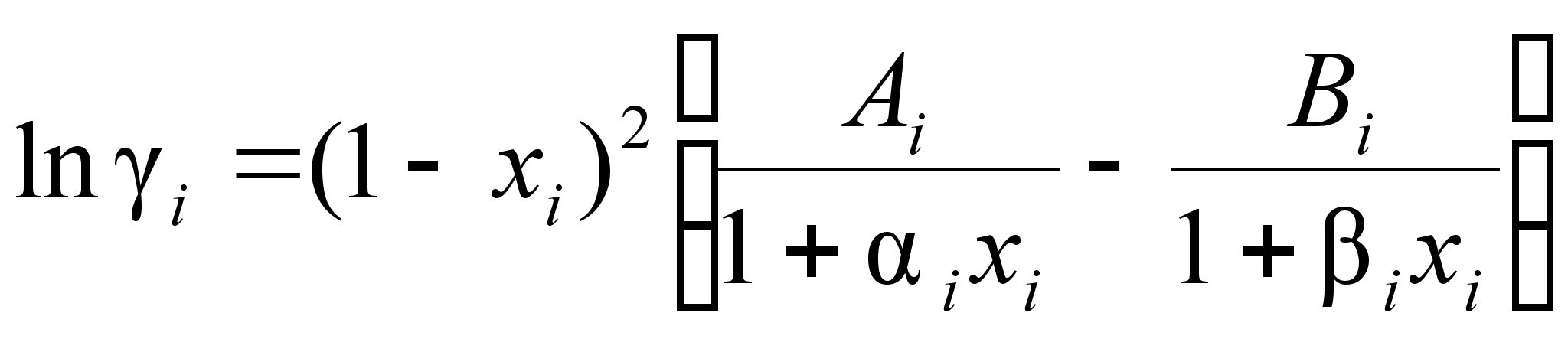
(97)
Разделив
левую и правую
части данного
уравнения на
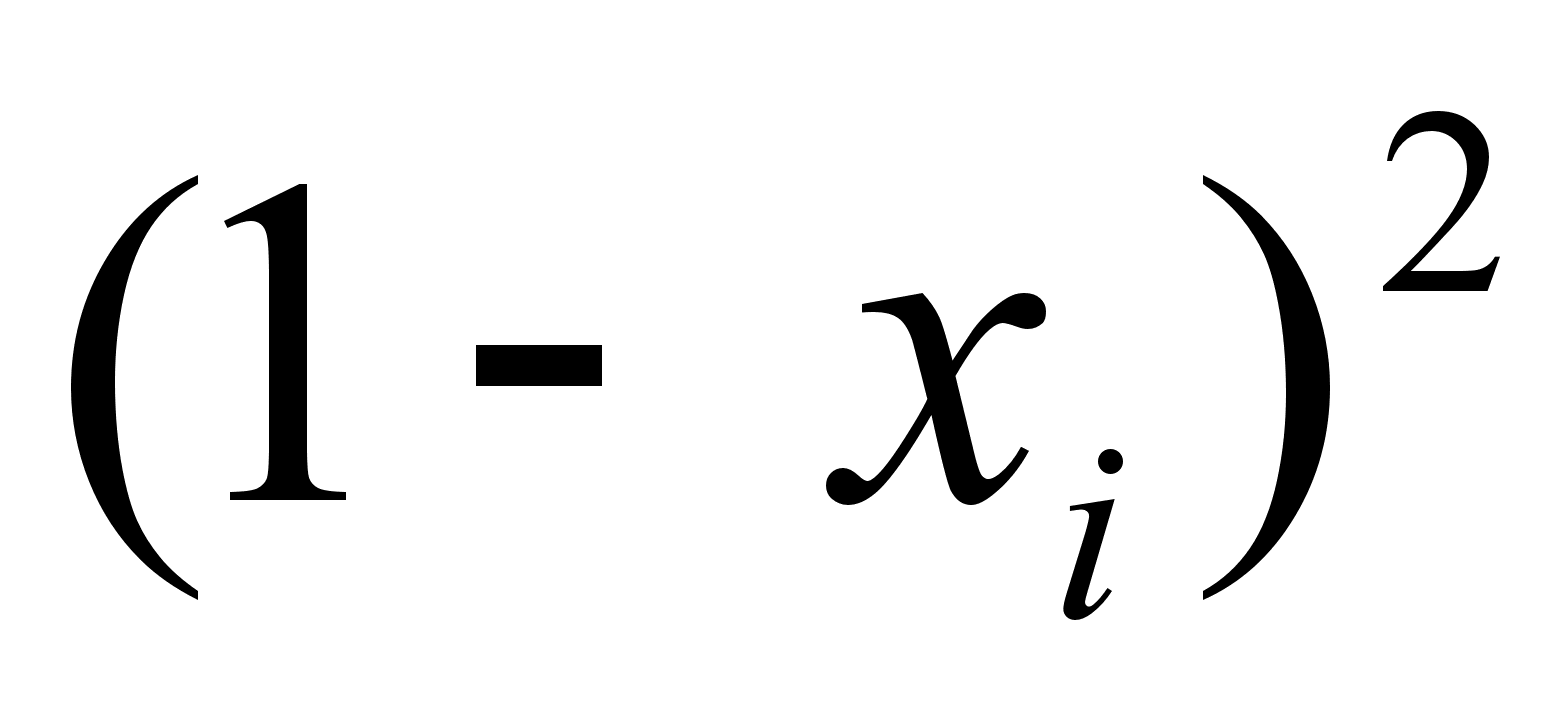 и имея в виду,
что
и имея в виду,
что
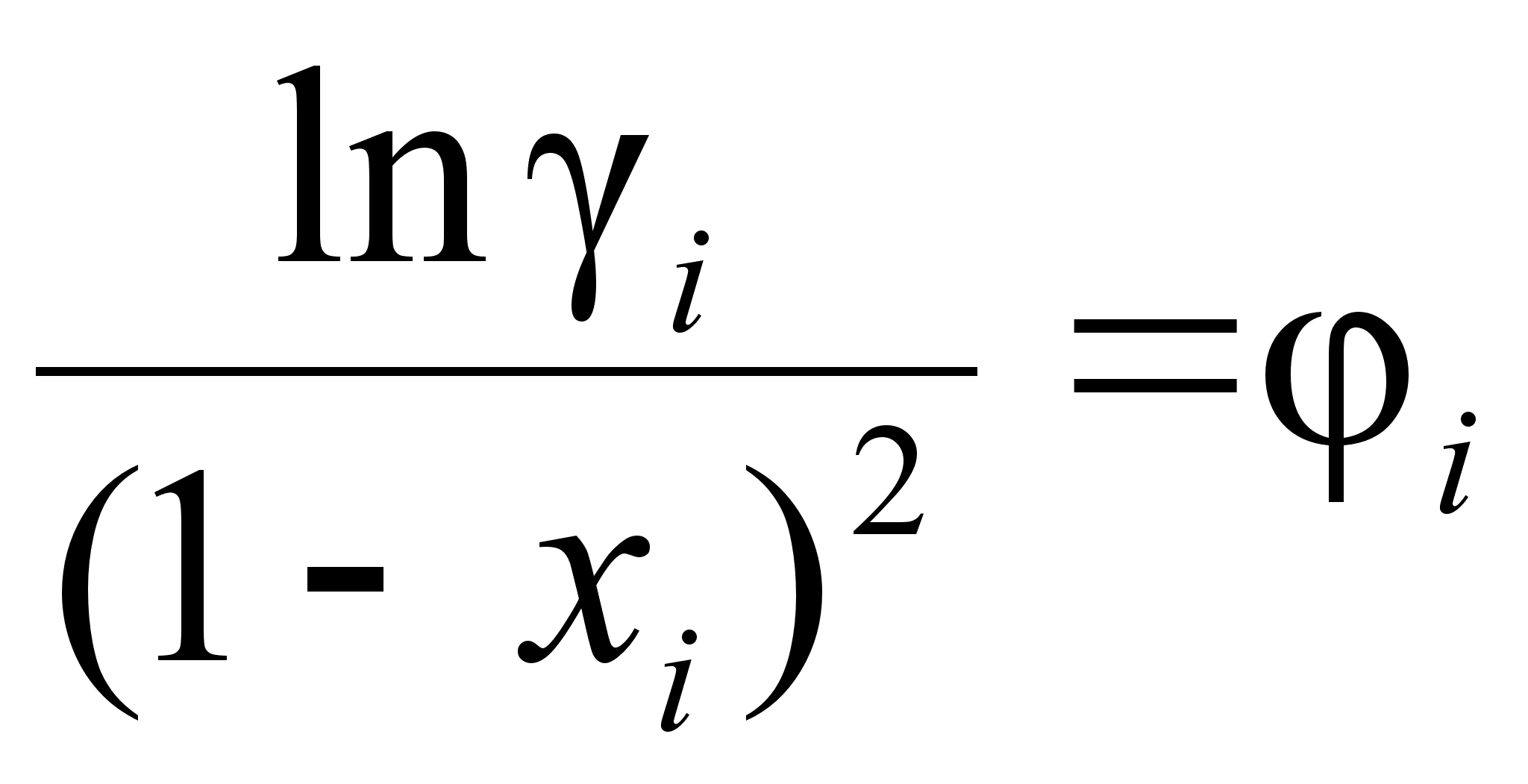 (о функции
(о функции
 скажем далее),
запишем выражение:
скажем далее),
запишем выражение:
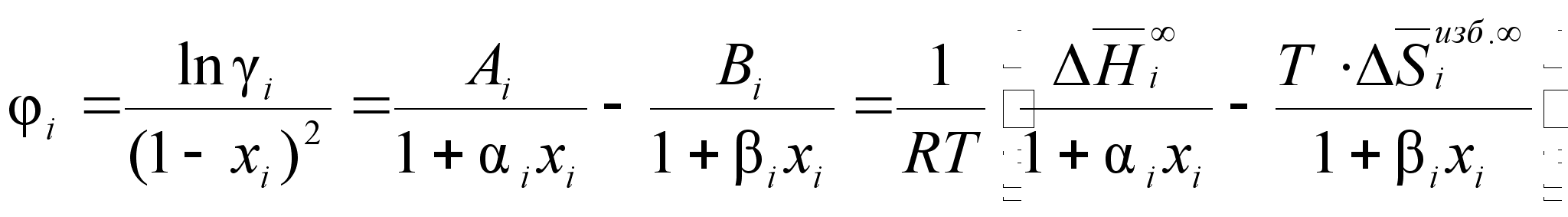
(98)
.
Из уравнения
(98) видно, что при
 :
:
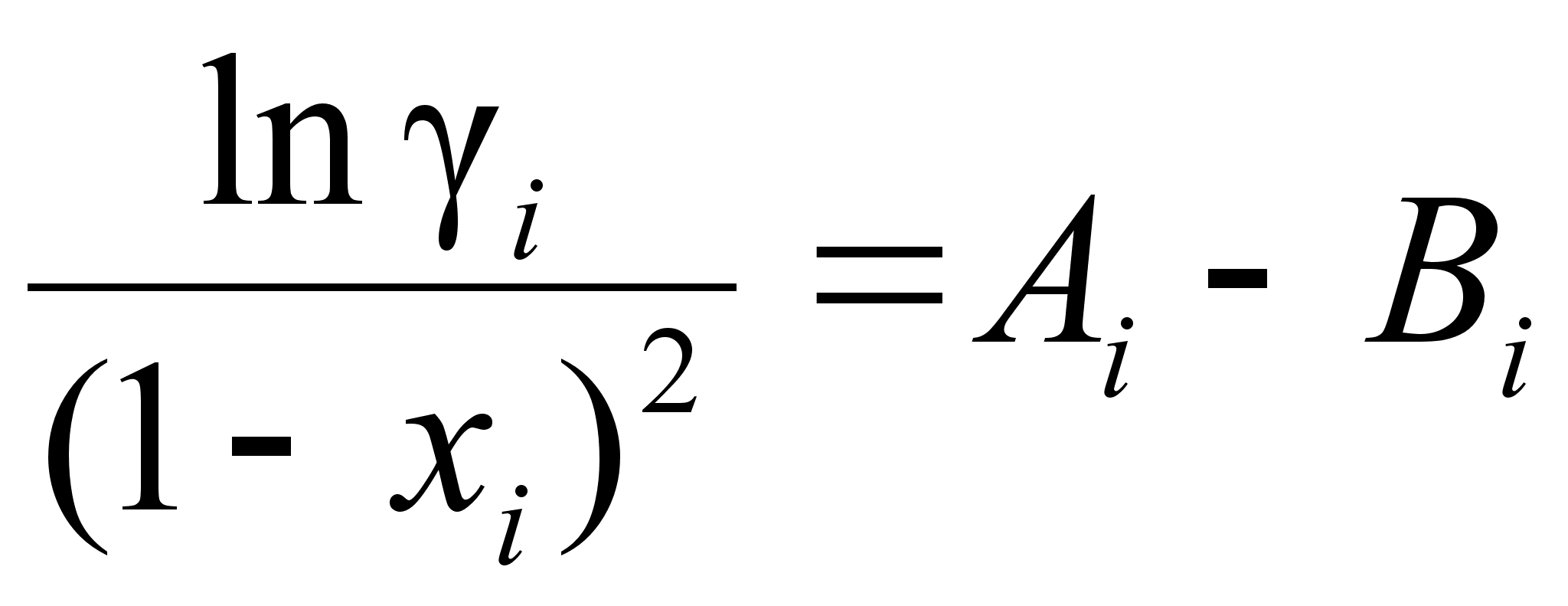
(99)
,а
(100)
при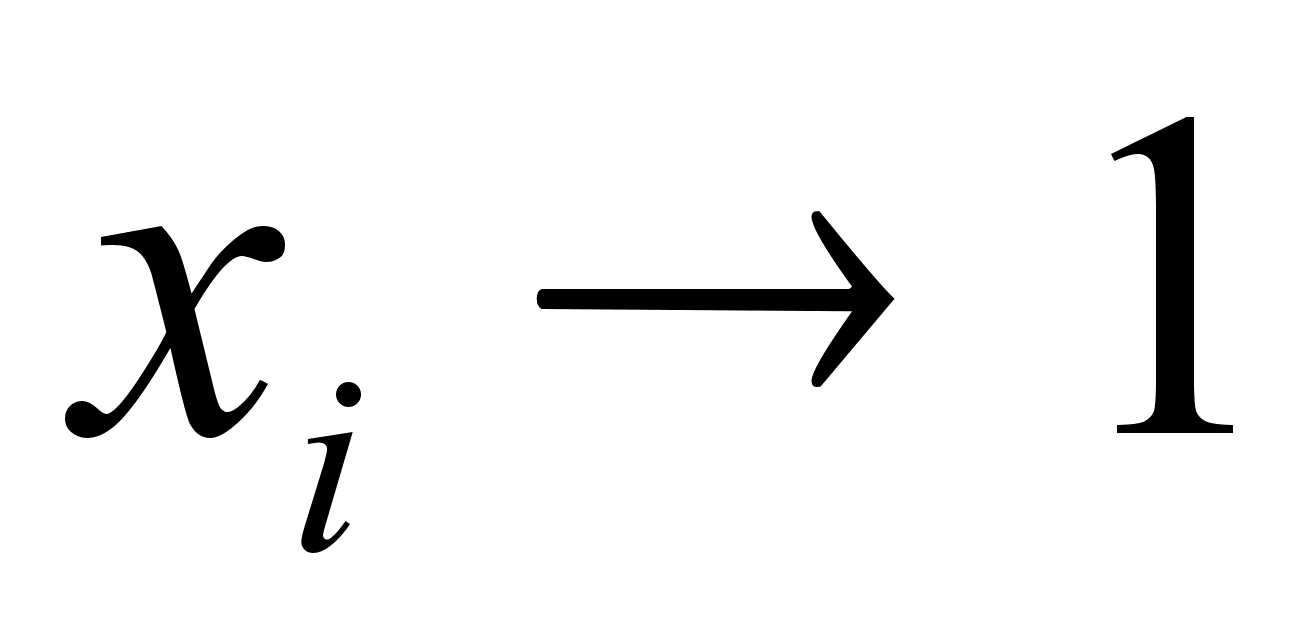 :
:
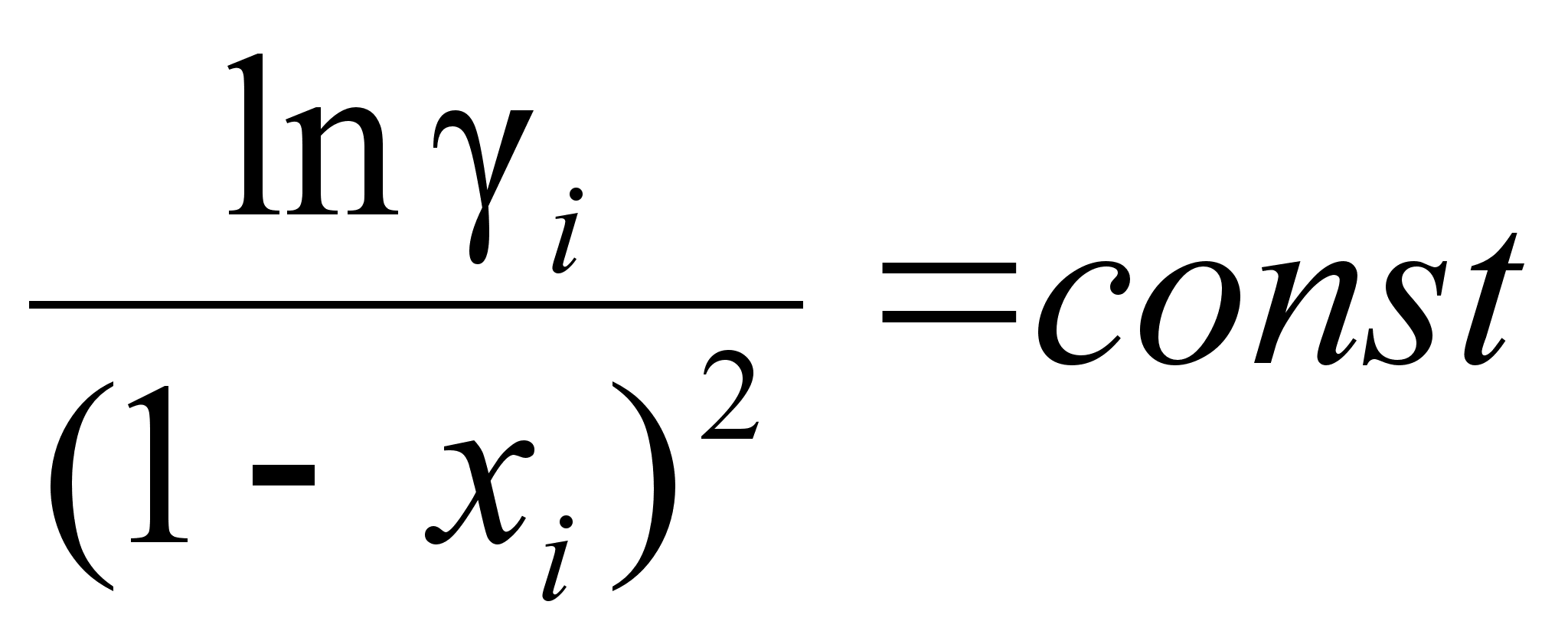 .
.
2.2 Функция .
Функция
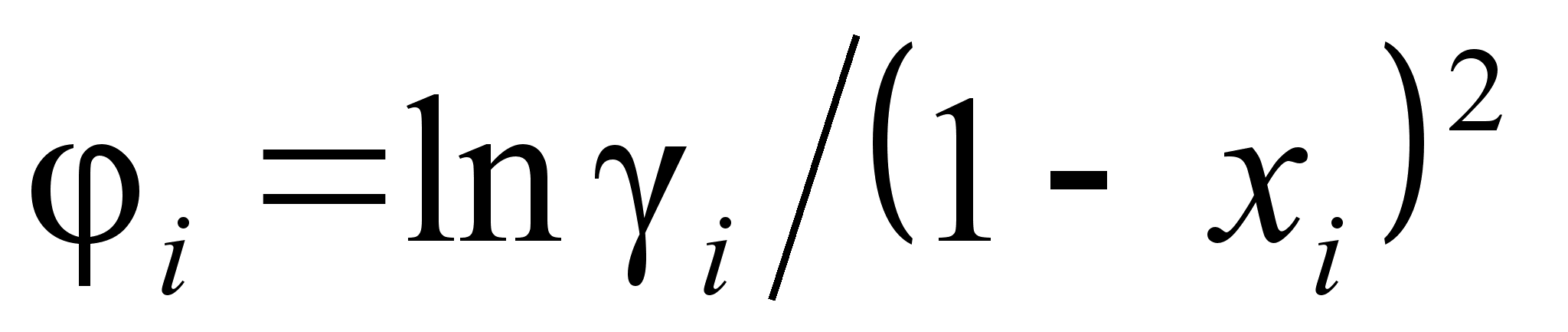 впервые была
введена Л.С.
Даркеном и Р.В.
Гурри [2] для
упрощения
интегрирования
уравнения
Гиббса-Дюгема
при определении
активности
одного компонента
бинарной системы
из известной
активности
другого компонента.
Они же показали,
что функция
i
для металлических
расплавов имеет
прямолинейный
характер. В
работах других
исследователей
также утверждается,
что при нанесении
на график величин
впервые была
введена Л.С.
Даркеном и Р.В.
Гурри [2] для
упрощения
интегрирования
уравнения
Гиббса-Дюгема
при определении
активности
одного компонента
бинарной системы
из известной
активности
другого компонента.
Они же показали,
что функция
i
для металлических
расплавов имеет
прямолинейный
характер. В
работах других
исследователей
также утверждается,
что при нанесении
на график величин
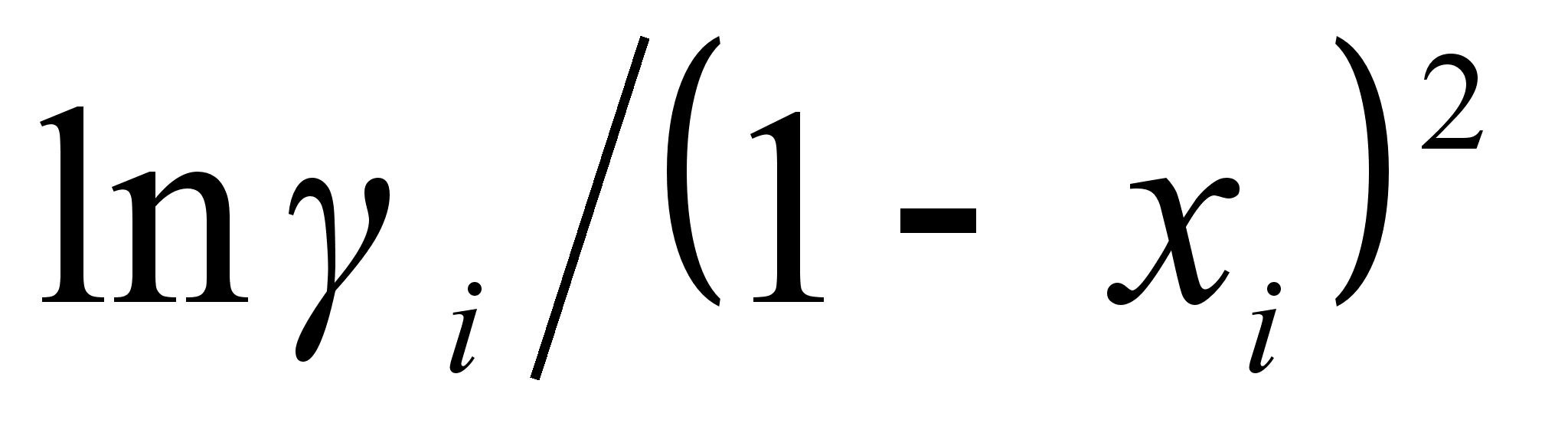 в функции (1
- xi)
экспериментальные
точки должны
ложиться на
прямую.
в функции (1
- xi)
экспериментальные
точки должны
ложиться на
прямую.
На рисунке
5 представлены
результаты
вычисления
функции
 для различных
систем в зависимости
от концентрации
компонента
в расплаве. Для
каждой системы
имеем две линии
– это
для различных
систем в зависимости
от концентрации
компонента
в расплаве. Для
каждой системы
имеем две линии
– это
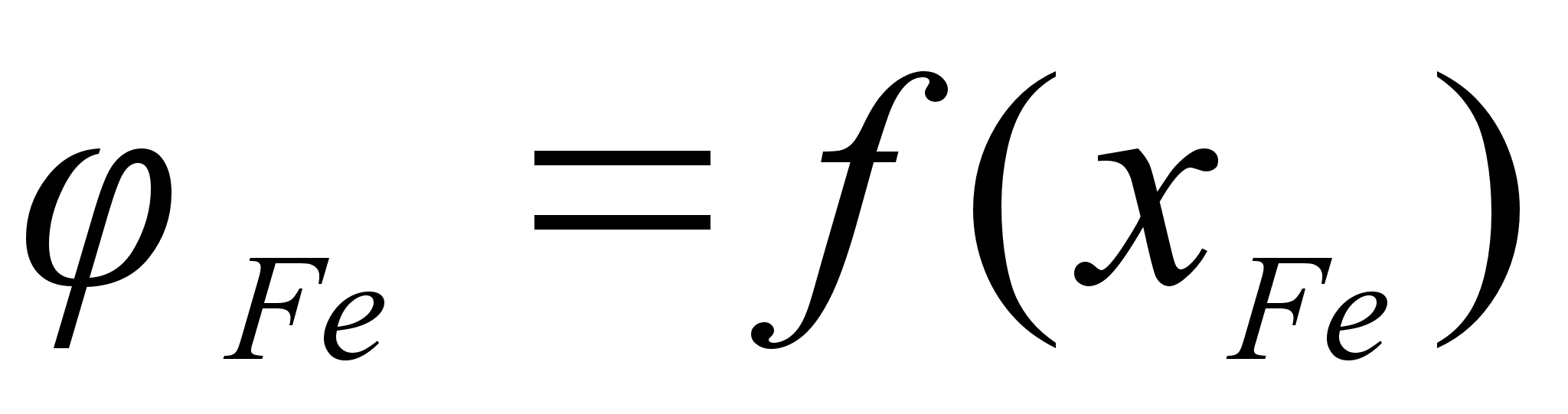 и
и
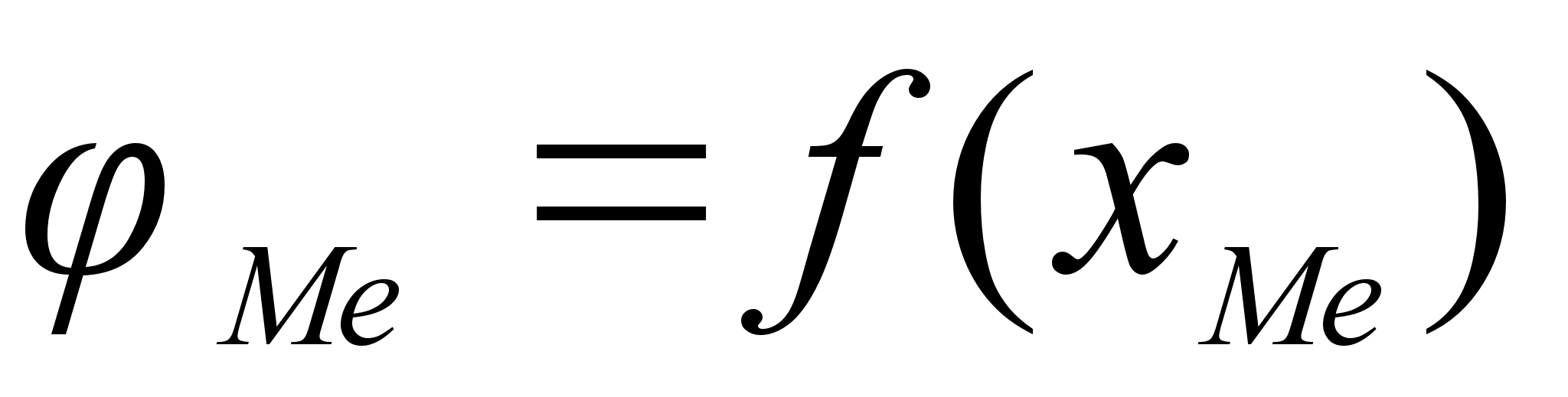 .
Цифрами обозначены
точки пересечения
этих линий в
расплавах:
.
Цифрами обозначены
точки пересечения
этих линий в
расплавах:
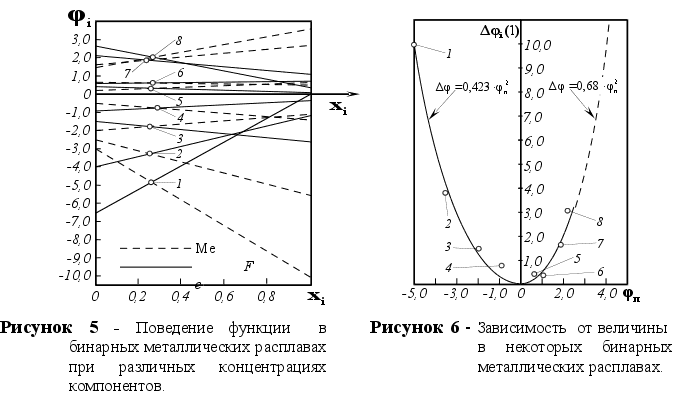 1-(Fe
– Si); 2-(Fe – Al); 3-(Fe – V); 4-(Fe –
Co); 5-(Fe – Mn); 6-(Fe – Cr) и
8-(Fe – Sn). Для
каждой точки
пересечения
линий характерно
своё значение
1-(Fe
– Si); 2-(Fe – Al); 3-(Fe – V); 4-(Fe –
Co); 5-(Fe – Mn); 6-(Fe – Cr) и
8-(Fe – Sn). Для
каждой точки
пересечения
линий характерно
своё значение
 .
Значения
.
Значения
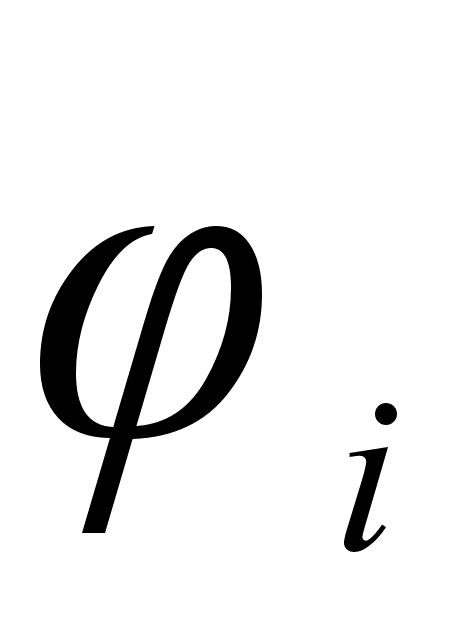 в точках пересечения
обозначены
через
в точках пересечения
обозначены
через
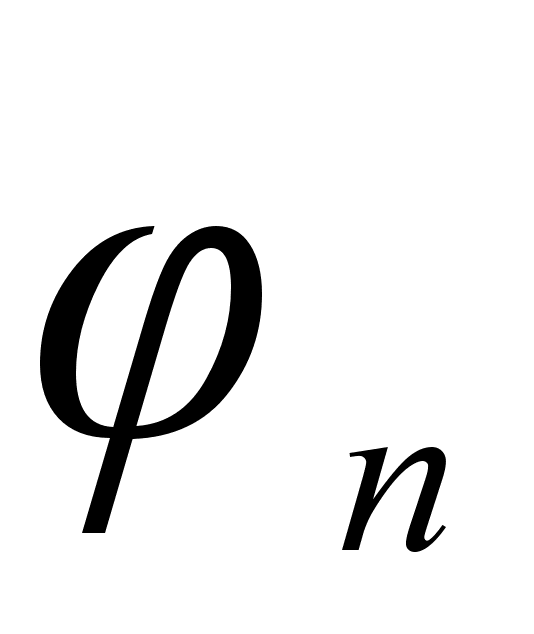 .
Из рисунка 5
видно, что чем
дальше система
от идеальности,
тем больше угол
между рассматриваемыми
прямыми. Пересекаются
линии всех
систем примерно
при одной и той
же концентрации
компонентов
в расплаве,
очень близкой
к значению
xi=0,25
(среднее значение
xi
для рассматриваемых
систем равно
0,251). Угол между
прямыми можно
характеризовать
величиной
.
Из рисунка 5
видно, что чем
дальше система
от идеальности,
тем больше угол
между рассматриваемыми
прямыми. Пересекаются
линии всех
систем примерно
при одной и той
же концентрации
компонентов
в расплаве,
очень близкой
к значению
xi=0,25
(среднее значение
xi
для рассматриваемых
систем равно
0,251). Угол между
прямыми можно
характеризовать
величиной
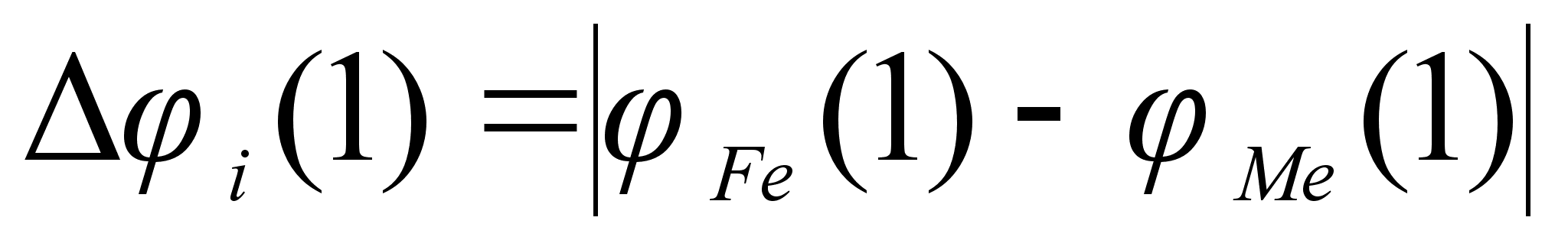 ,
т.е. абсолютным
значением
разности функций
,
т.е. абсолютным
значением
разности функций
 при xi=1
для конкретного
компонента
любой системы.
Это позволяет
предположить,
что между величиной
при xi=1
для конкретного
компонента
любой системы.
Это позволяет
предположить,
что между величиной
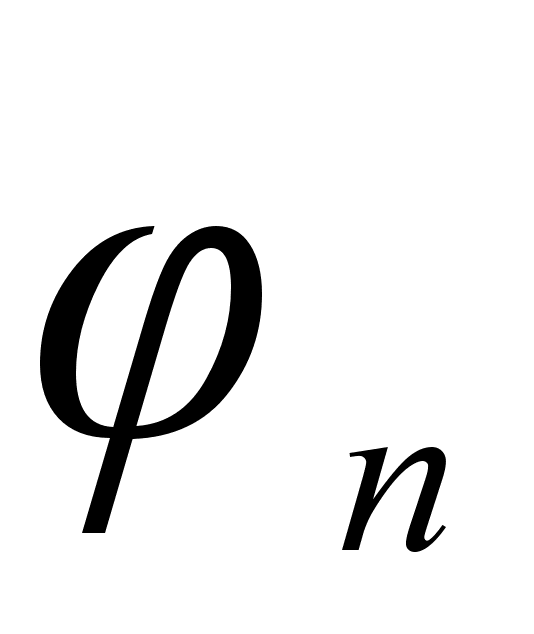 и функцией
и функцией
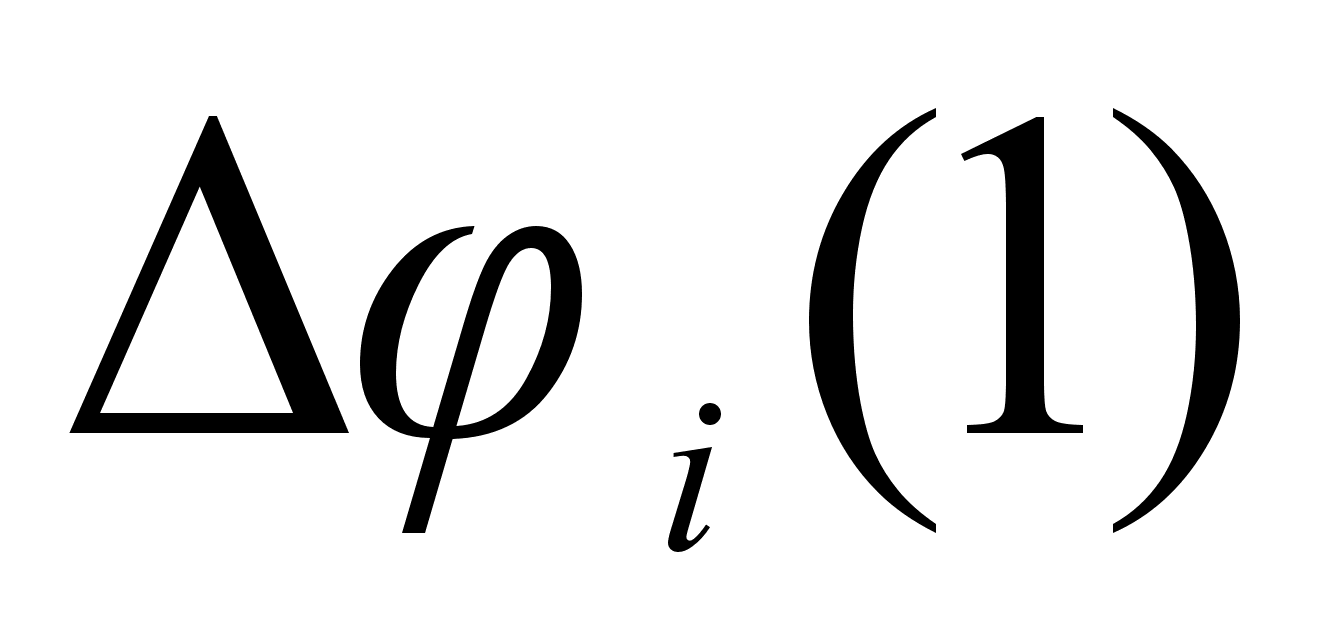 должна существовать
определенная
связь. Она показана
на рисунке 6.
Из рисунка
видно, что
зависимость
между
должна существовать
определенная
связь. Она показана
на рисунке 6.
Из рисунка
видно, что
зависимость
между
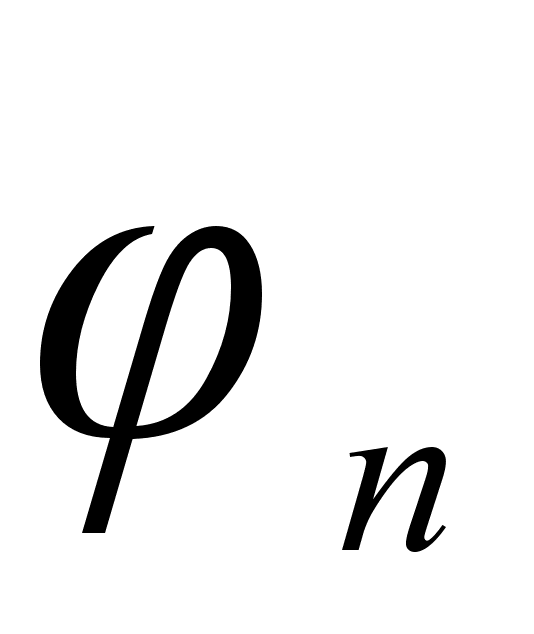 и
и
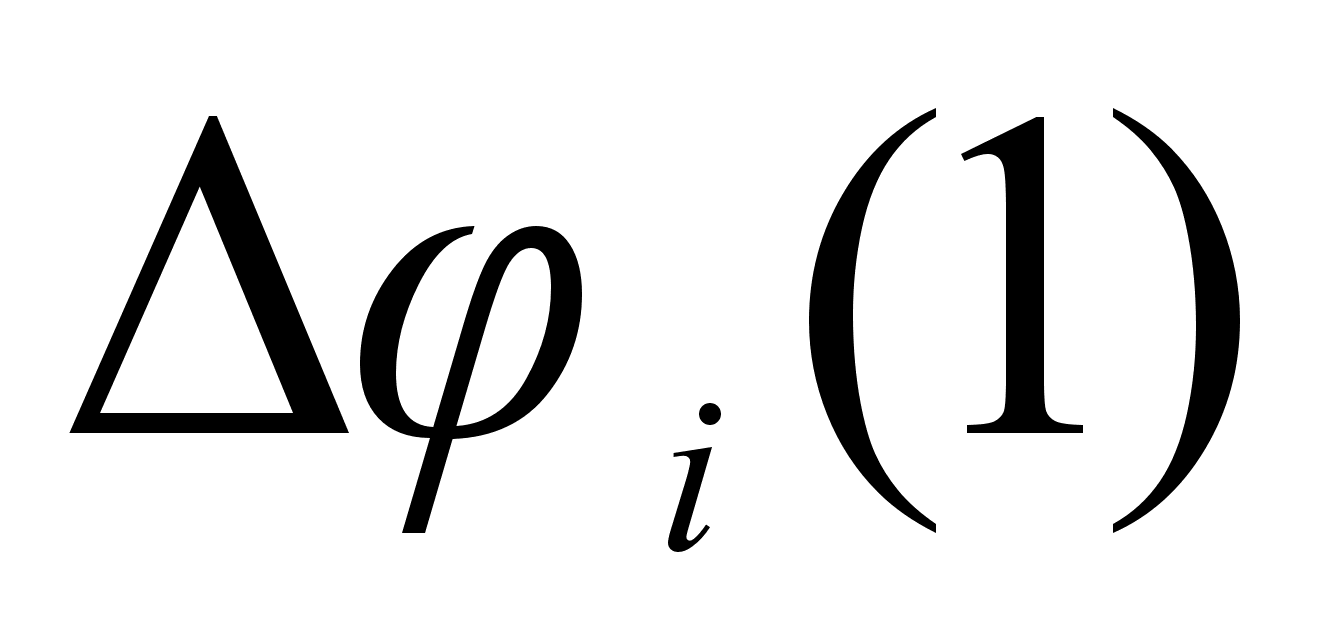 может быть
описана в общем
виде уравнением
параболы второй
степени, а именно:
может быть
описана в общем
виде уравнением
параболы второй
степени, а именно:
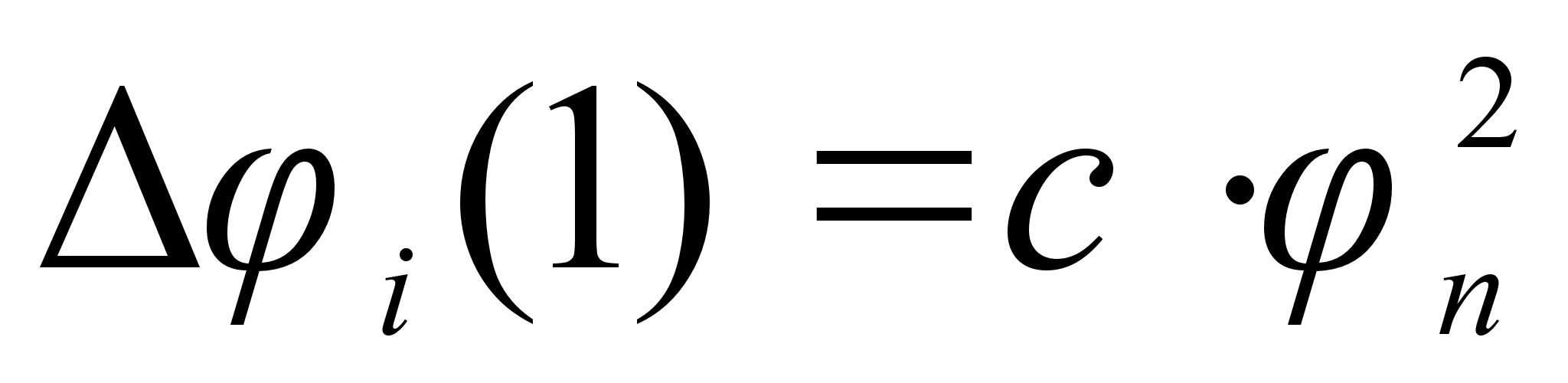 .
.
Для положительных
и отрицательных
значений
 уравнения
параболы отличаются,
их примерный
вид приведен
на этом же рисунке.
Это объясняется
тем, что растворы
с положительным
и отрицательным
отклонением
от закона Рауля
по своей природе
различаются:
для систем с
отрицательным
отклонением
никаких ограничений
нет, в то время
как для систем
с положительным
отклонением
ограничения
существуют.
Уравнения на
рисунке 6 могут
быть уточнены
при нанесении
на него дополнительных
данных.
уравнения
параболы отличаются,
их примерный
вид приведен
на этом же рисунке.
Это объясняется
тем, что растворы
с положительным
и отрицательным
отклонением
от закона Рауля
по своей природе
различаются:
для систем с
отрицательным
отклонением
никаких ограничений
нет, в то время
как для систем
с положительным
отклонением
ограничения
существуют.
Уравнения на
рисунке 6 могут
быть уточнены
при нанесении
на него дополнительных
данных.
Итак, в
данной главе
мы привели
концентрационные
уравнения,
связывающие
термодинамические
характеристики
с составом
бинарного
раствора с
неограниченной
растворимостью
компонентов.
В этих уравнениях
коэффициенты
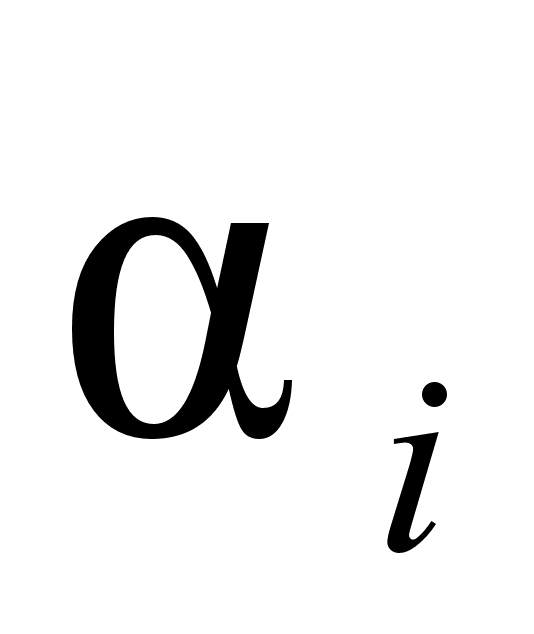 и
и
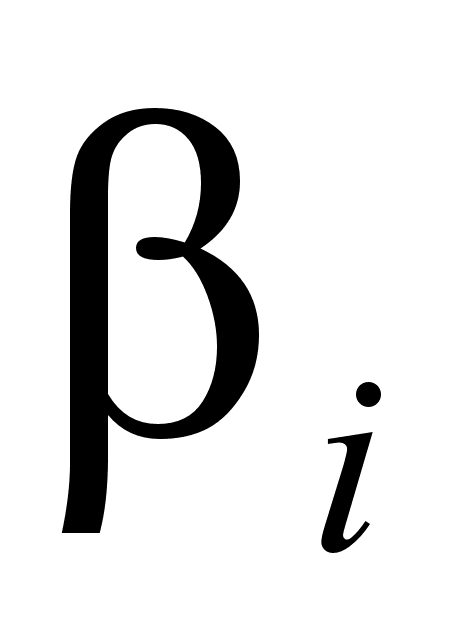 ,
наряду с другими
величинами
(
,
наряду с другими
величинами
(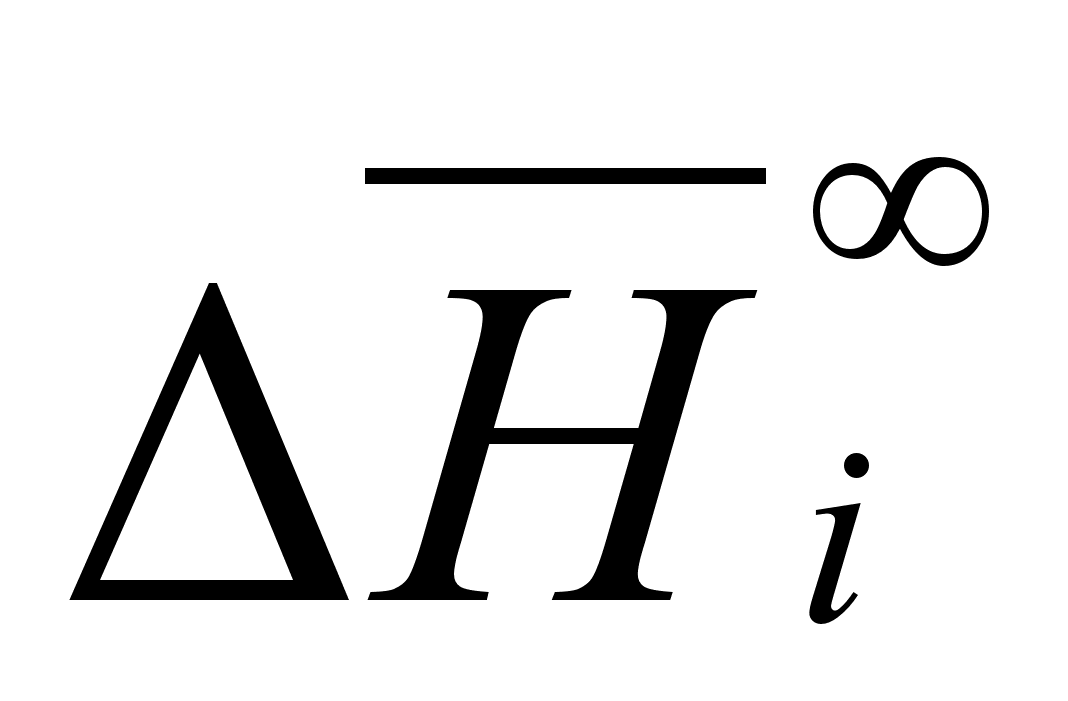 ,
,
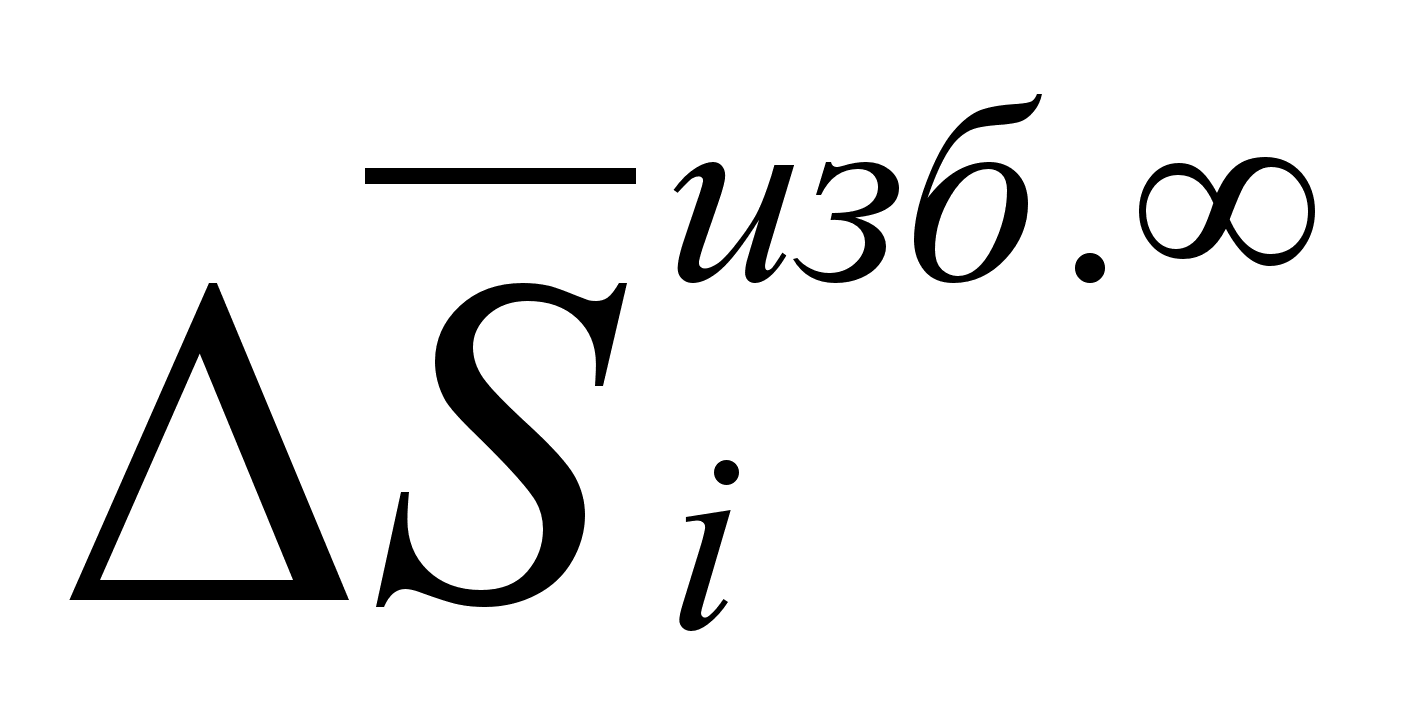 ,
T, xi
), определяют
степень отклонения
реального
раствора от
идеального.
,
T, xi
), определяют
степень отклонения
реального
раствора от
идеального.
Задача
исследователя
заключается
в том, чтобы по
имеющимся
экспериментальным
данным определить
неизвестные
величины
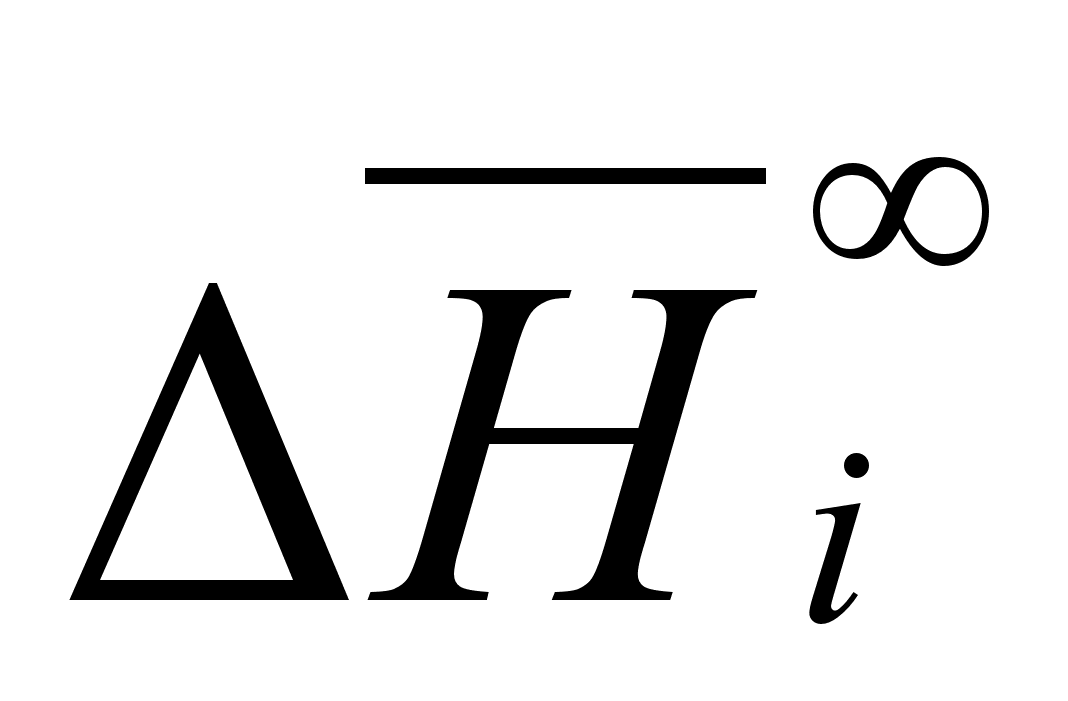 ,
,
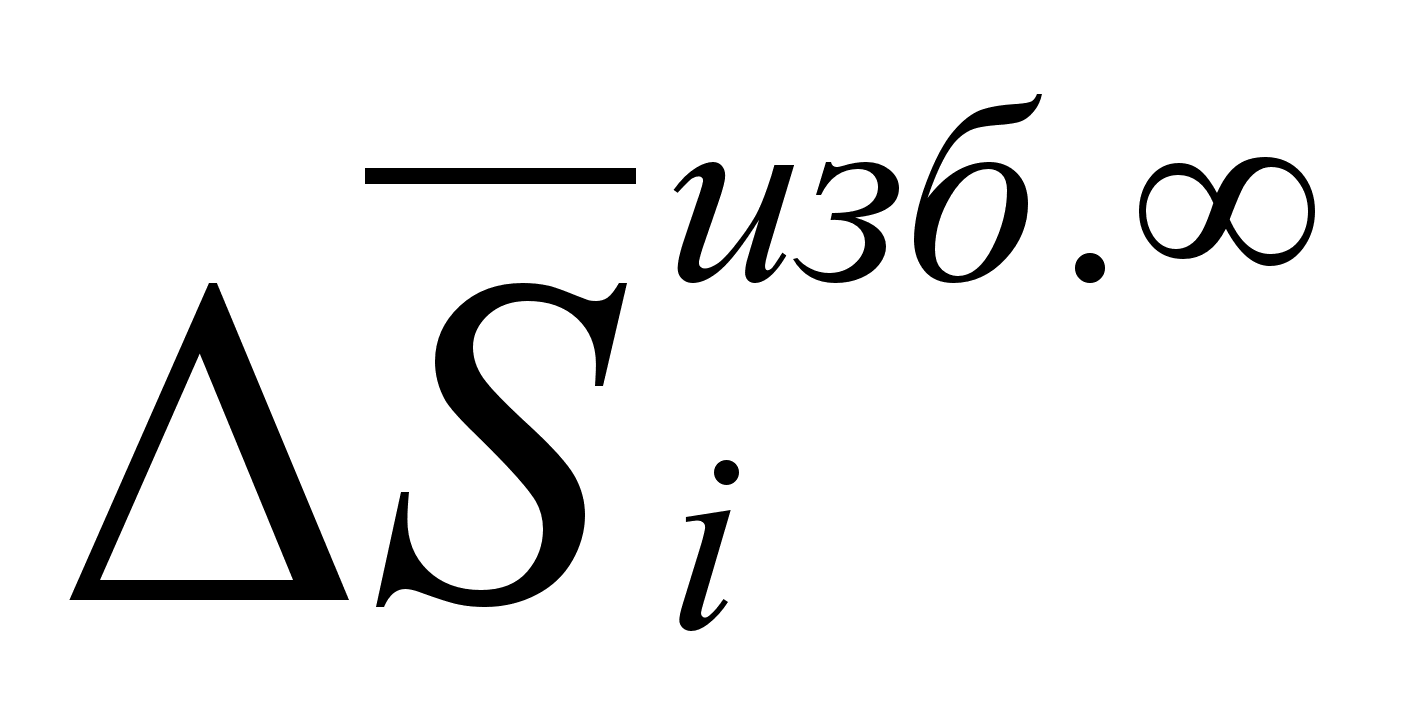 ,
,
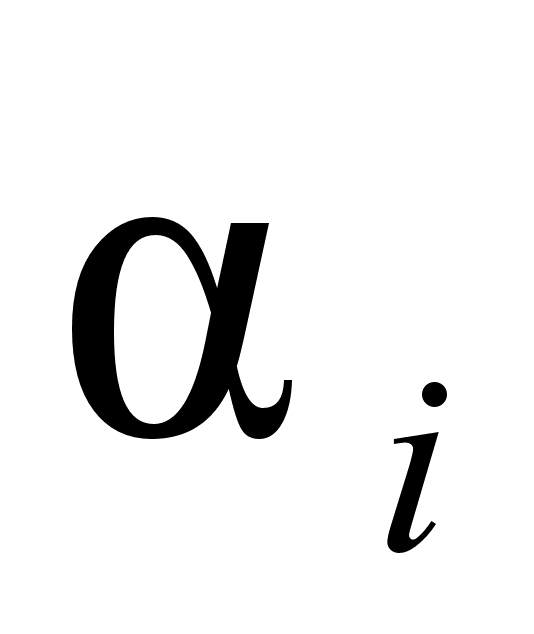 и
и
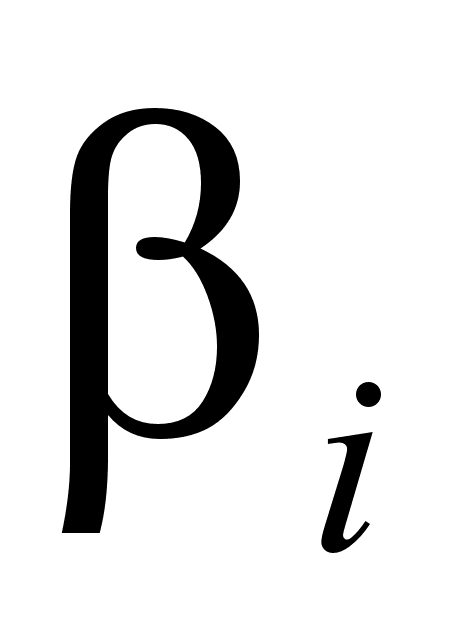 (при известной
температуре
и концентрации
компонентов),
входящие в
уравнение (98).
При любой методике
вычисления
этих величин
в первую очередь
определяются
численные
значения
(при известной
температуре
и концентрации
компонентов),
входящие в
уравнение (98).
При любой методике
вычисления
этих величин
в первую очередь
определяются
численные
значения
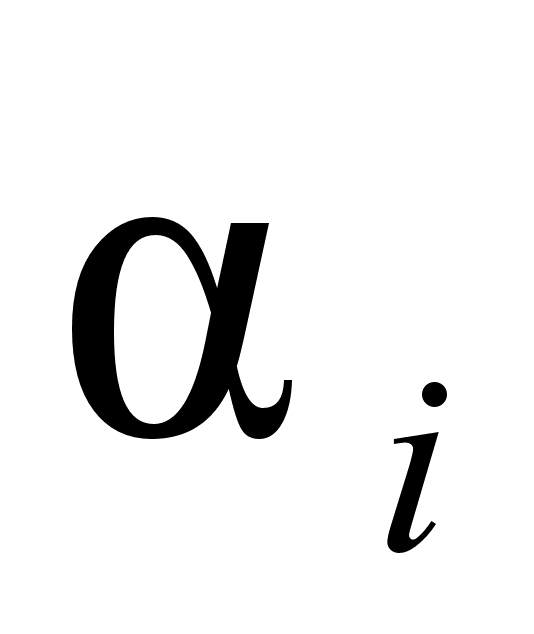 и
и
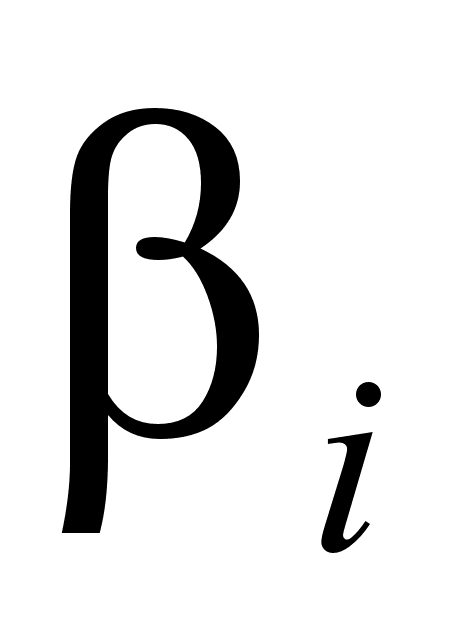 ,
а также их знаки,
и лишь затем
находятся
,
а также их знаки,
и лишь затем
находятся
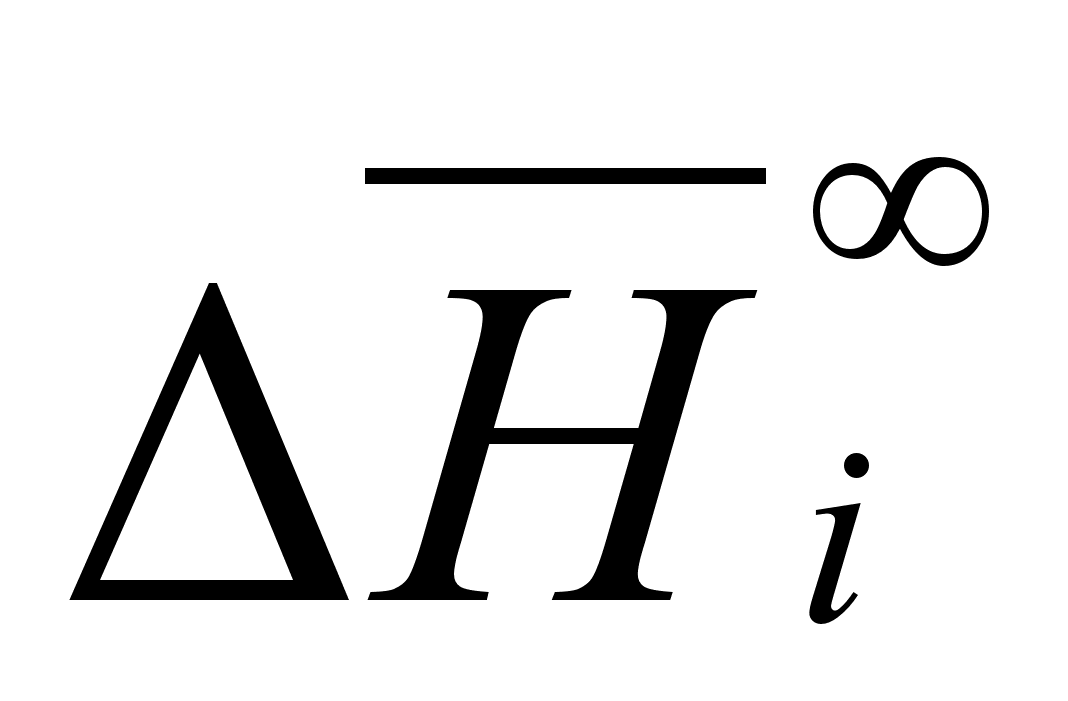 и
и
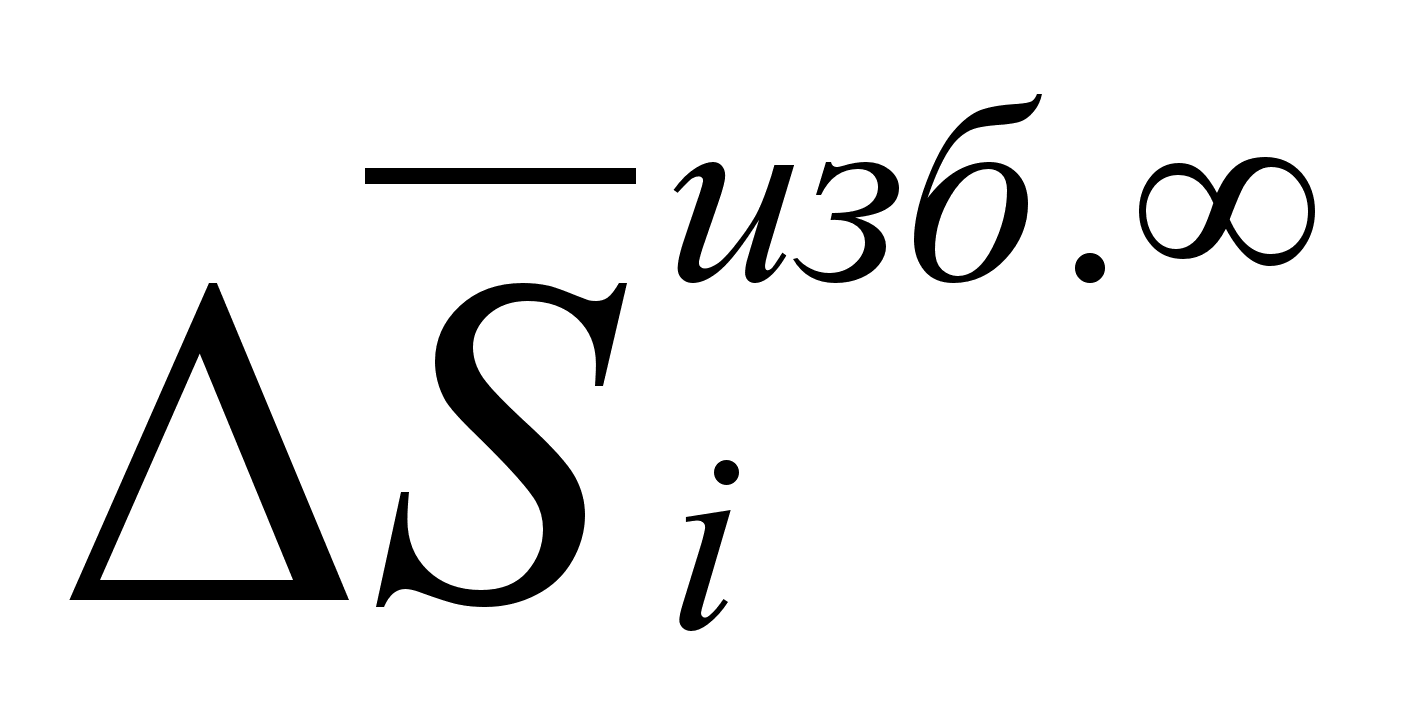 .
Поэтому следующая
глава нашей
работы посвящена
вопросам определения
коэффициентов
.
Поэтому следующая
глава нашей
работы посвящена
вопросам определения
коэффициентов
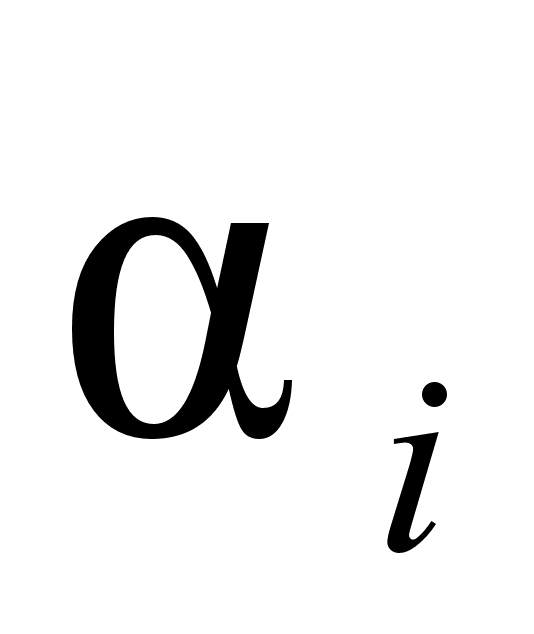 и
и
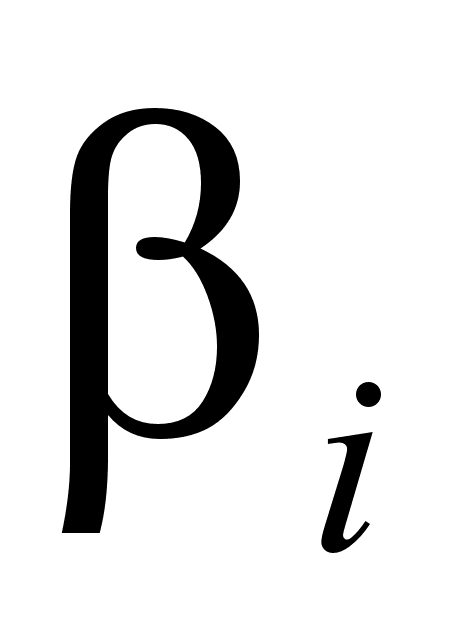 .
.
3
ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТОВ
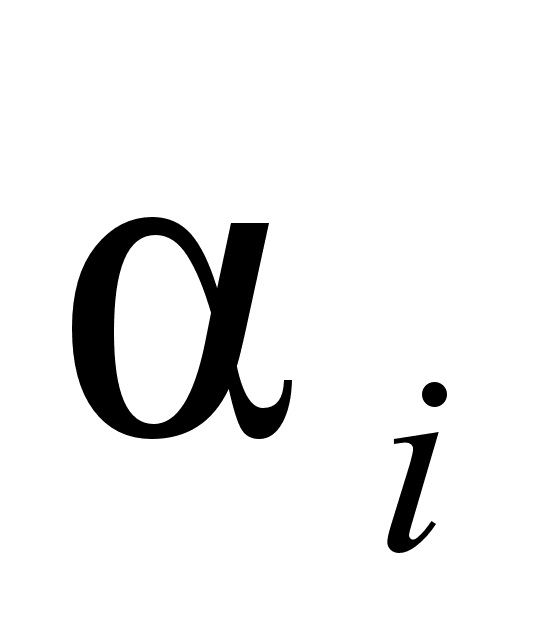 И
И
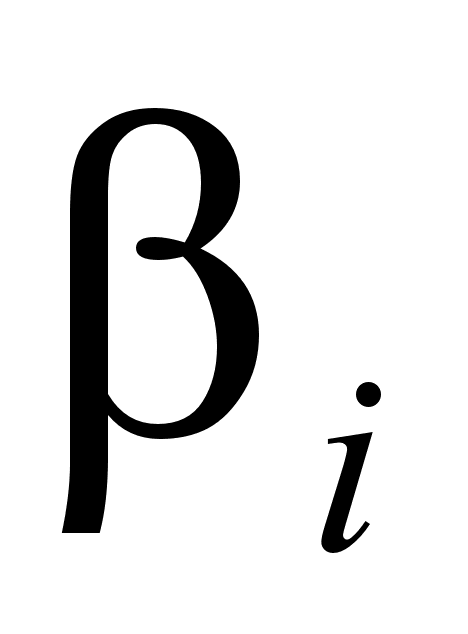
К
(101)
ак было сказано выше, коэффициенты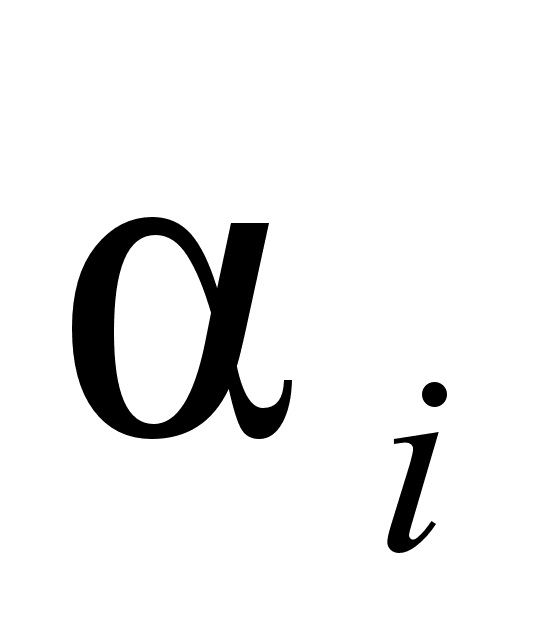 и
и
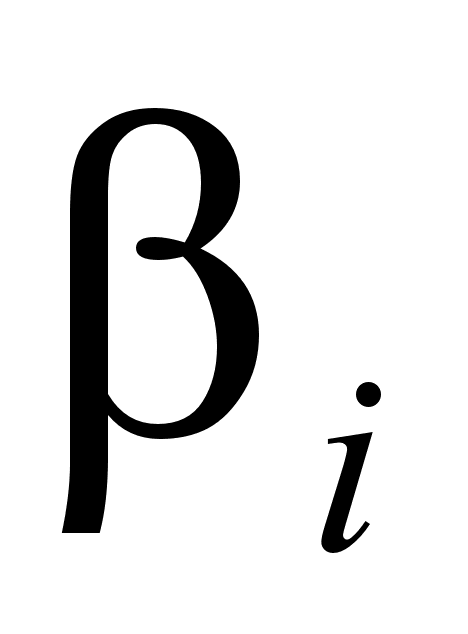 определяют
степень отклонения
раствора от
идеальности.
По условиям
вывода диапазон
значений этих
коэффициентов
одинаков и
равен:
определяют
степень отклонения
раствора от
идеальности.
По условиям
вывода диапазон
значений этих
коэффициентов
одинаков и
равен:
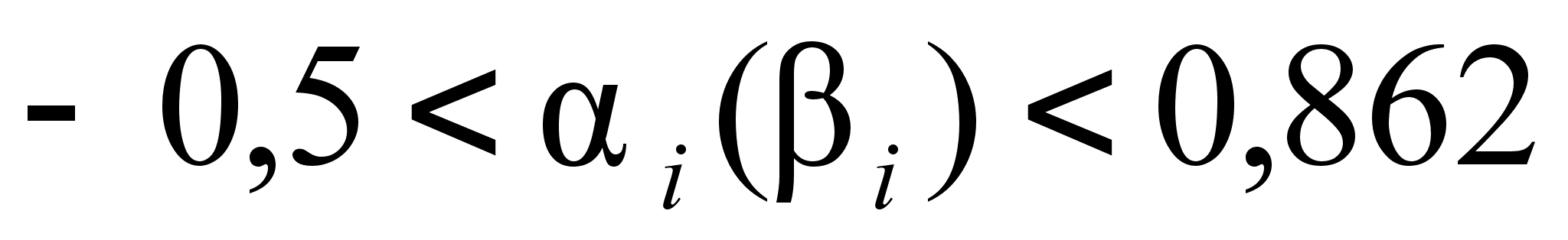
В
бинарных растворах
коэффициенты
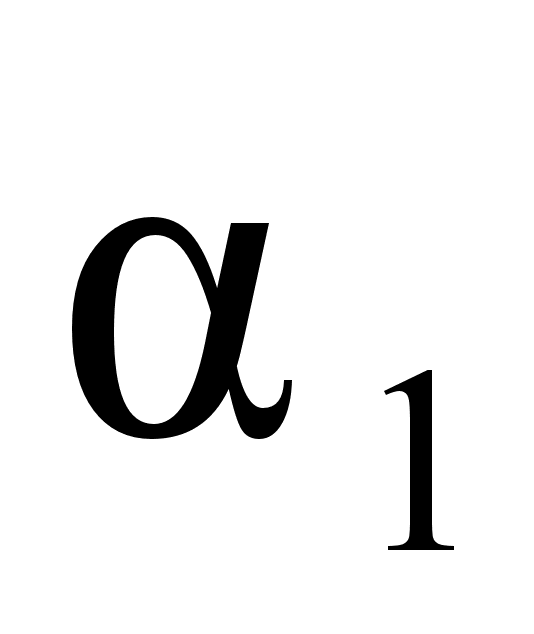 и
и
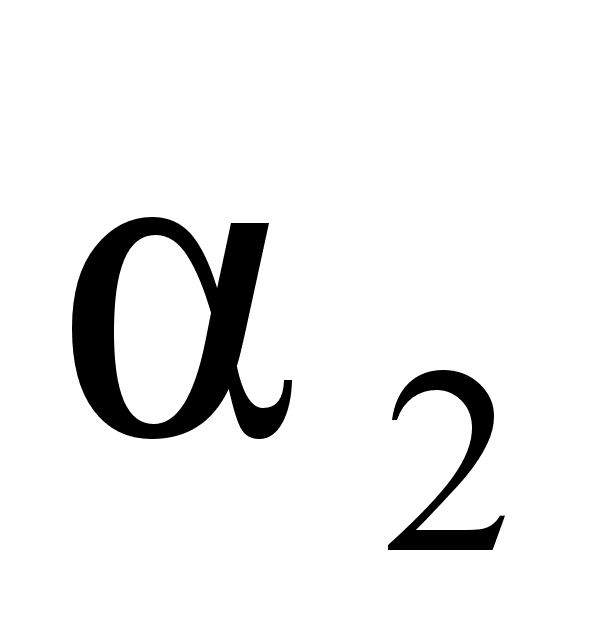 ,
равно как и
коэффициенты
,
равно как и
коэффициенты
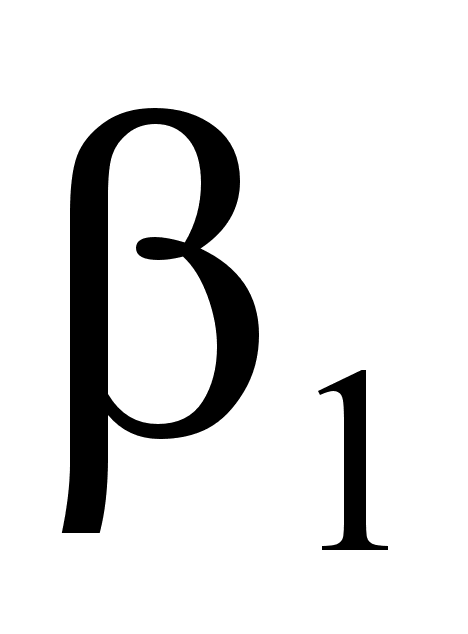 и
и
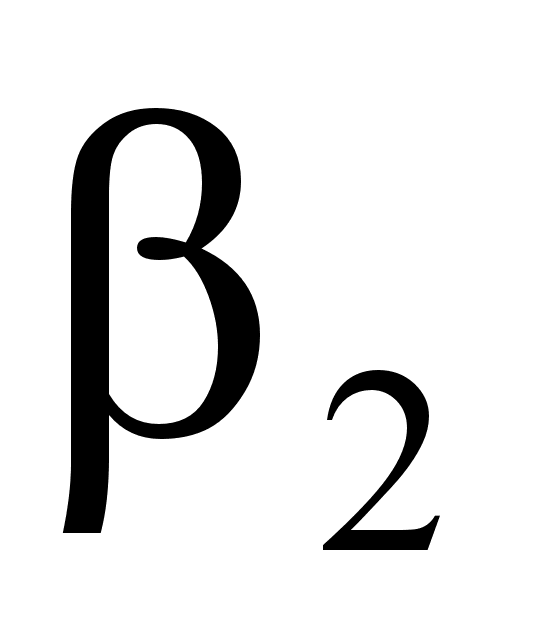 ,
связаны между
собой соотношениями:
,
связаны между
собой соотношениями:
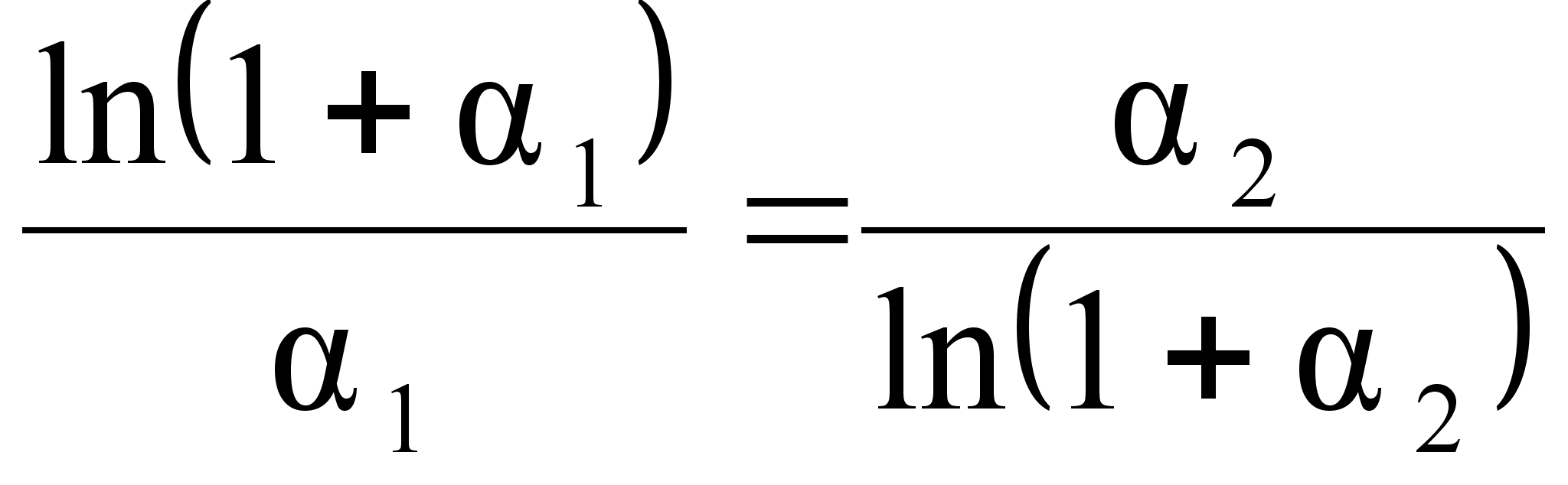
(102)
,
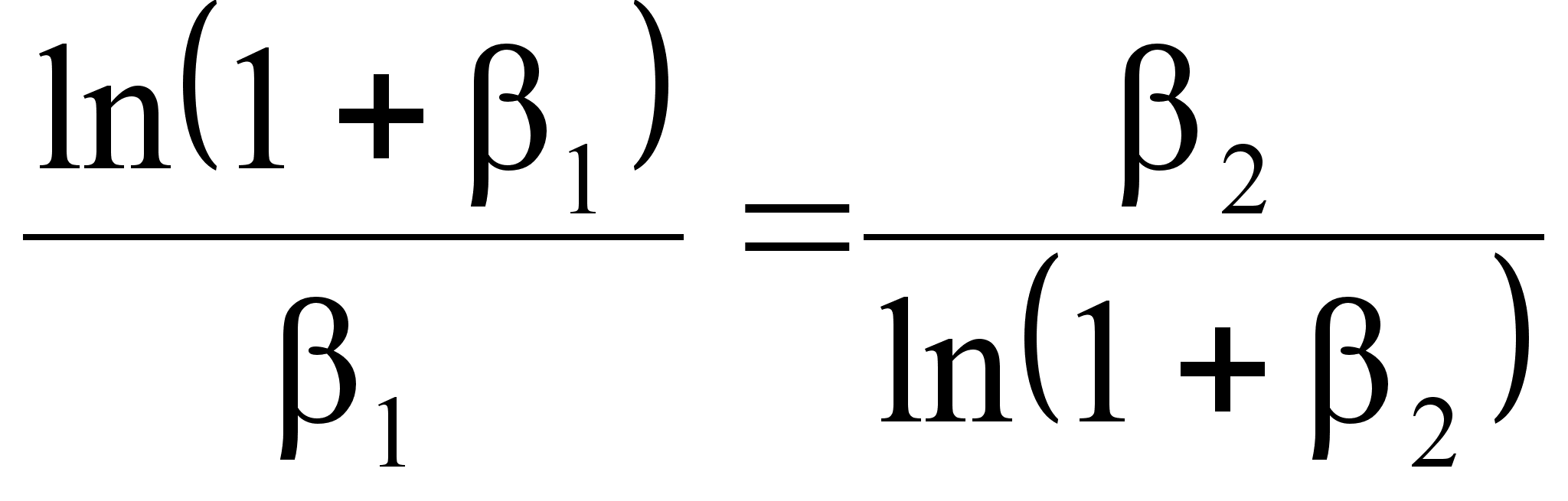
(103)
.
Коэффициенты
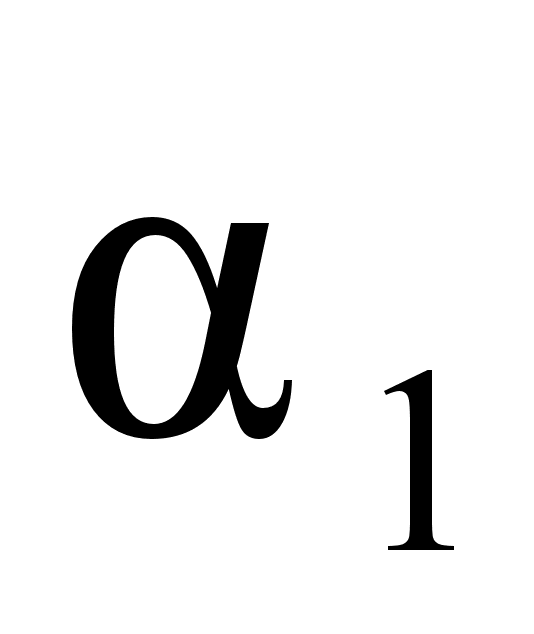 и
и
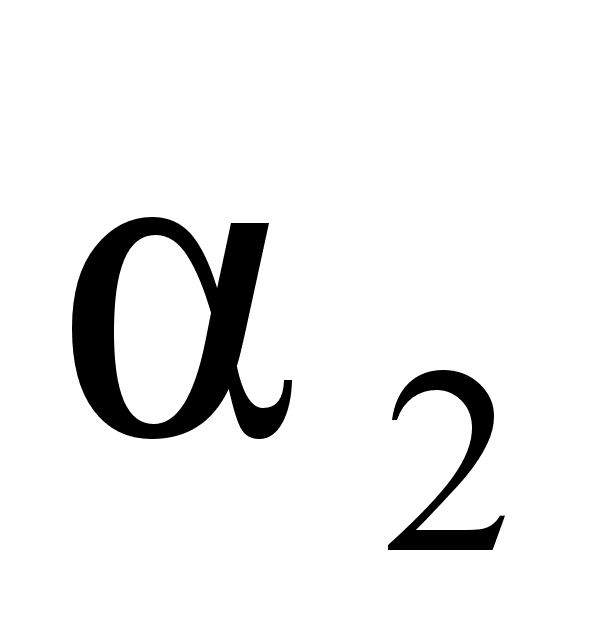 противоположны
по знаку. Противоположные
знаки также
имеют
противоположны
по знаку. Противоположные
знаки также
имеют
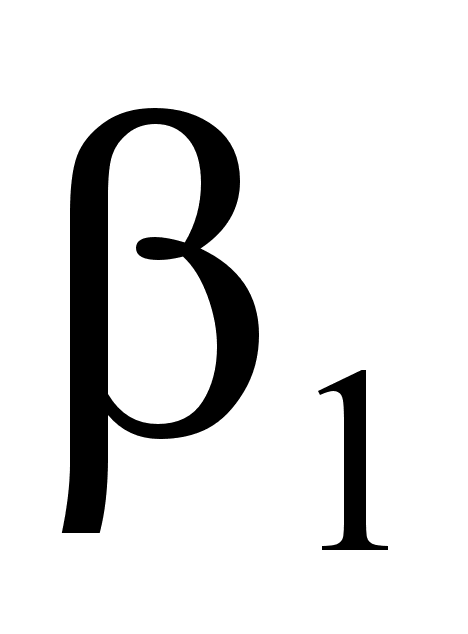 и
и
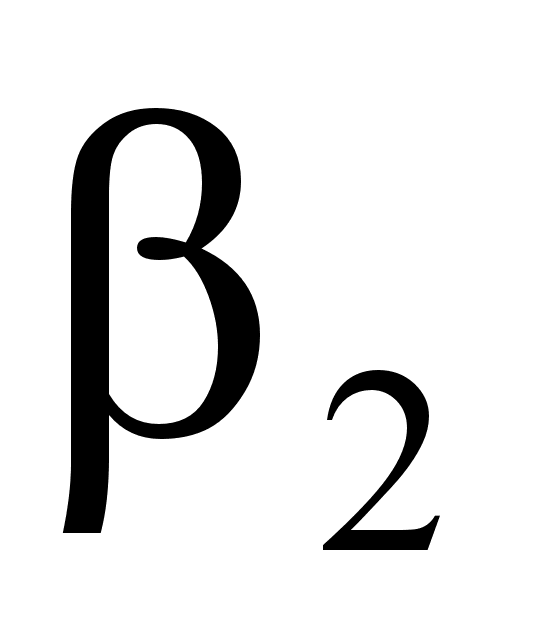 .
Определить
численное
значение
коэффициентов
.
Определить
численное
значение
коэффициентов
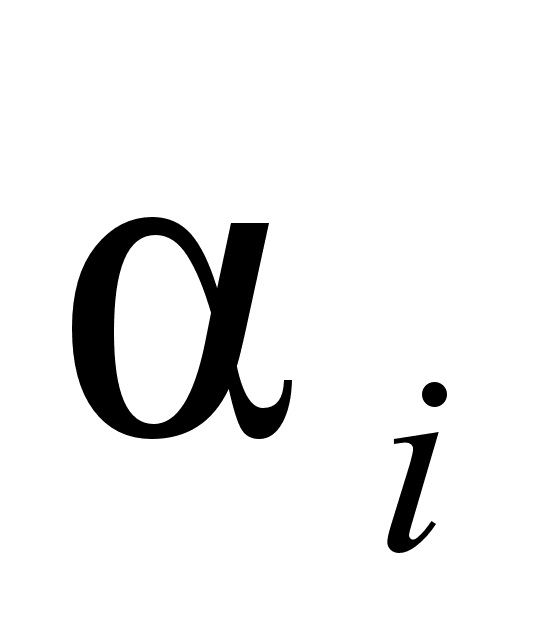 и
и
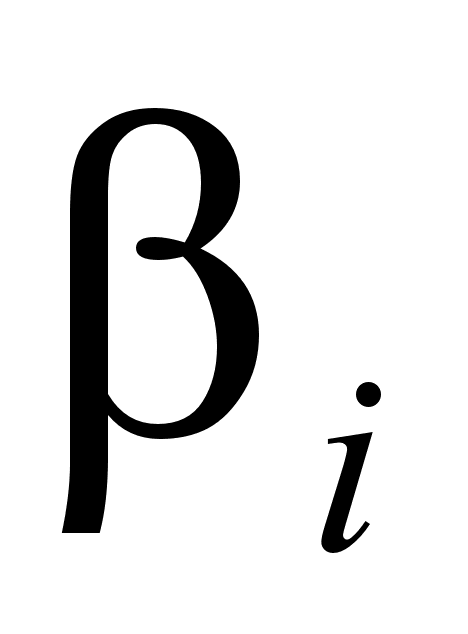 можно двумя
методами:
математическим
и графическим.
можно двумя
методами:
математическим
и графическим.
3.1 Математический метод.
При
чисто математическом
подходе, основываясь
на экспериментальных
данных, получим
систему четырех
уравнений типа
(98), решение которой
(например, методом
наименьших
квадратов)
позволяет найти
значения всех
неизвестных
величин:
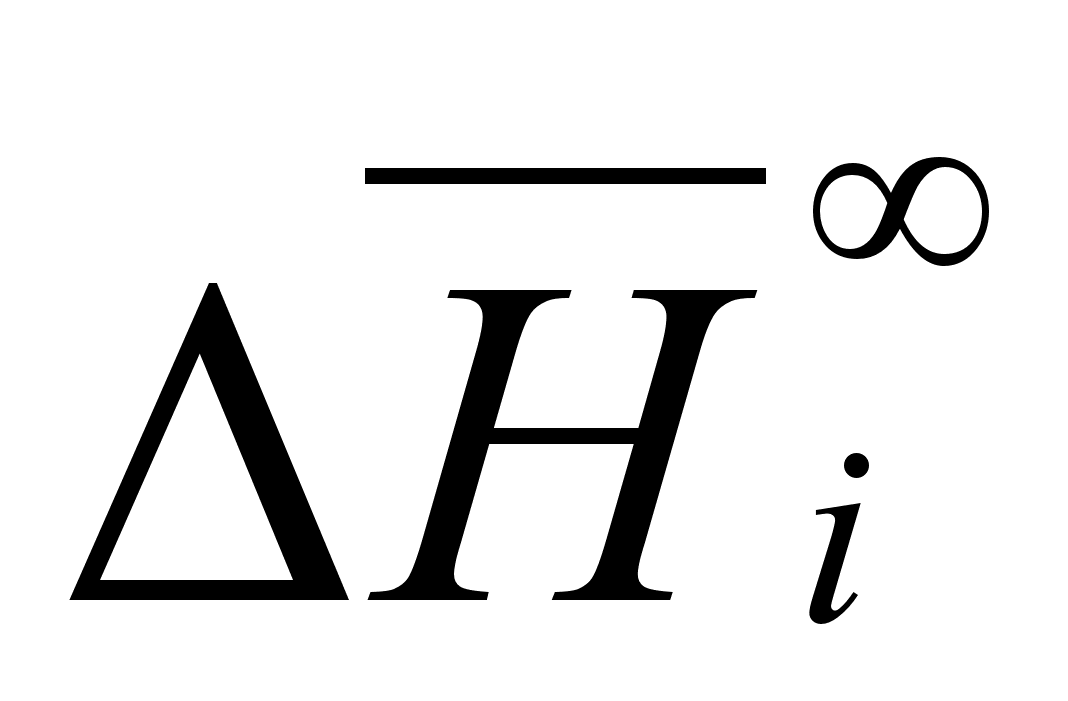 ,
,
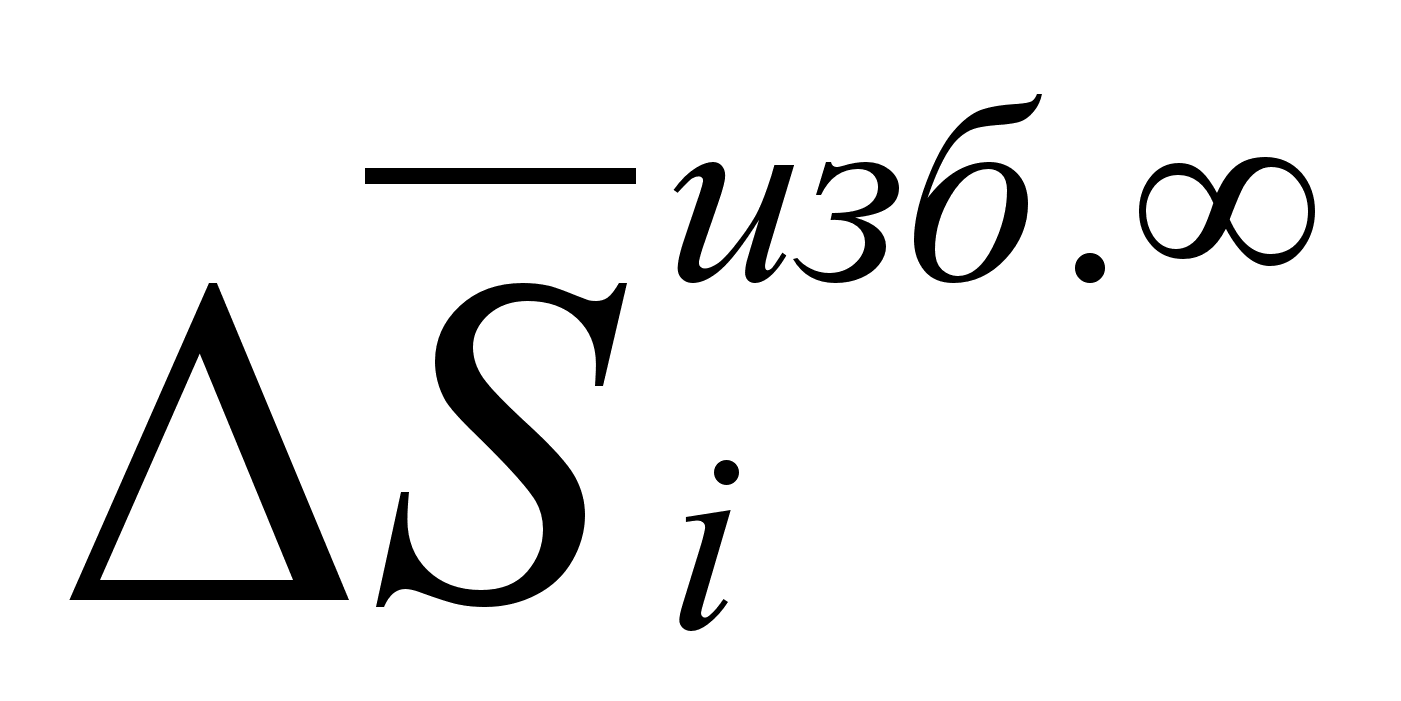 ,
,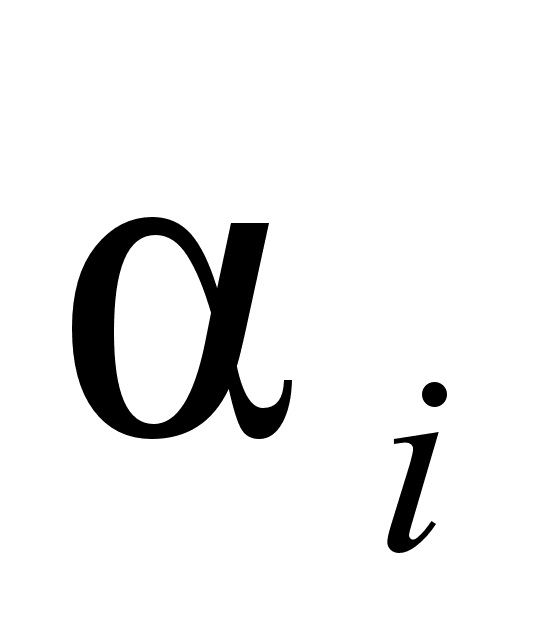 и
и
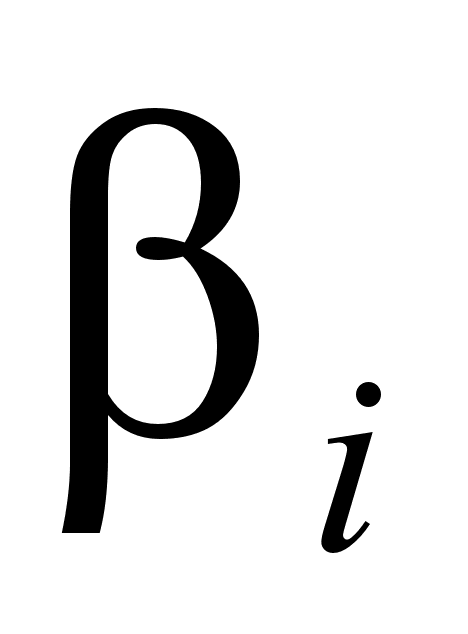 .
В процессе
решения возникает
ситуация, когда
надо определить,
какой из корней
квадратного
уравнения
коэффициент
.
В процессе
решения возникает
ситуация, когда
надо определить,
какой из корней
квадратного
уравнения
коэффициент
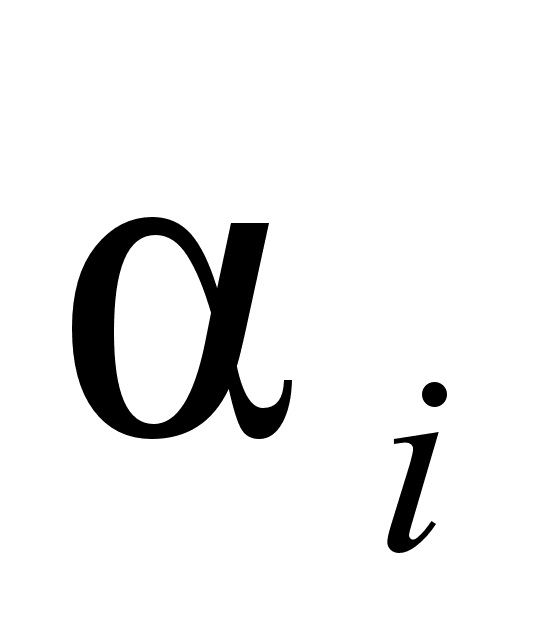 ,
а какой –
,
а какой –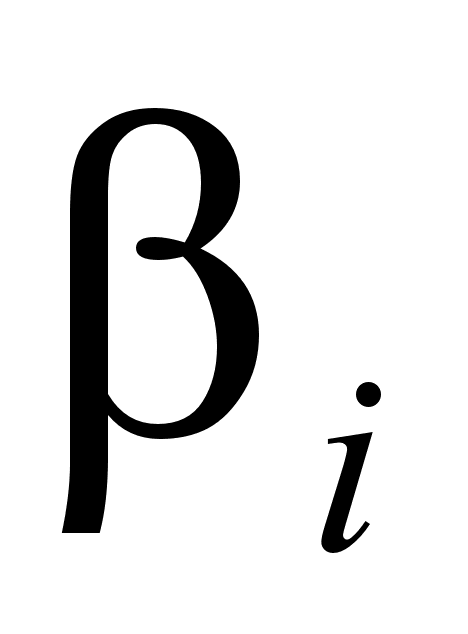 ,
т.е. нужно знать
знаки коэффициентов.
Способ определения
знака мы рассмотрим
ниже, в этой
главе.
,
т.е. нужно знать
знаки коэффициентов.
Способ определения
знака мы рассмотрим
ниже, в этой
главе.
Стоит сразу отметить весьма низкую точность результатов, рассчитанных математическим методом. Причины этого:
1
– абсолютные
значения величин
Ai
и Bi
отличаются
на порядок, а
иногда и на
два, от абсолютных
значений
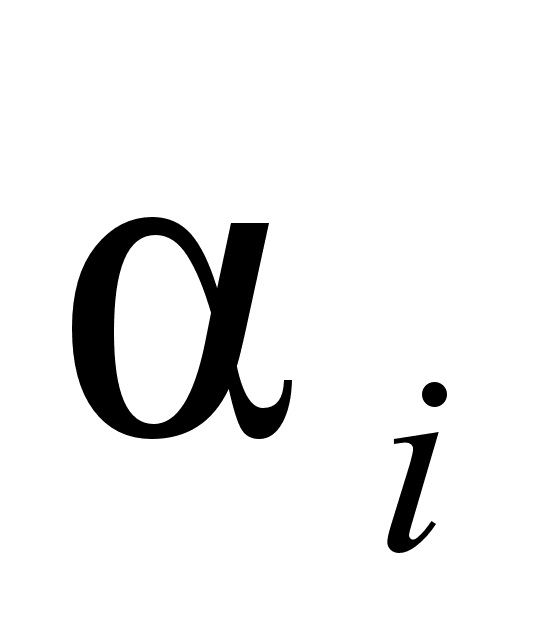 и
и
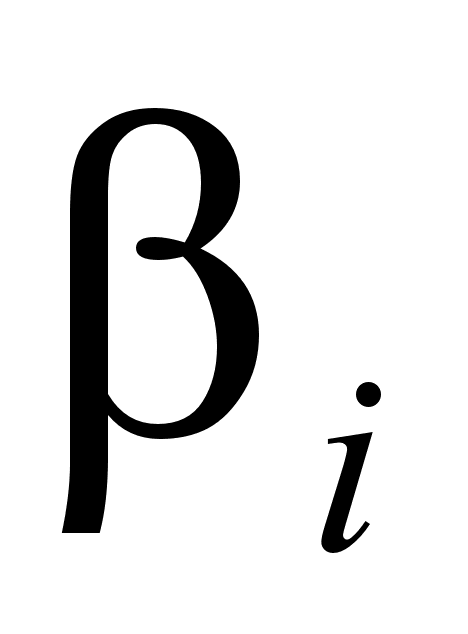 ,
что является
причиной погрешности
при решении.
,
что является
причиной погрешности
при решении.
2 – недостаточная точность экспериментальных данных; этот пункт рассмотрим подробнее.
Часто
в термодинамических
исследованиях
экспериментально
пользуясь
различными
методиками
определяют
связь активности
одного из компонентов
с его концентрацией
в растворе. При
этом график
функции
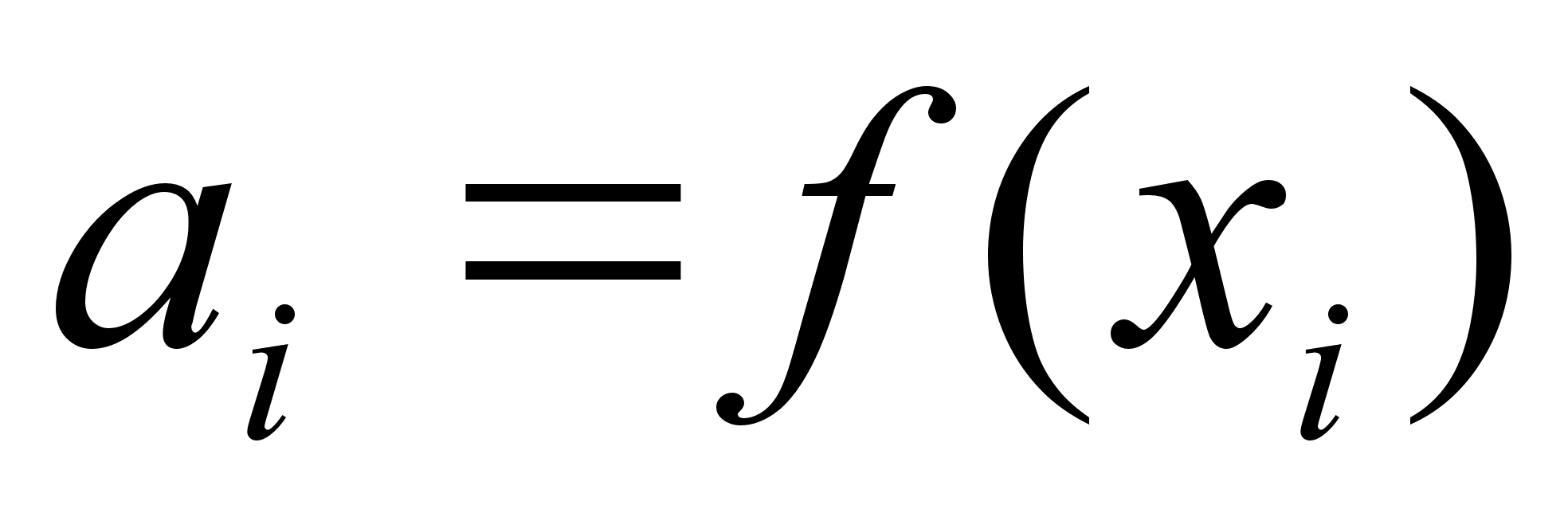 имеет следующие
особенности.
Кривая активности
в точках
имеет следующие
особенности.
Кривая активности
в точках
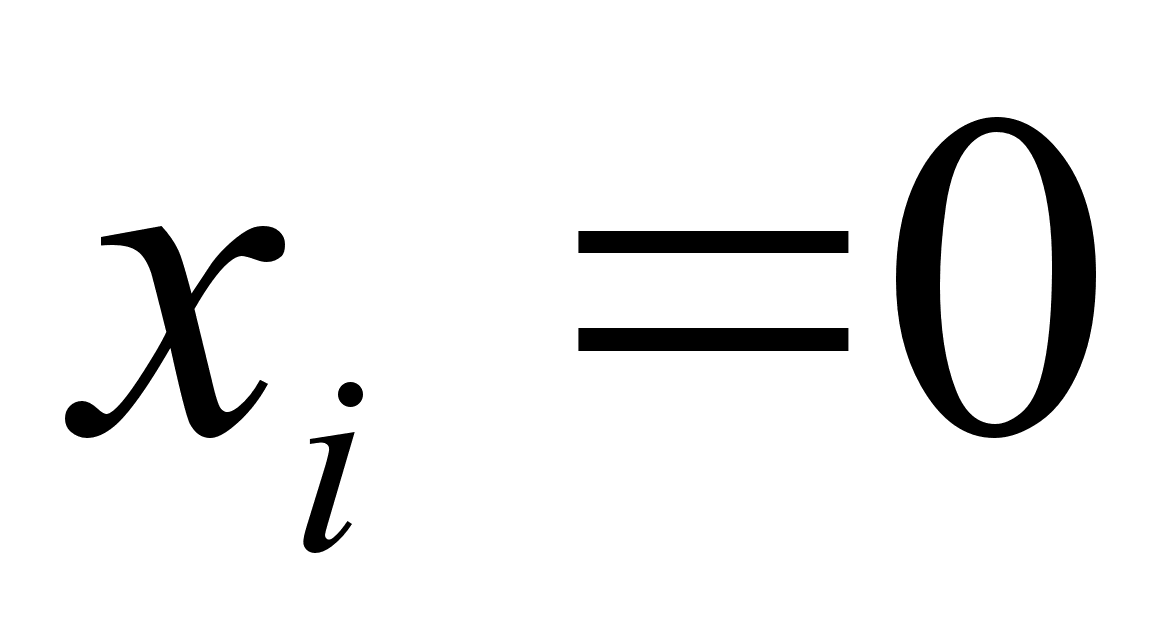 и
и
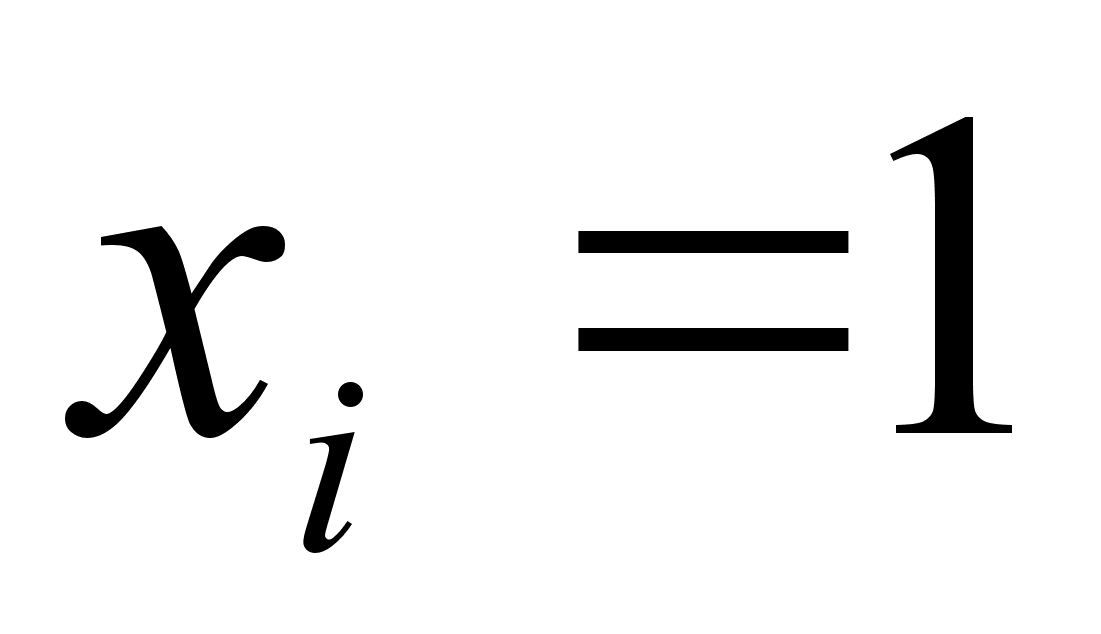 как бы жестко
закреплена;
при этом значения
ai
равны нулю и
единице соответственно.
Однако, в интервале
0
как бы жестко
закреплена;
при этом значения
ai
равны нулю и
единице соответственно.
Однако, в интервале
0
Различие
экспериментальных
данных становится
ещё более очевидно,
если их представить
в виде графика
зависимости
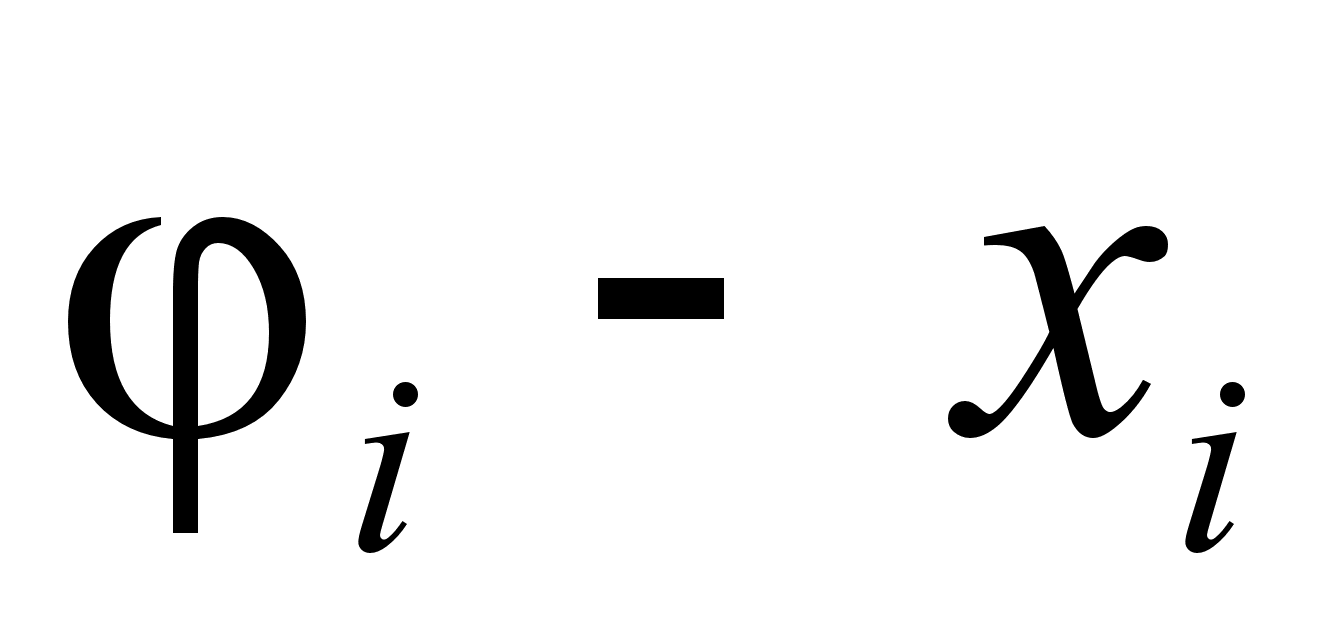 (см. рисунок
8). На рисунке
8 представлены
значения функции
(см. рисунок
8). На рисунке
8 представлены
значения функции
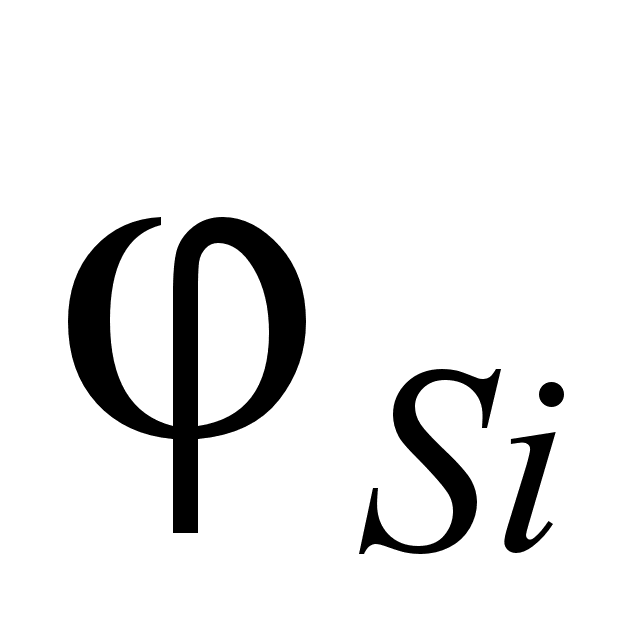 для различных
содержаний
кремния в расплаве
Fe
– Si
при Т=1873 К. Литературные
данные по активности
обработаны
в соответствии
с уравнением
(98). Как видим, все
графики имеют
разную форму,
и вдобавок,
весьма далеки
от прямой
зависимости.
Такой характер
данных, по-видимому,
связан с неточностью
измерений.
для различных
содержаний
кремния в расплаве
Fe
– Si
при Т=1873 К. Литературные
данные по активности
обработаны
в соответствии
с уравнением
(98). Как видим, все
графики имеют
разную форму,
и вдобавок,
весьма далеки
от прямой
зависимости.
Такой характер
данных, по-видимому,
связан с неточностью
измерений.
В
[8] дано следующее
объяснение
подобным неточностям.
В области составов
расплава вблизи
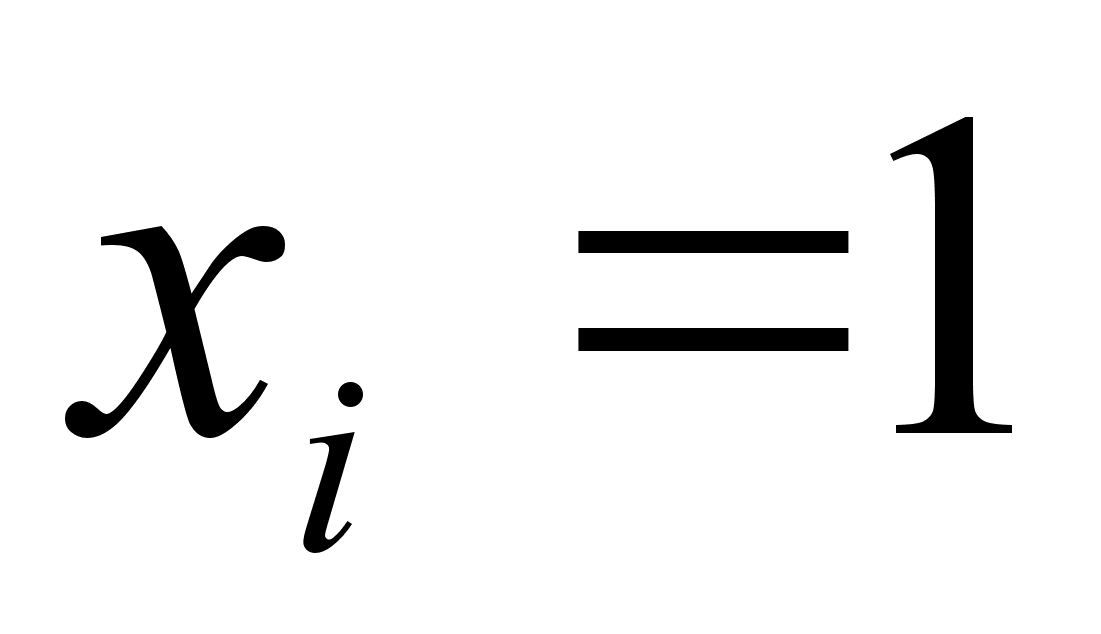 отклонения
от идеальности
и, следовательно,
величины
отклонения
от идеальности
и, следовательно,
величины
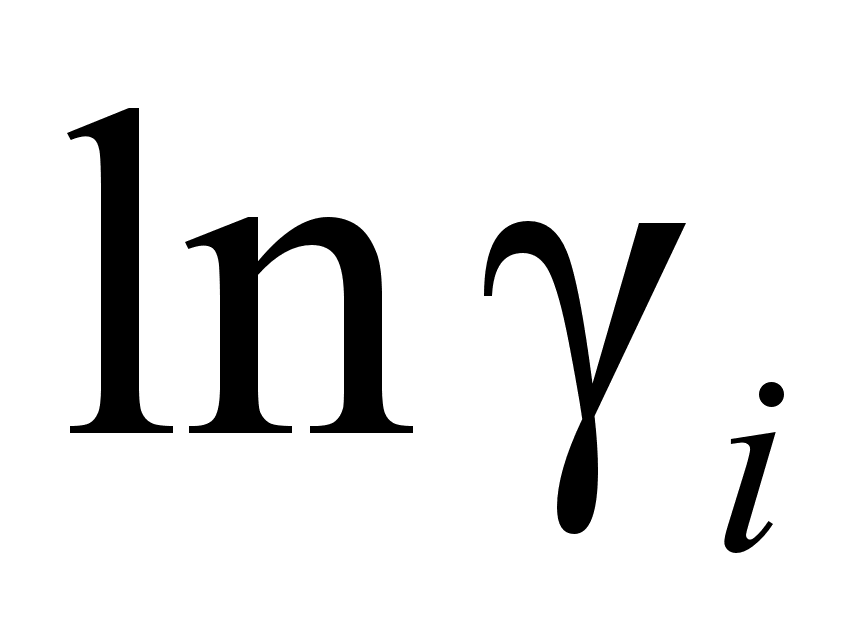 очень малы. Так
же малы и величины
очень малы. Так
же малы и величины
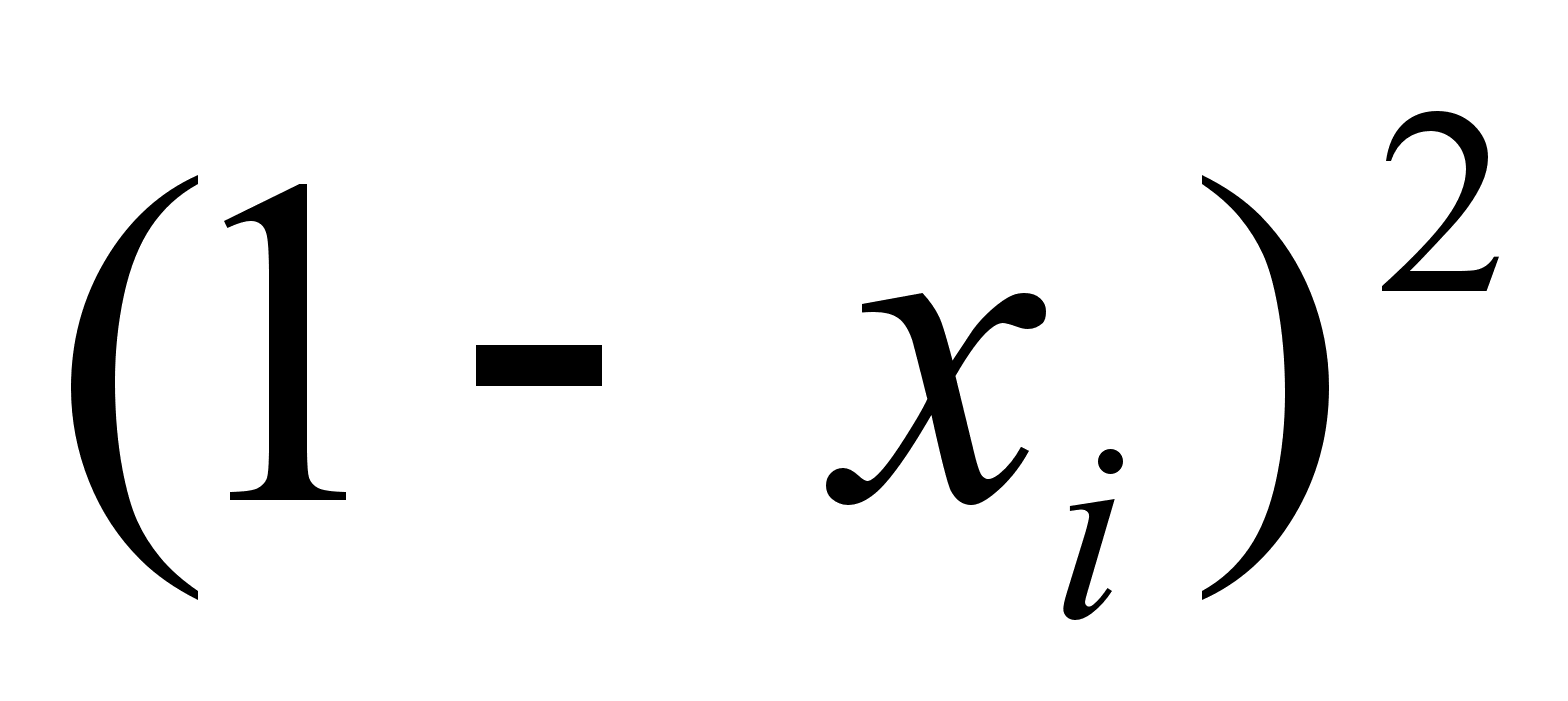 .
Поэтому для
достижения
удовлетворительных
результатов
при вычислении
функции
.
Поэтому для
достижения
удовлетворительных
результатов
при вычислении
функции
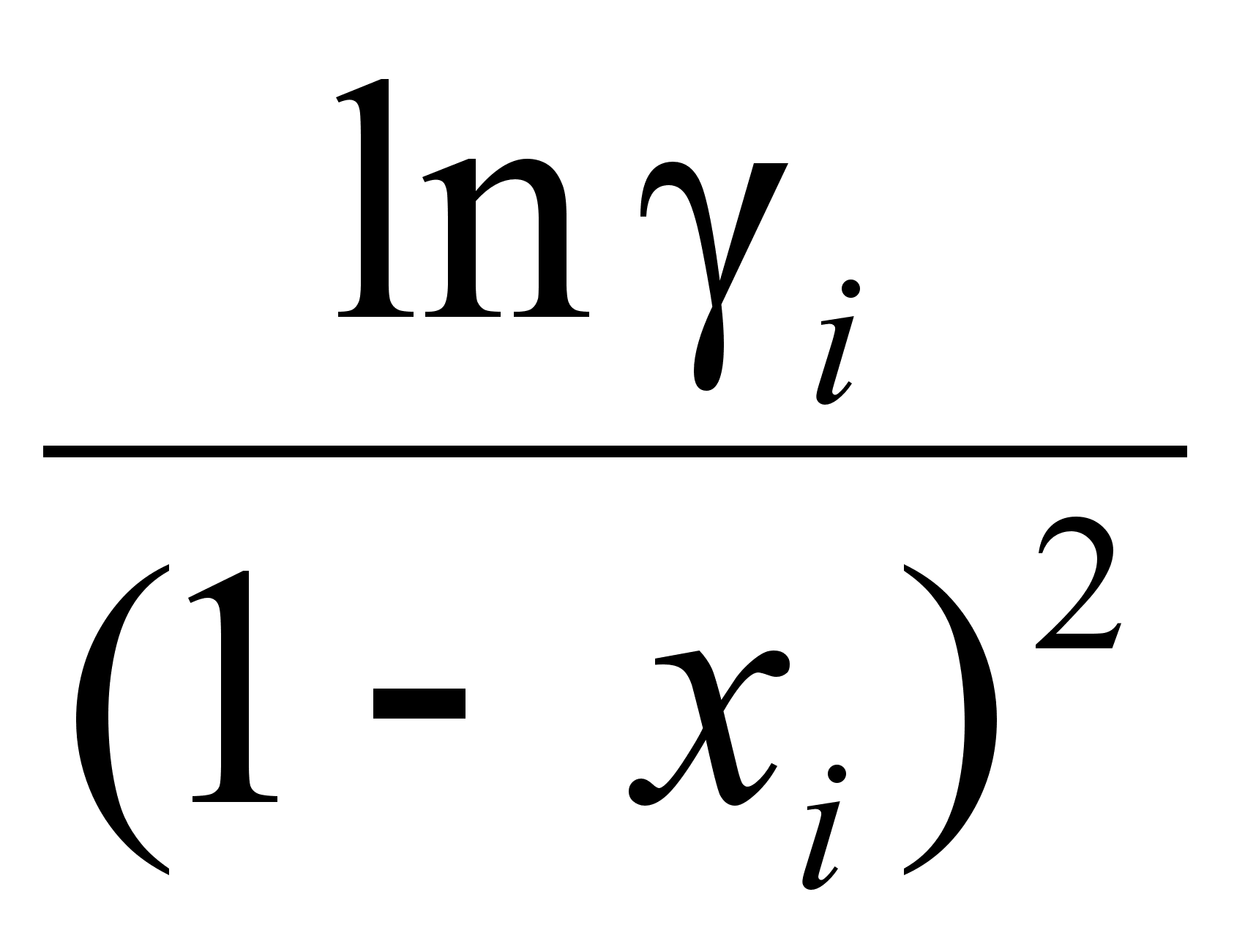 требуется
особенно высокая
точность
эксперимента.
В то же время
для наиболее
распространенных
методов исследования
термодинамических
свойств жидких
металлических,
солевых и других
систем как раз
характерно
требуется
особенно высокая
точность
эксперимента.
В то же время
для наиболее
распространенных
методов исследования
термодинамических
свойств жидких
металлических,
солевых и других
систем как раз
характерно
|
Лит. источник |
[10] |
[11] |
[12] |
[13] |
[14] |
[15] |
|||||||
| № |
xSi |
aSi |
Si |
aSi |
Si |
aSi |
Si |
aSi |
Si |
aSi |
Si |
aSi |
Si |
|
1 |
0,0 |
0,000 |
- |
0,00 |
- |
0,00 |
- |
0,00 |
- |
0,00 |
- |
0,00 |
- |
|
2 |
0,1 |
0,002 |
-4,83 |
0,009 |
-2,973 |
0,0011 |
-5,568 |
0,0008 |
-5,96 |
0,001 |
-5,685 |
0,008 |
-5,961 |
|
3 |
0,2 |
0,009 |
-4,845 |
0,026 |
-3,188 |
0,0051 |
-5,733 |
0,0043 |
-6,0 |
0,0045 |
-5,928 |
0,0083 |
-4,972 |
|
4 |
0,3 |
0,031 |
-4,632 |
0,076 |
-2,802 |
0,0198 |
-5,547 |
0,025 |
-5,07 |
0,0193 |
-5,599 |
0,030 |
-4,699 |
|
5 |
0,4 |
0,083 |
-4,368 |
0,164 |
-2,477 |
0,0669 |
-4,967 |
0,090 |
-4,14 |
0,0481 |
-5,884 |
0,080 |
-4,471 |
|
6 |
0,5 |
0,197 |
-3,726 |
0,285 |
-2,248 |
0,1779 |
-4,134 |
0,234 |
-3,04 |
0,162 |
-4,508 |
0,190 |
-3,870 |
|
7 |
0,6 |
0,427 |
-2,126 |
0,426 |
-2,141 |
0,3570 |
-3,245 |
0,455 |
-1,73 |
0,378 |
-2,888 |
0,415 |
-2,304 |
|
8 |
0,7 |
0,623 |
-1,295 |
0,525 |
-3,196 |
0,5567 |
-2,545 |
0,624 |
-1,28 |
0,582 |
-2,051 |
0,664 |
-0,926 |
|
9 |
0,8 |
0,745 |
-1,781 |
0,624 |
-6,212 |
0,7379 |
-2,020 |
0,770 |
-0,96 |
0,730 |
-2,289 |
0,780 |
-0,633 |
|
10 |
0,9 |
0,882 |
-2,00 |
0,830 |
-8,097 |
0,8890 |
-1,230 |
0,885 |
-1,68 |
0,879 |
-2,361 |
0,897 |
-0,334 |
|
11 |
1,0 |
1,000 |
- |
1,00 |
- |
1,00 |
- |
1,00 |
- |
1,00 |
- |
1,00 |
- |
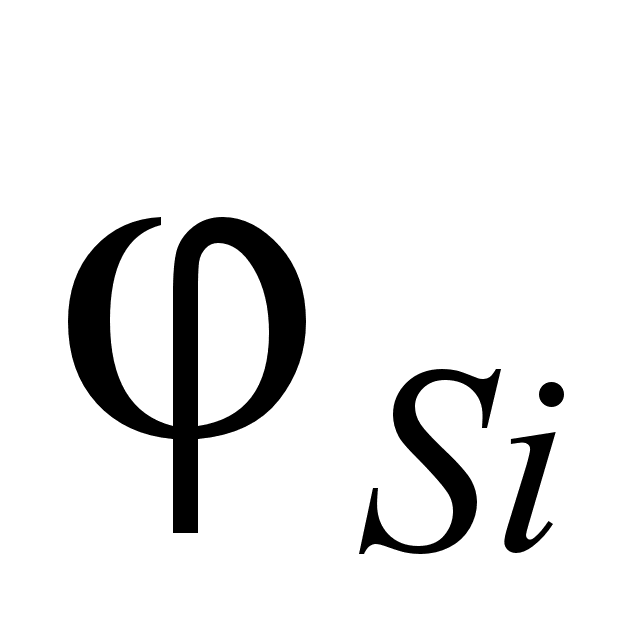 - xSi
для системы
Fe – Si
(при Т-1873 К)
- xSi
для системы
Fe – Si
(при Т-1873 К)
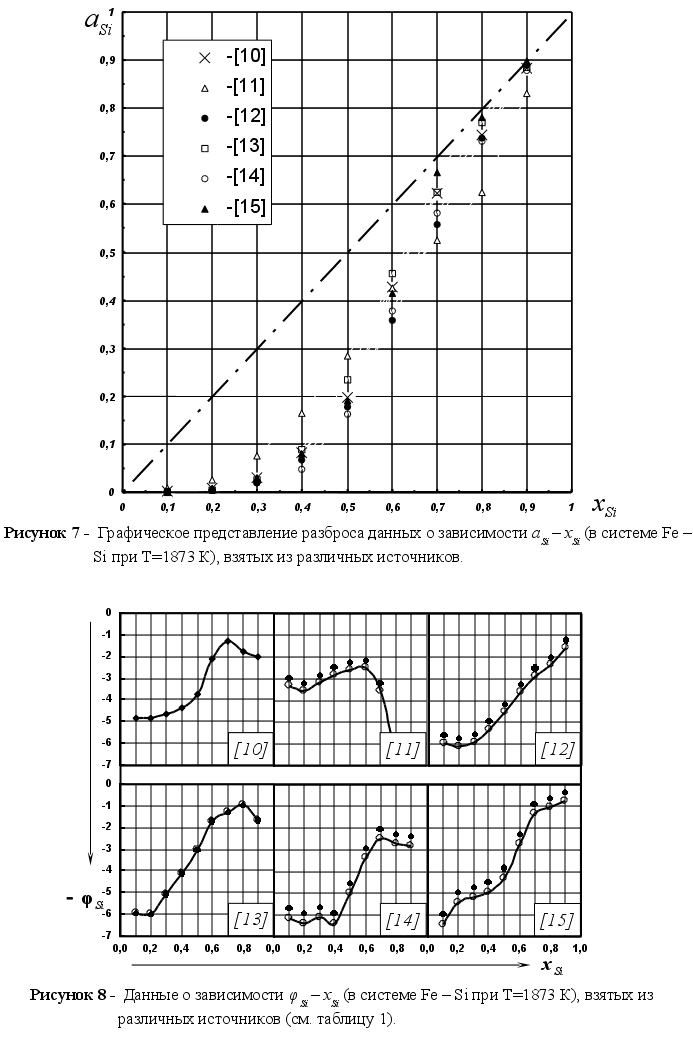
уменьшение точности измерений в области богатой компонентом, парциальные молярные характеристики которого определяются.
Из вышесказанного следует заключить: математический метод нежелателен в использовании в силу его неточности.
Проще и надежнее поставленная задача решается графически.
4.2 Графический метод.
Суть
данного метода
поясняет рисунок
9. На этом рисунке
Su
площадь под
линией ai=f(xi)=xi
в идеальном
расплаве; Sp
– площадь под
кривой ai=f(xi)
в реальном
расплаве;
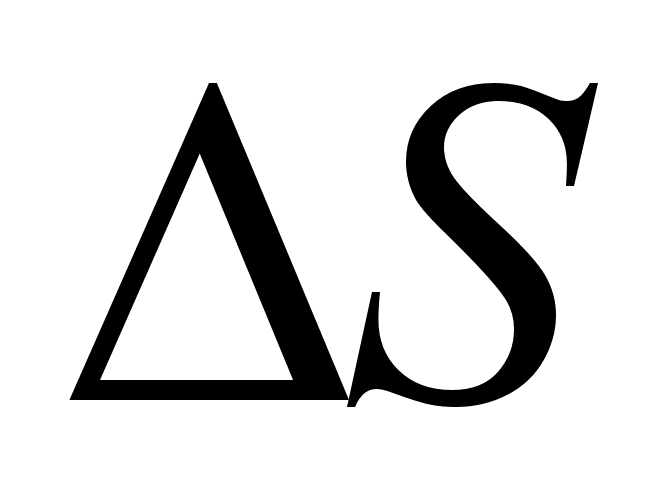 - абсолютное
значение разности
площадей Su
и Sp
:
- абсолютное
значение разности
площадей Su
и Sp
:
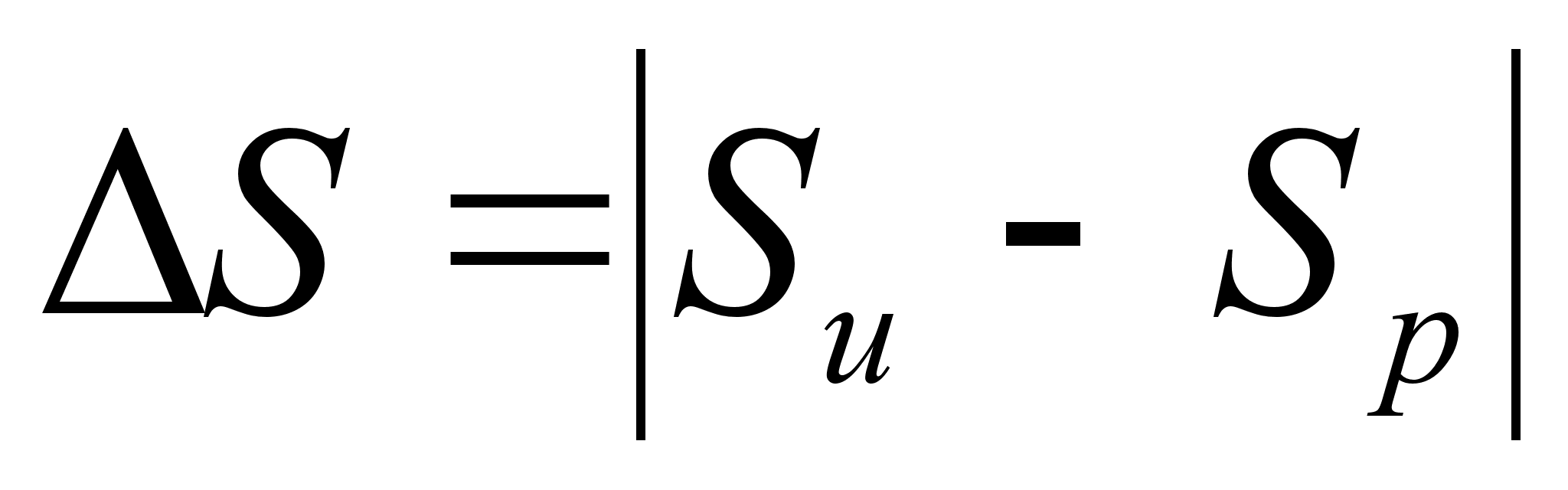
(104)
В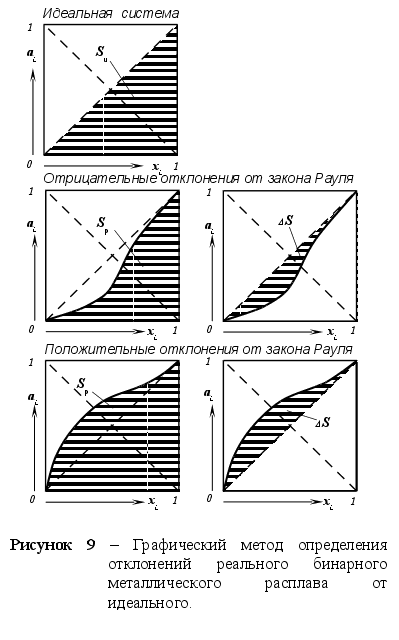 ведем
понятие интегрального
коэффициента
идеальности
реального
расплава К,
который равен:
ведем
понятие интегрального
коэффициента
идеальности
реального
расплава К,
который равен:
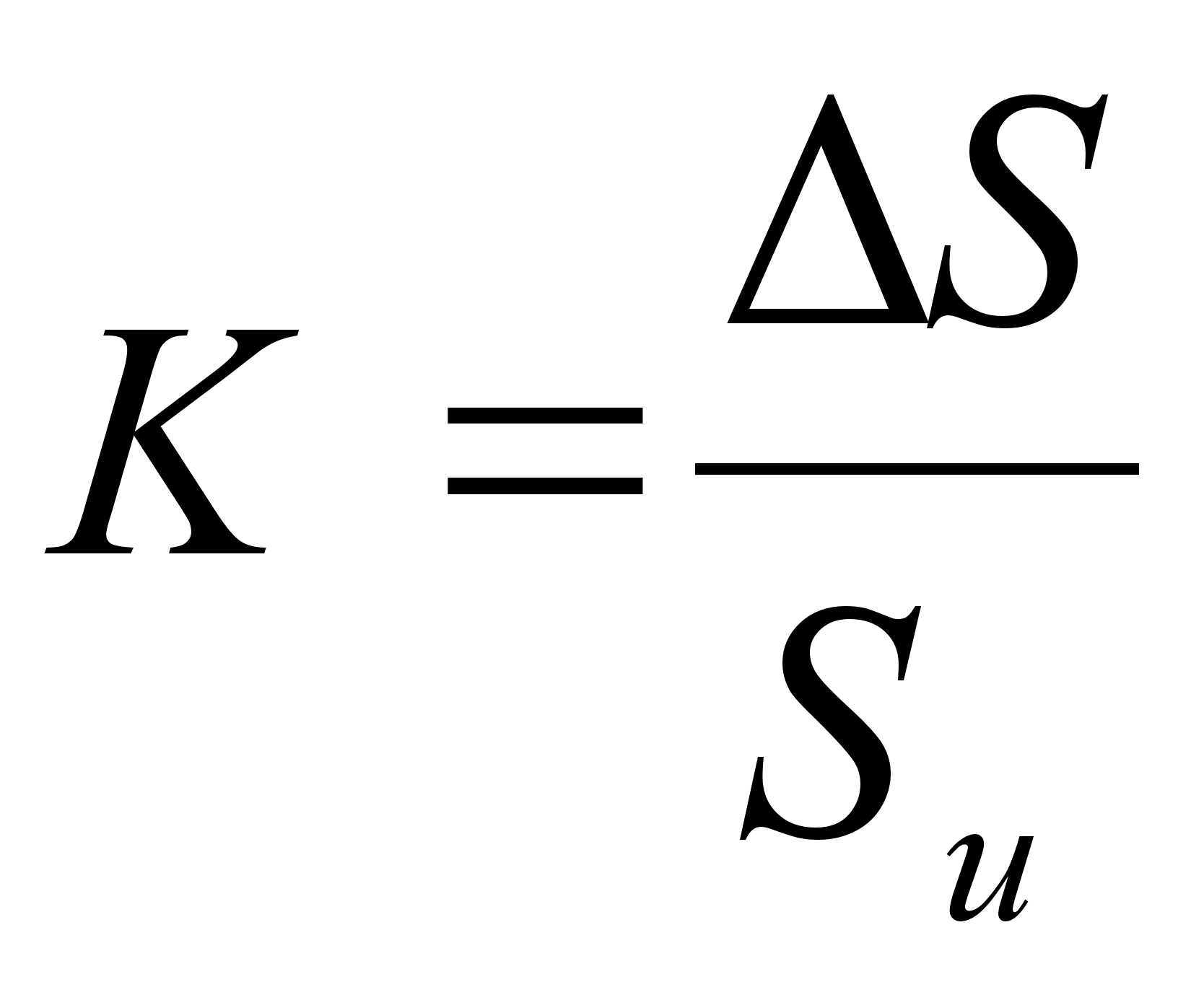
(105)
.
В
бинарном расплаве
для каждого
компонента
существует
своё значение
интегрального
коэффициента
идеальности,
т.е. К1
и К2.
Для нахождения
численных
значений
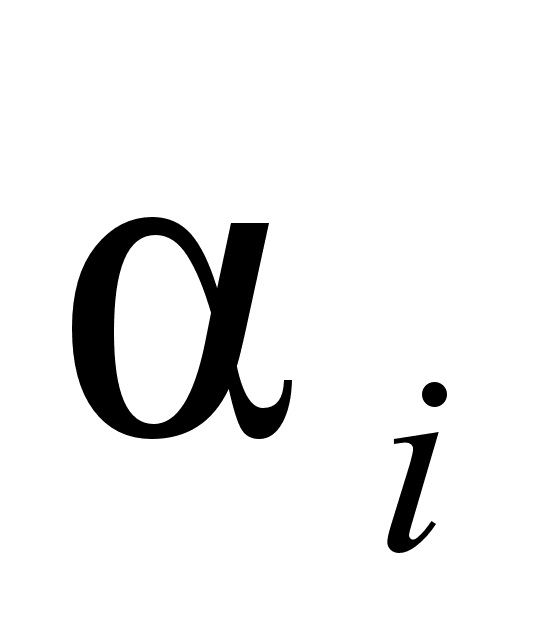 и
и
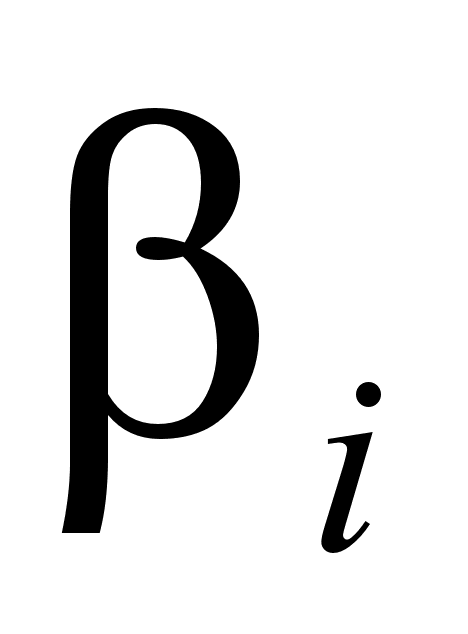 достаточно
умножить величину
Кi
на предельные
значения названных
коэффициентов,
а именно на
+0,862 или –0,5.
достаточно
умножить величину
Кi
на предельные
значения названных
коэффициентов,
а именно на
+0,862 или –0,5.
Чтобы
понять, как
можно определить
знаки коэффициентов
обратимся к
рисунку 10. На
этом рисунке
представлены
зависимости
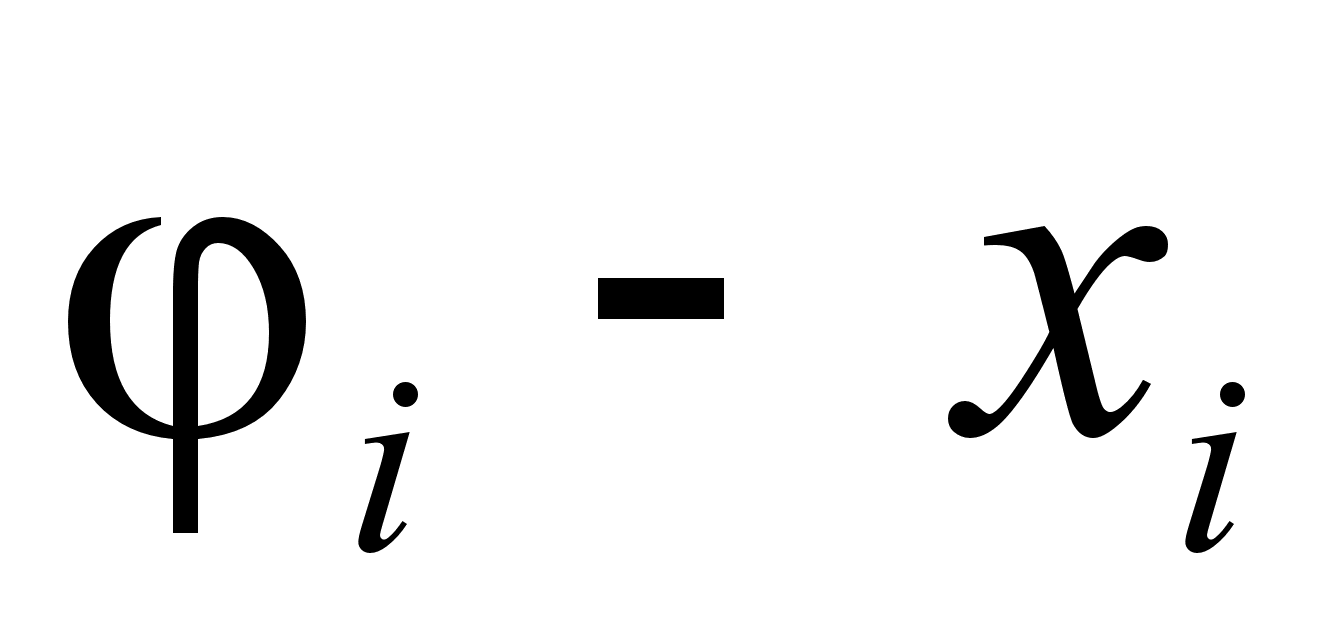 для трех
для трех
бинарных
расплавов,
характеризующихся
различными
отклонениями
от закона Рауля:
Fe
– Cu
при Т=1873 К [16] - сильное
положительное
отклонение;
Fe
– Si
при Т=1873 К (совместная
обработка
данных [10, 12, 15, 17, 18, 19] –
сильное отрицательное
отклонение;
Pd
– W
при Т=1973 К [20] –
знакопеременное
отклонения.
Здесь же приведены
и значения
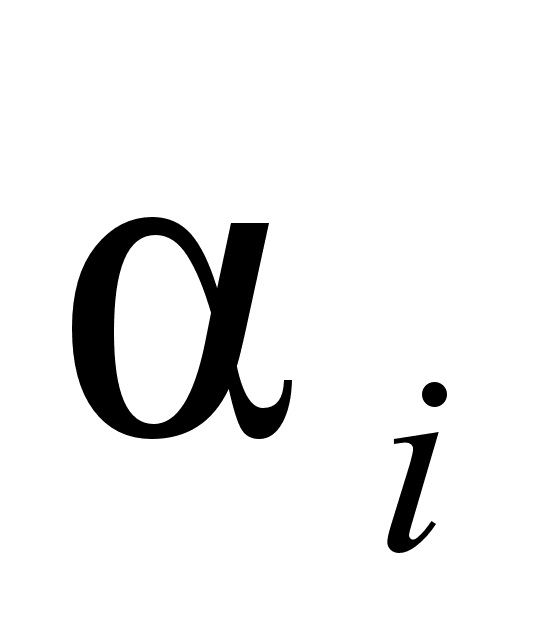 для компонентов
всех трех расплавов.
Из данного
рисунка можно
сделать вывод:
в тех случаях,
когда с ростом
для компонентов
всех трех расплавов.
Из данного
рисунка можно
сделать вывод:
в тех случаях,
когда с ростом
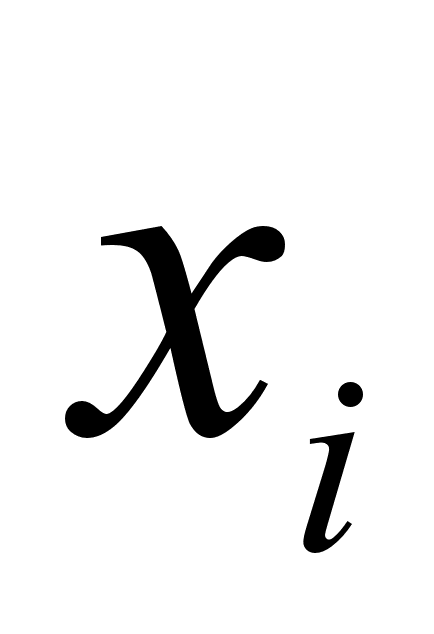 абсолютное
значение функции
абсолютное
значение функции
 уменьшается
– коэффициент
уменьшается
– коэффициент
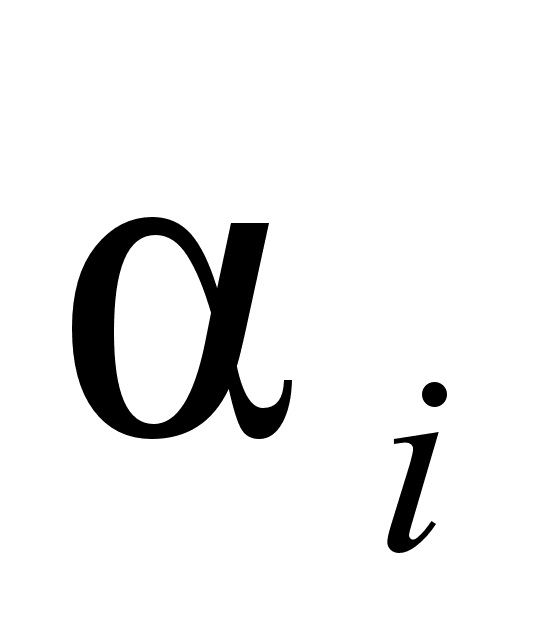 положительный,
и наоборот,
положительный,
и наоборот,
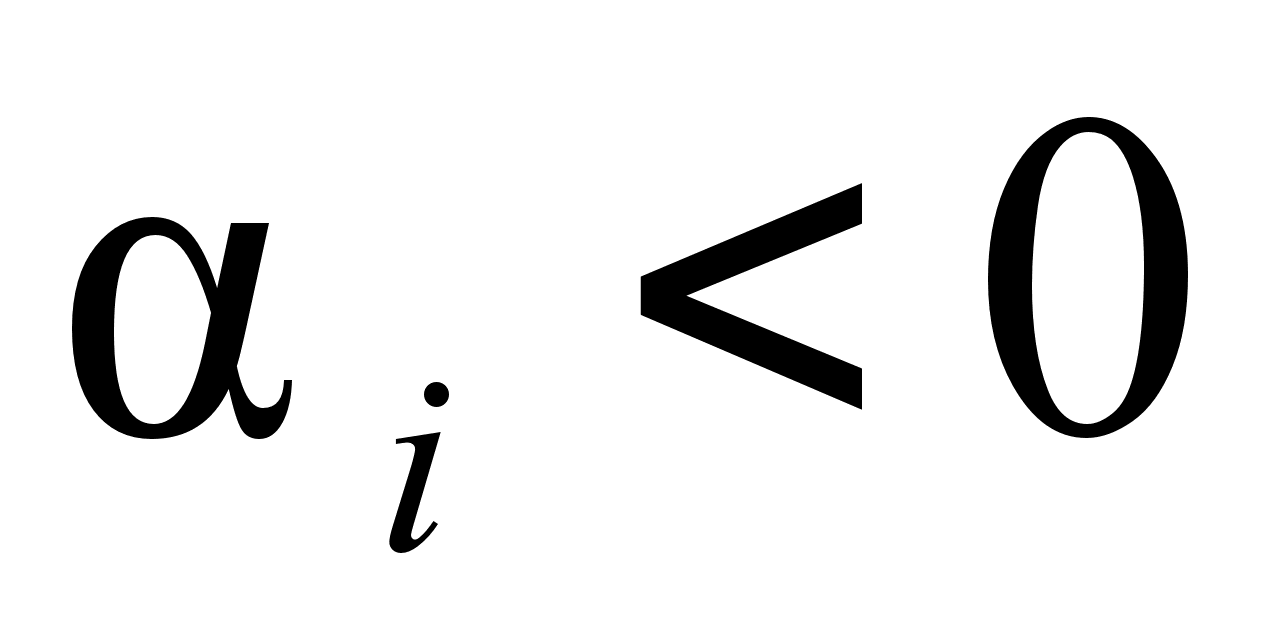 если функция
если функция
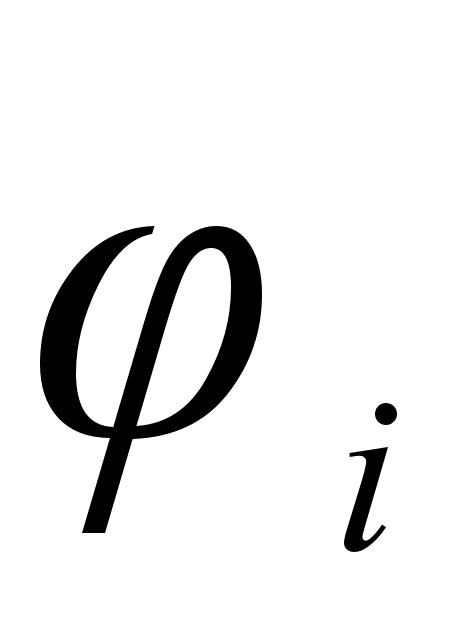 по абсолютному
значению возрастает.
Коэффициент
по абсолютному
значению возрастает.
Коэффициент
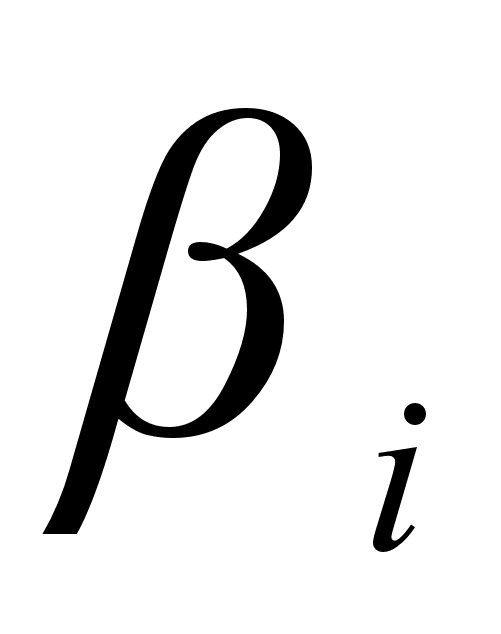 имеет, соответственно,
противоположный
знак.
имеет, соответственно,
противоположный
знак.
Пример.
В
системе Fe
– Cu
(рисунок 10) для
железа получено:
Su=0,5
, Sp=0,696,
и KFe=0,196/0,5=0,392.
Отсюда:
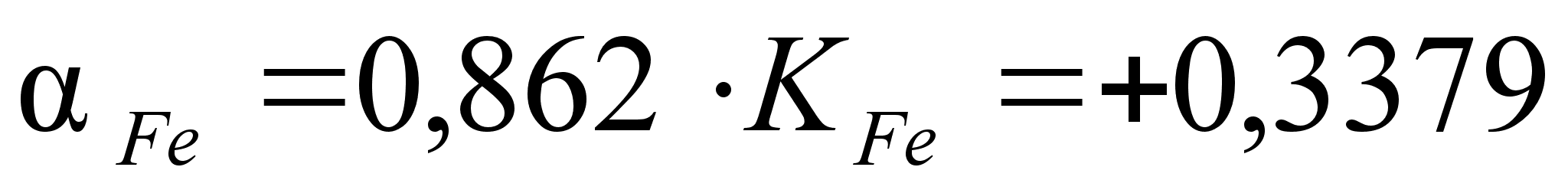
и
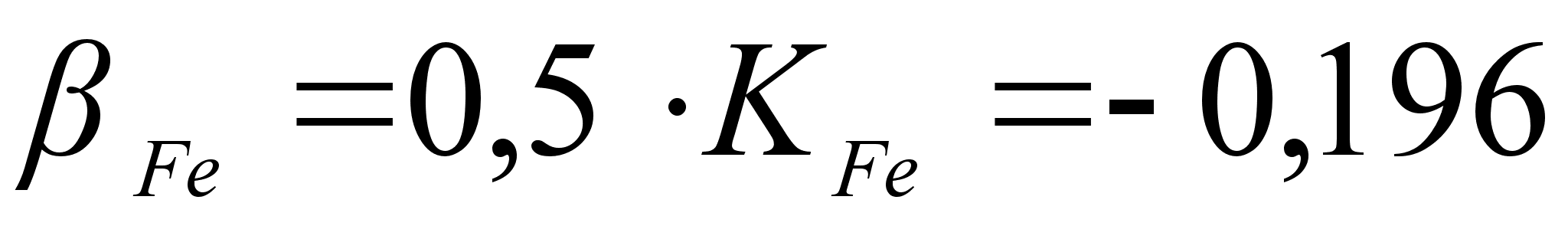 .
.
Значения
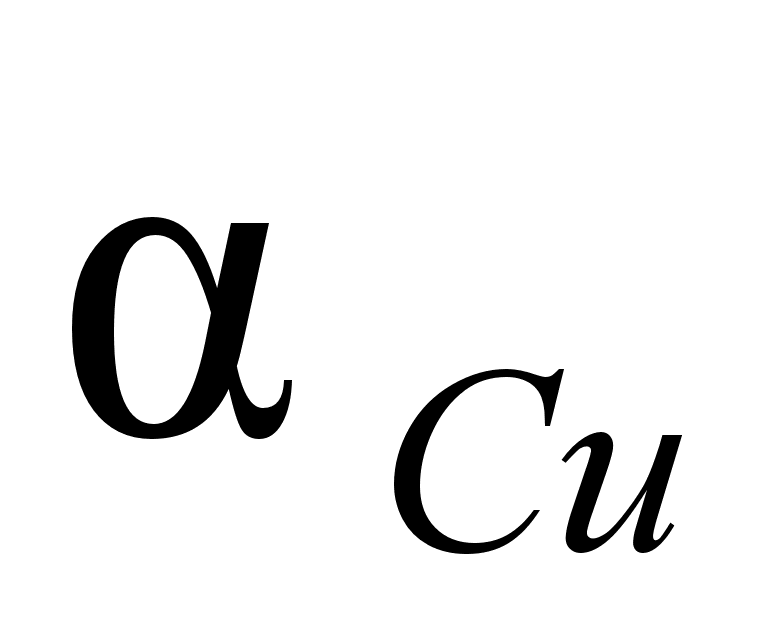 и
и
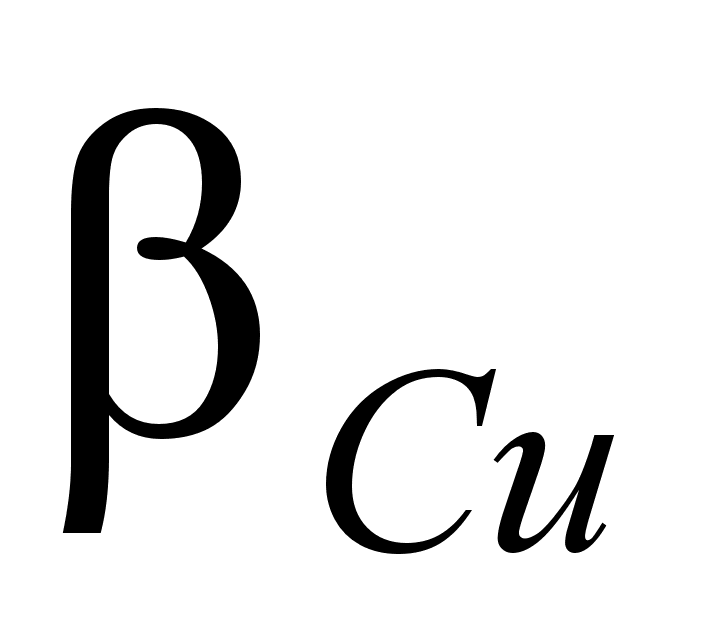 определены
из уравнений
(102) и (103). Они равны:
определены
из уравнений
(102) и (103). Они равны:
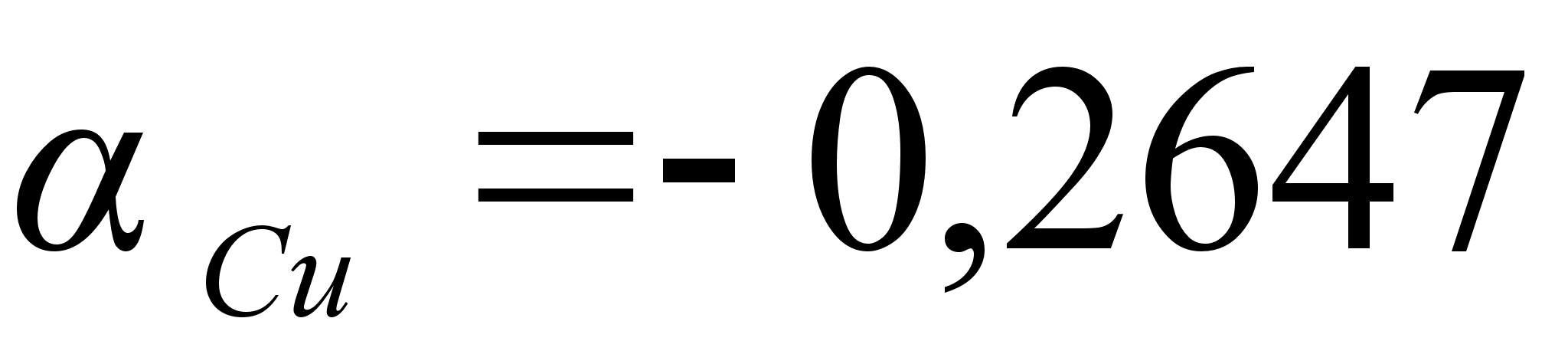
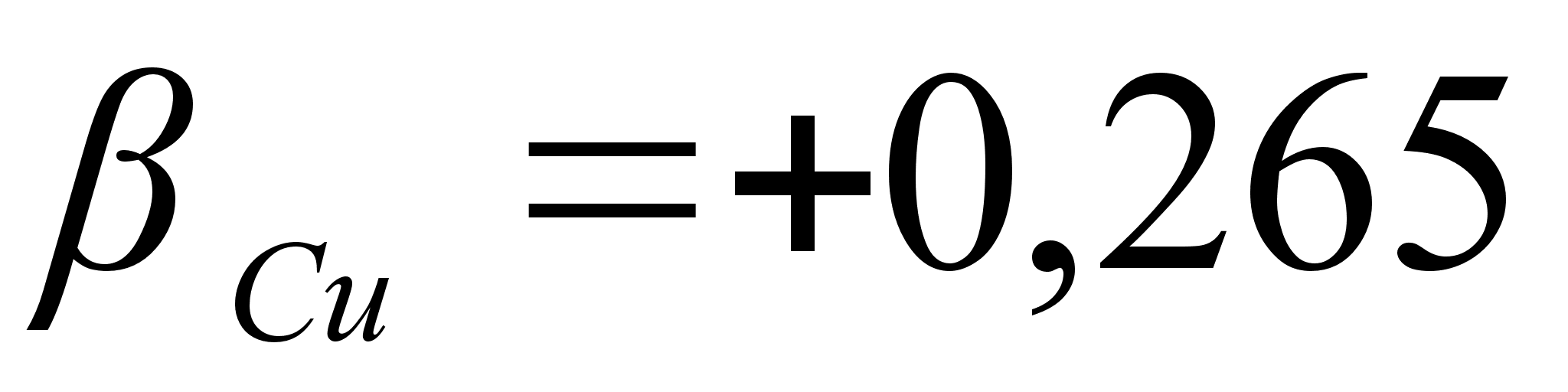 .
.
Величины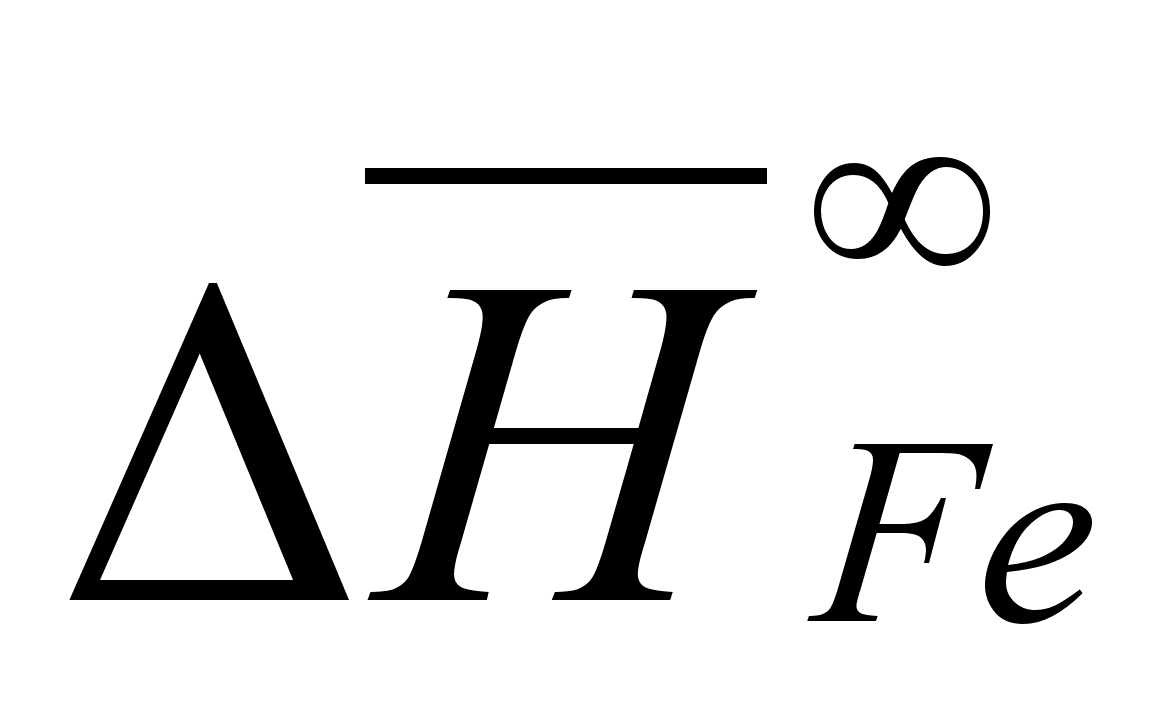 ,
,
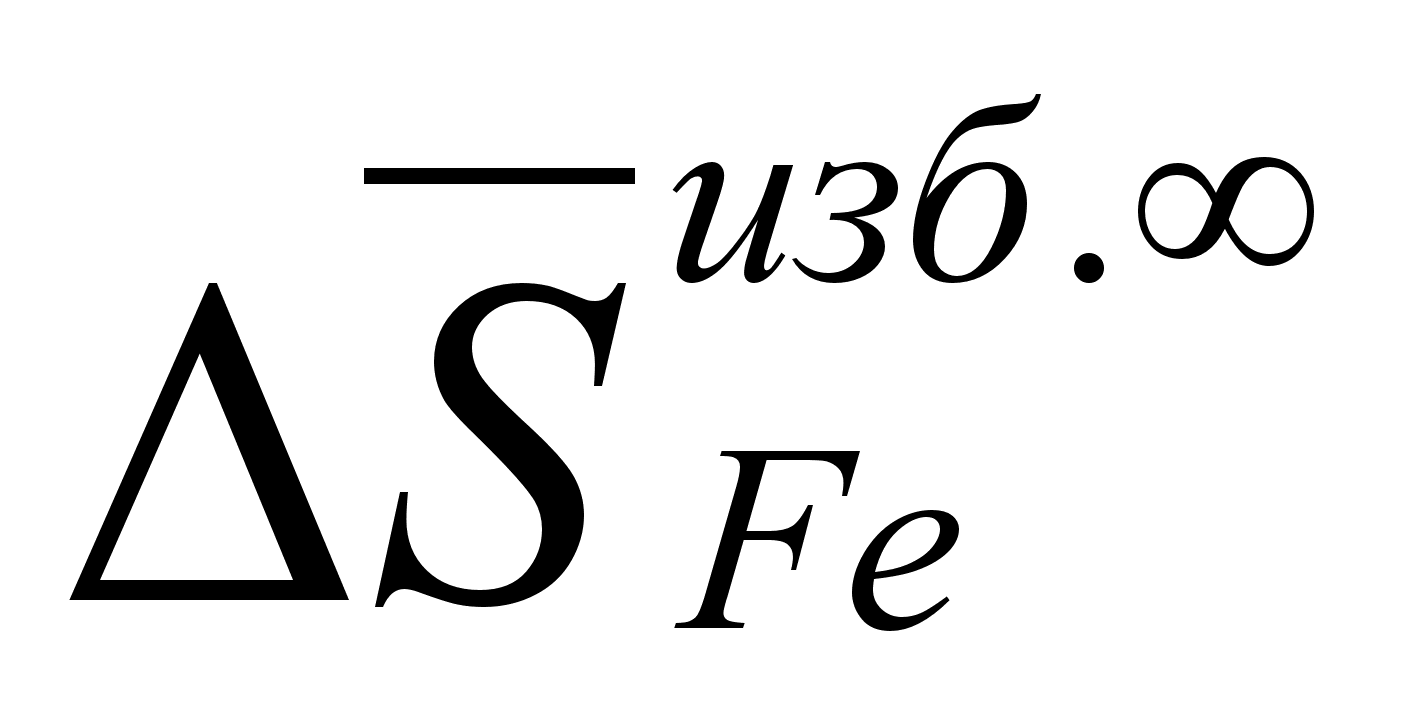 ,
,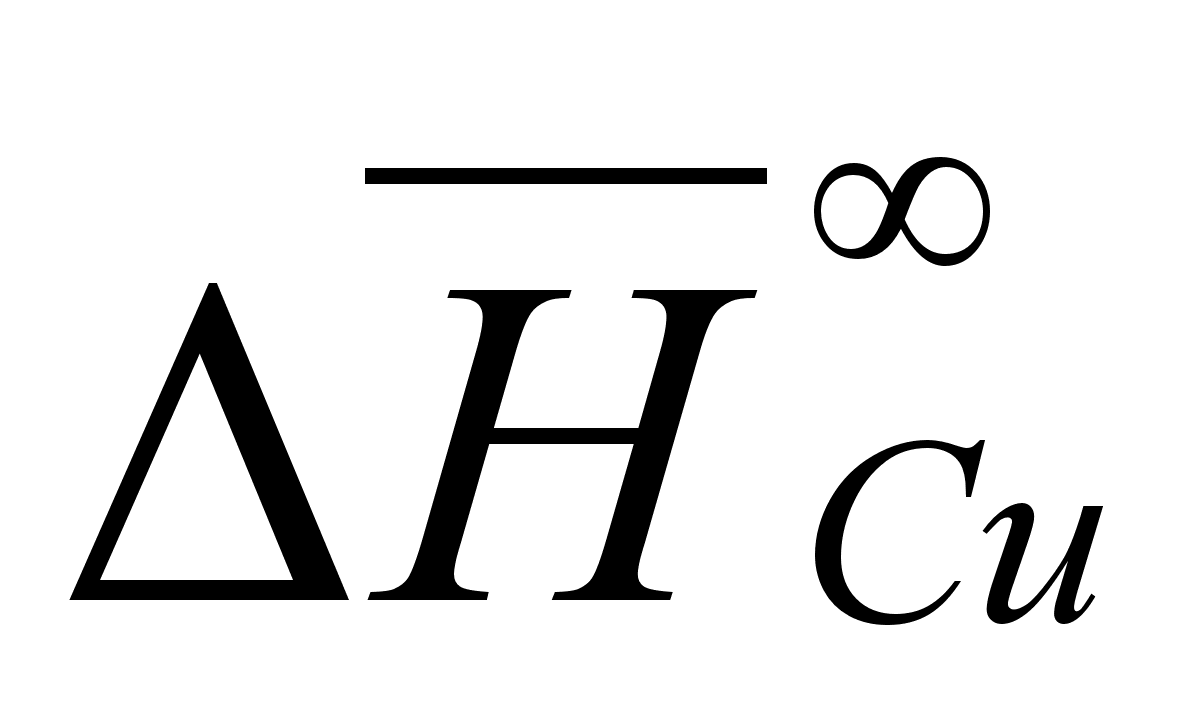 и
и
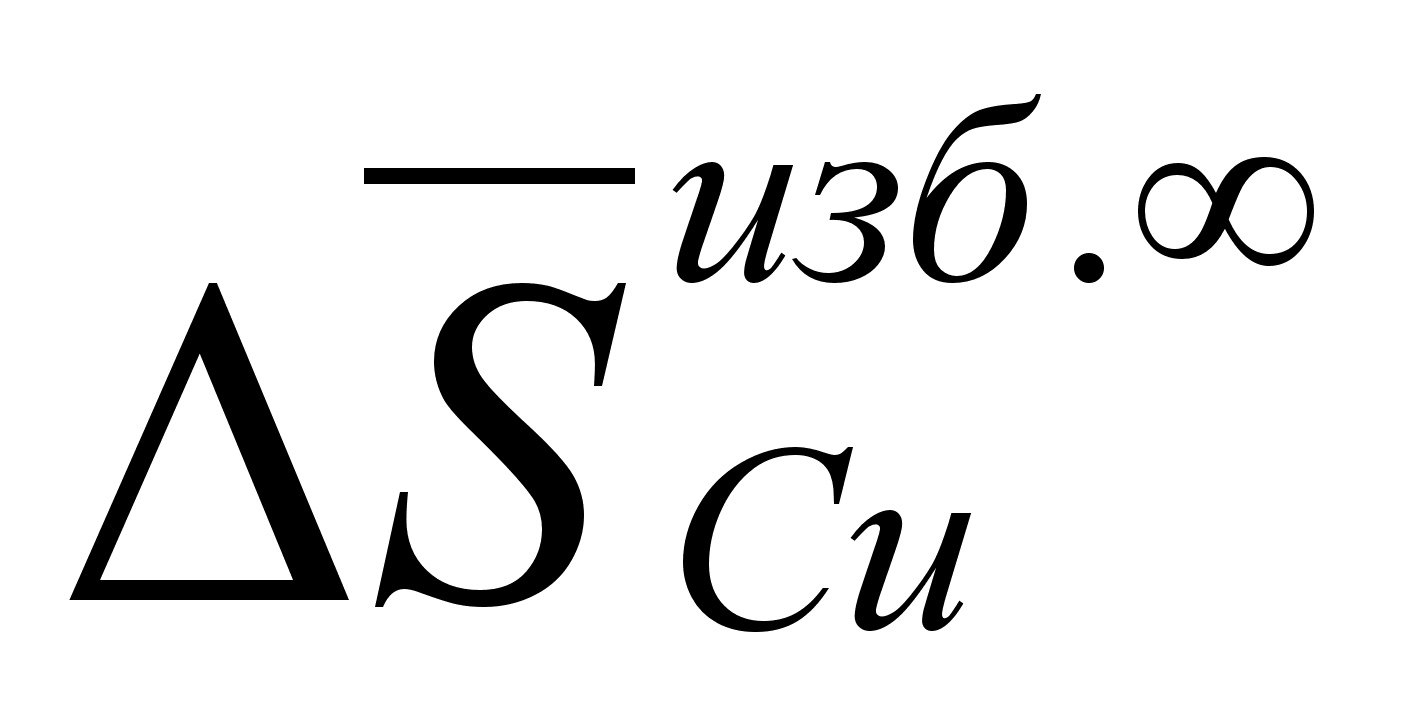 ,
при известных,
,
при известных,
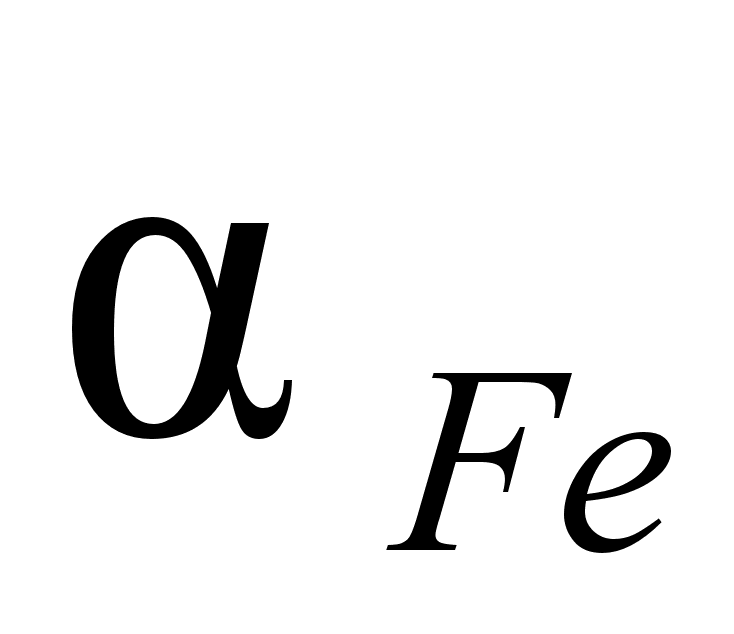 ,
,
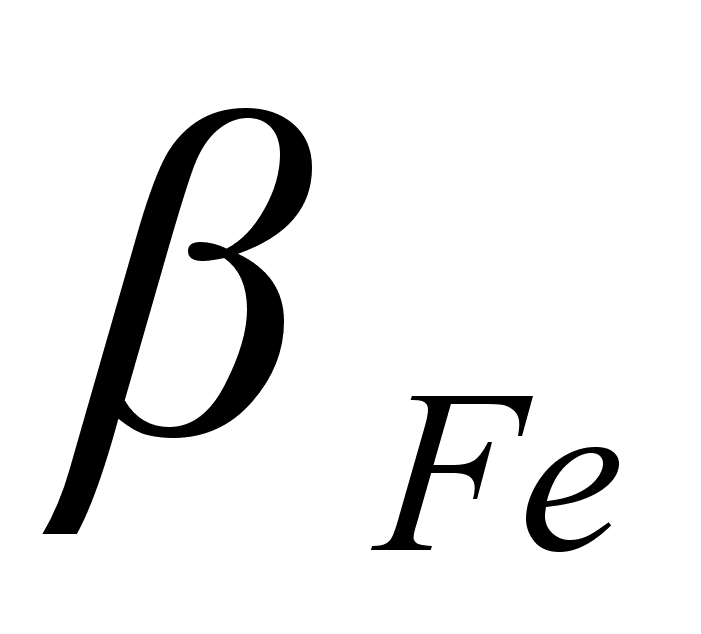 ,
,
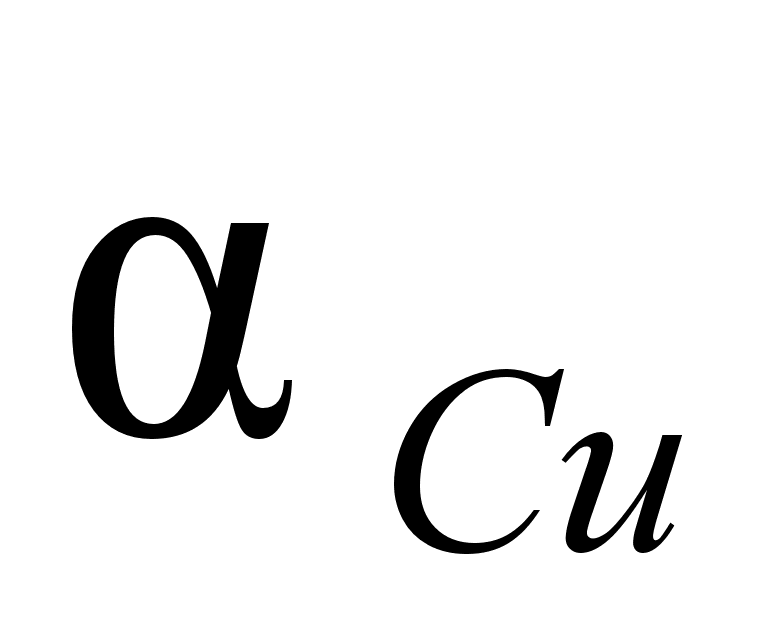 и
и
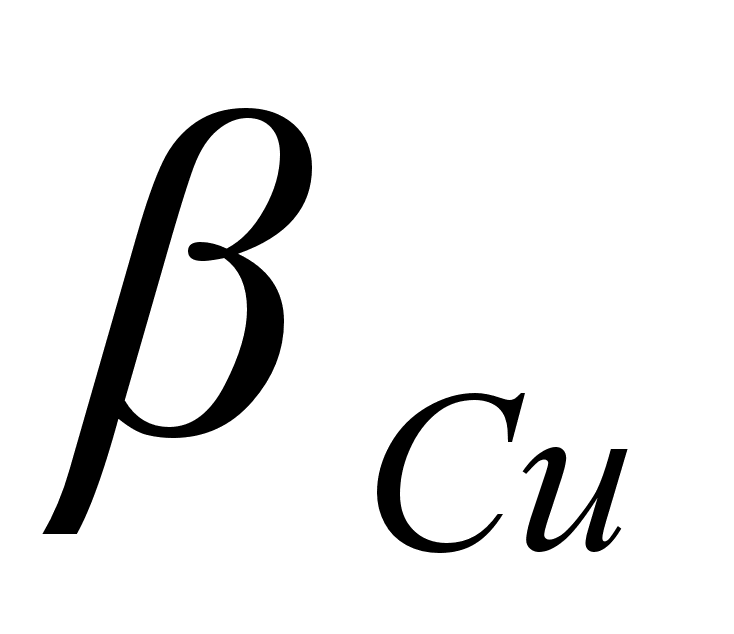 ,определяются
из уравнения
(98).
,определяются
из уравнения
(98).
Выводы:
1 – из двух рассмотренных
нами методов
вычисления
коэффициентов
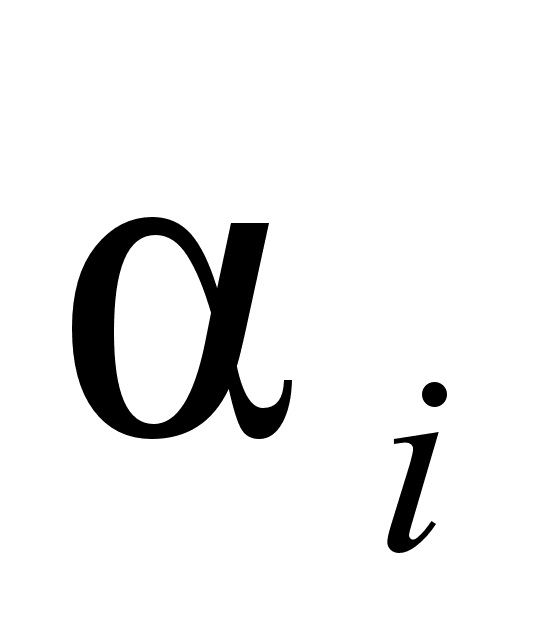 и
и
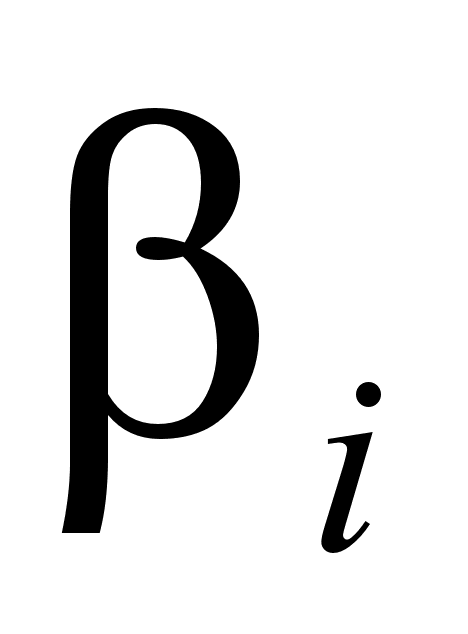 более рациональным
является графический
метод.
более рациональным
является графический
метод.
2 – показана возможность применения концентрационных уравнений для термодинамического описания металлических расплавов с любым характером отклонения от идеальности.
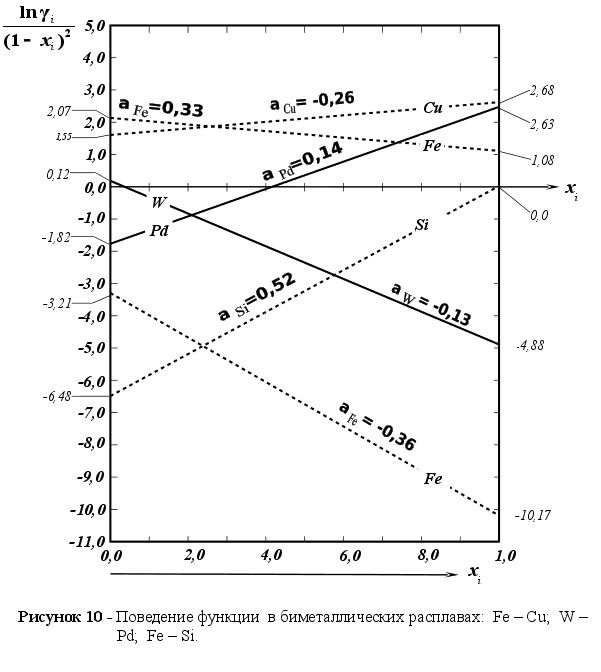
4 ИСПОЛЬЗОВАНИЕ
МЕТОДА НАИМЕНЬШИХ
КВАДРАТОВ ПРИ
РАСЧЕТЕ ФУНКЦИИ
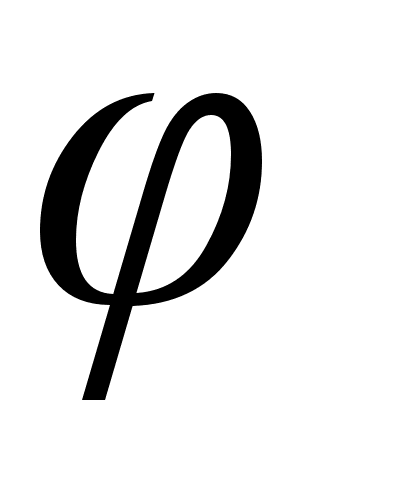
Функция
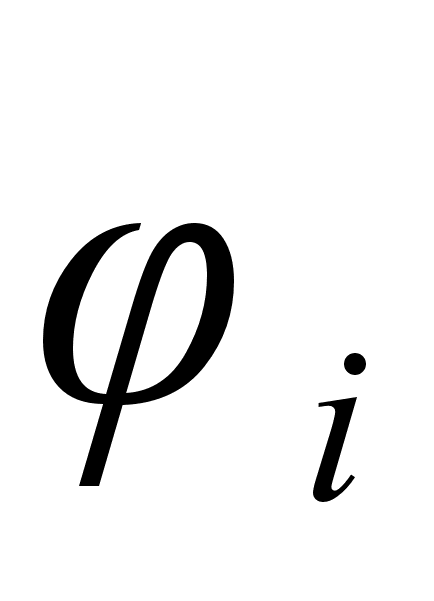 ,
как говорилось
ранее, имеет
прямолинейный
характер и
описывается
уравнением
,
как говорилось
ранее, имеет
прямолинейный
характер и
описывается
уравнением
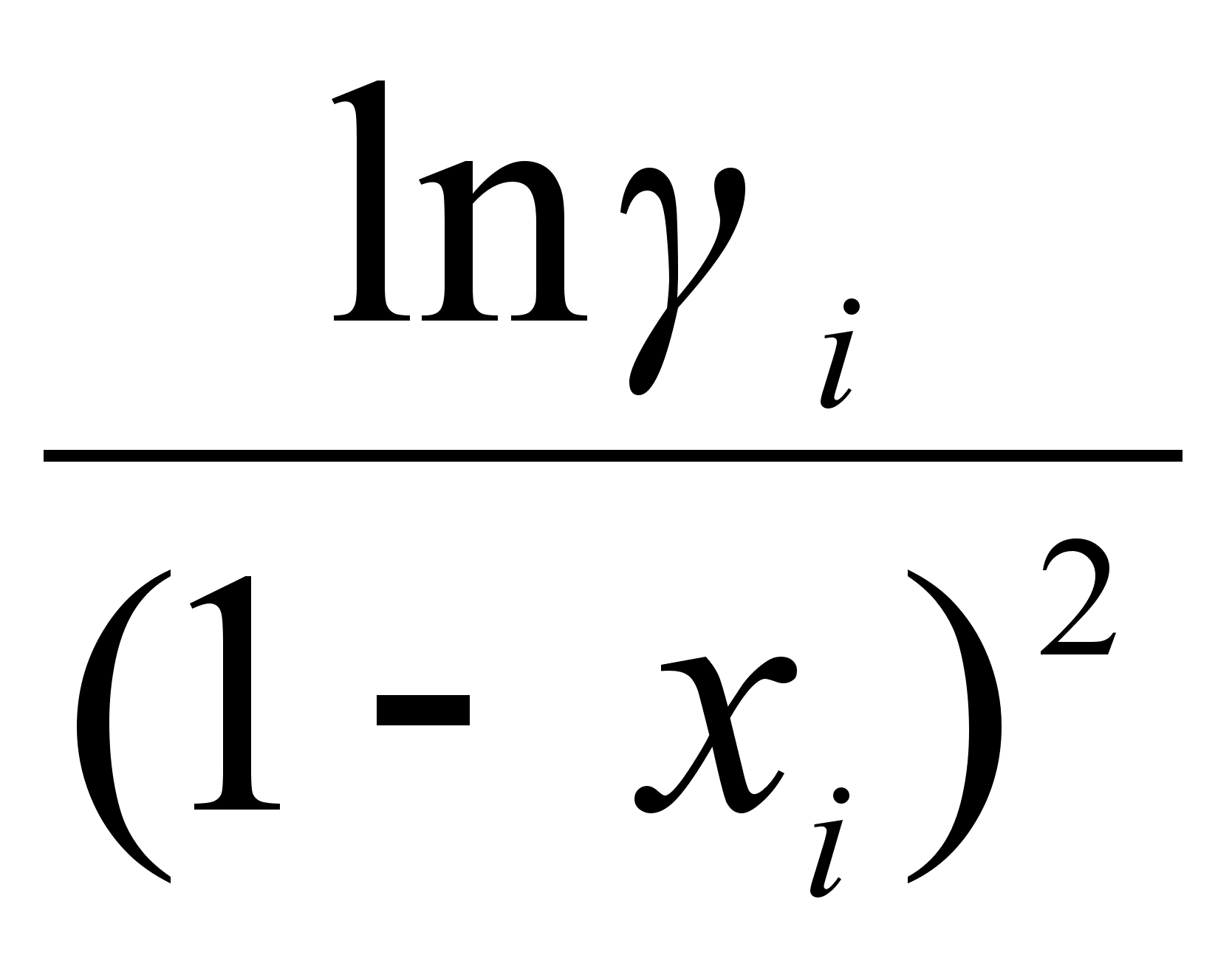 .
Однако, поскольку
это прямая, то
для упрощения
расчетов она
может быть
представлена
уравнением
:
.
Однако, поскольку
это прямая, то
для упрощения
расчетов она
может быть
представлена
уравнением
:
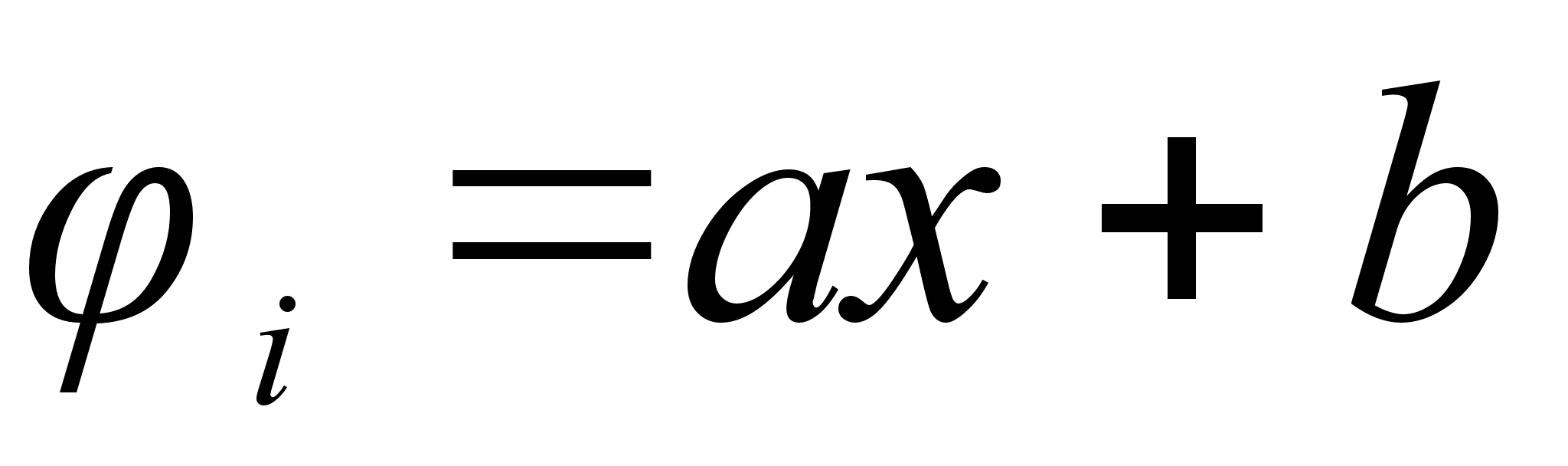
(106)
Вычисление коэффициентов в уравнении прямой линии по методу наименьших квадратов.
Для того чтобы подобрать значения коэффициентов а и b в линейной функции (уравнение (106)), отображающей экспериментальные данные, должно выполняться условие:
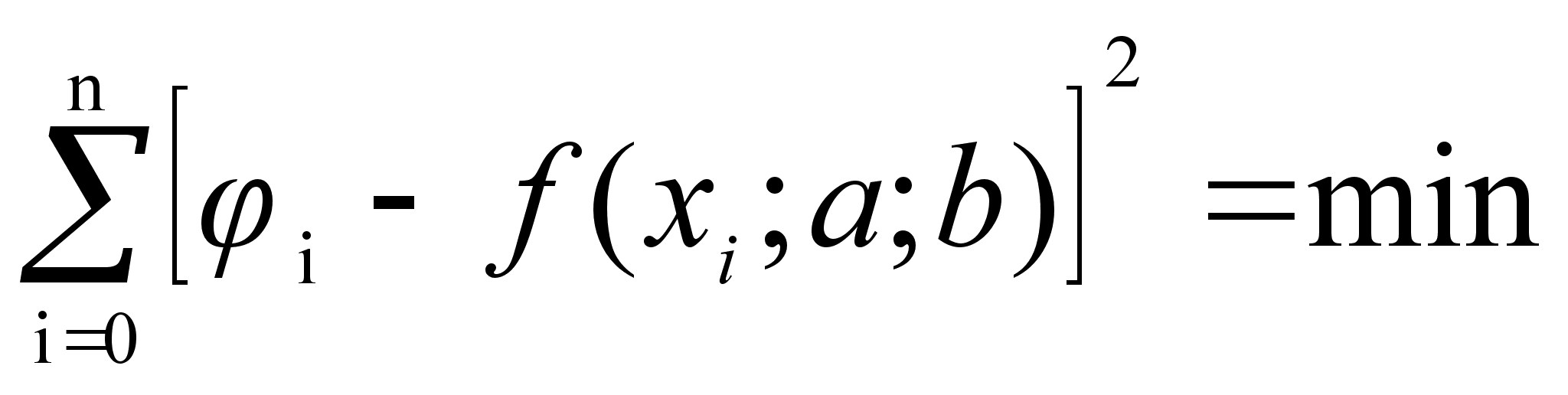
(107)
Найдем значение а и b, обращающую левую часть выражения (107) в минимум. Для этого продифференцируем её по а и b (частные производные) и приравняем производные к нулю:
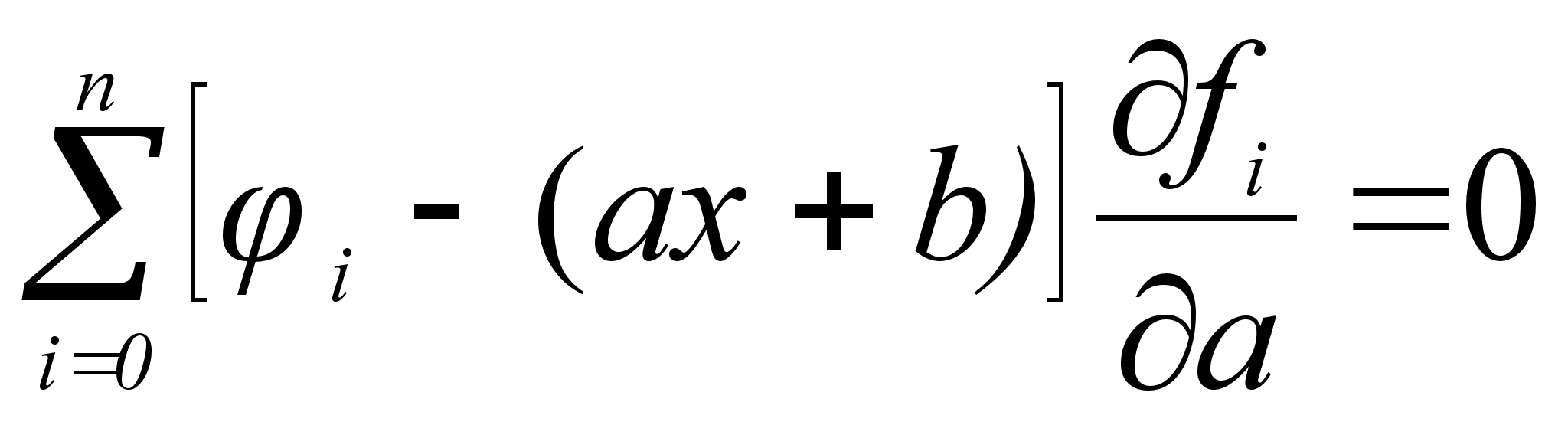

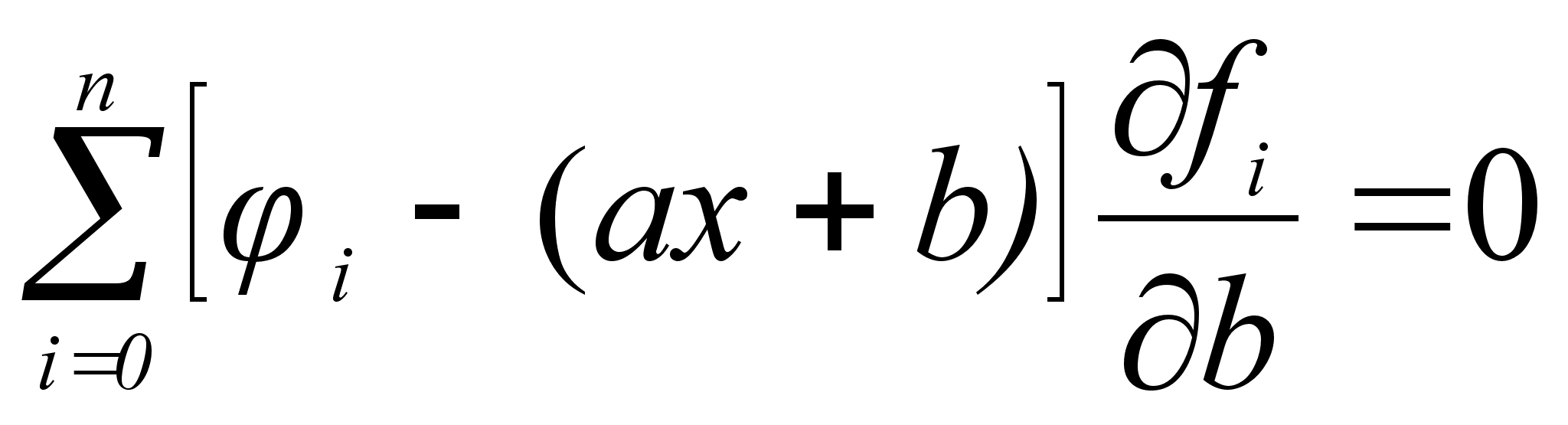
Дифференцируя выражение (106) по а и b, имеем:
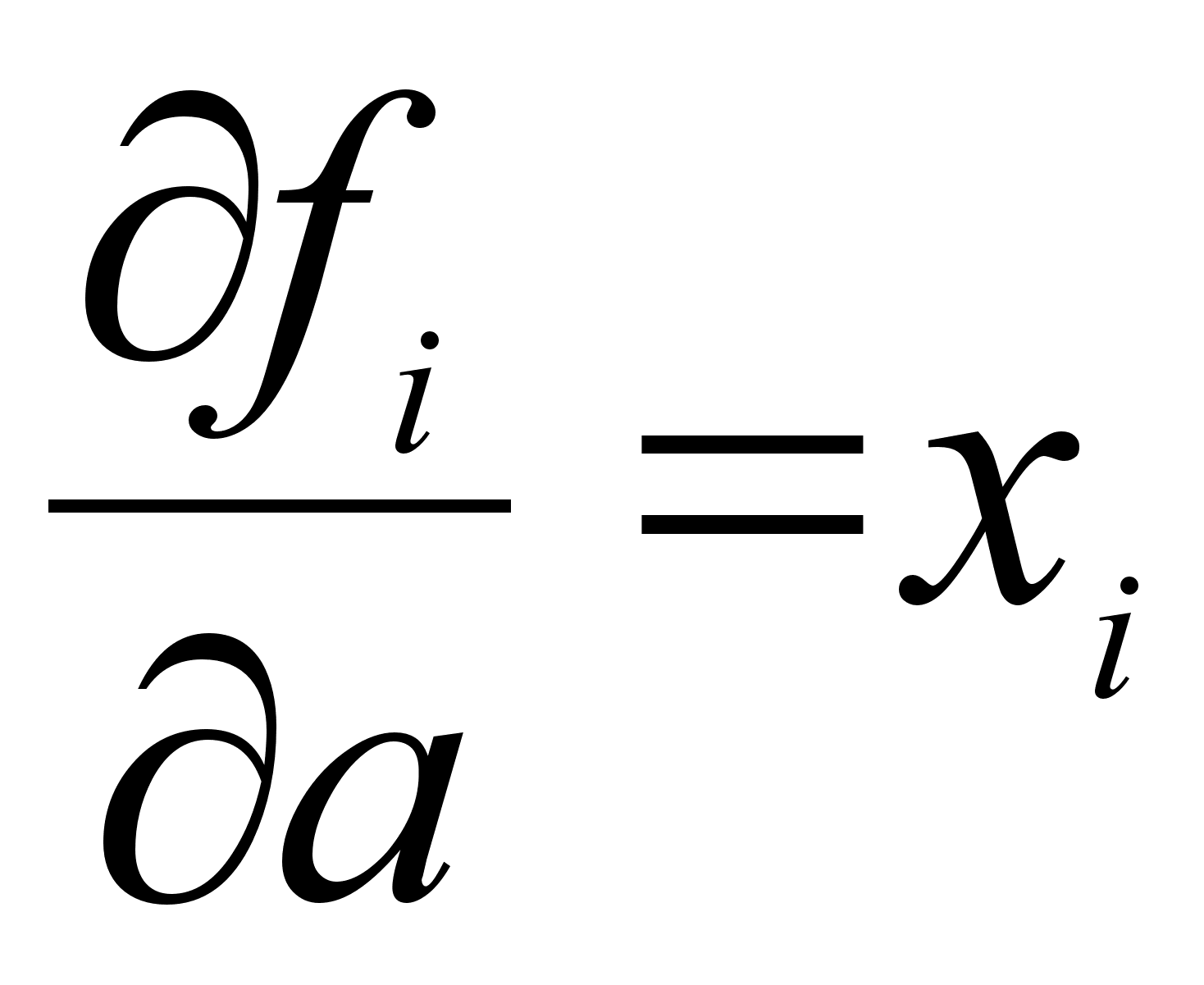

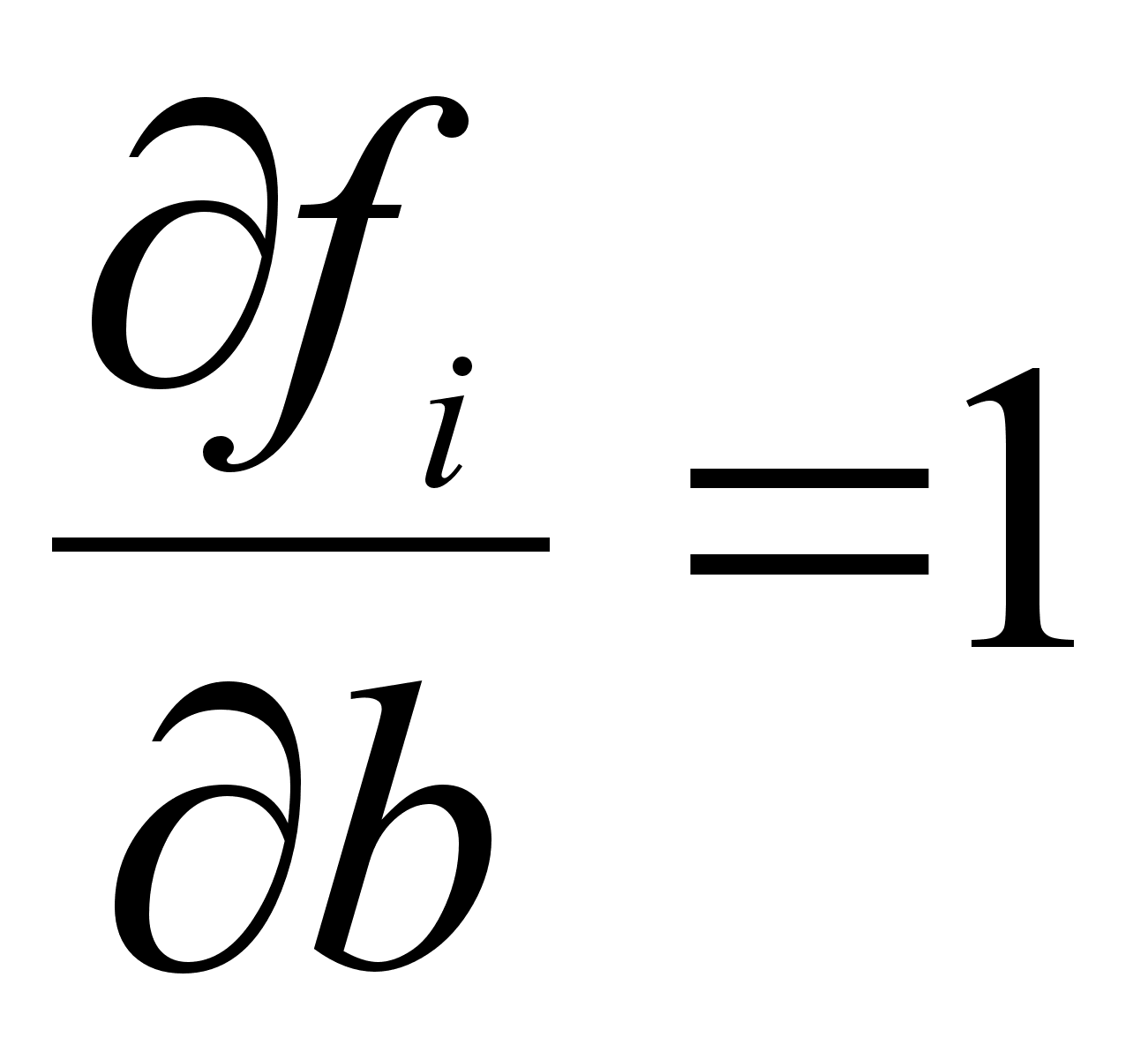
Подставляя в формулы (108), получим два уравнения для определения a и b:
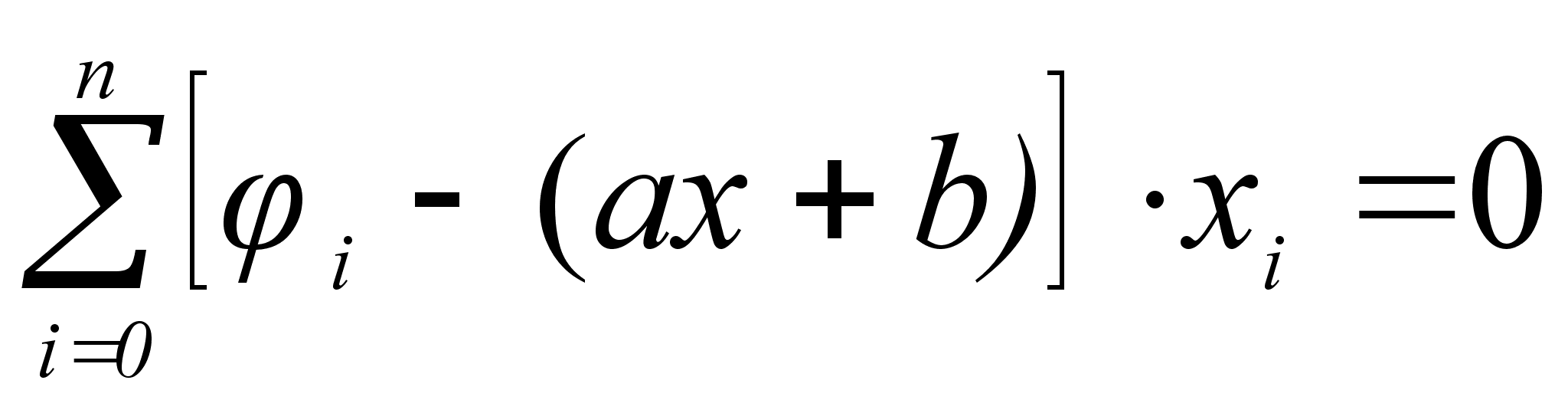 ;
;
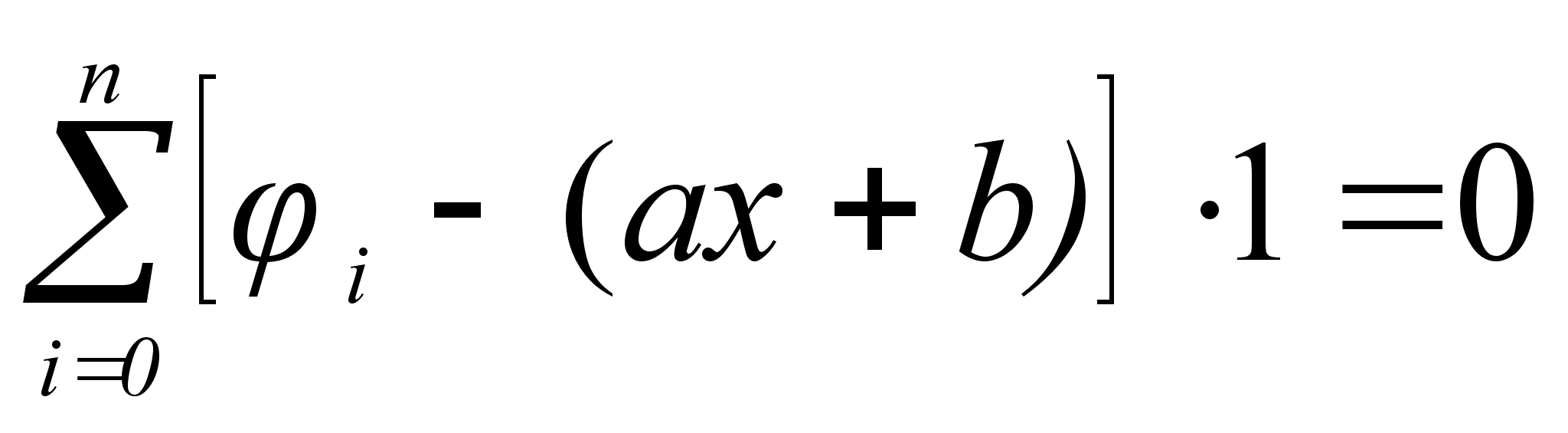 ,
,
или, раскрывая скобки и производя суммирование, получим:
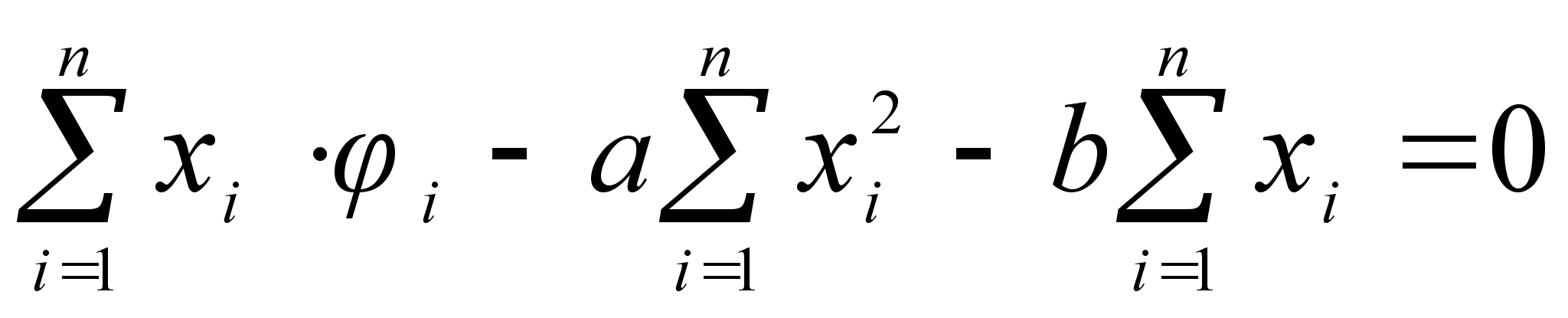

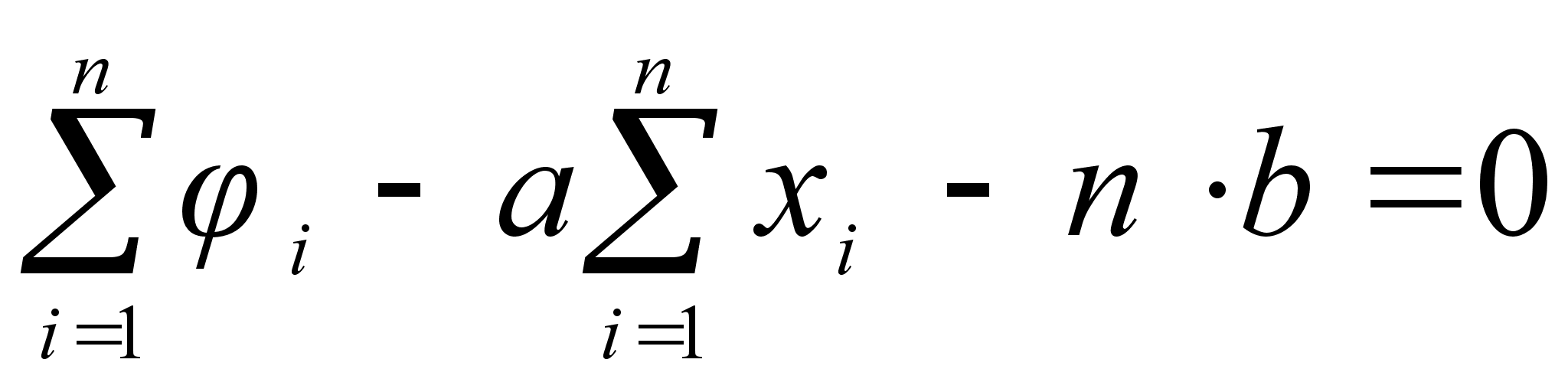
Эти уравнения можно записать иначе:
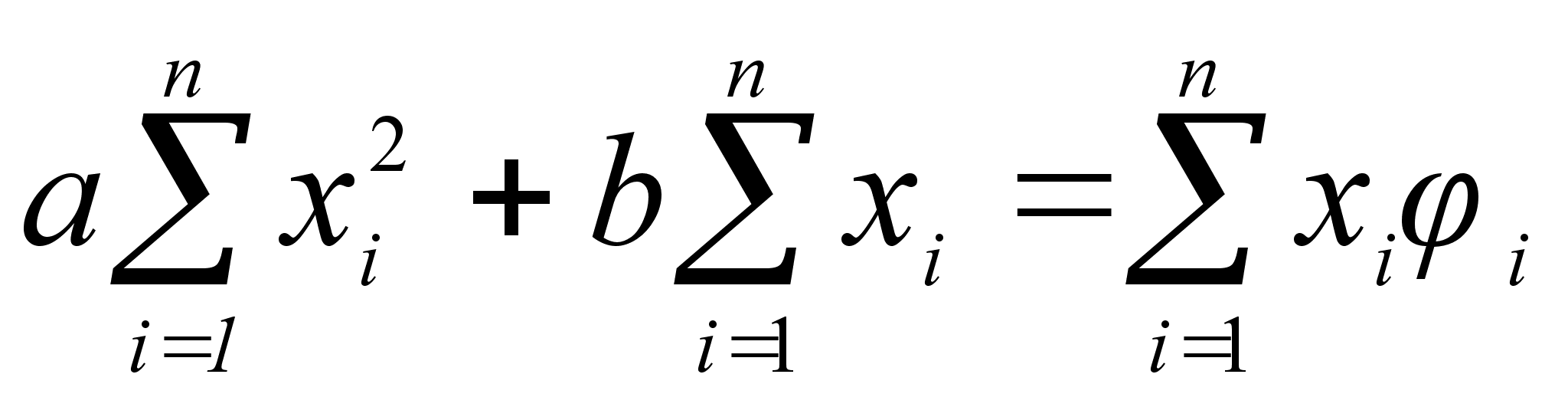

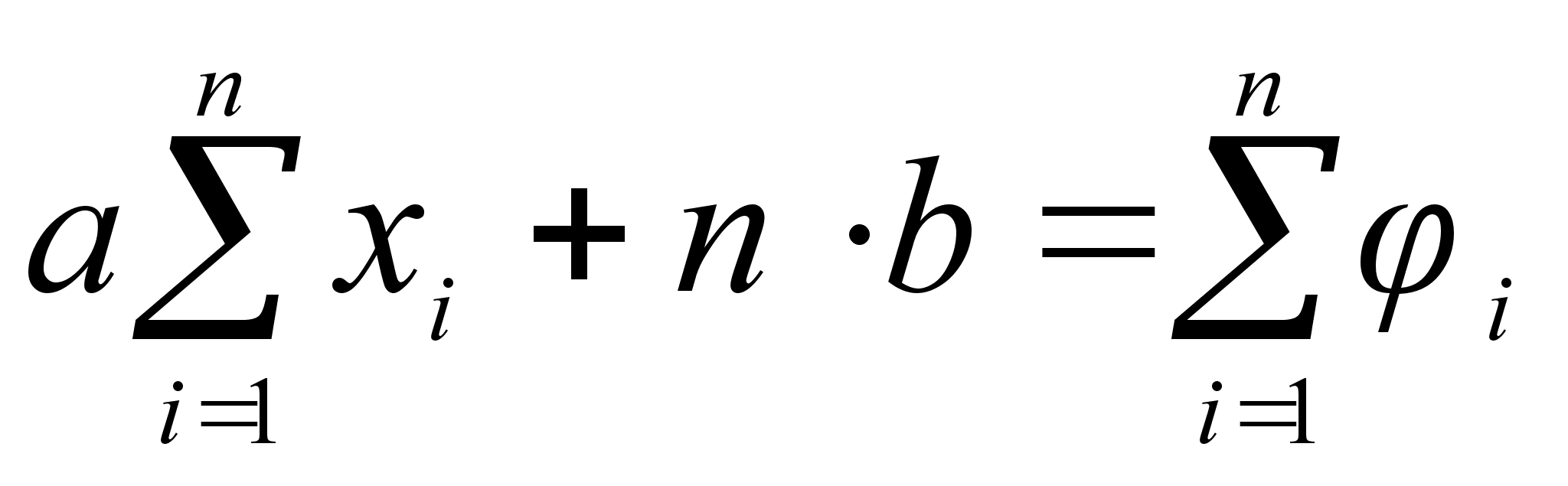
Для вычисления коэффициентов a и b достаточно составить таблицу в соответствии с экспериментальными данными, которая приведена ниже.
Таблица 2 – Исходные данные для вычисления коэффициентов a и b
| Исходные параметры для вычислений |
|
|||||||||
|
|
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 4,5 |
|
|
0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 | 2,85 |
|
|
- - - | - - - | - - - | - - - | - - - | - - - | - - - | - - - | - - - |
|
|
|
- - - | - - - | - - - | - - - | - - - | - - - | - - - | - - - | - - - |
|
Решая систему уравнений (111), подставив в эти уравнения данные из таблицы 2, определим численные значения коэффициентов a и b.
5 ПОДРОБНЫЙ АНАЛИЗ ПРИМЕНИМОСТИ КОНЦЕТРАЦИОННЫХ УРАВНЕНИЙ ДЛЯ ОПИСАНИЯ РЕАЛЬНЫХ СИСТЕМ С РАЗЛИЧНЫМ ХАРАКТЕРОМ ОТКЛОНЕНИЙ ОТ ЗАКОНА РАУЛЯ
5.1 Подробный анализ системы Fe – Cu.
Система Fe– Cu характеризуется положительным отклонением от закона Рауля.
5.1.1 Исходные данные к системе Fe – Cu.
В работе [16] на основе литературных и экспериментальных данных получены уравнения Крупновского для рассматриваемой системы, из которых выведены уравнения коэффициентов активности компонентов:
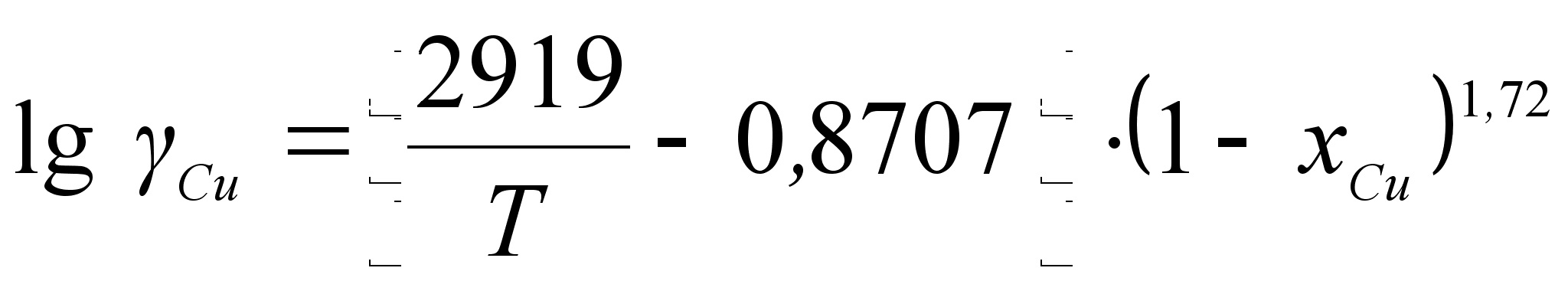
(112)
,
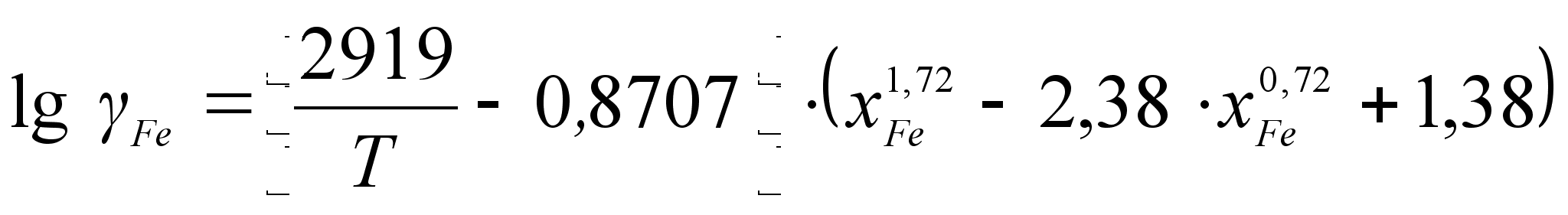
(113)
.По уравнениям (112) и (113) вычислены начальные исходные данные, которые приведены в таблице 3. По данным таблицы 3 построены рисунки 11 и 12.
5.1.2 Корректировка исходных данных
Из сравнения рисунков 11 и 12 видно, что расположение точек на рисунке 12, вычисленных по уравнению (113), в большей степени приближается к прямой линии, чем точки на рисунке 11.
Поэтому дальнейшему математическому анализу подвернем сначала термодинамические характеристики, относящиеся к железу, а затем, на их основании вычислим параметры меди.
Корректировка данных по железу. Обработаем данные таблицы 3 в соответствии с уравнением (106). Чтобы найти коэффициенты a и b, входящие в него, решим систему уравнений (111).

Таблица 3 –Исходные термодинамические характеристики компонентов в системе Fe – Cu.
-
Медь
Железо
xCu
Cu
aCu
Cu
XFe
Fe
aFe
Fe
0,1 3,748 0,3748 1,6311 0,1 4,47 0,447 1,8488 0,2 2,9415 0,5883 1,6853 0,2 3,0095 0,6019 1,7215 0,3 2,3573 0,7072 1,75 0,3 2,228 0,6684 1,6349 0,4 1,9306 0,7722
1,8272 0,4 1,7582 0,7033 1,5676 0,5 1,6173 0,8086 1,9229 0,5 1,4592 0,7296 1,5116 0,6 1,3875 0,8325 2,0469 0,6 1,2637 0,7582 1,4626 0,7 1,221 0,8547 2,2186 0,7 1,136 0,7952 1,4168 0,8 1,1045 0,8836 2,4854 0,8 1,0561 0,8449 1,3652 0,9 1,0306 0,9276 3,0177 0,9 1,0129 0,9116 1,2806
Составим таблицу, подобную таблице 2, с необходимыми параметрами для решения этой системы уравнений.
Таблица 4 – Необходимые параметры для решения системы уравнений (111), относящиеся к характеристикам железа.
Численные значения |
|
|||||||||
|
|
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 4,5 |
|
|
0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 | 2,85 |
|
|
1,8488 | 1,7215 | 1,6349 | 1,5676 | 1,5116 | 1,4626 | 1,4168 | 1,3652 | 1,2806 | 13,8096 |
|
|
0,185 | 0,3443 | 0,4905 | 0,627 | 07558 | 0,8776 | 0,9918 | 1,0922 | 1,1525 | 6,5166 |
Подставляя эти параметры в систему уравнений (111) получаем:
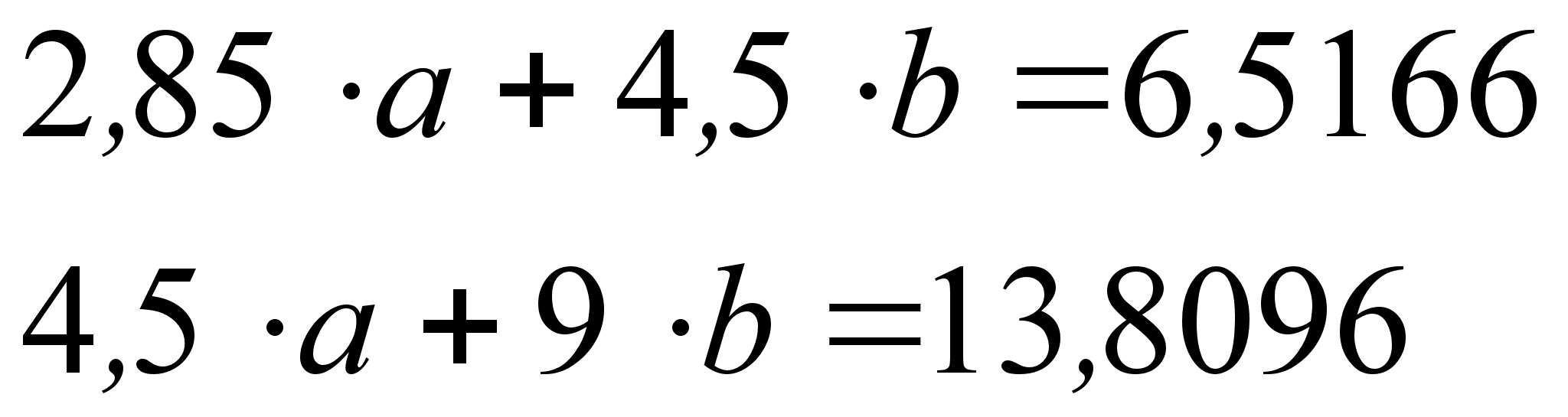

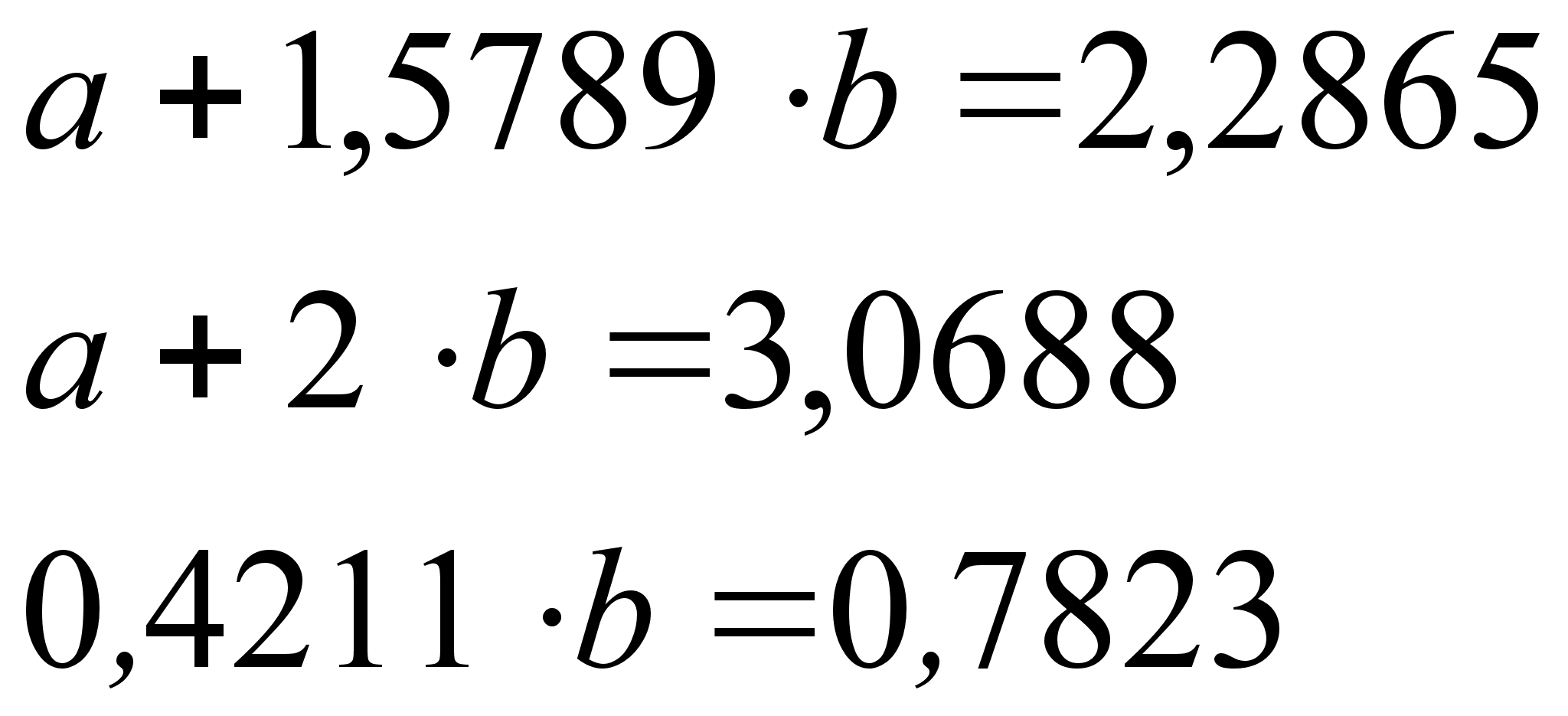
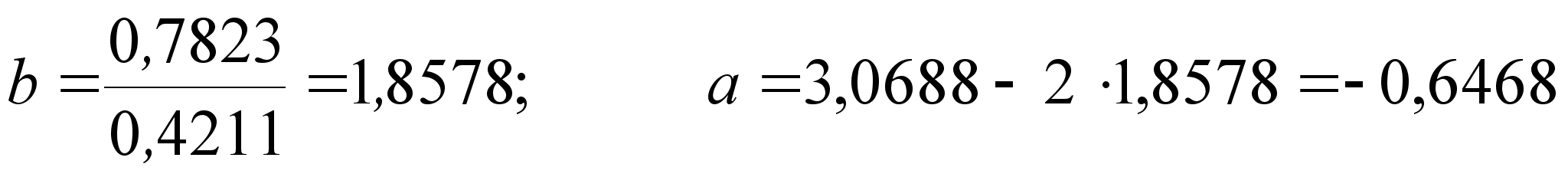
Следовательно, уравнение (106) для железа будет выглядеть так:
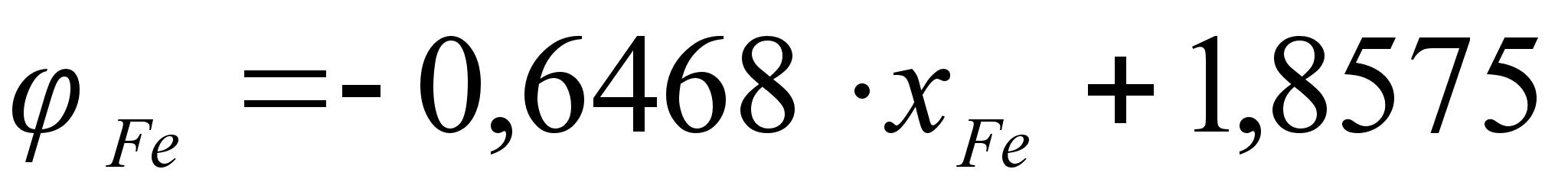
(114)
Из него
видно, что при
xFe=0:
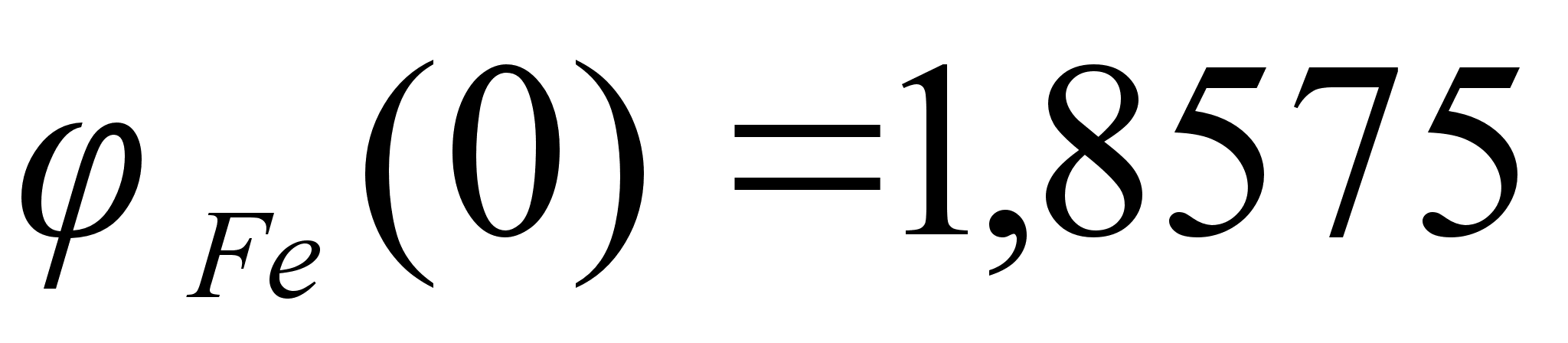 ,
а при xFe=1:
,
а при xFe=1:
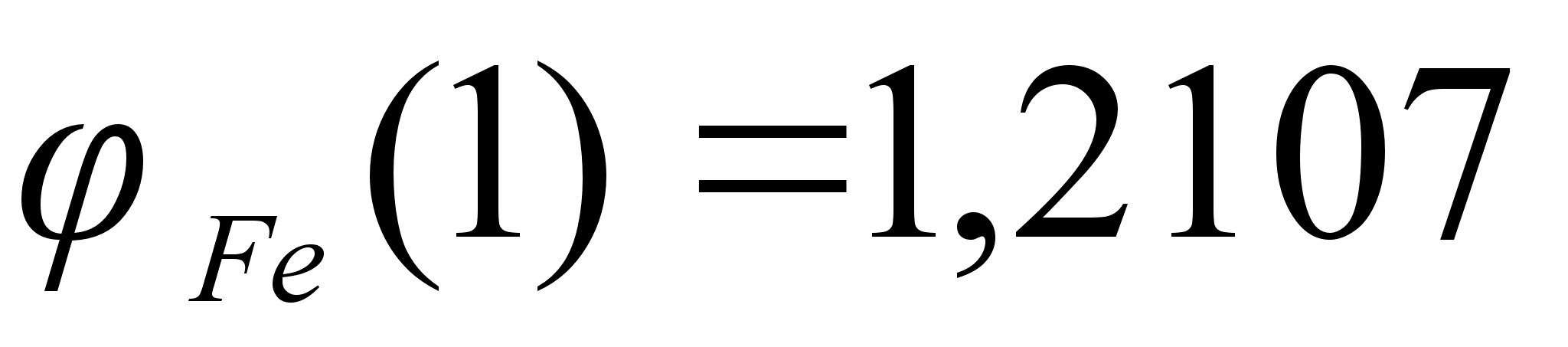 .
.
Корректировка данных по меди. Для меди ход решения будет аналогичным, поэтому запишем лишь конечное выражение, с учетом найденных коэффициентов а и b:
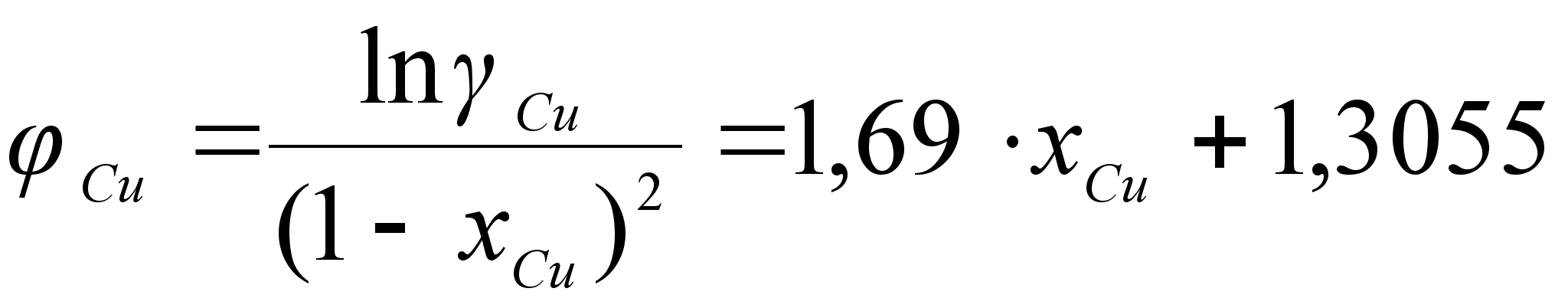
(115)
из
которого следует,
что
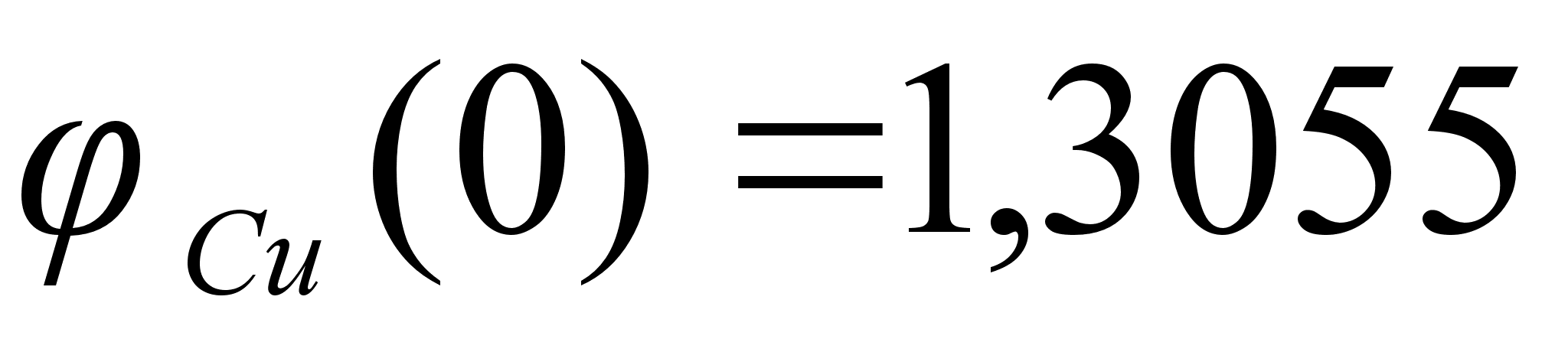 ,
,
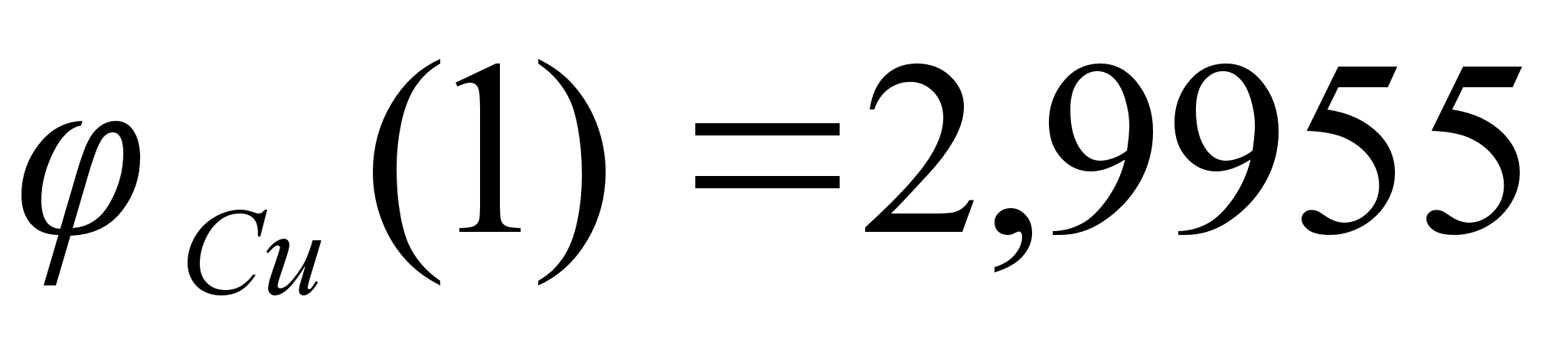 .
.
Значения
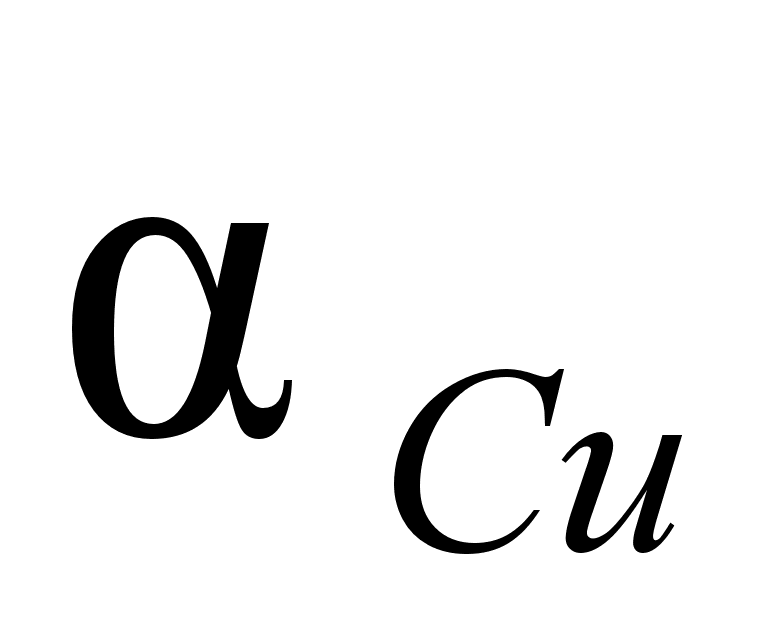 и
и
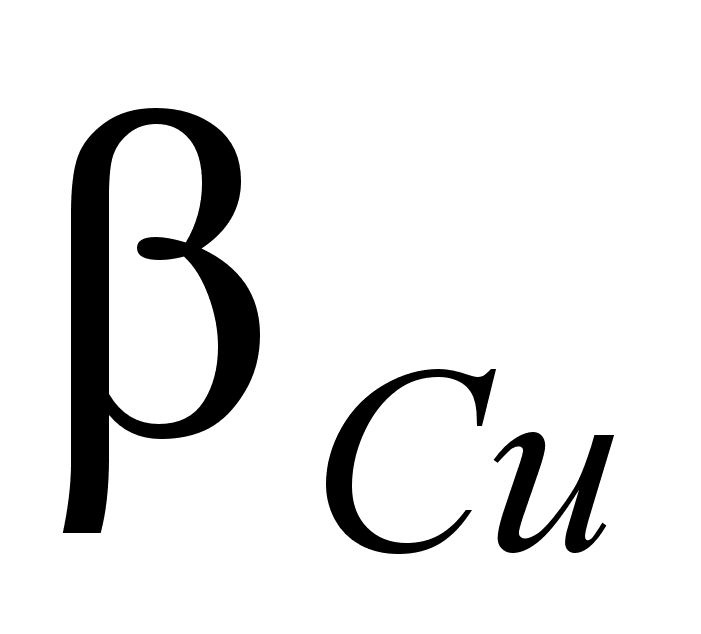 определим из
уравнений (102)
и (103):
определим из
уравнений (102)
и (103):
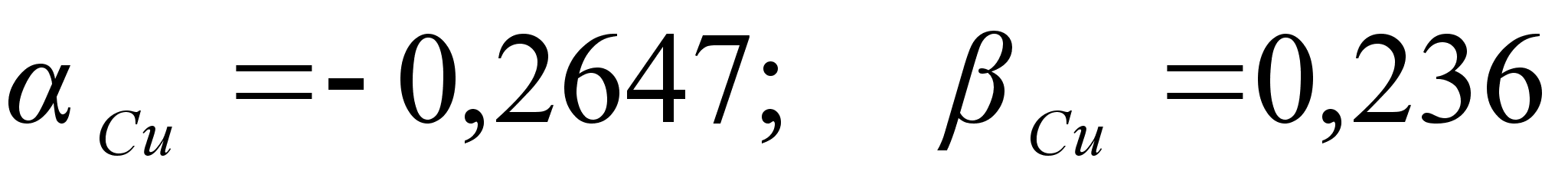
Линейные зависимости, в соответствии с уравнениями (114) и (115), изображены на рисунках 12 и 11 соответственно. В таблице 5 приведены скорректированные исходные данные по aFe, а также некоторым другим характеристикам.
Таблица 5 – Скорректированные исходные термодинамические характеристики для железа.
|
xFe |
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
|
Fe |
1,793 | 1,728 | 1,663 | 1,599 | 1,534 | 1,469 | 1,405 | 1,340 | 1,275 |
|
lnFe |
1,452 | 1,106 | 0,815 | 0,576 | 0,384 | 0,235 | 0,126 | 0,054 | 0,013 |
|
Fe |
4,272 | 3,022 | 2,259 | 1,778 | 1,467 | 1,265 | 1,135 | 1,055 | 1,013 |
|
aFe |
0,427 | 0,604 | 0,678 | 0,711 | 0,734 | 0,759 | 0,794 | 0,844 | 0,916 |
По данным таблицы 5 построен рисунок 13.
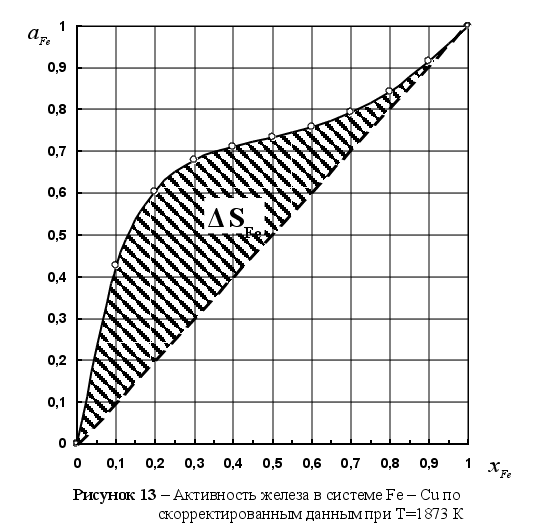
5.1.3
Вычисление
значений Аi,
Bi,
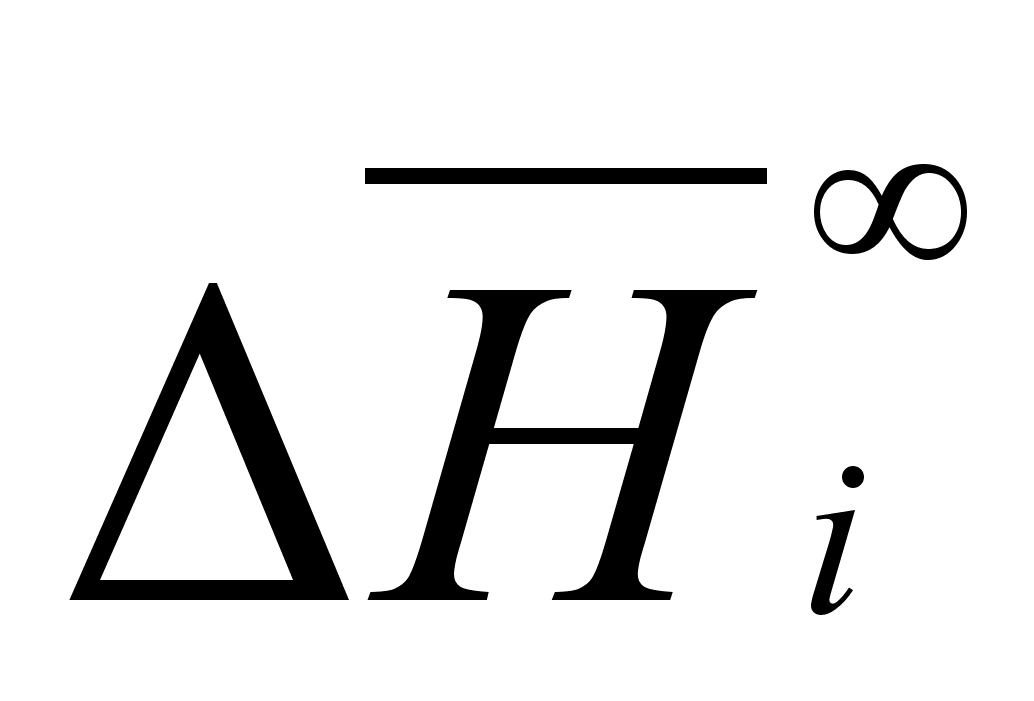 и
и
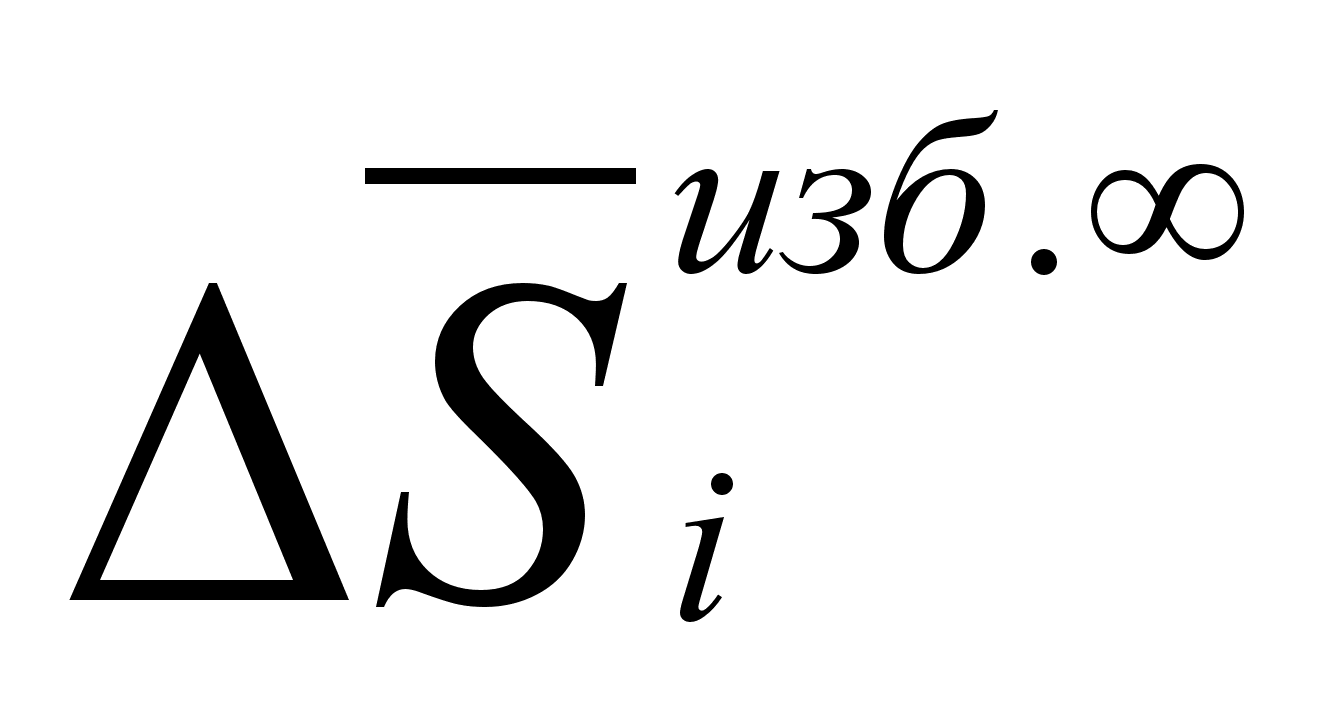 .
.
Железо.
Как было сказано
выше,
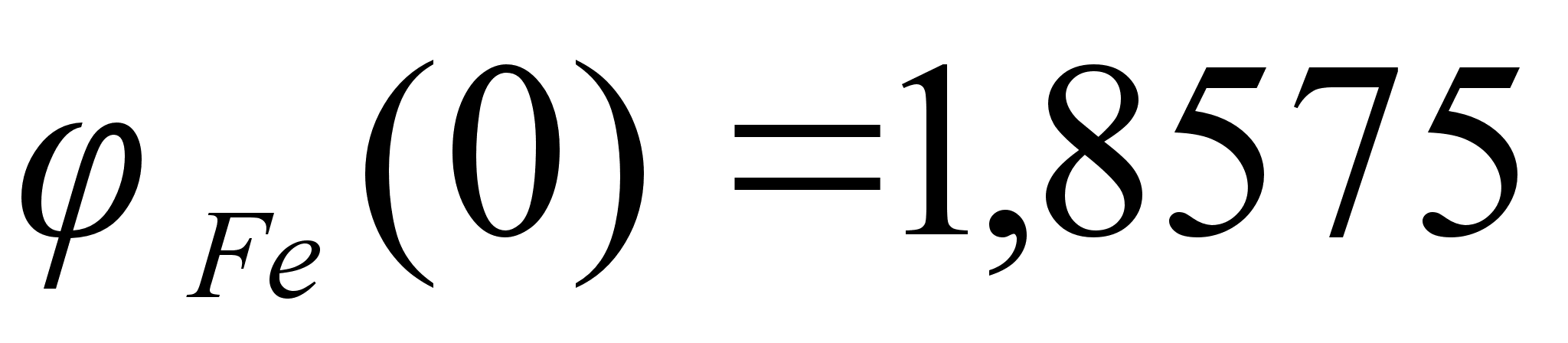 ;
;
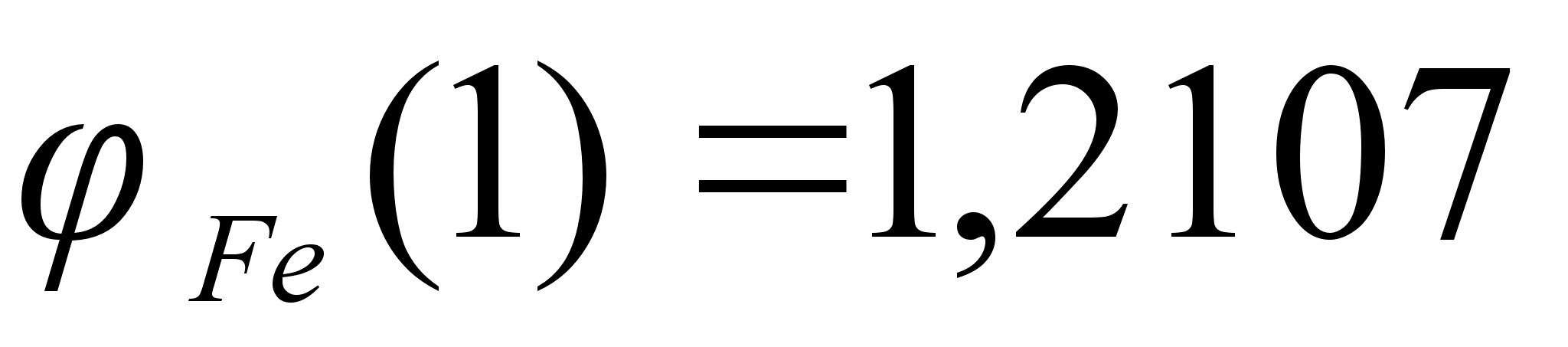 .
Значение величин
AFe
и BFe
найдем из уравнения
(98).
.
Значение величин
AFe
и BFe
найдем из уравнения
(98).
При xFe=0
имеем:
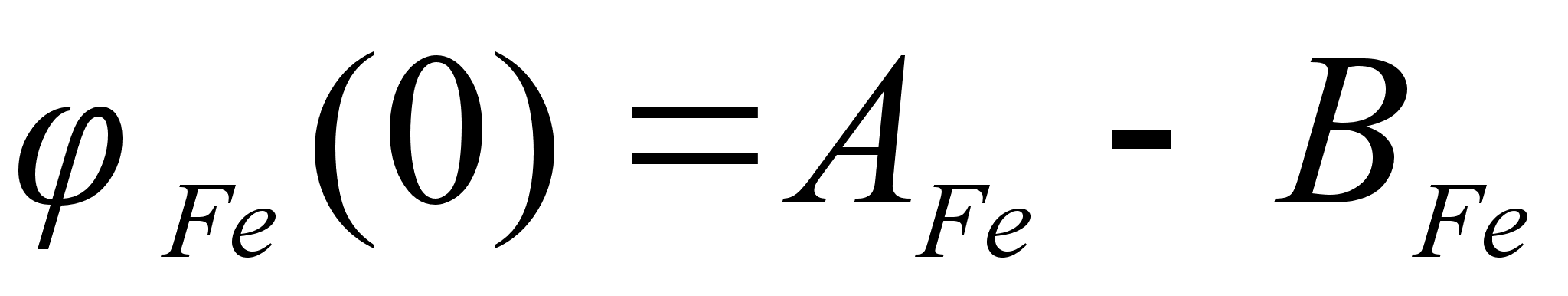 .
.
При xFe=1
имеем:
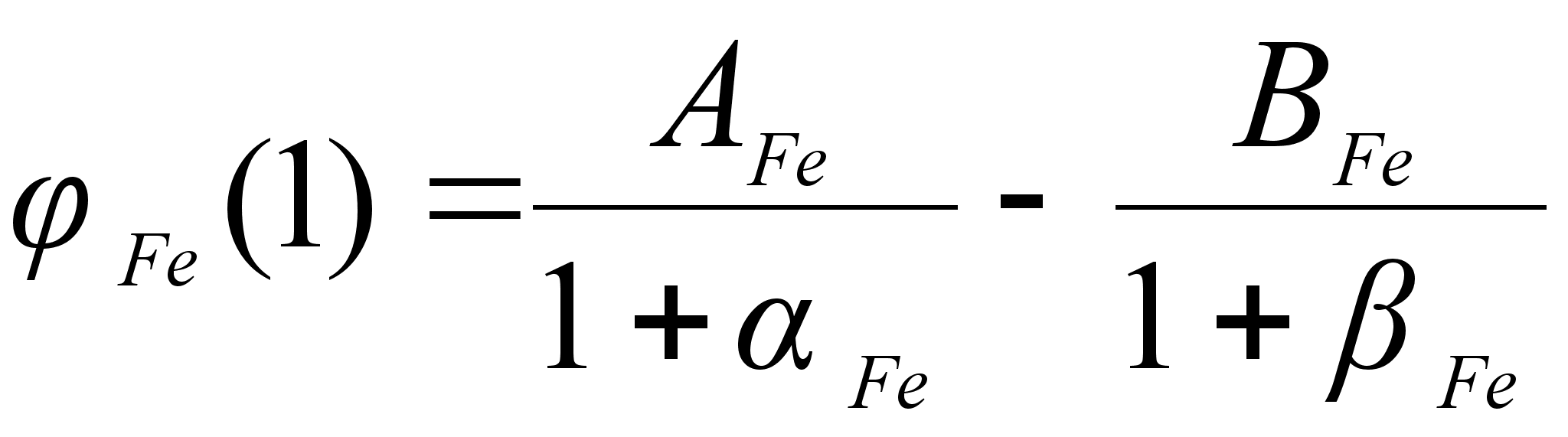 .
.
Вычислим:
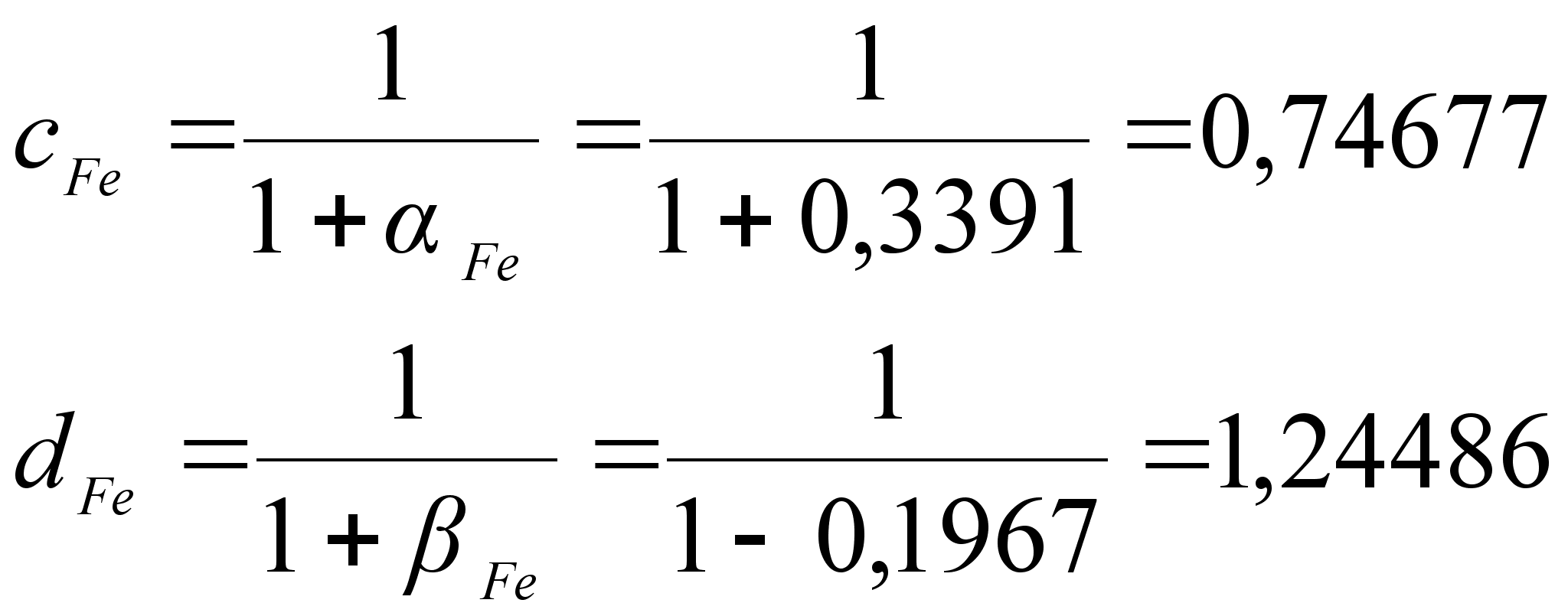
Тогда:
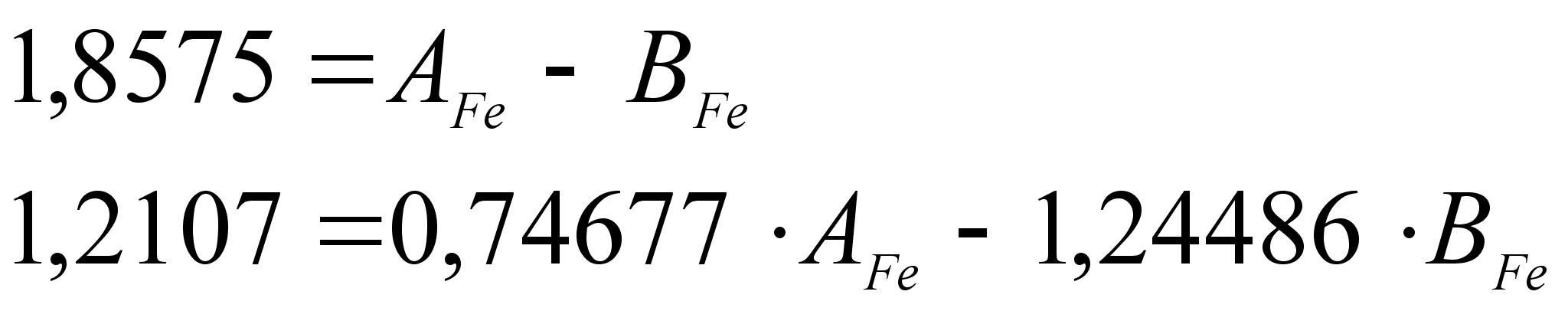

Решая систему уравнений (116), находим: AFe=2,2117; BFe=0,3542.
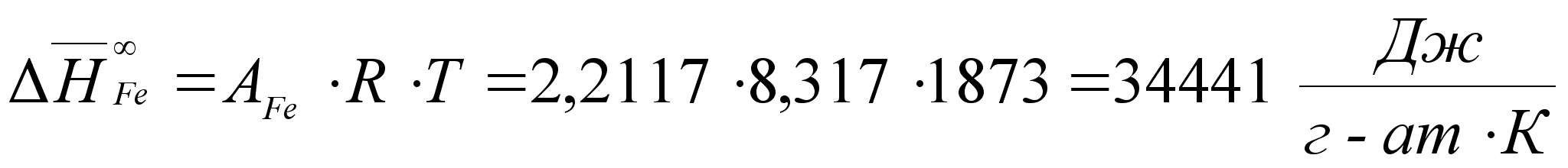 ,
,
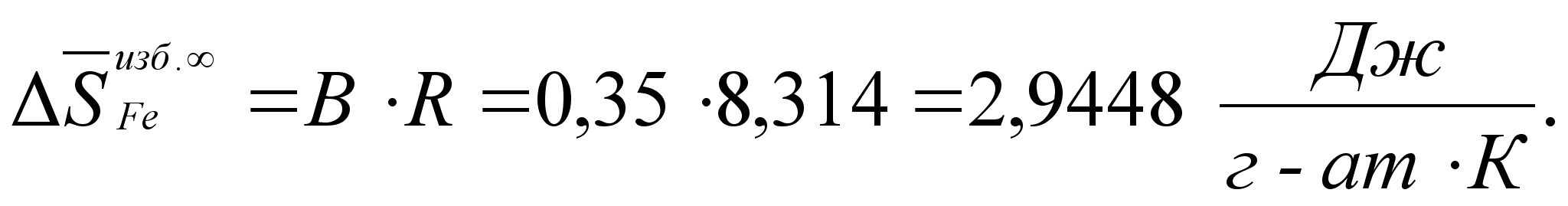
Медь. Зная характеристики железа в растворе Fe – Cu, вычислим термодинамические функции меди.
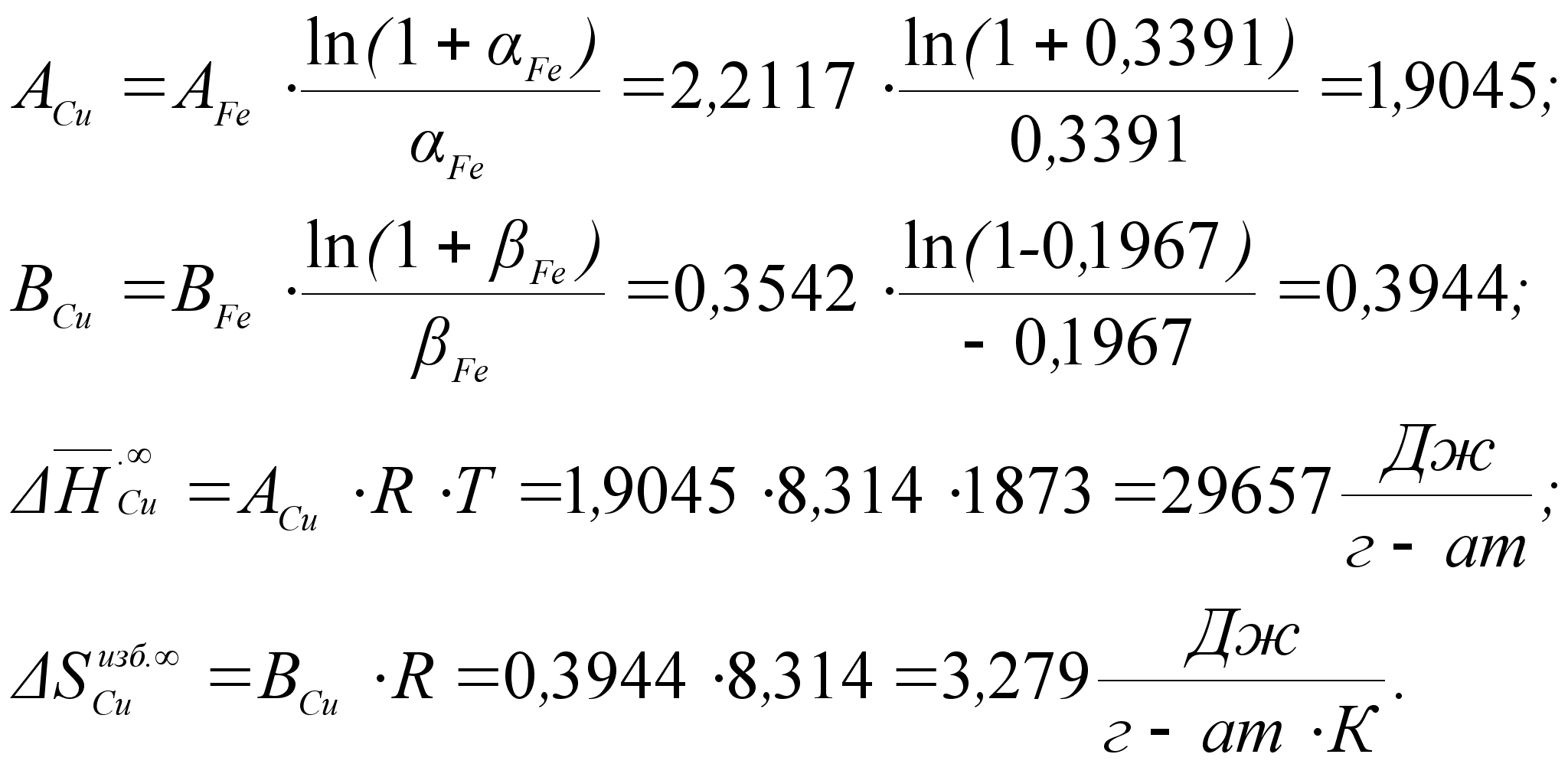
Окончательные результаты термодинамического анализа системы Fe – Cu приведены в таблицах 6 и 7.
Вывод: показана применимость концентрационных уравнений для нахождения термодинамических характеристик растворов с отрицательным отклонением от идеальности.
5.2 Подробный анализ системы Fe – Si.
Расплав Fe – Si представляет собой типичный пример системы с отрицательным отклонением от закона Рауля.
5.2.1 Исходные данные.
Исходные данные по активности компонентов в расплаве Fe – Si при Т=1873 К приведены в таблице 8. Все расчеты выполнены по данным для кремния.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
1,8575 |
1,778 |
1,703 |
1,631 |
1,563 |
1,498 |
1,436 |
1,377 |
1,319 |
1,264 |
1,2107 |
|
|
1,8575 |
1,440 |
1,01 |
0,799 |
0,563 |
0,375 |
0,230 |
0,124 |
0,053 |
0,013 |
0,0 |
|
|
6,408 |
4,221 |
2,973 |
2,224 |
1,755 |
1,454 |
1,258 |
1,132 |
1,054 |
1,013 |
1,0 |
|
|
0,0 |
0,422 |
0,595 |
0,667 |
0,702 |
0,727 |
0,755 |
0,792 |
0,843 |
0,911 |
1,0 |
|
|
34441 |
26982 |
20642 |
15318 |
10918 |
7362 |
4579 |
2505 |
1084 |
264 |
0 |
|
|
2,9448 |
2,433 |
1,962 |
1,533 |
1,151 |
0,817 |
0,534 |
0,307 |
0,14 |
0,036 |
0,0 |
Таблица 7 – Термодинамические характеристики меди в расплаве Fe – Cu при Т=1873 К.
| Функция |
Концентрация меди в расплаве - xCu |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
1,51 |
1,571 |
1,634 |
1,7 |
1,77 |
1,842 |
1,919 |
1,999 |
2,084 |
2,175 |
2,271 |
|
|
1,51 |
1,272 |
1,046 |
0,833 |
0,637 |
0,461 |
0,307 |
0,18 |
0,083 |
0,022 |
0,0 |
|
|
4,527 |
3,57 |
2,846 |
2,301 |
1,891 |
1,585 |
1,359 |
1,197 |
1,087 |
1,022 |
1,0 |
|
|
0,0 |
0,357 |
0,569 |
0,69 |
0,756 |
0,792 |
0,816 |
0,838 |
0,87 |
0,92 |
1,0 |
|
|
29657 |
24675 |
20041 |
15785 |
11941 |
8545 |
5641 |
3276 |
1505 |
389 |
0 |
|
|
3,279 |
2,595 |
2,004 |
1,5 |
1,079 |
0,733 |
0,46 |
0,253 |
0,11 |
0,027 |
0,0 |
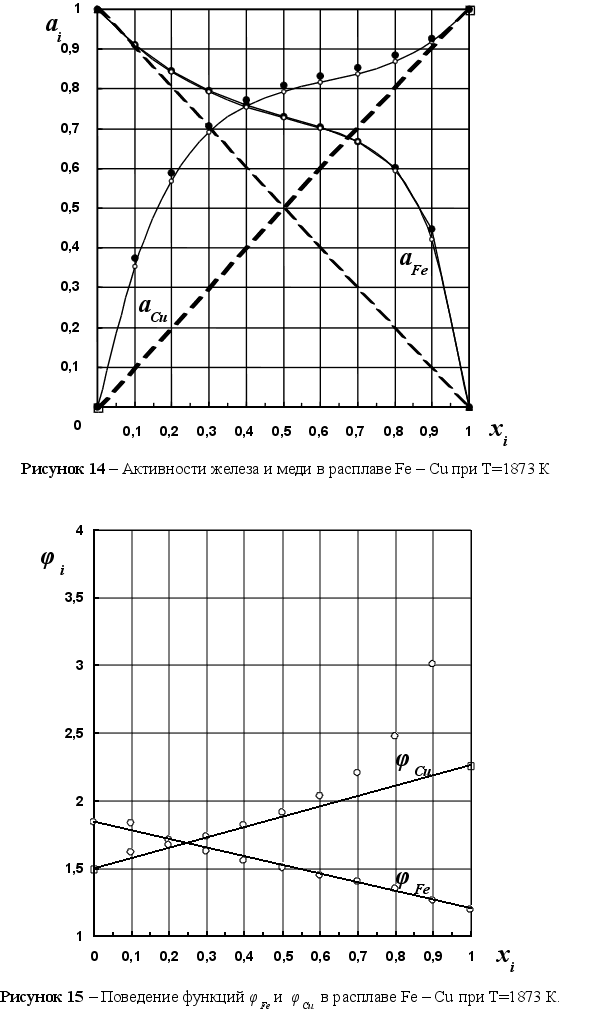
|
Лит. источник |
[7] |
[10] |
[11] |
[12] |
[13] |
[14] |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,1 | 0,0008 | 0,823 | 0,002 | 0,835 | 0,009 | 0,820 | 0,0010 | 0,8600 | 0,0008 | 0,8100 | 0,0010 | 0,8590 |
| 0,2 | 0,0083 | 0,556 | 0,009 | 0,600 | 0,026 | 0,608 | 0,0510 | 0,6489 | 0,0043 | 0,6650 | 0,0045 | 0,6650 |
| 0,3 | 0,0300 | 0,363 | 0,031 | 0,361 | 0,076 | 0,448 | 0,0198 | 0,4047 | 0,0250 | 0,4030 | 0,0193 | 0,4320 |
| 0,4 | 0,0800 | 0,213 | 0,083 | 0,160 | 0,164 | 0,264 | 0,0669 | 0,2030 | 0,0900 | 0,1900 | 0,0481 | 0,2130 |
| 0,5 | 0,1900 | 0,106 | 0,197 | 0,062 | 0,285 | 0,137 | 0,1779 | 0,0858 | 0,2340 | 0,0930 | 0,1620 | 0,0953 |
| 0,6 | 0,4150 | 0,040 | 0,427 | 0,027 | 0,426 | 0,056 | 0,3570 | 0,0344 | 0,4550 | 0,0450 | 0,3780 | 0,0344 |
| 0,7 | 0,6440 | 0,018 | 0,623 | 0,011 | 0,525 | 0,033 | 0,5567 | 0,0142 | 0,6240 | 0,0190 | 0,5820 | 0,0147 |
| 0,8 | 0,7800 | 0,010 | 0,745 | 0,005 | 0,624 | 0,022 | 0,7379 | 0,0058 | 0,7700 | 0,0070 | 0,7300 | 0,0074 |
| 0,9 | 0,8970 | 0,005 | 0,882 | 0,002 | 0,830 | 0,010 | 0,8890 | 0,0020 | 0,8850 | 0,0019 | 0,8790 | 0,0032 |
Таблица 8 - Активности компонентов в расплаве Fe – Si при Т=1873 К.
|
Лит. источник |
[17] |
[18] |
[19] |
[21] |
[22] |
[23] |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,1 | 0,00102 | 0,8795 | 0,00098 | - | 0,00115 | 0,8350 | 0,002 | 0,850 | 0,00158 | 0,8210 | 0,00006 | - |
| 0,2 | 0,00324 | 0,7130 | 0,00300 | - | 0,00716 | 0,3083 | 0,008 | 0,600 | 0,01000 | 0,6069 | 0,00040 | - |
| 0,3 | 0,01850 | 0,3936 | 0,01740 | - | 0,02763 | 0,3891 | 0,025 | 0,320 | 0,02860 | 0,3847 | 0,00189 | - |
| 0,4 | 0,11270 | 0,1542 | 0,10900 | - | 0,08300 | 0,2154 | 0,125 | 0,130 | 0,06050 | 0,1691 | 0,01004 | - |
| 0,5 | 0,34590 | 0,0601 | 0,34400 | - | 0,20330 | 0,1033 | 0,347 | 0,060 | 0,15450 | 0,0706 | 0,05250 | - |
| 0,6 | 0,51070 | 0,0382 | 0,50500 | - | 0,40490 | 0,0447 | 0,488 | 0,040 | 0,37860 | 0,0365 | 0,19400 | - |
| 0,7 | 0,62390 | 0,0267 | 0,63100 | - | 0,64000 | 0,0192 | 0,630 | 0,025 | 0,59580 | 0,0244 | 0,45100 | - |
| 0,8 | 0,74660 | 0,0155 | 0,74000 | - | 0,77370 | 0,0095 | 0,750 | 0,018 | 0,72960 | 0,0121 | 0,71700 | - |
| 0,9 | 0,87950 | 0,0060 | 0,88000 | - | 0,89060 | 0,0057 | 0,870 | 0,005 | 0,85950 | 0,0050 | 0,86600 | - |
Продолжение таблицы 8.
Термодинамические характеристики для железа получены путем вычислений, исходя из соответствующих характеристик кремния, по формулам, приведенным здесь ранее.
Для вычисления термодинамических характеристик используем основное уравнение (98).
В таблице
9 приведены
значения функции
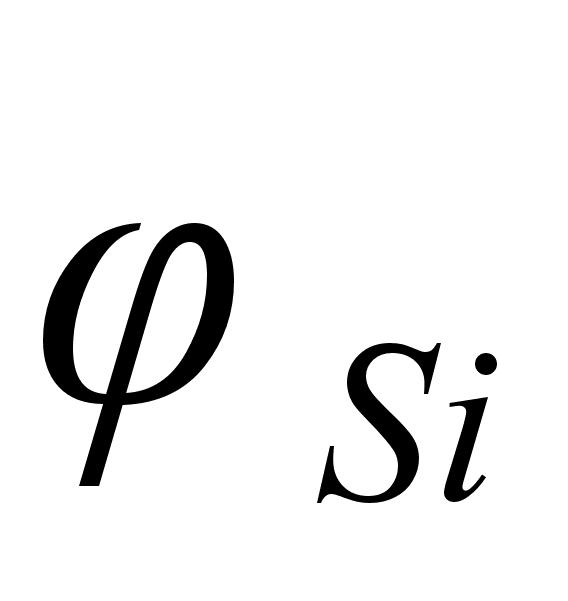 ,
вычисленные
по данным таблицы
8. На рисунках
(16 – 27) представлены
графики этой
функции, построенные
по данным таблицы
9. Точки, взятые
на графике в
«кружок», при
дальнейшей
математической
обработке не
учитывались.
,
вычисленные
по данным таблицы
8. На рисунках
(16 – 27) представлены
графики этой
функции, построенные
по данным таблицы
9. Точки, взятые
на графике в
«кружок», при
дальнейшей
математической
обработке не
учитывались.
5.2.2 Математическая обработка исходных литературных данных
Математическую обработку данных таблицы 9 производим в соответствии с уравнением (106) по методу наименьших квадратов. Требуется подобрать значения коэффициентов а и b в линейной функции, отображающей экспериментальные данные, приведенные в таблице 9 и на рисунках (16 – 27).
Проведенный анализ показал, что все рассматриваемые системы могут быть описаны уравнением:

(116)
Вычисленные
значения
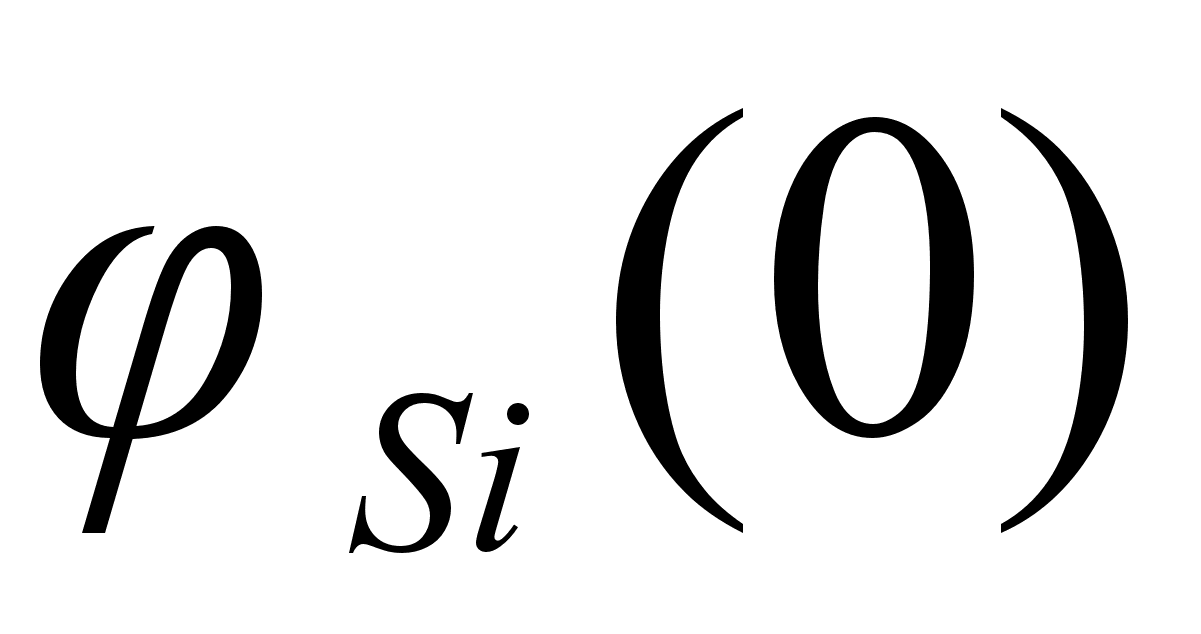 приведены в
таблице 10. На
рисунках (16 –
27) пунктирными
линиями нанесены
значения
приведены в
таблице 10. На
рисунках (16 –
27) пунктирными
линиями нанесены
значения
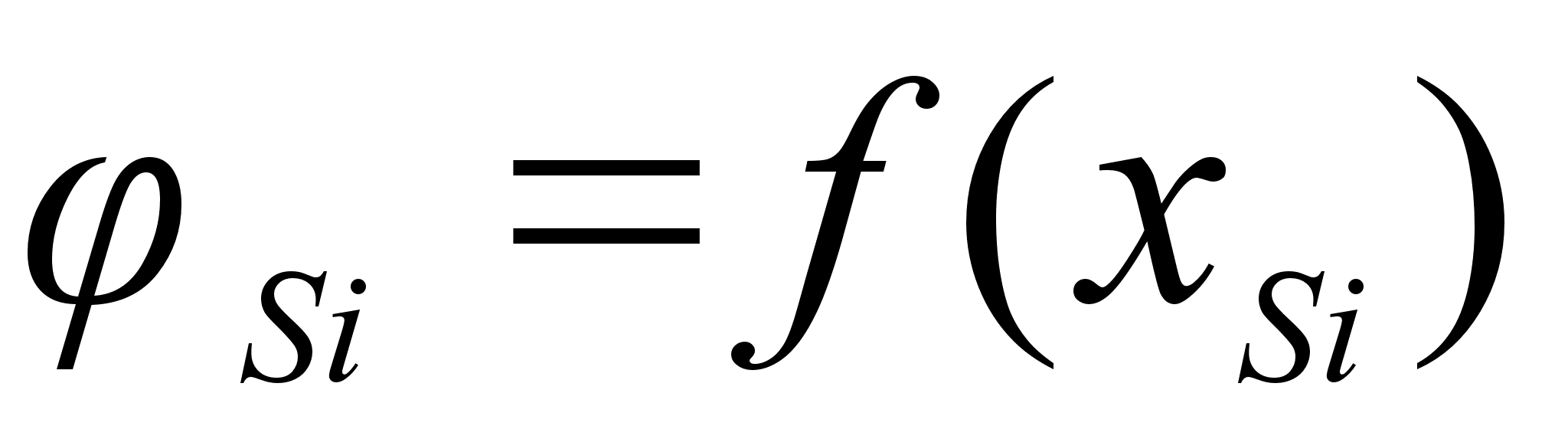 в соответствии
с уравнением
(120). Как следует
из уравнения
(116), значение
функции
в соответствии
с уравнением
(120). Как следует
из уравнения
(116), значение
функции
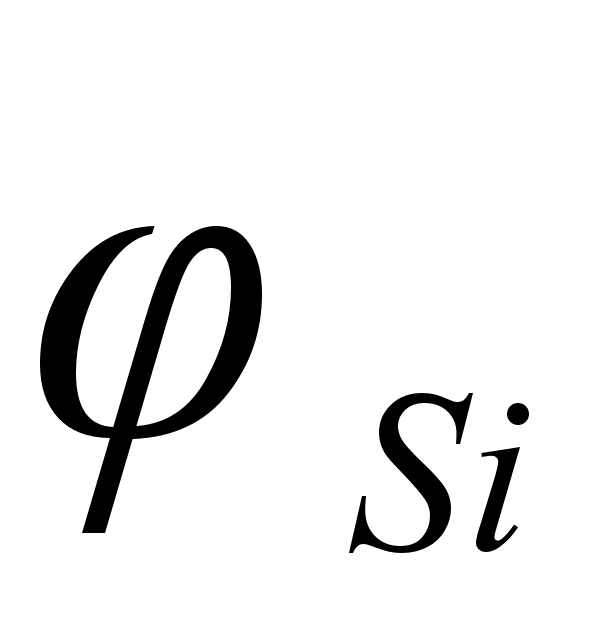 при
при
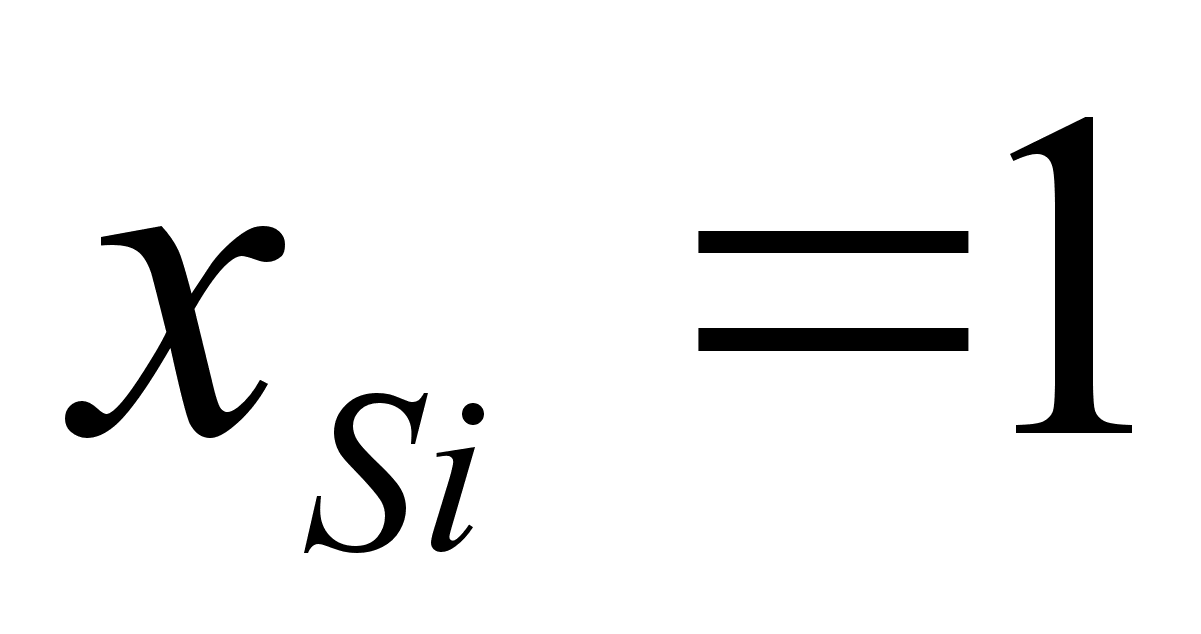 равно нулю.
Следовательно,
основным критерием
отбора наиболее
достоверных
данных из
рассматриваемых
литературных
источников
является величина
равно нулю.
Следовательно,
основным критерием
отбора наиболее
достоверных
данных из
рассматриваемых
литературных
источников
является величина
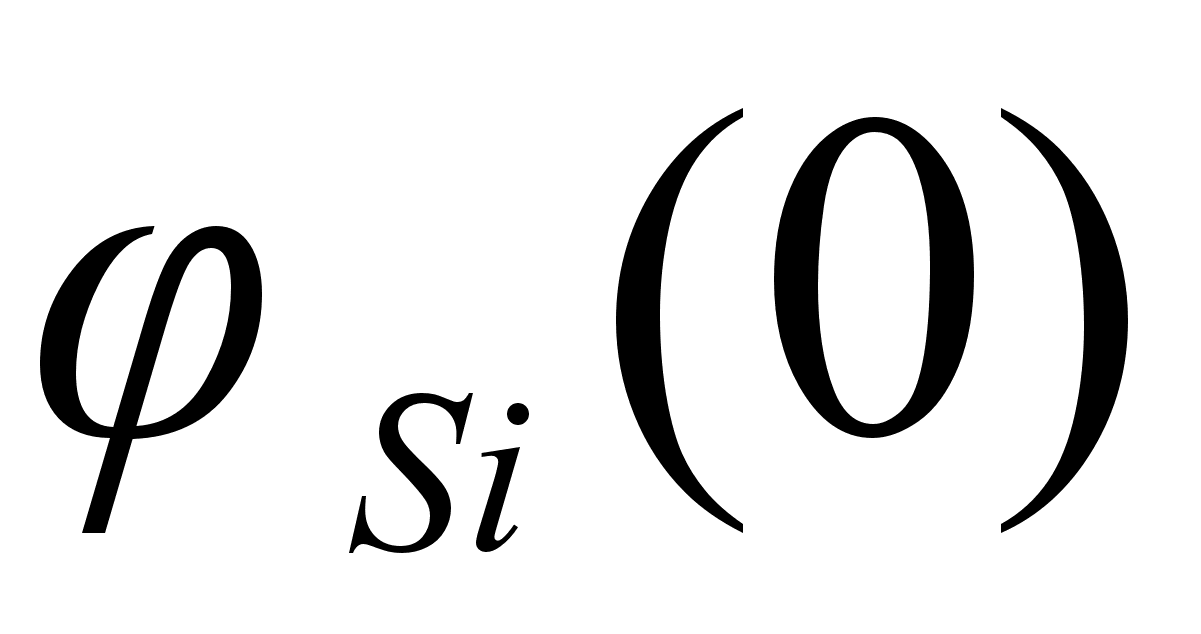 .
.
Из таблицы 10 видно, что данные [23] явно выпадают из общего ряда данных, поэтому в дальнейших расчетах мы их не учитываем.
Считая
величину
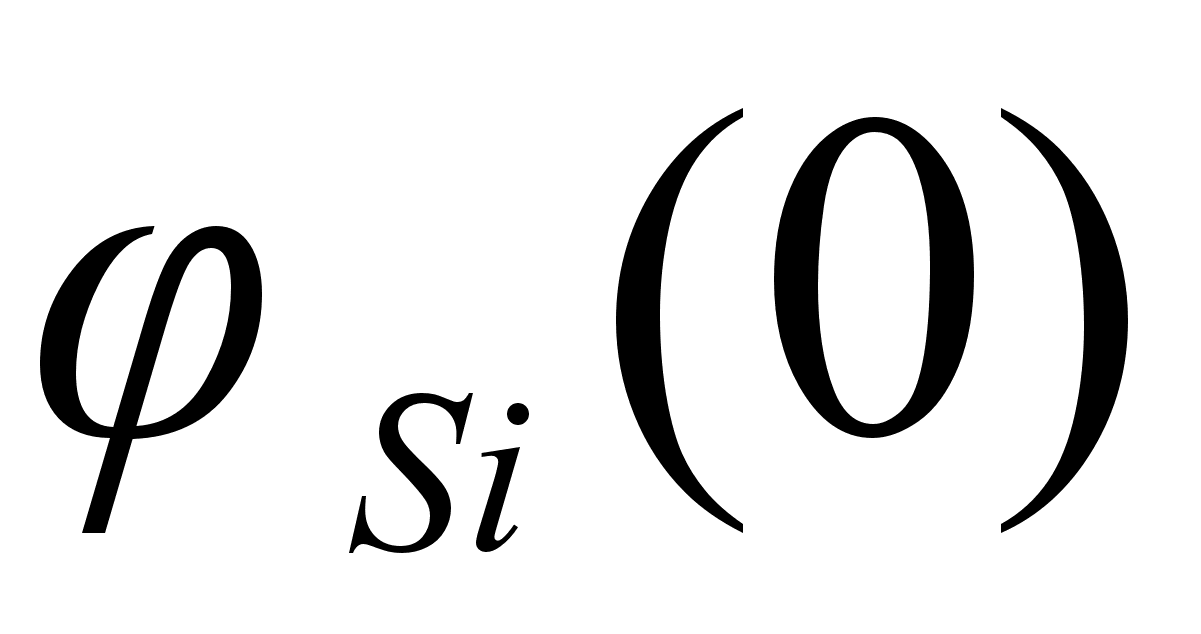 случайной, для
следующего
этапа отбора
исходных данных,
построим гистограмму
(см. рисунок
28).
случайной, для
следующего
этапа отбора
исходных данных,
построим гистограмму
(см. рисунок
28).
Таблица
9 – Значения
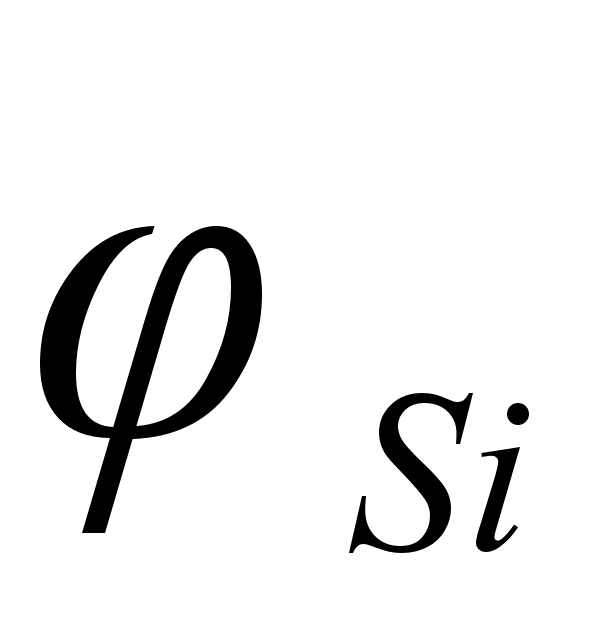 по
данным литературных
источников
по
данным литературных
источников
лит. источник |
значение концентрации Si | ||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| [7] | -5,961 | -4,972 | -4,699 | -4,471 | -3,870 | -2,304 | -0,926 | -0,633 | -0,334 |
| [10] | -4,830 | -4,845 | -4,632 | -4,368 | -3,726 | -1,126 | -1,295 | -1,781 | -2,020 |
| [11] | -2,973 | -3,188 | -2,802 | -2,477 | -2,248 | -2,141 | -3,196 | -6,212 | -8,097 |
| [12] | -5,568 | -5,733 | -5,547 | -4,967 | -4,134 | -3,245 | -2,545 | -2,020 | -1,230 |
| [13] | -5,960 | -6,000 | -5,070 | -4,140 | -2,890 | -1,730 | -1,280 | -0,950 | -1,700 |
| [14] | -5,658 | -5,928 | -5,599 | -5,884 | -4,508 | -2,888 | -2,051 | -2,289 | -2,361 |
| [17] | -5,661 | -6,442 | -5,686 | -3,519 | -1,474 | -1,007 | -1,279 | -1,727 | -2,304 |
| [18] | -5,710 | -6,550 | -5,810 | -3,610 | -1,500 | -1,080 | -1,150 | -1,950 | -2,250 |
| [19] | -5,513 | -5,203 | -4,867 | -4,368 | -3,600 | -2,458 | -0,996 | -0,836 | -1,050 |
| [21] | -1,711 | -4,681 | -5,071 | -3,231 | -1,461 | -1,291 | -1,171 | -1,613 | -3,390 |
| [22] |
-5,121 |
-4,681 | -4,797 | -5,247 | -4,698 | -2,871 | -1,791 | -2,303 | -4,604 |
| [23] | -9,159 | -9,710 | -10,341 | -10,236 | -9,015 | -7,057 | -4,885 | -2,738 | -3,851 |
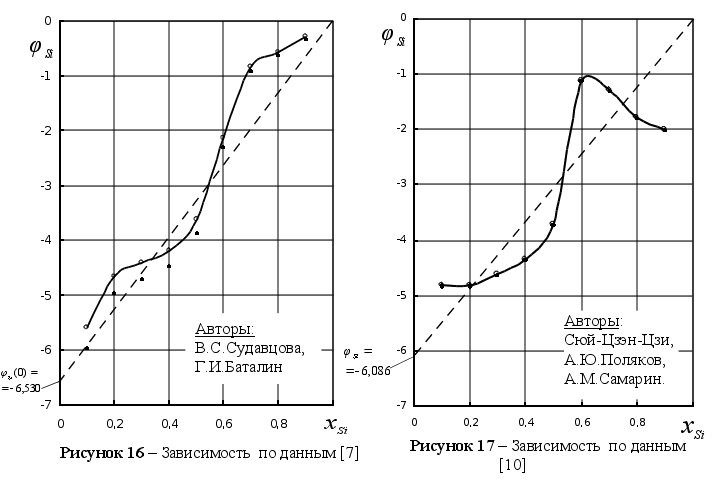
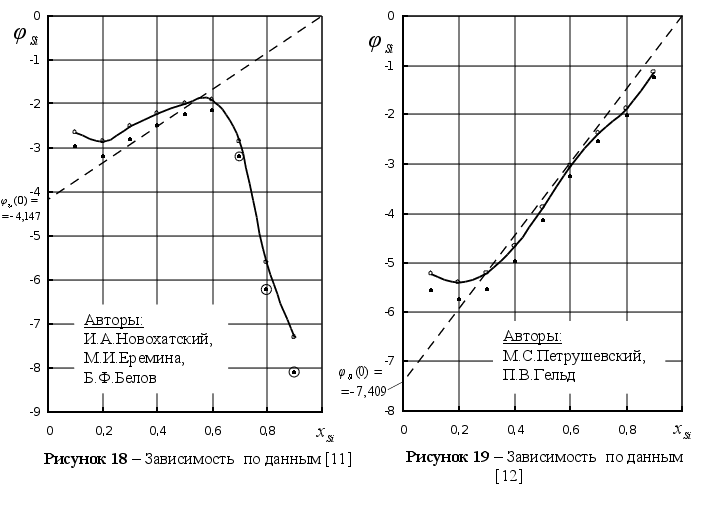

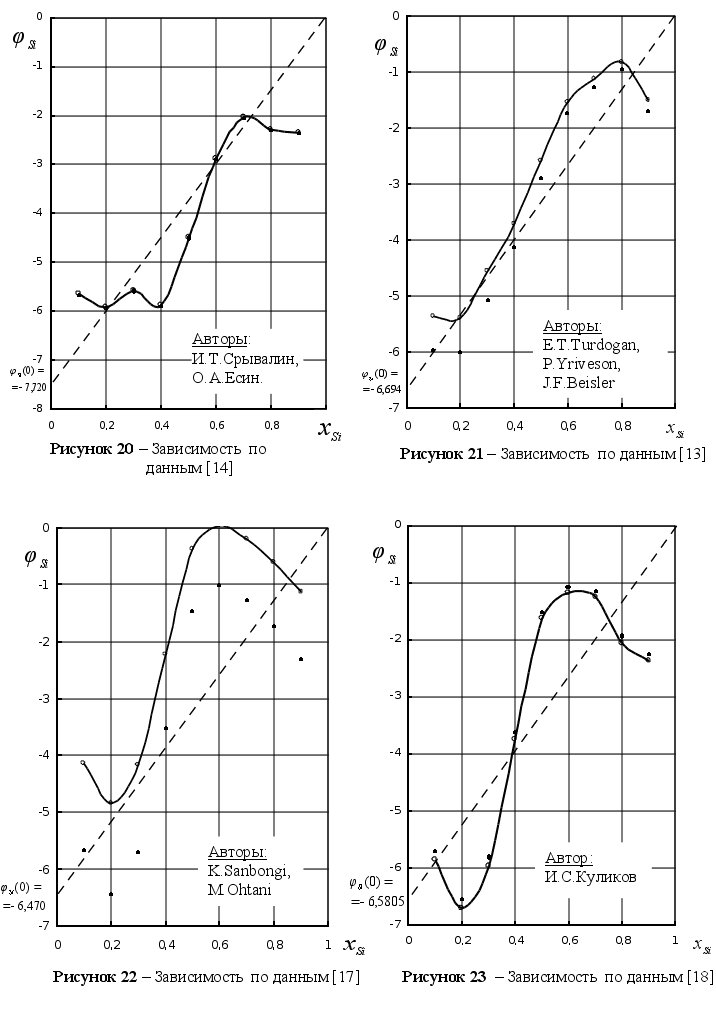
/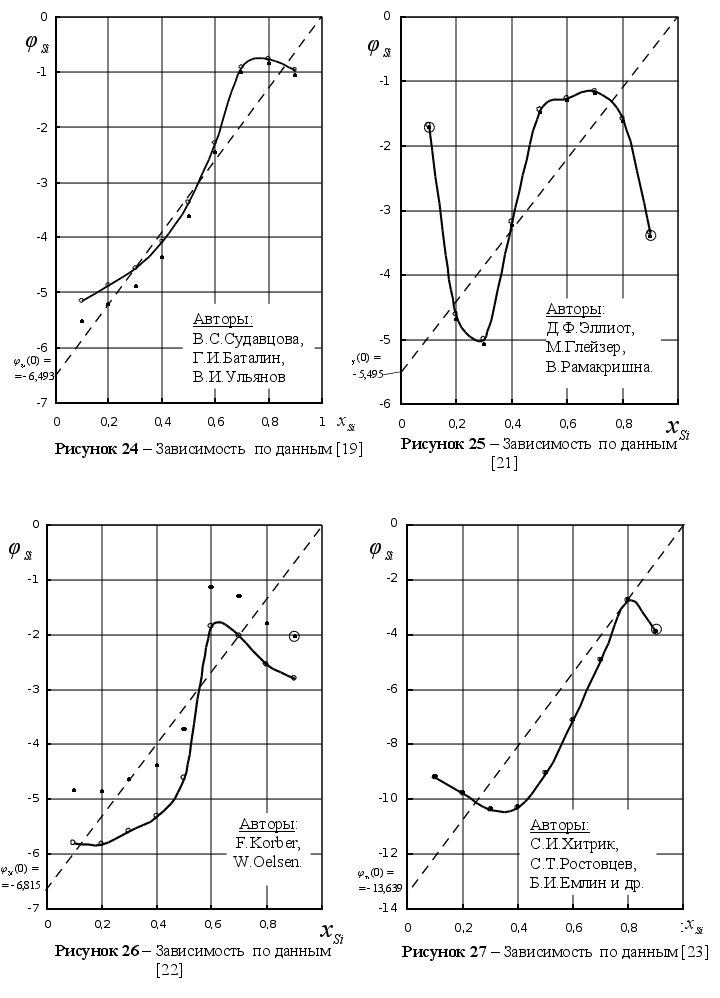
Таблица
10 – Значения
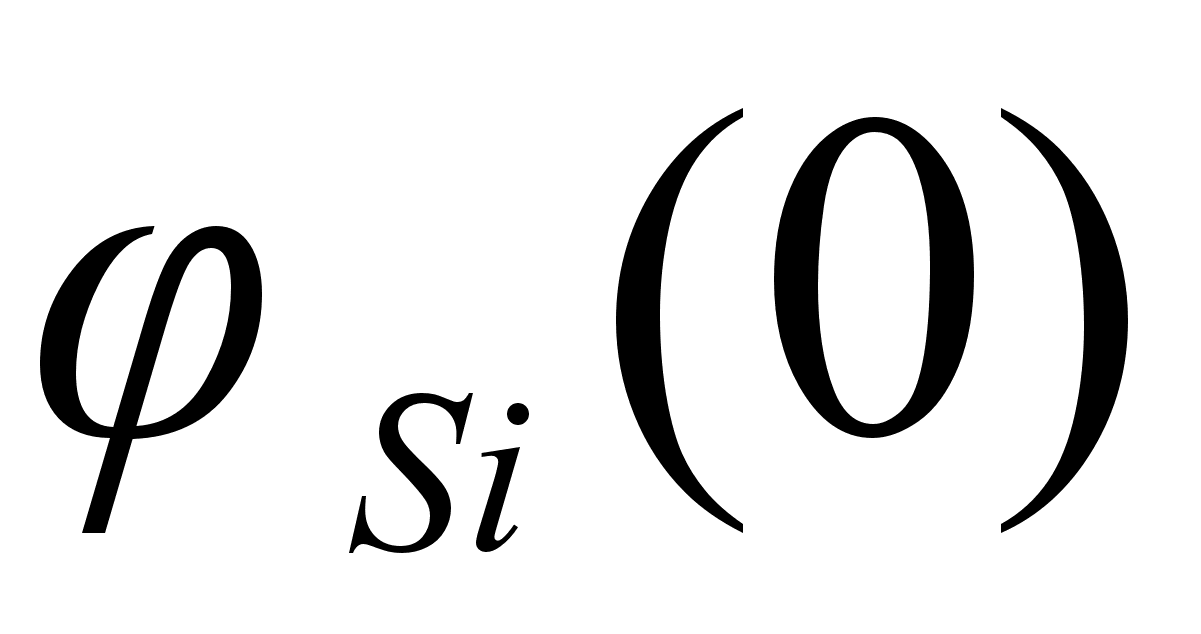 ,
вычисленные
по уравнению
(116)
,
вычисленные
по уравнению
(116)
| Литературный источник |
Значение
|
Литературный источник |
Значение
|
| [7] | -6,530 | [17] | -6,470 |
| [10] | -6,086 | [18] | -6,580 |
| [11] | -4,147 | [19] | -6,493 |
| [12] | -7,409 | [21] | -5,495 |
| [13] | -6,694 | [22] | -6,815 |
| [14] | -7,720 | [23] | -13,639 |
Н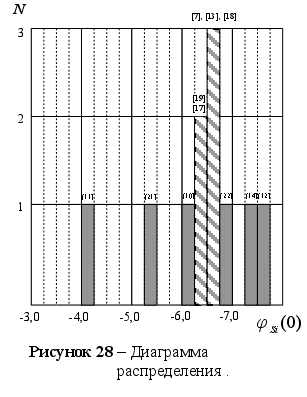 а
этой гистограмме
по оси абсцисс
представлен
диапазон значений
величины
а
этой гистограмме
по оси абсцисс
представлен
диапазон значений
величины
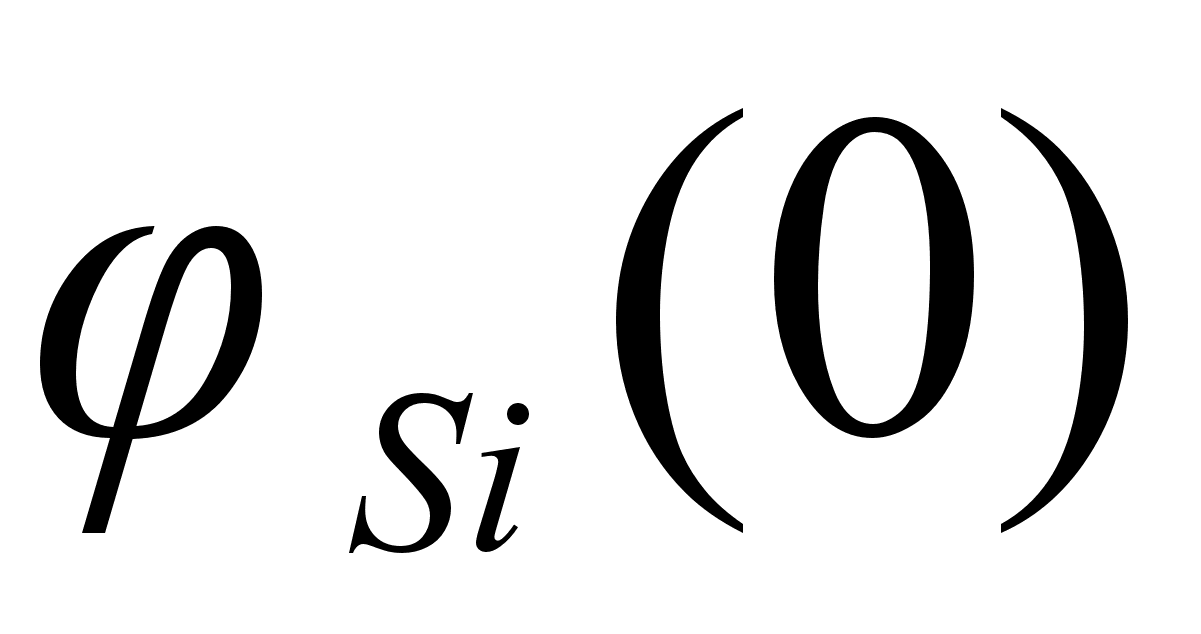 с интервалом
0,25. По оси ординат
мы откладываем
N
– число попаданий
значений
с интервалом
0,25. По оси ординат
мы откладываем
N
– число попаданий
значений
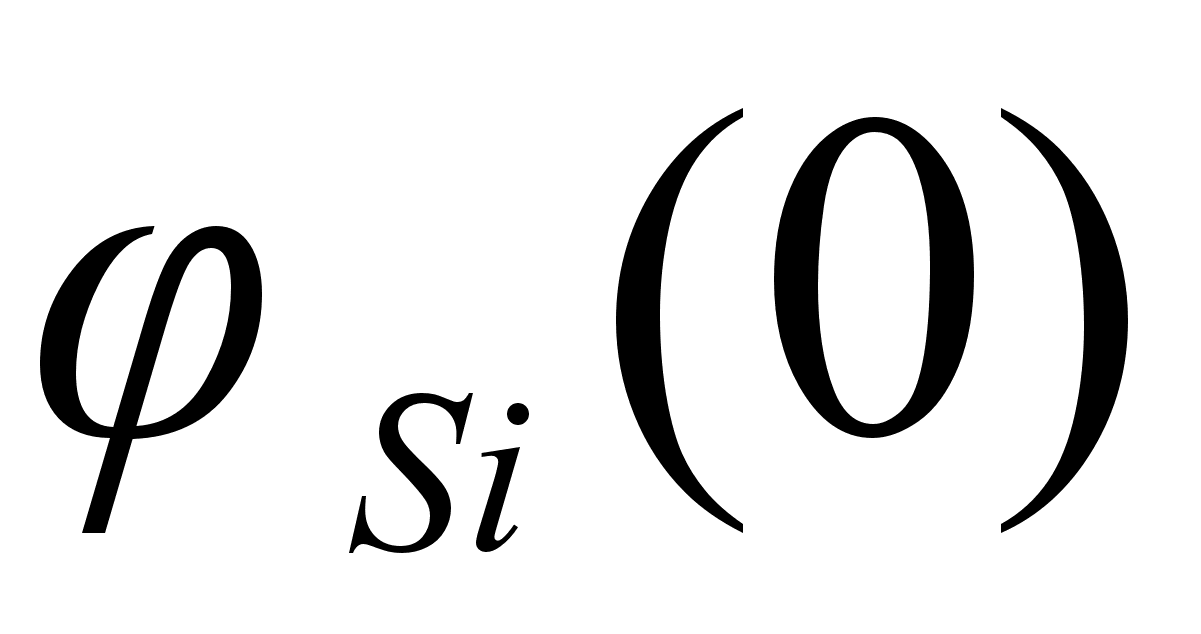 разных исследователей
в каждый интервал.
На основании
гистограммы
исключаем из
рассмотрения
данные следующих
литературных
источников:
[10], [11], [12], [14], [21], [22] и [23]. Дальнейшему
анализу подвергнем
данные из [7], [13],
[17], [18] и [19].
разных исследователей
в каждый интервал.
На основании
гистограммы
исключаем из
рассмотрения
данные следующих
литературных
источников:
[10], [11], [12], [14], [21], [22] и [23]. Дальнейшему
анализу подвергнем
данные из [7], [13],
[17], [18] и [19].
Вычислим
значение
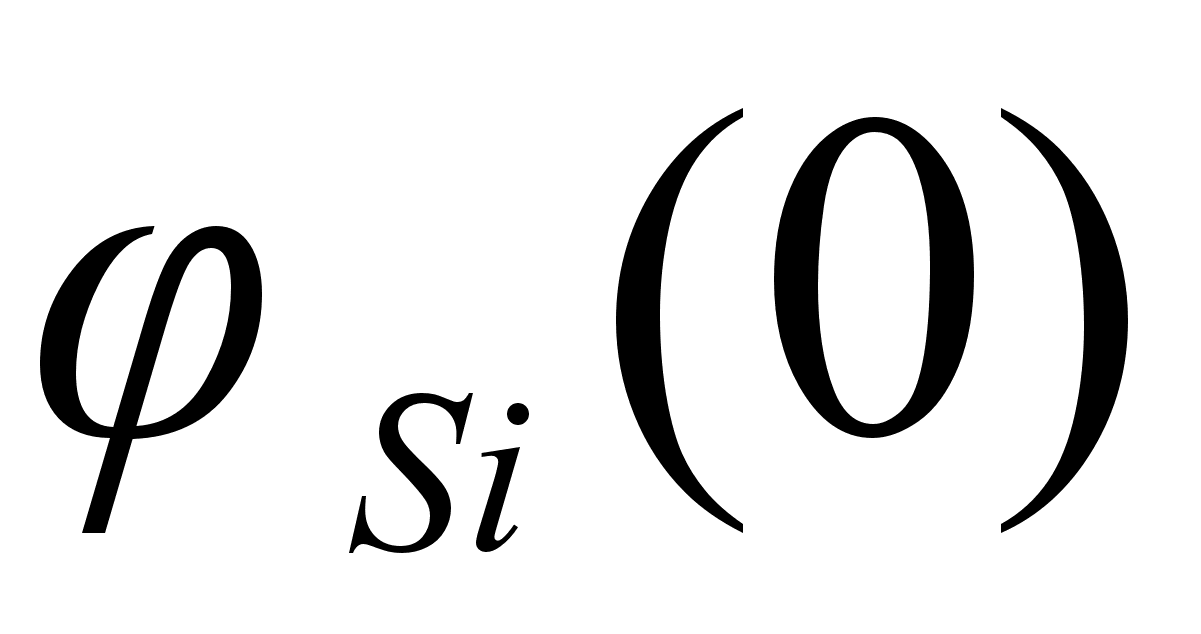 в соответствии
с уравнением
(116) по средним
значениям аSi
(таблица 11) методом
наименьших
квадратов.
в соответствии
с уравнением
(116) по средним
значениям аSi
(таблица 11) методом
наименьших
квадратов.
И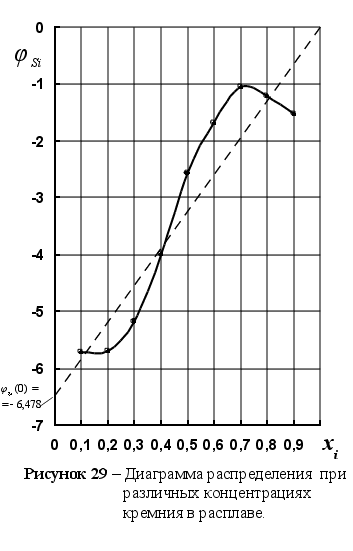 меем:
меем:
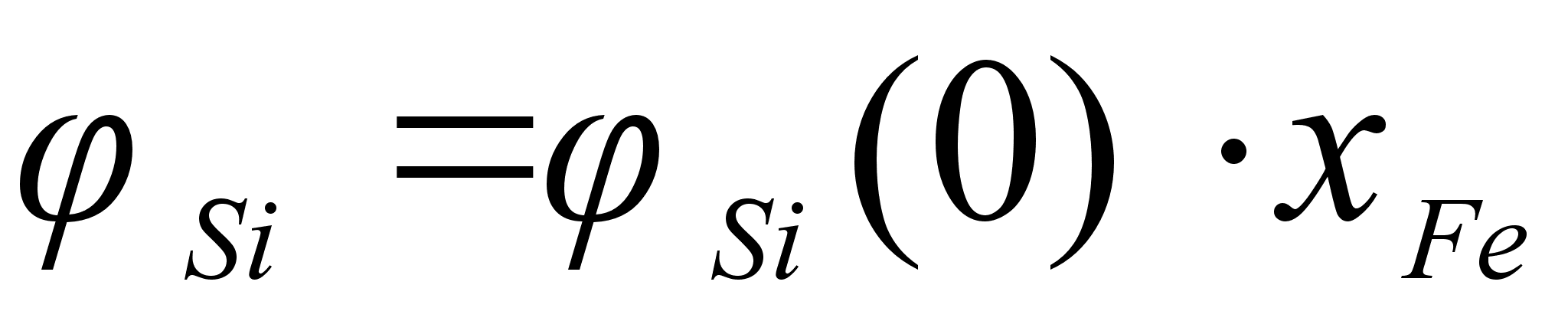
Требуется
определить
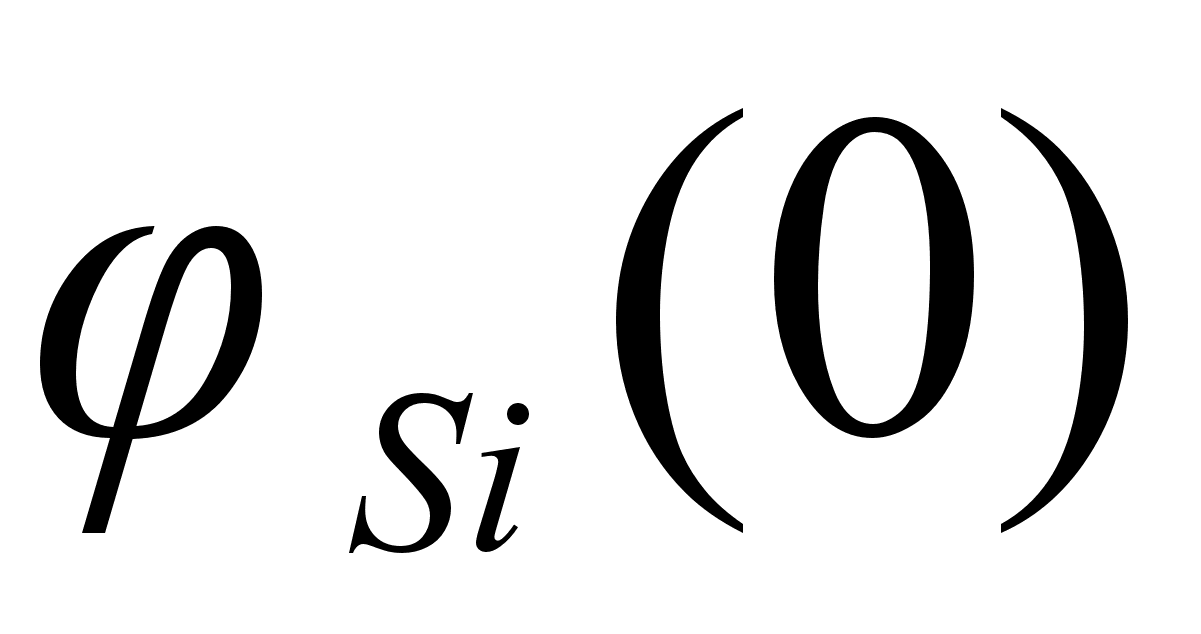 при известных
при известных
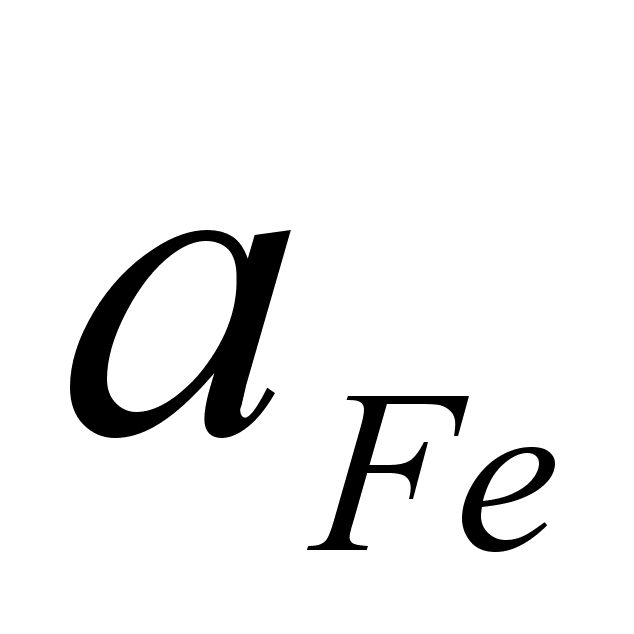 и
и
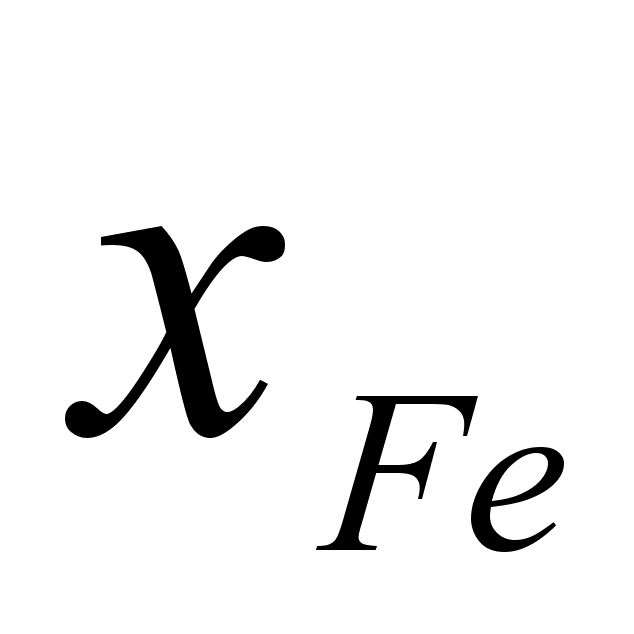 .
В соответствии
с методом наименьших
квадратов
запишем:
.
В соответствии
с методом наименьших
квадратов
запишем:
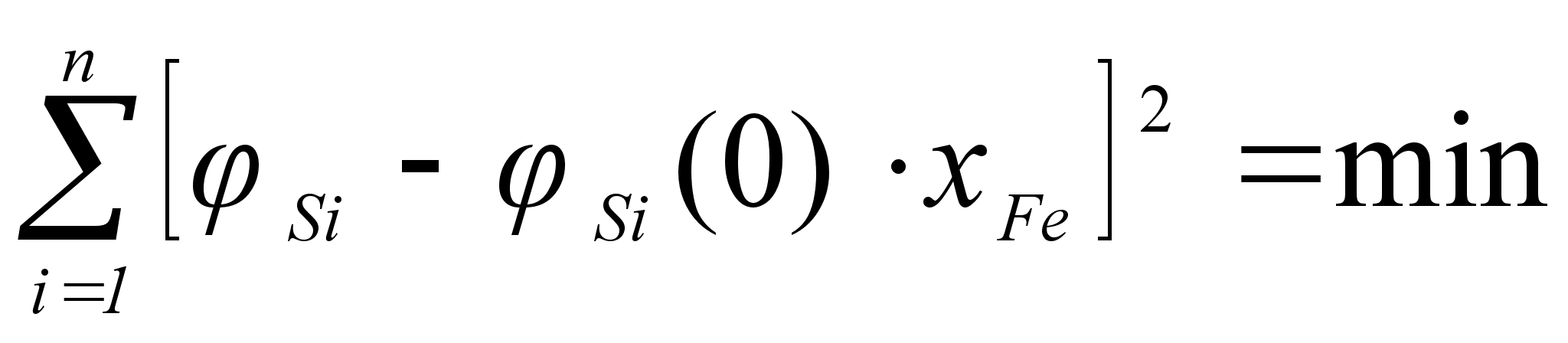
(117)
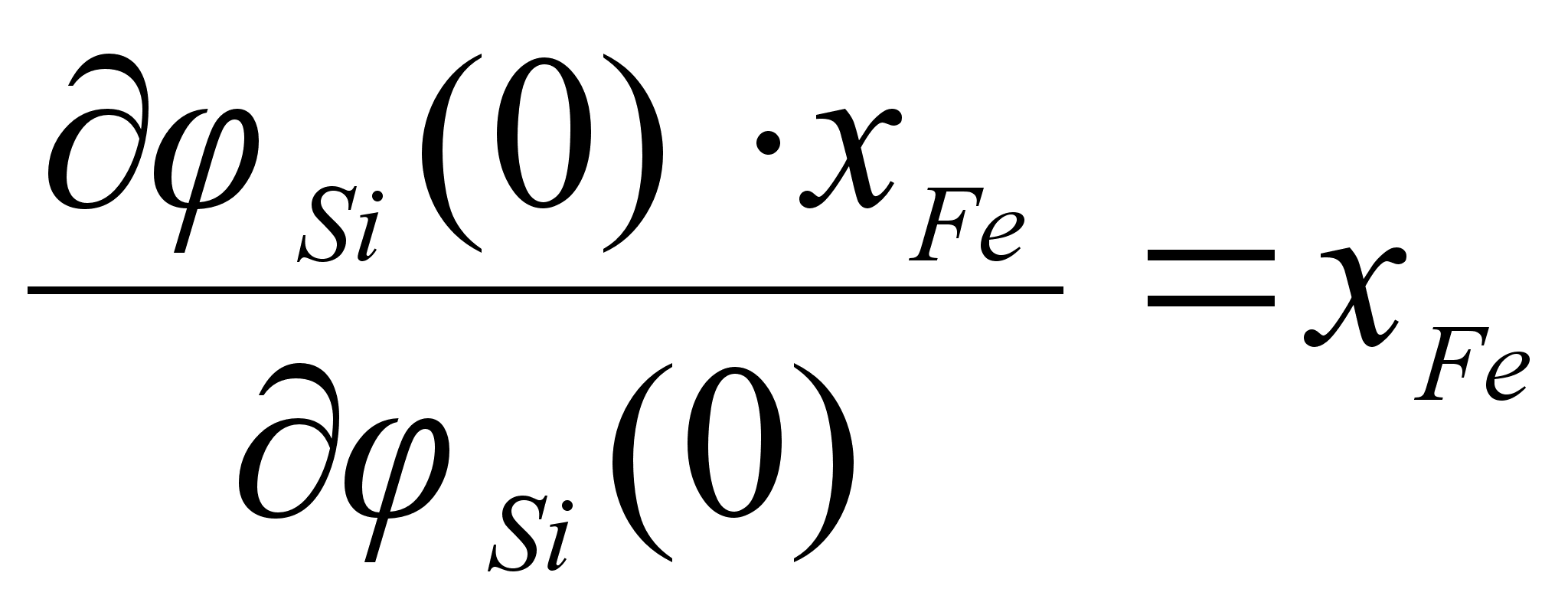
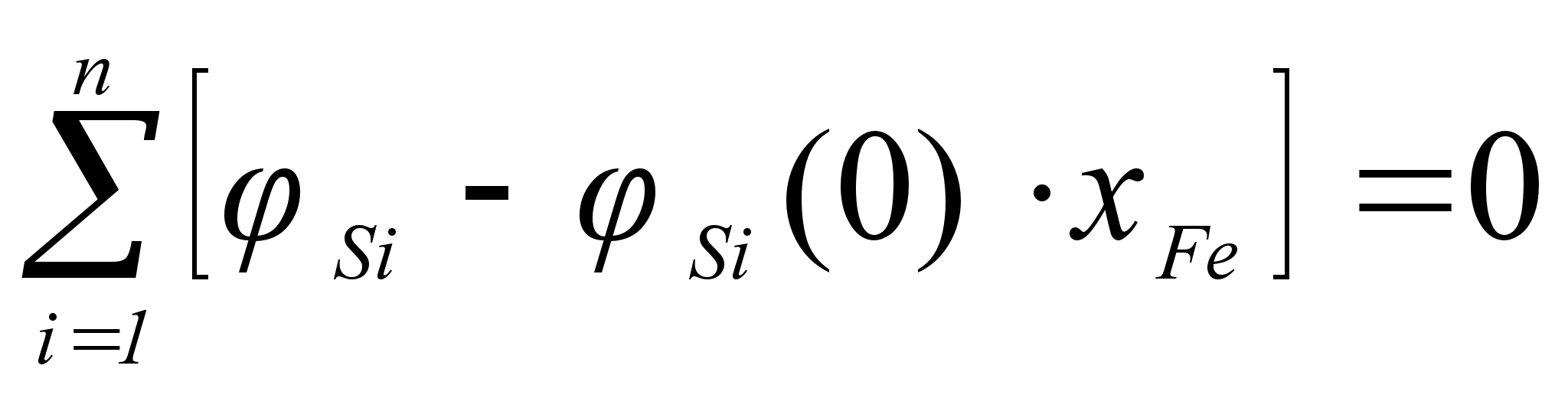
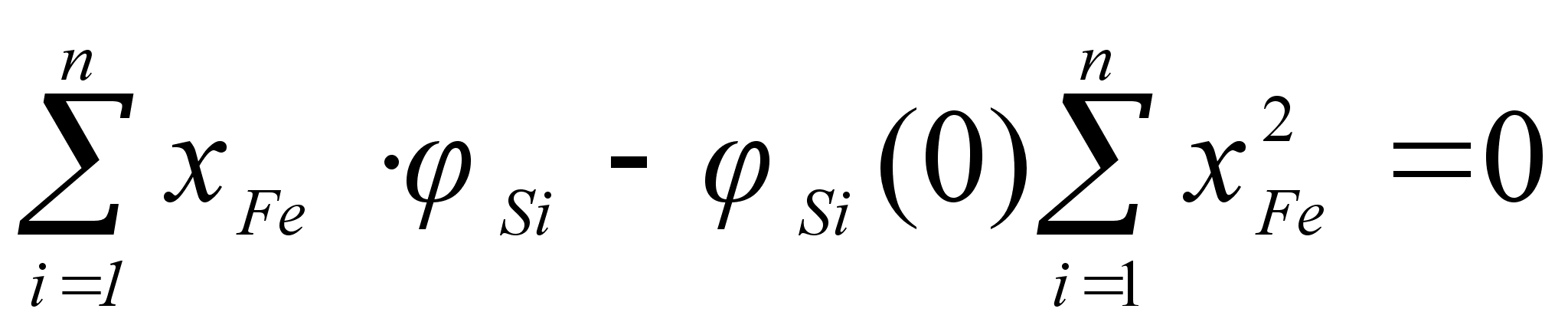
Откуда:
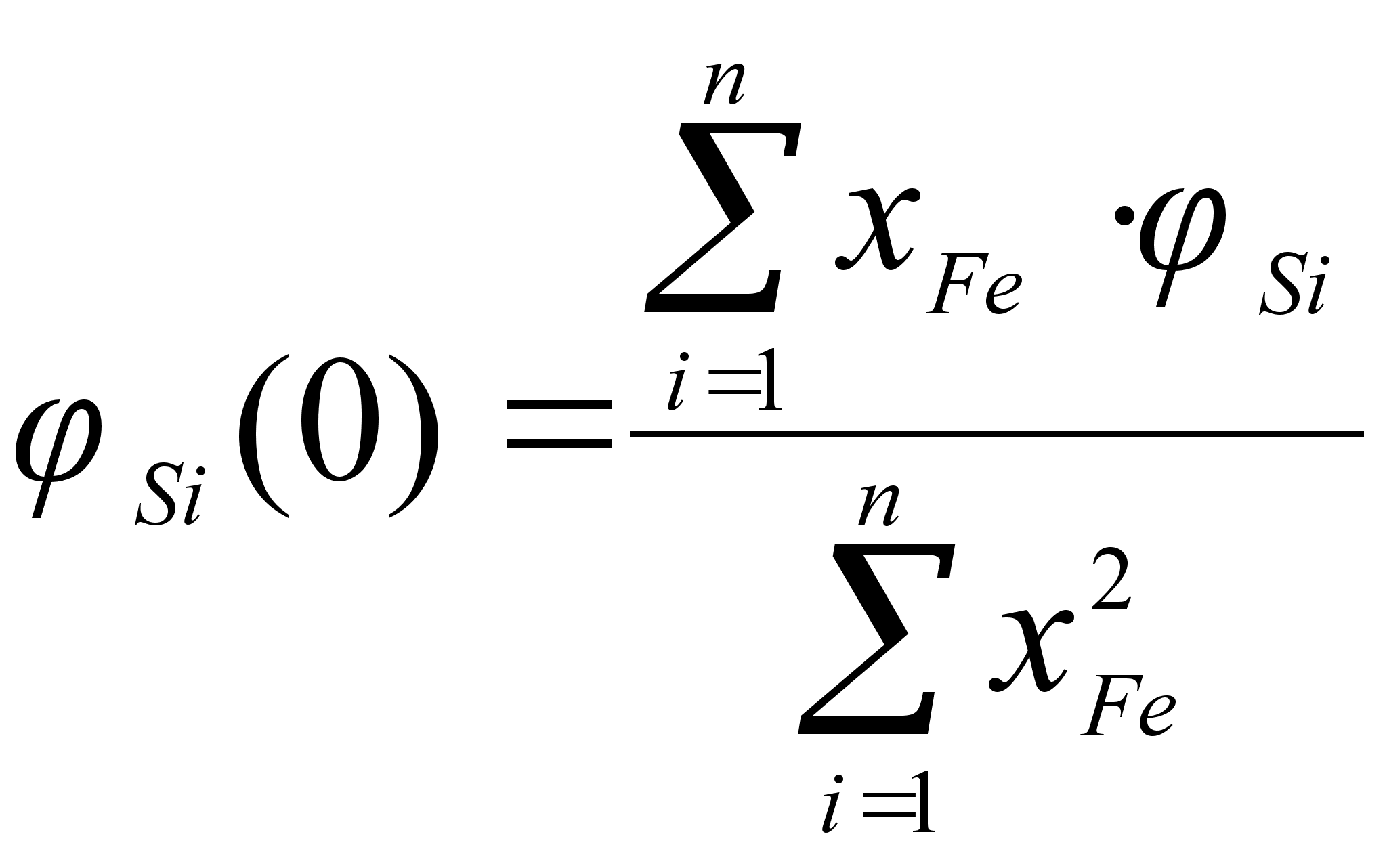
(118)
| Литератур. источник |
aSi |
Концентрация кремния в расплаве xSi |
||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| [7] |
a[7] |
0,00080 |
0,00830 |
0,03000 |
0,0800 |
0,1900 |
0,4150 |
0,6640 |
0,7800 |
0,8970 |
| [13] |
a[10] |
0,00080 |
0,00430 |
0,02500 |
0,0900 |
0,2340 |
0,4550 |
0,6240 |
0,7700 |
0,8850 |
| [17] |
a[12] |
0,00102 |
0,00324 |
0,01850 |
0,1127 |
0,3459 |
0,5107 |
0,6239 |
0,7466 |
0,8795 |
| [18] |
a[11] |
0,00100 |
0,00300 |
0,01740 |
0,1090 |
0,3440 |
0,5050 |
0,6310 |
0,7400 |
0,8800 |
| [19] |
a[8] |
0,00115 |
0,00716 |
0,02763 |
0,0830 |
0,2033 |
0,4049 |
0,6400 |
0,7737 |
0,8906 |
|
Средняя aSi |
0,00095 |
0,00520 |
0,02370 |
0,0949 |
0,2634 |
0,4581 |
0,6366 |
0,7621 |
0,8864 |
|
|
Si |
0,00950 |
0,00260 |
0,07900 |
0,2370 |
0,5270 |
0,7630 |
0,9090 |
0,9530 |
0,9850 |
|
|
lnSi |
-4,65600 |
-3,65000 |
-2,53800 |
-1,4390 |
-0,6410 |
-0,2700 |
-0,0950 |
-0,0490 |
-0,0150 |
|
|
Si |
-5,71900 |
-5,70300 |
-5,18000 |
-3,9960 |
-2,5640 |
-1,6870 |
-1,0550 |
-1,2130 |
-1,5230 |
По
образцу таблицы
2 строим таблицу
с исходными
данными для
вычисления
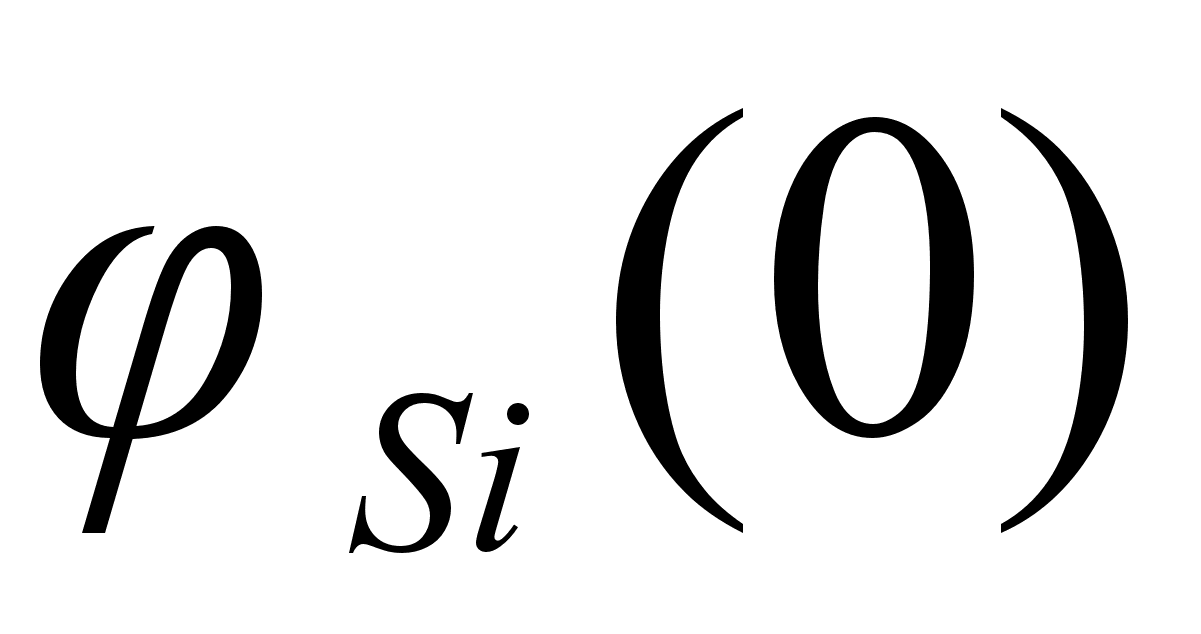 :
:
Таблица 12 – Исходные данные для вычисления по уравнению (118)
| Численные значения |
|
|||||||||
|
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
4,5 |
|
|
0,01 |
0,04 |
0,09 |
0,16 |
0,25 |
0,36 |
0,49 |
0,64 |
0,81 |
2,85 |
|
|
-1,523 |
-1,213 |
-1,055 |
-1,687 |
-2,564 |
-3,996 |
-5,18 |
-5,703 |
-5,719 |
- - - |
|
|
-0,1523 |
-0,2426 |
-0,3165 |
-0,6748 |
-1,282 |
-2,3976 |
-3,626 |
-4,5624 |
-5,1471 |
-18,4623 |
По
данным таблицы
12 в соответствии
с выражением
(118) вычислены
значения
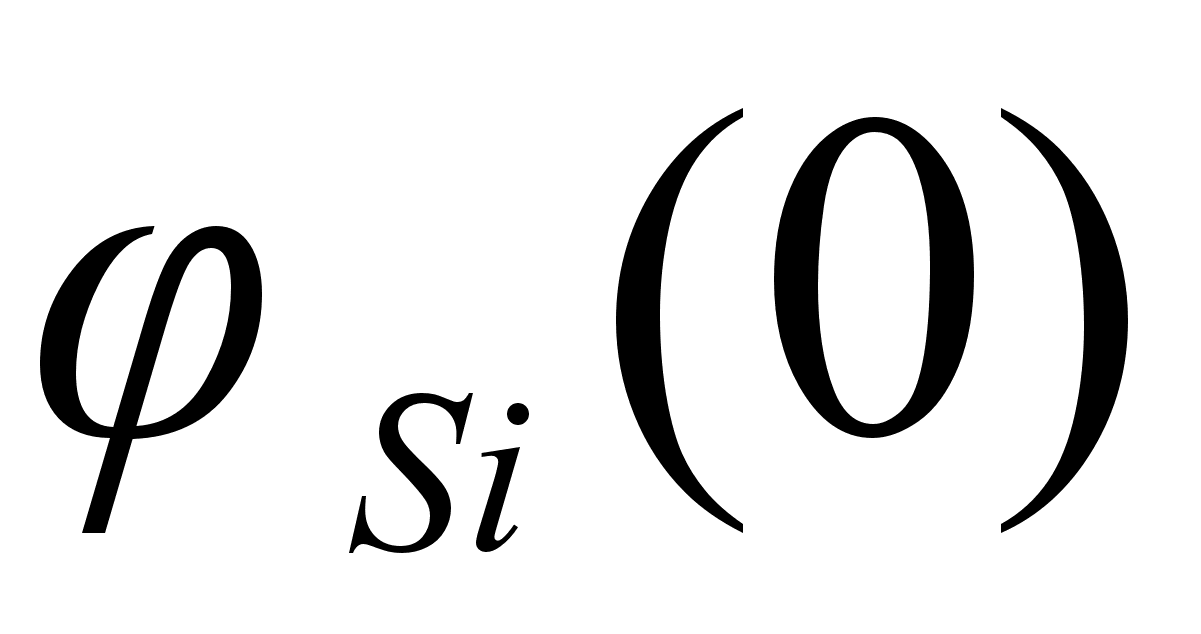 :
:
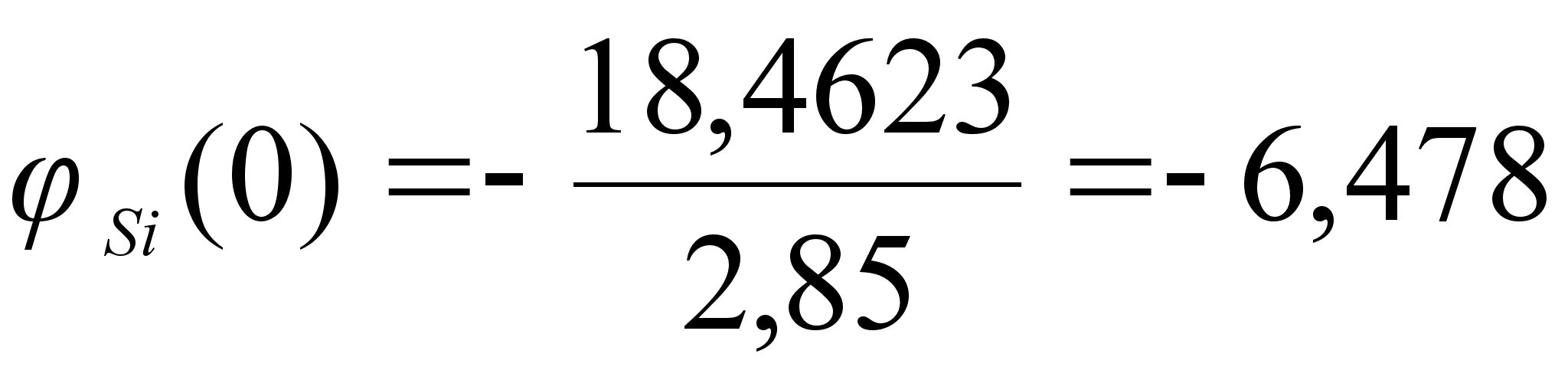
(119)
Теперь уравнение (116) можно записать в следующем виде:
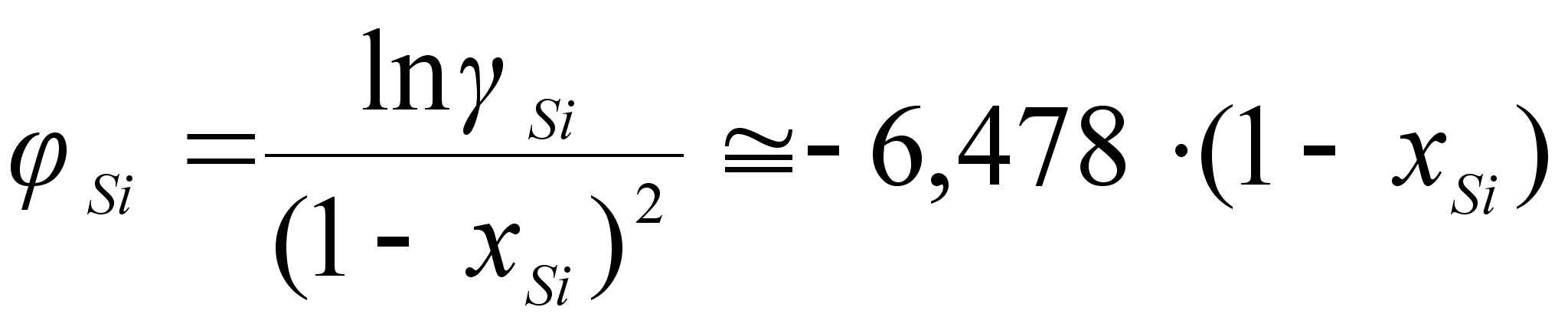
(120)
Значение
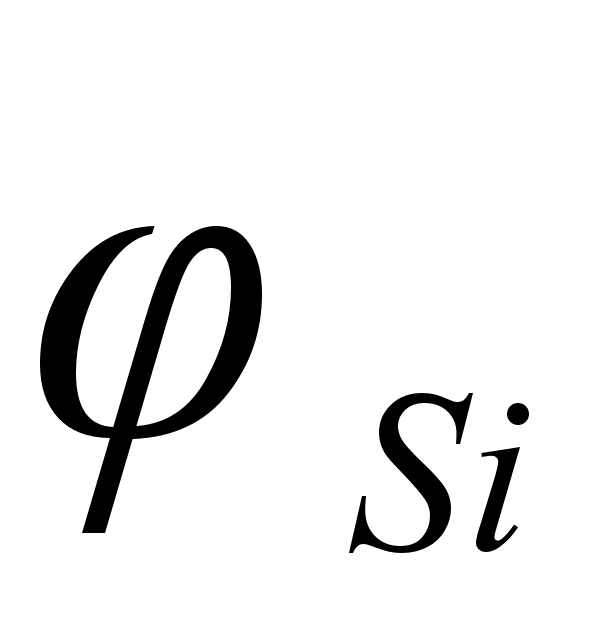 ,
вычисленное
по уравнению
(120) нанесены на
рисунок 29.
,
вычисленное
по уравнению
(120) нанесены на
рисунок 29.
В соответствии с уравнением (120), можно вычислить значения аSi, т.е. скорректировать (см. таблицу 13) исходные литературные данные, представленные ранее, в таблице 11.
5.2.3
Вычисление
значений Аi,
Bi,
 и
и
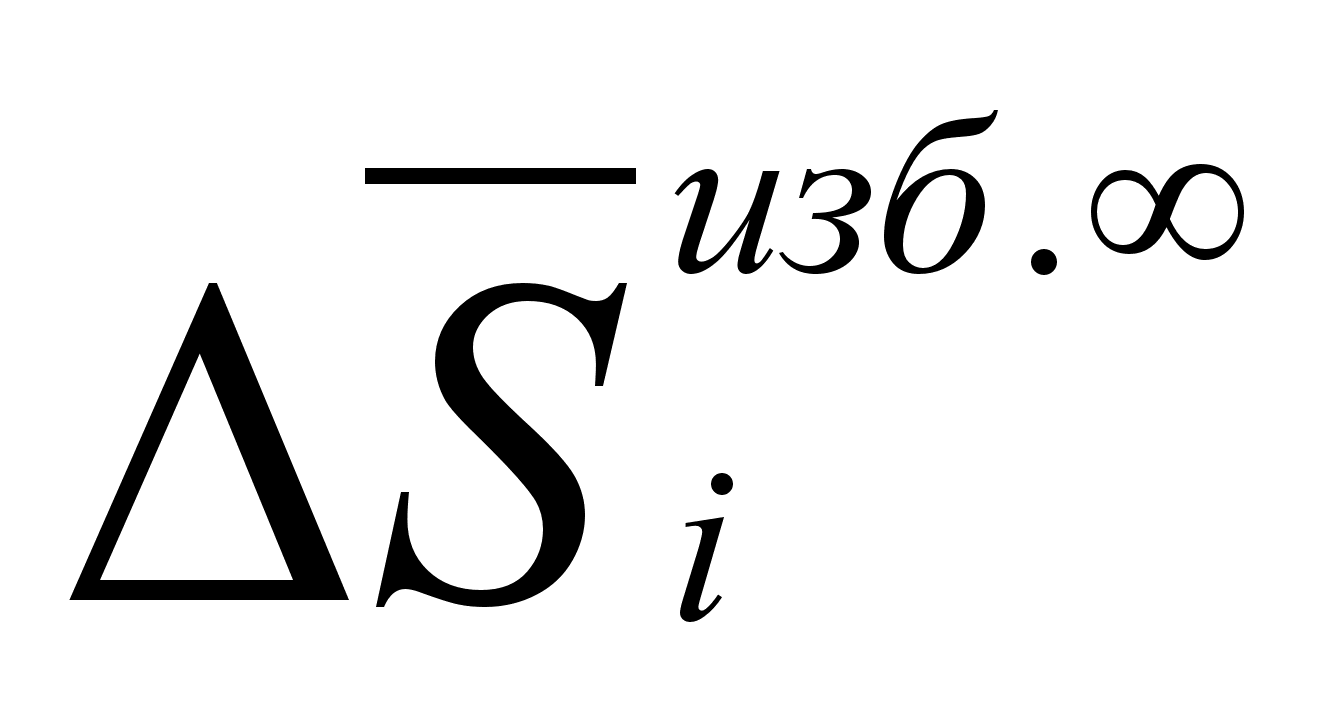 .
.
Термодинамические характеристики кремния
Термодинамические характеристики кремния вычислены из системы четырех уравнений типа (98) методом наименьших квадратов. В результате получено (при хSi 0):
ФункцияКонцентрация кремния в расплаве - xSi |
|||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
Si |
-6,478 |
-5,8110 |
-5,1650 |
-4,5200 |
-3,8740 |
-3,228 |
-2,583 |
-1,937 |
-1,291 |
-0,646 |
0,0 |
|
lnSi |
-6,478 |
-4,7070 |
-3,3060 |
-2,2150 |
-1,3950 |
-0,807 |
-0,413 |
-0,174 |
-0,052 |
-0,006 |
0 |
|
Si |
0,0015 |
0,0090 |
0,0370 |
0,1090 |
0,2480 |
0,446 |
0,662 |
0,840 |
0,950 |
0,994 |
1 |
|
aSi |
0,0000 |
0,0009 |
0,0073 |
0,0328 |
0,0992 |
0,223 |
0,397 |
0,588 |
0,760 |
0,894 |
1 |
Термодинамические
характеристики
кремния при
других его
концентрациях
рассчитываются
аналогичным
образом и приведены
в таблице 14. Для
сравнения в
этой таблице
даны, также,
усредненные
литературные
данные характеристик
 и
и
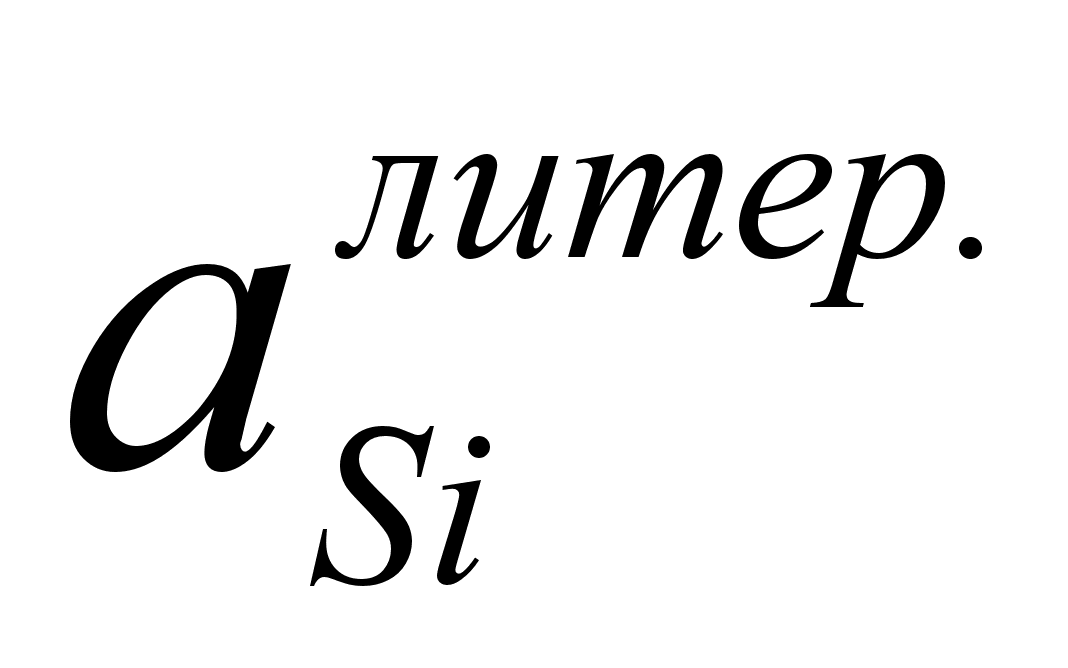 .
.
Термодинамические характеристики железа.
Значения
коэффициентов
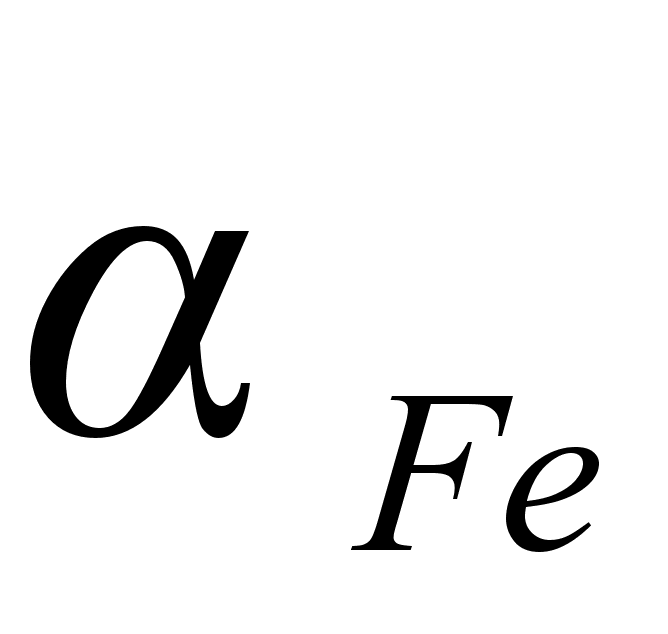 и
и
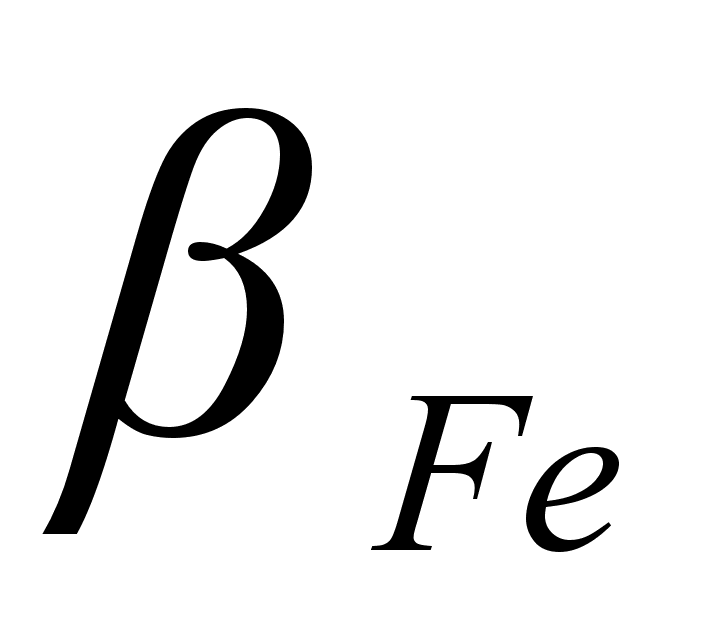 находим из
уравнения:
находим из
уравнения:
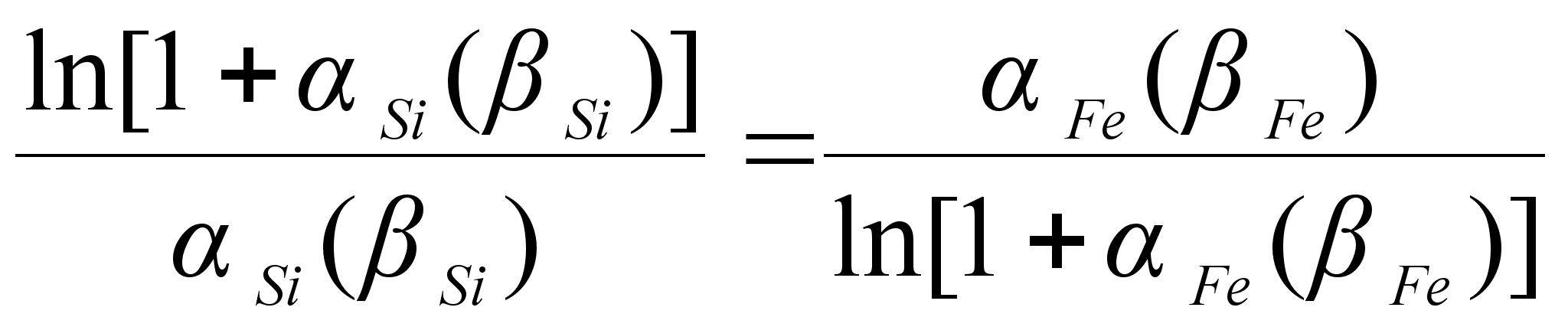
(121)
Получено:
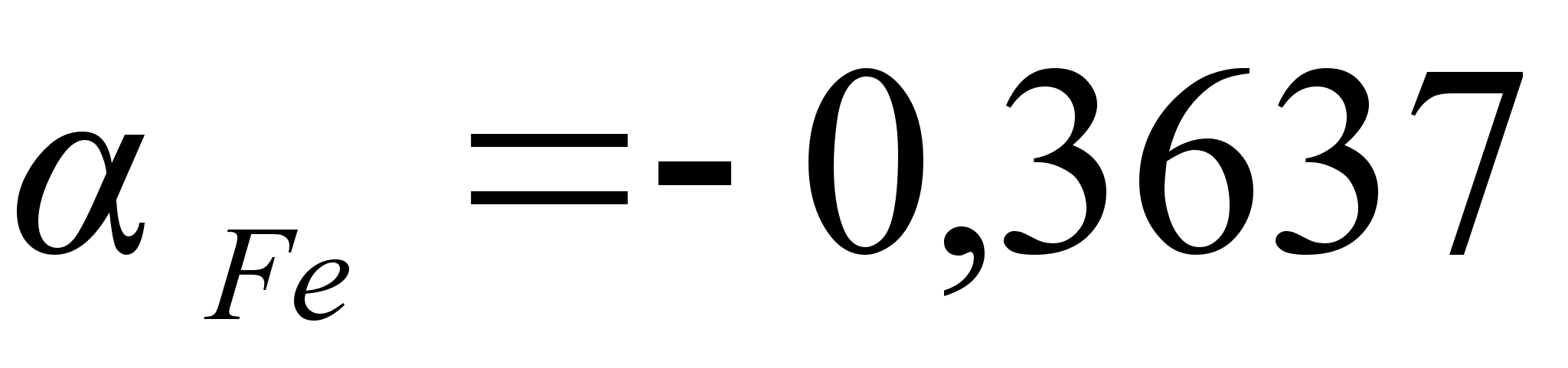 ,
,
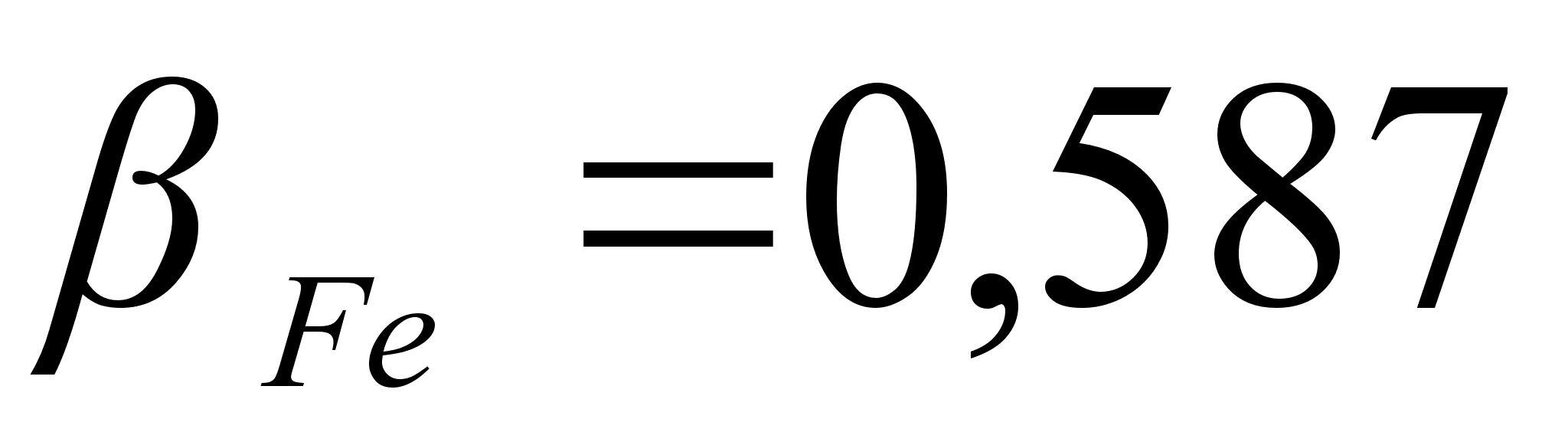 .
.
Величины
 и
и
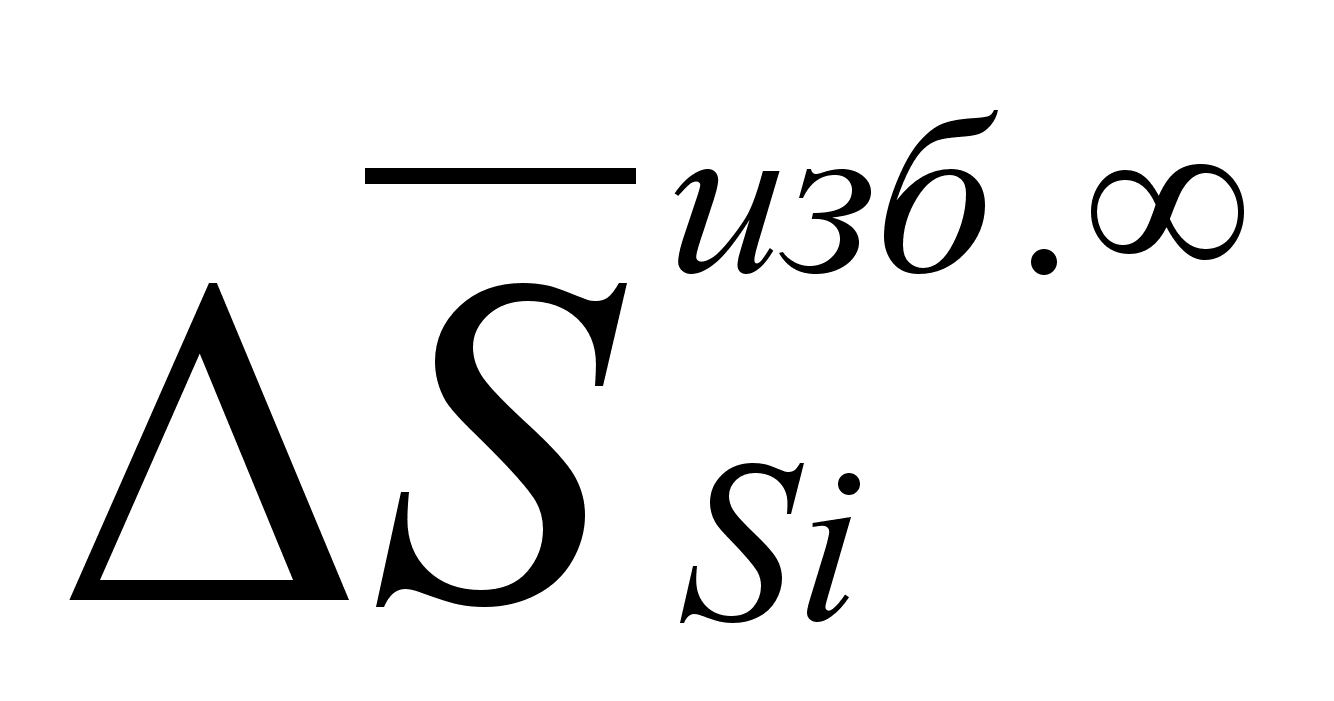 определяем
из выражений:
определяем
из выражений:
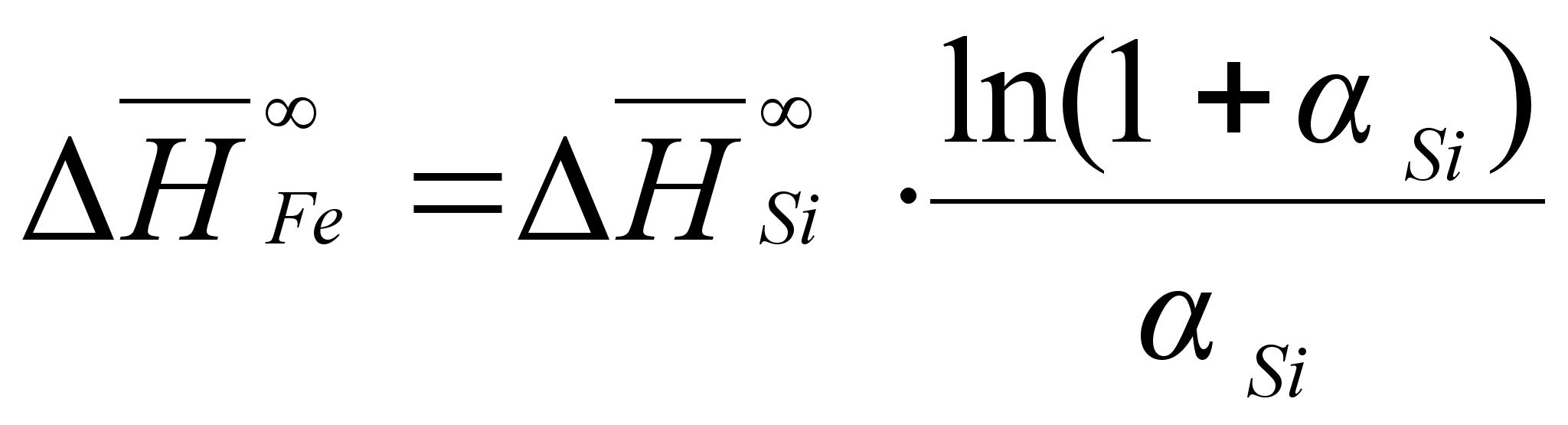
(122)
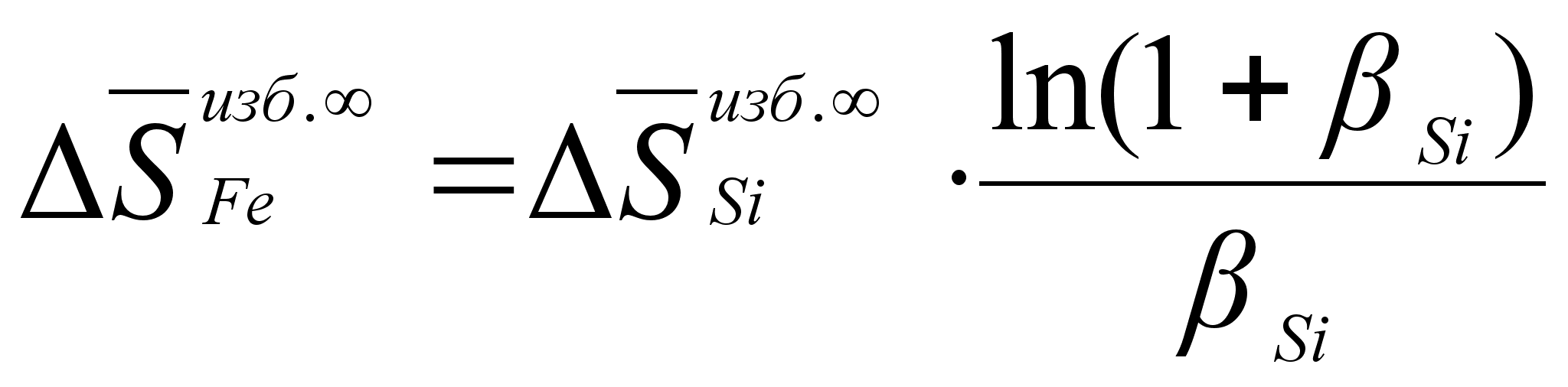
(123)
Они
равны:
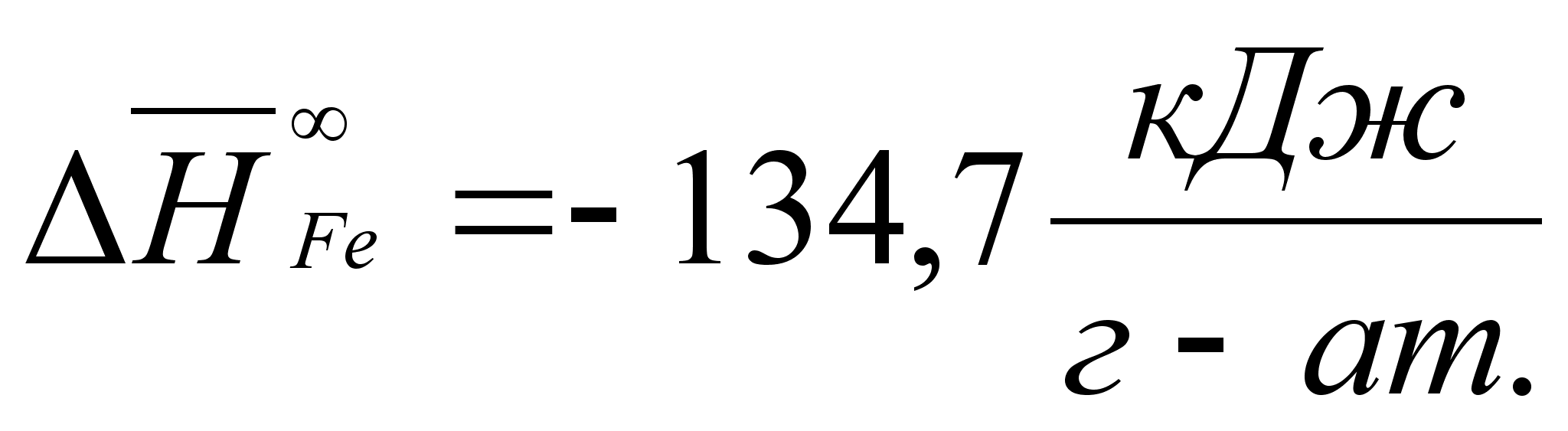 и
и
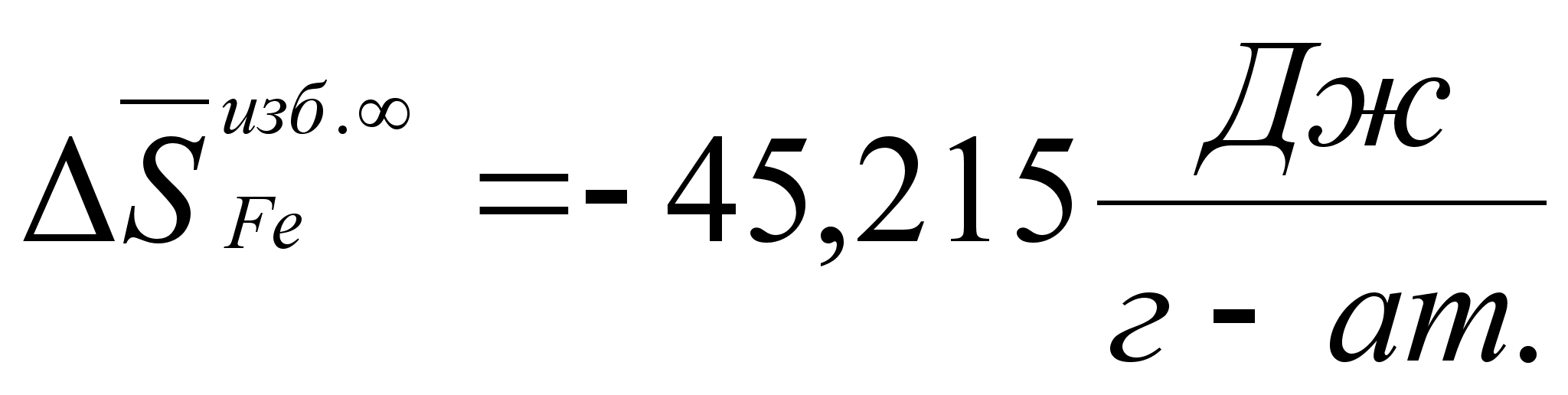 .
.
Отсюда вычисляются коэффициенты AFe и BFe:
AFe= -8,65, BFe= -5,438.
В таблице 14 представлены значения активности железа в расплаве Fe – Si, по данным разных авторов, а также среднее её значение и значение функции Fe .
Таблица 14 – Активность железа в выделенных работах, среднее её значение и некоторые другие термодинамические характеристики железа в расплаве Fe – Si.
| Литератур. источник |
aFe |
Концентрация кремния в расплаве xFe |
||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| [7] |
a[7] |
0,00080 |
0,00830 |
0,03000 |
0,0800 |
0,1900 |
0,4150 |
0,6640 |
0,7800 |
0,8970 |
| [13] |
a[10] |
0,00080 |
0,00430 |
0,02500 |
0,0900 |
0,2340 |
0,4550 |
0,6240 |
0,7700 |
0,8850 |
| [17] |
a[12] |
0,00102 |
0,00324 |
0,01850 |
0,1127 |
0,3459 |
0,5107 |
0,6239 |
0,7466 |
0,8795 |
| [18] |
a[11] |
0,00100 |
0,00300 |
0,01740 |
0,1090 |
0,3440 |
0,5050 |
0,6310 |
0,7400 |
0,8800 |
| [19] |
a[8] |
0,00115 |
0,00716 |
0,02763 |
0,0830 |
0,2033 |
0,4049 |
0,6400 |
0,7737 |
0,8906 |
|
Средняя aFe |
0,00095 |
0,00520 |
0,02370 |
0,0949 |
0,2634 |
0,4581 |
0,6366 |
0,7621 |
0,8864 |
|
|
Fe |
0,00950 |
0,00260 |
0,07900 |
0,2370 |
0,5270 |
0,7630 |
0,9090 |
0,9530 |
0,9850 |
|
|
lnFe |
-4,65600 |
-3,65000 |
-2,53800 |
-1,4390 |
-0,6410 |
-0,2700 |
-0,0950 |
-0,0490 |
-0,0150 |
|
|
Fe |
-5,71900 |
-5,70300 |
-5,18000 |
-3,9960 |
-2,5640 |
-1,6870 |
-1,0550 |
-1,2130 |
-1,5230 |
Для сравнения
литературных
данных и полученных
нами значений
Fe,
aSi,
 ,
,
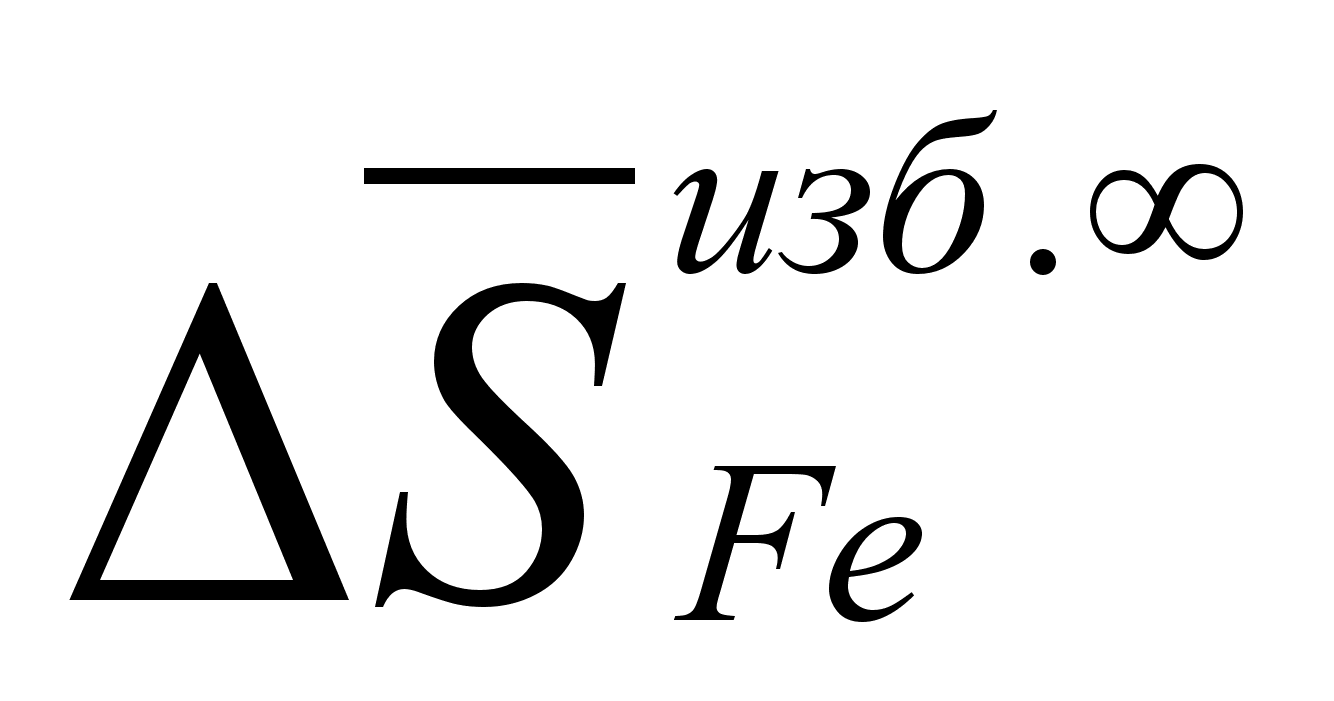 сведем их в
таблицу 16.
сведем их в
таблицу 16.
По данным таблиц 15 и 16 построены рисунки 30 и 31.
Вывод: Рассмотрена возможность применения концентрационных уравнений для растворов с отрицательным отклонением от идеальности.
| Функция |
Концентрация кремния в расплаве - xSi |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-6,4870 |
-5,81100 |
-5,1650 |
-4,5200 |
-3,8740 |
-3,2280 |
-2,5830 |
-1,9370 |
-1,2910 |
-0,6460 |
0,0 |
|
|
-6,4780 |
-4,70700 |
-3,3060 |
-2,2150 |
-1,3950 |
-0,8070 |
-0,4130 |
-0,1740 |
-0,0520 |
-0,0060 |
0,0 |
|
|
0,0015 |
0,00900 |
0,0370 |
0,1090 |
0,2480 |
0,4460 |
0,6620 |
0,8400 |
0,9500 |
0,9940 |
1,0 |
|
|
0,0000 |
0,00090 |
0,0073 |
0,0328 |
0,0992 |
0,2230 |
0,3970 |
0,5880 |
0,7600 |
0,8940 |
1,0 |
|
|
-167,4800 |
-128,91000 |
-97,0300 |
-70,9300 |
-49,8600 |
-33,1900 |
-20,390 |
-11,030 |
-4,7200 |
-1,1400 |
0,0 |
|
|
-35,5600 |
-29,98000 |
-24,7100 |
-19,7600 |
-15,2000 |
-11,0700 |
-7,4500 |
-4,4200 |
-2,0800 |
-0,5500 |
0,0 |
|
|
- - - - |
-5,71900 |
-5,7030 |
-5,1800 |
-3,9960 |
-2,5640 |
-1,6870 |
-1,0550 |
-1,2130 |
-1,5230 |
- - - |
|
|
0,0000 |
0,00095 |
0,0052 |
0,0237 |
0,0949 |
0,2634 |
0,4581 |
0,6366 |
0,7621 |
0,8864 |
1,0 |
Таблица 16 – Основные термодинамические характеристики железа в расплаве Fe – Si при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-3,2120 |
-3,8400 |
-4,4620 |
-5,0860 |
-5,7190 |
-6,3690 |
-7,0430 |
-7,7500 |
-8,4990 |
-9,3010 |
-10,168 |
|
|
-3,2120 |
-3,1100 |
-2,8560 |
-2,4920 |
-2,0590 |
-1,5920 |
-1,1270 |
-0,6975 |
-0,3400 |
-0,0930 |
0,000 |
|
|
-0,0403 |
0,0446 |
0,0575 |
0,0827 |
0,1276 |
0,2035 |
0,3240 |
0,4978 |
0,7118 |
0,9112 |
1,000 |
|
|
0,0000 |
0,0045 |
0,0115 |
0,0248 |
0,0510 |
0,1017 |
0,1944 |
0,3485 |
0,5694 |
0,8201 |
1,000 |
|
|
-134,700 |
-113,22 |
-92,9700 |
-74,0900 |
-56,7500 |
-41,1600 |
-27,5700 |
-16,260 |
-7,6000 |
-2,0000 |
0,000 |
|
|
-42,2100 |
-34,590 |
-25,9000 |
-18,8400 |
-13,1800 |
-8,7400 |
-5,3500 |
-2,8800 |
-1,2300 |
-0,3000 |
0,000 |
|
|
--- |
-3,7850 |
-4,6050 |
-5,4560 |
-5,2610 |
-6,8330 |
-7,0860 |
-6,5790 |
-5,7510 |
-7,2690 |
--- |
|
|
0,0000 |
0,0047 |
0,0105 |
0,0207 |
0,0420 |
0,0906 |
0,1931 |
0,3872 |
0,6356 |
0,8369 |
1,000 |


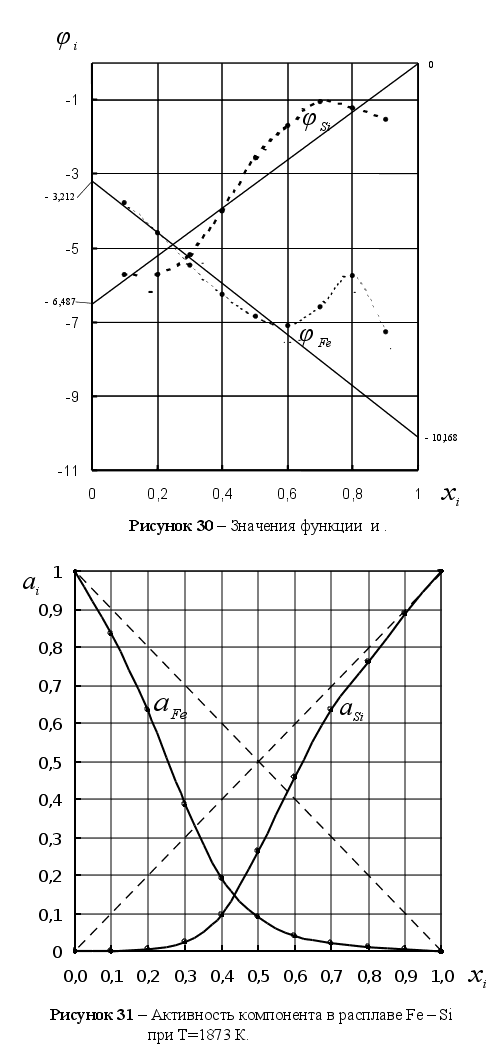
5.3 Система W – Pd
Данная система характеризуется знакопеременным отклонением от закона Рауля для палладия.
5.3.1 Исходные данные.
В работе [20] активность вольфрама вычислялась по давлению его паров над расплавом по методу Кнудсена [3], активность вольфрама определялась графическим интегрированием уравнения Гиббса – Дюгема. В основу вычисления термодинамических характеристик палладия были положены данные по активности вольфрама.
Таблица 17 – Исходные данные для системы W – Pd при 1973 К [20].
-
Вольфрам
Палладий
xW
aW
W
W
xPd
aPd
Pd
Pd
0,1 0,05 0,5 -0,8557 0,1 0,06 0,6 -0,6306 0,2 0,11 0,55 -0,9341 0,2 0,12 0,6 -0,7982 0,3 0,17 0,5667 -1,1592 0,3 0,23 0,7667 -0,5423 0,4 0,23 0,576 -1,5372 0,4 0,36 0,9 -0,2927 0,5 0,31 0,62 -1,9121 0,5 0,50 1,0
0,00 0,6 0,39 0,65 -2,6924 0,6 0,67 1,1167 0,6897 0,7 0,50 0,7143 -3,7386 0,7 0,78 1,1143 1,2024 0,8 0,63 0,7875 -5,9723 0,8 0,87 1,0875 2,097 0,9 0,873 0,97 -3,0459 0,9 0,918 1,02 1,9803
Суть метода
Кнудсена в
конечном счете
сводится к
определению
убыли массы
расплава, вследствие
испарения
вещества в
вакууме. При
использовании
этого метода
исследуемый
расплав помещают
в сосуд, в крышке
которого имеется
маленькое
отверстие с
точно измеренной
площадью. Убыль
массы вещества
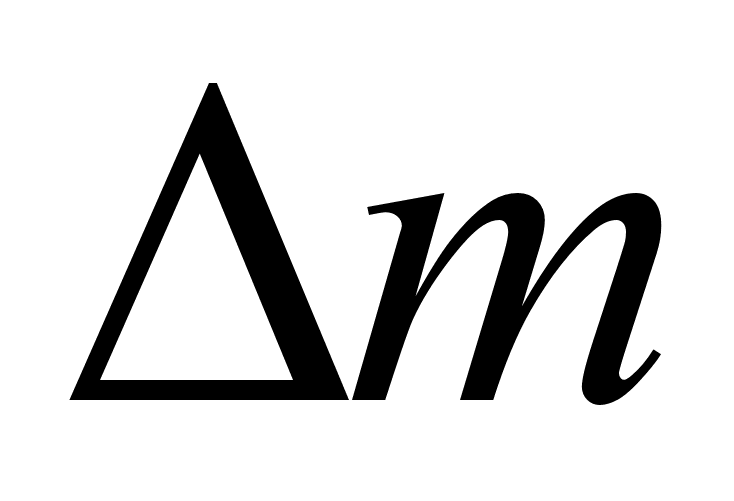 связано с истечением
(эффузией) его
через отверстие
при постоянной
разности между
давлением
насыщенного
пара металла
при температуре
Р опыта
и остаточным
давлением при
вакуумировании
Рост
, пропорциональна
времени
связано с истечением
(эффузией) его
через отверстие
при постоянной
разности между
давлением
насыщенного
пара металла
при температуре
Р опыта
и остаточным
давлением при
вакуумировании
Рост
, пропорциональна
времени
 и площади отверстия
S.
Если Р>>Рост.
, то можно записать:
и площади отверстия
S.
Если Р>>Рост.
, то можно записать:
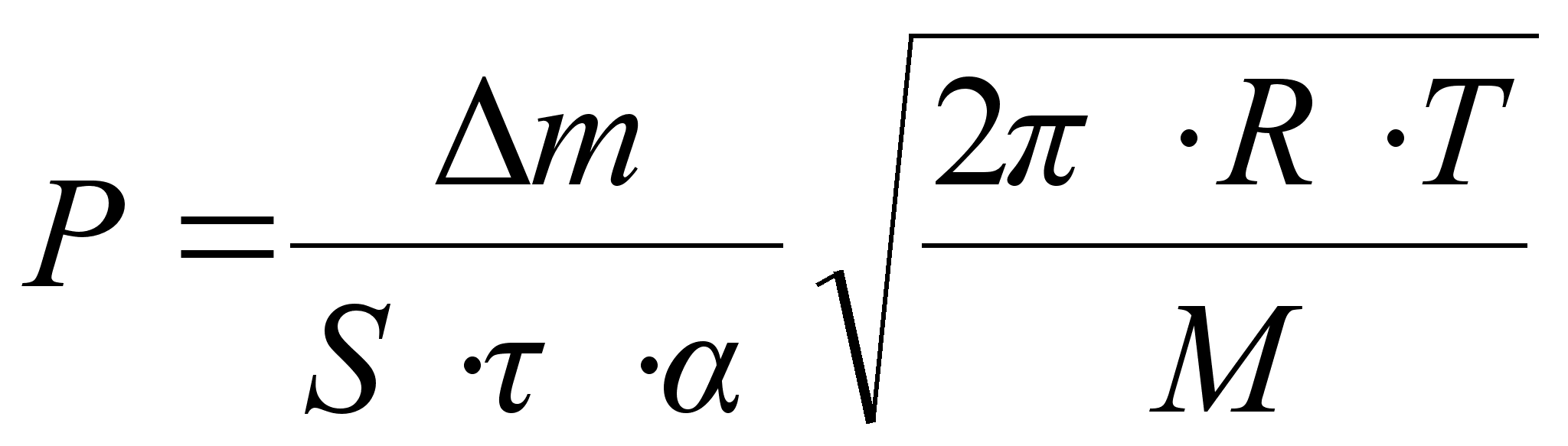
(124)
здесь
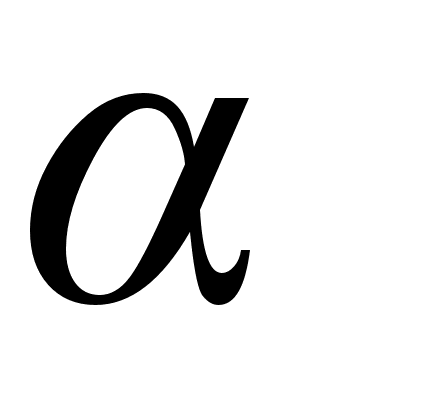 -
коэффициент
испарения,
учитывающий
прежде всего
состояние
поверхности;
-
коэффициент
испарения,
учитывающий
прежде всего
состояние
поверхности;
М – молекулярный вес испаряющегося металла.
Уравнение (124) известно как классическая формула Кнудсена и выведено на основании молекулярно – кинетической теории при следующих допущениях:
отсутствуют столкновения молекул между собой как в объеме эффузионной камеры, так и в области эффузионного отверстия;
длина свободного пробега частицы велика по сравнению с размерами эффузионного отверстия;
все атомы, попавшие в эффузионное отверстие, проходят через него, не изменяя направления движения, так как края отверстия бесконечно тонки.
Первые два условия обычно выполняются, если давление пара не превышает 1,3 – 13,3 Па, а радиус отверстия не более 1 мм.
По исходным
данным построим
графики функций
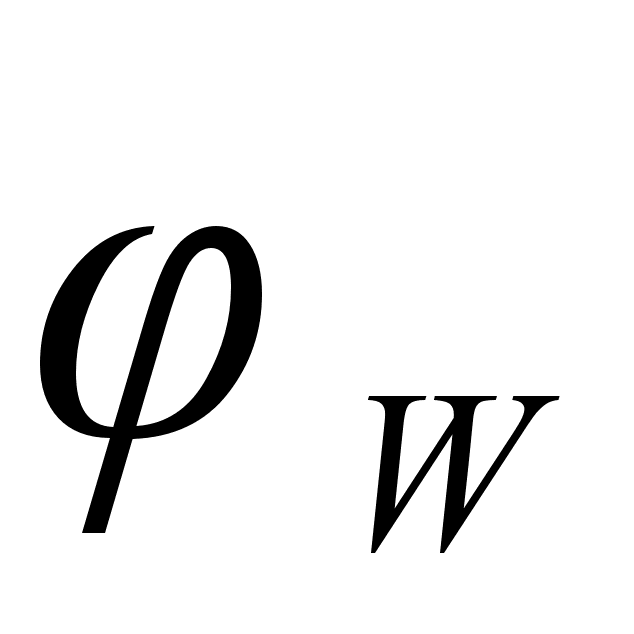 и
и
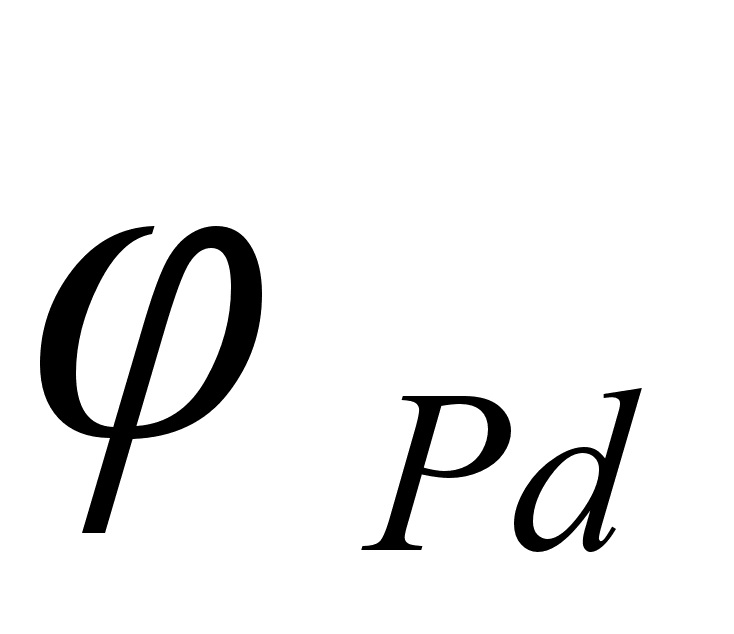 (рисунки 32 и 33). На
этих же рисунках
проведены
прямые линии,
полученные
путем обработки
первичных
литературных
данных в соответствии
с уравнением
прямой.
(рисунки 32 и 33). На
этих же рисунках
проведены
прямые линии,
полученные
путем обработки
первичных
литературных
данных в соответствии
с уравнением
прямой.
5.3.2 Корректировка исходных данных.
Приведем вычисление коэффициентов в уравнении прямой для вольфрама (таблица 18).
Таблица
18 – Необходимые
параметры для
вычисления
коэффициентов
в уравнении
прямой для
функции
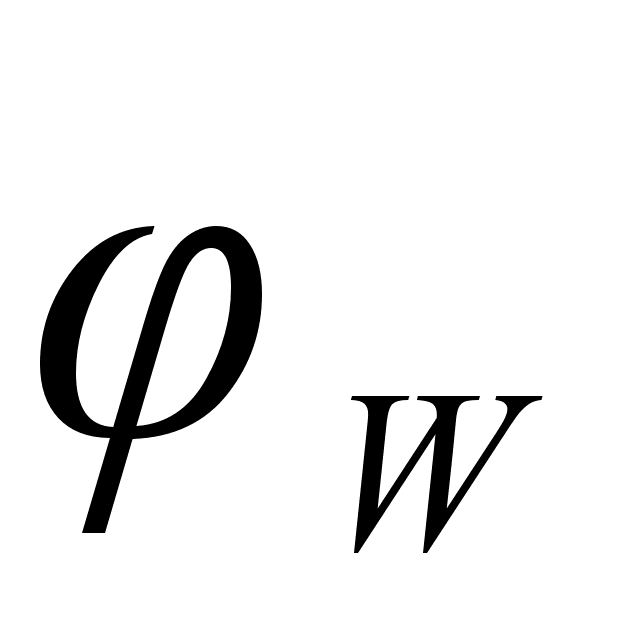 .
.
Численные значения |
|
|||||||||
|
|
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 4,5 |
|
|
0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 | 2,85 |
|
|
-0,8557 | -0,9341 |
-1,1592 |
-1,5372 | -1,9121 | -2,6924 | -3,7386 | -5,9723 | -3,0459 | -21,8475 |
|
|
-0,0856 | -0,1868 | -0,3478 | -0,6149 | -0,956 | -1,6154 | -2,617 | -4,7778 | -2,7413 | -13,9426 |
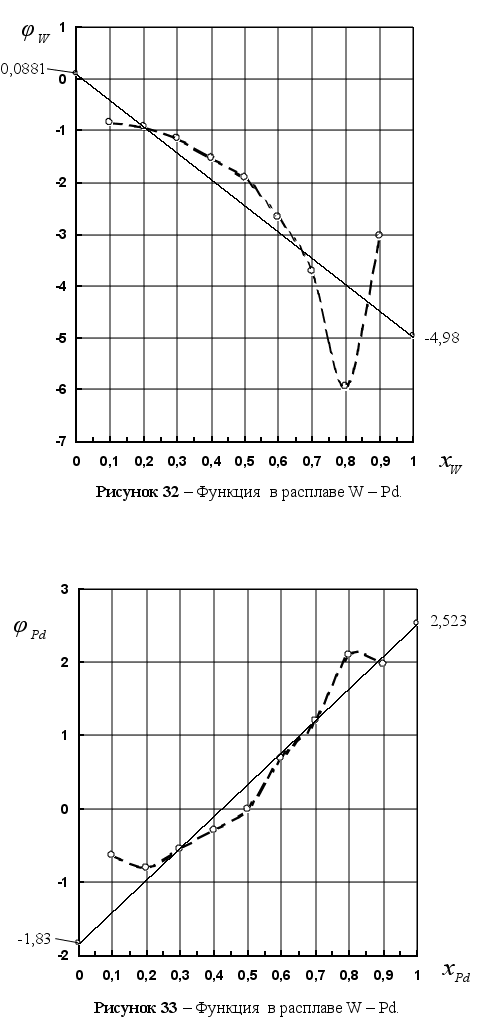
Вычисления:
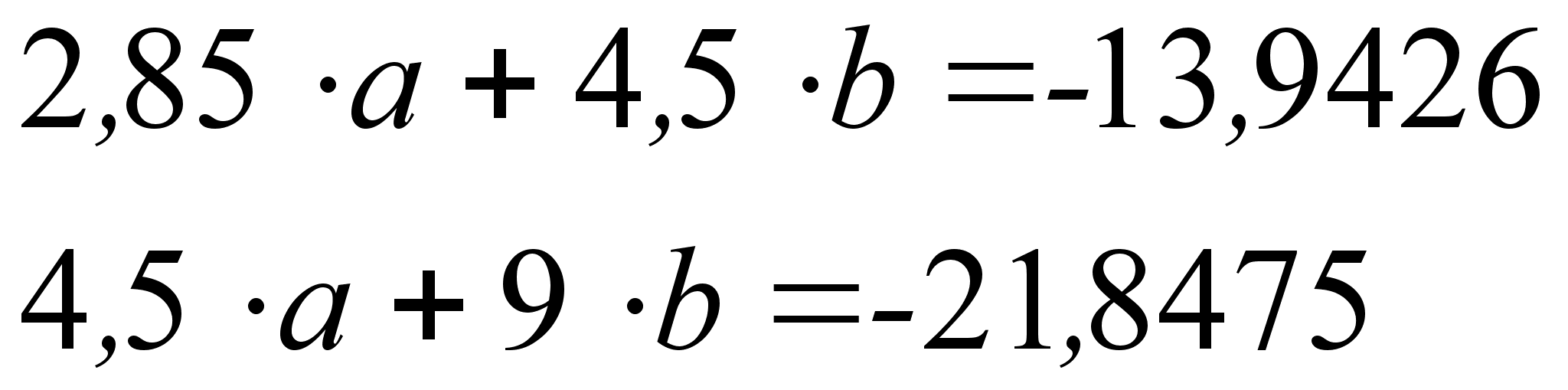
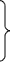
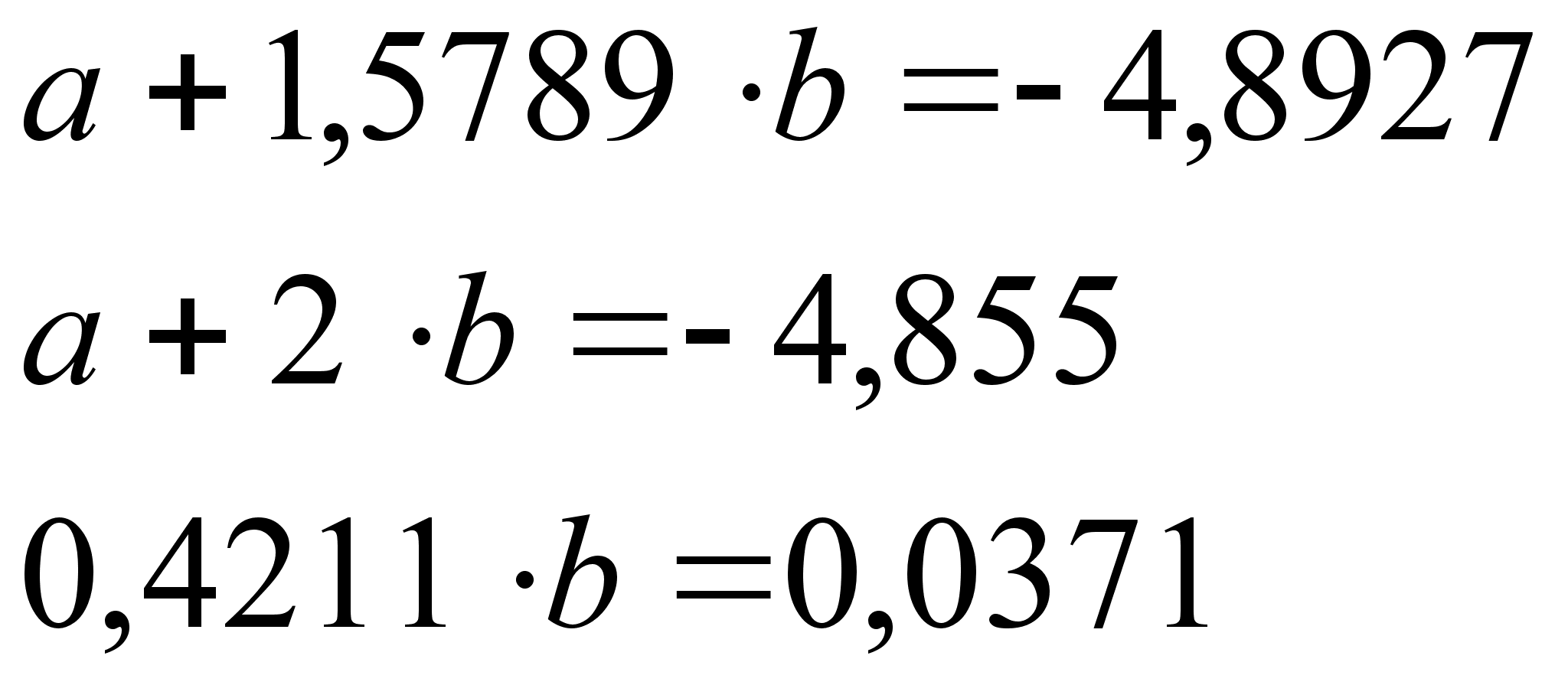

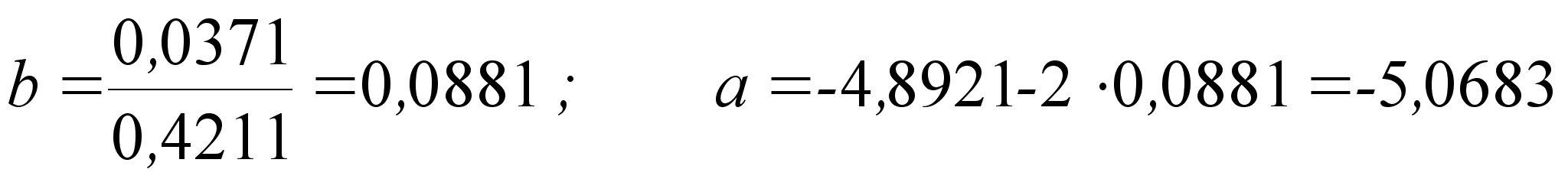 .
.
Таким
образом, для
функции
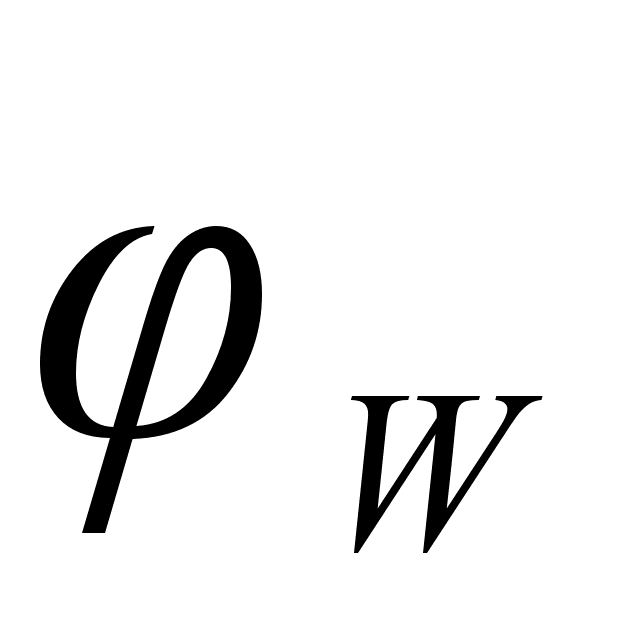 получено выражение:
получено выражение:
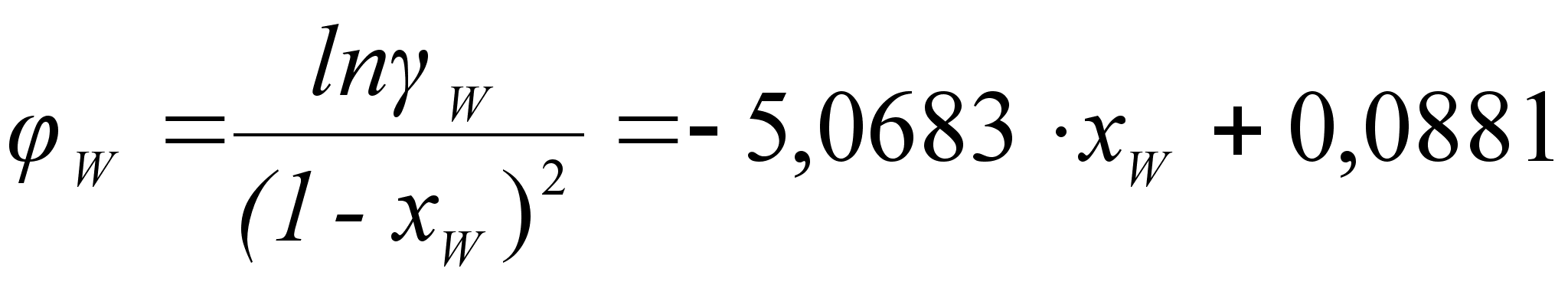
(125)
Уравнение
для
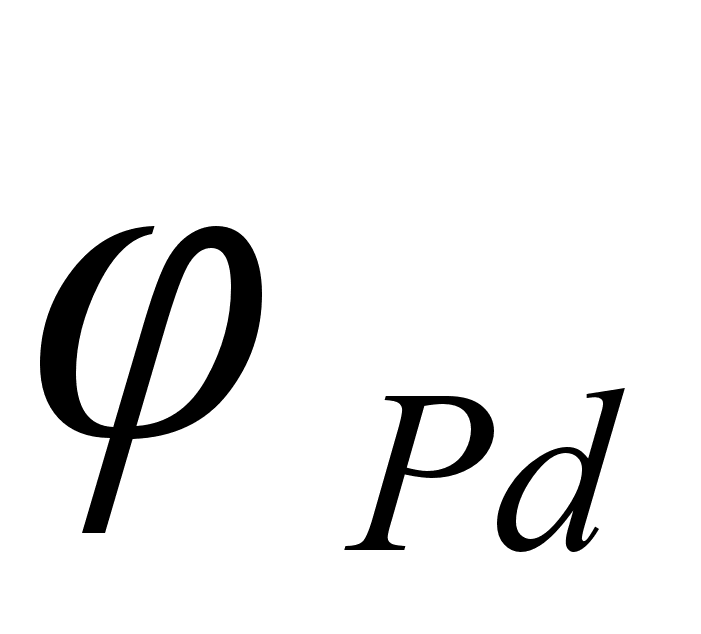 ,
полученное
аналогичным
образом имеет
вид:
,
полученное
аналогичным
образом имеет
вид:
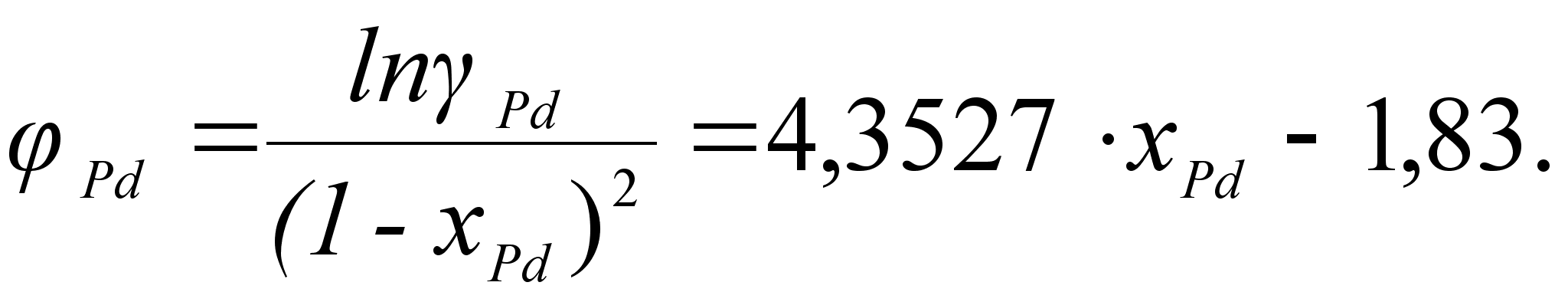
(126)
Исходные данные, скорректированные в соответствии с уравнением (125) приведены в таблице 19.
Таблица 19 – Скорректированные исходные данные для вольфрама.
|
|
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
|
|
-0,4183 | -0,9256 | -1,422 | -1,939 | -2,446 | -2,953 | -3,46 | -3,997 | -4,473 |
|
|
0,0712 | 0,1106 | 0,1487 | 0,199 | 0,2713 | 0,374 | 0,5127 | 0,6826 | 0,8606 |
По данным
таблицы 19 построим
рисунок 34, на
котором изображена
функция:
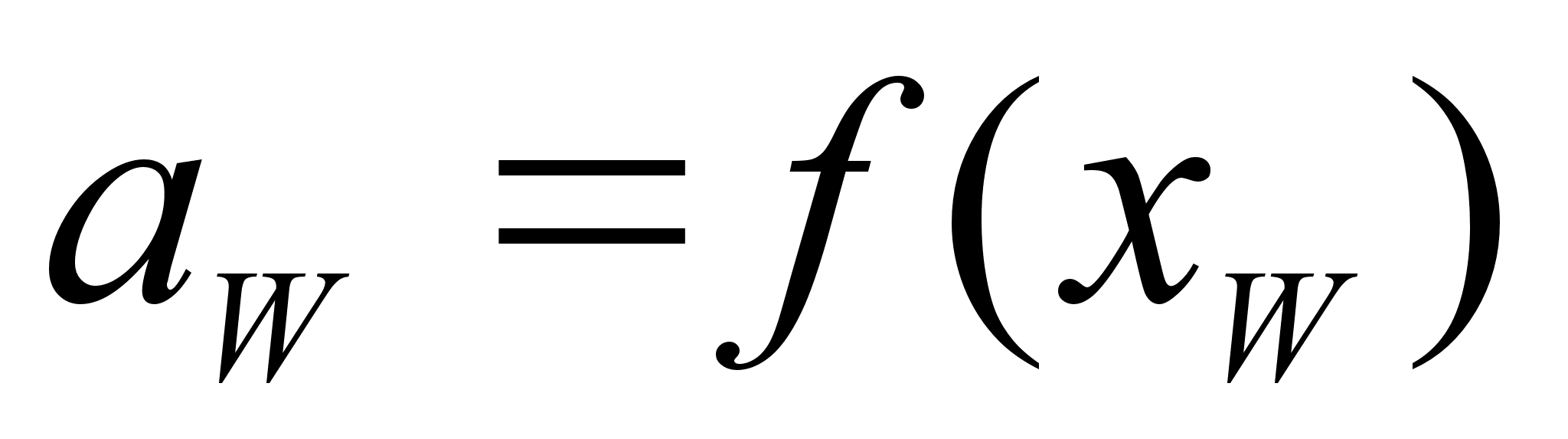 .
Из этого рисунка
получаем:
.
Из этого рисунка
получаем:
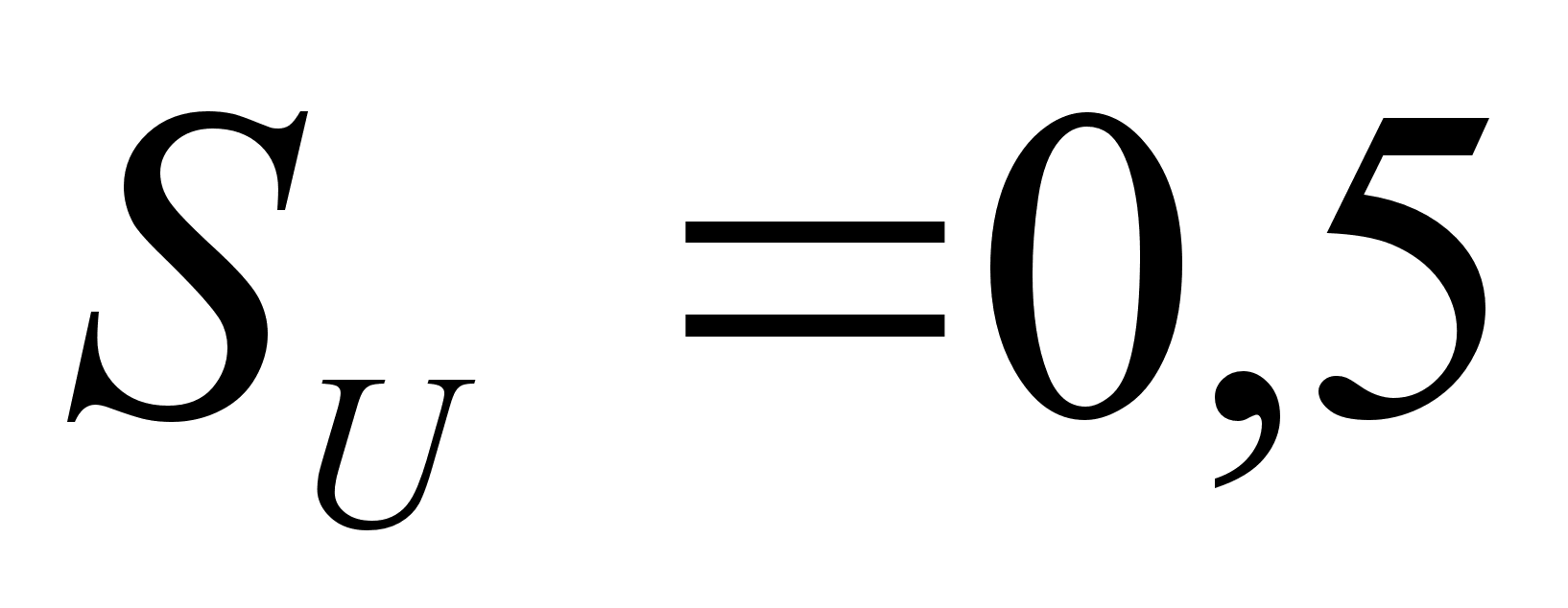 ;
;
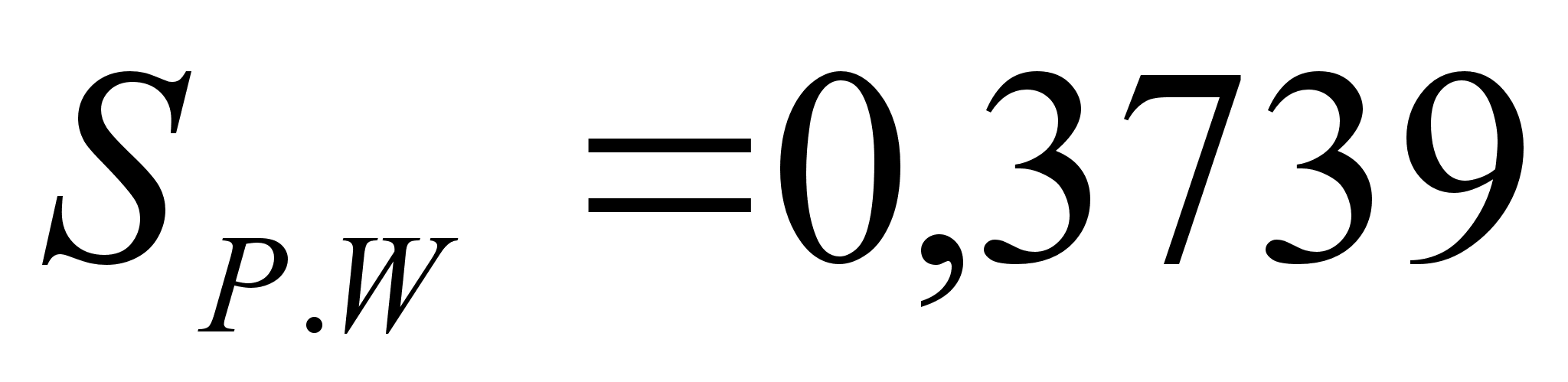 ;
;
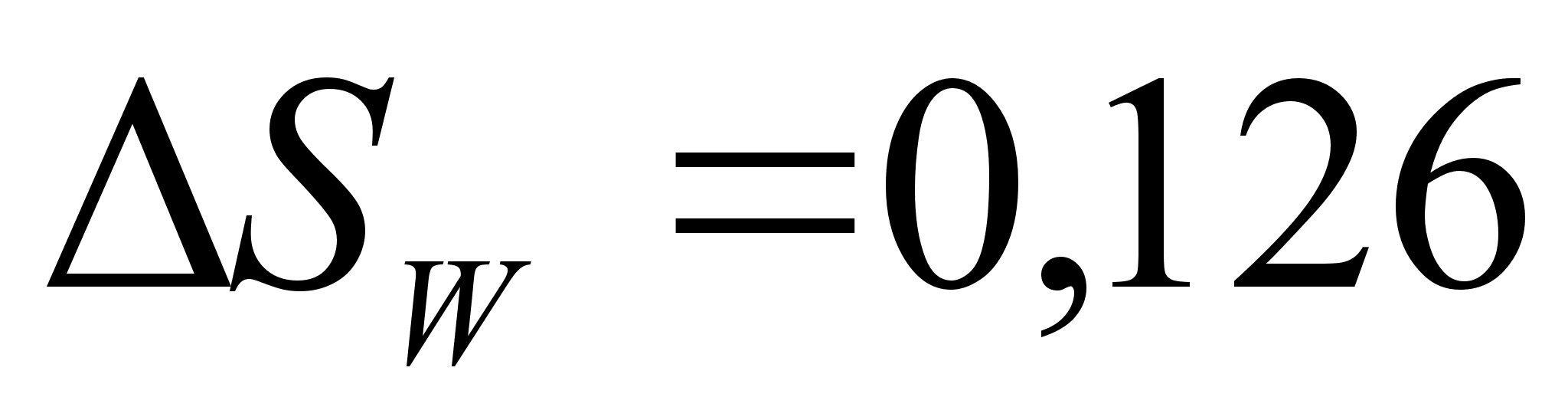 .
Коэффициент
отклонения
площади от
идеальности
равен:
.
Коэффициент
отклонения
площади от
идеальности
равен:
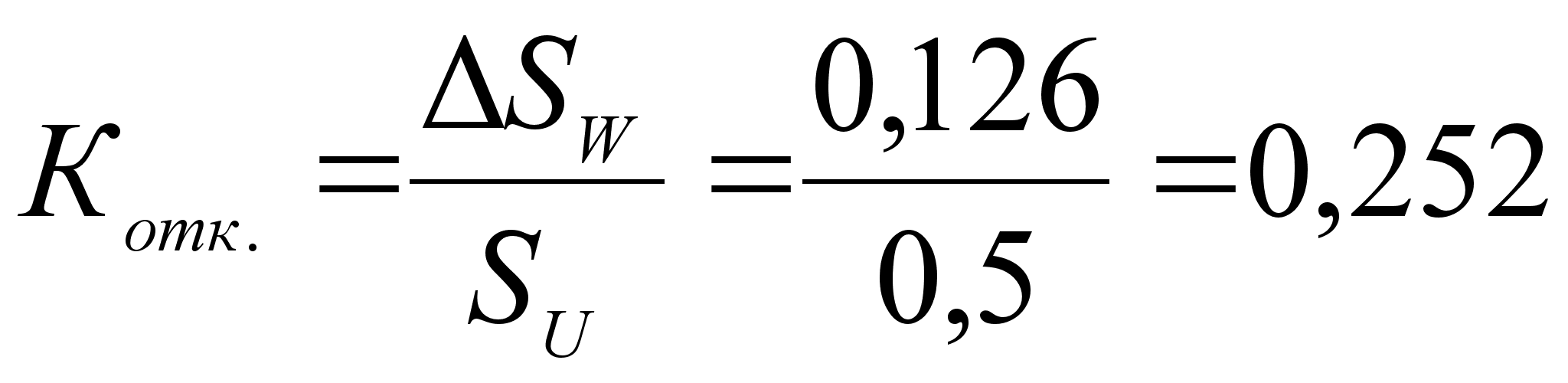 .
.
Графическим методом определены:
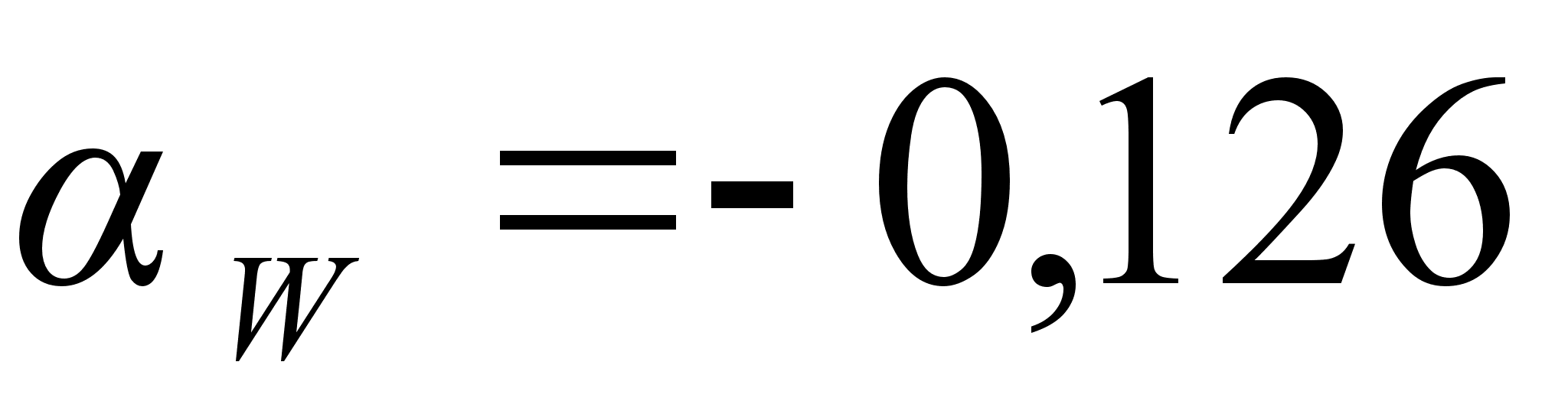 и
и
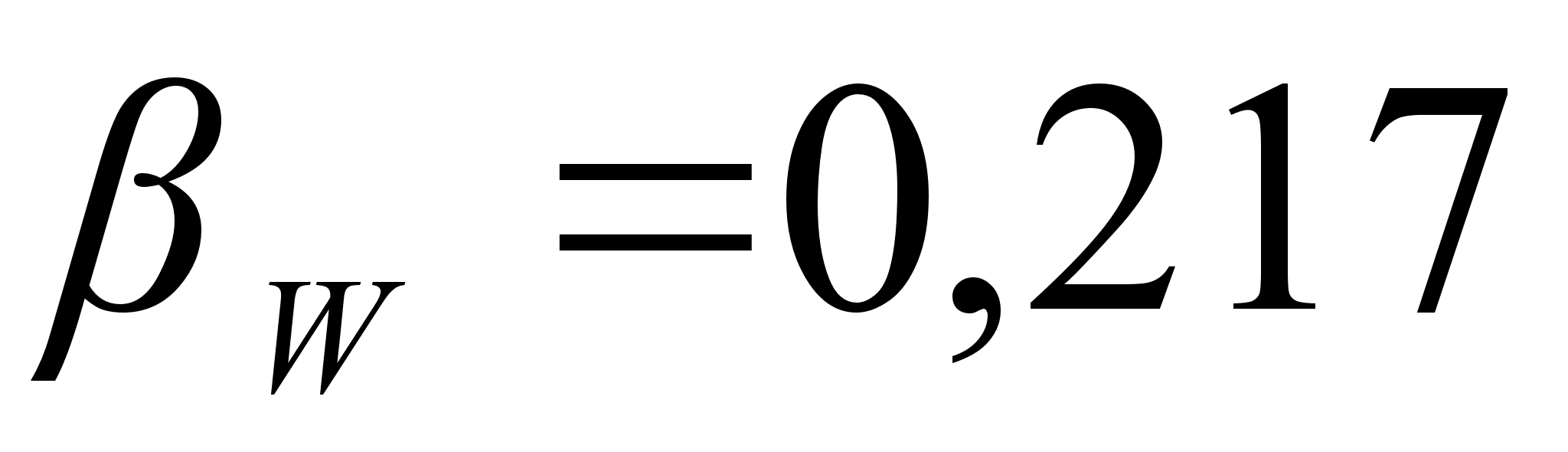 .
.
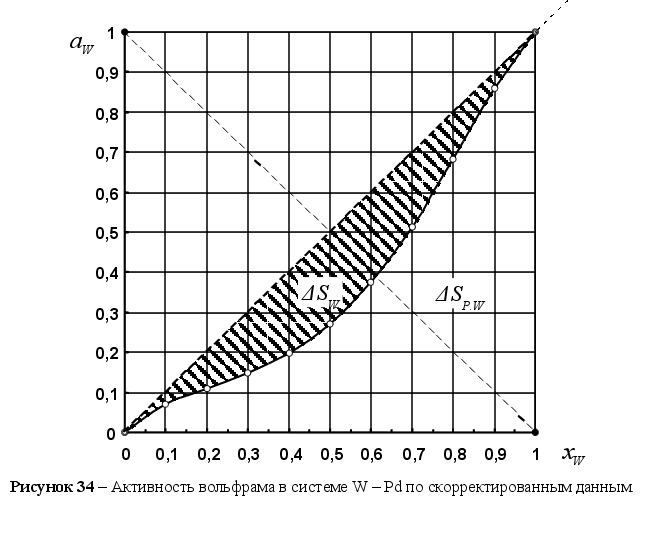
Из уравнения:
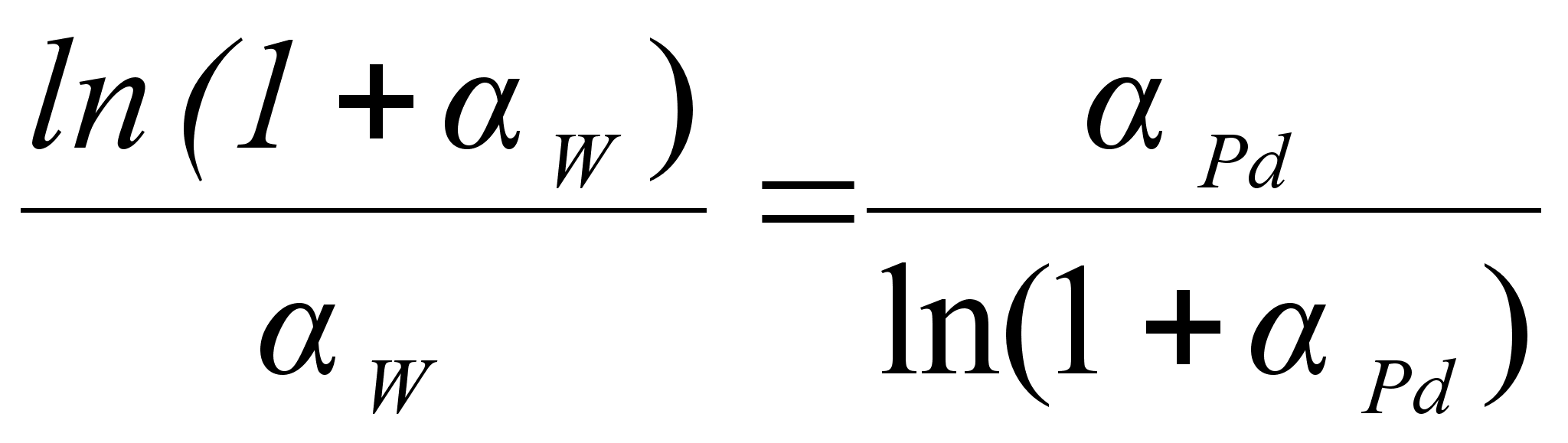 ,
,
определены:
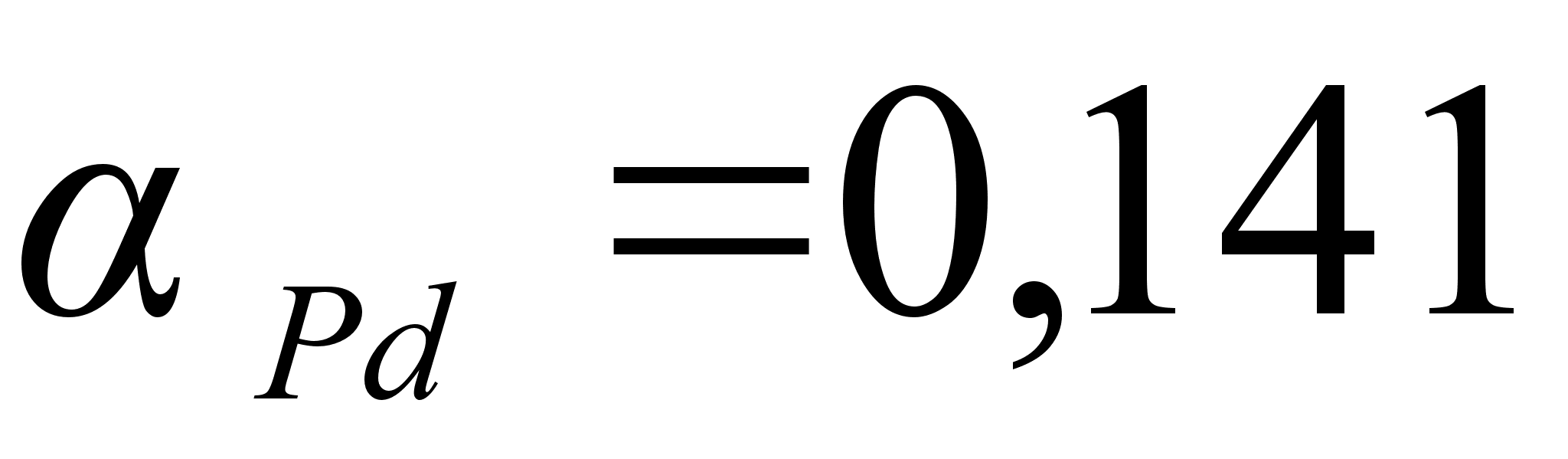 и
и
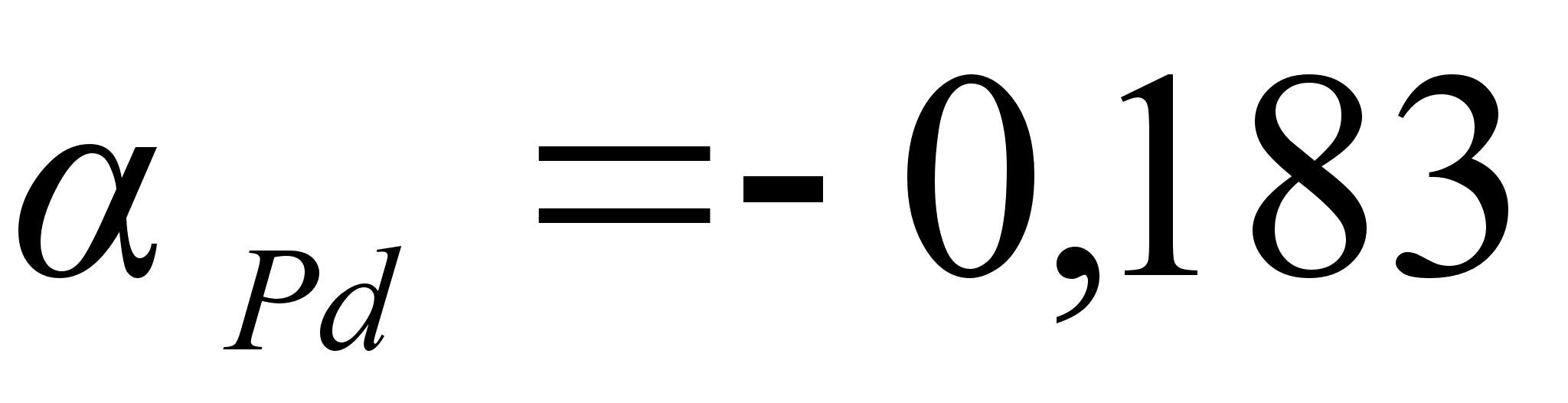 .
.
Далее, по уравнению (98) вычислим другие термодинамические характеристики для компонентов расплава W – Pd.
5.1.3 Вычисление
значений Аi,
Bi,
 и
и
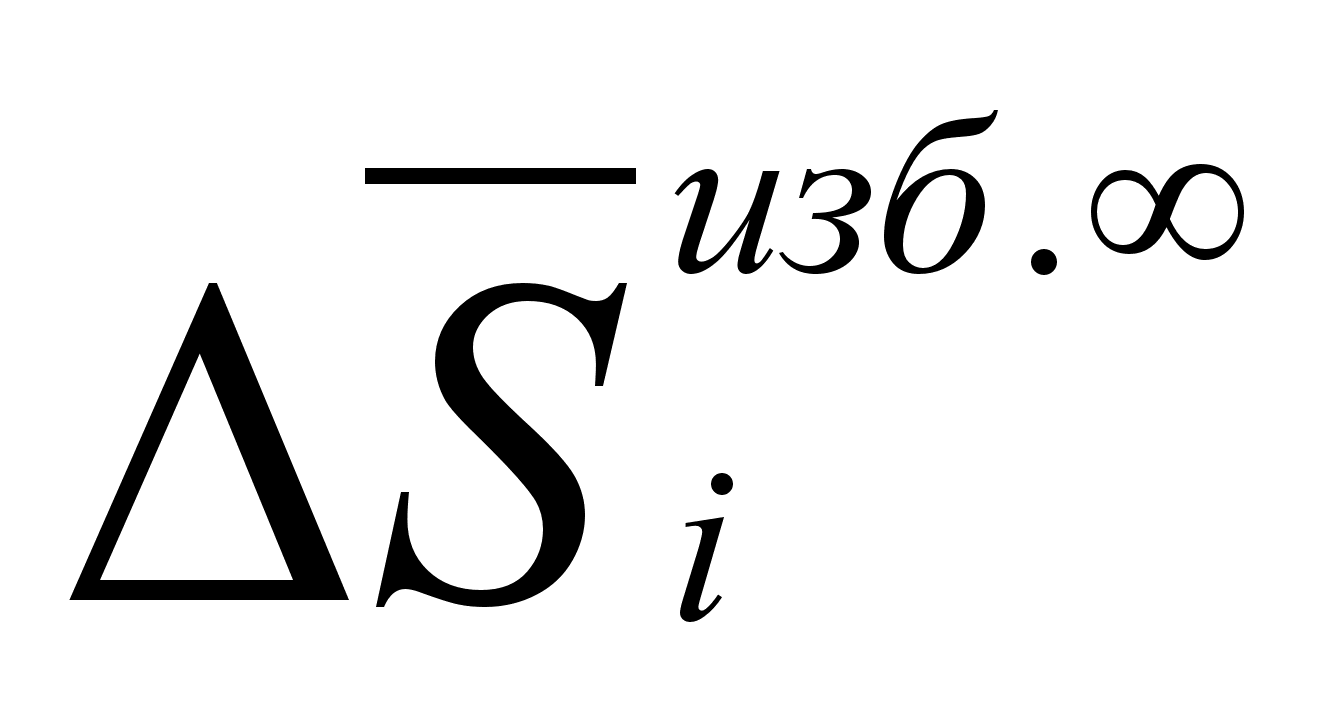 .
.
Термодинамические характеристики вольфрама в расплаве W – Pd.
|
|
|
|
|
|
|
|
|
|
|
Термодинамические характеристики палладия в расплаве W – Pd.
|
|
|
|
|
|
|
|
|
|
|
По приведенным термодинамическим характеристикам вычислим значения основных термодинамических характеристик компонентов в расплаве W – Pd при различных их концентрациях (таблицы 20 и 21).
По данным этих таблиц построены графики (рисунки 35 и 36).
Вывод: Показана применимость концентрационных уравнений для термодинамического описания бинарных металлических расплавов со знакопеременным отклонением от идеальности.
| Функция |
Концентрация вольфрама в расплаве - xW |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
0,1286 |
-0,399 |
-0,918 |
-1,429 |
-1,934 |
-2,433 |
-2,927 |
-3,417 |
3,904 |
-4,389 |
-4,872 |
|
|
0,1286 |
-0,323 |
-0,587 |
-0,700 |
-0,696 |
-0,608 |
-0,468 |
-0,308 |
-0,156 |
-0,044 |
0,00 |
|
|
1,137 |
0,724 |
0,556 |
0,496 |
0,498 |
0,544 |
0,626 |
0,735 |
0,855 |
0,957 |
1,00 |
|
|
0,00 |
0,0724 |
0,1112 |
0,1489 |
0,1994 |
0,2722 |
0,3756 |
0,5147 |
0,6843 |
0,8614 |
1,00 |
|
|
-253,26 |
-207,76 |
-166,28 |
-128,97 |
-96,01 |
-67,57 |
-43,84 |
-25,00 |
-11,27 |
-2,86 |
0,00 |
|
|
-129,4 |
-102,6 |
-79,4 |
-59,5 |
-42,86 |
-29,20 |
-18,30 |
-10,10 |
-4,40 |
-1,10 |
0,00 |
Таблица 20 – Вычисленные термодинамические характеристики вольфрама в расплаве W – Pd при Т=1873 К.
| Функция |
Концентрация палладия в расплаве - xPd |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-1,823 |
-1,402 |
-0,977 |
-0,548 |
-0,115 |
0,325 |
0,770 |
1,223 |
1,684 |
2,153 |
2,633 |
|
|
-1,823 |
-1,135 |
-0,625 |
-0,269 |
-0,041 |
0,081 |
0,123 |
0,110 |
0,067 |
0,022 |
0,00 |
|
|
0,167 |
0,321 |
0,535 |
0,764 |
0,960 |
1,085 |
1,131 |
0,112 |
1,070 |
1,022 |
1,00 |
|
|
0,00 |
0,0321 |
0,107 |
0,2293 |
0,3838 |
0,5423 |
0,6787 |
0,7814 |
0,8557 |
0,9196 |
1,00 |
|
|
-229,61 |
-183,40 |
-142,92 |
-107,94 |
-78,20 |
-53,60 |
-33,87 |
-18,81 |
-8,25 |
-2,04 |
0,00 |
|
|
-101,2 |
-83,5 |
-67,2 |
-52,5 |
-39,3 |
-27,8 |
-18,2 |
-10,4 |
-4,7 |
-1,2 |
0,0 |
Таблица 21 – Вычисленные термодинамические характеристики палладия в расплаве W – Pd при Т=1873 К.
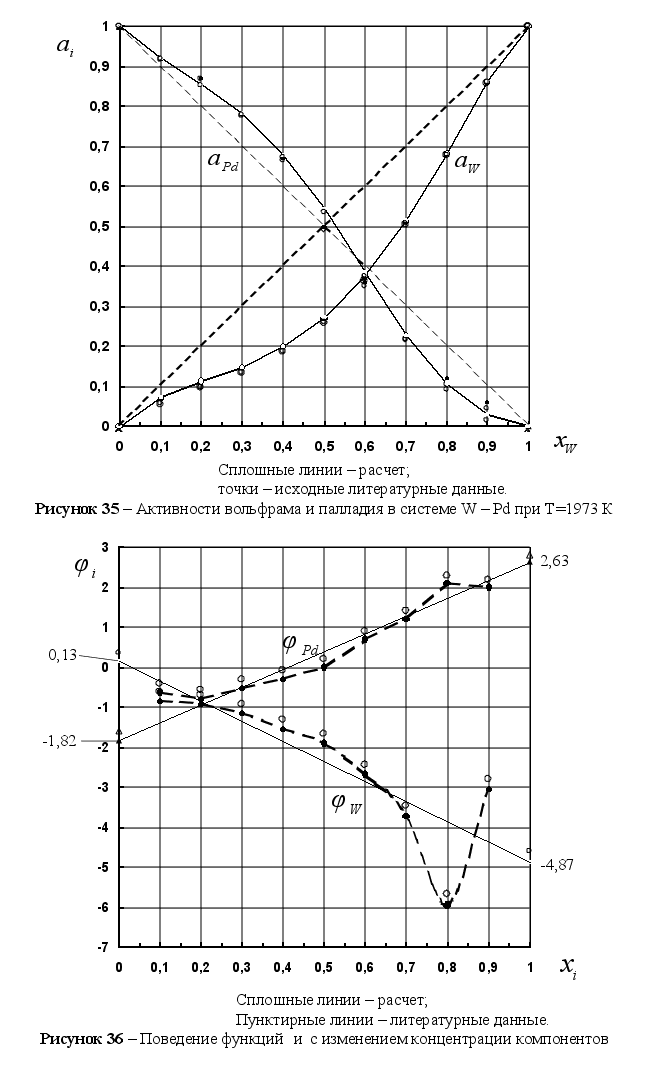
6 СИСТЕМЫ С РАЗЛИЧНЫМ ОТКЛОНЕНИЕМ ОТ ИДЕАЛЬНОСТИ
6.1 Системы с положительным отклонением от идеальности.
6.1.1 Система Fe – Mn.
Исходные данные. Исходные данные, взятые из разных источников, представлены в таблице 22.
Таблица 22 – Исходные данные для марганца.
| Функция |
xMn |
||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
|
aMn [21] |
0,124 | 0,242 | 0,364 | 0,46 | 0,54 | 0,634 | 0,708 | 0,81 | 0,905 |
|
aMn [25] |
0,137 | 0,257 | 0,363 | 0,46 | 0,552 | 0,638 | 0,725 | 0,813 | 0,904 |
|
aMn [26] |
0,122 | 0,239 | 0,351 | 0,455 | 0,552 | 0,644 | 0,731 | 0,817 | 0,905 |
|
aMn средн. |
0,128 | 0,246 | 0,359 | 0,460 | 0,548 | 0,639 | 0,721 | 0,813 | 0,905 |
|
|
0,01 | 0,04 | 0,09 | 0,16 | 0,25 | 0,36 | 0,49 | 0,64 | 0,81 |
|
|
0,305 | 0,323 | 0,366 | 0,388 | 0,367 | 0,394 | 0,328 | 0,403 | 0,554 |
|
|
0,030 | 0,065 | 0,11 | 0,155 | 0,183 | 0,236 | 0,230 | 0,322 | 0,499 |
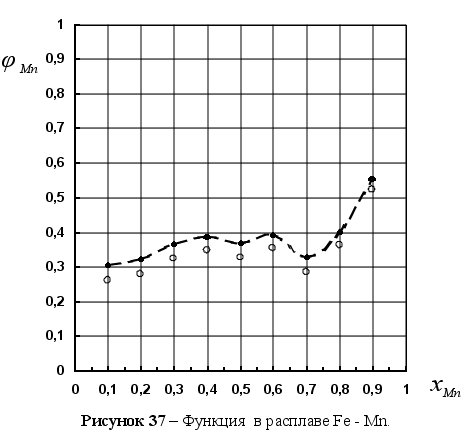
По этим данным
построим график
зависимости
функции
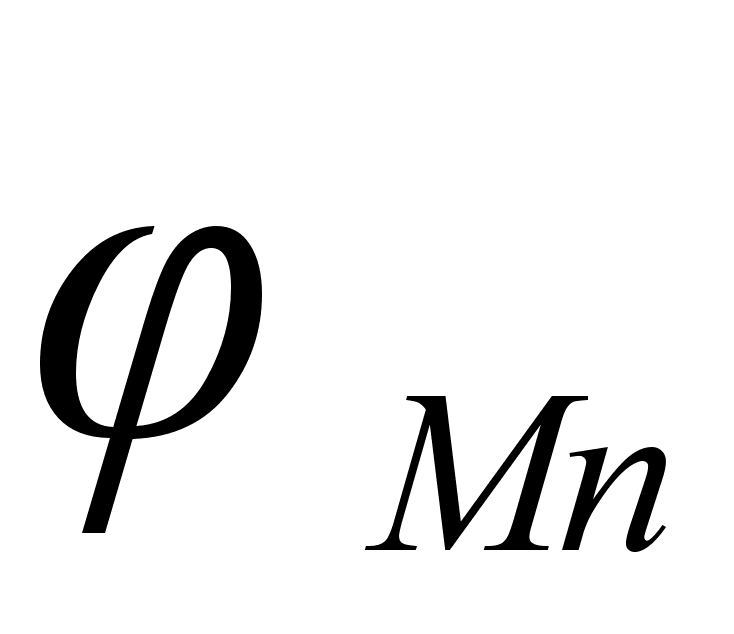 от концентрации
марганца в
расплаве (рисунок
37).
от концентрации
марганца в
расплаве (рисунок
37).
Корректировка данных.
Уравнение
прямой для
функции
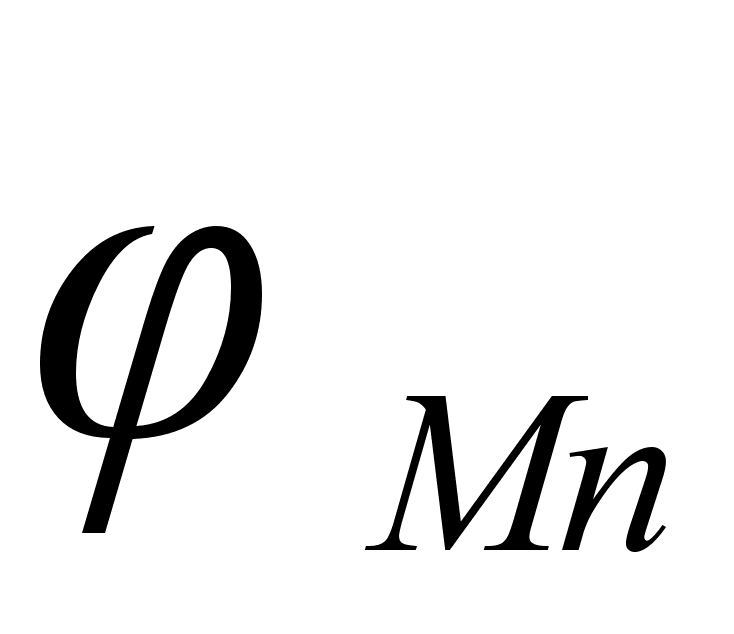 будет выглядеть
так:
будет выглядеть
так:
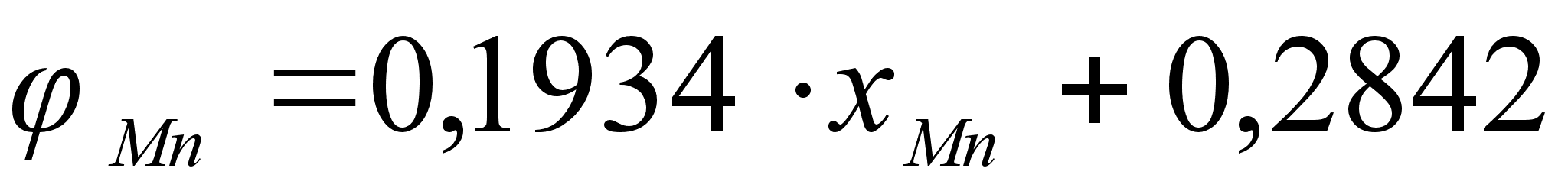
(127)
Таблица 23 – Скорректированные исходные данные для марганца.
|
|
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|
|
0,2842 | 0,304 | 0,323 | 0,342 | 0,362 | 0,381 | 0,400 | 0,420 | 0,439 | 0,458 | 0,478 |
|
|
0,00 | 0,128 | 0,246 | 0,355 | 0,456 | 0,550 | 0,640 | 0,727 | 0,814 | 0,904 | 1,00 |
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики марганца в расплаве Fe – Mn :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Функция |
Концентрация марганца в расплаве - xMn |
|||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| р а с ч е т |
|
0,2842 |
0,304 |
0,324 |
0,343 |
0,363 |
0,382 |
0,401 |
0,421 |
0,440 |
0,459 |
0,478 |
|
|
0,2842 |
0,246 |
0,207 |
0,168 |
0,131 |
0,095 |
0,064 |
0,038 |
0,018 |
0,005 |
0,00 |
|
|
|
1,329 |
1,279 |
1,23 |
1,183 |
1,139 |
1,10 |
1,066 |
1,039 |
1,018 |
1,005 |
1,00 |
|
|
|
0,00 |
0,128 |
0,246 |
0,355 |
0,456 |
0,55 |
0,64 |
0,727 |
0,814 |
0,904 |
1,00 |
|
| опыт |
|
- - - - |
0,305 |
0,323 |
0,366 |
0,388 |
0,367 |
0,394 |
0,328 |
0,403 |
0,554 |
- - - - |
|
|
0,00 |
0,128 |
0,246 |
0,359 |
0,460 |
0,548 |
0,639 |
0,721 |
0,813 |
0,905 |
1,00 |
Таблица 24 – Вычисленные термодинамические характеристики марганца в расплаве Fe – Mn при Т=1873 К.
Таблица 25 – Вычисленные термодинамические характеристики железа в расплаве Fe – Mn при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
|||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| р а с ч е т |
|
0,3814 |
0,362 |
0,343 |
0,324 |
0,305 |
0,285 |
0,266 |
0,246 |
0,227 |
0,207 |
0,1877 |
|
|
0,3814 |
0,293 |
0,220 |
0,159 |
0,110 |
0,071 |
0,043 |
0,022 |
0,009 |
0,002 |
0,00 |
|
|
|
1,463 |
1,341 |
1,246 |
1,172 |
1,116 |
1,074 |
1,043 |
1,022 |
1,009 |
1,002 |
1,00 |
|
|
|
0,00 |
0,134 |
0,249 |
0,352 |
0,446 |
0,537 |
0,626 |
0,716 |
0,807 |
0,902 |
1,00 |
|
| опыт |
|
н е т |
||||||||||
|
|
д а н н ы х |
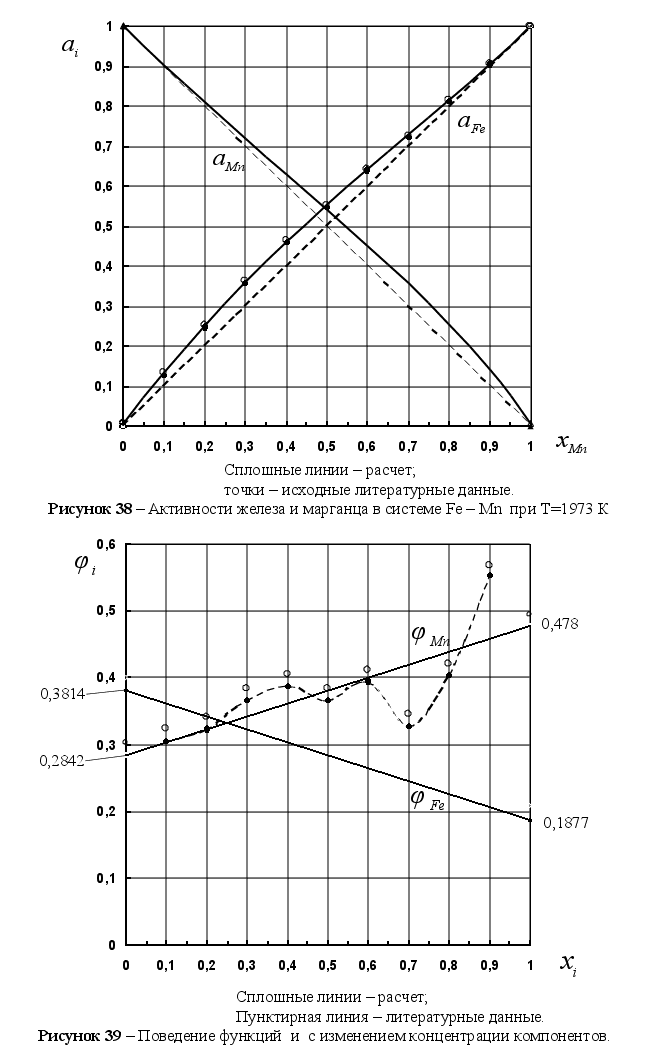
6.1.2 Система Fe – Sn.
|
xSn |
олово |
железосредние значения |
||||||
|
aSn [27] |
aSn [28] |
aSn [29] |
aFe [27] |
aFe [28] |
aFe [29] |
|||
|
aSn |
aFe |
|||||||
| 0,1 | 0,415 | 0,350 | 0,540 | 0,91 | 0,920 | 0,910 | 0,435 | 0,913 |
| 0,2 | 0,70 | 0,680 | 0,750 | 0,825 | 0,860 | 0,830 | 0,710 | 0,838 |
| 0,3 | 0,89 | 0,870 | 0,870 | 0,780 | 0,790 | 0,755 | 0,877 | 0,782 |
| 0,4 | 0,91 | 0,920 | 0,920 | 0,755 | 0,760 | 0,760 | 0,917 | 0,758 |
| 0,5 | 0,925 | 0,930 | 0,930 | 0,760 | 0,760 | 0,760 | 0,928 | 0,760 |
| 0,6 | 0,915 | 0,930 | 0,930 | 0,760 | 0,750 | 0,760 | 0,925 | 0,757 |
| 0,7 | 0,93 | 0,940 | 0,940 | 0,750 | 0,745 | 0,750 | 0,937 | 0,748 |
| 0,8 | 0,97 | 0,955 | 0,960 | 0,710 | 0,710 | 0,720 | 0,962 | 0,713 |
| 0,9 | 0,98 | 0,970 | 0,975 | 0,675 | 0,620 | 0,675 | 0,975 | 0,657 |
По средним значениям активности компонентов вычислим их коэффициенты активности и функции .
aFe
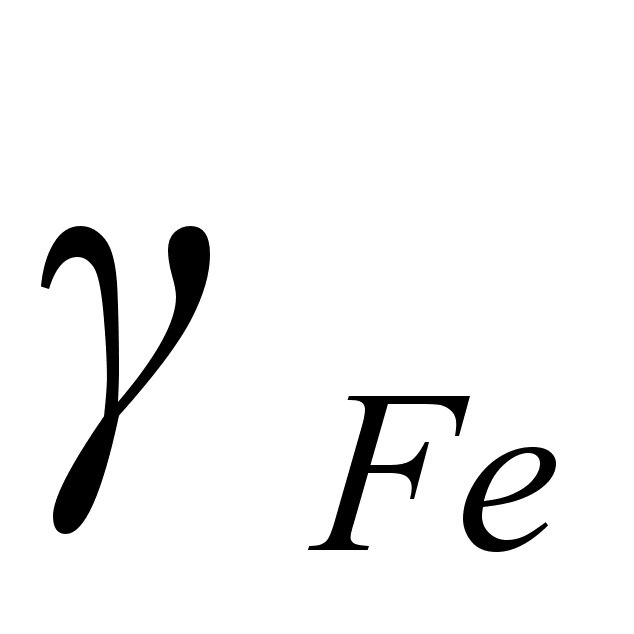
Корректировка данных.
Уравнение
прямой для
функции
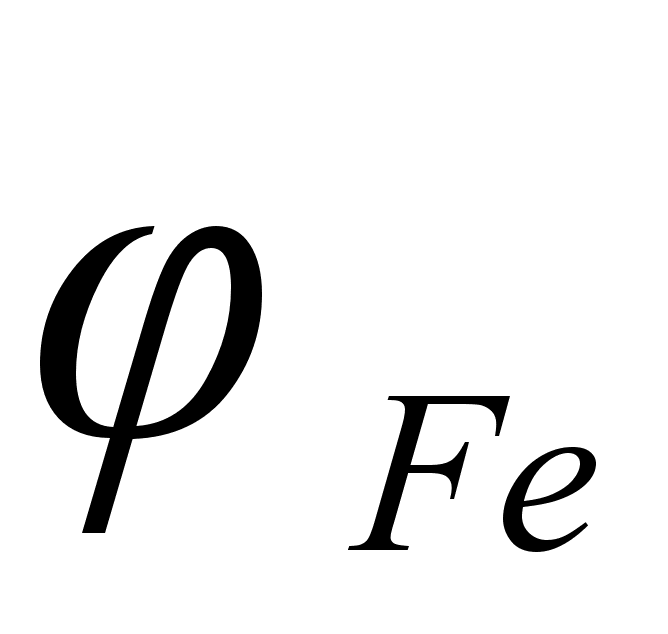 будет выглядеть
так:
будет выглядеть
так:
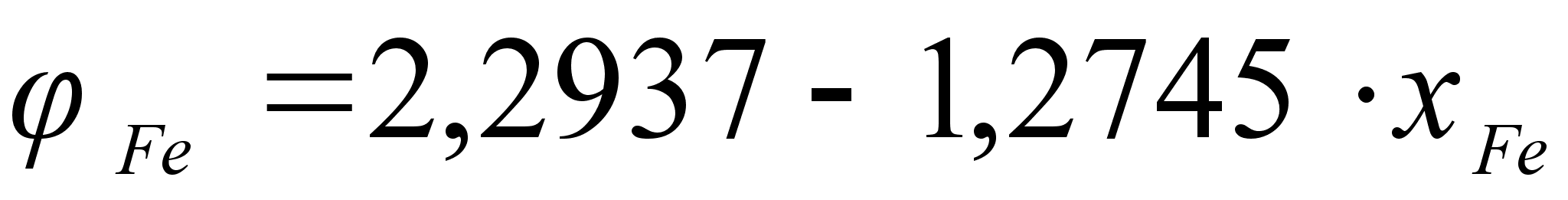
(128)
Таблица 28 – Скорректированные исходные данные для железа.
|
|
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|
|
2,2937 | 2,166 | 2,039 | 1,911 | 1,784 | 1,656 | 1,529 | 1,402 | 1,274 | 1,147 | 1,019 |
|
|
0,0 | 0,578 | 0,737 | 0,765 | 0,760 | 0,757 | 0,766 | 0,794 | 0,842 | 0,910 | 1,00 |
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики железа в расплаве Fe – Sn :
|
|
|
|
|
|
|
|
|
|
|
Характеристики олова:
|
|
|
|
|
|
|
|
|
|
|
Таблица 29 – Вычисленные термодинамические характеристики железа в расплаве Fe – Sn при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
2,2937 |
2,139 |
1,993 |
1,854 |
1,722 |
1,595 |
1,473 |
1,356 |
1,241 |
1,129 |
1,019 |
|
|
2,2937 |
1,732 |
1,275 |
0,908 |
0,620 |
0,399 |
0,236 |
0,122 |
0,05 |
0,011 |
0,00 |
|
|
9,912 |
5,654 |
3,579 |
2,480 |
1,859 |
1,490 |
1,266 |
1,13 |
1,051 |
1,011 |
1,00 |
|
|
0,0 |
0,565 |
0,716 |
0,744 |
0,743 |
0,745 |
0,760 |
0,791 |
0,841 |
0,910 |
1,00 |
|
|
42914 |
33377 |
25362 |
18702 |
13251 |
8886 |
5498 |
2993 |
1289 |
313 |
0,00 |
|
|
8,212 |
6,816 |
5,521 |
4,337 |
3,271 |
2,334 |
1,535 |
0,889 |
0,407 |
0,105 |
0,00 |
| Функция |
Концентрация олова в расплаве - xSn |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
1,6154 |
1,735 |
1,859 |
1,988 |
2,121 |
2,262 |
2,409 |
2,564 |
2,790 |
2,906 |
3,095 |
|
|
1,615 |
1,406 |
1,19 |
0,974 |
0,764 |
0,565 |
0,385 |
0,231 |
0,109 |
0,029 |
0,00 |
|
|
5,03 |
4,078 |
3,287 |
2,648 |
2,146 |
1,760 |
1,470 |
1,260 |
1,115 |
1,029 |
1,00 |
|
|
0,0 |
0,408 |
0,657 |
0,795 |
0,859 |
0,880 |
0,882 |
0,882 |
0,892 |
0,927 |
1,00 |
|
|
35901 |
30002 |
24482 |
19379 |
14737 |
10606 |
7044 |
4117 |
1905 |
496 |
0,00 |
|
|
9,393 |
7,387 |
5,671 |
4,223 |
3,019 |
2,042 |
1,274 |
0,699 |
0,303 |
0,074 |
0,00 |
Таблица 30 – Вычисленные термодинамические характеристики олова в расплаве Fe – Sn при Т=1873 К.
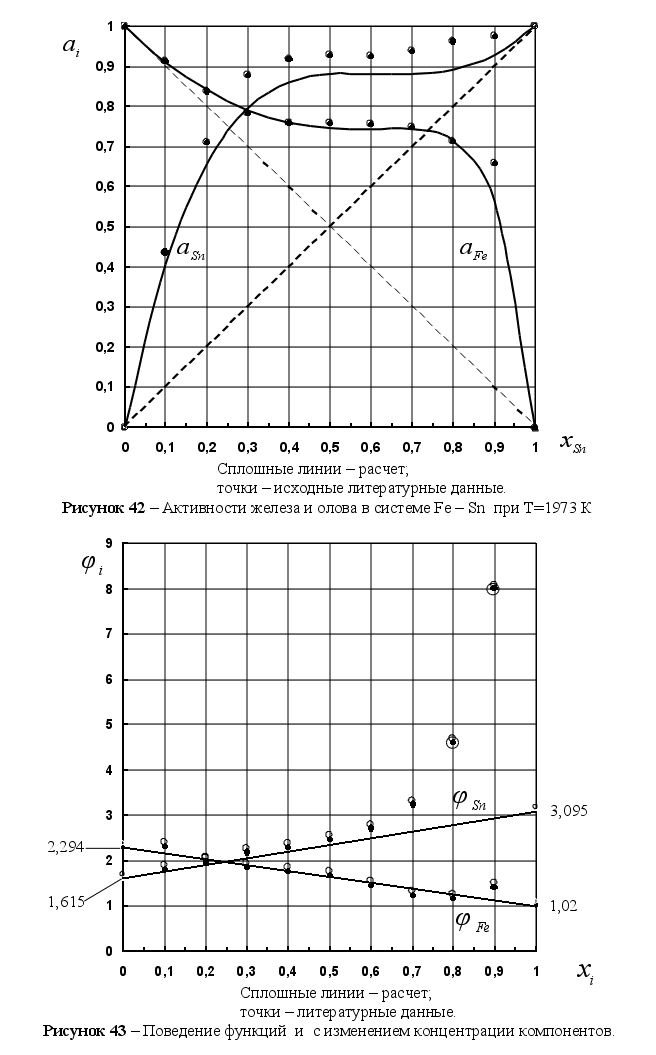
6.1.3 Система Fe – Cr.
Исходные данные. Исходные данные взяты из литературного источника [18].
| Функция |
Концентрация
хрома в расплаве
–
|
||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
|
|
5398 | 3989 | 3010 | 2436 | 2007 | 1529 | 1003 | 669 | 323 |
|
|
0,192 | 0,296 | 0,399 | 0,475 | 0,542 | 0,627 | 0,736 | 0,815 | 0,906 |
|
|
0,805 | 0,613 | 0,582 | 0,477 | 0,323 | 0,275 | 0,557 | 0,464 | 0,664 |
По этим данным
построим график
функции
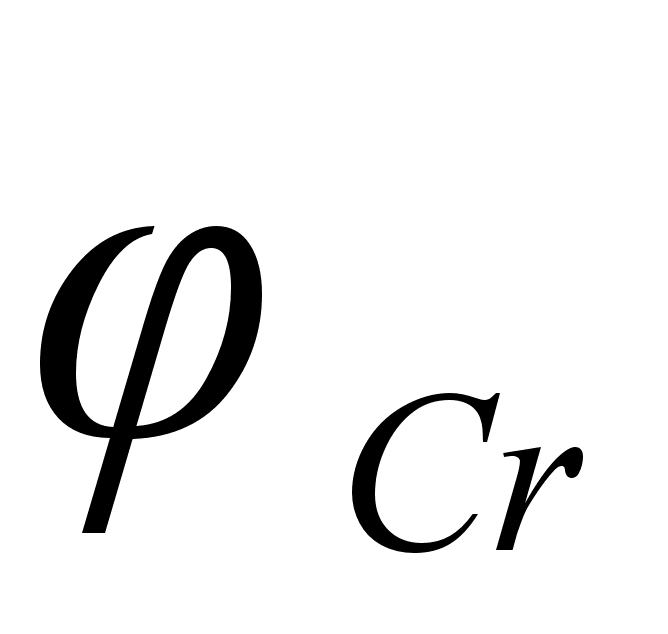 (см. рисунок
44).
(см. рисунок
44).
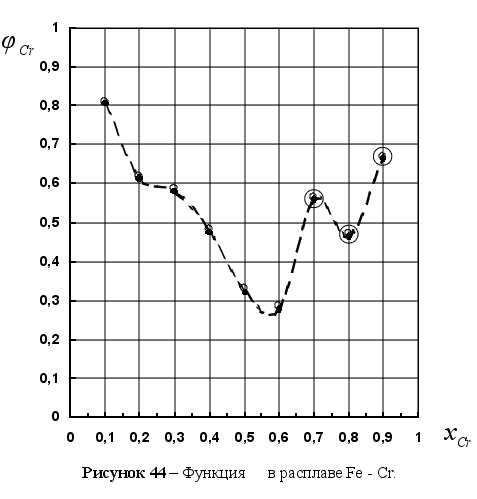
Корректировка данных. В процессе корректировки данных точки, обведенные не графике кругами, мы в расчет не принимаем.
Уравнение
прямой для
функции
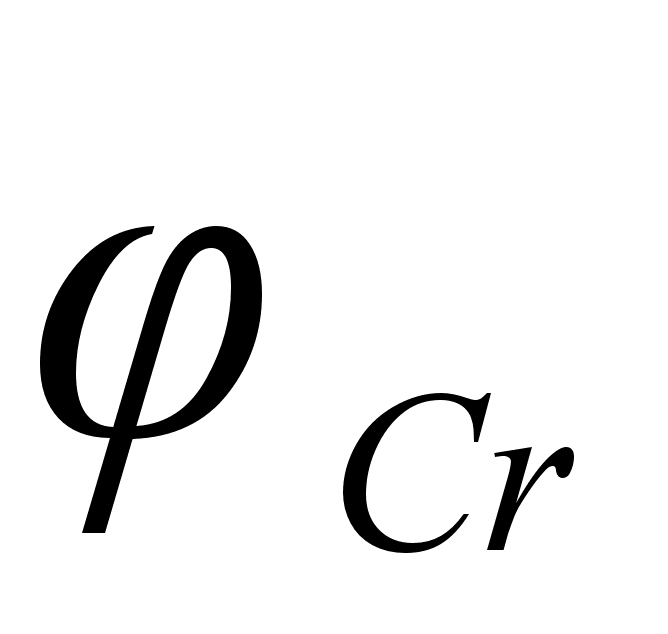 :
:
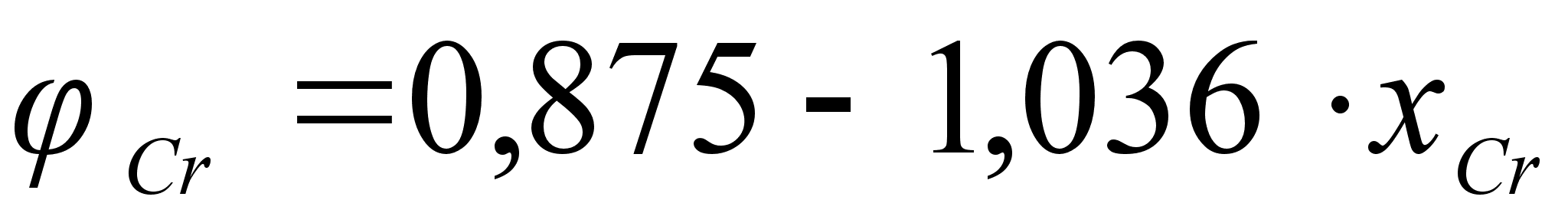
(129)
Таблица 32 – Скорректированные исходные данные для хрома.
|
|
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|
|
0,875 |
0,771 | 0,668 | 0,564 | 0,461 | 0,357 | 0,253 | 0,150 | 0,046 | -0,057 | -0,161 |
|
|
0,00 | 0,187 | 0,307 | 0,396 | 0,472 | 0,547 | 0,625 | 0,710 | 0,801 | 0,899 | 1,00 |
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики хрома в расплаве Fe – Cr :
|
|
|
|
|
|
|
|
|
|
|
Характеристики железа:
|
|
|
|
|
|
|
|
|
|
|
| Функция |
Концентрация хрома в расплаве - xCr |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
0,875 |
0,768 |
0,663 |
0,558 |
0,453 |
0,349 |
0,246 |
0,144 |
0,042 |
-0,06 |
-0,161 |
|
|
0,875 |
0,622 |
0,424 |
0,273 |
0,163 |
0,087 |
0,039 |
0,013 |
0,002 |
-0,006 |
0,00 |
|
|
2,399 |
1,864 |
1,529 |
1,314 |
1,177 |
1,091 |
1,040 |
1,013 |
1,002 |
0,999 |
1,00 |
|
|
0,00 |
0,186 |
0,306 |
0,394 |
0,471 |
0,546 |
0,624 |
0,709 |
0,801 |
0,899 |
1,00 |
|
|
125519 |
100899 |
79122 |
60124 |
43845 |
30224 |
19202 |
10723 |
4731 |
1174 |
0,00 |
|
|
68,889 |
56,049 |
44,484 |
34,211 |
25,248 |
17,613 |
11,324 |
6,399 |
2,857 |
0,718 |
0,00 |
Таблица 34 – Вычисленные термодинамические характеристики железа в расплаве Fe – Cr при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
0,351 |
0,454 |
0,557 |
0,661 |
0,766 |
0,871 |
0,977 |
1,083 |
1,191 |
1,299 |
1,407 |
|
|
0,351 |
0,368 |
0,357 |
0,324 |
0,276 |
0218 |
0,156 |
0,097 |
0,048 |
0,013 |
0,00 |
|
|
1,42 |
1,444 |
1,428 |
1,383 |
1,317 |
1,243 |
1,169 |
1,102 |
1,049 |
1,013 |
1,00 |
|
|
0,00 |
0,144 |
0,286 |
0,415 |
0,527 |
0,622 |
0,701 |
0,772 |
0,839 |
0,912 |
1,00 |
|
|
120949 |
98674 |
78530 |
60564 |
44824 |
31358 |
20219 |
11459 |
5131 |
1293 |
0,00 |
|
|
70,466 |
56,813 |
44,683 |
34,053 |
24,905 |
17,216 |
10,969 |
6,142 |
2,718 |
0,676 |
0,00 |
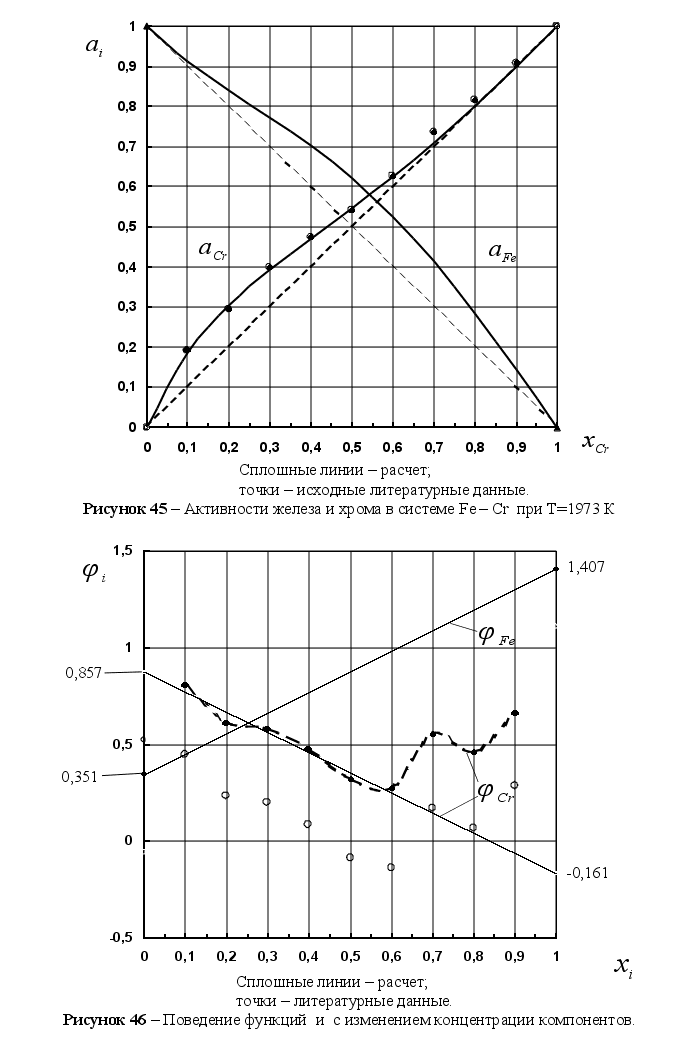
6.2 Системы с отрицательным отклонением от идеальности.
6.2.1 Система Fe – Al.
Таблица 35 – Исходные данные по коэффициентам активности компонентов в растворе Fe – Al, при Т=1876 К.
|
Концентрация железа в расплаве – xFe |
|||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
|
|
0,011 | 0,042 | 0,124 | 0,234 | 0,337 | 0,550 | 0,733 | 0,875 | 0,968 |
|
|
0,946 | 0,820 | 0,682 | 0,525 | 0,376 | 0,266 | 0,184 | 0,118 | 0,081 |
Таблица 36 – Обработанные исходные данные для системы Fe – Al.
железо |
алюминий
|
aFe |
|
|
|
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|
|
-2,647 | -2,924 | -3,201 | -3,478 | -3,754 | -4,031 | -4,308 | -4,585 | -4,861 | -5,138 | -5,415 |
|
|
0,00 | 0,0094 | 0,0258 | 0,055 | 0,1035 | 0,183 | 0,301 | 0,463 | 0,659 | 0,855 | 1,00 |
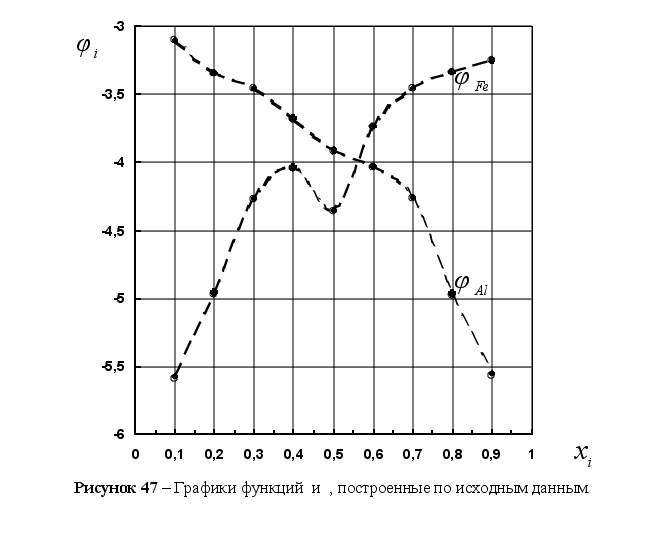
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики алюминия в расплаве Fe – Al :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Функция |
Концентрация алюминия в расплаве - xAl |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-2,647 |
-2,927 |
-3,203 |
-3,478 |
-3,751 |
-4,023 |
-4,297 |
-4,572 |
-4,849 |
-5,130 |
-5,425 |
|
|
-2,647 |
-2,371 |
-2,050 |
-1,704 |
-1,305 |
-1,006 |
-0,688 |
-0,411 |
-0,194 |
-0,051 |
0,00 |
|
|
0,071 |
0,093 |
0,129 |
0,182 |
0,259 |
0,366 |
0,503 |
0,663 |
0,824 |
0,950 |
1,00 |
|
|
0,00 |
0,009 |
0,026 |
0,055 |
0,104 |
0,183 |
0,302 |
0,464 |
0,659 |
0,855 |
1,00 |
|
|
-113287 |
-93492 |
-75289 |
-58773 |
-44042 |
-31209 |
-20389 |
-11713 |
-5319 |
-1359 |
0,00 |
|
|
-38,477 |
-30,206 |
-23,153 |
-17,212 |
-12,289 |
-8,30 |
-5,170 |
-2,832 |
-1,227 |
-0,299 |
0,00 |
Таблица 39 – Вычисленные термодинамические характеристики железа в расплаве Fe – Al при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-4,026 |
-3,749 |
-3,475 |
-3,201 |
-2,927 |
-2,652 |
-2,376 |
-2,096 |
-1,813 |
-1,524 |
-1,229 |
|
|
-4,026 |
-3,037 |
-2,224 |
-1,568 |
-1,054 |
-0,663 |
-0380 |
-0,189 |
-0,073 |
-0,015 |
0,00 |
|
|
0,018 |
0,048 |
0,108 |
0,208 |
0,349 |
0,515 |
0,684 |
0,828 |
0,930 |
0,985 |
1,00 |
|
|
0,00 |
0,005 |
0,022 |
0,063 |
0,139 |
0,258 |
0,410 |
0,580 |
0,744 |
0,886 |
1,00 |
|
|
-125269 |
-99284 |
-76793 |
-57581 |
-41449 |
-28214 |
-17706 |
-9770 |
-4261 |
-1046 |
0,00 |
|
|
-33,409 |
-27,758 |
22,512 |
-17,703 |
-13,370 |
-9,551 |
-6,293 |
-3,648 |
-1,672 |
-0,432 |
0,00 |
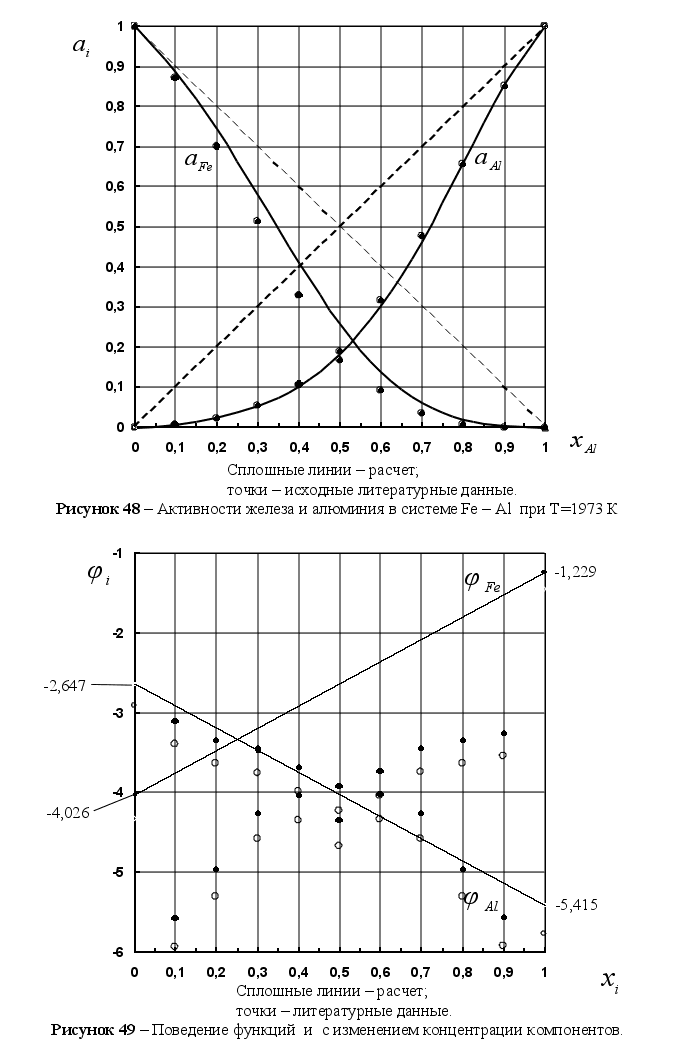
6.2.2 Система Fe – Co.
Исходные данные.
Таблица 40 – Литературные данные по [31] при 1873 К.
|
xCo |
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 |
|
aCo |
0,05 | 0,10 | 0,17 | 0,23 | 0,325 | 0,44 | 0,58 | 0,74 | 0,89 |
|
aFe |
0,90 | 0,80 | 0,67 | 0,56 | 0,43 | 0,30 | 0,175 | 0,09 | 0,03 |
|
Концентрация компонента в расплаве – xi |
||||||||||
| функция | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |||||
|
|
Расч. |
Литер. |
Расч. |
Литер. |
Расч. |
Литер. |
Расч. |
Литер. |
Расч. |
Литер. |
|
|
0,82 | 0,96 | 0,89 | 0,97 | 0,96 | 0,98 | 0,98 | 0,99 | 1,0 | 1,0 |
|
|
0,74 | 1,01 | 0,9 | 1,02 | 0,95 | 1,03 | 0,98 | 1,04 | 1,0 | 1,0 |
|
|
0,890 | 0,930 | 0,950 | 0,985 | 1,00 | |||||
|
|
0,875 | 0,960 | 0,990 | 1,010 | 1,00 | |||||
|
|
0,178 | 0,372 | 0,570 | 0,788 | 1,00 | |||||
|
|
0,175 | 0,384 | 0,594 | 0,808 | 1,00 |
Таблица 42 – Средние значения aCo и aFe по данным литературных источников [31] и [11].
| активность |
концентрация кобальта в расплаве - xCo. |
|||||||||
| 0,1 | 0,2 | 0, 3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| [31] |
aCo |
0,050 | 0,1000 | 0,1700 | 0,230 | 0,3250 | 0,440 | 0,5800 | 0,740 | 0,890 |
|
aFe |
0,900 | 0,8000 | 0,6900 | 0,560 | 0,4300 | 0,300 | 0,1750 | 0,090 | 0,030 | |
| [11] |
aCo |
0,080 | 0,1750 | 0,2700 | 0,384 | 0,4900 | 0,594 | 0,7500 | 0,808 | 0,910 |
|
aFe |
0,900 | 0,7880 | 0,6750 | 0,570 | 0,4900 | 0,372 | 0,2700 | 0,178 | 0,100 | |
| средн. знач. |
aCo |
0,065 | 0,1375 | 0,2200 | 0,307 | 0,4075 | 0,517 | 0,6650 | 0,774 | 0,900 |
|
aFe |
0,900 | 0,7940 | 0,6825 | 0,565 | 0,4450 | 0,336 | 0,2225 | 0,134 | 0,065 |
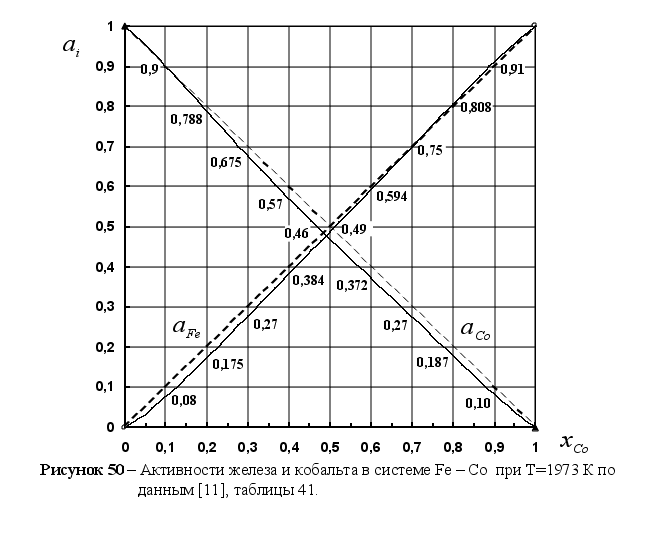
По данным
таблицы 42 вычислим
значения функций
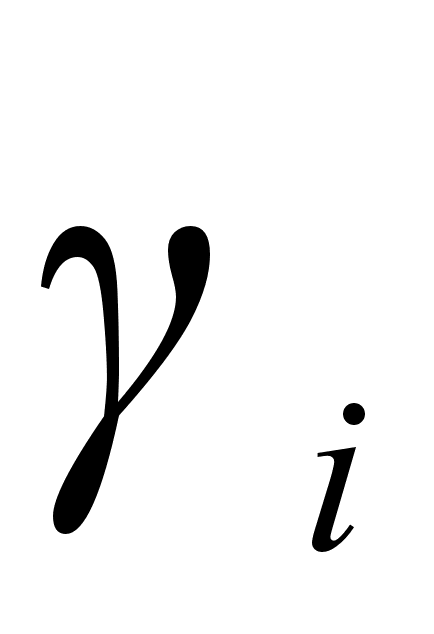 и
и
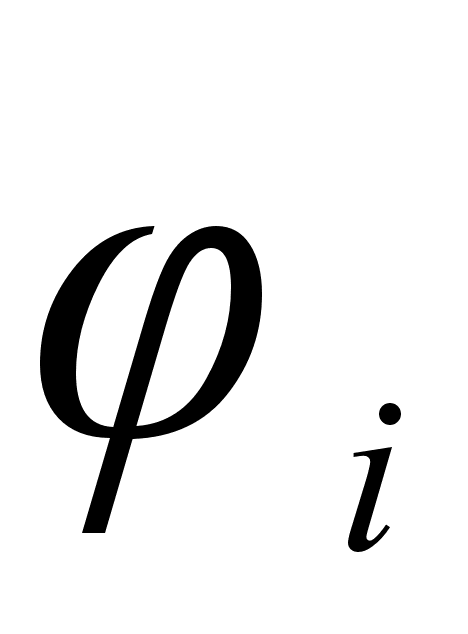 для компонентов
расплава Fe
– Co.
Эти вычисления
приведены в
таблице 43.
для компонентов
расплава Fe
– Co.
Эти вычисления
приведены в
таблице 43.
Таблица 43 – Обработанные исходные данные для системы Fe – Co.
железо |
кобальтaFe |
|
|
|
|
0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|
|
-0,7466 | -0,676 | -0,606 | -0,536 | -0,466 | -0,396 | -0,326 | -0,256 | -0,186 | -0,115 | -0,0453 |
|
|
0,00 | 0,058 | 0,136 | 0,231 | 0,338 | 0,453 | 0,570 | 0,684 | 0,794 | 0,839 | 1,00 |
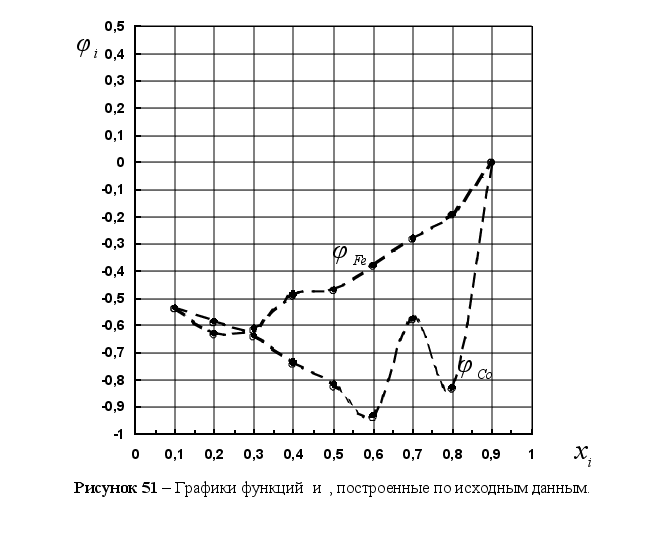
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики железа в расплаве Fe – Co:
|
|
|
|
|
|
|
|
|
|
|
Характеристики кобальта:
|
|
|
|
|
|
|
|
|
|
|
Термодинамические характеристики компонентов, при различных их концентрациях, приведены в таблицах 45 и 46. По данным этих таблиц построены графики (рисунки 52 и 53)
Таблица 45 – Вычисленные термодинамические характеристики железа в расплаве Fe – Co при Т=1873 К.
| Функция |
Концентрация железа в расплаве - xFe |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-0,747 |
-0,675 |
-0,604 |
-0,533 |
-0,463 |
-0,392 |
-0,322 |
-0,253 |
-0,183 |
-0,114 |
-0,0457 |
|
|
-0,747 |
-0,547 |
-0,387 |
-0,261 |
-0,167 |
-0,098 |
-0,052 |
-0,023 |
-0,007 |
-0,001 |
0,00 |
|
|
0,474 |
0,579 |
0,679 |
0,770 |
0,847 |
0,907 |
0,950 |
0,978 |
0,993 |
0,999 |
1,00 |
|
|
0,00 |
0,058 |
0,136 |
0,231 |
0,339 |
0,453 |
0,570 |
0,684 |
0,794 |
0,899 |
1,00 |
|
|
----- |
-0,532 |
-0,626 |
-0,610 |
-0,484 |
-0,466 |
-0,376 |
-0,281 |
-0,188 |
0,00 |
---- |
|
|
0,00 |
0,065 |
0,134 |
0,2225 |
0,336 |
0,415 |
0,565 |
0,6825 |
0,794 |
0,90 |
1,00 |
|
|
-126148 |
-101590 |
-79807 |
-60754 |
-44382 |
-30647 |
-19504 |
-10910 |
-4,822 |
-1199 |
0,00 |
|
|
-61,144 |
-49,694 |
-39,398 |
-30,267 |
-22,313 |
-15,548 |
-9,985 |
-5,636 |
-2,514 |
-0,631 |
0,00 |
| Функция |
Концентрация кобальта в расплаве - xCo |
||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
|
|
-0,393 |
-0,463 |
-0,534 |
-0,604 |
-0,675 |
-0,747 |
-0,818 |
-0,890 |
-0,963 |
-1,035 |
-1,1082 |
|
|
-0,393 |
-0,375 |
-0,341 |
-0,296 |
-0,243 |
-0,187 |
-0,131 |
-0,080 |
-0,039 |
-0,010 |
0,00 |
|
|
0,675 |
0,687 |
0,711 |
0,744 |
0,784 |
0,830 |
0,877 |
0,923 |
0,962 |
0,990 |
1,00 |
|
|
0,00 |
0,069 |
0,142 |
0,223 |
0,314 |
0,415 |
0,526 |
0,646 |
0,77 |
0,891 |
1,00 |
|
|
0,00 |
0,065 |
0,1375 |
0,220 |
0,307 |
0,4075 |
0,517 |
0,665 |
0,774 |
0,900 |
1,00 |
|
|
------ |
-0,532 |
-0,585 |
-0,633 |
-0,735 |
-0,818 |
-0,931 |
0,570 |
-0,826 |
0,00 |
----- |
|
|
-122620 |
-99866 |
-79342 |
-61082 |
-45127 |
-31514 |
-20282 |
-11474 |
-5128 |
-1289 |
0,00 |
|
|
-62,2 |
-50,2 |
-39,522 |
-30,151 |
-22,072 |
-15,274 |
-9,74 |
-5,46 |
-2,418 |
-0,602 |
0,00 |
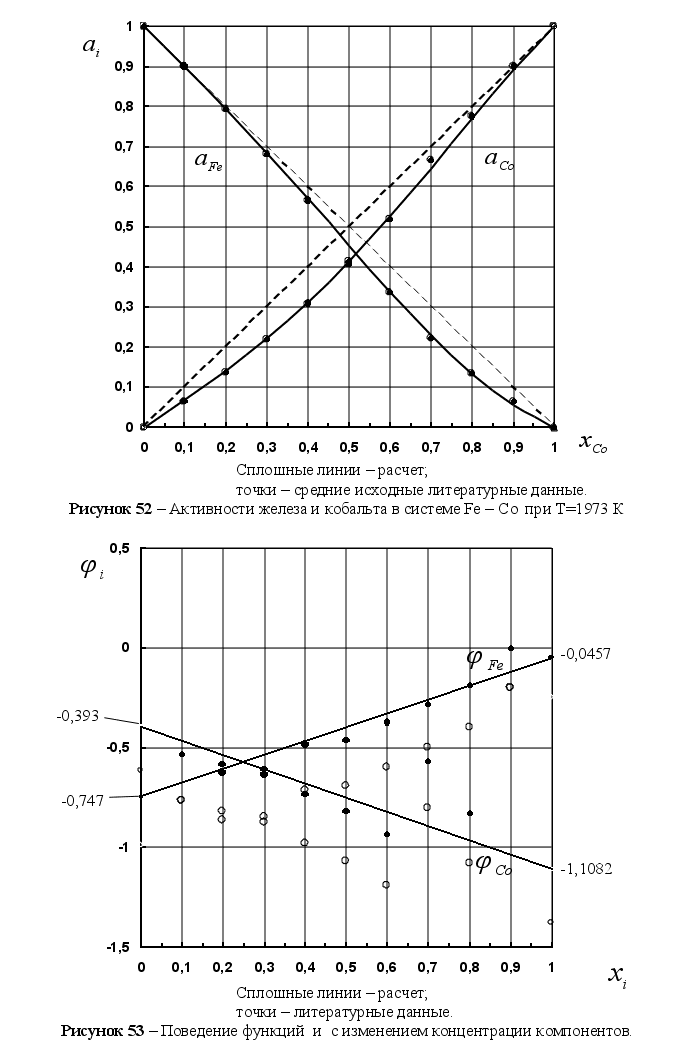
6.2.3 Система Fe – V.
Таблица 47 – Исходные данные при Т=1873 К.
-
функция Концентрация железа в расплаве – xFe.
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 aFe
0,02 0,06 0,13 0,22 0,34 0,47 0,61 0,76 0,89 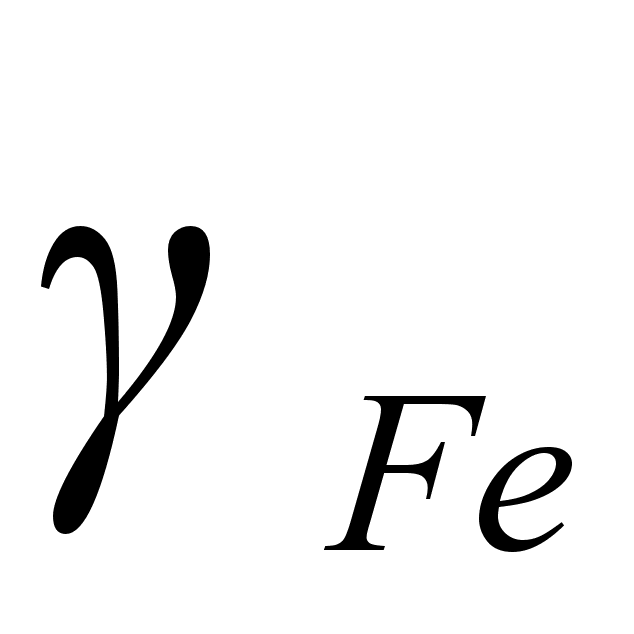
0,200 0,300 0,433 0,550 0,680 0,783 0,871 0,950 0,990 aV
0,89 0,76 0,61 0,47 0,34 0,22 0,13 0,06 0,02 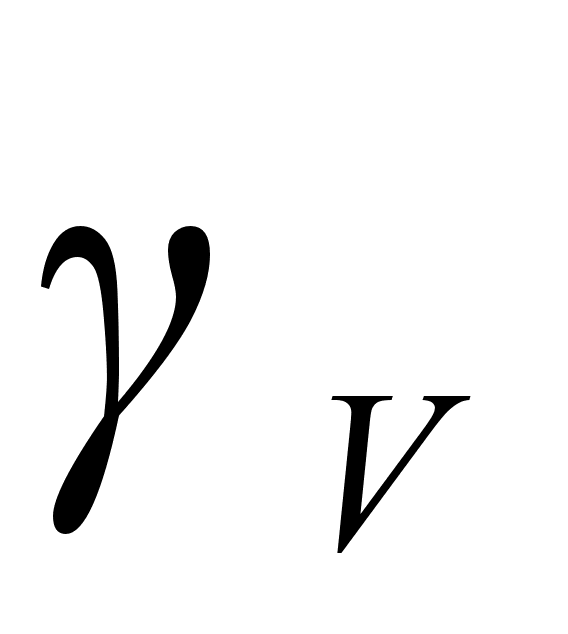
0,990 0,950 0,871 0,783 0,680 0,550 0,434 0,300 0,200
Таблица 48 – Обработанные исходные данные для системы Fe – V.
-
железо
ванадий
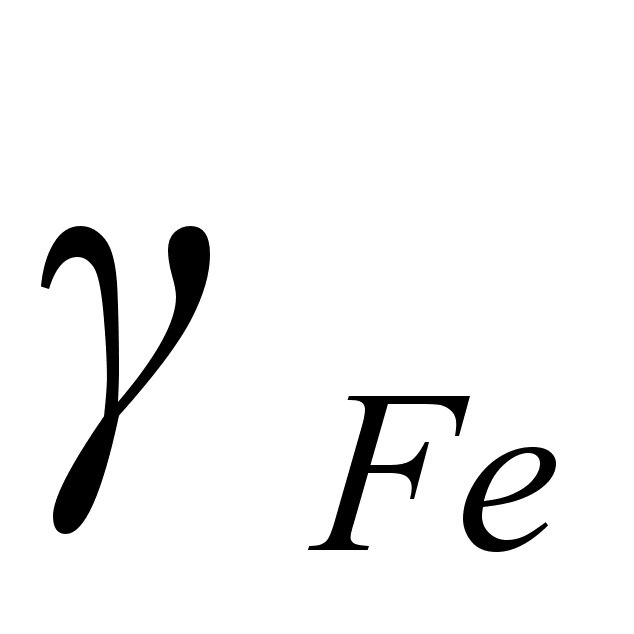
aFe
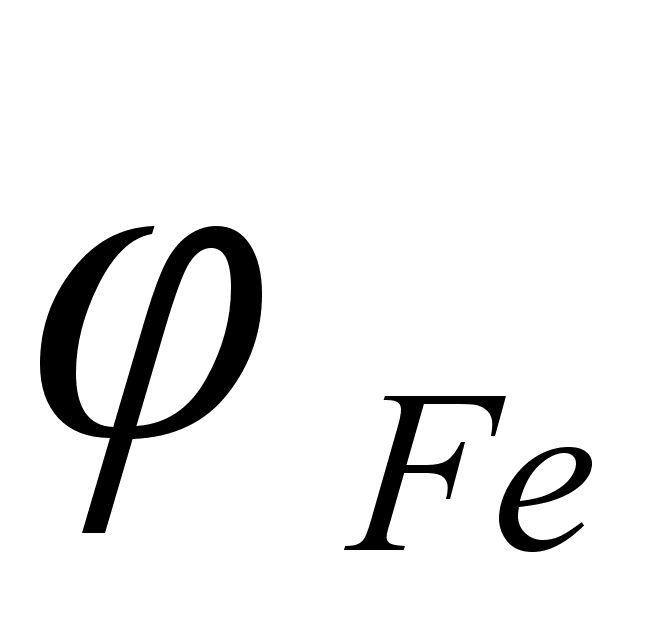
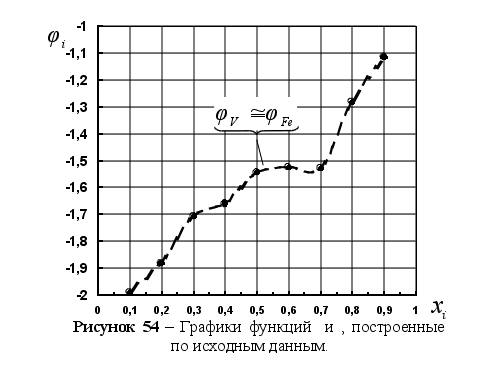
Уже из таблицы 48 становится очевидным, что термодинамические данные ванадия и железа абсолютно симметричны. Построим график функций i компонентов раствора (рисунок 54).
Продолжать расчеты будем по ванадию.
Корректировка данных.
Уравнение прямой для функции
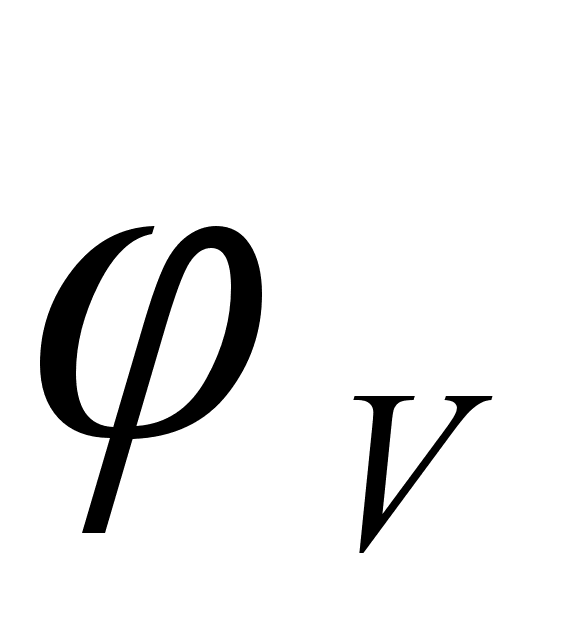 будет выглядеть
так:
будет выглядеть
так: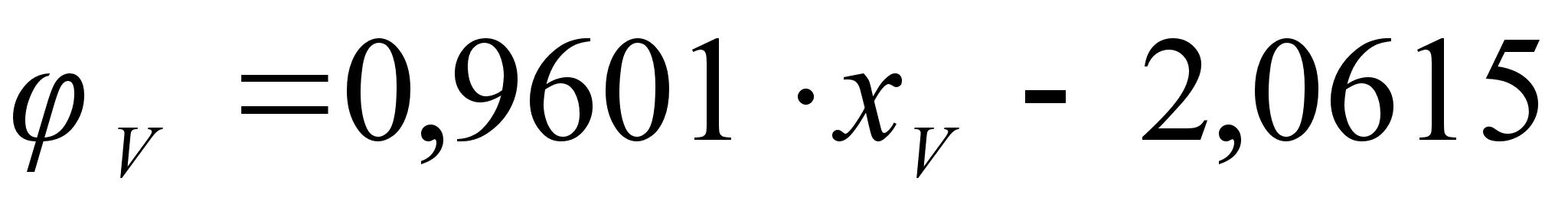
Таблица 49 – Скорректированные исходные данные для ванадия.
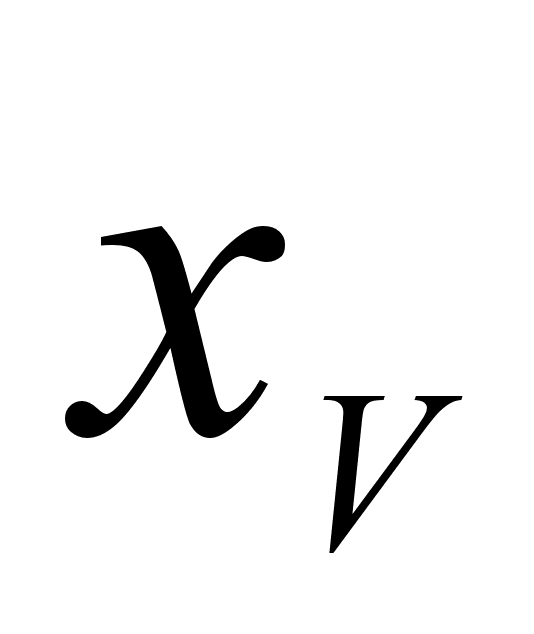
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 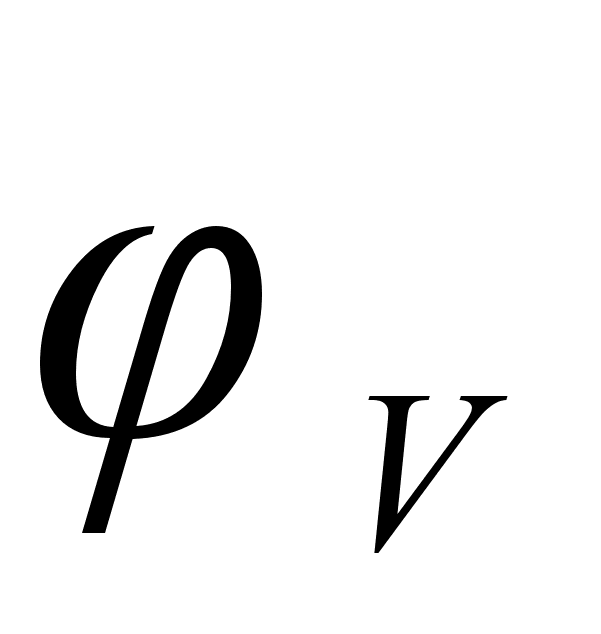
-2,0615 -1,965 -1,869 -1,773 -1,677 -1,581 -1,485 -1,389 -1,293 -1,197 -1,101 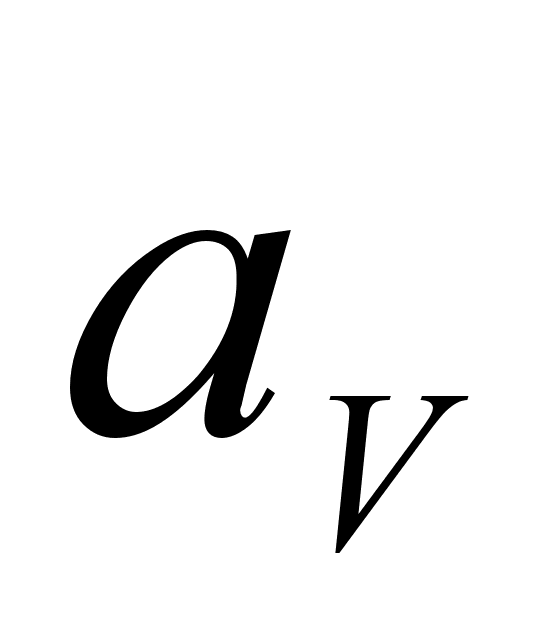
0,000 0,0204 0,0605 0,1258 0,2187 0,3367 0,4731 0,6177 0,7597 0,8893 1,000 (132)
Термодинамические характеристики компонентов. Вычисленные термодинамические характеристики ванадия в расплаве Fe – V :
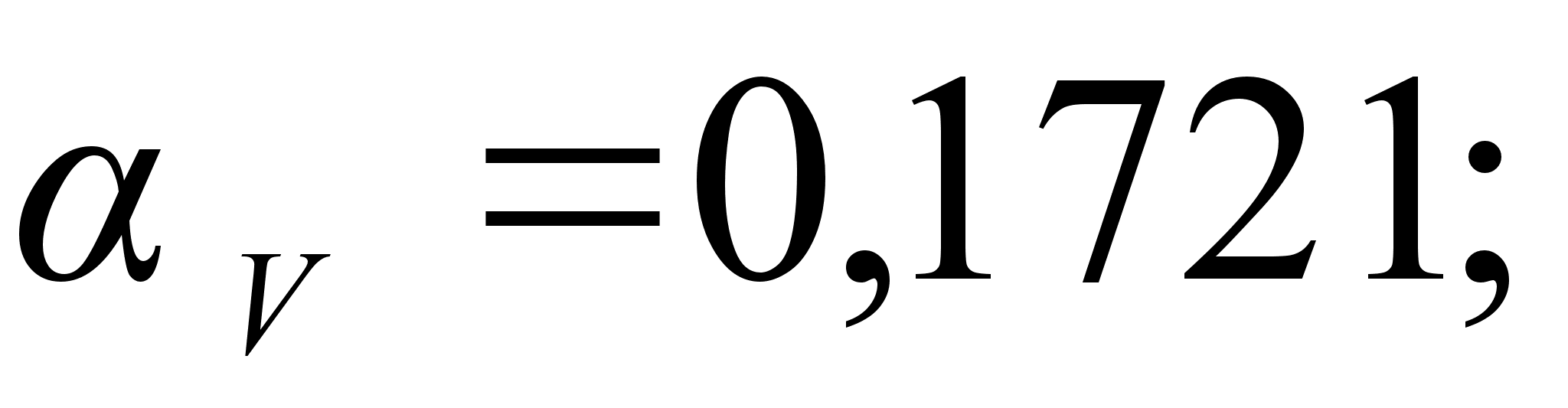
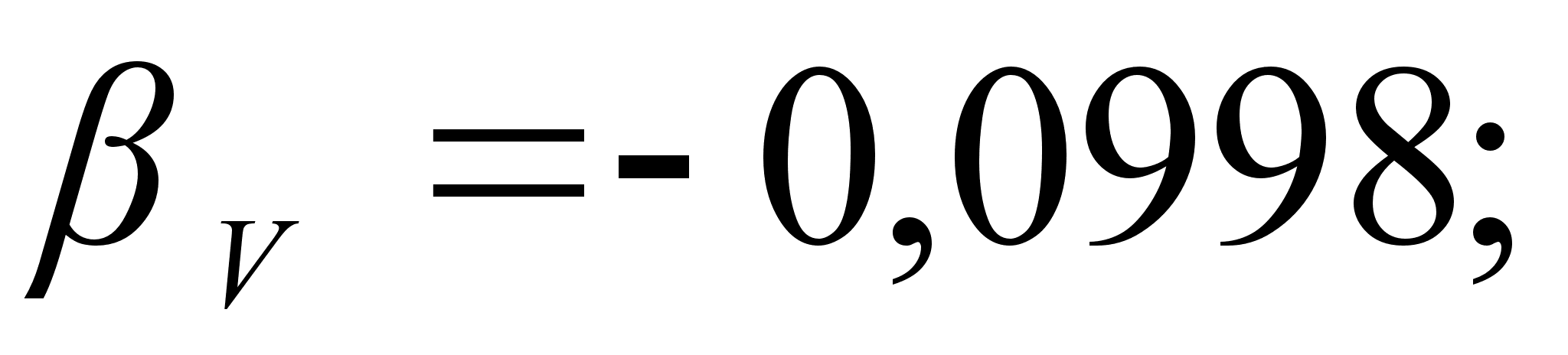
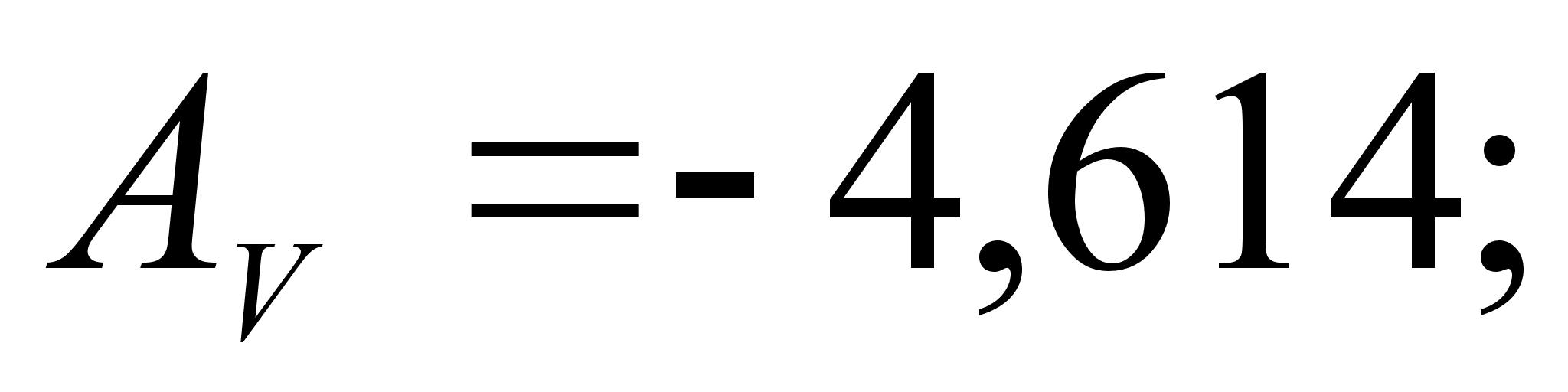
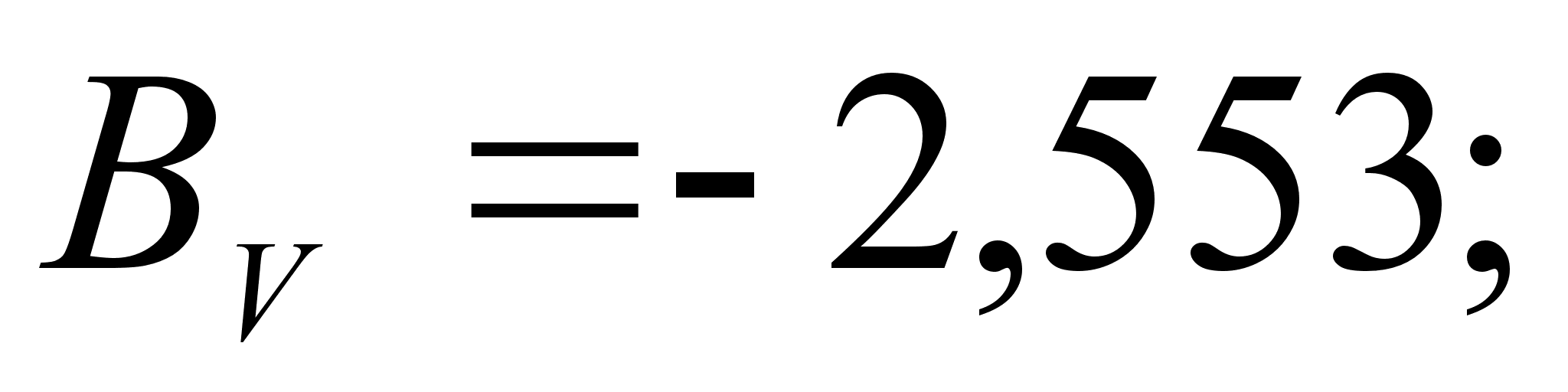
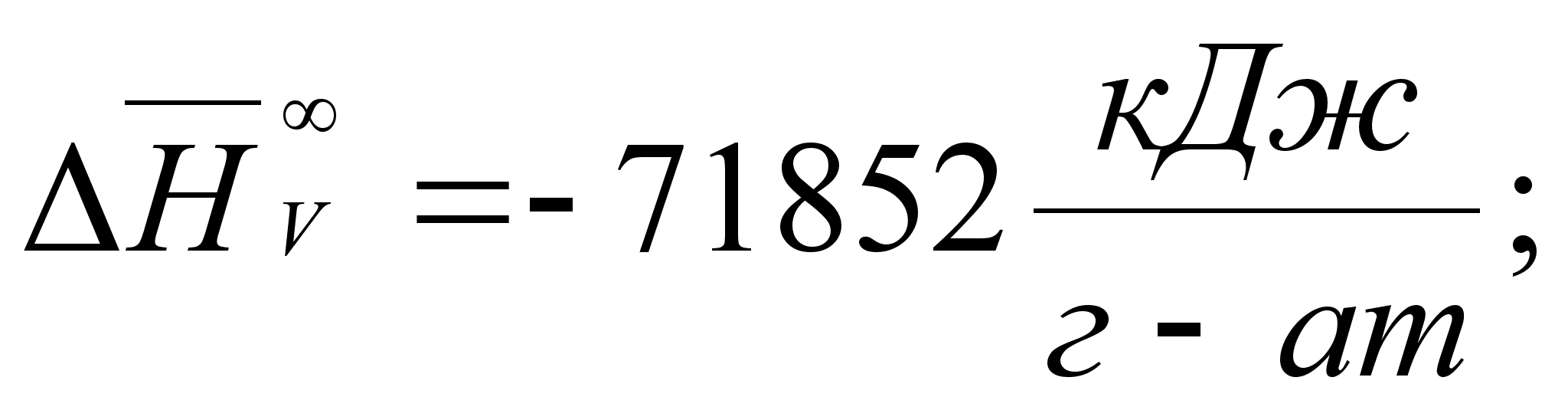
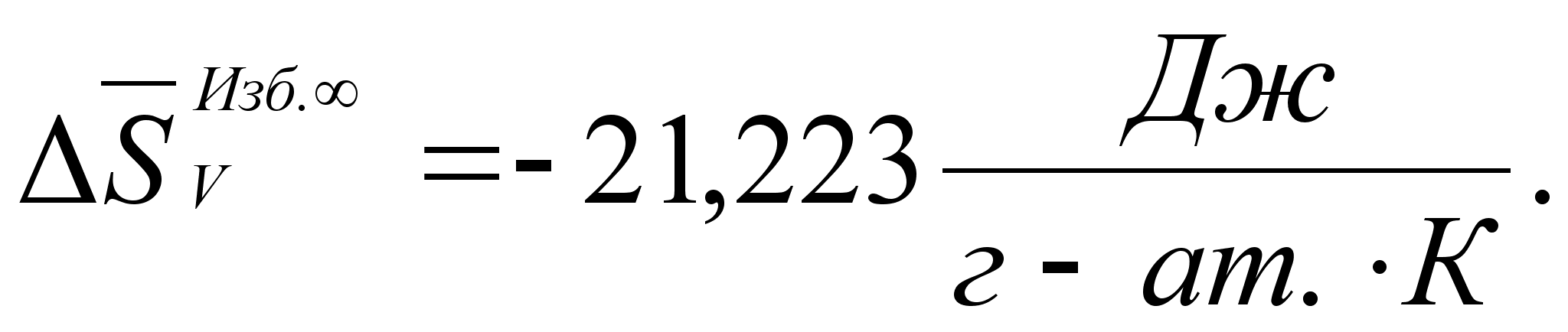
Характеристики железа: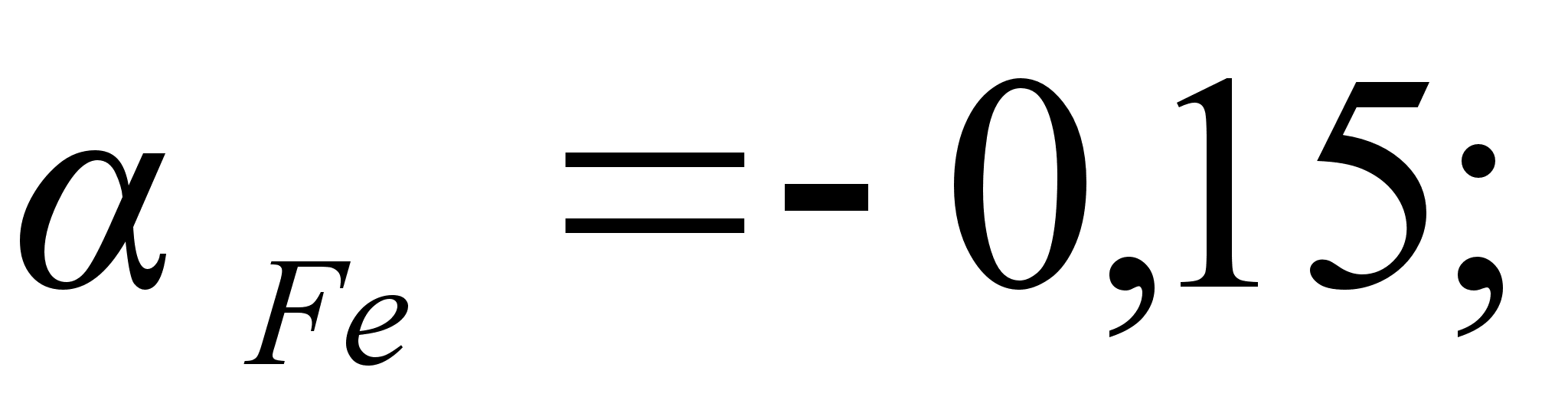
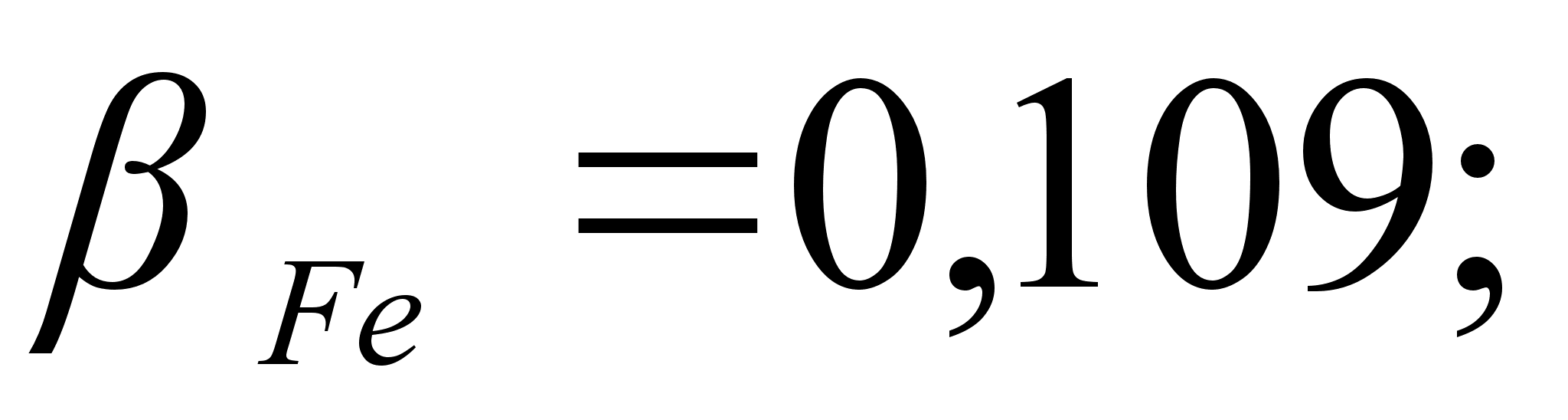
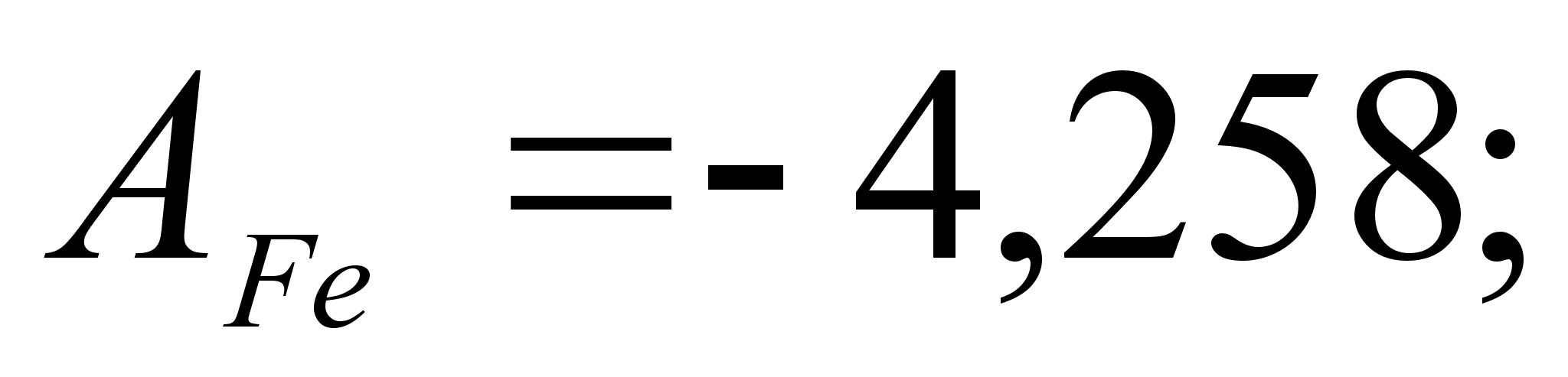
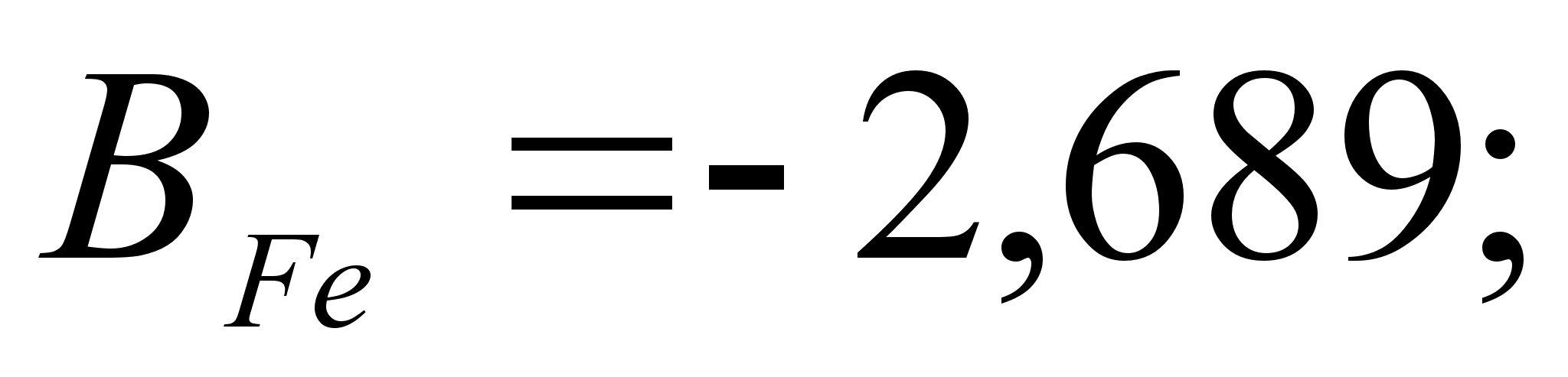
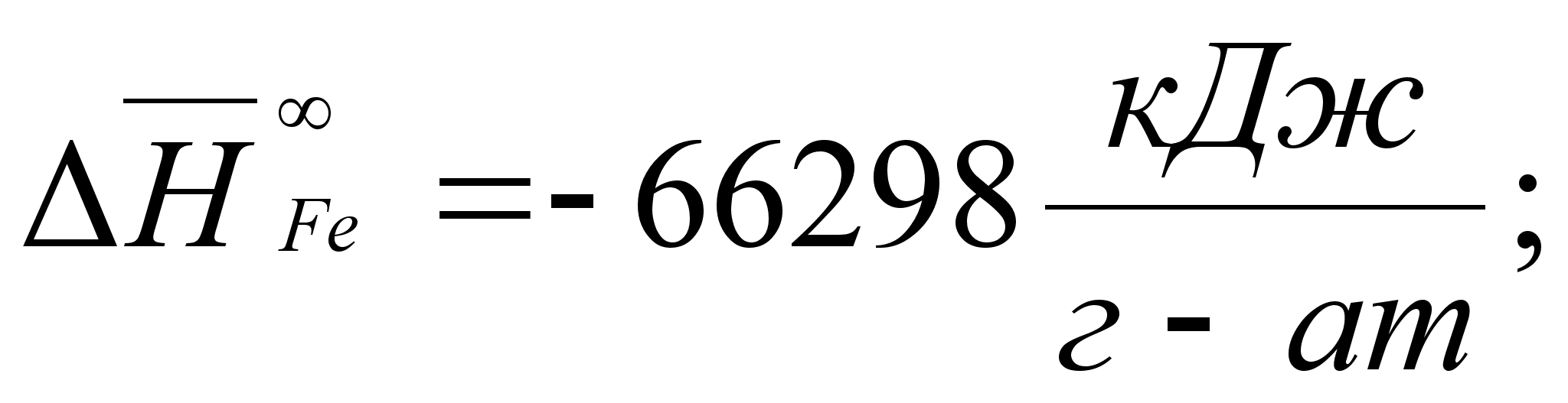
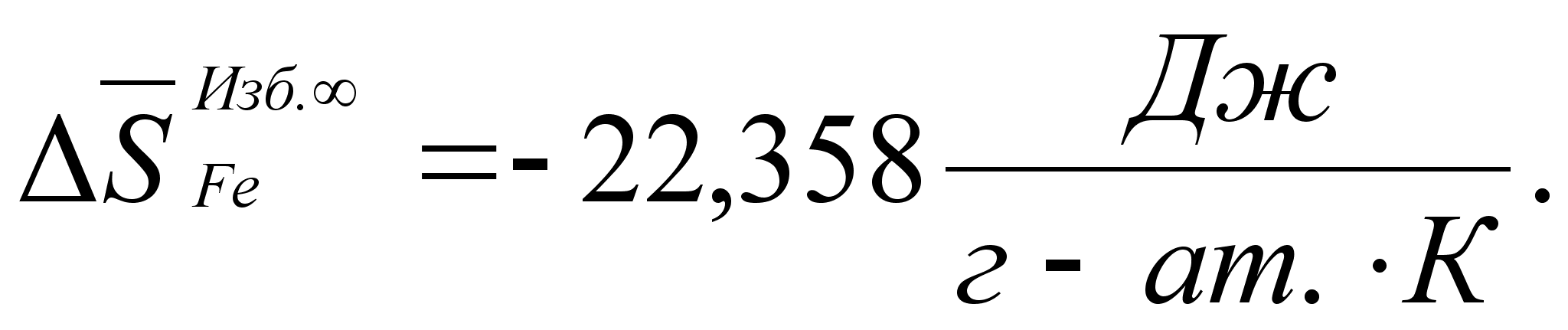
Таблица 50 – Вычисленные термодинамические характеристики ванадия в расплаве Fe – V при Т=1873 К.Функция Концентрация ванадия в расплаве - xV .
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 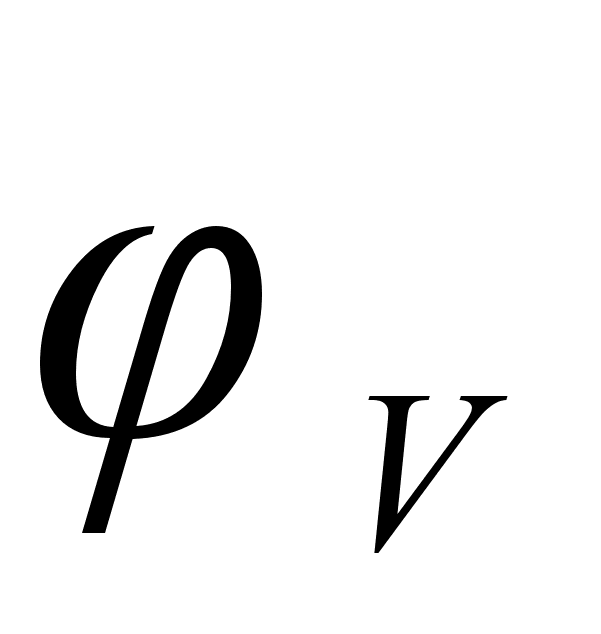
-2,061
-1,957
-1,855
-1,756
-1,658
-1,561
-1,467
-1,373
-1,281
-1,190
-1,100
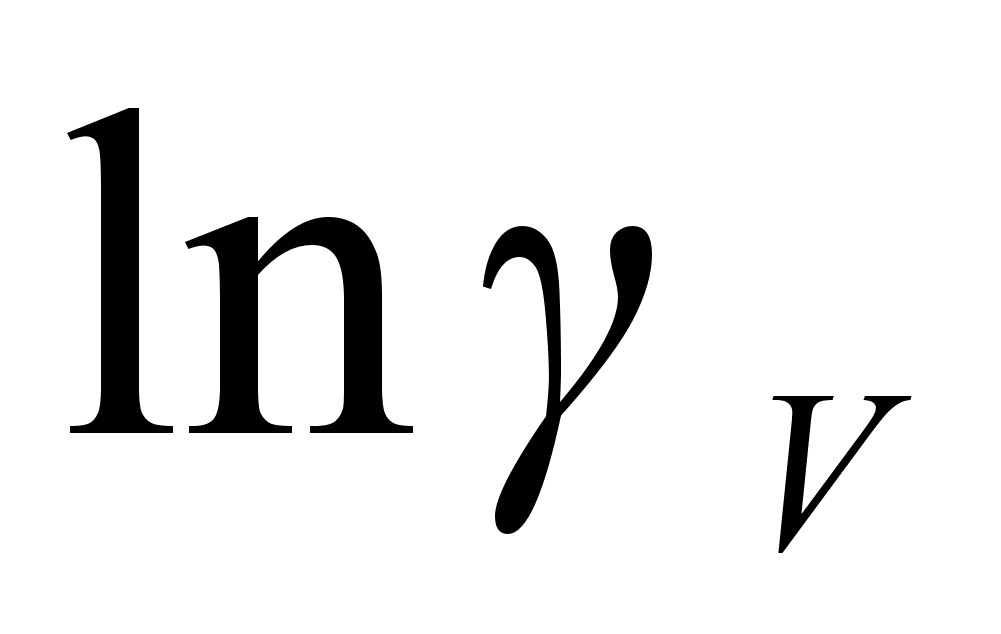
-2,061
-1,585
-1,188
-0,860
-0,597
-0,390
-0,235
-0,124
-0,051
-0,012
0,00
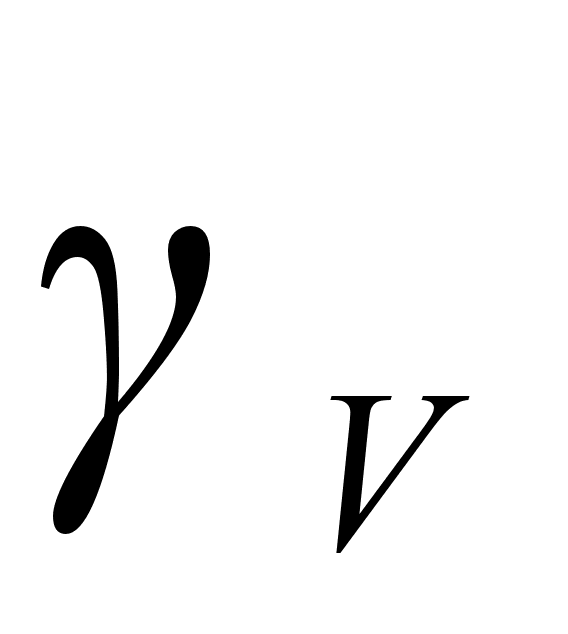
0,127
0,205
0,305
0,423
0,551
0,677
0,791
0,884
0,950
0,988
1,00
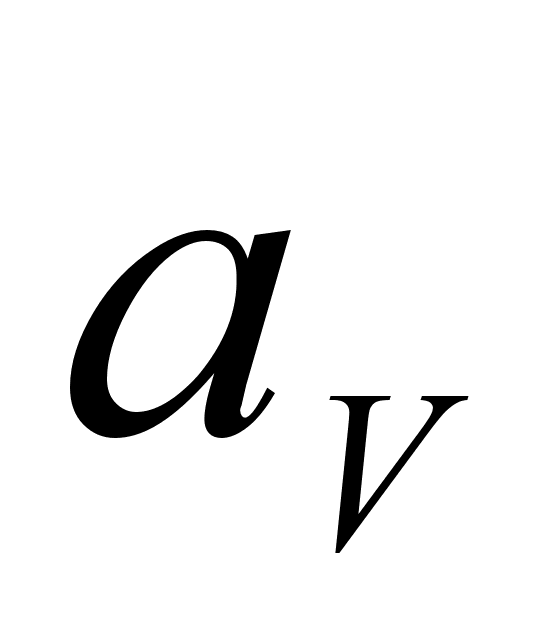
0,00
0,02
0,061
0,127
0,220
0,338
0,475
0,619
0,760
0,889
1,00
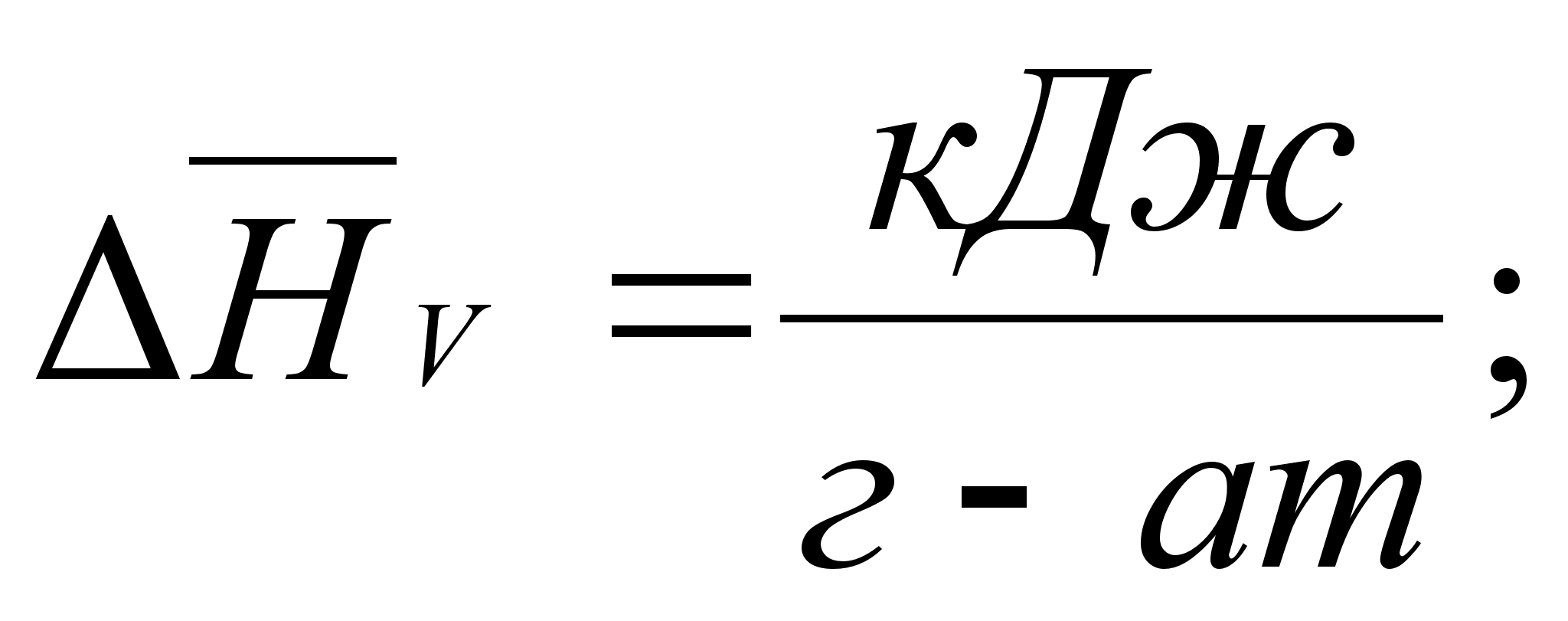
-71852
-57215
-44455
-33479
-24201
-16540
-10420
-5771
-2526
-622
0,00

-21,223
-17,364
-13,859
-10,720
-7,958
-5,584
-3,612
-2,054
-0,923
-0,233
0,00
Таблица 51 – Вычисленные термодинамические характеристики железа в расплаве Fe – V при Т=1873 К.
Функция Концентрация железа в расплаве - xFe
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 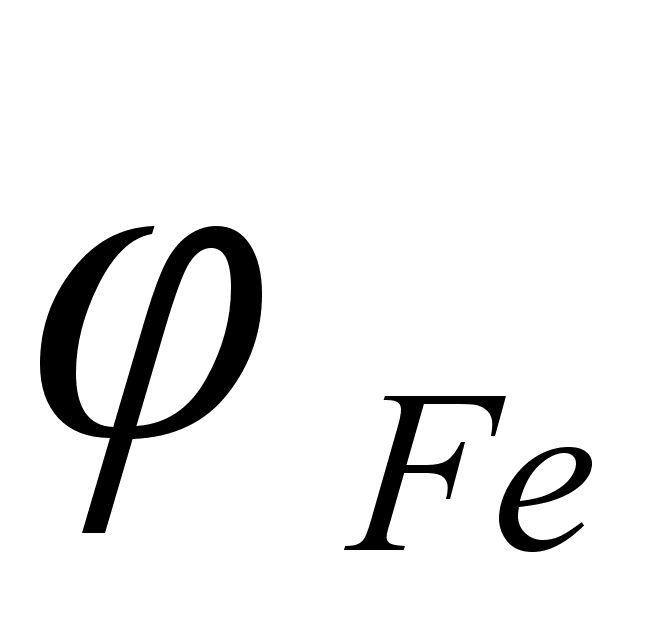
-1,569
-1,663
-1,758
-1,855
-1,953
-2,053
-2,155
-2,259
-2,365
-2,474
-2,585
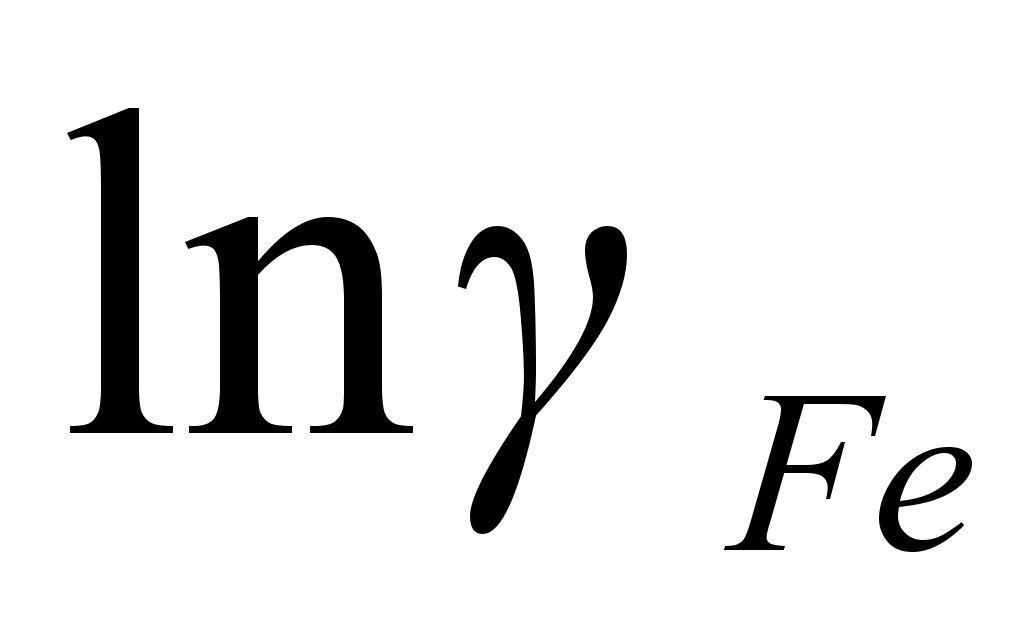
-1,569
-1,347
-1,125
-0,909
-0,703
-0,513
-0,345
-0,203
-0,095
-0,025
0,00
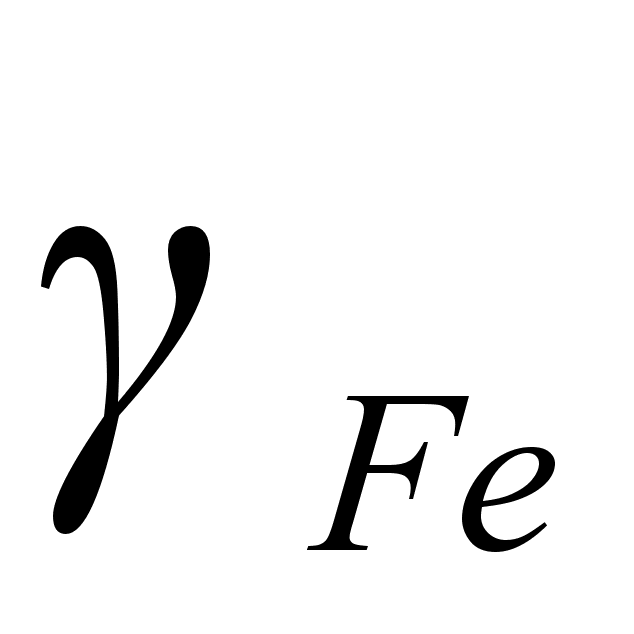
0,208
0,260
0,325
0,403
0,495
0,599
0,708
0,816
0,910
0,976
1,00
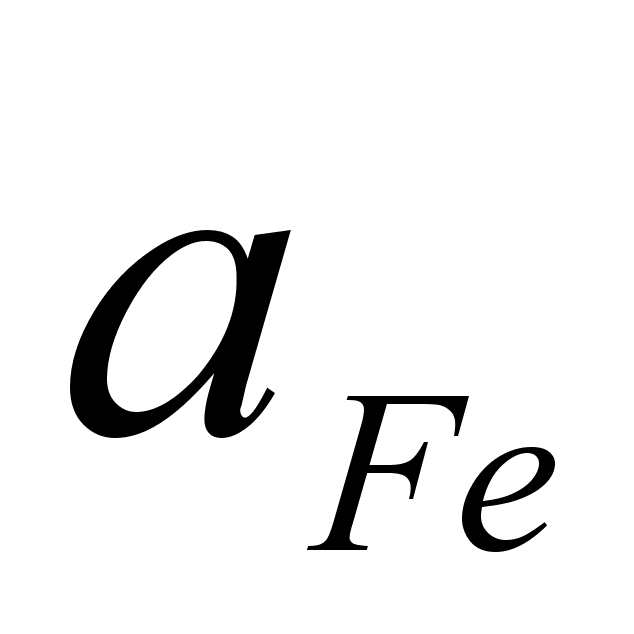
0,00
0,026
0,065
0,121
0,198
0,299
0,425
0,571
0,728
0,878
1,00
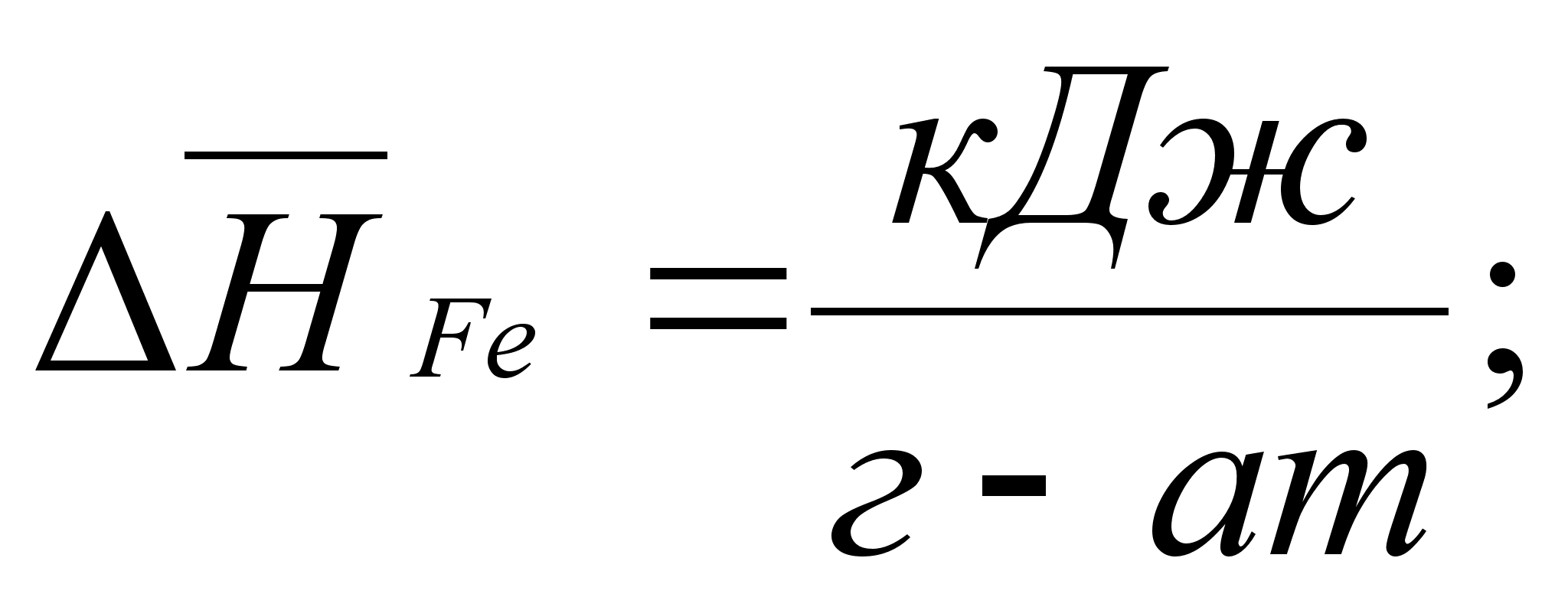
-66298
-54519
-43743
-34017
-25391
-17918
-11657
-6667
-3014
-766
0,00
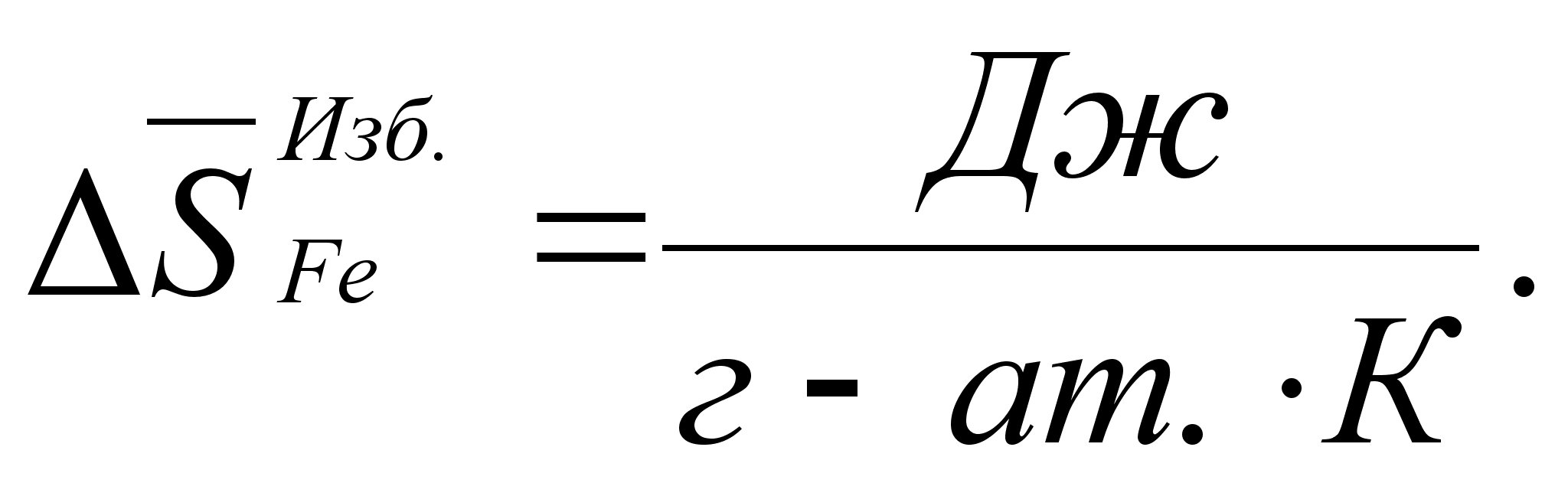
-22,358
-17,915
-14,004
-10,609
-7,713
-5,301
-3,358
-1,870
-0,823
-0,204
0,00
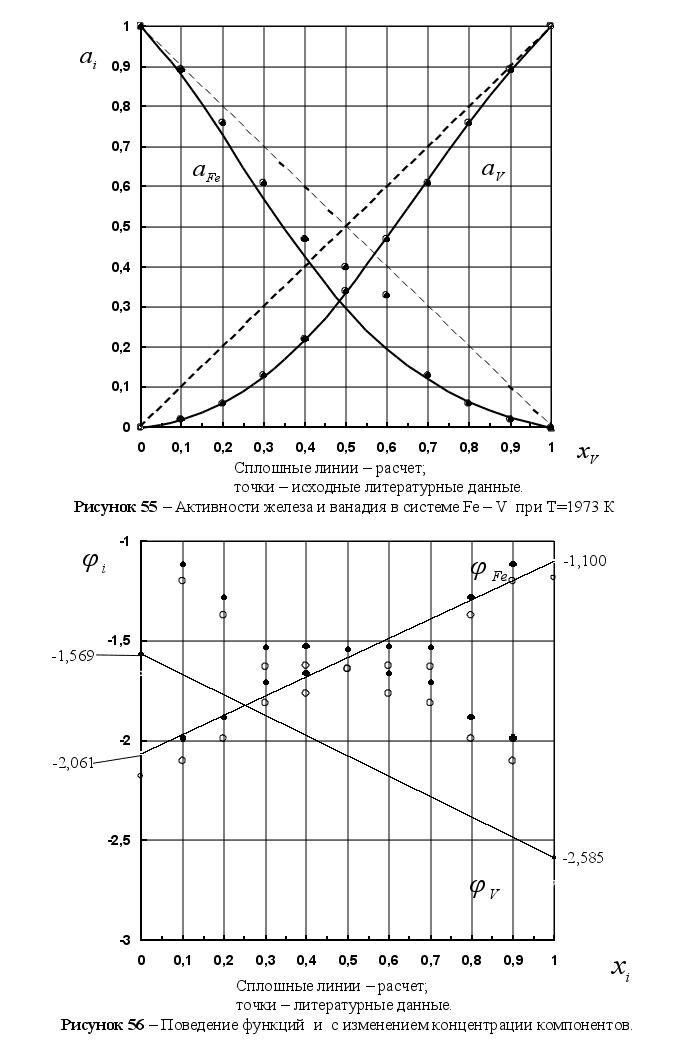
121
6 ОБОБЩЕНИЕ РЕЗУЛЬТАТОВ, ВЫВОДЫ
С целью выявления общих закономерностей для рассмотренных выше бинарных систем, обобщим данные, полученные нами в результате термодинамического анализа. Для этого все термодинамические функции систем сведем в таблицы 52 – 60. В этих же таблицах приведены уравнения зависимости функции
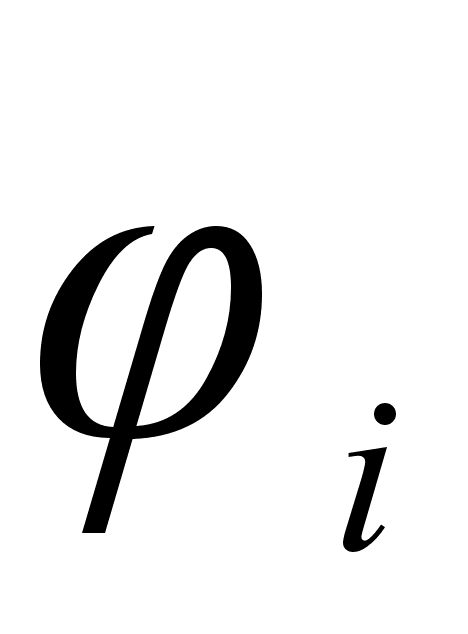 от концентрации
рассматриваемых
компонентов
в расплаве,
полученные
из данных итоговых
таблиц для
каждой системы.
от концентрации
рассматриваемых
компонентов
в расплаве,
полученные
из данных итоговых
таблиц для
каждой системы.На рисунке 56 представлены графики вычисленных нами функций
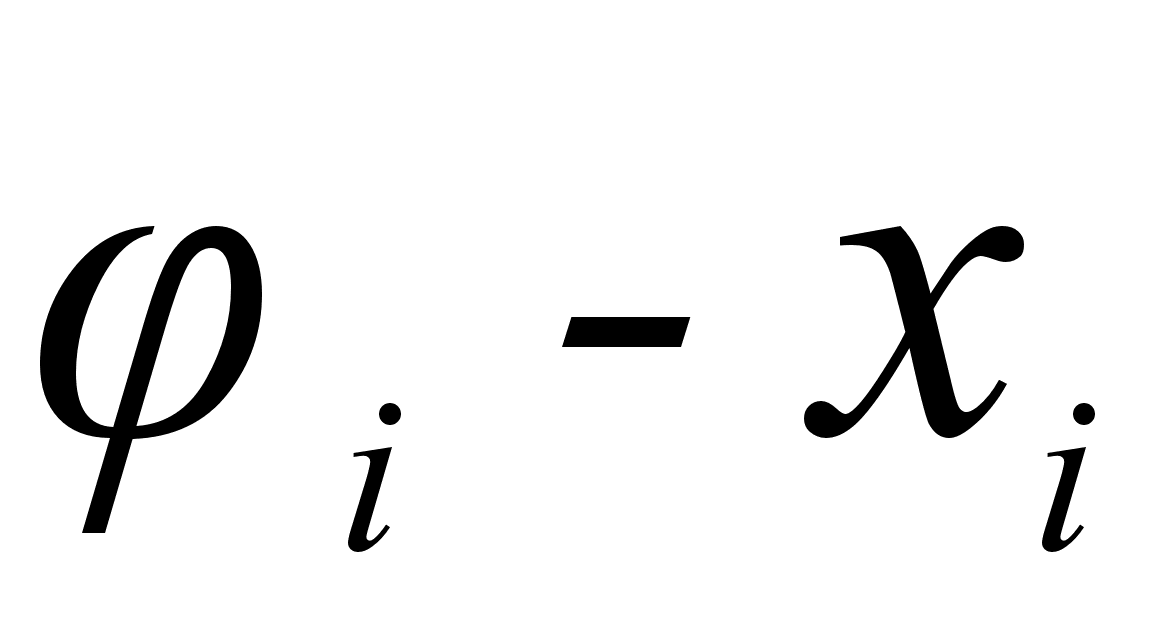 для рассмотренных
систем. Для
каждой системы
имеем две линии
-
для рассмотренных
систем. Для
каждой системы
имеем две линии
-
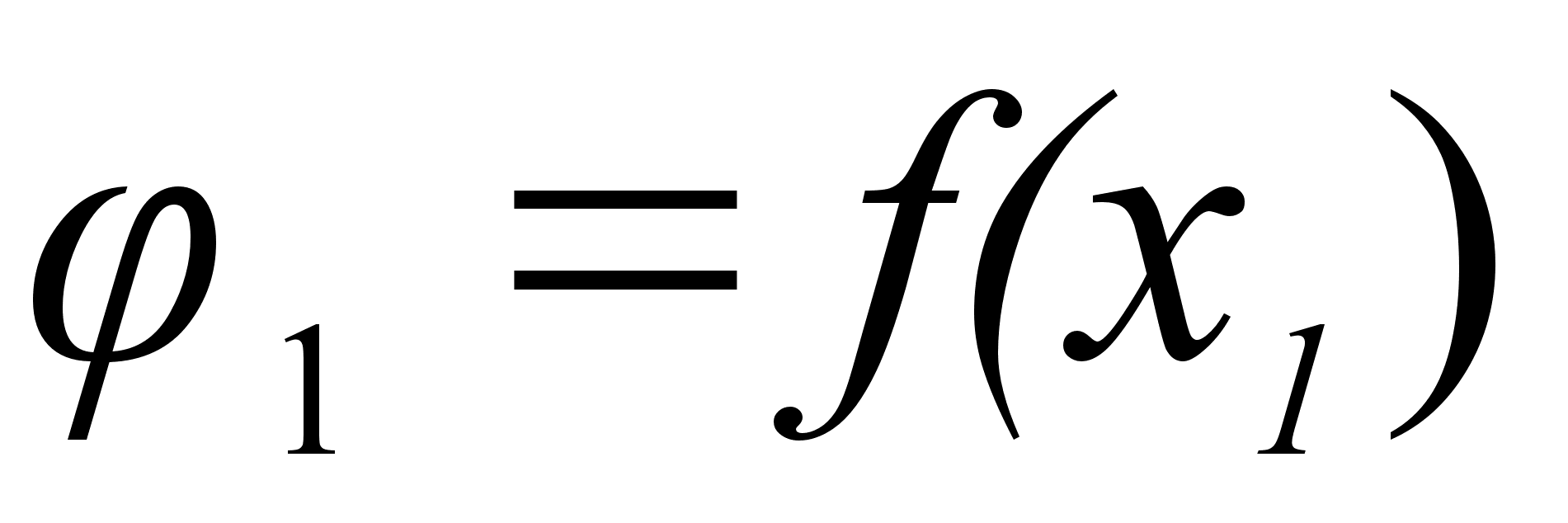 и
и
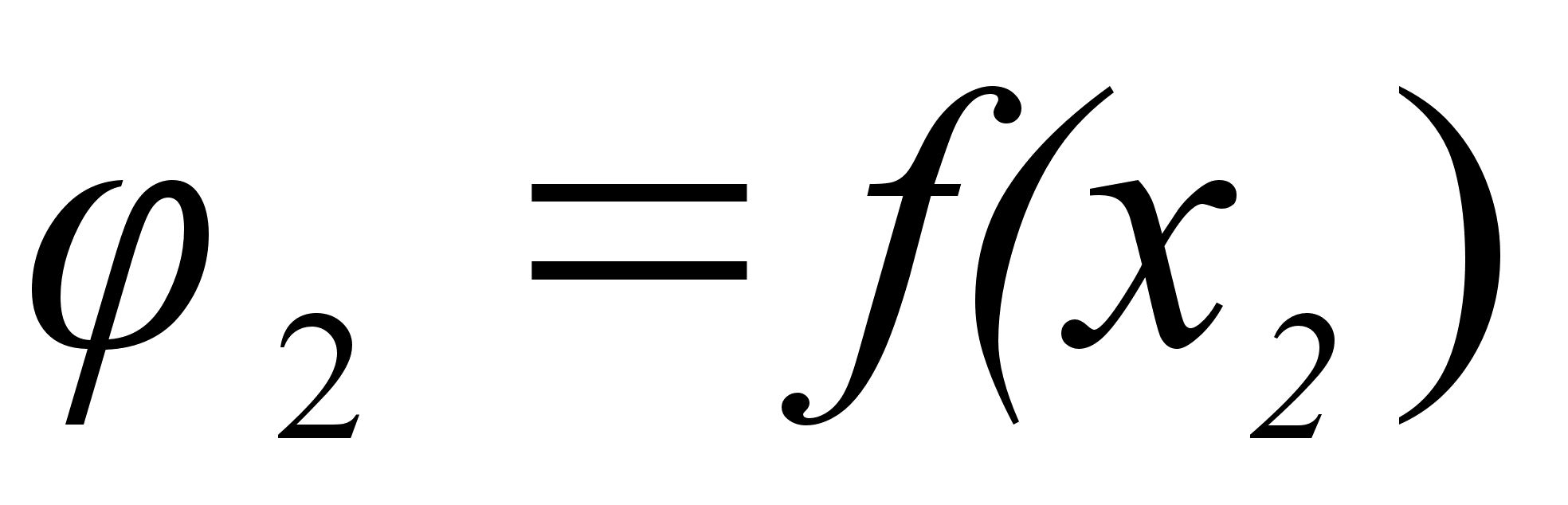 .
Цифрами обозначены
точки пересечения
этих линий в
расплавах:
.
Цифрами обозначены
точки пересечения
этих линий в
расплавах:1-(Fe – Si); 2-(Fe – Al); 3-(Fe – V); 4-(Fe – Co); 5-(Pd – W); 6-(Fe – Mn); 7-(Fe – Cu); 8-(Fe – Cr) и 9-(Fe – Sn).
Таблица 52 – Термодинамические характеристики компонентов системы Fe – Si.
железо
кремний
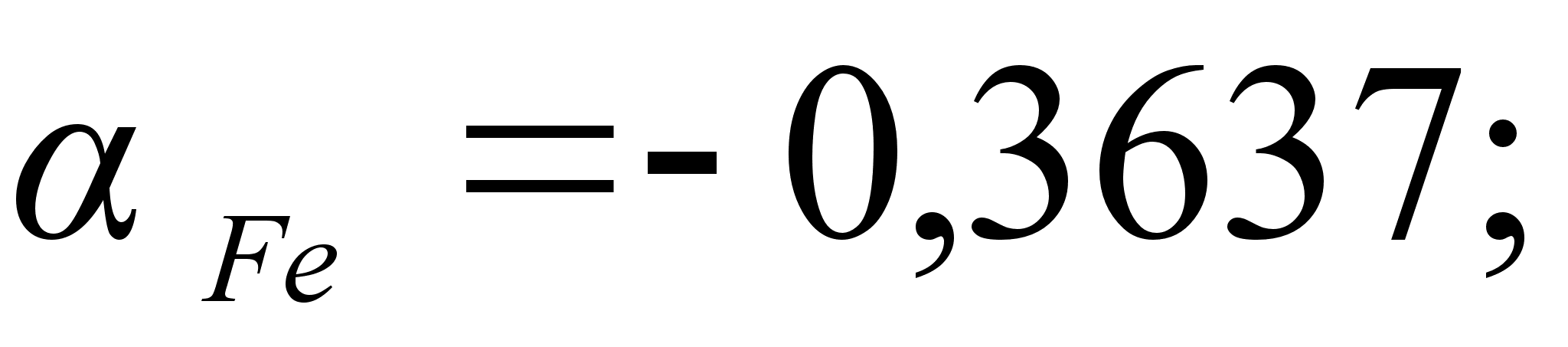
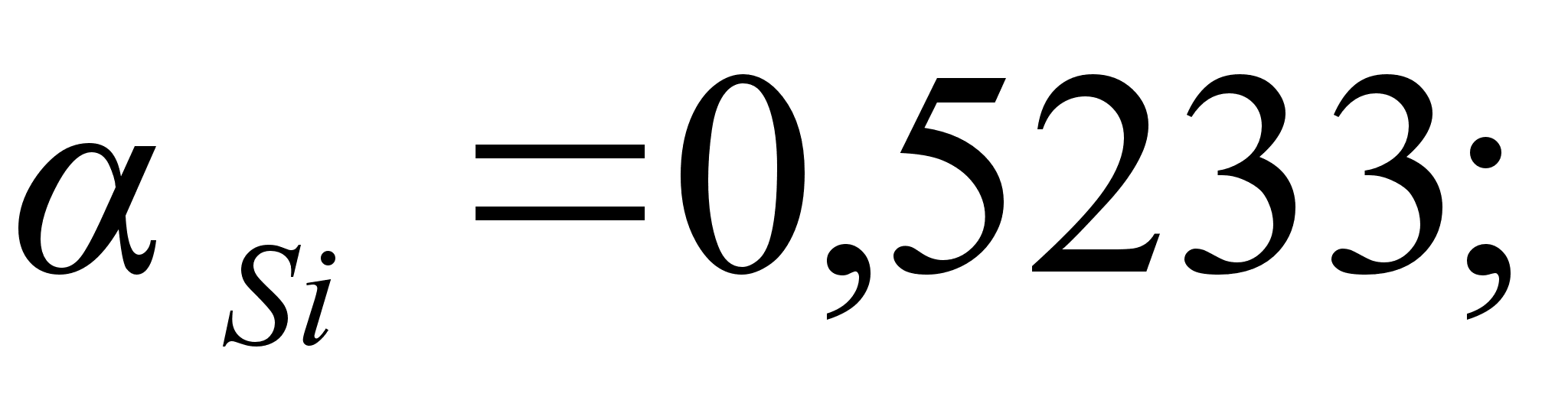
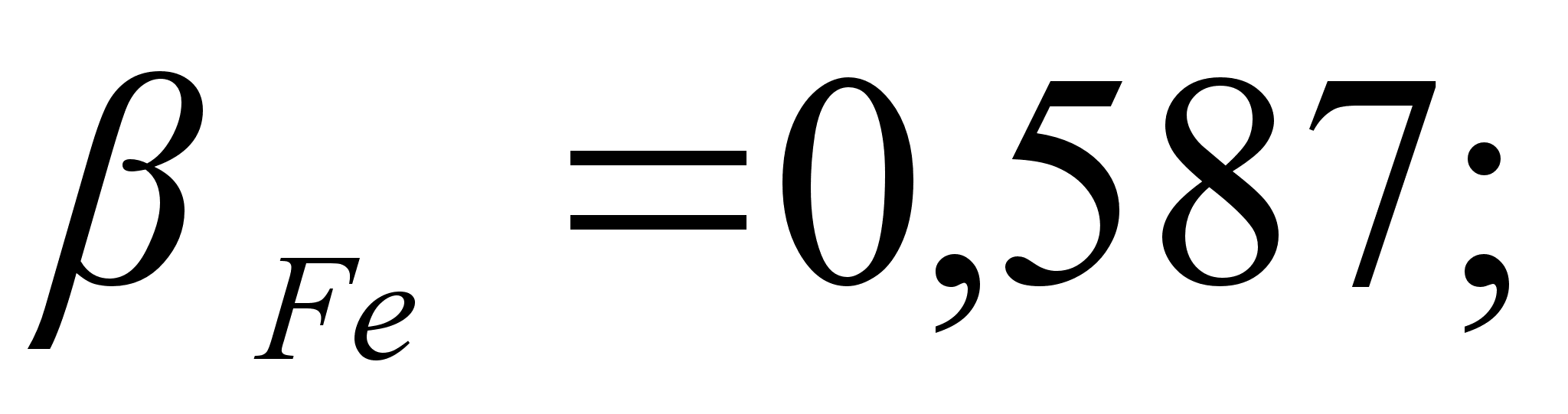
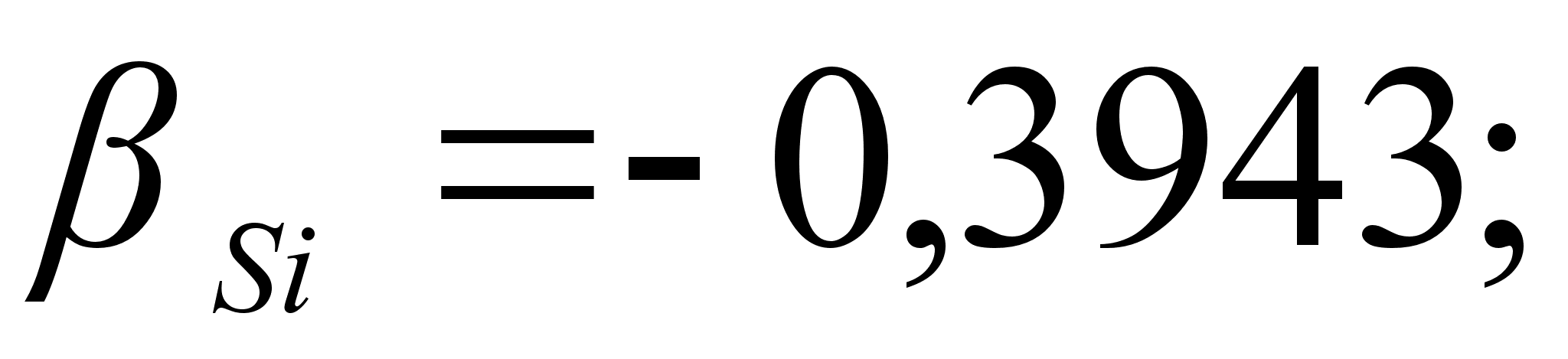
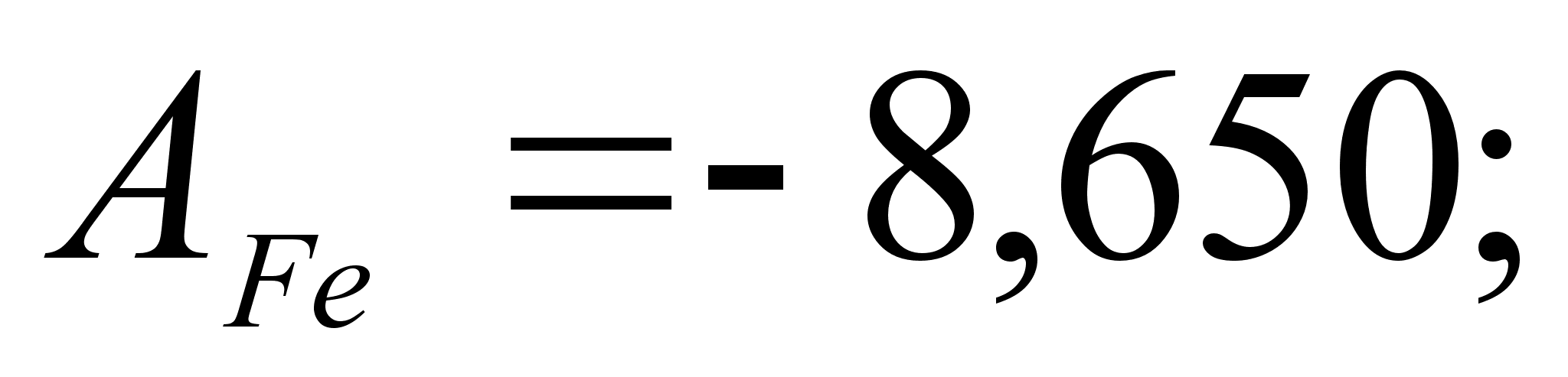
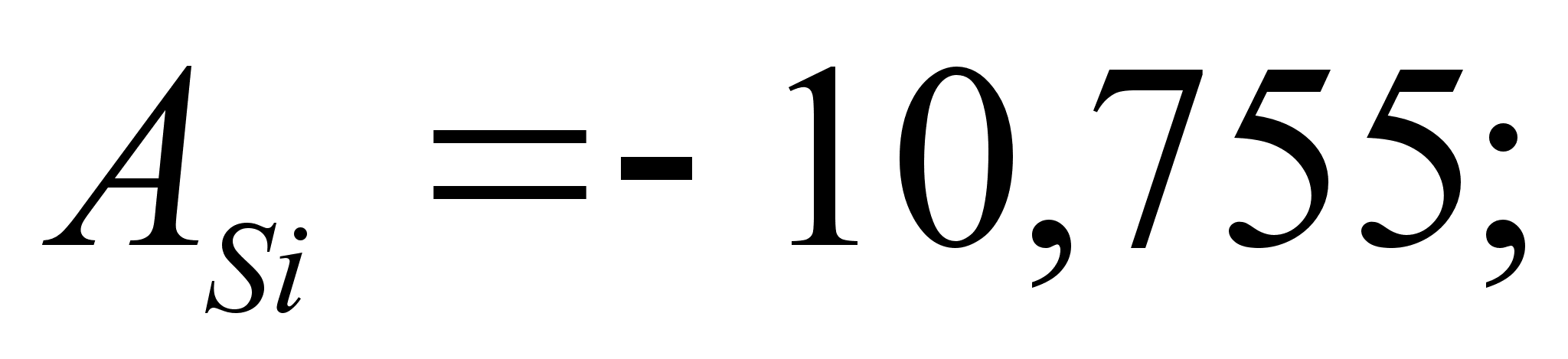
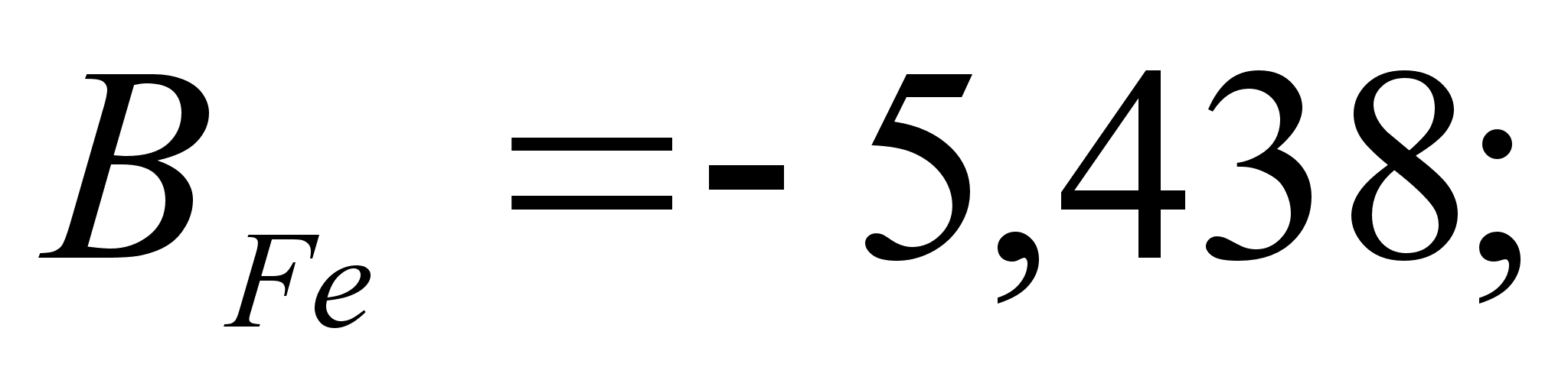
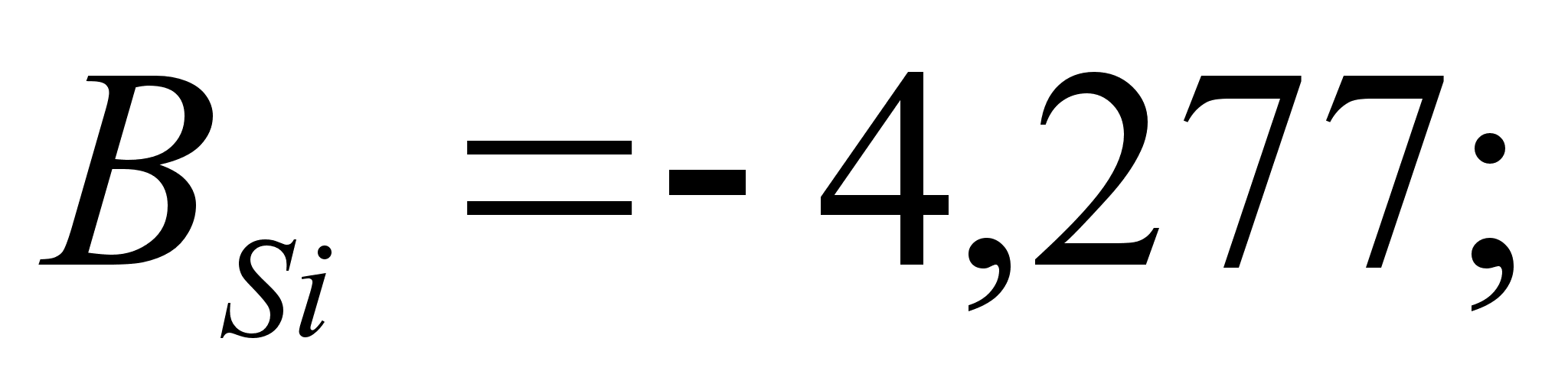
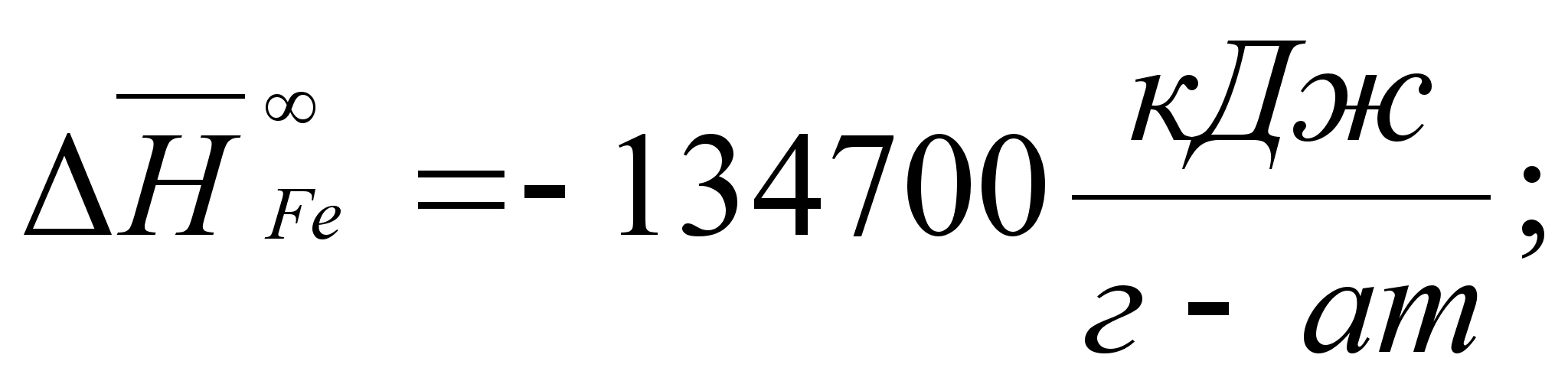
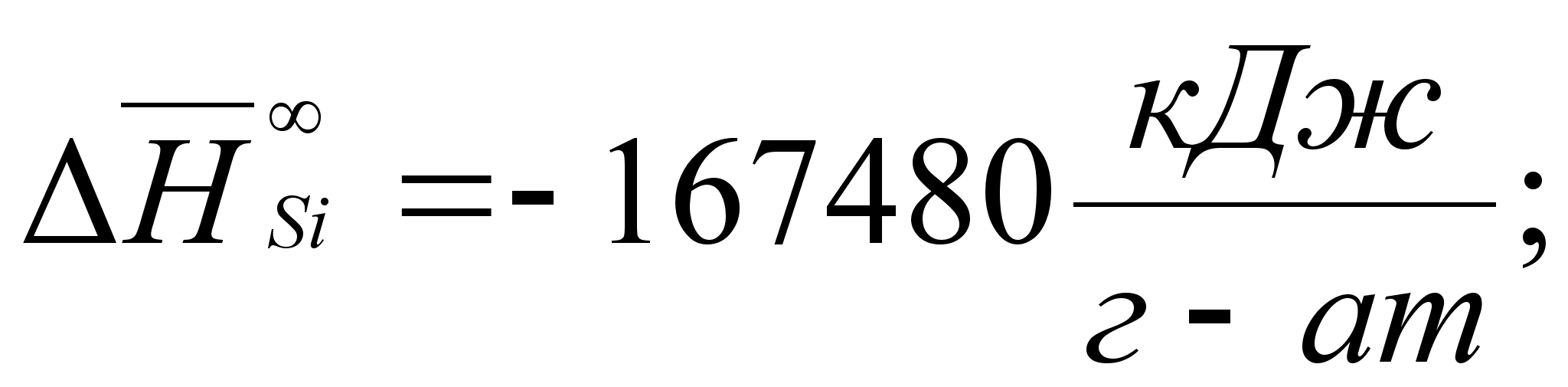
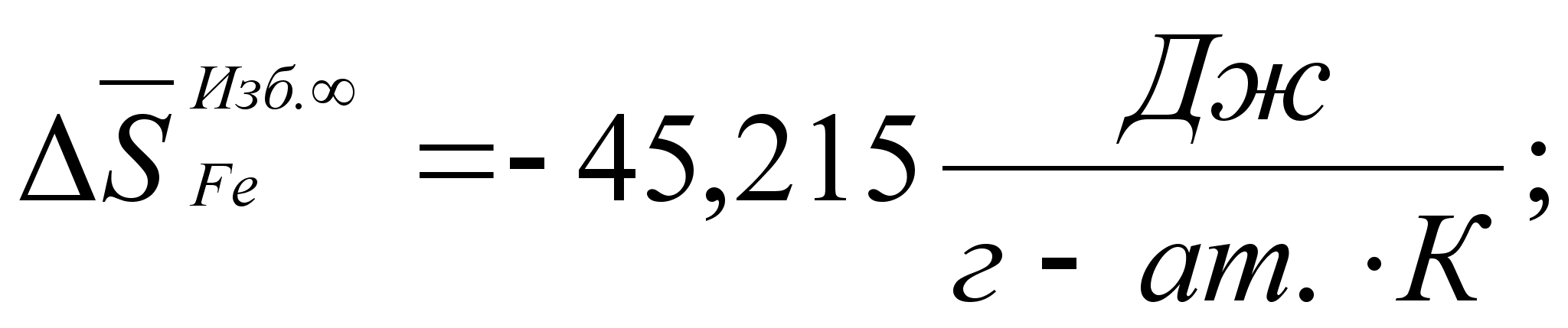
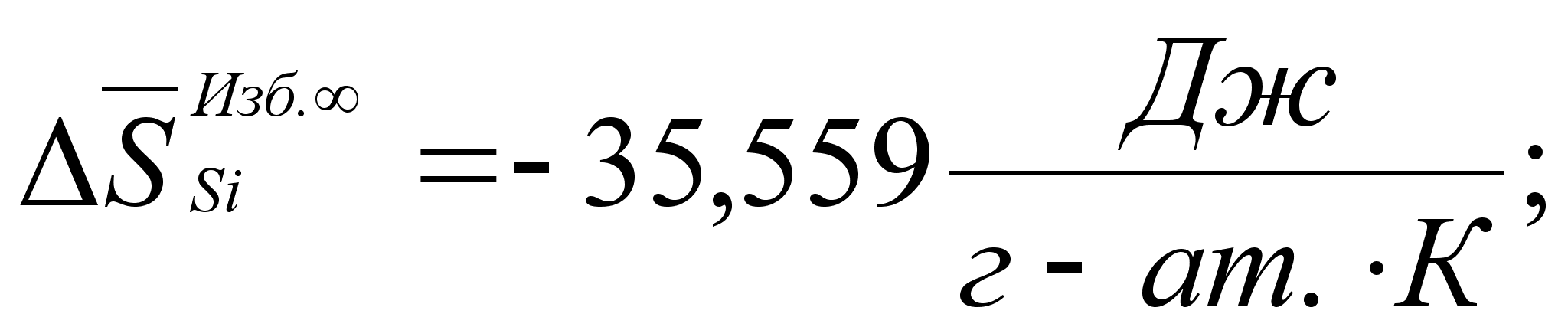
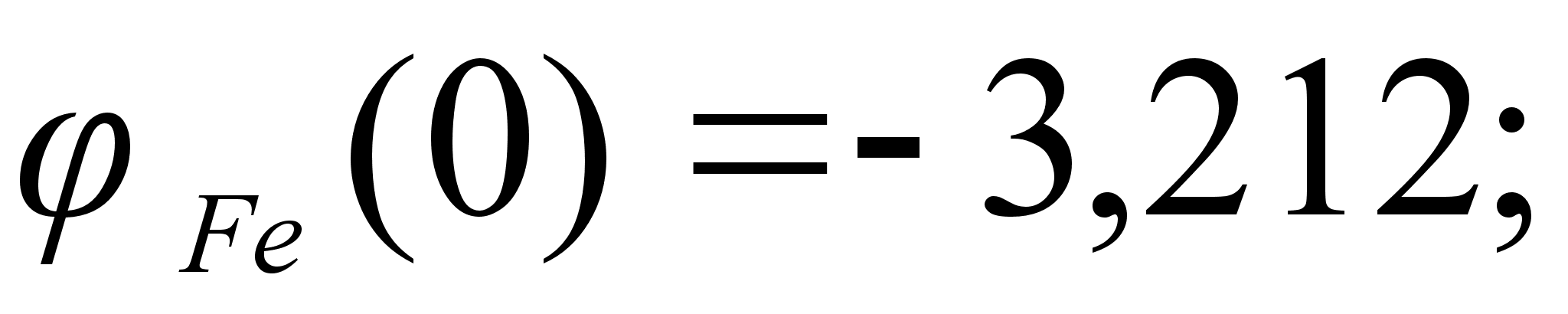
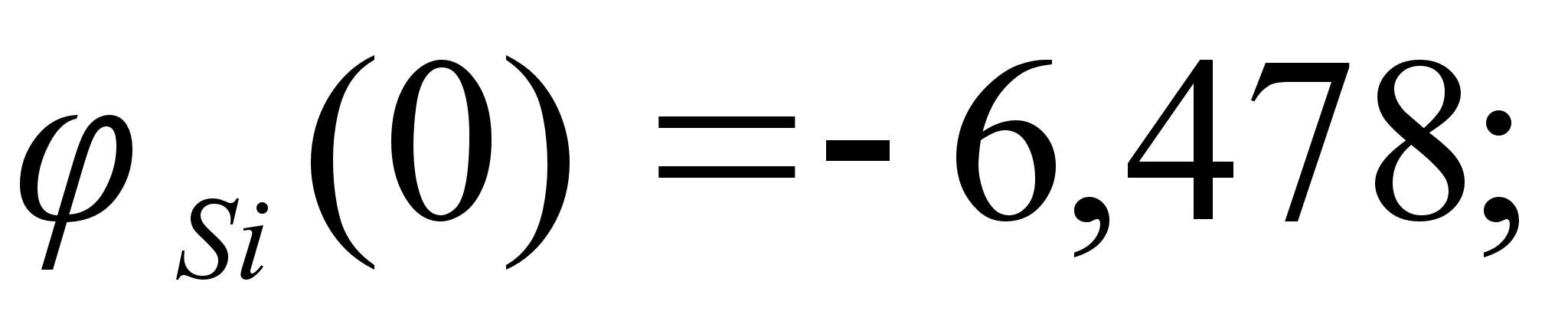
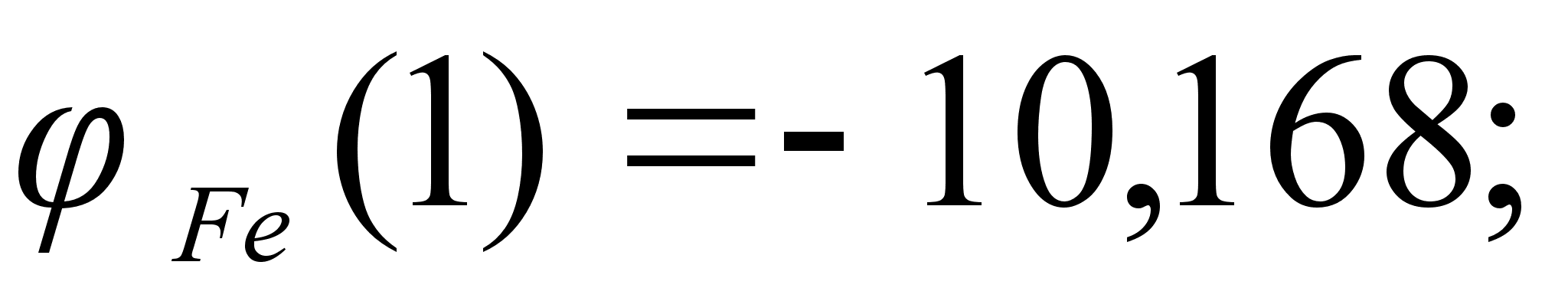
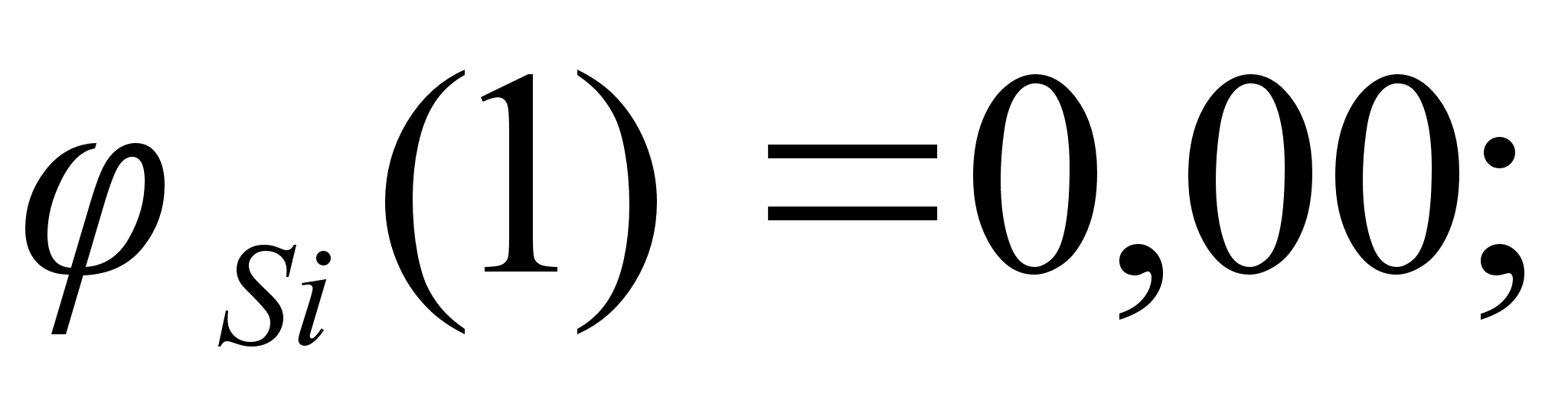
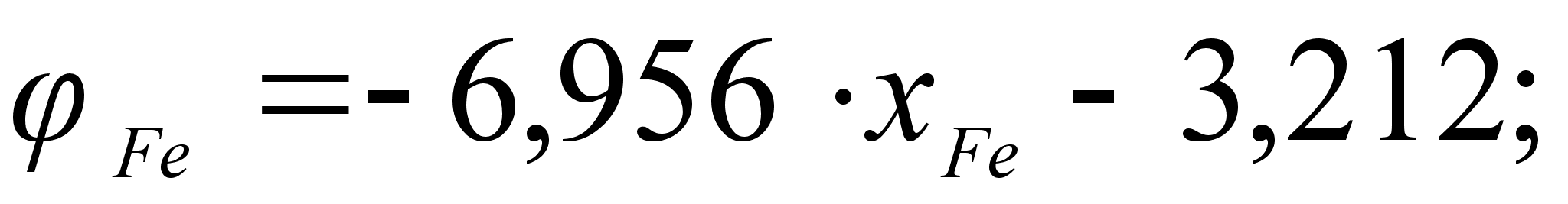
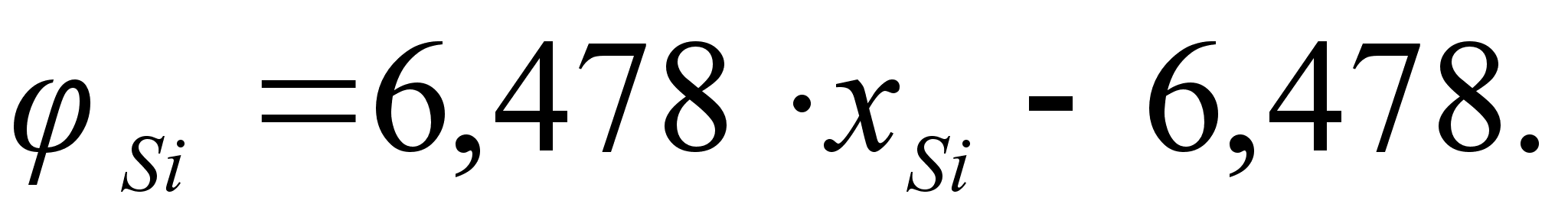
Таблица 53 – Термодинамические характеристики компонентов системы Fe – Al.
железо
алюминий
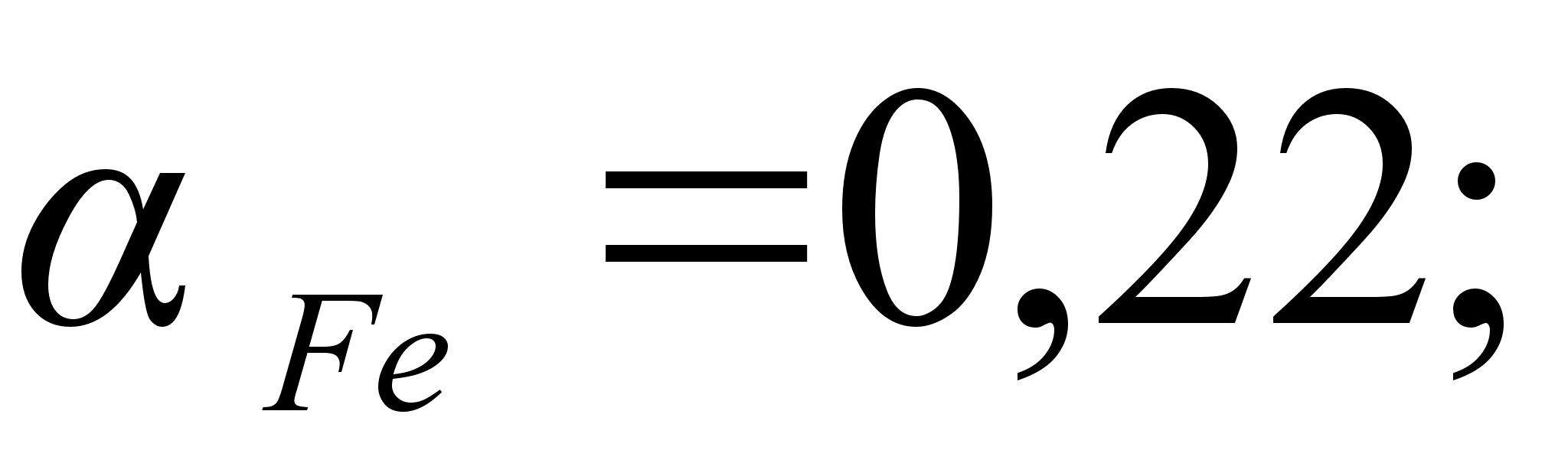
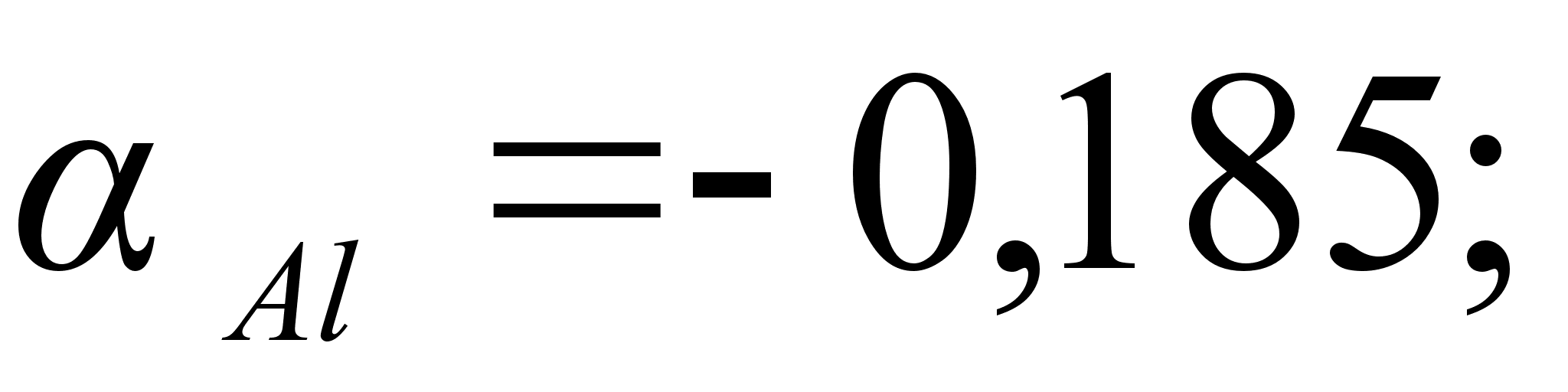
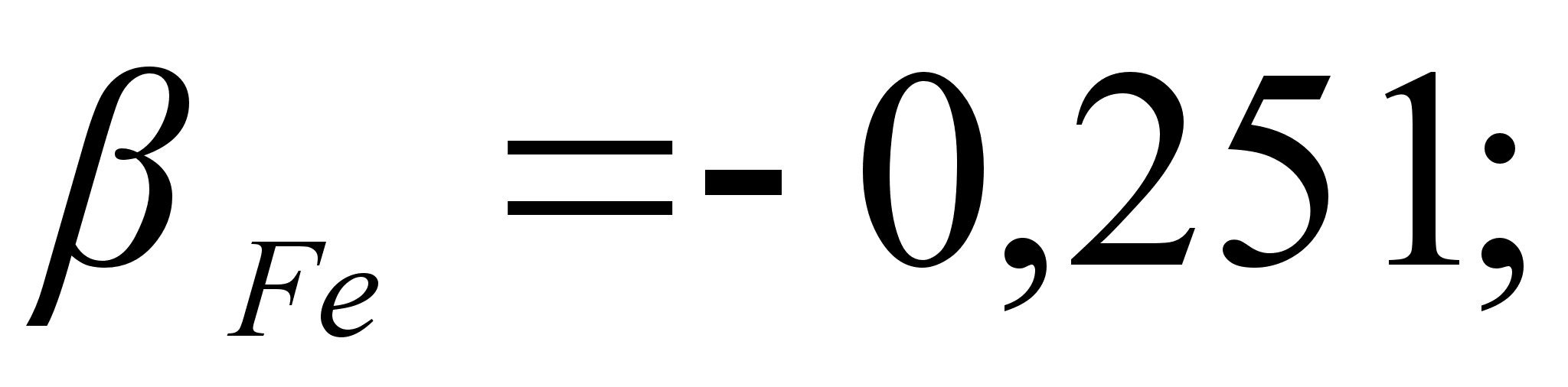
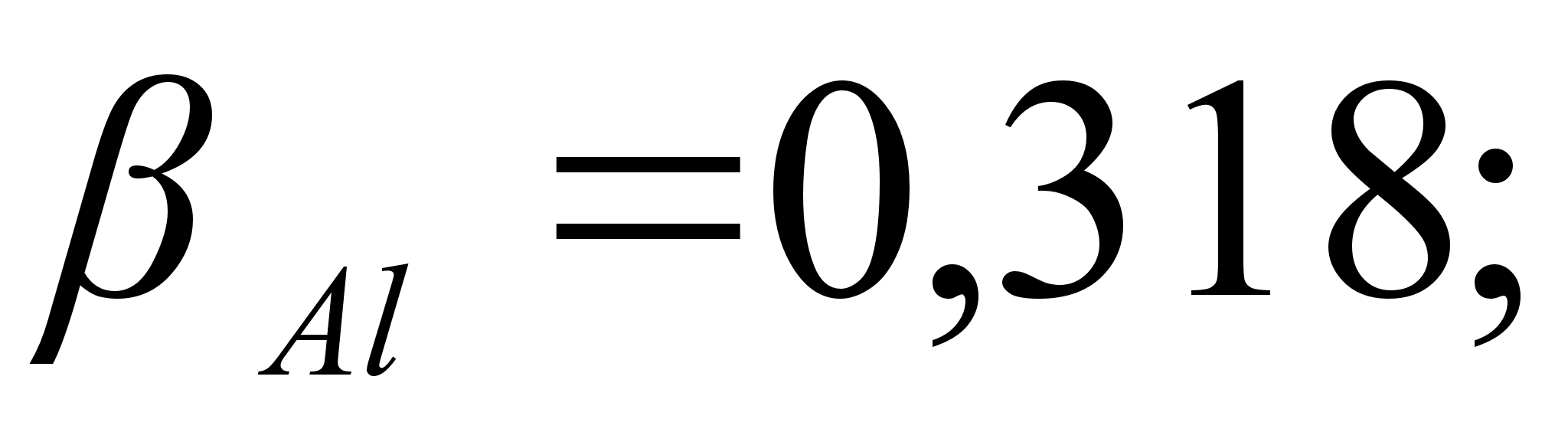
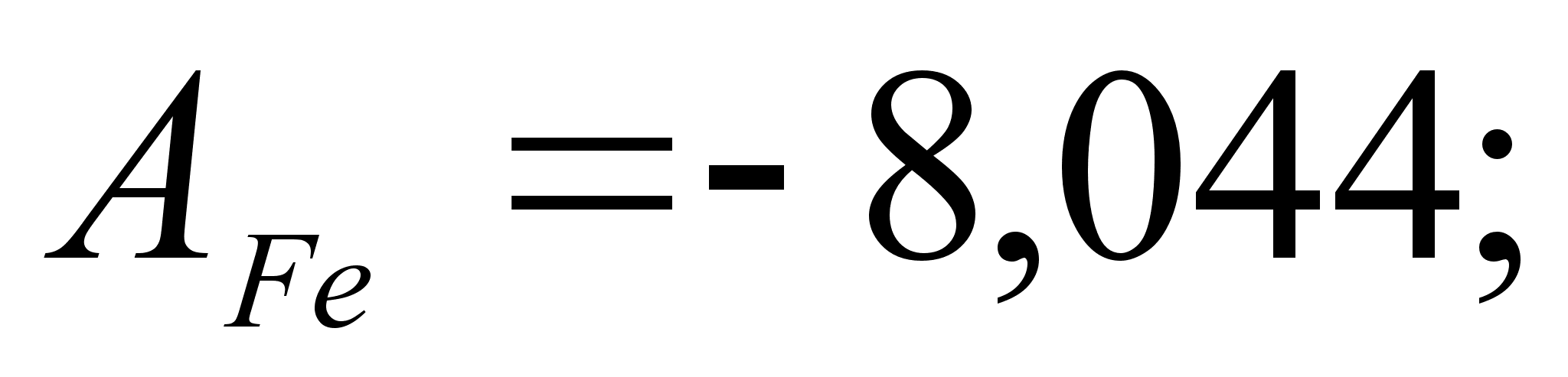
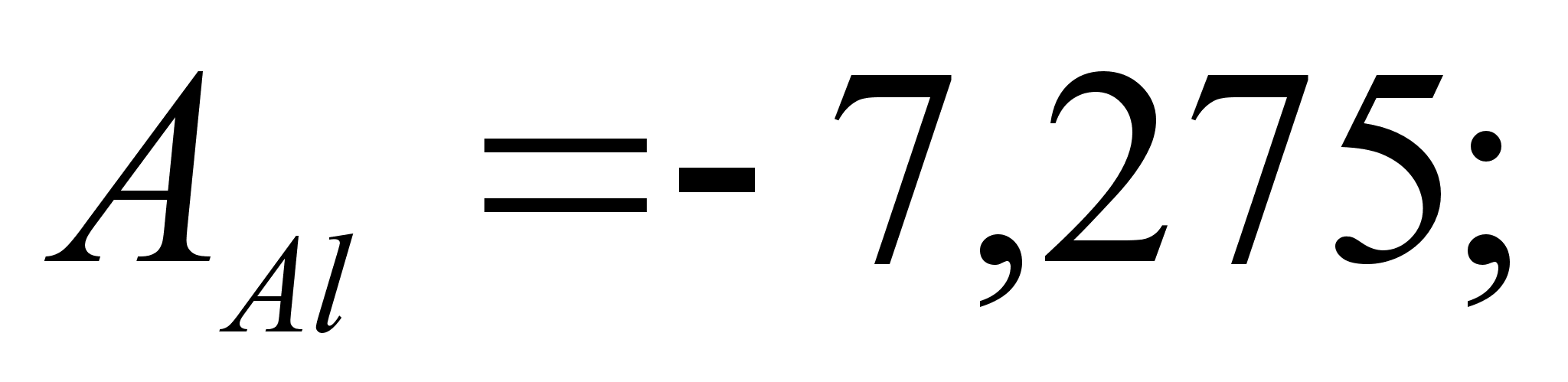
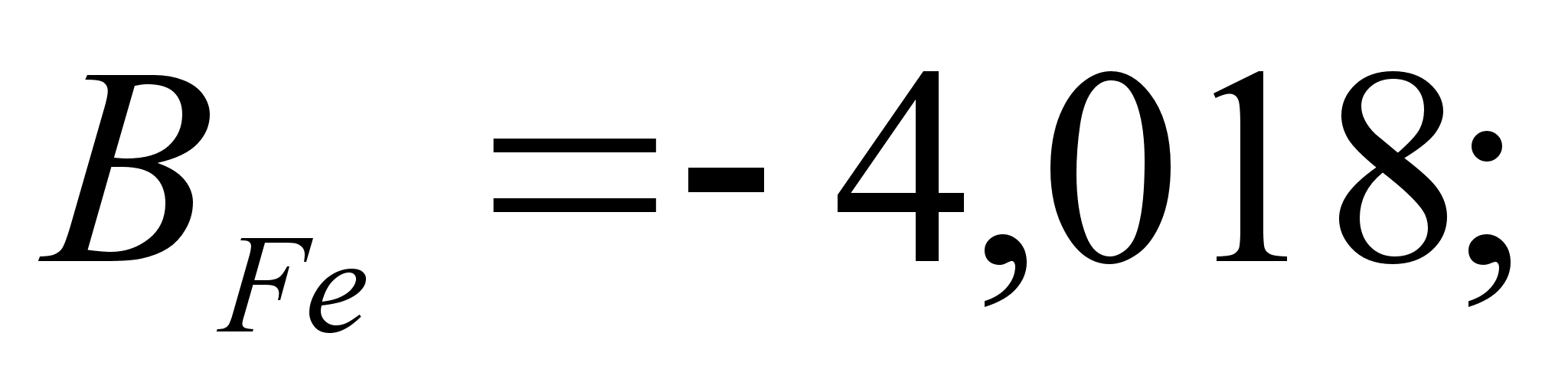
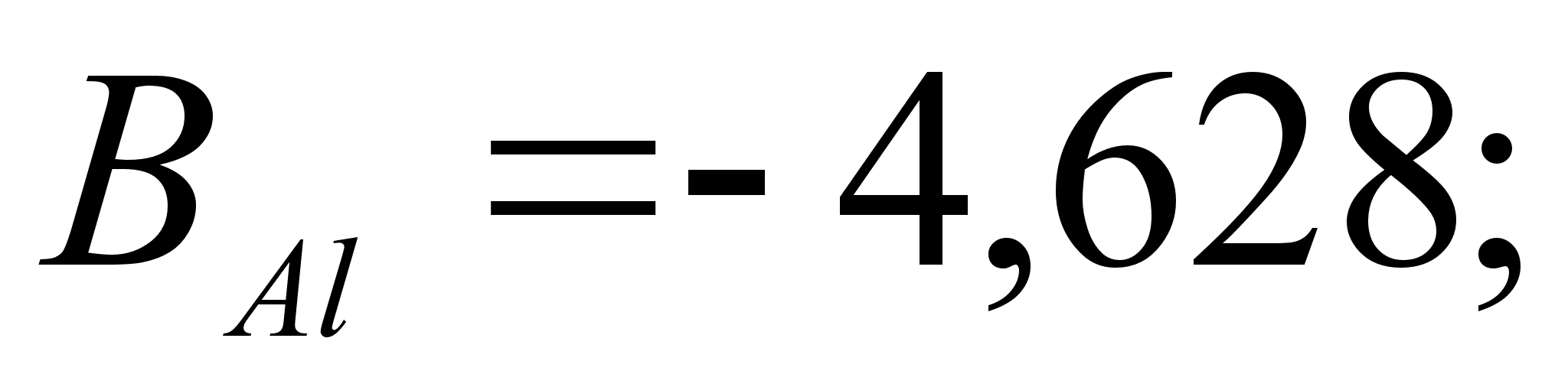
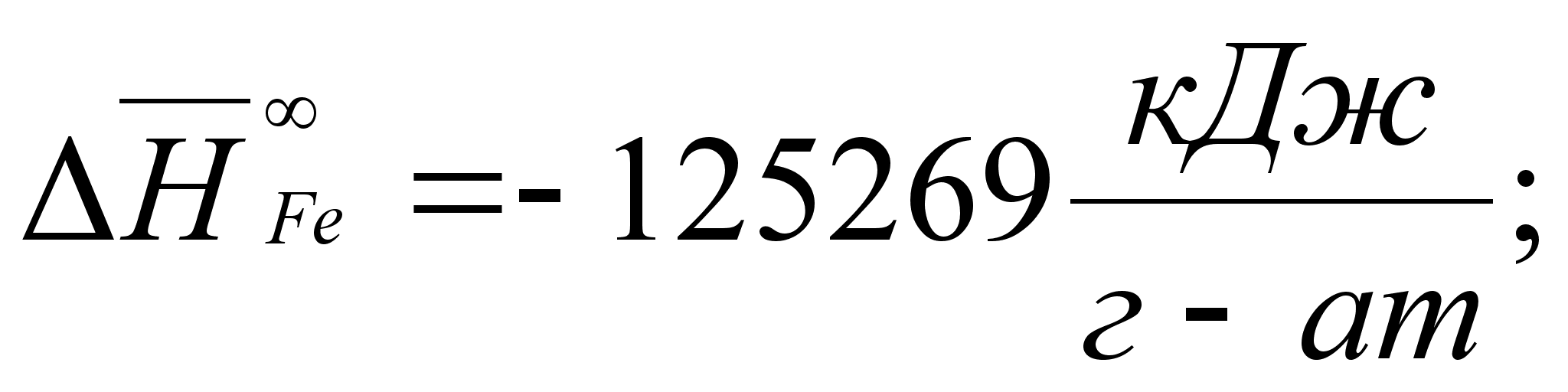
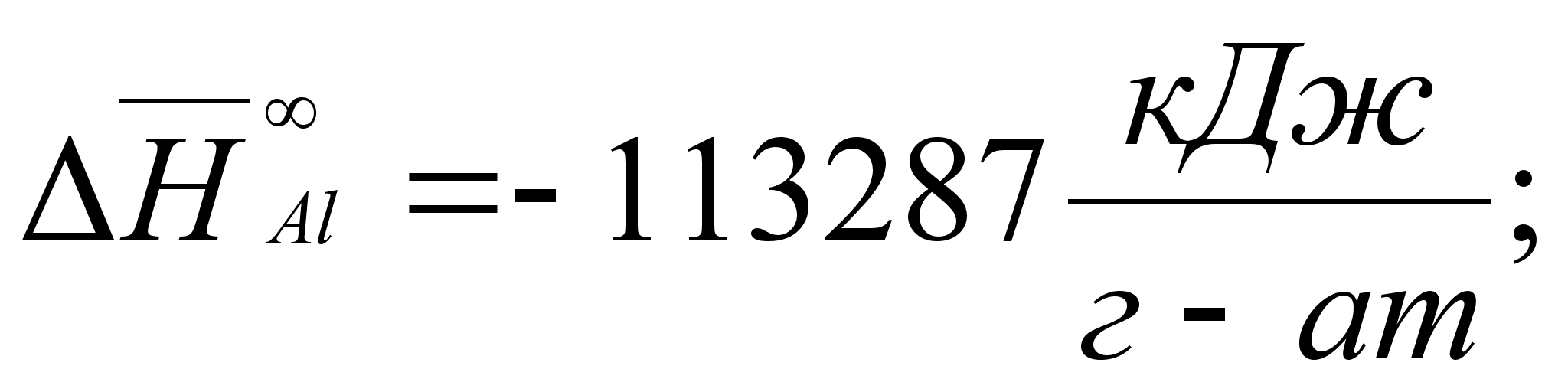
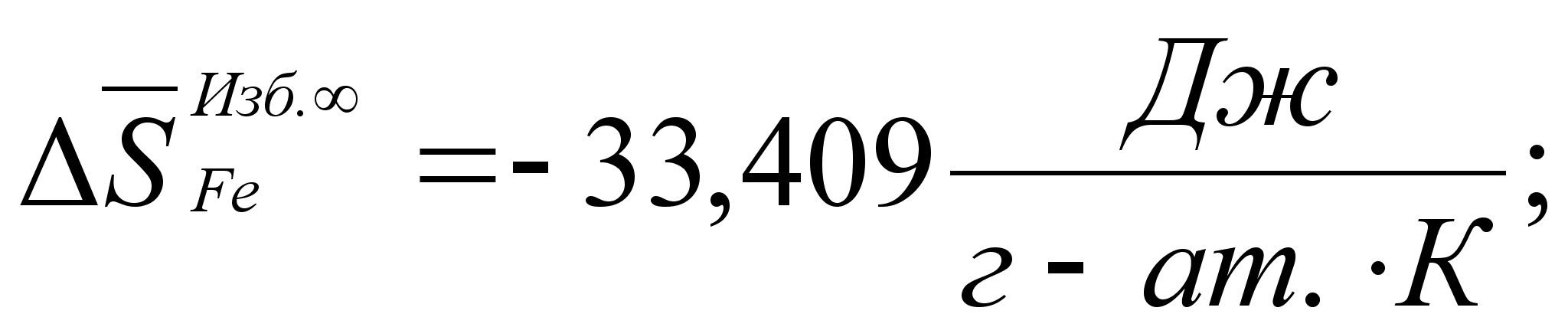
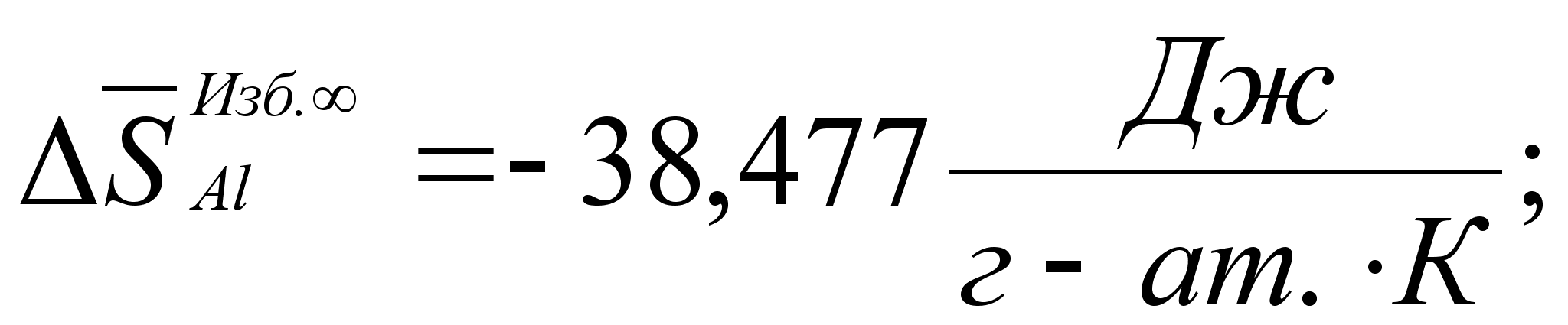
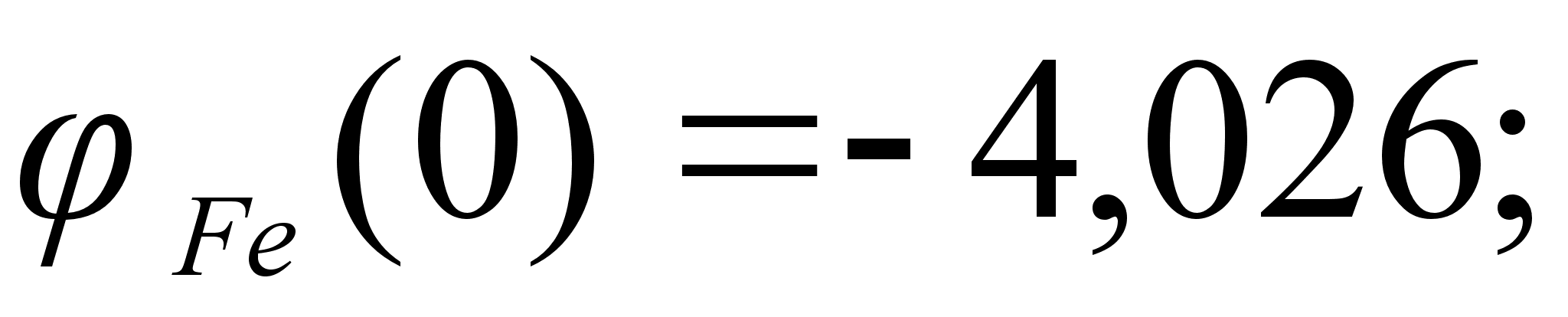
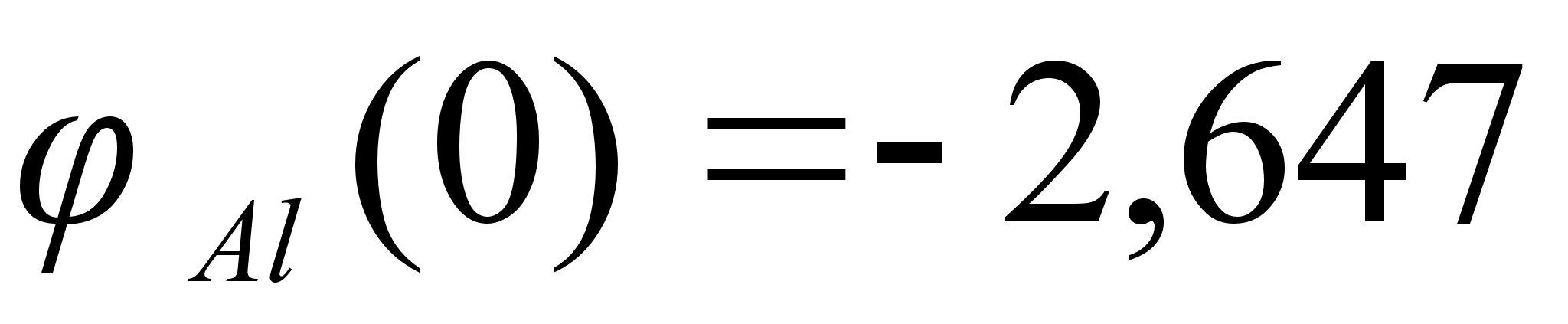
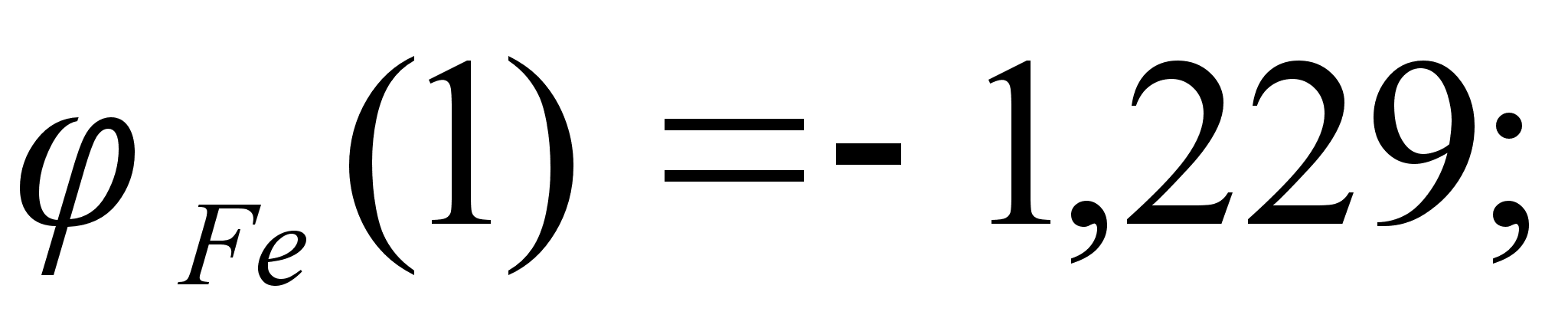
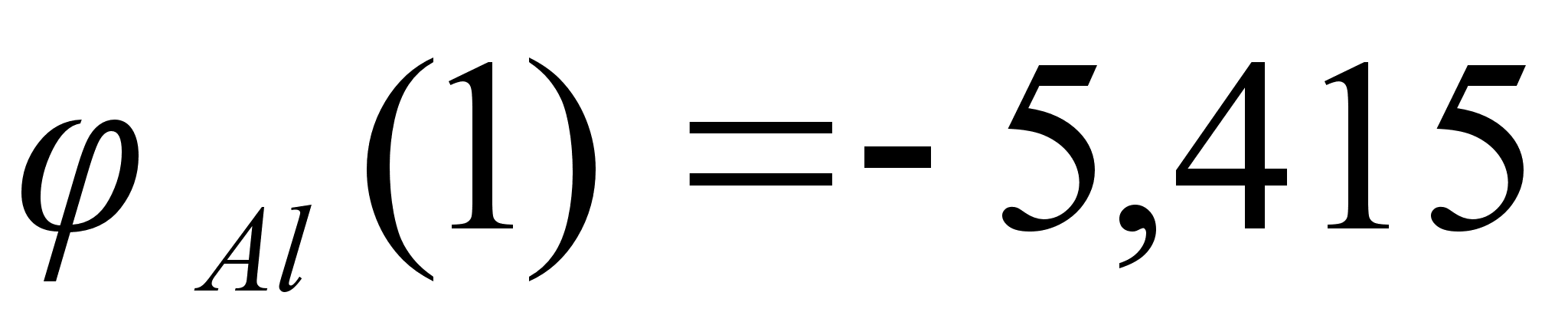
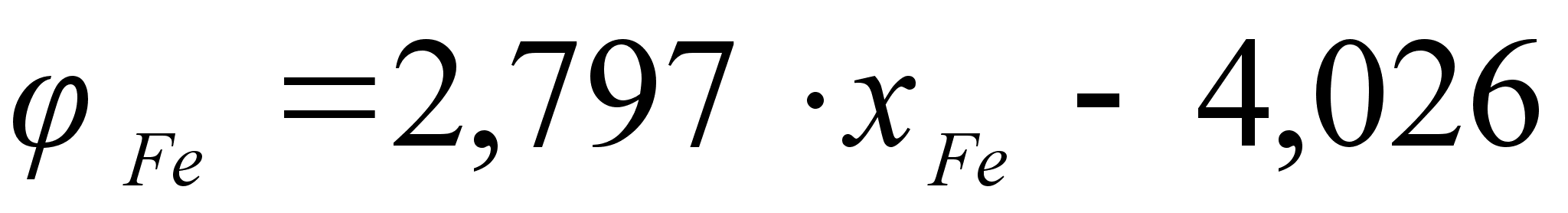 ;
;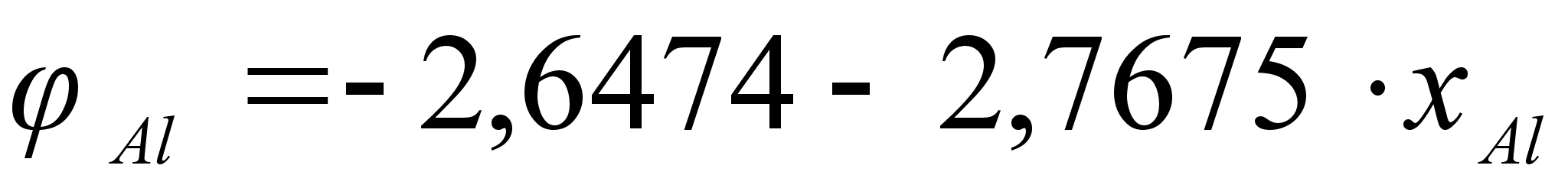 .
.
Таблица 54 – Термодинамические характеристики компонентов системы Fe – V.железо
ванадий
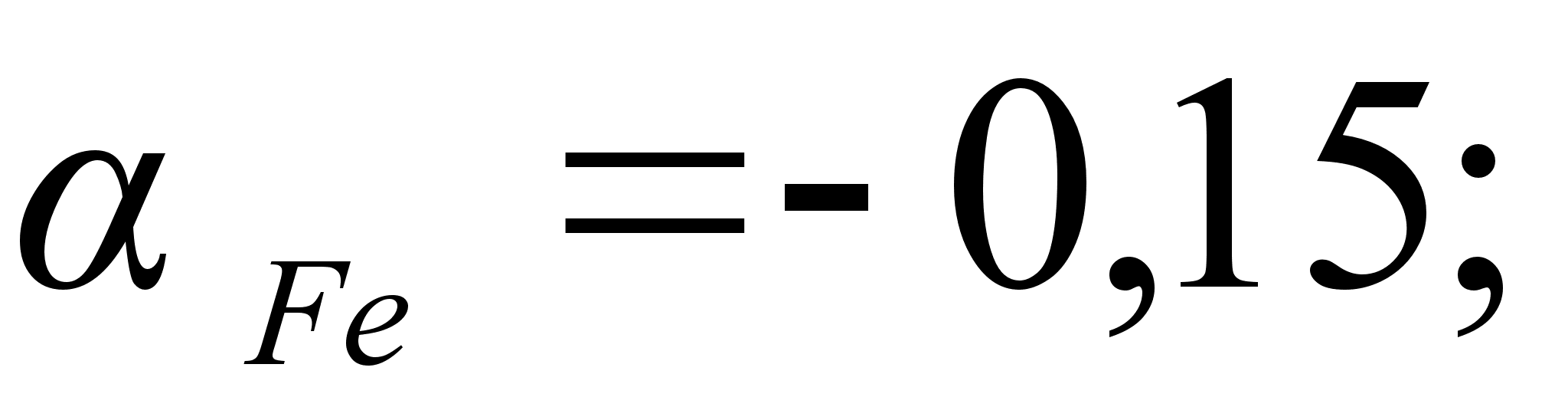
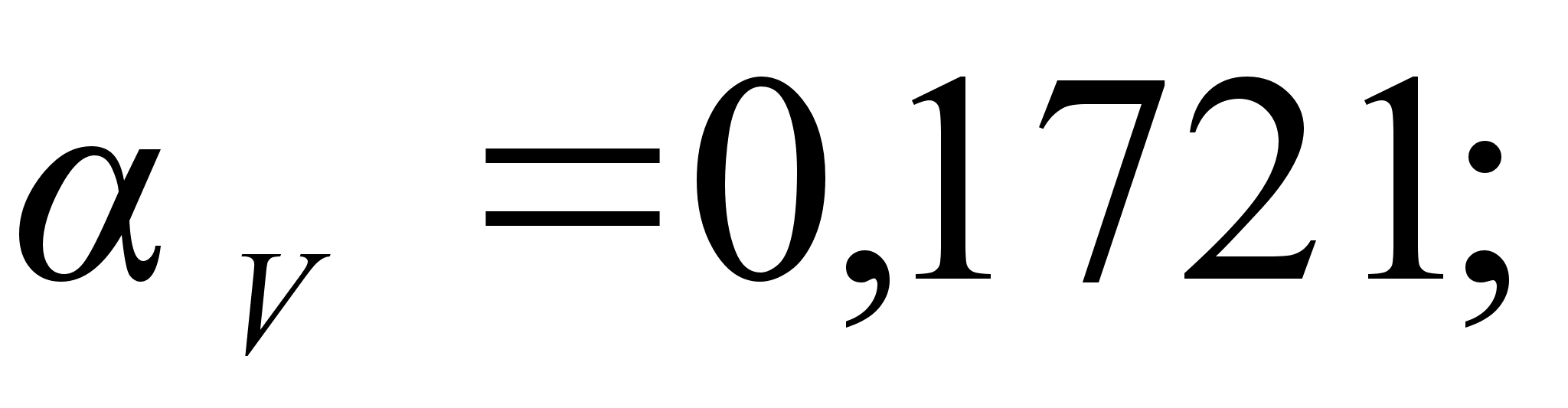
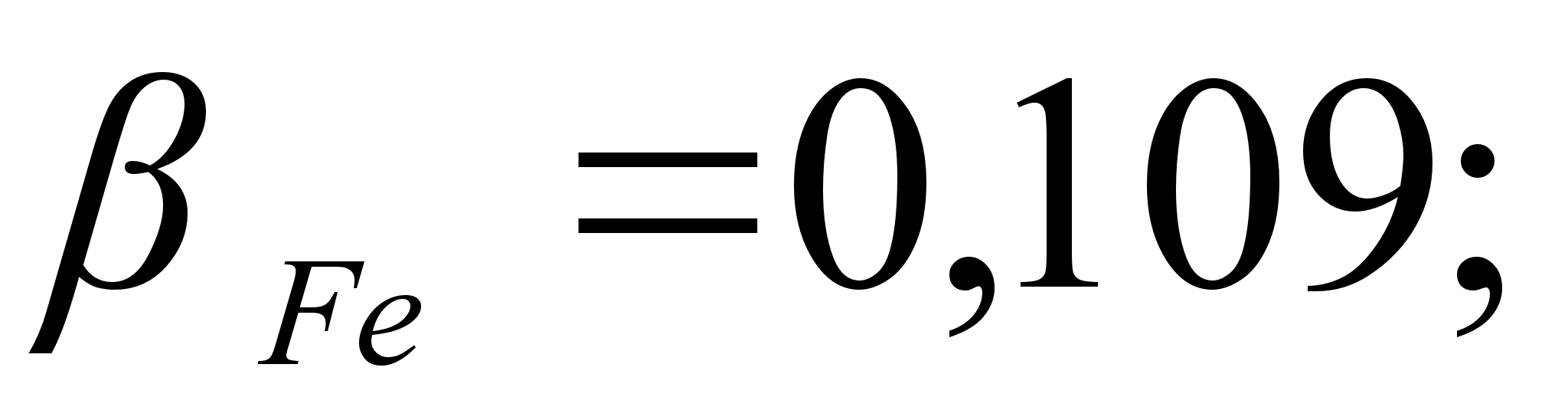
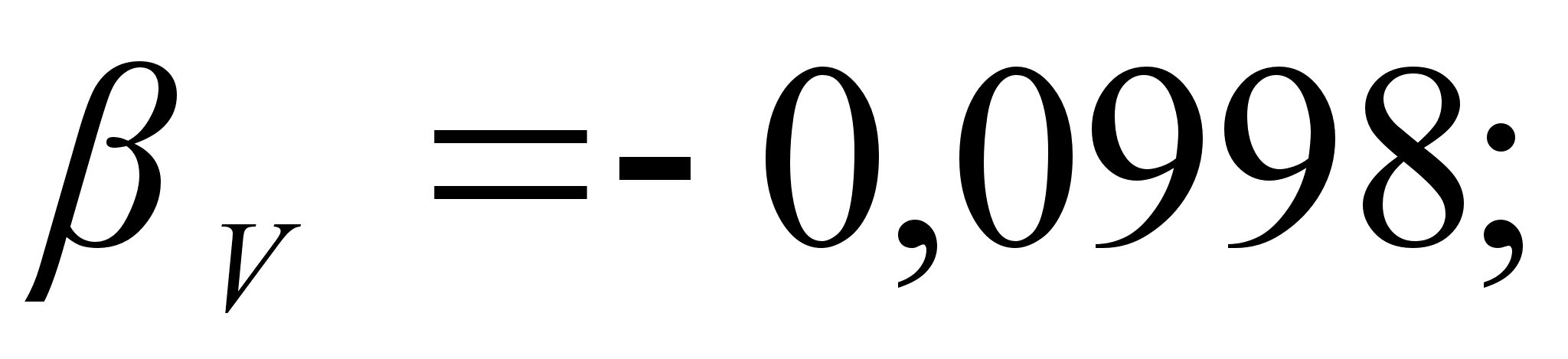
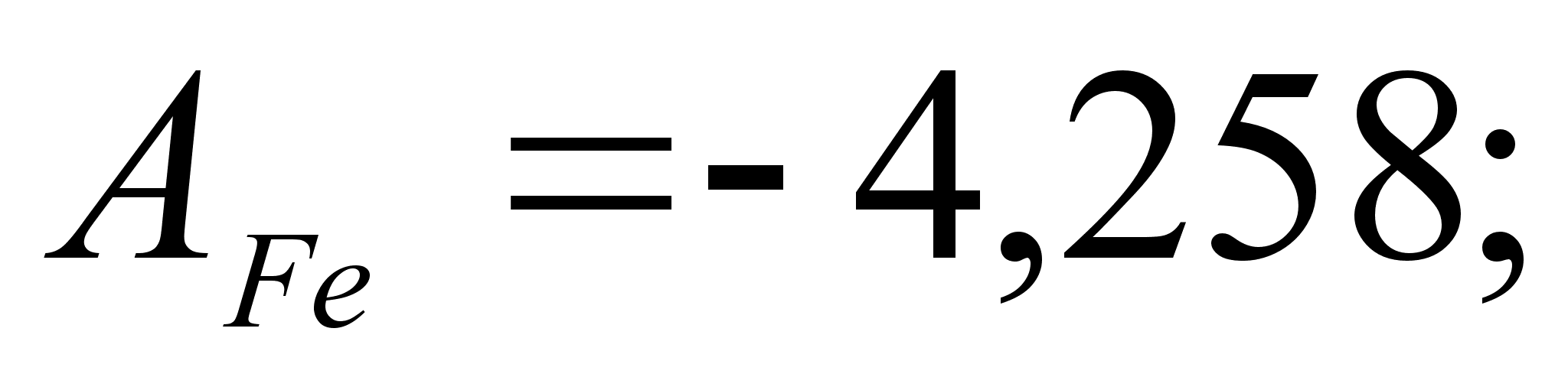
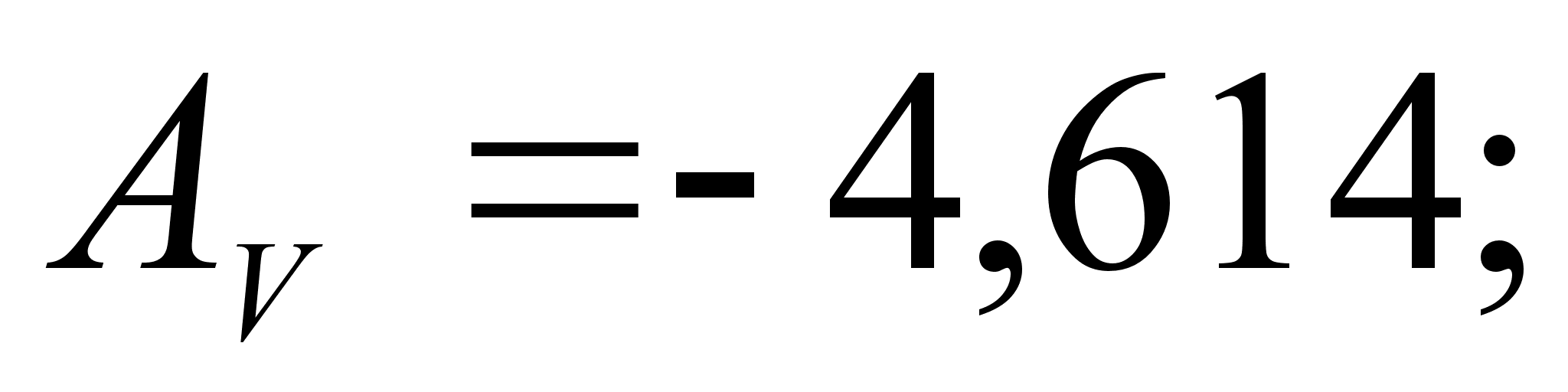
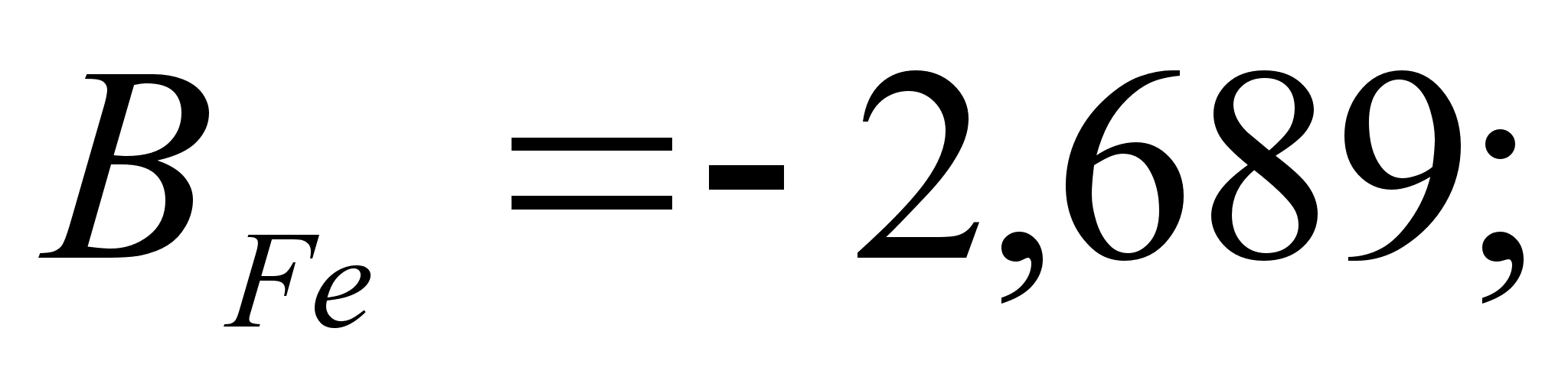
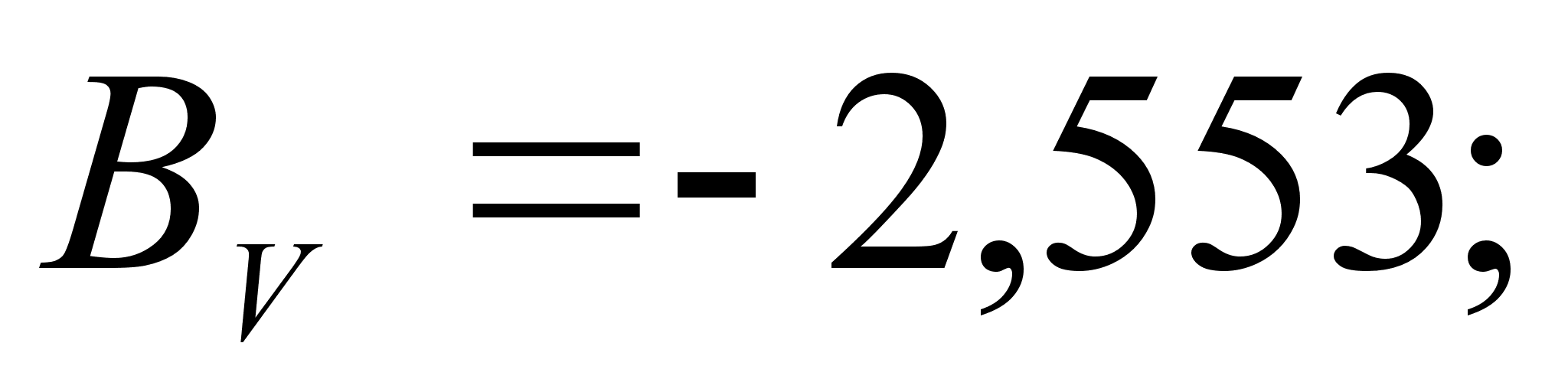
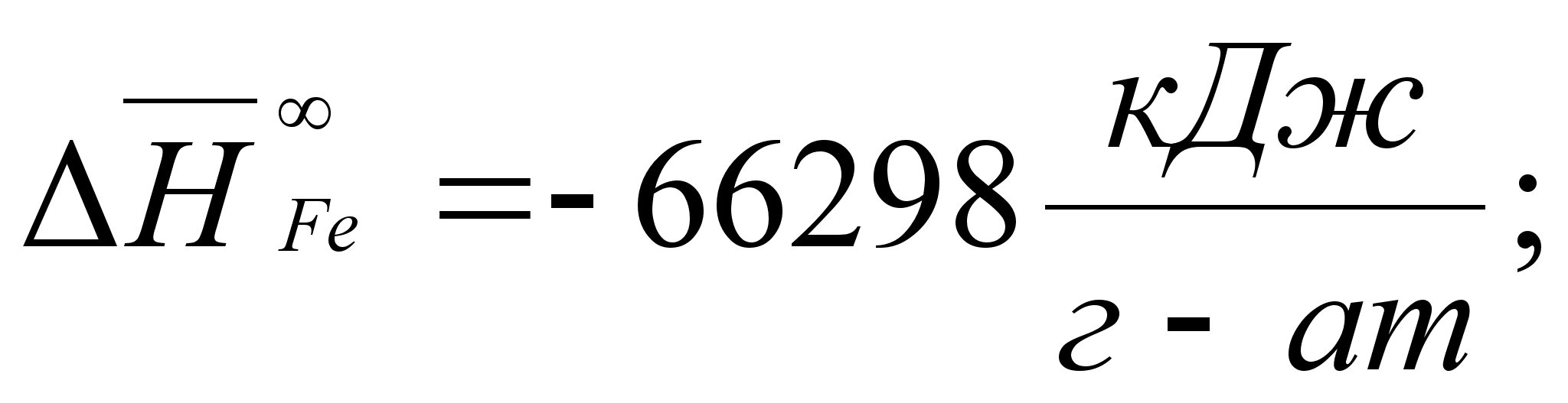
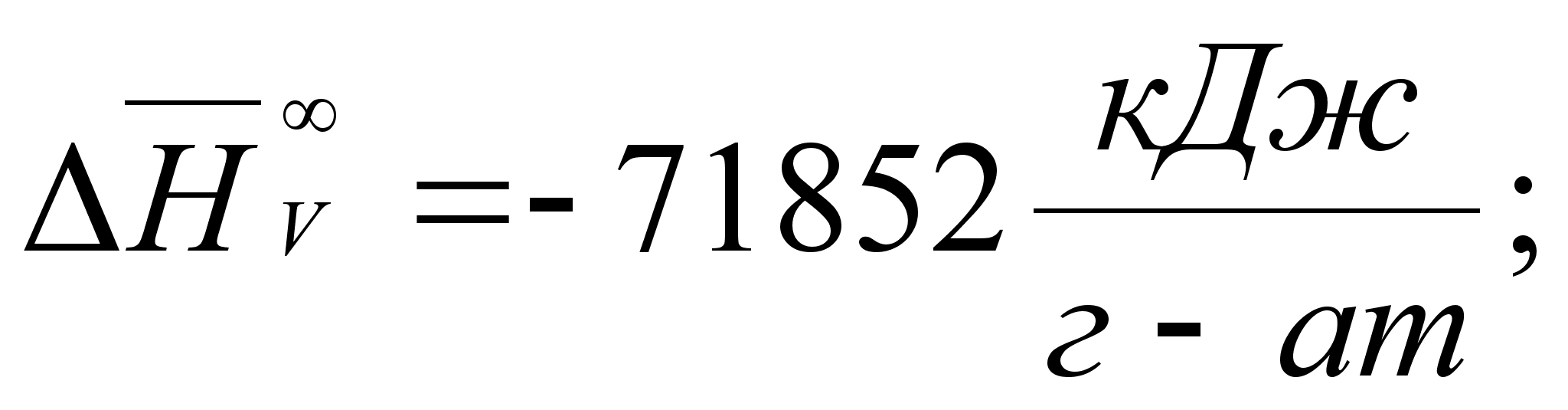
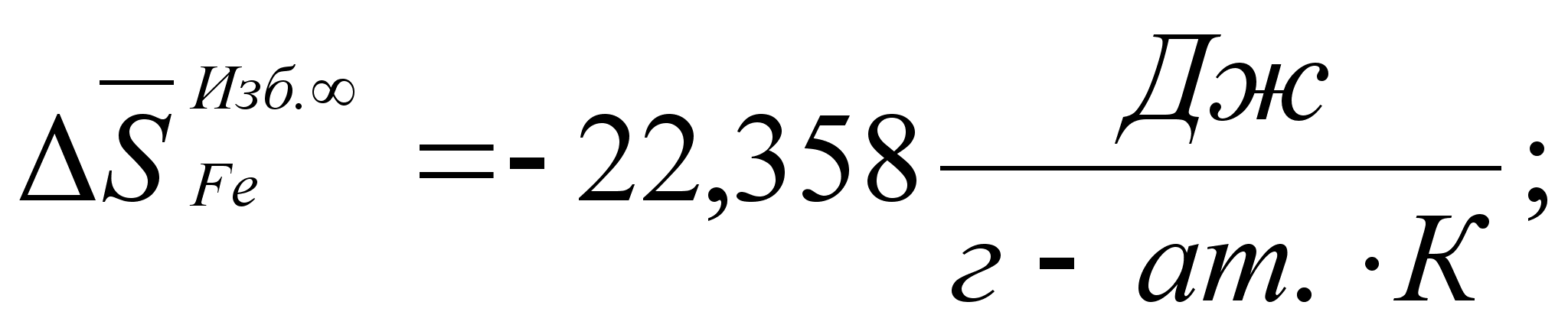
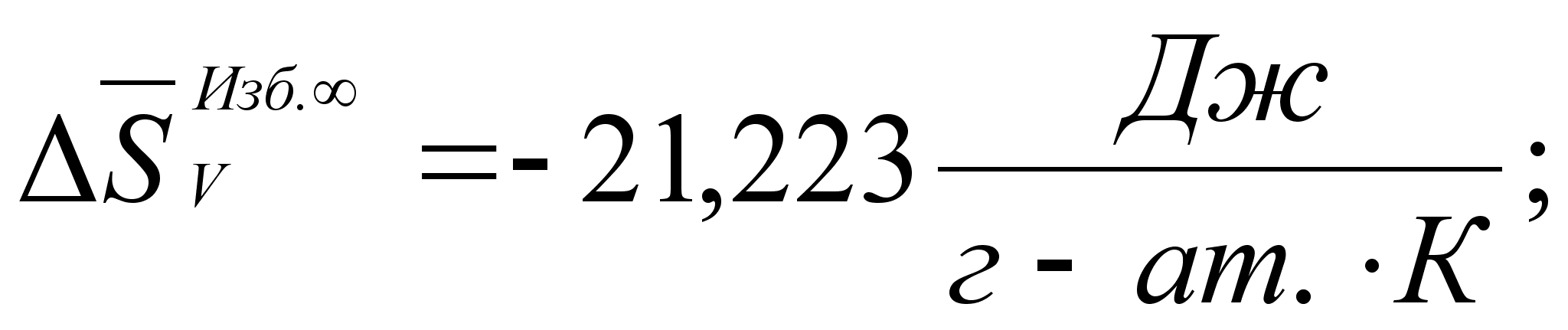
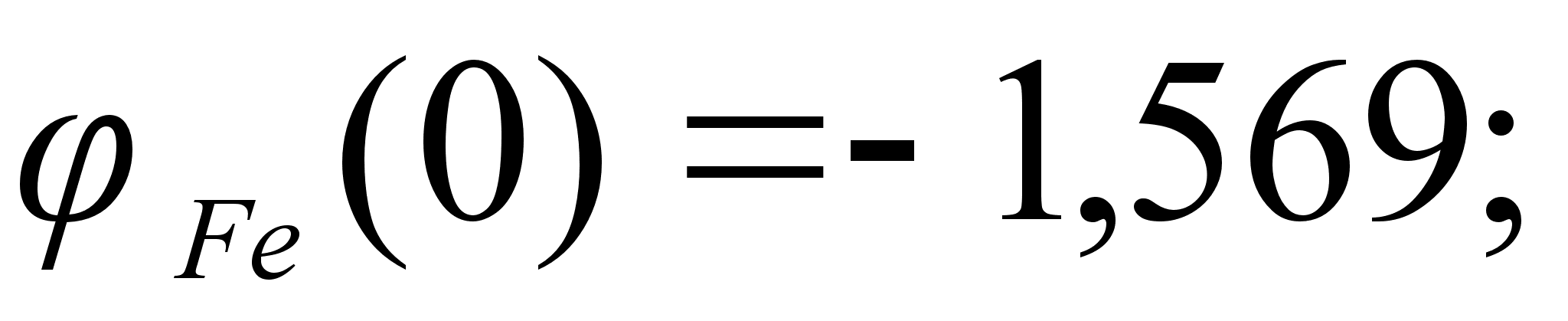
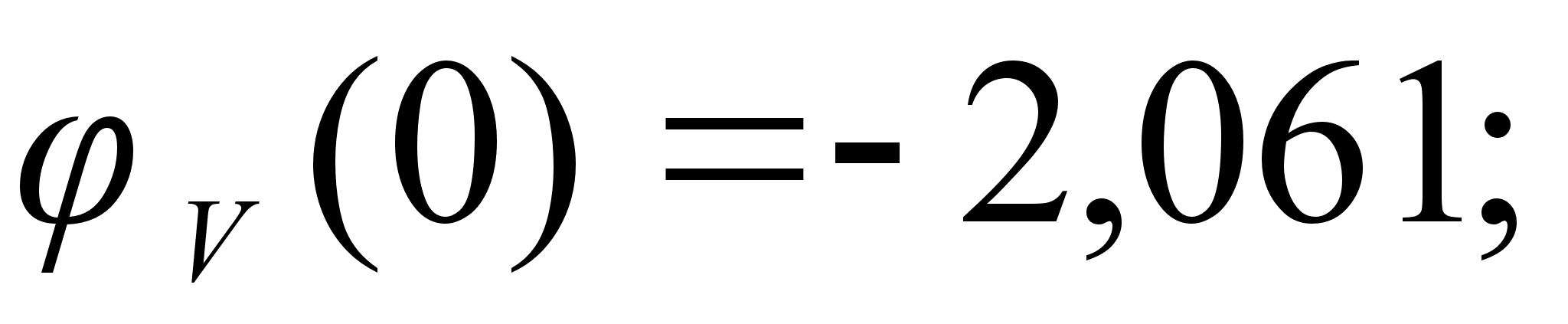
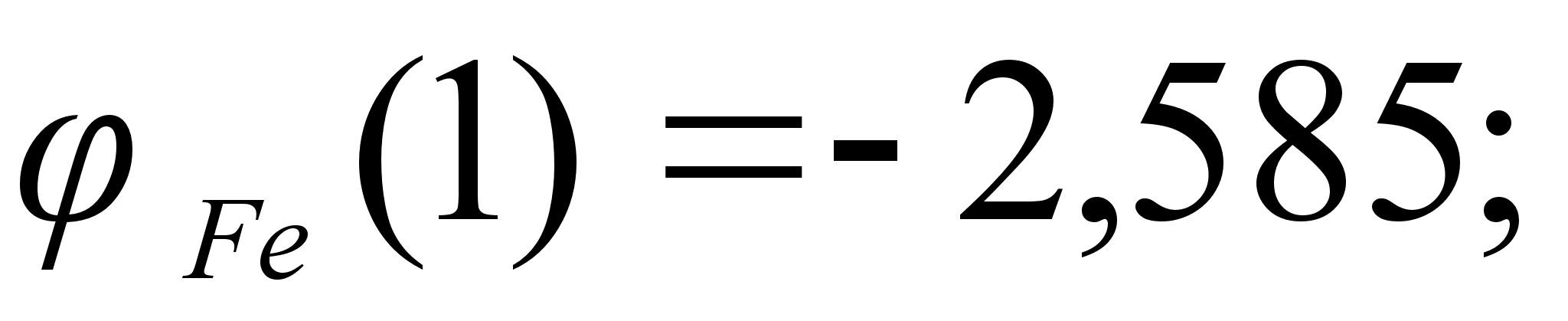
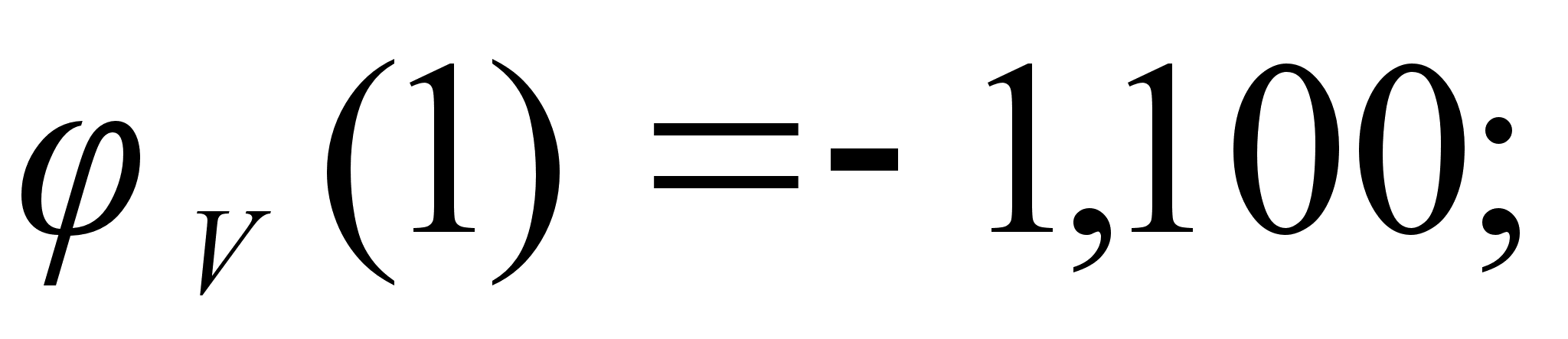
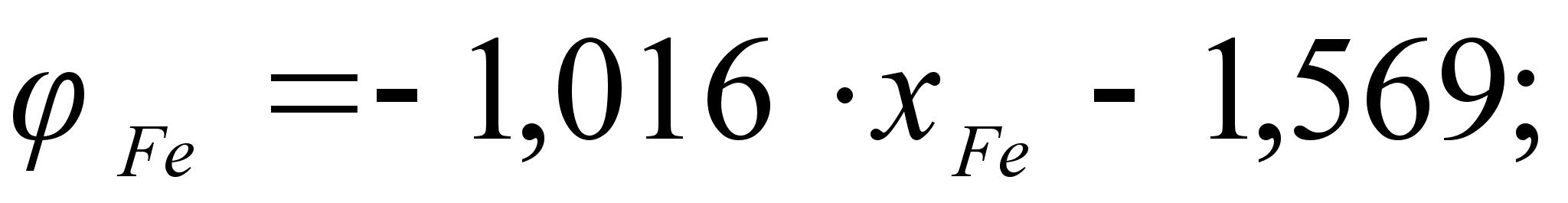
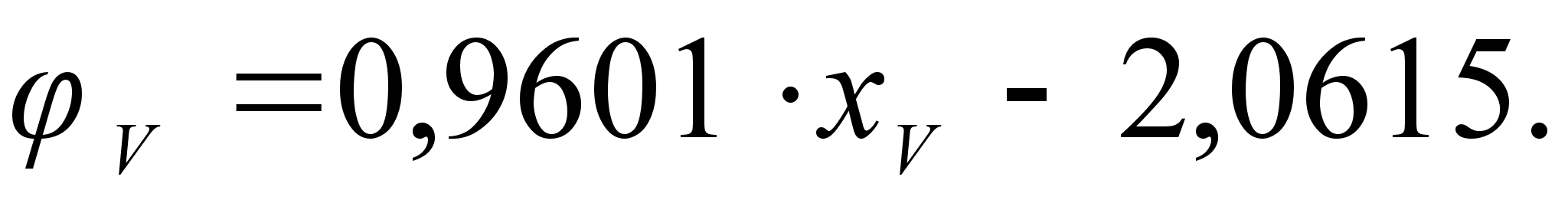
Таблица 55 – Термодинамические характеристики компонентов системы Fe – Co.
железо
кобальт
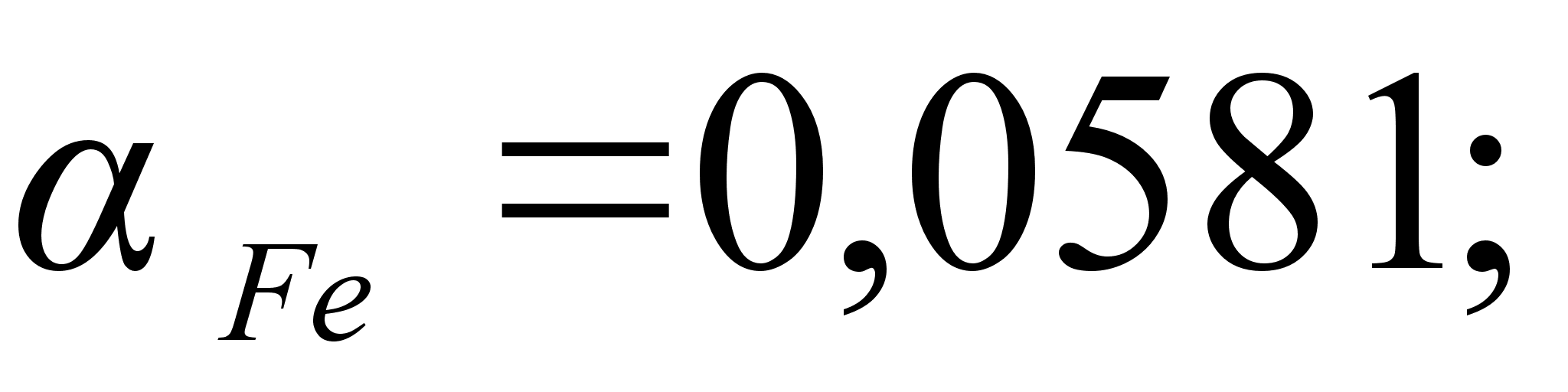
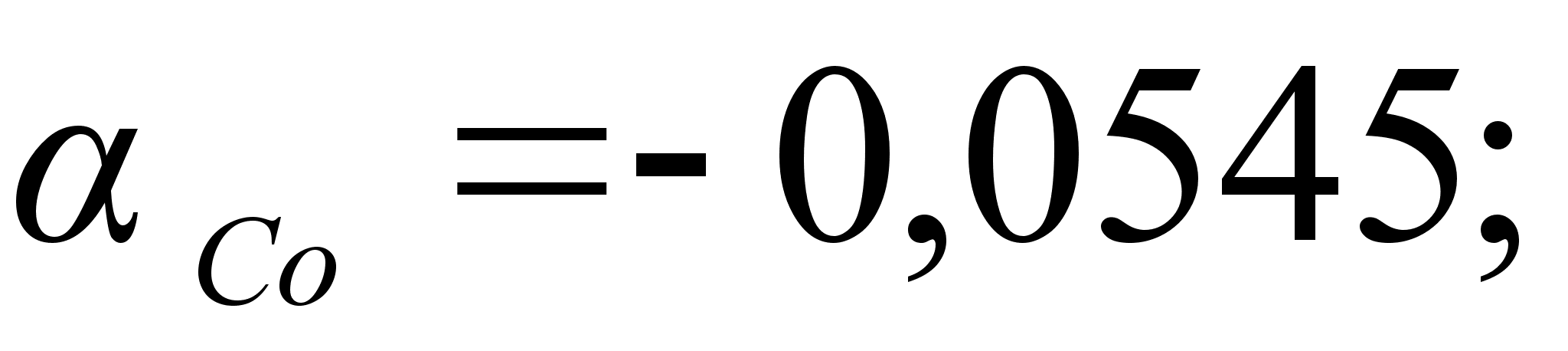
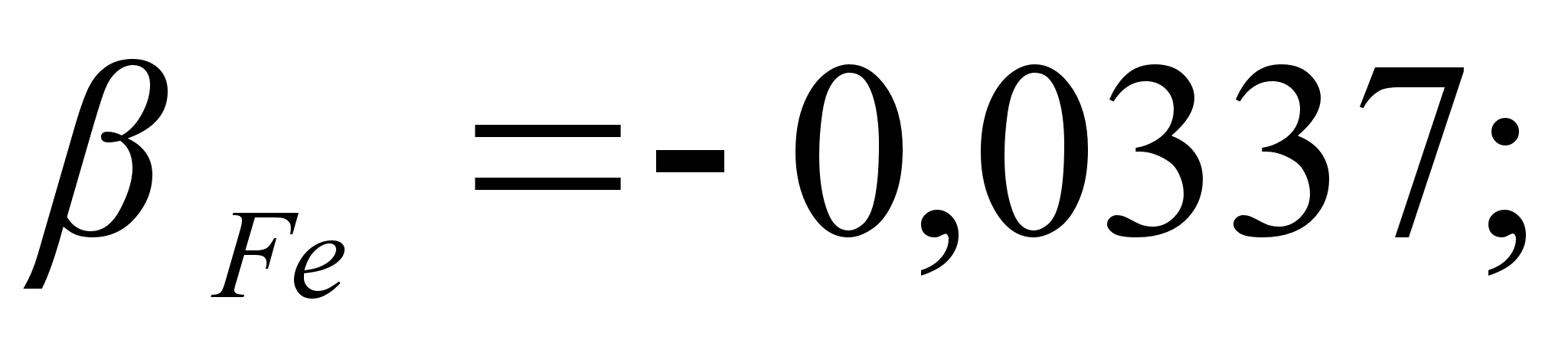
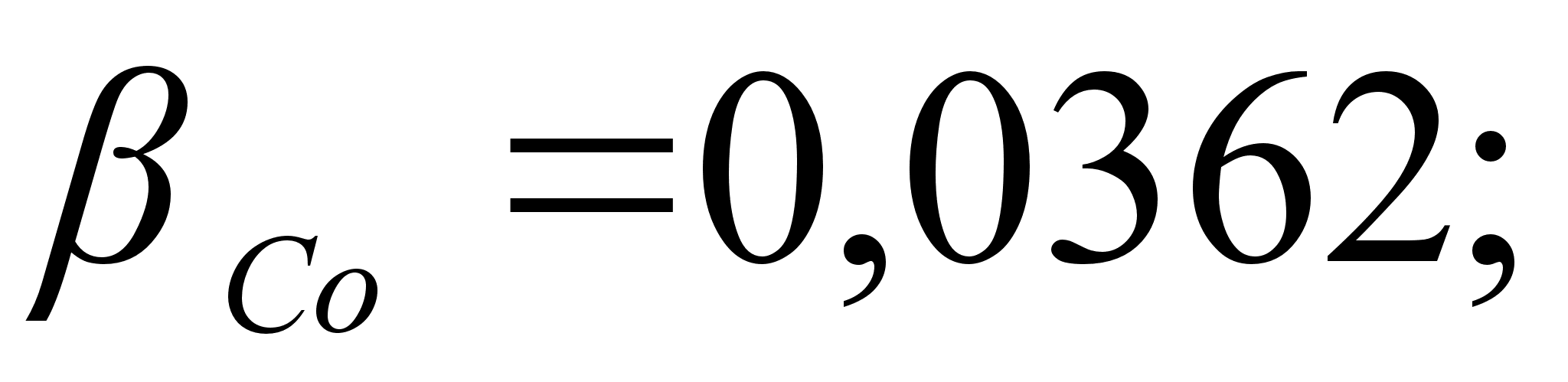
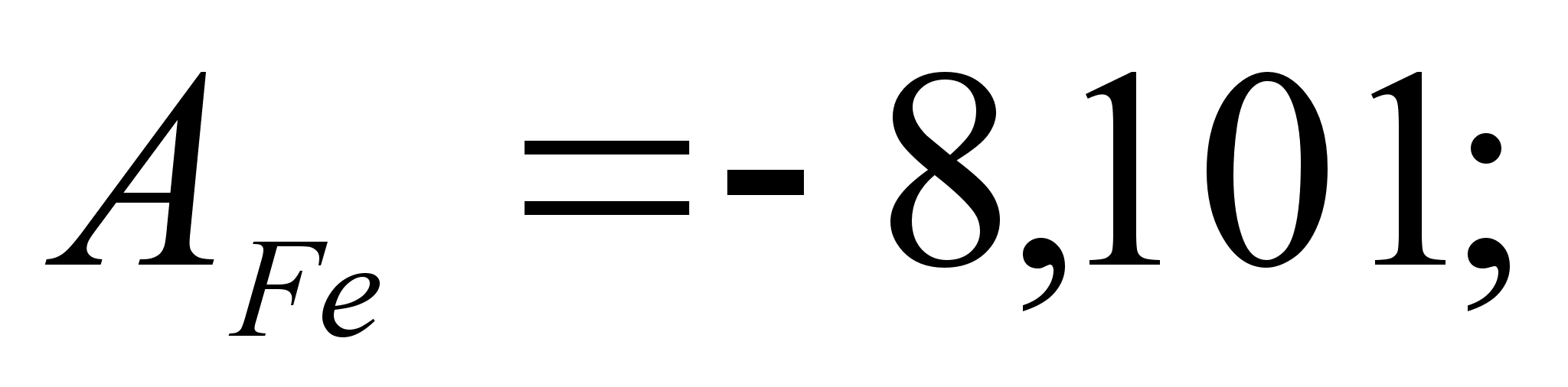
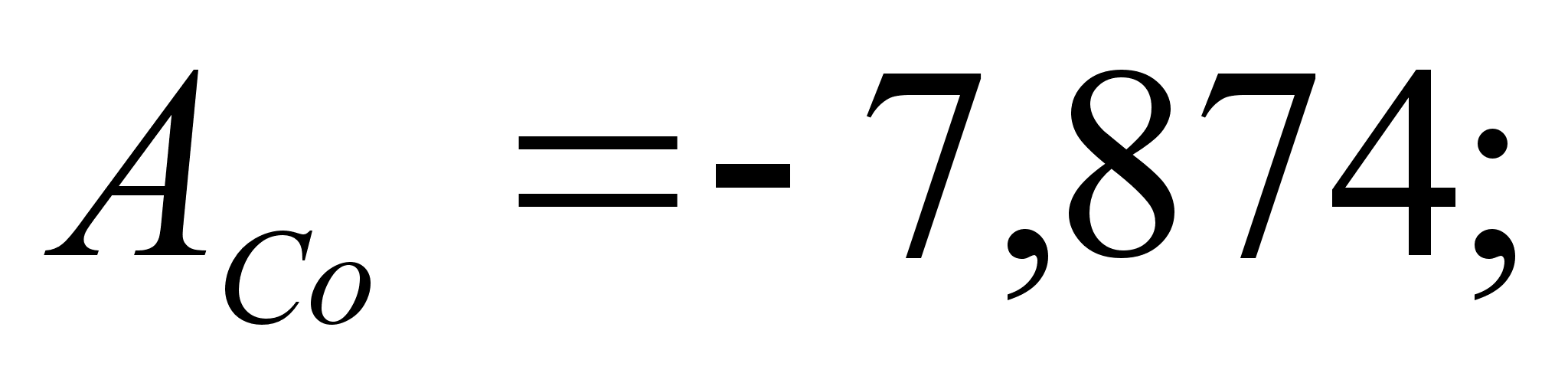
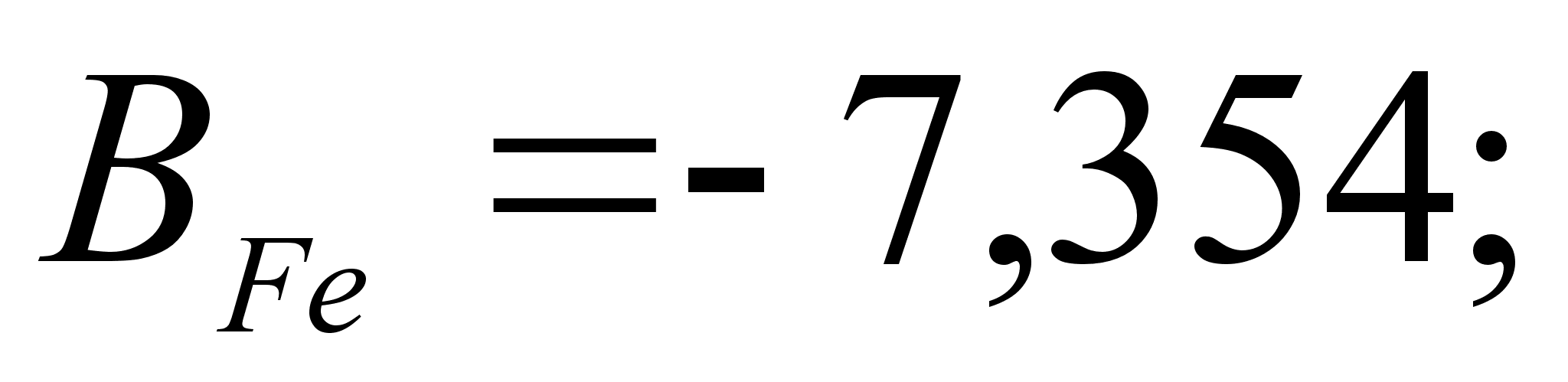
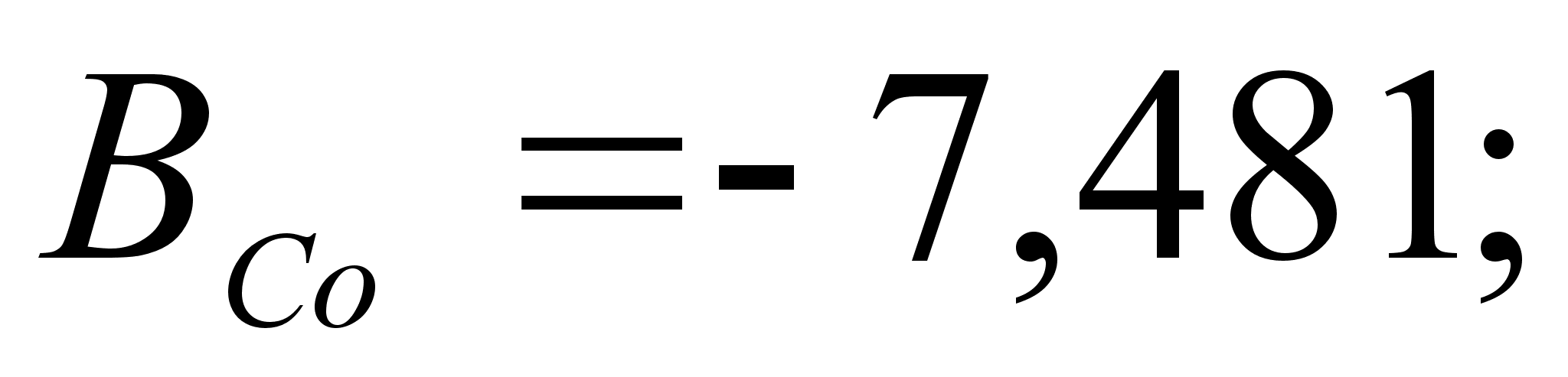
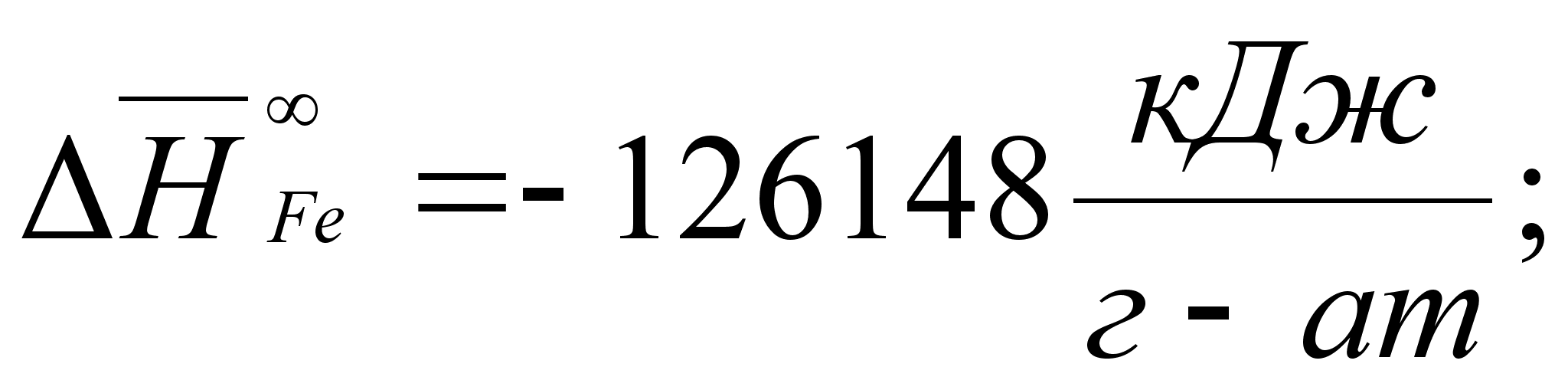
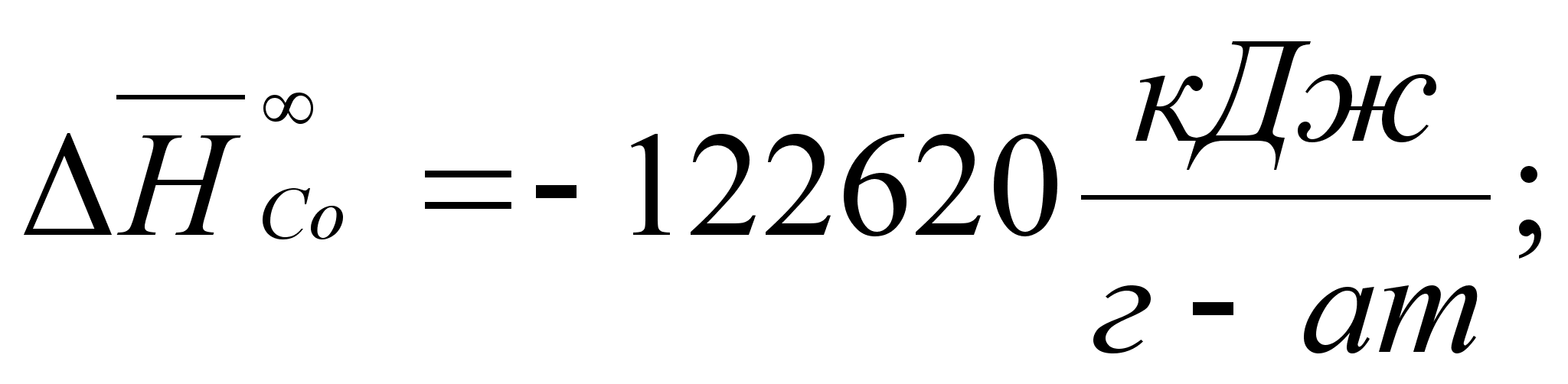
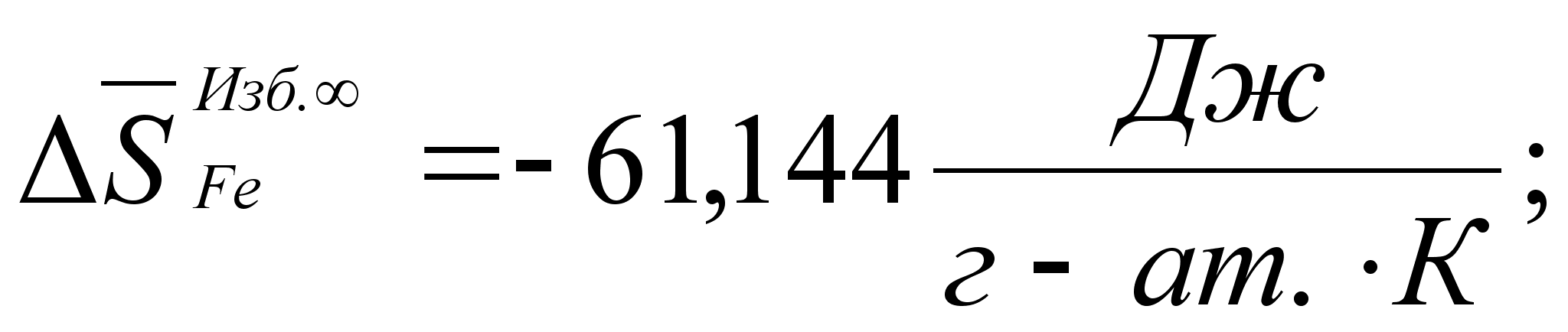
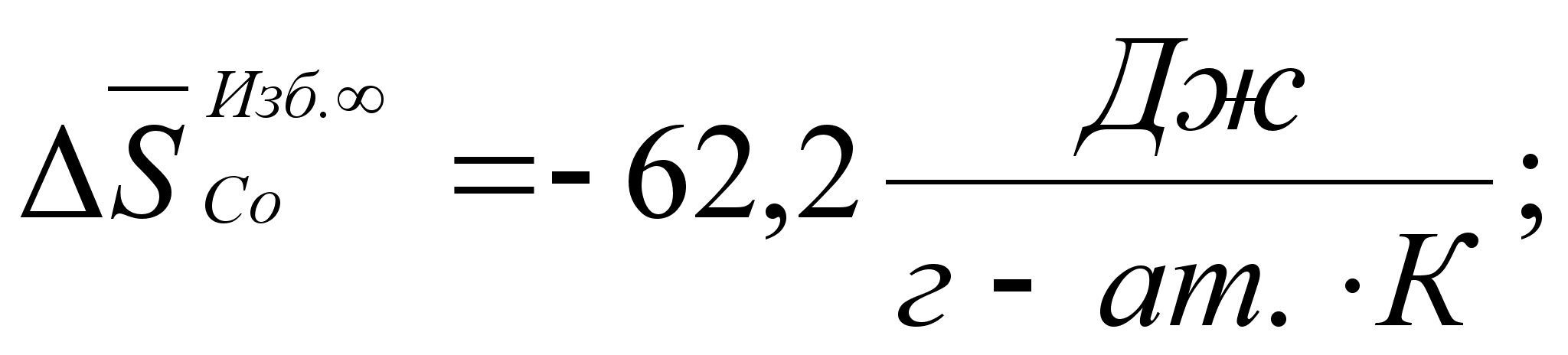
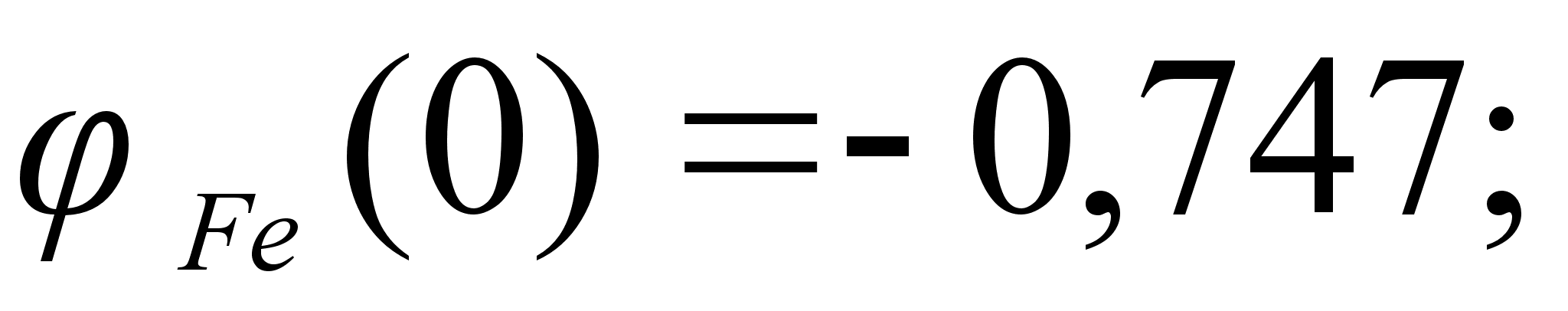
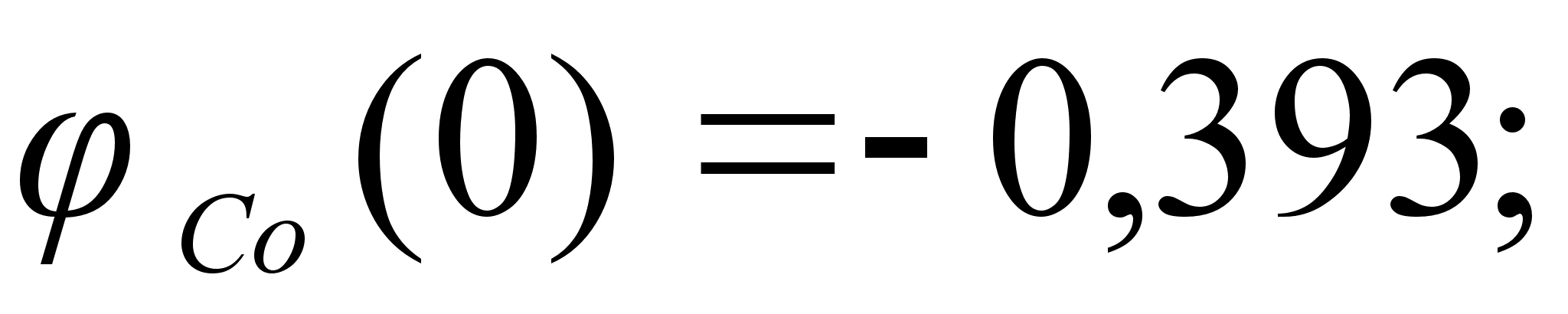
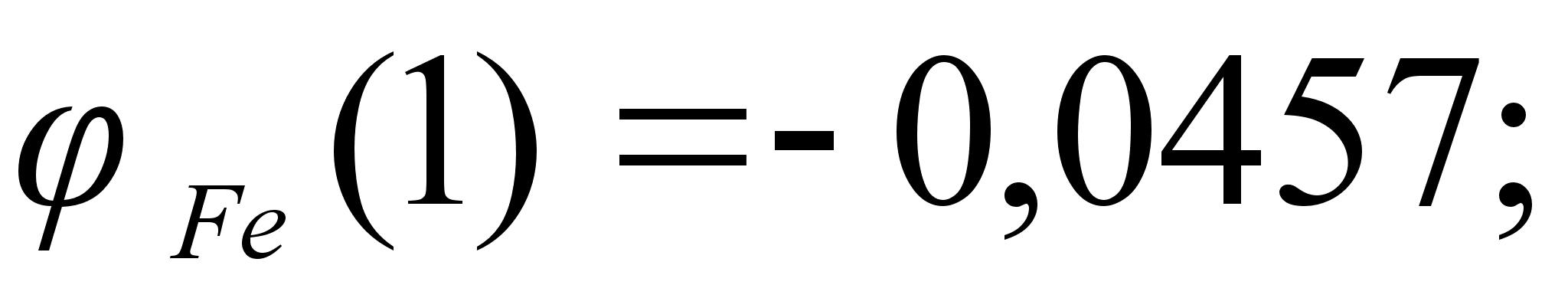
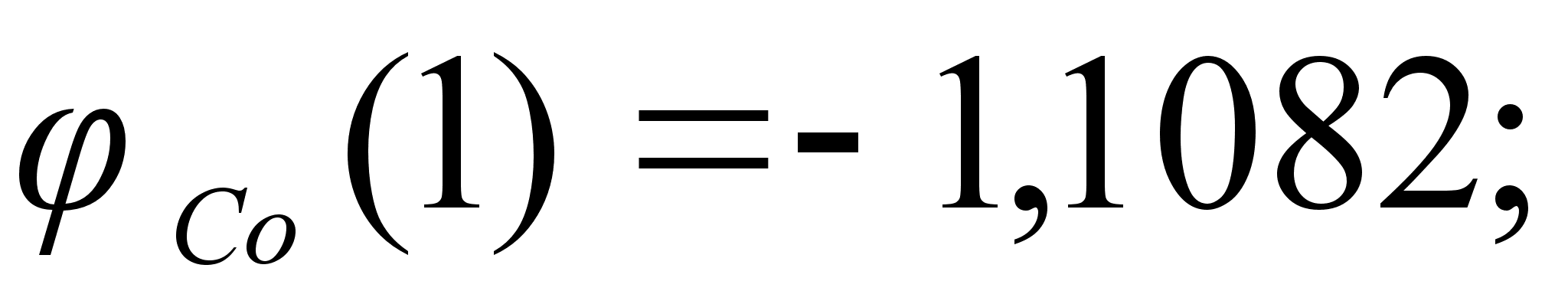
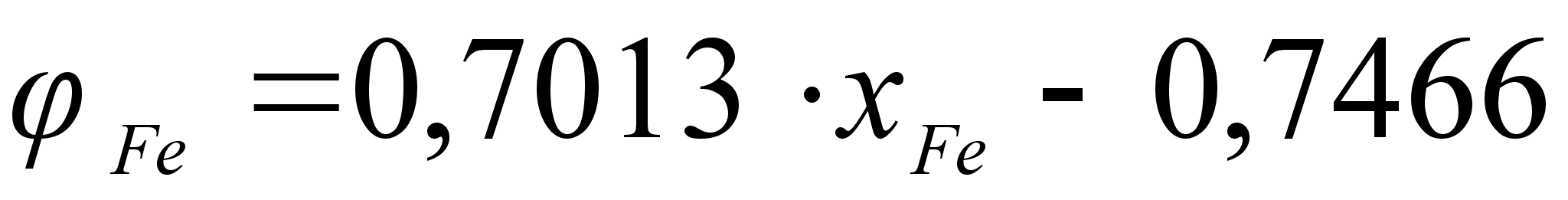 ;
;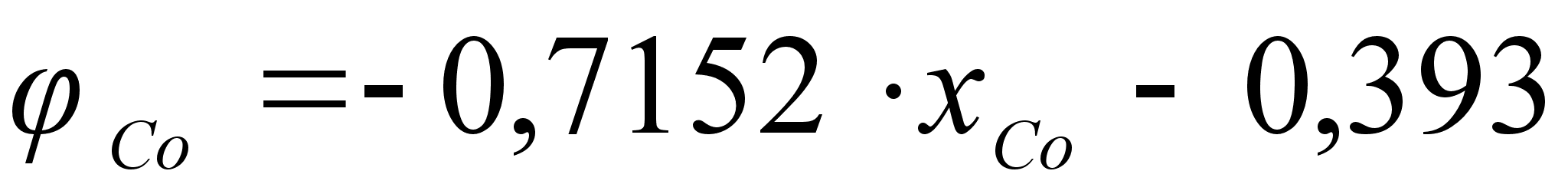 .
.
Таблица 56 – Термодинамические характеристики компонентов системы W – Pd..
вольфрам
палладий
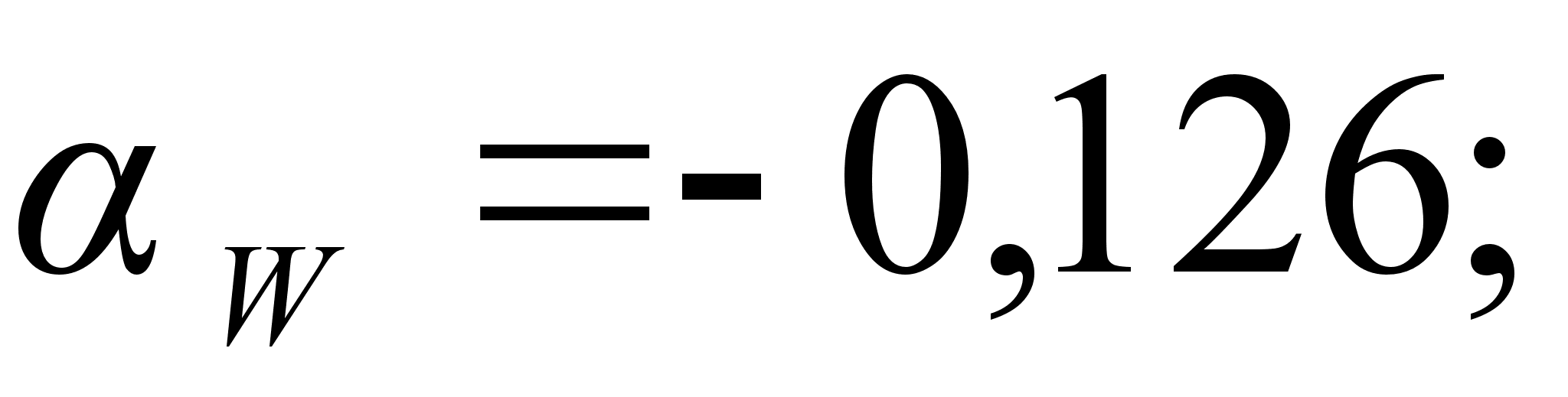
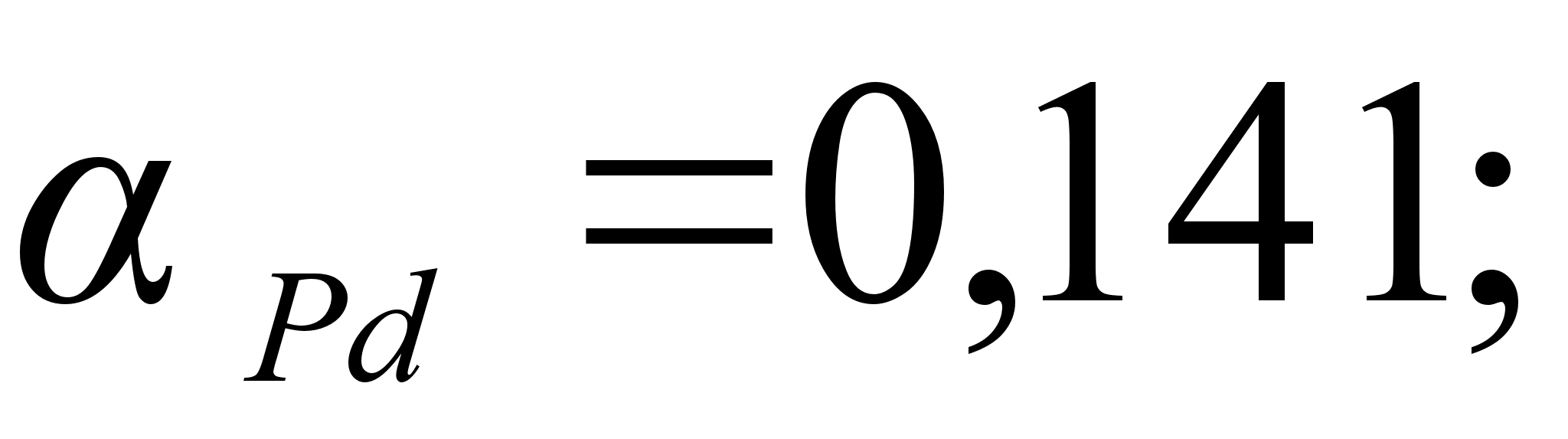
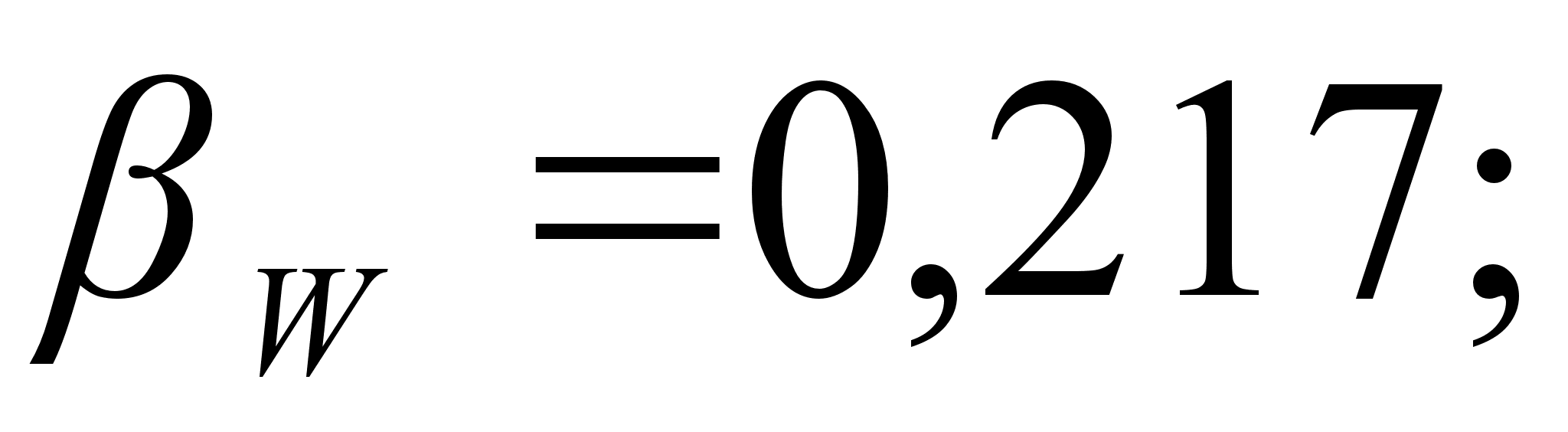
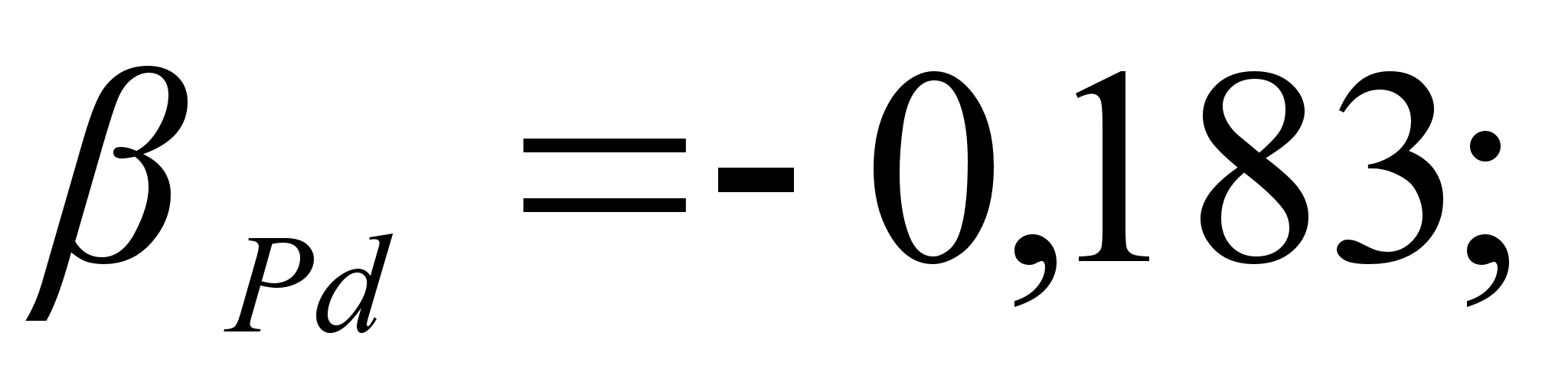
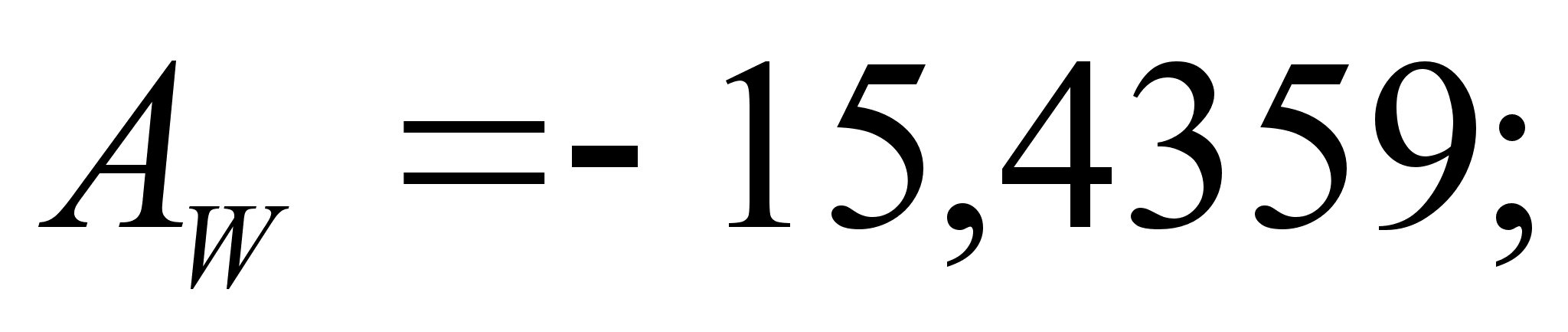
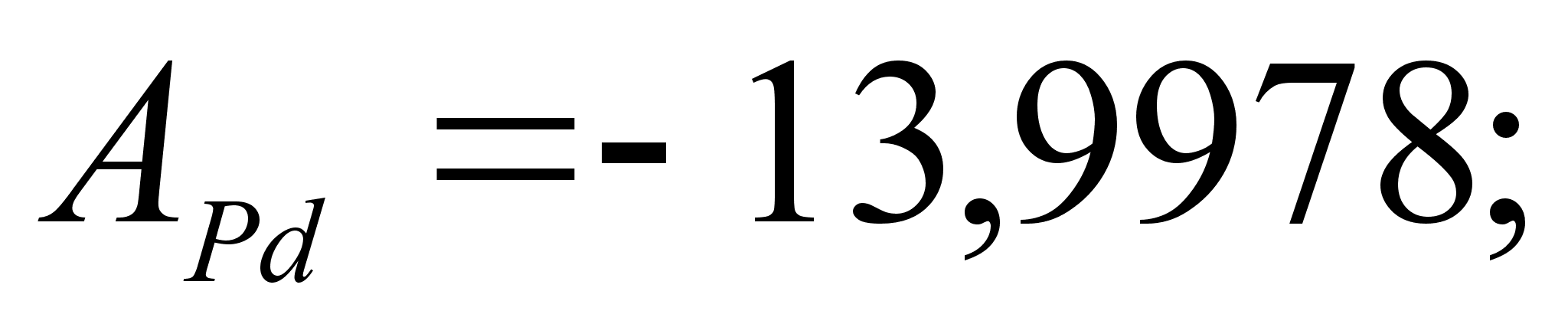
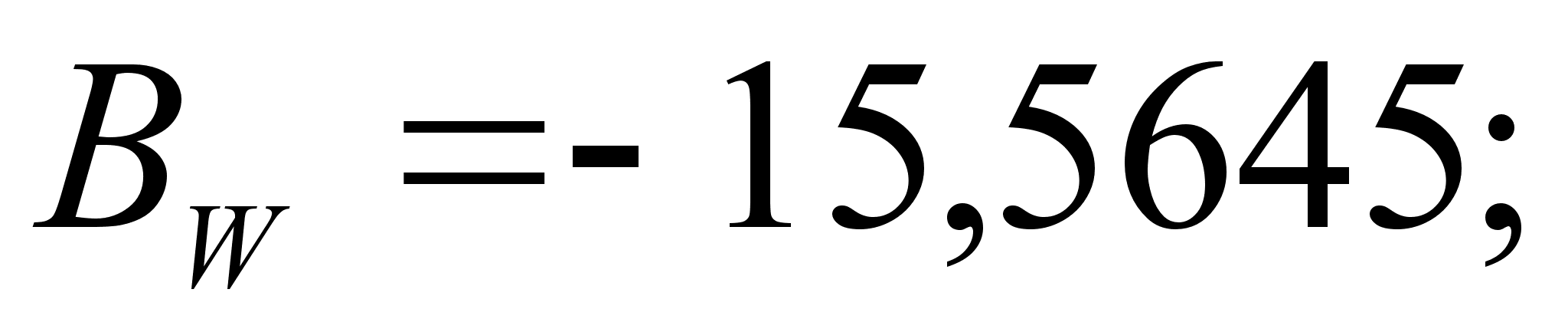
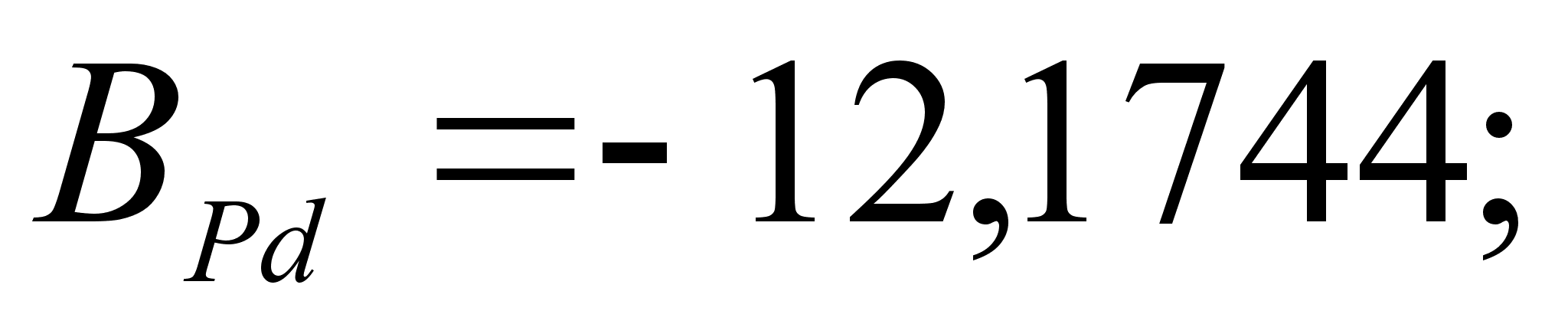
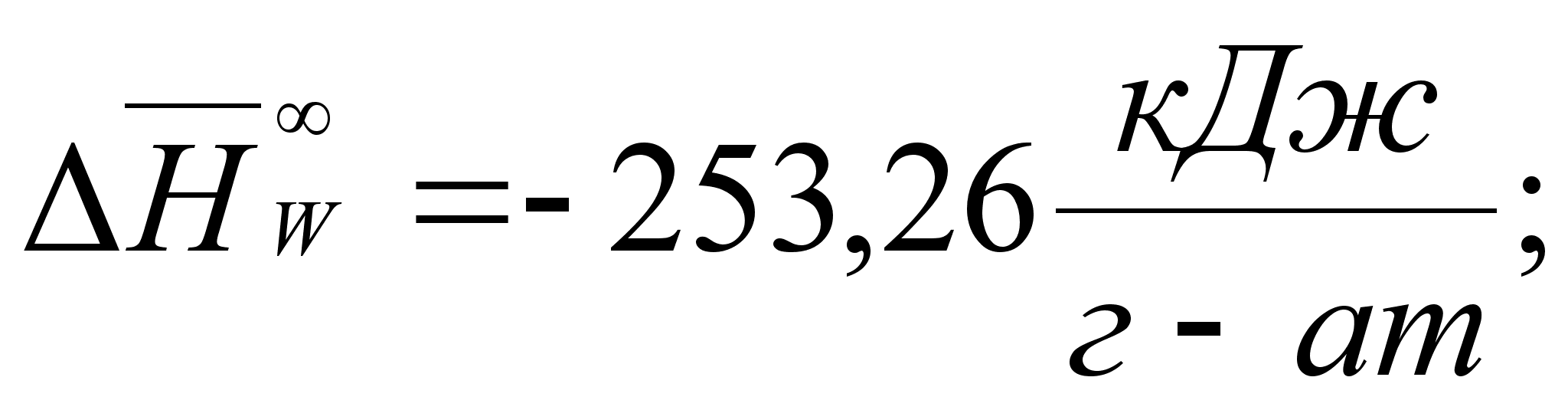
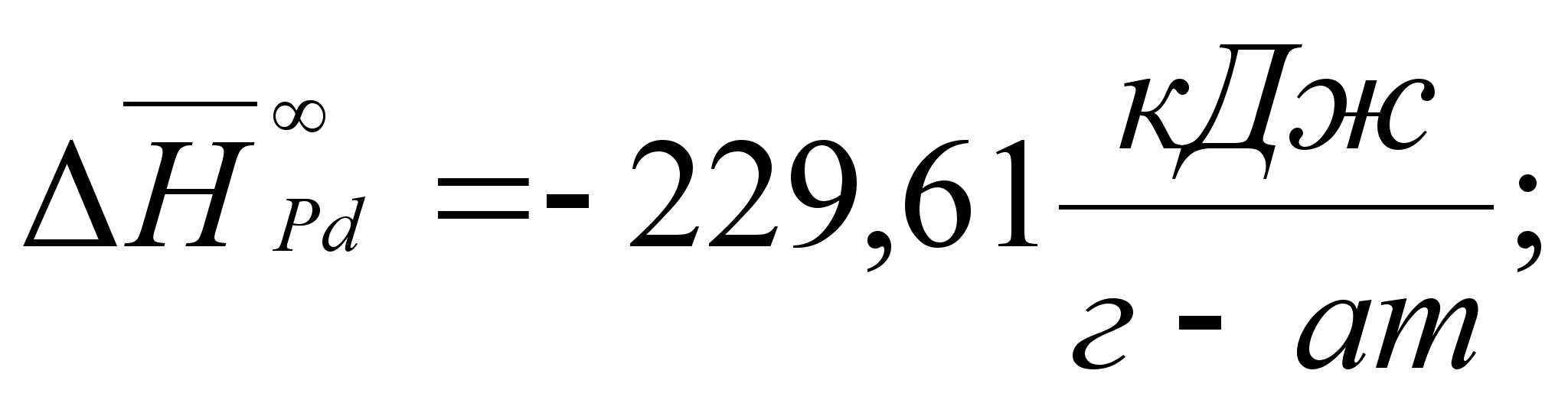
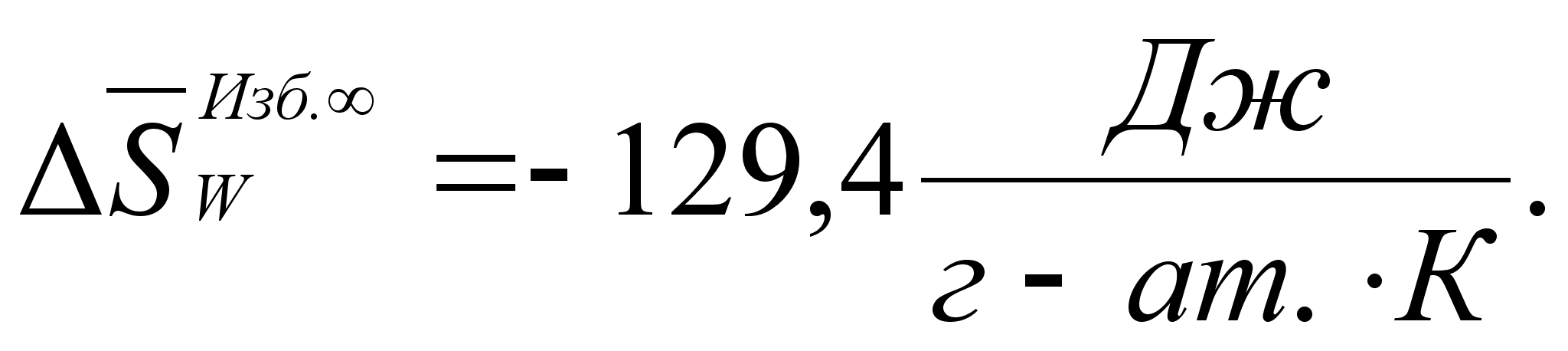
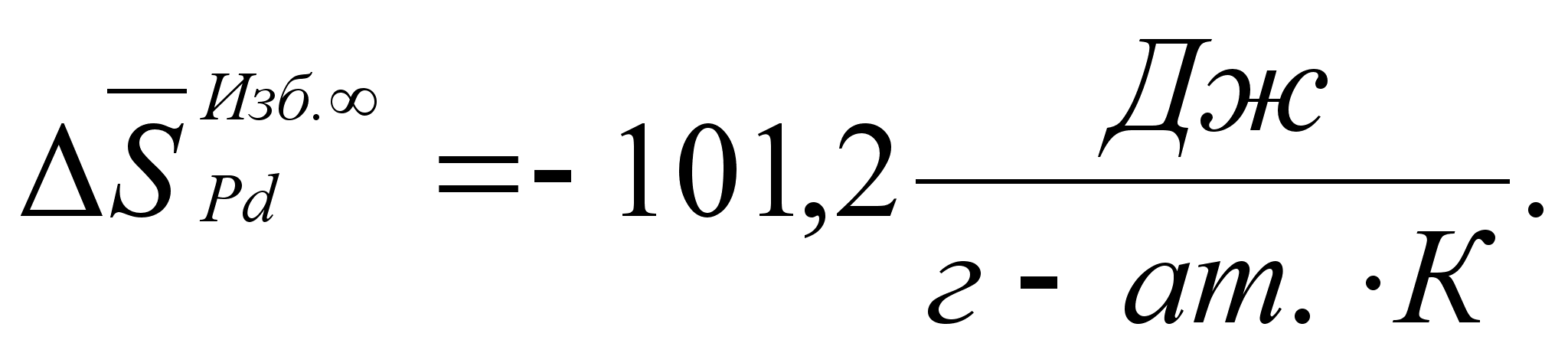
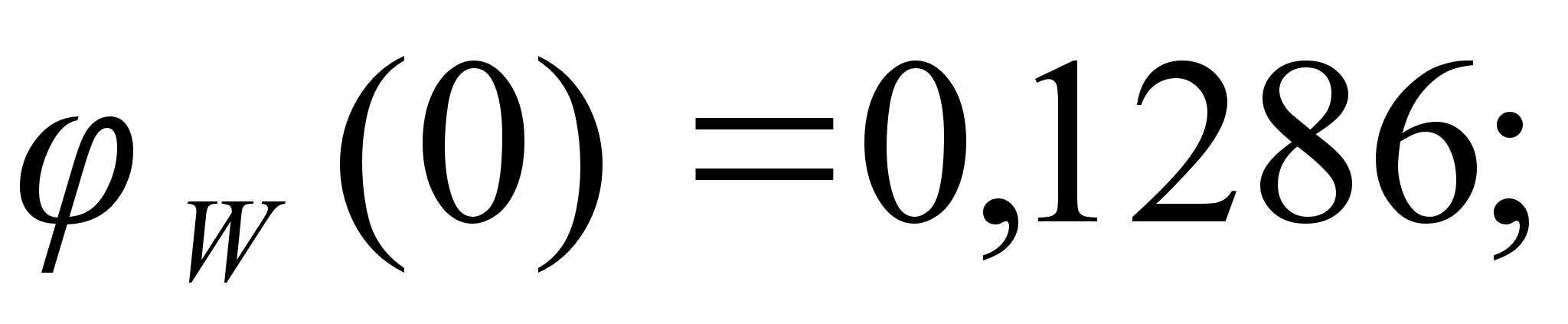
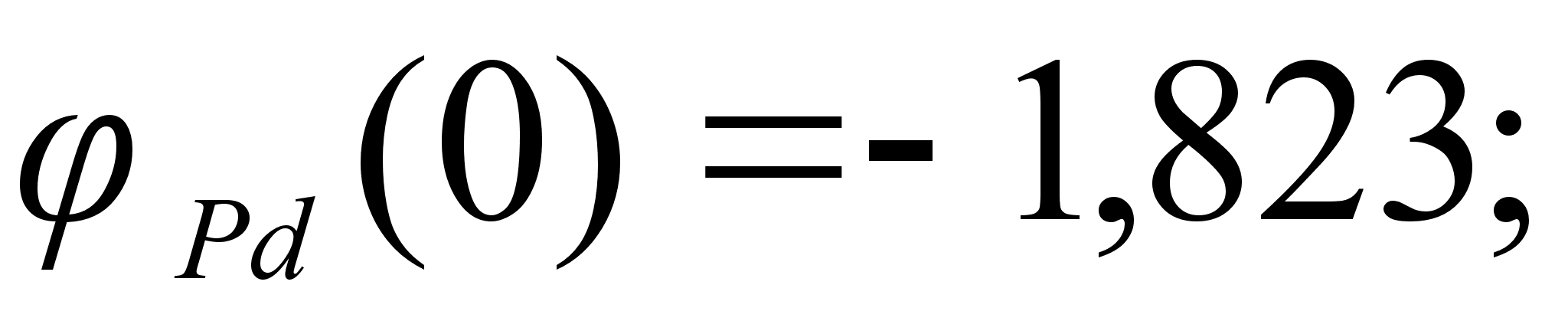
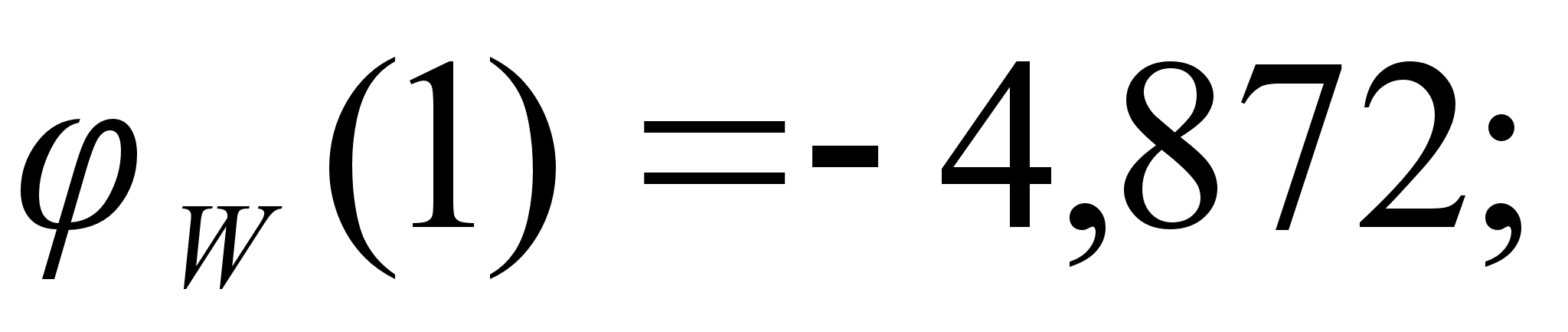
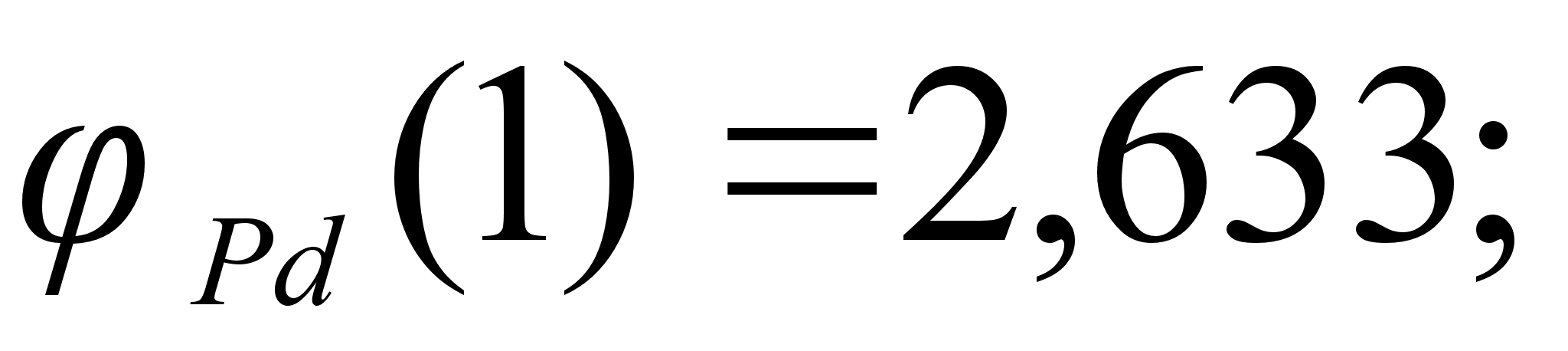
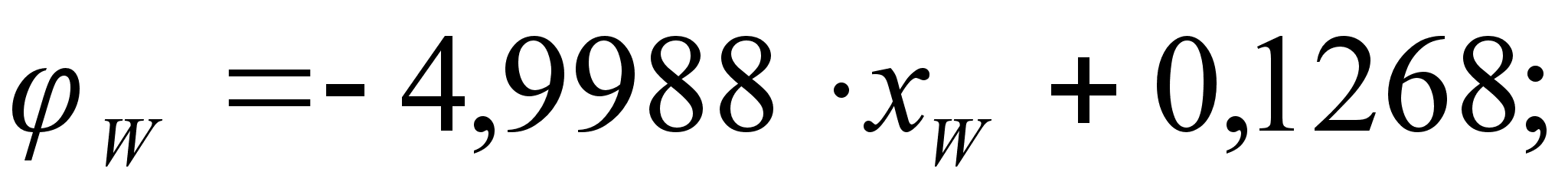
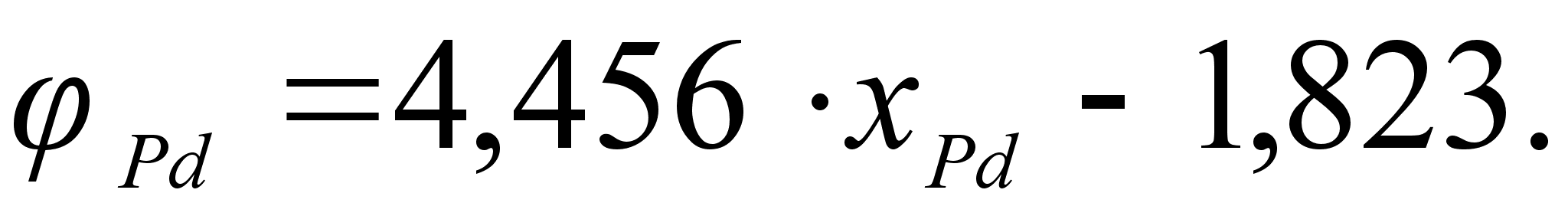
Таблица 57 – Термодинамические характеристики компонентов системы Fe – Mn.
железо
марганец
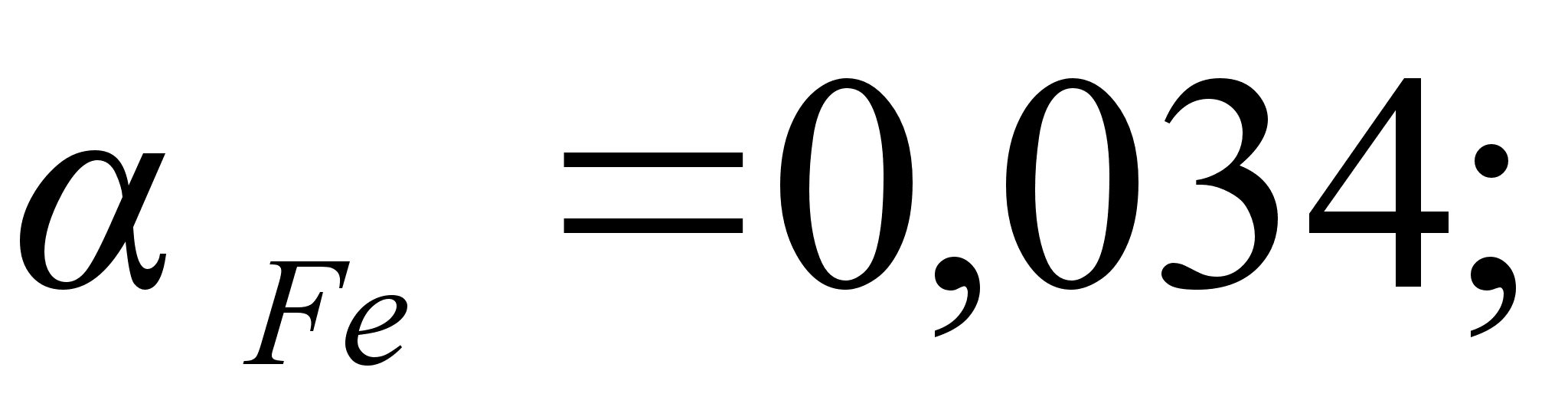
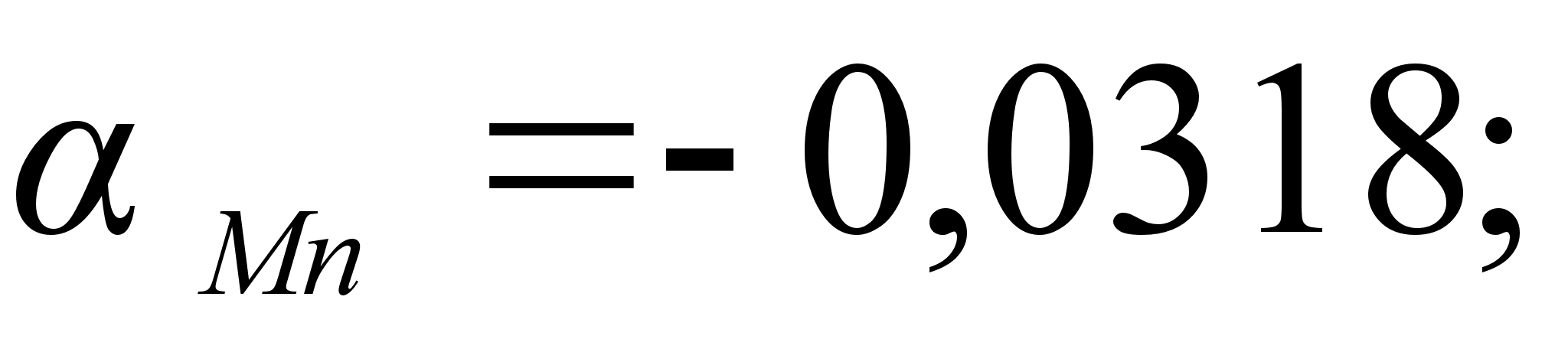
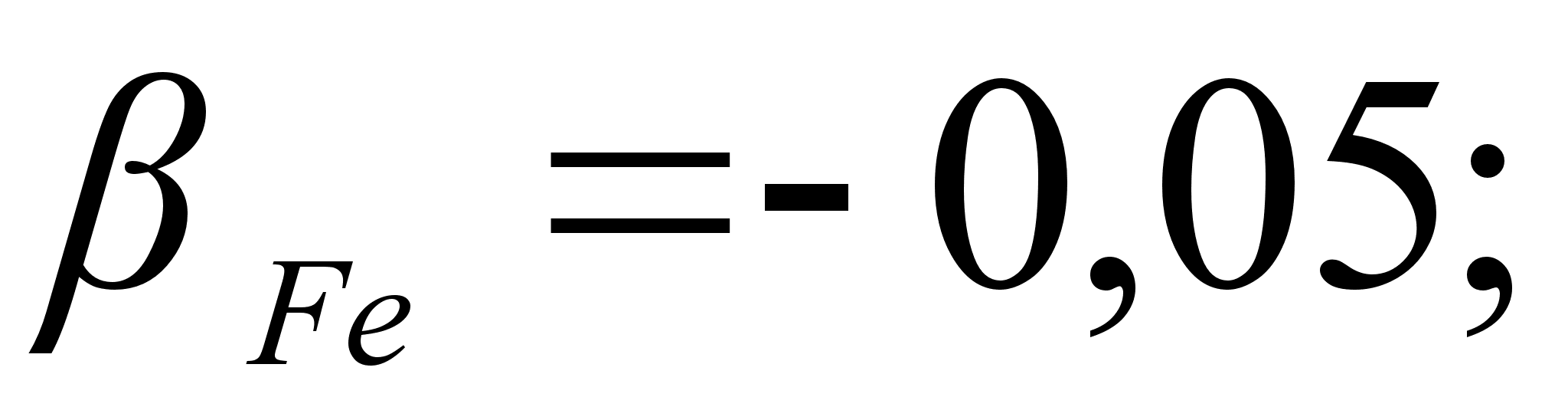
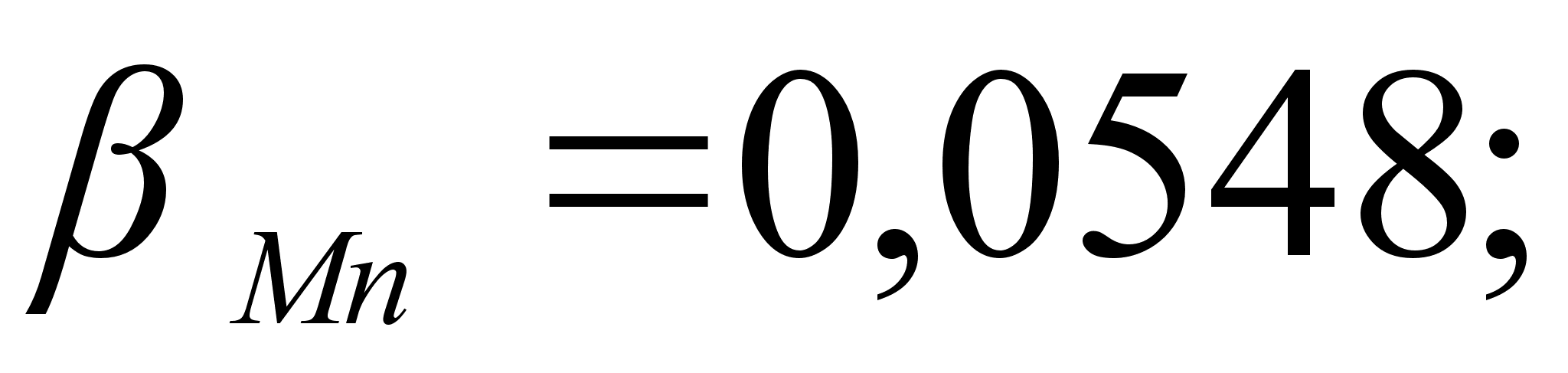
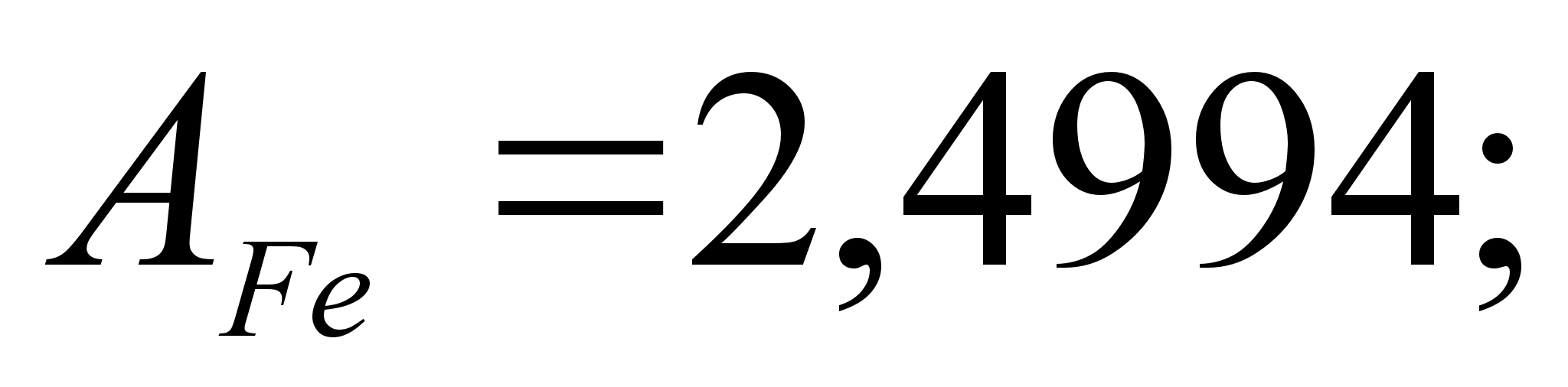
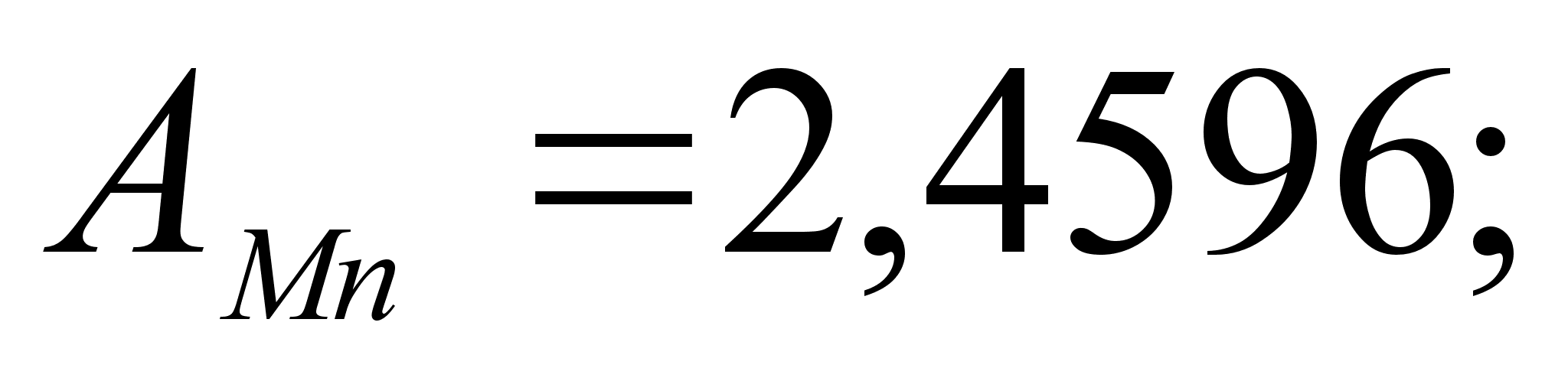
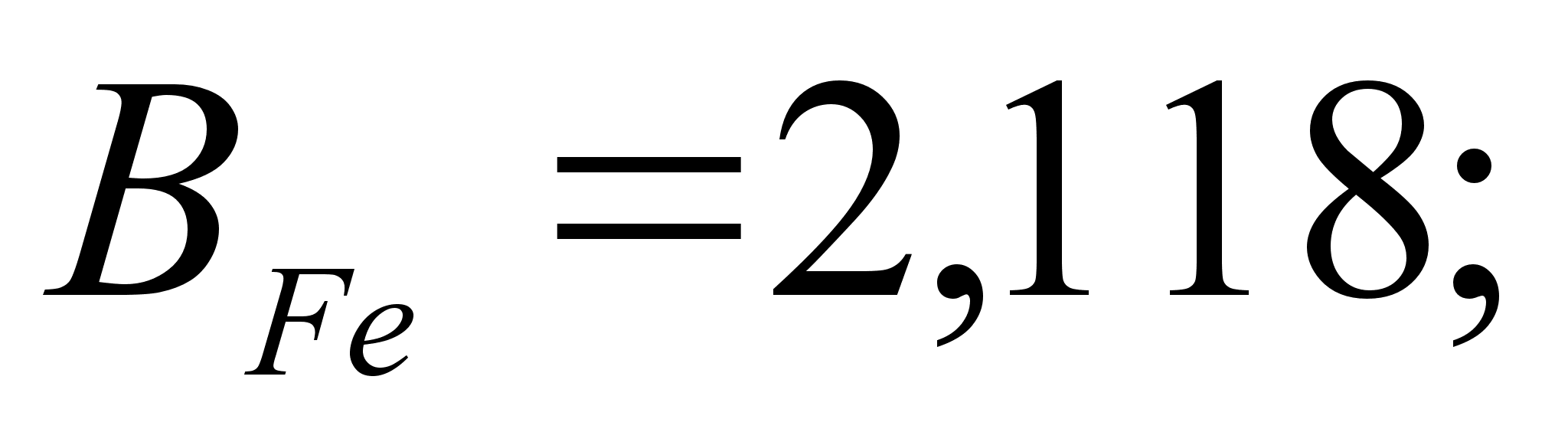
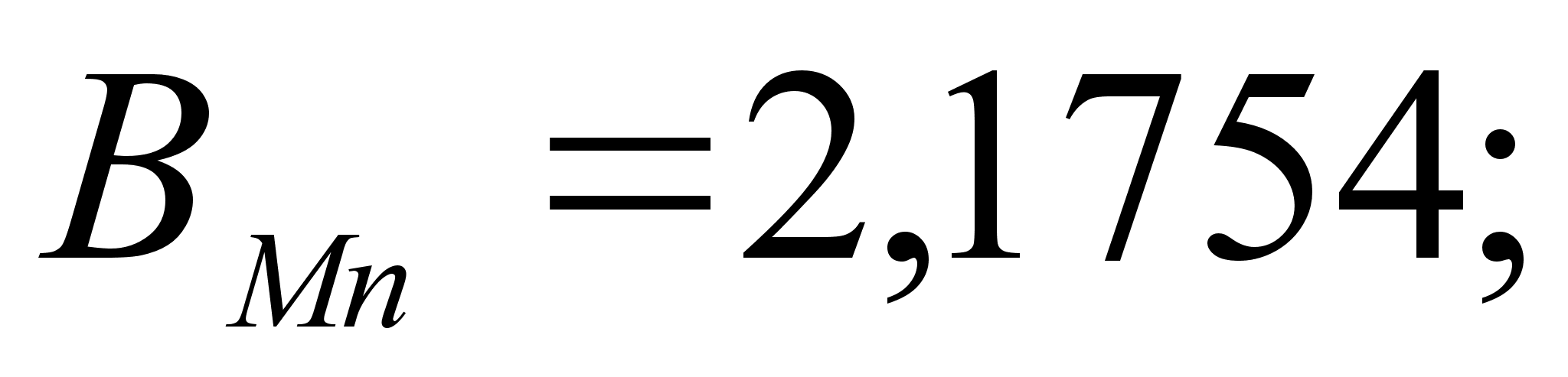
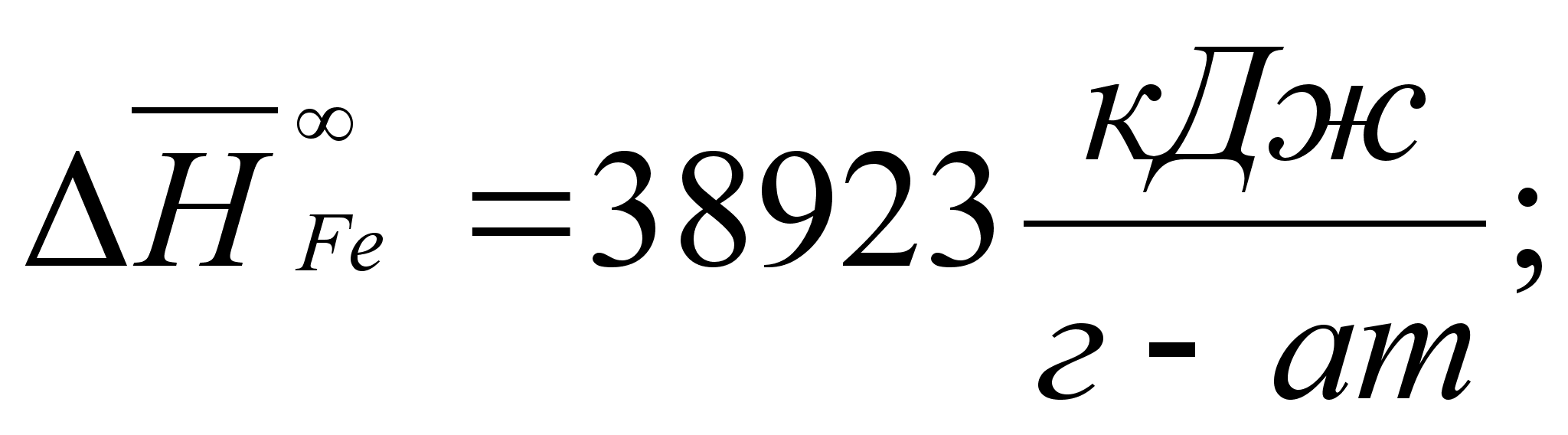
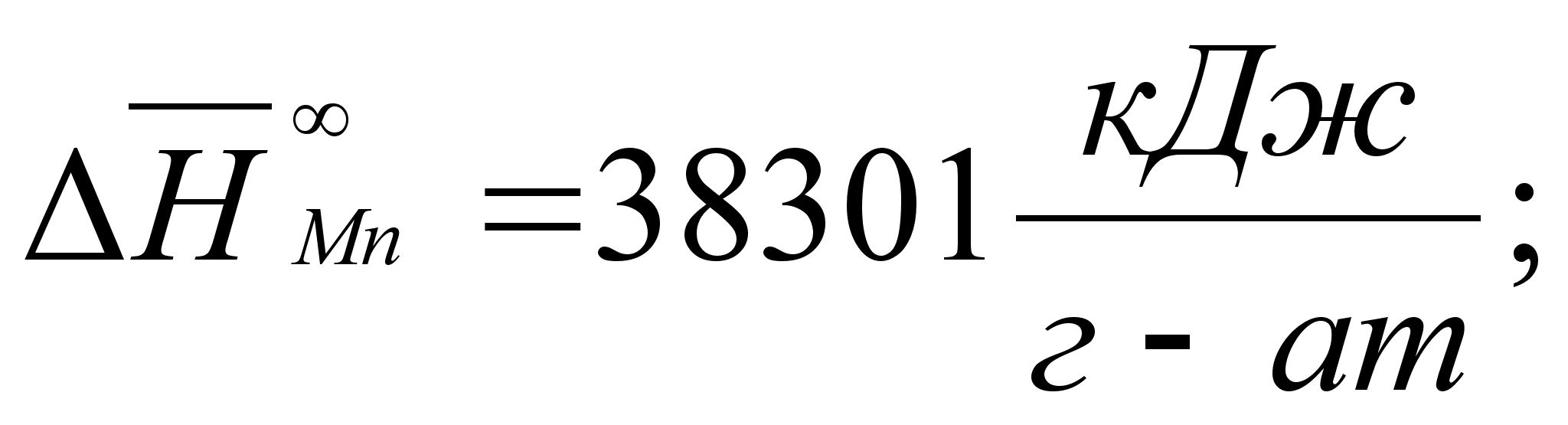
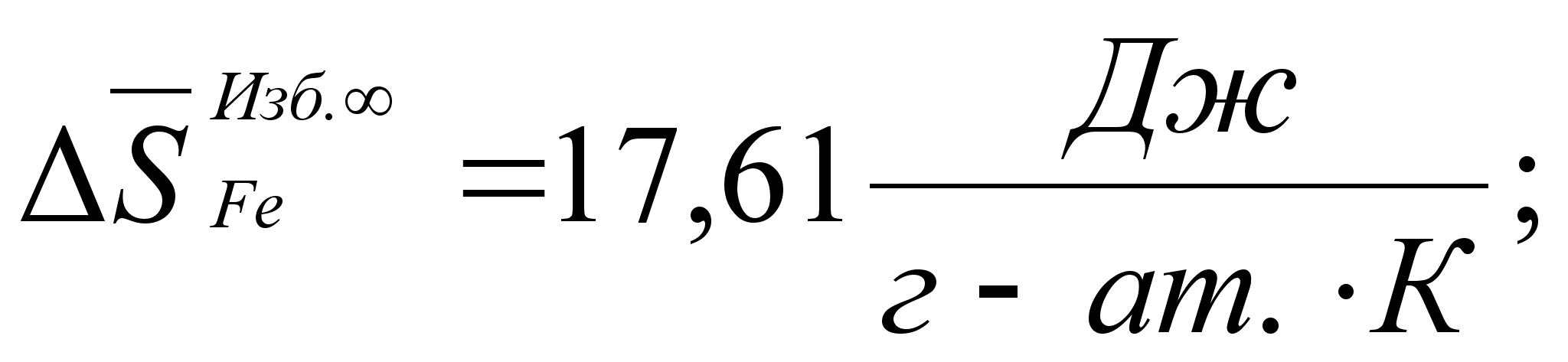
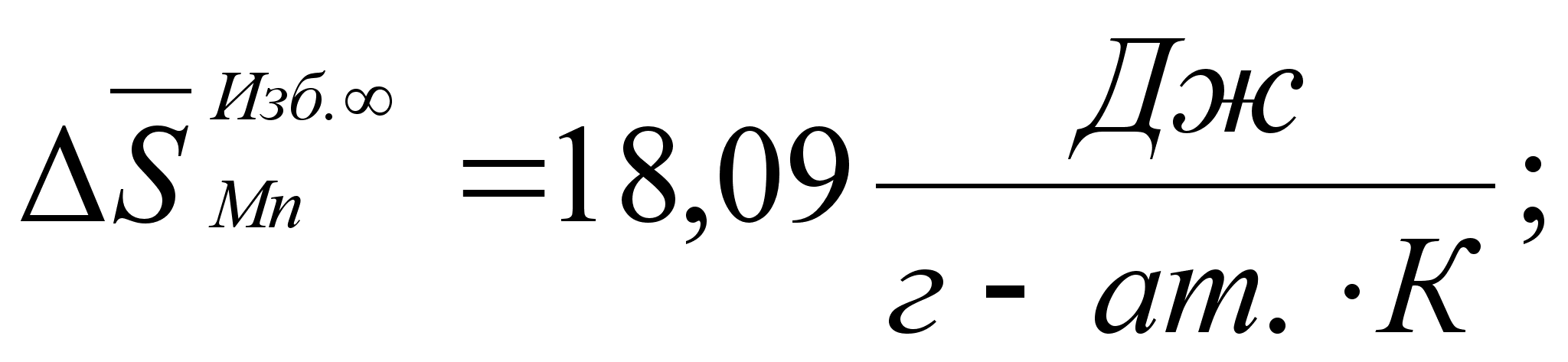
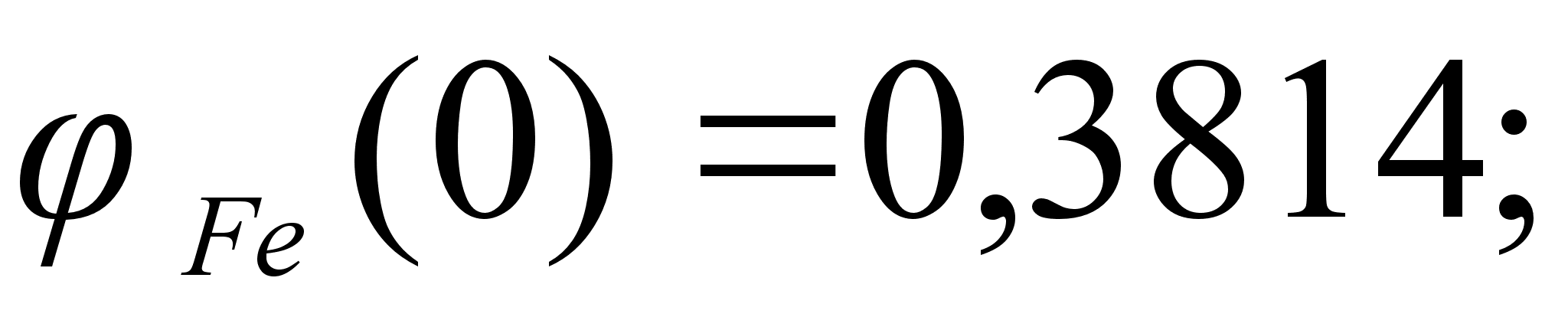
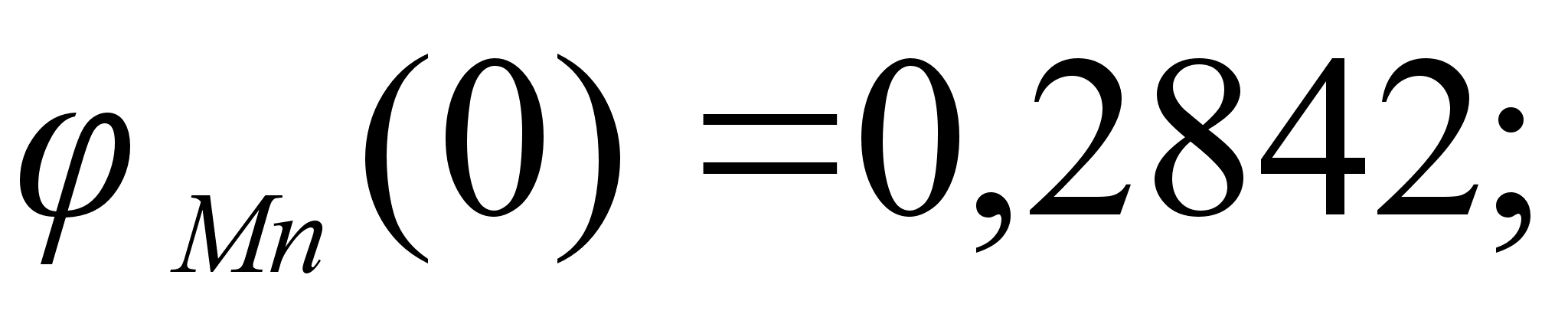
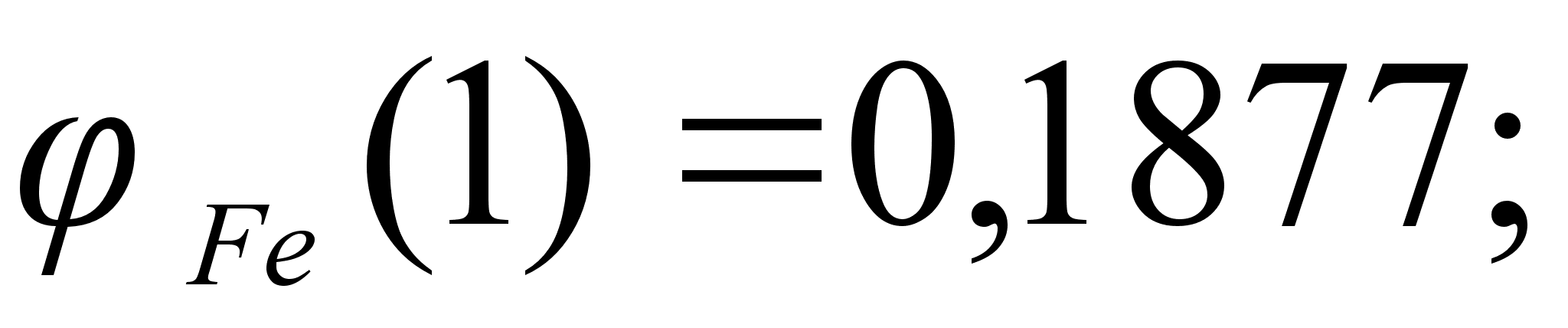
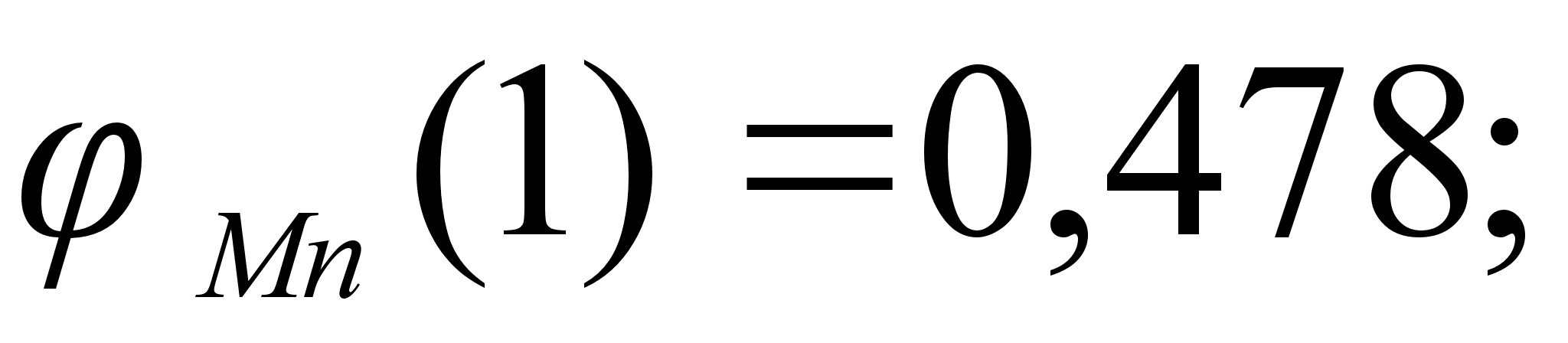
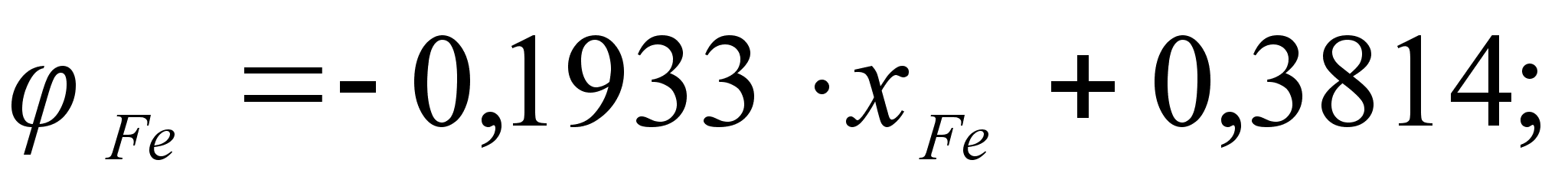
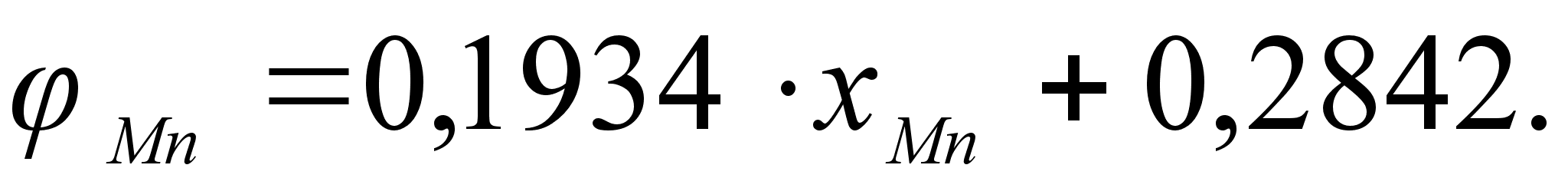
Таблица 58 – Термодинамические характеристики компонентов системы Fe – Cr.
железо
хром
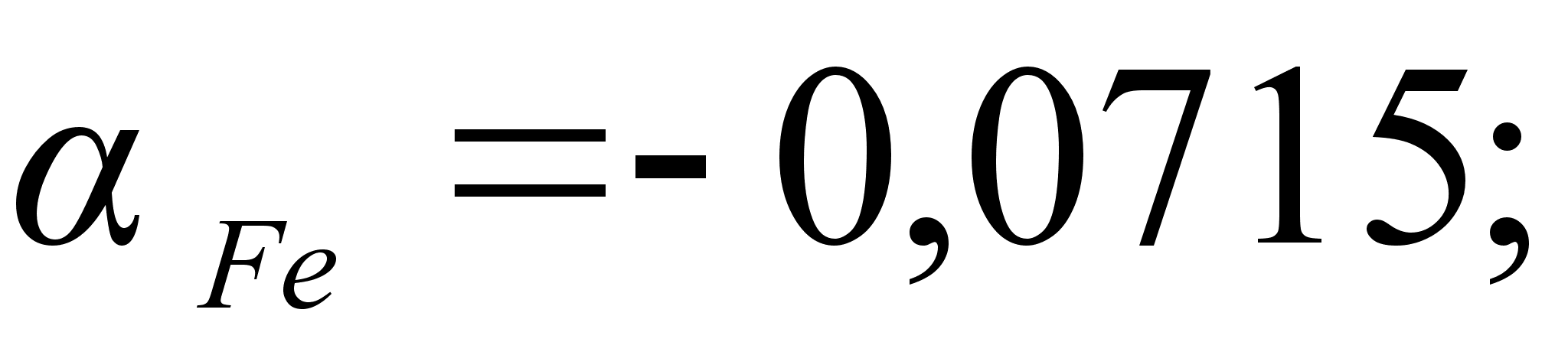
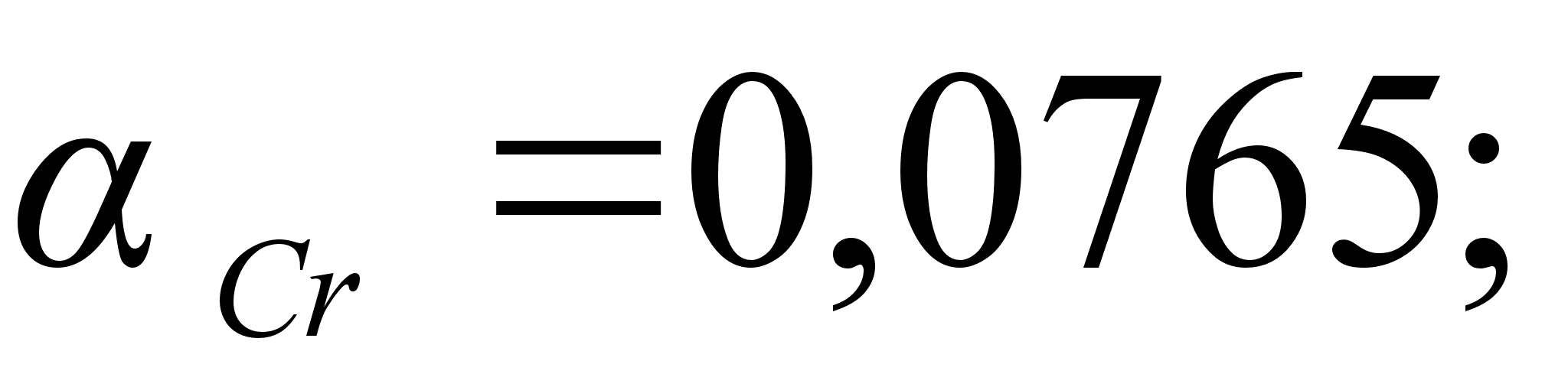
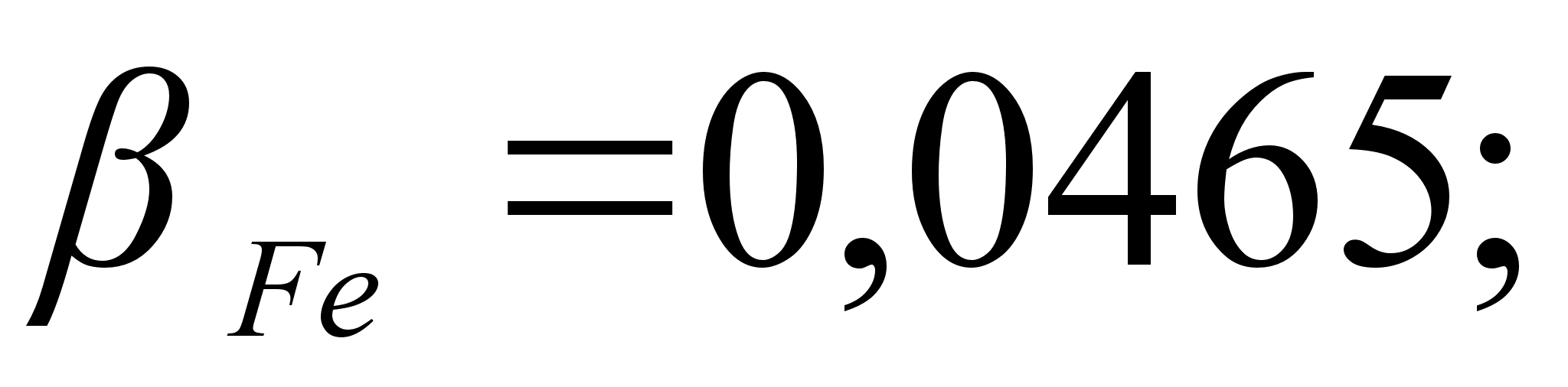
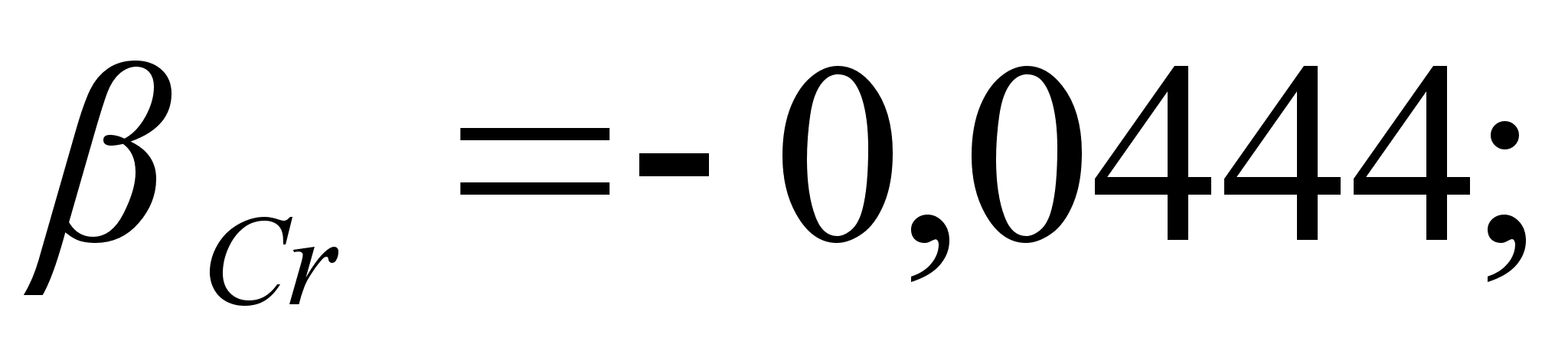
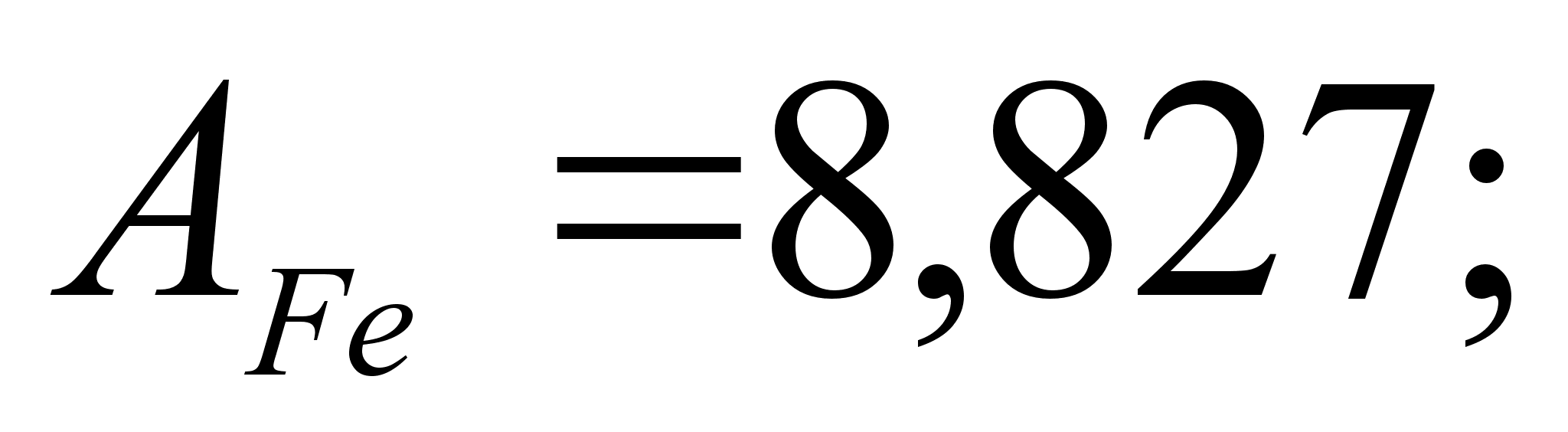
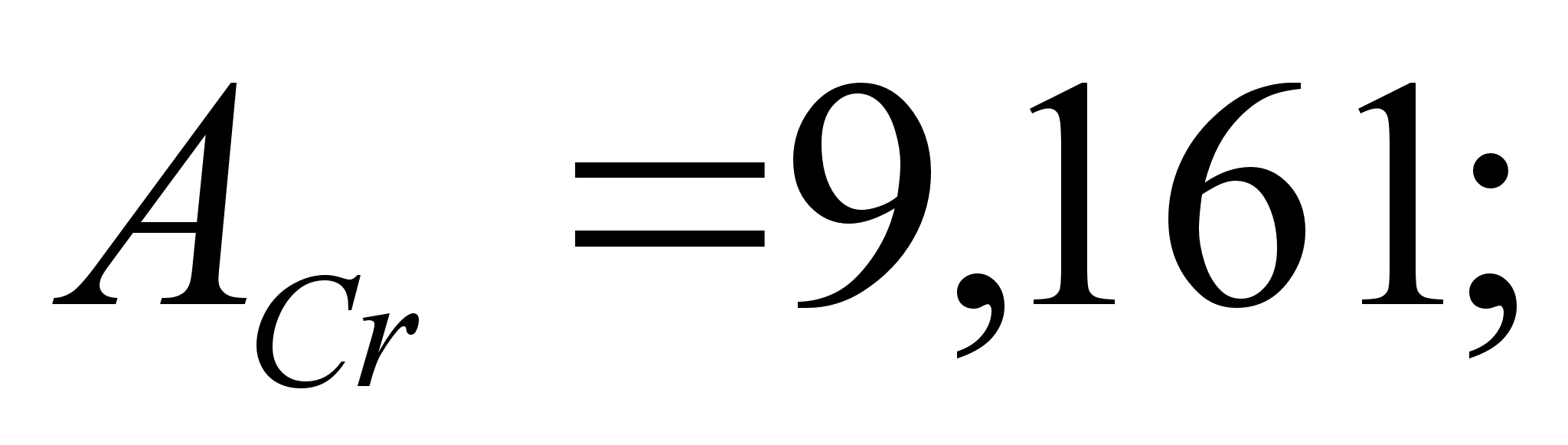
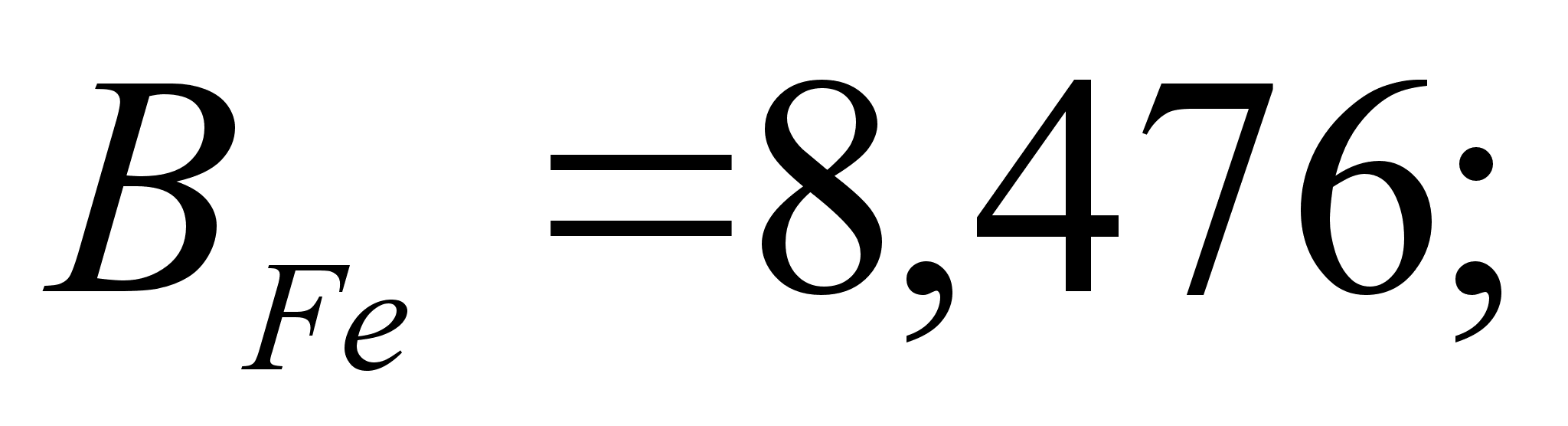
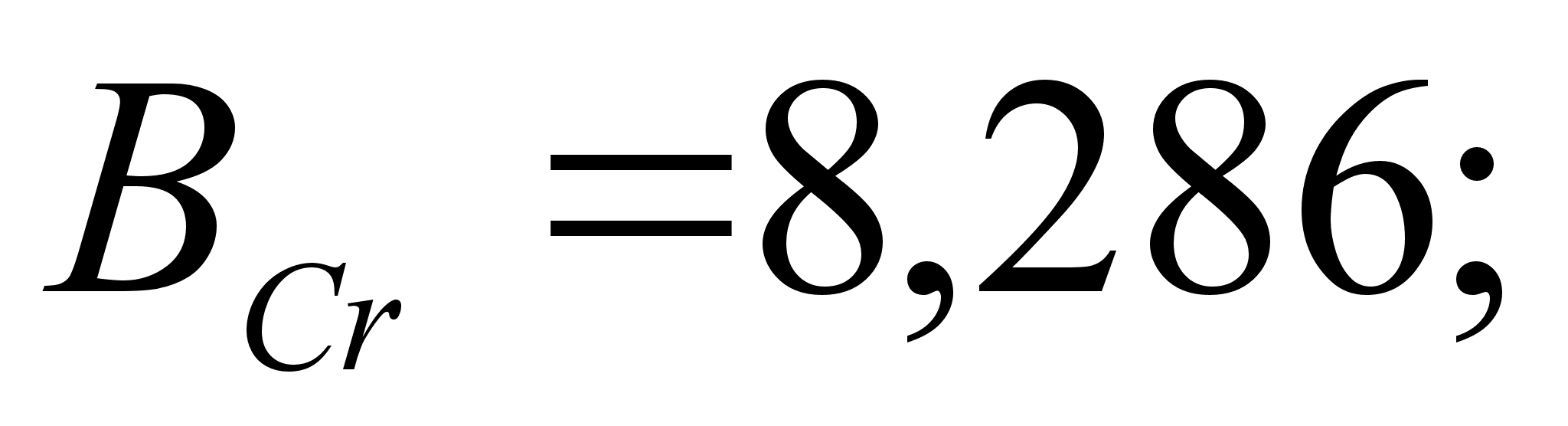
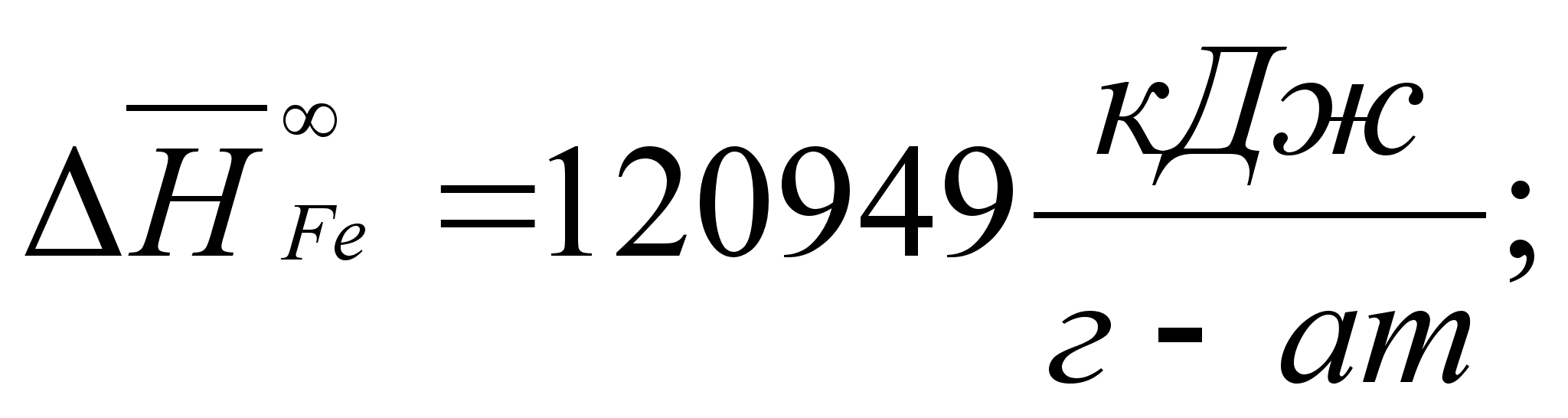
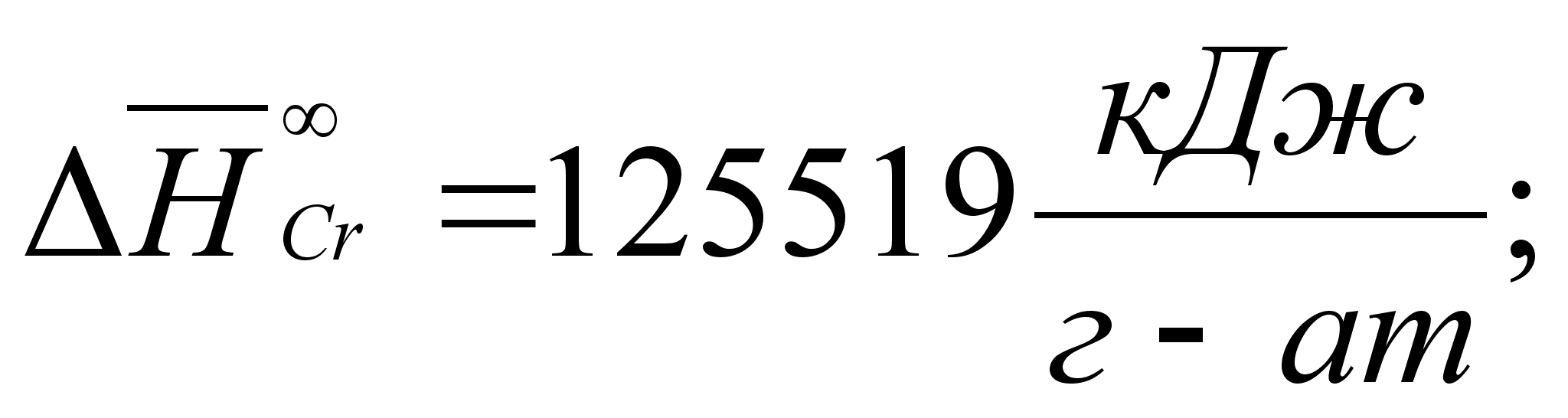
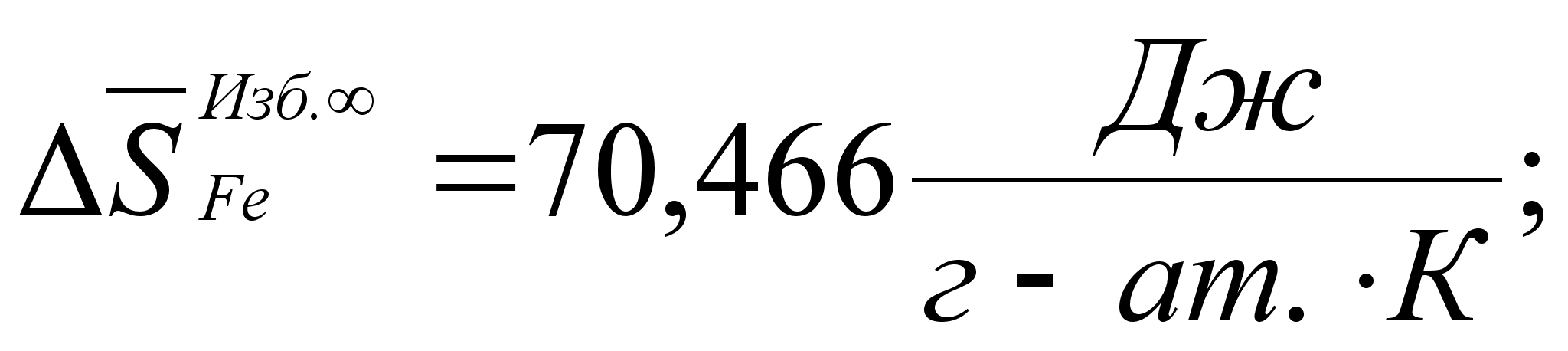
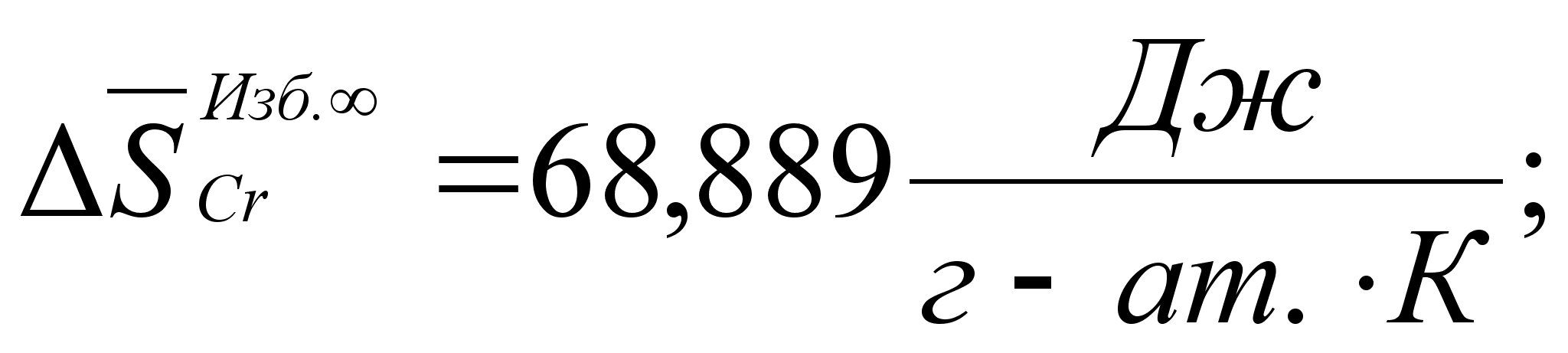
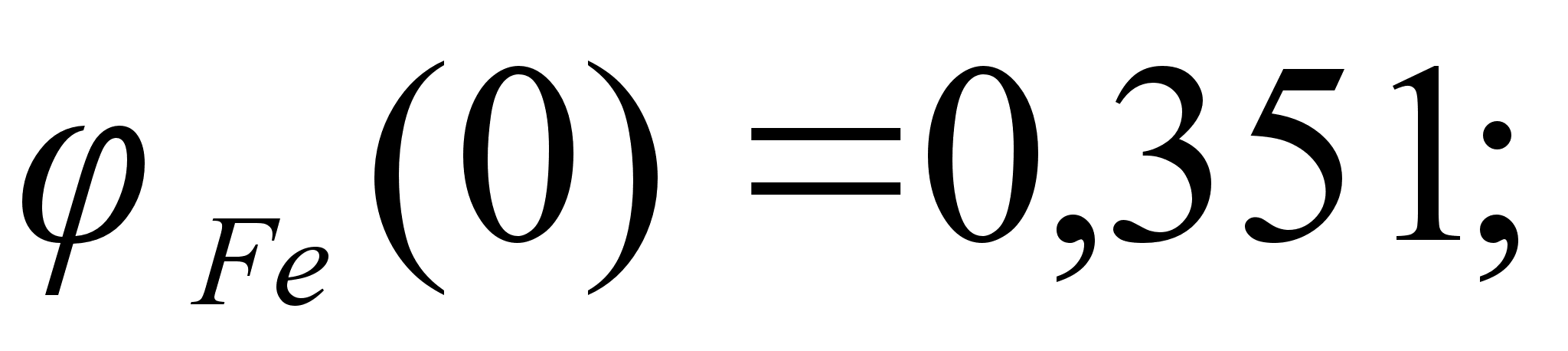
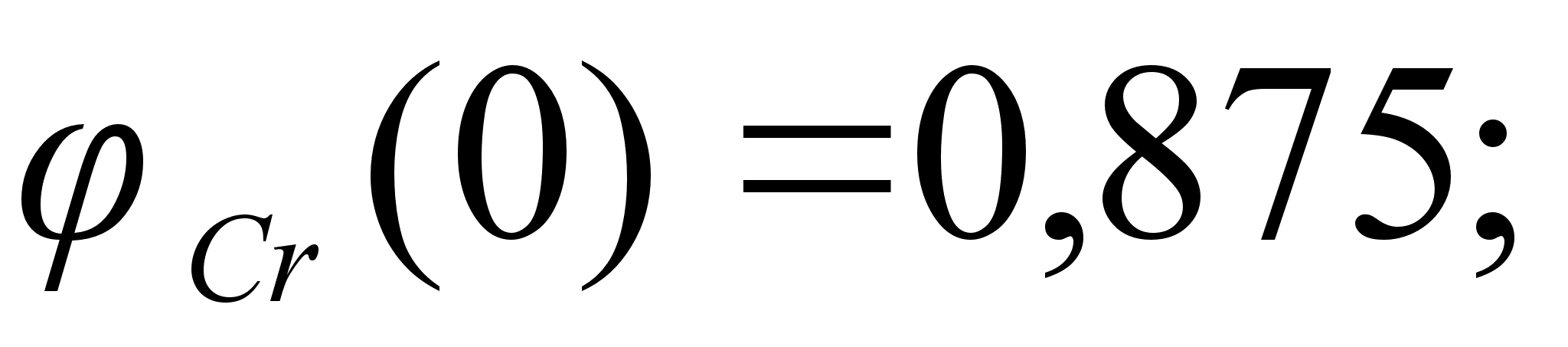
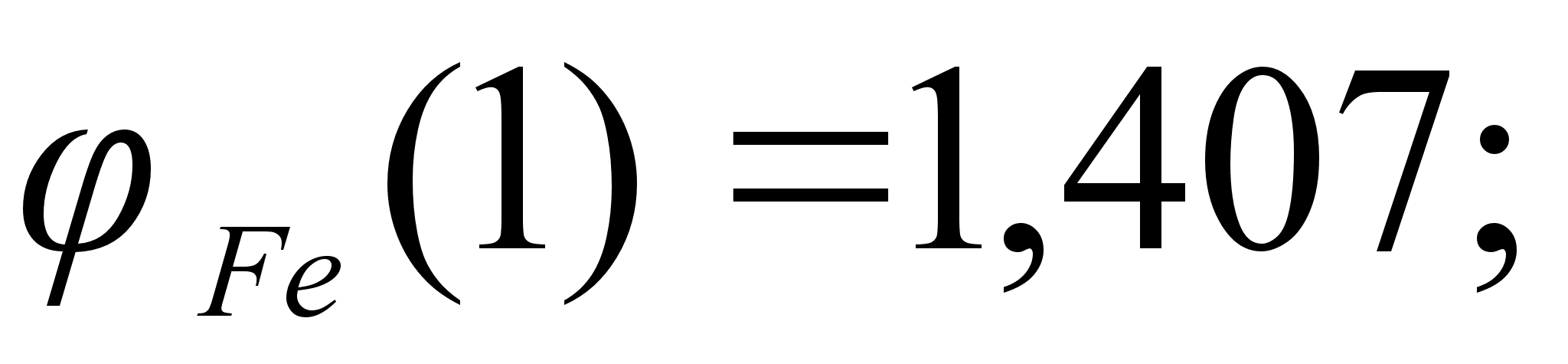
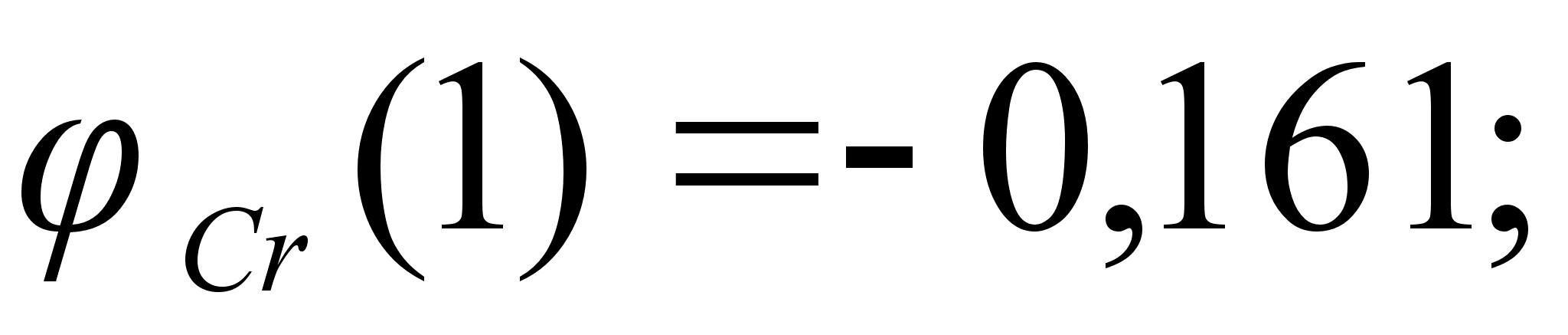
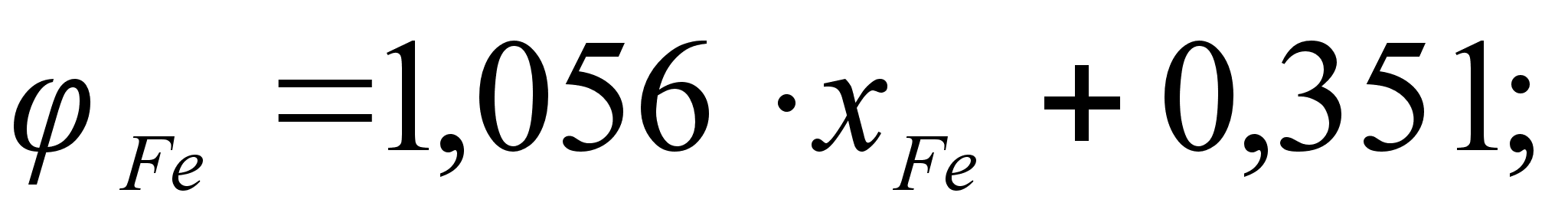
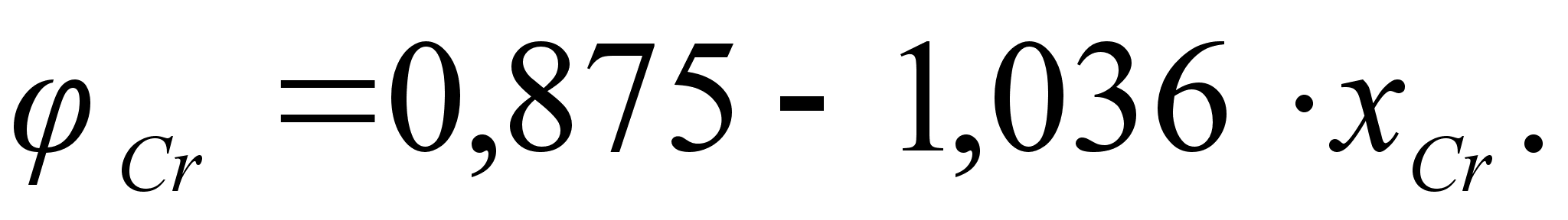
Таблица 59 – Термодинамические характеристики компонентов системы Fe – Cu.
железо
медь
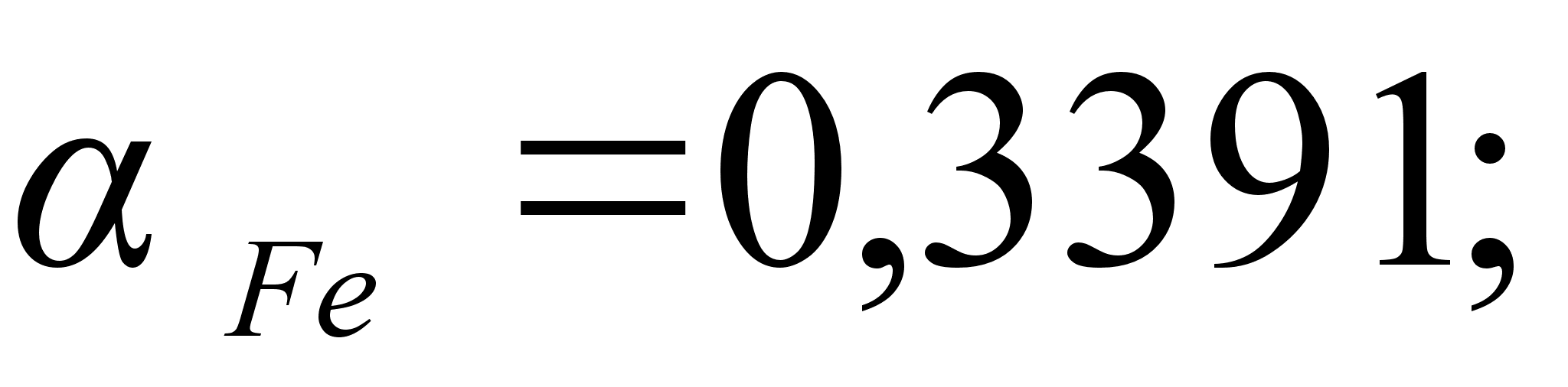
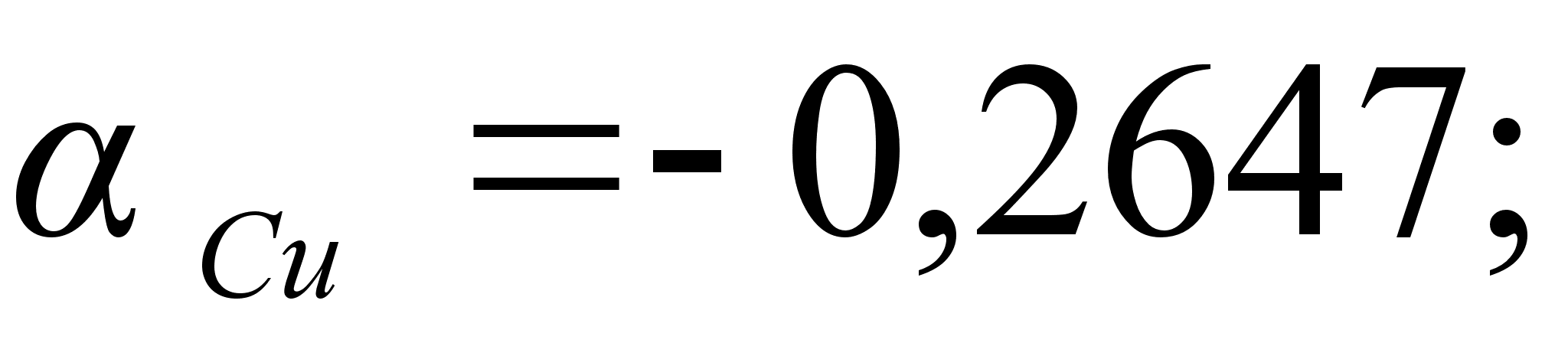
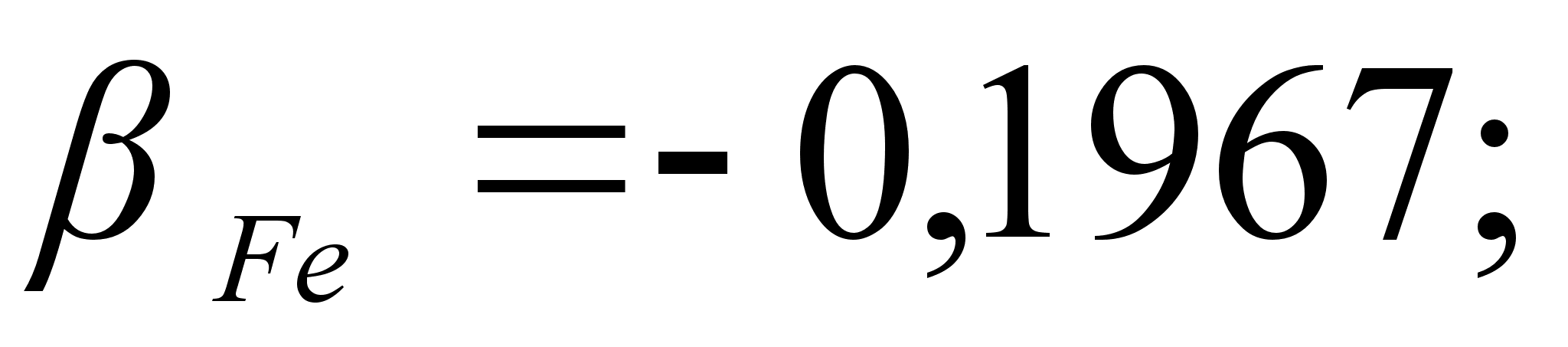
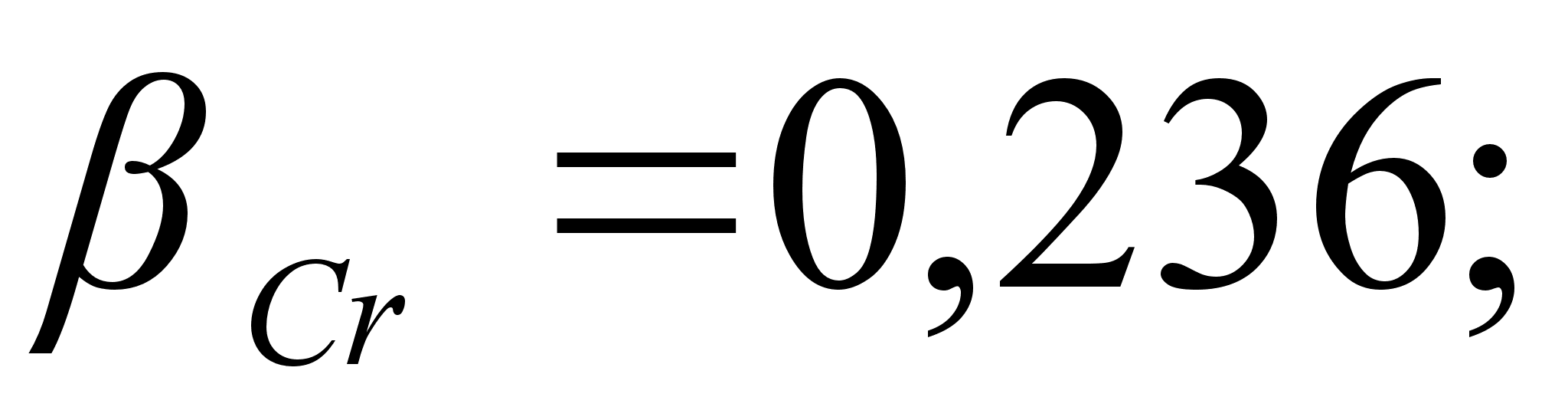
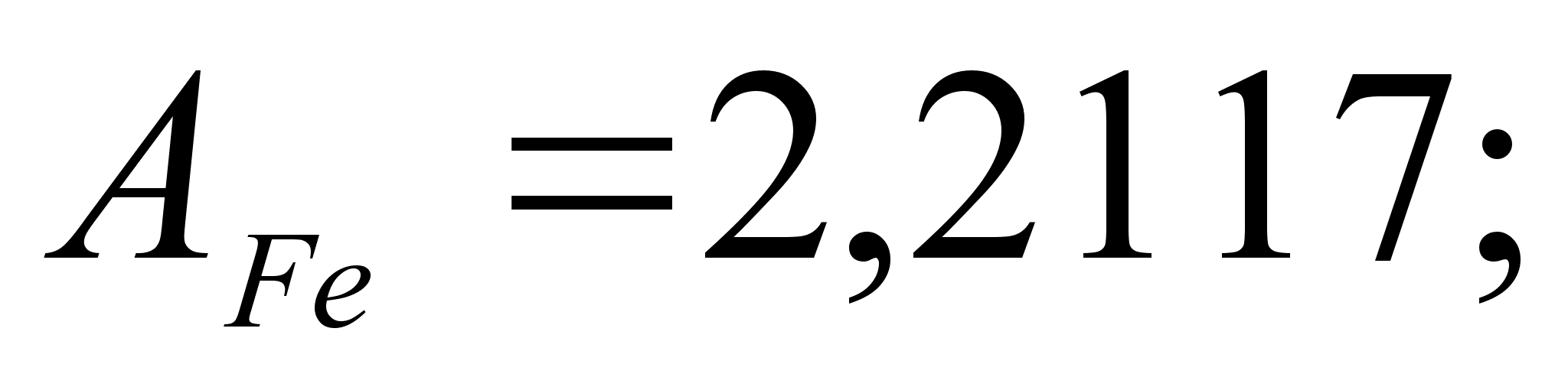
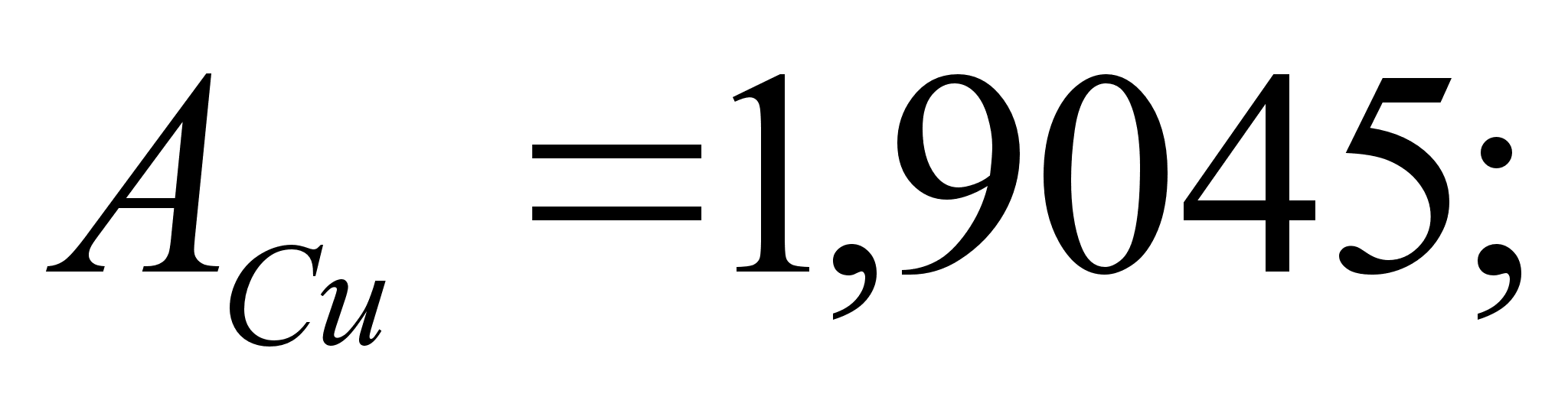
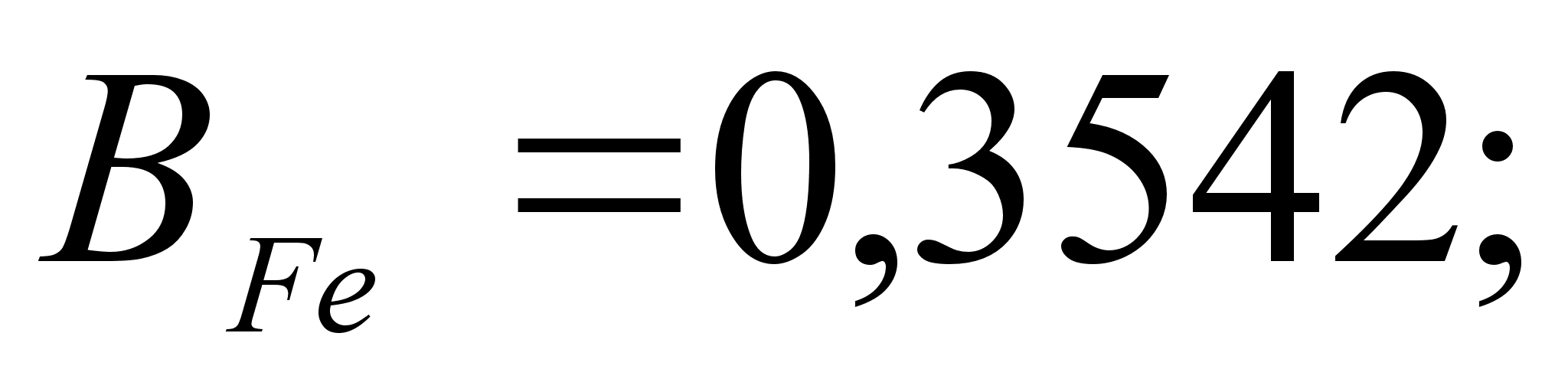
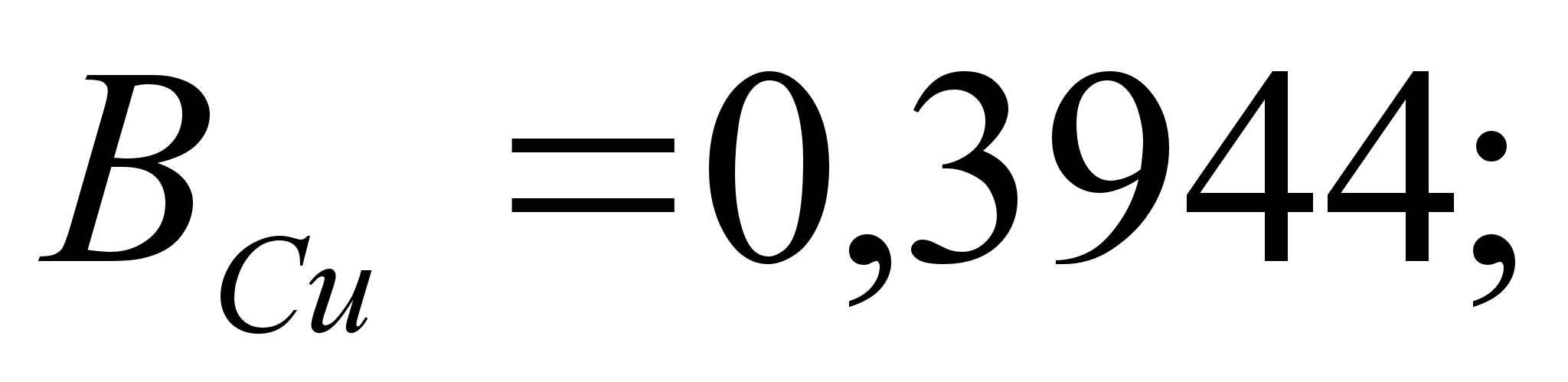

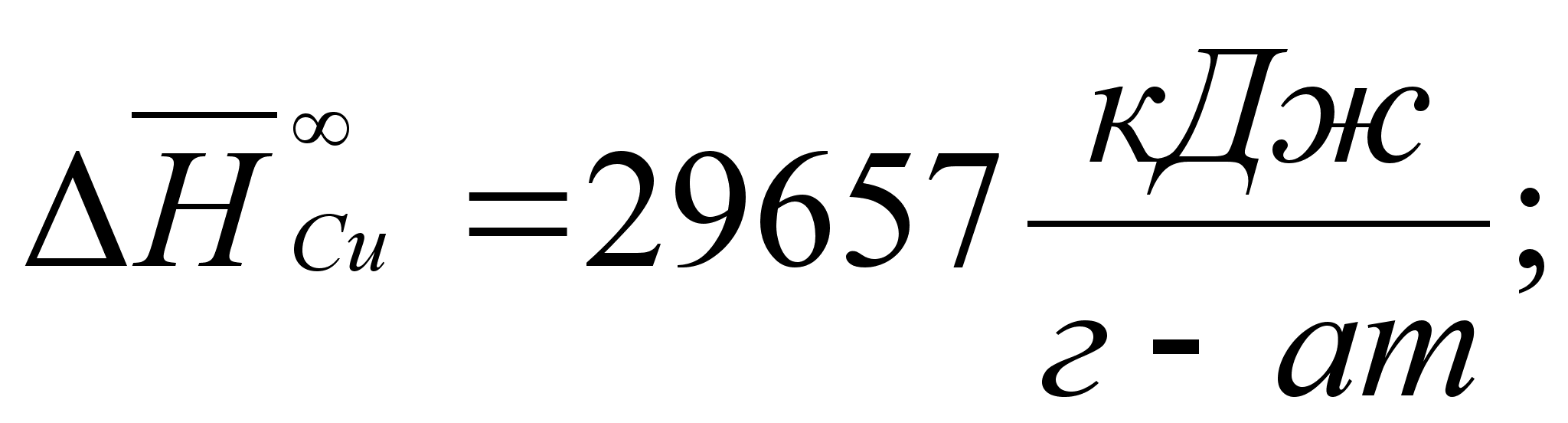
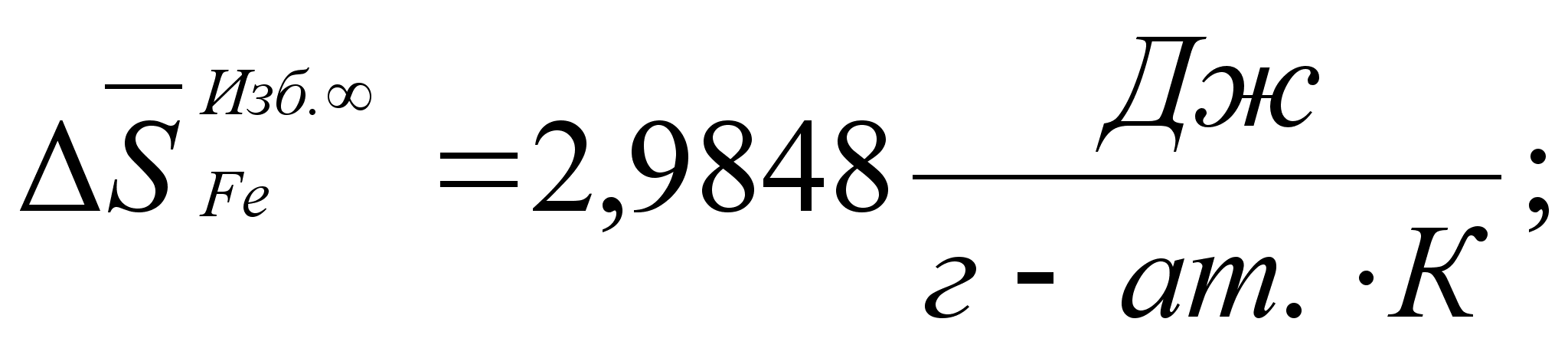
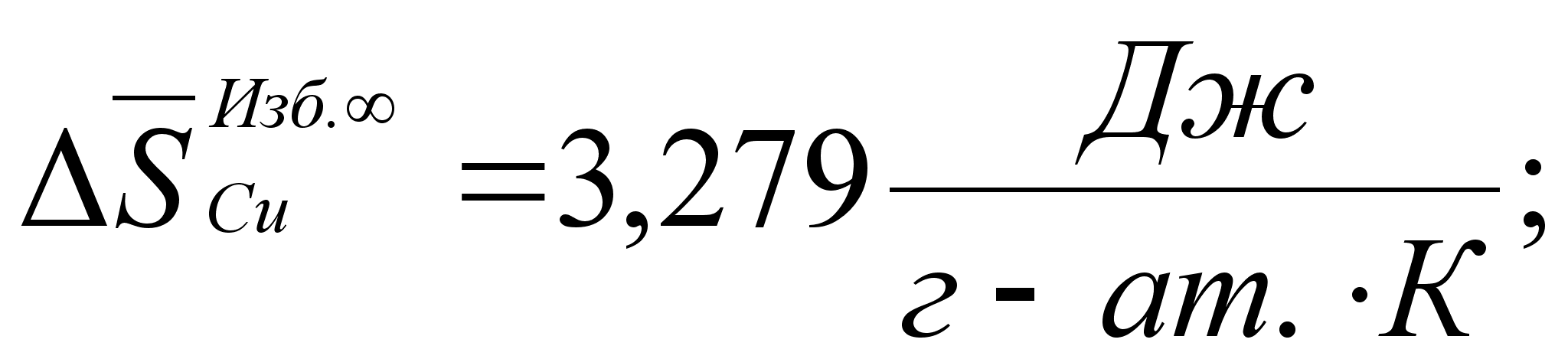
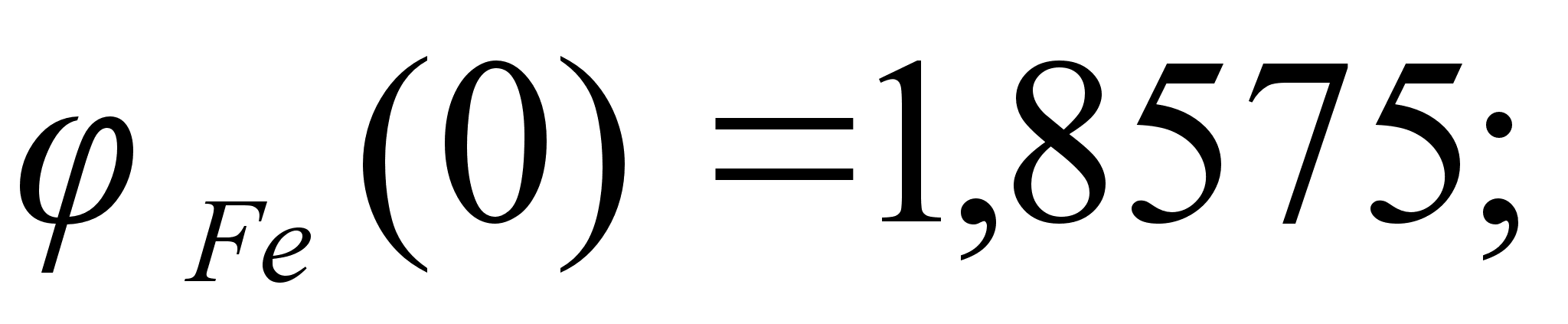
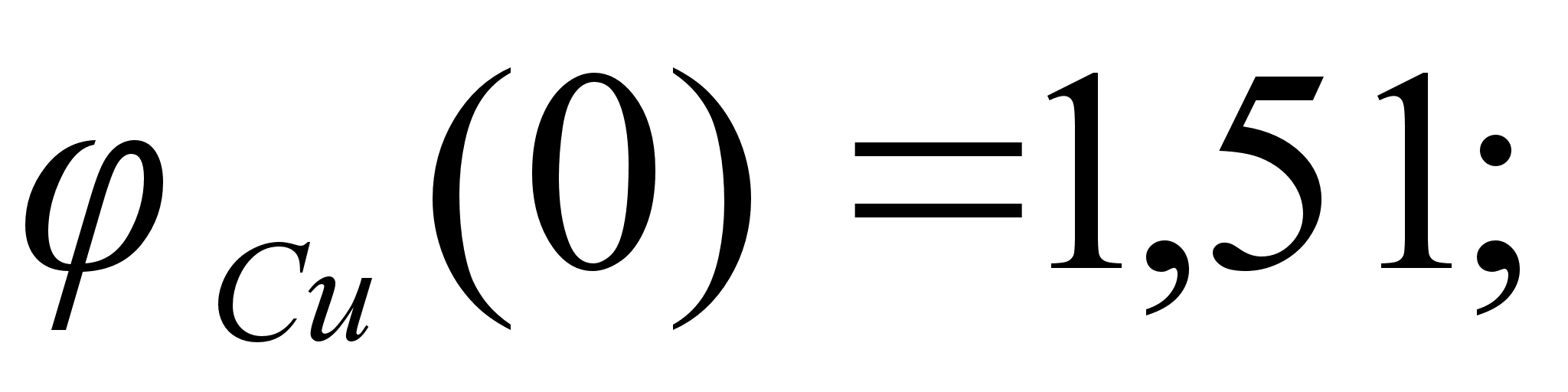
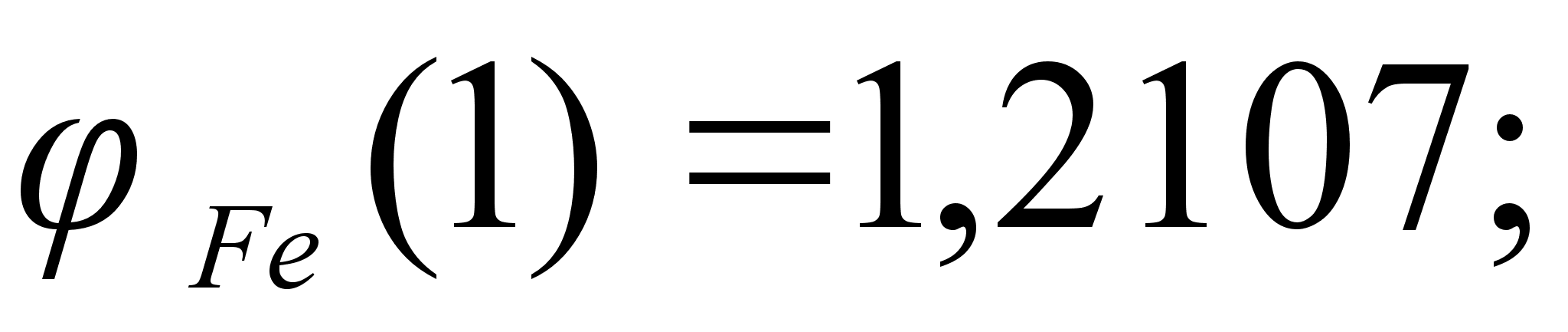
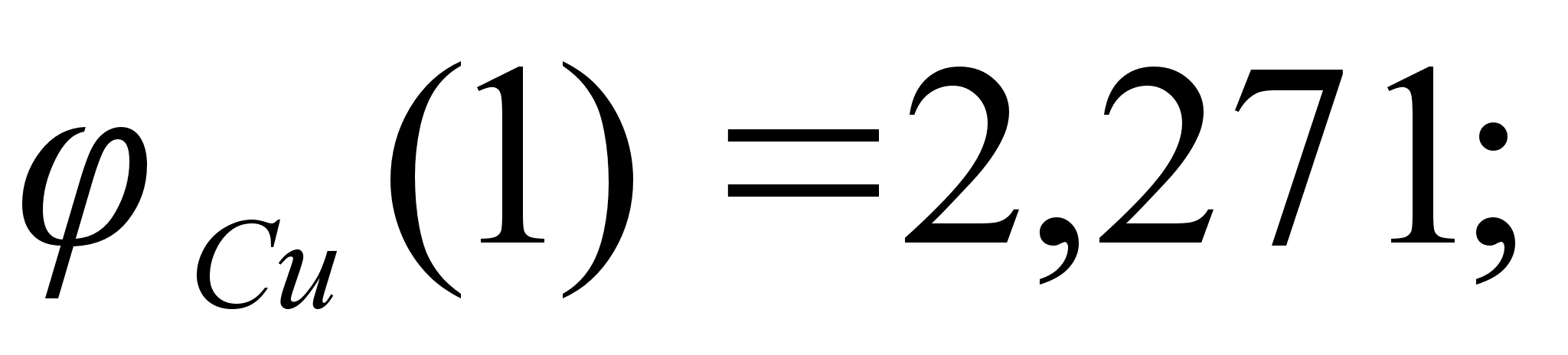
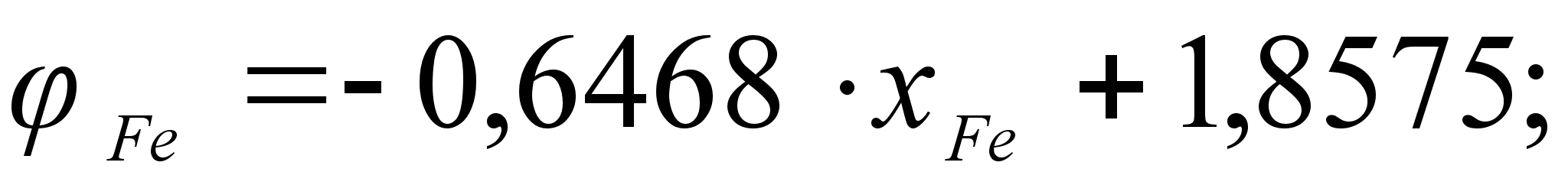
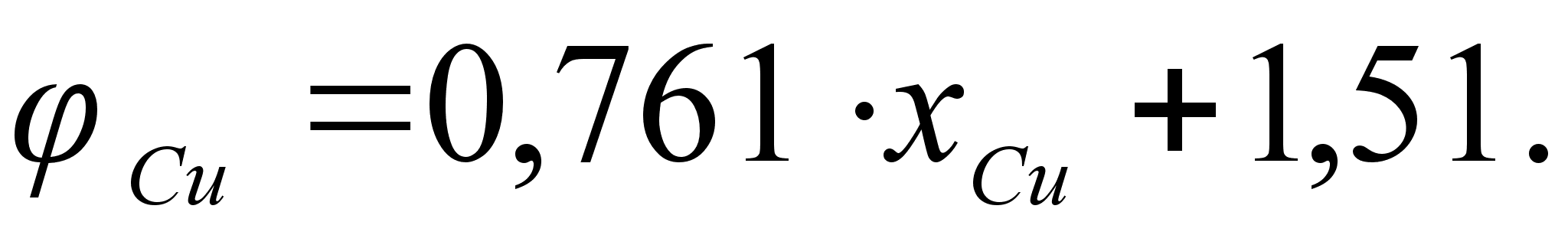
Таблица 60 – Термодинамические характеристики компонентов системы Fe – Sn.
железо
олово
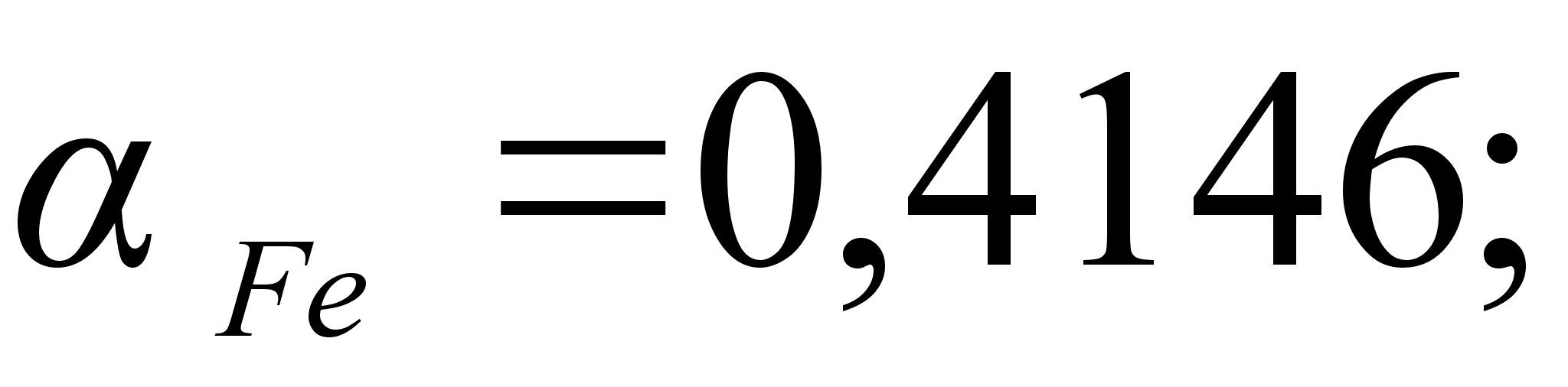
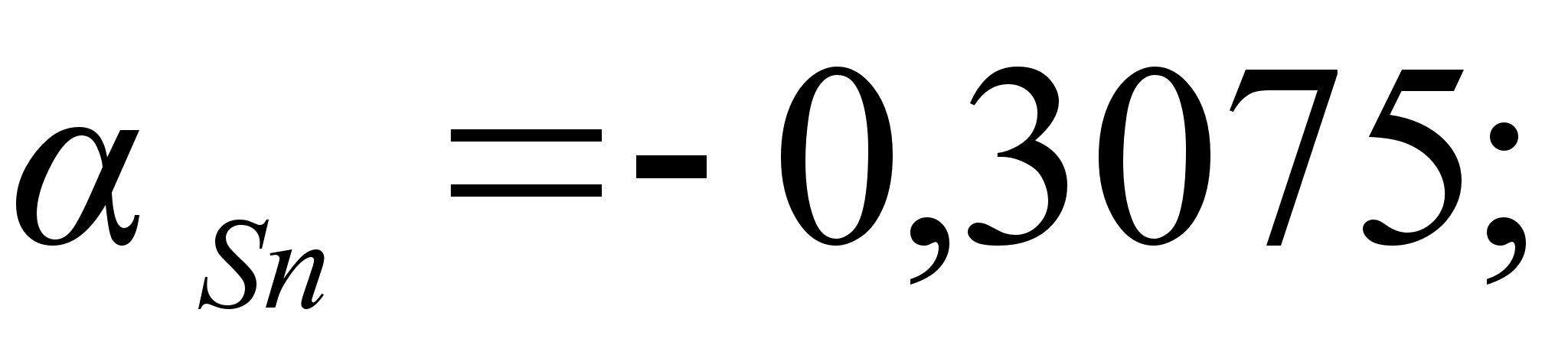
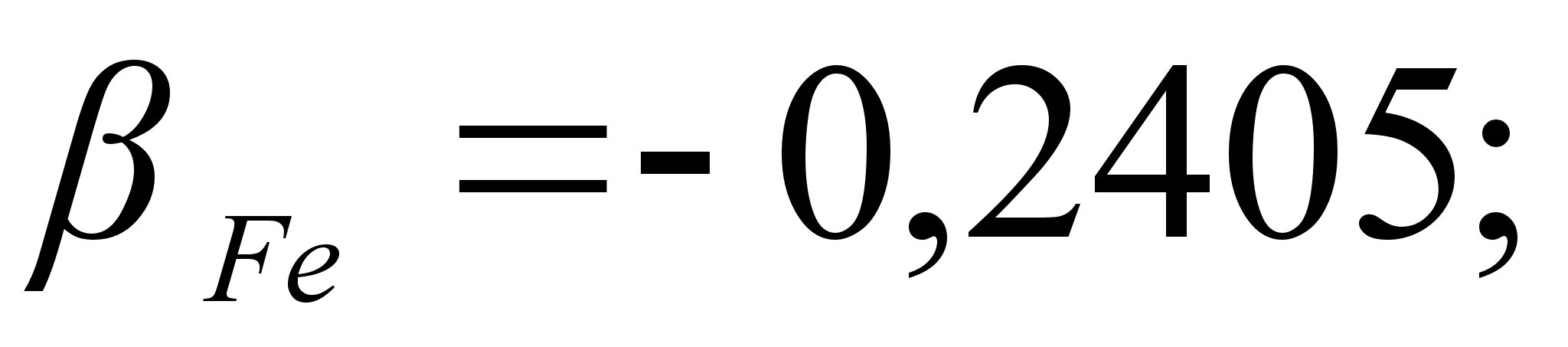
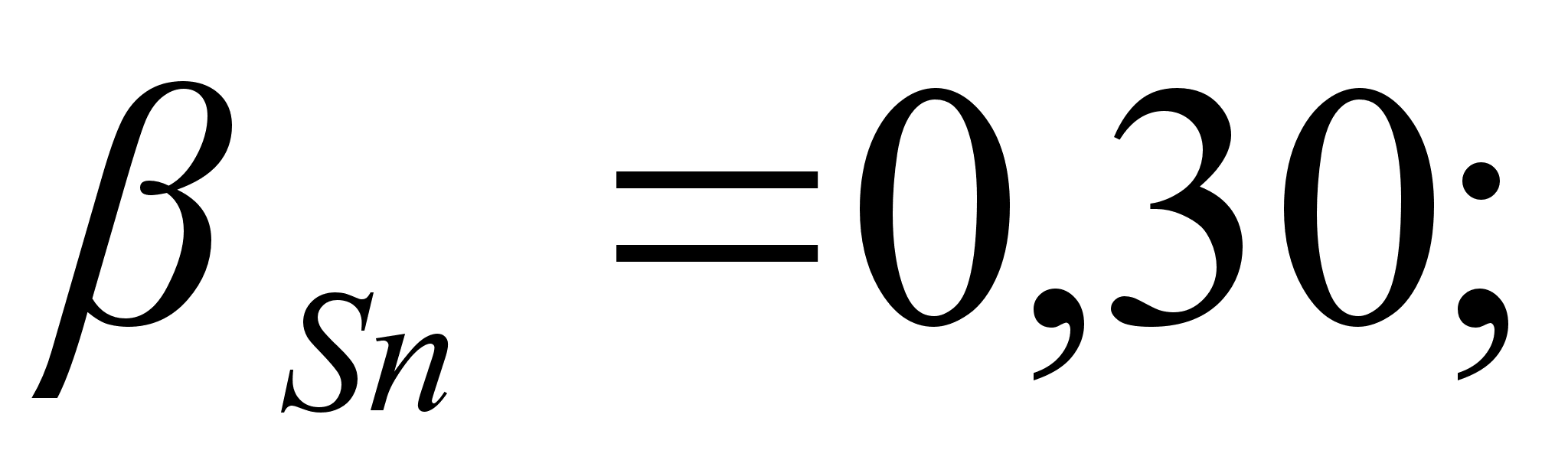
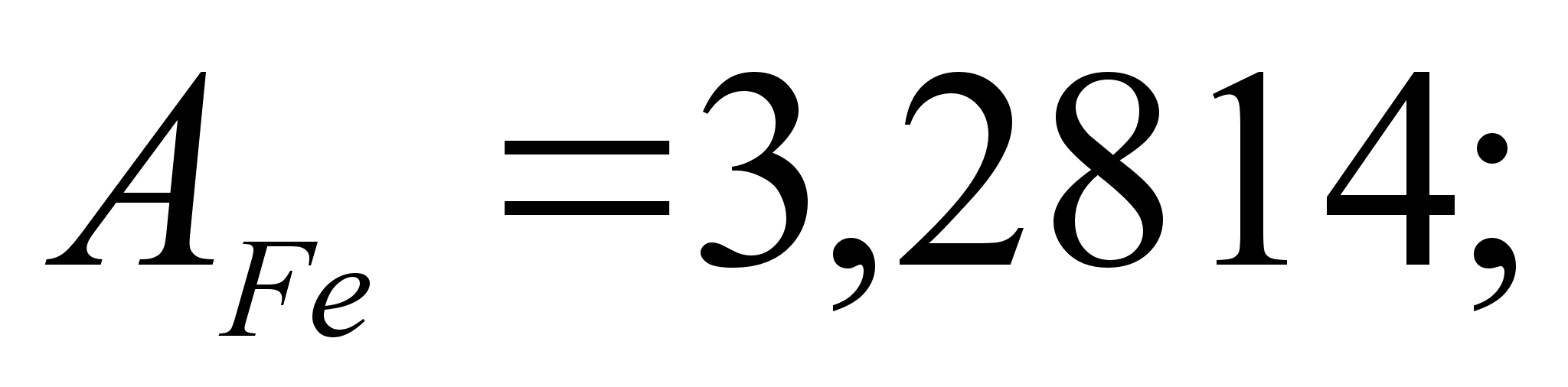
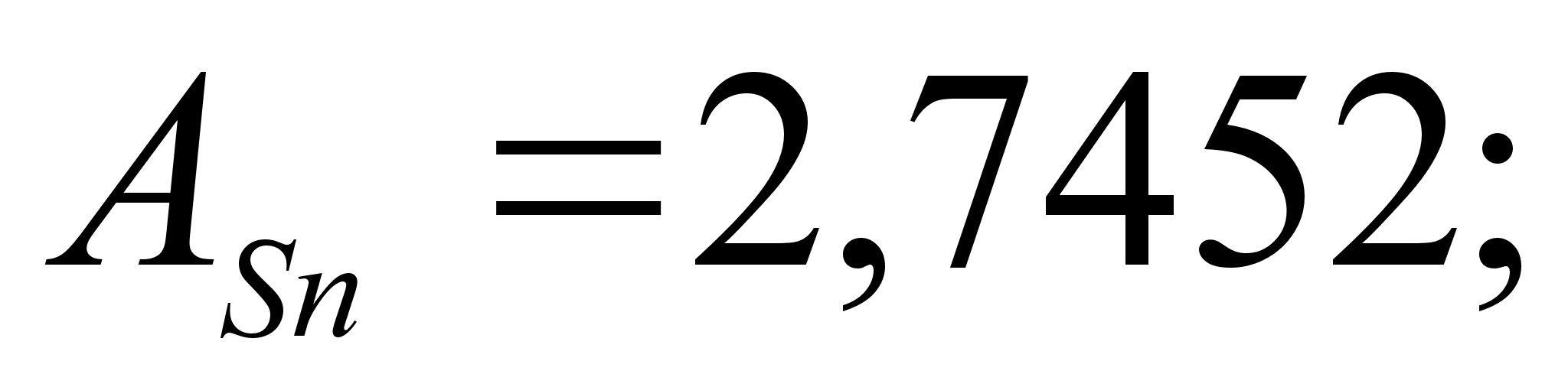
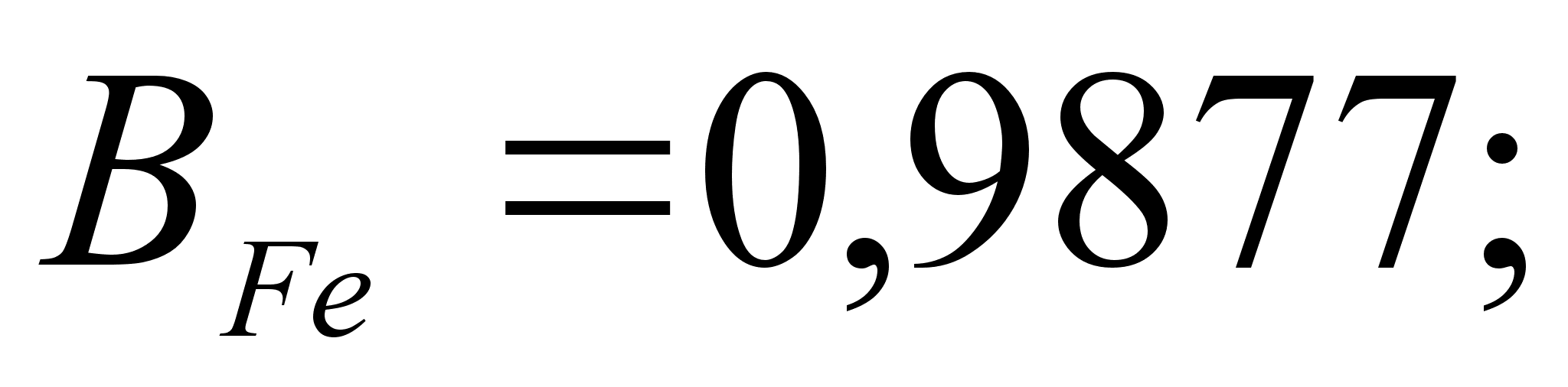
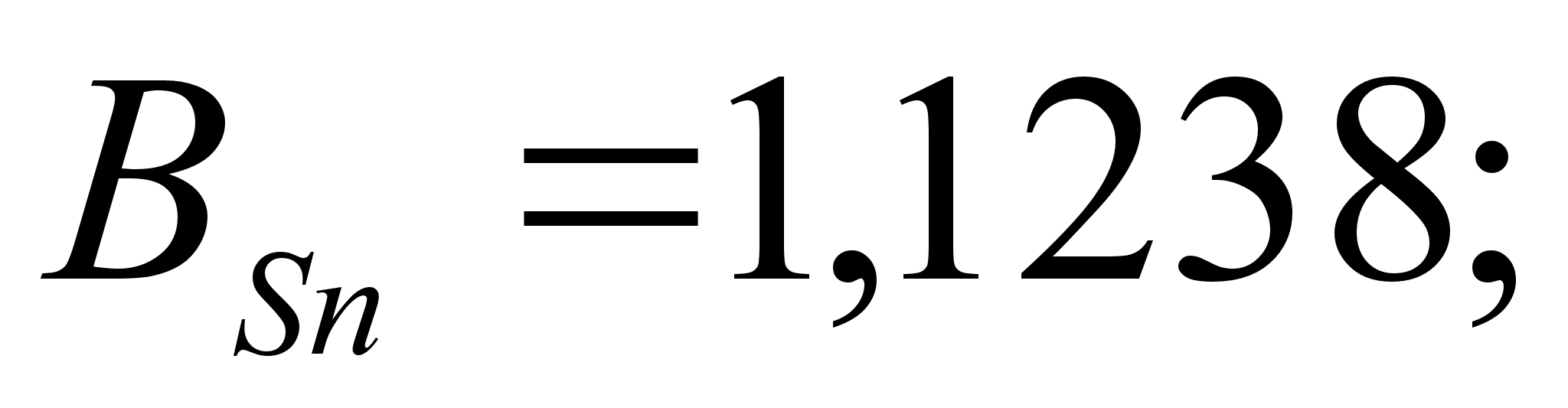
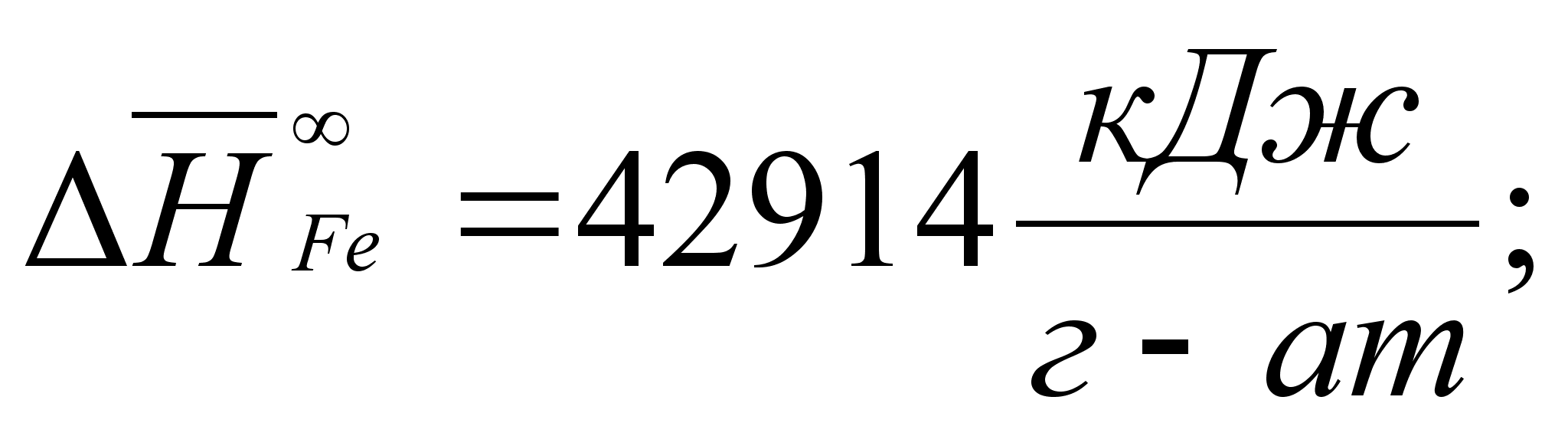
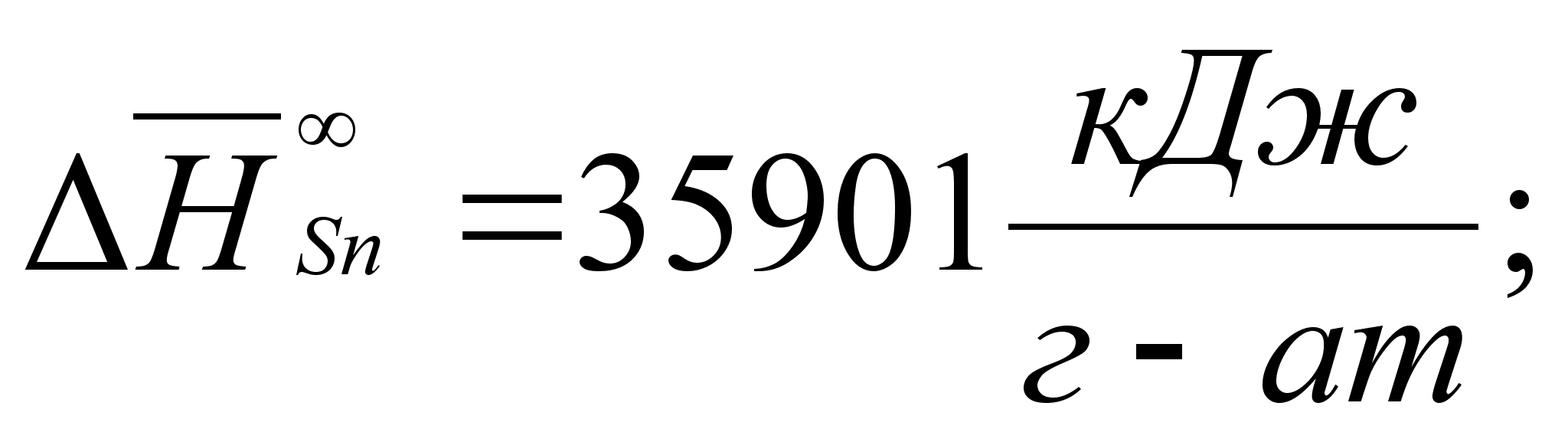
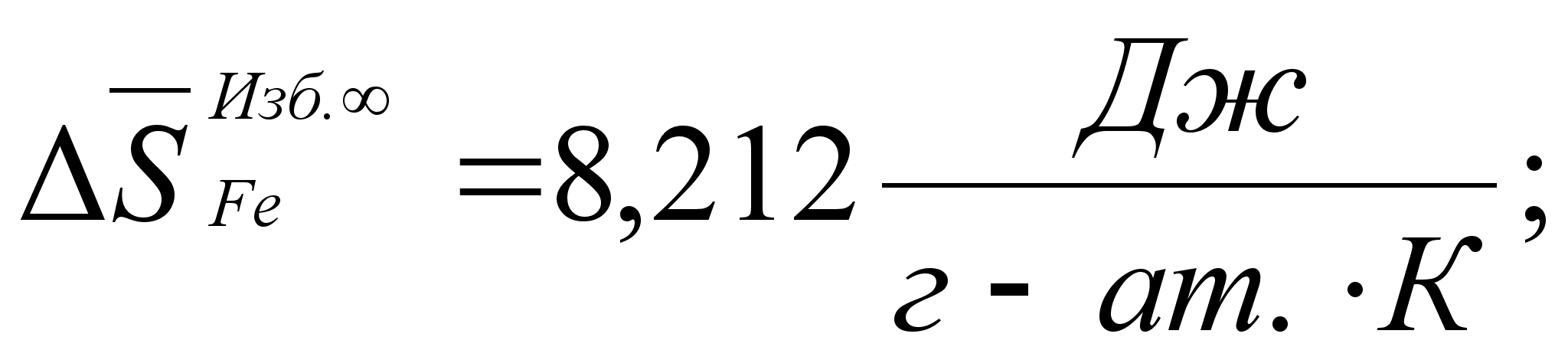
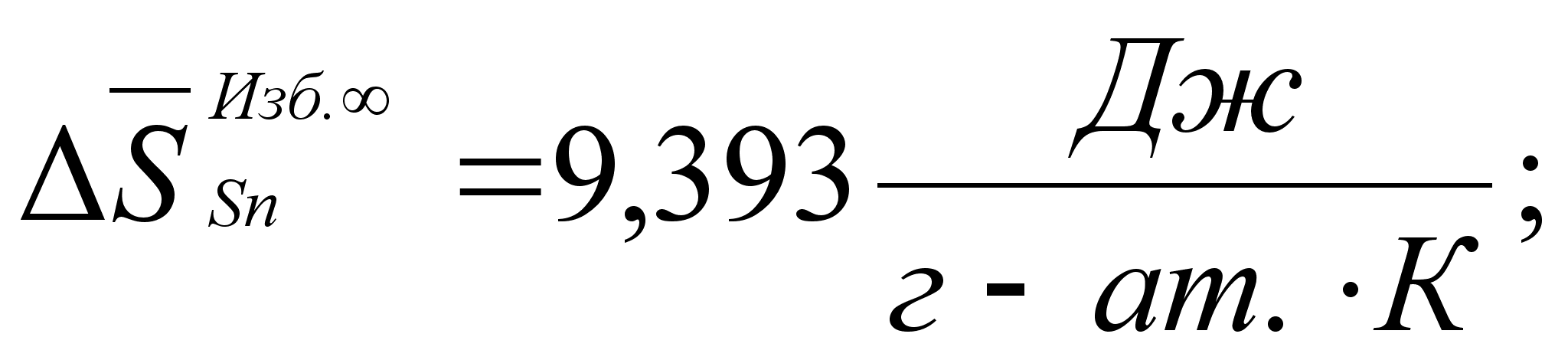
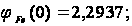
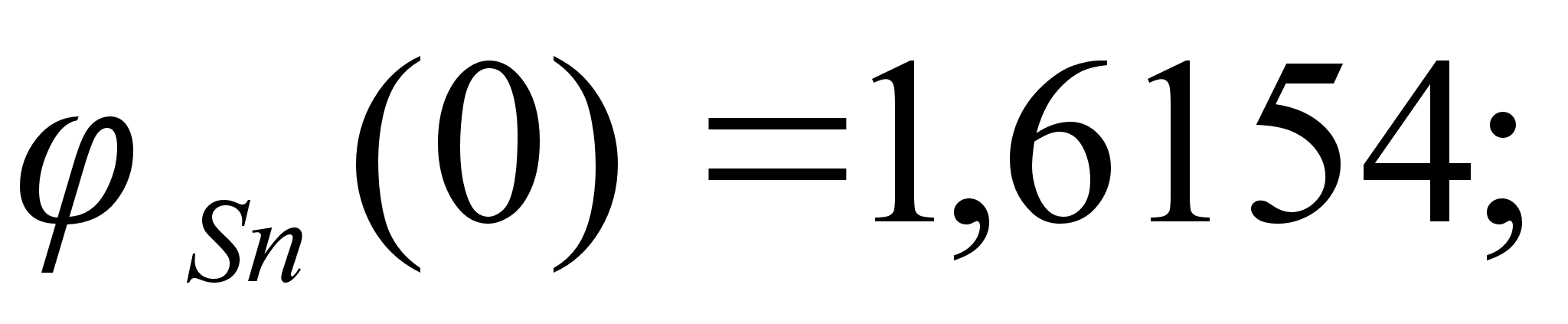
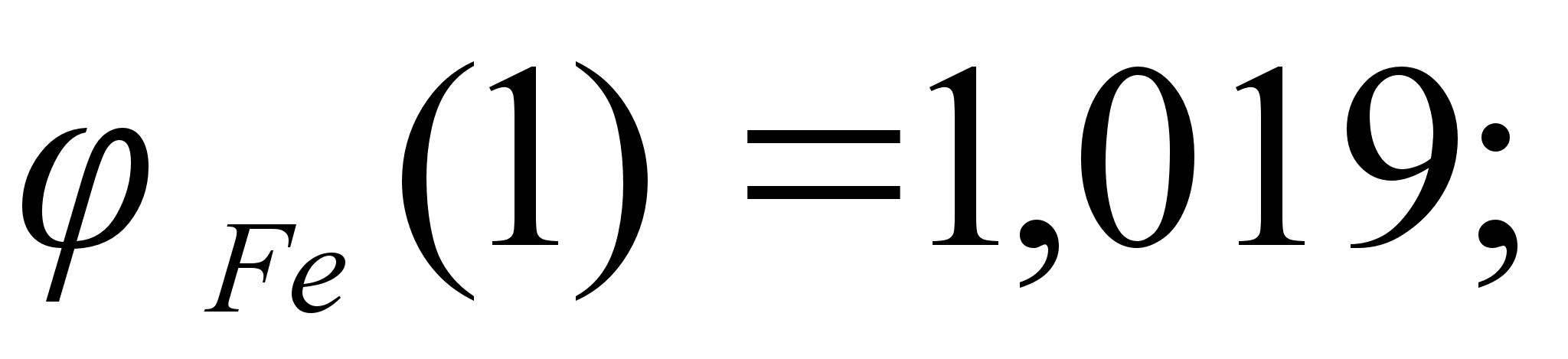
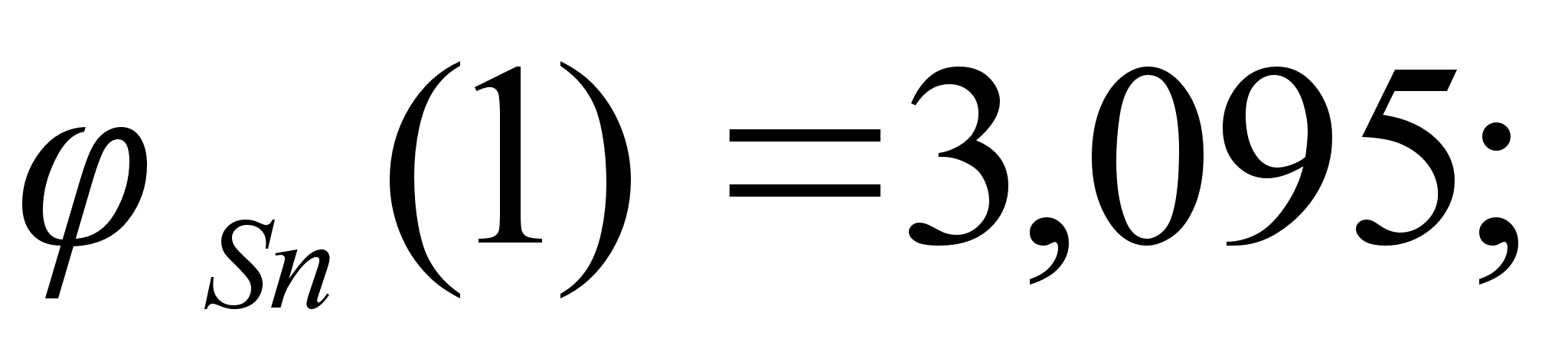
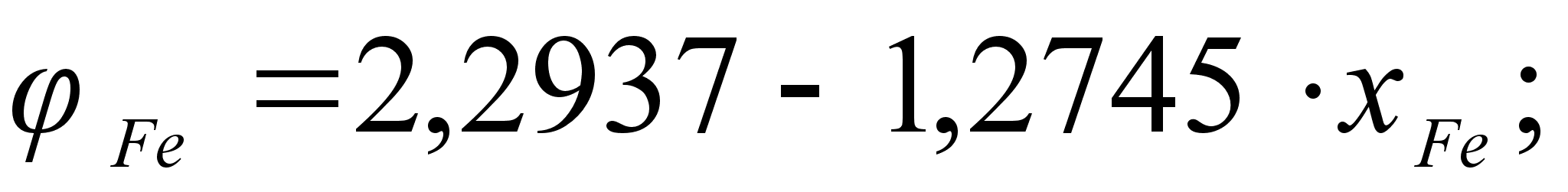
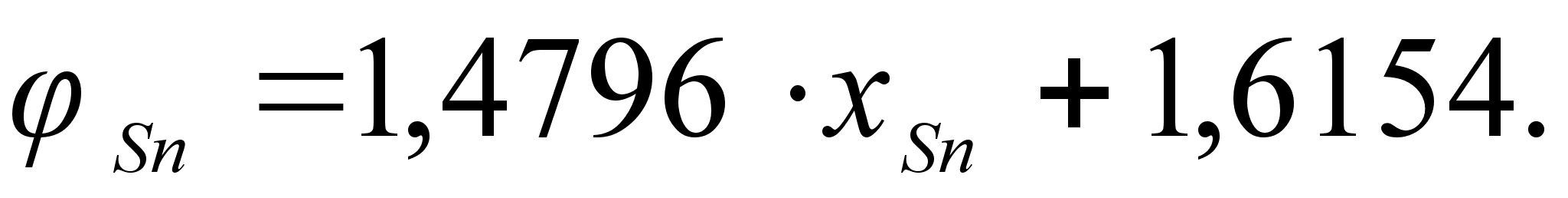
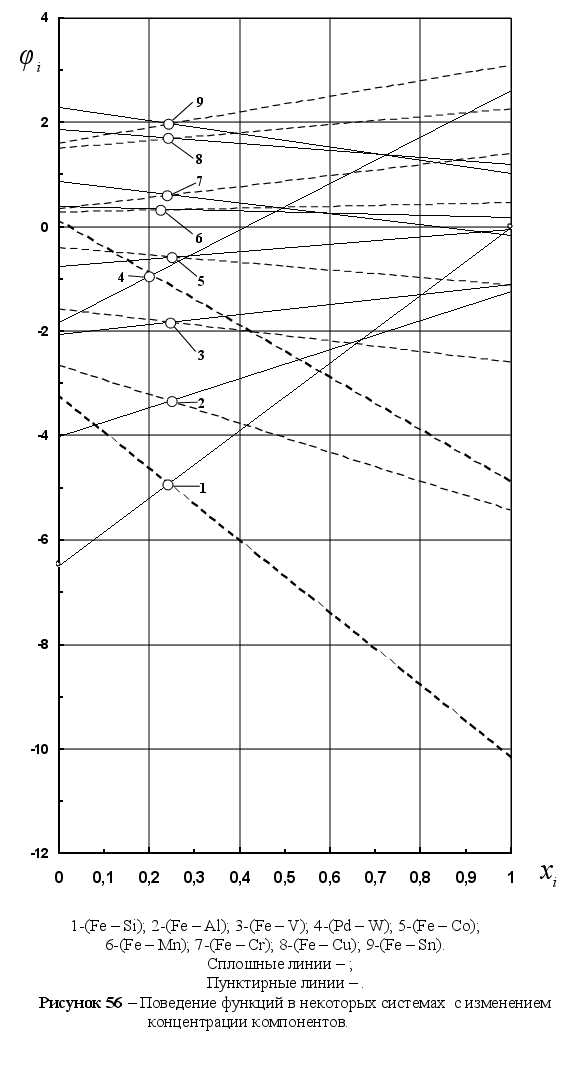
Как уже говорилось, при
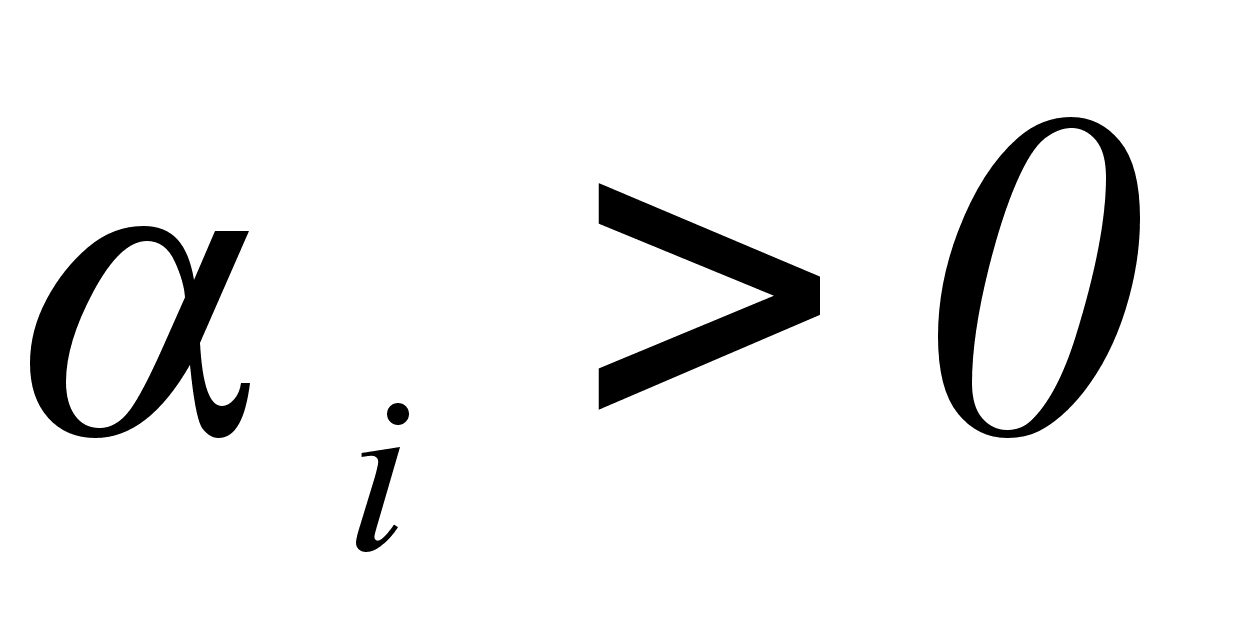 функция
функция
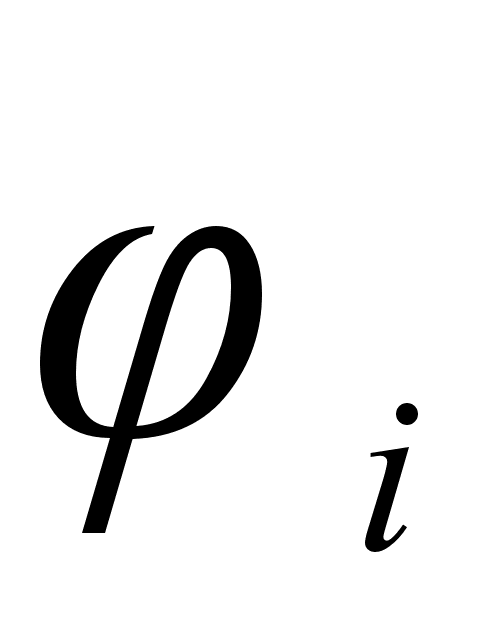 по абсолютному
значению должна
убывать, и наоборот.
Сплошные линии
на рисунке 56
относятся к
компоненту
у которого
по абсолютному
значению должна
убывать, и наоборот.
Сплошные линии
на рисунке 56
относятся к
компоненту
у которого
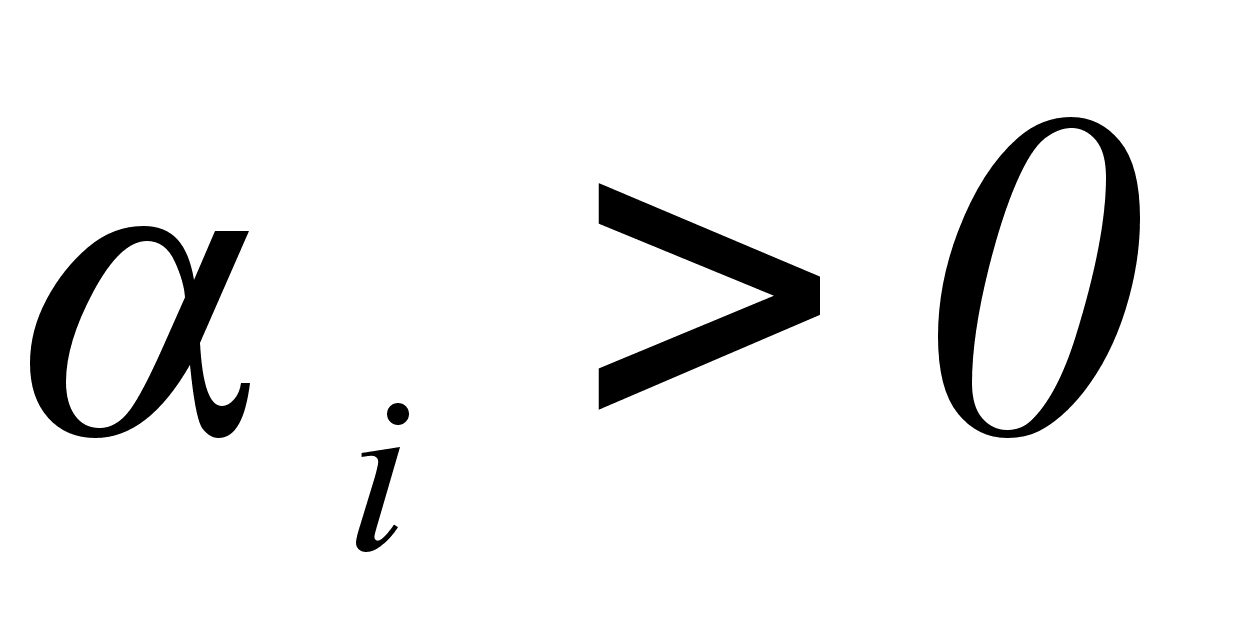 ,
пунктирные
– к компоненту
с
,
пунктирные
– к компоненту
с
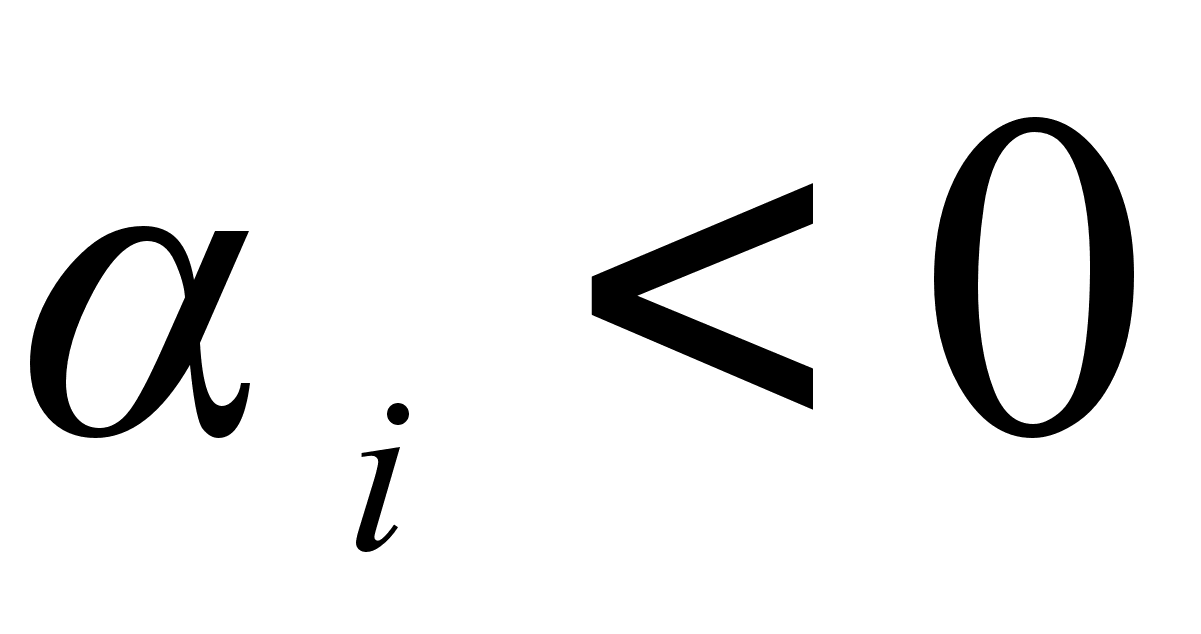 .
.
Каждой точке пересечения линий соответствует свое значение
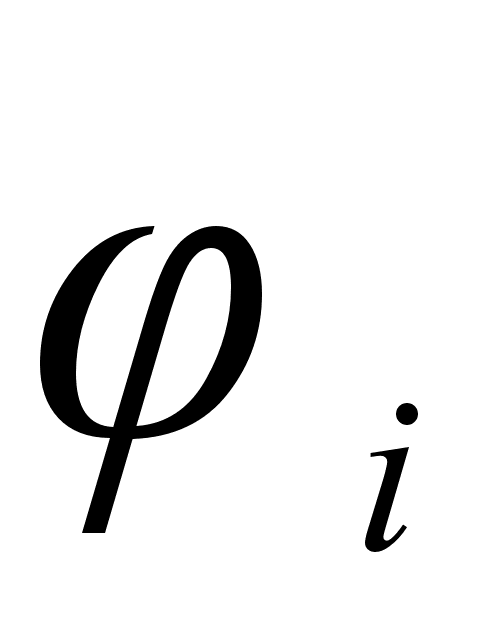 .
Значения
.
Значения
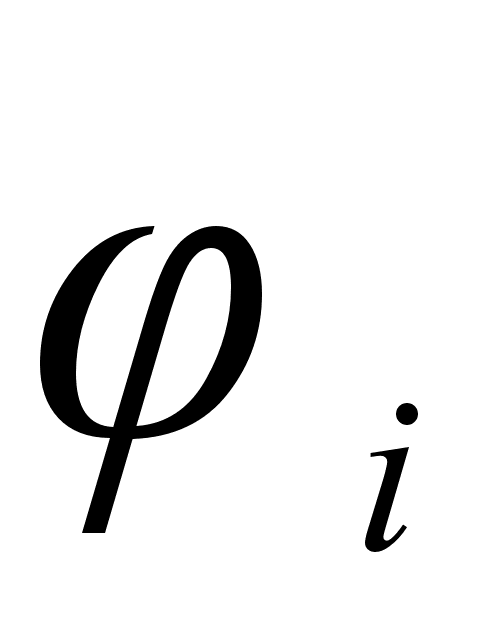 в точках пересечения
обозначим
в точках пересечения
обозначим
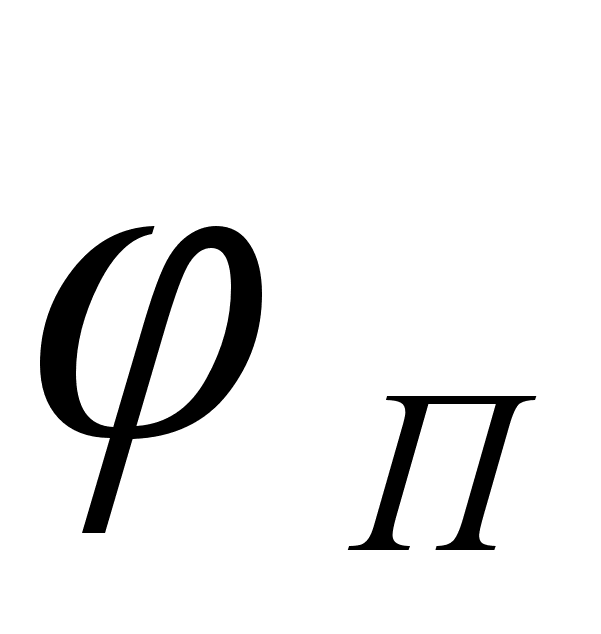 .
Таким образом,
приравняв друг
к другу уравнения
линейных функций
.
Таким образом,
приравняв друг
к другу уравнения
линейных функций
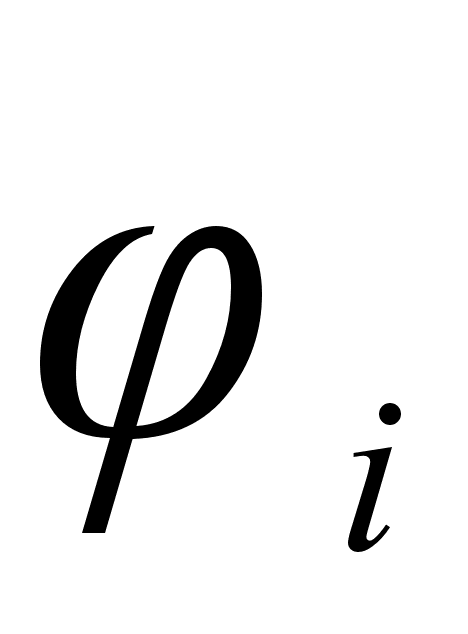 обоих компонентов
бинарного
раствора мы
найдем значения
концентраций
этих компонентов
в точках пересечения
графиков их
функций
обоих компонентов
бинарного
раствора мы
найдем значения
концентраций
этих компонентов
в точках пересечения
графиков их
функций
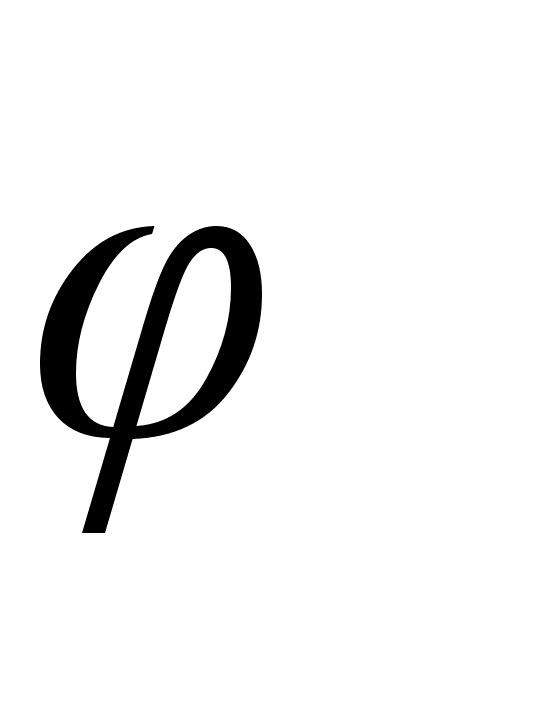 .
Значения
концентраций,
соответствующих
точкам пересечения
графиков обозначим
.
Значения
концентраций,
соответствующих
точкам пересечения
графиков обозначим
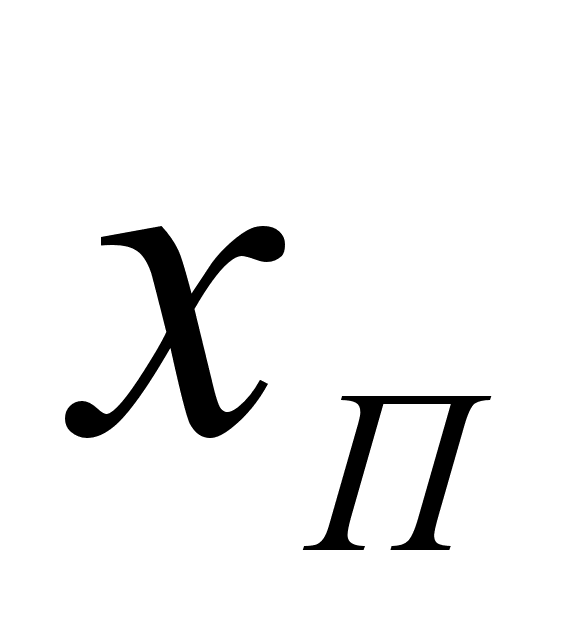 .
.Результаты вычислений
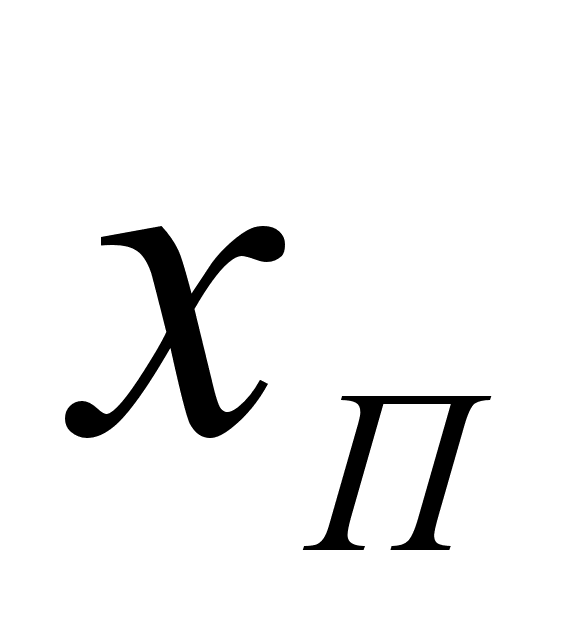 и соответствующие
этим концентрациям
и соответствующие
этим концентрациям
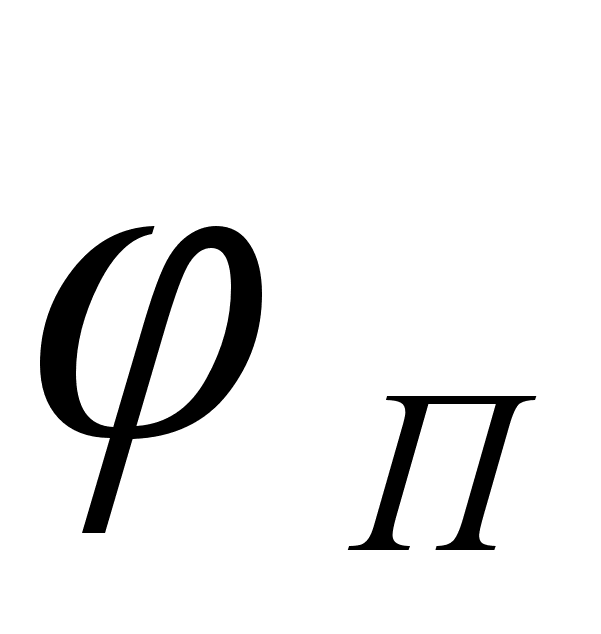 приведены в
таблице 61. Во
всех системах
прямые пересекаются
примерно при
одинаковых
значениях
приведены в
таблице 61. Во
всех системах
прямые пересекаются
примерно при
одинаковых
значениях
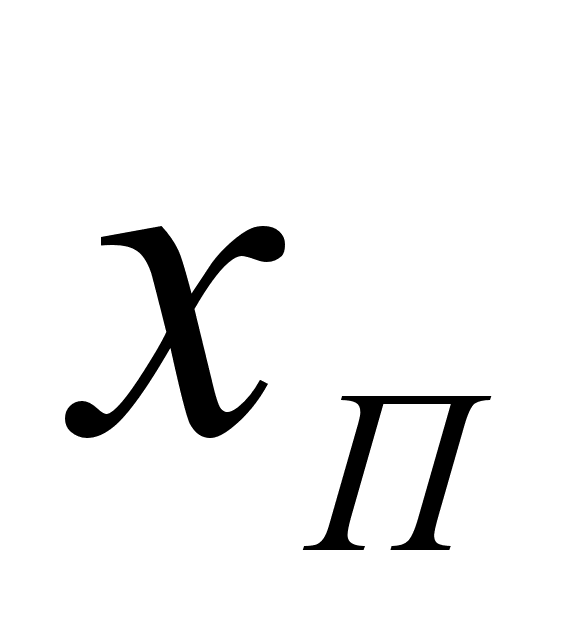 .
В среднем
.
В среднем
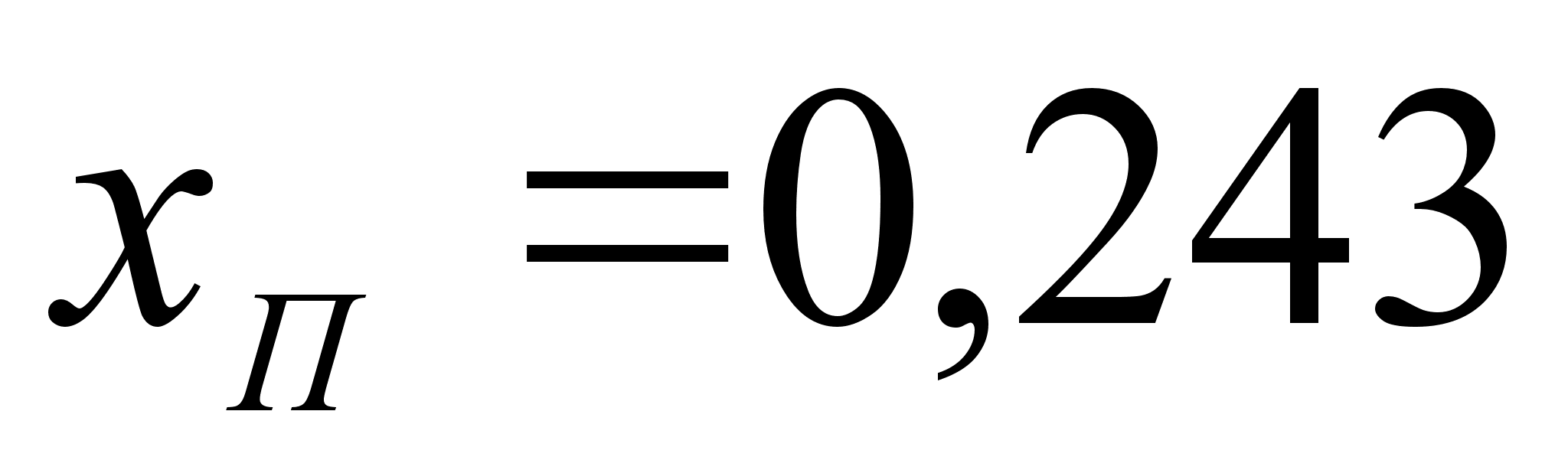 .
.
Из рисунка 56 видно, что чем большее отклонение от идеальности имеет система, тем на больший угол расходятся рассматриваемые прямые. Угол между прямыми можно характеризовать величинойСистема 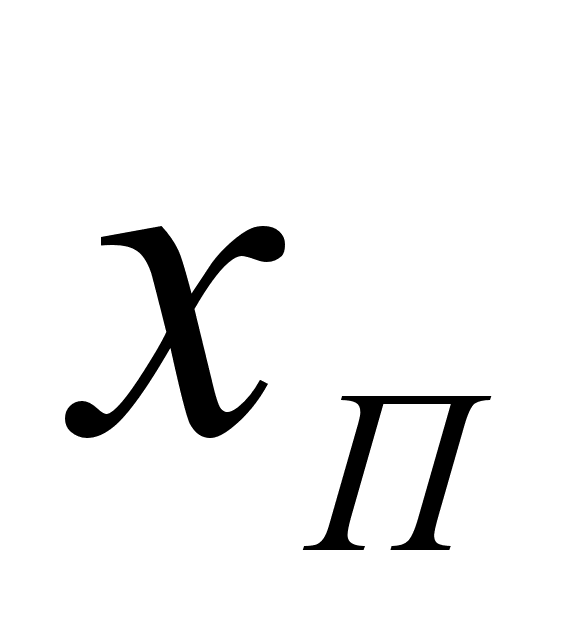
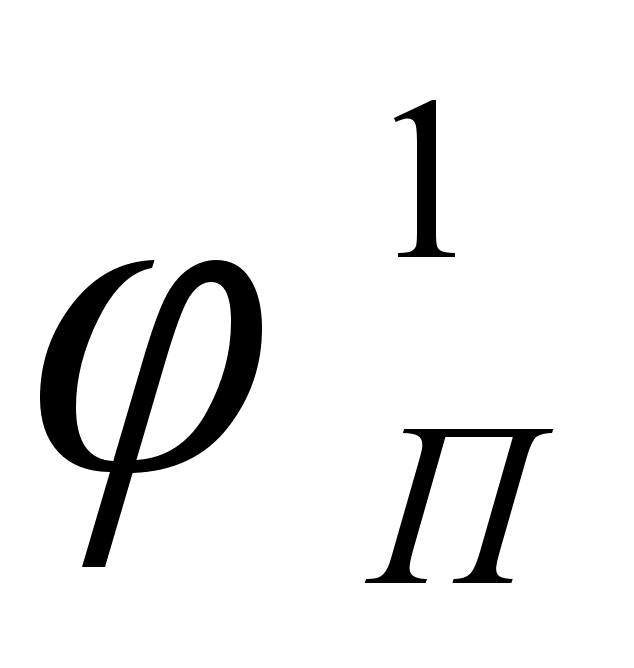
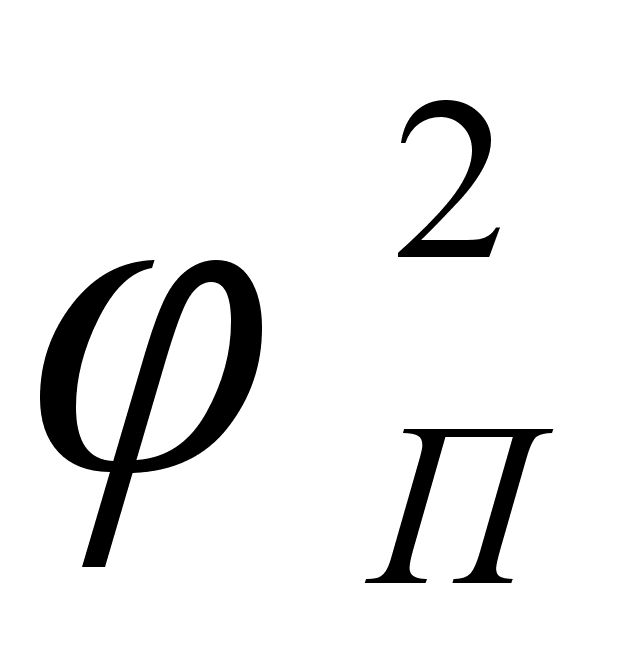
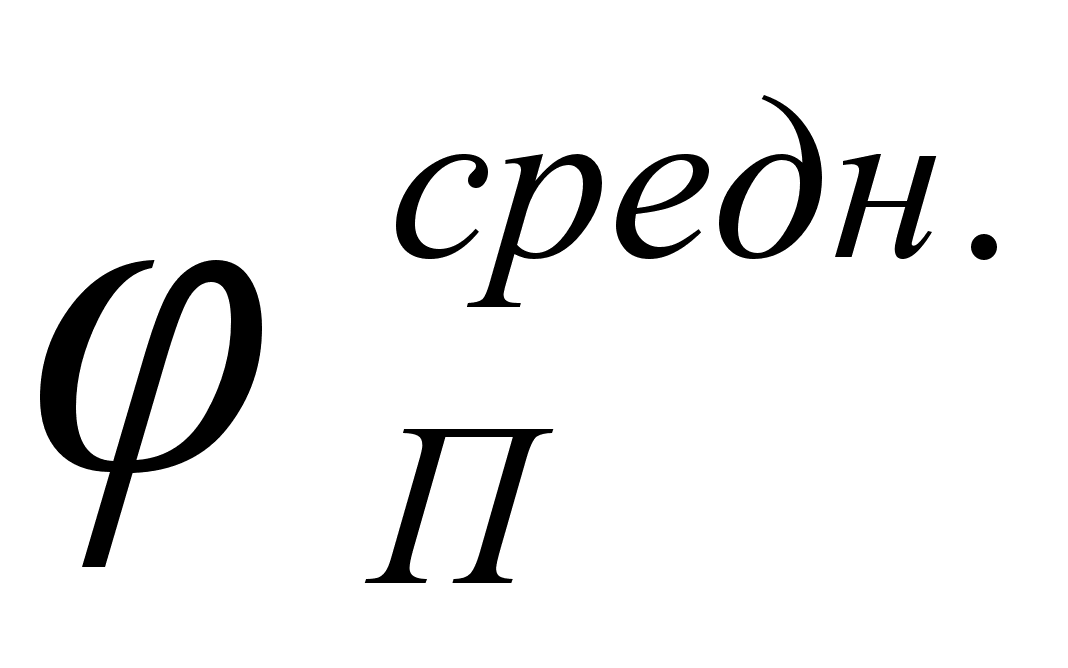
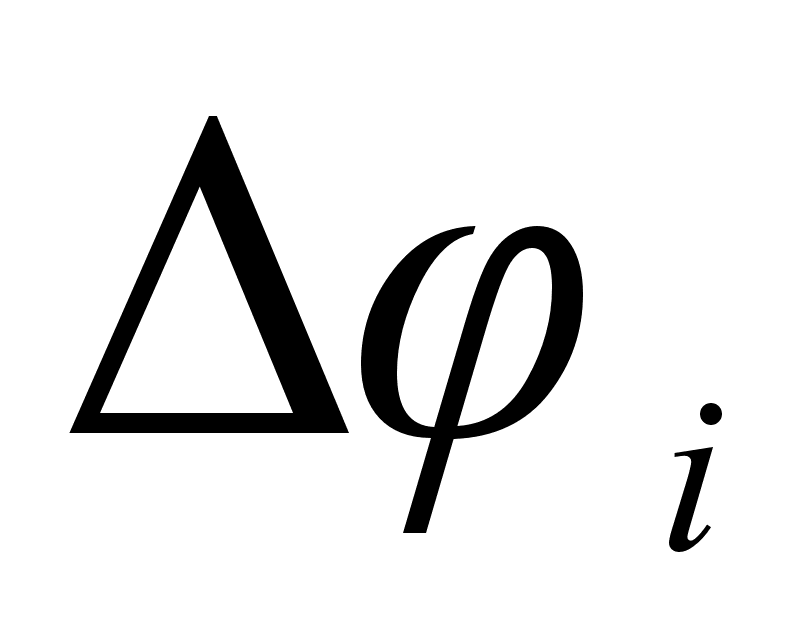
1-(Fe – Si) 0,243 -4,902 -4,904 -4,903 10,168 2-(Fe – Al) 0,248 -3,332 -3,334 -3,333 4,186 3-(Fe – V) 0,249 -1,822 -1,822 -1,822 1,485 4-(Pd – W)
0,206 -0,903 -0,905 -0,904 7,505 5-(Fe – Co) 0,250 -0,572 -0,572 -0,572 1,0625 6-(Fe – Mn) 0,251 0,333 0,333 0,333 0,5903 7-(Fe – Cr) 0,250 0,615 0,616 0,6155 1,568 8-(Fe – Cu) 0,247 1,698 1,698 1,698 1,060 9-(Fe – Sn) 0,246 1,980 1,979 1,9795 2,076 Средн. знач. 0,243 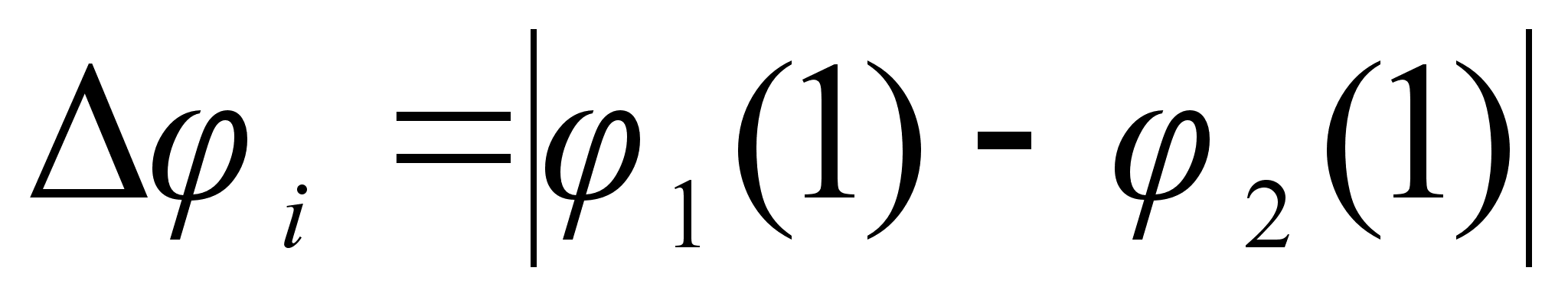 , т.е. абсолютным
значением
разности функций
, т.е. абсолютным
значением
разности функций
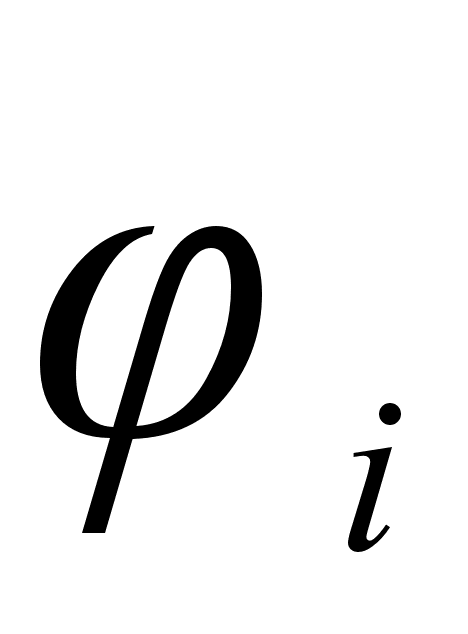 при концентрациях
компонентов
при концентрациях
компонентов .
Значения
.
Значения
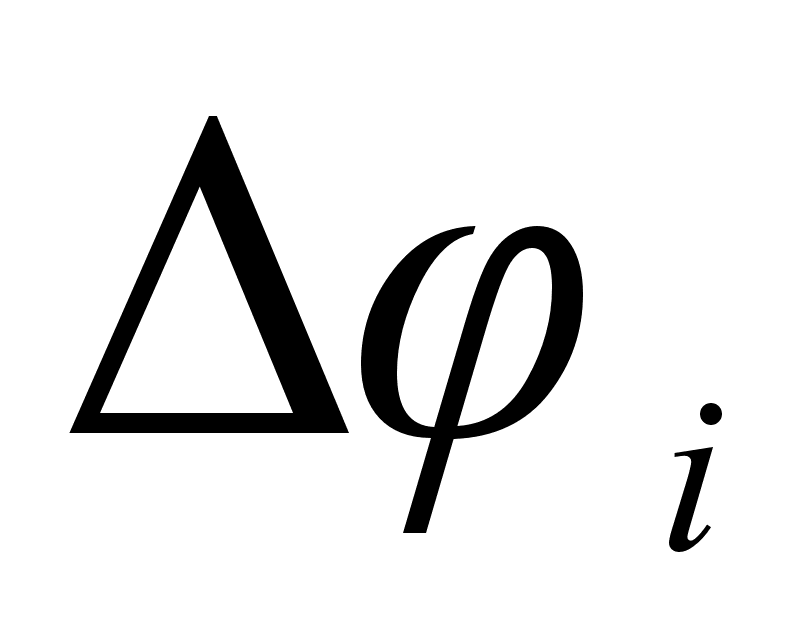 для рассматриваемых
систем приведены
в таблице 61.
для рассматриваемых
систем приведены
в таблице 61.
Таблица 61 – обобщенные данные для рассматриваемых бинарных систем.
Построим график в координатах
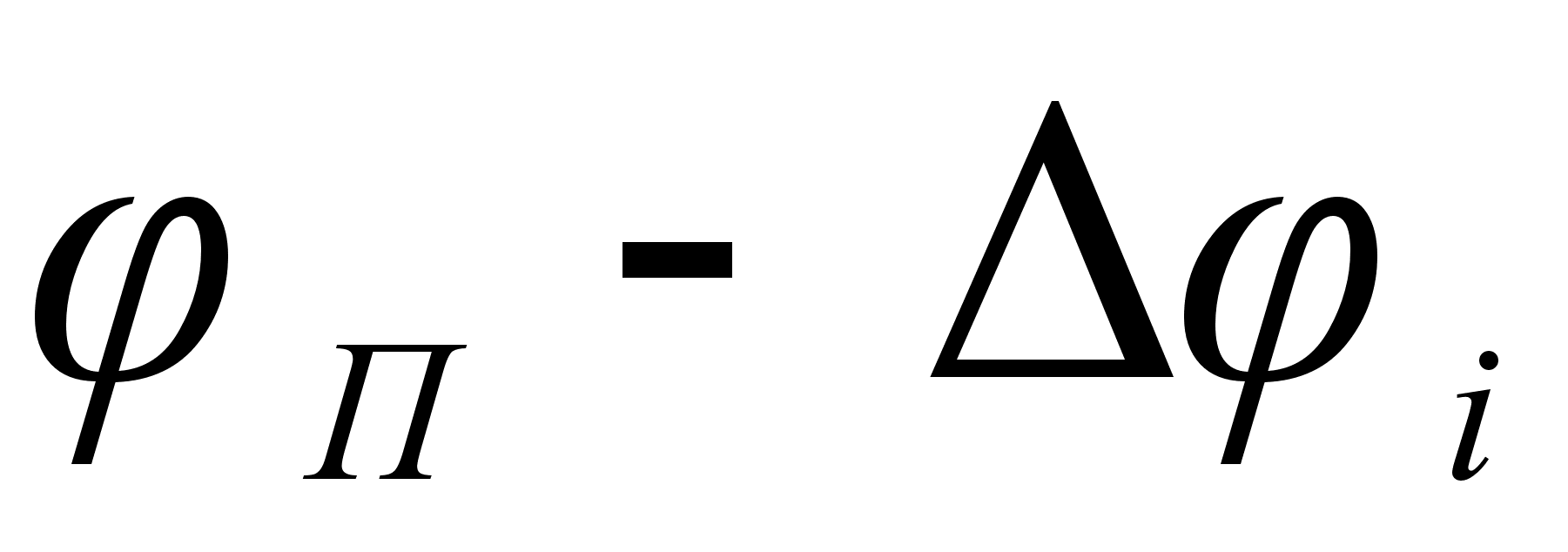 (см. рисунок
57). Из этого рисунка
видно, что
зависимость
между
(см. рисунок
57). Из этого рисунка
видно, что
зависимость
между
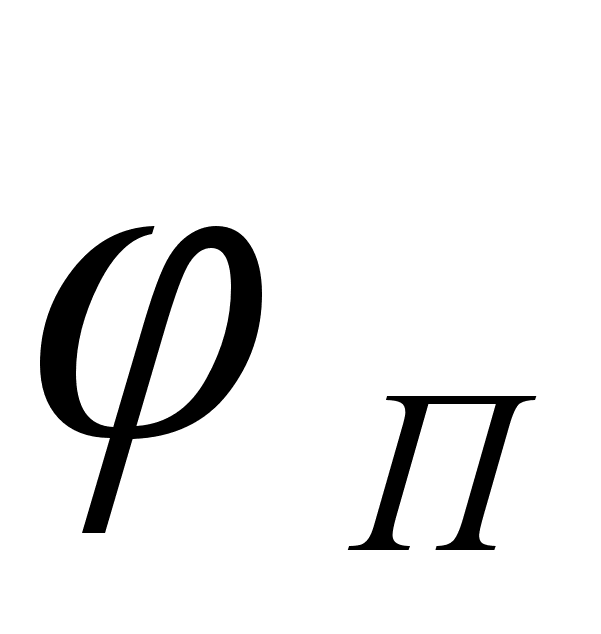 и
и
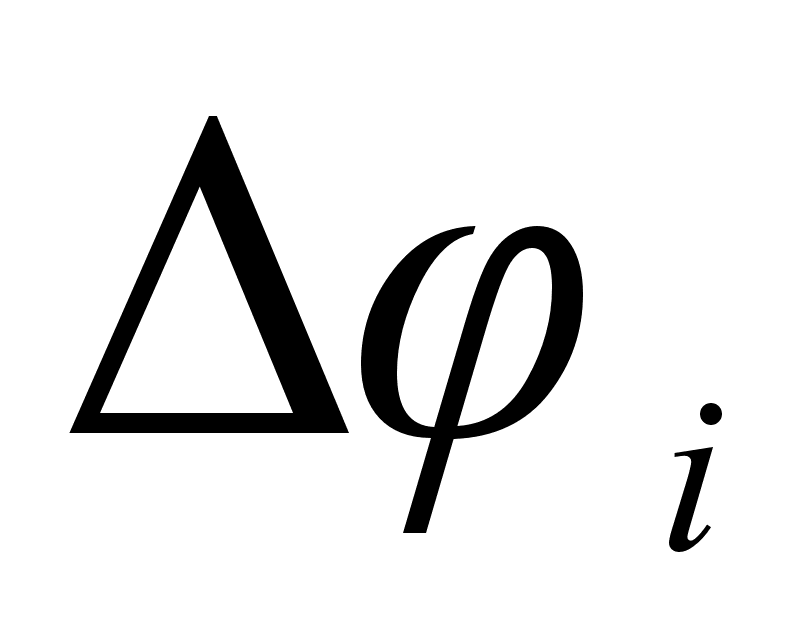 может быть
описана в общем
виде уравнением
параболы второй
степени:
может быть
описана в общем
виде уравнением
параболы второй
степени: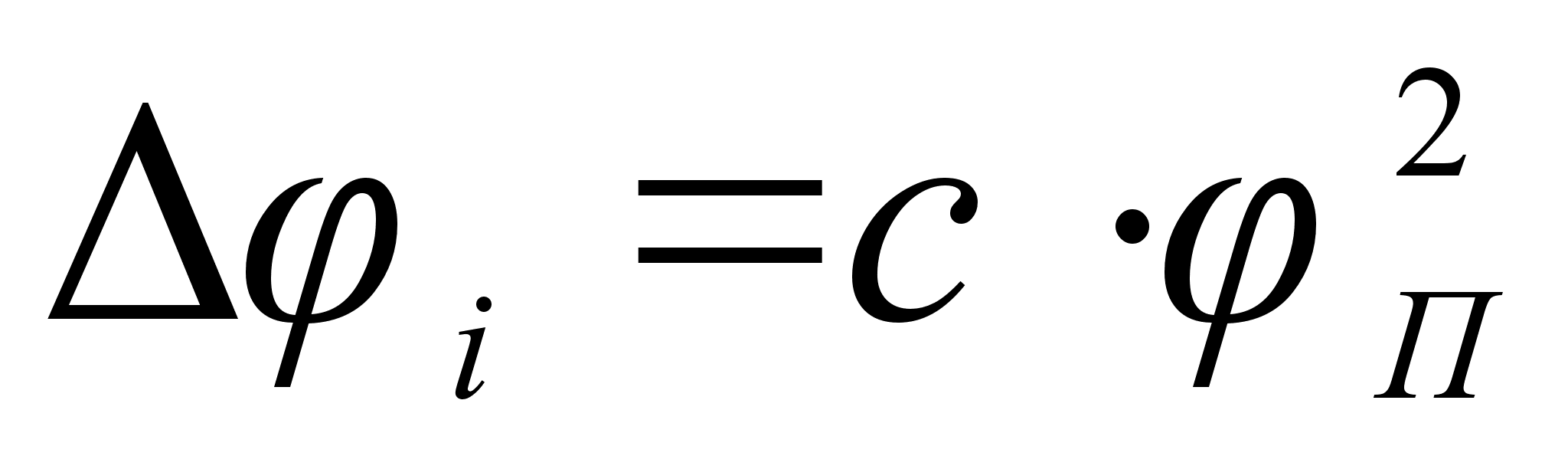
(133)
Вычислим значение коэффициента с в уравнении (133) методом наименьших квадратов. Формула для вычислений:
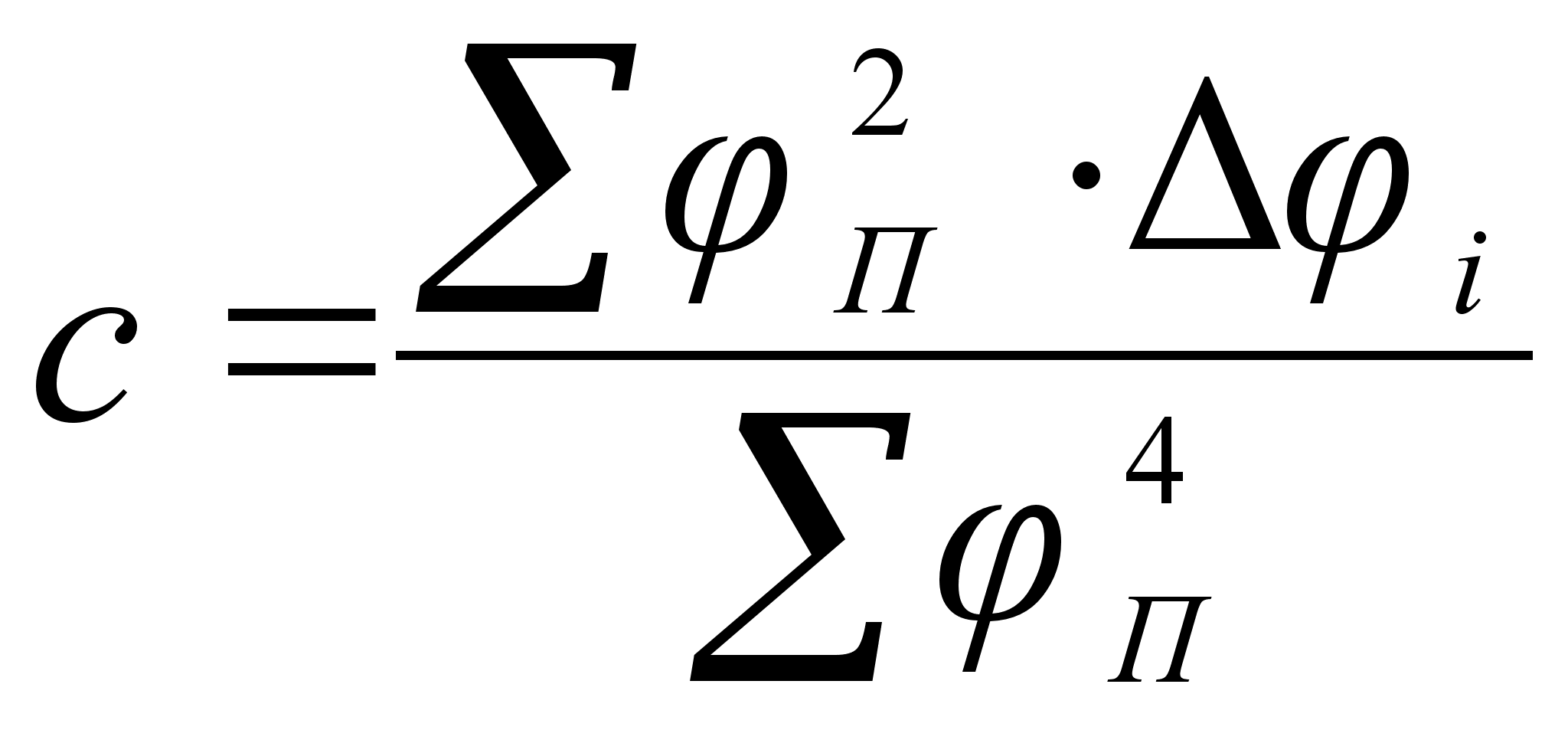
(134)
Таблица 62 – Расчетные данные для отрицательных значений
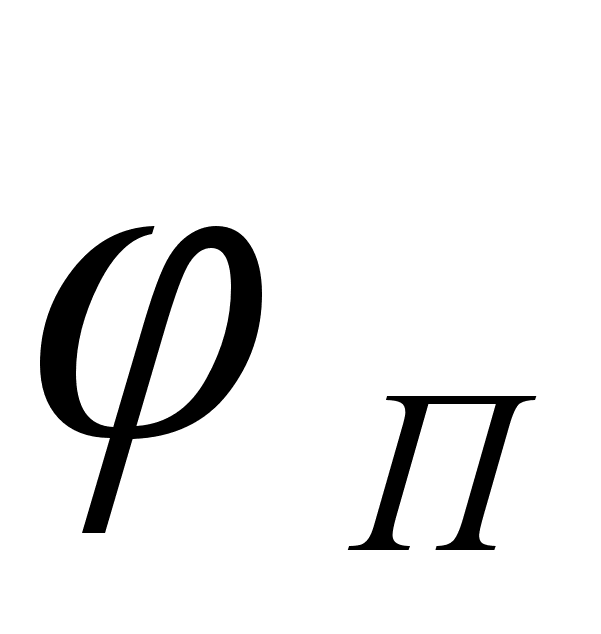 .
.-
функция Значения
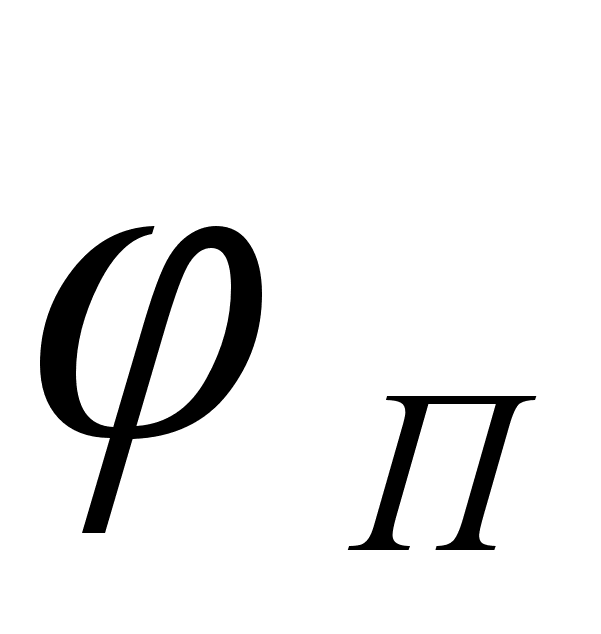
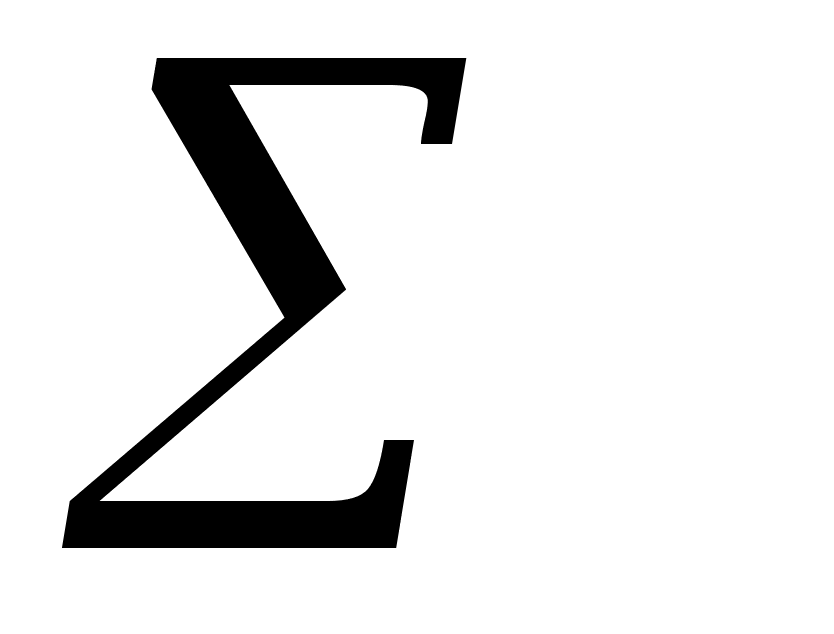
-4,903 -3,999 -1,822 -0,572 
24,039 11,109 3,320 0,327 ----- 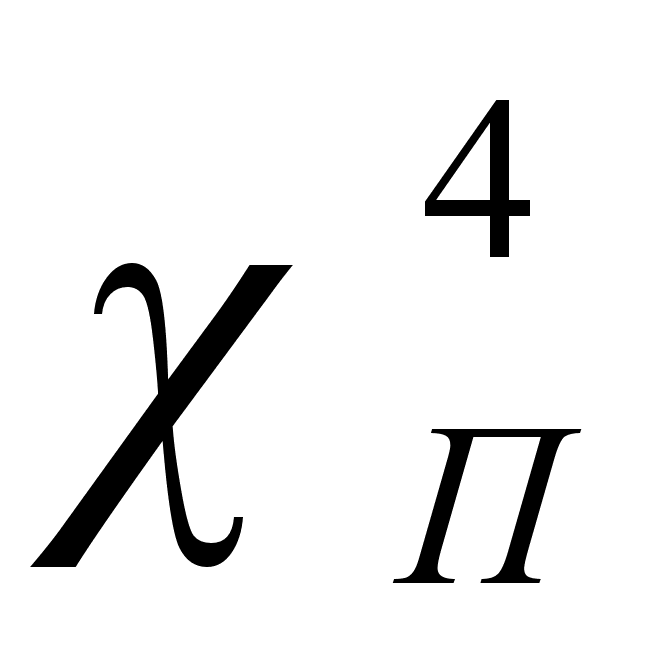
557,890 123,410 11,020 0,107 692,427 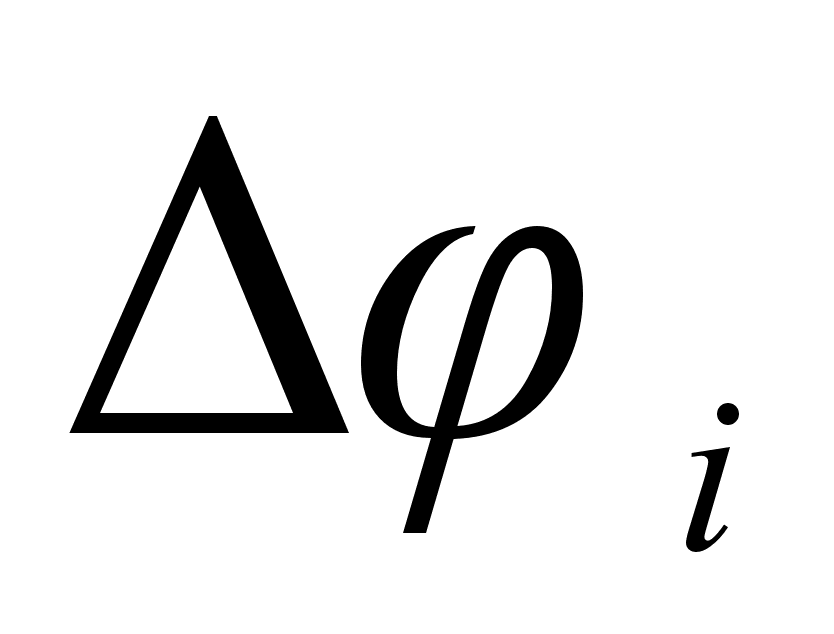
10,168 4,186 1,485 1,0625 ----- 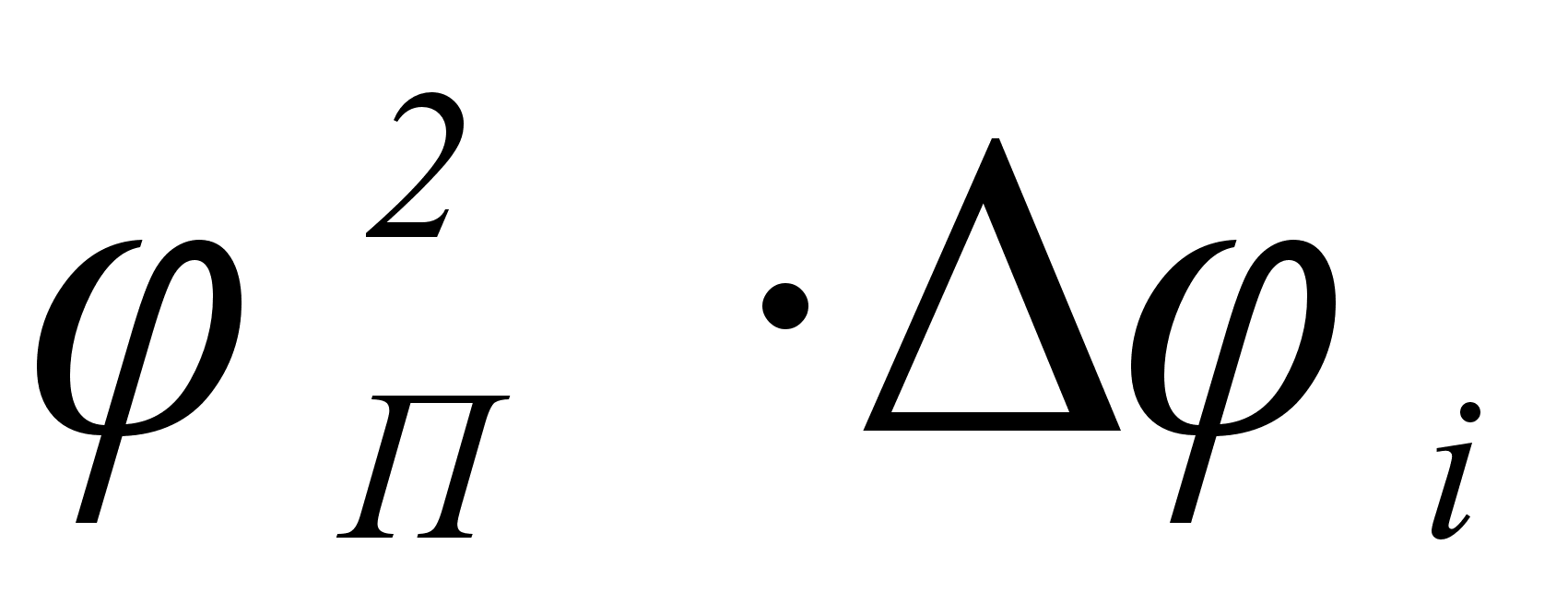
244,429 46,502 4,930 0,347 296,208
Подставив данные из этой таблицы в уравнение (134) получим:
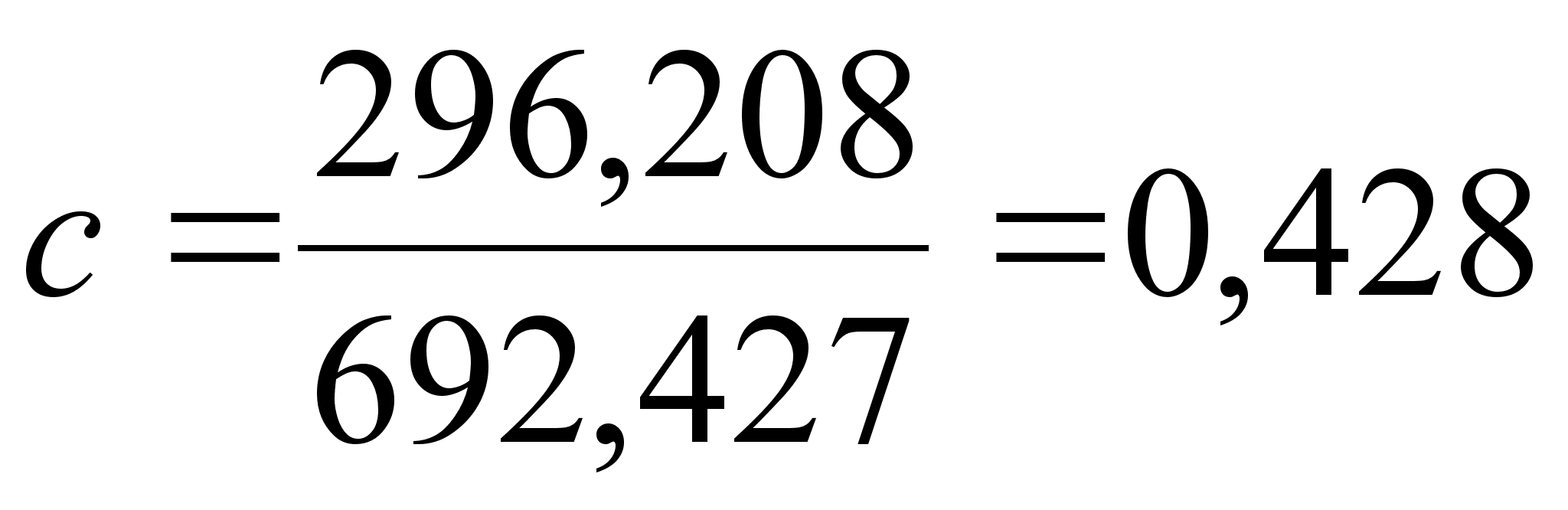
Таким образом, для отрицательных значений
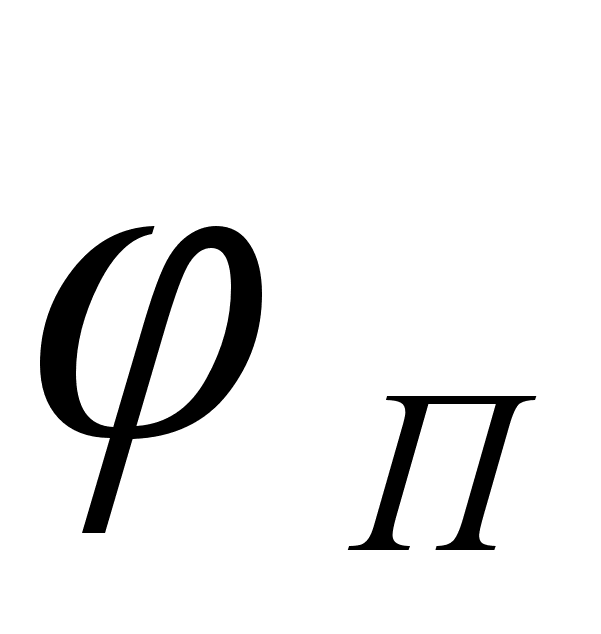 имеем:
имеем: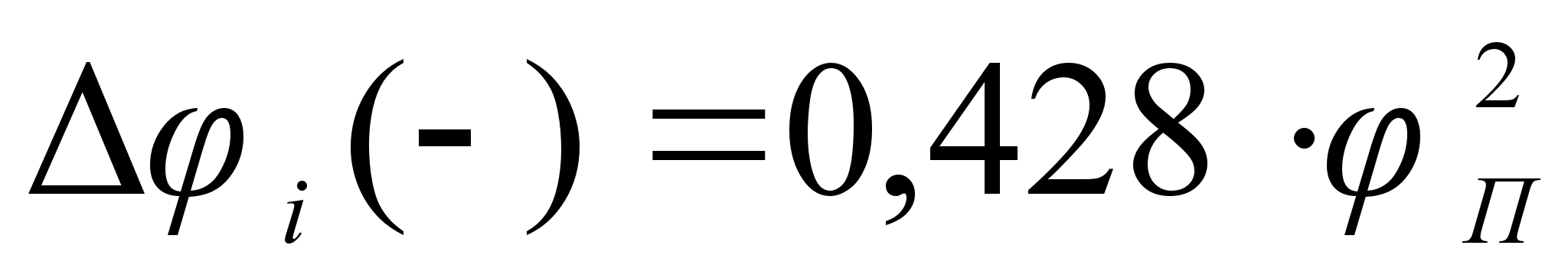
(135)
Для положительных значений
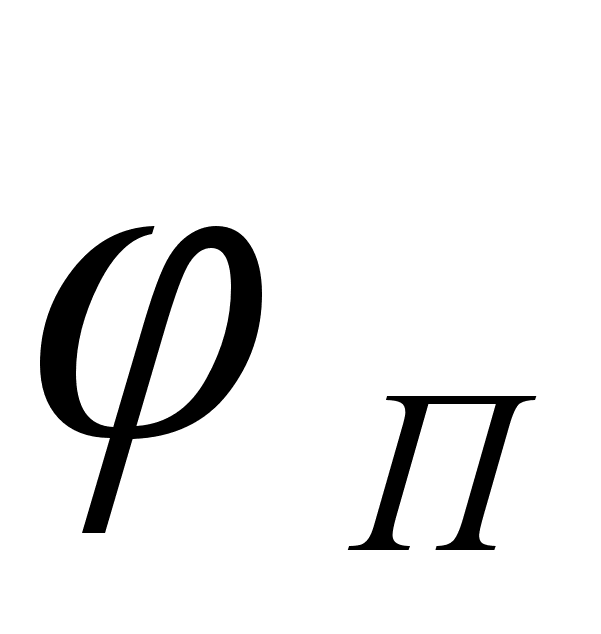 составим такую
же таблицу.
составим такую
же таблицу.Таблица 63 – Расчетные данные для положительных значений
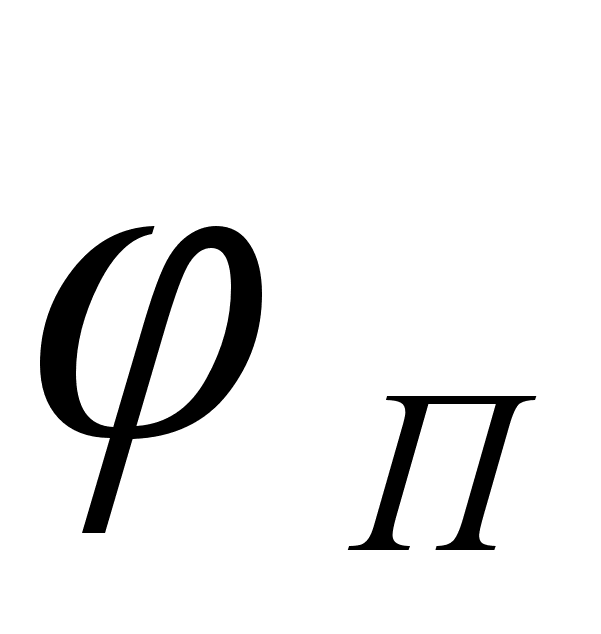 .
.-
функция Значения
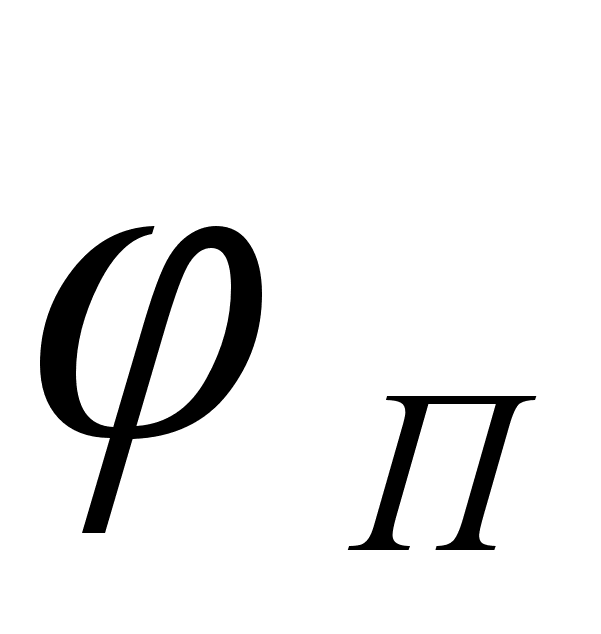
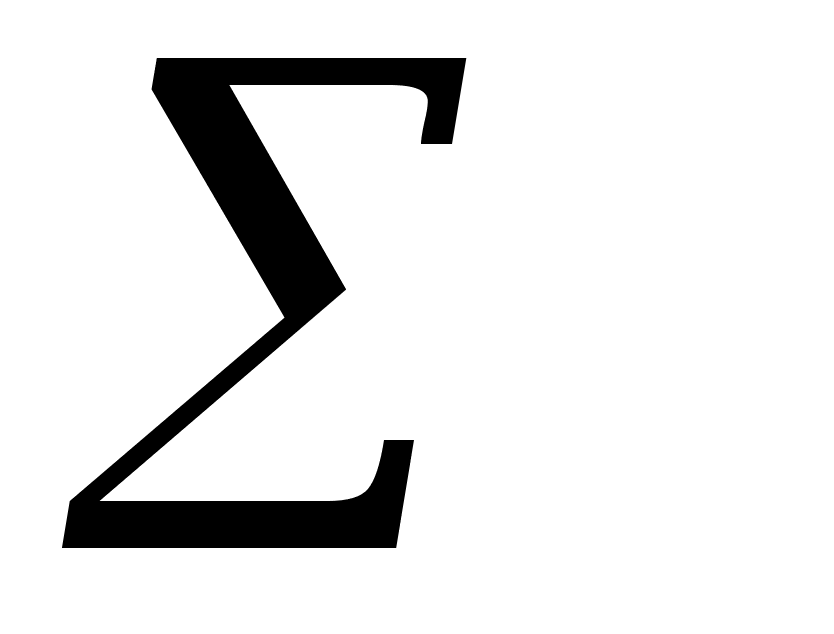
0,333 0,6155 1,698 1,9795 
0,111 0,379 2,883 3,918 ----- 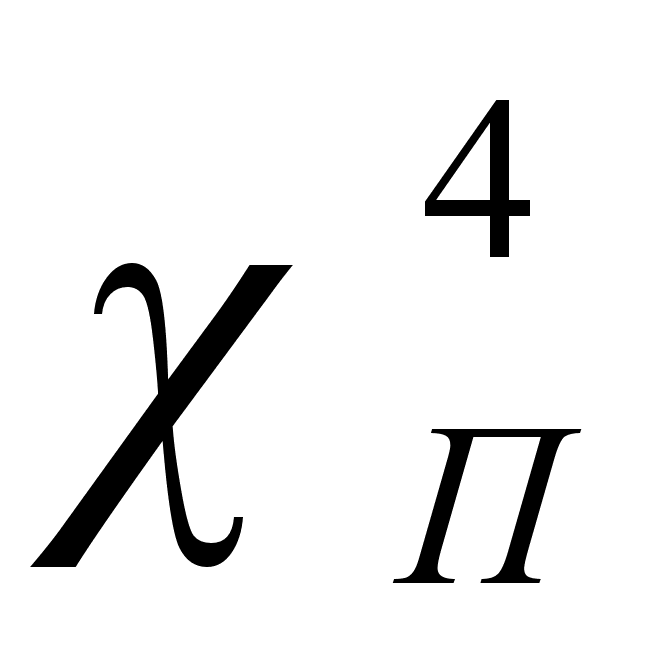
0,012 0,1435 8,313 15,354 23,8225 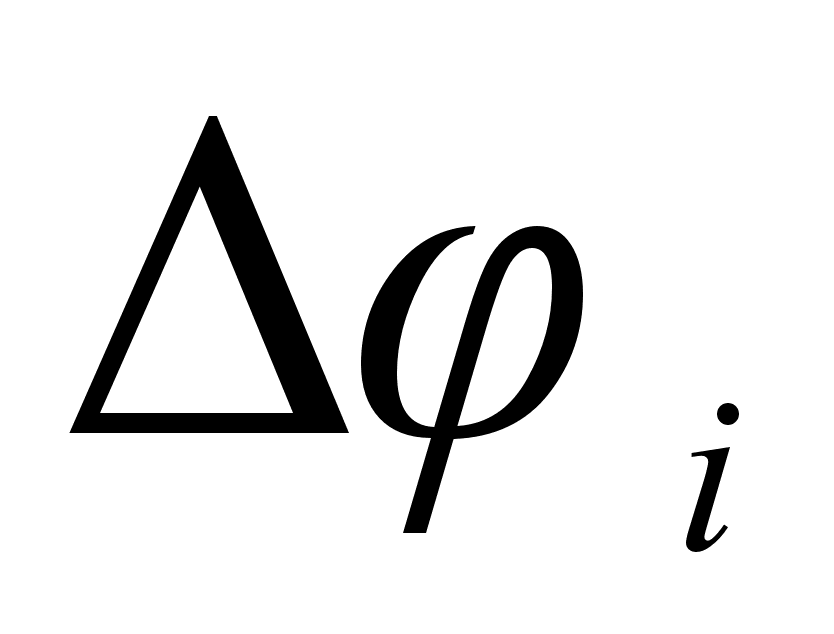
0,2903 1,568 1,060 2,076 ----- 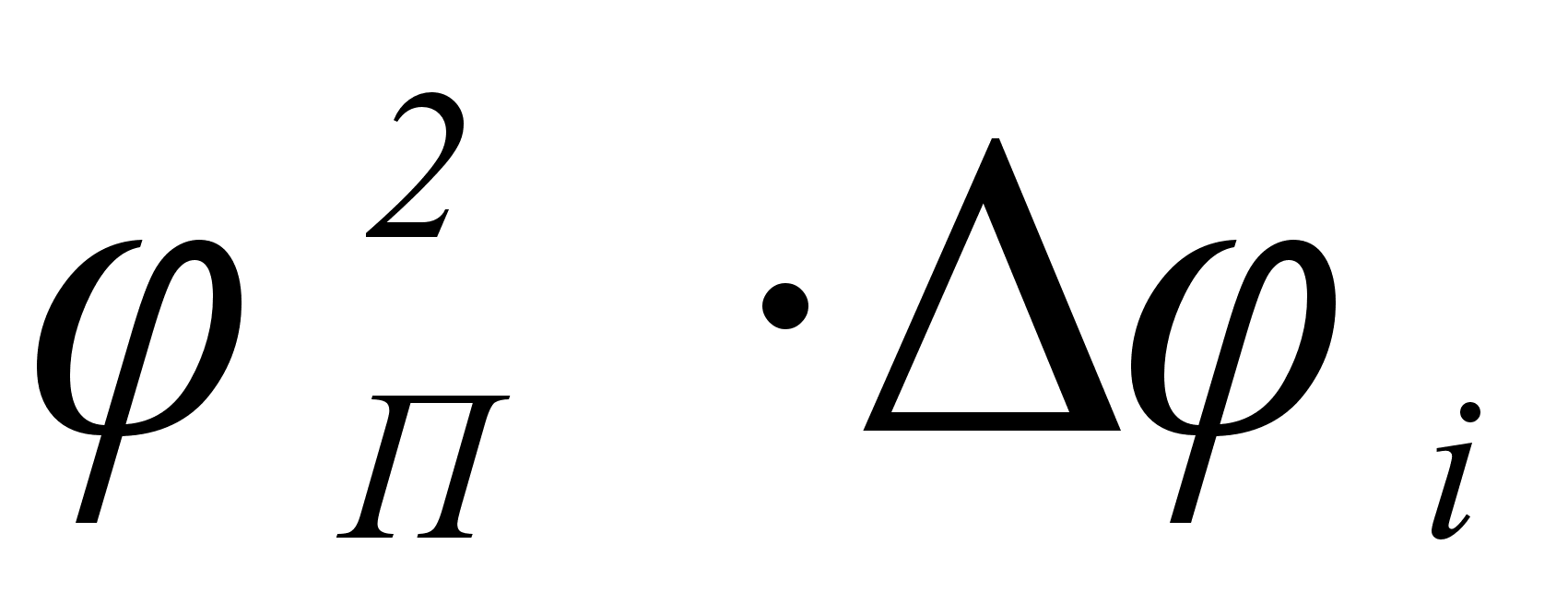
0,032 0,594 3,056 8,134 11,816
Для положительных значений
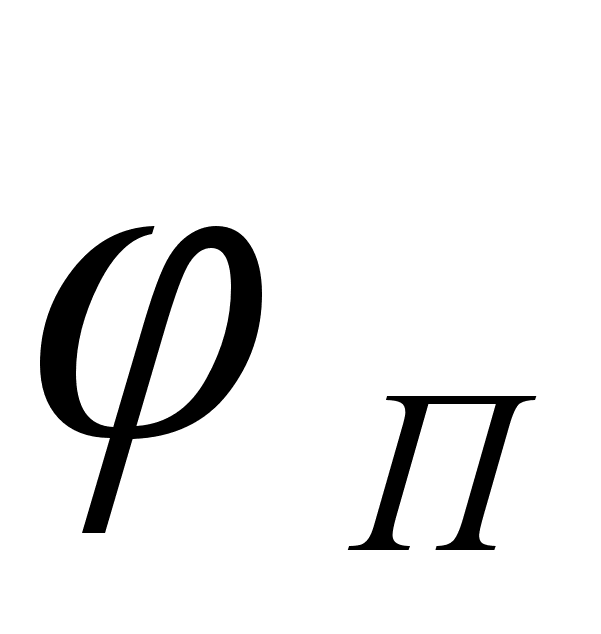 имеем:
имеем: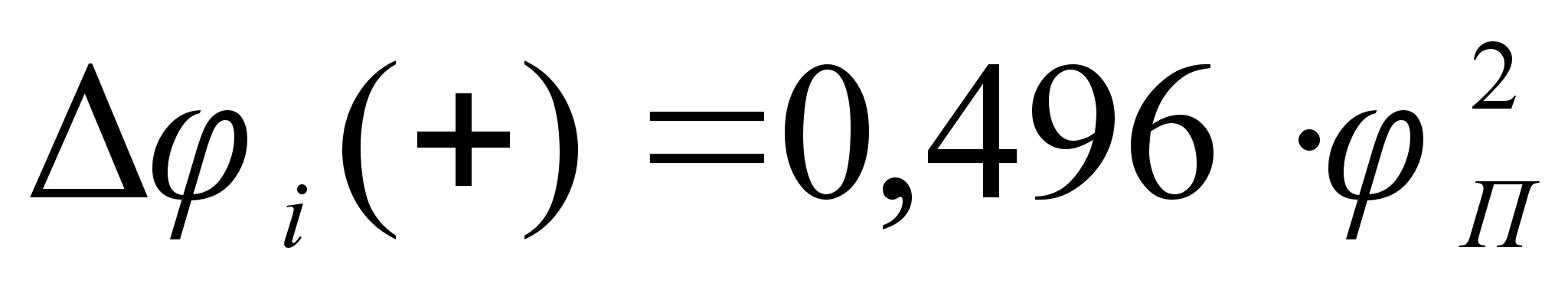
(136)
Вычислим значения функции
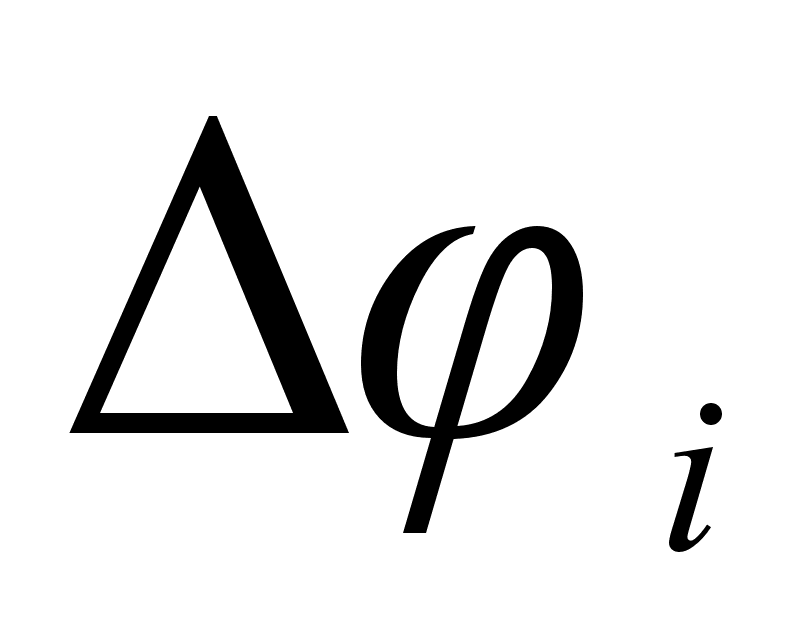 по уравнениям
(135) и (136) и занесем
их в таблицу
64.
по уравнениям
(135) и (136) и занесем
их в таблицу
64.Таблица 64 – Значения функции
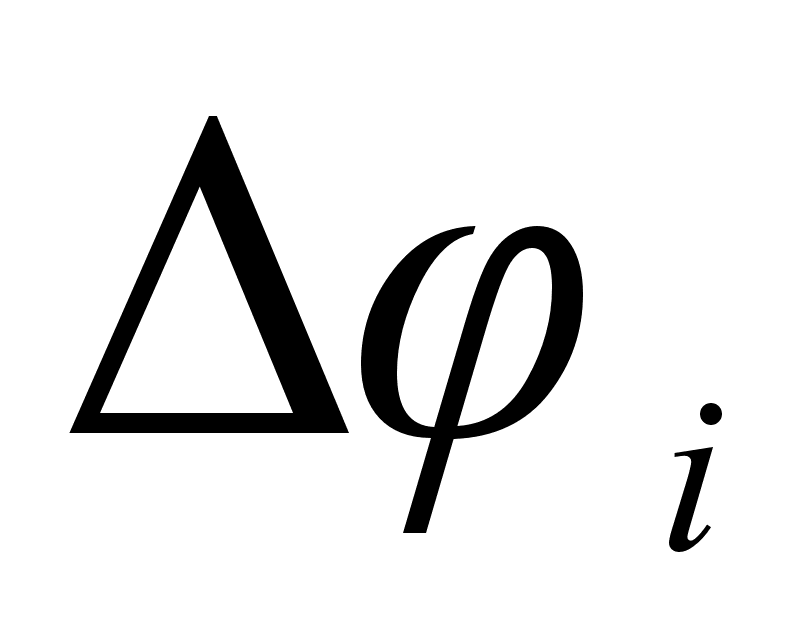 .
.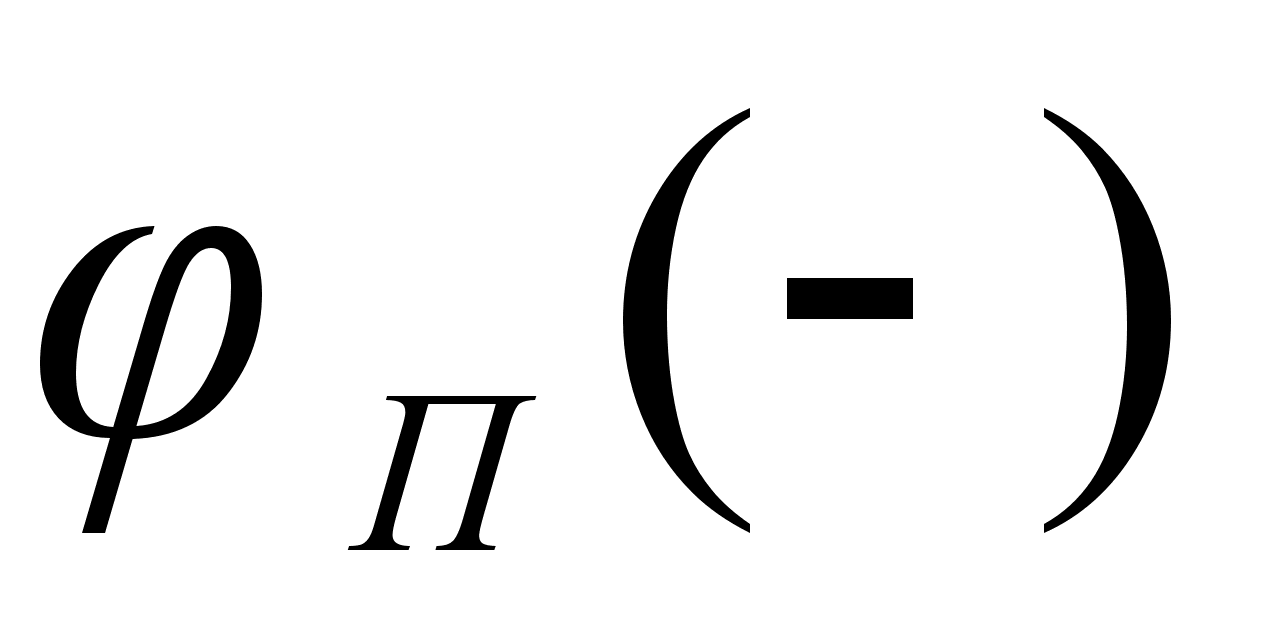
-5,0 -4,5 -4,0 -3,5 -3,0 -2,5 -2,0 -1,5 -1,0 -0, 5 0,0 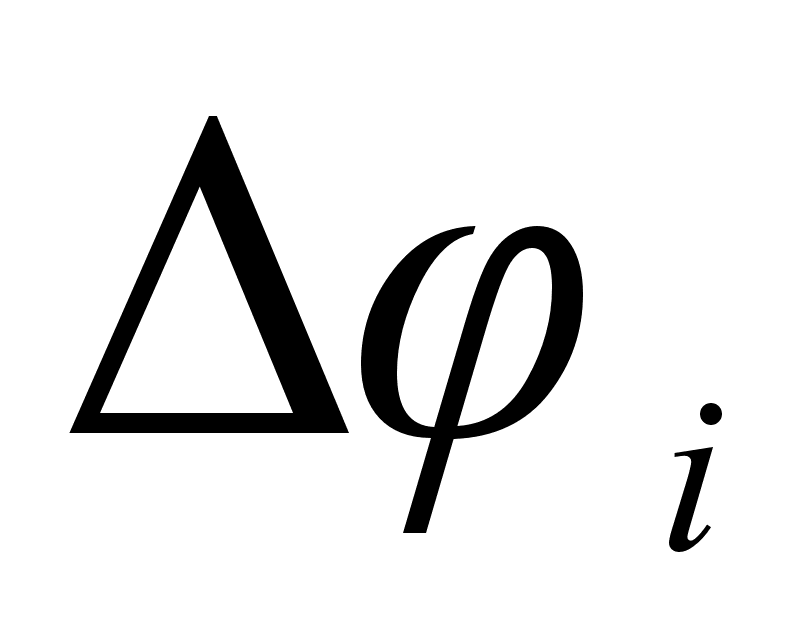
10,70 8,667 6,848 5,243 3,852 2,675 1,712 0,963 0,428 0,107 0,00 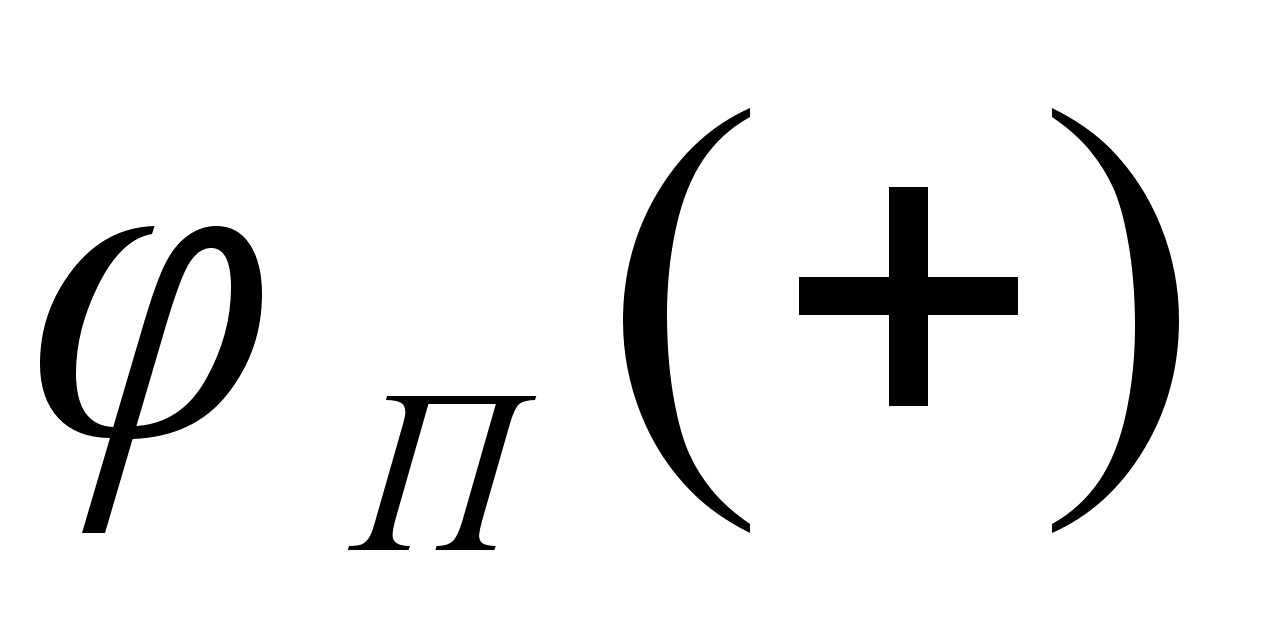
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 --- 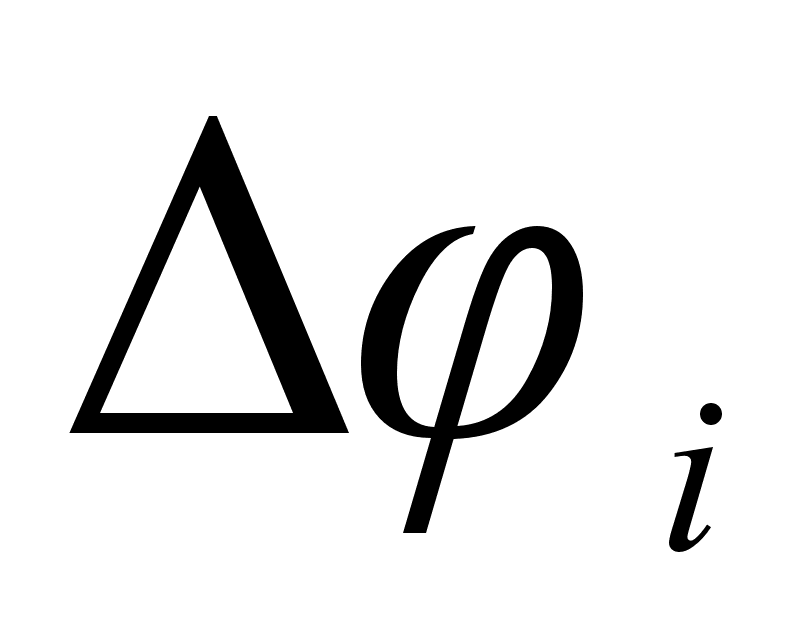
0,124 0,496 1,116 1,984 3,100 4,464 6,076 7,936 10,044 12,40 --- Значения
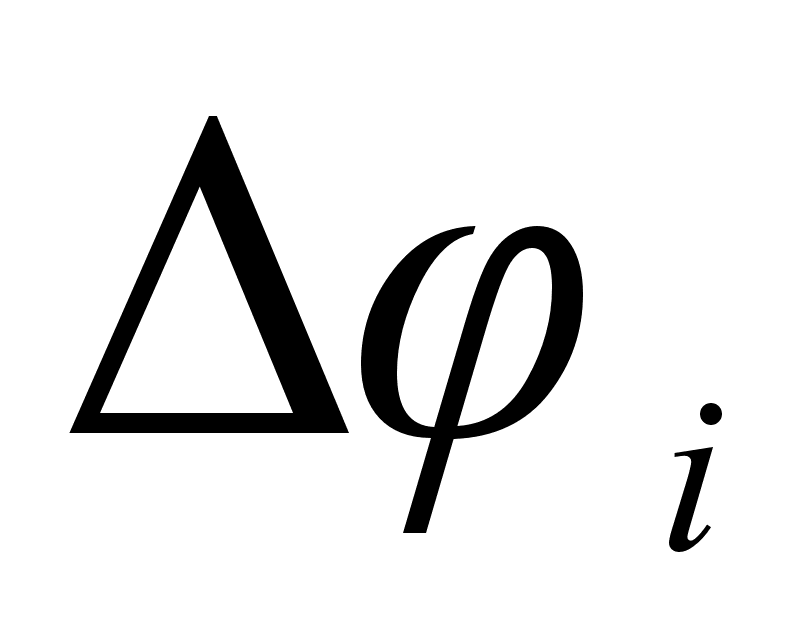 ,
приведенные
в данной таблице,
нанесены на
рисунок 57.
,
приведенные
в данной таблице,
нанесены на
рисунок 57.
Итак, в целом, по данной работе можно сделать следующие выводы:
1 – на примере систем с различными отклонениями от идеальности, нами доказана применимость уравнения (98), полученного автором работы [9], к нахождению всех термодинамических характеристик раствора, основываясь лишь на данных об активности (или какой-либо другой характеристике) одного из компонентов этой системы;
2 – опробован графический способ определения коэффициентов альфа и бета в концентрационном уравнении (98);
3 – расчеты подтверждают тот факт, что точки пересечения графиков функций
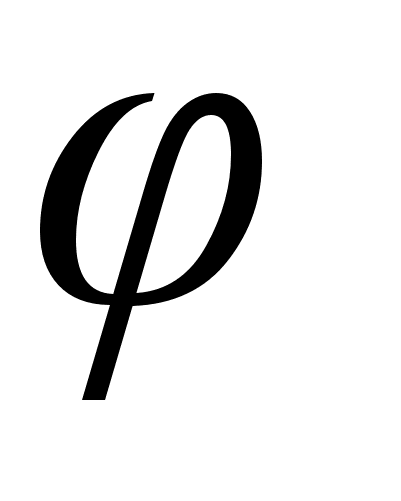 для обоих компонентов
во всех рассмотренных
нами бинарных
металлических
системах
соответствуют
концентрациям
компонентов
близким, в среднем,
к 0,245;
для обоих компонентов
во всех рассмотренных
нами бинарных
металлических
системах
соответствуют
концентрациям
компонентов
близким, в среднем,
к 0,245;4 – нами показано, что экспериментальные данные в виде точек в координатной плоскости
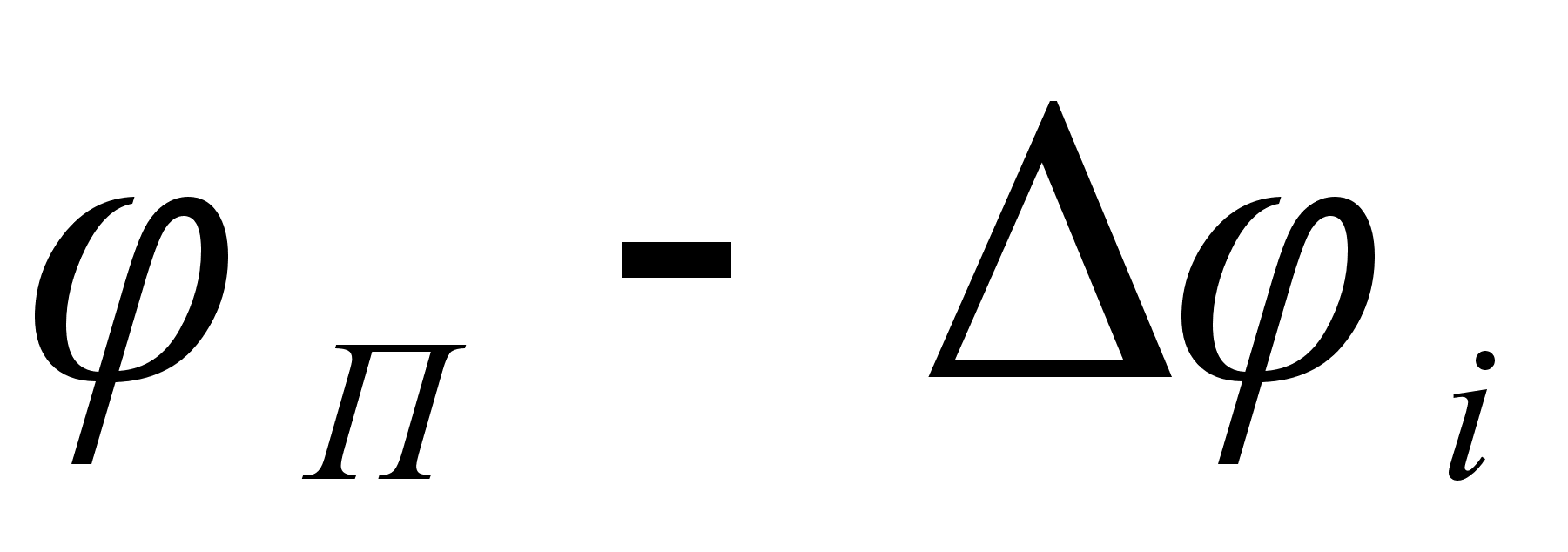 ложатся на
кривую, описываемую
уравнением
параболы второй
степени. Однако,
как видно из
рисунка 57, знакопеременная
система W
– Pd
(точка 4) не описывается
ни уравнением
(135), ни (136). Причины
этого нам пока
не ясны. Вероятно,
это результат
недостаточной
корректности
исходных данных.
ложатся на
кривую, описываемую
уравнением
параболы второй
степени. Однако,
как видно из
рисунка 57, знакопеременная
система W
– Pd
(точка 4) не описывается
ни уравнением
(135), ни (136). Причины
этого нам пока
не ясны. Вероятно,
это результат
недостаточной
корректности
исходных данных.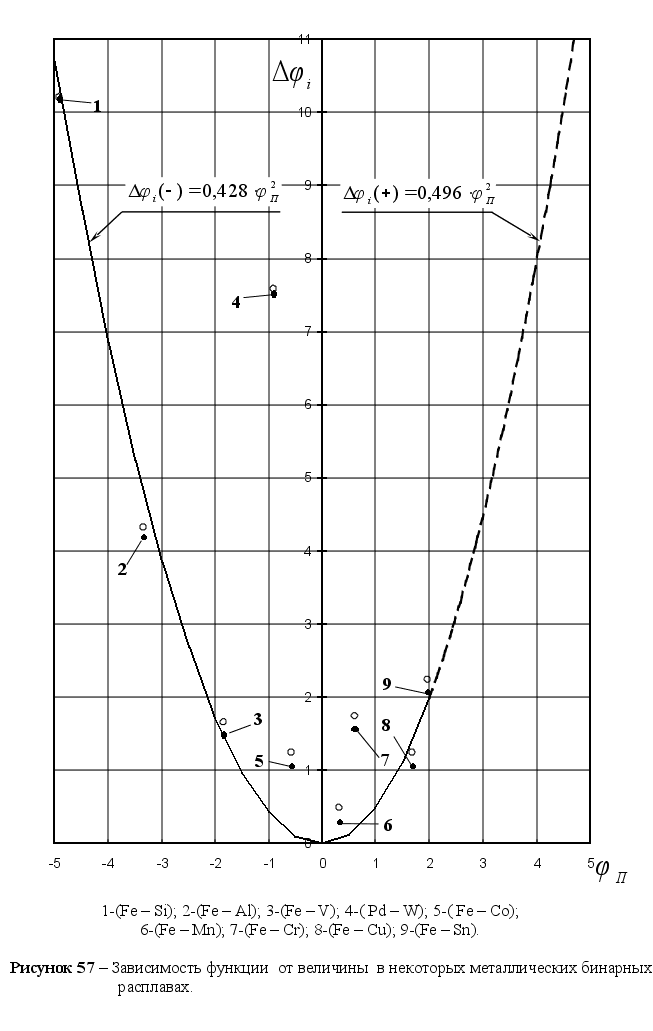
Государственный комитет Российской Федерации по высшему образованию
Сибирский государственный индустриальный университет
Факультет электротермических технологий
Кафедра электрометаллургии стали и ферросплавов
Бородин И.С. Термодинамические характеристики расплавов на основе железа: дипломная работа по специальности «Металлургия черных металлов» (110100), специализации «Электрометаллургия стали и ферросплавов» (110103). Новокузнецк, 2000. – 124 с. табл. 64, ил.57, источников 32, чертежей 10 листов.
Проведен подробный термодинамический анализ компонентов бинарных металлических растворов с различными отклонениями от закона Рауля, основанный на использовании концентрационных уравнений.
Опробован графический способ определения коэффициентов альфа и бета в указанных выше уравнениях, связывающих термодинамические функции компонентов раствора с их концентрацией.
На основании рассмотренных растворов выявлены некоторые закономерности, являющиеся справедливыми для всех бинарных металлических систем.
Исполнитель ___________________ Бородин И.С.
ANNOTATION
Borodin I.S. The thermodynamic characteristics molten solutions on the basis of iron: degree work on a speciality " Metallurgy of ferrous metals " (110100), specialization " Electrometallurgy of steel and ferroalloys " (110103). Novokuznetsk, 2000. - 124 p., Tab. 64, ill. 57, sources 32, drawings 10 of sheets.
The detailed thermodynamic analysis of components of binary metal molten solutions with various deviations from the Raul`s law, based on use of the concentration equations is carried out.
The graphic way of definition of factors alpha and beta in the mentioned above equations connecting thermodynamic functions of components of a solution to their concentration is tested.
On the basis of the considered solutions some laws being fair for all binary metal systems are revealed.
The executor____________________ Borodin I.S.
СОДЕРЖАНИЕ Введение _______________________________________________ 7 1 Термодинамика растворов 1.1 Основные понятия ____________________________________ 8 1.2 Растворы ____________________________________________ 13 2 Концентрационные уравнения для бинарных растворов с полной взаимной растворимостью 2.1 Вывод концентрационных уравнений ____________________ 31 2.2 Функция ___________________________________________
34 3 Определение коэффициентов альфа и бета 3.1 Математический метод ________________________________ 37 3.2 Графический метод ___________________________________ 39 4 Использование метода наименьших квадратов при расчете функции
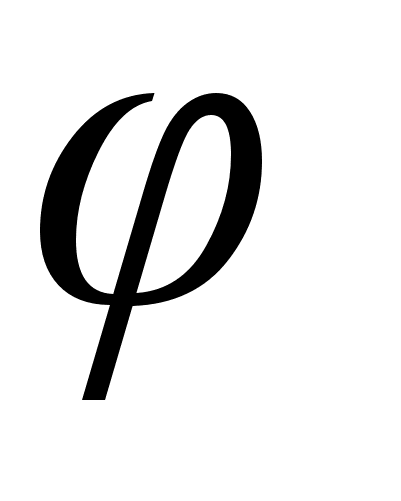 ______________________________________________
______________________________________________44 5 Подробный анализ применимости концентрационных уравнений для описания реальных систем с различным характером отклонений от закона Рауля 5.1 Подробный анализ системы Fe – Cu _____________________ 46 5.2 Подробный анализ системы Fe – Si ______________________ 51 5.3 Подробный анализ системы W – Pd ______________________ 69 6 Системы с различным отклонением от идеальности 6.1 Системы с положительным отклонением от идеальности ____ 78 6.2 Системы с отрицательным отклонением от идеальности ____ 95 7 Обобщение результатов анализа, выводы _____________________ 112 Список использованных источников ________________________ 122
ВВЕДЕНИЕ
Вопросы теории растворов занимают важное место в термодинамике. Образование растворов существенно изменяет условия протекания химических реакций. Как и в природе, так и в технике постоянно приходится иметь дело с растворами, а не с чистыми веществами.
Химически чистые вещества представляют собой лишь предельное состояние, которое никогда в действительности не достигается. Получаемое в современной технике методами вакуумной и зонной плавок чистейшие металлы все же содержат ничтожные количества (10-6 %) примесей, главным образом металлоидов, и по существу являются растворами. [1]
Самое чистое железо, которое может быть получено в настоящее время, содержит примесей до нескольких тысячных долей процента. Можно считать, что основная разница между бессемеровской сталью и сталью, выплавленной в мартеновской печи, заключается в наличии в первой около 0,01% азота, влиянием которого на свойства стали нельзя пренебрегать. [2]
Химические реакции при выплавке чугуна и стали происходят в растворах. В доменных и сталеплавильных печах жидкие чугун и сталь взаимодействуют со шлаком – раствором окислов. [1]
Задача термодинамической теории расплавов состоит в том, чтобы связать различные свойства растворов и найти способы предсказания свойств растворов, исходя из свойств чистых компонентов. Однако, настоящее время, рассчитать изменение термодинамических функций в процессе сплавообразования, исходя из свойств исходных компонентов, не представляется возможным. Основным источником информации является экспериментальное исследование. [3]
В данной дипломной работе рассмотрена возможность расчета, на основании экспериментальных данных о концентрационной зависимости одной из термодинамических характеристик компонента, изменения остальных его свойств.
124
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Жуховицкий А.А., Шварцман Л.А. – Физическая химия. Издание 4-е, переработанное и дополненное. М.:Металлургия. 1987 г. – 542 с.
2 Даркен Л.С., Гурри Р.В. Физическая химия металлов: Пер. с англ., Н.Н. Сироты. – М.: Металлургиздат. 1960. – 582 с.
3 МорачевскийА.Г. Термодинамика расплавленных металлических и солевых систем. М.:Металлургия. 1987 г. – 239 с.
4 Глинка Н.Л. Общая химия: учебное пособие для вузов. – 25 издание исправленное/ под редакцией В.А.Рабиновича. Л.:Химия. 1986 г. – 704 с.
5 Казачков Е.А. Расчеты по теории металлургических процессов: учебное пособие для вузов. – М.:Металлургия. 1988 г. – 288 с.
6 Григорян В.А., Белянчиков Л.Н., Стомахин А.Я. Теоретические основы электросталеплавильных процессов. Издание 2-е, переработанное и дополненное. М.:Металлургия. 1987 г. – 272 с.
8 Морачевский А.Г., Сладков И.Б. Термодинамические расчеты в металлургии. Справочник. М.:Металлургия. 1985 г. – 356 с.
9 Воробьев А.А. Связь термодинамических функций с концентрацией компонентов в бинарных металлических расплавах. // Металлургия на пороге XXI века: достижения и прогнозы. Материалы Всероссийской научно-практической конференции. – Новокузнецк. 1999. с. 89 – 91.
10 Физико-химические методы исследования металлургических процессов. / П.П. Арсентьев, В.В. Яковлев, М.Г. Крашенинников и др. – М.: Металлургия, 1988. – 509 с.
11 Новохватский И.А., Еремина М.И., Белова Б.Ф. Определение активностей компонентов в бинарных металлических сплавах по растворимости в них газов. // ЖФХ. 1975. 49. № 3. С. 628 – 630.
12 Петрушевский М.С., Гельд Р.В. к расчету термодинамических характеристик железокремнистых расплавов.// Изв. вузов. Черная металлургия. 1969 г. №6. с.31 – 35.
13 Turdogan E.T., Yrieveson P. and Beisler J.F. Kinetic and Equilibrium Considerations for silicon reaction between silicate melts and graphite – saturated. Yron part 1: Reaction equilibrium // Transaction of the metallurgical society of AUME. 1963. v. 227. №6. p.1258 – 1265.
14 Срывалин И.Т., Есин О.А. Применение квазихимического метода к жидким железокремниевым сплавом // Изв. вузов. Черная металлургия. 1963 г. №5 с. 5 – 9.
15 Судавцова В.С., Баталин Г.И. Термодинамические свойства жидких сплавов эелеза с кремнием // Термодинамические свойства жидких сплавов. – Баку. ЭЛМ. 1975 с.151 – 154.
16 Nowakowski Jersy. Wspolczynniki aktywnosci skladnikow niektorych roztworow zawierajacych miedz.// Zesz nauk. AYH. 1974. №434. с. 137 – 151.
17 Sanbongi K. Ohtani M. Sci rep. Ynct. Tohocu univ., 1953, AS350. Цитируется по И.Т.Срывалину и О.Е.Есину. Применение квазихимического метода к жидким железокремниевым сплавам.// Изв. вузов. Черная металлургия. 1963 г. №5. с.5 – 9.
18 Куликов И.С. Раскисление металлов. М.:Металлургия. 1975 г. – 504 с.
19 Судавцова В.С., Баталин Г.И., Ульянов В.И. Термодинамические свойства жидких сплавов железа с кремнием// Изв. АН СССР. Неорганические материалы. 1975 г. №1. с. 66 – 71.
20 Ватолин Н.А., Тимофеев А.И., Дубинин Э.А. Давление пара жидких сплавов на основе палладия.//Ж.Ф.Х. 1971. 45. №8. с.2078 – 2029.
21 Эллиот Д.Ф., Глейзер М., Рамакришна В. Термохимия сталеплавильных процессов. – М.: Металлургия, 1969. – 252 с.
22 Korber F.,Oelsen W/ Mitt. K. – W. Ynst. Eisenforch., 1936. 18. s.109 – 130.
23 Хитрик С.И., Ростовцев С.Т., Емлин Б.И. и др. Активность кремния в ферросплавах.// Изв. вузов. Черная металлургия. 1970 г. №6. с.55 – 61.
24 Судавцова В.С., Баталин Г.И., Ульянов В.И. Термодинамические свойства жидких сплавов Si c Fe //изв. АН СССР. Неорг.материалы,1975.№1 с.66–67
25 Steiler J–M., Ribound P., Onillon M. и др. Determination de l’activite thermodinamique des constituents du systeme Fe – Mn liquide par une metode d’entrainement // C.r. Acad. Sci. 1973. c.277, №22, 1207 – 1210.
26 Санбонги К., Отани М. Исследование активности сопутствующих элементов в жидком железе (III) // Тыцу то хогане. 1954. с.1106 – 1109.
27 Петрушевский М.С., Абрамычева, Гельд П.В. К термодинамике жидких растворов, характеризующихся большим отклонением от закона Рауля // Изв. вузов, черная металлургия 1973, №6, с.5 – 8.
28 Еременко В.Н., Лукашенко Г.М., Притула В.Л. Термодинамические свойства жидких сплавов олова с железом, кобальтом и никелем // Ж.Ф.Х. 1971, 45. №8, с.1993 – 1995.
29 Еременко В.Н., Лукашенко Г.М., Притула В.Л. Термодинамические свойства расплавов системы Fe – Sn.//Изв. АН СССР. Металлы. 1972, №1.с.99 – 102.
30 Баталин Г.И., Белобородова Е.А., Стукало В.А. и Гончарук Л.В. Термодинамические свойства жидких сплавов алюминия с железом // Ж.Ф.Х. 1971. №8. С.2007 – 2009.
31 Цемехман Л.Ш., Вайсбург С.Е., Широкова З.Ф. Активности компонентов в бинарных расплавах Fe – Ni, Fe – Co, Ni – Co.// Ж.Ф.Х. 1975. 45. №3, с.628 – 630.
32 Воробьев А.А. Характеристика отклонений реальных растворов от идеальности. // Металлургия на пороге XXI века: достижения и прогнозы. Материалы Всероссийской научно-практической конференции. – Новокузнецк. 1999. С. 91 – 93.
Работы, похожие на Реферат: Термодинамические характеристики расплавов на основе железаОбщая и неорганическая химия Квантово-механическая модель атома. Квантовые числа. Атомные орбитали. Порядок заполнения орбиталей электронами Теория строения атома основана на ...
По уравнению изотермы вычисляют энергию Гиббса реакции, а также определяют направление и глубину ее самопроизвольного протекания при данных условиях, если известны стандартная ...
Противоположный случай, когда парциальные давления паров компонентов оказываются меньше вычисленных - отрицательные отклоненияПричиной отклонений от закона Рауля является то ...Раздел: Рефераты по химии
Тип: учебное пособиеМеталлы и сплавы МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ Национальный аэрокосмический университет им. Н.Е. Жуковского "Харьковский авиационный институт" АВИАЦИОННОЕ ...
В момент окончания процесса кристаллизации при достаточной скорости диффузии концентрация твердого раствора должна быть равна исходной концентрации сплава.
Вторая кривая (верхняя, 882°С - Сb) определяет границу между областями (a+b) и b, а точка пересечения ее с осью абсцисс Сb соответствует минимально необходимой концентрации второго ...Раздел: Промышленность, производство
Тип: учебное пособиеОсновы химии Глава 1. Общие химические и экологические закономерности. С чего начинается химия? Cложный ли это вопрос? На него каждый ответит по-своему. В середней ...
Термодинамической системой может быть любой макро***ческий объект (тело или группа тел, находящихся во взаимодействии, клоба с раствором вещества, штатив с набором химических ...
На следующем рисунке (рис.10.1.) кривой "а" показано уменьшение концентрации исходного вещества, а кривой "б" -увеличение концентрации продукта реакции с течением времени"ѭ".Раздел: Рефераты по химии
Тип: рефератТехнология получения монокристаллического Si ... им. Баумана Физико-химические основы технологии электронных средств Реферат на тему: Технология получения монокристаллического Si Преподаватель:
В условиях термодинамического равновесия концентрация этих дефектов NШ задается уравнением
Получаемый таким образом технический кремний содержит 98 -99 % Si, 1 -2 % Fe, Аu, В, Р, Са, Cr, Cu, Mg, Mn, Ni, Ti, V, Zn и др.Раздел: Рефераты по радиоэлектронике
Тип: рефератНанесение и получение металлических покрытий химическим способом Кафедра xxx Аттестационная работа по теме: "НАНЕСЕНИЕ МЕТАЛЛИЧЕСКИХ ПОКРЫТИЙ ХИМИЧЕСКИМ СПОСОБОМ" на соискание степени бакалавра по направлению xxx ...
На рентгенограммах Со-Fe-Р-пленок, полученных из раствора с 25 % железа выявляется наличие двух фаз ѭ-Со и ѭ-Fe.
Ионы цинка меди, железа, никеля вызывают восстановление палладия во всем объеме раствора Уже при концентрации ионов цинка 0,0004г-ион/л стабильность раствора уменьшалась в семь раз ...Раздел: Промышленность, производство
Тип: дипломная работаИсследование возможности извлечения редких металлов из золы-уноса ТЭЦ ... Министерство общего и профессионального образования Российской Федерации ДИПЛОМНАЯ РАБОТА Исследование возможности извлечения редких металлов из золы ...
Возгоны промывают кислыми и щелочными растворами, эти растворы окисляют, к ним добавляют Fe(II), Fe(III), Ni, Cu или Al в виде солей в трехкратном отношении к германию и кремнию и ...
В этом объеме должно содержаться от 1 до 10 мкг железа, что соответствует концентрациям от 0,1 до 1 мг/л. Более концентрированные по содержанию железа сточные воды предварительно ...Раздел: Рефераты по технологии
Тип: рефератМетодические особенности изучения темы "Железо" на уроках ... ВВЕДЕНИЕ Железо играло и играет исключительную роль в материальной истории человечества. Первое металлическое железо, попавшее в руки человека, имело ...
Реактивы: железные опилки Fe, соль Мора (NH4)2SO4-FeSO4-6H2O, раствор хлорида железа (III) FeCl3, раствор гексационоферрата (III) калия K3[Fe(CN)6], раствор гексационоферрата (II ...
Суммы всех коэффициентов в полном и сокращенном ионных уравнениях реакции между растворами сульфата железа (II) с гидроксидом бария равныРаздел: Рефераты по педагогике
Тип: курсовая работаКоллоидная химия ВВЕДЕНИЕ Предметом физической химии является объяснение химических явлений на основе более общих законов физики. Физическая химия рассматривает две ...
Поскольку для каждой химической реакции стандартное изменение термодинамического потенциала ѬF° и ѬG° есть строго определенная величина, то произведение равновесных парциальных ...
Показатель степени при концентрации каждого из реагирующих веществ в кинетическом уравнении химической реакции (в уравнении (II.4) соответственно x, y и z) есть частный порядок ...Раздел: Рефераты по химии
Тип: учебное пособиеХимический анализ катионов ГОУ СПО "Спасский АПТ" АНАЛИТИЧЕСКАЯ ХИМИЯ (Контрольные, лабораторные и практические работы. Примерные вопросы и задания к итоговой аттестации) С ...
Пример 1. Вычислите: а) массовую долю (ѭ, %); б) молярную (С, моль/дм3), в) молярную концентрацию эквивалента (С (1/z, А)); г) моляльную (Сm) концентрации раствора Н3РО4 ...
Количество растворителя должно соответствовать концентрации раствора определяемого компонента.Раздел: Рефераты по химии
Тип: учебное пособие
-
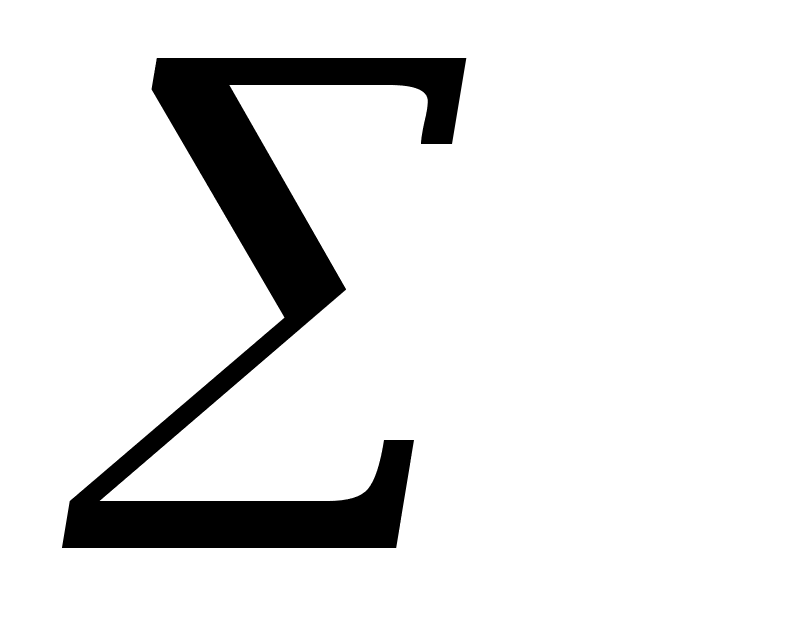
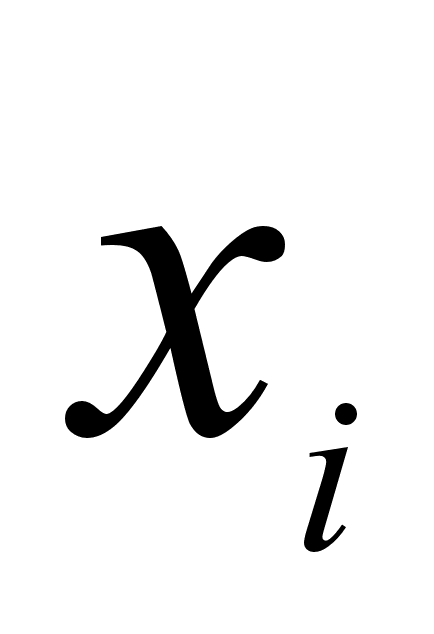
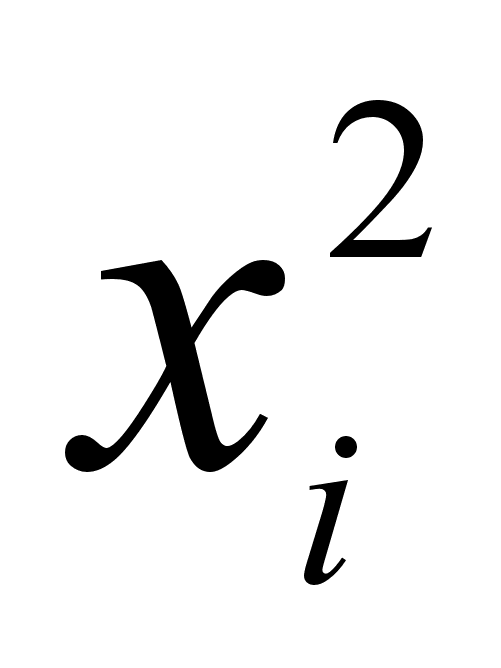
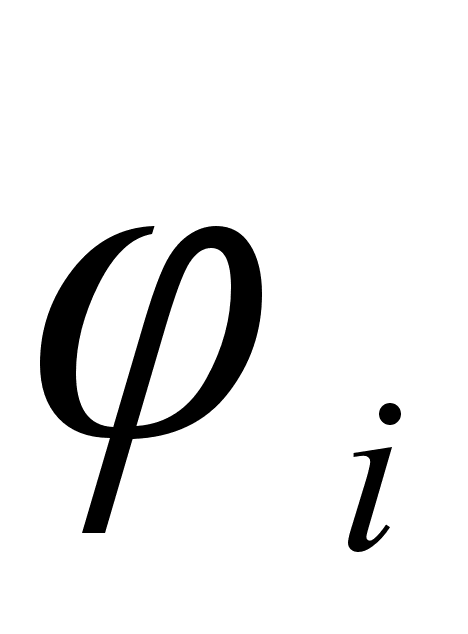
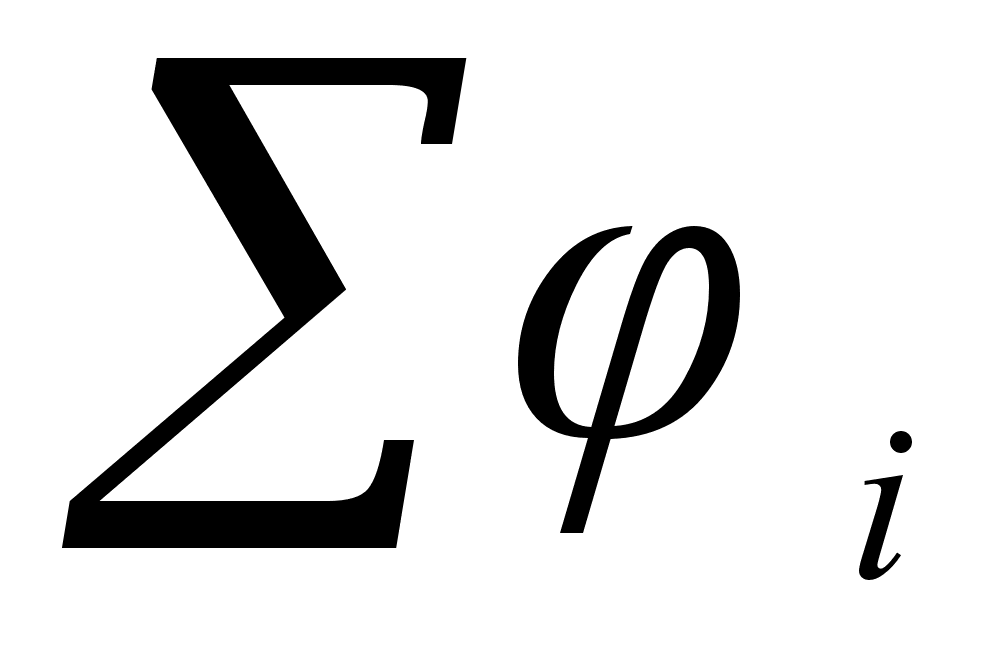
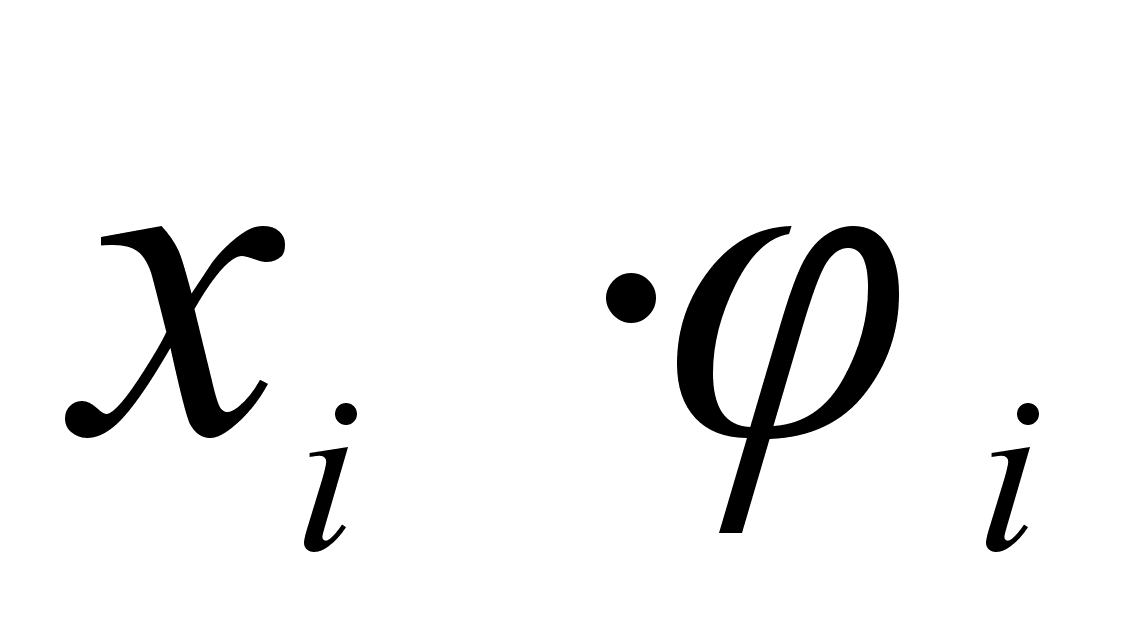
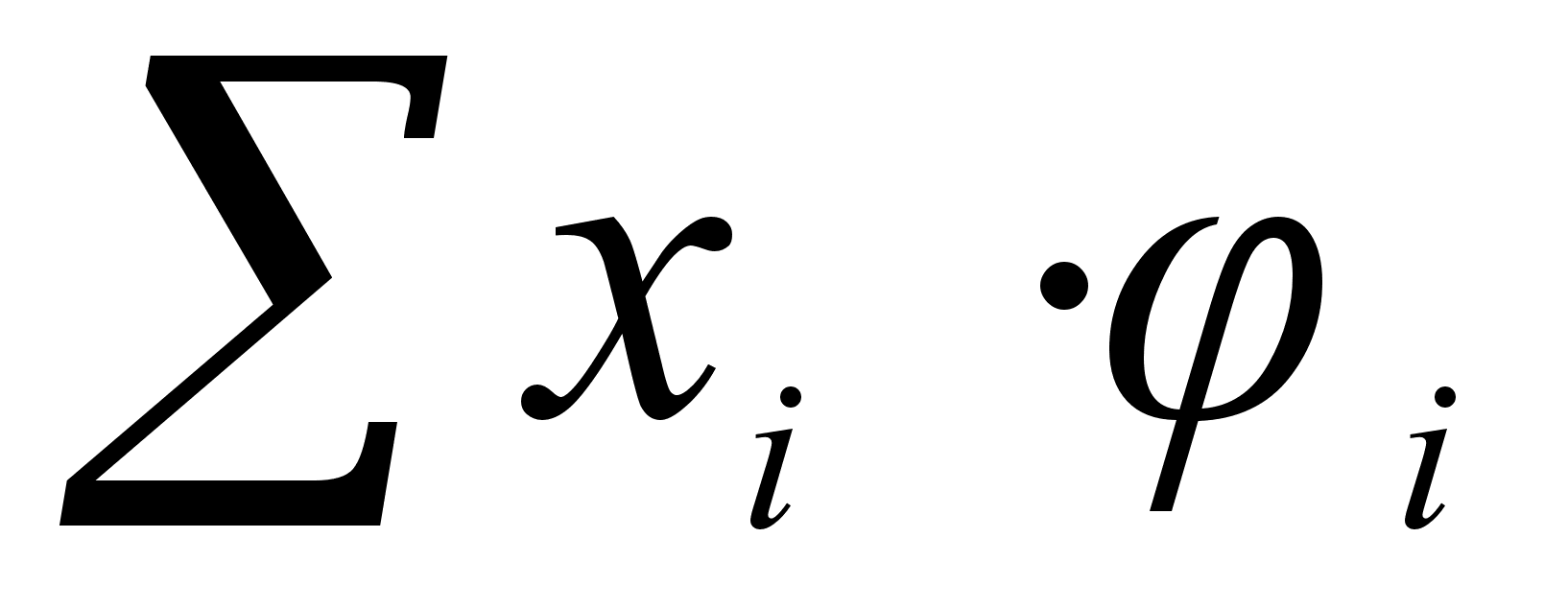
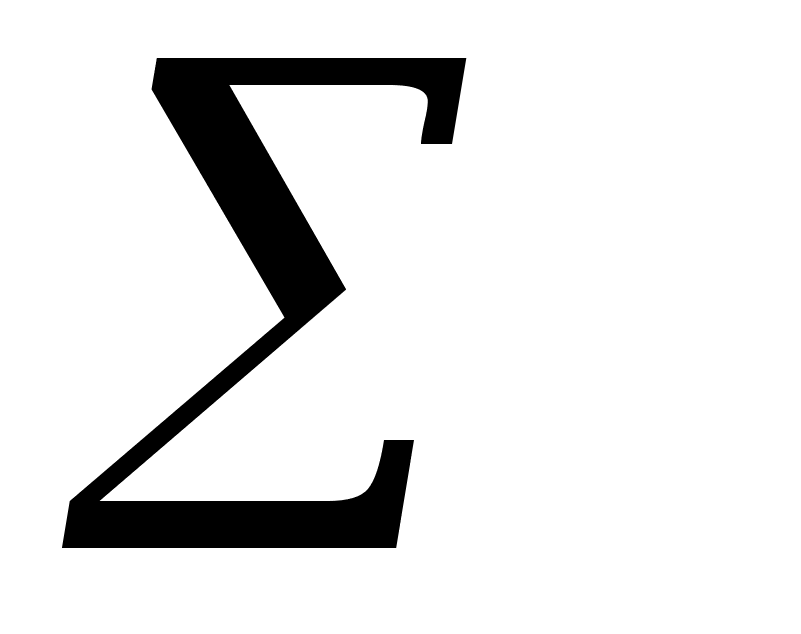
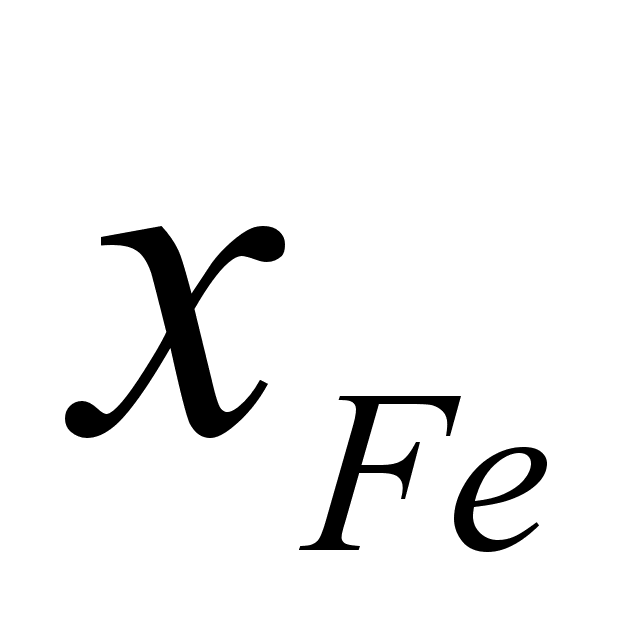
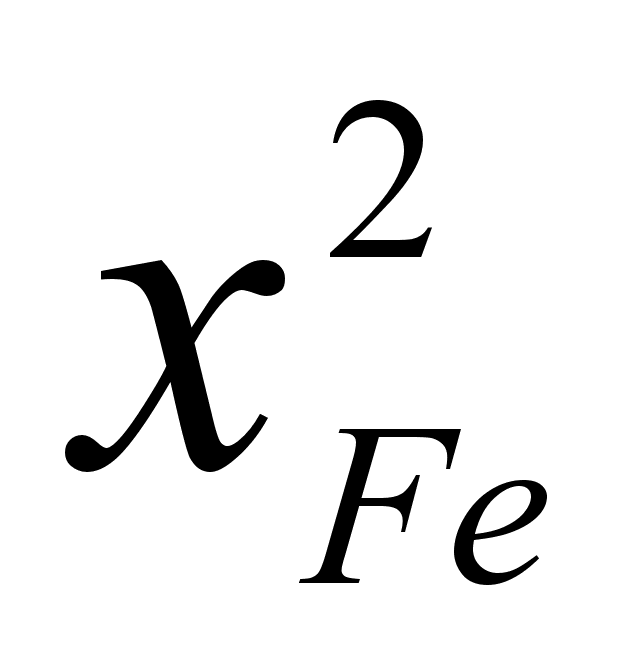
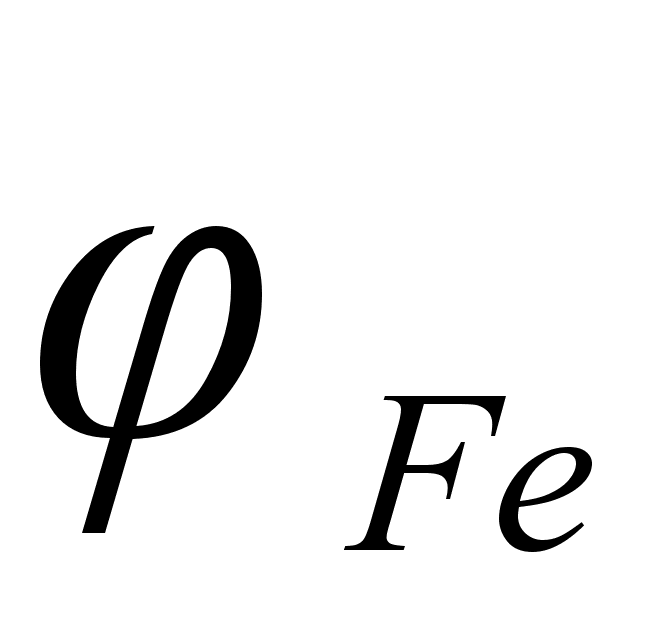
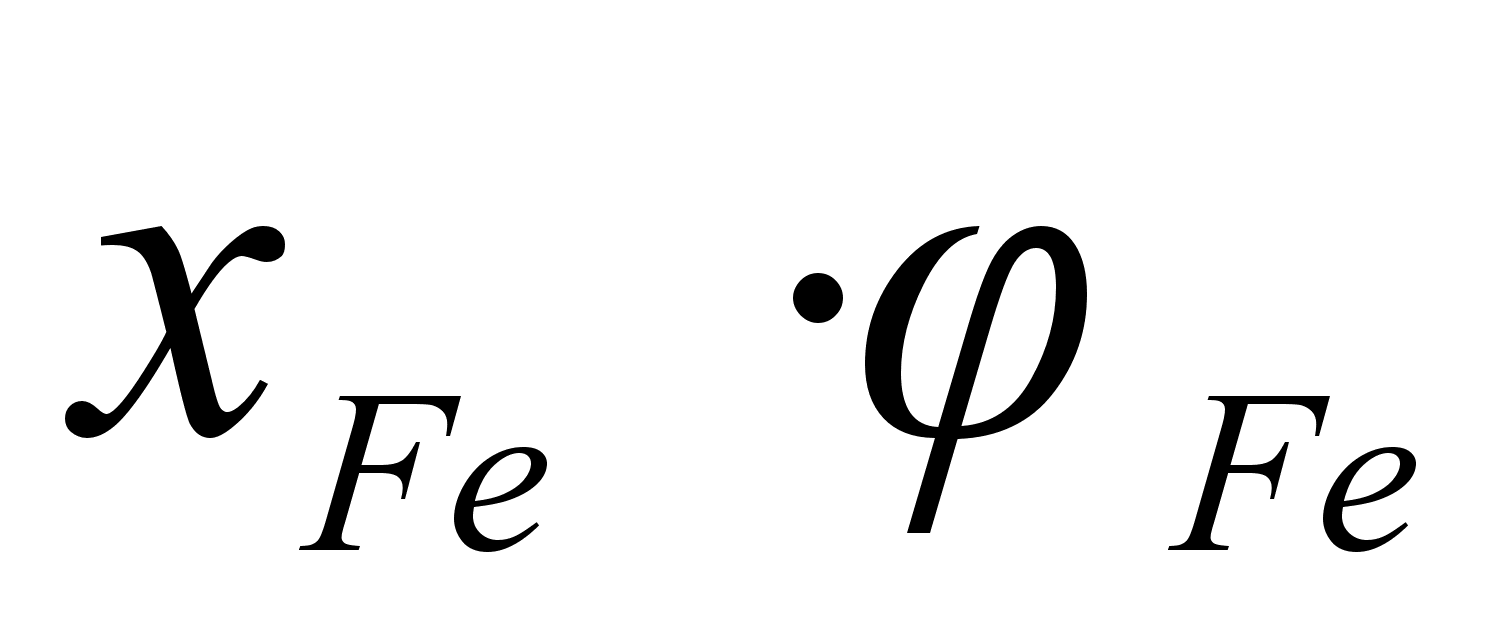
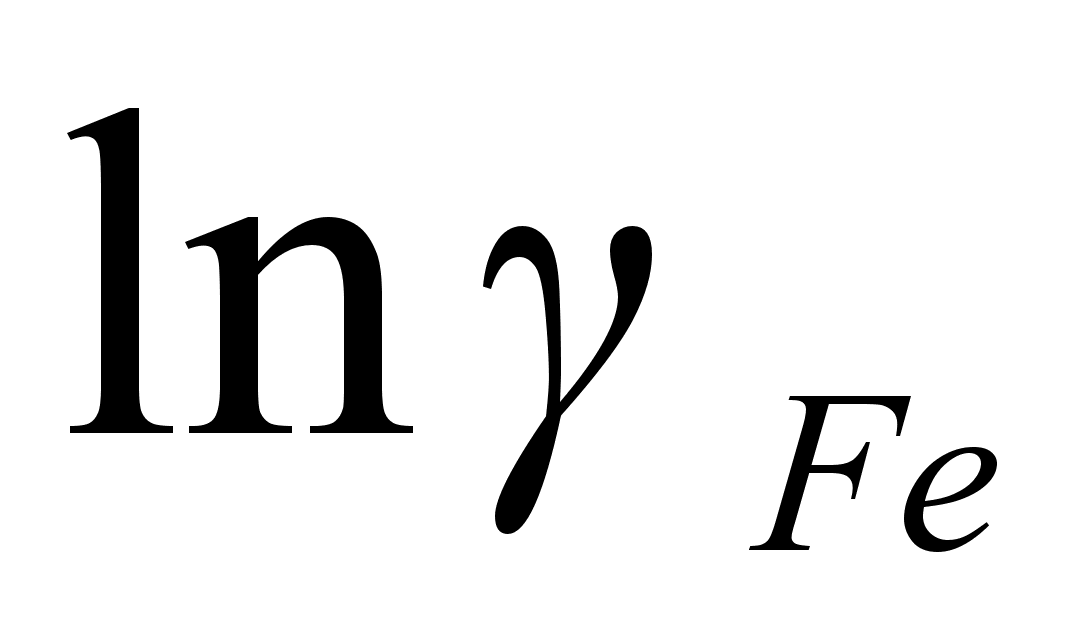
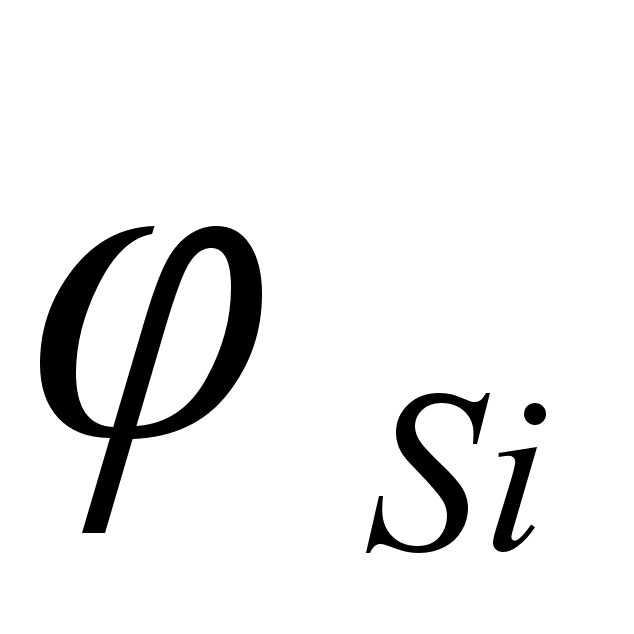
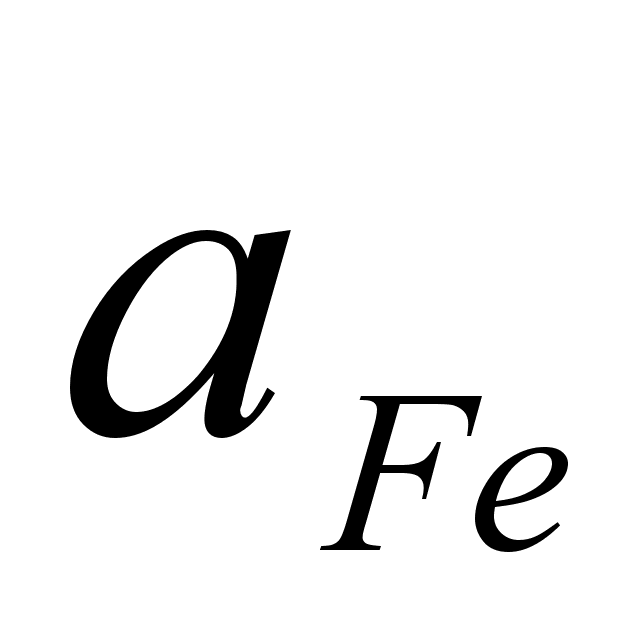
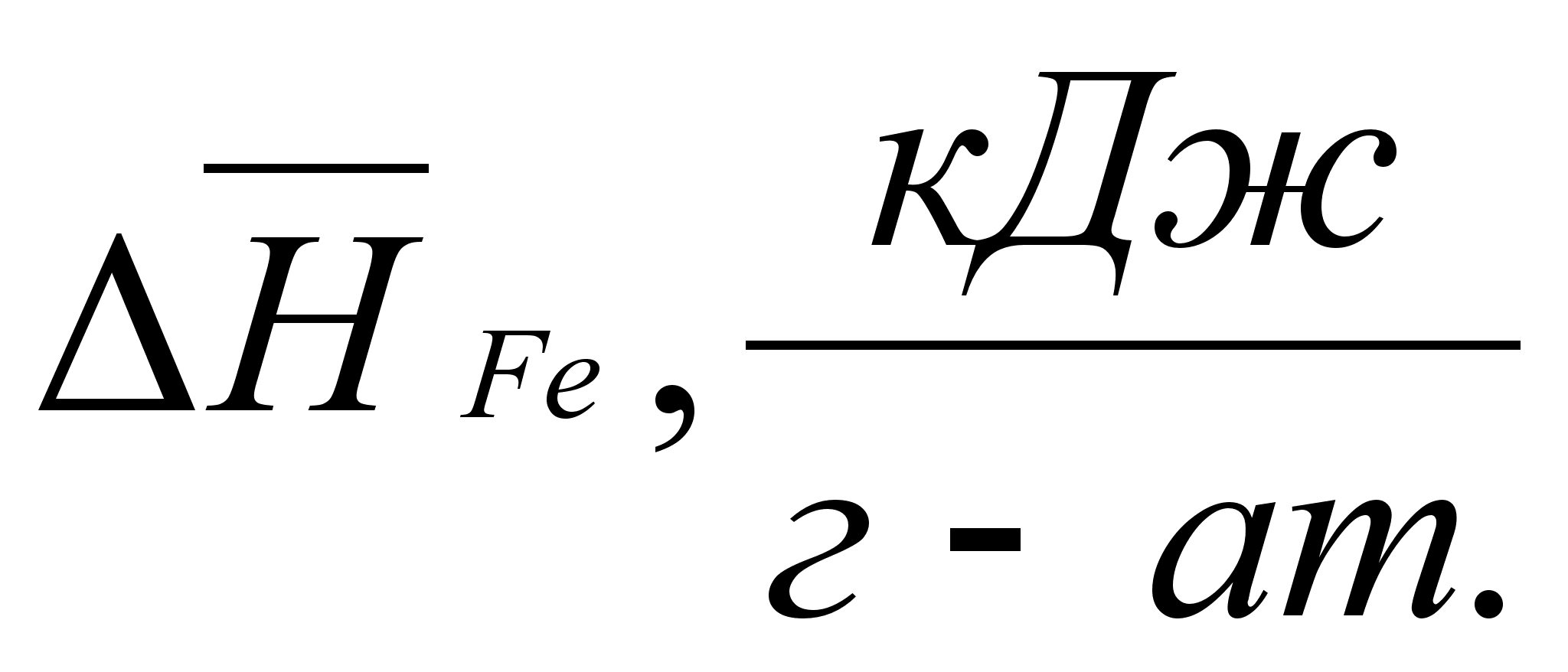
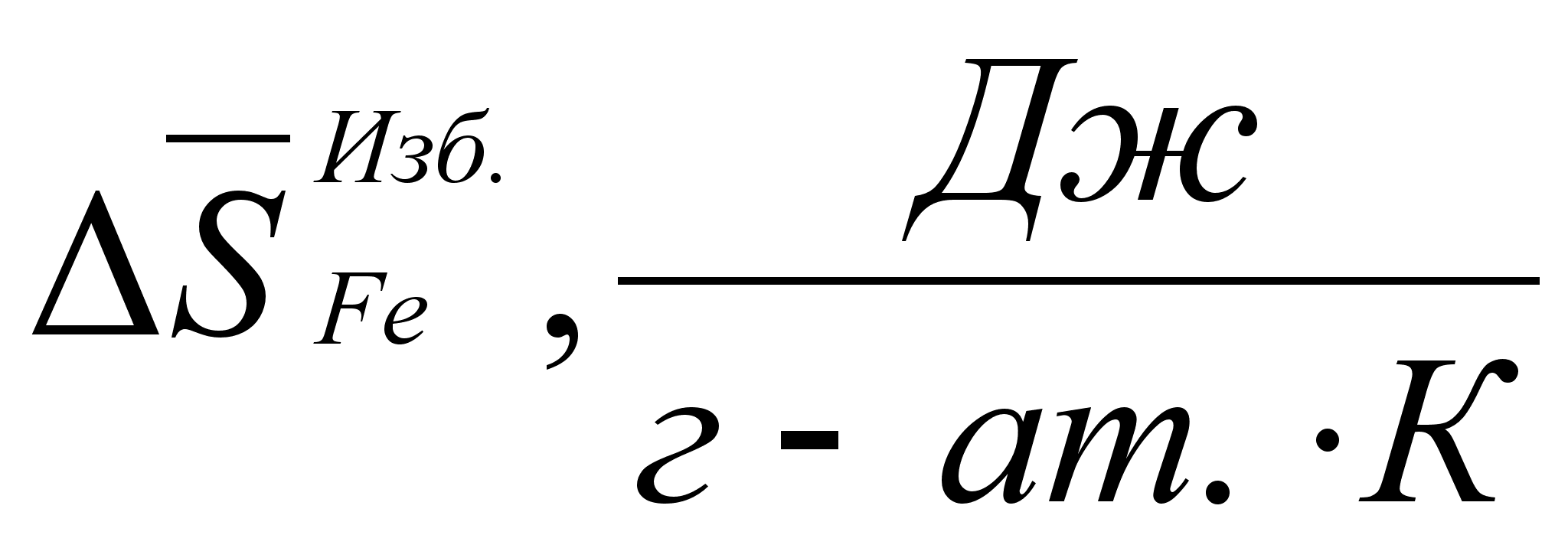
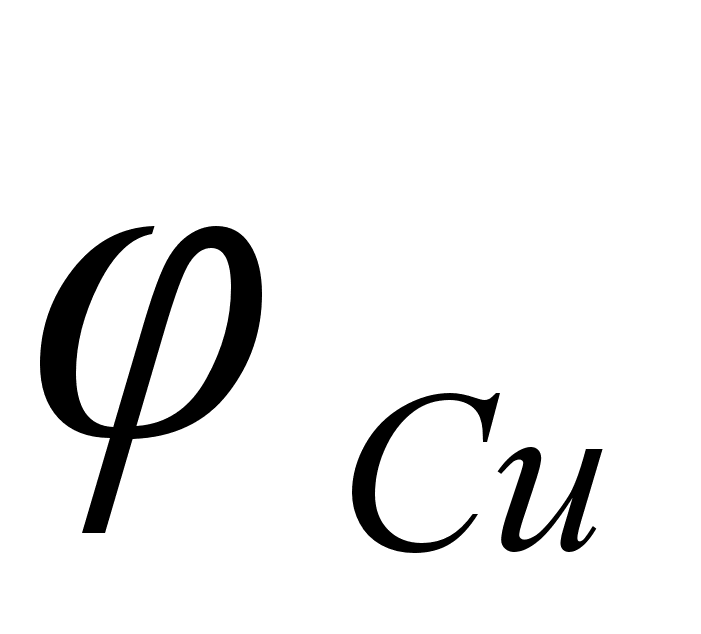
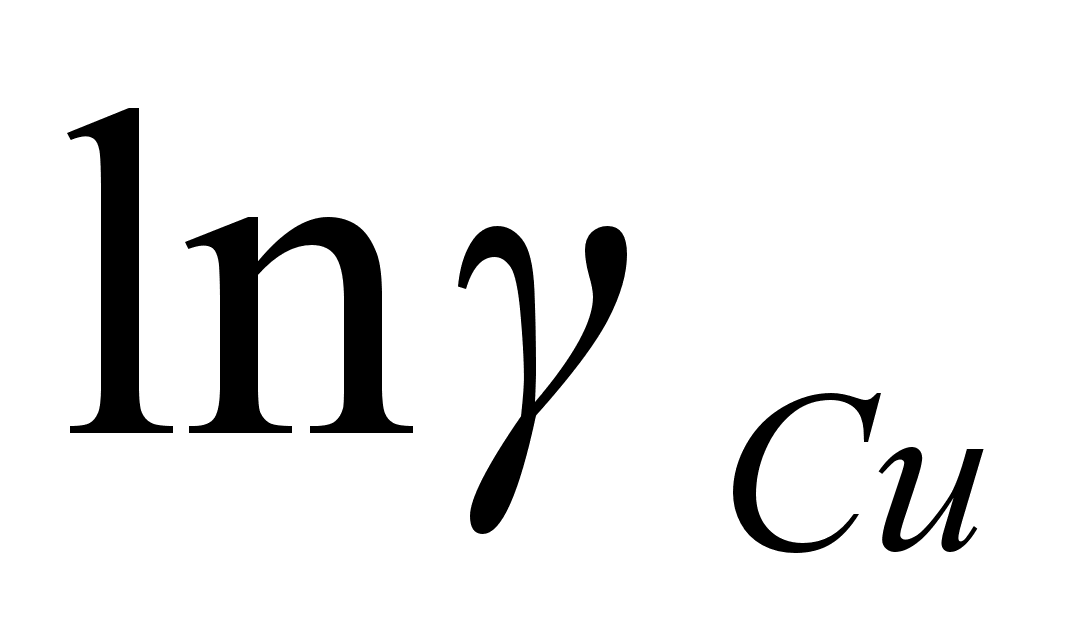
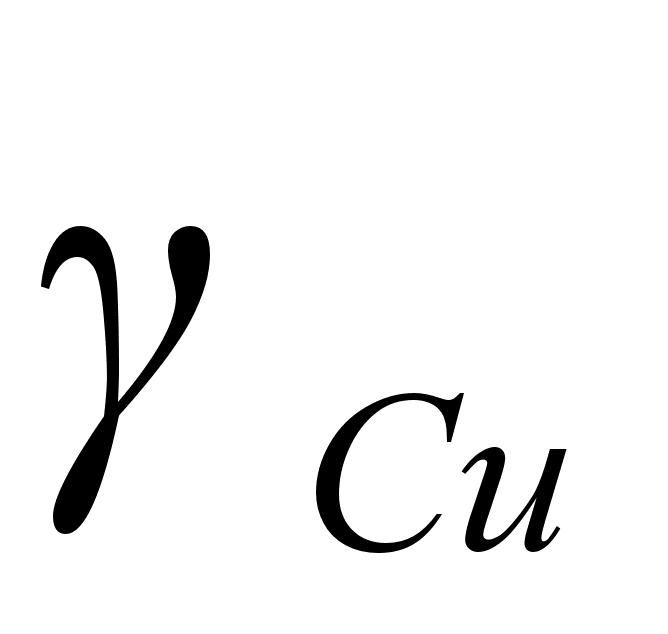
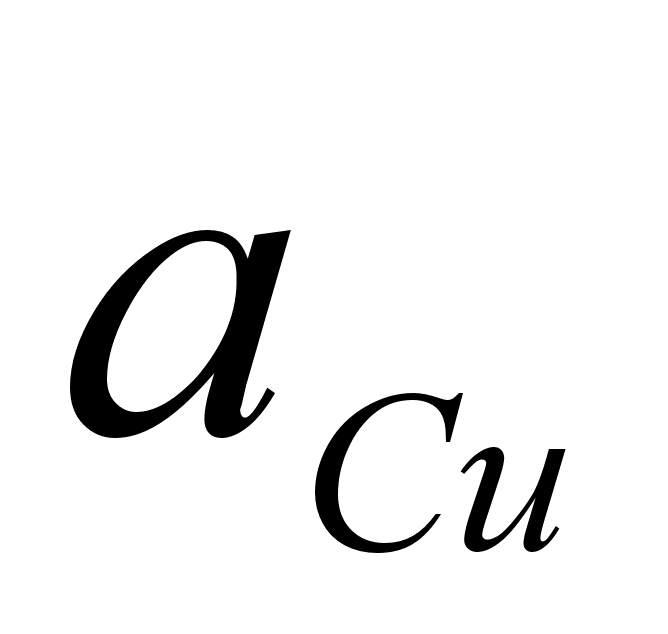
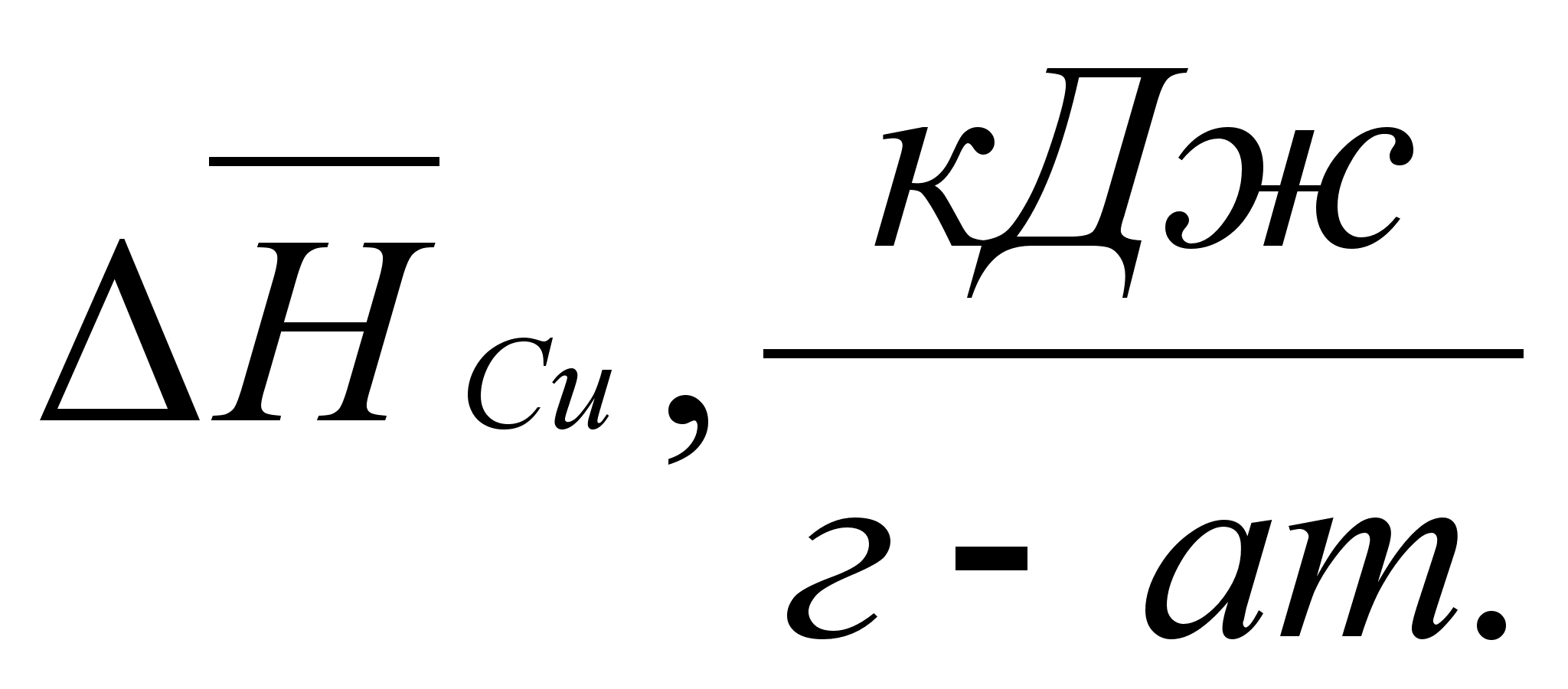
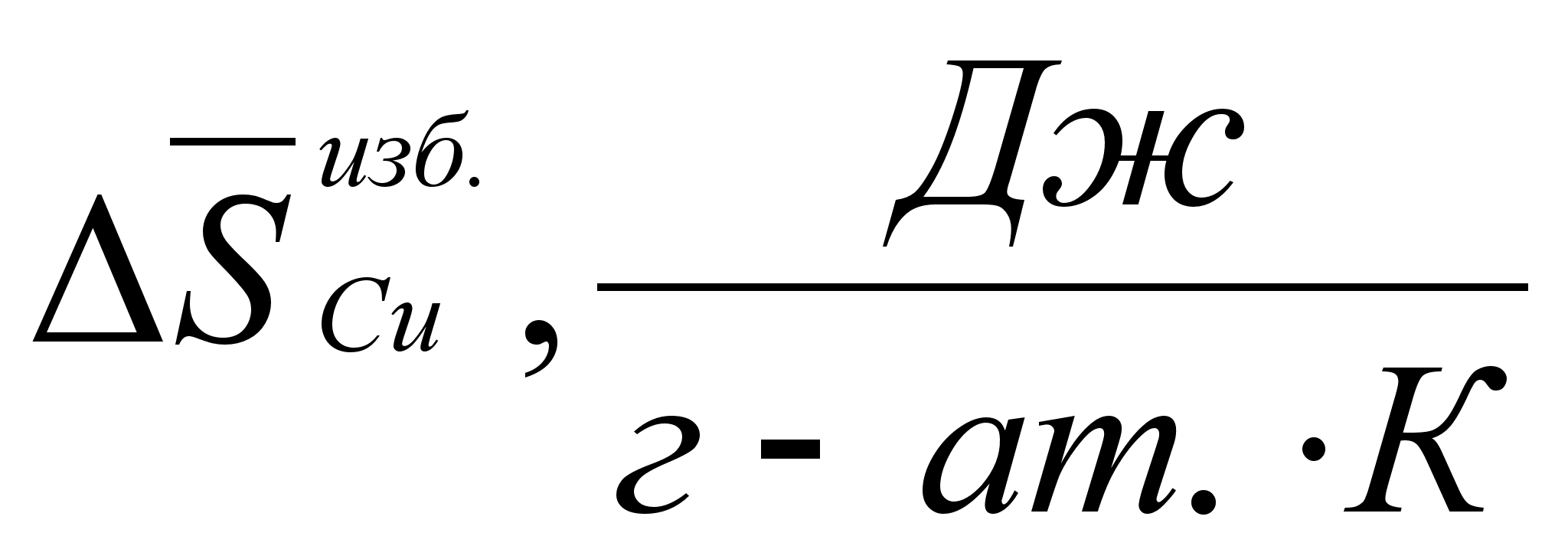
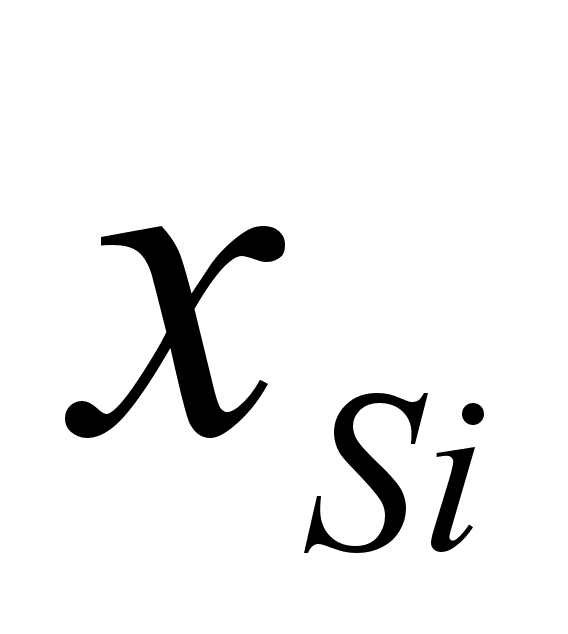
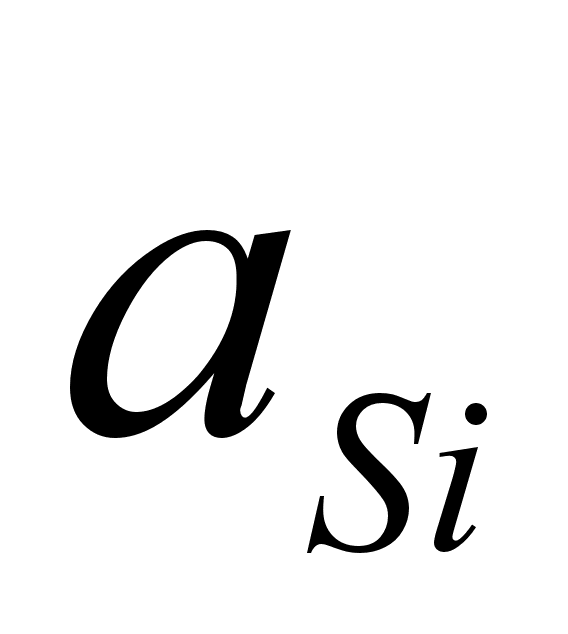
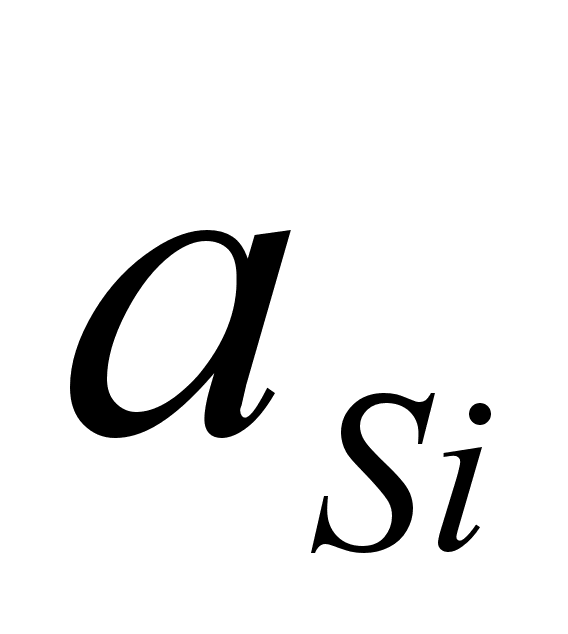
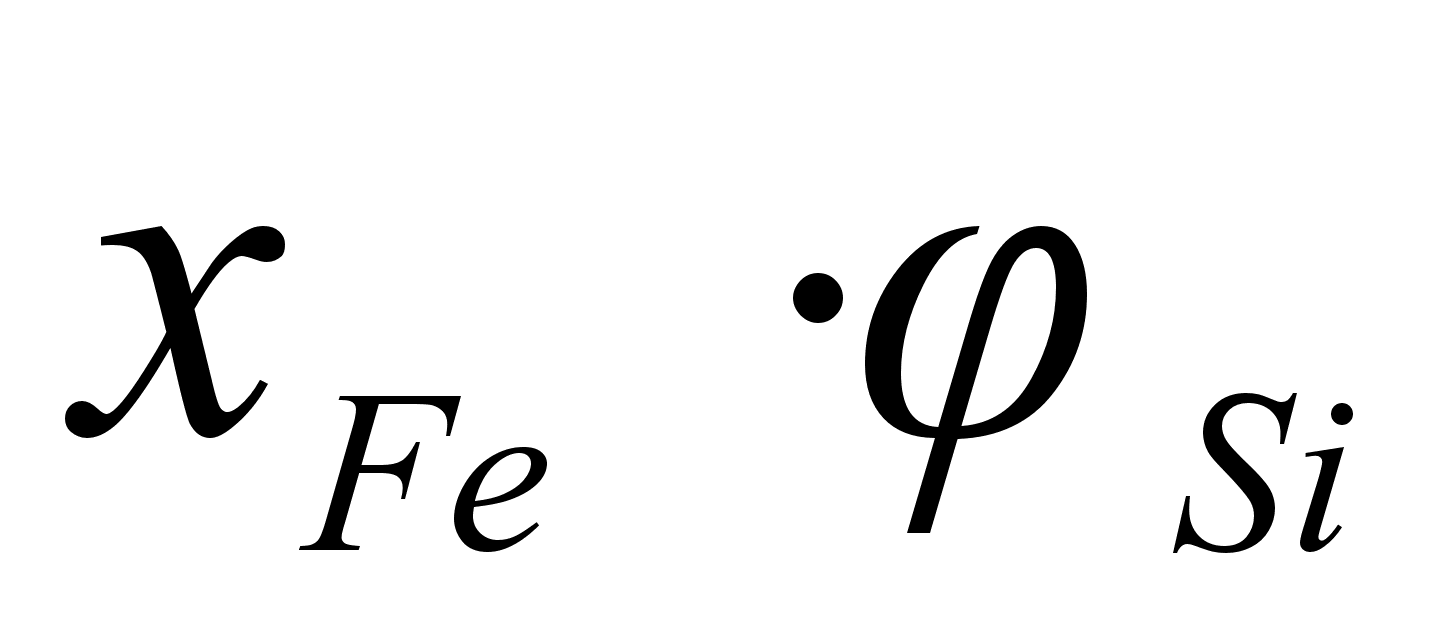
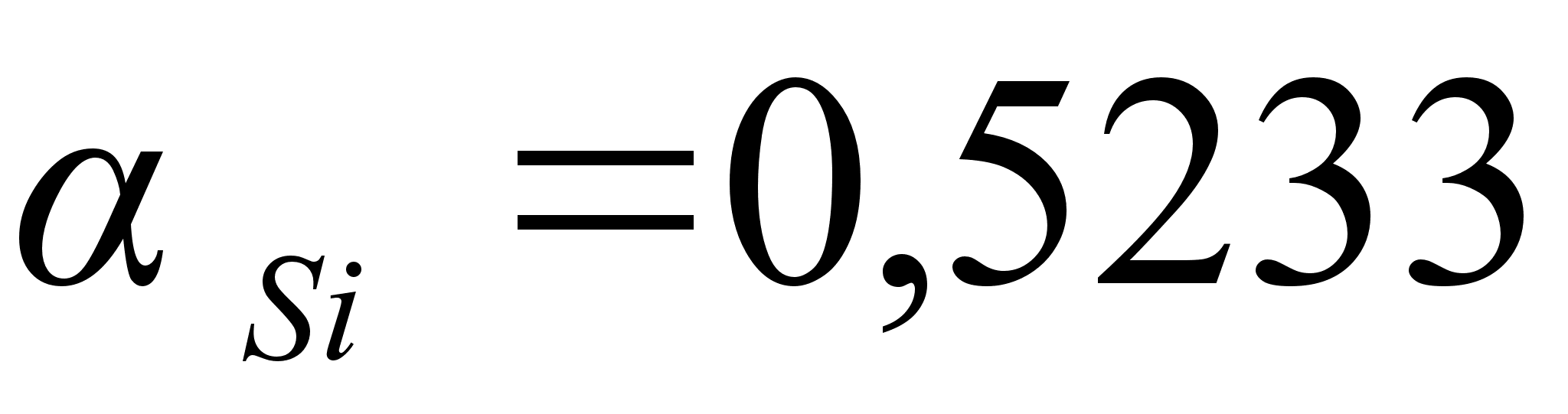
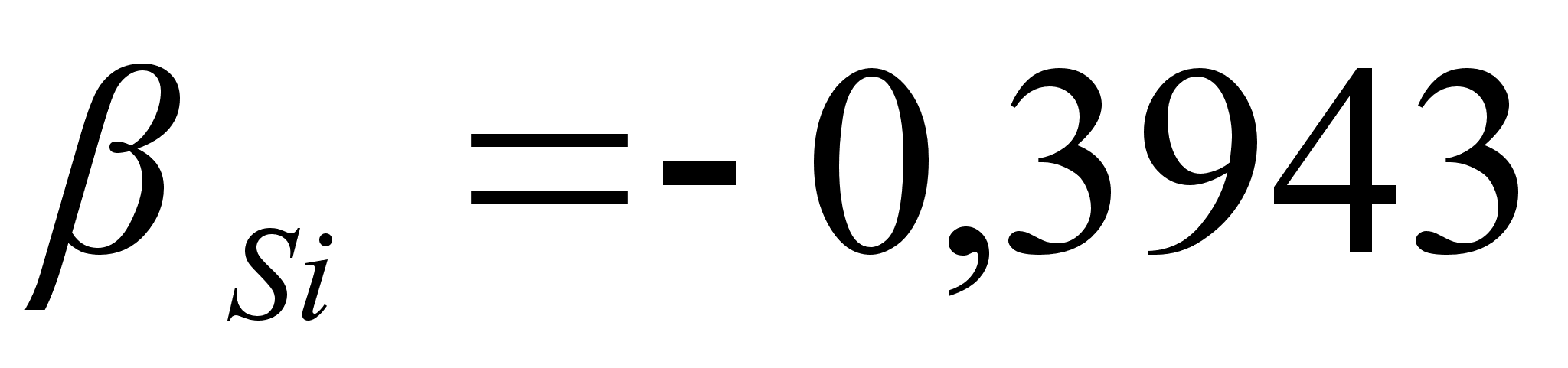
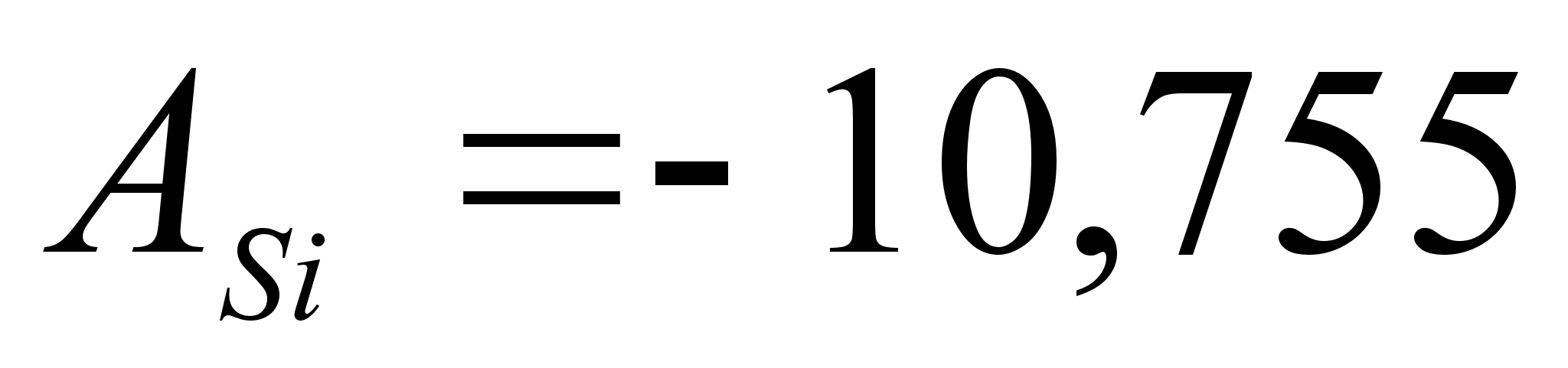
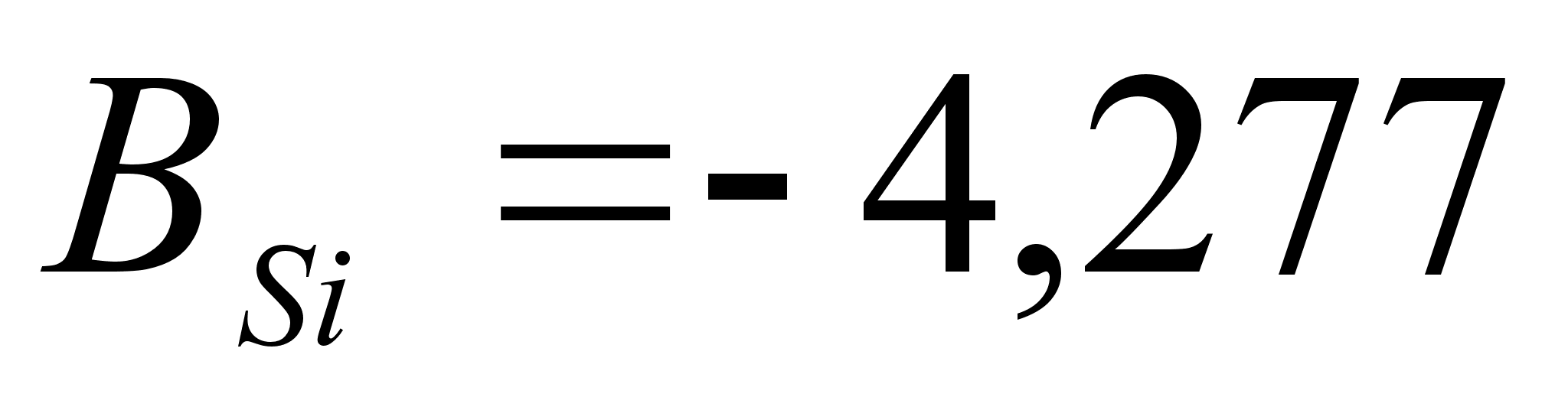
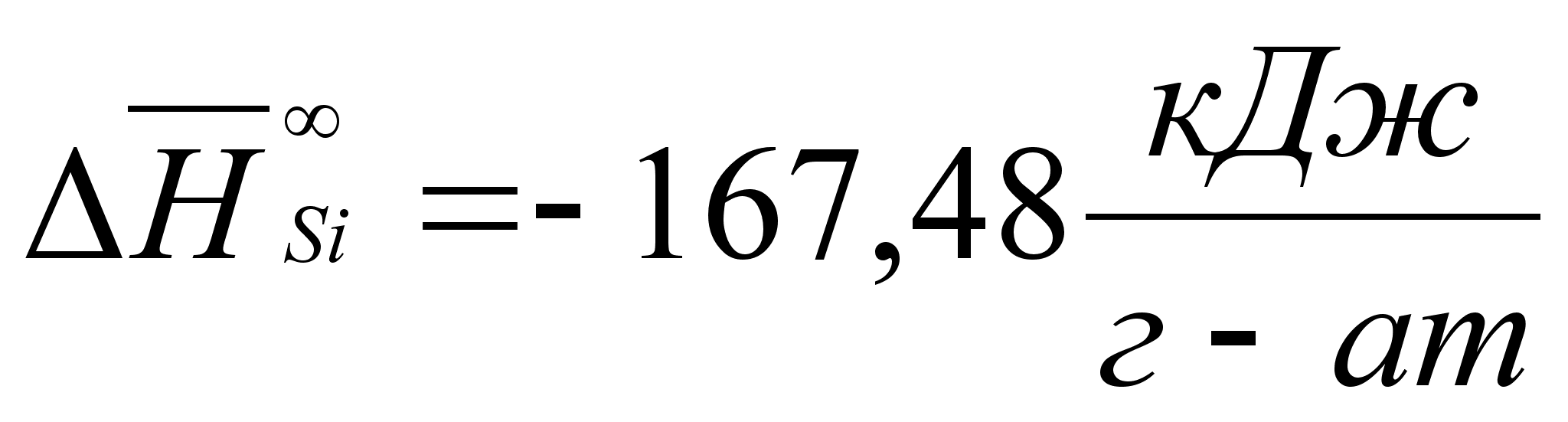
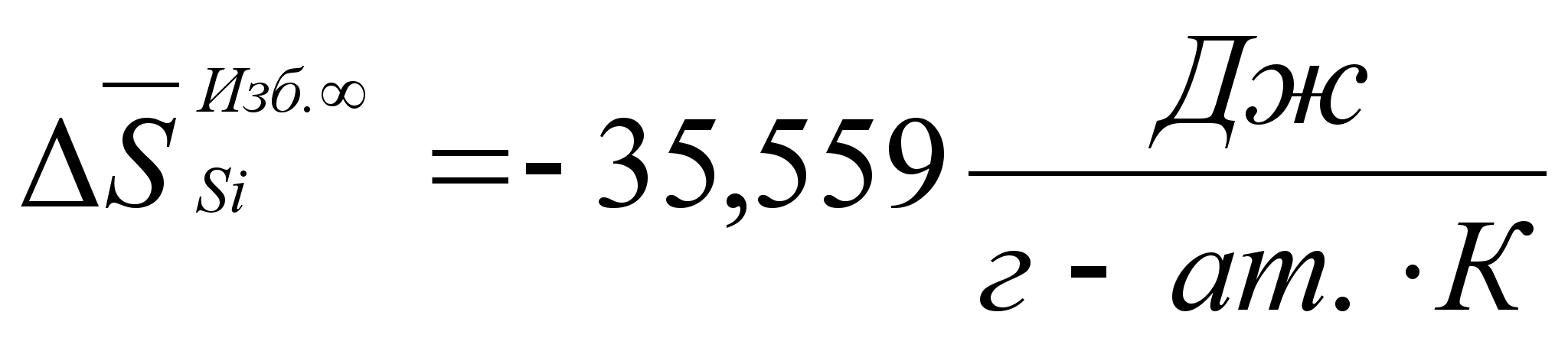
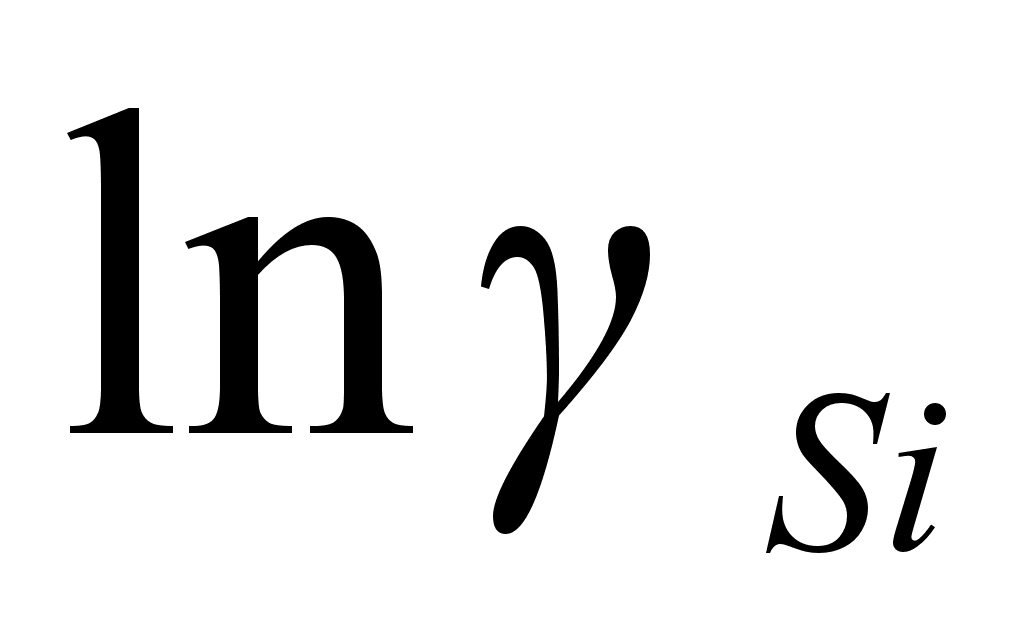
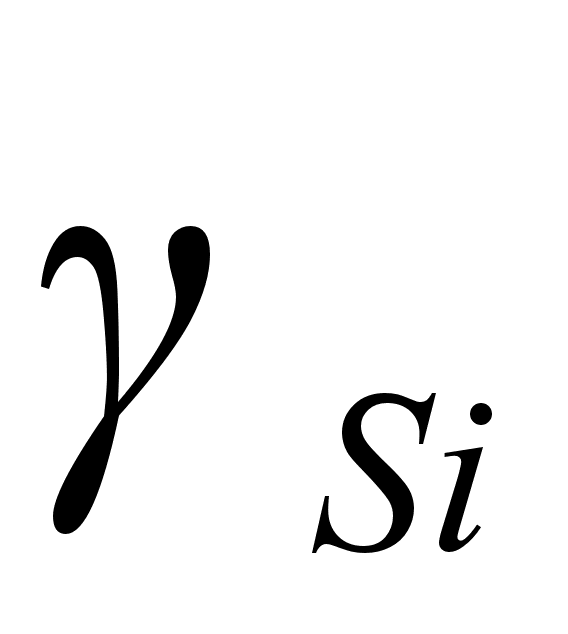
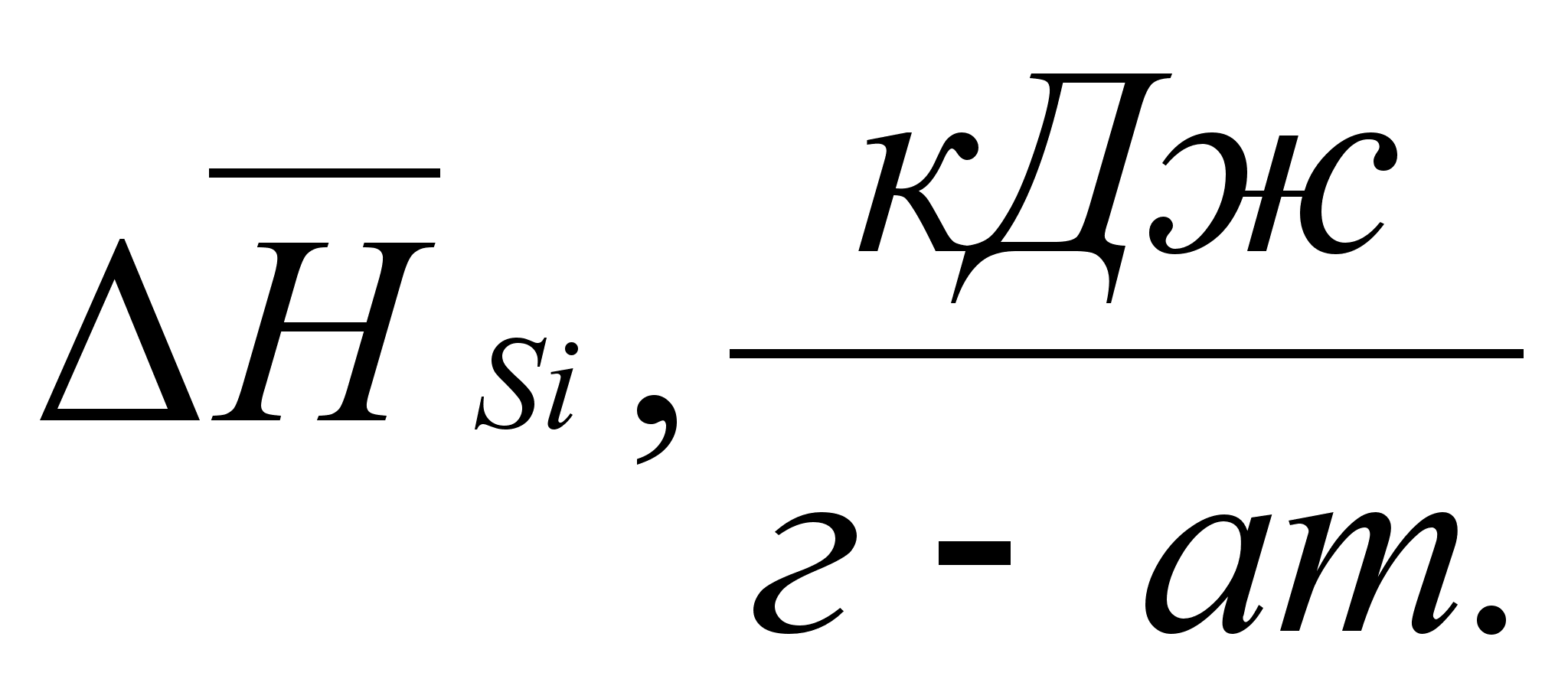
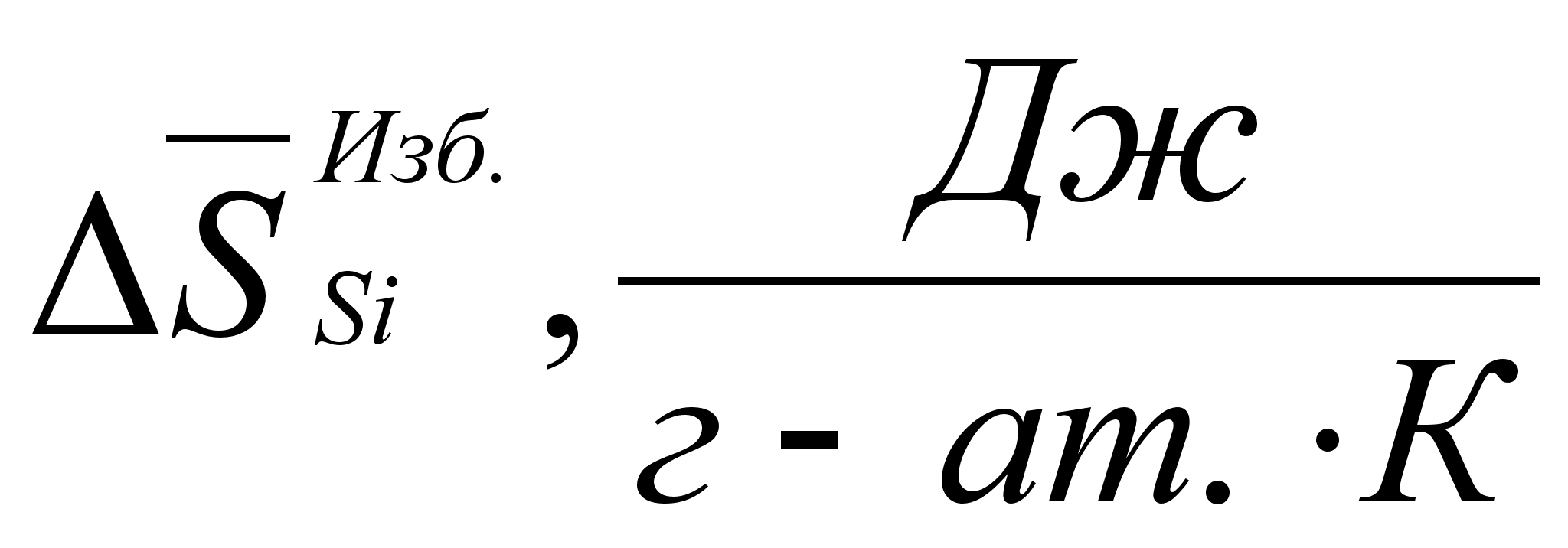
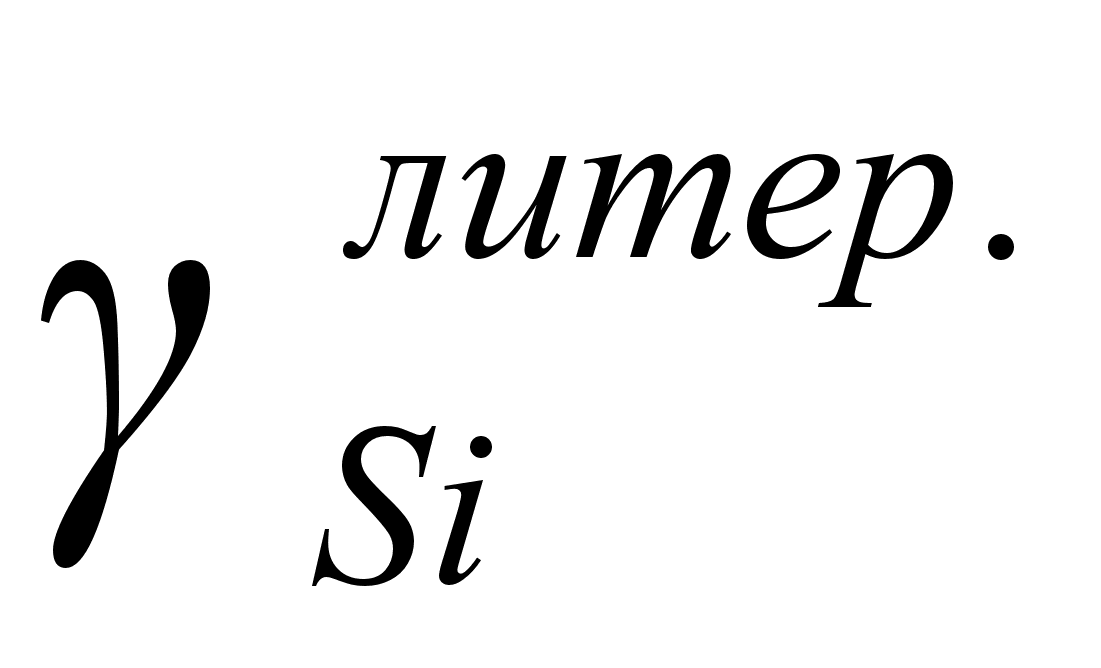
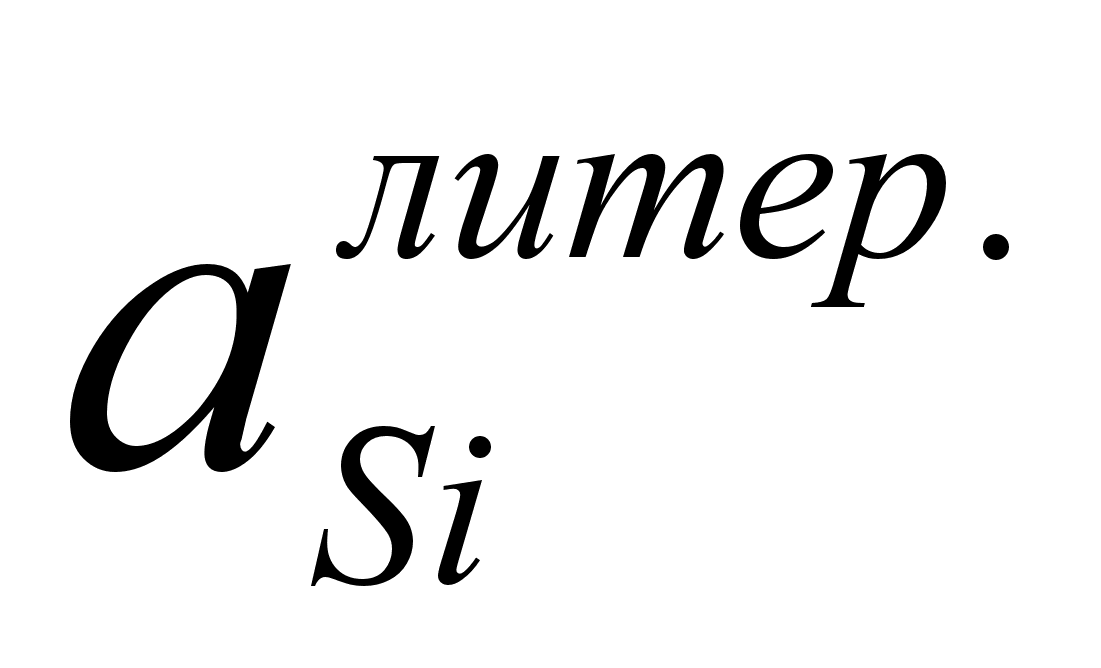
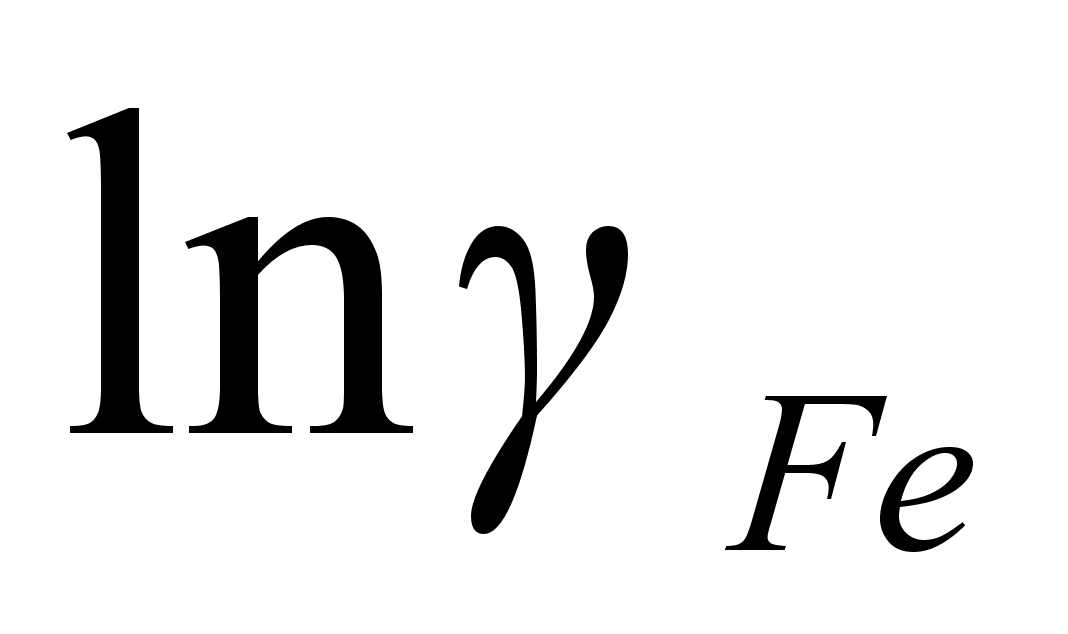
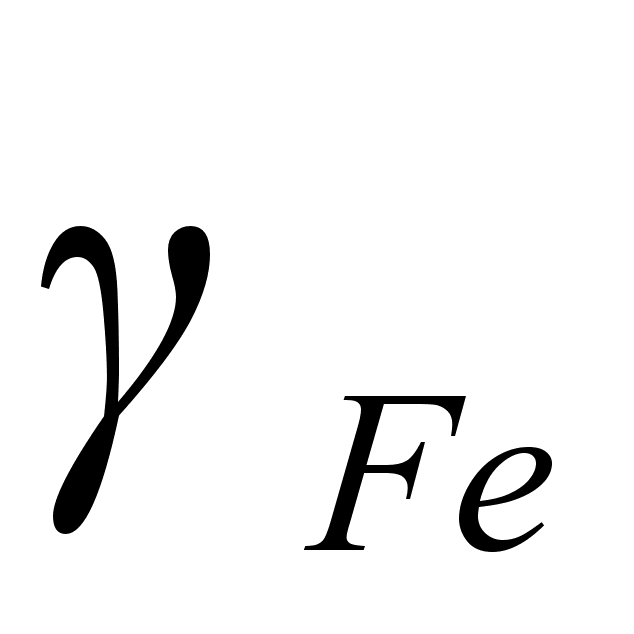

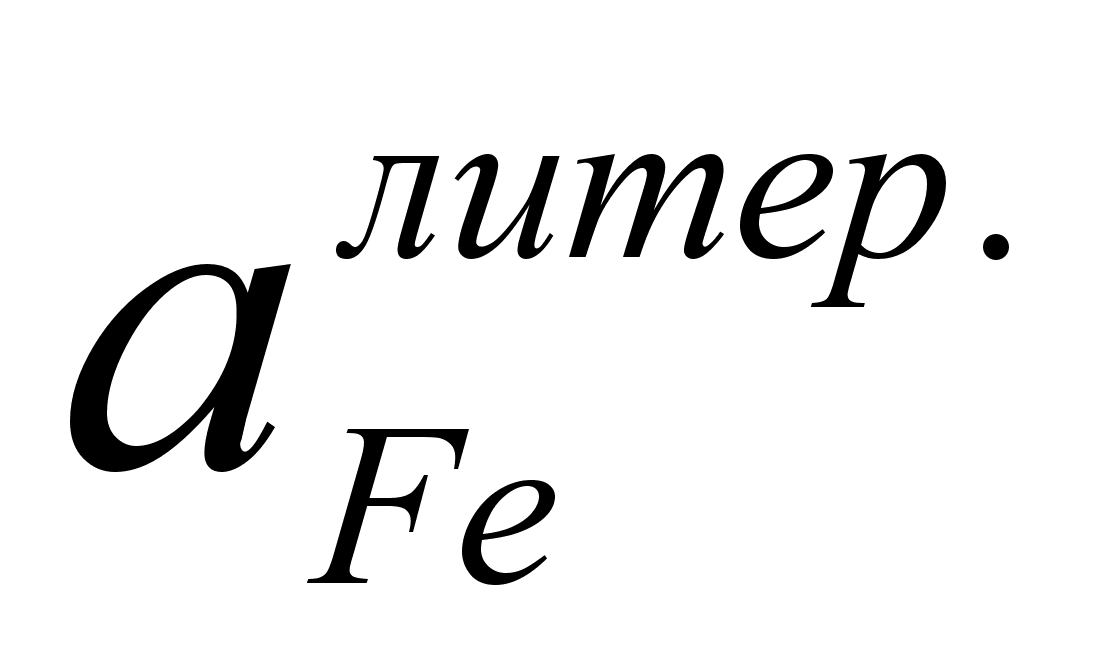
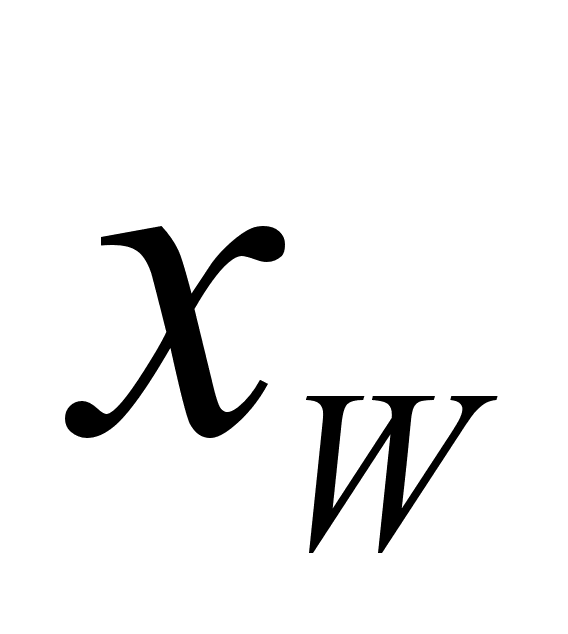
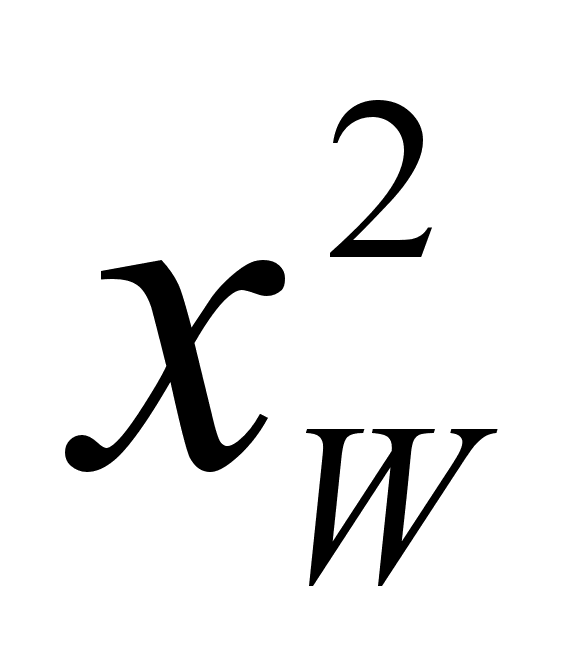
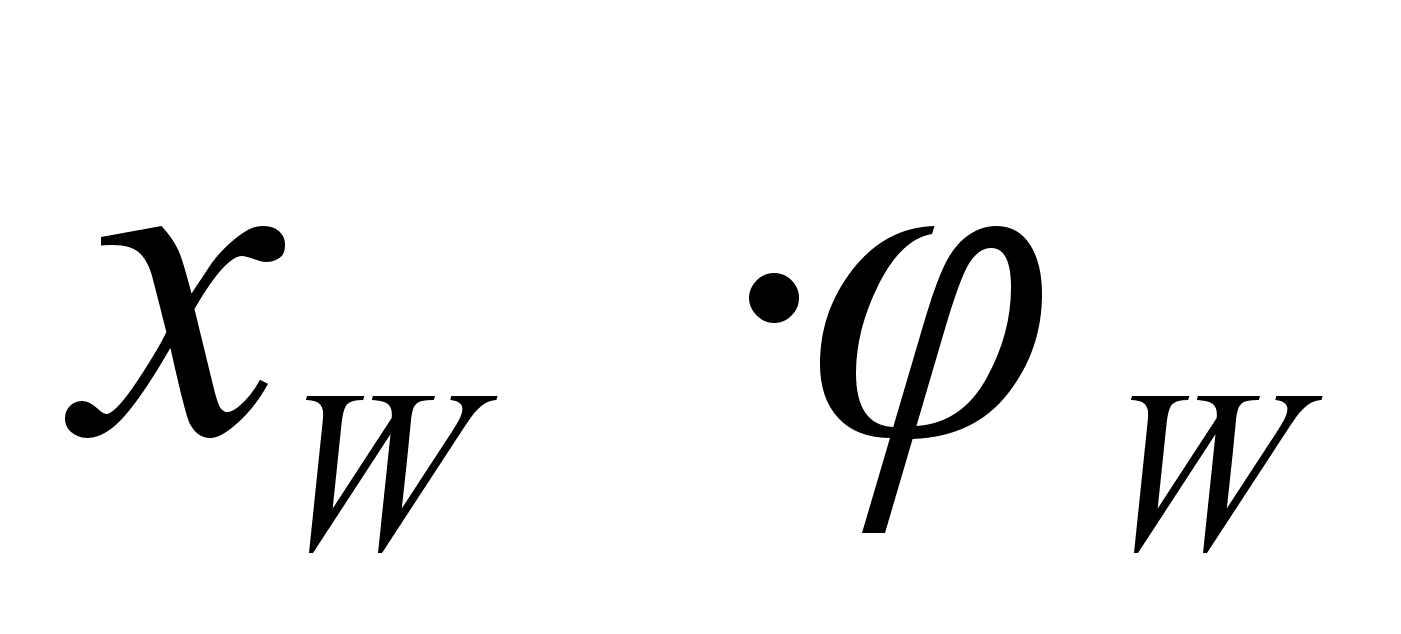
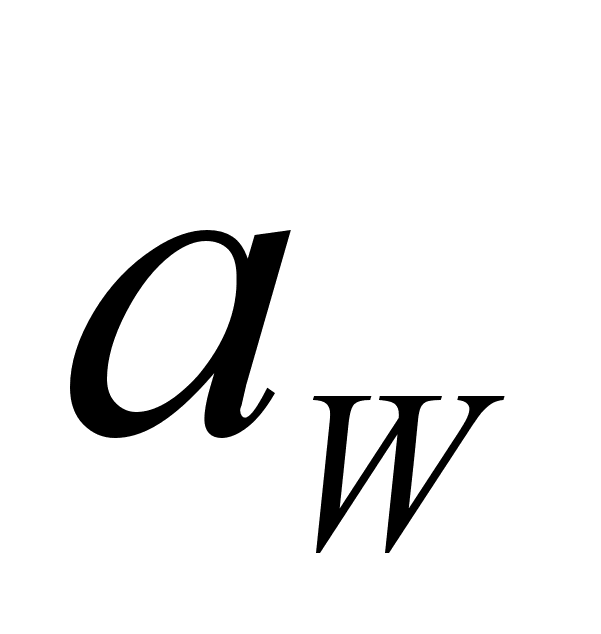
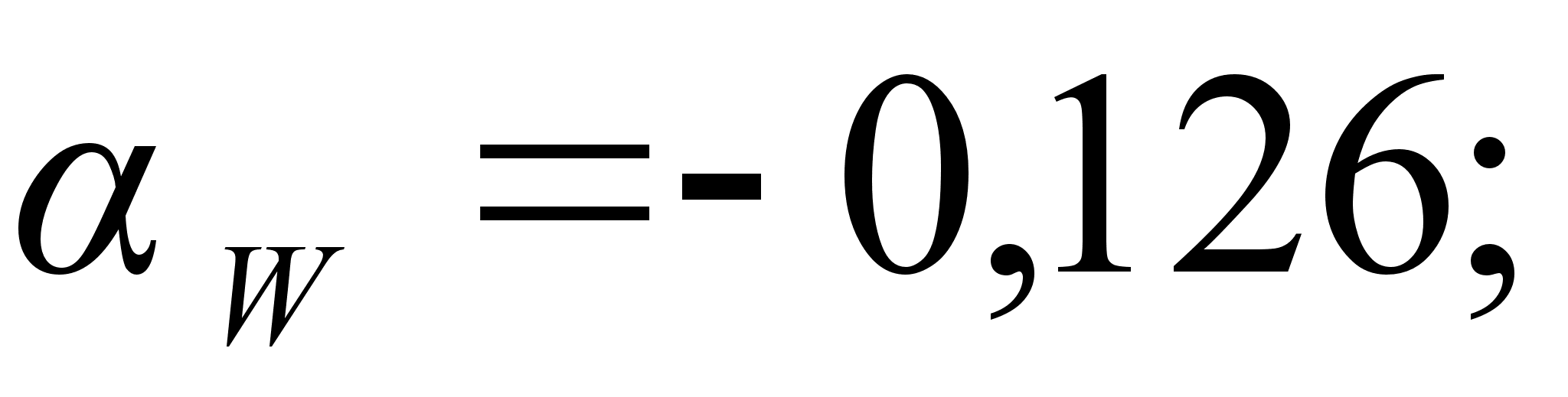
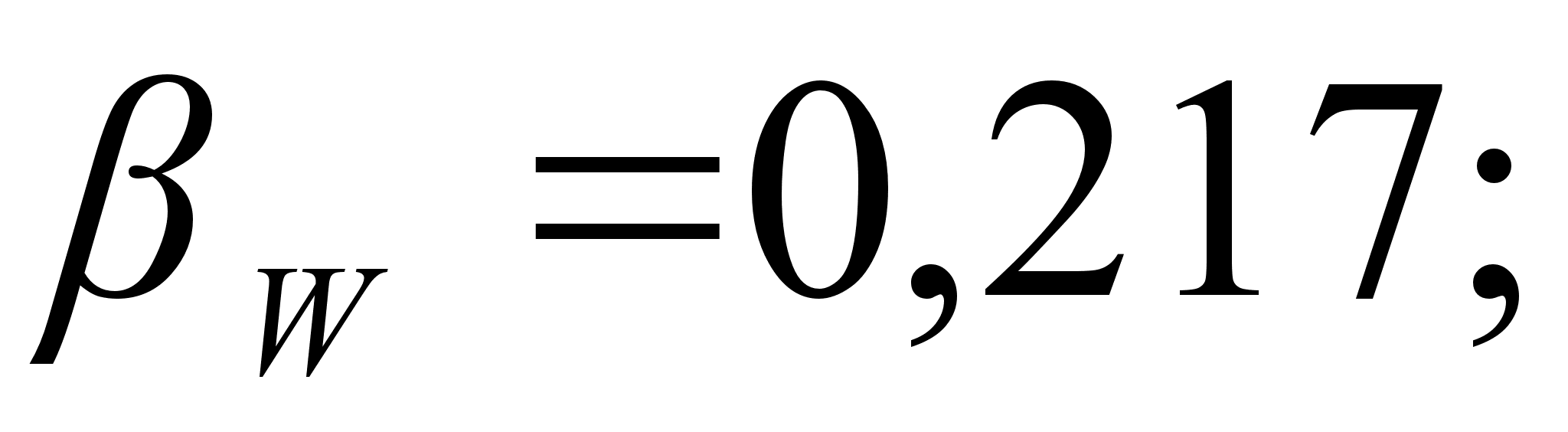
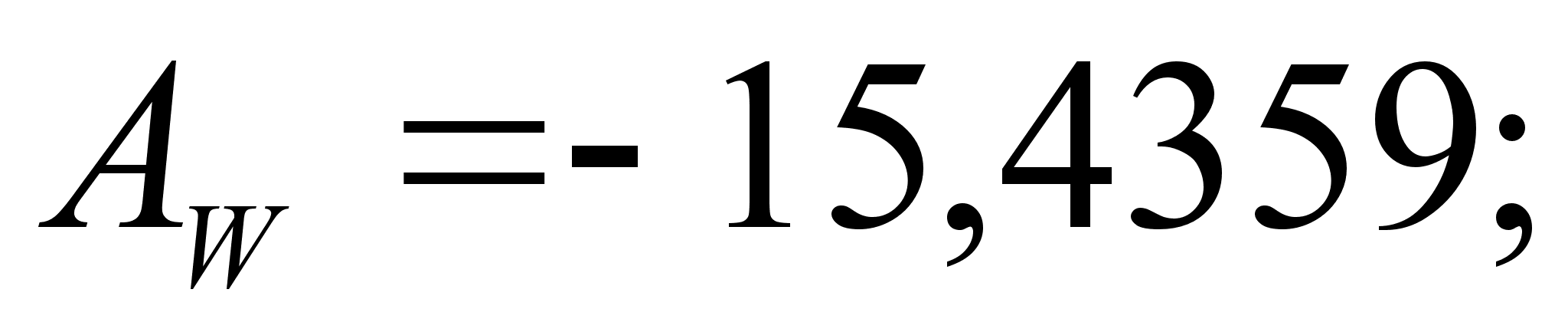
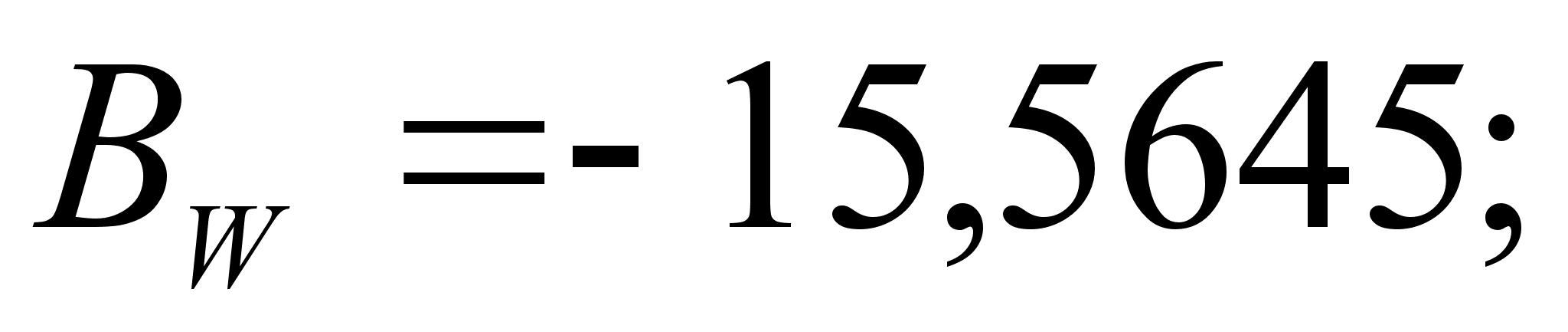
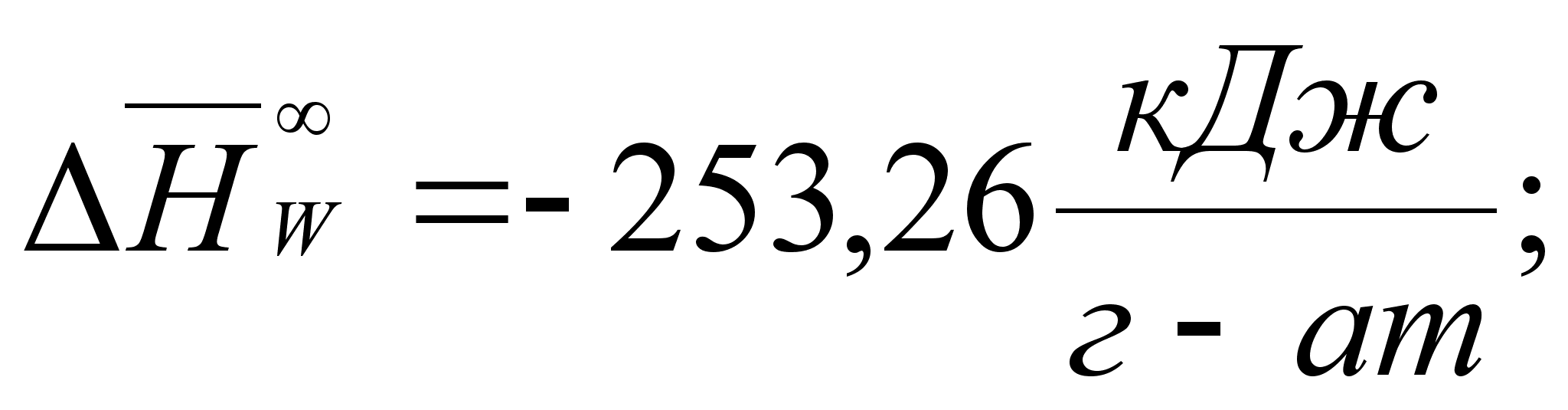
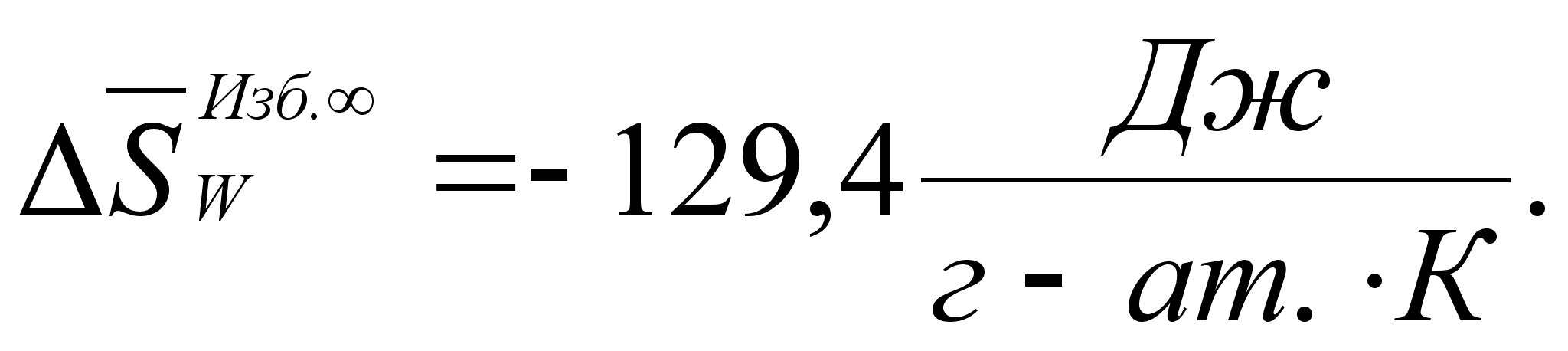
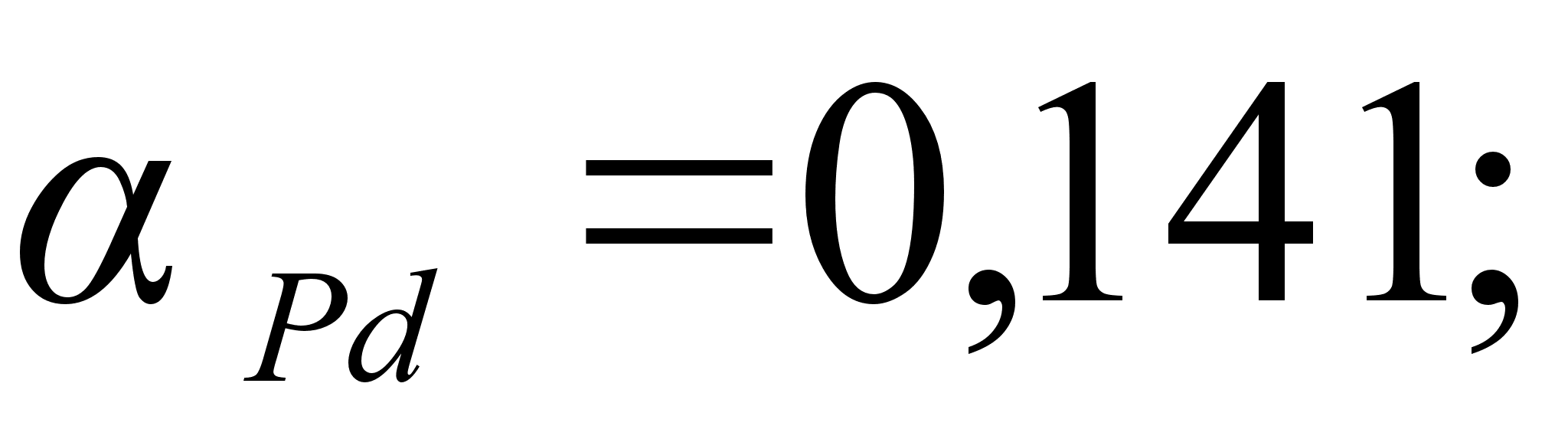
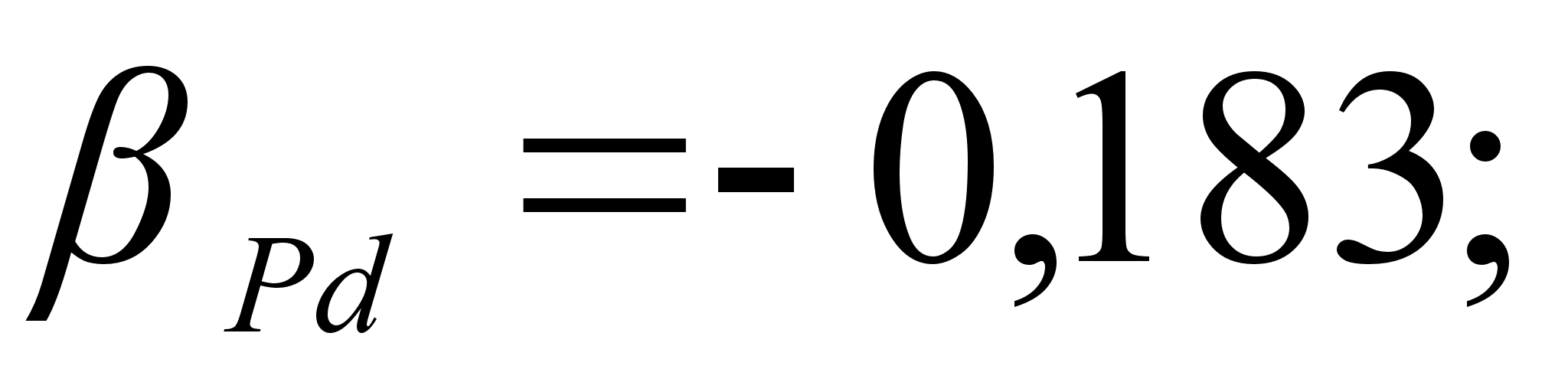
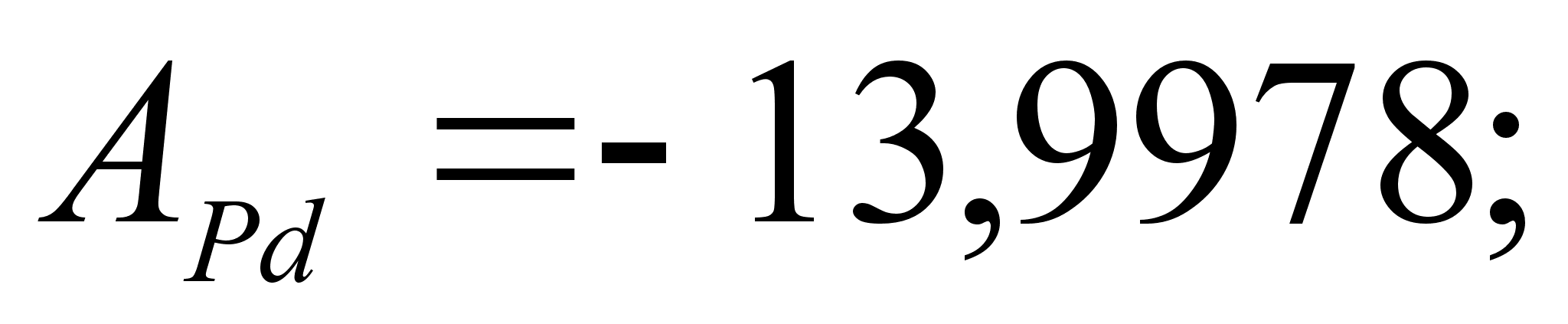
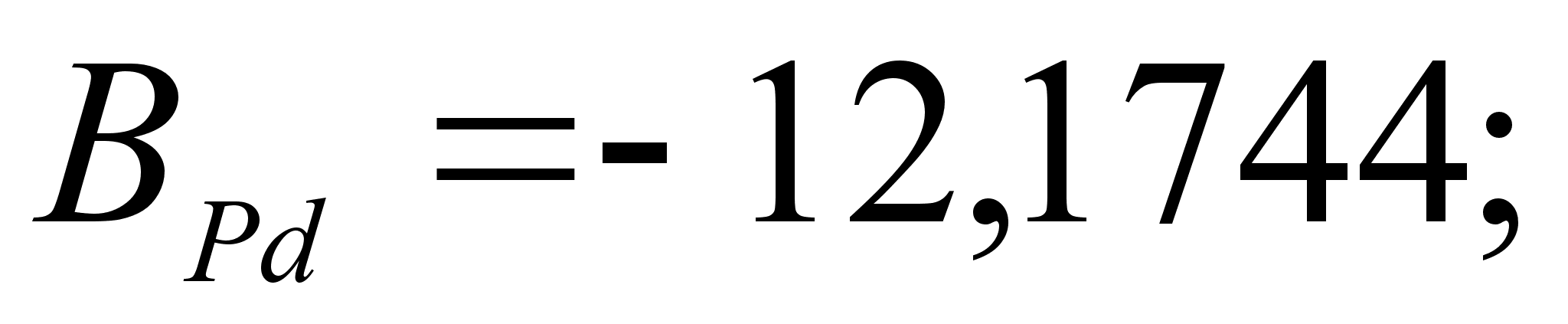
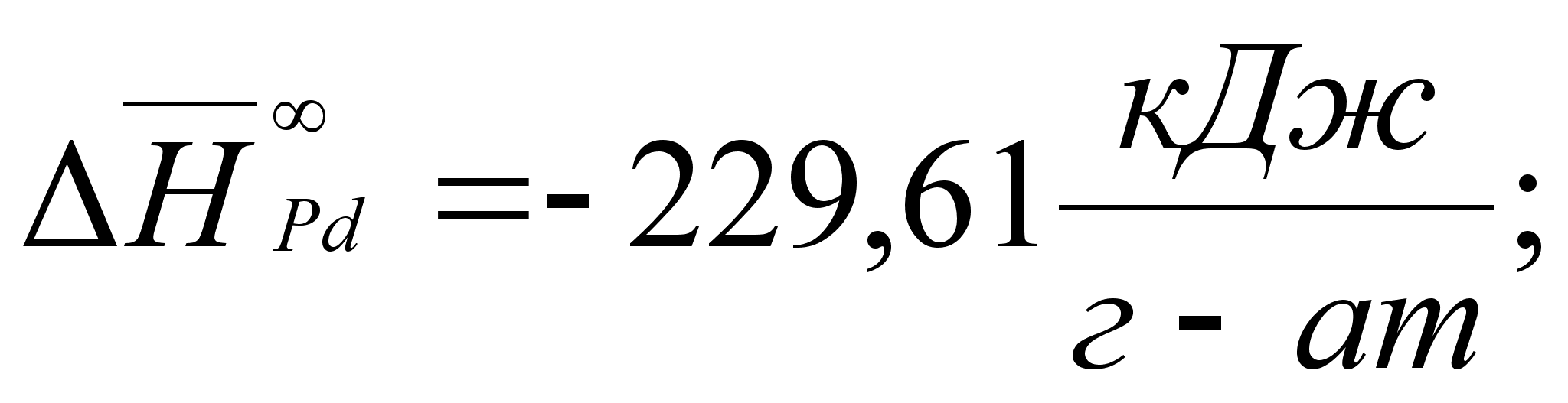
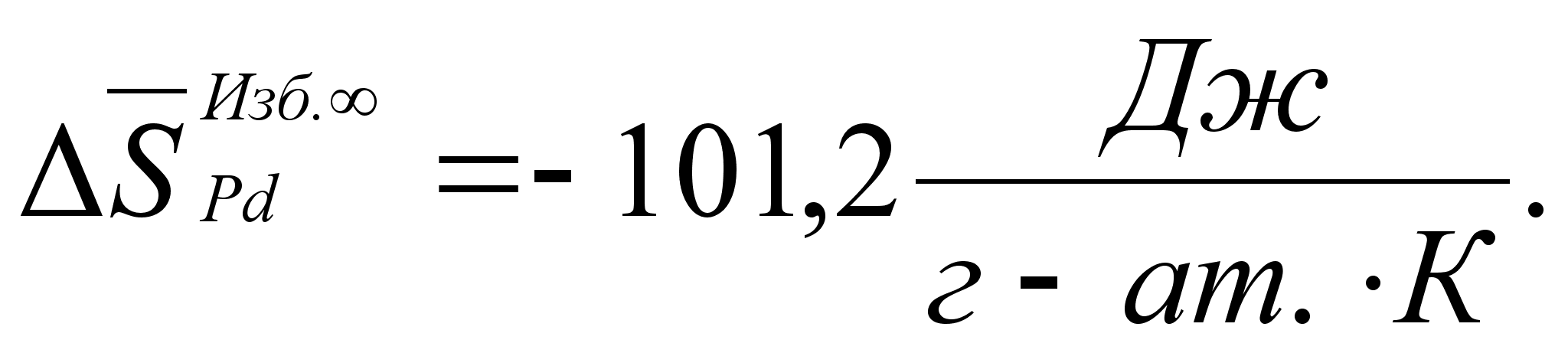
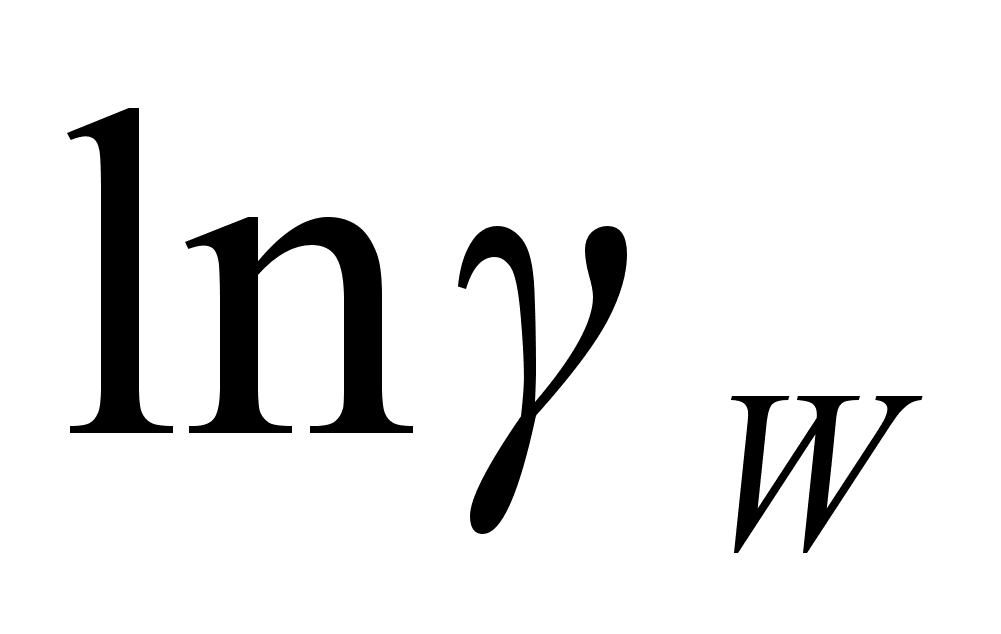
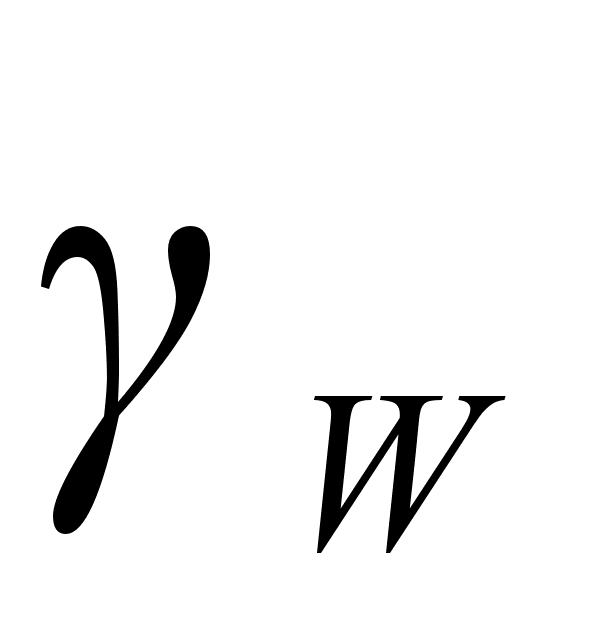
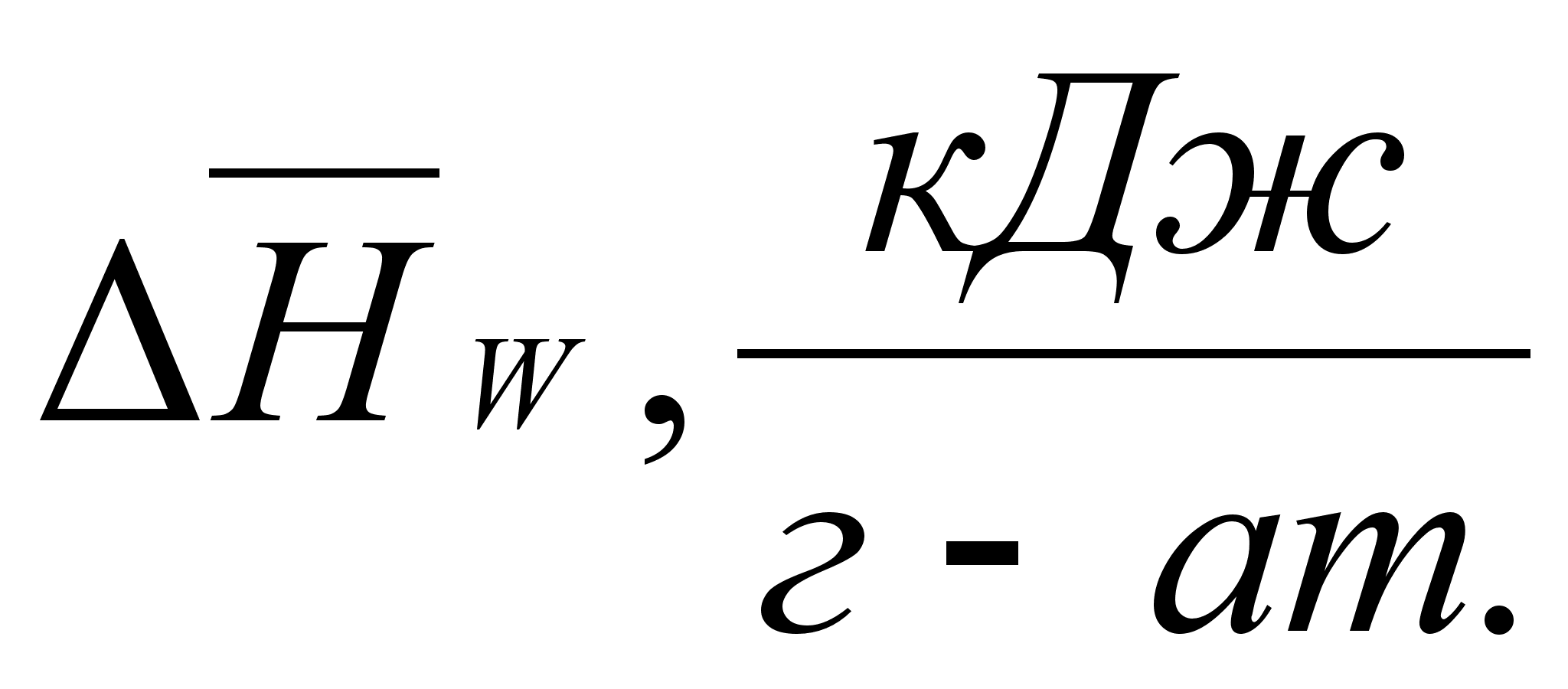
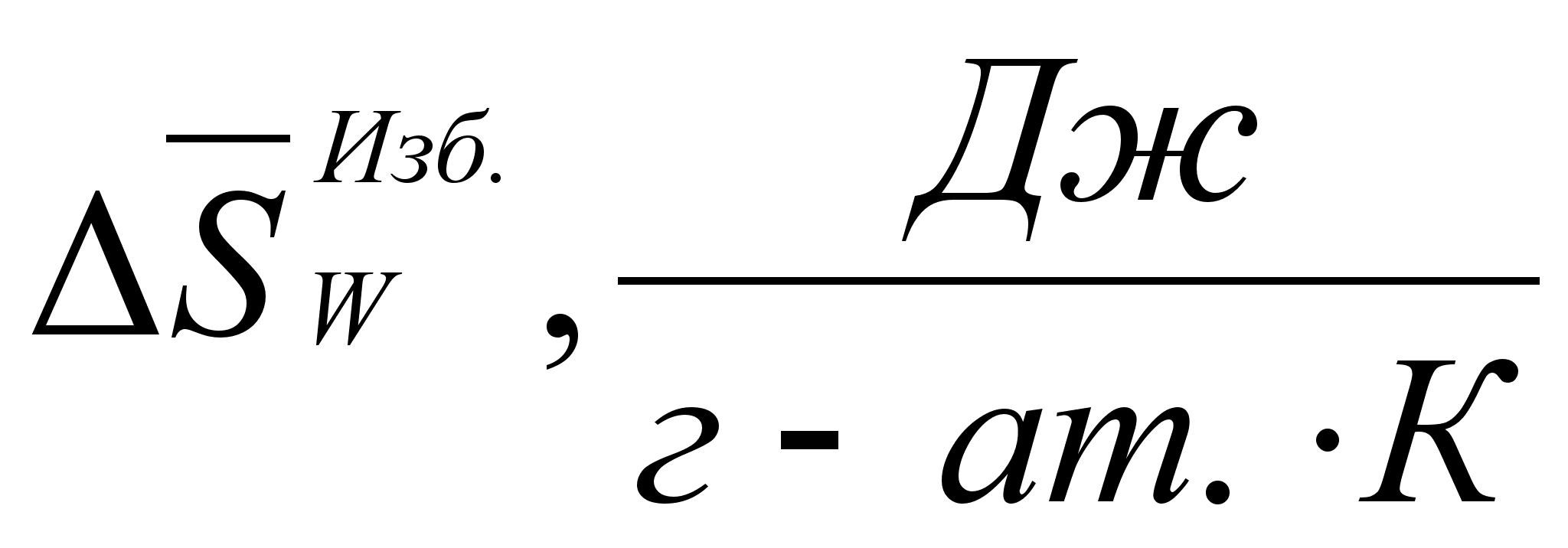
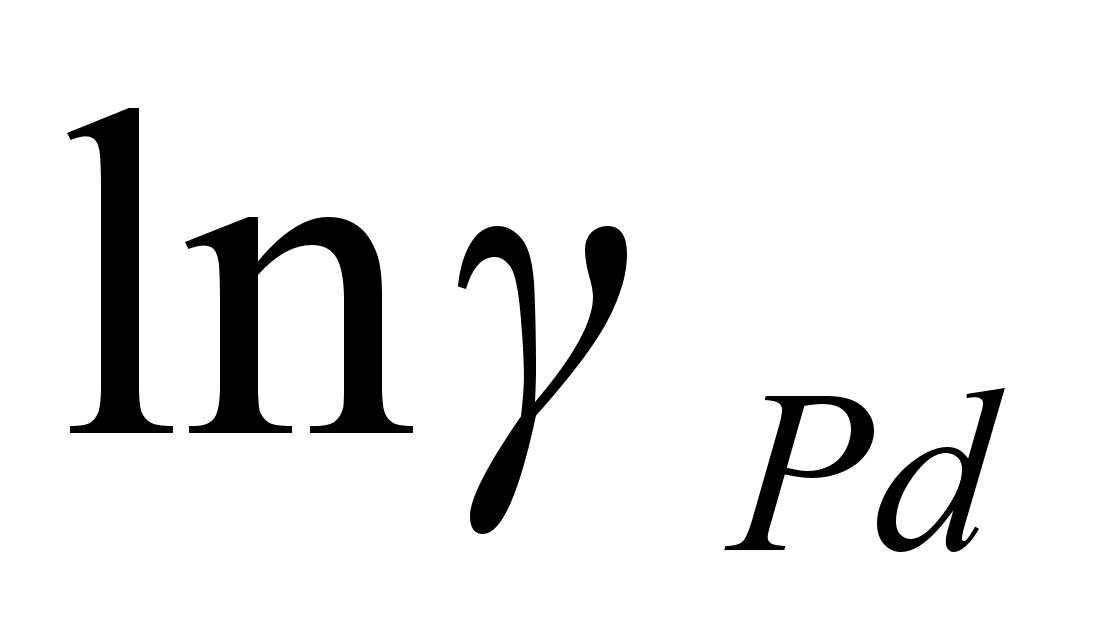
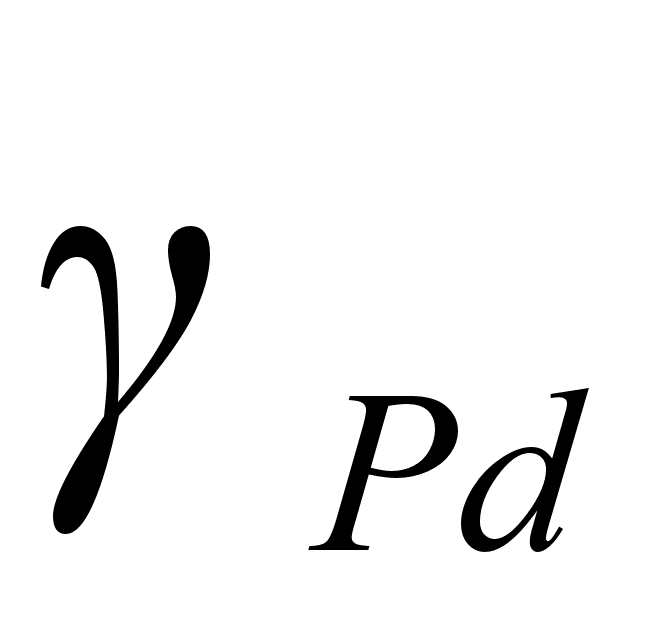
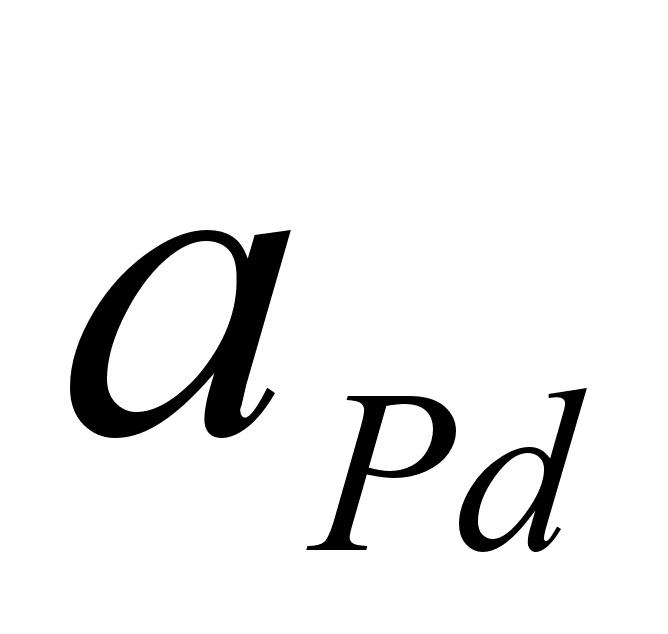
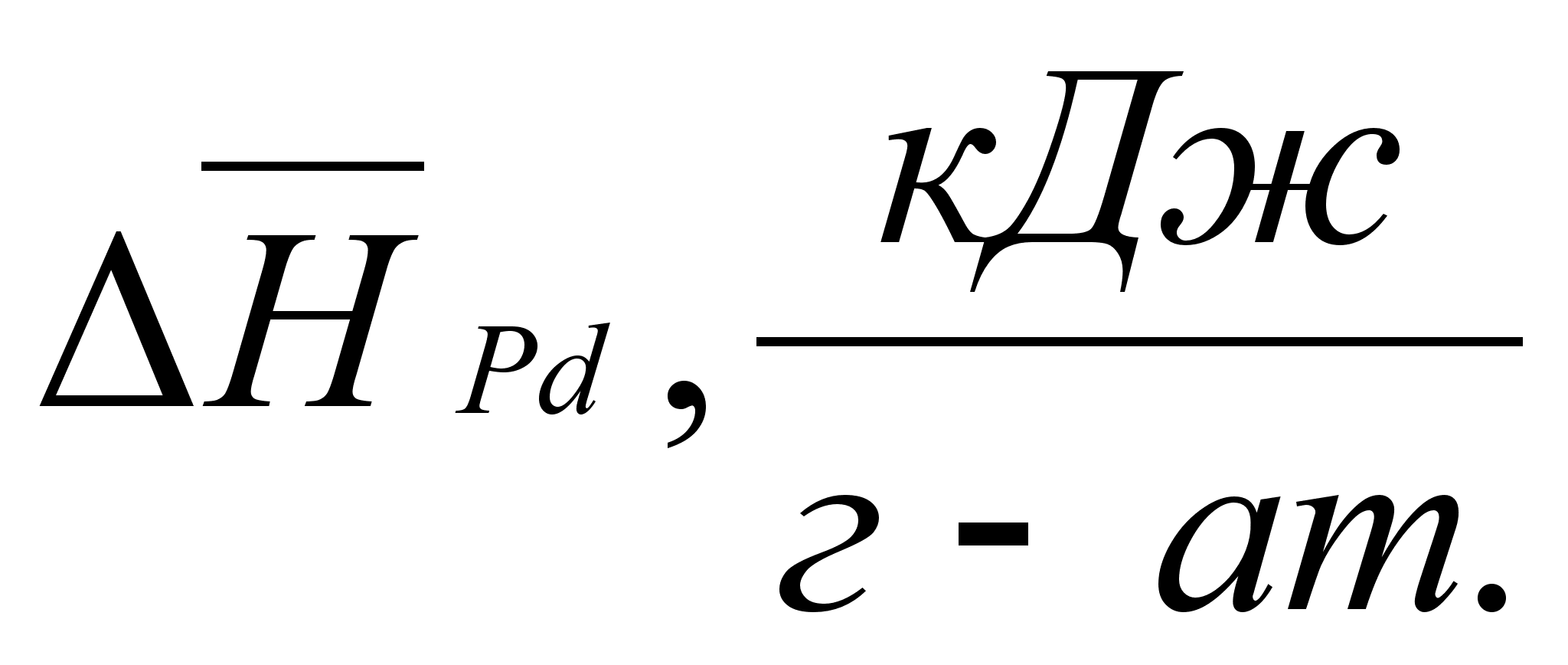
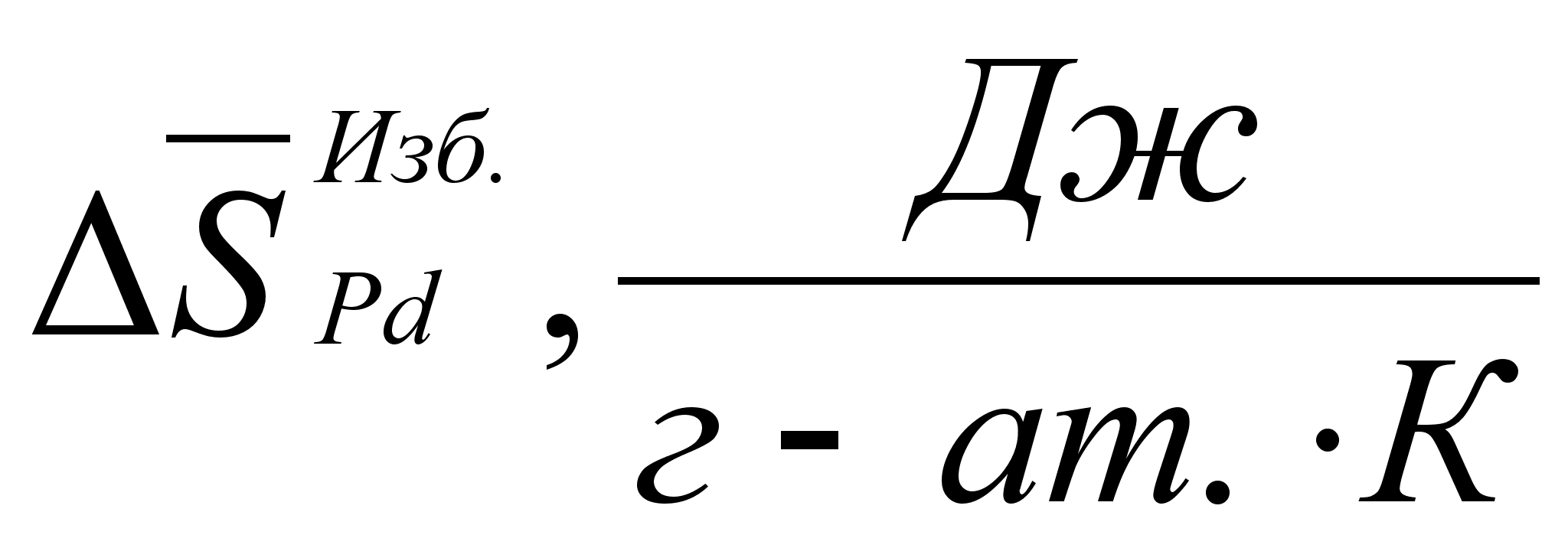
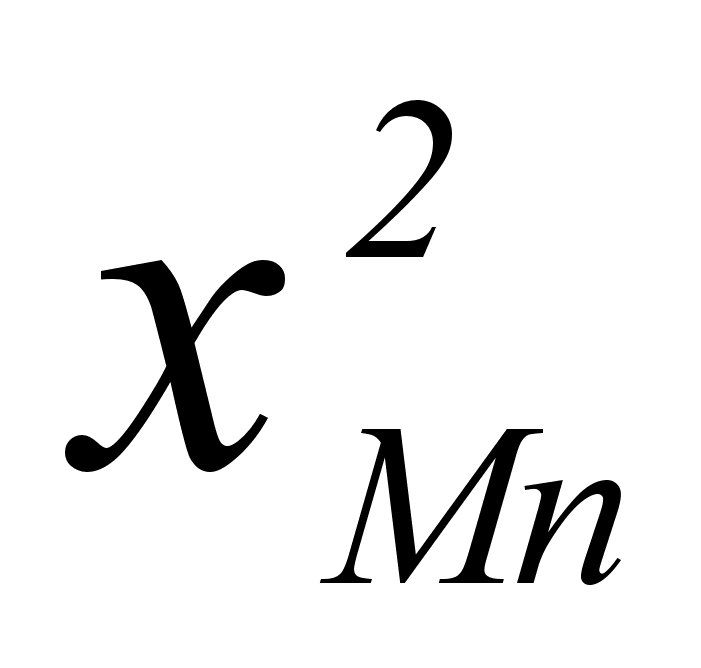
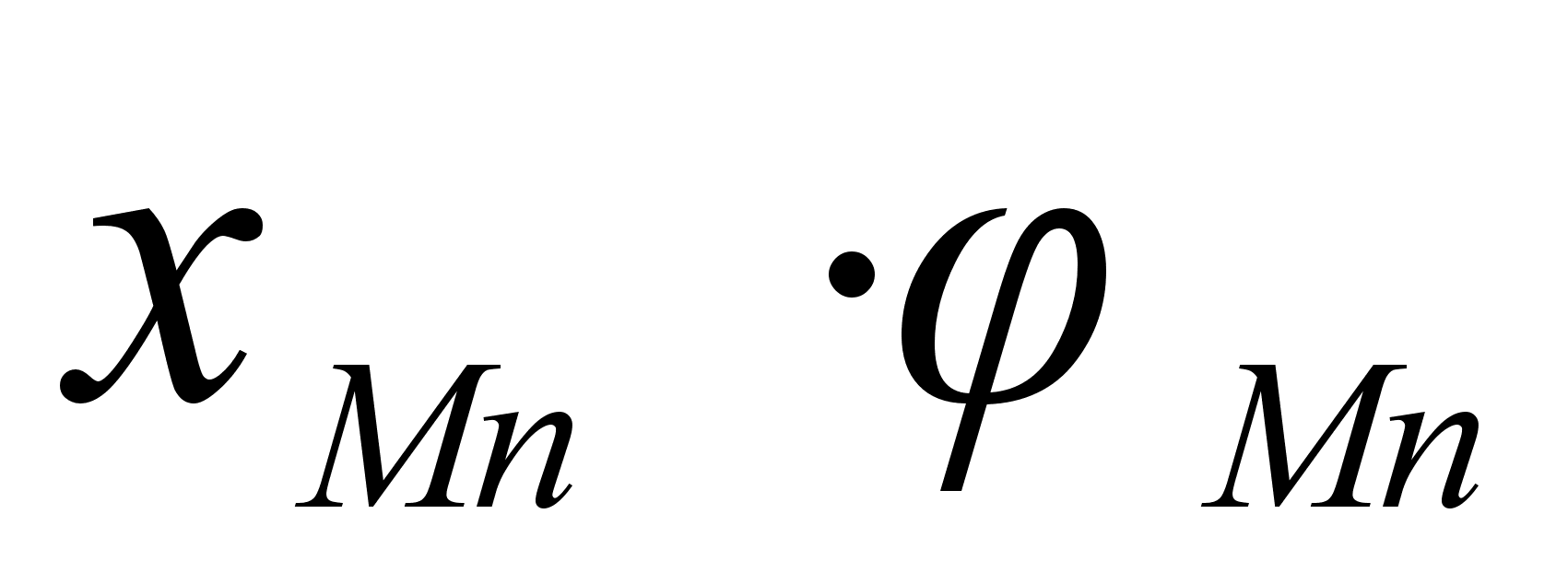
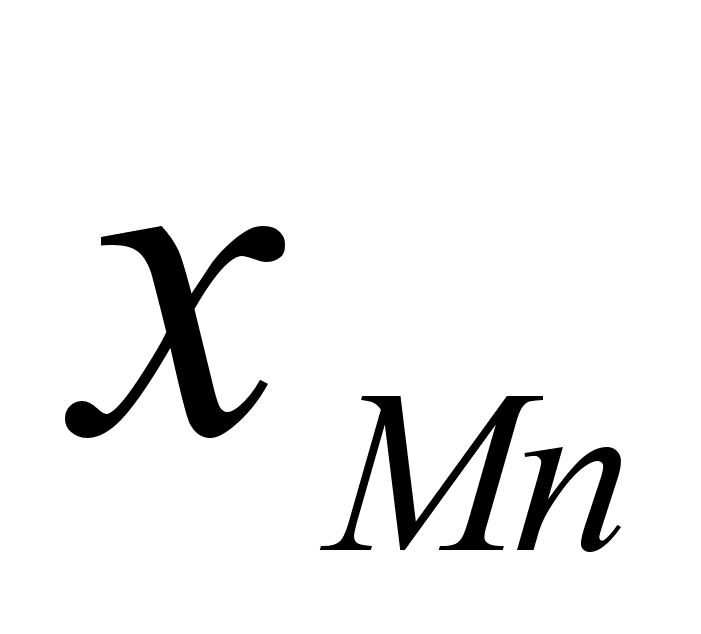
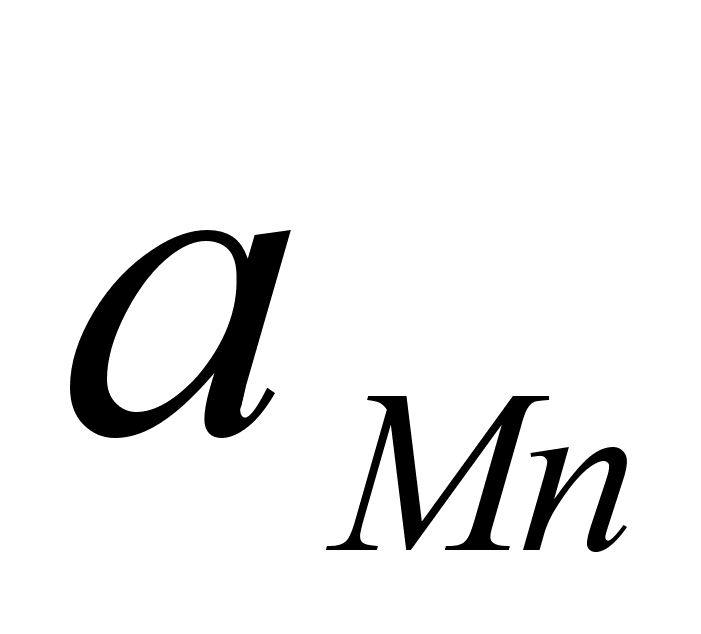
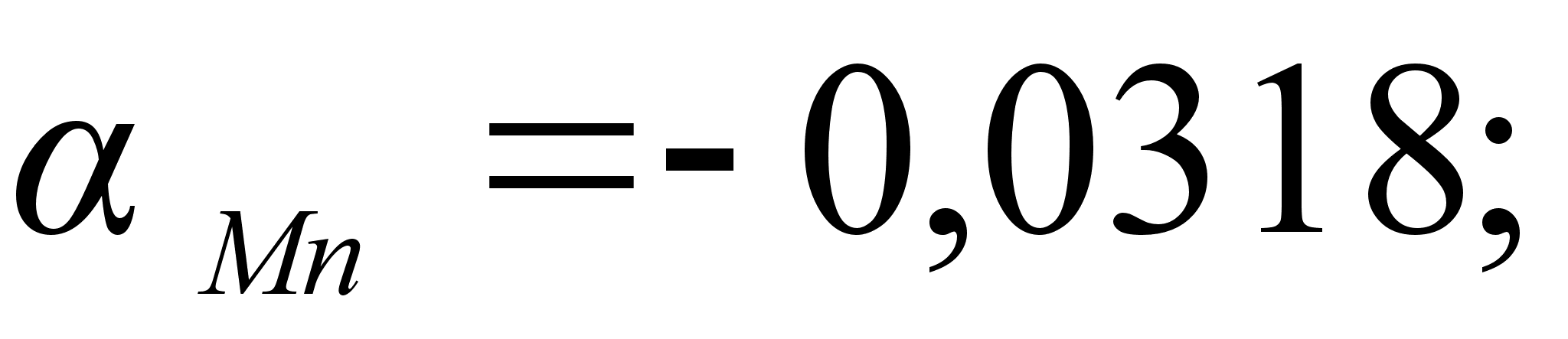
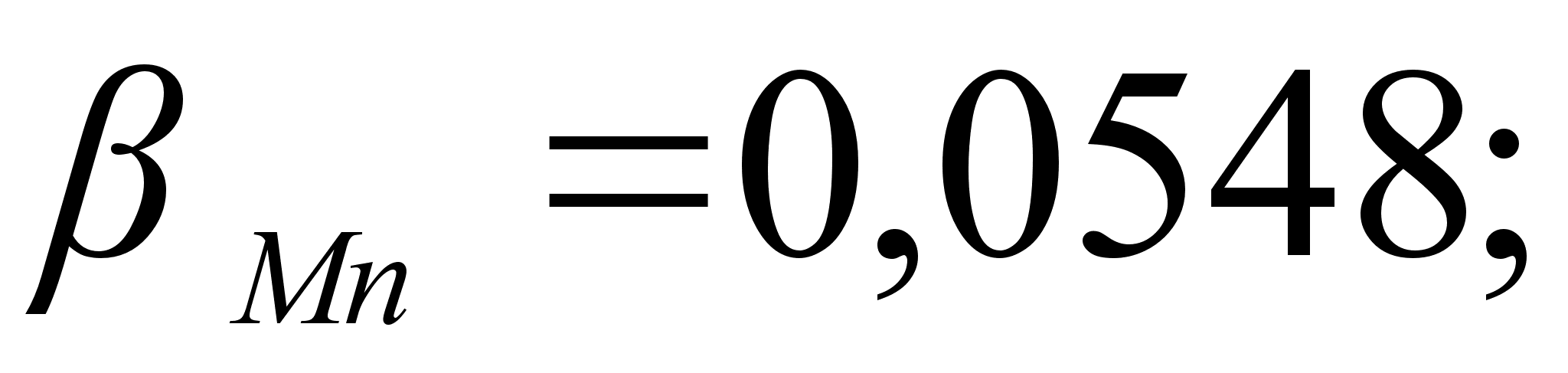
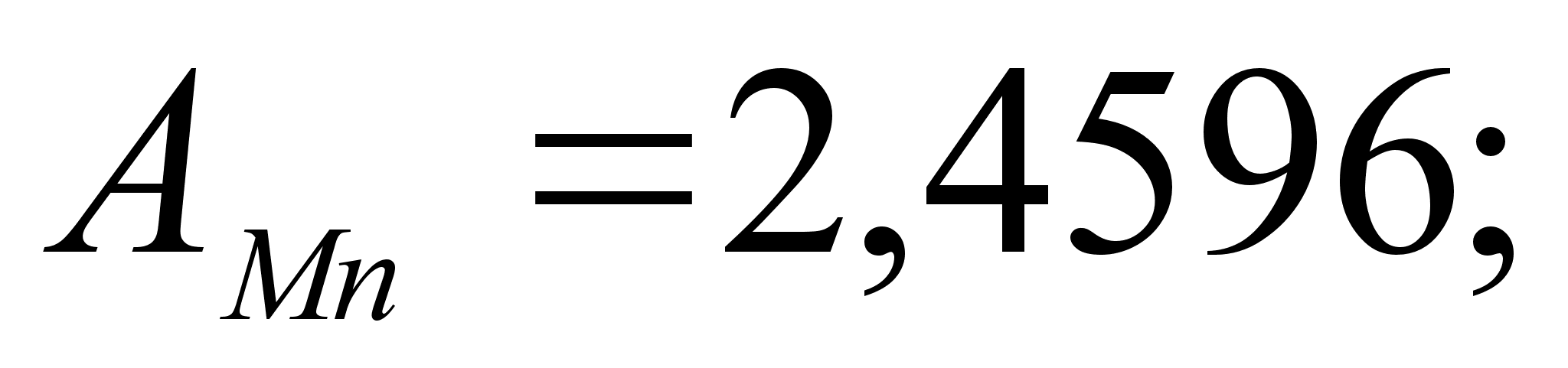
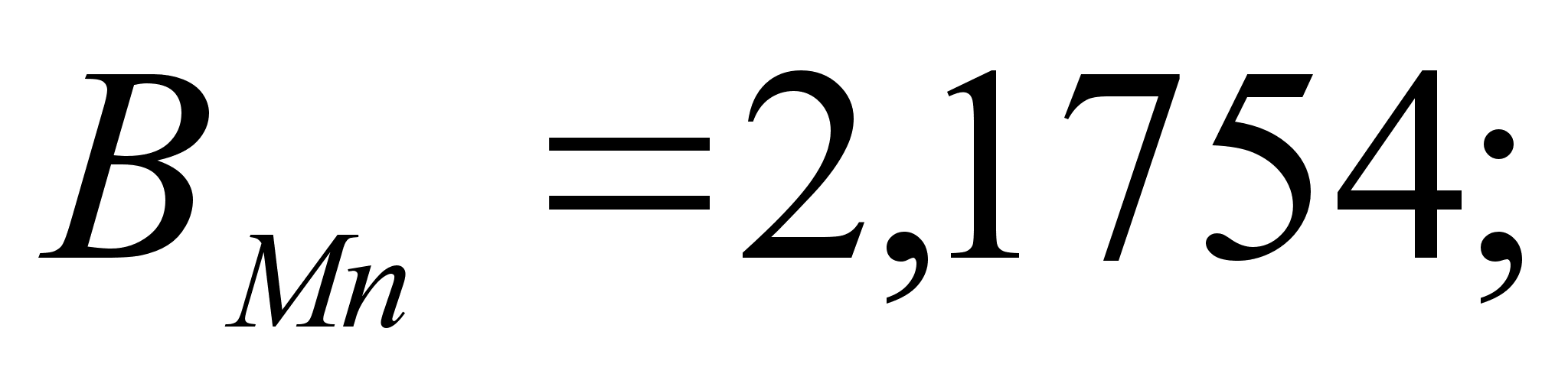
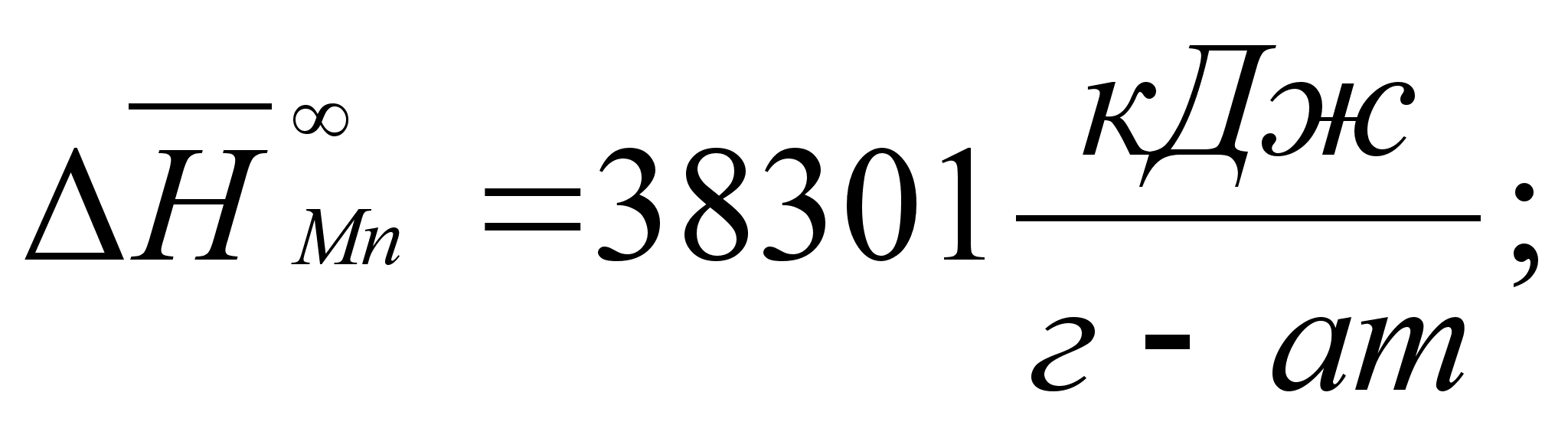
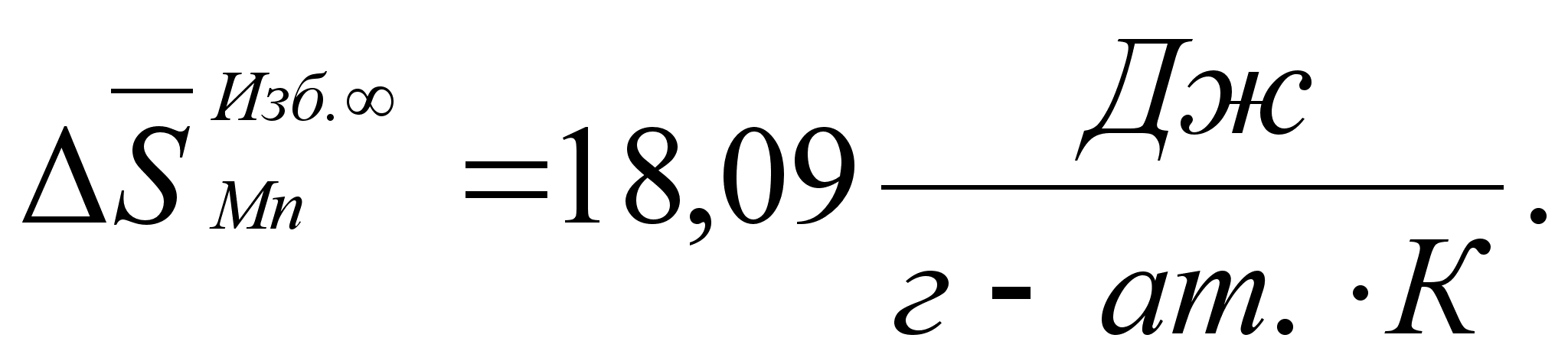
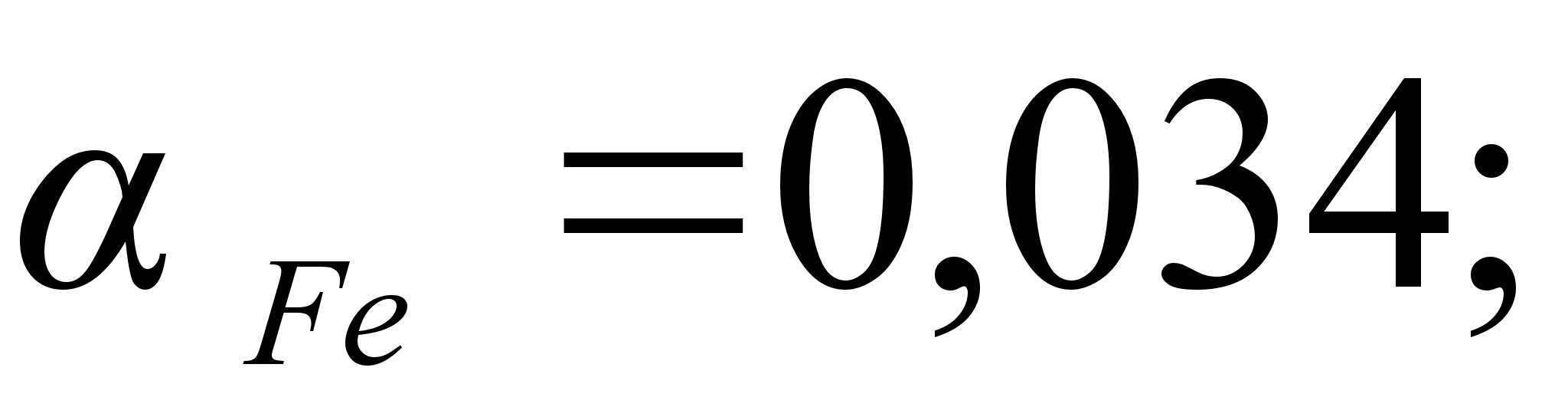
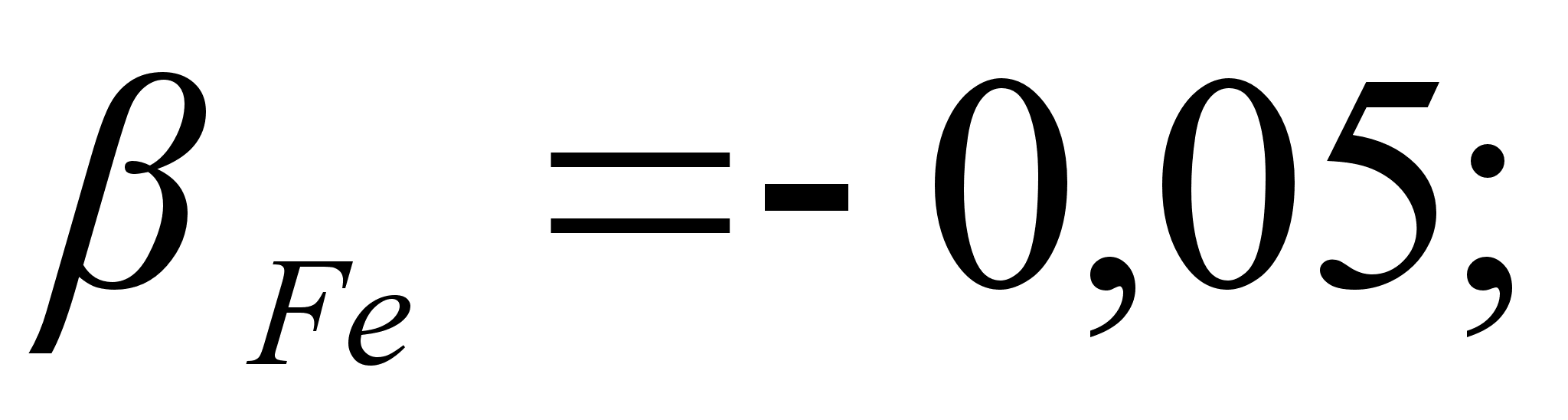
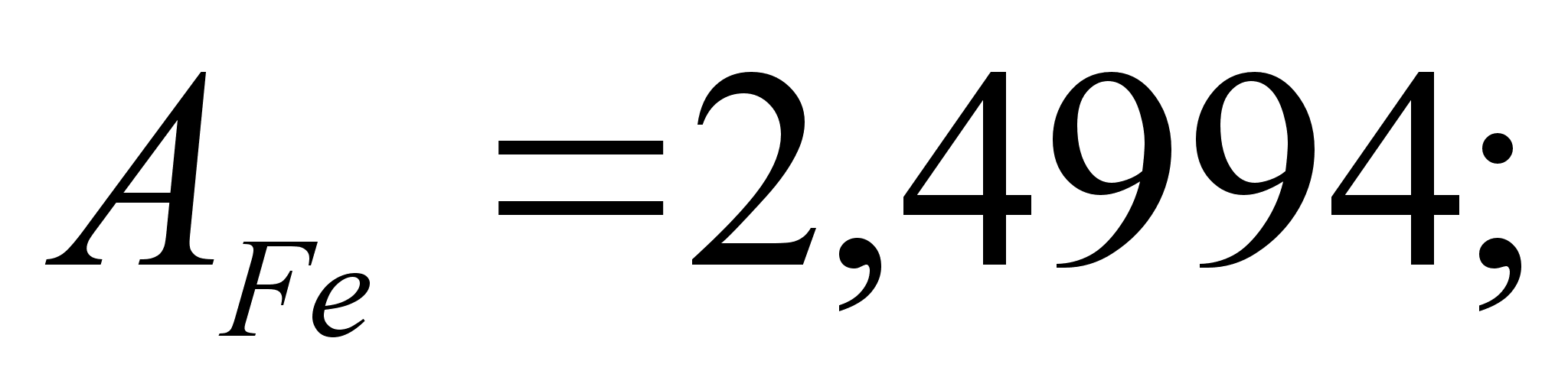
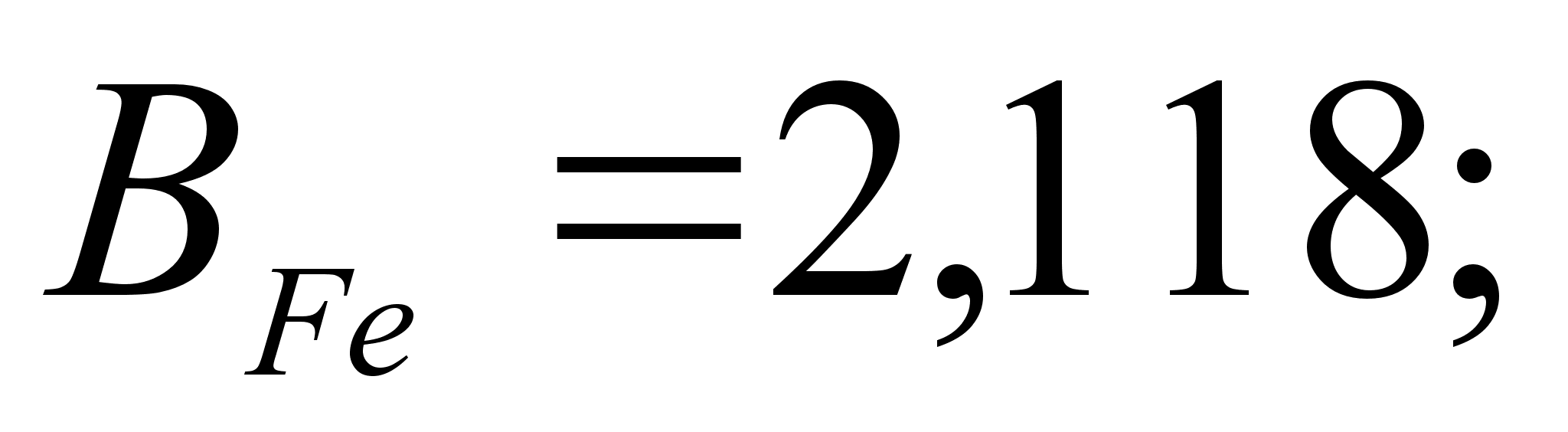
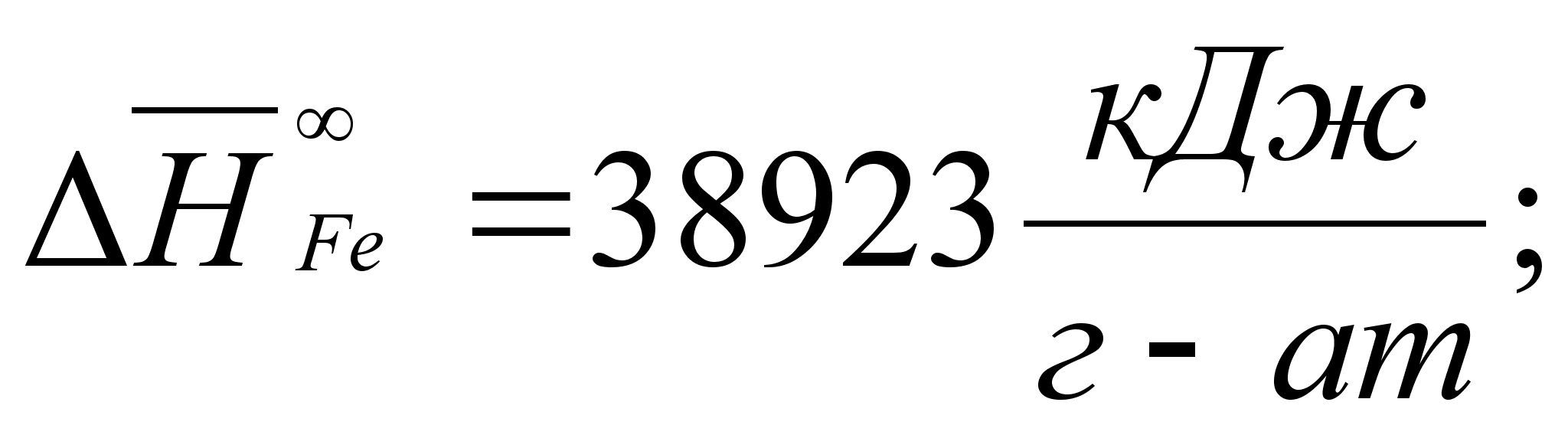
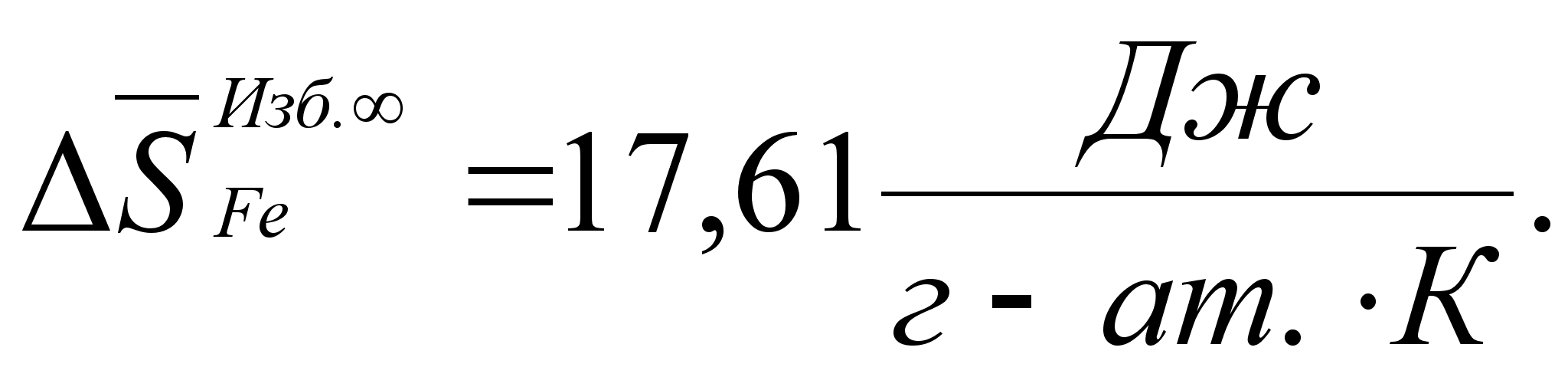
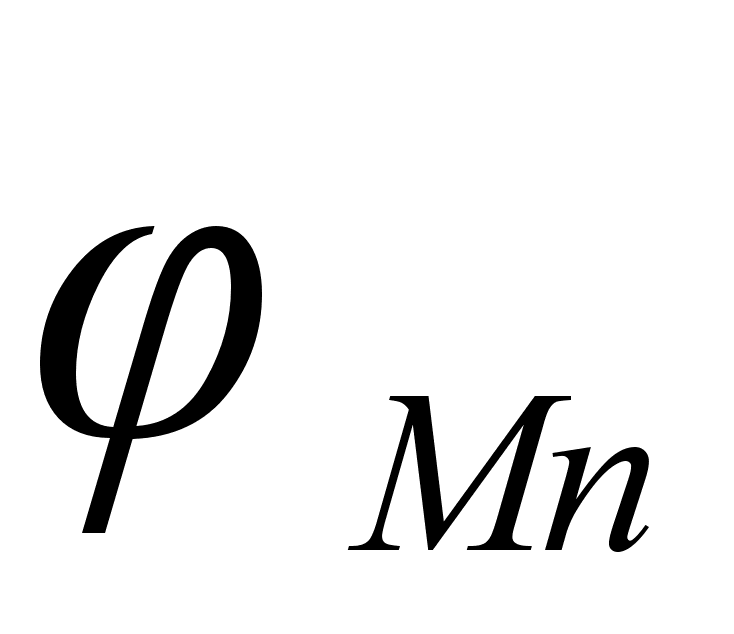
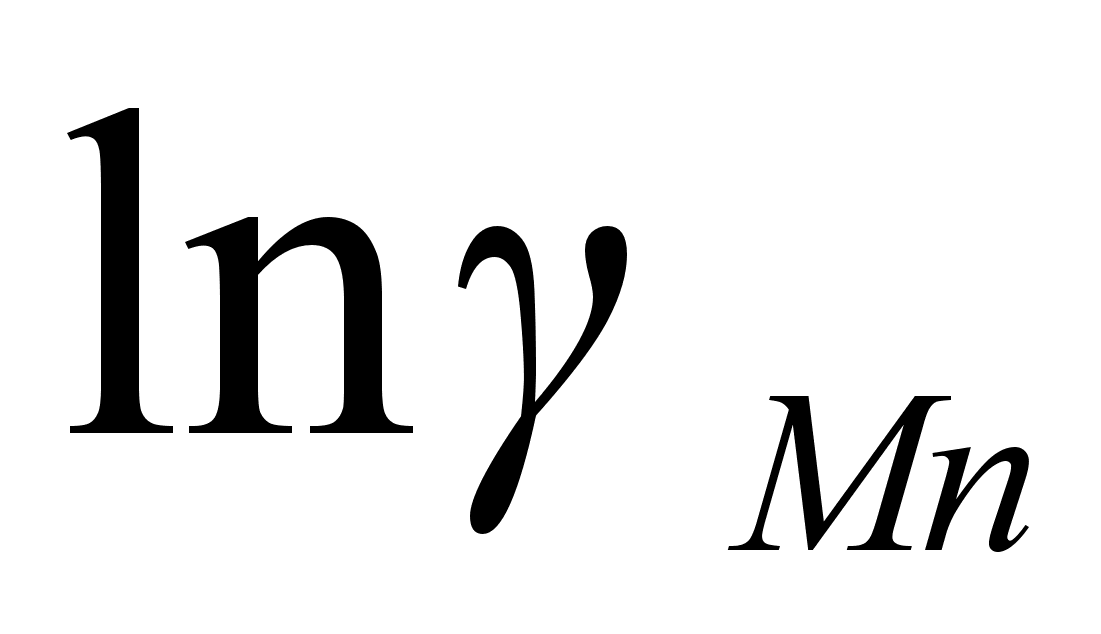
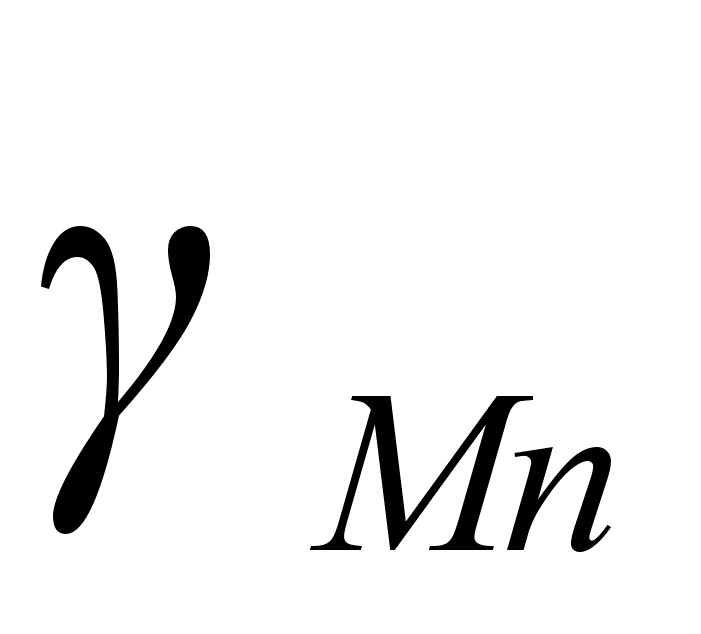

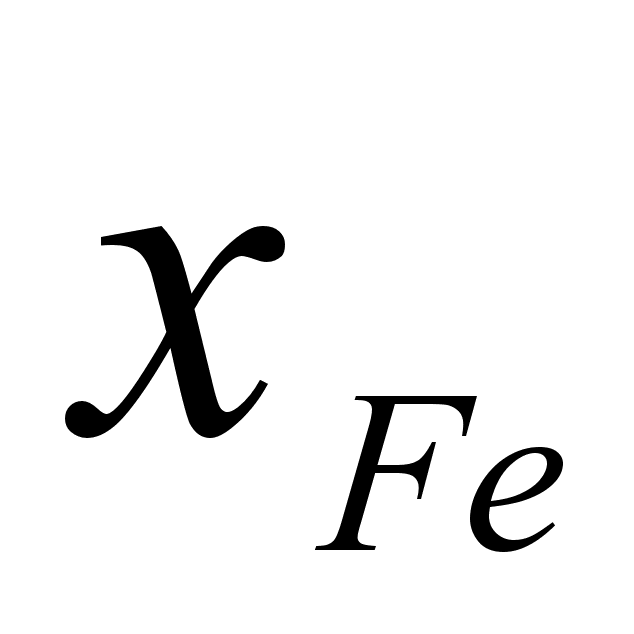
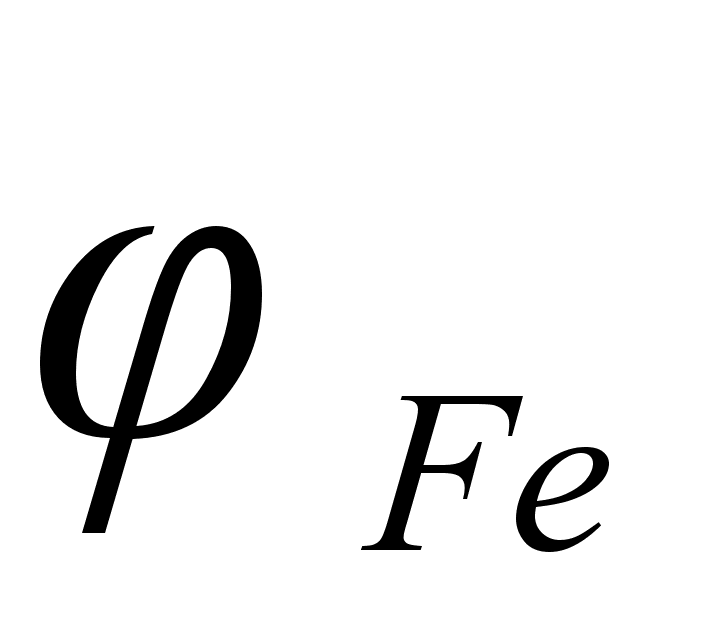
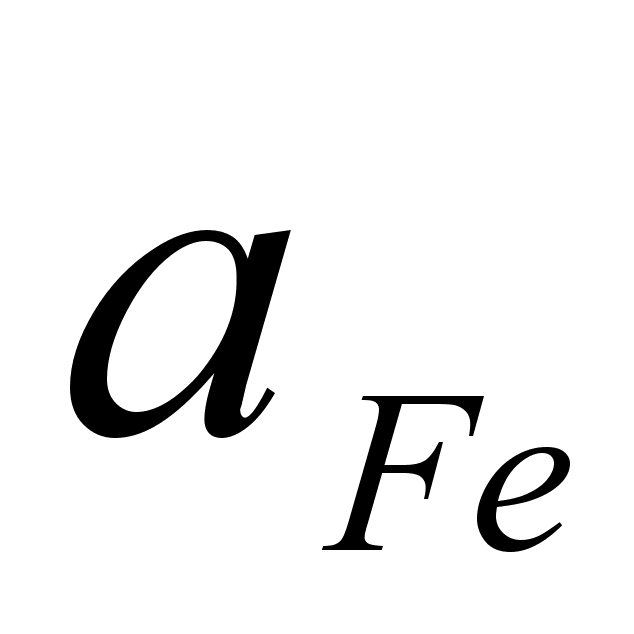
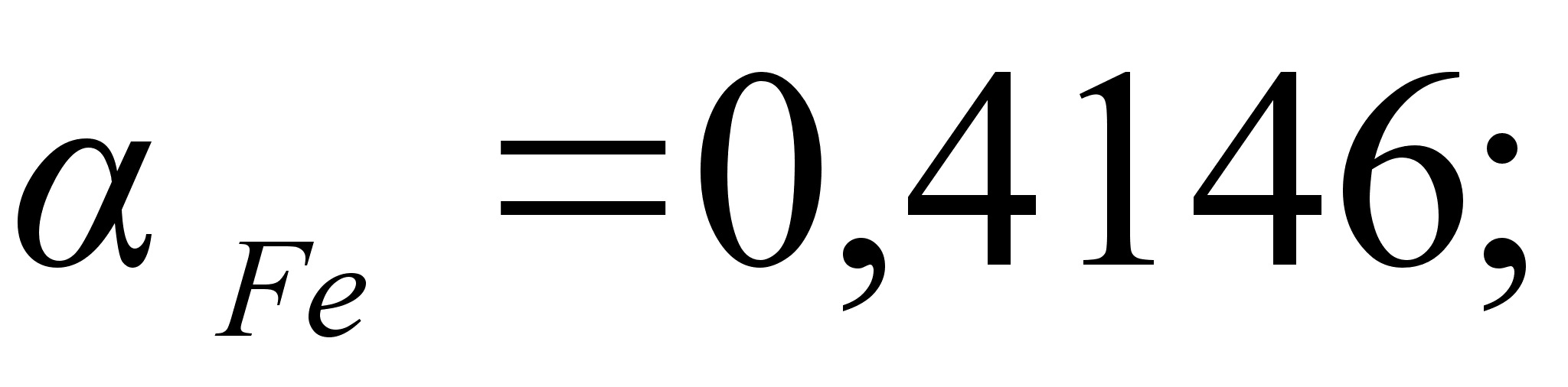
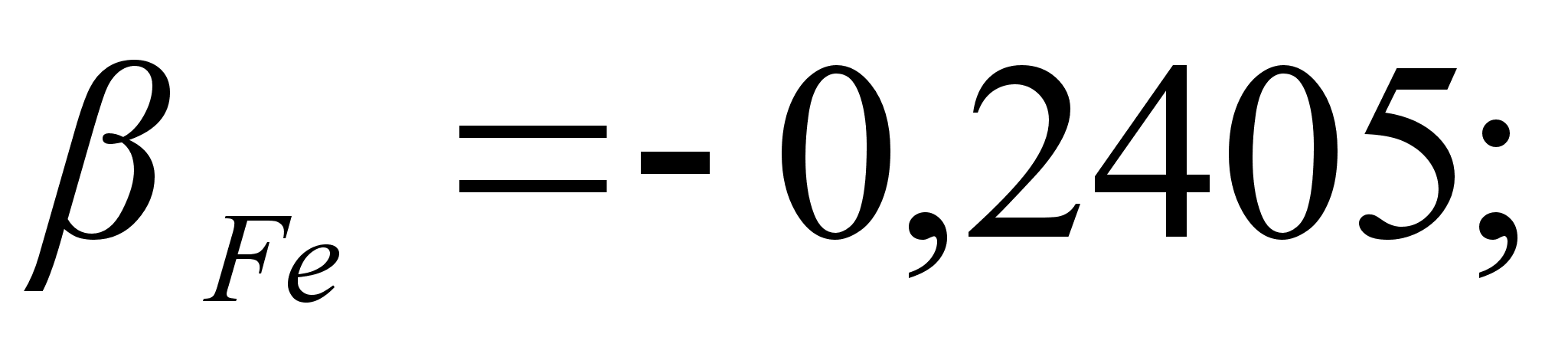
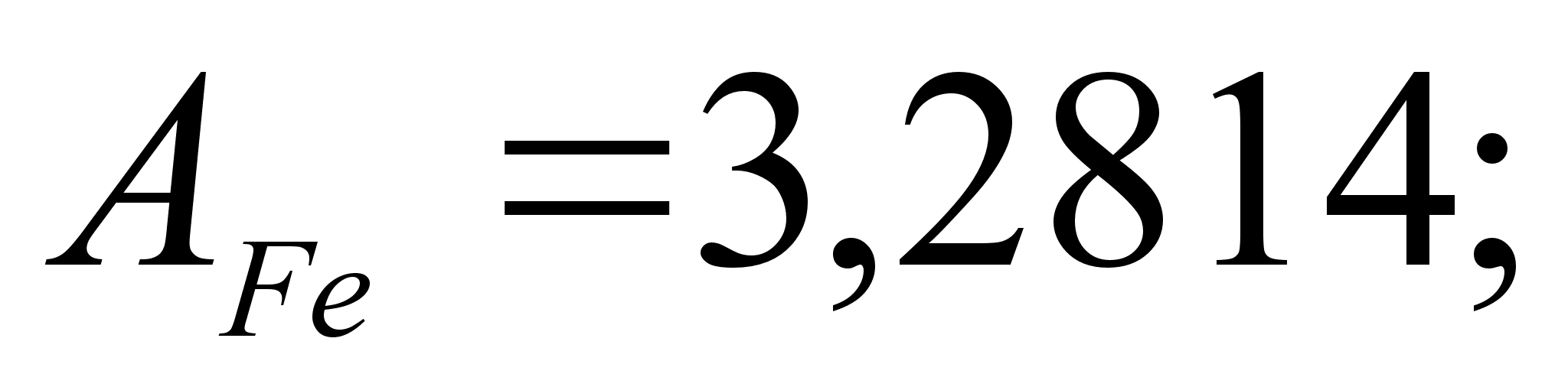
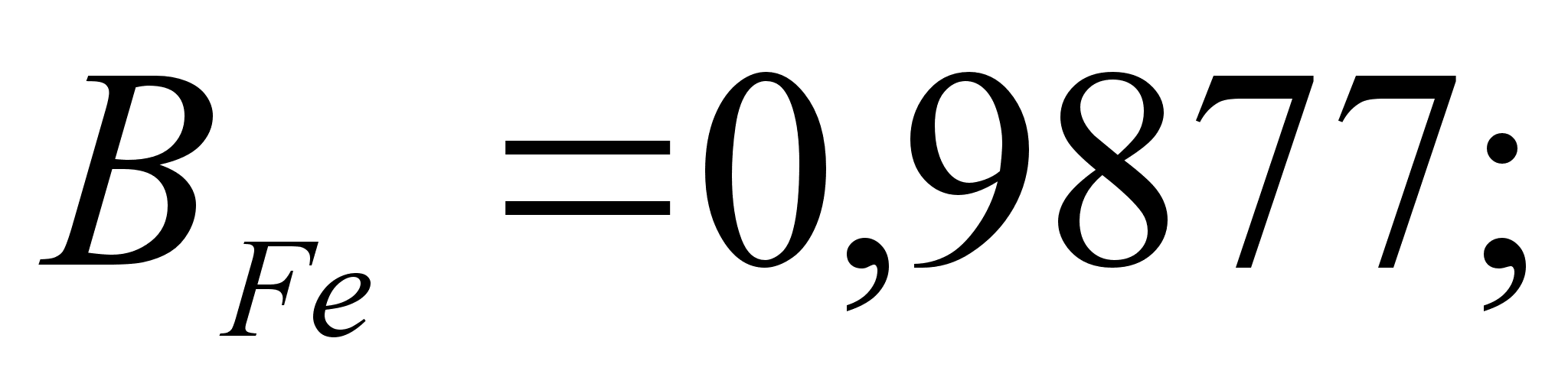
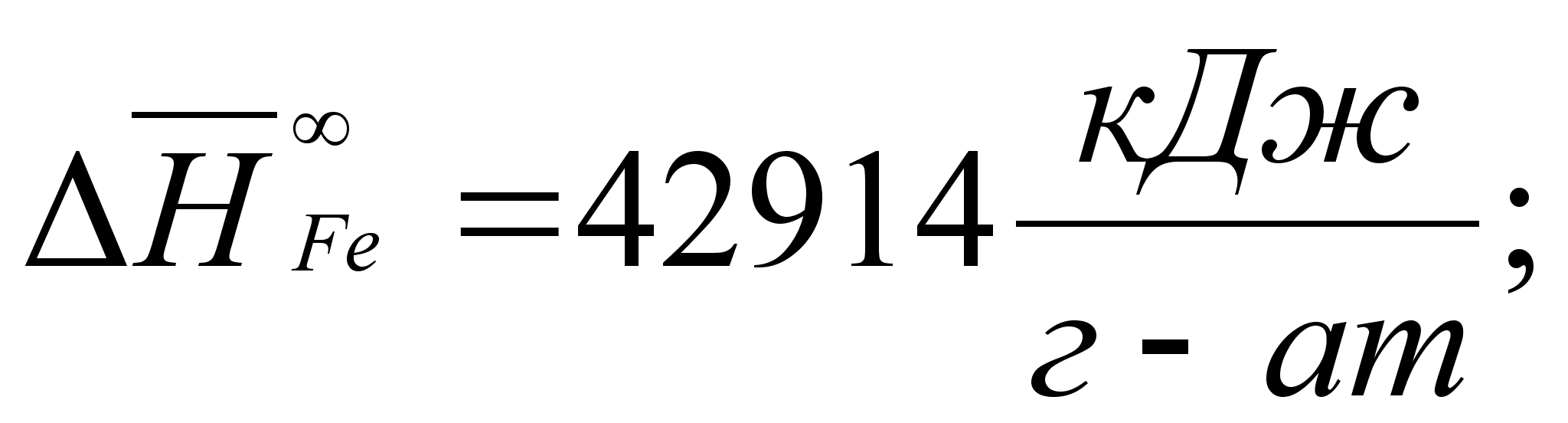
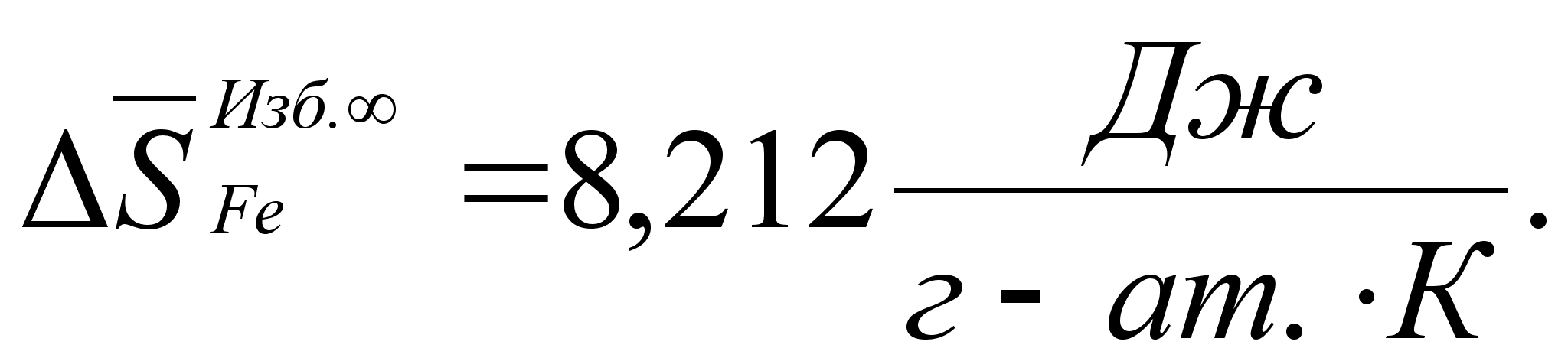
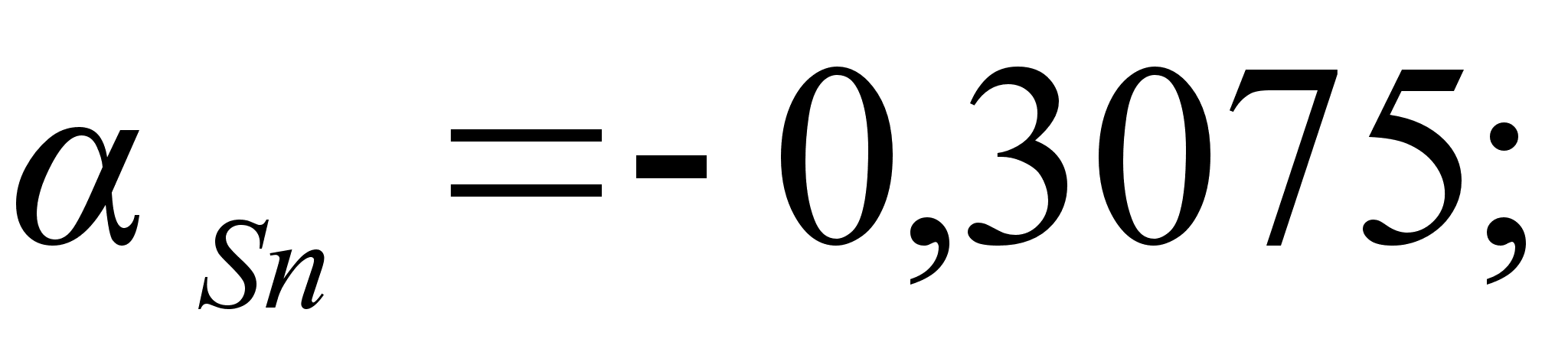
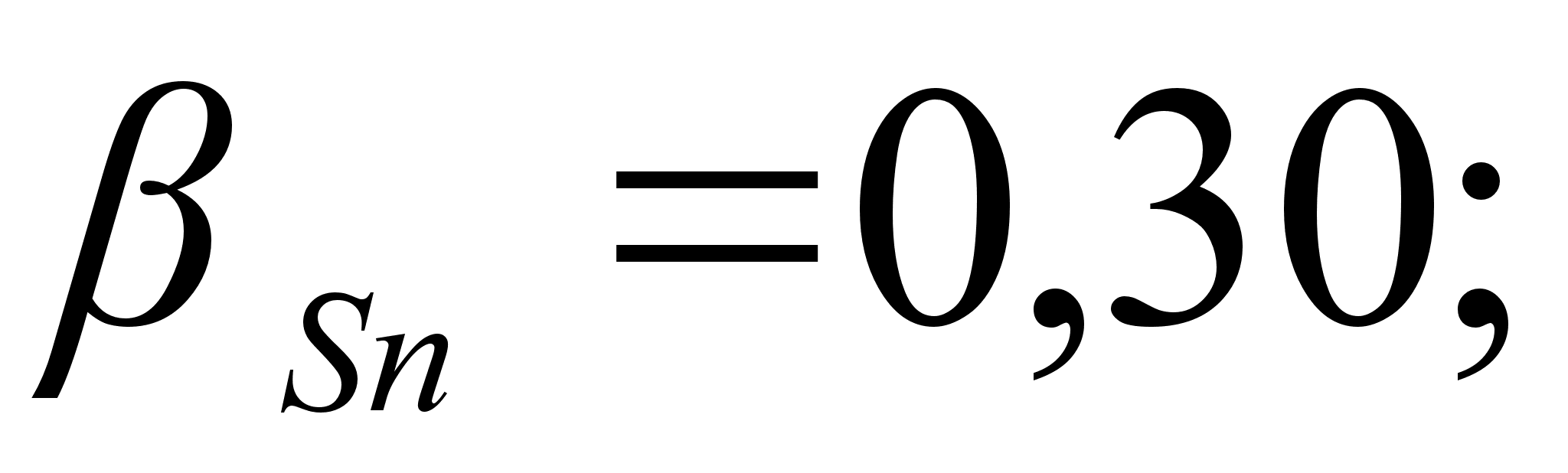
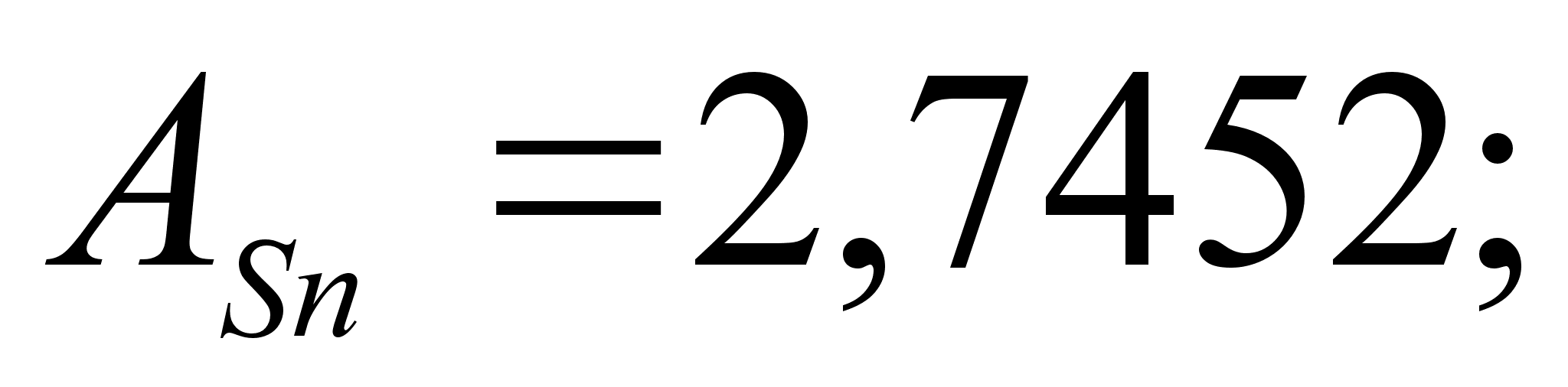
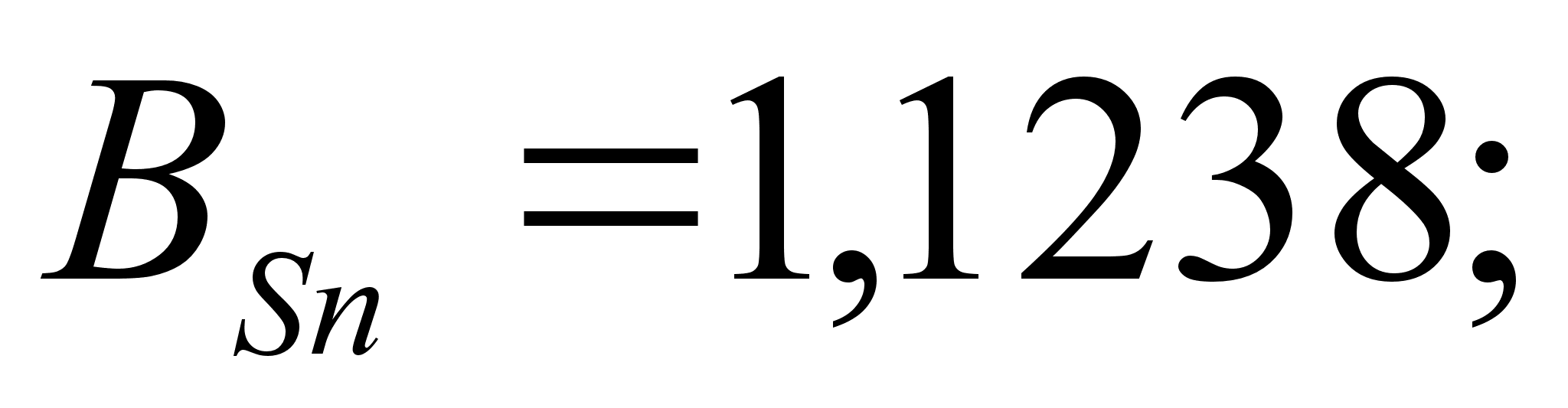
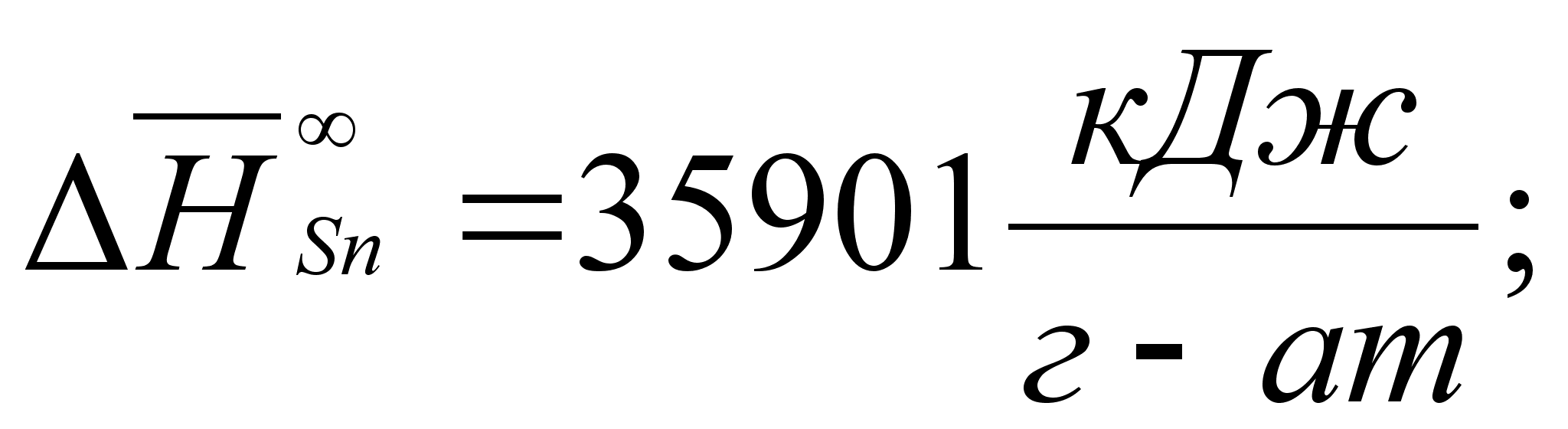
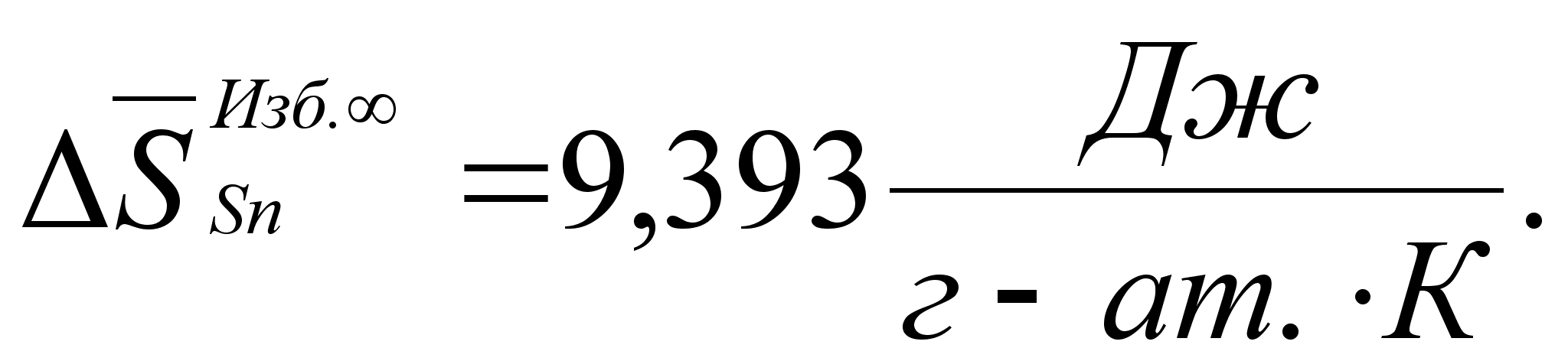
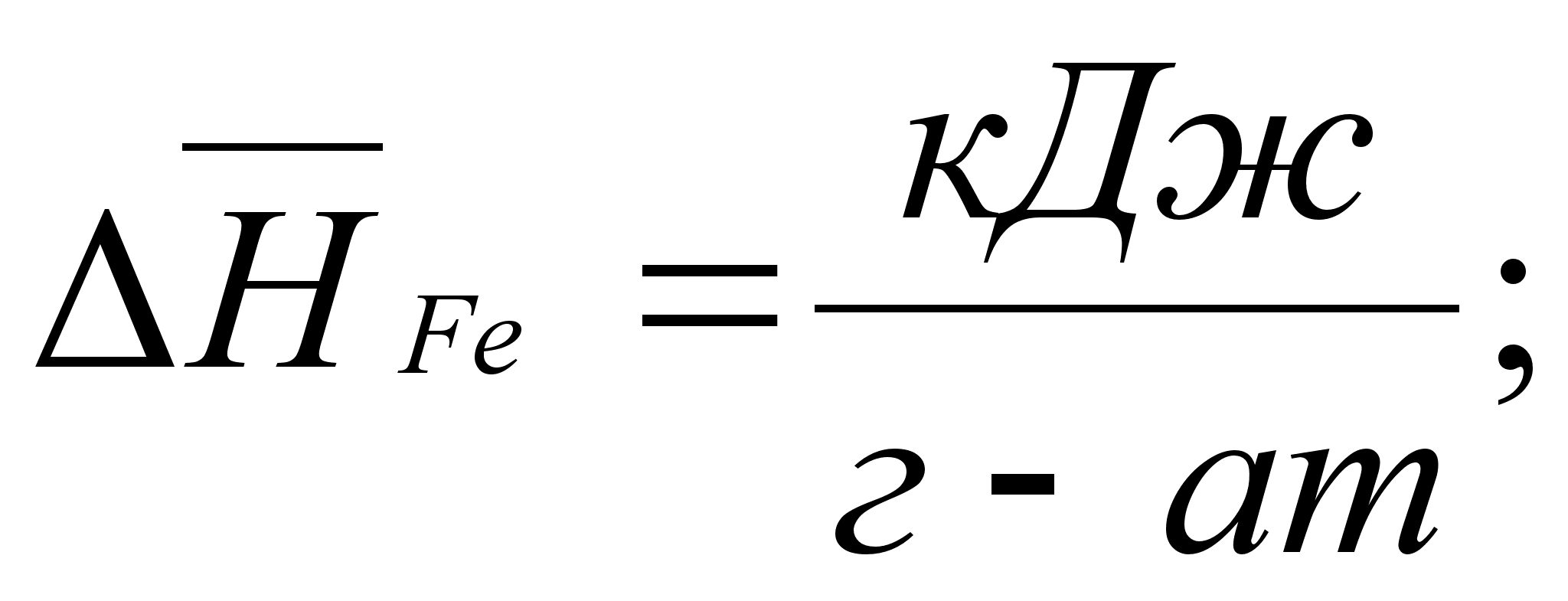
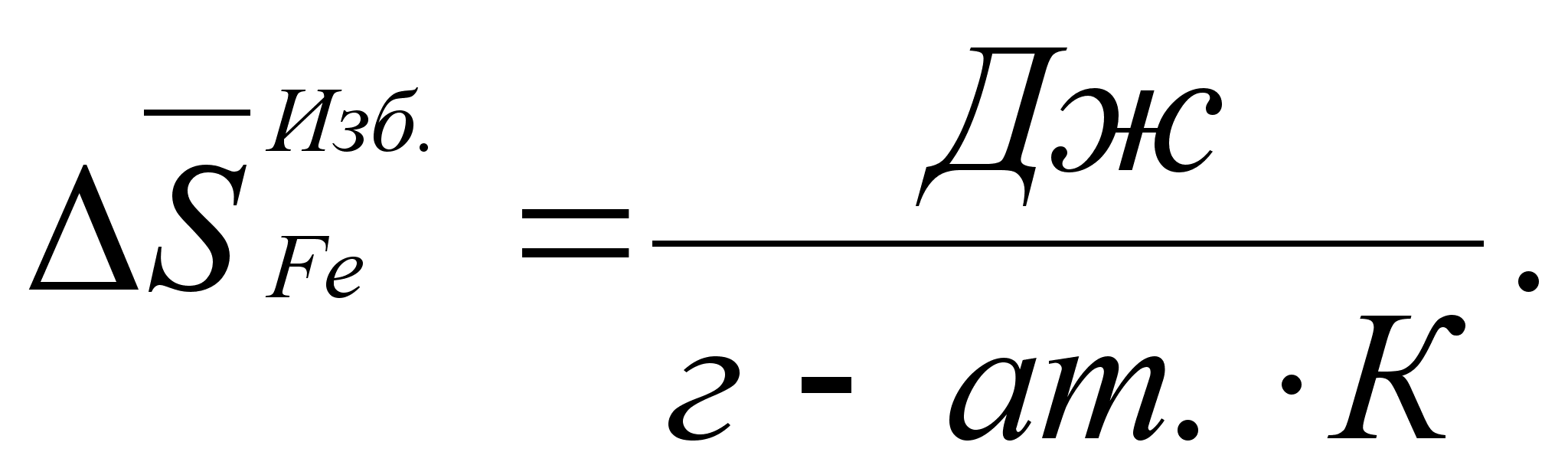
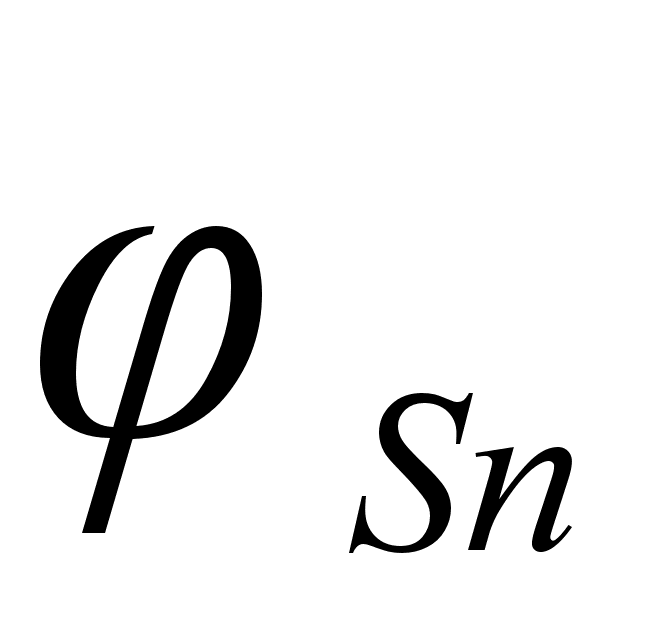
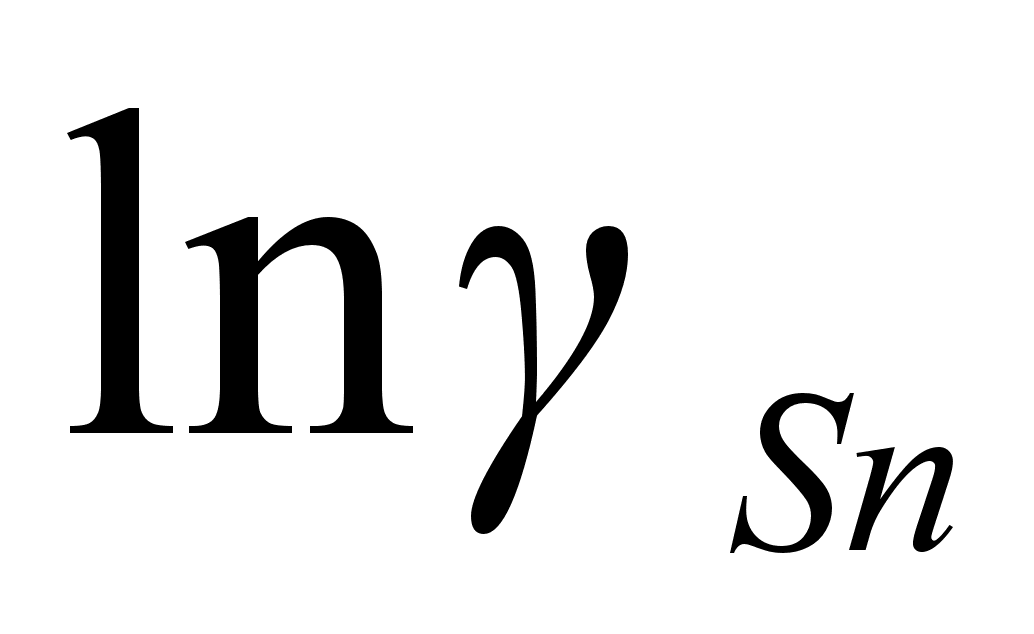
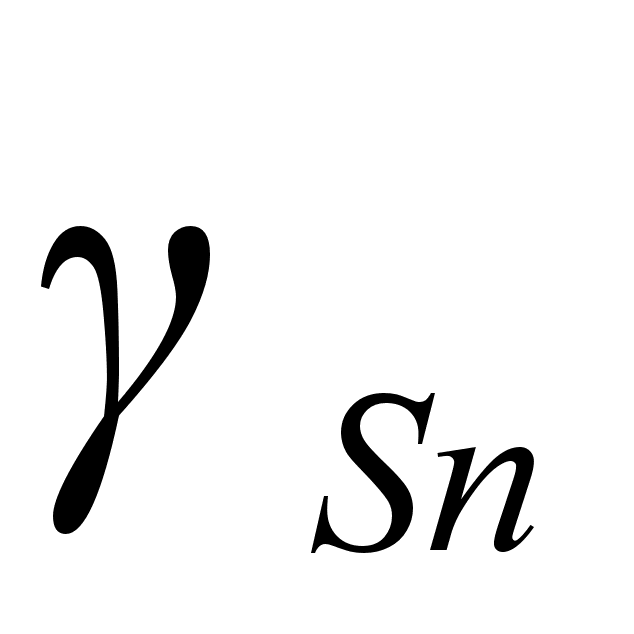
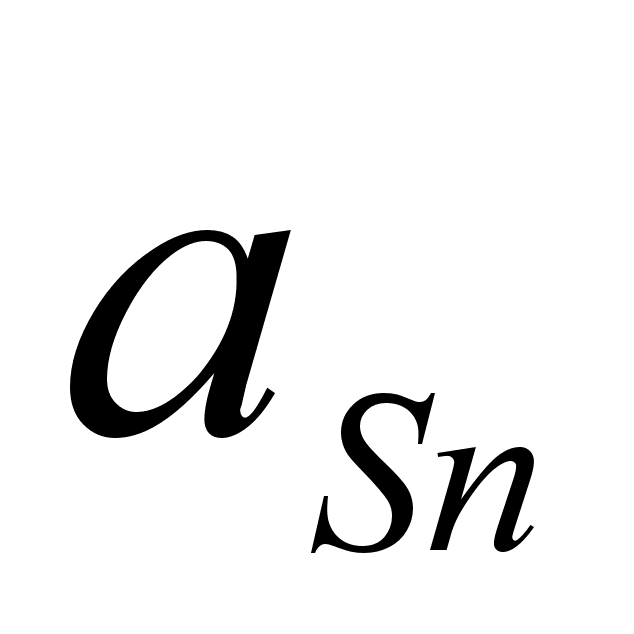
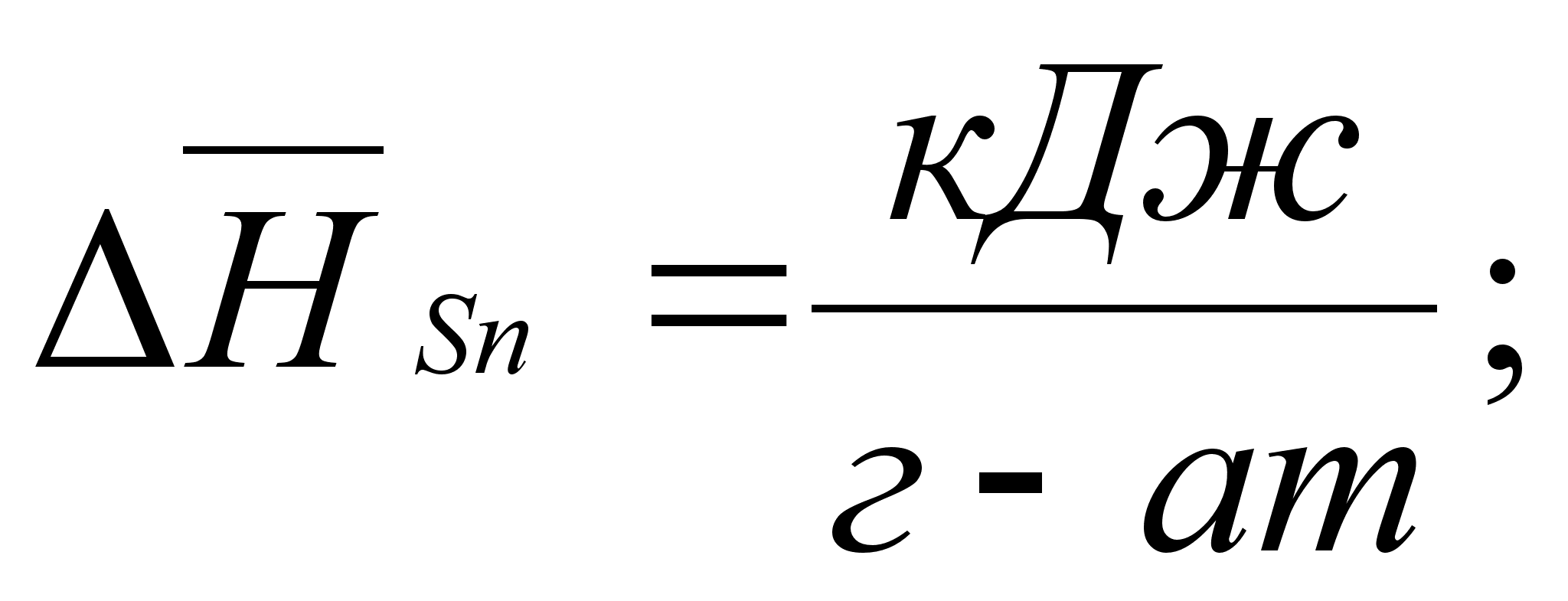
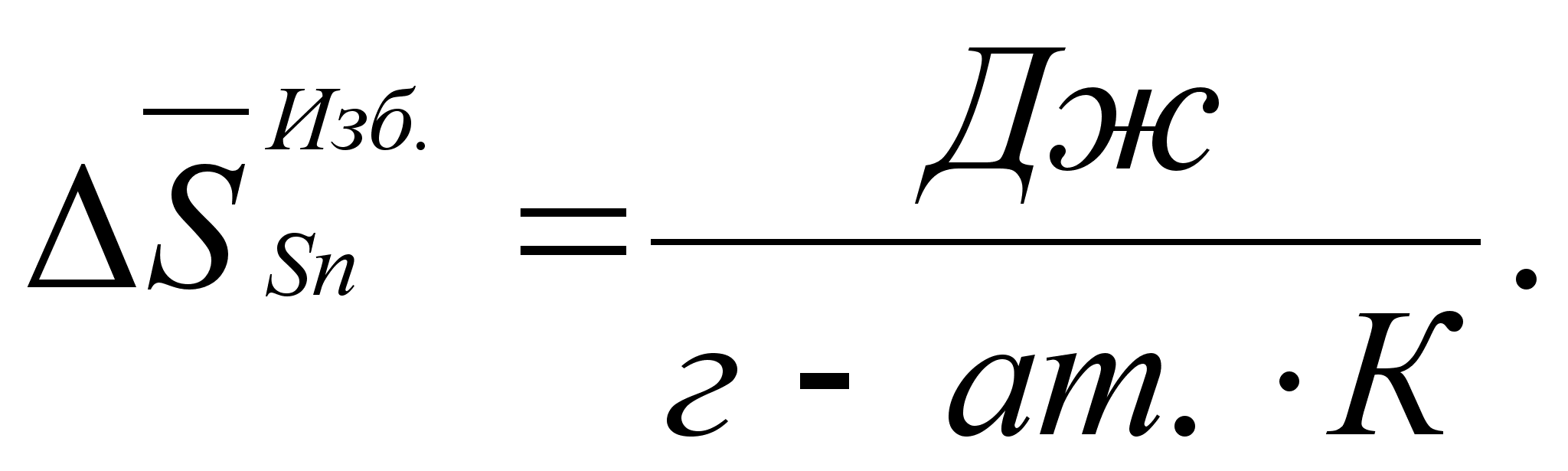
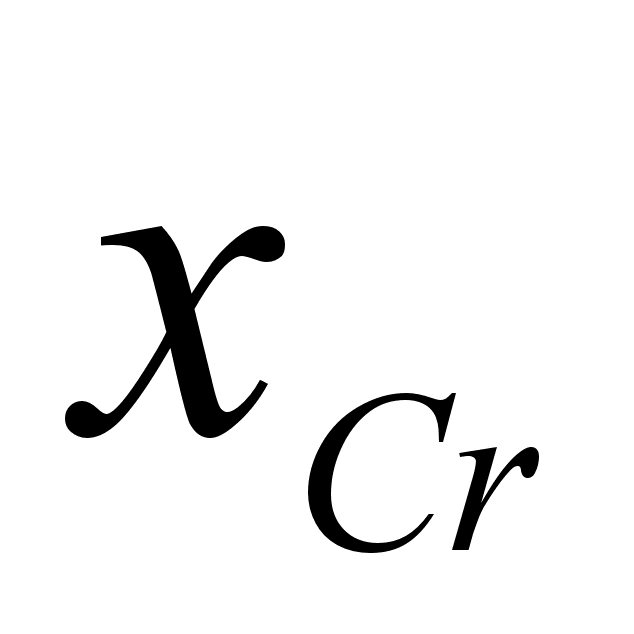 .
.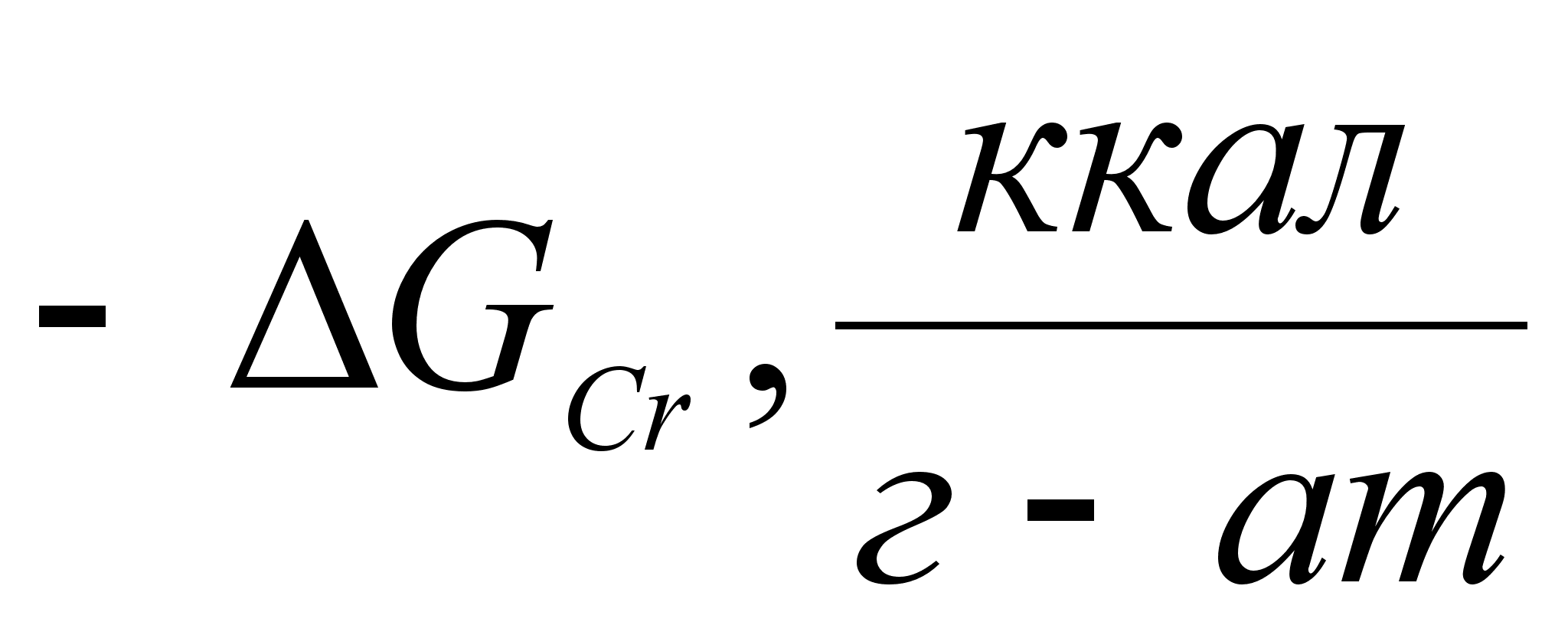
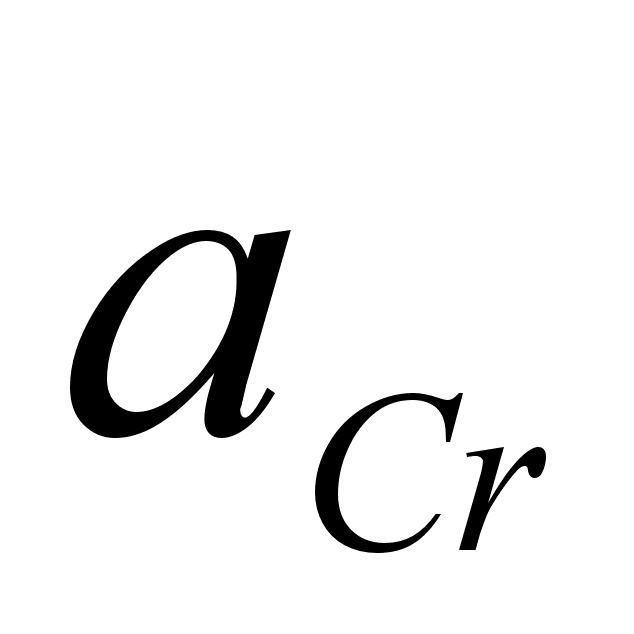
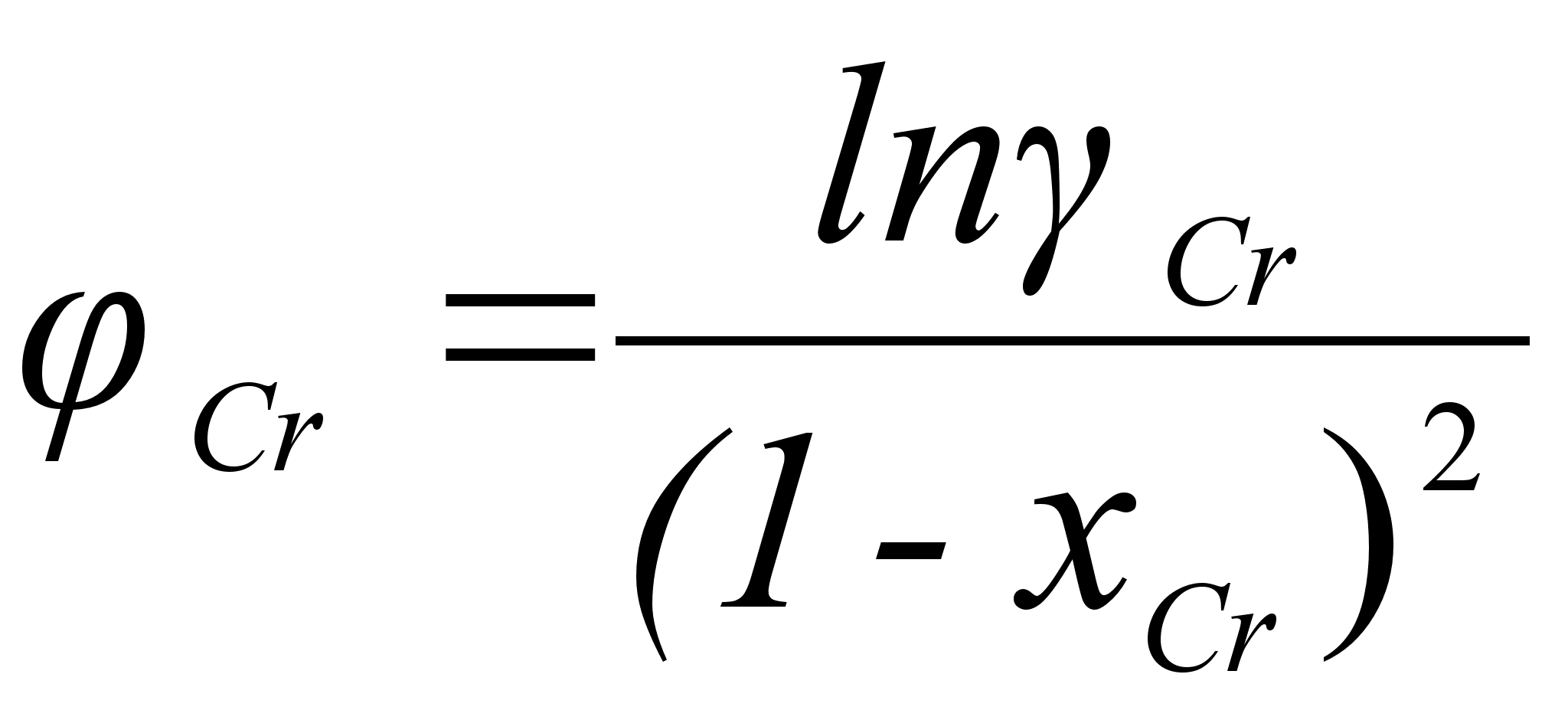
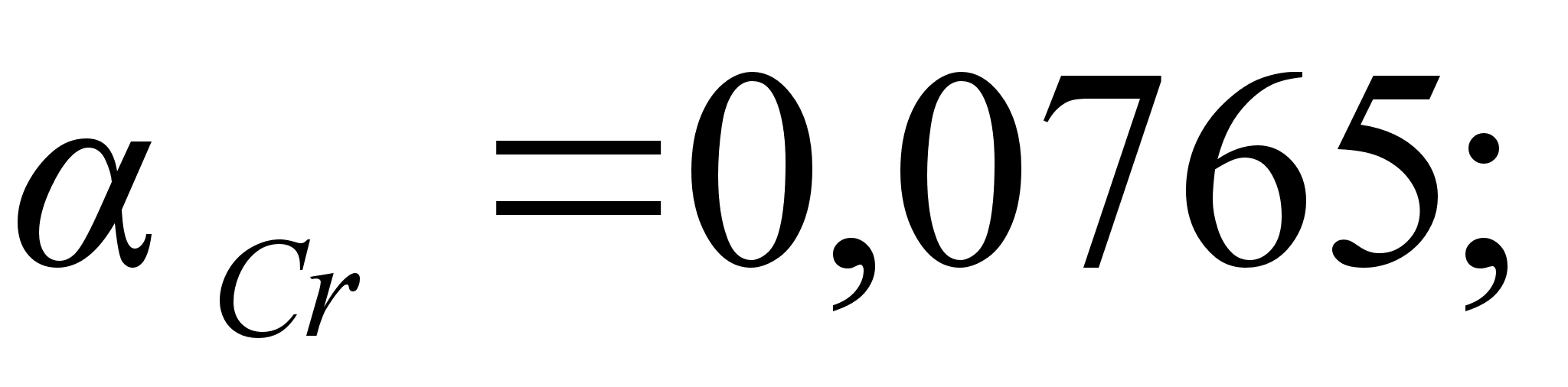
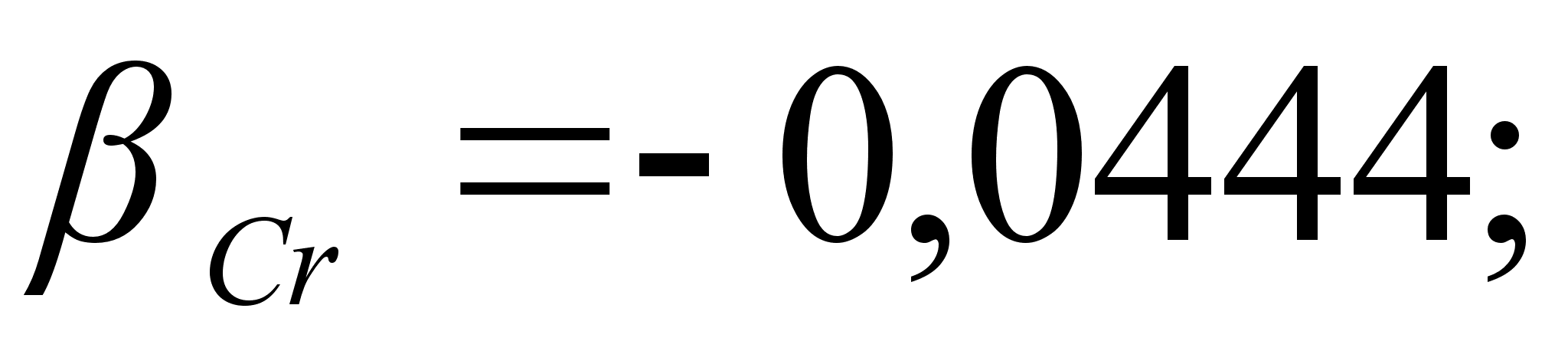
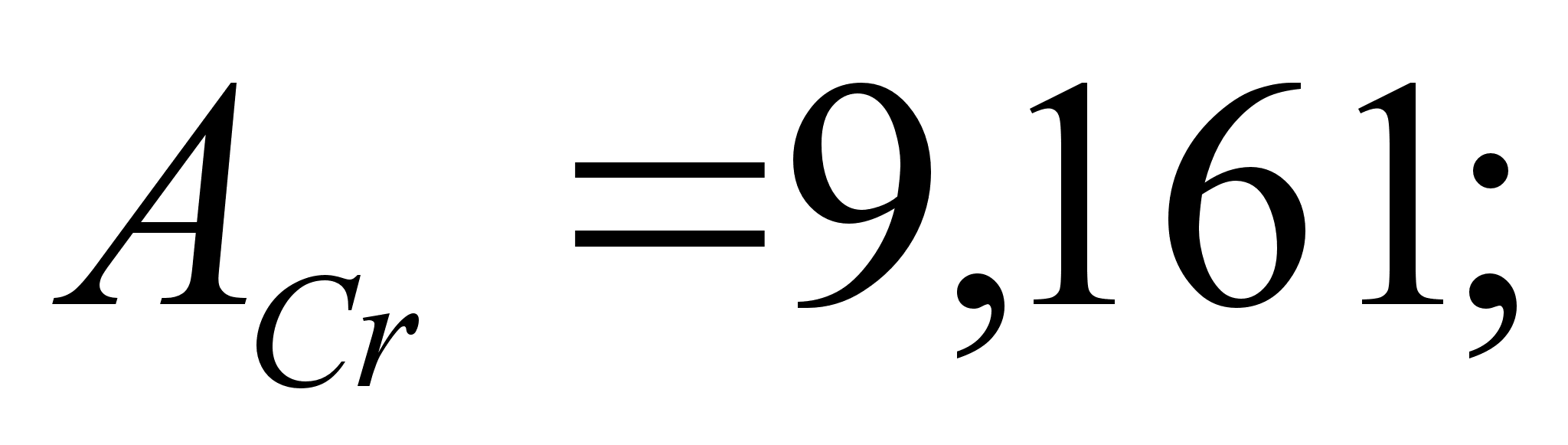
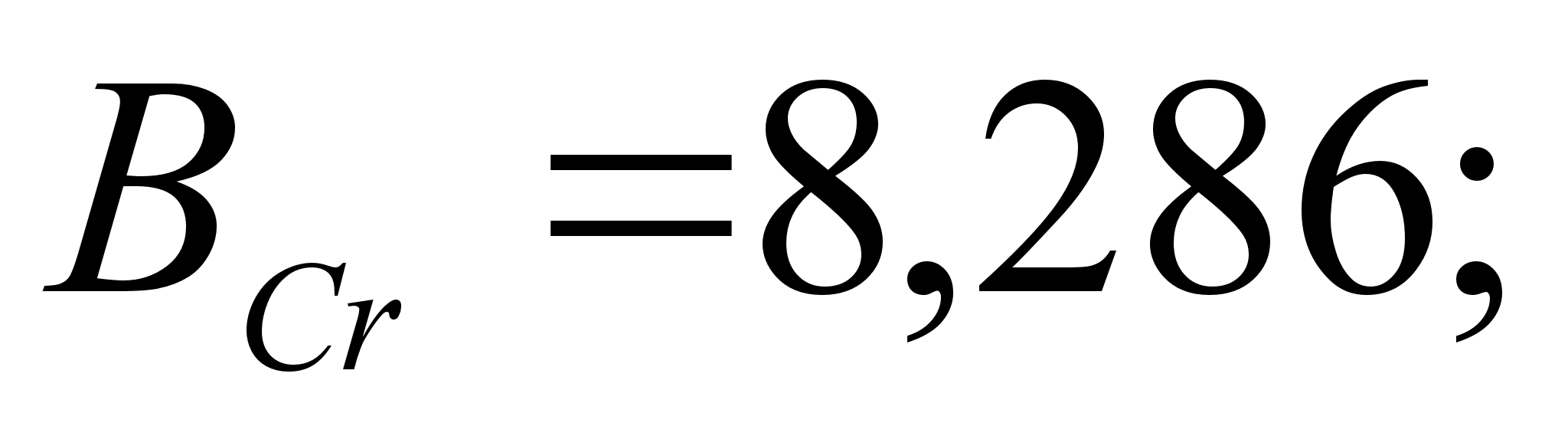
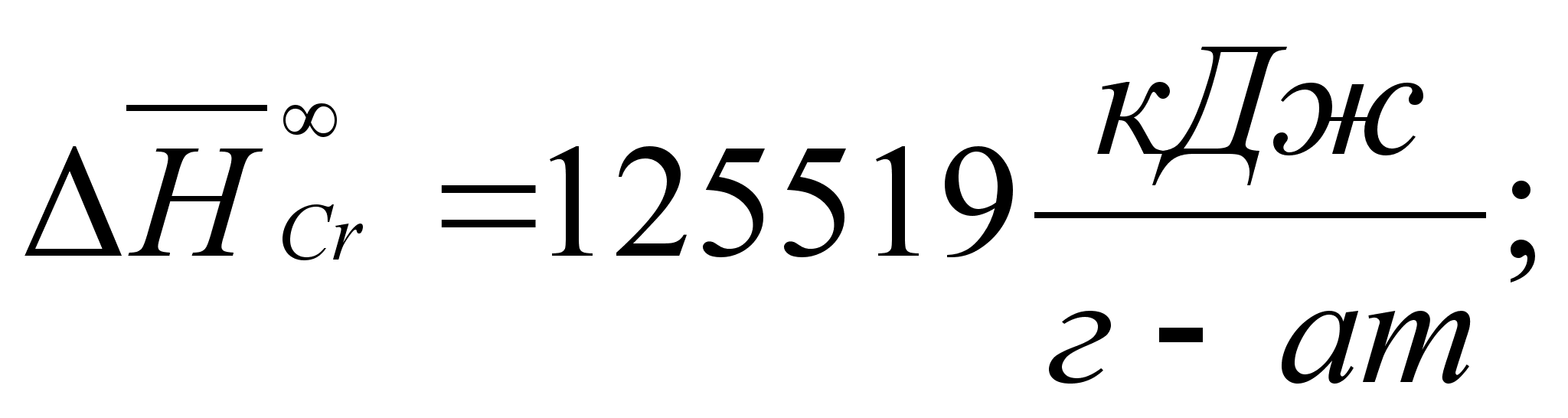
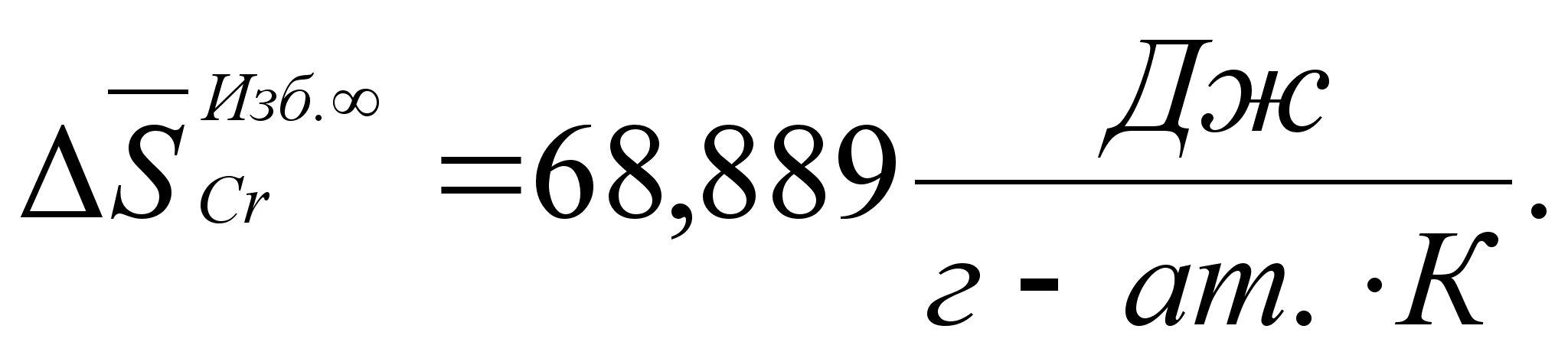
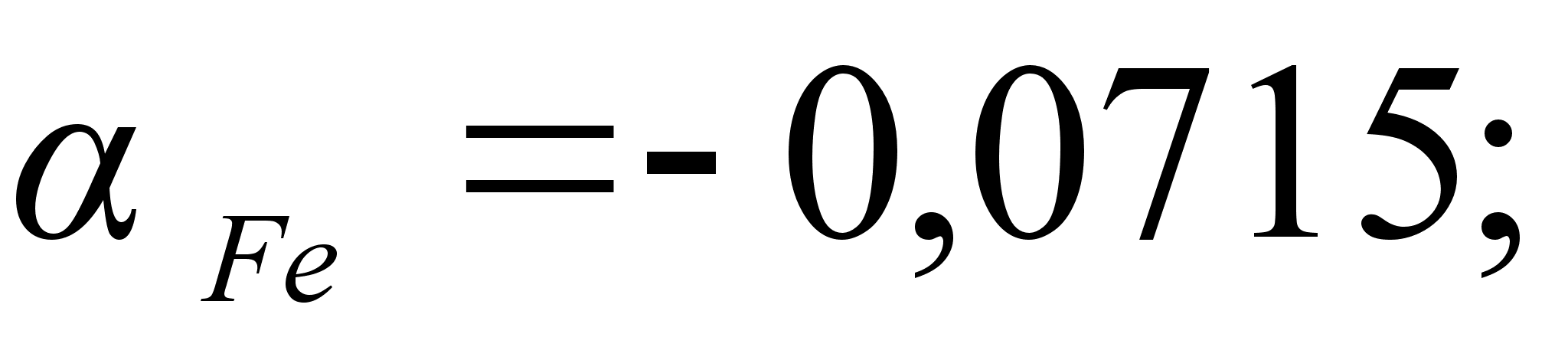

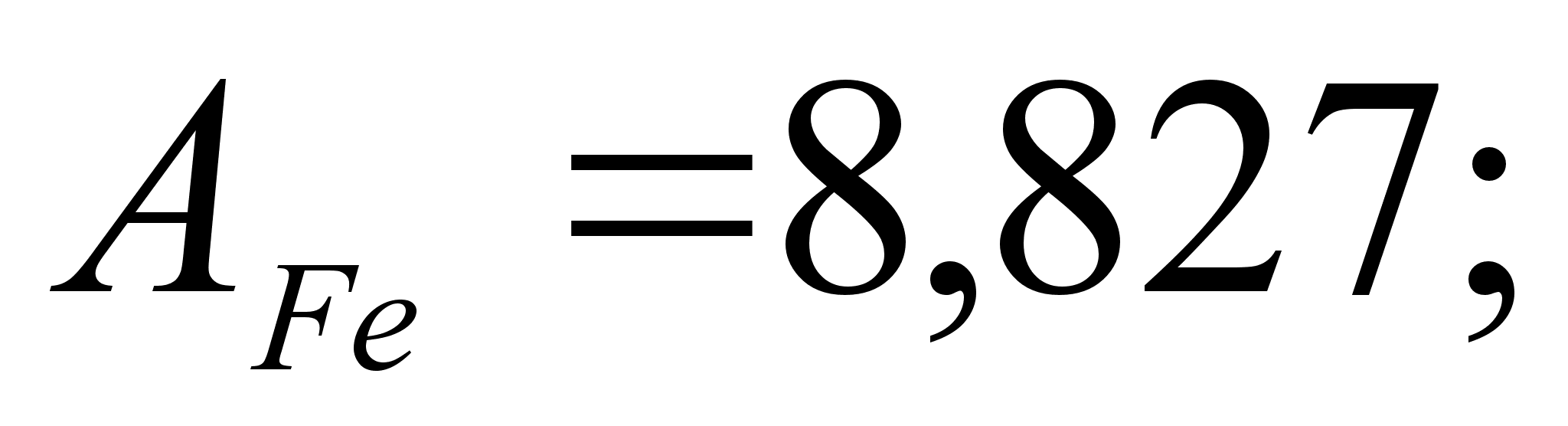
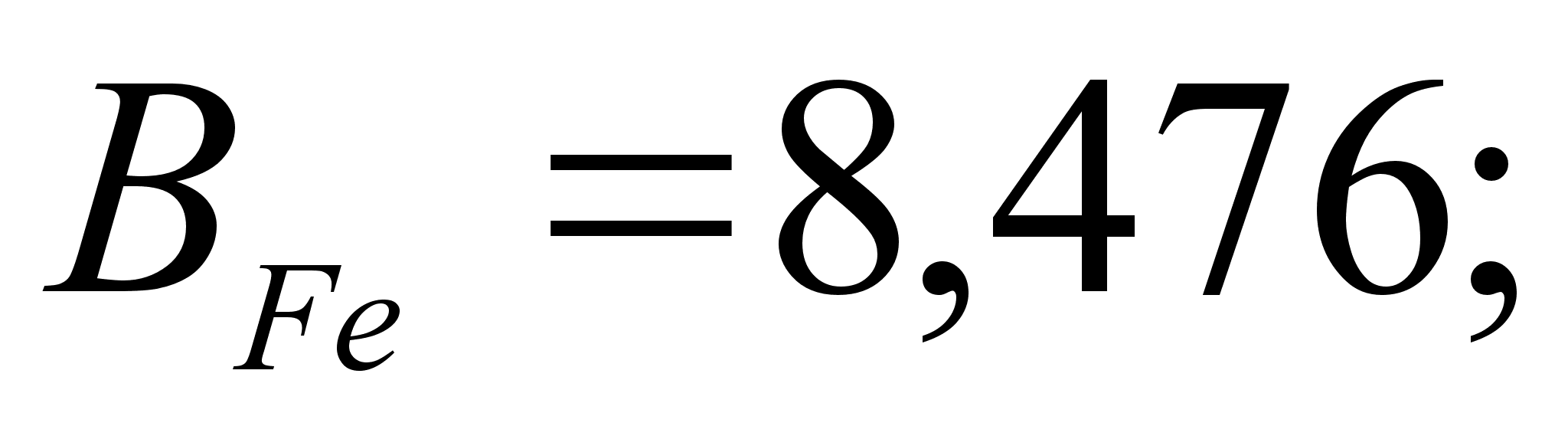
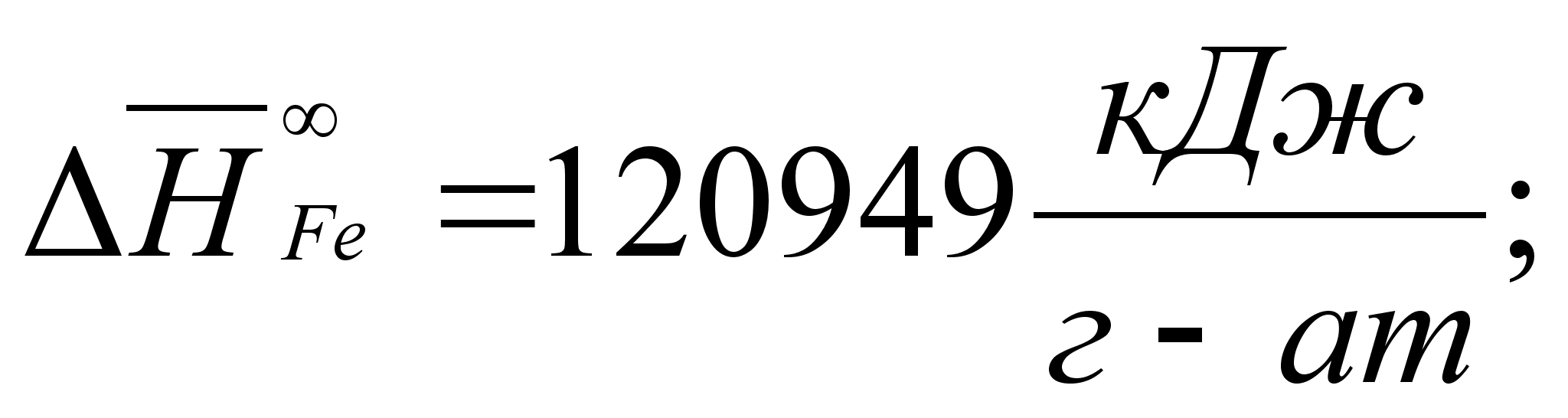
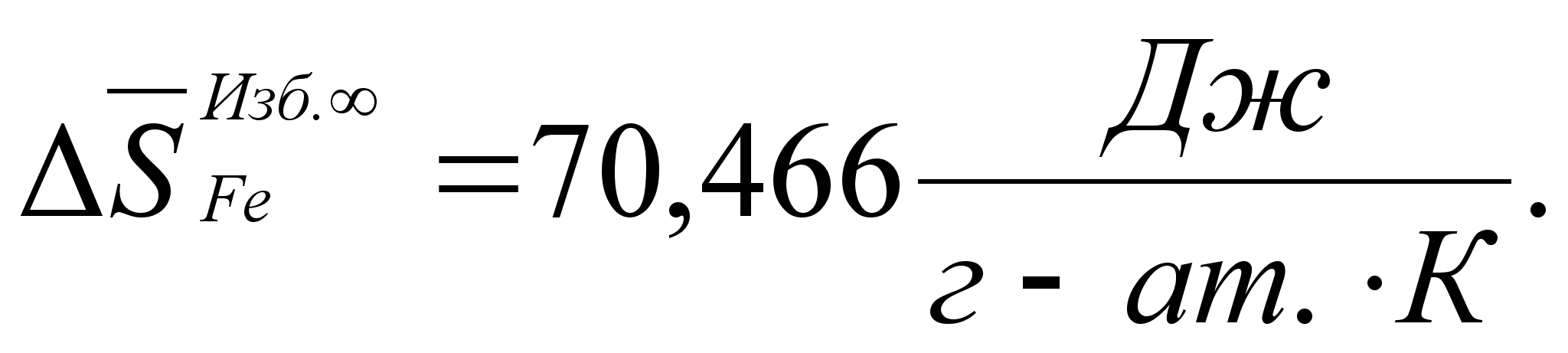
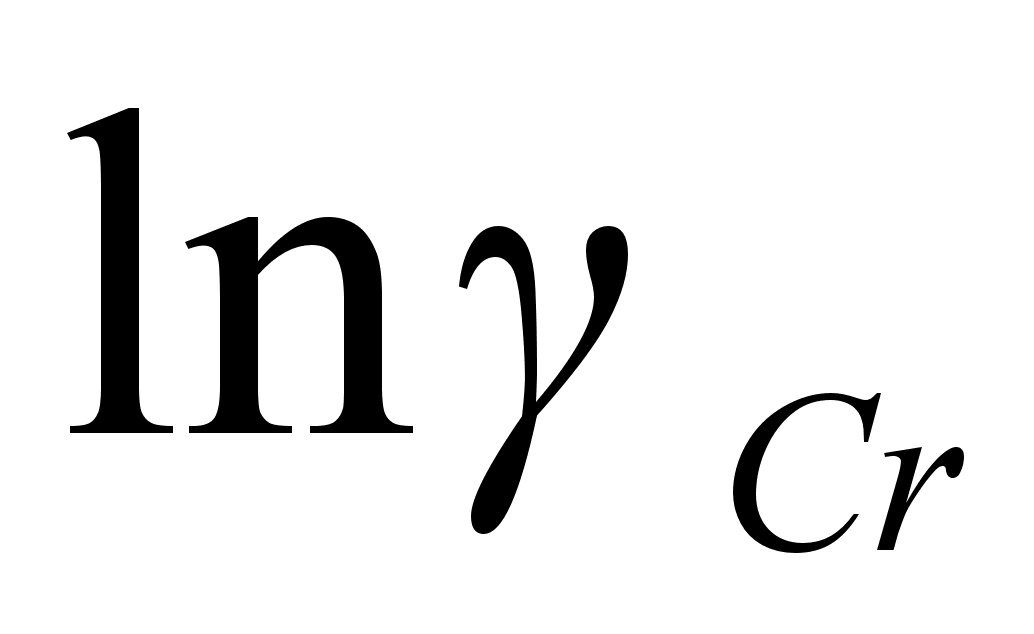
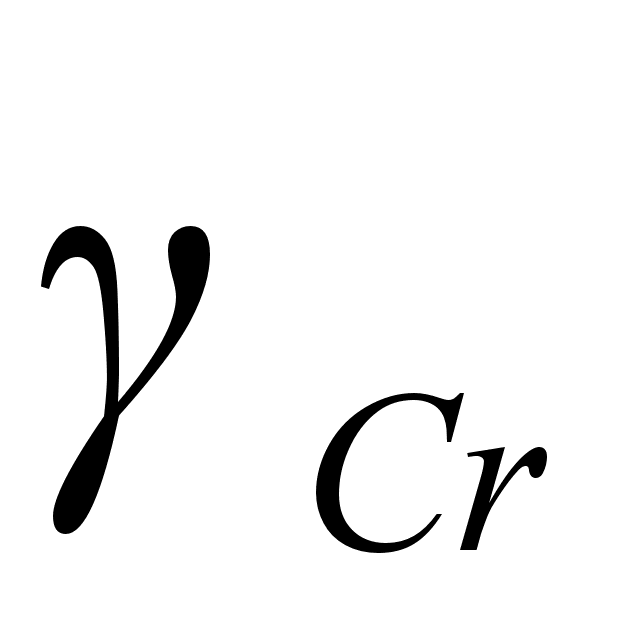
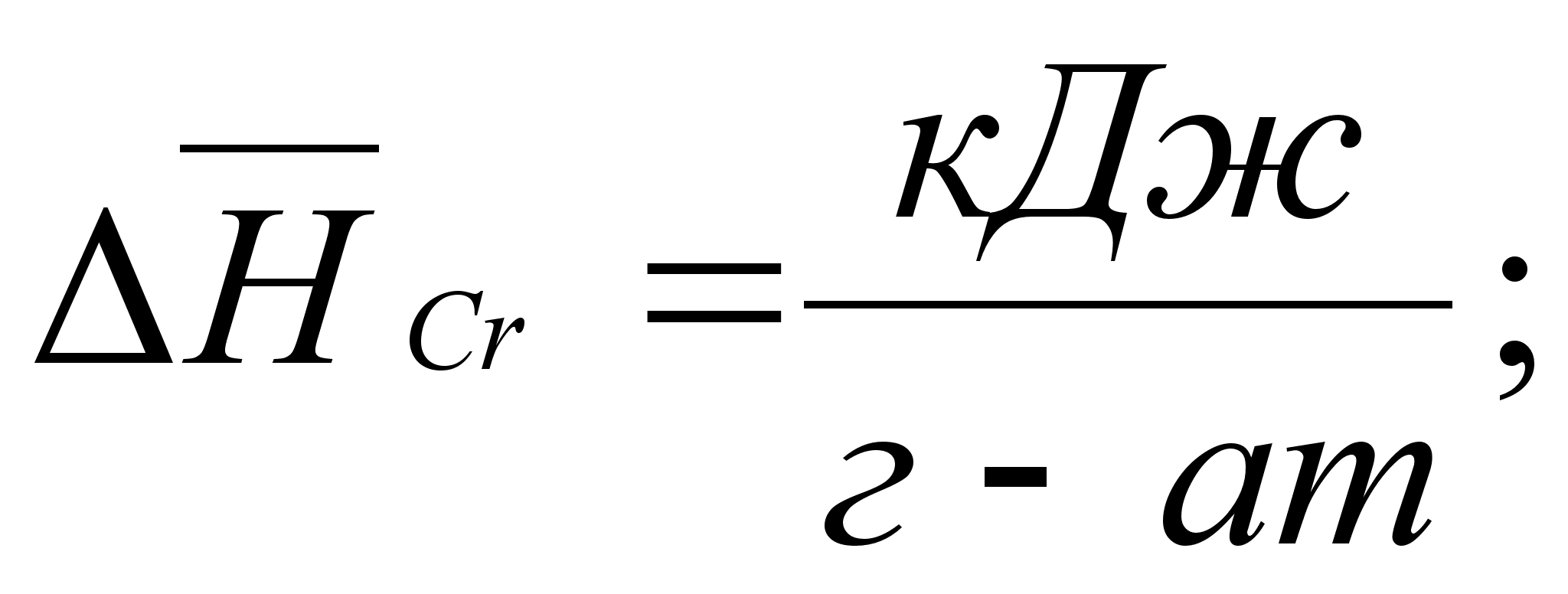
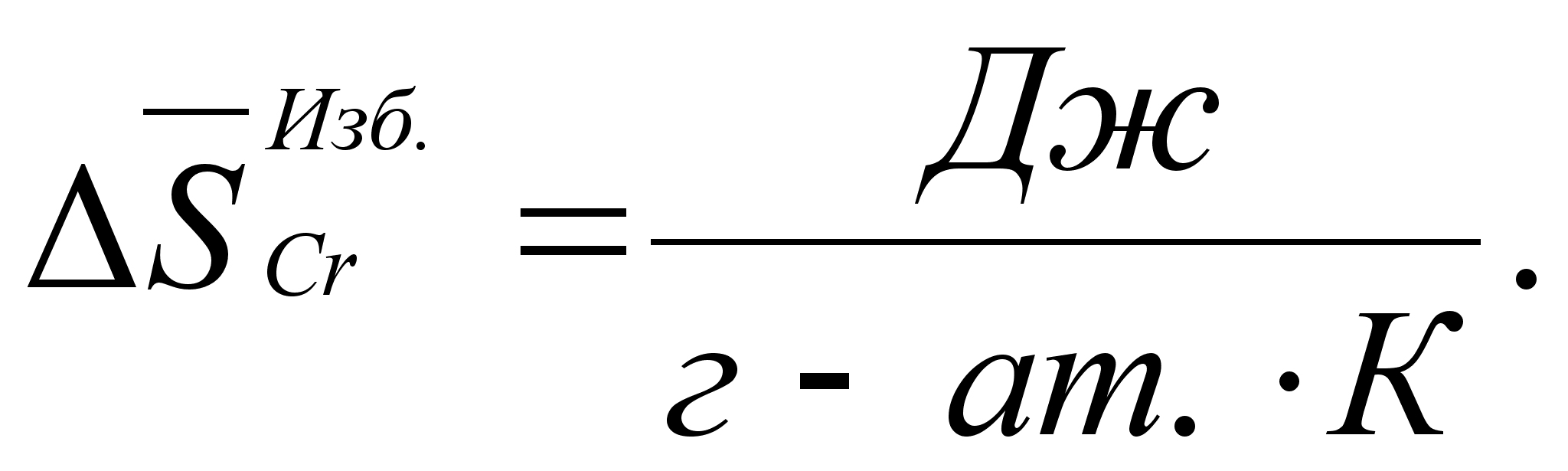
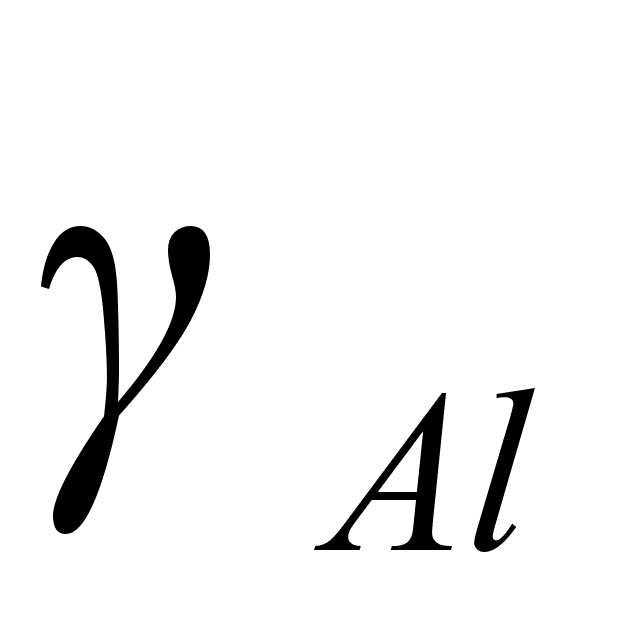
 будет выглядеть
так:
будет выглядеть
так:
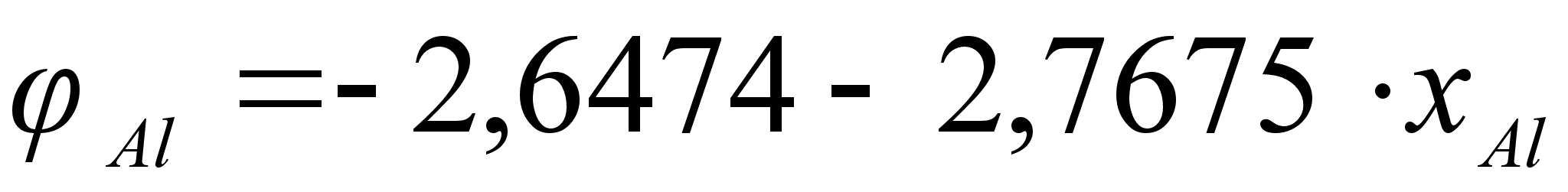
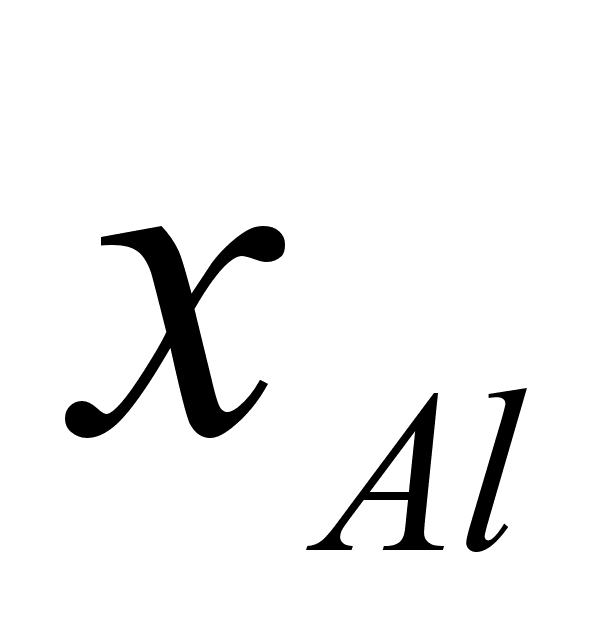


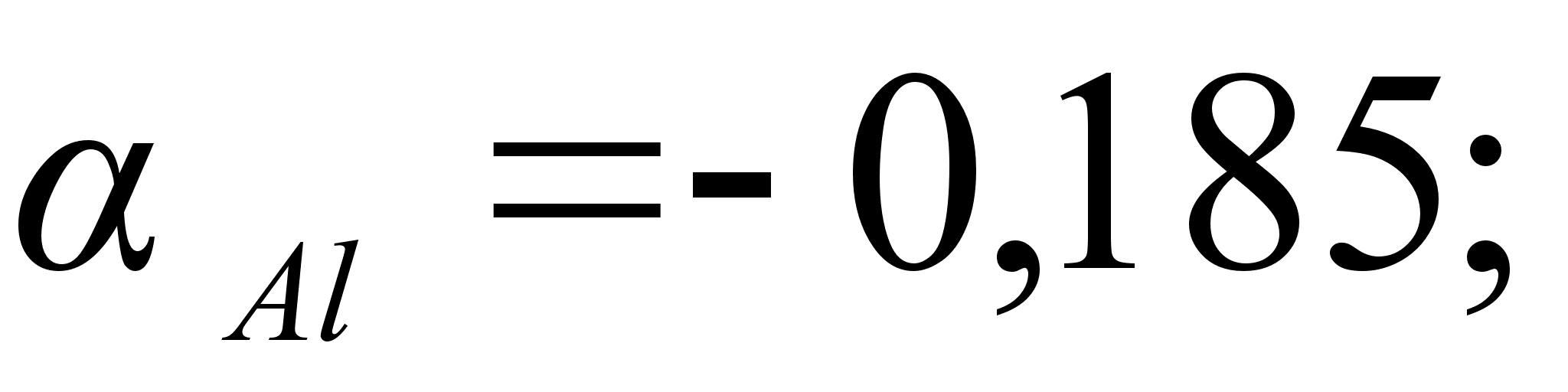
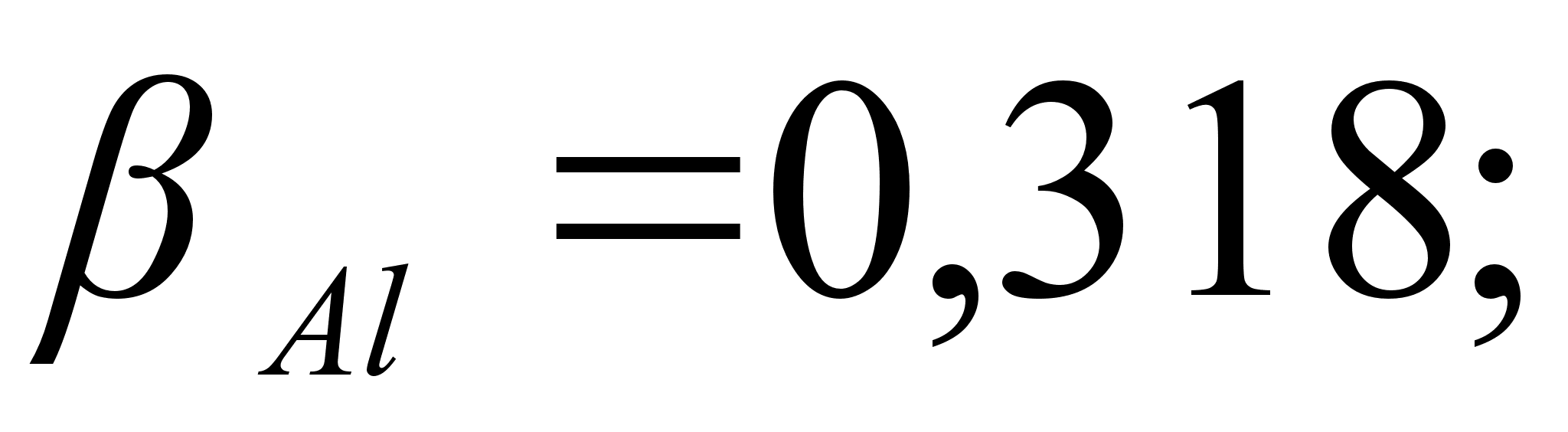
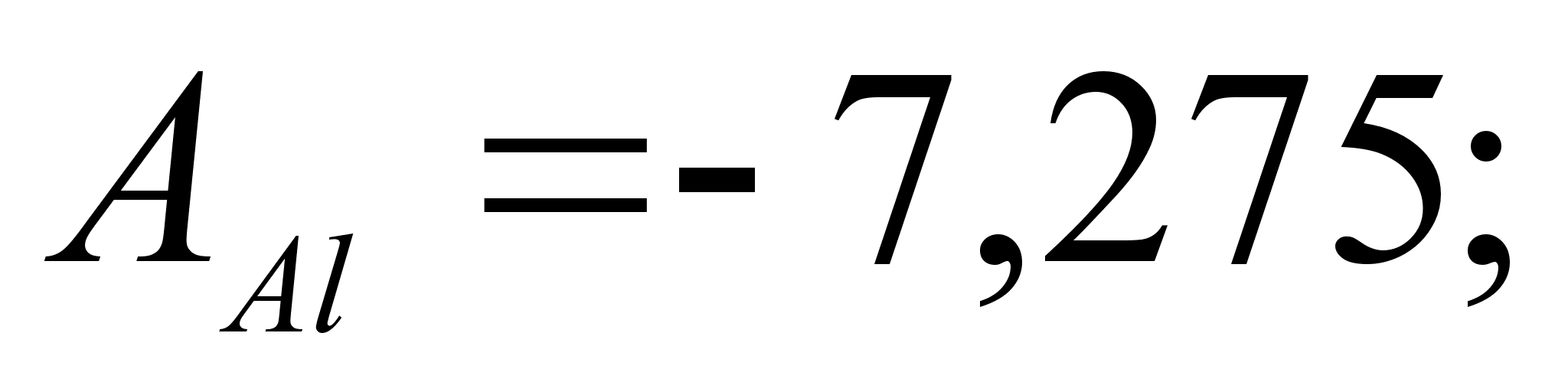
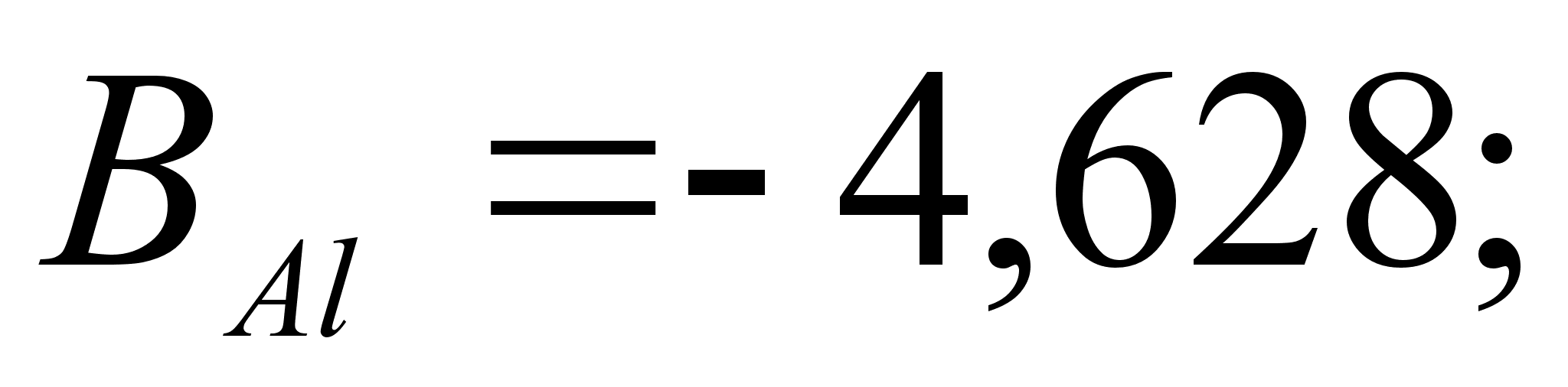
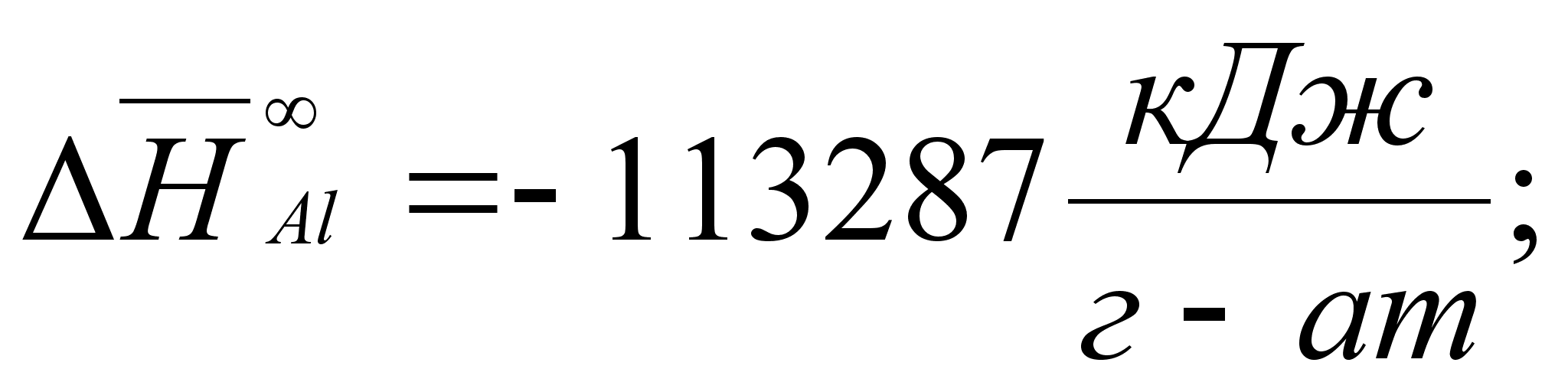
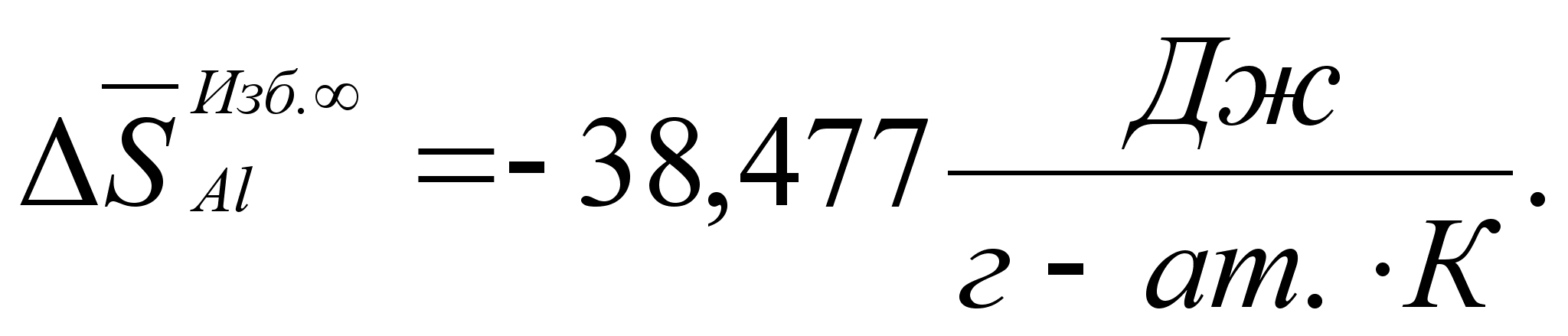
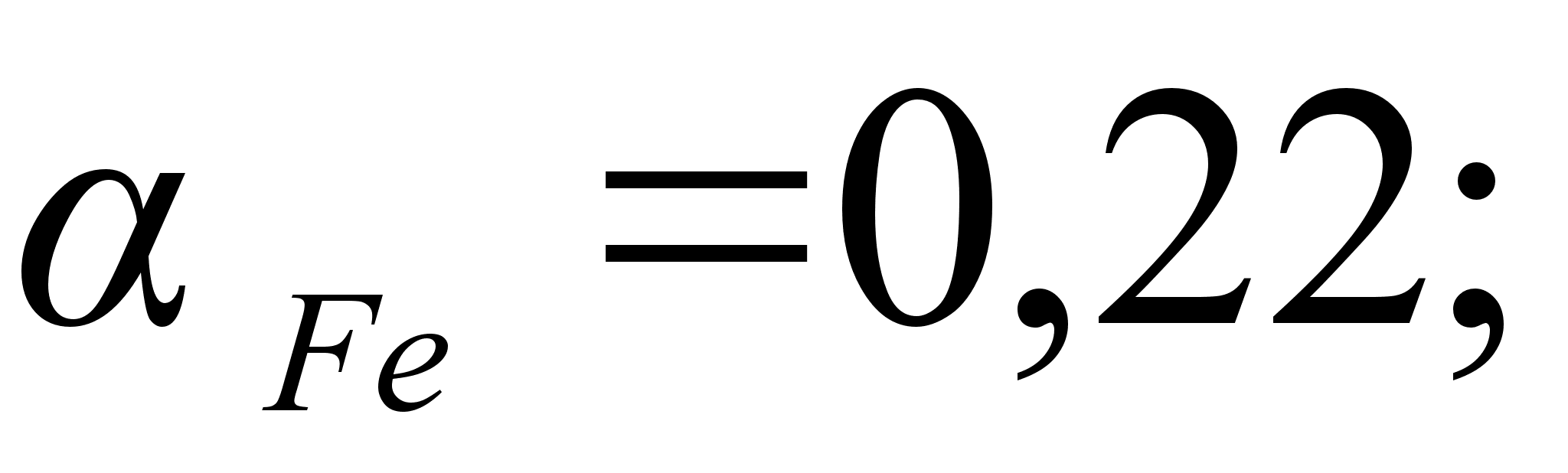
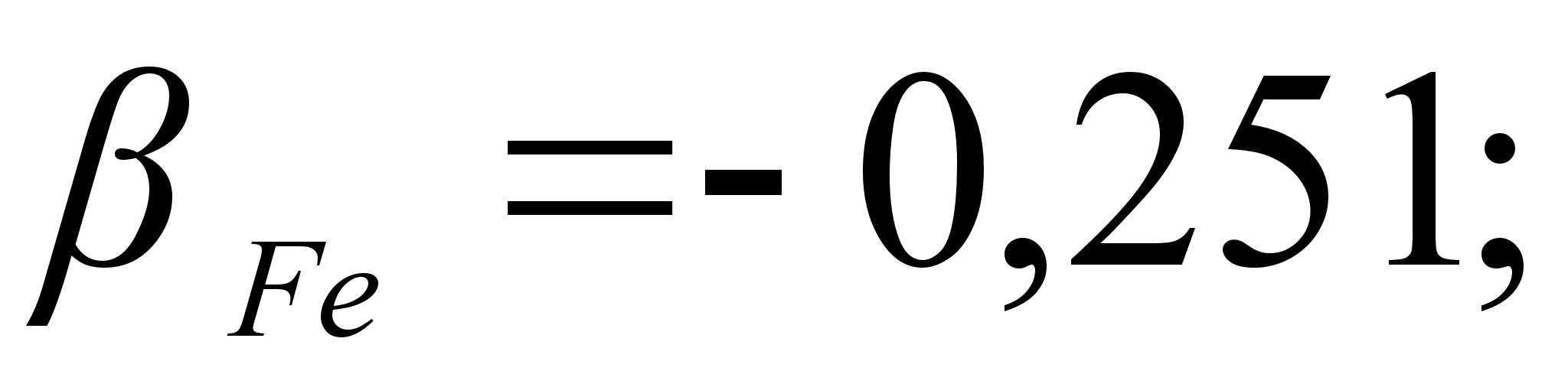
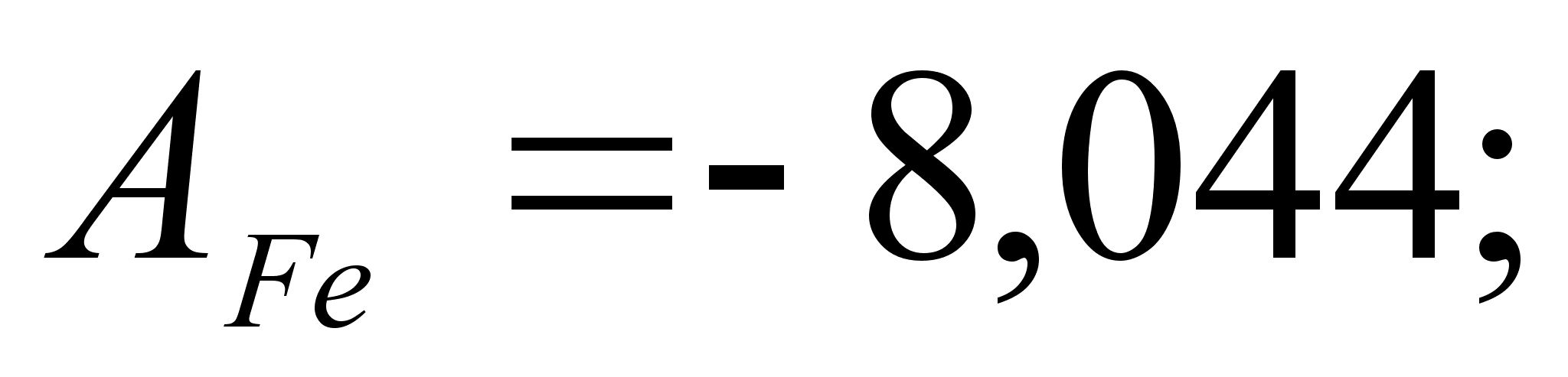
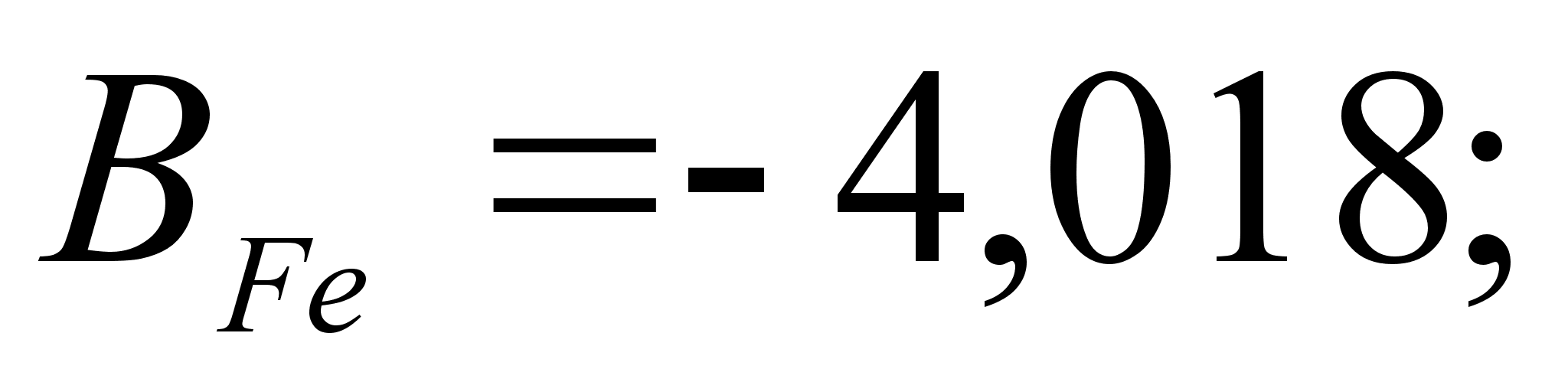

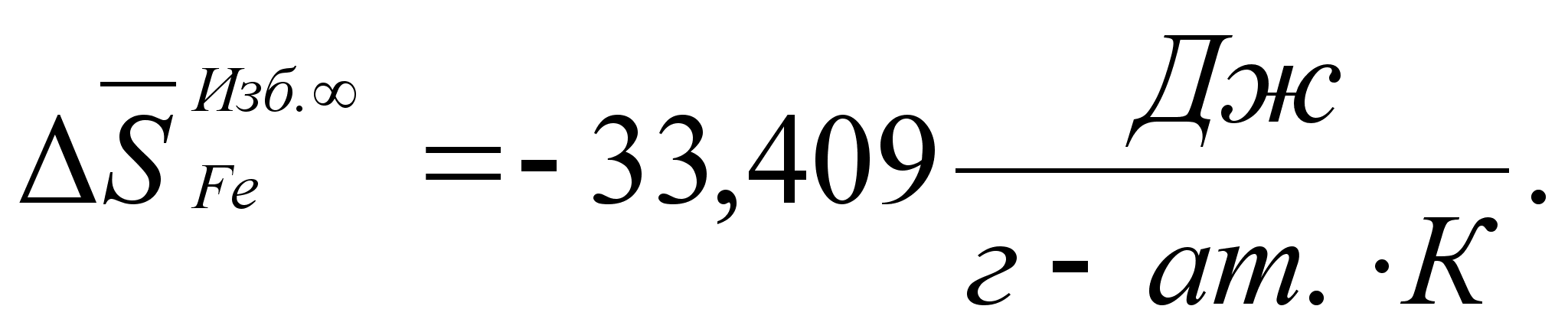

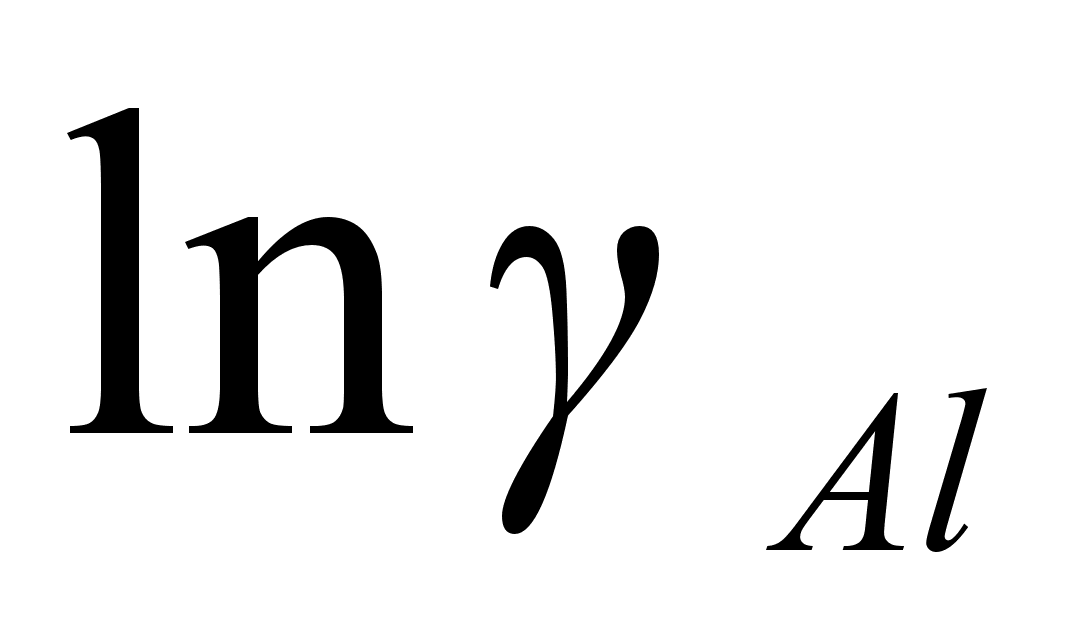
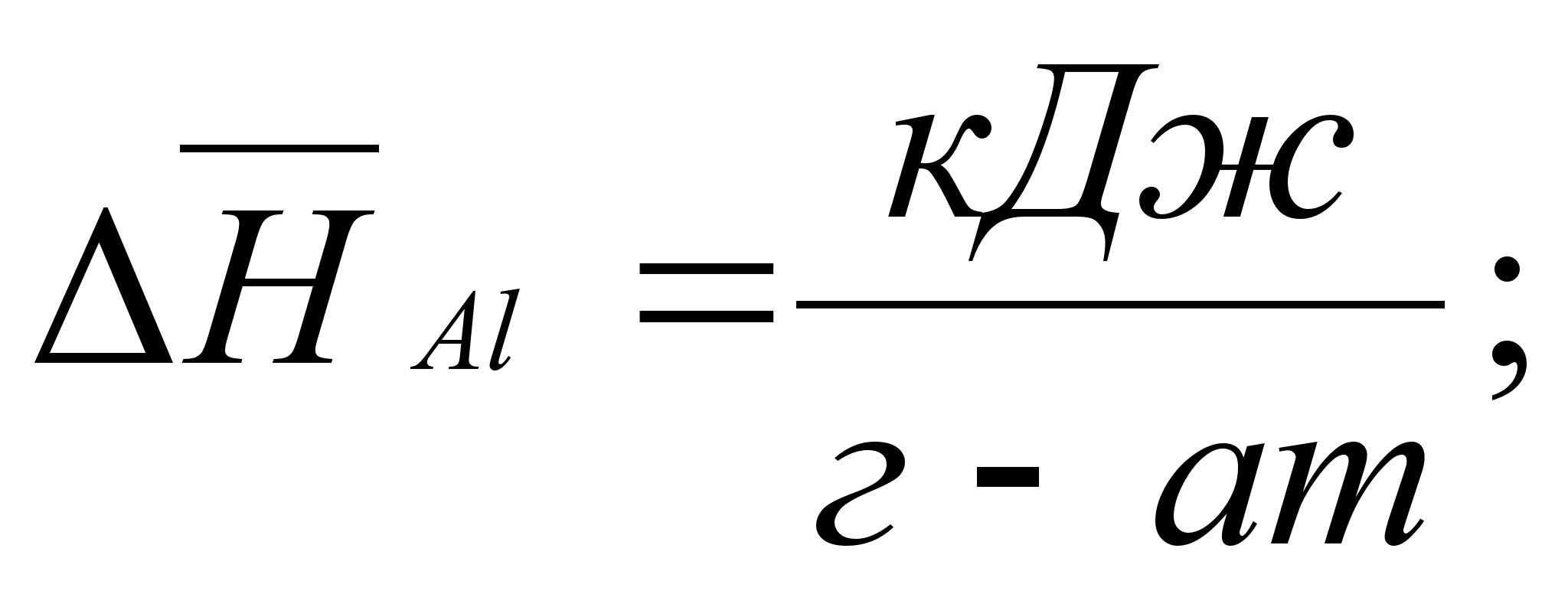
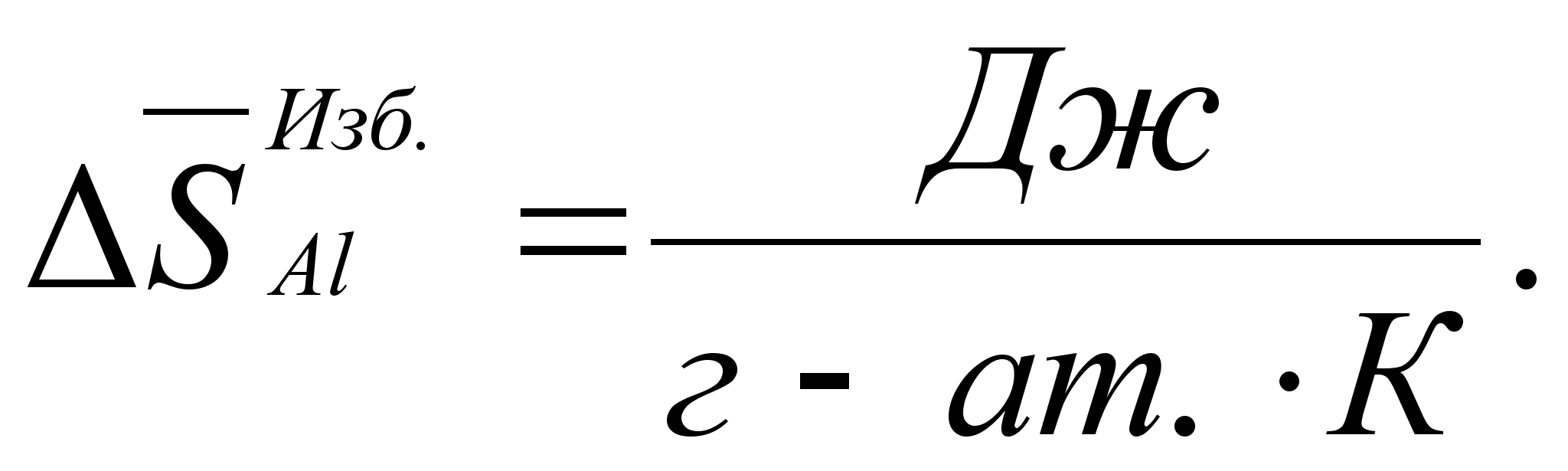
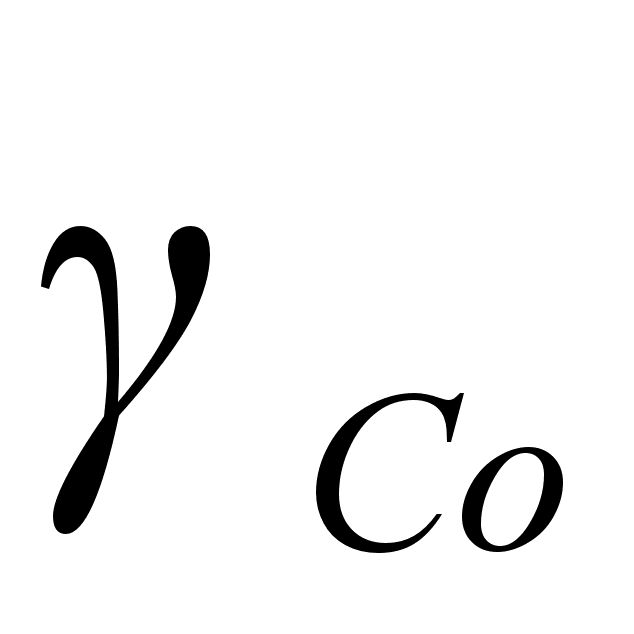
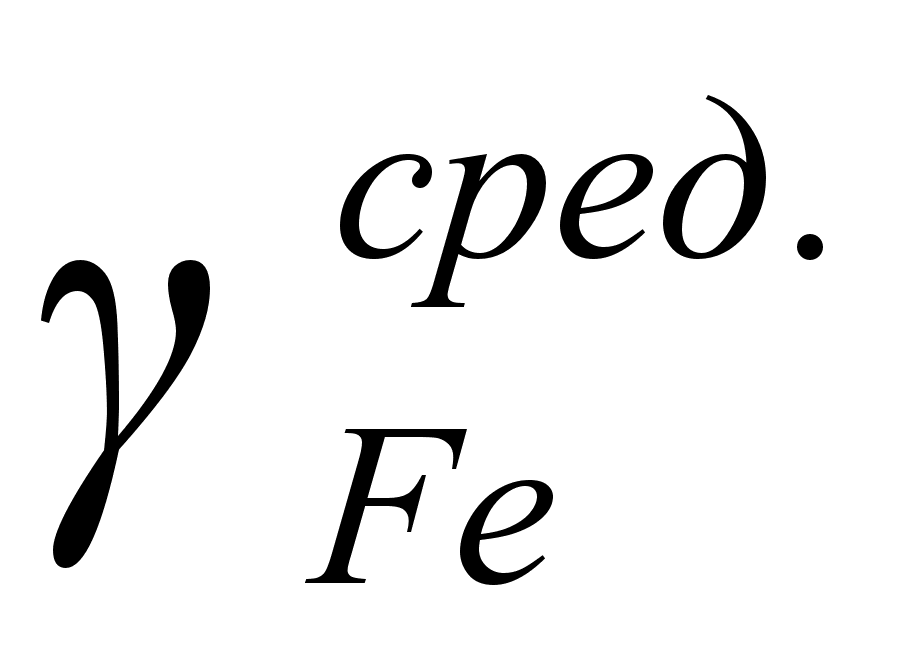
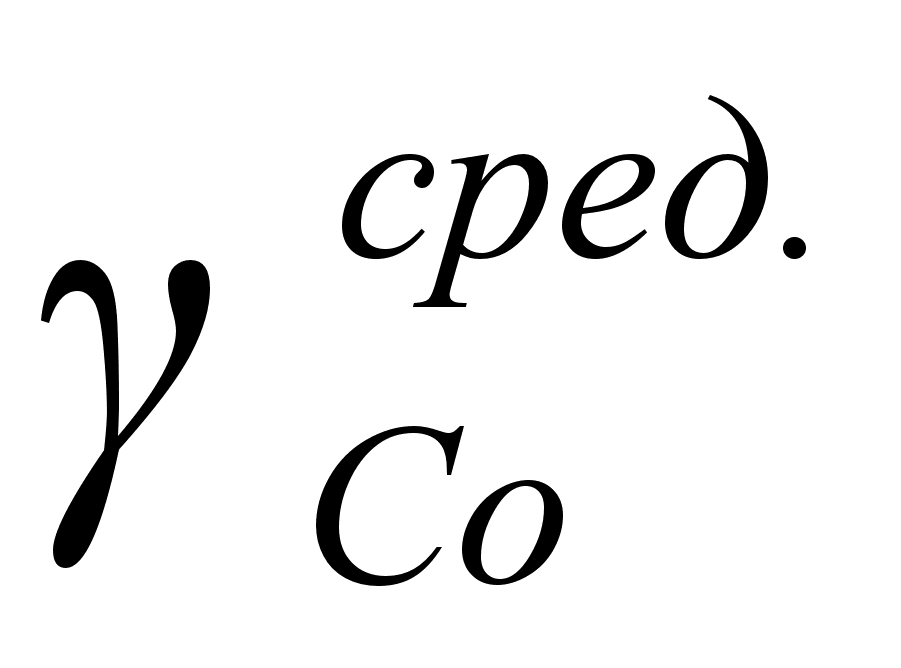
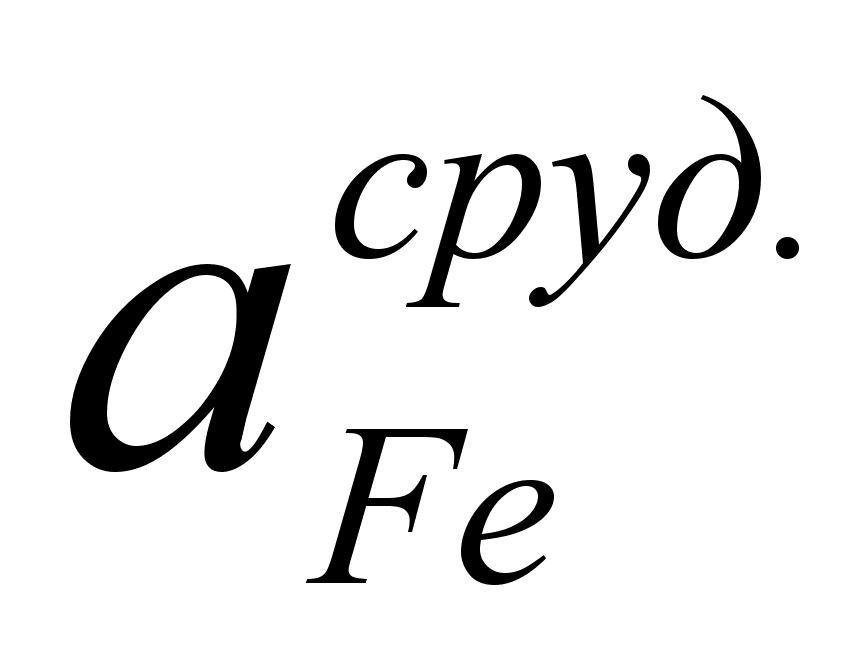
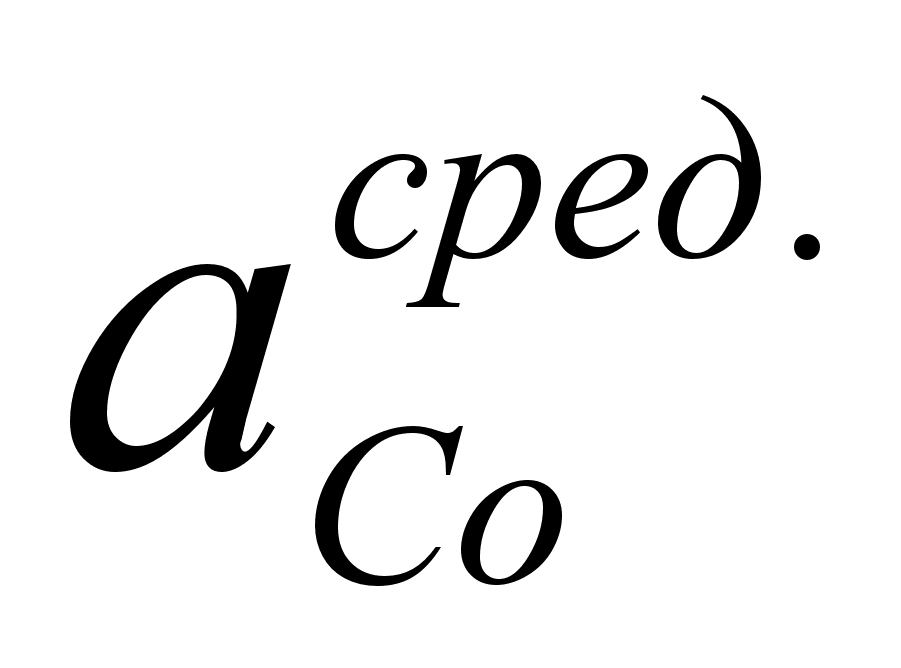
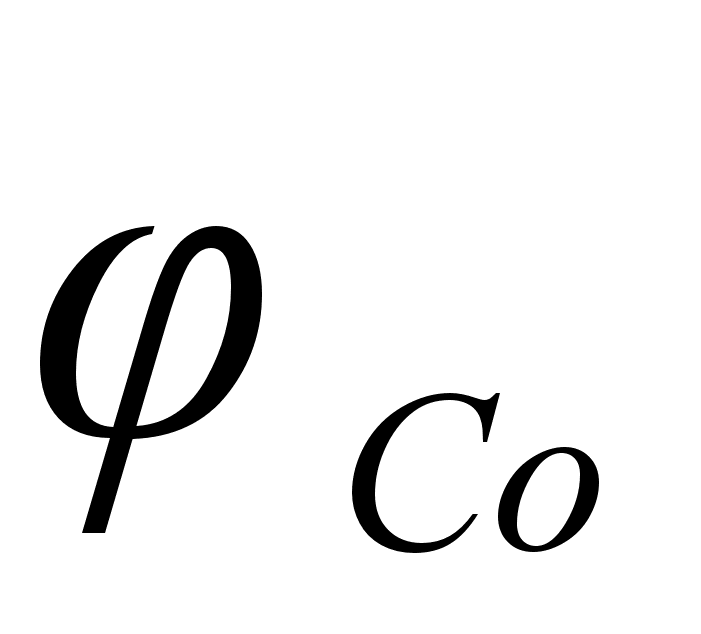 и
и