Доклад: Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских кривых.
Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность 1) ![]() =
=![]() (x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны
(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны
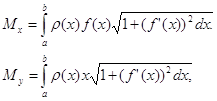
моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам
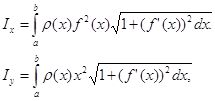
а координаты центра масс ![]() и
и ![]() — по формулам
— по формулам
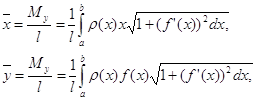
где l— масса дуги, т. е.
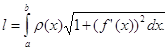
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох
и Оу дуги цепной линии y=chx при 0≤x≤1.
1) Всюду в задачах, где плотность не указана, предполагается, что
кривая однородна и ![]() =1.
=1.
Имеем: ![]() Следовательно,
Следовательно,
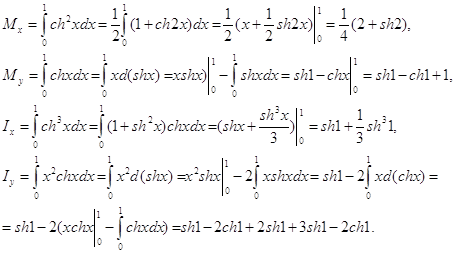
Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.
Имеем: ![]()
Отсюда получаем:
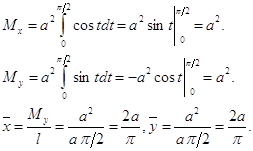
В приложениях часто оказывается полезной следующая
Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Пример 3. Найти координаты центра масс
полуокружности ![]()
Вследствие симметрии ![]() . При вращении
полуокружности вокруг оси Ох получается сфера, площадь поверхности которой
равна
. При вращении
полуокружности вокруг оси Ох получается сфера, площадь поверхности которой
равна ![]() , а
длина полуокружности равна па. По теореме Гульдена имеем
, а
длина полуокружности равна па. По теореме Гульдена имеем ![]()
Отсюда ![]() , т.е. центр масс C имеет координаты
C
, т.е. центр масс C имеет координаты
C![]() .
.
2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.
Пример 4. Скорость прямолинейного движения
тела выражается формулой ![]() (м/с). Найти путь, пройденный телом
за 5 секунд от начала движения.
(м/с). Найти путь, пройденный телом
за 5 секунд от начала движения.
Так как путь, пройденный телом со
скоростью ![]() (t) за отрезок времени [t1,t2], выражается интегралом
(t) за отрезок времени [t1,t2], выражается интегралом
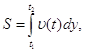
то имеем:
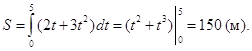
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru/
| Применение дифференциального и интегрального исчисления к решению ... | |
|
Отдел образования гомельского городского Исполнительного комитета Государственное учреждение образования "Гимназия №71 г. Гомеля" Конкурсной работы ... Если дуга кривой задана уравнением y=f(x), a=x=b, и имеет плотность =(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности ... |
Раздел: Рефераты по математике Тип: реферат |
| Приложения определенного интеграла к решению некоторых задач механики ... | |
|
Приложения определенного интеграла к решению некоторых задач механики и физики 1. Моменты и центры масс плоских кривых. Если дуга кривой задана ... Если дуга кривой задана уравнением y=f(x), a=x=b, и имеет плотность 1) =(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Основы программирования на языке Паскаль | |
|
Как работать с книгой Внимательно прочитайте соответствующий раздел теории (одну главу), разберите все примеры, чтобы вам все было понятно, при этом ... 3. Прямоугольник, ограниченный осями OX, ОУ и прямыми x=-2, y=-4. Процедура Arc (Х, Y, Beg А, End А, R); вычерчивает дугу окружности Beg А и End А, соответственно, начальный и конечный углы дуги. |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Кинематический анализ механизма транспортирования ткани | |
|
Кинематический анализ механизма верхней и нижней реек швейной машины 131-42+3 класса. Реферат Отчет с., 1 ч., 46 рис., 3 табл., 88 источников, 1 прил ... D.W.Levis и C.K.Gyory в работе [35] показывают, что траектория точки шатуна плоского механизма является кривой, которую можно описать рядом парных координат. Введём неподвижную систему координат O1 X Y, центр которой связан с осью вращения O1. |
Раздел: Рефераты по технологии Тип: реферат |
| Построение графика функции различными методами (самостоятельная работа ... | |
|
Беловский Филиал Кемеровского Государственного Университета Построение графика функции различными методами (самостоятельная работа учащихся) Дипломная ... Здесь формируется умение находить вершину и ось симметрии графиков квадратичных функций, заданных формулами y=ax2+q, y=a(x+p)2, y=a(x+p)2+q. Рассматриваются некоторые примеры ... Дело в том , что если, скажем, на интервале (a; b) функция y=f(x) принимает только положительные значения, то график её на этом интервале лежит выше оси Ох. |
Раздел: Рефераты по математике Тип: реферат |