Учебное пособие: Приложения определенного интеграла к решению некоторых задач механики и физики
Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских
кривых. Если дуга
кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность 1) 
=(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны
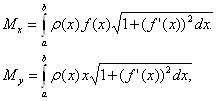
моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам
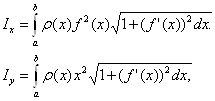
а координаты центра масс 
и 
— по формулам
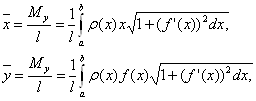
где l— масса дуги, т. е.
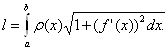
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох
и Оу дуги цепной линии y=chx при 0≤x≤1.
1)
Всюду в задачах, где плотность не указана, предполагается, что кривая однородна
и =1.
◄ Имеем: 
Следовательно,
►
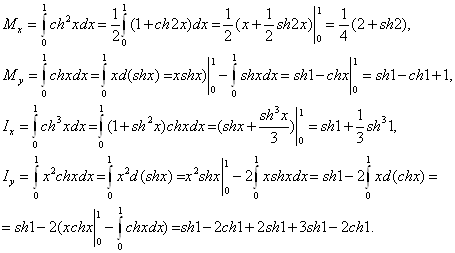Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.
◄ Имеем: 
Отсюда получаем:
►
В приложениях часто оказывается полезной следующая
Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Пример 3. Найти координаты центра масс полуокружности 
◄Вследствие симметрии 
. При вращении полуокружности вокруг
оси Ох получается сфера, площадь поверхности которой равна 
, а длина полуокружности равна па. По теореме Гульдена
имеем 
Отсюда 
, т.е. центр масс C имеет координаты C
.
2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.
Пример 4. Скорость прямолинейного движения
тела выражается формулой 
(м/с). Найти путь, пройденный телом
за 5 секунд от начала движения.
◄ Так как путь, пройденный
телом со скоростью 
(t) за отрезок времени [t1,t2], выражается интегралом
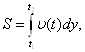
то имеем:
►
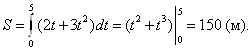Пример 5. Какую работу необходимо затратить для того, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту /i? Чему равна работа, если тело удаляется в бесконечность?
<4| Работа переменной силы / (#), действующей вдоль оси Ох на отрезке [а, Ь], выражается интегралом
| Применение дифференциального и интегрального исчисления к решению ... | |
|
Отдел образования гомельского городского Исполнительного комитета Государственное учреждение образования "Гимназия №71 г. Гомеля" Конкурсной работы ... Если дуга кривой задана уравнением y=f(x), a=x=b, и имеет плотность =(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности ... |
Раздел: Рефераты по математике Тип: реферат |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Уравнение (x-2)2 + (y+3)2 - 25 = 0 задает окружность с центром в точке C(2,-3) и радиусом 5. Окружность разбивает плоскость на две части - внутреннюю и внешнюю. Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox. |
Раздел: Рефераты по математике Тип: дипломная работа |
| Электрические аппараты | |
|
Раздел 1. Основы теории электрических аппаратов Лекция № 1 Электрический аппарат - это электротехническое устройство, которое используется для ... Касательная к кривой в начале координат отсекает на прямой too отрезок, равный в выбранном масштабе постоянной времени Т. Джоулев интеграл предохранителя состоит из джоулева интеграла нагрева до температуры плавления вставки Спл и джоулева интеграла гашения образовавшейся дуги Сгаш..С целью сокращения ... |
Раздел: Рефераты по физике Тип: учебное пособие |
| Полный курс лекций по математике | |
|
МАТЕМАТИКА Тема 1. Роль математики в современном мире. Основные этапы становления математики. Тема 2. Аксиоматический метод построения научной теории ... Гипербола, заданная уравнением симметрична относительно осей координат (Рис 2). Она пересекает ось ох в точках А1( -а, 0) и А2(+а, 0) - вершинах гиперболы и не пересекает ось оу. Мы ввели понятие определенного интеграла от функции y = f(x) на отрезке а; b , когда функция y = f(x) была интегрируема (и, следовательно, ограничена) на конечном отрезке а; b ... |
Раздел: Рефераты по математике Тип: реферат |
| Графики и их функции | |
|
Министерство образования Российской Федерации Муниципальное общеобразовательное учреждение "Средняя общеобразовательная школа №22" Графики и их ... Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f(x). Горизонтальную ось Ох называют осью абсцисс ... Для этого выберем прямоугольную систему координат так, чтобы ось Ох проходила через фокусы, а начало координат делило отрезок F1F2 пополам (см. приложение 14). |
Раздел: Рефераты по математике Тип: реферат |