Реферат: Высшая математика
Задание №2. Вопрос №9.
Задание №3. Вопрос №1.
Задание №12. Вопрос №9.
Задание №13. Вопрос №2.
Задание №18. Вопрос №9
Часть II.
Задание №8. Вопрос №8.
Задание №12. Вопрос №9.
Задание №14. Вопрос №2.
Задание №15. Вопрос №6.
Задание №18. Вопрос №9.
Дополнительно Часть I.
Задание №7. Вопрос №1.
Задание №9. Вопрос №8.
Задание №11. Вопрос №6.
Задание №15. Вопрос №1.
Дополнительно Часть II.
Задание №7. Вопрос №1.
Задание №9. Вопрос №8.
Задание №11. Вопрос №6.
Задание №15. Вопрос №1.
Часть I. Задание №2. Вопрос №9.В штате гаража числится 54 водителя. Сколько свободных дней может иметь каждый водитель в месяц (30 дней), если ежедневно 25% автомашин из имеющихся 60 остаются в гараже для профилактического ремонта.
Решение:
|
|
машин ежедневно остается в гараже на профилактическом ремонте. |
|
60-15=45 |
машин с водителями ежедневно уходят в рейс. |
|
54-45=9 |
водителей из штата гаража ежедневно не выходит в рейс из-за профилактического ремонта автомашин. |
|
|
количество водителей в течение месяца, не выходящих в рейс из-за профилактического ремонта автомашин. |
|
|
дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. |
Ответ:Каждый водитель из штата гаража в течение месяца может иметь 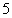 свободных дней.
свободных дней.
Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если 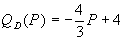 ,
, 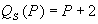 .
.
Решение:
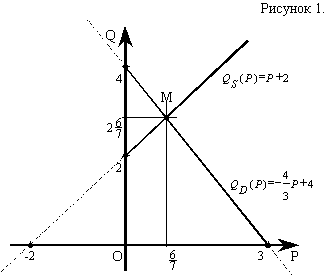
Построим в плоскости POQ график функции спроса Q=QD(P) и предложения Q=QS(P). Для этого найдем координаты пересечения с осями координат:
|
С осью OP (Q=0): |
С осью OQ (P=0): |
|
|
Для Q=QS(P): |
Для Q=QD(P): |
|
|
|
|
|
Т.к. функции QS(P) и QD(P) – линейные функции, то их графиками являются прямые, для построения которых достаточно определить их точки пересечения с осями координат. Они найдены, значит можно производить построение графика (рис.1).
Найдем точку равновесия графиков функции спроса и предложения (М), в которой спрос равен предложению. Для этого решим систему:
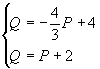 , из этой системы получаем:
, из этой системы получаем: 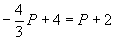
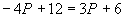
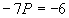
 , тогда
, тогда 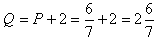 ,
значит координаты т.M
,
значит координаты т.M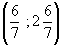 .
.
Ответ:Координаты точки равновесия равны  ,
, 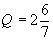
Используя правила вычисления производных и таблицу, найдите производные следующих функций:

Решение:
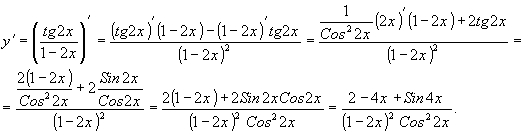
Ответ:Производная заданной функции равна 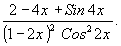
Используя дифференциал функции, найдите приближенное значение
числа: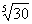
Решение:
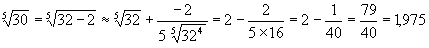
Ответ:Приближенное значение заданного числа равно 1,975.
Задание №18. Вопрос №9Исследуйте функцию и постройте ее график: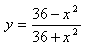
Решение:
Область определения данной функции: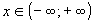 .
Найдем точки пересечения с осями координат:
.
Найдем точки пересечения с осями координат:
|
С осью OY |
С осью OX (y=0): |
|
|
|
|
Точка пересечения: |
Точки пересечения: |
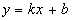 ,
где:
,
где:
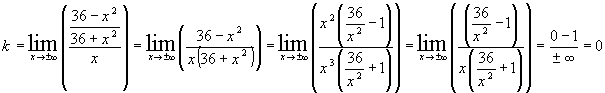
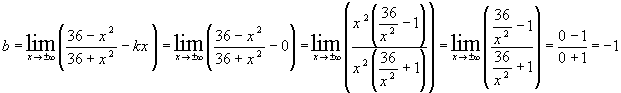 т.к.
правая и левая наклонные асимптоты совпадают, то уравнение имеет вид:
т.к.
правая и левая наклонные асимптоты совпадают, то уравнение имеет вид: 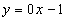 ,
т.е.
,
т.е. 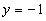 - уравнение горизонтальной
асимптоты.
- уравнение горизонтальной
асимптоты.
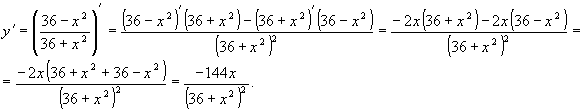
Т.к. если у функции есть точка экстремума, то в этой точке
первая производная функции равна нулю, т.е. 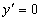 :
:
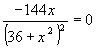 , дробь равна
нулю, если ее числитель равен нулю, т.е.
, дробь равна
нулю, если ее числитель равен нулю, т.е. 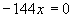 ,
отсюда x=0, следовательно
,
отсюда x=0, следовательно 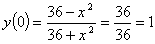 ,
значит точка
,
значит точка 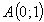 - точка экстремума
функции.
- точка экстремума
функции.
На участке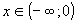 производная
производная 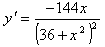 > 0, значит,
при
> 0, значит,
при 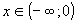 , заданная функция возрастает.
, заданная функция возрастает.
На участке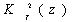 производная
производная 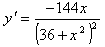 < 0, значит,
при
< 0, значит,
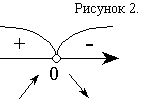
при  , заданная функция убывает
(рис 2.).
, заданная функция убывает
(рис 2.).
Следовательно 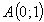 - точка максимума заданной функции
- точка максимума заданной функции 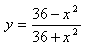 .
.
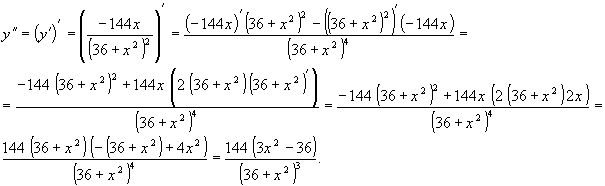
Т.к. если у функции есть точка перегиба, то в этой точке вторая производная функции равна нулю, т.е. 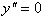 :
:
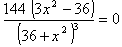 , дробь равна нулю, если
ее числитель равен нулю, т.е.
, дробь равна нулю, если
ее числитель равен нулю, т.е. 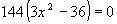 ,
значит
,
значит 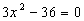 , тогда
, тогда 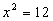 ,
отсюда
,
отсюда 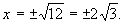
Отсюда 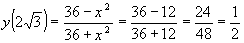 ,
, 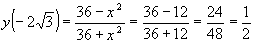 .
.
На участке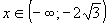 производная
производная 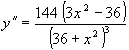 >0, значит это участок вогнутости графика функции.
>0, значит это участок вогнутости графика функции.
На участке 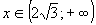 производная
производная 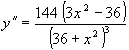 >0,
>0,
значит это тоже участок вогнутости графика функции.
Следовательно, при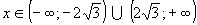 график заданной функции является вогнутым.
график заданной функции является вогнутым.
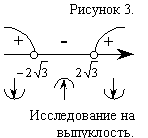
На участке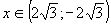 производная
производная 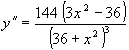 <0, значит, при
<0, значит, при 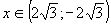 график заданной функции является выпуклым (рис. 3).
график заданной функции является выпуклым (рис. 3).
Следовательно, точки 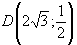 ,
,  - точки перегиба графика заданной функции
- точки перегиба графика заданной функции 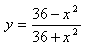 .
.
Выполненные исследования заданной функции позволяют построить ее график (см. рис. 4).
 Часть II.
Задание №8. Вопрос №8.
Часть II.
Задание №8. Вопрос №8.
Фирма производит товар двух видов в количествах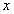 и
и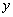 . Задана функция полных издержек
. Задана функция полных издержек 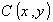 . Цены этих товаров на рынке равны
. Цены этих товаров на рынке равны 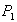 и
и 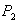 . Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.
. Определить, при каких объемах выпуска достигается максимальная прибыль, найти эту прибыль.
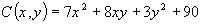 ,
, 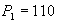 ,
,
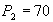
Решение:
Пусть  - функция прибыли, тогда
- функция прибыли, тогда
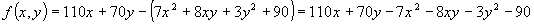
Найдем первые частные производные функции f(x,y):
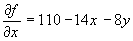 ,
, 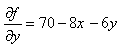 . Найдем стационарные точки графика функции
. Найдем стационарные точки графика функции 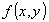 . Для этого решим систему:
. Для этого решим систему:
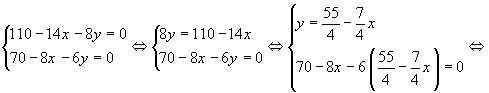
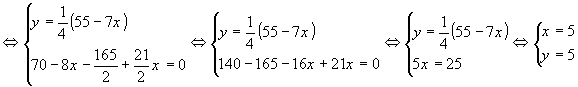
Следовательно 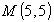 - стационарная точка. Проверим ее на экстремум, для этого
- стационарная точка. Проверим ее на экстремум, для этого
введем обозначения: 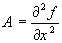 ,
, 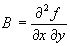 ,
, 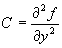 ,
,
тогда 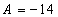 ,
, 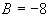 ,
,
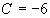 ,
, 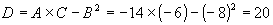 .
Т.к. A>0, то экстремум есть, а т.к.
.
Т.к. A>0, то экстремум есть, а т.к. 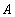 < 0,
то это максимум. Следовательно, при объемах выпуска
< 0,
то это максимум. Следовательно, при объемах выпуска 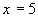 и
и
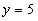 , достигается максимальная прибыль
равная:
, достигается максимальная прибыль
равная:
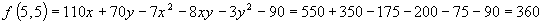
Ответ: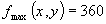 и достигается при объемах выпуска
и достигается при объемах выпуска 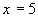 и
и 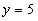 .
.
Вычислить неопределенный интеграл: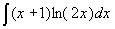
Решение:
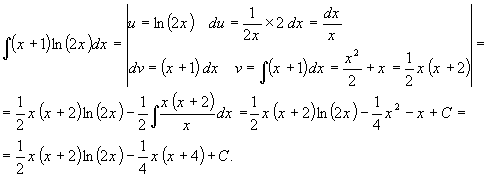
Ответ: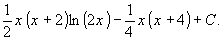
Вычислить несобственный интеграл (или установить его расходимость) 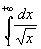 .
.
Решение:

Ответ:Данный несобственный интеграл – расходящийся.
Задание №15. Вопрос №6.Решить уравнение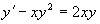
Решение:
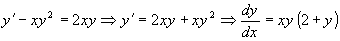 . Разделив обе части на
. Разделив обе части на 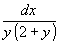 , получим
, получим 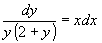 . Проинтегрируем полученное уравнение
. Проинтегрируем полученное уравнение 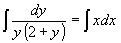 . Представим
. Представим 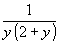 , как
, как 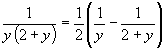 , тогда
, тогда
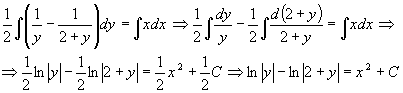
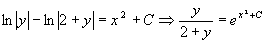
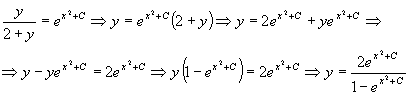
Ответ:Решением данного уравнения является 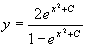 .
.
Найти общее решение уравнения: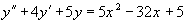
Решение:
Найдем корни характеристического уравнения: 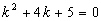 , тогда
, тогда 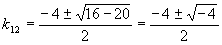 , следовательно
, следовательно 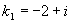 ,
, 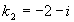 , тогда
, тогда
фундаментальную систему решений образуют функции:
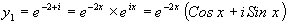 ,
, 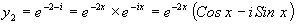
Т.к. действительные и мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решений 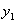 и
и 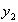 , возьмем
, возьмем 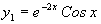 ,
, 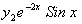 , тогда общее решение однородного уравнения будет иметь вид:
, тогда общее решение однородного уравнения будет иметь вид: 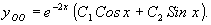
Представим правую часть уравнения, как 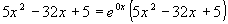 и сравним с выражением, задающим правую часть специального вида:
и сравним с выражением, задающим правую часть специального вида:
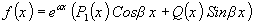 . Имеем
. Имеем 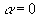 ,
, 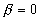 , тогда т.к.
, тогда т.к. 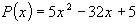 - многочлен второй степени, то общий вид правой части:
- многочлен второй степени, то общий вид правой части: 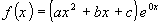 . Найдем частные решения:
. Найдем частные решения:
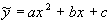 ,
, 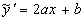 ,
, 
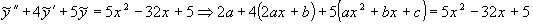
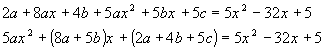
Сравним коэффициенты при 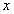 слева и справа, найдем
слева и справа, найдем 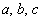 , решив систему:
, решив систему:
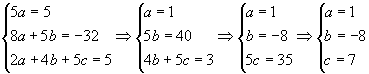 , отсюда
, отсюда 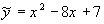 .
.
Тогда общее решение заданного неоднородного линейного уравнения имеет вид: 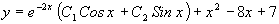 .
.
Ответ: 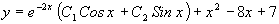 .
.
Найти предел: 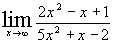 .
.
Решение:
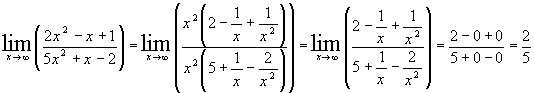 .
.
Ответ:Заданный предел равен 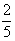 .
.
Найдите уравнение асимптот и постройте их графики:
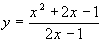 .
.
Решение:
Область определения данной функции: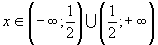 .
Т.к. точка
.
Т.к. точка 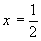 не входят в область значений функции, то это точка разрыва, а т.к.
не входят в область значений функции, то это точка разрыва, а т.к. 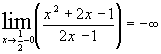 и
и 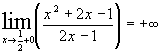 , следовательно, уравнение
, следовательно, уравнение 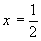 – уравнение вертикальной асимптоты.
Уравнения правой и левой наклонных асимптот имеют вид:
– уравнение вертикальной асимптоты.
Уравнения правой и левой наклонных асимптот имеют вид: 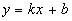 , где:
, где:
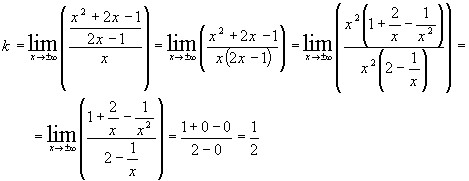
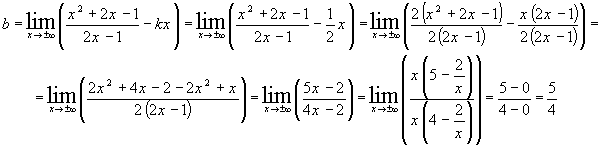
т.к. правая и левая наклонные асимптоты совпадают, то уравнение наклонной
асимптоты имеет вид: 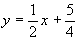 .
.
Для построения графиков асимптот (см. рис. 5), найдем
точки пересечения наклонной асимптоты 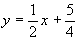 с осями
с осями
координат:
С осью OX: точка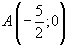 ,
,
с осью OY: точка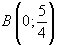
Ответ: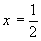 и
и 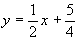 – уравнения асимптот заданной функции.
– уравнения асимптот заданной функции.
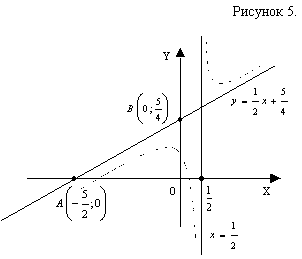 Задание №11. Вопрос №6.
Задание №11. Вопрос №6.
Исходя из определения производной, докажите: 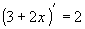 .
.
Решение:
Т.к. по определению производная функции 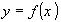 в точке
в точке 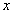 вычисляется по формуле
вычисляется по формуле 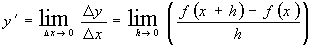 , тогда приращение
, тогда приращение 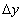 в точке
в точке 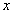 :
: 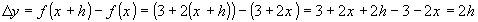 .
.
Следовательно 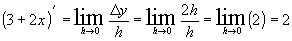 .
.
Ответ: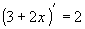 .
.
Найдите пределы, используя правило Лопиталя: 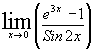 .
.
Решение:
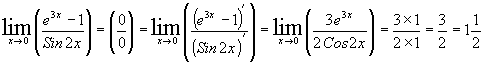 .
.
Ответ:Заданный предел равен 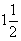 .
.
Написать в точке 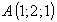 уравнение касательной плоскости к поверхности, заданной уравнением:
уравнение касательной плоскости к поверхности, заданной уравнением: 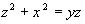 .
.
Решение:
Уравнение касательной плоскости к графику функции 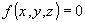 в точке
в точке 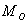 имеет вид:
имеет вид: 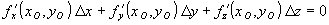 . Поэтому, продифференцируем заданное уравнение поверхности:
. Поэтому, продифференцируем заданное уравнение поверхности: 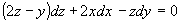 . Подставив в полученное уравнение координаты точки
. Подставив в полученное уравнение координаты точки 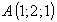 вместо значений переменных, и заменив дифференциалы переменных на их приращения, получим:
вместо значений переменных, и заменив дифференциалы переменных на их приращения, получим:
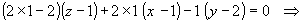
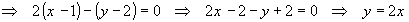 .
.
Ответ:Уравнение касательной плоскости к заданной поверхности в заданной точке 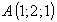 имеет вид
имеет вид 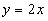 .
.
Найти наибольшее и наименьшее значение функции 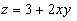 в области:
в области: 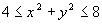 .
.
Решение:
Т.к. заданная функция дифференцируется в замкнутой ограниченной области, то свое наибольшее/наименьшее значение она достигает или в стационарной точке внутри области дифференцирования, или на границе области.
Найдем стационарные точки заданной функции, для этого решим систему:
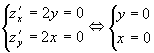 , точка
, точка 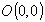 не принадлежит заданной области дифференцирования, значит стационарных точек внутри области нет, следовательно, наибольшее/наименьшее значение функцией достигается на границе области дифференцирования. Граница области ограничена окружностями
не принадлежит заданной области дифференцирования, значит стационарных точек внутри области нет, следовательно, наибольшее/наименьшее значение функцией достигается на границе области дифференцирования. Граница области ограничена окружностями 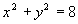 и
и 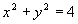 . Найдем наибольшее/наименьшее значение на границах области дифференцирования. Для этого составим функцию Лагранжа:
. Найдем наибольшее/наименьшее значение на границах области дифференцирования. Для этого составим функцию Лагранжа:
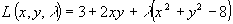 , тогда
, тогда 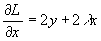 ,
,
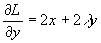 , следовательно, система уравнений
для определения координат экстремальной точки имеет вид:
, следовательно, система уравнений
для определения координат экстремальной точки имеет вид:
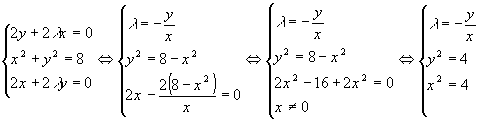
Эта система имеет четыре решения:
|
|
Точка |
|
|
Точка |
|
|
Точка |
|
|
Точка |
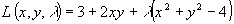 , тогда
, тогда 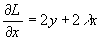 ,
,
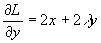 ,
,
следовательно, система уравнений для определения координат экстремальной точки имеет вид:
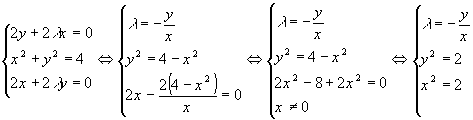
Эта система также имеет четыре решения:
|
|
Точка |
|
|
Точка |
|
|
Точка |
|
|
В точке |
Следовательно, заданная функция 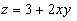 в заданной области дифференцирования достигает наибольшего значения в точках
в заданной области дифференцирования достигает наибольшего значения в точках
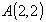 и
и 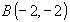 и наименьшего в точках
и наименьшего в точках 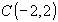 и
и 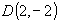 при этом графики функций
при этом графики функций 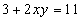 и
и 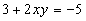 касаются окружности
касаются окружности 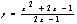 в точках
в точках 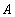 ,B,
и
,B,
и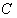 ,
, 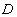 соответственно (см. рис.6).
соответственно (см. рис.6).
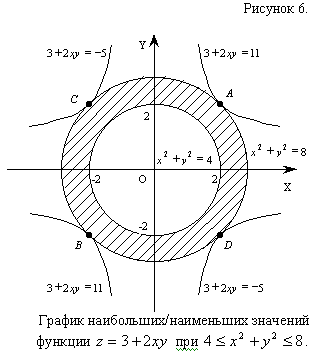
Ответ:Заданная функция 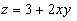 при условии
при условии 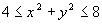 имеет
имеет 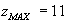 и
и 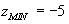 .
.
Вычислить неопределенный интеграл: 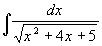 .
.
Решение:
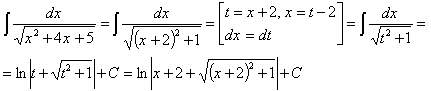
Ответ:
Заданный неопределенный интеграл равен 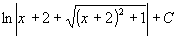 .
.
Задание №15. Вопрос №1.
Решить уравнение: 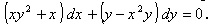 .
.
Решение:
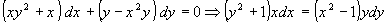 . Разделив обе части на
. Разделив обе части на 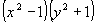 , получим
, получим 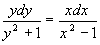 . Проинтегрируем полученное уравнение:
. Проинтегрируем полученное уравнение:
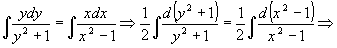
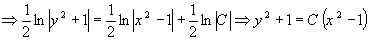 .
.
Ответ:
Решением данного уравнения является 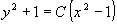 .
.
| Методика решения иррациональных уравнений и неравенств в школьном ... | |
|
Содержание Введение § 1. Анализ школьных учебников по алгебре и началам анализа 1.1. "Алгебра, 8", авт. А. Г. Мордкович 1.2. "Алгебра и начала анализа ... При решении уравнений или неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Задания 1-3 -с выбором ответа, задания 4-7 - с кратким ответом, задание 8 - с развернутым ответом. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Рациональные уравнения и неравенства | |
|
Содержание I. Рациональные уравнения. 1) Линейные уравнения. 2) Системы линейных уравнений. 3) Квадратные уравнения и уравнения, сводящиеся к ним. 4 ... где a, b, c, a - заданные числа, отличные от нуля; y = y(x), z = z(x) - некоторые функции от x. Разделим обе части уравнения на (x2 - x + 1)2 1 0: Для этого нужно начертить графики обоих уравнений и найти координаты точек их пересечения. |
Раздел: Рефераты по математике Тип: реферат |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Эллипс, заданный уравнением (2.10), симметричен относительно осей координат. Запишем каноническое уравнение гиперболы: x2/a2 - y2/b2 = 1. Асимптоты гиперболы задаются уравнениями y = = 0,5 x, значит, b/a = 1/2, откуда a=2b. |
Раздел: Рефераты по математике Тип: дипломная работа |
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... Главная ось курсового гироскопа находится в горизонтальной плоскости и занимает произвольное по отношению к осям ЛА положение, например, в исходном состоянии перпендикулярна к оси ... Если при курсе 0°, 90°, 180° и 270° поперечная ось ЛА совпадает с осью внутренней рамы или с главной осью гироскопа, то карданная ошибка в этих случаях равна нулю. |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| ... уроков при изучении темы "Квадратные уравнения" в 8 классе | |
|
ГОУ СПО "Кунгурское педагогическое училище" ПЦК преподавателей естественно-математических дисциплин Выпускная квалификационная работа по методике ... К ним можно отнести переход от уравнения к совокупности уравнений после предварительного разложения на множители; переход от уравнения к системе после приравнивания суммы квадратов ... 3.5 "Решение уравнений" (каждой команде учитель раздает карточки с заданиями, учащиеся решают вместе и выносят ответы на доску. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
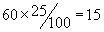
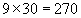
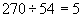
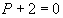
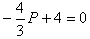
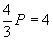
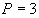
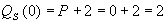
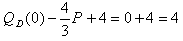
 :
:
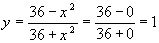
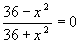 , дробь равна нулю,
если ее числитель равен нулю, т.е.
, дробь равна нулю,
если ее числитель равен нулю, т.е.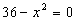
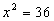
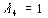
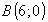 ,
,
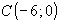
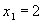 ,
, 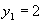 ,
,
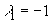
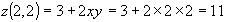 .
.
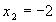 ,
, 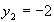 ,
,
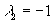
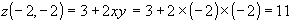 .
.
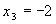 ,
, 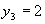 ,
,
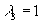
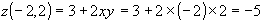 .
.
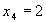 ,
, 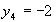 ,
,
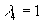
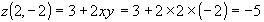 .
.
 ,
, 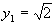 ,
, 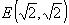 – точка условного максимума, при этом функция
– точка условного максимума, при этом функция 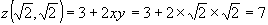 .
.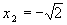 ,
, 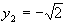 ,
, 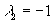
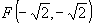 – точка условного максимума, при этом функция
– точка условного максимума, при этом функция 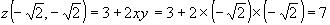 .
.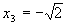 ,
, 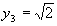 ,
, 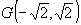 – точка условного минимума, при этом функция
– точка условного минимума, при этом функция 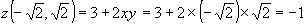 .
.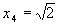 ,
, 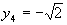 ,
, 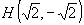 – точка условного минимума, при этом функция
– точка условного минимума, при этом функция 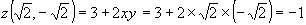 .
.