Реферат: Линейные системы уравнений
Реферат
Тема: «Линейные системы уравнений»
Содержание
1. Уравнения, векторы, матрицы, алгебра
2. Умножение матриц как внешнее произведение векторов
3. Нормы векторов и матриц
4. Матрицы и определители
5. Собственные значения и собственные векторы
6. Ортогональные матрицы из собственных векторов
7. Функции с матричным аргументом
8. Вычисление проекторов матрицы
Пример использования числовых характеристик матриц
10. Оценка величины и нахождение собственных значений
Литература
1. Уравнения, векторы, матрицы, линейная алгебра
Многие из рассмотренных нами задач сводились к формированию систем линейных алгебраических или дифференциальных уравнений, которые требовалось решить. Пока системы включали в себя не более трех-четырех переменных, их несложно было решать известными классическими методами: методом определителей (Крамера) или методом исключения переменных (Гаусса). С появлением цифровых вычислительных машин порядок алгебраических уравнений, решаемых методом исключений вырос в несколько десятков раз. Однако выявилось множество причин, по которым решение таких систем получить не удавалось. Появившиеся различные модификации метода исключения не привели к существенным улучшениям ситуации с получением решений. Появление же систем с количеством переменных более многих сотен и тысяч заставили обратиться и развивать итерационные методы и методы эквивалентных векторно-матричных преобразований применительно к решению линейных систем алгебраических уравнений.
Основные теоретические результаты были получены путем обобщения известных классических методов функционального анализа и алгебры конечномерных линейных пространств на векторно-матричные представления систем линейных алгебраических и дифференциальных уравнений.
Общая форма записи линейной системы алгебраических уравнений с n неизвестными может быть представлена следующим образом:
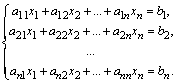
Здесь ![]() – неизвестные,
– неизвестные,
![]() – заданные числа,
– заданные числа,
![]() – заданные числовые
коэффициенты.
– заданные числовые
коэффициенты.
Последовательность записи уравнений в системе и обозначение неизвестных в последней не играет роли. В этом плане удобно при анализе и исследованиях системы использовать упорядоченную индексацию натурального ряда для неизвестных, значений правых частей и коэффициентов в уравнениях, однозначно привязывая, тем самым, каждое слагаемое и каждое уравнение к определенной позиции в общей записи. В результате можно выделить в данной записи уравнений три позиционно упорядоченных неделимых объекта:
список переменных – ![]() ,
,
список правых частей – ![]() и
и
матрицу коэффициентов – 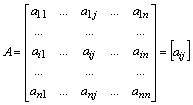 .
.
Первые два объекта в линейной алгебре называют вектором-строкой, а второй – квадратной матрицей.
Операции с векторами,
матрицами должны быть определены так, чтобы однозначно отображать допустимые
эквивалентные преобразования исходной системы алгебраических уравнений. В
предельных случаях задания векторов и матриц: ![]() ,
,
![]() – аддитивные и
мультипликативные операции должны переходить в аналогичные операции со скалярными
величинами.
– аддитивные и
мультипликативные операции должны переходить в аналогичные операции со скалярными
величинами.
Если рассмотреть i-тую строку исходной системы
![]() ,
,
то в ней кроме
упорядоченного расположения компонент ![]() присутствует
упорядоченное по индексу j размещение коэффициентов
присутствует
упорядоченное по индексу j размещение коэффициентов ![]() , которые могут
рассматриваться как вектор-строка
, которые могут
рассматриваться как вектор-строка ![]() .
Результатом суммы покомпонентного перемножения двух векторов-строк должно быть
число. В линейной алгебре такая операция с векторами определена и названа скалярным
или внутренним произведением векторов:
.
Результатом суммы покомпонентного перемножения двух векторов-строк должно быть
число. В линейной алгебре такая операция с векторами определена и названа скалярным
или внутренним произведением векторов:
![]() .
.
Скалярное произведение
линейно, так как обладает основными свойствами линейных преобразований ![]() , и коммутативно.
, и коммутативно.
Определение скалярного произведения позволяет переписать исходную систему уравнений в виде вектора с компонентами из скалярных произведений:
![]()
или
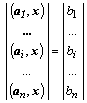 .
.
Вторая форма представления векторов в форме столбцов более наглядна в смысле зрительного установления покомпонентного равенства двух векторов: стоящего слева от знака равенства и справа. Эта форма, форма вектора-столбца принята за каноническую (основную).
Левый вектор-столбец в
записи каждой строки содержит вектор неизвестных и естественно желание вынести
его за прямые скобки. Оставшиеся коэффициенты упорядочены, как в матрице ![]() . Теперь для представления
исходной системы уравнений в виде
. Теперь для представления
исходной системы уравнений в виде ![]() несложно
определить векторно-матричную операцию
несложно
определить векторно-матричную операцию ![]() ,
результатом которой является вектор с i-той компонентой, равной
,
результатом которой является вектор с i-той компонентой, равной ![]() .
.
Аксиоматическое построение линейной (векторной) алгебры с рассмотренными базовыми операциями позволило установить важные и полезные свойства, как самих объектов алгебры, так и их алгебраических выражений.
2. Умножение векторов и матриц
Среди n-мерных векторов и векторных операций над ними важно выделить сумму n векторов, умноженных на числовые константы:
![]() ,
,
которая при произвольном
выборе ![]() в частности может
оказаться нулевым вектором (с нулевыми компонентами) или одним из суммируемых
векторов
в частности может
оказаться нулевым вектором (с нулевыми компонентами) или одним из суммируемых
векторов ![]() . Если нулевой вектор при
суммировании не нулевых векторов можно получить лишь в случае, когда все
. Если нулевой вектор при
суммировании не нулевых векторов можно получить лишь в случае, когда все ![]()
![]() ,
то такие векторы в наборе называют линейно независимыми. Такими
векторами в частности будут единичные векторы
,
то такие векторы в наборе называют линейно независимыми. Такими
векторами в частности будут единичные векторы ![]() , у которых все компоненты
нулевые, кроме единичной компоненты, расположенной на j-строке.
, у которых все компоненты
нулевые, кроме единичной компоненты, расположенной на j-строке.
Линейно независимый набор единичных векторов с геометрической точки зрения можно рассматривать как n-мерную систему координат. Набор компонент любого вектора в этой n-мерной системе определяет координаты точки конца вектора, исходящего из начала координат, а также являются длинами проекций вектора на координатных осях.
Среди матриц размера ![]() и операций с ними в первую
очередь необходимо отметить операцию умножения матрицы на матрицу.
Необходимость введения операции умножения матриц возникает уже при первом
взгляде на полученную векторную форму записи линейного уравнения
и операций с ними в первую
очередь необходимо отметить операцию умножения матрицы на матрицу.
Необходимость введения операции умножения матриц возникает уже при первом
взгляде на полученную векторную форму записи линейного уравнения ![]() . Векторы слева и справа
имеют равные компоненты. Так как коэффициенты в строках матрицы в общем
произвольны по величине, то соответствующие компоненты вектора x
не обязаны быть равными компонентам вектора y. Последнее
означает, что умножение вектора x на матрицу A вызвало
изменение длины и направления вектора x. Если аналогичное
преобразование выполняется над вектором правой части до решения уравнения, то
вектор левой части должен быть преобразован так же:
. Векторы слева и справа
имеют равные компоненты. Так как коэффициенты в строках матрицы в общем
произвольны по величине, то соответствующие компоненты вектора x
не обязаны быть равными компонентам вектора y. Последнее
означает, что умножение вектора x на матрицу A вызвало
изменение длины и направления вектора x. Если аналогичное
преобразование выполняется над вектором правой части до решения уравнения, то
вектор левой части должен быть преобразован так же:
![]() .
.
Фактически мы имеем дело с заменой системы координат. Рассмотрим методику вычисления коэффициентов результирующей матрицы уравнения:

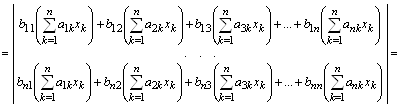
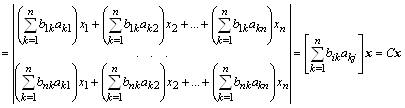 ,
,
где ![]() – элемент матрицы С,
равный скалярному произведению вектор-строки
– элемент матрицы С,
равный скалярному произведению вектор-строки ![]() матрицы В на вектор-столбец
матрицы В на вектор-столбец ![]() матрицы А.
матрицы А.
Произведение матриц в общем случае не коммутативно. Ассоциативный и распределительный законы в матричных выражениях выполняются.
3. Нормы векторов и матриц
Интерпретация упорядоченного набора чисел, как вектора в многомерном пространстве, позволяет говорить и о его длине. В прямоугольной системе координат по известным длинам проекций на координатные оси длину самого вектора вычисляют, как корень квадратный из суммы квадратов проекций:
![]() ,
,
где ![]() – компоненты вектора
– компоненты вектора ![]() ,
,
![]() – евклидова норма
вектора, его длина.
– евклидова норма
вектора, его длина.
В качестве нормы в литературе иногда используют квадрат длины вектора или другое выражение с компонентами вектора, лишь бы оно обладало свойствами расстояния: было положительным, линейным и удовлетворяло неравенству треугольника.
Деление вектора на величину его нормы называют нормированием, т.е. приведением вектора к единичной длине.
Норма матрицы в принципе тоже может быть определена в виде корня квадратного из суммы квадратов ее элементов или другими выражениями со свойствами расстояний. Однако в ряде случаев работы с векторно-матричными выражениями нормы векторов и матриц должны быть согласованными ввиду того, что результатом произведения матрицы на вектор является опять же вектор. Если выражение для нормы вектора принято, то
![]() ,
,
где функция sup говорит о том, что из всех отношений норм, стоящих в числителе и знаменателе, взятых при любом векторе x, кроме нулевого, выбирается наименьшее, т.е. это функция выбора нижней границы значений. Согласованная матричная норма для евклидовой нормы вектора удовлетворяет неравенству
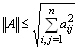 .
.
Нормы вектора и матрицы служат, в основном, для сопоставительной оценки матриц и векторов, указывая на возможный диапазон представления строгих числовых характеристик. К числу последних, в первую очередь, нужно отнести определители матриц, собственные значения и собственные векторы матриц и ряд других.
4. Матрицы и определители
Упорядоченный набор коэффициентов из системы линейных алгебраических уравнений используется для получения числовой характеристики, величина которой инвариантна по отношению к эквивалентным преобразованиям системы. Речь идет об определителе матрицы. Важное свойство определителей матрицы обнаруживается в связи с вычислением произведения матриц:
![]()
Учитывая это свойство и зная, что определитель единичной матрицы det(E)=1, можно найти матрицу B и ее определитель из уравнения:
![]()
откуда следует, что ![]() и
и ![]() .
.
Из свойств определителей нелишне помнить и такие:
![]()
где ![]() – транспонированная
матрица A,
– транспонированная
матрица A,
n – размер квадратной матрицы A,
![]() – матрица перестановки
строк или столбцов,
– матрица перестановки
строк или столбцов,
s, c=0,1,…, n – число выполненных перестановок строк и / или столбцов.
Если обратная матрица исходной системы уравнений определена, то, используя эквивалентные преобразования их векторно-матричной записи, решение уравнений можно представить в следующем виде:
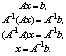
Умножив вектор правых частей на обратную матрицу, получим вектор решения.
Классический способ вычисления обратной матрицы использует определители и осуществляется по формуле:
 ,
,
где ![]() – алгебраическое
дополнение, а
– алгебраическое
дополнение, а ![]() – минор матрицы A,
получаемый вычислением определителя матрицы A, в которой вычеркнуты j-тая
строка и i-тый столбец.
– минор матрицы A,
получаемый вычислением определителя матрицы A, в которой вычеркнуты j-тая
строка и i-тый столбец.
Такой способ вычисления определителя представляет в основном теоретический интерес, так как требует выполнения неоправданно большого числа операций.
Очень просто вычисляется определитель, если матрица диагональная или треугольная. В этом случае определитель равен произведению диагональных элементов. Кстати и решения уравнений, имеющих такие матрицы коэффициентов, получаются тривиально. Поэтому основные усилия разработчиков методов решения алгебраических уравнений направлены на поиск и обоснование эквивалентных преобразований матрицы с сохранением всех ее числовых характеристик, но имеющих в конце преобразований диагональную или треугольную форму.
5. Собственные значения и собственные векторы
Рассмотрим теоретические основы и методы, позволяющие выполнять эквивалентные матричные преобразования.
Найдем вектор, который под воздействием матрицы A изменяет только свою величину, но не направление. Для системы уравнений это означает, что вектор решения должен быть пропорционален с некоторым коэффициентом вектору правой части:
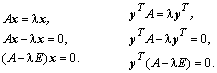
В результате несложных
преобразований получены однородные векторно-матричные уравнения в столбцовой и
в строчной формах с некоторым числовым параметром ![]() и
неизвестным вектором-столбцом x и вектором-строкой
и
неизвестным вектором-столбцом x и вектором-строкой ![]() , представляющих
собственное состояние системы. Однородная система может иметь отличное от нуля
решение лишь в том случае, когда определитель ее равен нулю. Это следует из
формул получения решения методом определителей (Крамера), в которых и
определитель знаменателя, и определитель числителя оказываются равными нулю.
, представляющих
собственное состояние системы. Однородная система может иметь отличное от нуля
решение лишь в том случае, когда определитель ее равен нулю. Это следует из
формул получения решения методом определителей (Крамера), в которых и
определитель знаменателя, и определитель числителя оказываются равными нулю.
Полагая, что решение все
же существует, т.е. ![]() и
и ![]() , удовлетворить уравнению можно
только за счет приравнивания нулю определителя однородной системы:
, удовлетворить уравнению можно
только за счет приравнивания нулю определителя однородной системы:
![]()
Раскрыв определитель и
сгруппировав слагаемые при одинаковых степенях неизвестного параметра, получим
алгебраическое уравнение степени n относительно ![]() :
:
![]()
Это уравнение называется характеристическим уравнением матрицы и имеет в общем случае n корней, возможно комплексных, которые называются собственными значениями матрицы и в совокупности составляют спектр матрицы. Относительно n корней различают два случая: все корни различные или некоторые корни кратные.
Важным свойством характеристического уравнения матрицы A является то, что согласно теореме Гамильтона-Кели, матрица A удовлетворяет ему:
![]()
где 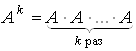 – k-тая степень
матрицы.
– k-тая степень
матрицы.
Подставляя каждое ![]() в однородную систему,
получим векторно-матричные уравнения для нахождения векторов
в однородную систему,
получим векторно-матричные уравнения для нахождения векторов ![]() или векторов-строк
или векторов-строк ![]() . Эти векторы называются
соответственно правыми собственными векторами и левыми собственными
векторами матрицы.
. Эти векторы называются
соответственно правыми собственными векторами и левыми собственными
векторами матрицы.
Решение однородных
уравнений имеет некоторую специфику. Если ![]() (как
в равной мере и
(как
в равной мере и ![]() ) является
решением, то, будучи умноженным на произвольную константу, оно тоже будет
являться решением. Поэтому в качестве собственных векторов берут такие векторы,
которые имеют норму, равную единице, и тогда:
) является
решением, то, будучи умноженным на произвольную константу, оно тоже будет
являться решением. Поэтому в качестве собственных векторов берут такие векторы,
которые имеют норму, равную единице, и тогда:
![]()
Если все собственные числа различны, то собственные векторы матрицы A образуют систему n линейно независимых векторов таких, что
![]()
6. Ортогональные матрицы из собственных векторов
Из правых собственных
векторов можно составить матрицу T, а из левых – матрицу ![]() , которые обладают
уникальными свойствами по отношению к матрице A.
, которые обладают
уникальными свойствами по отношению к матрице A.
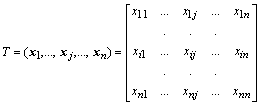
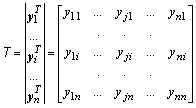
Умножив матрицу A
слева на матрицу ![]() , а справа – на
матрицу T, после несложных преобразований получим:
, а справа – на
матрицу T, после несложных преобразований получим:
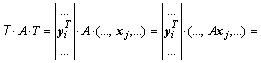
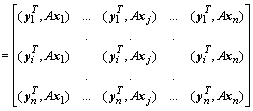 .
.
Каждое скалярное
произведение ![]() в матрице, принимая во
внимание линейную независимость собственных векторов, полученных для различных
собственных значений, можно преобразовать так:
в матрице, принимая во
внимание линейную независимость собственных векторов, полученных для различных
собственных значений, можно преобразовать так:
![]()
Поэтому, результатом преобразования матрицы A будет диагональная матрица с собственными значениями, расположенными на диагонали:
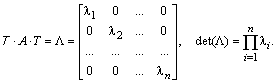
Если вместо A
взять единичную матрицу и проделать аналогичные преобразования, то станет
очевидным равенство ![]() , откуда следует
, откуда следует ![]() . Последнее позволяет для
преобразования матрицы A в диагональную обходиться только системой
правых собственных векторов-столбцов:
. Последнее позволяет для
преобразования матрицы A в диагональную обходиться только системой
правых собственных векторов-столбцов:

Последнее показывает, что
умножение матрицы A на ![]() слева и
на S справа, где S – произвольная не особая матрица, преобразует
ее в некоторую матрицу B, которая имеет определитель, равный
определителю матрицы A. Такие преобразования матриц называют
эквивалентными (подобными).
слева и
на S справа, где S – произвольная не особая матрица, преобразует
ее в некоторую матрицу B, которая имеет определитель, равный
определителю матрицы A. Такие преобразования матриц называют
эквивалентными (подобными).
Продолжая использовать T-матрицу, несложно получить следующие важные результаты:
![]() .
.
7. Функции с матричным аргументом
Пусть теперь задана некоторая матричная функция от матрицы A:
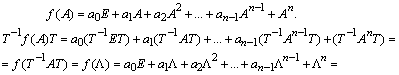
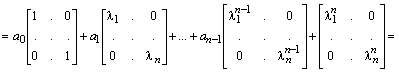
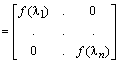 .
.
С другой стороны очевидно и обратное

![]() ,
,
где ![]() – матрица с одной единицей
на i-том месте диагонали (
– матрица с одной единицей
на i-том месте диагонали (![]() ).
).
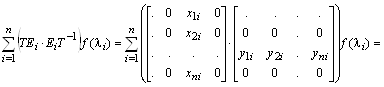
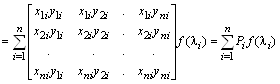
где ![]() – проекторы матрицы
A, образуемые умножением одноименных правых и левых собственных векторов
по правилам умножения прямоугольных матриц с размерами соответственно
– проекторы матрицы
A, образуемые умножением одноименных правых и левых собственных векторов
по правилам умножения прямоугольных матриц с размерами соответственно ![]() и
и ![]() . Сумма проекторов
. Сумма проекторов ![]() .
.
Проекторы обладают
свойствами идемпотентных матриц, т.е. матриц, все степени которых равны
первой. Для невырожденных проекторов (![]() )
матрицы A (
)
матрицы A (![]() ) справедливо:
) справедливо:

Представление функции от матрицы A в виде взвешенной суммы проекций называется спектральным разложением матричной функции по собственным значениям матрицы A:
![]() .
.
Если в качестве матричных
функций взять ![]() и
и ![]() , то их спектральные
разложения будут следующими:
, то их спектральные
разложения будут следующими:
![]()
8. Вычисление проекторов матрицы
Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
![]()
По известному спектру ![]() проекторы матрицы можно
найти и методом неопределенных коэффициентов. Для чего выбирают такие функции
от матрицы A, которые вычисляются очевидным образом, например, такие:
проекторы матрицы можно
найти и методом неопределенных коэффициентов. Для чего выбирают такие функции
от матрицы A, которые вычисляются очевидным образом, например, такие:
![]()
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
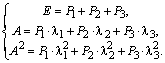
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:

где ![]() – значения i-тых
произ-водных функции в точках, соответствующих различным (не кратным) корням
характеристического многочлена,
– значения i-тых
произ-водных функции в точках, соответствующих различным (не кратным) корням
характеристического многочлена,
![]() – число кратных корней
– число кратных корней ![]() ,
,
![]() – проекторы кратных корней, в выражении
которых содержатся
– проекторы кратных корней, в выражении
которых содержатся
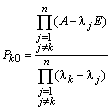 – проекторы различных корней.
– проекторы различных корней.
9. Пример использования числовых характеристик матриц
Знание собственных значений матрицы и ее проекторов позволяет выполнять вычисления аналитических функций получающихся, например, при решениях систем линейных дифференциальных уравнений, при исследованиях эквивалентных матричных преобразований и пр.
Для примера построим
матрицу с заданными собственными значениями ![]() и
собственными векторами, основанными на векторах
и
собственными векторами, основанными на векторах ![]() .
.
Сначала необходимо
убедиться в линейной независимости исходных векторов и добиться того, чтобы
левые и правые одноименные собственные векторы оказались ортогональными, т.е. ![]() . Проверка линейной
независимости может быть объединена с процессом ортогонализации заданной
системы векторов методом Грама-Шмидта.
. Проверка линейной
независимости может быть объединена с процессом ортогонализации заданной
системы векторов методом Грама-Шмидта.
Для заданных векторов
построим систему векторов ![]() таких,
что
таких,
что ![]() , следующим образом:
, следующим образом:

Откуда последовательно
находятся коэффициенты ![]() :
:
![]()
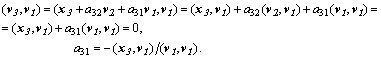
![]()
![]()
Взаимной ортогональности
векторов v можно было бы добиваться и так, чтобы каждый ![]() был ортогонален каждому
был ортогонален каждому ![]() , положив
, положив ![]() и приравняв нулю скалярные
произведения
и приравняв нулю скалярные
произведения ![]() :
:
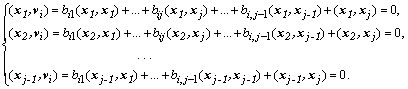
Определитель этой системы называют определителем Грама:
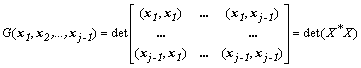 ,
,
где ![]() - матрица, в общем случае
комплексно сопряженная с матрицей
- матрица, в общем случае
комплексно сопряженная с матрицей
![]() , составленной из
заданных векторов.
, составленной из
заданных векторов.
Если грамиан
положителен, а он всегда неотрицателен, то векторы ![]() линейно
независимы, а если равен нулю, то зависимы. Это один из способов проверки
конкретного набора векторов на их линейную независимость.
линейно
независимы, а если равен нулю, то зависимы. Это один из способов проверки
конкретного набора векторов на их линейную независимость.
Для заданного выше набора
векторов ![]() определитель произведения матрицы
X на транспонированную X* будет равен
определитель произведения матрицы
X на транспонированную X* будет равен
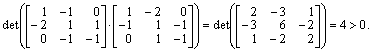
Таким образом, заданная система векторов линейно независима. Для построения ортонормированной системы векторов последовательно вычислим коэффициенты и ортогональные векторы:
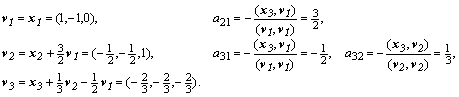
После нормирования
векторы образуют правую систему собственных векторов. Транспонированная Т-матрица
с этими векторами есть ![]() -матрица (
-матрица (![]() ); ее строки являются
собственными левосторонними векторами:
); ее строки являются
собственными левосторонними векторами:
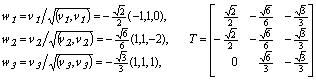 .
.
Внешнее (матричное)
произведение каждого нормированного вектора ![]() самого
на себя дает нам проекторы искомой матрицы:
самого
на себя дает нам проекторы искомой матрицы:
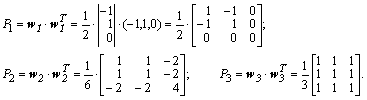
Умножая каждое
собственное значение ![]() из заданного
набора на свой проектор и суммируя, получим:
из заданного
набора на свой проектор и суммируя, получим:
![]() .
.
Аналогично получается обратная матрица:
![]() .
.
С помощью этих же проекторов вычисляется любая аналитическая функция, аргументом которой является матрица A:
![]() .
.
10. Оценка величины и нахождение собственных значений
Краткое рассмотрение основных теоретических положений линейной алгебры позволяет сделать следующие выводы: для успешного решения систем линейных алгебраических уравнений и вычислений матричных функций необходимо уметь находить ее собственные значения и собственные векторы.
Для любой матрицы A с действительными компонентами и любого ненулевого вектора v существует отношение Рэлея, связывающее скалярное произведение векторов v и Av с минимальным и максимальным собственными значениями:
![]() .
.
К высказанному необходимо сделать еще ряд замечаний, связанных со случаями, когда исходная матрица имеет кратные собственные значения или оказывается вырожденной.
Характеристическое
уравнение матрицы A с кратным корнем ![]() можно
записать в виде
можно
записать в виде
![]() .
.
На основании этой записи
можно составить минимальное характеристическое уравнение ![]() , для которого матрица A
также является корнем:
, для которого матрица A
также является корнем:
![]() .
.
Особенности в части
определения собственных значений и векторов обычно возникают в несимметричных
матрицах (![]() ). Некоторые из них
никакими подобными преобразованиями не удается свести к диагональной. Например,
не поддаются диагонализации матрицы n-го порядка, которые не имеют n линейно
независимых собственных векторов. Однако любая матрица A
размера
). Некоторые из них
никакими подобными преобразованиями не удается свести к диагональной. Например,
не поддаются диагонализации матрицы n-го порядка, которые не имеют n линейно
независимых собственных векторов. Однако любая матрица A
размера ![]() с помощью преобразования
подобия может быть приведена к прямой сумме жордановых блоков или к канонической
жордановой форме:
с помощью преобразования
подобия может быть приведена к прямой сумме жордановых блоков или к канонической
жордановой форме:
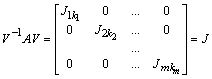 ,
,
где A –
произвольная матрица размера ![]() ;
;
 – жорданов блок размера
– жорданов блок размера ![]() ;
;
V – некоторая невырожденная
матрица размера ![]() .
.
Характеристическое
уравнение жорданова блока размера ![]() независимо
от количества единиц в верхней диагонали записывается в виде произведения
независимо
от количества единиц в верхней диагонали записывается в виде произведения ![]() одинаковых сомножителей и,
следовательно, имеет только
одинаковых сомножителей и,
следовательно, имеет только ![]() кратных
корней:
кратных
корней:
![]() .
.
Если выразить матрицу V в
форме вектора с компонентами в виде векторов-столбцов ![]() , то из равенства AV=VJ для
каждого жорданового блока следует соотношение
, то из равенства AV=VJ для
каждого жорданового блока следует соотношение
![]() .
.
Здесь ![]() в зависимости от структуры
верхней диагонали, в которой может быть либо ноль, либо единица. Если жордановы
блоки имеют размер
в зависимости от структуры
верхней диагонали, в которой может быть либо ноль, либо единица. Если жордановы
блоки имеют размер ![]() , то мы имеем
случай симметричной матрицы или матрицы с различными собственными значениями.
, то мы имеем
случай симметричной матрицы или матрицы с различными собственными значениями.
При поиске решений систем линейных уравнений с несимметричными матрицами, последние стремятся теми или иными приемами свести к выражению с симметричными матрицами.
Один из возможных подходов к решению несимметричных линейных систем состоит в замене исходной системы эквивалентной системой:
![]() .
.
Недостаток этого подхода
состоит в том, что мера обусловленности произведения матрицы A на
свою транспонированную, оцениваемая отношением ![]() ,
оказывается больше, чем у матрицы A.
,
оказывается больше, чем у матрицы A.
Под мерой обусловленности понимают отношение наибольшего собственного значения матрицы к наименьшему. Это отношение влияет на скорость сходимости итерационных процедур при решении уравнений.
Итак, основными алгебраическими системами уравнений можно считать неоднородные системы уравнений с симметричными матрицами коэффициентов.
Литература
1. Вержбицкий В.М. Основы численных методов: Учебник для вузов – 3-е изд. М: Высшая школа, 2009. – 840 с.
2. Самарcкий А.А. Задачи и упражнения по численным методам. Изд. 3 Изд-во: КомКнига, ЛКИ, 2006. – 208 с.
3. Турчак Л.И., Плотников П.В. Основы численных методов. Изд-во: ФИЗМАТЛИТ®, 2003. – 304 с.
4. Хеннер Е.К., Лапчик М.П., Рагулина М.И. Численные методы. Изд-во: «Академия/Academia», 2004. – 384c.
5. Чистяков С.В. Численные и качественные методы прикладной математики. СПб: 2004. – 268 с.
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... В разделе "Линейная алгебра" основное внимание уделяется матрицам, определителям и системам линейных уравнений, поскольку в экономических исследованиях широко используются ... Итак, = (l - 2)2 = (l+2)2. Корни характеристического уравнения =0 - это числа l1 = 2 и l2 = -2. Другими словами, мы нашли собственные значения матрицы A. Для нахождения собственных ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... Линейная алгебра и теория матриц определяют множество операций над матрицами, которые непо-средственно поддерживаются (т.е. выполняются как стандартные операции) в MATLAB-е. В ... Второй и третий столбцы матрицы V являются одинаковыми и поэтому полного набора линейно-неза-висимых собственных векторов не существует (и поэтому не существует обратная матрица V ... |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Способы решения систем линейных уравнений | |
|
очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того ... Заметим, что в i-й строке матрицы В расположены алгебраические дополнения элементов j-го столбца определителя = Умножим каждое уравнение системы (14) на алгебраические дополнения элементов i-го столбца определителя =, т.е. первое уравнение умножим на А1i, второе - на А2i и т.д., наконец ... |
Раздел: Рефераты по математике Тип: реферат |
| Достаточно общая теория управления (Расовые доктрины в России: их ... | |
|
Достаточно общая теория управления _ Постановочные материалы учебного курса факультета прикладной математики - процессов управления Санкт ... Потеря управления может быть вызвана и выпадением из вектора некоторых объективно необходимых для управления процессом целей, и выпадением всего вектора или каких-то его фрагментов ... Если вектор ошибки может быть интерпретирован в форме числового алгебраического п-мерного вектора (столбец чисел), то в качестве его меры может выступать какая-либо из норм1 ... |
Раздел: Остальные рефераты Тип: реферат |
| Классификации гиперболических дифференциальных уравнений в частных ... | |
|
Содержание Введение 1. Гиперболические уравнения как подкласс дифференциальных уравнений в частных производных. Классификация уравнений в частных ... Свойства решений уравнения (5) существенно зависят от знаков корней (алгебраического относительно l) уравнения Очень важно, что если само уравнение теплопроводности линейно, то с в левой части разностного уравнения является константой, а ф в его правой части может зависеть только от первой ... |
Раздел: Рефераты по математике Тип: контрольная работа |