Реферат: Способы решения систем линейных уравнений

– очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается. Поэтому первая глава моего реферата посвящена теме матриц и определителей. В ней я рассматривала различные действия над матрицами, свойства определителей, метод Гаусса вычисления ранга матрицы, а так же некоторые другие теоретические вопросы. Во второй главе непосредственно рассматриваются системы линейных уравнений и некоторые методы их решения: правило Крамера, метод Гаусса, а так же теорема Кронекера – Капелли. И в той и в другой главах приведены примеры, которые составляют практическую часть моего реферата.

Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, определителей и систем линейных уравнений; изучить современное состояние данного вопроса; отобрать и классифицировать исследуемый материал; а также провести практическую часть работы. Давайте рассмотрим некоторые примеры важнейших моментов этой работы.

Пусть дана система n линейных уравнений с n неизвестными:

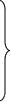
a₁₁x₁ + a₁₂x₂ + …+ a_1n x_n = b₁ ;

a₂₁x₁ + a₂₂x₂ + …+ a_2n x_n = b₂ ;

……………………………………

a_n1x₁ + a_n2x₂ + …+ a_nnx_n = b_n ;

a). Если , то система (1) имеет единственное решение,

которое может быть найдено по формулам Крамера: x₁=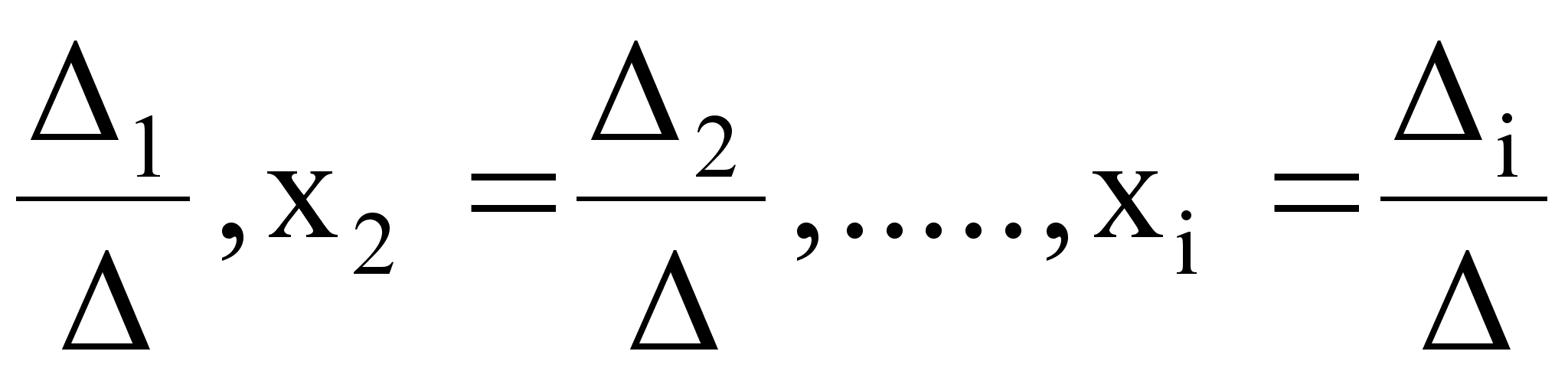, где

определитель n-го порядка _i ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b₁ , b₂ ,..., b_n.

б). Если , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет. Например:

решить систему уравнений

.

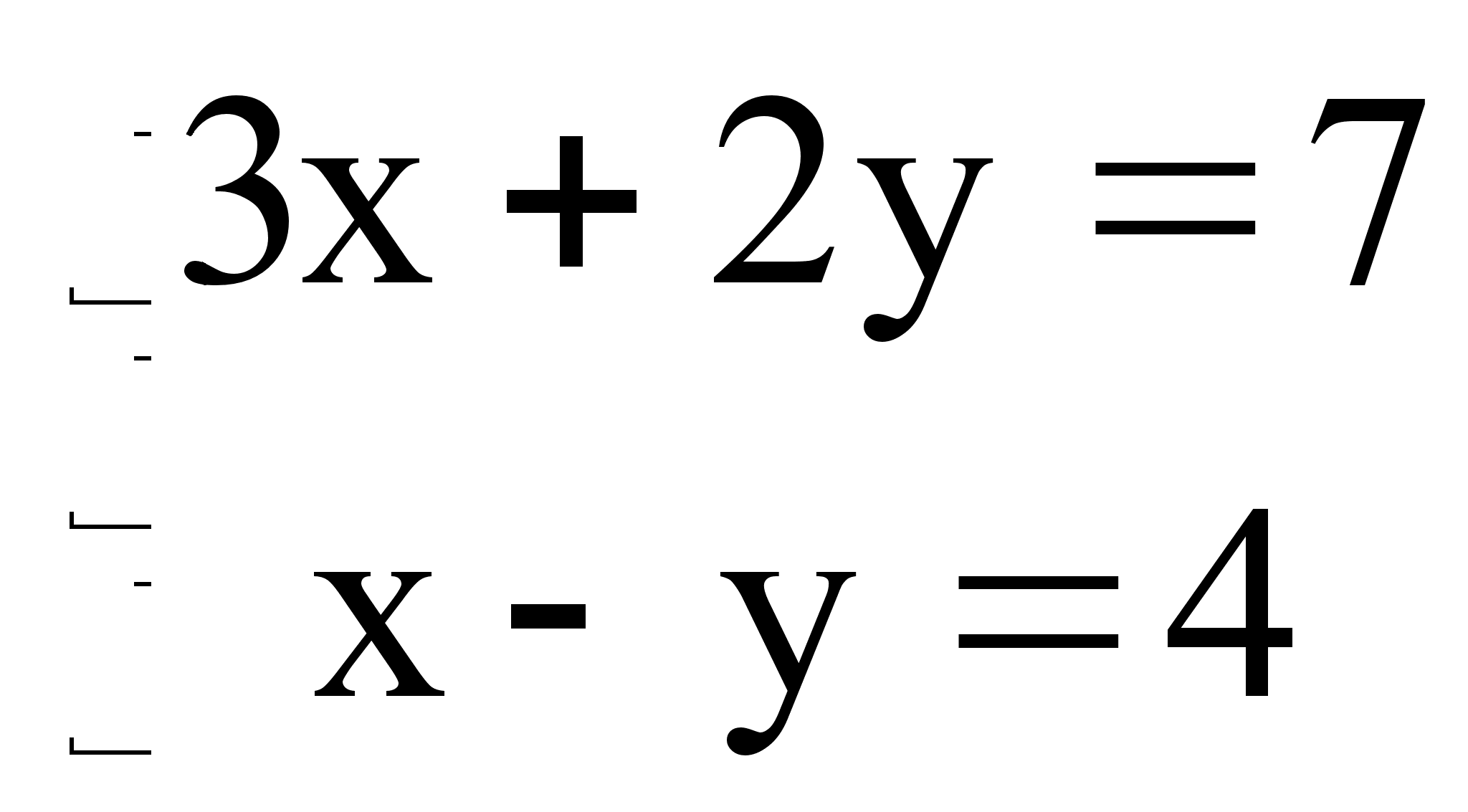Вычислим определитель системы:

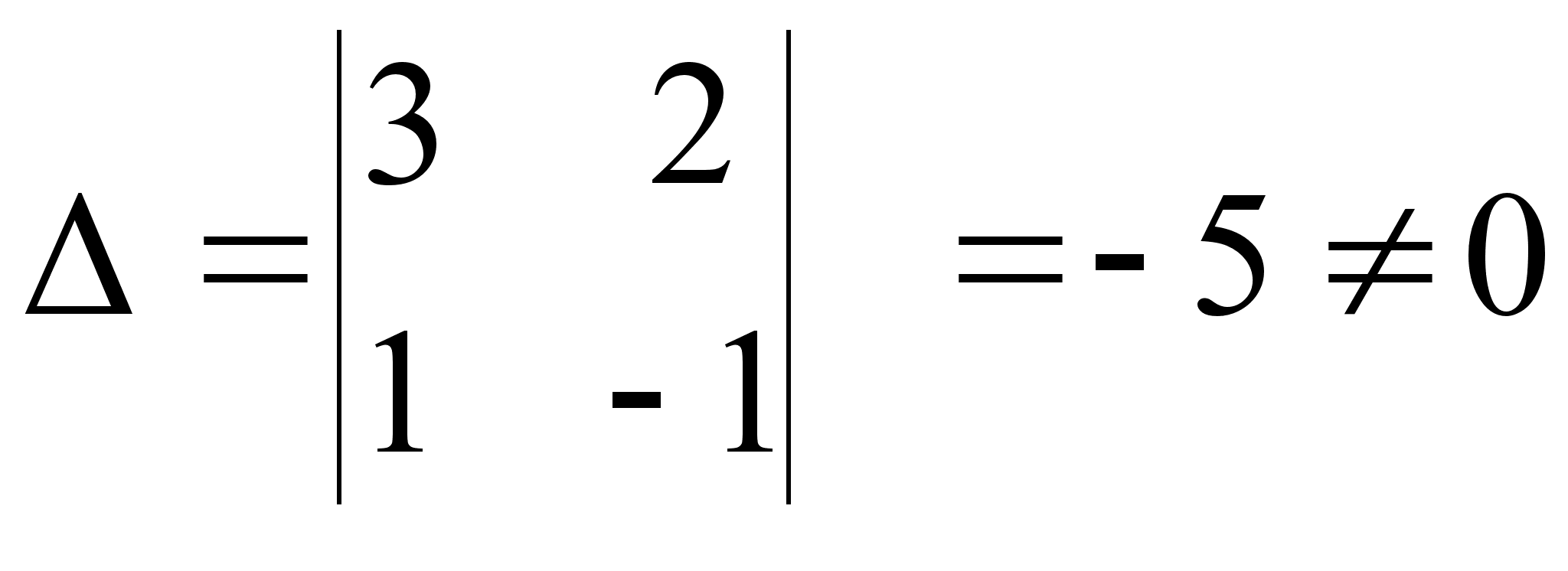
Так как определитель не равен нулю, система уравнений может быть решена по формулам Крамера. Найдем определители ∆x , ∆y:

.

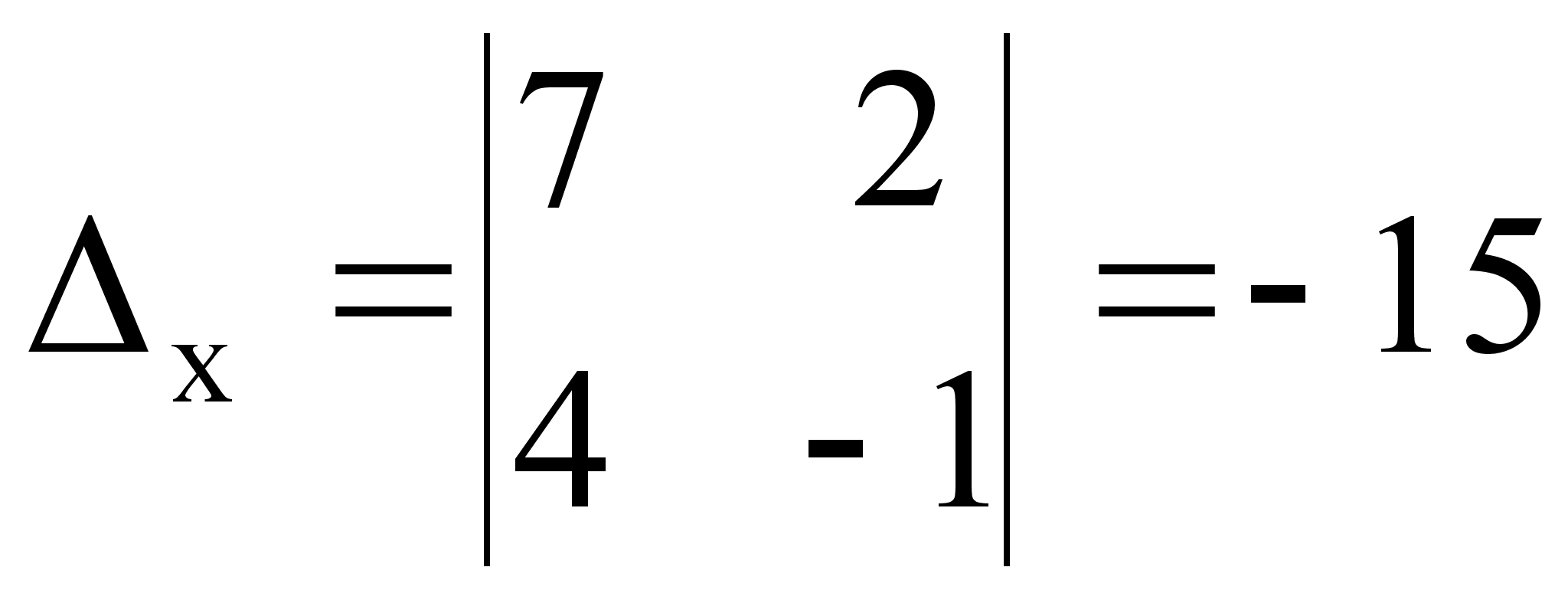
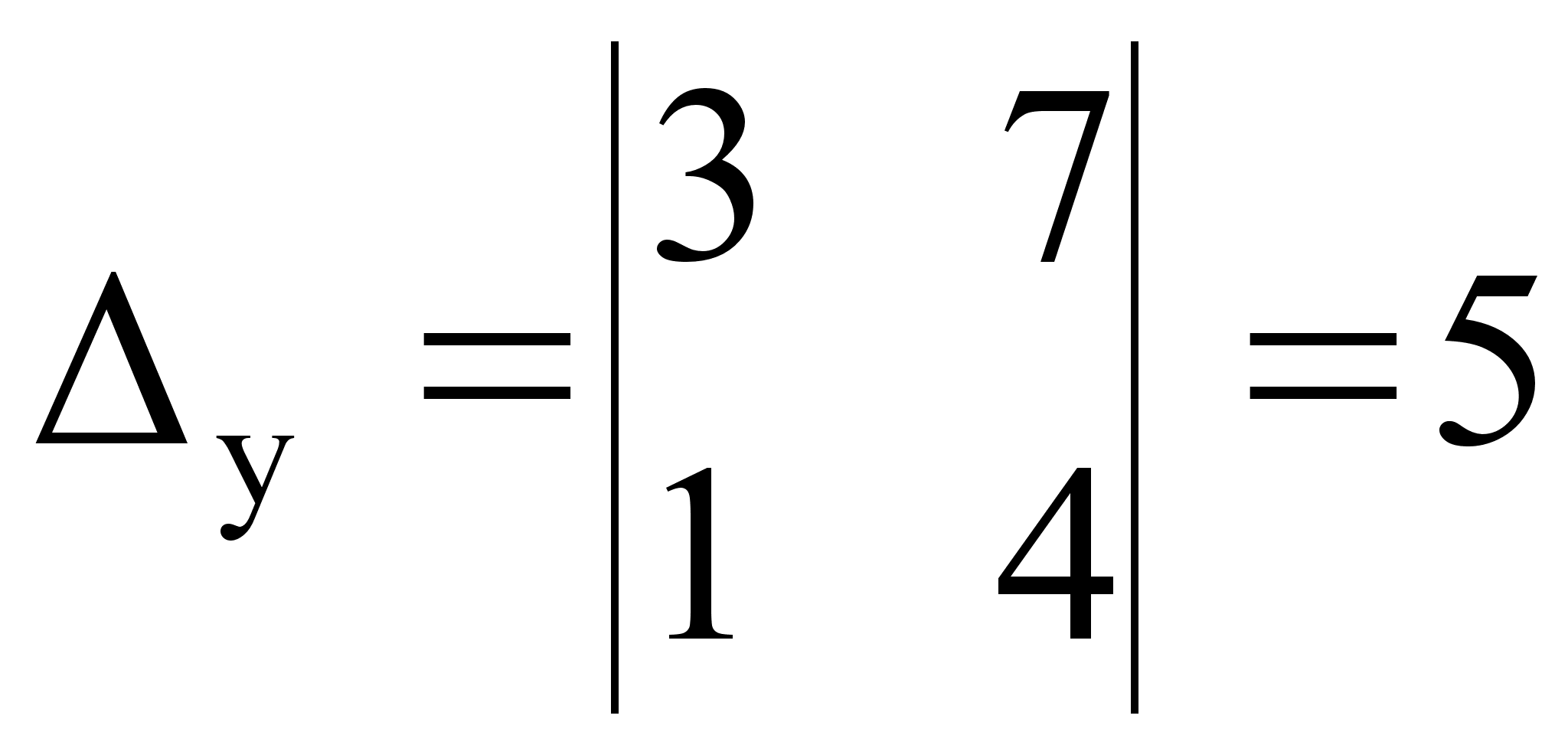
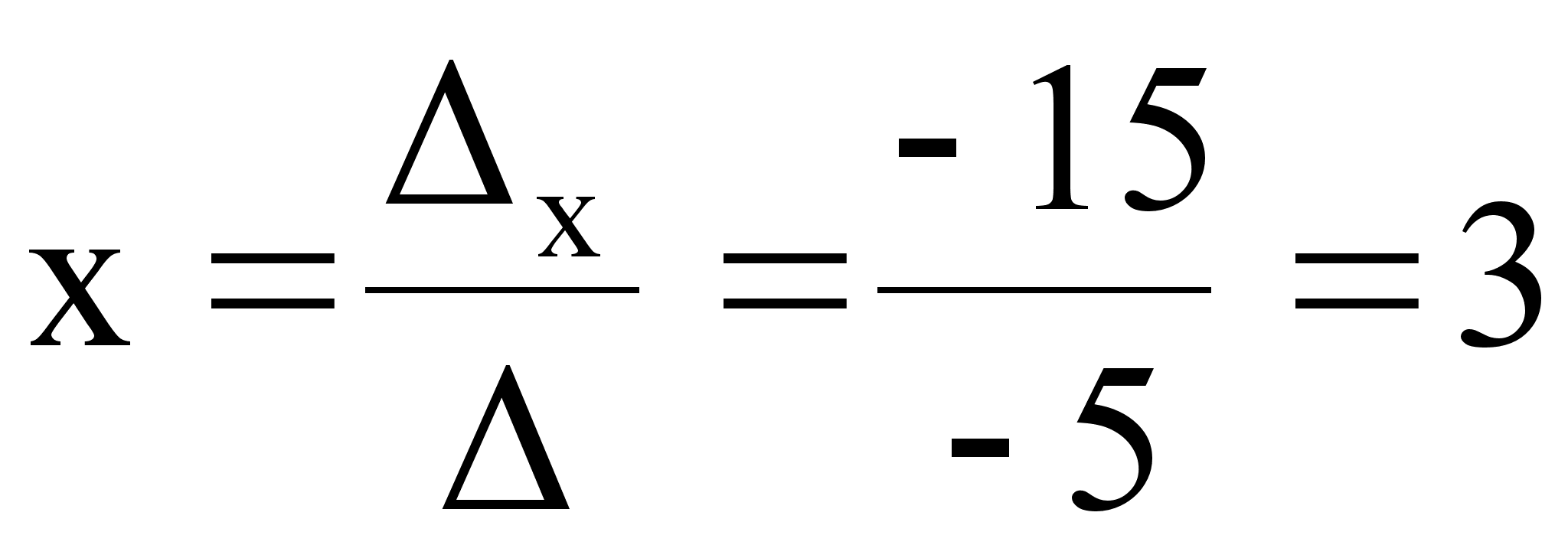
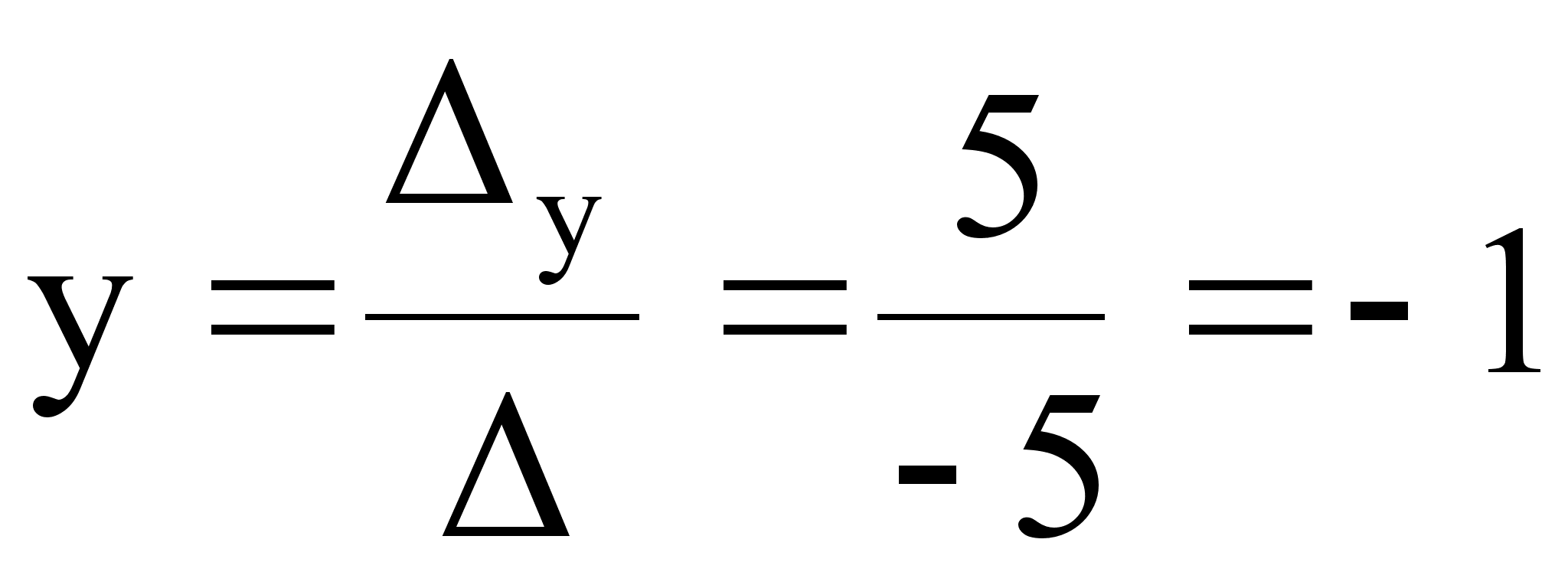Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: , _x1, _x2, …,x_n. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

а₁₁х₁ + а₁₂х₂ + …+ а_1nх_n = b₁;

а₂₁х₁ + а₂₂х₂ + …+ а_2nх_n = b₂;

_. ……………………………………

а_m1х₁ + а_m2х₂ + …+ а_mnх_n = b_m

Метод Гаусса решения системы (19) заключается в последовательном исключении переменных. Например:

Решить методом Гаусса систему уравнений

x₁ – 2x₂ + x₃ + x₄ = –1;

3x₁ + 2x₂ – 3x₃ – 4x₄ = 2;

2x₁ – x₂ + 2x₃ – 3x₄ = 9;

x₁ + 3x₂ – 3x₃ – x₄ = –1.

Р е ш е н и е. Составим матрицу В и преобразуем ее. Для удобства вычислений отделим вертикальной чертой столбец, состоящий из свободных членов:

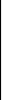1 –2 1 1 –1

B = 3 2 –3 –4 2 .

2 –1 2 –3 9

1 3 –3 –1 –1

Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу, эквивалентную исходной:

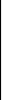
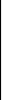1 –2 1 1 –1

0 8 –6 –7 5

0 3 0 –5 11

0 5 –4 –2 0

Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:

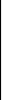
1 –2 1 1 –1

0 –1 –6 8 –28

0 0 –1 0 –3

0 0 0 19 –19

Из коэффициентов последней матрицы составим систему, равносильную исходной:

x₁ – 2x₂ + x₃ + x₄ = –1;

• X₂ – 6x₃ + 8x₄ = –28;

– x₃ = –3;

19x₄ = –19.

Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x₄ = –1, из третьего х₃ = 3. Подставив значения х₃ и x₄ во второе уравнение, найдем x₂ = 2. Подставив значения x₂, x₃, x₄ в первое уравнение, найдем x₁ = 1.

Теорема совместности Кронекера – Капелли звучит следующим образом: Для того, чтобы система неоднородных линейных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу её основной матрицы. Рассмотрим следующий пример:

Рассмотрим систему

5x₁ – x₂ + 2x₃ + x₄ = 7;

2x₁ + x₂ – 4x₃ – 2x₄ = 1;

x₁ – 3x₂ + 6x₃ – 5x₄ = 0.

Ранг основной матрицы этой системы равен 2, так как сцществует отличный от нуля минор второго порядка этой матрицы, например

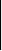
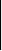5 –1 = 7,

2 1

а все миноры третьего порядка равны нулю.

Ранг расширенной матрицы этой системы равен 3, так как существует отличный от нуля минор третьего порядка этой матрицы, например

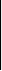
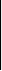5 –1 7

2 1 1 = –35.

1 –3 0

Согласно критерию Кронекера – Капелли система несовместна, т.е. не имеет решений.

В процессе работы я узнала много нового: какие действия можно выполнять над матрицами, какой путь решения систем линейных уравнений наиболее простой и быстрый, а так же многие другие теоретические вопросы и провела практические исследования, приводя примеры в тексте.

Тема решения систем линейных уравнений предлагается на вступительных экзаменах в различные математические вузы, на выпускных экзаменах, поэтому умение их решать очень важно.

Реферат может использоваться как учащимися, так и преподавателями в процессе факультативных занятий, как пособие для самостоятельного изучения по теме „Способы решения систем линейных уравнений ”, а также в качестве дополнительного материала.

МОУ Гимназия № 11

Способы решения систем линейных уравнений

Анжеро-Судженск

2004г.

МОУ Гимназия № 11

Способы решения систем линейных уравнений

Реферат по математике

Выполнила:

Ученица 9² класса

Бойко Юлия

Научный

Руководитель:

Клокова Татьяна

Васильевна.

Анжеро-Судженск

2004г.

Содержание:

Введение. 2

Глава I. Матрицы и действия над ними. 5

1.1. Основные понятия. –

1.2. Действия над матрицами. 8

1.3. Обратная матрица. 11

1.4. Ранг матрицы. 16

Глава II. Системы линейных уравнений. 23

2.1. Основные понятия. –

2.2. Система n линейных уравнений с n неизвестными. Правило

Крамера. 24

2.3. Однородная система n линейных уравнений с n

неизвестными. 28

2.4. Метод Гаусса решения общей системы линейных

уравнений. 30

2.5. Критерий совместности общей системы линейных

уравнений. 37

Заключение. 45

Список литературы. 46

-1-

Введение.

Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных уравнений, т.е. системы m уравнений 1ой степени с n неизвестными:

a₁₁x₁ + … + a_1n x_n = b₁ ;

a₂₁x₁ + … + a_2n x_n = b₂ ;

………………………………

a_m1x₁+ … + a_mnx_n = b_m .

Здесь x₁, … , x_n – неизвестные, а коэффициенты записаны так, что индексы при них указывают на номер уравнения и номер неизвестного. Значение систем 1ой степени определяется не только тем, что они простейшие. На практике часто имеют дело с заведомо малыми величинами, старшими степенями которых можно пренебречь, так что уравнения с такими величинами сводятся в первом приближении к линейным. Не менее важно, что решение систем линейных уравнений составляет существенную часть при численном решении разнообразных прикладных задач. Ещё Г.Лейбниц (1693) обратил внимание на то, что при изучении систем линейных уравнений наиболее существенной является таблица, состоящая из коэффициентов, и показал, как из этих коэффициентов (в случае m = n) строить так называемые определители, при помощи которых исследуются системы линейных уравнений. Впоследствии такие матрицы, или матрицы, стали предметом самостоятельного изучения, так как обнаружилось, что их роль не исчерпывается приложениями к теории систем линейных уравнений. Современная алгебра, понимаемая как учение об операциях над любыми математическими объектами, является одним из разделов математики, формирующих общие понятия и методы для всей математики. Для современной алгебры характерно то, что в центре внимания оказываются свойства операций, а не объектов, над которыми проводятся данные операции. Классическим разделом алгебры является линейная алгебра, т.е. теория

-2-

векторных пространств и модулей, частью которых являются сформировавшиеся ещё в XIX веке теория линейных уравнений и теория матриц. Идеи и методы линейной алгебры применяются во многих разделах математики. Так, основным предметом изучения функционального анализа являются бесконечномерные векторные пространства.

Г.Крамером в 1750 году было установлено правило, применимое к любой системе n линейных уравнений c n неизвестными. Оно носит название правила Крамера. Построение полной теории произвольных систем линейных уравнений было закончено только спустя 100 лет Л.Кронекером.

Применение правила Крамера при практическом решении большого числа линейных уравнений может встретить различные трудности, так как нахождение определителей высокого порядка связано с весьма большими вычислениями. Поэтому были разработаны методы численного (приближённого) решения систем линейных уравнений, наиболее известным из которых является метод Гаусса. Система линейных уравнений может иметь как одно единственное решение (определённая система), так и несколько (и даже бесконечное множество) решений (неопределённая система); может также оказаться, что система линейных уравнений не имеет ни одного решения (несовместная система). Вопрос о совместности системы линейных уравнений, т.е. вопрос о существовании решения системы линейных уравнений, решается сравнением ранга матриц [а_ij] и [a_ij, b_j ]. Если ранги совпадают, то система совместна; если ранг матрицы В строго больше ранга матрицы А, то система несовместна (теорема Кронекера-Капелли).

Несколько уравнений вида a₁x₁ + …+ a_nx_n= b образуют систему линейных уравнений

a_j1x₁ + …+ a_jnx_n = b_j , j = 1, …, m,

которую можно записать как

x₁a₁ + …+ x_na_n = b,

где а₁, …, а_n, b m-мерные векторы, являющиеся столбцами расширенной матрицы В системы. Отсюда следует, что различные линейные уравнения в функциональных пространствах, линейные дифференциальные уравнения, линейные интегральные уравнения

-3-

являются бесконечномерными аналогами обычных систем линейных уравнений.

Способы решения систем линейных уравнений – очень интересная и важная тема. Системы уравнений и методы их решения рассматриваются в школьном курсе математики, но недостаточно широко. А для того, чтобы перейти к исследованию данной темы, также нужно было познакомиться с темой матриц и определителей. Этот же материал вообще в школьной программе не изучается. В процессе знакомства с данной работой приобретаются навыки, с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее.

Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, определителей и систем линейных уравнений; изучить современное состояние данного вопроса; отобрать и классифицировать исследуемый материал; а также провести практическую часть работы.

-4-

Глава I. Матрицы и действия над ними.

1. Основные понятия.

Матрица размерами m Ч n – совокупность mn чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, например (обозначим за А)

2 5 2

А= 3 10 7 - матрица.

6 -3 -4

Числа, из которых состоит матрица, называются элементами матрицы. В общем виде матрицы:

а₁₁ a₁₂ … a_1n

a₂₁ a₂₂ … a_2n

M = a₃₁ a₃₂ … a_3n

…………………

a_m1 a_m2 … a_mn

они обозначаются буквами с двумя индексами: 1ый индекс указывает номер строки, а 2ой – номер столбца, в которых содержится этот элемент.

Если m = n, то матрица называется квадратной, а число строк (или столбцов) – её порядком.

Две матрицы, имеющие одинаковое количество строк и столбцов, называются матрицами одинакового типа. Две матрицы А = [a_ij] и В = [b_ij] одинакового типа называются равными, если a_ij = b_ij при всех i и j.

Матрица, состоящая из одной строки (одного столбца), называется матрицей-строкой (матрицей-столбцом), а матрица, у которой все элементы а_ij = 0, – нулевой или нуль матрицей.

Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ, а элементы квадратной

-5-

матрицы порядка n,сумма индексов каждого из которых равна n+1, –

побочную диагональ.

Сумма элементов главной диагонали квадратной матрицы называется следом матрицы. Квадратные матрицы, у которых все элементы вне главной диагонали равны нулю, называются диагональными (обозначается Е):

1 0 … 0

Е = 0 1 … 0

………………

0 0 … 1

Квадратная матрица, все элементы которой, стоящие ниже (выше) главной диагонали, равны нулю, называется треугольной:

a₁₁ а₁₂ … а_1n b₁₁ 0 … 0

А = 0 а₂₂ … а_2n ; B = b₂₁ b₂₂ … 0

……………… ………………

0 0 … a_nn b_n1 b_n2 … b_nn

Диагональная матрица является частным случаем треугольной. Преобразование элементов квадратной матрицы, состоящее в замене строк соответствующими столбцами, называется транспонированием матрицы. Таким образом, если

a₁₁ a₁₂ … a_1n

A = a₂₁ a₂₂ … a_2n ;

…………………

a_n1 a_n2 … a_nn

то

a₁₁ a₂₁ … a_n1

A^T = a₁₂ a₂₂ … a_n2 .

………………

a_1n a_2n … a_nn

Определитель n-го порядка матрицы

-6-

а₁₁ а₁₂ … а_1n

А = а₂₁ а₂₂ … а_2n

…………….…

а_n1 а _n2 … а_nn

есть число

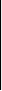
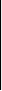а₁₁ а₁₂ … а_1n

∆ = а₂₁ а₂₂ … а_2n = ∑ (-1)^{I(k , k , …, k )} a_1k a_2k … a_nk

……………… (k₁, k₂, …, k_n)

а_n1 а_n2 … а_nn

Здесь суммирование распространяется на всевозможные перестановки индексов элементов а_ij, т.е. на всевозможные перестановки (k₁, k₂, …, k_n). Числа а_ij называют элементами определителя.

Квадратная матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю – вырожденной.

Определитель обладает некоторыми свойствами. Перечислим их:

1. При транспонировании матрицы её определитель не изменяется.

2. Если все элементы некоторой строки определителя состоят из

нулей, определитель равен нулю.

3.От перестановки двух строк определитель меняет знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Общий множитель всех элементов некоторой строки определителя можно вынести за знак определителя, или, если все элементы некоторой строки определителя умножить на одно и тоже число, то определитель умножается на это число.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, те же, что и у данного определителя; i-я строка определителя состоит из первых слагаемых элементов i-й строки данного определителя, а i-я

строка другого – из вторых слагаемых элементов i-й строки.

-7-

8. Определитель не изменяется, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число.

1.2. Действия над матрицами.

Основные операции, которые производятся над матрицами, – сложение, вычитание, умножение, а также умножение матрицы на число. Указанные операции являются основными операциями алгебры матриц – теории, играющей весьма важную роль в различных разделах математики и естествознания.

Суммой двух матриц А и В одинаковых размеров называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц А и В. Таким образом, если

а₁₁ … а_1n b₁₁ … b_1n

А = ………….. ; (1) В = …………… , то (2)

a_m1 … а_mn b_m1 … b_mn

a₁₁+ b₁₁ … a_1n + b_1n

A + B = ………………………

a_m1+ b_m1 … a_mn + b_mn

Операция нахождения суммы матриц называется сложением матриц и распространяется на случай конечного числа матриц одинаковы размеров.

Так же, как и сумма, определяется разность двух матриц

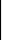
a₁₁ – b₁₁ … a_1n – b_1n

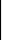A – B = ………………………

a_m1 – b_m1 … a_mn – b_mn

Операция нахождения разности двух матриц называется вычитанием матриц. Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:

-8-

1. А + В = В + А; (коммутативность)

2. А + (В + С) = (А + В) + С; (ассоциативность)

3. А + О = А.

Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.

Произведением матрицы А = [а_ij] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ. Произведение обозначим

λА. Таким образом от умножения матрицы (1) на число, получим:

a₁₁ … a_1n λa₁₁ … λa_1n

A = ………… , то λA = ………………

a_m1 … a_mn λa_m1 … λa_mn

Операция нахождения произведения матрицы на число называется умножением матрицы на число. Матрица –А = –1А называется противоположной матрице А. Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:

1. 1А = А;

2. (λ + μ)А = λА + μΑ;

3. λ(А + В) = λΑ+ λВ;

4) λ( μА) = (λμ)А;

5) А + (-А) = О.

Здесь А, В – произвольные матрицы; μ, λ - произвольные числа; О – нулевая матрица.

Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. Пусть матрицы А и В такие, что число столбцов матрицы А равно числу строк матрицы В:

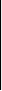
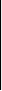
а₁₁ … а_1n b₁₁ … b _1n

A = …………… ; B = ………………

a_m1 … a_mn b_m1 … b_mn

В этом случае произведением матрицы А на матрицу В, которые

-9-

заданы в определенном порядке (А – 1ая, В – 2ая), является матрица С, элемент которой с_ij определяется по следующему правилу:

c_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj = ∑ ⁿ _{α = 1} a_iαb_αj,

где i = 1,2, …, m; j = 1, 2, …, k.

Для получения элемента с_ij матрицы произведения С = АВ нужно элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить. Например, если:

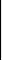1 2 3 7 8

А = ; В = 9 10 , то (1)

4 5 6 11 12

1 7 + 2 9 + 3 11 1 8 + 2 10 + 3 12 58 64

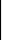АВ = = (2)

4 7 + 5 9 + 6 11 4 8 + 5 10 + 6 12 139 154

Число строк матрицы С = АВ равно числу строк матрицы А, а число столбцов – числу столбцов матрицы В.

Операция нахождения произведения двух матриц называется умножением матриц. Умножение матриц некоммутативно, т.е.

АВ ≠ ВА. Убедимся в примере матриц (1). Перемножив их в обратном порядке, получим:

39 54 69

ВА = 49 68 87 (3)

59 82 105

Сравнив правые части выражений (2) и (3), убедимся, что АВ ≠ ВА.

Матрицы А и В, для которых АВ = ВА, называются перестановочными. Например:

1 2 -3 2

А = ; В = перестановочны, т.к.

-2 0 -2 -4

-7 -6

АВ = ВА=

6. -4

-10-

Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:

1. А(ВС) = (АВ)С; (ассоциативность)

2. λ(АВ) = (λА)В = А(λВ);

3. А(В + С) = АВ + АС. (дистрибутивность)

Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ - произвольное число.

Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1ом множителе равно числу строк во 2ом, в остальных случаях произведение не определяется. А также, если матрицы А и В – квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.

1.3.Обратная матрица.

Пусть дана квадратная матрица

a₁₁ … a_1n

A = …………… ,

a_m1 … a_mn

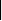
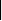= A – её определитель.

Если существует матрица Х такая, что АХ = ХА = Е, где Е – единичная матрица, то матрица Х называется обратной по отношению к матрице А, а сама матрица А – обратимой. Обратная матрица для А обозначается А^-1.

Теорема 1.1. Для каждой обратимой матрицы существует только одна обратная ей матрица.

Д о к а з а т е л ь с т в о. Пусть для матрицы А наряду с матрицей Х существует еще хотя бы одна отличная от Х обратная матрица, которую обозначим за Х₁. Тогда должны выполняться следующие условия: ХА = Е, АХ₁ = Е. Умножив второе равенство на матрицу Х, получим ХАХ₁ = ХЕ =Х. Но, т.к. ХА = Е, то предыдущее равенство можно записать в виде ЕХ₁ = Х или Х = Х₁.

Т е о р е м а д о к а з а н а.

Найдем теперь выражение для матрицы А^-1 при условии, что матрица

-11-

А – обратимая. Пусть дана обратимая квадратная матрица А с элементами а_ij. Обозначим через А_ij алгебраическое дополнение элемента а_ij в определителе ∆ матрицы А и составим матрицу В:

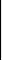А₁₁ A₂₁ … A_n1

B = …………………… (4)

A_1n A_2n … A_nn

Заметим, что в i-й строке матрицы В расположены алгебраические дополнения элементов j-го столбца определителя ∆. Матрица (4) называется присоединённой для матрицы А. Докажем, что матрицы А и В удовлетворяют матричному равенству

АВ = ВА = ∆Е. (5)

Для этого вычислим элемент, стоящий в i-й строке и j-м столбце произведения АВ. Искомый элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:

a_i1A_j1 + a_i2A_j2 + … + a_inA_jn. (6)

Согласно правилу разложения определителя по элементам строки (или столбца) выражение (6) равно определителю ∆ при i = j и нулю при i ≠ j. Следовательно, мы установили, что произведение АВ есть матрица вида

∆ 0 … 0 1 0 … 0

0 ∆ … 0 = ∆ 0 1 … 0

…………… ……………

0 0 … ∆ 0 0 … 1

Таким образом, АВ = ∆Е. Аналогично доказывается и равенство

ВА = ∆Е.

Пусть теперь А – невырожденная матрица (т.е. ∆ ≠ 0). Тогда, умножив обе части равенства (5) на числовой множитель 1/∆ , получим

(7)

Сравнивая равенства (5) и (7) и учитывая единственность обратной

-12-

матрицы, замечаем, что

Таким образом, доказано, что, во-первых, обратимы только невырожденные матрицы, и, во-вторых, для матрицы А обратной является матрица

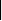
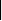
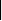
П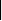усть А невырожденная матрица, тогда АА^-1 = Е. Переходя в этом равенстве к определителям, получаем А А^-1 = 1, откуда

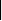
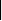
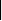
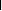
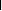А^-1 = А ^-1.

Таким образом, определитель обратной матрицы равен обратной величине определителя данной матрицы. Из этого следует, что если матрица А – невырожденная, то обратная матрица А^-1 также невырожденная.

Пусть теперь дана матрица А^-1. Для неё обратной будет матрица

(А^-1)^-1.Поэтому из определения обратной матрицы будем иметь

А^-1(А^-1) ^-1 = Е. Умножив это соотношение слева на А, получим

АА^-1(А^-1) ^-1 = АЕ или (А^-1) ^-1 = А.

-13-

Пример 1. Найти матрицу обратную матрице

1 2 3

А = –3 –1 1 .

2 1 –1

Р е ш е н и е. Проверим, обратима матрица А или нет, т.е. является ли она невырожденной:

1 2 3 1 2 5

∆_А = –3 –1 1 = –3 –1 0 = 5 –3 1 = 5 (–3 + 2) = –5 ≠ 0.

2 1 –1 2 1 0 2 1

Найдем алгебраические дополнения всех элементов матрицы А:

А₁₁ = –1 1 = 0; А₁₂ = –­­ –3 1 = –1;

1 –1 2 –1

А₁₃ = –3 –1 = –1; А₂₁ = – 2 3 = 5;

2 1 1 –1

А₂₂ = 1 3 = –7; А₂₃ = – 1 2 = 3;

2 –1 2 1

А₃₁ = 2 3 = 5; А₃₂ = 1 3 = –10;

–1 1 –3 1

А₃₃ = 1 2 = 5.

–3 –1

Составим присоединённую матрицу для матрицы А:

0 5 5

–1 –7 –10 .

–1 3 5

Отсюда находим обратную матрицу:

0 5 5

А^-1 = – –1 –7 –10 .

–1 3 5

-14-

Пример 2. Найти неизвестную матрицу Х из уравнения АХ = В, если:

А = 2 3 ; В = 3 4 .

1 2 -1 1

Р е ш е н и е. Умножив обе части данного матричного уравнения слева на матрицу А^-1, получим:

А^-1АХ = А^-1В; Х = А^-1В.

Найдем А^-1: ∆_А = 1, А₁₁ = 2, А₁₂ = -1, А₂₁ = -3, А₂₂ = 1, следовательно,

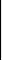
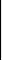
А^-1 = 2 -3 .

-1 1

Найдем матрицу Х:

Х = А^-1В = 2 -3 3 4 = 9 5 .

-1 1 -1 1 -4 -3

-15-

1.4. Ранг матрицы.

Рассмотрим произвольную прямоугольную матрицу

а₁₁ … а_1n

A = …………… (8)

a_m1 … a_mn

Выделим некоторое число k строк этой матрицы и такое же число столбцов. Элементы матрицы (8), стоящие на пересечение выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Если не все числа а_ij матрицы А равны нулю, то всегда можно указать число r такое, что у матрицы А имеется минор,

имеющий порядок r + 1 и выше, равен нулю.

Число r, представляющее собой наибольший из порядков отличных от нуля миноров матрицы А, называется рангом матрицы и обозначается rangA. Если все элементы а_ij равны нулю, то ранг матрицы принимается равным нулю. Отличный от нуля минор r-го порядка матрицы A (таких миноров у матрицы А может быть несколько, но все они имеют один и тот же порядок r) называется базисным минором матрицы А. Строки и столбцы, из которых построен базисный минор, называют базисными. Понятие ранга матрицы широко применяется в различных приложениях теории матриц.

Выделим в матрице А произвольно k строк. Пусть это будут строки

a₁, а₂, …, а_k:

а_α11, а_α12, …, а_α1n;

а_α21, а_α22, …, а_α2n;

……………………

а_αk1, а_αk2, …, а_αkn.

-16-

Если существуют такие числа λ₁, λ₂, …, λ_k, не все равные нулю, что для элементов некоторой другой, отличной от выделенной, строки i выполняются следующие соотношения:

(9)

то говорят, что i-я строка линейно выражается через строки

α₁, α₂, …, α_k. В случае, если равенства (9) выполняются тогда и только тогда, когда все числа λ₁, λ₂, …, λ_k – нули, то говорят, что i-я строка линейно зависима от строк α₁, α₂, …, α_k. Аналогичным образом можно ввести понятие линейной зависимости и линейной независимости между столбцами матрицы.

Теорема 1.2.(о базисном миноре) Любая строка матрицы А является линейной комбинацией её базисных строк.

Д о к а з а т е л ь с т в о. Предположим, что базисный минор матрицы (8) расположен в её верхнем левом углу, т.е. в первых r строках и первых r столбцах. Такое предположение не уменьшает общности рассуждения. Пусть k – номер любой строки матрицы А (k может принимать значения от 1 до m), а l – номер любого её столбца (l может принимать значения от 1 до n).

Рассмотрим следующий минор матрицы (8):

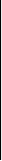
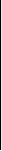a₁₁ a₁₂ … a_1r a_1l

a₂₁ a₂₂ … a₁₁ a_1l

∆ = ……………………… (10)

a_r1 a_r2 … a_rr a_rl

………………………

a_k1 a_k2 … a_kr a_kl

Если k < r, то ∆ = 0, так как в нем имеется две одинаковые строки. Аналогично ∆ = 0 и при l < r.

Разложив определитель ∆ по элементам последнего столбца, получим

a_1lA_1l + a_2lA_2l + … + a_rlA_rl + a_klA_kl = 0,

-17-

Придавая l значения, получаем:

(11)

Равенства (11) показывают, что k-я строка матрицы А является линейной комбинацией первых r строк с коэффициентами

λ₁, λ₂, …, λ_r. Так как эти равенства справедливы при любом k от 1 до n, то т е о р е м а д о к а з а н а полностью.

Основываясь на теореме о базисном миноре, докажем справедливость следующих предложений.

1. Ранг матрицы не изменяется, если к ней приписать строку, являющуюся линейной комбинацией строк матрицы.

Действительно, базисные строки исходной матрицы будут также базисными строками в дополнительной матрице, так как строку из линейной комбинации всех строк исходной матрицы можно

представить как линейную комбинацию базисных строк.

2. Ранг матрицы А не изменится, если вычеркнуть из неё строку, являющуюся линейной комбинацией остальных строк матрицы.

В самом деле, исходная матрица А получается из матрицы с вычеркнутой строкой путем добавления строки, являющейся линейной комбинацией строк матрицы А. Таким образом, предложение 2 сводится к предложению 1.

Нахождение ранга матрицы, как это следует из его определения, требует вычисления большого числа миноров (т.е. определителей разных порядков) матрицы. Однако этот процесс можно упростить: вычисляя ранг матрицы, гораздо удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор r-го порядка, отличный от нуля, то при следующем шаге нужно вычислять миноры (r + 1)-го порядка, окаймляющие прежний минор. Если все они равны нулю, то ранг матрицы равен r.

Другим простым способом вычисления ранга матрицы является метод Гаусса, основанный на так называемых элементарных преобразованиях, выполняемых над матрицей. Такими преобразованиями будем считать:

-18-

1. вычеркивание строки состоящей из нулей;

2. прибавление к элементам одной из строк соответствующих элементов других строк, умноженных на любое число;

3. перестановку двух столбцов.

Теорема 1.3. Элементарные преобразования не изменяют ранга матрицы.

Д о к а з а т е л ь с т в о. Преобразование 1 следует из теоремы о линейной комбинации элементов любой строки матрицы. В самом деле, так как нулевая строка не может быть базисной, то её исключение, как и включение, не изменит ранга матрицы.

Преобразование 3 очевидно, так как перестановка двух столбцов матрицы не нарушает никаких линейных зависимостей между её строками.

Остается рассмотреть преобразование 2. Пусть к k элементам i-ой строки матрицы А прибавляются соответствующие элементы j-ой строки, умноженные на число k. Указанное преобразование можно выполнить в два приёма: сначала добавить к матрице А новую строку

с элементами a_il + ka_jl, вставив её после i-й строки, затем из полученной матрицы вычеркнуть j-ю строку. При первой операции ранг полученной матрицы будет равен рангу матрицы А согласно предложению 1, а при второй операции – согласно предложению 2.

Т е о р е м а д о к а з а н а.

Метод Гаусса вычисления ранга матрицы заключается в том, что путем элементарных преобразований можно привести данную матрицу А к виду

b_1l b₁₂ … b_1r … b_1n

B = 0 b₂₂ … b_2r … b_2n

…………………………… ,

0 0 … b_rr … b_rn

в котором все диагональные элементы b_1l, b₂₂, …, b_rr отличны от нуля, а элементы других строк, расположенные ниже диагональных, равны нулю.

Учитывая, что ранг не меняется при элементарных преобразованиях, имеем rang A = rang B.

-19-

Пример 1. Вычислить ранг матрицы

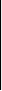
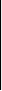1 –2 –1 3

А = 2 0 1 –1 .

–1 –2 –2 4

7 –6 –1 7

Р е ш е н и е. Выберем минор второго порядка, стоящий в верхнем левом углу:

М₂ = 1 –2 = 4.

2. 0

Т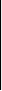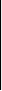ак как М₂ ≠ 0, то, следовательно, ранг матрицы не меньше двух. Составляем миноры третьего порядка, окаймляющие минор второго порядка отличный от нуля. Для этого добавим к М₂ третью строку и третий столбец:

1 –2 –1

М₃ = 2 0 1 = 2 + 4 + 2 – 8 = 0.

–1 –2 –2

Заменим третий столбец четвертым:

1 –2 3

М′₃ = 2 0 –1 = –2 – 12 – 2 + 16 = 0.

–1 –2 4

В миноре М₃ заменим третью строку четвертой:

1 –2 –1

М″₃ = 2 0 1 = –14 + 12 + 6 – 4 = 0.

7 –6 –1

В миноре М′₃ заменим третью строку четвертой:

1 –2 3

М′″₃ = 2 0 –1 = 14 – 36 – 6 + 28 = 0.

7 –6 7

Все миноры третьего порядка, окаймляющие минор второго порядка, равны нулю. А это значит, что rang A = 2.

-20-

Пример 2. Найти ранг матрицы

1 2 3 4 5

A = 2 1 1 3 5 .

1 2 3 1 7

–2 2 4 –1 2

Р е ш е н и е. Произведем следующие элементарные преобразования над матрицей А. Путем умножения элементов строк на числа и сложения их с соответствующими элементами других строк добьемся, чтобы все элементы первого столбца, кроме первого, были бы нулями. Один нуль там уже имеется, поэтому, сложив четвертую строку со второй, умноженной на два, получим

1 2 3 4 5

B = 0 –3 –5 –5 –5 .

0 0 0 –3 2

0 6 10 7 12

Применим теперь элементарные преобразования таким образом, чтобы в матрице В все элементы второго столбца, кроме первых двух, были бы нулями. Один нуль там уже имеется, поэтому, сложив четвертую строку со второй, умноженной на 2, получим

1 2 3 4 5

С = 0 –3 –5 –5 –5 .

0 0 0 –3 2

0 0 0 –3 2

Оставив три строки матрицы С без изменения и сложив четвертую строку с третьей, умноженной на –1, получим

1 2 3 4 5

D = 0 –3 –5 –5 –5 .

0 0 0 –3 2

0 0 0 0 0

-21-

Очевидно, что ранг матрицы D равен трем, так как минор третьего порядка

1 2 5

М = 0 –3 –5 = –6 ≠ 0,

0 0 2

а все миноры четвертого порядка, окаймляющие минор М, равны нулю. На основании теоремы 1.3. заключаем, что rang А = 3.

-22-

Глава II. Системы линейных уравнений.

2.1. Основные понятия

В самом общем случае система линейных уравнений имеет следующий вид:

a₁₁x₁ + a₁₂x₂ + …+ a_1n x_n = b₁ ;

a₂₁x₁ + a₂₂x₂ + …+ a_2n x_n = b₂ ; (13)

……………………………………

a_m1x₁+ a_m2x₂ + …+ a_mnx_n = b_m ;

где х₁, х₂, …, х_n - неизвестные, значения которых подлежат нахождению. Как видно из структуры системы (2.1), в общем случае число неизвестных не обязательно должно быть равно числу уравнений самой системы. Числа а₁₁, а₁₂, … , а_mn называются коэффициентами системы, а b₁, b₂, … , b_m - её свободными членами. Для удобства коэффициенты системы а_ij

(i = 1, 2, . . ., m; j = 1, 2, . . .,n) и свободные члены b_i (i=1, 2, . . .,m) снабжены индексами. Первый индекс коэффициентов а_ij соответствует номеру уравнения, а второй индекс – номеру неизвестной х_i, при которой коэффициент поставлен. Индекс свободного члена b_i соответствует номеру уравнения, в которое входит b_i.

Дадим определения некоторых понятий, необходимых при изучении системы уравнений. Решением системы уравнений (13) называется всякая совокупность чисел α₁, α₂, α_n, которая будучи поставлена в систему (13) на место неизвестных х₁, х₂, …, х_n, обращает все уравнения системы в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решений. Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет по крайней мере два различных решения.

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.

-23-

2.2. Система n линейных уравнений с n

неизвестными. Правило Крамера.

Пусть дана система n линейных уравнений с n неизвестными:

a₁₁x₁ + a₁₂x₂ + …+ a_1n x_n = b₁ ;

a₂₁x₁ + a₂₂x₂ + …+ a_2n x_n = b₂ ; (14)

……………………………………

a_n1x₁ + a_n2x₂ + …+ a_nnx_n = b_n ;

Определителем системы (14) называется определитель, составленный из коэффициентов а_ij.

a₁₁ a₁₂ … a_1n

∆ = a₂₁ a₂₂ … a_2n

…………………………

a_n1 a_n2 … a_nn

Рассмотрим случай, когда ∆ ≠ 0. Докажем, что в этом случае система (14) является определенной, т.е. имеет одно единственное решение. Как и ранее, через А_ij будем обозначать алгебраическое дополнение элемента а_ij в определителе ∆.

Умножим каждое уравнение системы (14) на алгебраические дополнения элементов i-го столбца определителя ∆, т.е. первое уравнение умножим на А_1i, второе – на А_2i и т.д., наконец, последнее уравнение – на А_ni, а затем все полученные уравнения системы сложим. В результате будем иметь

(a₁₁x₁ + a₁₂x₂ + …+ a_1ix_i + …+ a_1nx_n) A_1i + (a₂₁x₁ + a₂₂x₂ + …+ a_2ix_i +

+ …+ a_2nx_n) A_2i + …+ (a_n1x₁ + a_n2x₂ + …+ a_nix_i + …+ a_nx_nn) A_ni = b₁A_1i + b₂A_2i + …+ b_nA_ni

или, сгруппировав члены относительно известных x₁, x₂, …, x_n, получим

(a₁₁A_1i + a₂₁A_2i + …+ a_n1A_ni) x₁ + … +

+ (a_1iA_1i + a_2iA_2i + …+ a_niA_ni) x_i + … +

+ (a_1nA_1i + a_2nA_2i + …+ a_nnA_ni) x_n =

= b₁A_1i + b₂A_2i + …+ b_nA_ni. (15)

Коэффициент при неизвестной х_i равен определителю ∆, а коэффициенты при всех других неизвестных равны нулю. Свободный

-24-

член уравнения (15) отличается от коэффициента при х₁ тем, что коэффициенты а_1i, а_2i, …, а_ni заменены свободными членами

b₁, b₂, …, b_n уравнения (14). Следовательно, выражение

b₁A_1i + b₂A_2i + …+ b_nA_ni есть определитель i-го порядка, отличающийся от определителя только i-м столбцом, который заменен столбцом свободных членов. Обозначив этот определитель ∆x_i, будем иметь

a₁₁ a₁₂ … b₁ … a_1n

∆x_i = a₂₁ a₂₂ … b₂ … a_2n .

………………………………

a_n1 a_n2 … b_n … a_nn

Таким образом, уравнение (15) можно записать в виде

∆х =∆x_i, (16)

откуда при ∆ ≠ 0

х = ——

Придавая индексу i значения 1, 2, …, n, получаем:

х₁ = —— ;

х₂ = —— ;

(17)

………………

х_n = —— .

Рассмотренный метод решения системы уравнений называется правилом Крамера, а формулы (17) – формулами Крамера.

-25-

Пример 1. Решить систему уравнений

x₂ + 2x₂ + x₂ – x₂ = 1;

2x₂ + x₂ – ­­­x₂ – 3x₂ = 1;

x₂ – 3x₂ + 2x₂ + 2x₂ = –2;

3x₂ + x₂ + 3x₂ – 4x₂ = –3.

Р е ш е н и е. Вычислим определитель системы:

1 2 1 -1 1 0 0 0 -3 -3 -1

∆ = 2 1 -1 -3 = 2 -3 -3 -1 = -5 1 3 =

1 -3 2 2 1 -5 1 3 -5 0 -1

3 1 3 -4 3 -5 0 -1

-18 0 8

= -5 1 3 = -18 8 _{= 18 + 40 = 58.}

-5 0 -1 -5 -1

Поскольку ∆ ≠ 0, система уравнений может быть решена по формулам Крамера. Найдем определители ∆x₁ – ∆x₄:

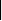
1 2 1 –1 1 0 0 0 –1 –2 –2

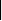
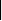_{∆х1 =} 1 1 –1 –3 ₌ 1 –1 –2 –2 = 1 4 0 =

–2 –3 2 2 2 1 4 0 7 6 –7

–3 1 3 –4 –3 7 6 –7

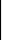
–1 2 –2 2 –2

= 1 0 0 = – –22 –7 = – (–14 – 48) =58;

7 22 –7

1 1 1 –1 1 0 0 0 –1 –3 –1

∆х₂ = 2 1 –1 –3 = 2 –1 –3 –1 = –3 1 3 =

1 –2 2 2 1 –3 1 3 –6 0 –1

3 –3 3 –4 3 –6 0 –1

–10 0 8 –10 8

= –3 1 3 = –6 –1 = 19 + 48 = 58;

–6 0 –1

-26-

1 2 1 –1 1 0 0 0 –3 –1 –1

∆х₃ = 2 1 1 –3 = 2 –3 –1 –1 = –5 –3 3 =

1 –3 –2 2 1 –5 –3 3 –5 –6 –1

3 1 –3 –4 3 –5 –6 –1

= – (70 – 12) = –58.

Таким же образом высчитываем ∆х₄ и получаем: ∆х₁ = ∆х₂ = –∆х₃ = ∆х₄, и, следовательно, х₁ = х₂ = –х₃ = х₄ = 1.

-27-

2.3. Однородная система п линейных уравнений , с n неизвестными

Линейное уравнение называется однородным, если его свободный член равен нулю. Система линейных уравнений называется однородной, если все входящие в нее уравнения являются линейными однородными уравнениями.

Однородная система п линейных уравнений с п неизвестными имеет вид:

а₁₁х₁ + а₁₂х₂ + …+ а_1nх_n = 0;

а₂₁х₁ + а₂₂х₂ + …+ а_2nх_n = 0; (18)

…………………………………

а_n1х₁ + а_n2х₂ + …+ а_nnх_n = 0.

Непосредственной проверкой убеждаемся в том, что однородная система линейных уравнений (18) имеет нулевое решение:

х₁ = 0, х₂ = 0, . . . , х_п = 0.

Таким образом, однородная система линейных уравнений (18) всегда

совместна. Поэтому важно выяснить, при каких условиях она является определенной. Покажем, что однородная система п линейных уравнений с п неизвестными имеет ненулевые решения тогда и только тогда, когда определитель ее равен нулю.

В самом деле, пусть  = 0. Так как однородная система уравнений (18) является частным случаем неоднородной системы, то к ней применимо правило Крамера. Но для однородной системы все x_i = 0, так как каждый из этих определителей содержит столбец из нулей (b_i = 0). Поэтому система, равносильная системе (16), будет иметь вид

_x1= 0, _x2=0;. . .,_xn= 0

Из этой системы следует, что однородная система (18) имеет единственное нулевое решение, если Δ 0; если же  = 0, то из условий (16) следует, что она имеет бесчисленное множество решений.

-28-

Пример 1. Решить систему уравнений

2x₁ + x₂ – 2x₃ = 0;

3x₁ – x₂ – x₃ = 0;

x₁ + 3x₂ – x₃ = 0.

Р е ш е н и е. Определитель системы

2 1 –2 2 1 0

 = 3 –1 –1 = 3 –1 2 = –2 2 1 = –2 (6 – 1) = –10

1 3 –1 1 3 0 1 3

Так как Δ 0, то система линейных однородных уравнений имеет единственное нулевое решение: х₁ = х₂ = х₃ = 0.

Пример 2. Решить систему уравнений

x₁ – 5x₂ = 0;

2x₁ – 10x₂ = 0;

Решение. Вычислим определитель системы:

= 1 –5 =0

2 –10

Так как  = 0, то система линейных однородных уравнений имеет бесчисленное множество решений.

-29-

2.4. Метод Гаусса решения общей

системы с линейных уравнений

Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: , _x1, _x2, …,x_n. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

а₁₁х₁ + а₁₂х₂ + …+ а_1nх_n = b₁;

а₂₁х₁ + а₂₂х₂ + …+ а_2nх_n = b₂; (19)

_. ……………………………………

а_m1х₁ + а_m2х₂ + …+ а_mnх_n = b_m

Требуется найти все решения системы уравнений (19). Будем производить над системой элементарные преобразования: исключение из системы уравнения вида

0х₁ + 0х₂ + …+ 0х_n = 0 (20)

и прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое число .

Очевидно, что если мы проделаем над уравнениями системы (19) любое из приведенных выше преобразований, то получим систему, равносильную исходной. При необходимости систему (19) будем подвергать еще одному виду преобразований – перенумерации переменных и уравнений. Идея этого преобразования заключается в следующем. Если, например, возникает необходимость, чтобы в каком-то уравнении системы (например, в k -м) неизвестная x₁ стояла на первом месте, то в результате перенумерации соответствующее уравнение запишется в виде

a_kix₁ + ... + a_k2x₂ + … + a_k1x_i+ ... + a_knx_n = b_k,

т. е. вместо прежней неизвестной х_i мы будем писать х₁, а вместо

x₁ – х_i

Метод Гаусса решения системы (19) заключается в

-30-

последовательном исключении переменных.

Если среди уравнений системы есть хотя бы одно уравнение вида

0x_l + 0x₂+ ... + 0x_n= b , (21)

причем b 0, то совершенно очевидно, что ни одна система значений х₁, х₂..., х_п не удовлетворяет этому уравнению, а следовательно, и системе в целом, поэтому система несовместна.

Пусть теперь система (19) не содержит уравнений вида (20) или (21). Это значит, что в каждом уравнении системы хотя бы один из коэффициентов отличен от нуля. Пусть a₁₁0 (в противном случае, применив элементарные преобразования, мы сможем добиться, чтобы первый коэффициент первого уравнения был отличен от нуля). Оставив первое уравнение без изменения, исключим из всех уравнений системы (19), начиная со второго, неизвестную х₁. Для этого из второго уравнения вычтем первое, умноженное на a₂₁/a₁₁, затем из третьего уравнения вычтем также первое, но уже умноженное на a₃₁/a₁₁, и так до последнего уравнения. В результате этих преобразований мы получим равносильную систему

а₁₁х₁ + а₁₂х₂ + … + а_1nх_n = b_1;

а′₂₂х₂ + …+ а′_2nх_n = b′_2;

………………………… (22)

а′_m2х₂ + …+ а′_mnх_n = b′_m

Заметим, что в системе (22) число уравнений может быть и меньше m, так как среди них могут оказаться уравнения вида (20), которые, как мы условились ранее, можно отбросить.

Пусть а₂₂ 0. Применим те же самые рассуждения и исключим из последних п – 2 уравнений системы (22) неизвестную х₂ путем вычитания из третьего уравнения второго, умноженного на a′₃₂/a′₂₂ , из четвертого уравнения — второго, умноженного на a′₃₄/a′₂₂ и т. д. В результате получим систему

а₁₁х₁ + а₁₂х₂ + а₁₃х₃ + …+ а_1nх_n = b_1;

а′₂₂х₂ + а′₂₃х₃ + …+ а′_2nх_n = b′_2;

а′′₃₃х₃ + …+ а″₃х_n = b″_3;

……………………………

а″_m3х₃ +…+а″_mnх_n = b″_m.

Продолжая этот процесс, систему (19) приведем к равносильной системе вида

-31-

c₁₁х₁ + c₁₂х₂ + c₁₃х₃ + …+ c_1kх_k + …+ c_1nх_n = d_1;

c₂₂х₂ + c₂₃х₃ + …+ c_2kх_k + …+ c_2nх_n = d_2;

c₃₃х₃ + …+ c_3kх_k + …+ c_3nх_n = d_3; (23)

………………………………………

c_kkх_k + …+c_knх_n = d_k.

в которой коэффициенты c_11, c_22, . . ., c_kk отличны от нуля.

Может оказаться, что в процессе преобразования на каком-то шаге в полученной системе окажется уравнение вида (21). В этом случае система (19) не имеет решений. Предположим теперь, что среди уравнений полученной системы нет уравнения вида (21). Тогда для решения системы (19) необходимо решить систему (23), что не составляет особого труда. Рассмотрим два возможных случая.

1. k = n (это частный случай, когда число уравнений совпадает с числом неизвестных). Тогда последнее уравнение системы (23) имеет вид с_ппх_п = d_n, откуда х_п = d_n /c_nn. Подставив это значение в предпоследнее уравнение системы (23), имеющее вид

c_n-1n-1x_n-1 + c_n-1nx_n= d_n-1, найдем значение неизвестной x_n-1 и т. д.; наконец, из первого уравнения найдем неизвестную x₁ Таким образом, в случае k = п система уравнений (19) имеет единственное решение.

2. k < n. Тогда из последнего уравнения системы (23), найдем неизвестную x_k, выраженную через неизвестные х_k+1, х_k+2, . . . x_{n :}

x_k = (d_kk – c_{k k+1}x_k+1 – … – c_knx_n).

Подставив это значение неизвестной в предпоследнее уравнение системы (23), найдем выражение для неизвестной х_k-1,и т. д.; наконец, подставив значения неизвестных х_k, х_k-1, . . . x₂ в первое уравнение системы (23), получим выражение для неизвестной x₁. В результате указанная система уравнений (19) приводится к виду

x₁ = d′₁ + c′_{1 k+1}x_k+1 + …+ c′_1nx_n;

x₂ = d′₂ + c′_{2 k+1}x_k+1 + …+ c′_2nx_n; (24)

………………………………………

x_k = d′_k + c′_{k k+1} x_k+1 + …+ c_knx_n.

-32-

Неизвестные х_k+1, х_k+2, …, х_п называются свободными. Им можно придать различные значения и затем из системы (19) найти значения неизвестных х_1, х₂, …, х_k. Таким образом, в случае k < п совместная система уравнений (19) имеет бесчисленное множество решений.

Заметим, что если в процессе приведения системы (19) к системе (24) была произведена перенумерация неизвестных, то в системе (24) необходимо вернуться к их первоначальной нумерации.

На практике процесс решения системы уравнений облегчается тем, что указанным выше преобразованиям подвергают не саму систему, а матрицу

a₁₁ a₁₂ … a_1n b₁

a₂₁ a₂₂ … a_2n b₂

……………………… …… (25)

a_m1 a_m2 … a_mn b_m

составленную из коэффициентов уравнений системы (19) и их свободных членов. При этом каждому элементарному преобразованию, проведенному над системой (19), соответствует преобразование над матрицей (25): вычеркивание строки, все элементы которой состоят из нулей, прибавление к элементам некоторой строки соответствующих элементов другой строки, умноженных на некоторое число, и перестановка двух столбцов матрицы (25).

-33-

Пример 1. Решить методом Гаусса систему уравнений

x₁ – 2x₂ + x₃ + x₄ = –1;

3x₁ + 2x₂ – 3x₃ – 4x₄ = 2;

2x₁ – x₂ + 2x₃ – 3x₄ = 9;

x₁ + 3x₂ – 3x₃ – x₄ = –1.

Р е ш е н и е. Составим матрицу В и преобразуем ее. Для удобства вычислений отделим вертикальной чертой столбец, состоящий из свободных членов:

1 –2 1 1 –1

B = 3 2 –3 –4 2 .

2 –1 2 –3 9

1 3 –3 –1 –1

Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу, эквивалентную исходной:

1 –2 1 1 –1

0 8 –6 –7 5

0 3 0 –5 11

0 5 –4 –2 0

Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:

1 –2 1 1 –1

0 –1 –6 8 –28

0 0 –1 0 –3

0 0 0 19 –19

Из коэффициентов последней матрицы составим систему, равносильную исходной:

-34-

x₁ – 2x₂ + x₃ + x₄ = –1;

• X₂ – 6x₃ + 8x₄ = –28;

– x₃ = –3;

19x₄ = –19.

Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x₄ = –1, из третьего х₃ = 3. Подставив значения х₃ и x₄ во второе уравнение, найдем x₂ = 2. Подставив значения x₂, x₃, x₄ в первое уравнение, найдем x₁ = 1.

-35-

Пример 2. Найти общее решение системы уравнений

x₁ + 3x₂ – 2x₃ = 10;

2x₁ + 7x₂ + 3x₃ = 0;

3x₁ + 10x₂ + x₃ = 10.

Р е ш е н и е. Составим матрицу В и преобразуем её:

1 3 –2 10 1 3 –2 10 1 3 –2 10

В = 2 7 3 0 ~ 0 1 7 –20 ~ .

3 10 1 10 0 1 7 –20 0 1 7 –20

Из коэффициентов полученной матрицы составим систему, равносильную исходной:

x₁ + 3x₂ – 2x₃ = 10;

x₂ + 7x₃ = –20.

Из второго уравнения выразим x₂ через x₃: х₂ = –20 – 7x₃. Поставив в первое уравнение системы значение x₃, получим x₁ = 70 + 23x₃. Итак, имеем общее решение исходной системы:

x₁ = 70 + 23x₃;

x₂ = –20 – 7x₃.

-36-

Пример 3. Решить систему уравнений

x₁ + x₂ – 3x₃ = 5;

2x₁ – 3x₂ + 2x₃ = –3;

3x₁ + 2x₂ + x₃ = 7.

Р е ш е н и е. Составим матрицу В и преобразуем ее:

1 1 –3 5 1 1 –3 5 1 1 –3 5

В = 2 –3 2 –3 ~ 0 –5 8 –13 ~ 0 –5 8 –13 .

3 –2 –1 7 0 –5 8 –8 0 0 0 5

Составим систему уравнений, равносильную исходной:

x₁ + x₂ – 3x₃ = 5;

– 5x₂ + 8x₃ = –13;

0x₁ + 0x₂ + 0x₃ = 5.

Система уравнений решений не имеет, так как мы получили уравнение 0x₁ + 0x₂ + 0x₃ = 5, которое не имеет решений.

-37-

2.5. Критерий совместности общей

системы линейных уравнений.

Как уже было отмечено, под общей системой линейных уравнений мы понимаем систему (14) в которой число неизвестных необязательно совпадает с числом уравнений.

Пусть дана общая система линейных уравнений (14) и требуется установить признак существования решения этой системы, т.е. условия, при которых система (14)является совместной.

Из коэффициентов при неизвестных и свободных членов системы (14) составим матрицу

a₁₁ a₁₂ … a_1n

A = a₂₁ a₂₂ … a_2n

……………………

a_m1 a_m2 … a_mn

которую назовем основной матрицей системы (14), и матрицу

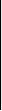
a₁₁ a₁₂ … a_1n b₁

B = a₂₁ a₂₂ … a_2n b₂

……………………… …… (26)

a_m1 a_m2 … a_mn b_m

которую назовем расширенной матрицей системы (14).

Теорема 2.1. Для того чтобы система (14) линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу ее основной матрицы.

Д о к а з а т е л ь с т в о. Необходимость. Пусть система (14) совместна и c₁, c₂, ..., с_п – некоторое ее решение. Тогда имеют место равенства:

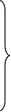а₁₁с₁ + а₁₂с₂ + …+ а_1nс_n = b₁;

а₂₁с₁ + а₂₂с₂ + …+ а_2nс_n = b₂;

_. ……………………………………

а_m1с₁ + а_m2с₂ + …+ а_mnс_n = b_m

из которых следует, что последний столбец расширенной матрицы (26) есть линейная комбинация остальных ее столбцов с коэффициентами с₁, с₂, ..., с_п. Согласно предложению 2, последний столбец матрицы В

-38-

может быть вычеркнут без изменения ее ранга. При этом мы из матрицы В получим матрицу А. Таким образом, если ci, c_z, ..., с_п — решение системы уравнении (14), то rang А = rang В.

Достаточность. Пусть теперь rang A = rang В. Покажем, что при этом система уравнений (14) совместна. Рассмотрим r базисных столбцов матрицы А. Очевидно, что они будут базисными столбцами и матрицы В. Согласно теореме о базисных строках и столбцах, последний столбец матрицы В можно представить как линейную комбинацию базисных столбцов, а следовательно, и как линейную комбинацию всех столбцов матрицы А, т. е.

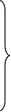b₁ = а₁₁с₁ + а₁₂с₂ + …+ а_1nс_n ;

b₂ = а₂₁с₁ + а₂₂с₂ + …+ а_2nс_n ;

_. …………………………………

b_m = а_m1с₁ + а_m2с₂ + …+ а_mnс_n,

где c₁, c₂, ..., с_п — коэффициенты линейных комбинаций. Таким образом, системе (27) удовлетворяют значения x₁ = c₁, ..., х_п = с_п, следовательно, она совместна. Т е о р е м а д о к а з а н а.

Доказанная теорема совместности системы линейных уравнений называется теоремой Кронекера – Капелли.

-39-

Пример 1. Рассмотрим систему

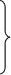5x₁ – x₂ + 2x₃ + x₄ = 7;

2x₁ + x₂ – 4x₃ – 2x₄ = 1;

x₁ – 3x₂ + 6x₃ – 5x₄ = 0.

Ранг основной матрицы этой системы равен 2, так как сцществует отличный от нуля минор второго порядка этой матрицы, например

5 –1 = 7,

2 1

а все миноры третьего порядка равны нулю.

Ранг расширенной матрицы этой системы равен 3, так как существует отличный от нуля минор третьего порядка этой матрицы, например

5 –1 7

2 1 1 = –35.

1 –3 0

Согласно критерию Кронекера – Капелли система несовместна, т.е. не имеет решений.

-40-

Пример 2. При каких k совместна система уравнений

x + ky = 3,

kx + 4y = 6?

Поскольку r ≠ 0, то эта система совместна в двух случаях: когда ∆ ≠ 0

И когда R = r = 1. Поэтому рассмотрим два случая.

1) Если ∆ = 0, т.е. если r ≠ 0, т.е. если k² ≠ 4, то по правилу Крамера система имеет единственное решение.

Значит, для любого k, кроме k = 2 и k = –2, система имеет единственное решение.

2) Если R = r = 1, т.е. если

1 k = 3 k = 1 3 = 0,

k 4 6 4 k 6

т.е. если k = 2, то система совместна.

Подводя итог, получаем, что исходная система совместна при любых k кроме k = –2.

-41-

Используя критерий Кронекера – Капелли, проведем исследование системы двух линейных уравнений с двумя неизвестными x и y:

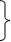a₁x + b₁y = c₁,

a₂x + b₂y = c₂. (26)

Основная матрица этой системы

a₁ b₁

a₂ b₂

имеет ранг r, причем 0 < r < 2.

Расширенная матрица

a₁ b₁ с₁

a₂ b₂ с₂

имеет ранг R, причем 0 < r < R. Очевидно, что r < R < r+1.

Имеют место следующие утверждения.

Пусть дана система двух линейных уравнений с двумя неизвестными (26). Тогда:

1. Если r = R = 0, т.е. если все коэффициенты a₁, a₂, b₁, b₂, c₁, c₂ равны нулю, то любая пара действительных чисел является решением системы (26).

2. Если r = 0, R = 1, т.е. a₁ = a₂ = b₁ = b₂ = 0 и c + c ≠ 0, то система (26) не имеет решений.

3. Если r =1, R = 1, то система (26) имеет бесконечно много решений, но не любая пара действительных чисел есть её решение.

4. Если r = 1, R = 2, то система (26) не имеет решений.

5. Если r = 2, R = 2, то система (26) имеет единственное решение, которое можно найти по правилу Крамера.

Справедливы и обратные утверждения.

1. Если система (26) имеет единственное решение, то r = R =2.

2. Если любая пара действительных чисел является решением системы (26), то r = R = 0.

3. Если система (26) не имеет решений, то r ≠ R, т.е. либо r =0 и

R = 1, либо r =1 и R = 2.

4. Если система (26) имеет бесконечно много решений, но не любая пара действительных чисел является её решением, то r = R = 1.

Приведём доказательство этих утверждений только в том случае, когда оба уравнения системы (26) являются уравнениями первой

-42-

степени, т.е. когда выполняются условия a + b ≠ 0, a + b ≠ 0. В этом случае каждое уравнение этой системы в отдельности определяет прямую на плоскости, где задана система координат xOy. Это дает возможность придать геометрический характер дальнейшим рассуждениям при исследовании системы (26)

Теорема 2.2. Пусть две прямые заданы уравнениями

a₁x + b₁y – c₁ = 0,

a₂x + b₂y – c₂ = 0, (27)

где a + b ≠ 0, a + b ≠ 0.

1. Для того, чтобы две прямые пересеклись, необходимо и достаточно, чтобы r = R = 2.

2. Для того, чтобы две прямые были параллельными, но не совпадали, необходимо и достаточно, чтобы r = 1, R = 2.

3. Для того, чтобы две прямые совпадали, необходимо и достаточно, чтобы r = R = 1.

Д о к а з а т е л ь с т в о. Сначала докажем достаточность условий.

1. Если r = R = 2, то система (27) имеет единственное решение, которое легко найти по правилу Крамера, а это означает, что прямые имеют одну общую точку, т.е. пересекаются.

2. Если r = 1, R = 2, то система (27) несовместна и поэтому прямые не имеют общих точек, т.е. параллельны и не совпадают.

3. Если r = R = 1, то все миноры второго порядка основной и расширенной матриц равны нулю, т.е.

a₁ b₁ = 0, c₁ b₁ = 0, a₁ c₁ = 0.

a₂ b₂ c₂ b₂ a₂ c₂

Эти условия можно переписать так:

a₁b₂ = b₁a₂, (28)

c₁b₂ = b₁c₂, (29)

a₁c₂ = c₁a₂. (30)

Рассмотрим теперь все возможные случаи.

а) Если а₁ = 0, то b₁ ≠ 0, так как a₁ + b₁ ≠ 0. Тогда из (28) следует, что а₂ = 0, а так как a₂ + b₂ ≠ 0, то b₂ ≠ 0. Тогда из (29) находим, что c₁/b₁ = c₂/b₂ = α и при этом уравнения прямых примут вид

b₁(y – α) = 0, b₂(y – α) = 0. Поскольку b₁ ≠ 0, b₂ ≠ 0, то отсюда вытекает, что эти прямые совпадают с прямой y – α = 0.

б) Если b₁ = 0, то а₁ ≠ 0, а из (28) тогда следует, что b₂ = 0(причем

-43-

а₂ ≠ 0). Тогда из (30) имеем c₁/a₁ = c₂/a₂ = β, и поэтому уравнения прямых примут вид а₁(x – β) = 0, а₂(x – β) = 0. Поскольку

а₁ ≠ 0, а₂ ≠ 0, то отсюда вытекает, что эти прямые совпадают с прямой x – β = 0.

в) Если а₁ ≠ 0 и b₁ ≠ 0, то из (28) вытекает, что а₂/a₁ = b₂/b₁ = γ, а из (29) и (30) вытекает, что с₂ = b₂c₁/b₁ = a₂c₁/a₁. Т.е. получаем, что

а₂ = γа₁, b₂ = γb₁, c₂ = γc₁, и поэтому уравнения прямых примут вид

a₁x + b₁y – c₁ = 0, γ(a₁x + b₁y – c₁)= 0. Поскольку γ ≠ 0, то отсюда вытекает, что эти прямые совпадают.

Теперь докажем необходимость условий. Доказательство проведём методом от противного.

1. Пусть прямые пересекаются. Докажем, что r = R = 2. Если бы оказалось, что r = 1, R = 2, то по доказанному прямые были бы параллельны и не совпадали. Если бы оказалось, что r = R = 1, то по доказанному прямые оказались бы совпавшими.

Следовательно, r = R = 2.

2. Пусть прямые параллельны. Докажем, что r = 1, R = 2. Если бы оказалось, что r = R = 2, то по доказанному прямые оказались бы пересекающимися. Если бы оказалось, что r = R = 1, то по доказанному прямые оказались бы совпавшими.

Следовательно, r = 1, R = 2.

3. Пусть прямые совпадают. Докажем, что r = R = 1. Если бы оказалось, что r = R = 2, то по доказанному прямые оказались бы пересекающимися. Если бы оказалось бы, что r = 1, R = 2, то по доказанному прямые были бы параллельны.

Следовательно, r = R = 1.

Т е о р е м а д о к а з а н а п о л н о с т ь ю.

-44-

Заключение.

Работа над рефератом была очень интересной.

− в процессе работы я узнала много нового;

− я научилась пользоваться научной литературой, сопоставлять и сравнивать различные точки зрения, выделять главное;

− теперь я знаю, какие действия можно выполнять над матрицами, какой путь решения систем линейных уравнений наиболее простой и быстрый, и ещё в своей работе я изучила многие другие теоретические вопросы;

− также весь материал я исследовала не только теоретически, но и практически, приводя некоторые примеры в тексте.

Тема решения систем линейных уравнений предлагается на вступительных экзаменах в различные математические вузы, на выпускных экзаменах, поэтому умение их решать очень важно.

Реферат может использоваться как учащимися, так и преподавателями в процессе факультативных занятий, как пособие для самостоятельного изучения по теме „Способы решения систем линейных уравнений ”, а также в качестве дополнительного материала.

-45-

Список литературы:

1. А.А.Дадаян. Алгебра и геометрия./А.А.Дадаян, В.А.Дударенко. Минск: „Вышэйная школа”, 1989г.

2. Ф.Р.Гантмахер. Теория матриц (издание третье)./Ф.Р.Гантмахер. Москва: „Наука”, главная редакция физико-математической литературы, 1967г.

3. Математический энциклопедический словарь. Москва: „Советская энциклопедия”, 1988г.

4. Л.Андреева. Реферат по математике „Системы уравнений”./Л.Андреева. Анжеро-Судженск. 1999г.

5. Д.К.Фаддеев. „Сборник задач по высшей алгебре”./ Д.К.Фадеев, И.С.Саминский. Москва: „Наука”, 1977г.

-46-