Реферат: Шпаргалки на экзамен в ВУЗе (1 семестр, математика)
1) Основные понятия линейной алгебры. Задачи о перевозках.
Элементы линейной алгебры. Задачи о перевозках. На 2-х складах А1 и А2 сосредоточено а1, а2 тон однородного груза, которые нужно доставить в 3-и пункта назад в В1, В2, В3, потребн пунктов назначения, равны в1, в2, в3 тон. Известно стоимость перевозки одной тонны груза, из каждого пункта отправления в каждый пункт назначения. Требуется составить такой план перевозки, при котором общая стоимость перевозок была бы наименьшей.
А1+А2=В1+В2+В3 Хij – груз(тон) Сij – цена 1т груза.
С=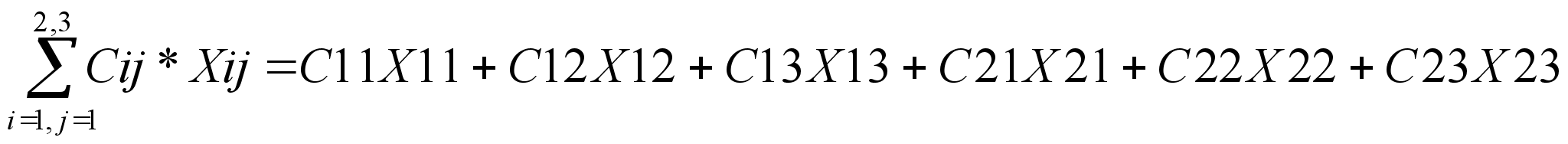
Т.о
задача ставится
к нахожд неизвестного
X
и ij
удовлетвор
системе Ур-ий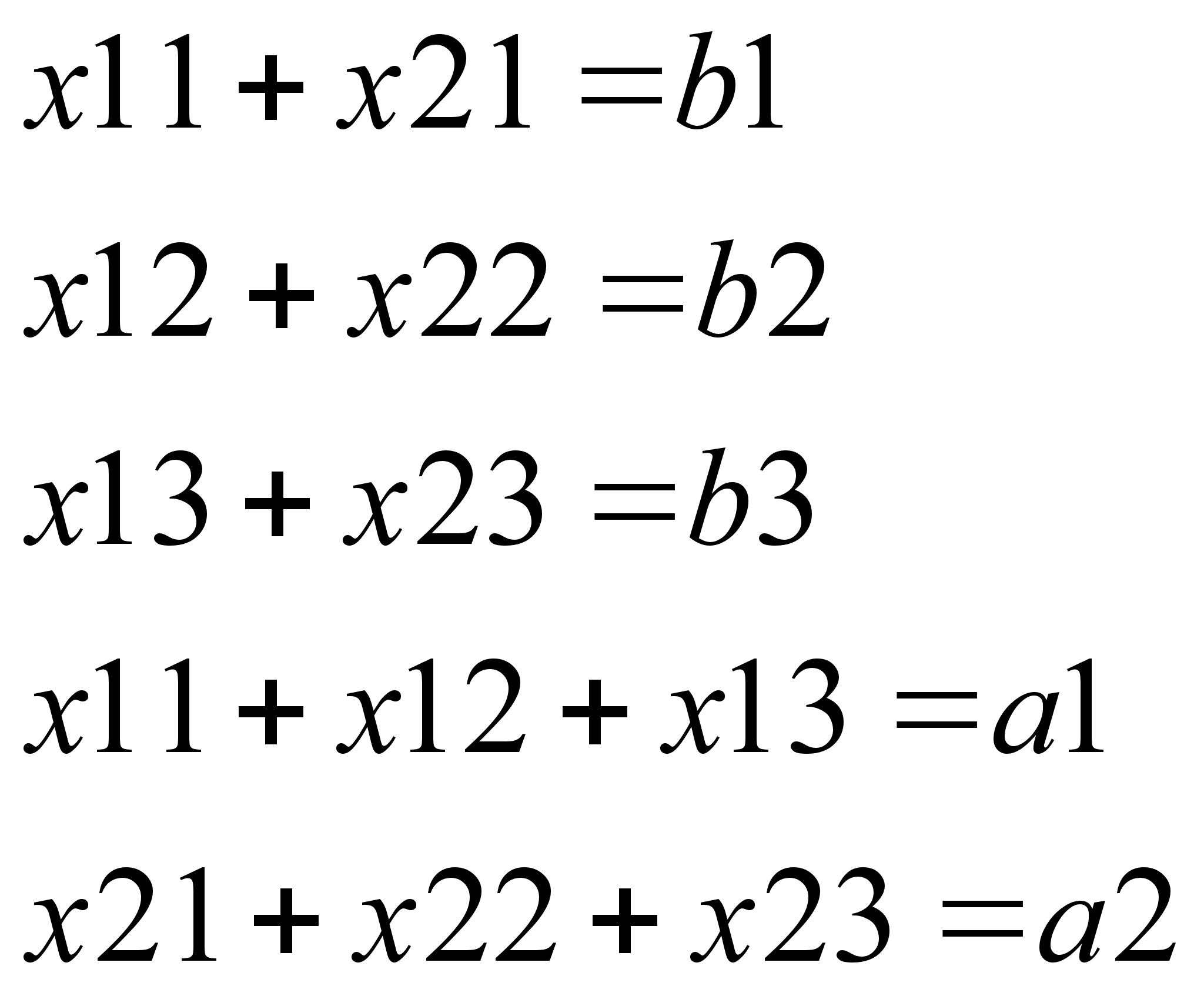
Причем найден Ур-е должны быть такими чтобы ф-я приняла миним з-я. Для реш сформир задачи необходимо уметь решать системы лин Ур-й , т.к. система явл сист лин Ур-й относит xij. Сист m лин Ур-й с n нейзв x1, x2,…,Xn имеет вид а11x1+а12x2+…+a1nXn=b1; a21x1+a22x2+…+a2nXn=b2;…….;am1x1+am2x2+…amnxn=bm.Коэфициенты аij при неизвестн xij (j =1,2,…n), для удобства обозн одной буквой с 2-я индексами i-номер Ур-нии, j- неизвстного
|
10)Метод
Гаусса.(Карл
Фридрих Гаусс
(1777-1855) немецкий
математик)В
отличие от
матричного
метода
и метода
Крамера,
метод Гаусса
может быть
применен к
системам линейных
уравнений с
произвольным
числом уравнений
и неизвестных.
Суть метода
заключается
в последовательном
исключении
неизвестных.Рассмотрим
систему линейных
уравнений: |
|
11)
Векторы,
действия над
ними.Определение.
Вектором
называется
направленный
отрезок (упорядоченная
пара точек).
К векторам
относится
также и нулевой
вектор, начало
и конец которого
совпадают.Определение.
Длиной
(модулем)
вектора называется
расстояние
между началом
и концом
вектора. |
|
12)Скалярное
произведение
векторов, его
св-ва и вычисления.
Определение.
Скалярным
произведением
векторов
|
|
13)Векторное
произведение
векторов. Его
св-ва и вычисление.
Определение.
Векторным
произведением
векторов
3
Свойства
векторного
произведения
векторов:1)
|
|
14)Смешенное
произведение
векторов его
св-ва и вычисления.Определение.
Смешанным
произведением
векторов
Свойства смешанного произведения: 1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю;б)два из векторов коллинеарны;в)векторы компланарны. 2) 4) Для
нахождения
длины высоты
пирамиды найдем
сначала площадь
основания
CD.
Sосн
=
|
|
15) Общее вычисление прямой на плоскостиОпределение. Любая прямая на плоскости может быть задана уравнением первого порядкаАх + Ву + С = 0,причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. |
|
Уравнение
прямой может
быть рассмотрено
как уравнение
линии пересечения
двух плоскостей.Как
было рассмотрено
выше, плоскость
в векторной
форме может
быть задана
уравнением: |
|
17)Взаимное
расположение
двух плоскостей
характеризуется
двумя возможностями.1).
Две плоскости
не имеют общих
точек, и , в таком
случае, они
называются
параллельными
(на рис. 28
Две
плоскости
имеют хотя
бы одну общую
точку, и в таком
случае они
называются
пересекающимися.
Если две плоскости
имеют общую
точку, то они
имеют общую
прямую, на которой
лежат обе общие
точки этих
плоскостей
(аксиома). Таким
образом, две
плоскости
пересекаются
по прямой (на
рис. 28
Пересекающиеся плоскости образуют четыре двугранных угла. Если один из них прямой, тогда и остальные углы тоже прямые, а плоскости называются перпендикулярными. В качестве параллельных плоскостей на каждом шагу встречаем параллельные грани одного дома. Плоскости стен домов перпендикулярны плоскости земли. |
|
18) Взаимное расположение двух прямых на плоскости.Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. |
|
Взаимное
расположение
двух прямых
и пространстве
характеризуется
следующими
тремя возможностями.1)Прямые
лежат в одной
плоскости и
не имеют общих
точек - параллельные
прямые. 2)Прямые
лежат и одной
плоскости и
имеют одну
общую точку
- прямые пересекаются.
3)В пространстве
две прямые
могут быть
расположены
еще так, что
не лежат ни
в одной плоскости.
Такие прямые
называются
скрещивающимися
(не пересекаются
и не параллельны).
Теорема. Если
одна из двух
прямых лежит
в некоторой
плоскости, а
другая пересекает
эту плоскость
и точке, которая
не лежит на
первой прямой,
то эти прямые
скрещиваются.
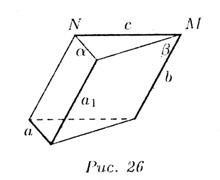
На рис. 26 прямая
a лежит в плоскости Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
На рис.
26 прямые a и b
скрещиваются.
Черен прямую
а проведена
плоскость
Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты. |
|
2)Матрицы,действия
над матрицами.Привести
пример.Определение.
Матрицей
размера
mn,
где m-
число строк,
n-
число столбцов,
называется
таблица чисел,
расположенных
в определенном
порядке. Эти
числа называются
элементами
матрицы.Место
каждого элемента
однозначно
определяется
номером строки
и столбца, на
пересечении
которых он
находится.
Элементы матрицы
обозначаются
aij,
где i-
номер строки,
а j-
номер столбца.
А = |
|
20)Взаимное расположение прямой и плоскости. Для выяснения взаимного расположения прямой (x=b1t+x0; y=b2t+y0; z=b3t+z0) b(b1, b2, b3)-направляющий вектор прямой Ax+By+Cz+D=0 Чтобы найти точку пересечения прямой и плоскости, надо решить сист Ур-ий A(b1t+x0)+B(b2t+y0)+C(b3t+z0)+D=0; Ab1t+Ax0+Bb2t+By0+Cb3t+Cz0+D=0; (Ab1+Bb2+Cb3)t=-(Ax0+By0+Cz0+D). 1Случай: Ab1+Bb2+Cb3=0, определяет единственное решение, т.к. получаем конкретное значение параметра t, подставив которое в исходное Ур-е прямой получаем точки пересеч с данной плоскостью 2Случай: Пусть выражение Ab1+Bb2+Cb3=0, Ax0+By0+Cz0+D=0, т.к. левая часть не может быть равна правой, это говорит о том что прямая параллельна плоскости. 3Случай: Пусть Ab1+Bb2+Cb3=0, Ax0+By0+Cz0+D=0, Ур-ям удовлетворяют любые знач t след прямая лежит в плоскости. |
|
О М r1 r2
F1 F2
F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0) с – половина расстояния между фокусами; a – большая полуось;
b
– малая полуось.Теорема.
Фокусное
расстояние
и полуоси эллипса
связаны соотношением:a2
= b2
+ c2.Доказательство:
В случае, если
точка М находится
на пересечении
эллипса с
вертикальной
осью, r1
+ r2
= 2 |
|
22)ГиперболаОпределение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
y M(x, y) b r1 r2 x F1 a F2 c
По определению
r1
– r2=
2a.
F1,
F2
– фокусы гиперболы.
F1F2
= 2c.Выберем
на гиперболе
произвольную
точку М(х, у).
Тогда:
обозначим
с2
– а2
= b2
(геометрически
эта величина
– меньшая
полуось)
|
|
23)Парабола. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.Расположим начало координат посередине между фокусом и директрисой.
А у М(х, у)
О
F
x
p/2 p/2 Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.Из геометрических соотношений: AM = MF; AM = x + p/2;MF2 = y2 + (x – p/2)2 (x + p/2)2 = y2 + (x – p/2)2 x2 +xp + p2/4 = y2 + x2 – xp + p2/4 y2 = 2px Уравнение директрисы: x = -p/2. Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4. Из уравнения параболы получаем, что р = 4. r = x + p/2 = 4; следовательно:x = 2; y2 = 16; y = 4. Искомые точки: M1(2; 4), M2(2; -4).
|
|
25)Общее ур-е линии второго порядкаКривые 2го порядка описываются с помощью общего ур-я: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где
а) Каноническое ур-е эллипса
Если a=b, то x2+b2=a2 - ур-е окружности. б) Ур-е гиперболы: x2/a2-y2/b2=1
в) ур-е параболы: y2=2px или y=ax2 г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2) д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1 |
|
О B a Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме. |
|
Основные действия с комплексными числами вытекают из действий с многочленами.1) Сложение и вычитание.
3)
Деление.
Приравнивая,
получим
Отсюда:
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений. |
|
27) Комплексные числа, тригонометрическая форма записи комплексного числа. Действия над комплексными числами в тригонометрической форме.(продолжение 26-1-2) Тригонометрическая
форма числа.Из
геометрических
соображений
видно, что
Очевидно,
что комплексно
– сопряженные
числа имеют
одинаковые
модули и противоположные
аргументы. |
|
28)Основные элементарные ф-ии.Функция - это зависимость одной величины от другой. Если существует взаимооднозначное соответствие между переменной х одного множества и переменной у другого множества, то она называется функциональной зависимостью. y=f(x). Определение способа задания: -аналитически (y=kx+b) -графический (график) -таблично
-алгоритмически (с помощью ЭВМ) Классификация функций: Элементарные: - функции, которые получаются из основных элементарных ф-ций с помощью алгебраических действий (+,-,*,/,введение в степень). Основные элементарные ф-ции: 1. y=xn - степенная 2. y=ax - показательная 3. y=logax - логарифмическая 4. y=sinx, y=cosx - тригонометрические. Сложные: Y=f(U), где U=(x), Y=f[(x)] Если ф-ция у зависит от промежуточного аргумента U, который зависит от независимой переменной х, то y=f[(x)] называется сложным заданием х. |
|
29)Предел ф-ии
A + A A - a - a a + x
П А2 А1 a Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x). |
|
3)Обратная матрица, ее вычисление.Привести пример.Определим операцию деления матриц как операцию, обратную умножению.Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию: XA
= AX = E,где Е - единичная
матрица того
же самого порядка,
что и матрица
А, то матрица
Х называется
обратной
к матрице
А и обозначается
А-1.Каждая
квадратная
матрица с
определителем,
не равным нулю
имеет обратную
матрицу и притом
только одну. Рассмотрим
общий подход
к нахождению
обратной
матрицы.Исходя
из определения
произведения
матриц, можно
записать:AX
= E
eij
= 1, i = j .Таким
образом, получаем
систему уравнений:
Таким
образом, А-1= |
|
30)Основные
теоремы о
пределахТеорема
1.
Определение.
Функция f(x)
называется
ограниченной
вблизи
точки х = а, если
существует
такое число
М>0, что f(x)
Доказательство.
Пусть
|
|
31)Первый
замечательный
предел В
силу четности
входящих в
неравенство
ф-ий, докажем
это неравенство
на промежутке
2.
следовательно,
что
|
|
32) Второй замечательный предел lim(n)(1+1/n)^n=e Док-во:
x+
n x:n=[x] => nx Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n(1+1/n)^x (1+1/n)^(n+1) (4) Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х+, n) lim(n)(1+1/(n+1))=lim(n)(1+1/(n+1))^n+1-1= lim(n)(1+1/(n+1))^n+1lim(n)1/(1+1/(n+1))=e lim(n)(1+1/n)^n+1= lim(n)(1+1/n)^n lim(n)(1+1/n)=e1=e |
|
33)Бесконечно
малые величины
и их св-ваОпределение.
Функция f(x)
называется
бесконечно
малой
при ха,
где а может
быть числом
или одной из
величин ,
+
или -,
если
Используя
понятие бесконечно
малых функций,
приведем
доказательство
некоторых
теорем о пределах,
приведенных
выше.Доказательство
теоремы 2.
Представим
f(x)
= A
+ (x),
g(x)
= B
+ (x),
где A
+ B
= const,
(х)
+ (х)
– бесконечно
малая, значит Теорема
доказана.Доказательство
теоремы 3.
Представим
f(x)
= A
+ (x),
g(x)
= B
+ (x),
где AB
= const,
(х)
и (х)
– бесконечно
малые, значит |
|
34)Эквивалентные
бесконечно
малые величины
и их св-ваПусть
(х),
(х)
и (х)
– бесконечно
малые функции
при х
а. Будем обозначать
эти функции
,
и
соответственно.
Эти бесконечно
малые функции
можно сравнивать
по быстроте
их убывания,
т.е. по быстроте
их стремления
к нулю.Например,
функция f(x)
= x10
стремится к
нулю быстрее,
чем функция
f(x)
= x.Определение.
Если
Так
как tg5x
~ 5x
и sin7x
~ 7x
при х
0, то, заменив
функции эквивалентными
бесконечно
малыми, получим: |
|
3
Определение.
Функция называется
бесконечно
большой при
ха,
где а – чосли
или одна из
величин ,
+
или -,
если
|
|
3 f(x0)+ f(x0) f(x0)-
x0- x0 x0+
Пример разрывной функции: f(x0)+ f(x0) f(x0)- x0
Определение.
Функция f(x)
называется
непрерывной
в точке х0,
если для любого
положительного
числа >0
существует
такое число
>0,
что для любых
х, удовлетворяющих
условию |
|
37)Св-ва
функций непрерывных
на отрезке.Свойство
1: (Первая
теорема Вейерштрасса
(Вейерштрасс
Карл (1815-1897)- немецкий
математик)).
Функция, непрерывная
на отрезке,
ограничена
на этом отрезке,
т.е. на отрезке
[a,
b]
выполняется
условие –M
f(x)
M.Доказательство
этого свойства
основано на
том, что функция,
непрерывная
в точке х0,
ограничена
в некоторой
ее окрестности,
а если разбивать
отрезок [a,
b]
на бесконечное
количество
отрезков, которые
“стягиваются”
к точке х0,
то образуется
некоторая
окрестность
точки х0.Свойство
2: Функция,
непрерывная
на отрезке
[a,
b],
принимает на
нем наибольшее
и наименьшее
значения.Т.е.
существуют
такие значения
х1
и х2,
что f(x1)
= m,
f(x2)
= M,
причем m
f(x)
M
Отметим эти
наибольшие
и наименьшие
значения функция
может принимать
на отрезке и
несколько
раз (например
– f(x)
= sinx).
Разность между
наибольшим
и наименьшим
значением
функции на
отрезке называется
колебанием
функции
на отрезке.
Свойство
3: (Вторая
теорема Больцано
– Коши). Функция,
непрерывная
на отрезке
[a,
b],
принимает на
этом отрезке
все значения
между двумя
произвольными
величинами.
Свойство
4: Если
функция f(x)
непрерывна
в точке х = х0,
то существует
некоторая
окрестность
точки х0,
в которой функция
сохраняет
знак. Свойство
5: (Первая
теорема Больцано
(1781-1848) – Коши). Если
функция f(x)-
непрерывная
на отрезке
[a,
b]
и имеет на концах
отрезка значения
противоположных
знаков, то
существует
такая точка
внутри этого
отрезка, где
f(x)
= 0. Т.е.
если
sign(f(a))
sign(f(b)), то
х0:
f(x0)
= 0. Определение.
Функция f(x)
называется
равномерно
непрерывной
на отрезке
[a,
b],
если для любого
>0
существует
>0
такое, что для
любых точек
х1[a,b]
и x2[a,b]
таких, что х2
– х1<
верно неравенство
f(x2)
– f(x1)
<
Отличие равномерной
непрерывности
от “обычной”
в том, что для
любого
существует
свое ,
не зависящее
от х, а при “обычной”
непрерывности
зависит от
и х. Свойство
6: Теорема
Кантора (Кантор
Георг (1845-1918)- немецкий
математик).
Функция, непрерывная
на отрезке,
равномерно
непрерывна
на нем.(Это
свойство
справедливо
только для
отрезков, а
не для интервалов
и полуинтервалов.)
Пример.
Ф Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
|
|
3
f(x0 +x) f P M f(x0) x x0 x0 + x
Пусть
f(x)
определена
на некотором
промежутке
(a, b).
Тогда
Физический
смысл производной
функции f(t),
где t-
время, а f(t)-
закон движения
(изменения
координат) –
мгновенная
скорость
движения. Соответственно,
вторая производная
функции- скорость
изменения
скорости, т.е.
ускорение.
Определение.
Правой (левой)
производной
функции f(x)
в точке х = х0
называется
правое (левое)
значение предела
отношения
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.Например: f(x) = x- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точкеПонятно, что это условие не является достаточным. |
|
1.
Значит,
Поэтому,
по свойствам
пределов,
Докажем
теперь формулу
|
|
4)Определители 2-го порядка.Св-ва.Определители 2-ого и 3-го порядков Любые 4 числа, расположенные в виде квадратной таблицы, называются квадратной матрицей второго порядка. Каждой квадратной матрице 2-ого порядка можно поставить в соответствие число, называемое её определителем и обозначаемое D=|A|.Определители n-ного порядка.Определитель n-ого порядка равен сумме произведений элементов 1-ой строки на их алгебраические дополнения (Aij соответствующее элементу aij и равно Aij = (-1)i+j *Mij) Результат разложения не зависит от того, по какой строке (столбцу) производится разложение: 2 -1 0 4 0 3 = (3 столбец) = -2 4 5 Свойство1. Важным свойством определителей является следующее соотношение: det A = det AT; Свойство 2.det ( A B) = det A det B.Свойство 3. det (AB) = detAdetB Свойство
4.
Если в квадратной
матрице поменять
местами какие-либо
две строки
(или столбца),
то определитель
матрицы изменит
знак, не изменившись
по абсолютной
величине.Свойство
5. При
умножении
столбца (или
строки) матрицы
на число ее
определитель
умножается
на это число.Определение:
Столбцы (строки)
матрицы называются
линейно
зависимыми,
если существует
их линейная
комбинация,
равная нулю,
имеющая нетривиальные
(не равные нулю)
решения.Свойство
6. Если
в матрице А
строки или
столбцы линейно
зависимы, то
ее определитель
равен нулю.Свойство
7. Если
матрица содержит
нулевой столбец
или нулевую
строку, то ее
определитель
равен нулю.
(Данное утверждение
очевидно, т.к.
считать определитель
можно именно
по нулевой
строке или
столбцу.)Свойство
8. Определитель
матрицы не
изменится,
если к элементам
одной из его
строк(столбца)
прибавить(вычесть)
элементы другой
строки(столбца),
умноженные
на какое-либо
число, не равное
нулю.Свойство
9. Если
для элементов
какой- либо
строки или
столбца матрицы
верно соотношение:
d
= d1
d2
, e
= e1
e2
, f
= f1
f2
, то
верно:
|
|
40)Логарифмич
дифференцирование.Производная
степеннопоказ
ф-ииРассмотрим
функцию
|
|
41)Производная
сложной ф-ииТеорема.
Пусть
y
= f(x);
u
= g(x),
причем область
значений функции
u
входит в область
определения
функции
f.Тогда (
с учетом того,
что если x0,
то u0,
т.к. u
= g(x)
– непрерывная
функция) Тогда
Теорема доказана. |
|
42)Производная ф-и задана неявно и параметрическиОпр. Функция z=f(x,y) наз. Заданной неявно, если она определена равенством, неразрешенным относительно z .F(x,y,z)=0 x+y+z=ez - это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде.x2+y2+z2=0 - не задает никакой функции. Теорема: Если ф-я F(x,y,z) непрерывна в т. р0(x0,y0,z0) и ее производная по z Fz(x,y,z)0, то равенство F(x,y,z)=0 однозначно определяет в неявном виде функцию z=f(x,y), при этом эта функция дифференцируема и ее производная находится по формулам: z/x= Fx(x,y,z)/Fz(x,y,z) z/y=Fz (x,y,z)/Fy(x,y,z)Док-во: Найдем полный дифференциал функции dF(x,y,z)=F/x*dx+F/y*dy+F/x*dz F(x0,y0,z0)=0dF=0F/x*dx+F/y*dy+F/x*dz=0 dz=(F/x)/(F/z)*dx(F/y)/(F/z)*dy (*) С другой стороны: z=f(x,y), dz=z/x*dx+z/y*dy (**) Сравнивая (*) и(**) z/x= Fx(x,y,z)/Fz(x,y,z)z/y=Fz (x,y,z)/Fy(x,y,z)
Пусть
дана функция |
|
43) Диффиренциал ф-ии, его свойства.ОпределениеФункция y=f(x) называется диф. в точке x, если приращение функции можно представить в виде Df = Dx+o(Dx), A- const Если f(x) диф. в точке x, то df=A·Dx– дифференциал функции в точке x Функция имеет в точке x производную Ы она дифференцируема. в этой точке Док-во: $ f’(x)= lim Df/DxЮ Df/Dx=f’(x)+a Df=f’(x)Dx+aDxЮf-диф. Df = ADx+aDx Df/Dx=A+a Ю $ lim Df/Dx =A = f’(x) Следствие: для диф. функции константа A равна производной функции в точке x Свойства: Пусть f(x) и g(x)- диф.
Доказательство: d(f*g)= (fg)’ dx= (gf’+fg’) dx = gf’ dx+ fg’ dx= gdf+fdg Дифференциал первого порядка обладает свойством инвариантности формы при замене независимой переменной Доказательство: y= f(x) dy= f’(x) dx x=j(t) dx=j’(t)dt y= f(j(t)) dy= (f(j)))’dt= f’(j(t))*j(t) dt = f’(x) dx Смысл Физический смысл дифференциала: x=x(t) dx= x(t) dt= u (мгновенное) Физич. диф.- это путь, который прошла бы точка, если ее движение стало бы равномерным со скоростью, взятой в момент времени t Геометрический смысл дифференциала: Геометрически дифференциал равен приращению ординаты вдоль касательной к графику функции, проведенной в заданной точке. |
|
44)Инвариантная
форма записи
дифференциала
первого порядка.Пусть
y
= f(x),
x
= g(t),
т.е у- сложная
функция.Тогда
dy
= f(x)g(t)dt
= f(x)dx.Видно,
что форма записи
дифференциала
dy
не зависит
от того, будет
ли х независимой
переменной
или функцией
какой- то другой
переменной,
в связи с чем
эта форма записи
называется
инвариантной
формой записи
дифференциала.Однако,
если х- независимая
переменная,
то dx
= x,
но если х зависит
от t,
тох
dx.
Таким образом
форма записи
dy
= f(x)x
не является
инвариантной.
Пример.
Найти производную
функции
|
|
45)Основные
теоремы о
дифференцируемых
ф-яхТеорема:
Если f(x)
и g(x)
дифферен. в
точке х, то:
Теорема о произв. сложной функции:Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x). Теорема
о произв. обратной
функции.
|
|
46)Правило
Лопиталя.Пример(Лопиталь
(1661-1704) – французский
математик)К
разряду
неопределенностей
принято относить
следующие
соотношения: где
- точка, находящаяся
между а и х.
Учитывая, что
f(a)
= g(a)
= 0: Теорема
доказана. Пример:
Найти предел
|
|
47)Экстремум
ф-ииОпределение.
Функция f(x)
имеет в точке
х1
максимум, если
ее значение
в этой точке
больше значений
во всех точках
некоторого
интервала,
содержащего
точку х1.
Функция f(x)
имеет в точке
х2
минимум, если
f(x2
+x)
> f(x2)
при любом х
(х
может быть и
отрицательным).Очевидно,
что функция,
определенная
на отрезке
может иметь
максимум и
минимум только
в точках, находящихся
внутри этого
отрезка. Нельзя
также путать
максимум и
минимум функции
с ее наибольшим
и наименьшим
значением на
отрезке – это
понятия принципиально
различные.Определение.
Точки максимума
и минимума
функции называются
точками
экстремума.
Теорема.
(необходимое
условие существования
экстремума)
Если
функция f(x)
дифференцируема
в точке х = х1
и точка х1
является точкой
экстремума,
то производная
функции обращается
в нуль в этой
точке.Доказательство.
Предположим,
что функция
f(x)
имеет в точке
х = х1
максимум.Тогда
при достаточно
малых положительных
х>0
верно неравенство:
Т.е. если
х0,
но х<0,
то f(x1)
0, а если х0,
но х>0,
то f(x1)
0.А возможно
это только в
том случае,
если при х0
f(x1)
= 0.Для случая,
если функция
f(x)
имеет в точке
х2
минимум теорема
доказывается
аналогично.Теорема
доказана.
Следствие.
Обратное
утверждение
неверно. Если
производная
функции в
некоторой
точке равна
нулю, то это
еще не значит,
что в этой точке
функция имеет
экстремум.
Красноречивый
пример этого
– функция у
= х3,
производная
которой в точке
х = 0 равна нулю,
однако в этой
точке функция
имеет только
перегиб, а не
максимум или
минимум.Определение.
Критическими
точками
функции называются
точки, в которых
производная
функции не
существует
или равна
нулю.Рассмотренная
выше теорема
дает нам необходимые
условия существования
экстремума,
но этого
недостаточно.Пример:
f(x)
= x
Пример:
f(x)
=
В точке х = 0 функция имеет минимум, но В точке х = 0 функция не имеет ни не имеет производной. максимума, ни минимума, ни производной. Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю.Теорема. (Достаточные условия существования экстремума) Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1)Если при переходе через точку х1 слева направо производная функции f(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.Доказательство. Пусть
|
|
4
Теорема
1. Если
во всех точках
интервала
(a,
b)
вторая производная
функции f(x)
отрицательна,
то кривая y
= f(x)
обращена
выпуклостью
вверх (выпукла).Доказательство.
Пусть х0
(a,
b).
Проведем
касательную
к кривой в этой
точке.Уравнение
кривой: y
= f(x);Уравнение
касательной:
|
|
49)АсимтотыПри
исследовании
функций часто
бывает, что
при удалении
координаты
х точки кривой
в бесконечность
кривая неограниченно
приближается
к некоторой
прямой.Определение.
Прямая называется
асимптотой
кривой,
если расстояние
от переменной
точки кривой
до этой прямой
при удалении
точки в бесконечность
стремится к
нулю.Следует
отметить, что
не любая кривая
имеет асимптоту.
Асимптоты
могут быть
прямые и наклонные.
Исследование
функций на
наличие асимптот
имеет большое
значение и
позволяет
более точно
определить
характер функции
и поведение
графика кривой.Вообще
говоря, кривая,
неограниченно
приближаясь
к своей асимптоте,
может и пересекать
ее, причем не
в одной точке,
как показано
на приведенном
ниже графике
функции
Вертикальные
асимптоты.Из
определения
асимптоты
следует, что
если
Обозначим
точку пересечения
кривой и перпендикуляра
к асимптоте
– М, Р – точка
пересечения
этого перпендикуляра
сасимптотой.
Угол между
асимптотой
и осью Ох обозначим
.
Перпендикуляр
МQ
к оси Ох пересекает
асимптоту в
точке N.Тогда
MQ
= y
– ордината
точки кривой,
NQ
=
Угол
- постоянный
и не равный
900,
тогда
Тогда
Т.к.
х,
то
Таким образом, прямая у = х + 2 является наклонной асимптотой.Построим график функции:
|
|
5)Определители 3-го порядка.Св-ва. 9 элементов aij, где i-номер строка, а j-номер столбца, располагаются в квадратную таблицу, называемую квадратной матрицей третьего порядка. Ей можно поставить в соответствие число, которое называется определителем 3-го порядка. Свойство1. Важным свойством определителей является следующее соотношение: det A = det AT; Свойство 2.det ( A B) = det A det B.Свойство 3. det (AB) = detAdetB Свойство
4.
Если в квадратной
матрице поменять
местами какие-либо
две строки
(или столбца),
то определитель
матрицы изменит
знак, не изменившись
по абсолютной
величине.Свойство
5. При
умножении
столбца (или
строки) матрицы
на число ее
определитель
умножается
на это число.Определение:
Столбцы (строки)
матрицы называются
линейно
зависимыми,
если существует
их линейная
комбинация,
равная нулю,
имеющая нетривиальные
(не равные нулю)
решения.Свойство
6. Если
в матрице А
строки или
столбцы линейно
зависимы, то
ее определитель
равен нулю.Свойство
7. Если
матрица содержит
нулевой столбец
или нулевую
строку, то ее
определитель
равен нулю.
(Данное утверждение
очевидно, т.к.
считать определитель
можно именно
по нулевой
строке или
столбцу.)Свойство
8. Определитель
матрицы не
изменится,
если к элементам
одной из его
строк(столбца)
прибавить(вычесть)
элементы другой
строки(столбца),
умноженные
на какое-либо
число, не равное
нулю.Свойство
9. Если
для элементов
какой- либо
строки или
столбца матрицы
верно соотношение:
d
= d1
d2
, e
= e1
e2
, f
= f1
f2
, то
верно:
|
|
50)Общая
схема исследования
ф-ии.Процесс
исследования
функции состоит
из нескольких
этапов:1)Область
существования
функции.Это
понятие включает
в себя и область
значений и
область определения
функции.2)Точки
разрыва. (Если
они имеются).3)Интервалы
возрастания
и убывания.4)Точки
максимума и
минимума.5)Максимальное
и минимальное
значение функции
на ее области
определения.6)Области
выпуклости
и вогнутости.7)Точки
перегиба.(Если
они имеются).8)Асимптоты.(Если
они имеются).9)Построение
графика.Применение
этой схемы
рассмотрим
на примере.Пример.
Исследовать
функцию
|
|
6)Системы
линейных уравнений
(n=2,3)Теорема
Крамера.(Габриель
Крамер (1704-1752) швейцарский
математик)Данный
метод также
применим только
в случае систем
линейных
уравнений,
где число
переменных
совпадает с
числом уравнений.
Кроме того,
необходимо
ввести ограничения
на коэффициенты
системы. Необходимо,
чтобы все
уравнения
были линейно
независимы,
т.е. ни одно
уравнение не
являлось бы
линейной
комбинацией
остальных.Для
этого необходимо,
чтобы определитель
матрицы системы
не равнялся
0.det
A
0;Действительно,
если какое-
либо уравнение
системы есть
линейная
комбинация
остальных,
то если к элементам
какой- либо
строки прибавить
элементы другой,
умноженные
на какое- либо
число, с помощью
линейных
преобразований
можно получить
нулевую строку.
Определитель
в этом случае
будет равен
нулю.
Теорема.
Система из n
уравнений с
n
неизвестными |
|
7)Система
линейных
Ур-ий.Теорема
Кронекра-Капели.
(Леопольд Кронекер
(1823-1891) немецкий
математик)Теорема:
Система
совместна
(имеет хотя
бы одно решение)
тогда и только
тогда, когда
ранг
матрицы системы
равен рангу
расширенной
матрицы.RgA
= RgA*.Очевидно,
что система
(1) может быть
записана в
виде:x1
7)Продолжение. +12
= 14
0; RgA
= 2;A*
=
|
|
8)Ранг
матрицы и его
вычисление.
Привести
пример.Рангом
матрицы А наз
наивысший из
порядков миноров
этой матрицы
не равных
нулю.А=(аij)=(a11
a12
… a1n;
a21
a22
… a2n;
…; am1
am2
… amn)
m*x
Возьмем и выделим
какой-нибудь
минор порядка
А (а11 а12; а21 а22). Если
этот минор
не равен нулю
то его строки(столбцы)
линейно независимы,
тогда первые
2-е строки этой
матрицы линейно
независ. Ранг
матрицы А будет
не меньше 2-х.
При нахождении
ранга матрицы
пользуются
методом окомляющих
миноров. Этот
метод состоит
в том что минор
второго порядка
окомляют одной
строкой и одним
столбцом, т.е
строят минор
3-го порядка.
Если же миноры
3-его порядка
окомляющие
данный минор
2-го порядка
равны нулю,
то матрица А
не содержит
миноров порядка
большего 2-х,
не равных нулю
и ее ранг равен
2-м.Если же есть
хотя бы один
минор 3-го порядка
который не
равен нулю,
то ранг матрицы
не менее 3-х и
процедуру
окомления
3-порядка продолжают,
в итоге будет
найден минор
4-го порядка
не равный нулю.
Для которого
все окомляющие
миноры n+1-го
порядка равны
нулю. Тогда
ранг матрицы
А равен n.
Разность матрицы
обозн. R(A).
Замечания:
1)Ранг нулевой
матрицы равен
нулю; 2)ранг
матрицы равен
max
числу его линейно
независимых
строк.Найдите
ранг матрицы
|
|
9)Сист
лин уравненийОпределение.
Система m
уравнений с
n
неизвестными
в общем виде
записывается
следующим
образом:
где aij
– коэффициенты,
а bi
– постоянные.
Решениями
системы являются
n
чисел, которые
при подстановке
в систему
превращают
каждое ее
уравнение в
тождество.Определение.
Если система
имеет хотя
бы одно решение,
то она называется
совместной.
Если система
не имеет ни
одного решения,
то она называется
несовместной.Определение.
Система называется
определенной,
если она имеет
только одно
решение и
неопределенной,
если более
одного.Определение.
Для системы
линейных уравнений
матрицаА =
|
Работы, похожие на Реферат: Шпаргалки на экзамен в ВУЗе (1 семестр, математика)
|
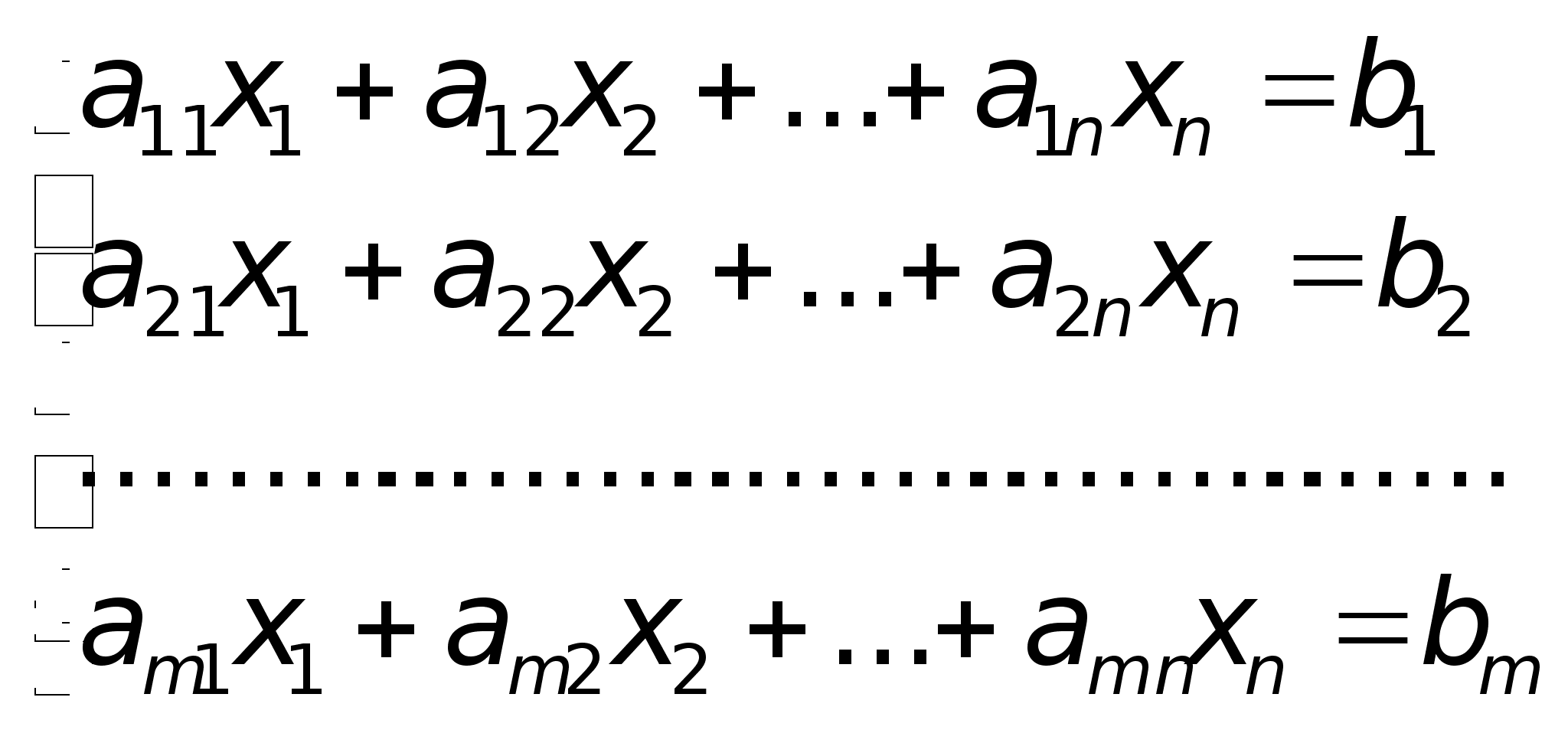 Разделим
обе части 1–го
уравнения
на a11
Разделим
обе части 1–го
уравнения
на a11
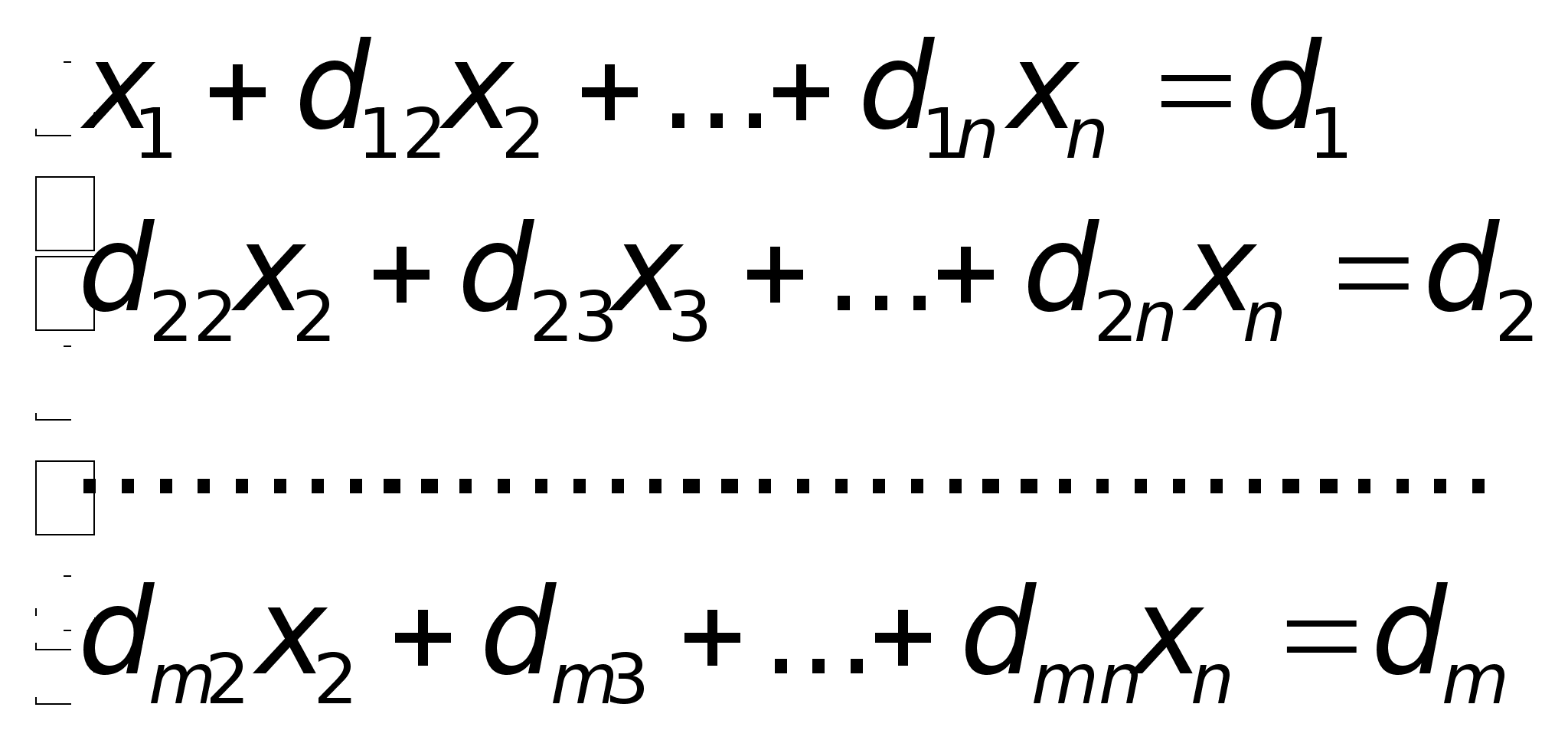 ,
где d1j
= 1j/a11,
j
= 2, 3, …, n+1
dij
= aij
– ai1d1j
i
= 2, 3, … , n;
j
= 2, 3, … , n+1.Далее
повторяем
эти же действия
для второго
уравнения
системы, потом
– для третьего
и т.д.Пример.
Решить систему
линейных уравнений
методом Гаусса.
,
где d1j
= 1j/a11,
j
= 2, 3, …, n+1
dij
= aij
– ai1d1j
i
= 2, 3, … , n;
j
= 2, 3, … , n+1.Далее
повторяем
эти же действия
для второго
уравнения
системы, потом
– для третьего
и т.д.Пример.
Решить систему
линейных уравнений
методом Гаусса.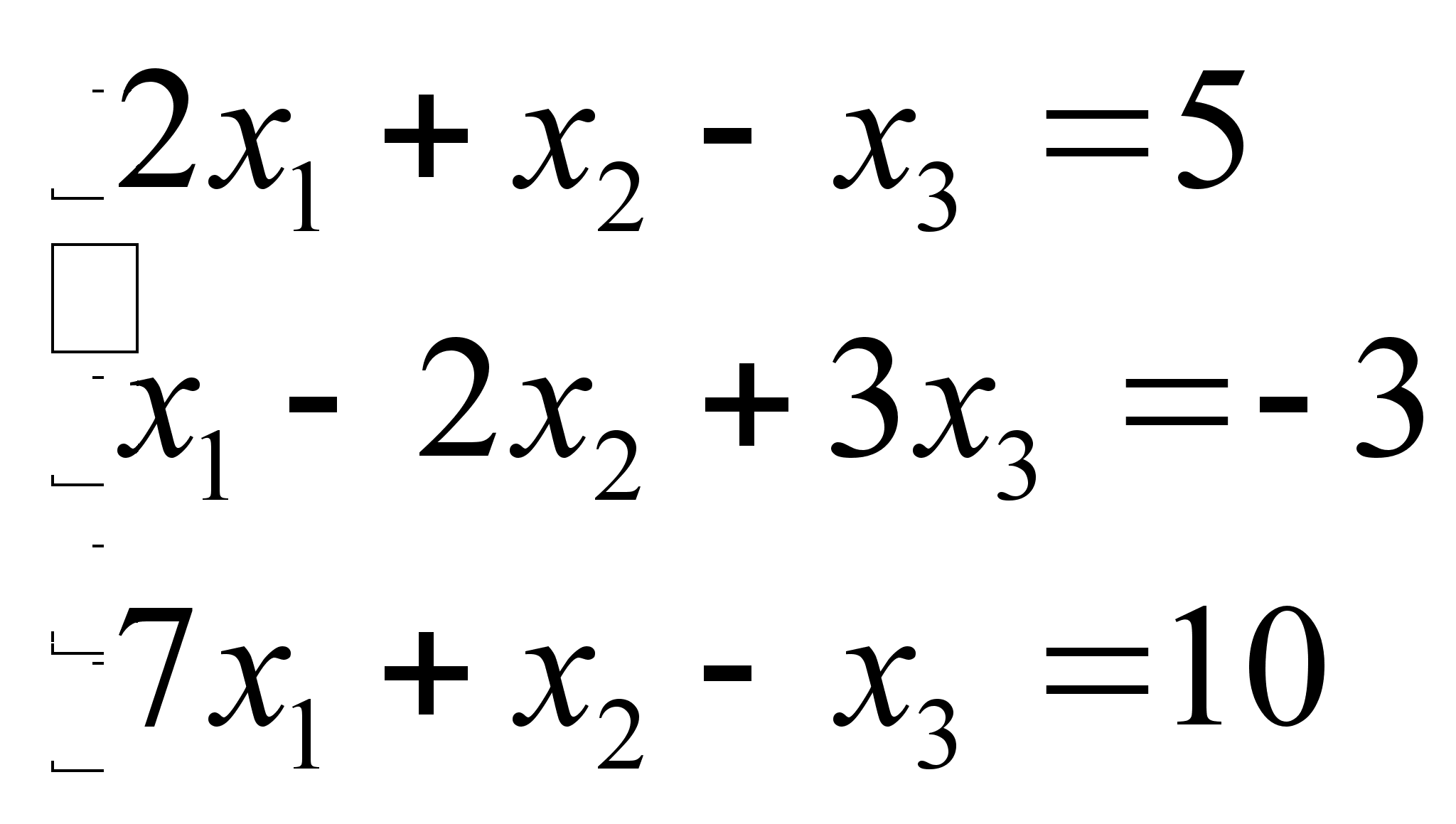 Составим
расширенную
матрицу системы.*
=
Составим
расширенную
матрицу системы.*
=
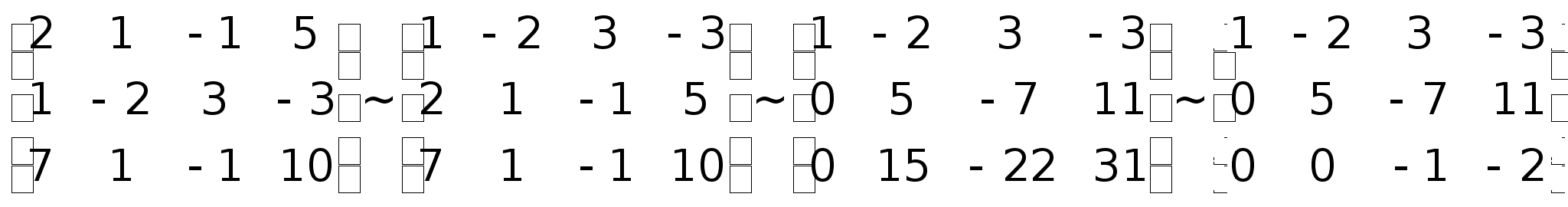 Таким
образом, исходная
система может
быть представлена
в виде:
Таким
образом, исходная
система может
быть представлена
в виде: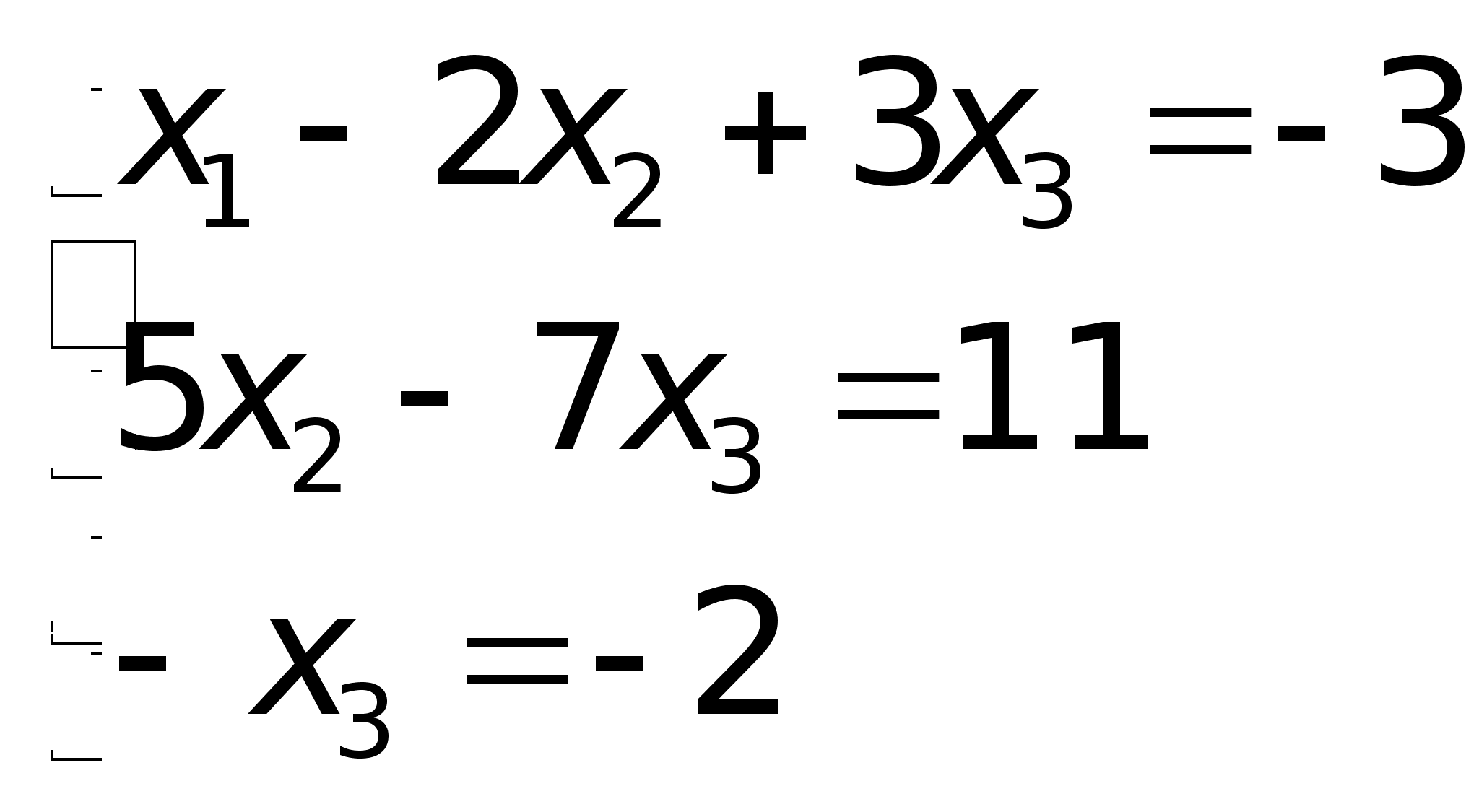 ,
откуда получаем:
x3
= 2; x2
= 5; x1
= 1.Пример.
Решить систему
методом Гаусса.
,
откуда получаем:
x3
= 2; x2
= 5; x1
= 1.Пример.
Решить систему
методом Гаусса.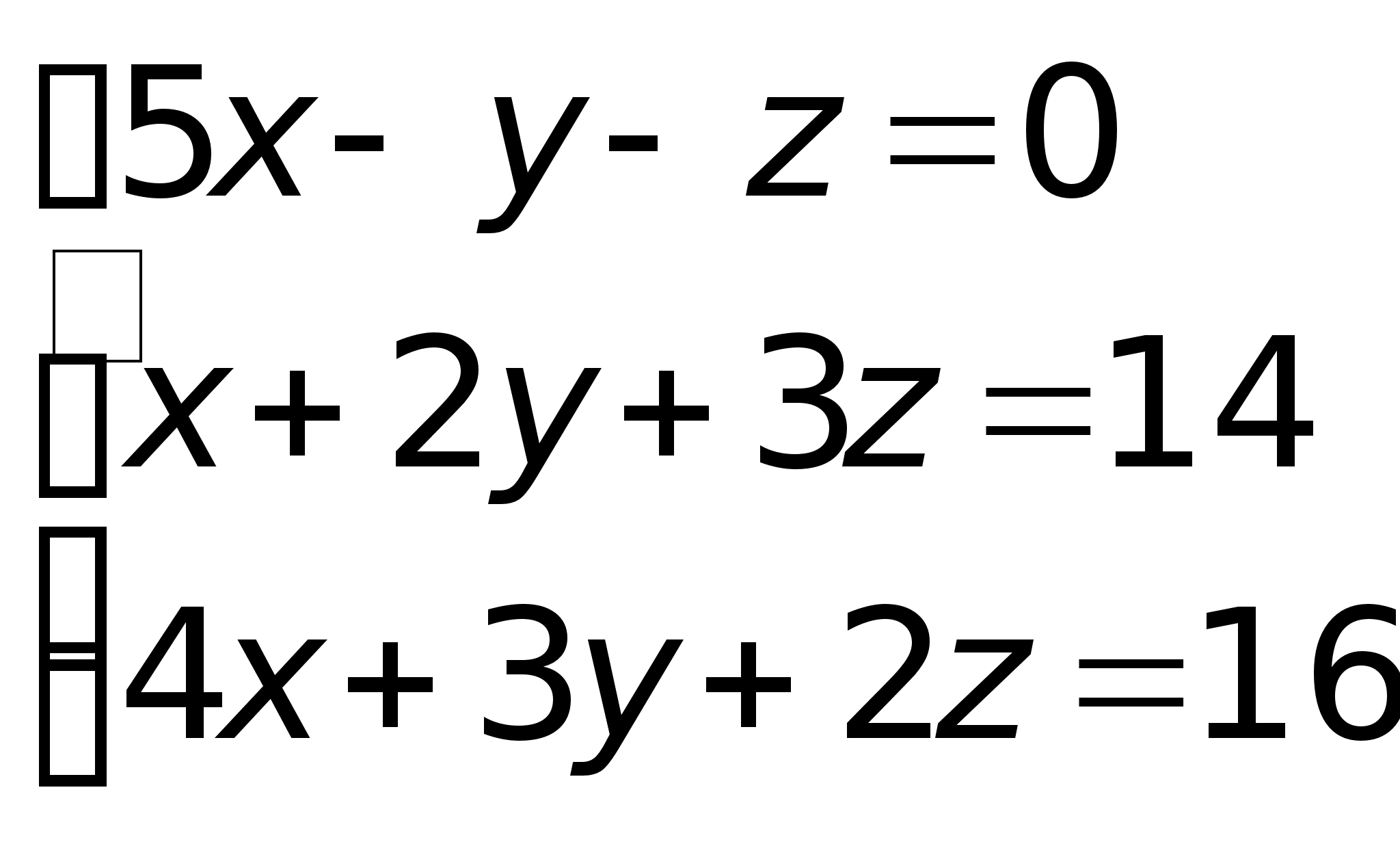 Составим
расширенную
матрицу системы.
Составим
расширенную
матрицу системы.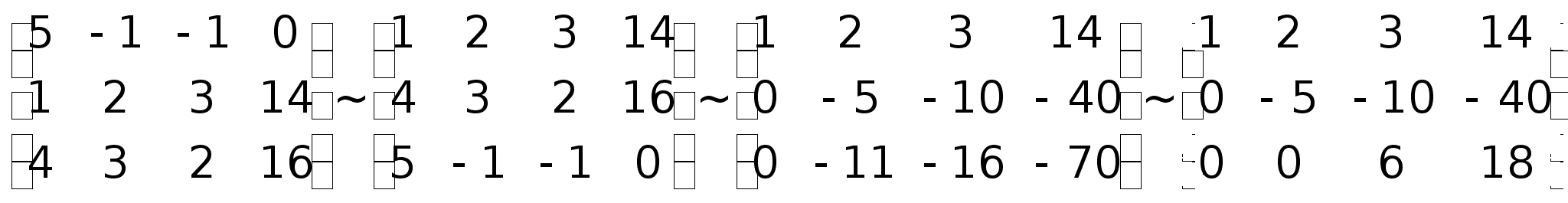 Таким
образом, исходная
система может
быть представлена
в виде:
Таким
образом, исходная
система может
быть представлена
в виде: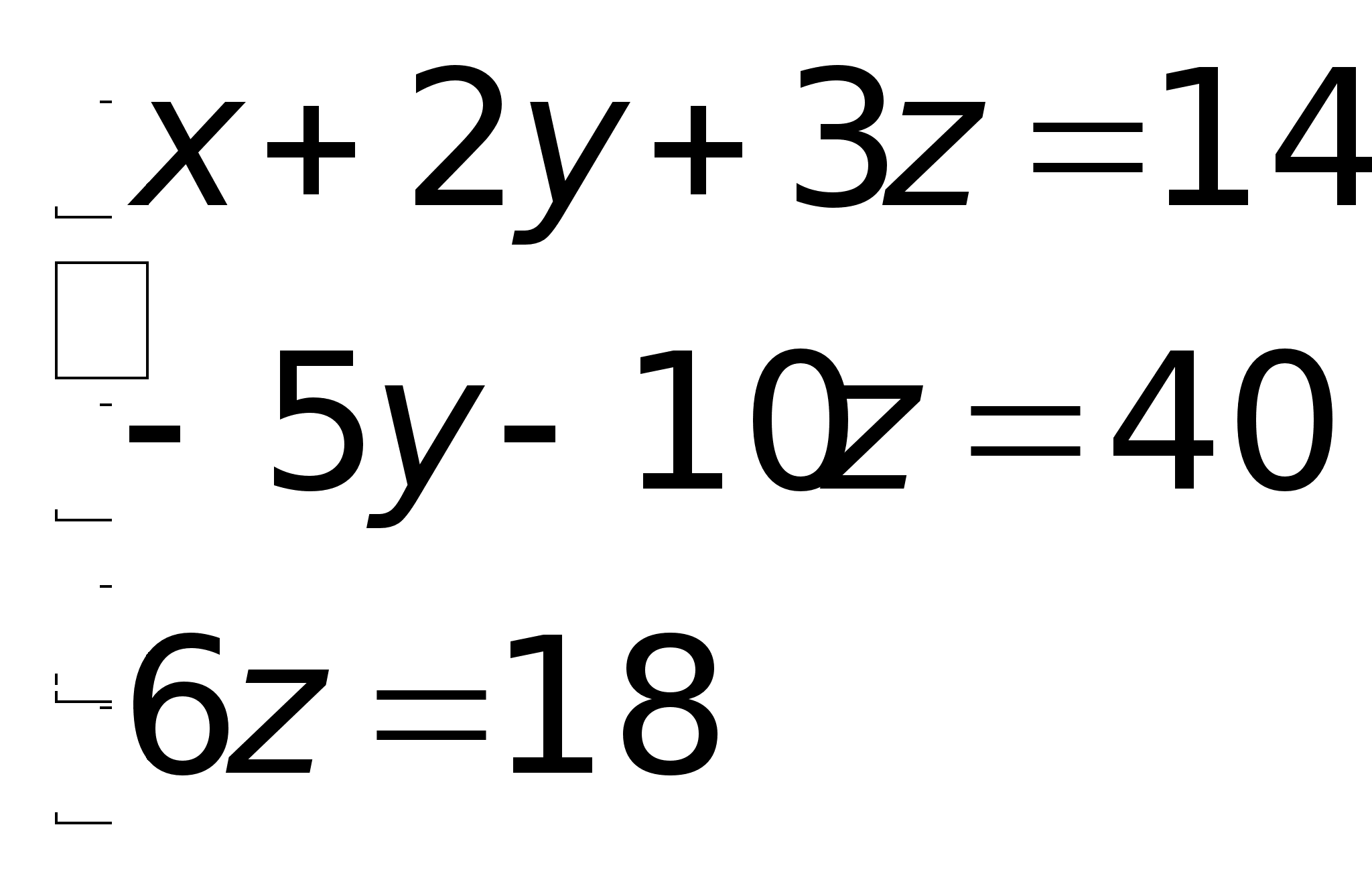 ,
откуда получаем:
z
= 3; y
= 2; x
= 1.Полученный
ответ совпадает
с ответом,
полученным
для данной
системы методом
Крамера и
матричным
методом.Для
самостоятельного
решения:
,
откуда получаем:
z
= 3; y
= 2; x
= 1.Полученный
ответ совпадает
с ответом,
полученным
для данной
системы методом
Крамера и
матричным
методом.Для
самостоятельного
решения: Ответ:
{1, 2, 3, 4}.
Ответ:
{1, 2, 3, 4}. Определение.
Векторы называются
коллинеарными,
если они расположены
на одной или
параллельных
прямых. Нулевой
вектор коллинеарен
любому вектору.Определение.
Векторы называются
компланарными,
если существует
плоскость,
которой они
параллельны.
Коллинеарные
векторы всегда
компланарны,
но не все компланарные
векторы коллинеарны.
Определение.
Векторы называются
равными,
если они коллинеарны,
одинаково
направлены
и имеют одинаковые
модули.Всякие
векторы можно
привести к
общему началу,
т.е. построить
векторы, соответственно
равные данным
и имеющие общее
начало. Из
определения
равенства
векторов следует,
что любой вектор
имеет бесконечно
много векторов,
равных ему.Определение.
Линейными
операциями
над векторами
называется
сложение и
умножение на
число.Суммой
векторов является
вектор -
Определение.
Векторы называются
коллинеарными,
если они расположены
на одной или
параллельных
прямых. Нулевой
вектор коллинеарен
любому вектору.Определение.
Векторы называются
компланарными,
если существует
плоскость,
которой они
параллельны.
Коллинеарные
векторы всегда
компланарны,
но не все компланарные
векторы коллинеарны.
Определение.
Векторы называются
равными,
если они коллинеарны,
одинаково
направлены
и имеют одинаковые
модули.Всякие
векторы можно
привести к
общему началу,
т.е. построить
векторы, соответственно
равные данным
и имеющие общее
начало. Из
определения
равенства
векторов следует,
что любой вектор
имеет бесконечно
много векторов,
равных ему.Определение.
Линейными
операциями
над векторами
называется
сложение и
умножение на
число.Суммой
векторов является
вектор -
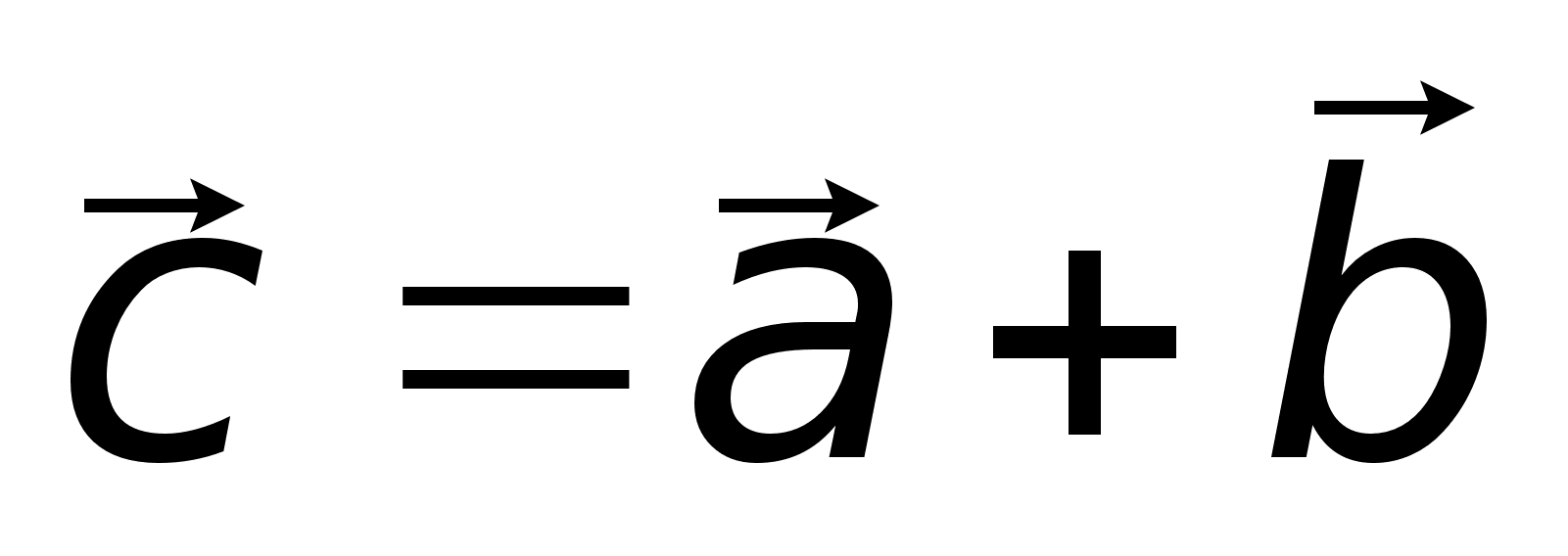 Произведение
-
Произведение
-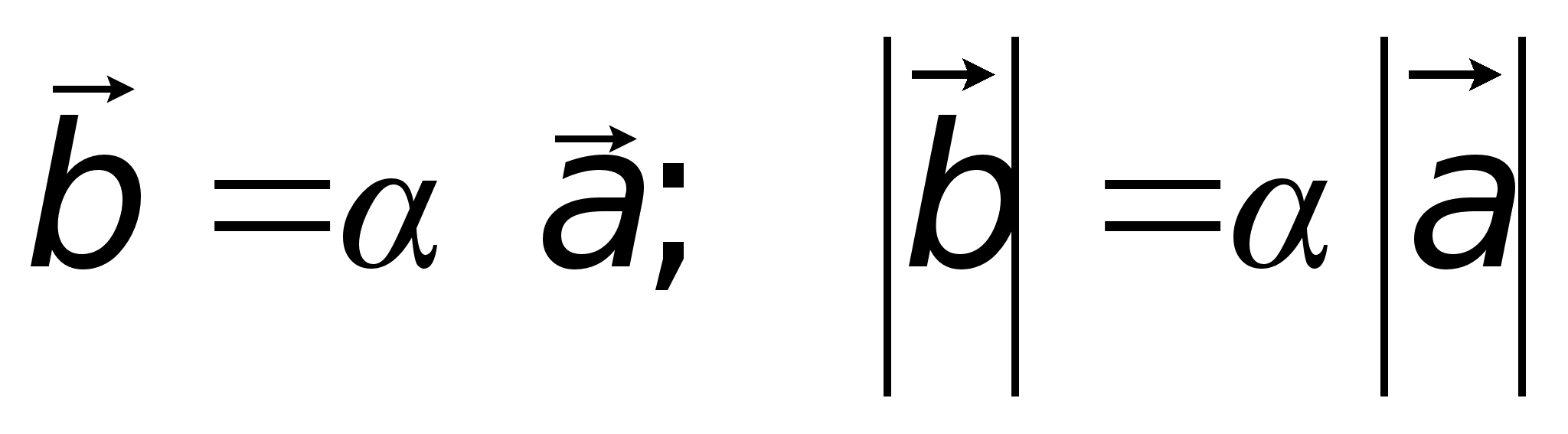 ,
при этом
,
при этом
 коллинеарен
коллинеарен
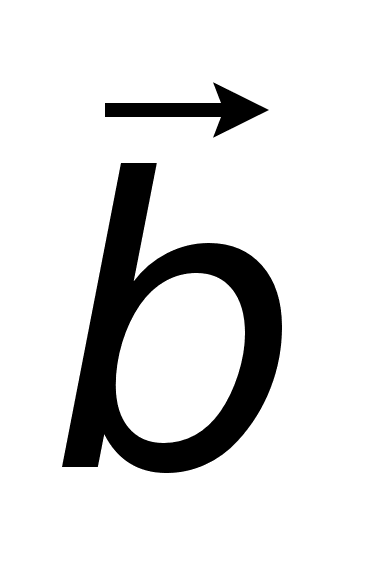 .Вектор
.Вектор
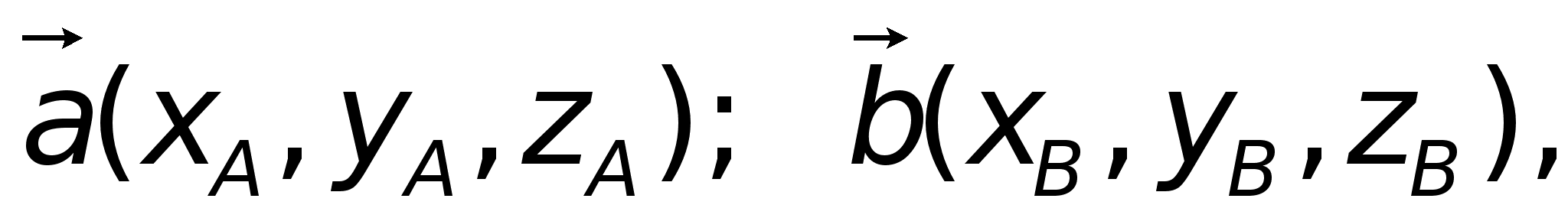 тогда
тогда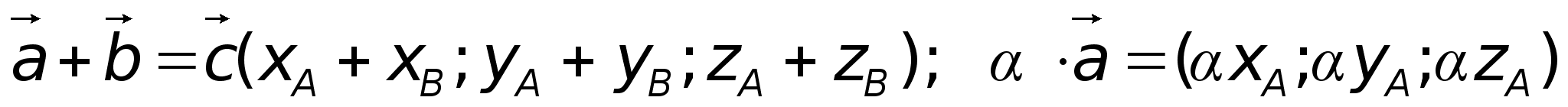
 и
и
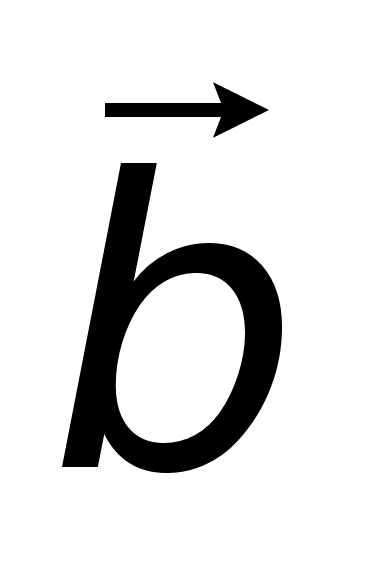 называется
число, равное
произведению
длин этих сторон
на косинус
угла между
ними.
называется
число, равное
произведению
длин этих сторон
на косинус
угла между
ними.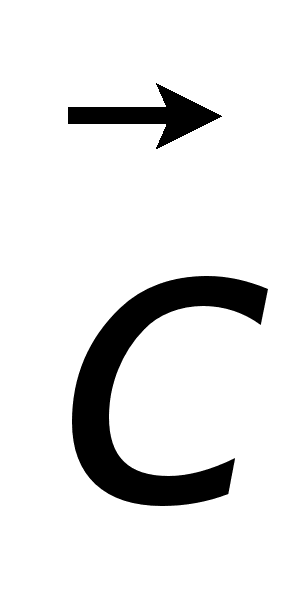 )
=
)
=
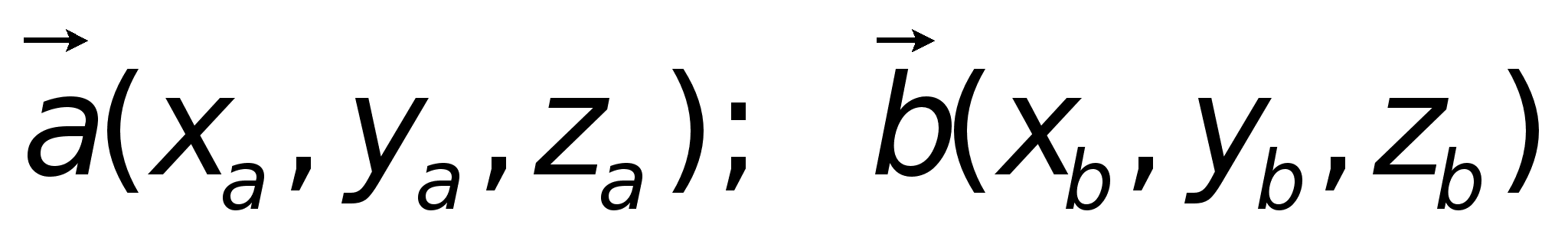 в
декартовой
прямоугольной
системе координат,
то
в
декартовой
прямоугольной
системе координат,
то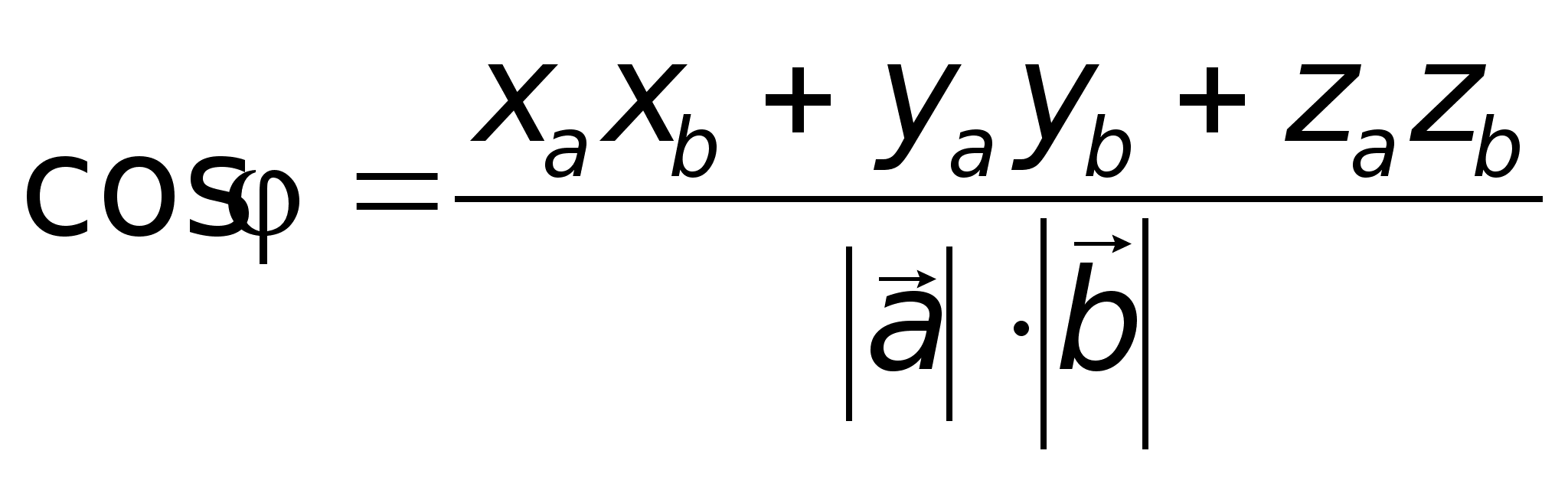 ;Пример.
Найти (5
;Пример.
Найти (5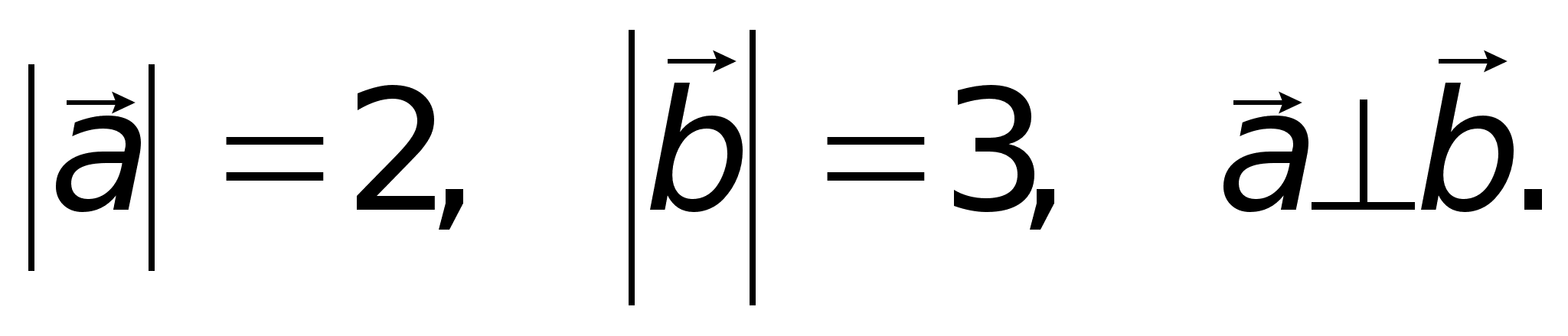 10
10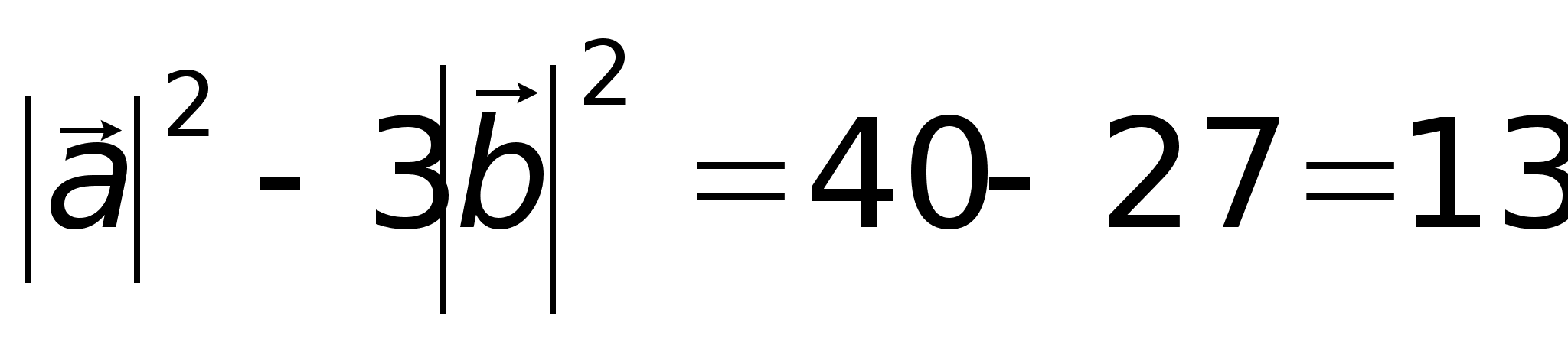 ,
т.к.
,
т.к.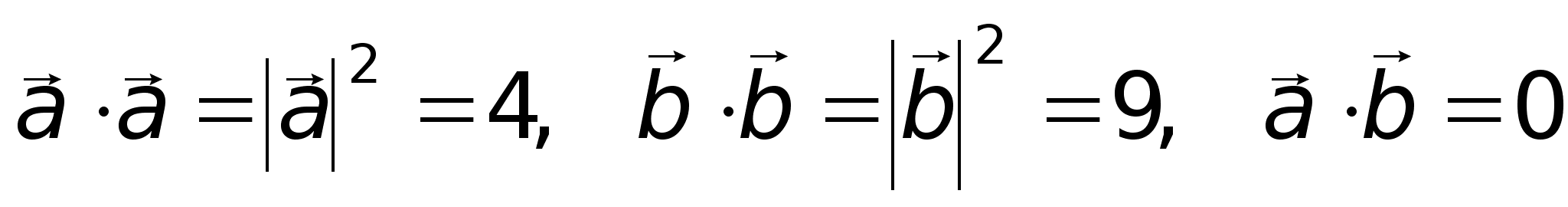 .
. и
и
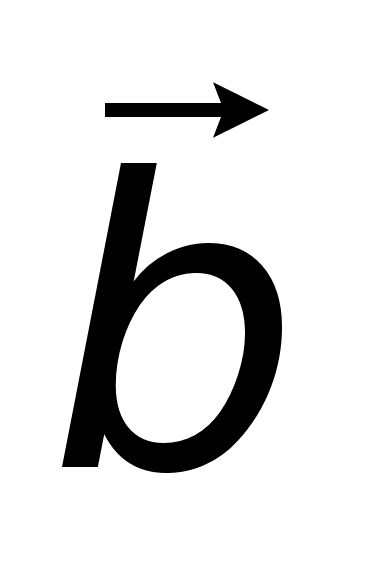 называется
вектор
называется
вектор
 ,
удовлетворяющий
следующим
условиям:1)
,
удовлетворяющий
следующим
условиям:1)
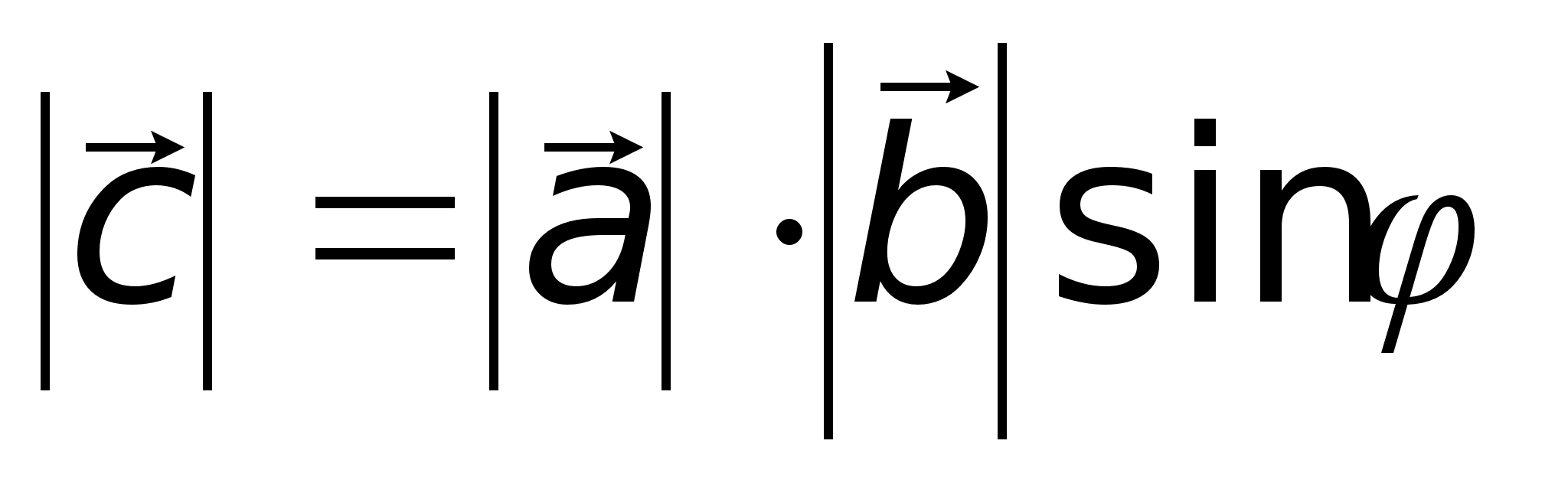 ,
где
,
где 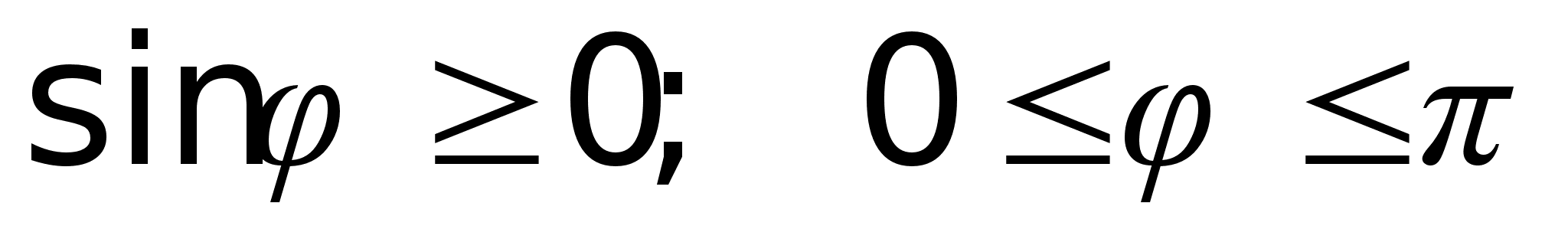 2)
вектор
2)
вектор
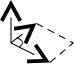 )
)
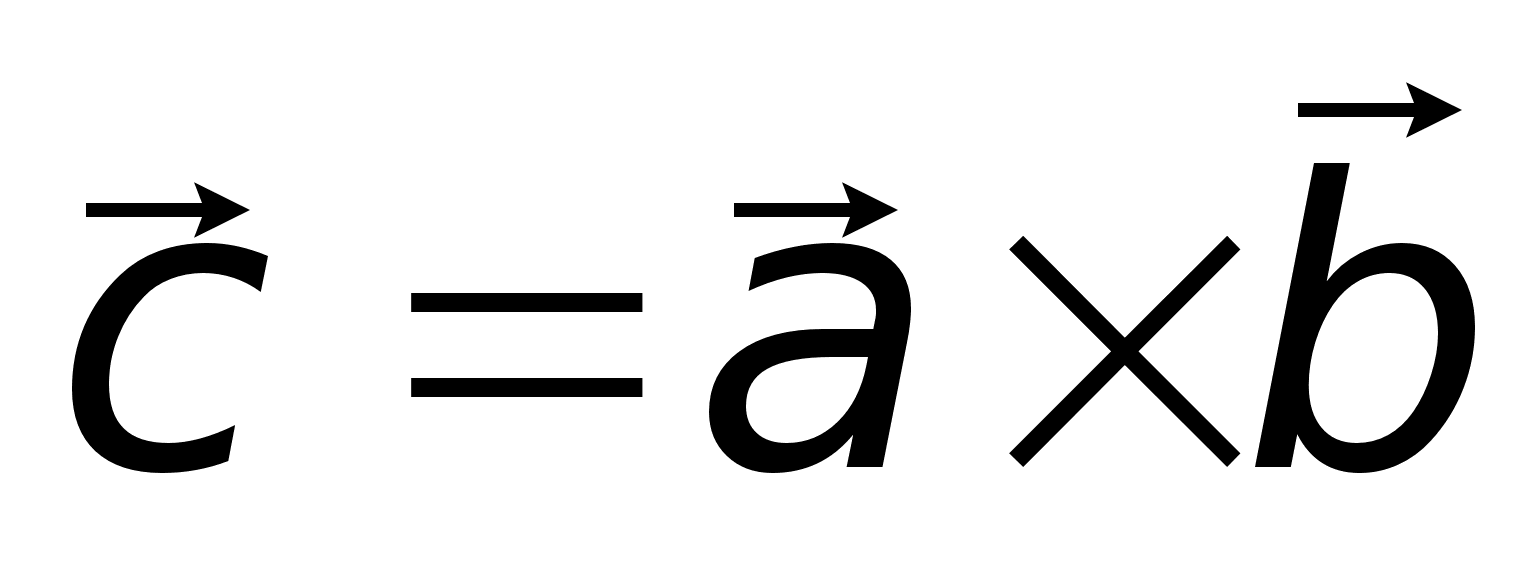 или
или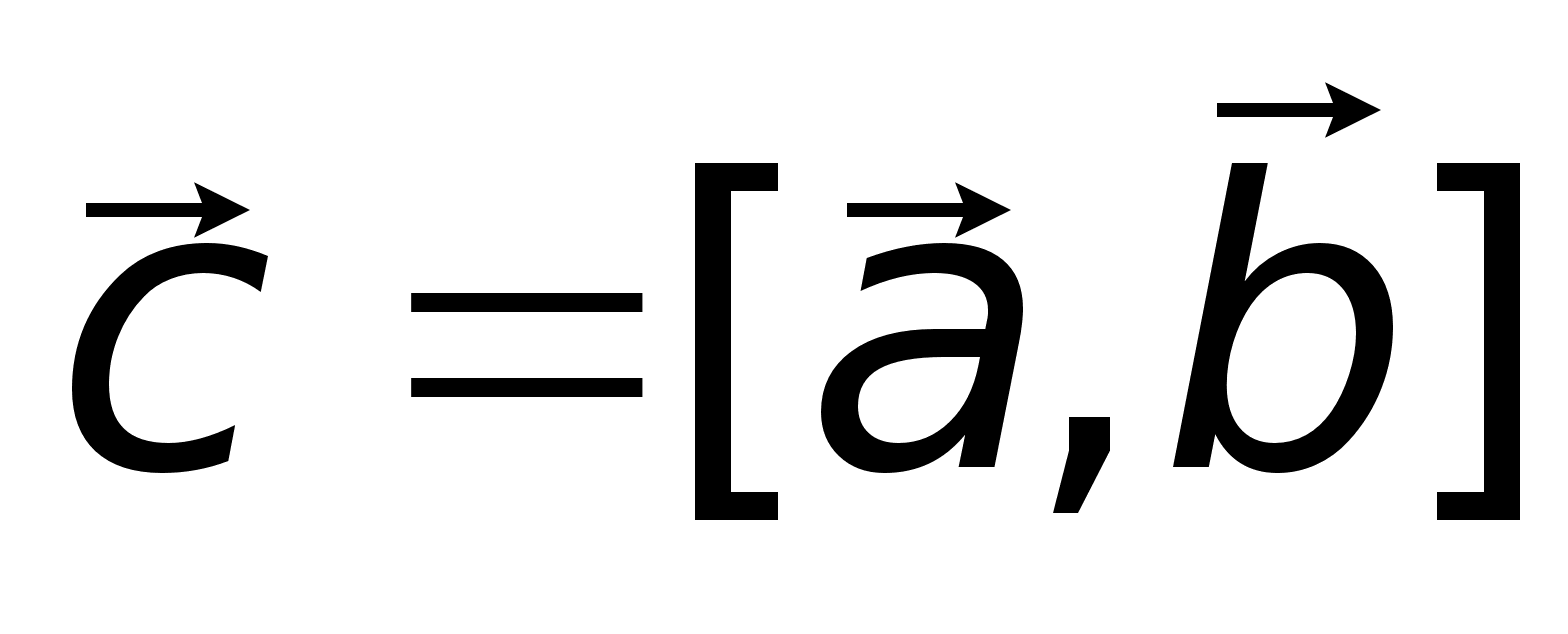 .
.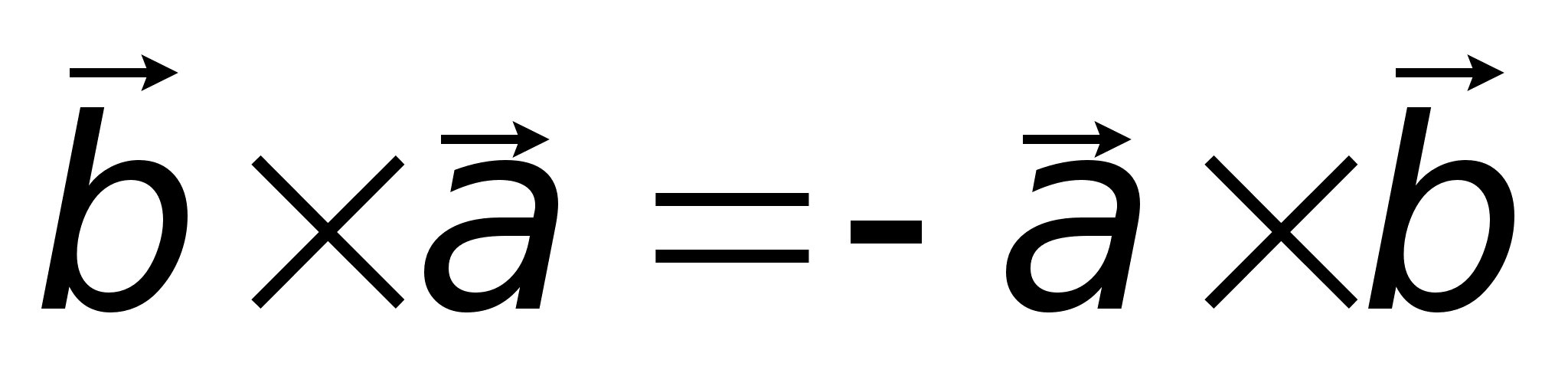 ;2)
;2)
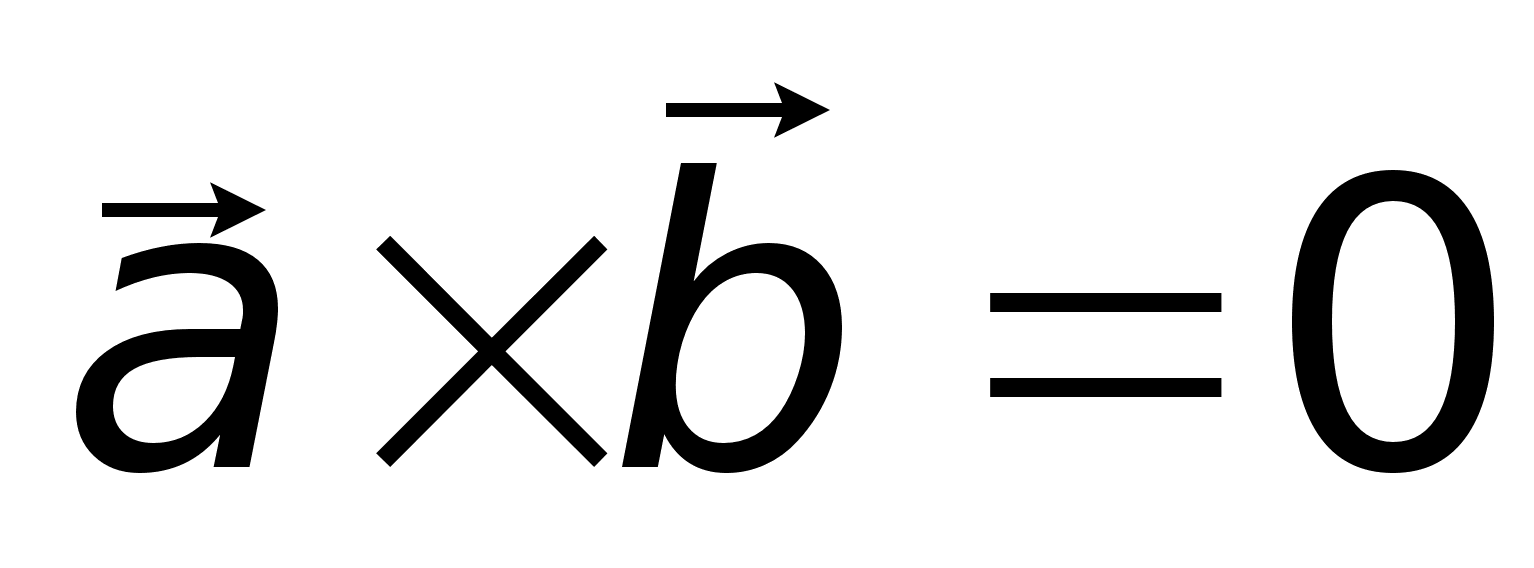 ,
если
,
если
 )
=
)
=
 ,
то
,
то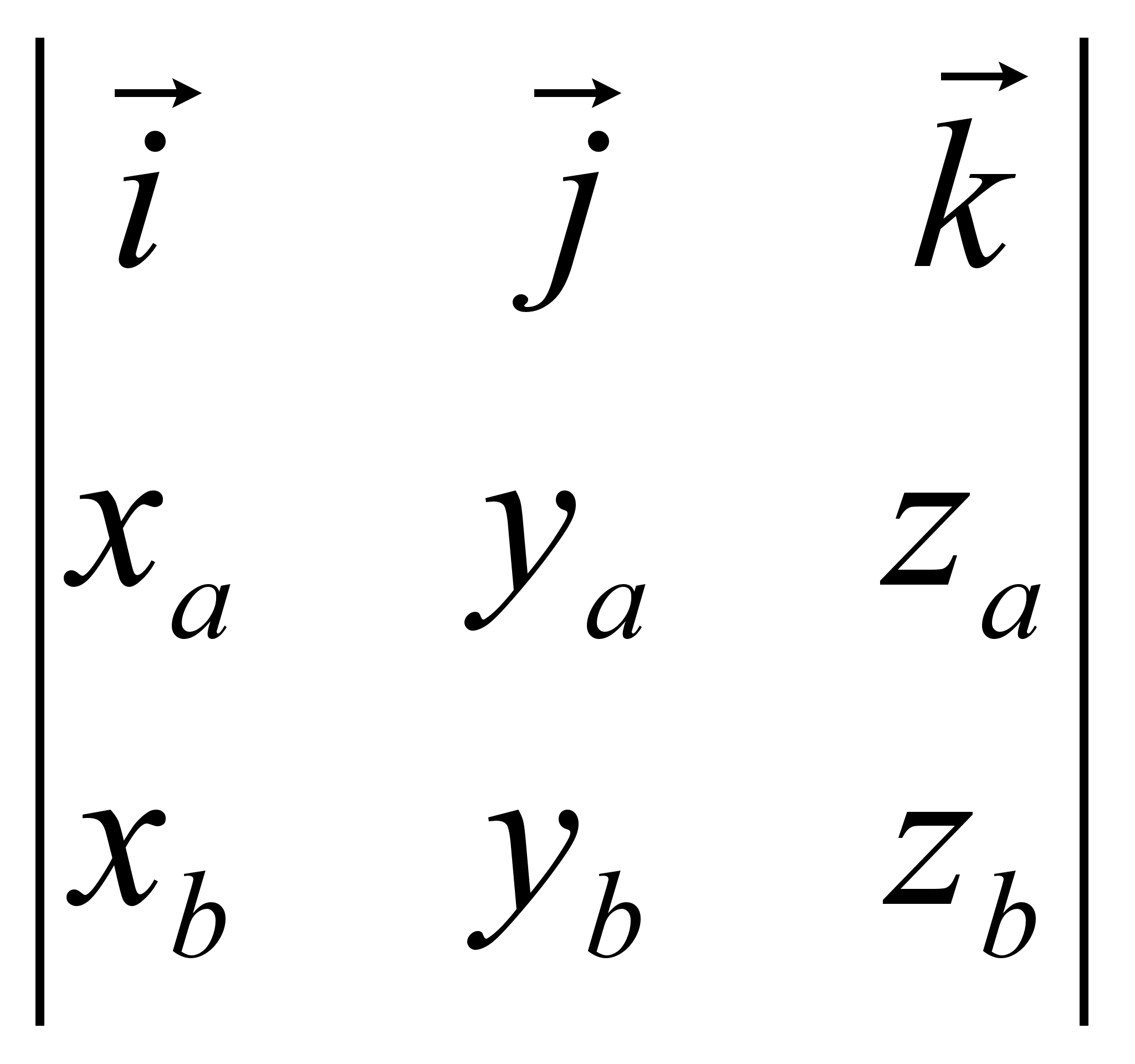 6)
Геометрическим
смыслом векторного
произведения
векторов является
площадь параллелограмма,
построенного
на векторах
6)
Геометрическим
смыслом векторного
произведения
векторов является
площадь параллелограмма,
построенного
на векторах
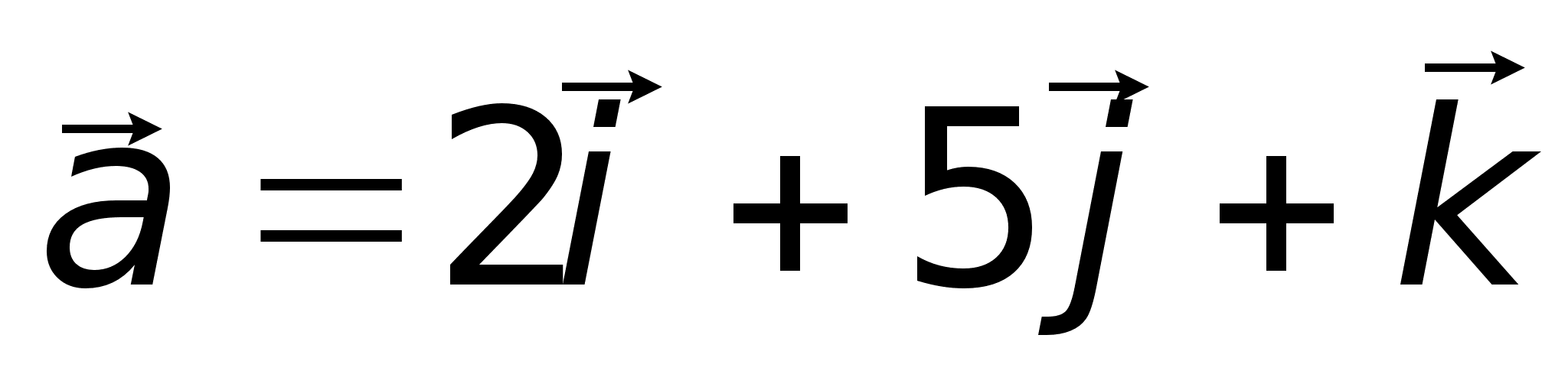 и
и
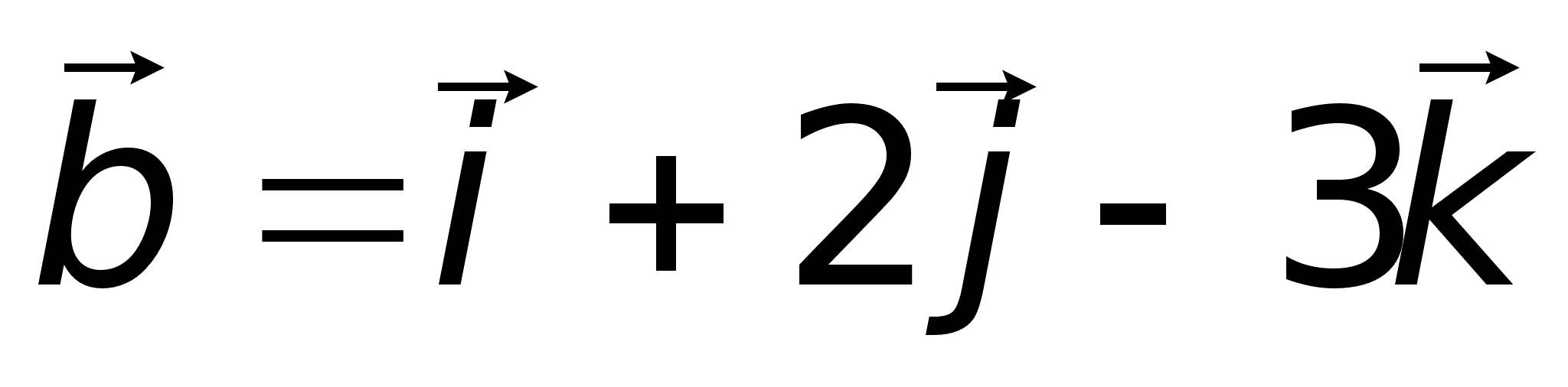 .
.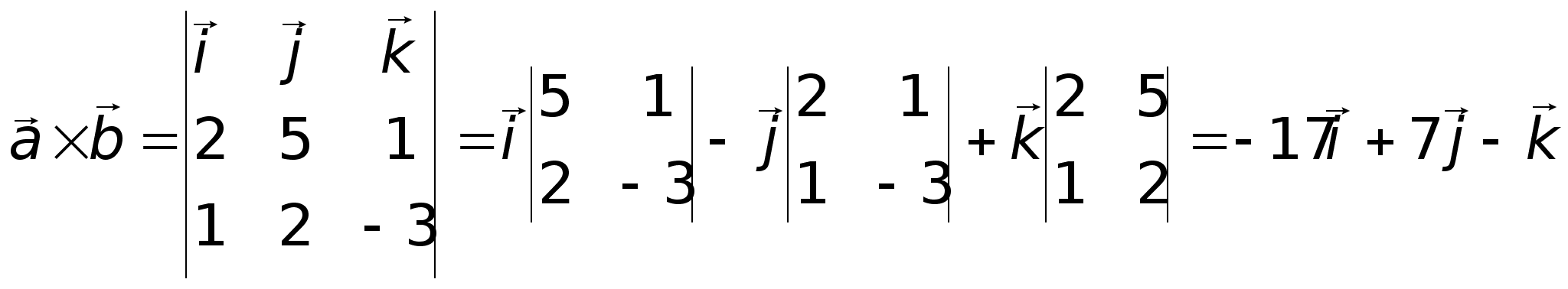 .
. ,
,
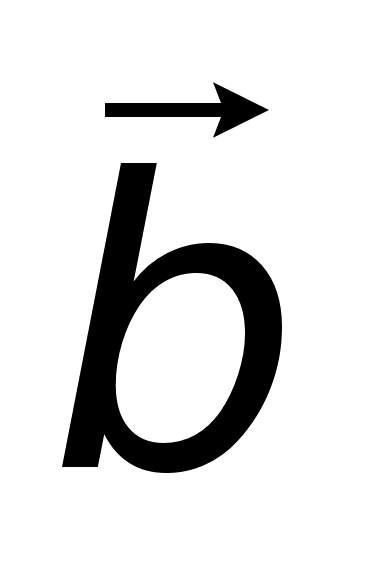 и
и
 называется
число, равное
скалярному
произведению
вектора
называется
число, равное
скалярному
произведению
вектора
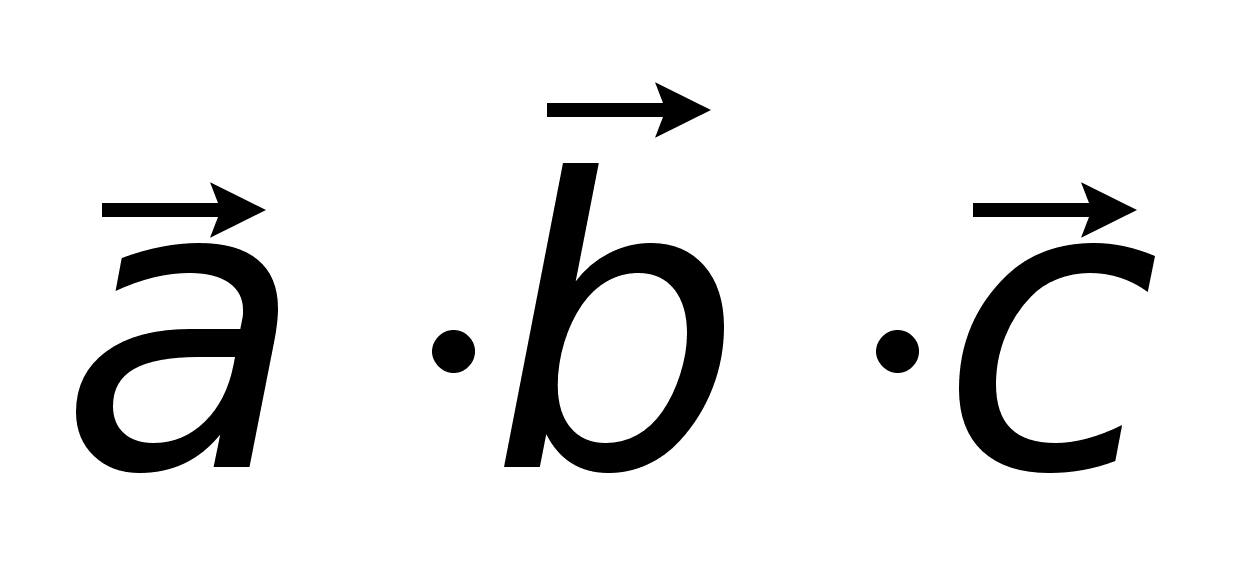 или
(
или
(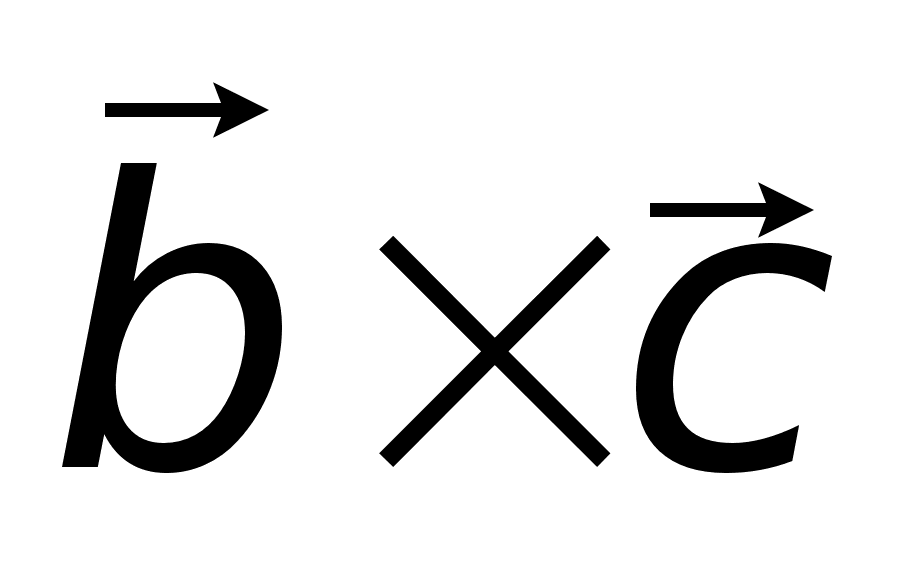
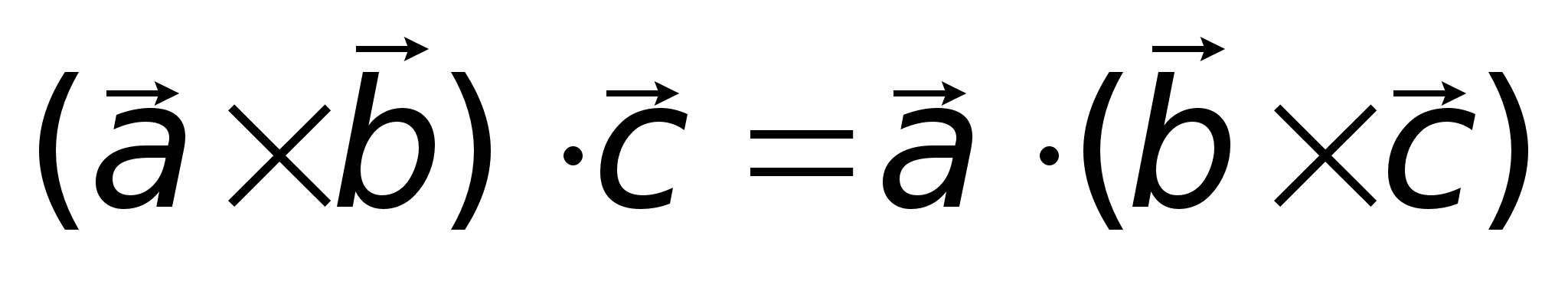 3)
3)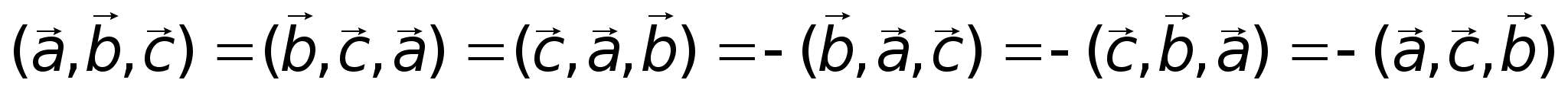
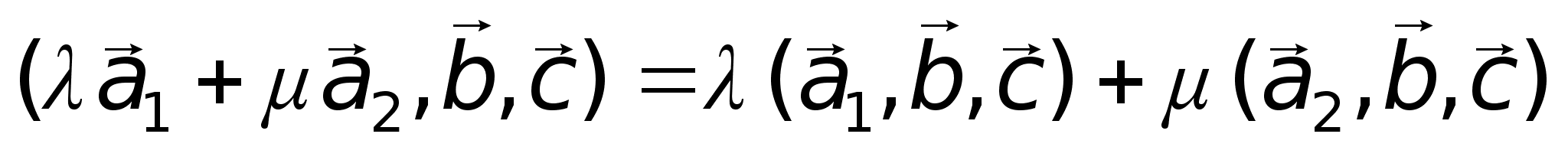 5)
Объем треугольной
пирамиды,
образованной
векторами
5)
Объем треугольной
пирамиды,
образованной
векторами
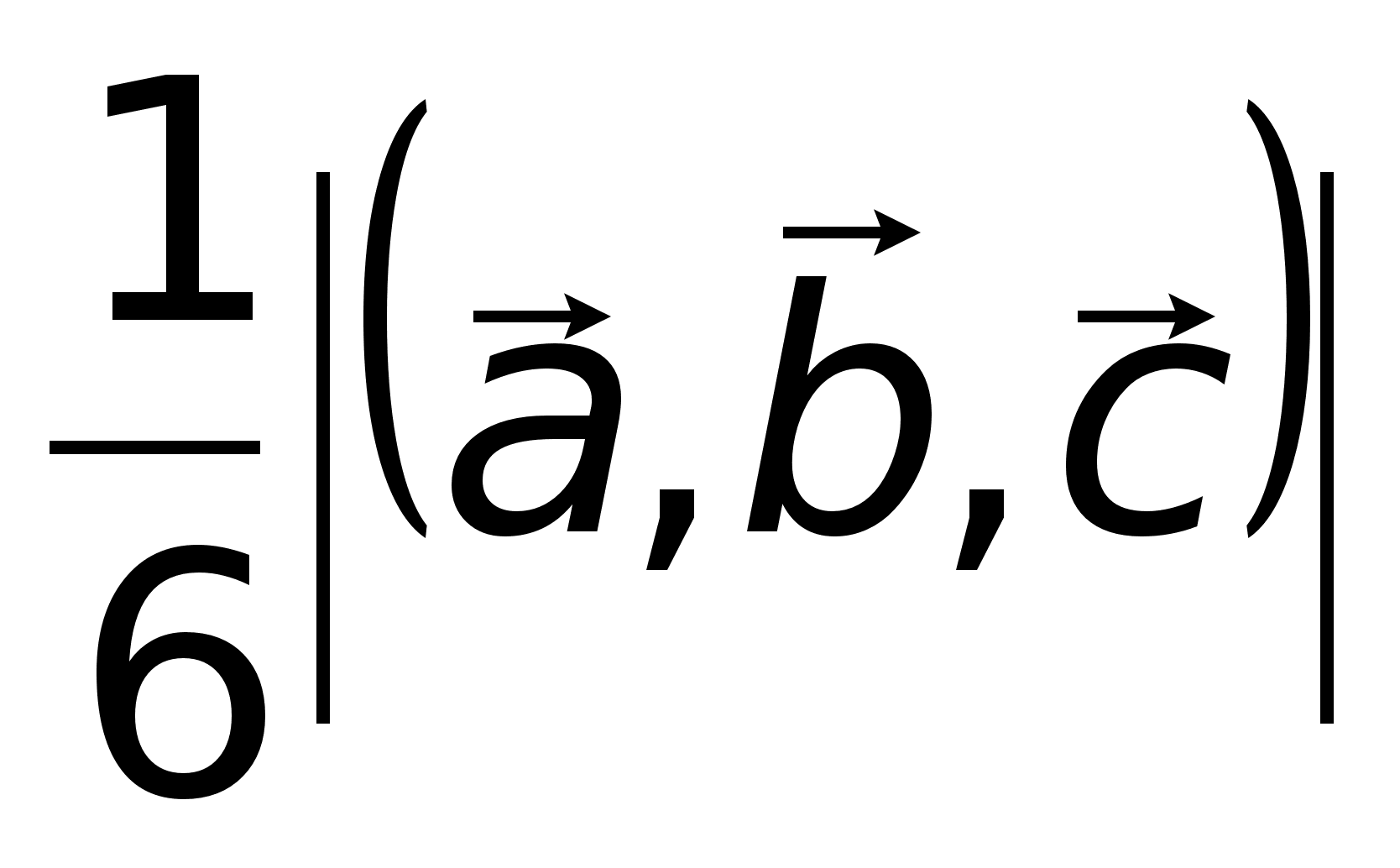 6)Если
6)Если
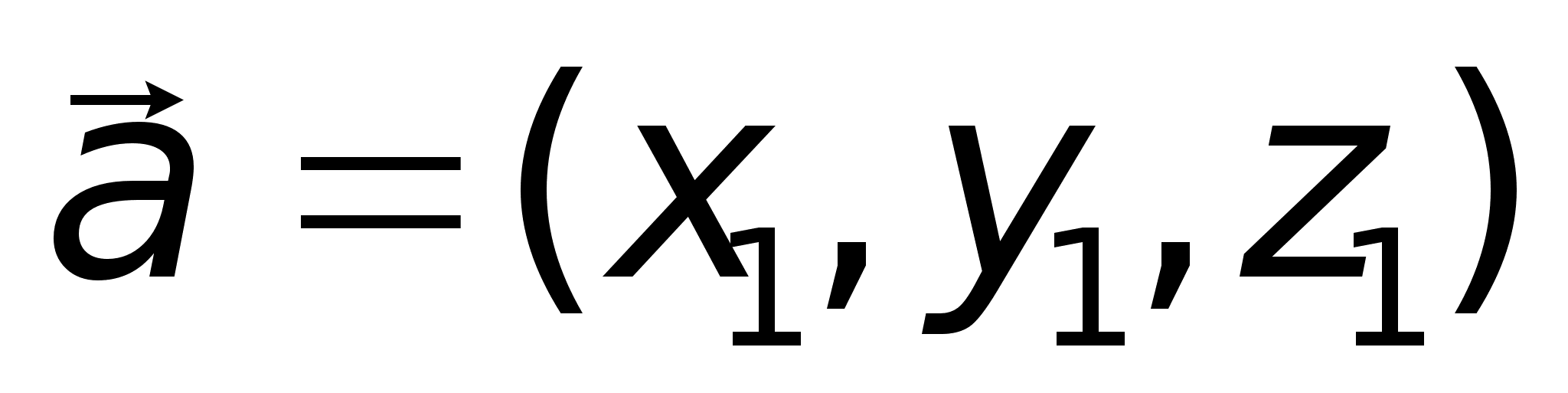 ,
,
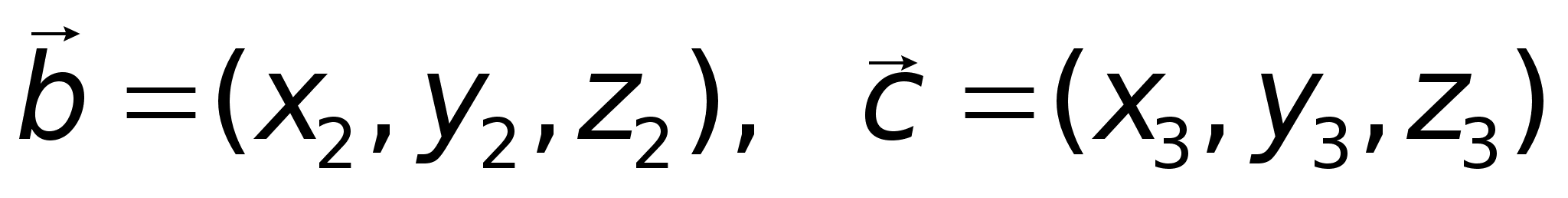 ,
то
,
то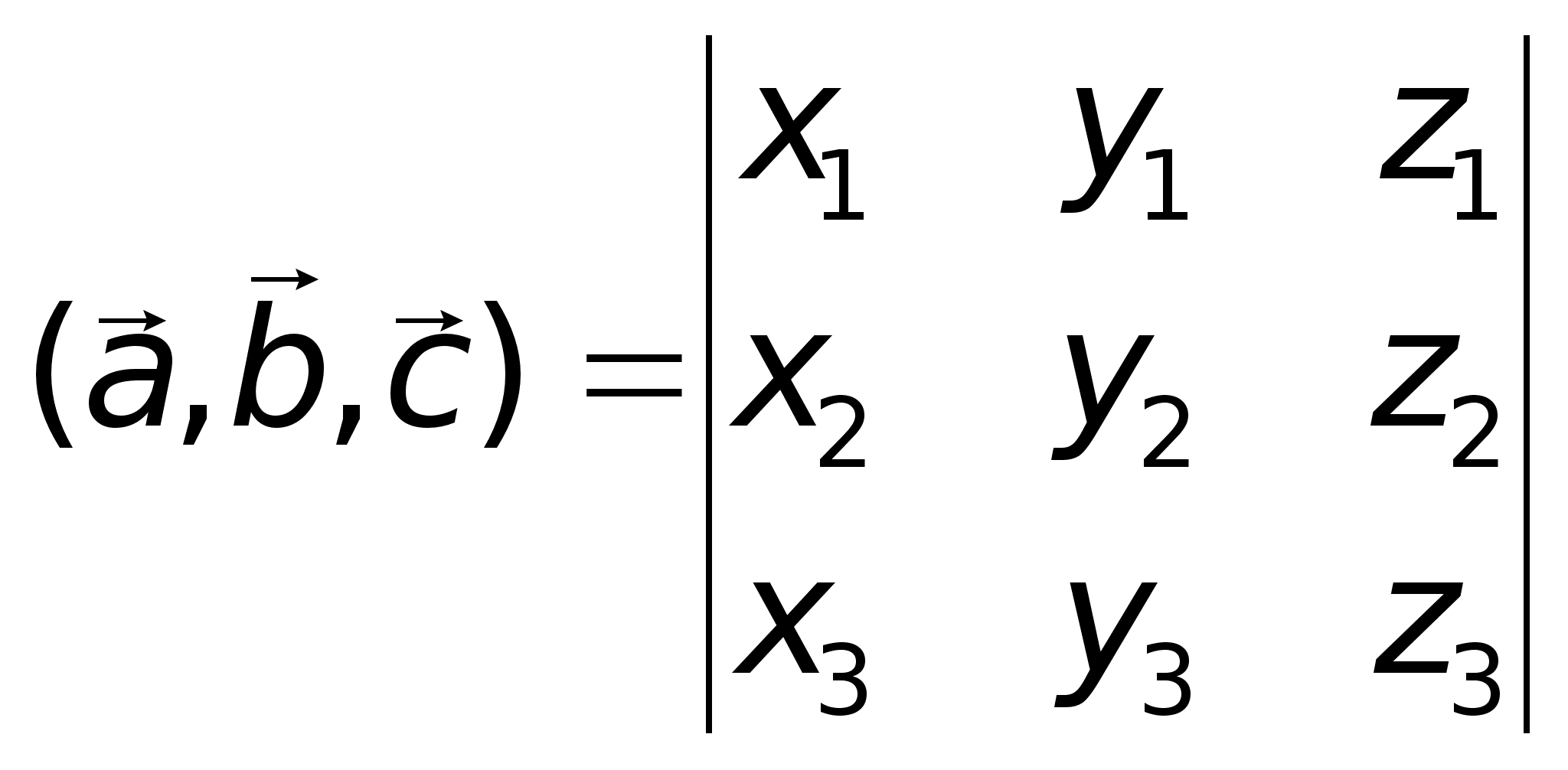 Пример.
Доказать, что
точки А(5; 7; 2), B(3;
1; -1), C(9;
4; -4), D(1;
5; 0) лежат в одной
плоскости.Найдем
координаты
векторов:
Пример.
Доказать, что
точки А(5; 7; 2), B(3;
1; -1), C(9;
4; -4), D(1;
5; 0) лежат в одной
плоскости.Найдем
координаты
векторов:
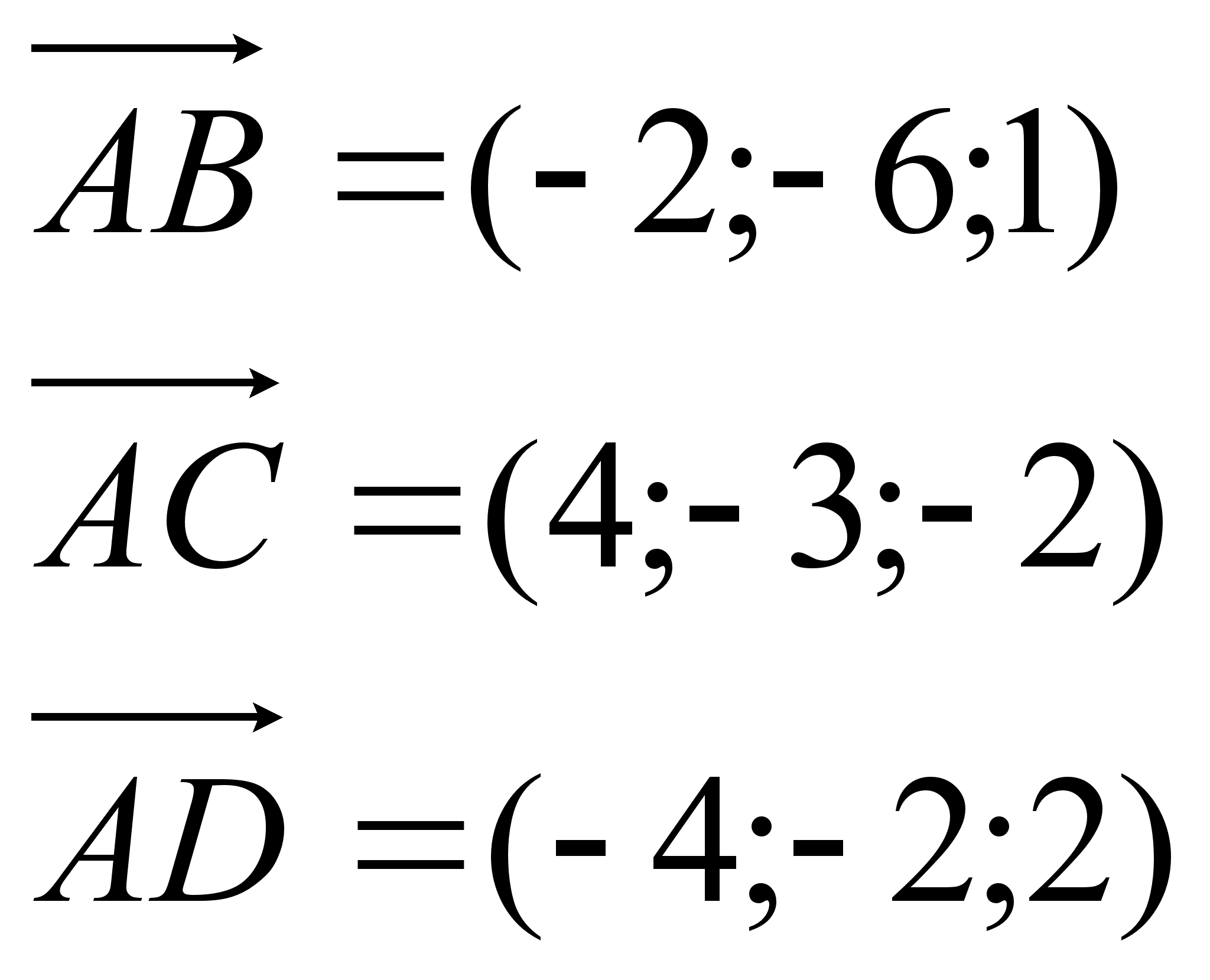 Найдем
смешанное
произведение
полученных
векторов:
Найдем
смешанное
произведение
полученных
векторов: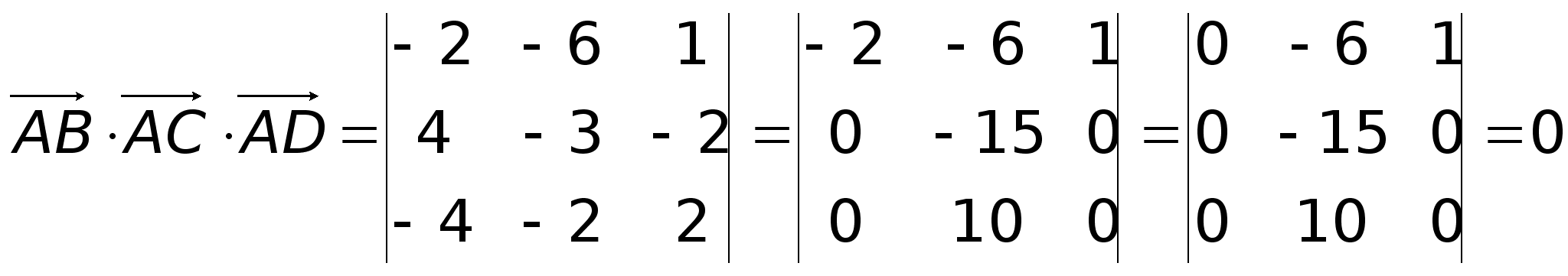 ,Таким
образом, полученные
выше векторы
компланарны,
следовательно
точки A,
B,
C
и D
лежат в одной
плоскости.Пример.
Найти объем
пирамиды и
длину высоты,
опущенной на
грань BCD,
если вершины
имеют координаты
A(0;
0; 1), B(2;
3; 5), C(6;
2; 3), D(3;
7; 2).Найдем координаты
векторов:
,Таким
образом, полученные
выше векторы
компланарны,
следовательно
точки A,
B,
C
и D
лежат в одной
плоскости.Пример.
Найти объем
пирамиды и
длину высоты,
опущенной на
грань BCD,
если вершины
имеют координаты
A(0;
0; 1), B(2;
3; 5), C(6;
2; 3), D(3;
7; 2).Найдем координаты
векторов:
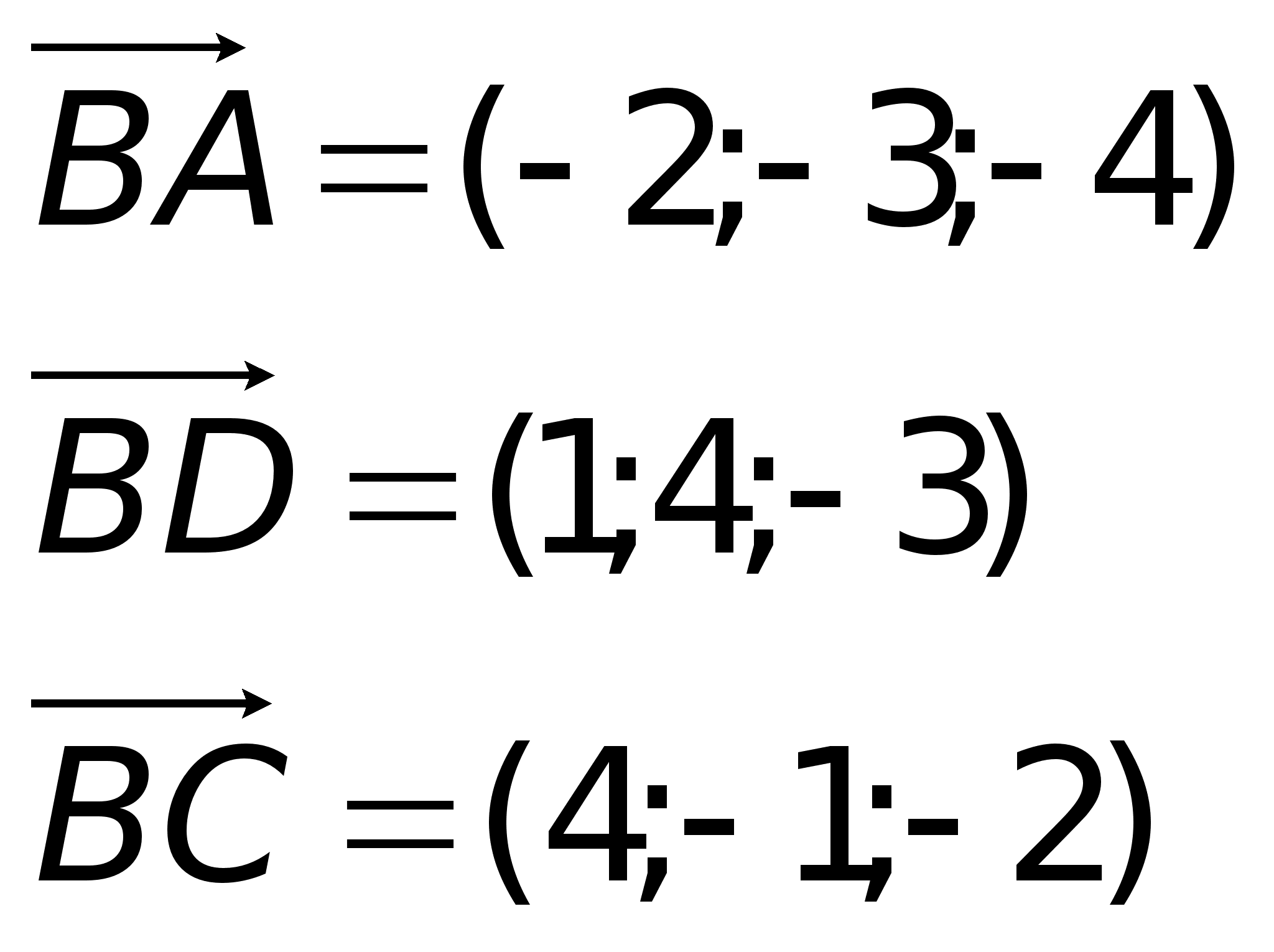 Объем
пирамиды
Объем
пирамиды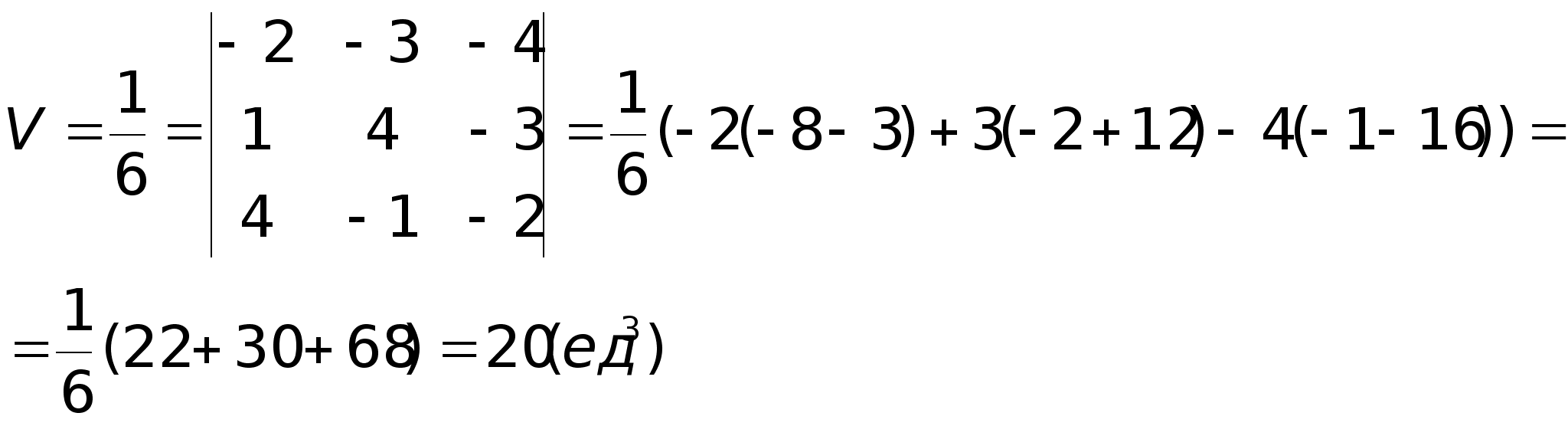
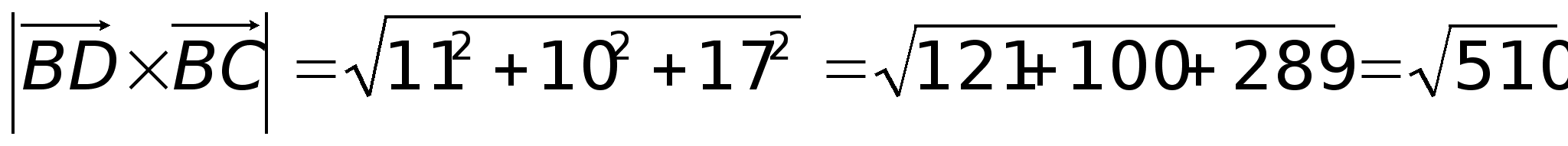
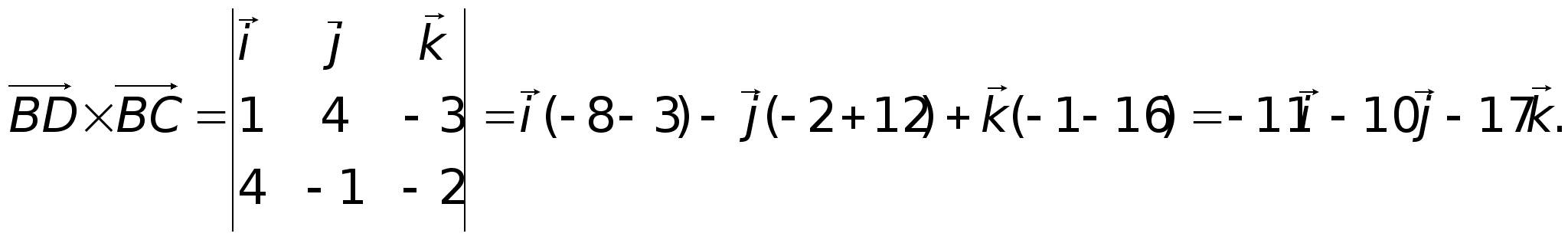
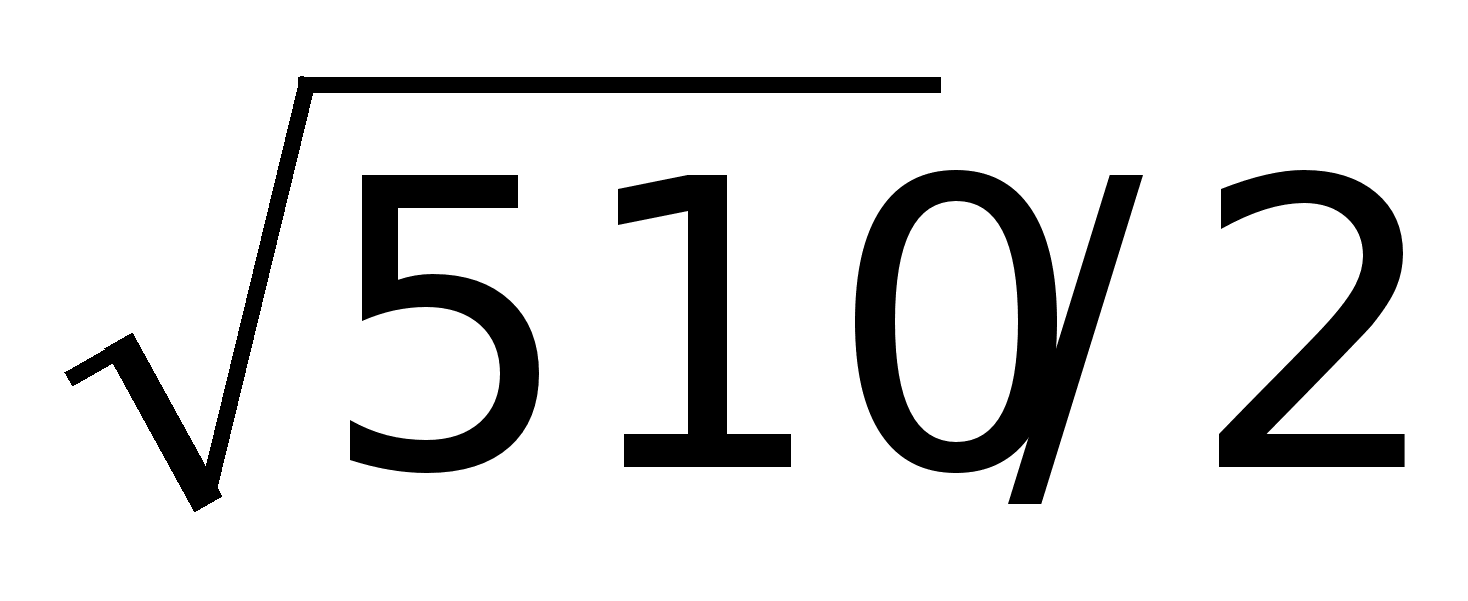 (ед2)Т.к.
V
=
(ед2)Т.к.
V
=
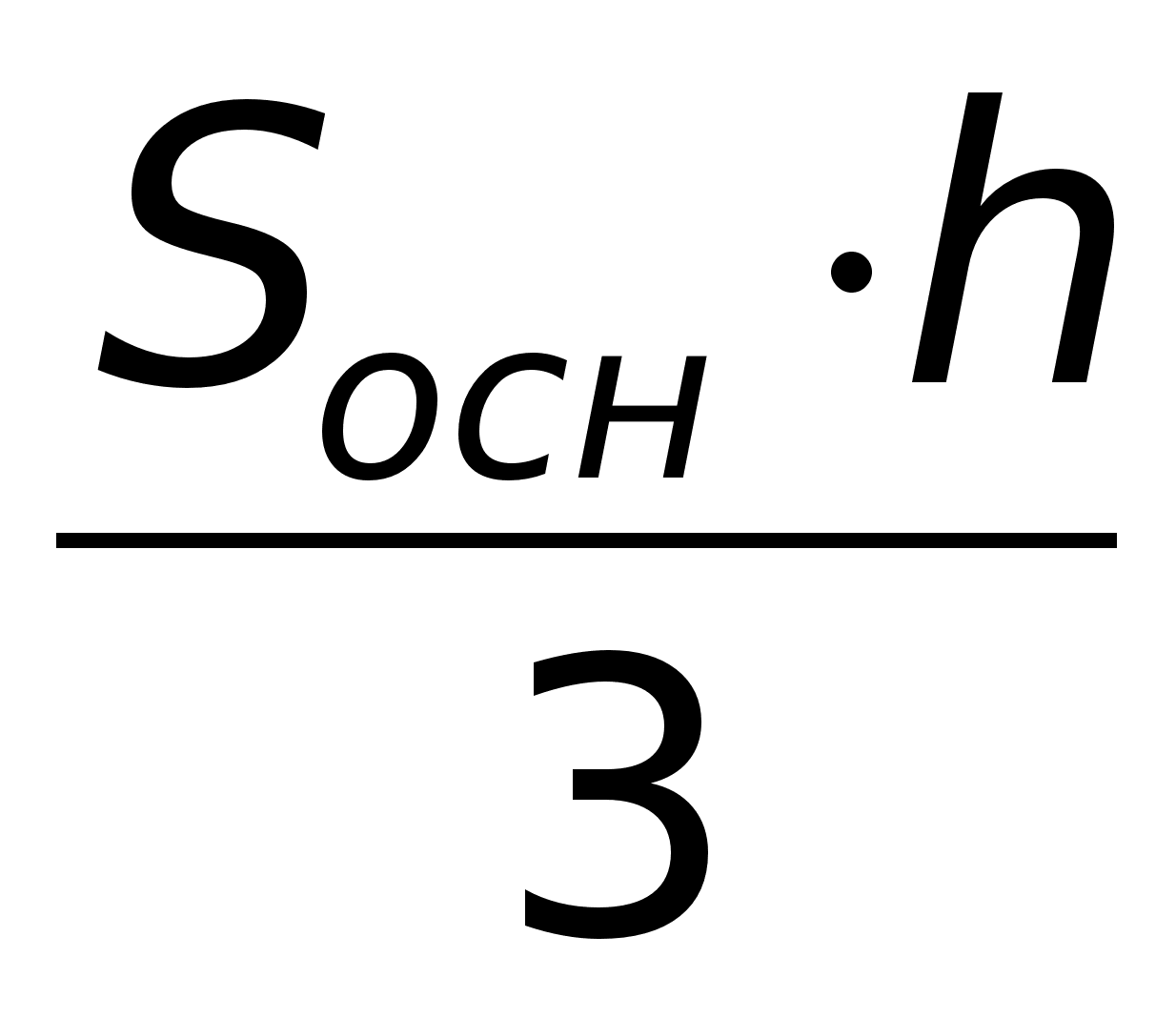 ;
(ед)
;
(ед)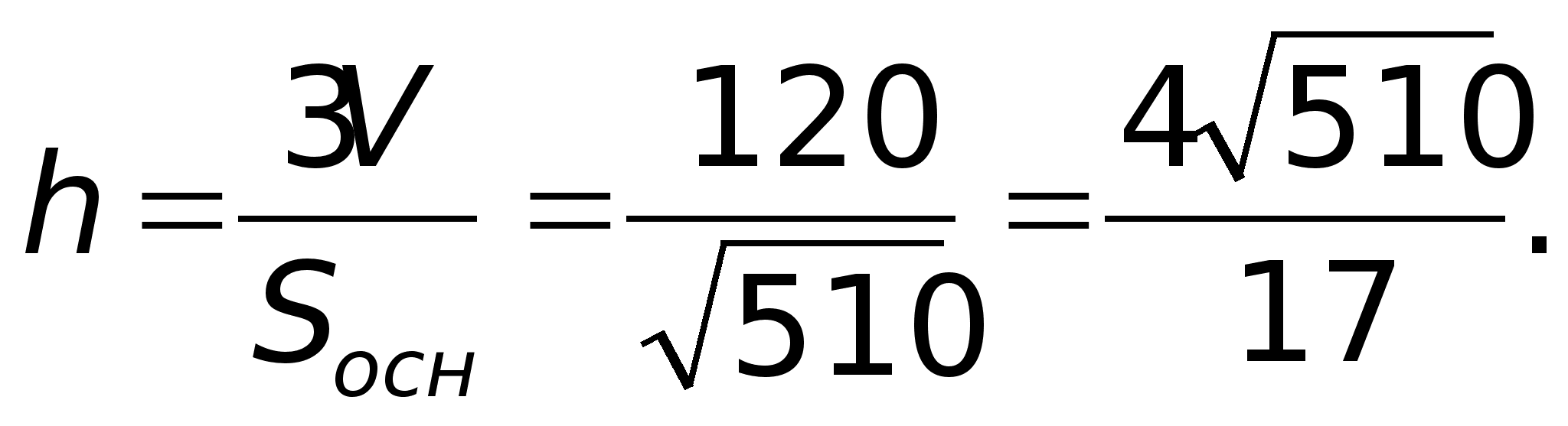

 +
D
= 0, где
+
D
= 0, где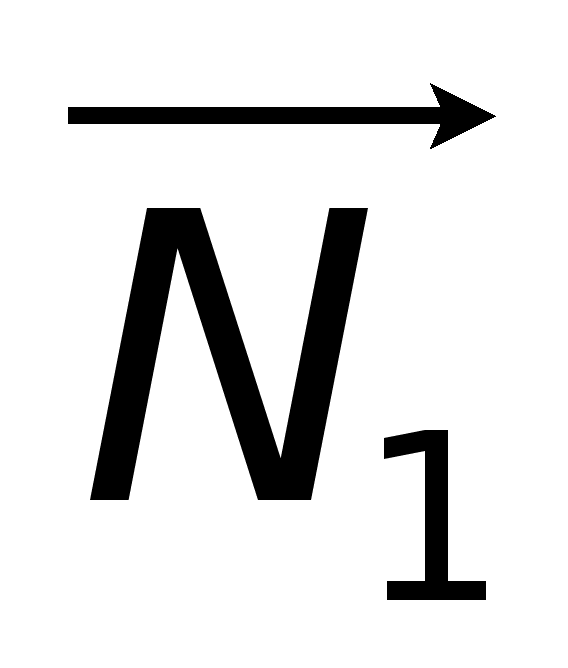
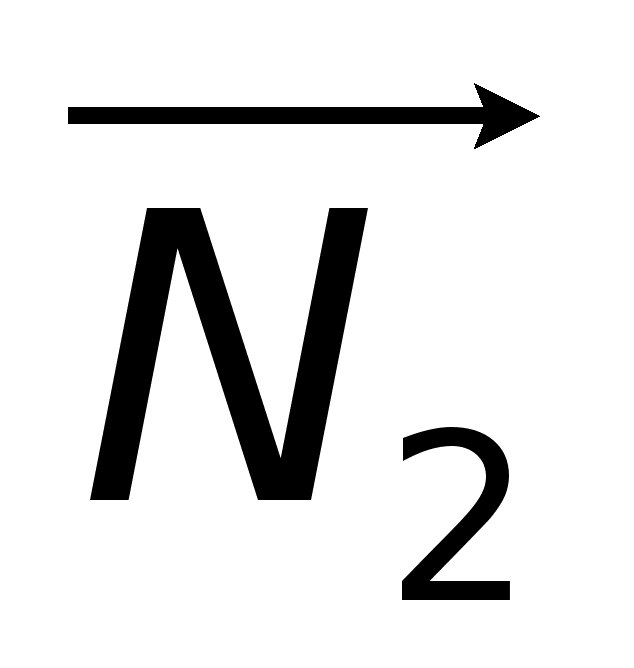
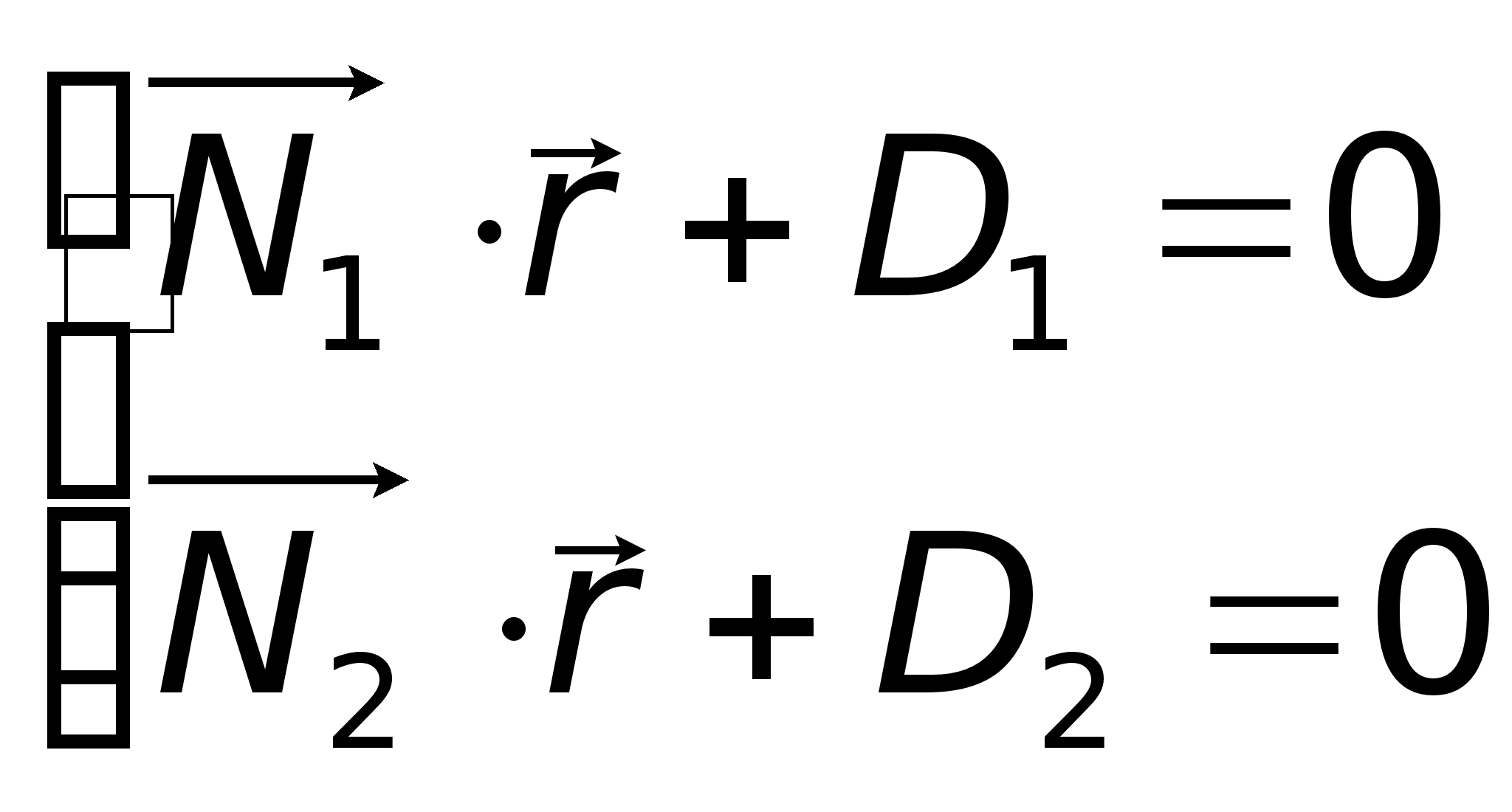 Общие
уравнения
прямой в координатной
форме:
Общие
уравнения
прямой в координатной
форме: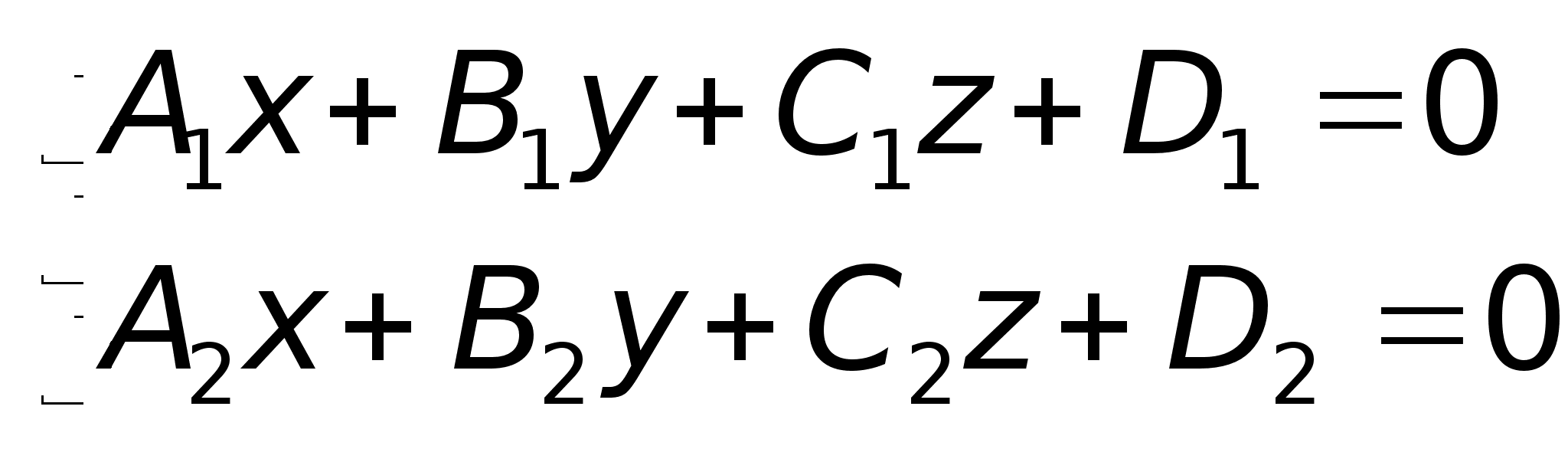 Практическая
задача часто
состоит в
приведении
уравнений
прямых в общем
виде к каноническому
виду.Для этого
надо найти
произвольную
точку прямой
и числа m,
n,
p.При
этом направляющий
вектор прямой
может быть
найден как
векторное
произведение
векторов нормали
к заданным
плоскостям.
Практическая
задача часто
состоит в
приведении
уравнений
прямых в общем
виде к каноническому
виду.Для этого
надо найти
произвольную
точку прямой
и числа m,
n,
p.При
этом направляющий
вектор прямой
может быть
найден как
векторное
произведение
векторов нормали
к заданным
плоскостям.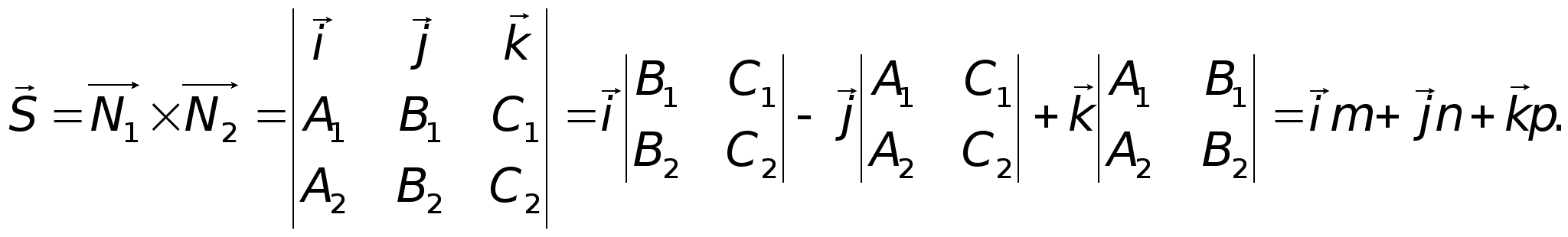 Пример.
Найти каноническое
уравнение,
если прямая
задана в виде:
Пример.
Найти каноническое
уравнение,
если прямая
задана в виде: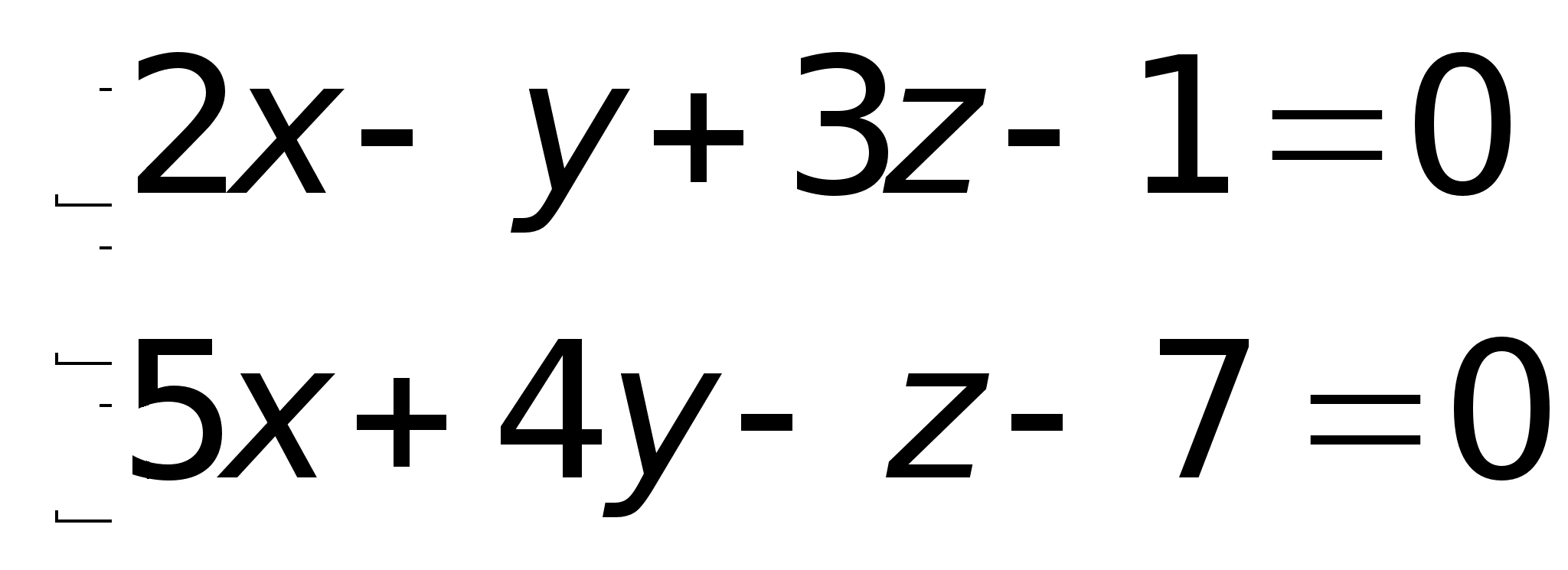 Для
нахождения
произвольной
точки прямой,
примем ее
координату
х = 0, а затем подставим
это значение
в заданную
систему уравнений.
Для
нахождения
произвольной
точки прямой,
примем ее
координату
х = 0, а затем подставим
это значение
в заданную
систему уравнений.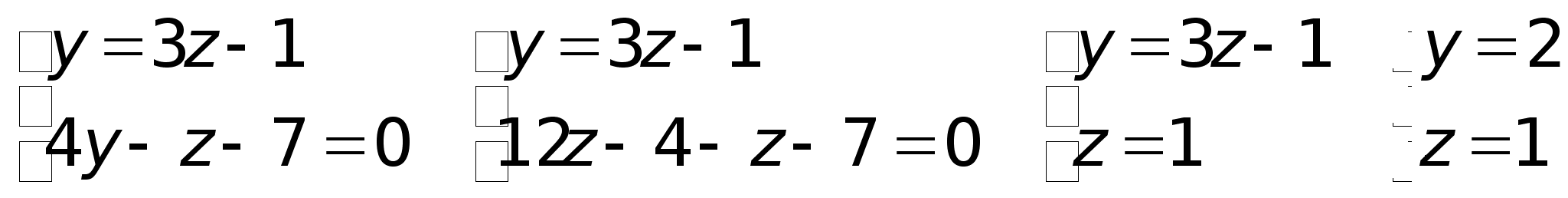 ,
т.е. А(0, 2, 1).Находим
компоненты
направляющего
вектора прямой.
,
т.е. А(0, 2, 1).Находим
компоненты
направляющего
вектора прямой.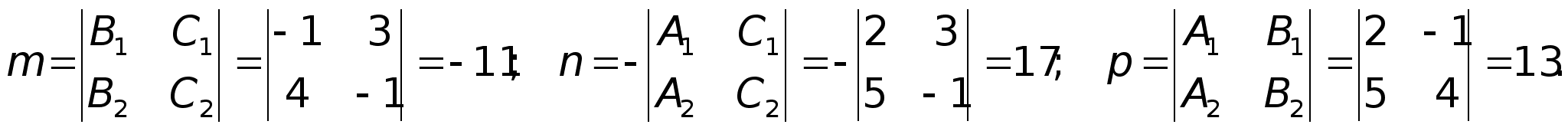 Тогда
канонические
уравнения
прямой:
Тогда
канонические
уравнения
прямой: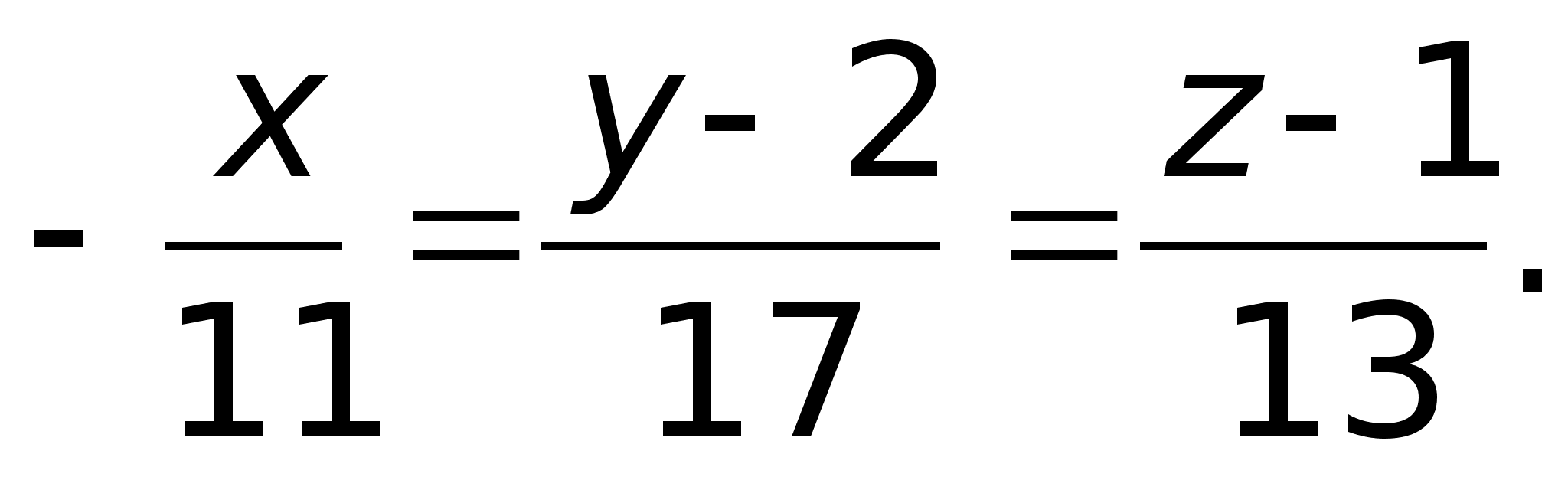 Пример.
Привести к
каноническому
виду уравнение
прямой, заданное
в виде:
Пример.
Привести к
каноническому
виду уравнение
прямой, заданное
в виде: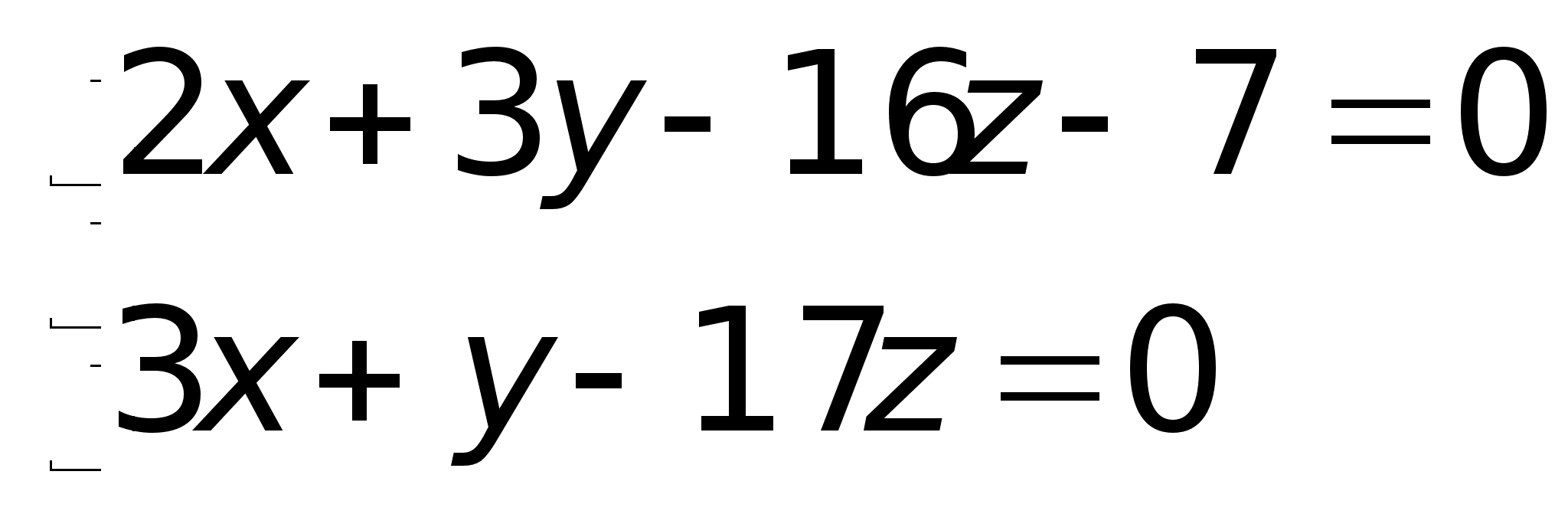 Для
нахождения
произвольной
точки прямой,
являющейся
линией пересечения
указанных
выше плоскостей,
примем z
= 0. Тогда:
Для
нахождения
произвольной
точки прямой,
являющейся
линией пересечения
указанных
выше плоскостей,
примем z
= 0. Тогда: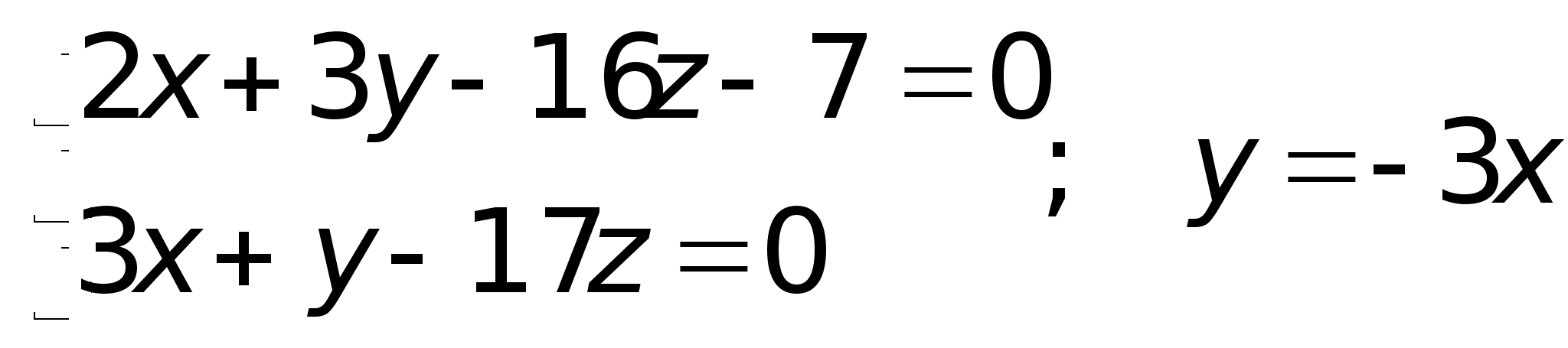 ;2x
– 9x
– 7 = 0; x
= -1; y
= 3; Получаем:
A(-1;
3; 0).Направляющий
вектор прямой:
;2x
– 9x
– 7 = 0; x
= -1; y
= 3; Получаем:
A(-1;
3; 0).Направляющий
вектор прямой:
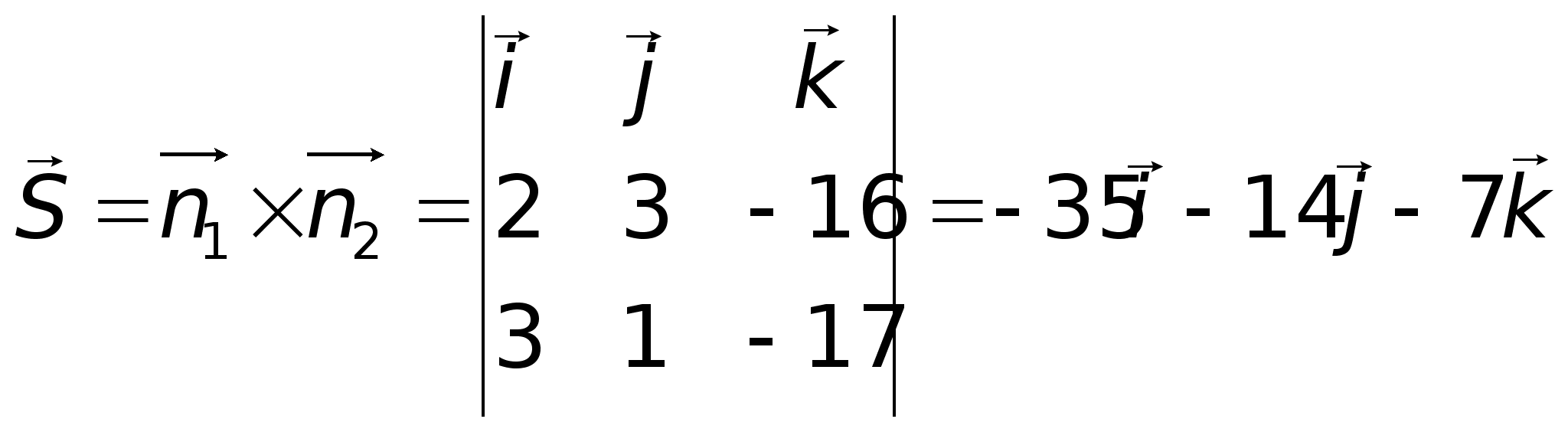 .Итого:
.Итого:
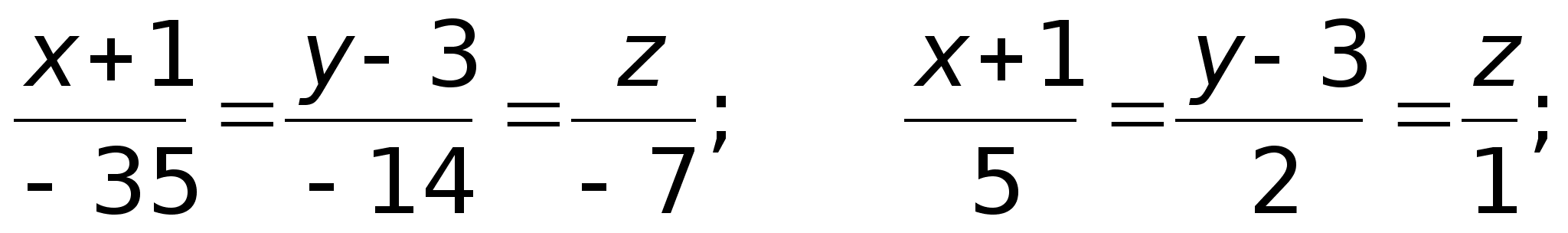
 ||
|| ).
).
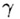 пересекаются
по прямой a, a
пересекаются
по прямой a, a
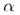 ,
а прямая с
пересекает
,
а прямая с
пересекает
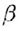 указана
прямая a1
|| b).
указана
прямая a1
|| b).
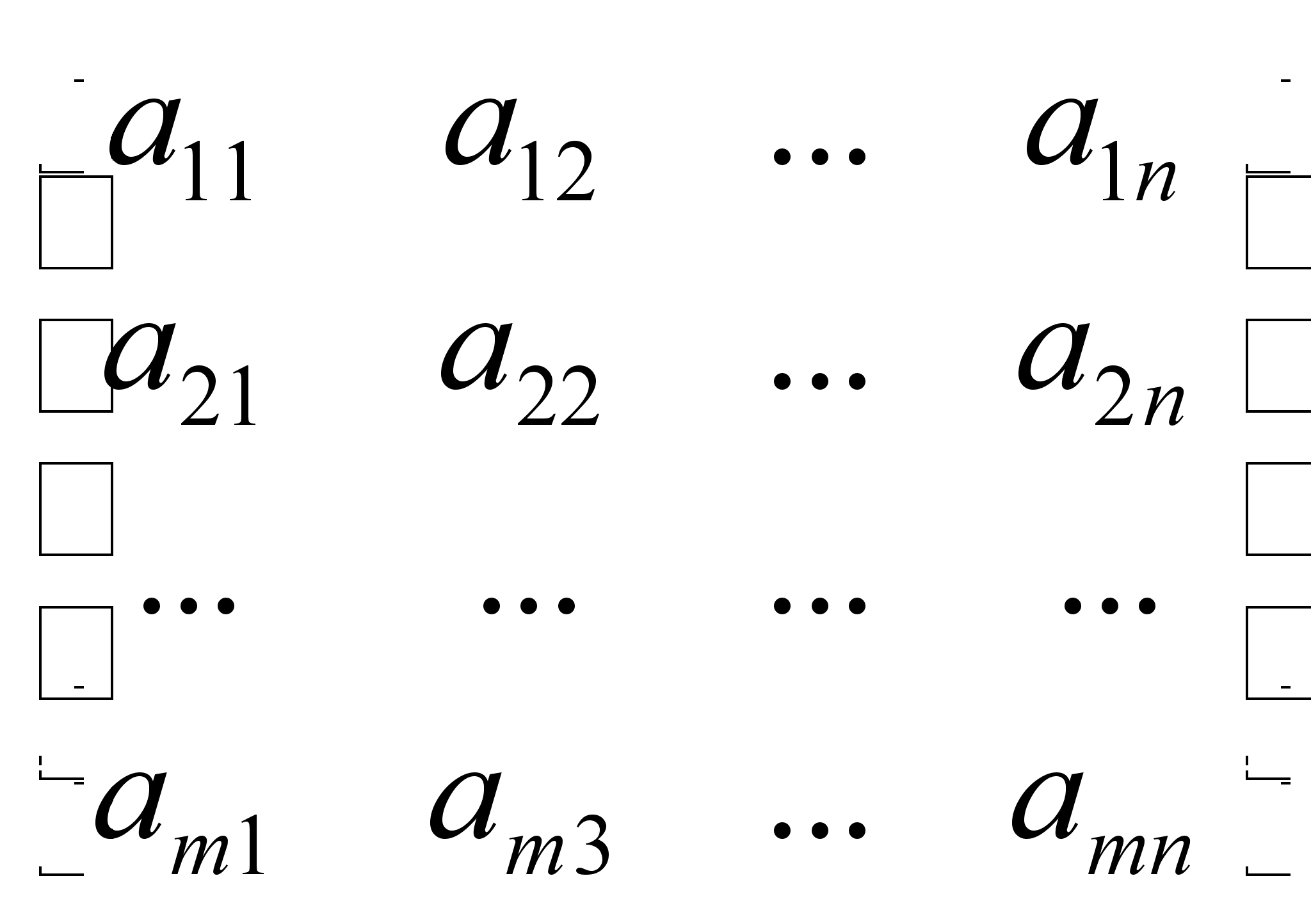 Основные действия
над матрицами.Матрица
может состоять
как из одной
строки, так
и из одного
столбца. Вообще
говоря, матрица
может состоять
даже из одного
элемента.Определение.
Если число
столбцов матрицы
равно числу
строк (m=n), то матрица
называется
квадратной.Определение.
Матрица вида:
Основные действия
над матрицами.Матрица
может состоять
как из одной
строки, так
и из одного
столбца. Вообще
говоря, матрица
может состоять
даже из одного
элемента.Определение.
Если число
столбцов матрицы
равно числу
строк (m=n), то матрица
называется
квадратной.Определение.
Матрица вида: =
E,называется
единичной
матрицей.Определение.
Если amn
= anm
, то
матрица называется
симметрической.Пример.
=
E,называется
единичной
матрицей.Определение.
Если amn
= anm
, то
матрица называется
симметрической.Пример. -
симметрическая
матрицаОпределение.
Квадратная
матрица вида
-
симметрическая
матрицаОпределение.
Квадратная
матрица вида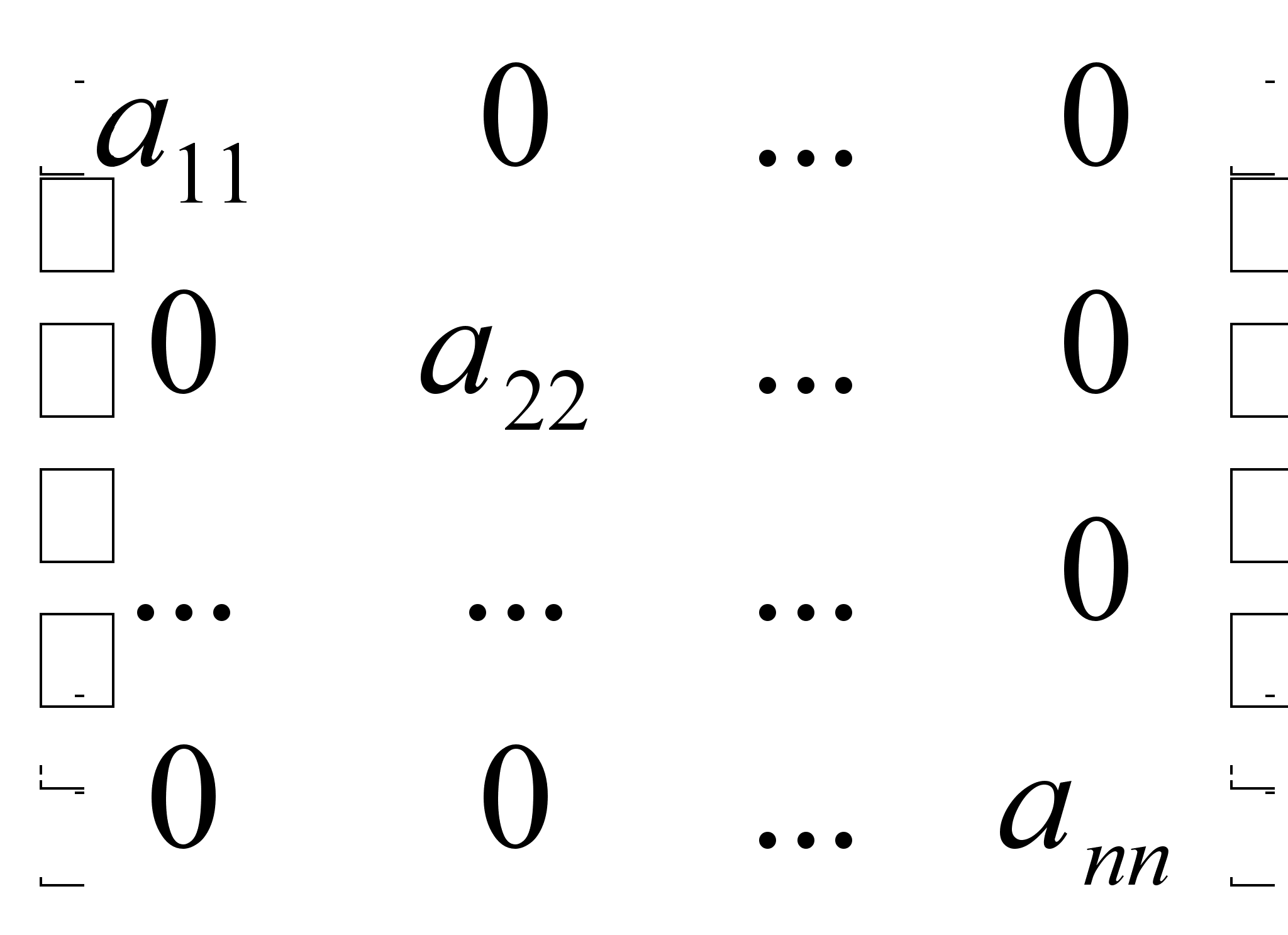 называется
диагональной
матрицей.
Сложение
и вычитание
матриц сводится
к соответствующим
операциям
над их элементами.
Самым главным
свойством
этих операций
является то,
что они определены
только для
матриц одинакового
размера. Таким
образом, возможно
определить
операции сложения
и вычитания
матриц:Определение.Суммой
(разностью)
матриц является
матрица, элементами
которой являются
соответственно
сумма (разность)
элементов
исходных
матриц.cij
= aij
называется
диагональной
матрицей.
Сложение
и вычитание
матриц сводится
к соответствующим
операциям
над их элементами.
Самым главным
свойством
этих операций
является то,
что они определены
только для
матриц одинакового
размера. Таким
образом, возможно
определить
операции сложения
и вычитания
матриц:Определение.Суммой
(разностью)
матриц является
матрица, элементами
которой являются
соответственно
сумма (разность)
элементов
исходных
матриц.cij
= aij
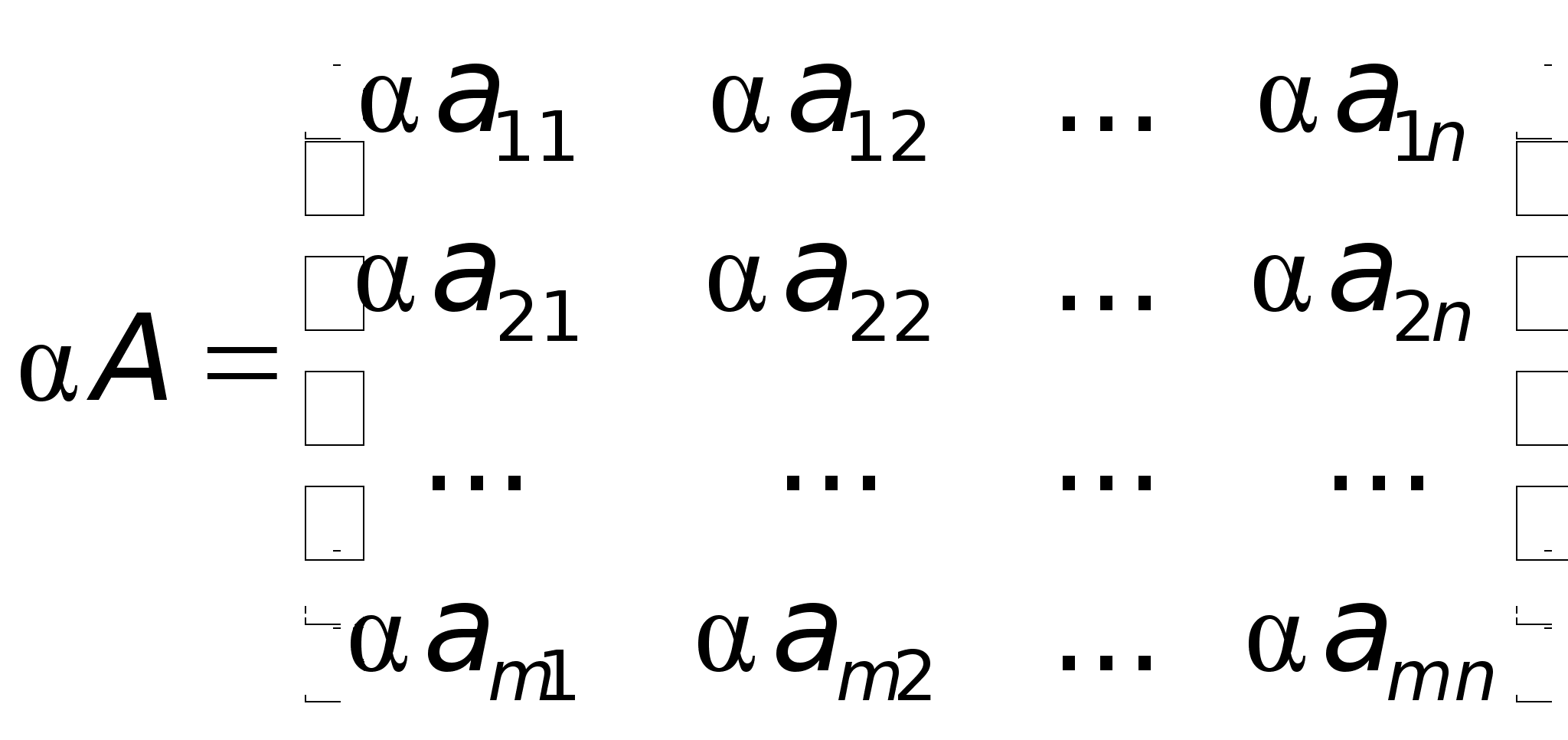
 ;
B
=
;
B
=
 ,
найти 2А + В.2А =
,
найти 2А + В.2А =
 ,
2А + В =
,
2А + В =
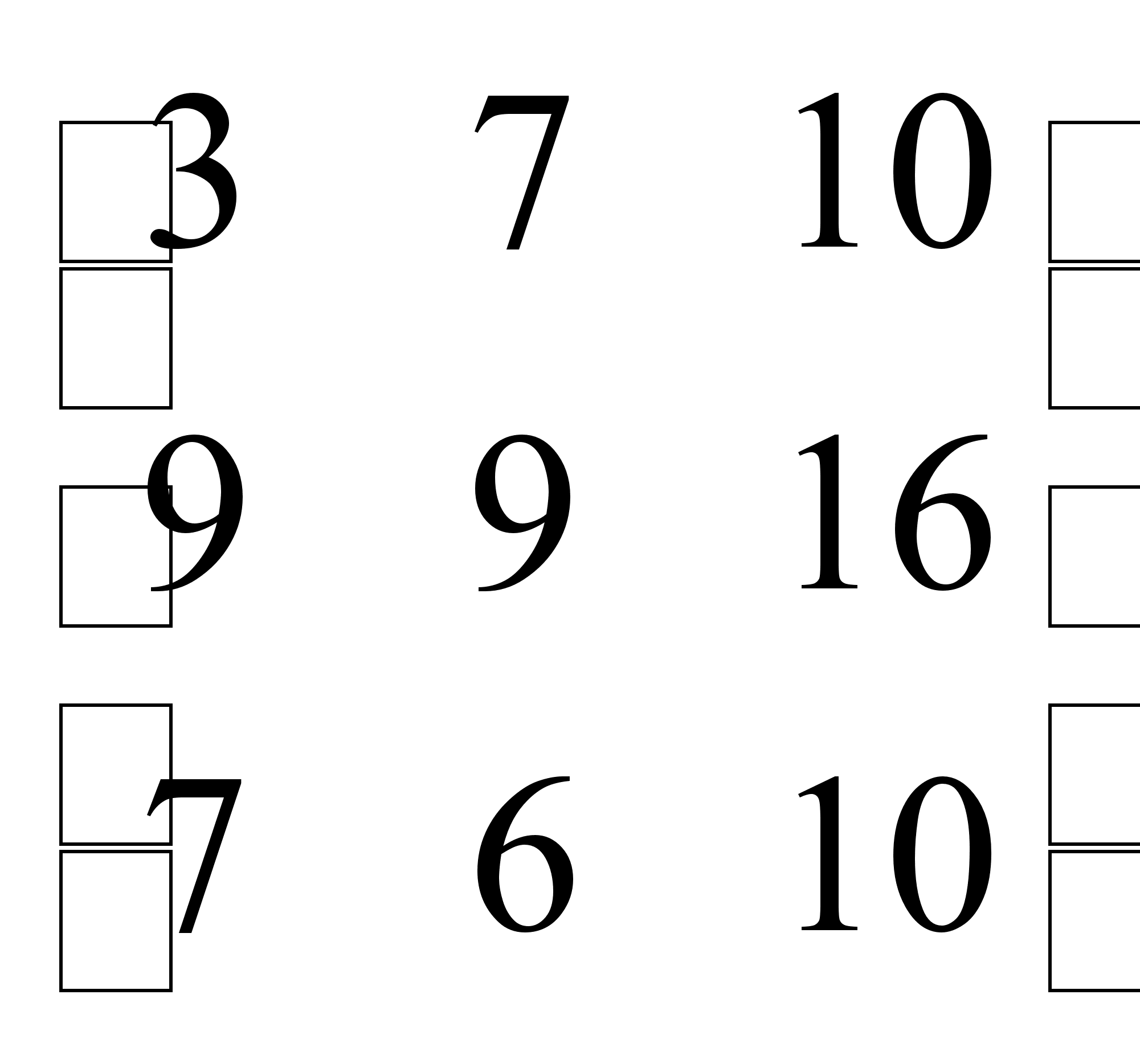 .
. пределение.
Эллипсом
называется
линия, заданная
уравнением
пределение.
Эллипсом
называется
линия, заданная
уравнением
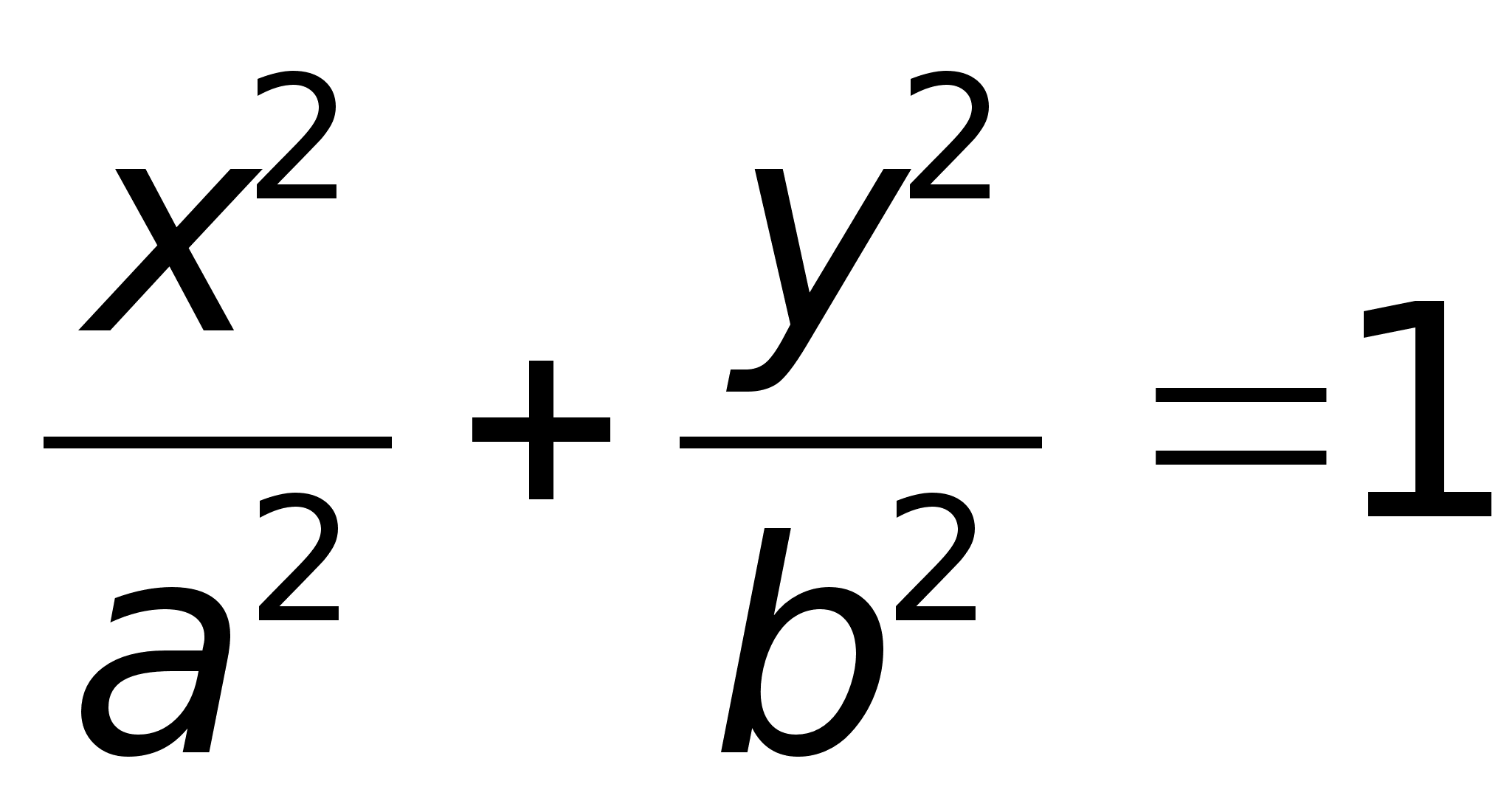 .Определение.
Фокусами
называются
такие две точки,
сумма расстояний
от которых
до любой точки
эллипса есть
постоянная
величина.
.Определение.
Фокусами
называются
такие две точки,
сумма расстояний
от которых
до любой точки
эллипса есть
постоянная
величина.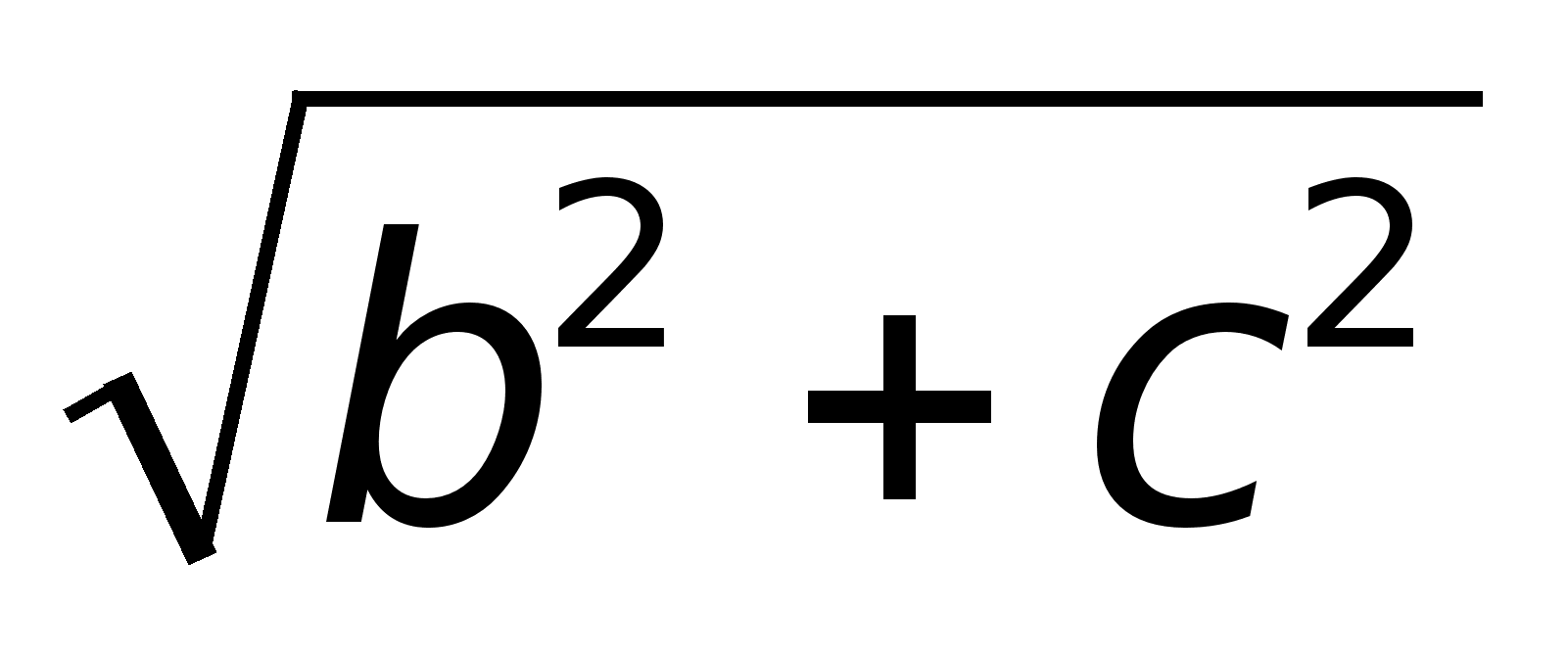 (по
теореме Пифагора).
В случае, если
точка М находится
на пересечении
эллипса с
горизонтальной
осью, r1
+ r2
= a
– c
+ a
+ c.
Т.к. по определению
сумма r1
+ r2
– постоянная
величина, то
, приравнивая,
получаем:a2
= b2
+ c2
r1
+ r2
= 2a.
Определение.
Форма эллипса
определяется
характеристикой,
которая является
отношением
фокусного
расстояния
к большей оси
и называется
эксцентриситетом.Е
= с/a.
Т.к. с Определение.
Величина k
= b/a
называется
коэффициентом
сжатия эллипса,
а величина 1
– k
= (a
– b)/a
называется
сжатием
эллипса.Коэффициент
сжатия и эксцентриситет
связаны соотношением:
k2
= 1 – e2.Если
a
= b
(c
= 0, e
= 0, фокусы сливаются),
то эллипс
превращается
в окружность.Если
для точки М(х1,
у1)
выполняется
условие:
(по
теореме Пифагора).
В случае, если
точка М находится
на пересечении
эллипса с
горизонтальной
осью, r1
+ r2
= a
– c
+ a
+ c.
Т.к. по определению
сумма r1
+ r2
– постоянная
величина, то
, приравнивая,
получаем:a2
= b2
+ c2
r1
+ r2
= 2a.
Определение.
Форма эллипса
определяется
характеристикой,
которая является
отношением
фокусного
расстояния
к большей оси
и называется
эксцентриситетом.Е
= с/a.
Т.к. с Определение.
Величина k
= b/a
называется
коэффициентом
сжатия эллипса,
а величина 1
– k
= (a
– b)/a
называется
сжатием
эллипса.Коэффициент
сжатия и эксцентриситет
связаны соотношением:
k2
= 1 – e2.Если
a
= b
(c
= 0, e
= 0, фокусы сливаются),
то эллипс
превращается
в окружность.Если
для точки М(х1,
у1)
выполняется
условие:
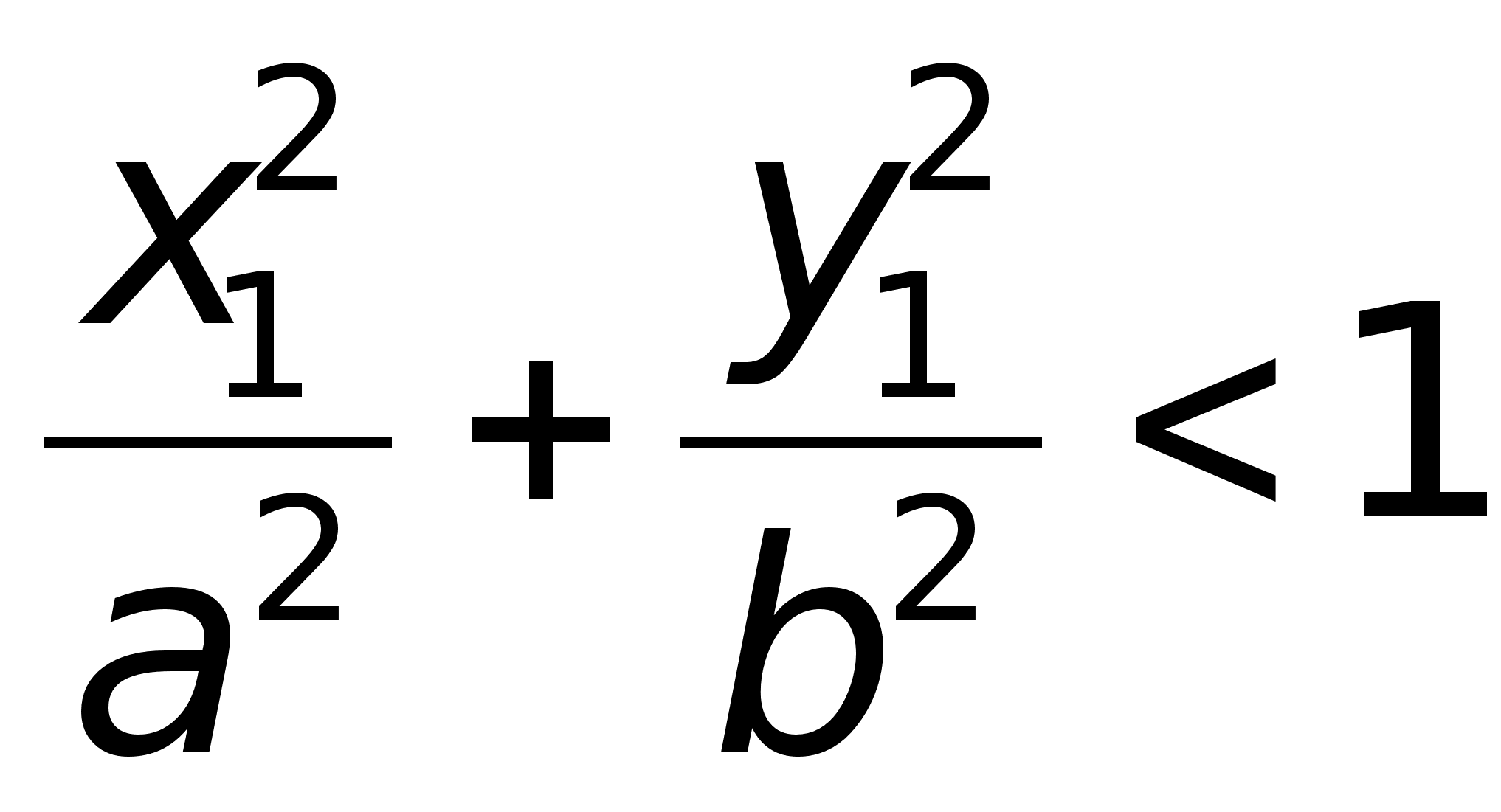 ,
то она находится
внутри эллипса,
а если
,
то она находится
внутри эллипса,
а если
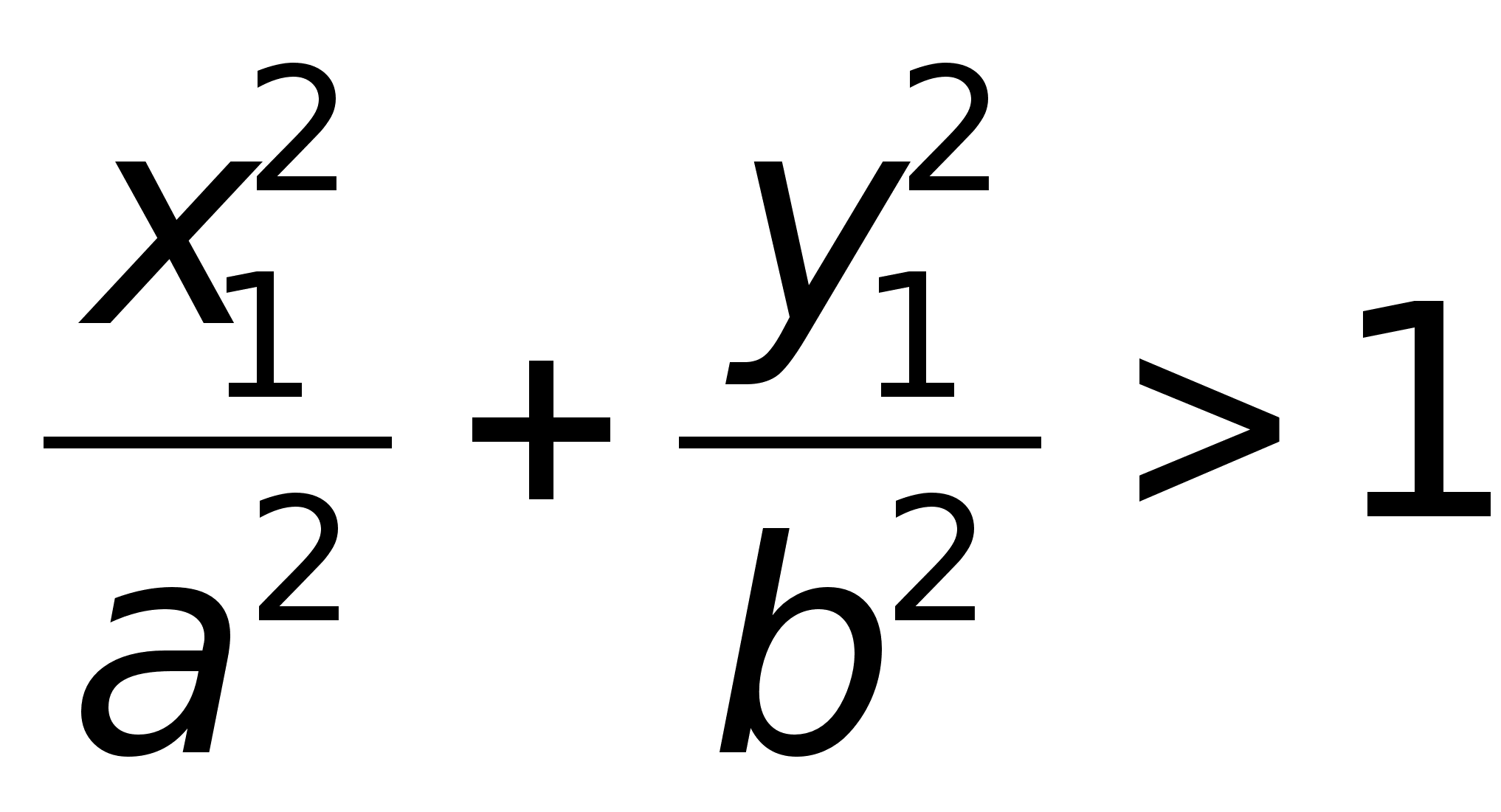 ,
то точка находится
вне эллипса.Теорема.
Для
произвольной
точки М(х, у),
принадлежащей
эллипсу верны
соотношения:r1
= a
– ex,
r2
= a
+ ex.
Доказательство.
Выше было
показано, что
r1
+ r2
= 2a.
Кроме того,
из геометрических
соображений
можно записать:
,
то точка находится
вне эллипса.Теорема.
Для
произвольной
точки М(х, у),
принадлежащей
эллипсу верны
соотношения:r1
= a
– ex,
r2
= a
+ ex.
Доказательство.
Выше было
показано, что
r1
+ r2
= 2a.
Кроме того,
из геометрических
соображений
можно записать: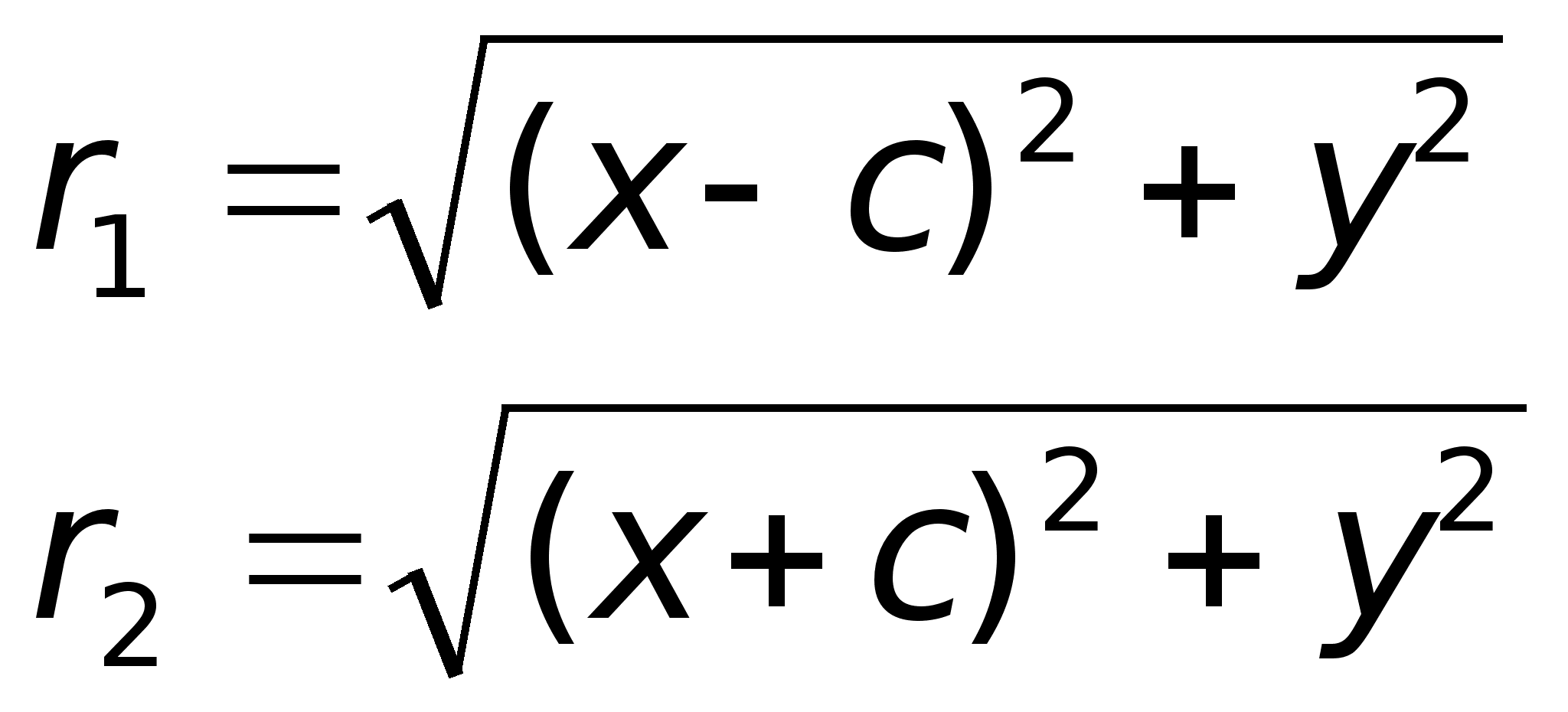
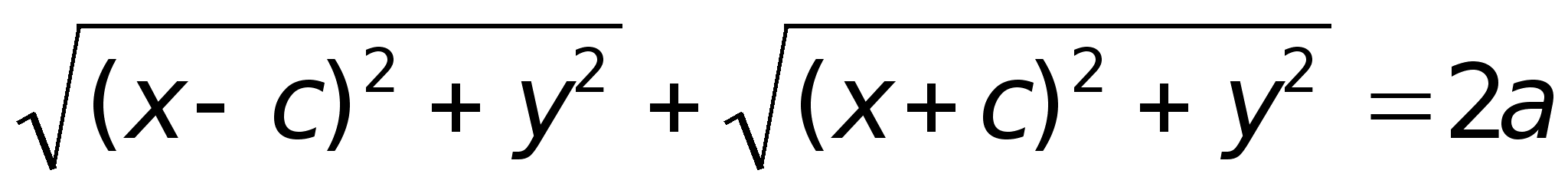 После
возведения
в квадрат и
приведения
подобных
слагаемых:
После
возведения
в квадрат и
приведения
подобных
слагаемых:
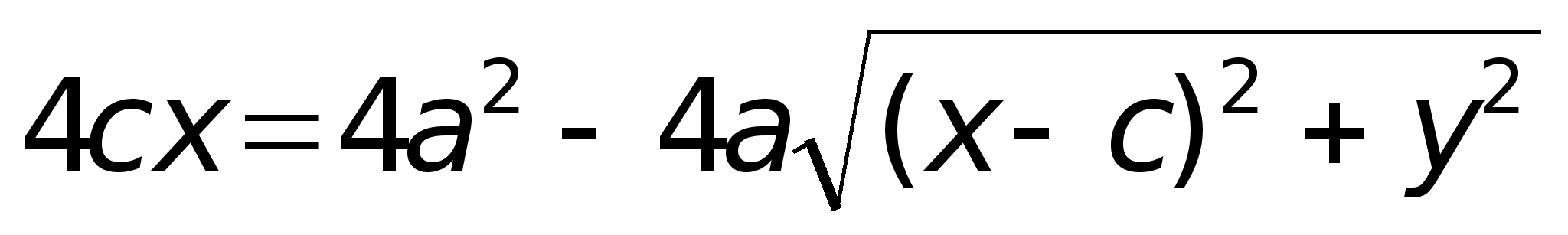
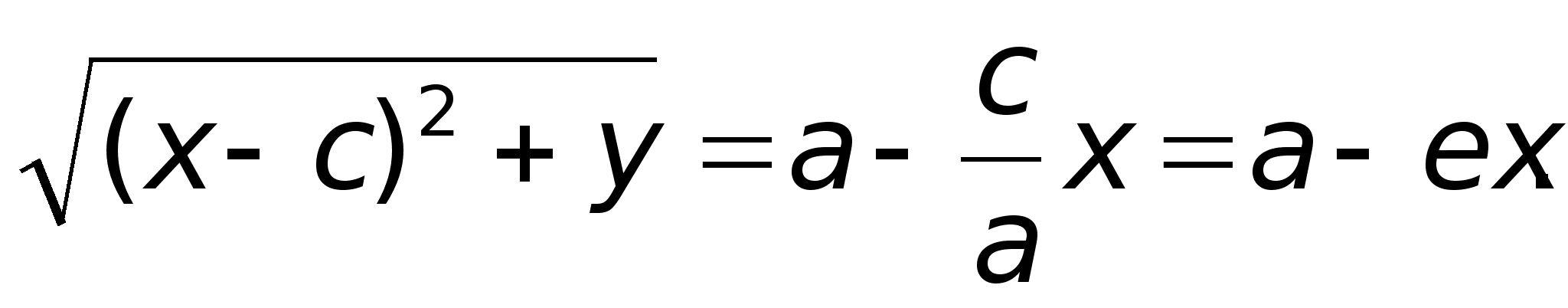 Аналогично
доказывается,
что r2
= a
+ ex.
Теорема
доказана.С
эллипсом связаны
две прямые,
называемые
директрисами.
Их уравнения:
x
= a/e;
x
= -a/e.Теорема.
Для
того, чтобы
точка лежала
на эллипсе,
необходимо
и достаточно,
чтобы отношение
расстояния
до фокуса к
расстоянию
до соответствующей
директрисы
равнялось
эксцентриситету
е.Пример.
Составить
уравнение
прямой, проходящей
через левый
фокус и нижнюю
вершину эллипса,
заданного
уравнением:
Аналогично
доказывается,
что r2
= a
+ ex.
Теорема
доказана.С
эллипсом связаны
две прямые,
называемые
директрисами.
Их уравнения:
x
= a/e;
x
= -a/e.Теорема.
Для
того, чтобы
точка лежала
на эллипсе,
необходимо
и достаточно,
чтобы отношение
расстояния
до фокуса к
расстоянию
до соответствующей
директрисы
равнялось
эксцентриситету
е.Пример.
Составить
уравнение
прямой, проходящей
через левый
фокус и нижнюю
вершину эллипса,
заданного
уравнением:
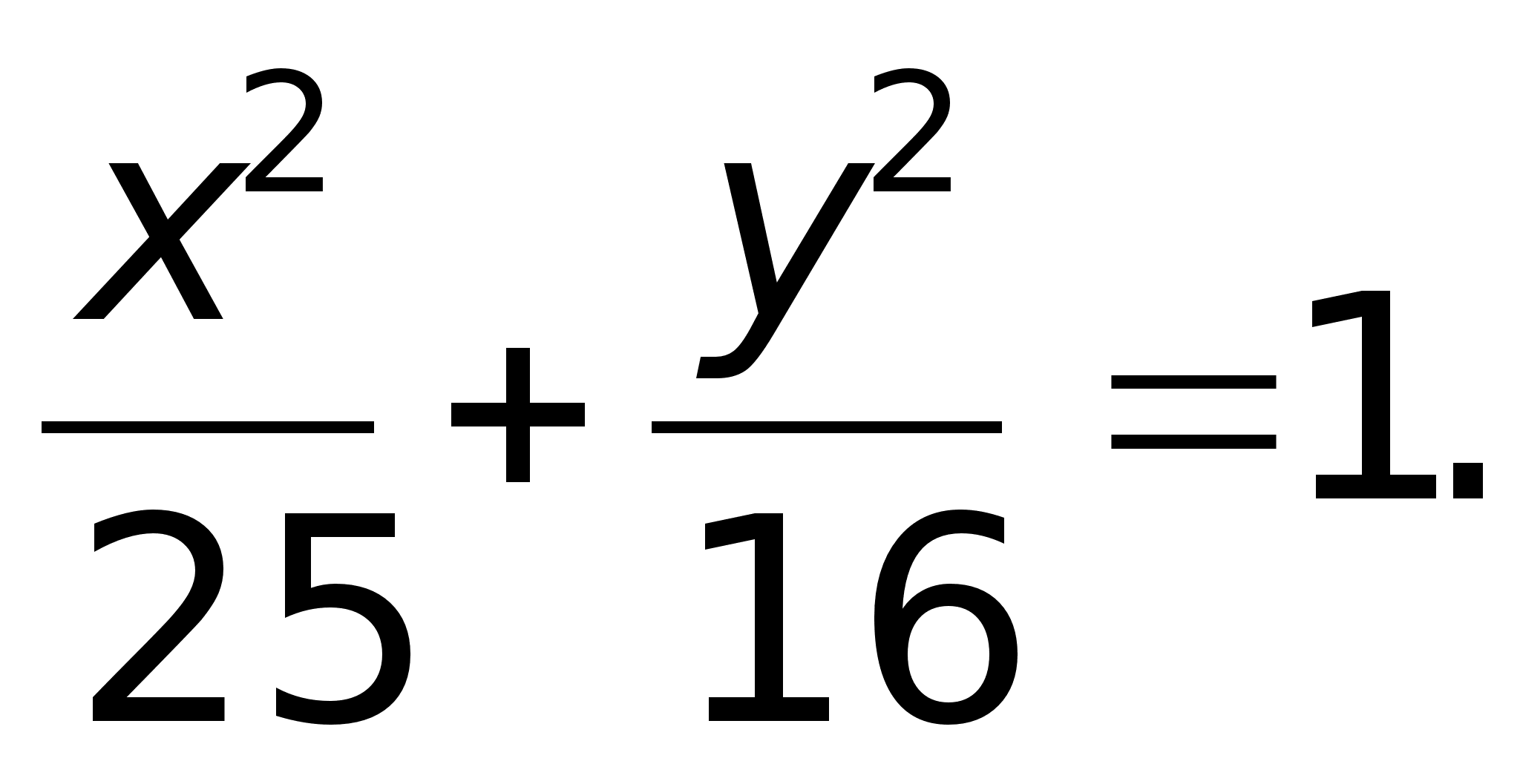 Координаты
нижней вершины:
x
= 0; y2
= 16; y
= -4. Координаты
левого фокуса:
c2
= a2
– b2
= 25 – 16 = 9; c
= 3; F2(-3;
0). Уравнение
прямой, проходящей
через две точки:
Координаты
нижней вершины:
x
= 0; y2
= 16; y
= -4. Координаты
левого фокуса:
c2
= a2
– b2
= 25 – 16 = 9; c
= 3; F2(-3;
0). Уравнение
прямой, проходящей
через две точки:
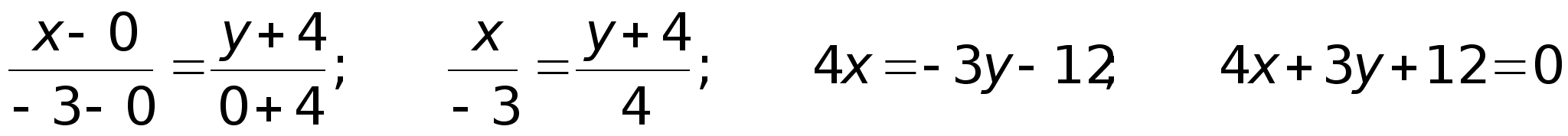 Пример.
Составить
уравнение
эллипса, если
его фокусы
F1(0;
0), F2(1;
1), большая ось
равна 2.Уравнение
эллипса имеет
вид:
Пример.
Составить
уравнение
эллипса, если
его фокусы
F1(0;
0), F2(1;
1), большая ось
равна 2.Уравнение
эллипса имеет
вид:
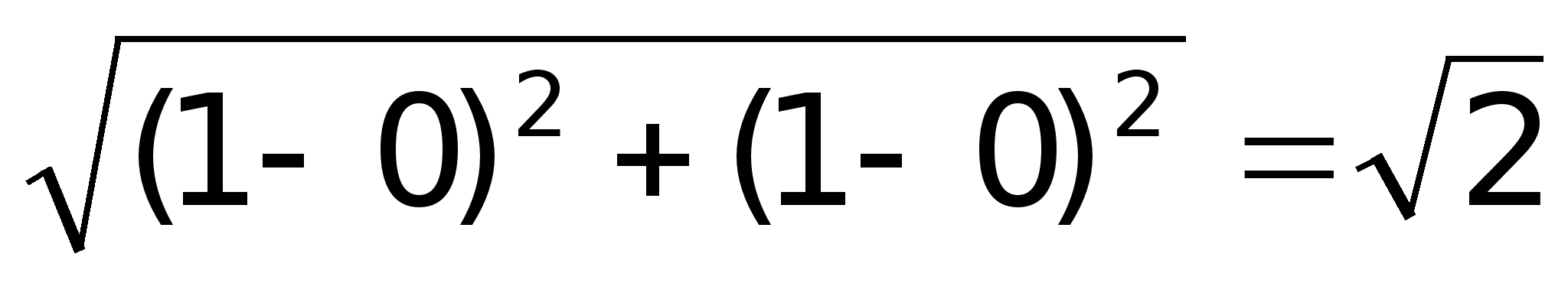 ,
таким образом,
a2
– b2
= c2
= Ѕпо условию
2а = 2, следовательно
а = 1, b
=
,
таким образом,
a2
– b2
= c2
= Ѕпо условию
2а = 2, следовательно
а = 1, b
=
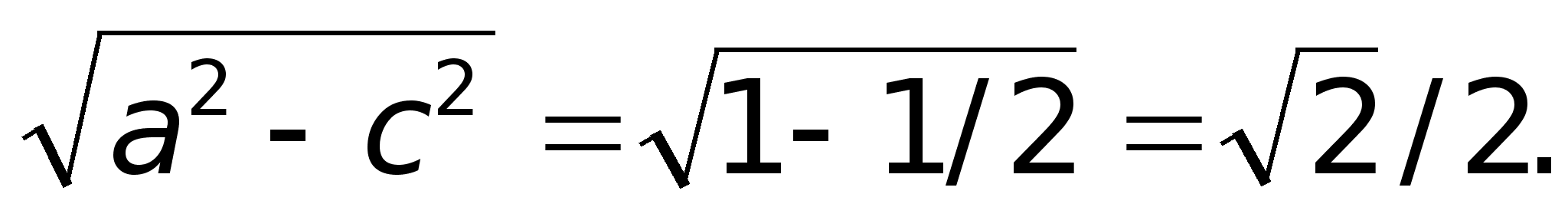 Итого:
Итого:
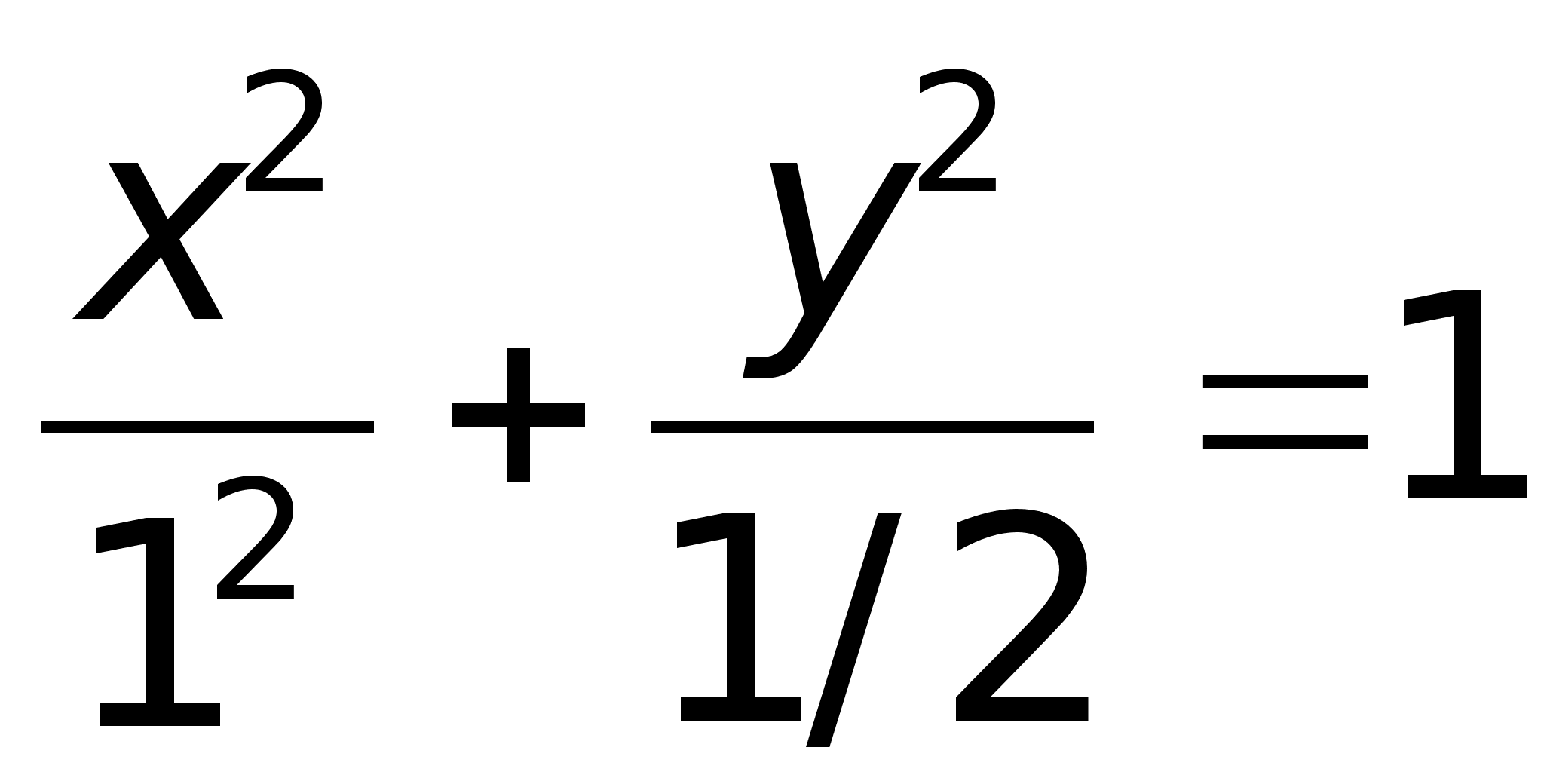 .
.
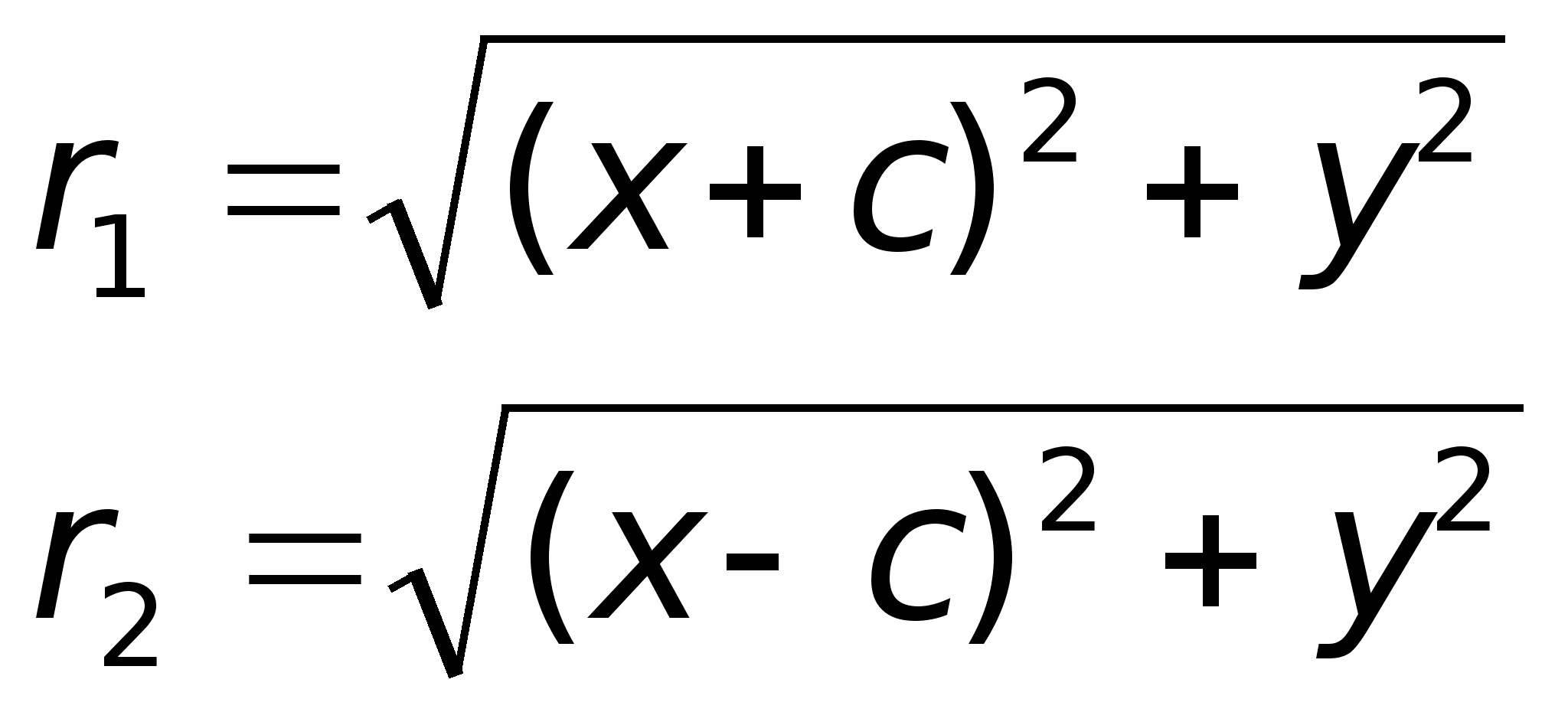
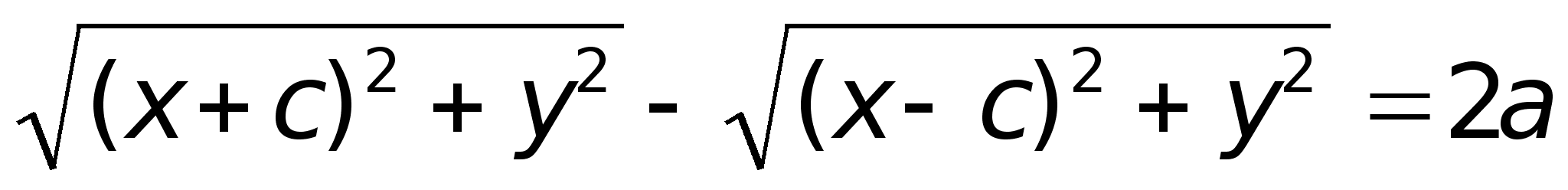
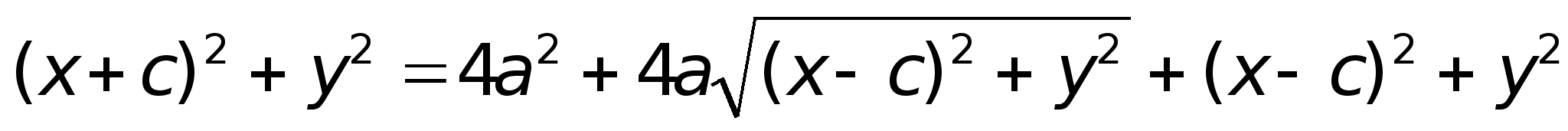
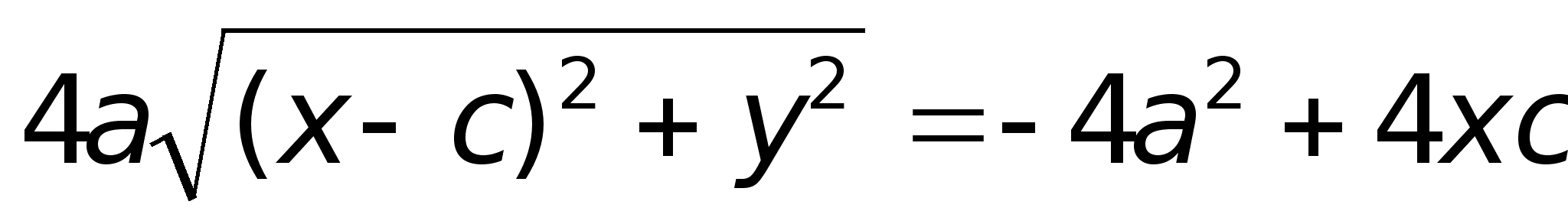
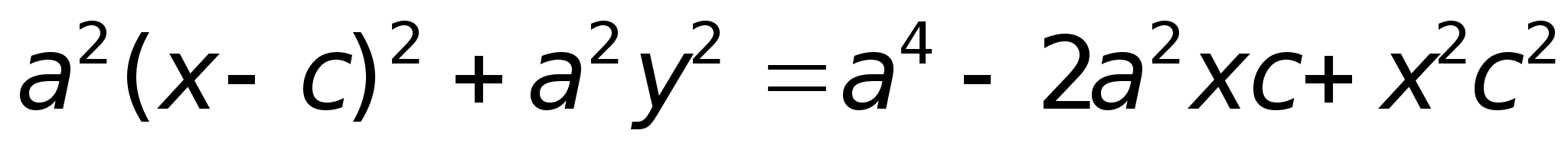
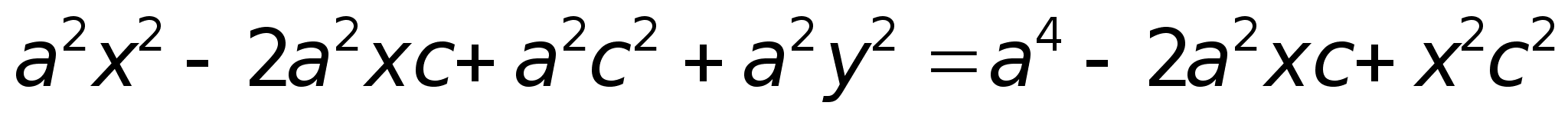
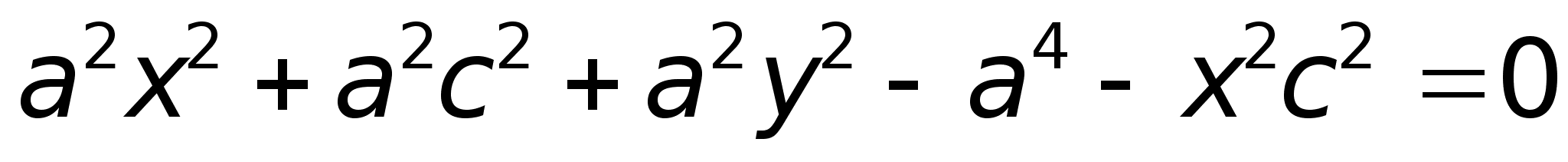
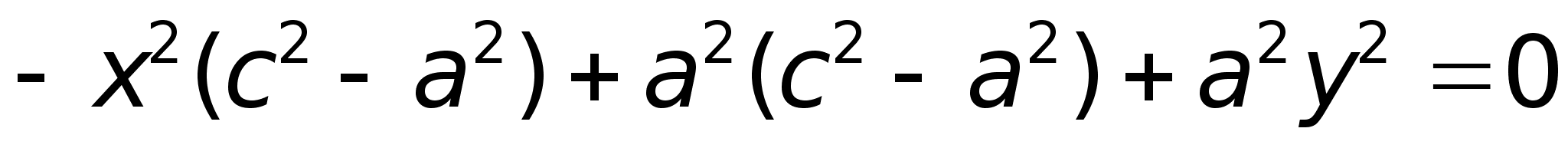
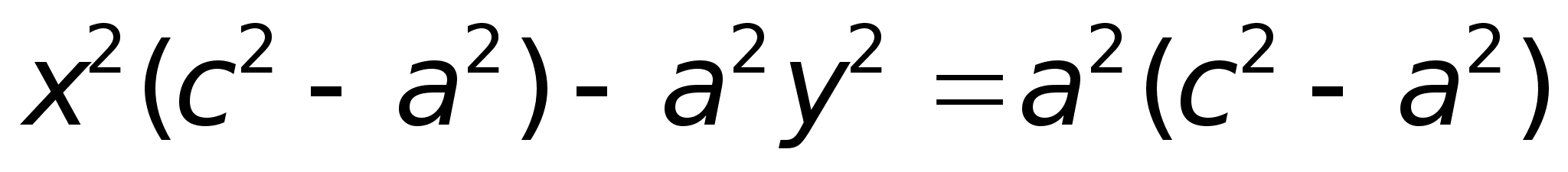
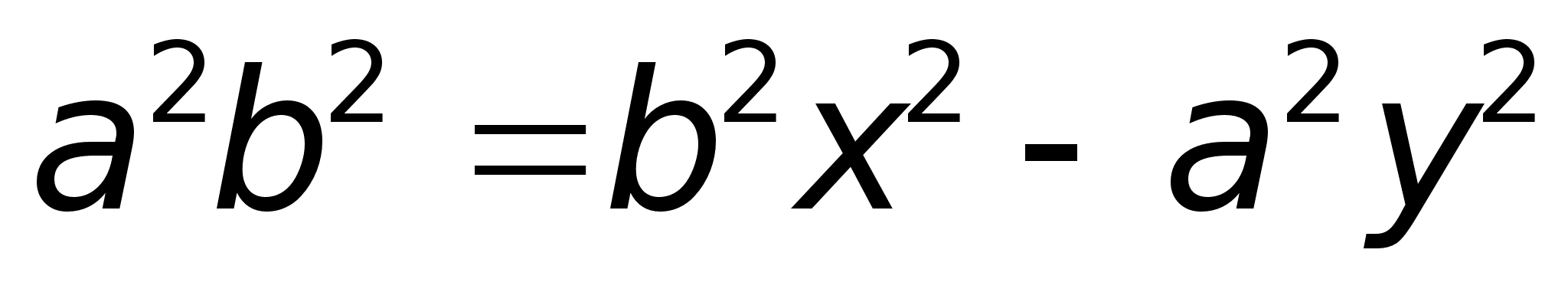
 Получили
каноническое
уравнение
гиперболы.Гипербола
симметрична
относительно
середины отрезка,
соединяющего
фокусы и относительно
осей координат.Ось
2а называется
действительной
осью гиперболы.Ось
2b
называется
мнимой осью
гиперболы.Гипербола
имеет две
асимптоты,
уравнения
которых
Получили
каноническое
уравнение
гиперболы.Гипербола
симметрична
относительно
середины отрезка,
соединяющего
фокусы и относительно
осей координат.Ось
2а называется
действительной
осью гиперболы.Ось
2b
называется
мнимой осью
гиперболы.Гипербола
имеет две
асимптоты,
уравнения
которых
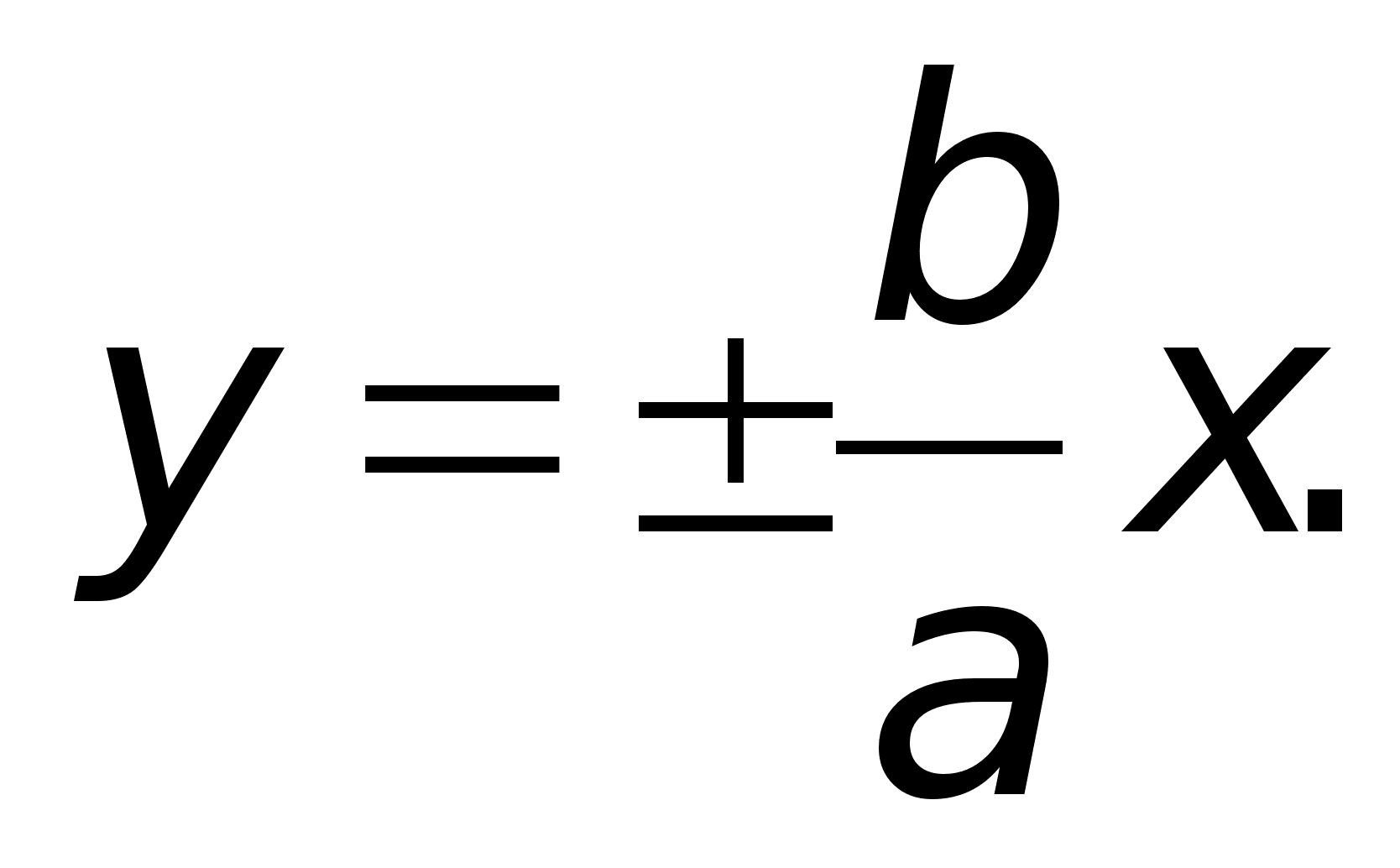 Определение.
Отношение
Определение.
Отношение
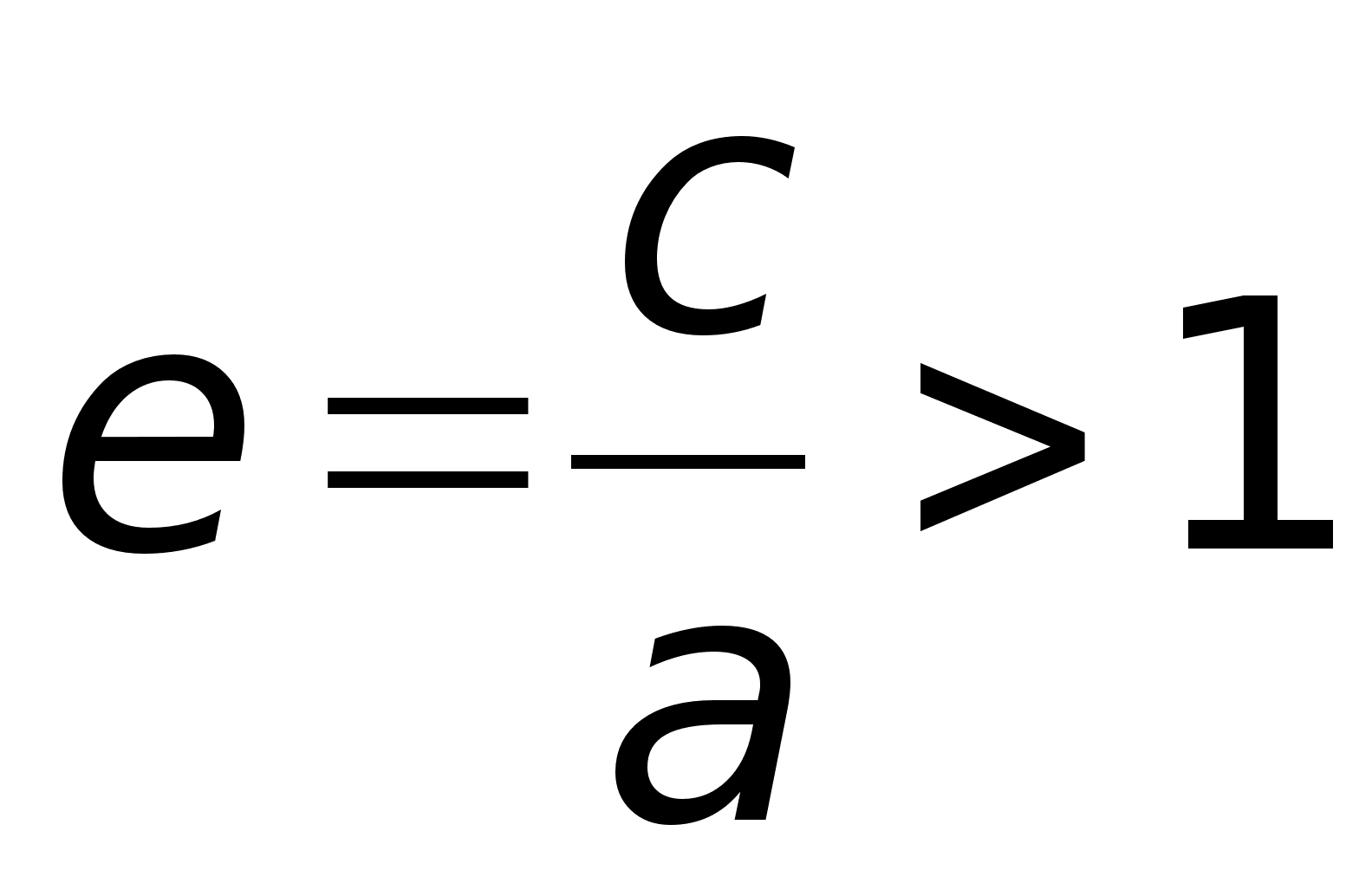 называется
эксцентриситетом
гиперболы,
где с – половина
расстояния
между фокусами,
а – действительная
полуось.С учетом
того, что с2
– а2
= b2:
называется
эксцентриситетом
гиперболы,
где с – половина
расстояния
между фокусами,
а – действительная
полуось.С учетом
того, что с2
– а2
= b2: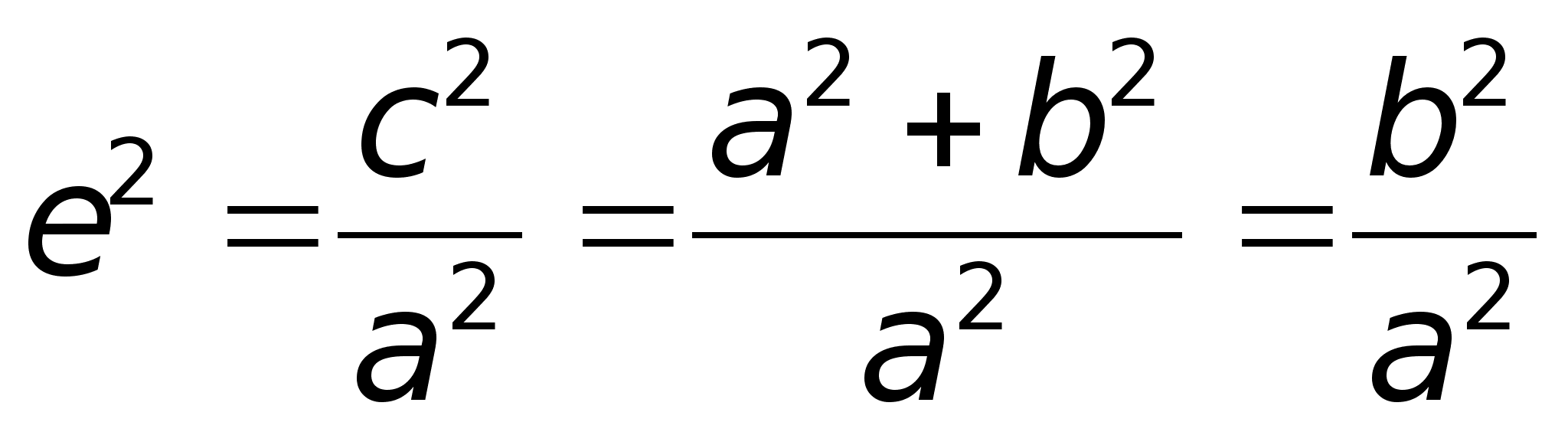
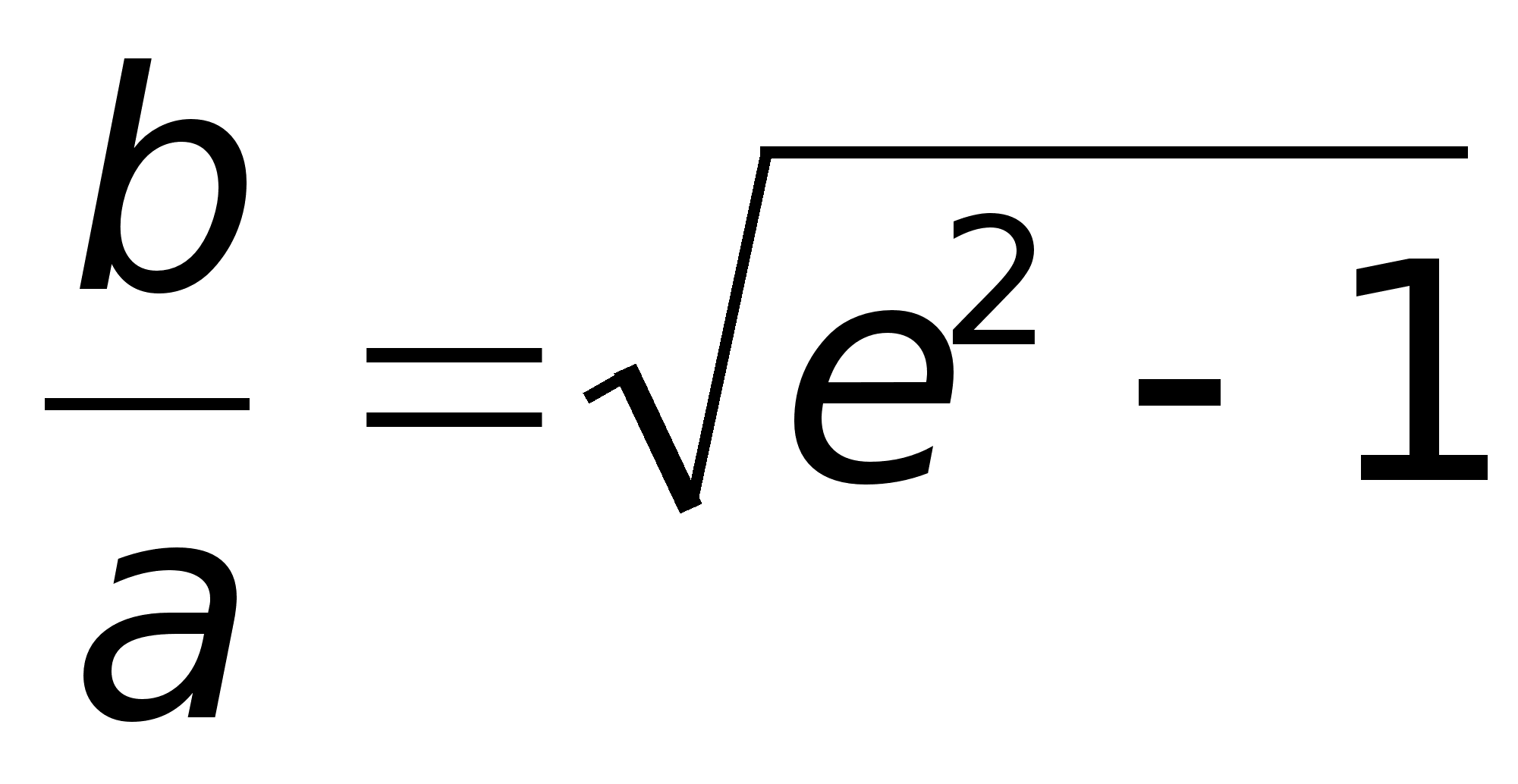 Если
а = b,
e
=
Если
а = b,
e
=
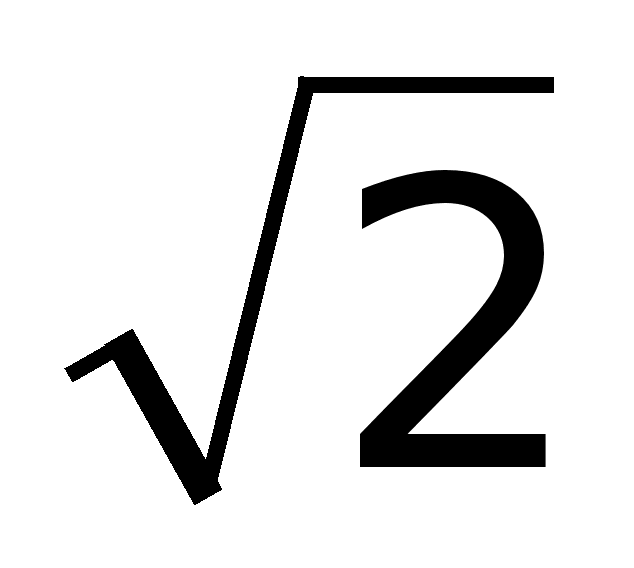 ,
то гипербола
называется
равнобочной
(равносторонней).Определение.
Две прямые,
перпендикулярные
действительной
оси гиперболы
и расположенные
симметрично
относительно
центра на
расстоянии
a/e от него, называются
директрисами
гиперболы.
Их уравнения:
,
то гипербола
называется
равнобочной
(равносторонней).Определение.
Две прямые,
перпендикулярные
действительной
оси гиперболы
и расположенные
симметрично
относительно
центра на
расстоянии
a/e от него, называются
директрисами
гиперболы.
Их уравнения:
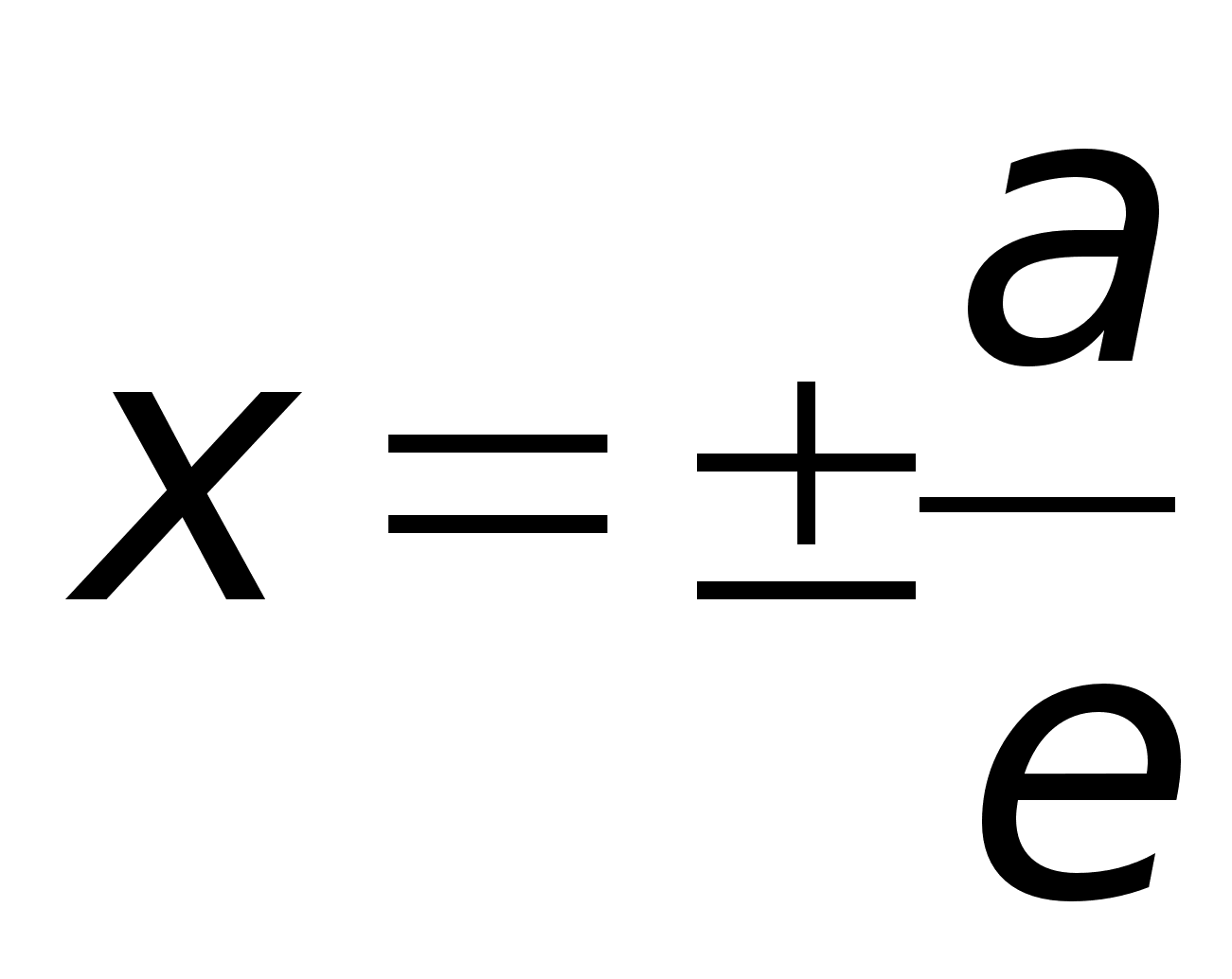 .Теорема.
Если
r
– расстояние
от произвольной
точки М гиперболы
до какого- либо
фокуса, d
– расстояние
от той же точки
до соответствующей
этому фокусу
директрисы,
то отношение
r/d
– величина
постоянная,
равная эксцентриситету.
.Теорема.
Если
r
– расстояние
от произвольной
точки М гиперболы
до какого- либо
фокуса, d
– расстояние
от той же точки
до соответствующей
этому фокусу
директрисы,
то отношение
r/d
– величина
постоянная,
равная эксцентриситету. 
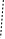

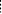
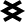
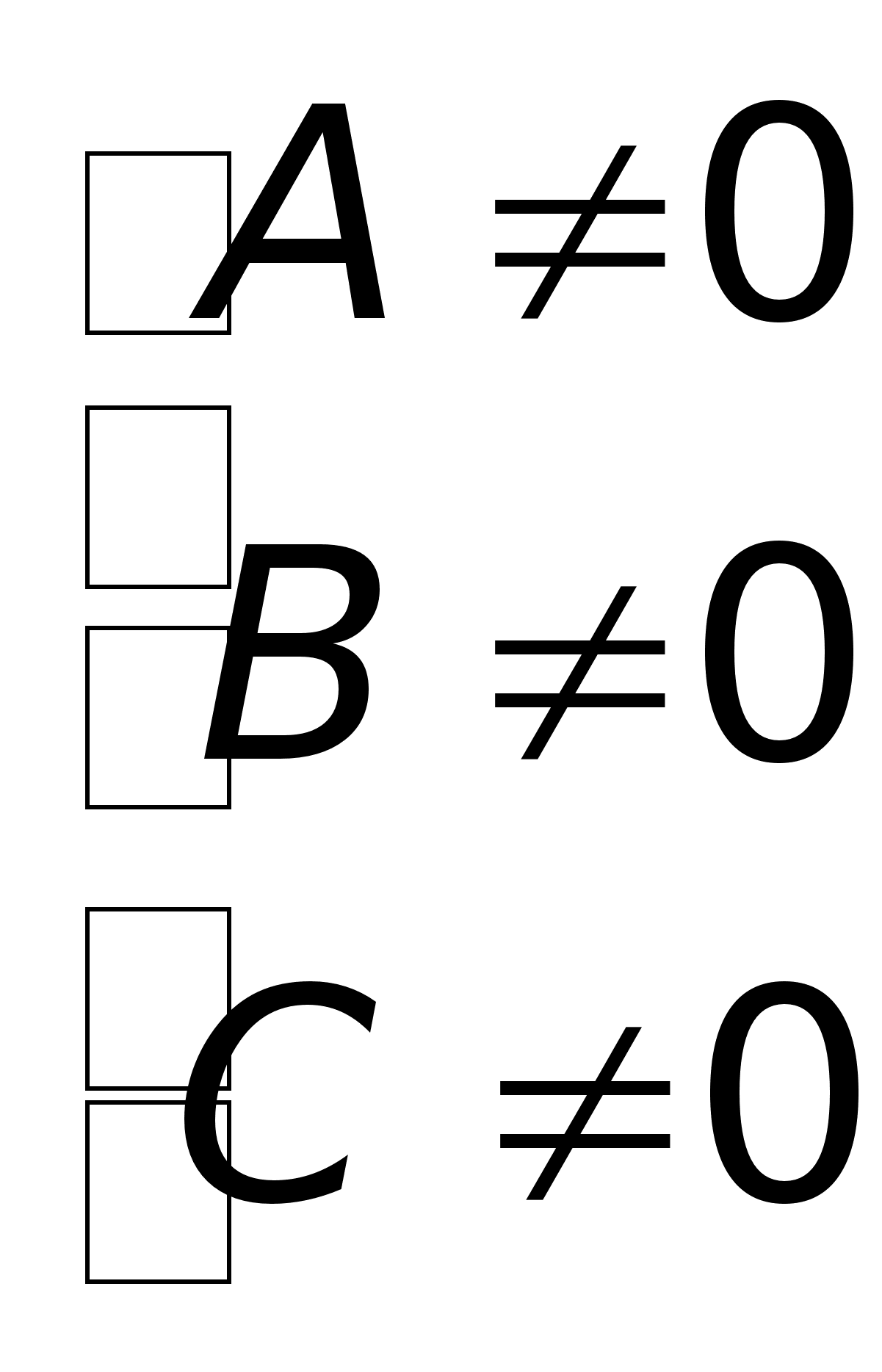
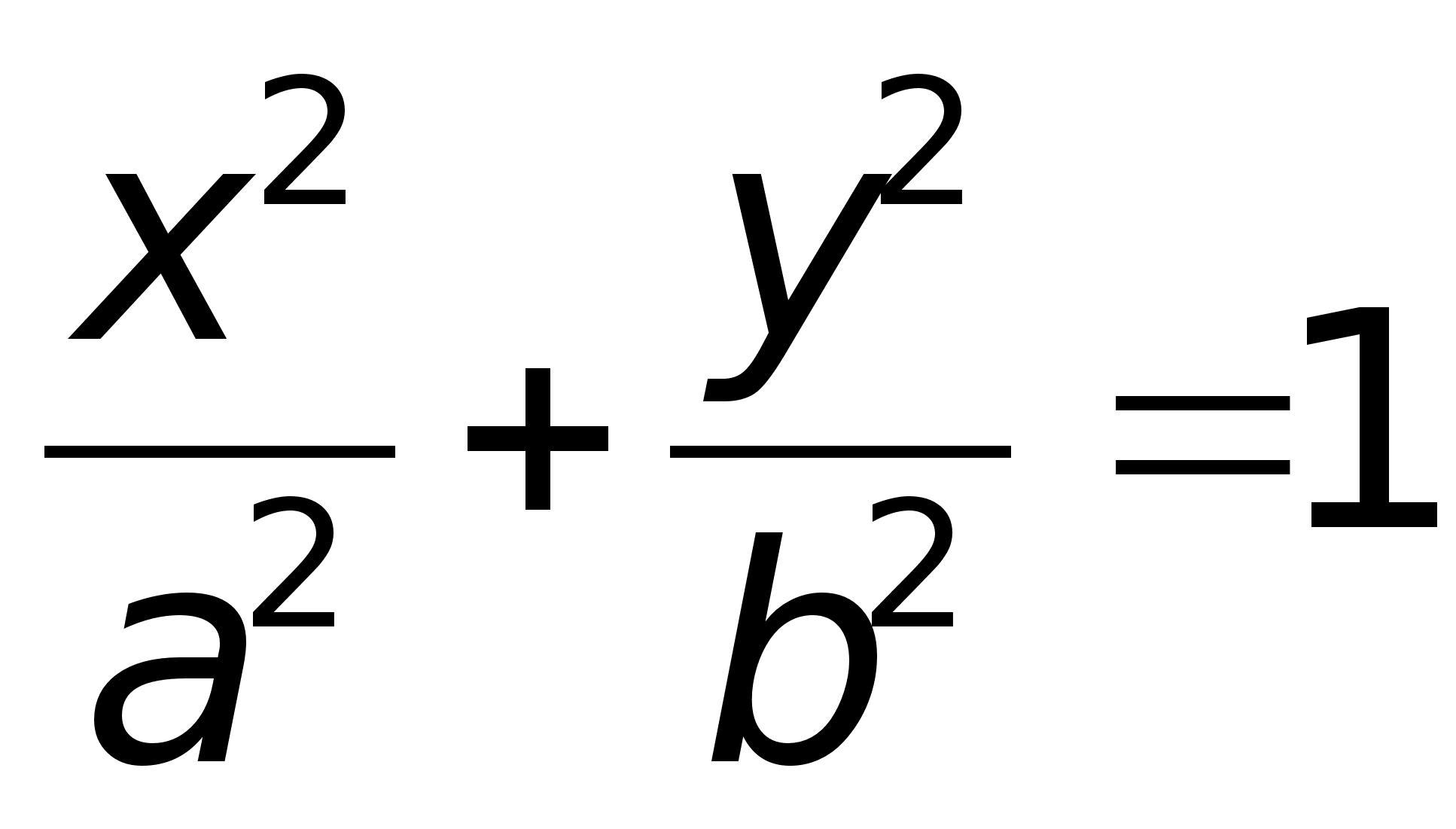 -
Каноническое
ур-е эллипса
-
Каноническое
ур-е эллипса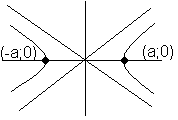
 пределение.
Комплексным
числом z
называется
выражение
пределение.
Комплексным
числом z
называется
выражение
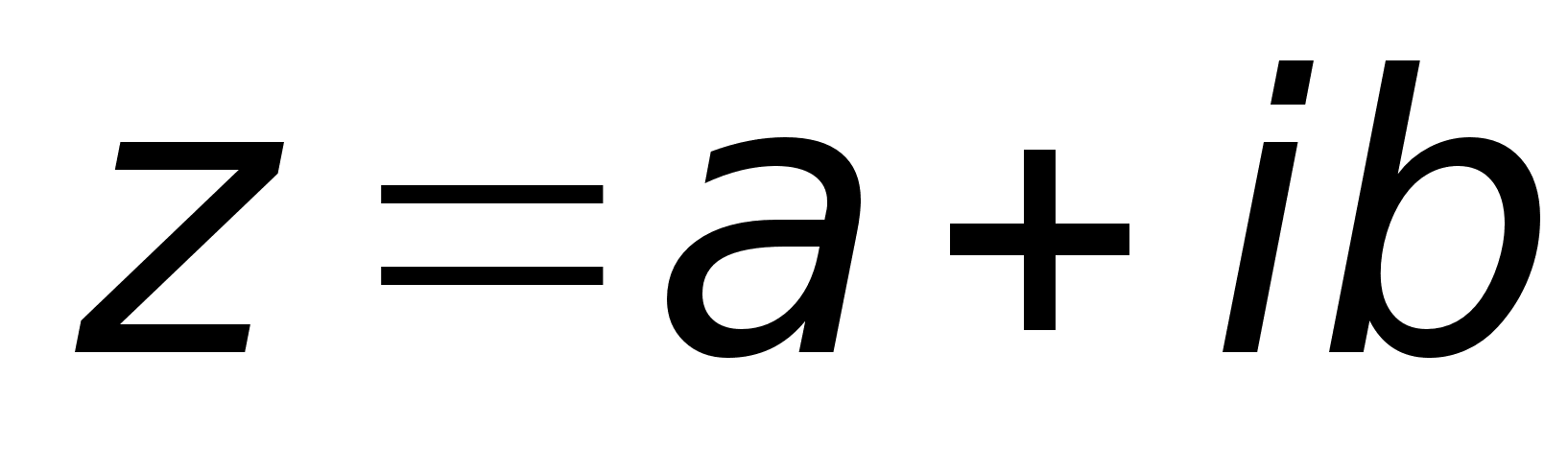 ,
где a
и b
– действительные
числа, i
– мнимая единица,
которая определяется
соотношением:
,
где a
и b
– действительные
числа, i
– мнимая единица,
которая определяется
соотношением: При
этом число a
называется
действительной
частью
числа z
(a
= Re
z),
а b-
мнимой
частью
(b
= Im
z).Если
a
=Re
z
=0, то
число z
будет чисто
мнимым, если
b
= Im
z
= 0, то
число z
будет действительным.Определение.
Числа
При
этом число a
называется
действительной
частью
числа z
(a
= Re
z),
а b-
мнимой
частью
(b
= Im
z).Если
a
=Re
z
=0, то
число z
будет чисто
мнимым, если
b
= Im
z
= 0, то
число z
будет действительным.Определение.
Числа
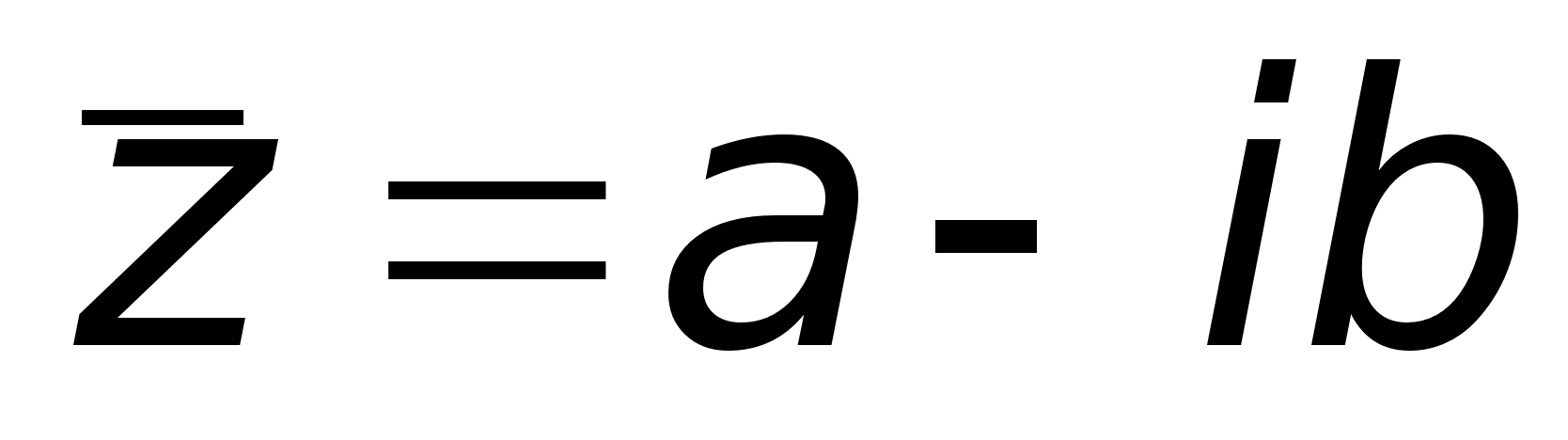 называются
комплексно
– сопряженными.
Определение.
Два комплексных
числа
называются
комплексно
– сопряженными.
Определение.
Два комплексных
числа
 и
и
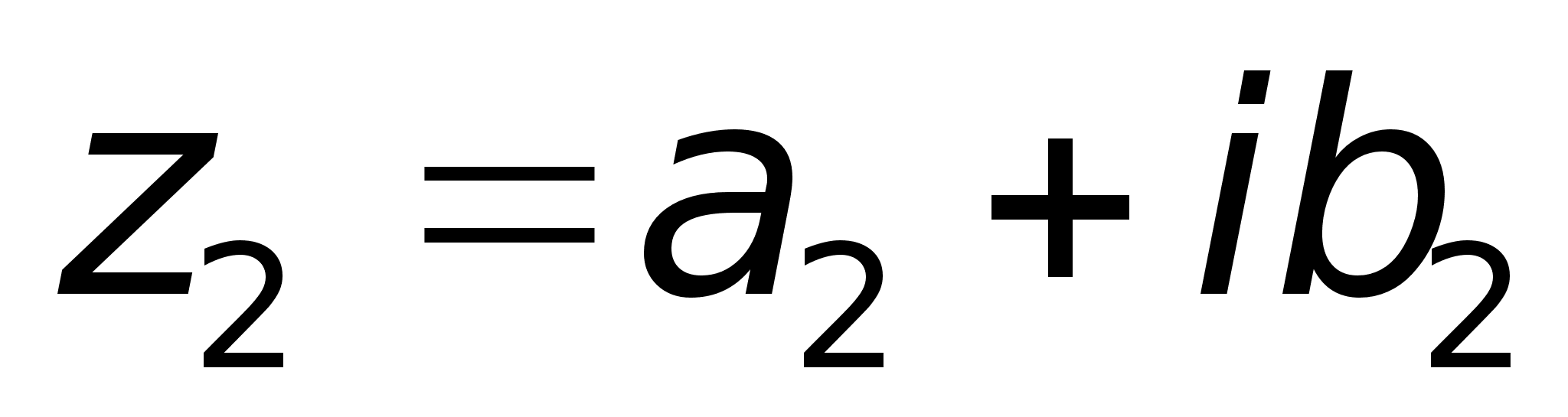 называются
равными, если
соответственно
равны их действительные
и мнимые
части:
называются
равными, если
соответственно
равны их действительные
и мнимые
части: Определение.
Комплексное
число равно
нулю, если
соответственно
равны нулю
действительная
и мнимая части.
Определение.
Комплексное
число равно
нулю, если
соответственно
равны нулю
действительная
и мнимая части.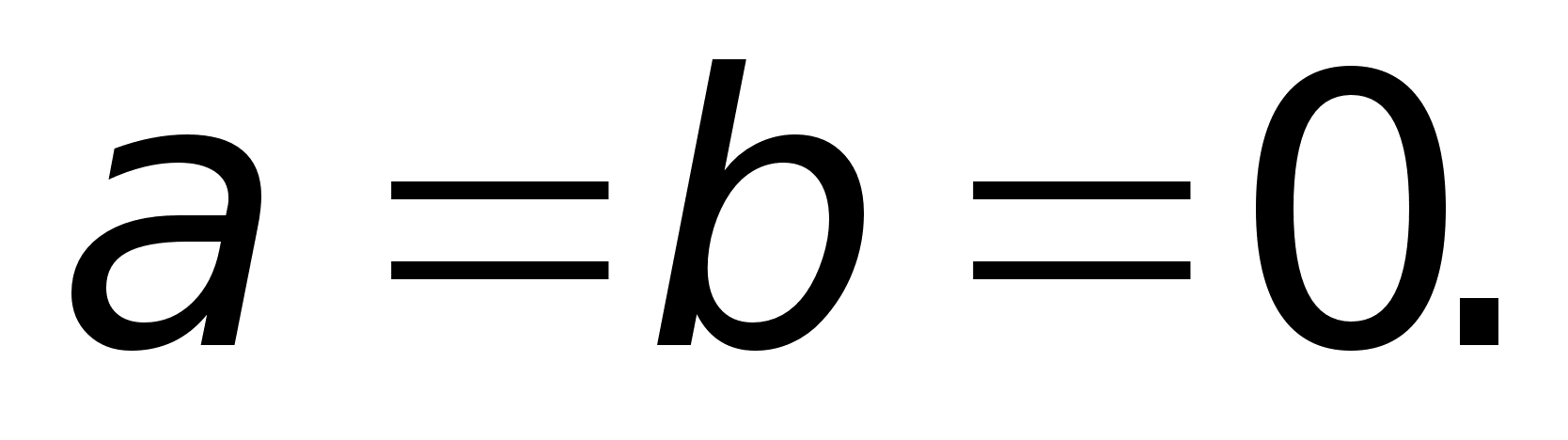 Понятие
комплексного
числа имеет
геометрическое
истолкование.
Множество
комплексных
чисел является
расширением
множества
действительных
чисел за счет
включения
множества
мнимых чисел.
Комплексные
числа включают
в себя все
множества
чисел, которые
изучались
ранее. Так
натуральные,
целые, рациональные,
иррациональные,
действительные
числа являются,
вообще говоря,
частными случаями
комплексных
чисел.Если
любое действительное
число может
быть геометрически
представлено
в виде точки
на числовой
прямой, то
комплексное
число представляется
точкой на
плоскости,
координатами
которой будут
соответственно
действительная
и мнимая части
комплексного
числа. При этом
горизонтальная
ось будет являться
действительной
числовой осью,
а вертикальная
- мнимой осью.
A(a,b)
Понятие
комплексного
числа имеет
геометрическое
истолкование.
Множество
комплексных
чисел является
расширением
множества
действительных
чисел за счет
включения
множества
мнимых чисел.
Комплексные
числа включают
в себя все
множества
чисел, которые
изучались
ранее. Так
натуральные,
целые, рациональные,
иррациональные,
действительные
числа являются,
вообще говоря,
частными случаями
комплексных
чисел.Если
любое действительное
число может
быть геометрически
представлено
в виде точки
на числовой
прямой, то
комплексное
число представляется
точкой на
плоскости,
координатами
которой будут
соответственно
действительная
и мнимая части
комплексного
числа. При этом
горизонтальная
ось будет являться
действительной
числовой осью,
а вертикальная
- мнимой осью.
A(a,b)
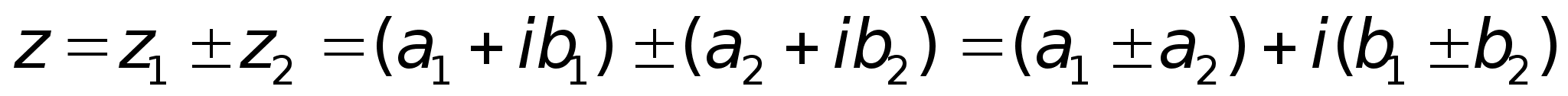 ;
;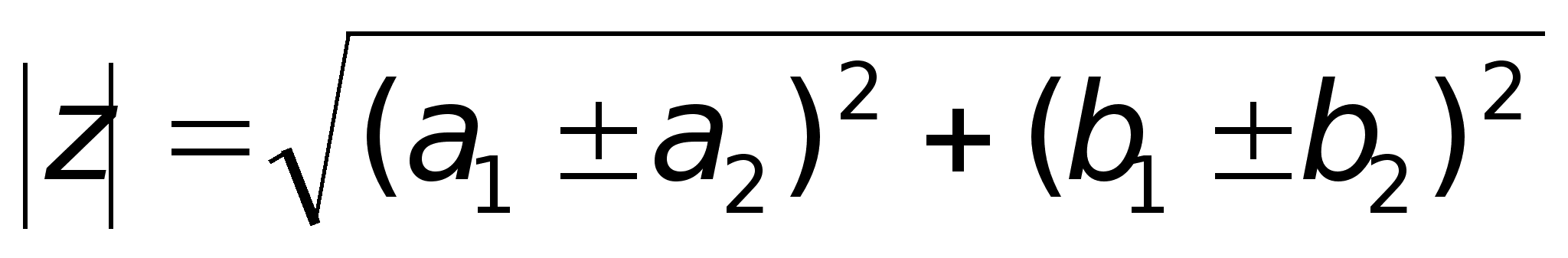 ;2)
Умножение.
;2)
Умножение.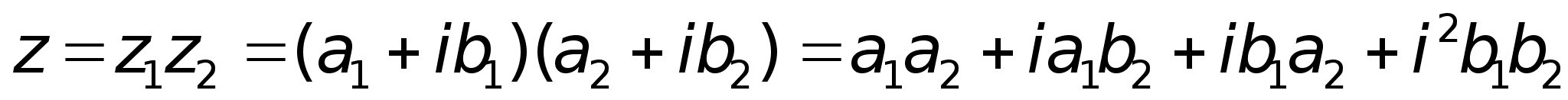
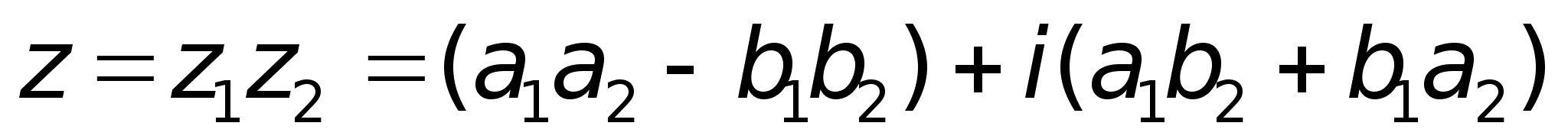 В
тригонометрической
форме:
В
тригонометрической
форме: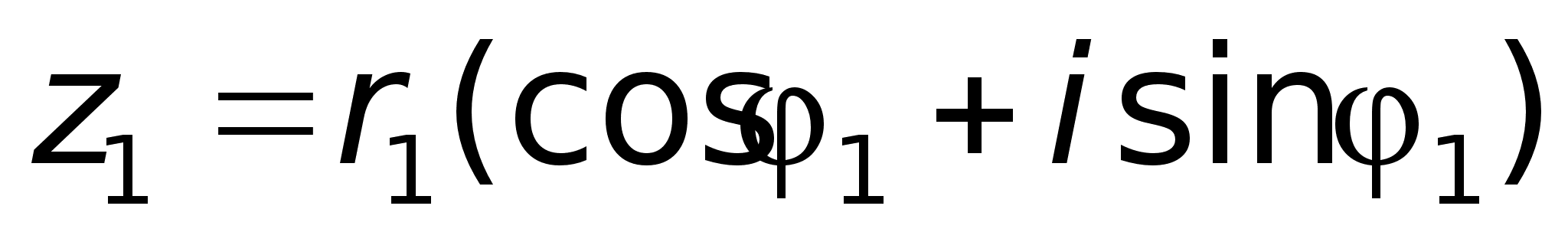 ,
,
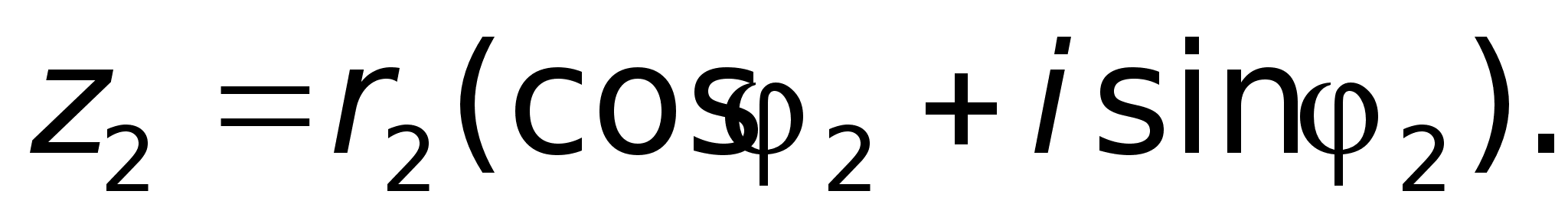
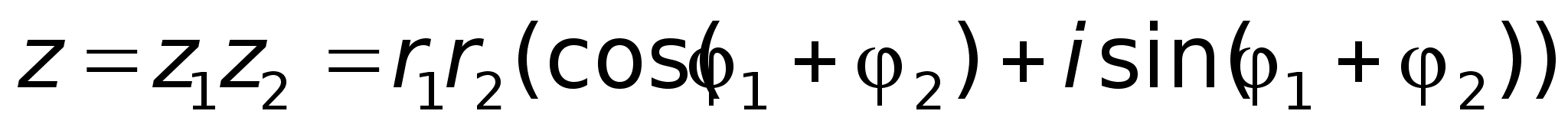 С
случае комплексно
– сопряженных
чисел:
С
случае комплексно
– сопряженных
чисел: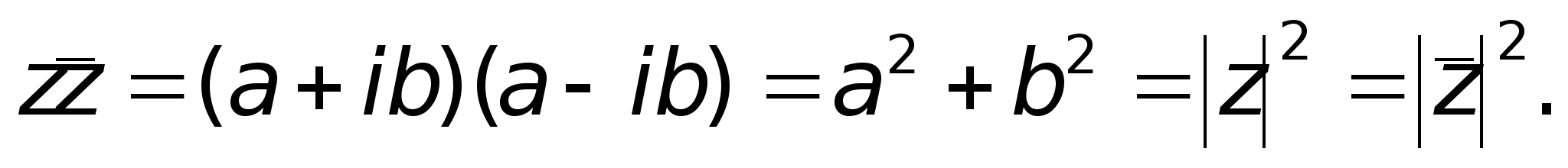
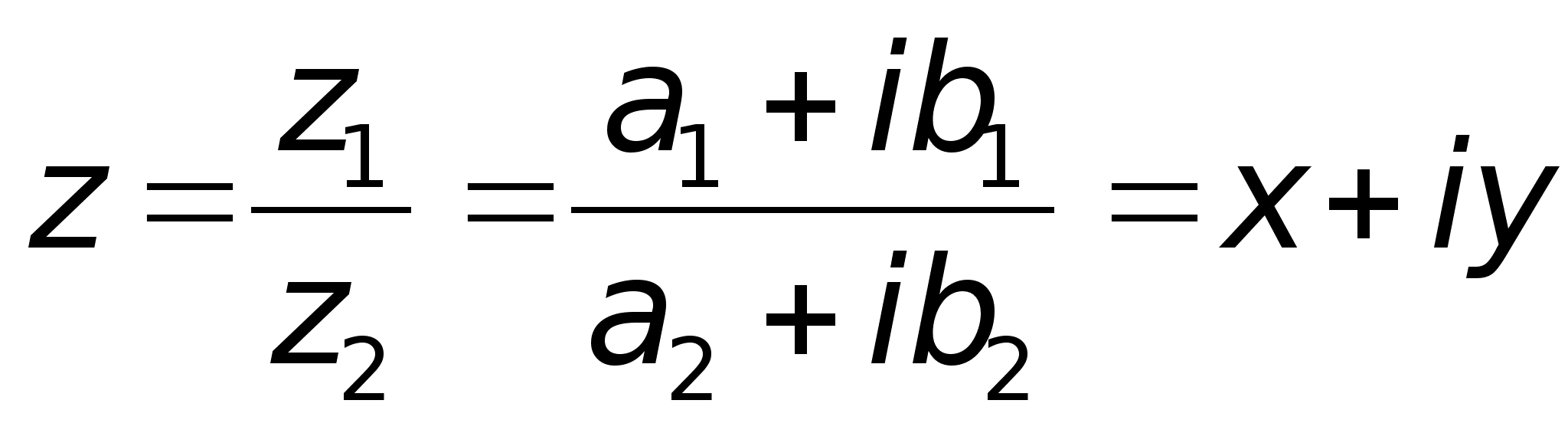
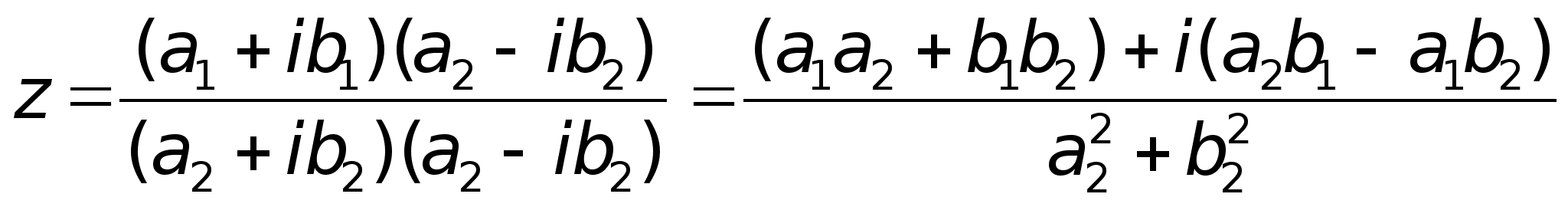
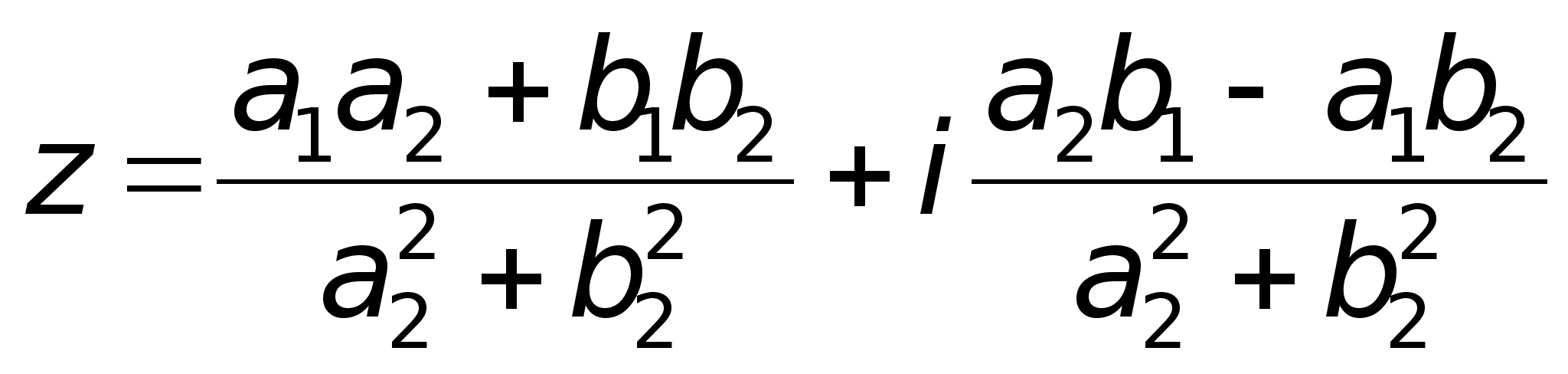 В
тригонометрической
форме:
В
тригонометрической
форме: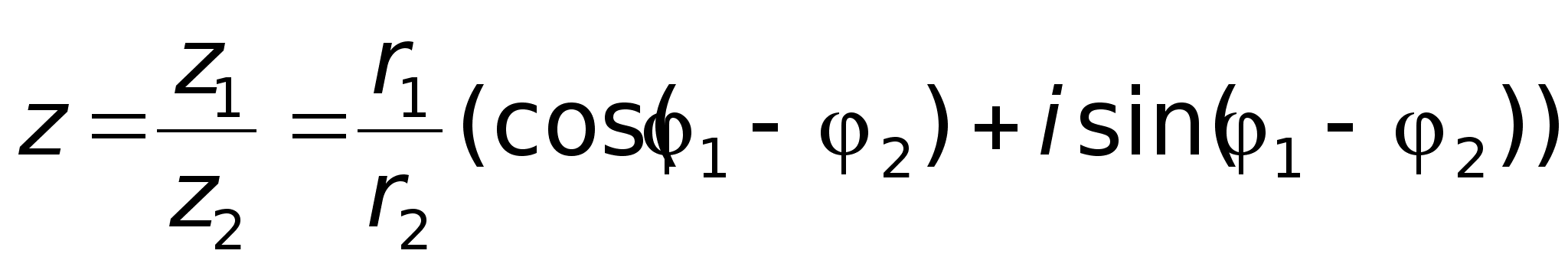 4)
Возведение
в степень.Из
операции умножения
комплексных
чисел следует,
что
4)
Возведение
в степень.Из
операции умножения
комплексных
чисел следует,
что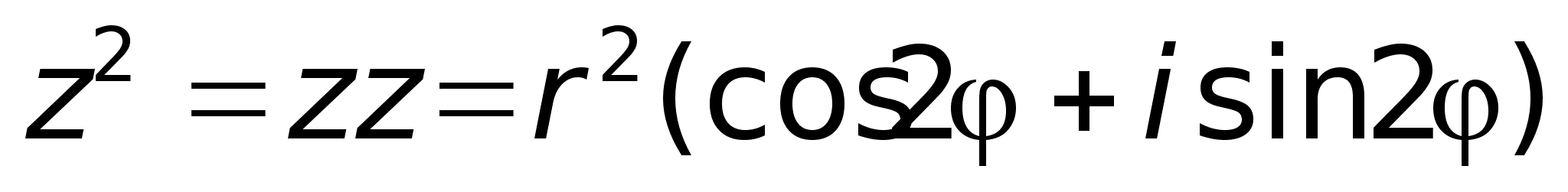 В
общем случае
получим:
В
общем случае
получим: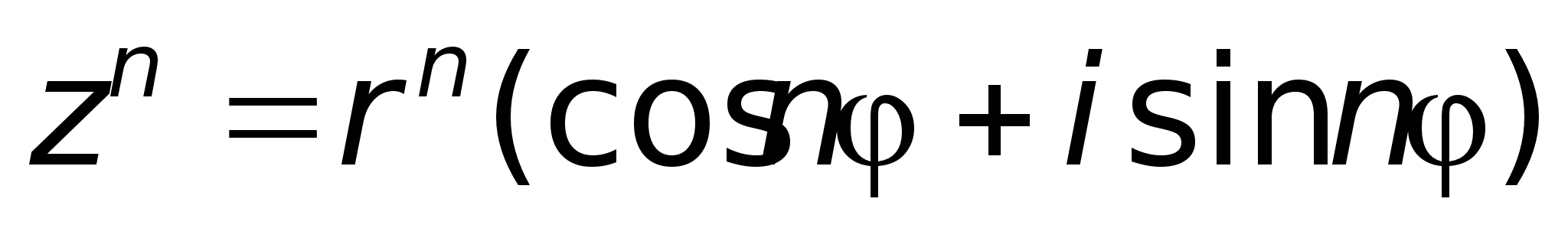 ,где
n
– целое
положительное
число. Это
выражение
называется
формулой
Муавра.(Абрахам
де Муавр (1667 –
1754) – английский
математик)Формулу
Муавра можно
использовать
для нахождения
тригонометрических
функций двойного,
тройного и
т.д. углов.Пример.
Найти формулы
sin2
,где
n
– целое
положительное
число. Это
выражение
называется
формулой
Муавра.(Абрахам
де Муавр (1667 –
1754) – английский
математик)Формулу
Муавра можно
использовать
для нахождения
тригонометрических
функций двойного,
тройного и
т.д. углов.Пример.
Найти формулы
sin2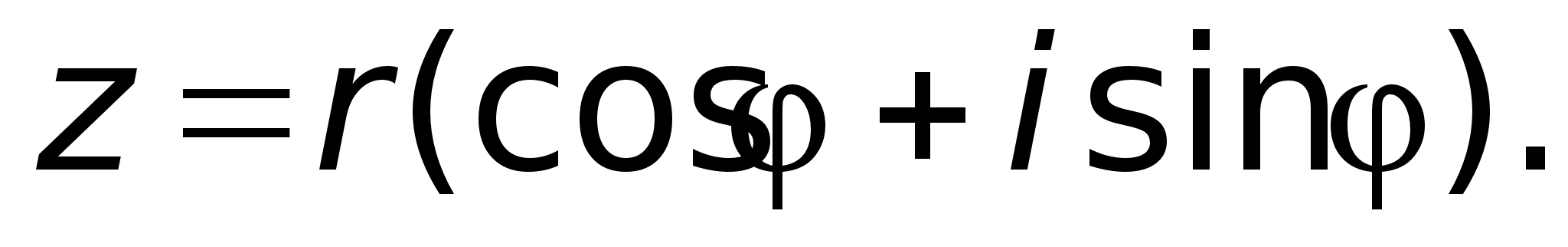 Тогда
с одной стороны
Тогда
с одной стороны
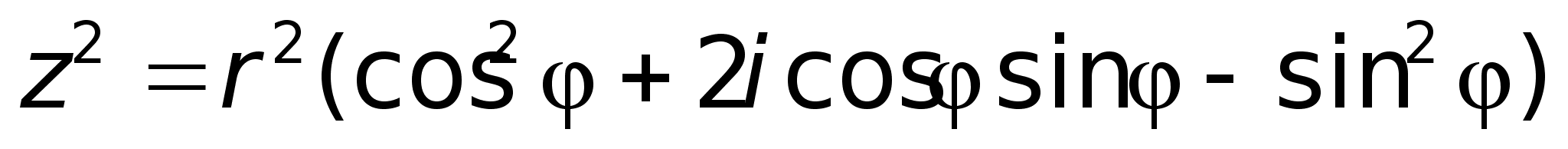 .По
формуле Муавра:
.По
формуле Муавра:
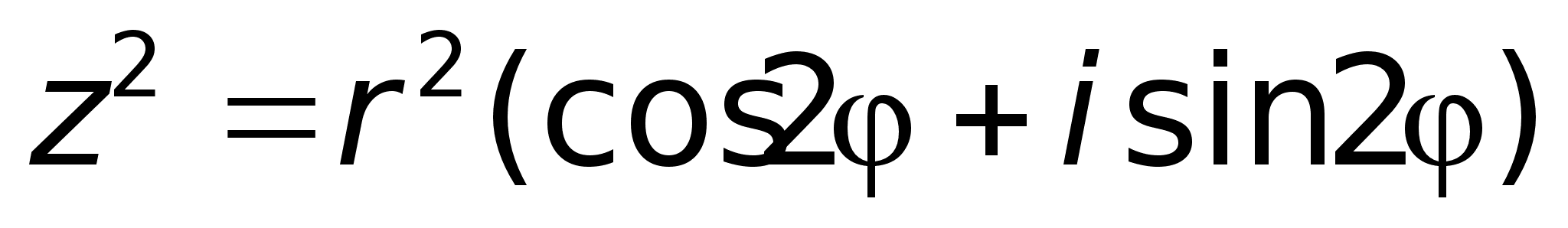
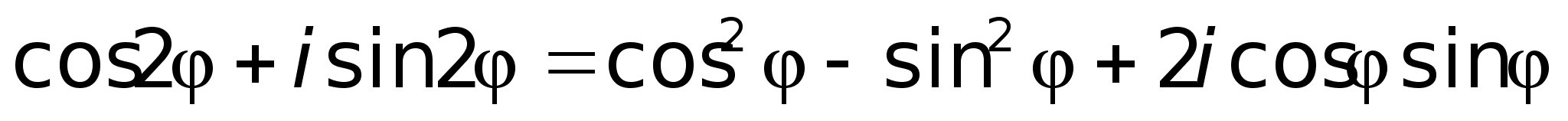 Т.к.
два комплексных
числа равны,
если равны
их действительные
и мнимые части,
то
Т.к.
два комплексных
числа равны,
если равны
их действительные
и мнимые части,
то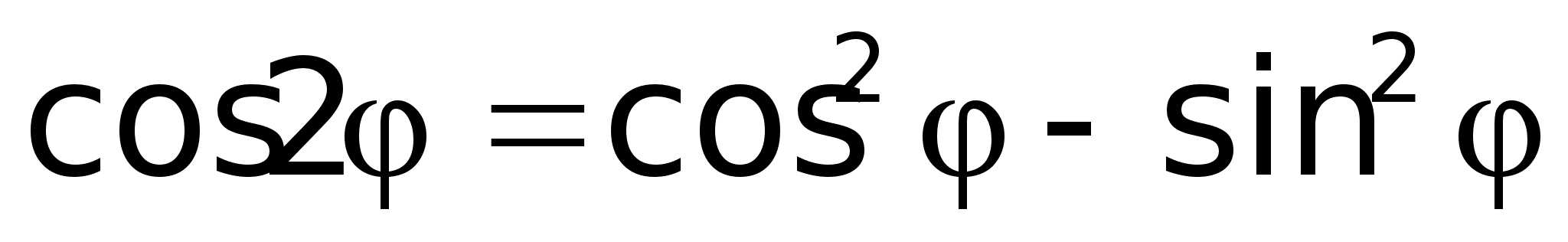
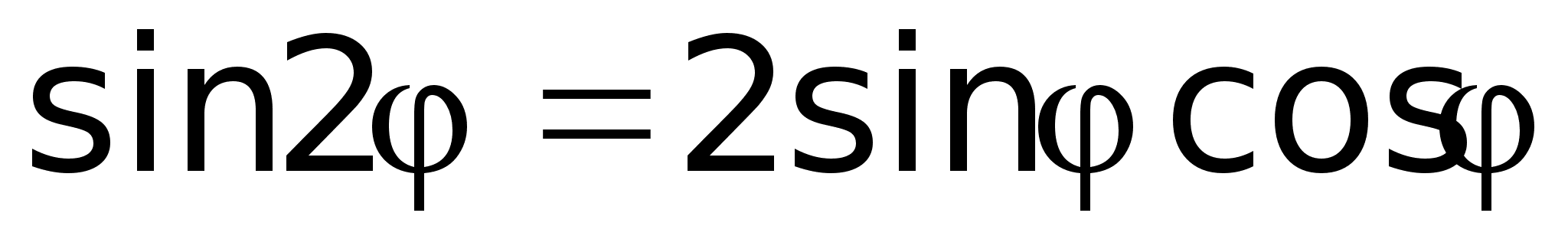 Получили
известные
формулы двойного
угла.5) Извлечение
корня из комплексного
числа.
Получили
известные
формулы двойного
угла.5) Извлечение
корня из комплексного
числа.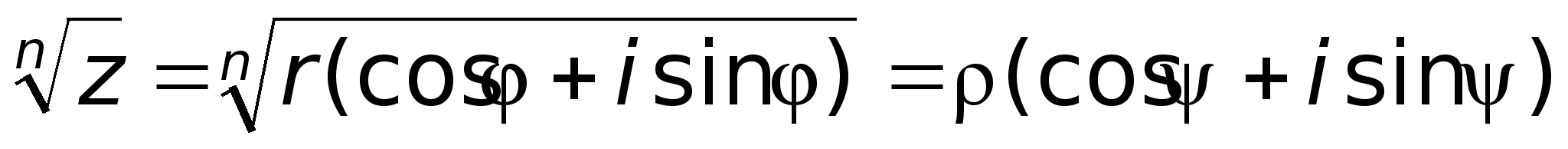 Возводя
в степень,
получим:
Возводя
в степень,
получим: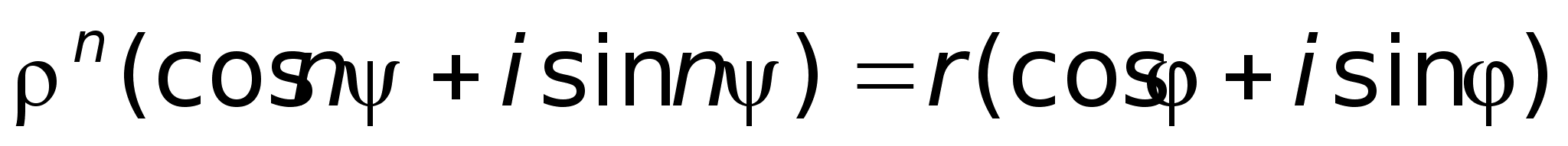
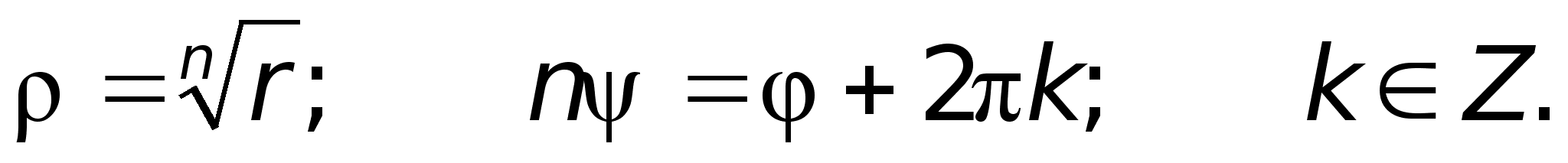
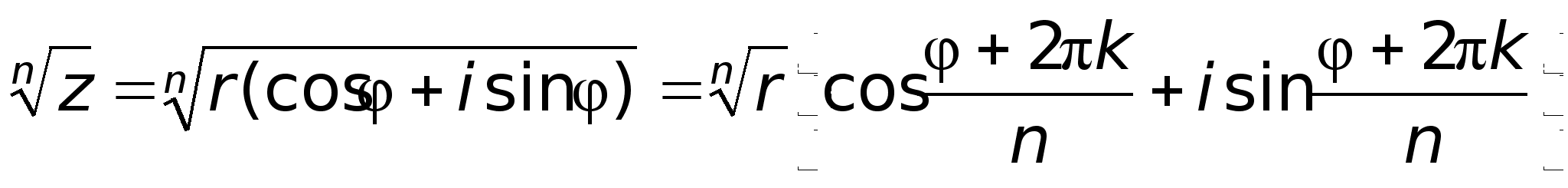
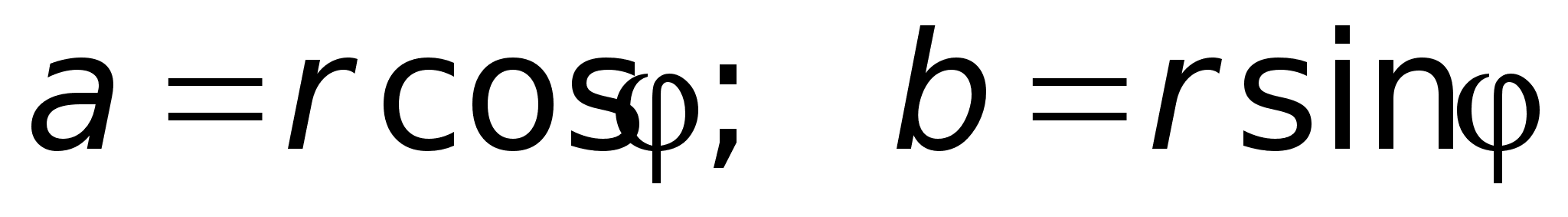 .
Тогда комплексное
число можно
представить
в виде:
.
Тогда комплексное
число можно
представить
в виде: Такая
форма записи
называется
тригонометрической
формой записи
комплексного
числа.При
этом величина
r
называется
модулем
комплексного
числа, а угол
наклона
Такая
форма записи
называется
тригонометрической
формой записи
комплексного
числа.При
этом величина
r
называется
модулем
комплексного
числа, а угол
наклона  .Из
геометрических
соображений
видно:
.Из
геометрических
соображений
видно: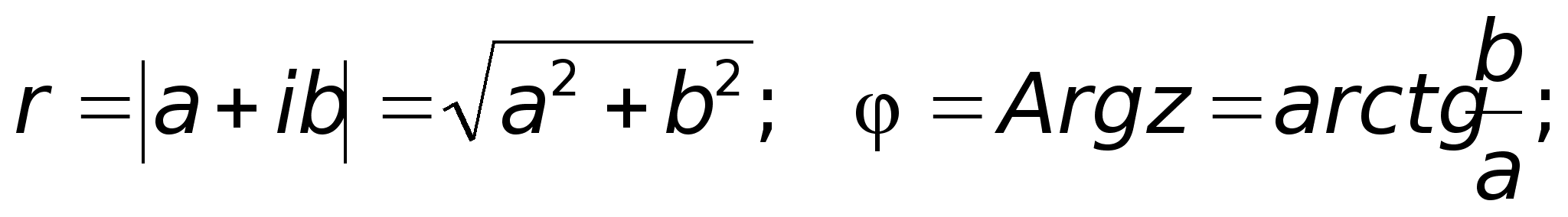

 f(x)
f(x)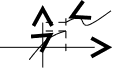 усть
функция f(x)
определена
в некоторой
окрестности
точки х = а (т.е.
в самой точке
х = а функция
может быть и
не определена)Определение.
Число А называется
пределом
функции f(x)
при х
усть
функция f(x)
определена
в некоторой
окрестности
точки х = а (т.е.
в самой точке
х = а функция
может быть и
не определена)Определение.
Число А называется
пределом
функции f(x)
при х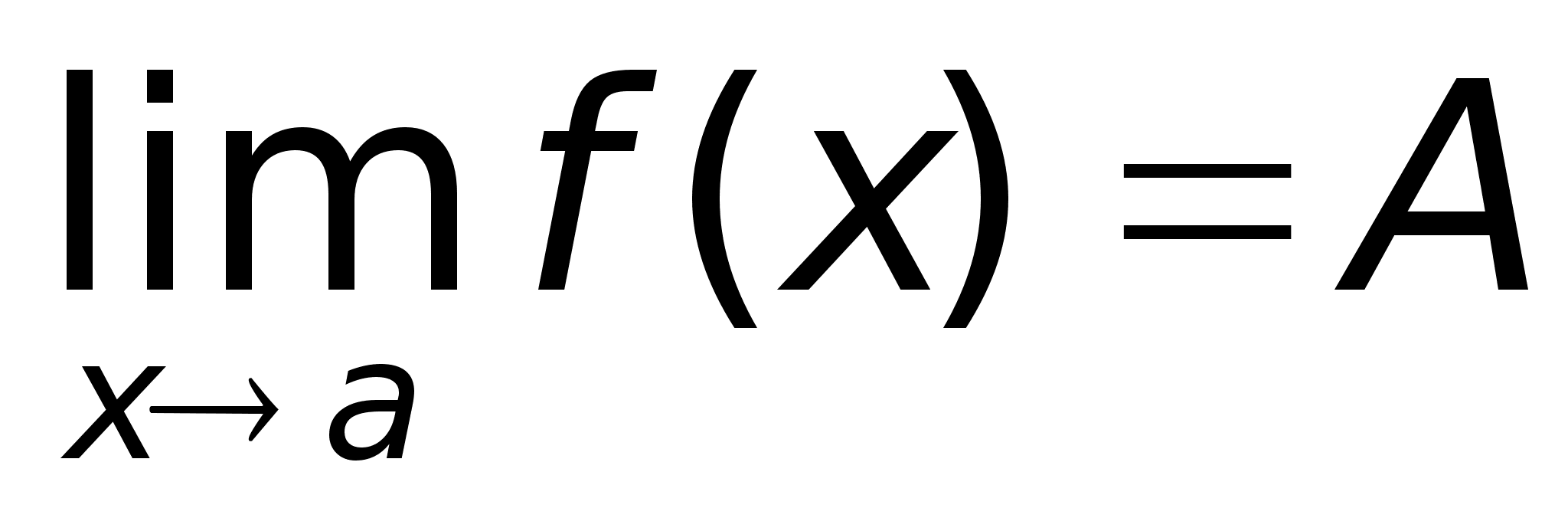 Определение.
Если f(x)
Определение.
Если f(x)
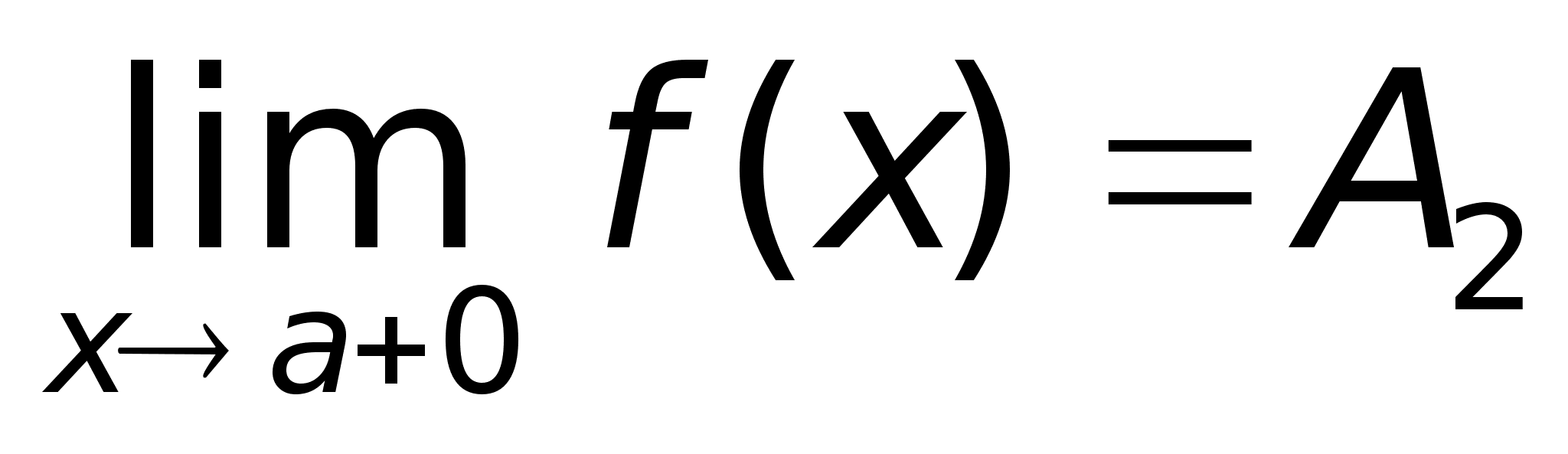 называется
пределом
функции f(x)
в точке х = а
справа.
f(x)
называется
пределом
функции f(x)
в точке х = а
справа.
f(x)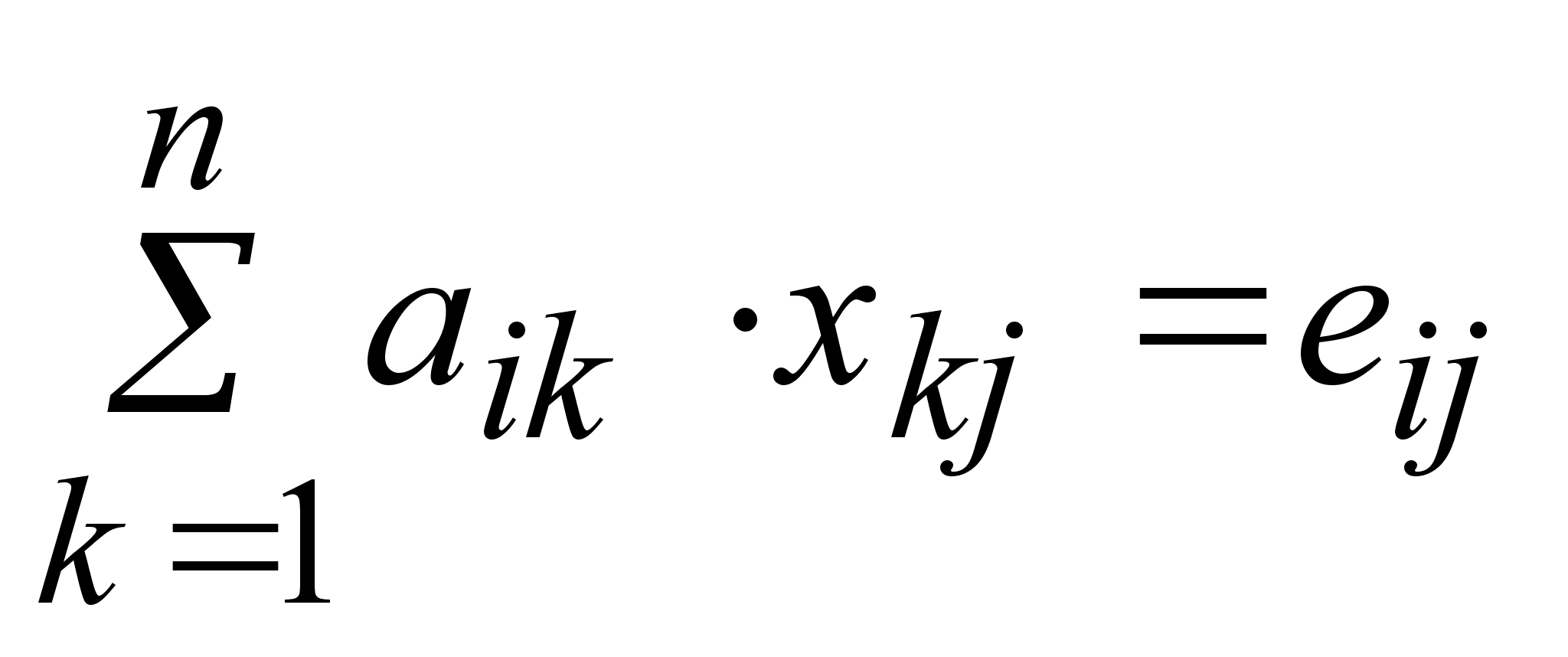 ,
i=(1,n),
j=(1,n),
eij
= 0, i
,
i=(1,n),
j=(1,n),
eij
= 0, i
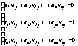 Решив эту систему,
находим элементы
матрицы Х. Пример.
Дана матрица
А =
Решив эту систему,
находим элементы
матрицы Х. Пример.
Дана матрица
А =
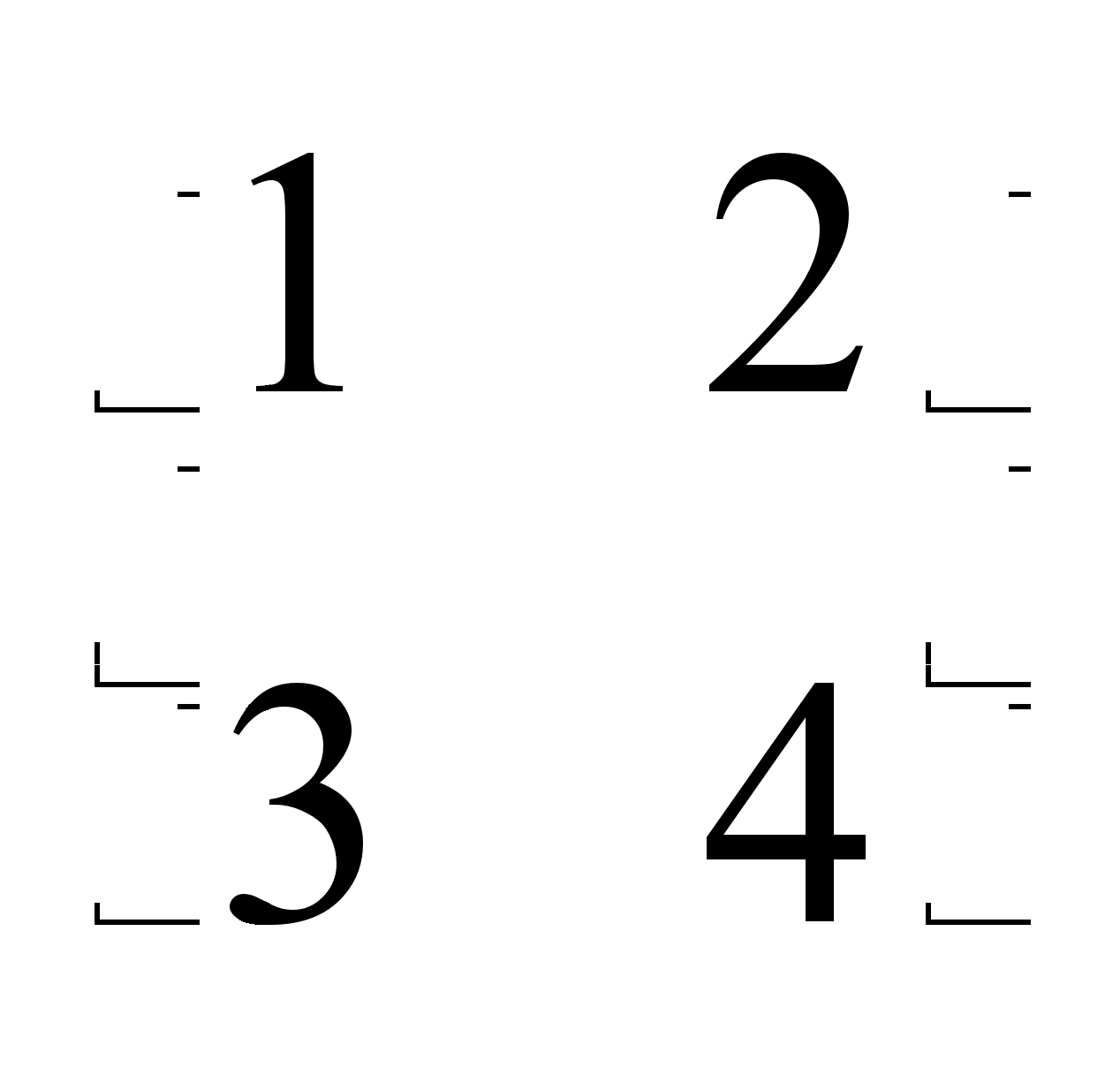 ,
найти А-
,
найти А-
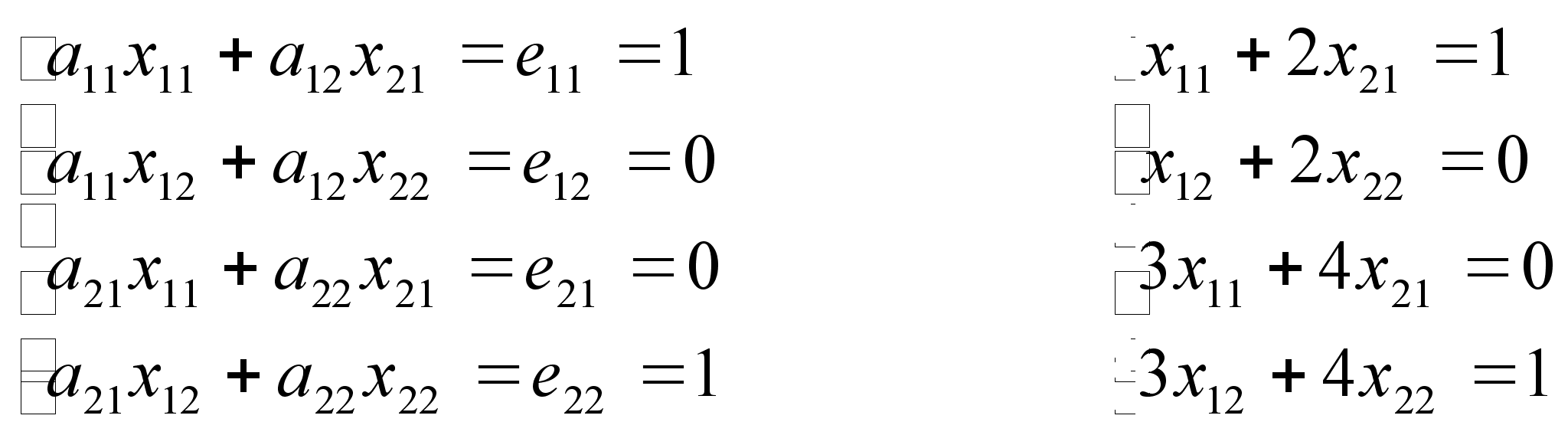
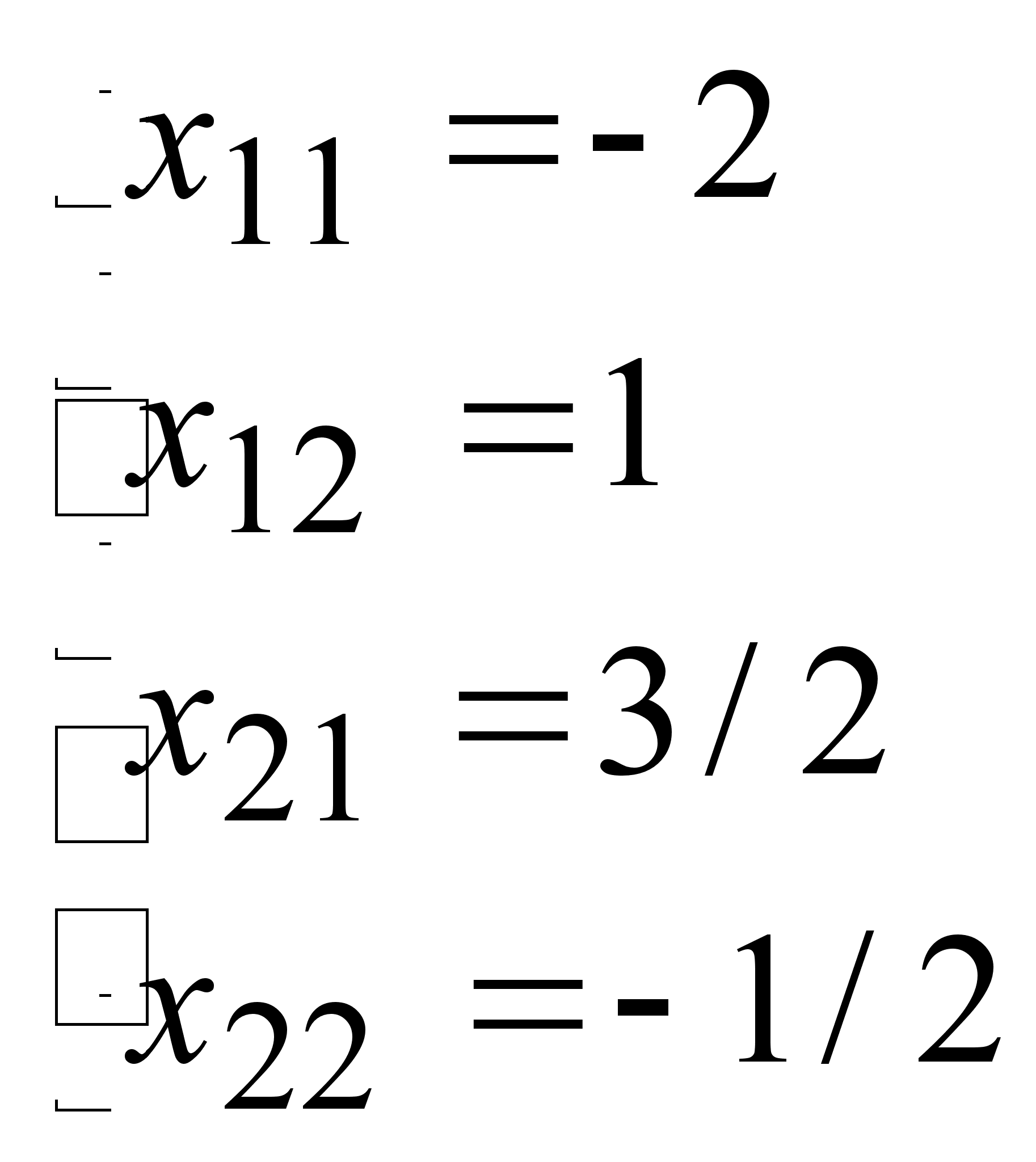
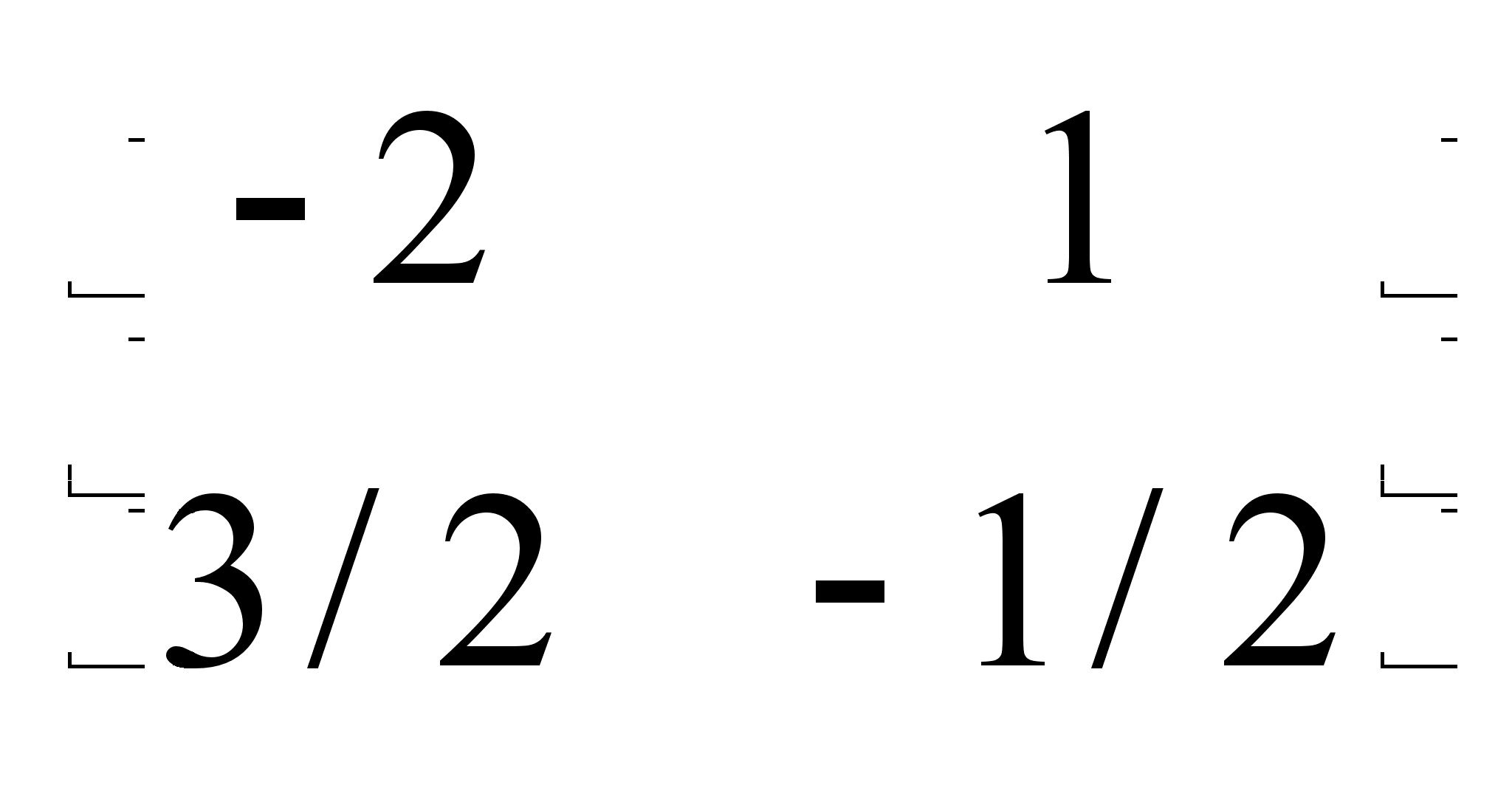 .Однако,
такой способ
не удобен при
нахождении
обратных матриц
больших порядков,
поэтому обычно
применяют
следующую
формулу:
.Однако,
такой способ
не удобен при
нахождении
обратных матриц
больших порядков,
поэтому обычно
применяют
следующую
формулу: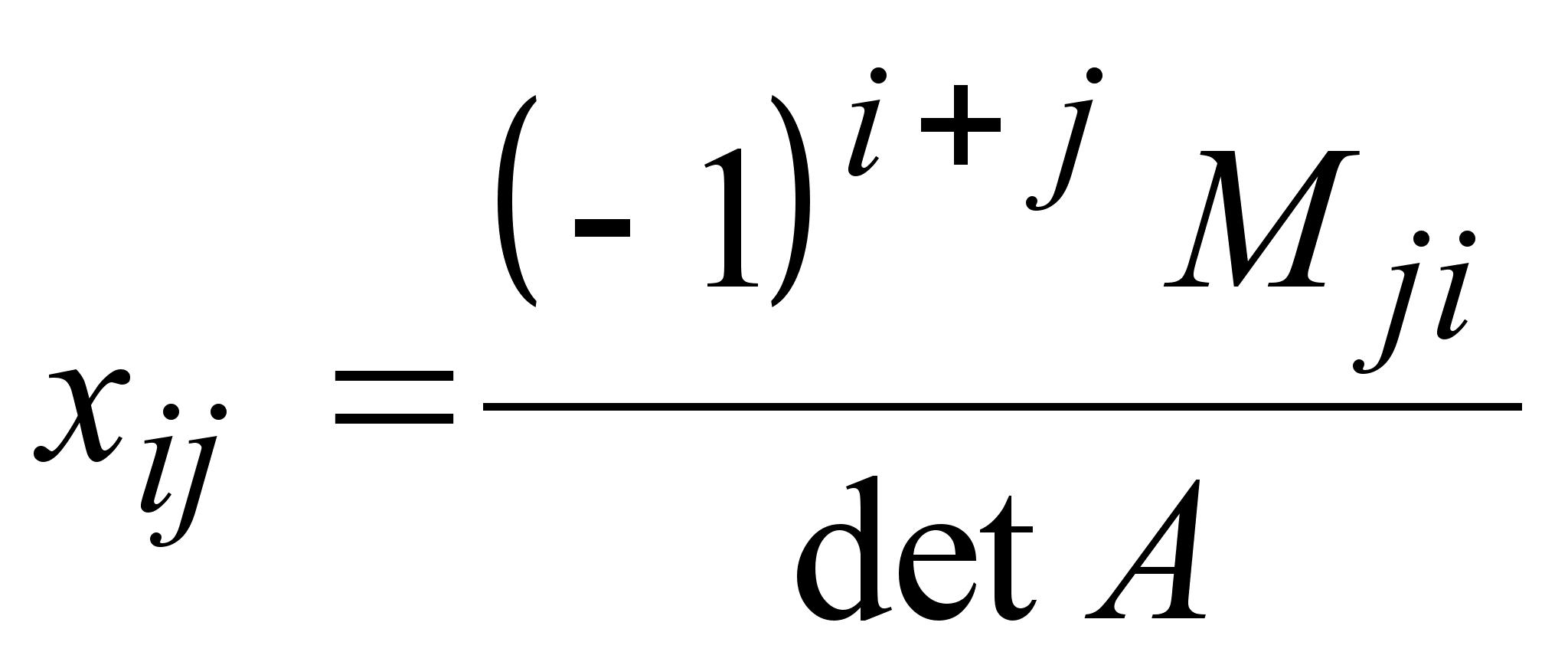 ,где
Мji-
,где
Мji-
 ,
найти А3.А2
= АА =
,
найти А3.А2
= АА =
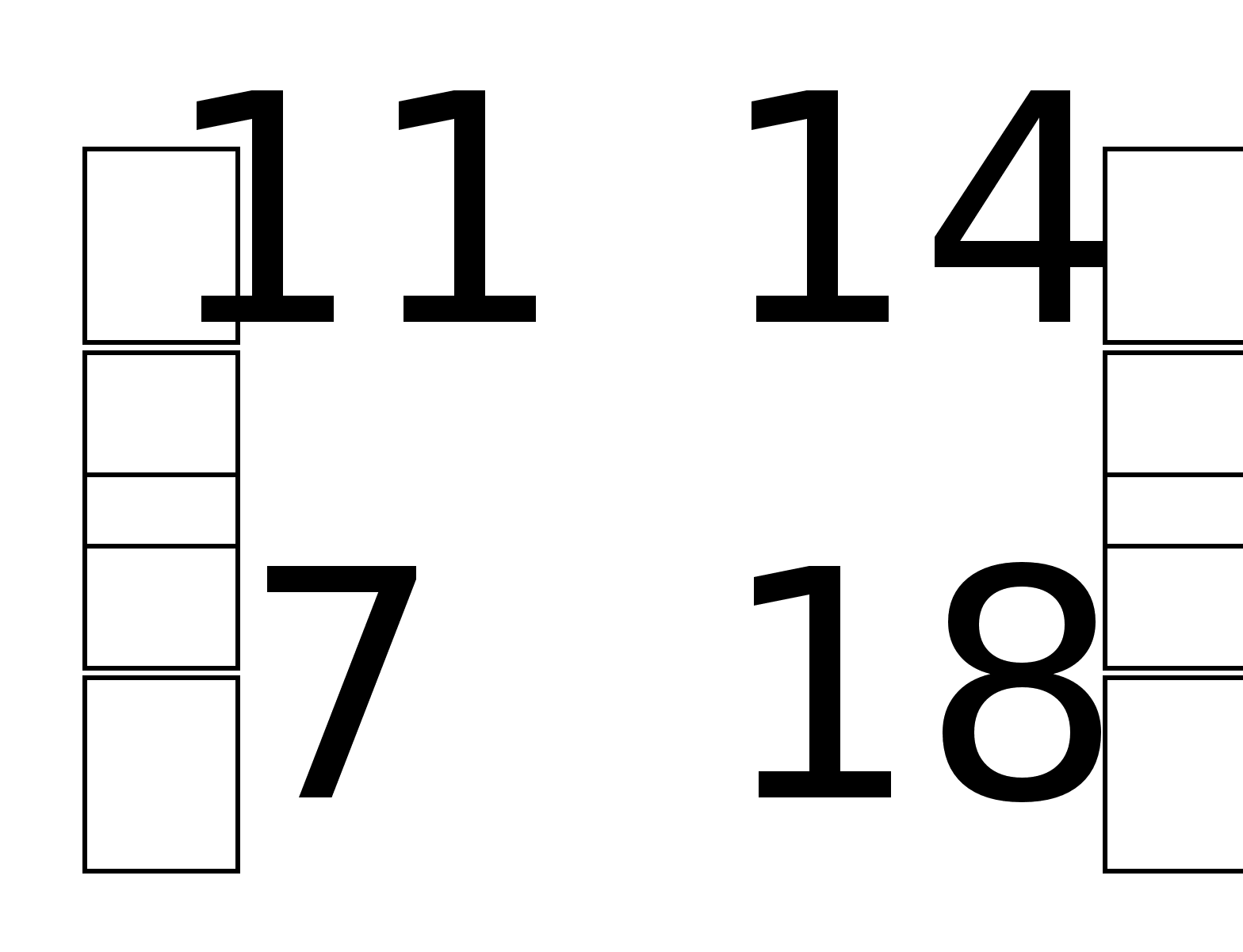 ;
A3
=
;
A3
=
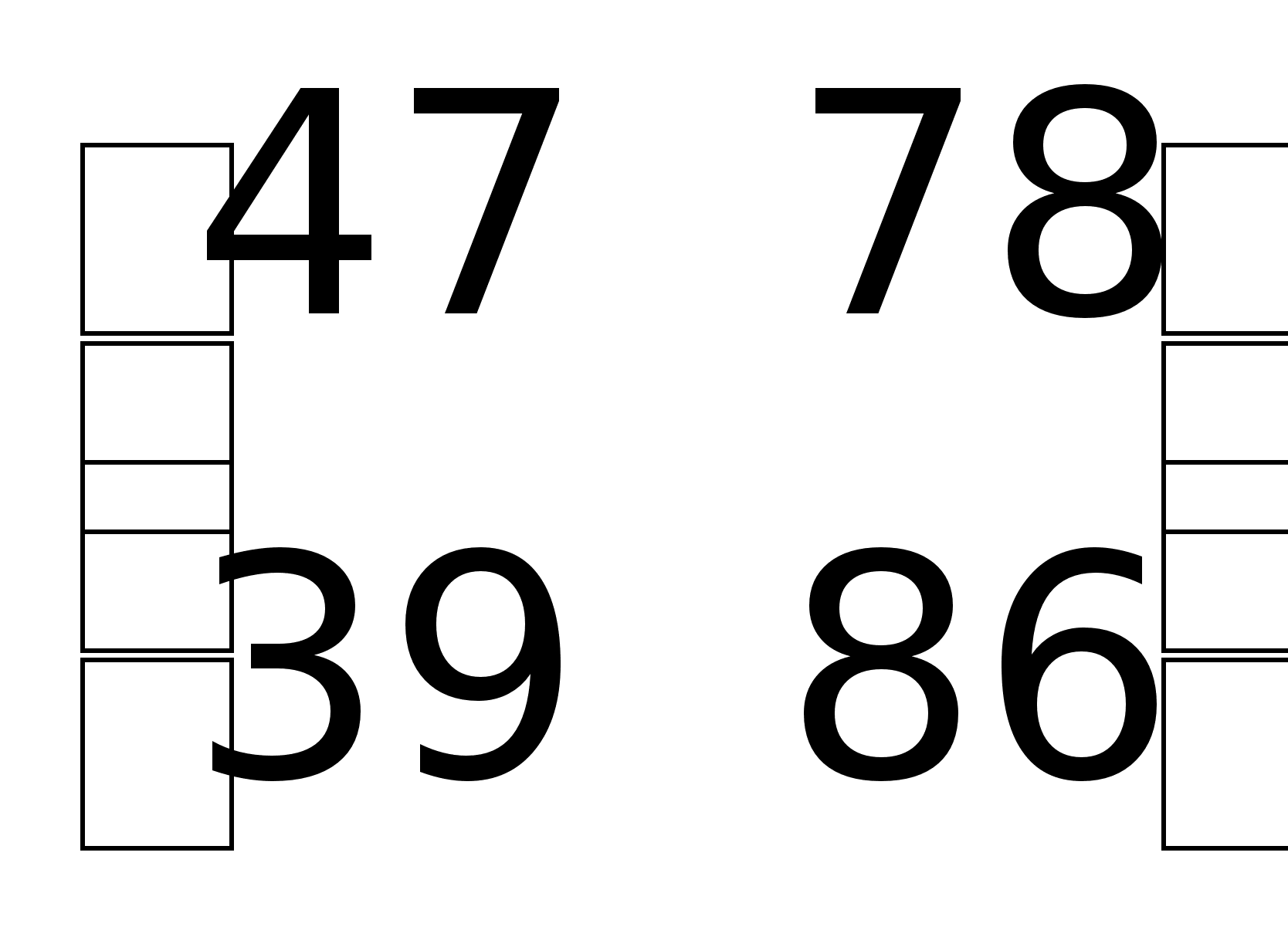 .Отметим,
что матрицы
.Отметим,
что матрицы
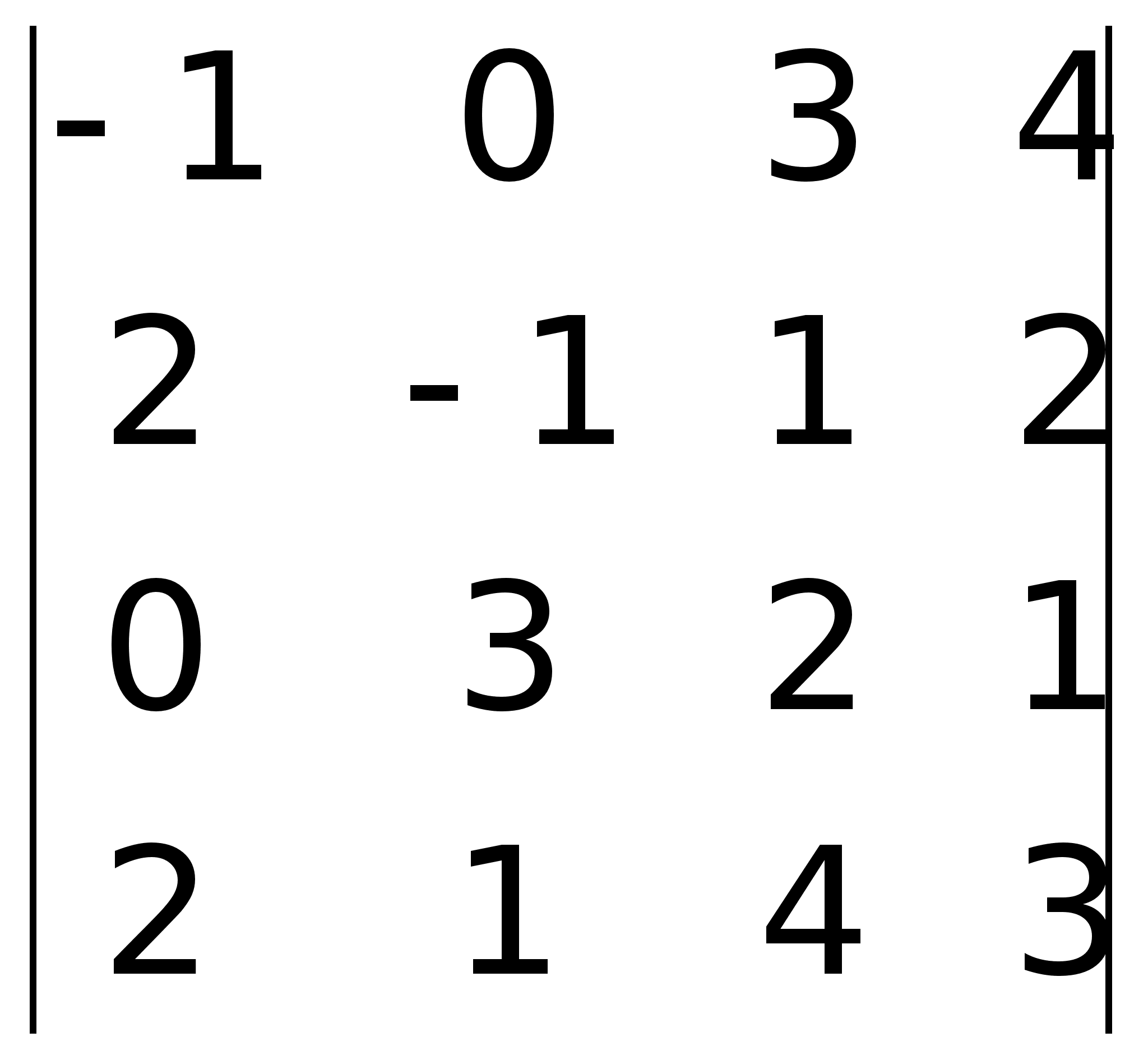 .
.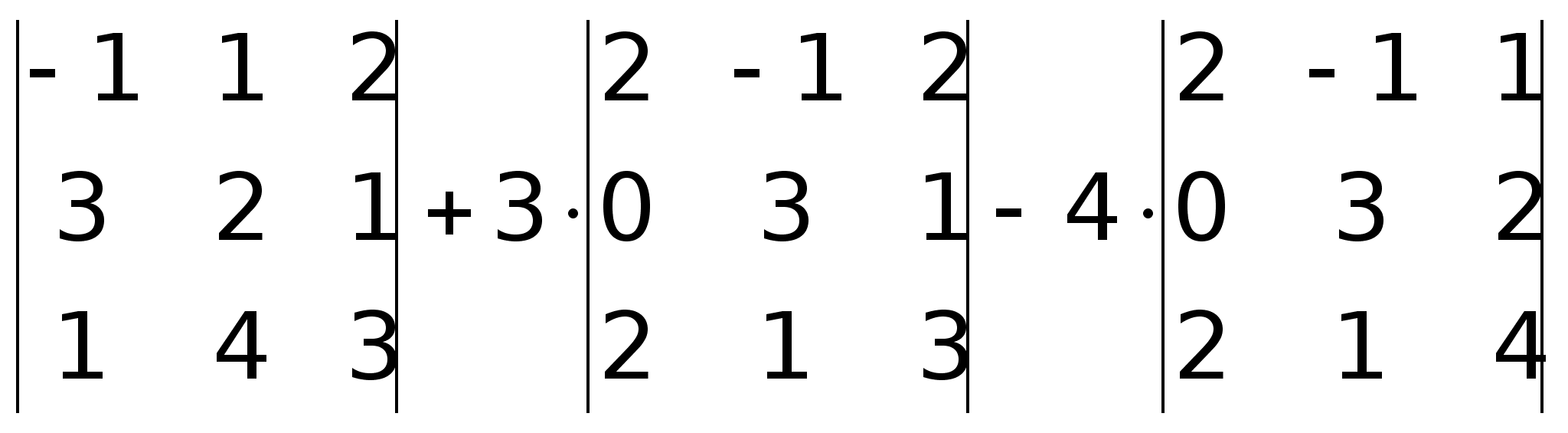
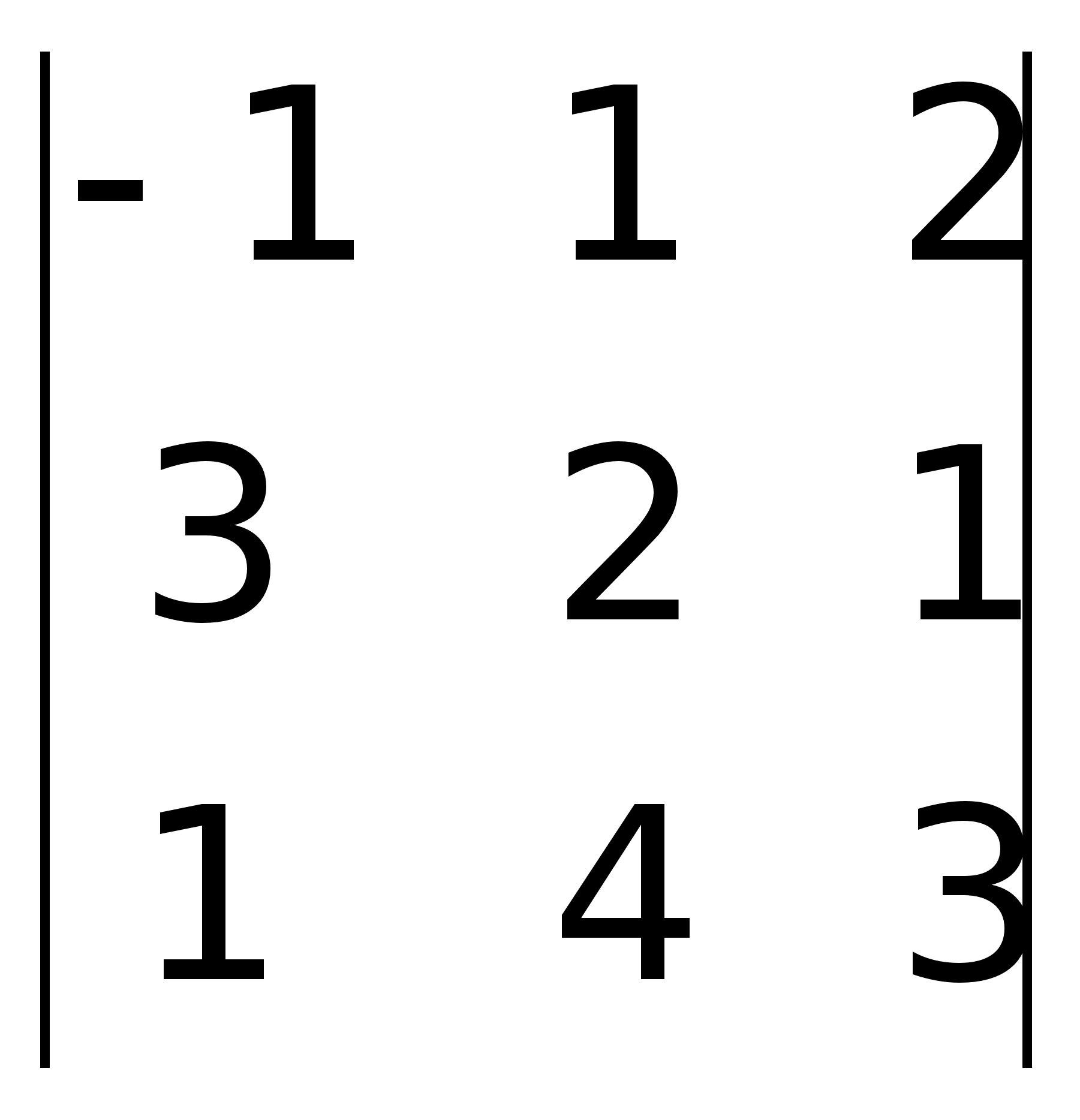 =
-1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 –
8 + 20 = 10.
=
-1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 –
8 + 20 = 10.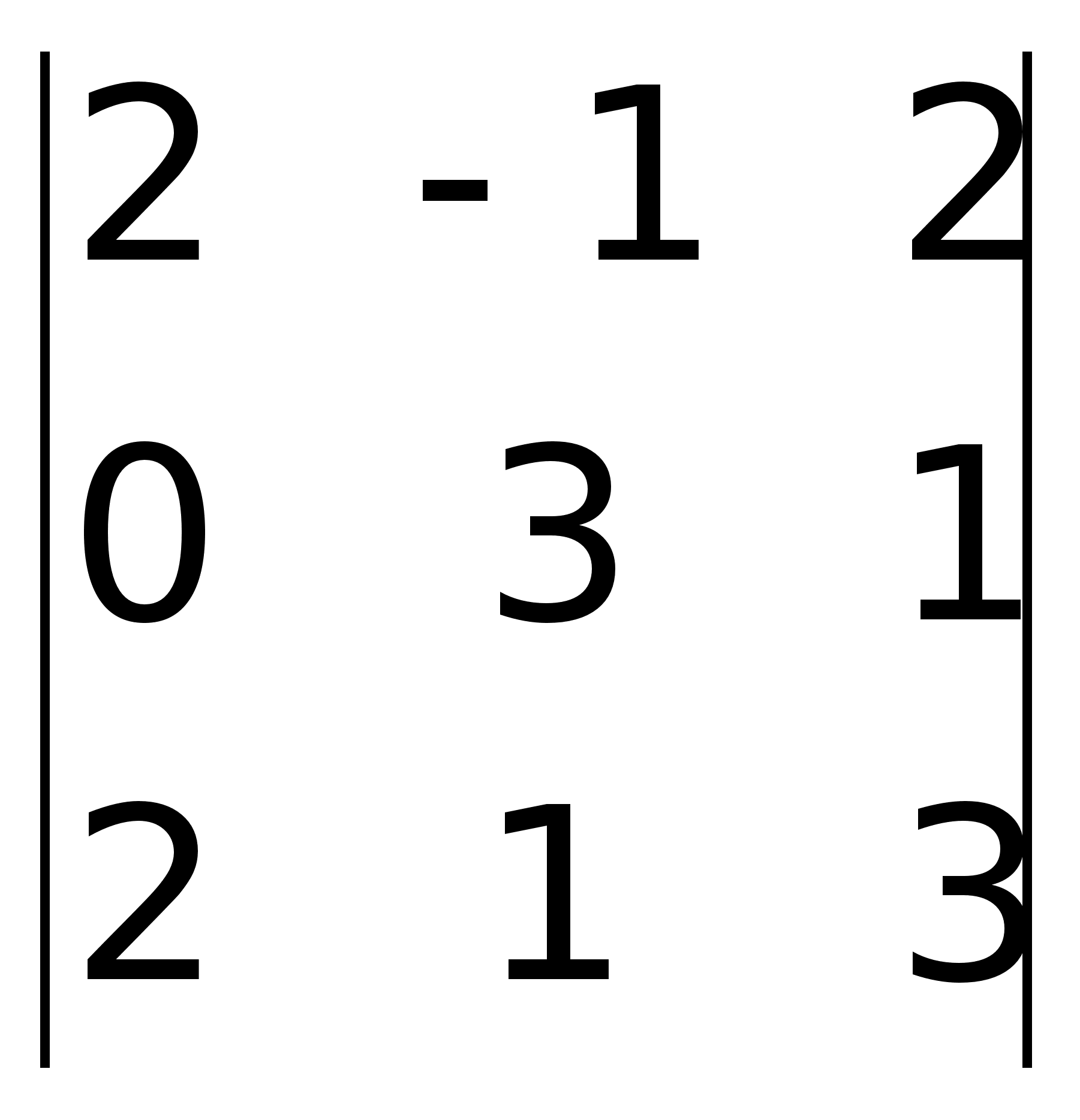 =
=
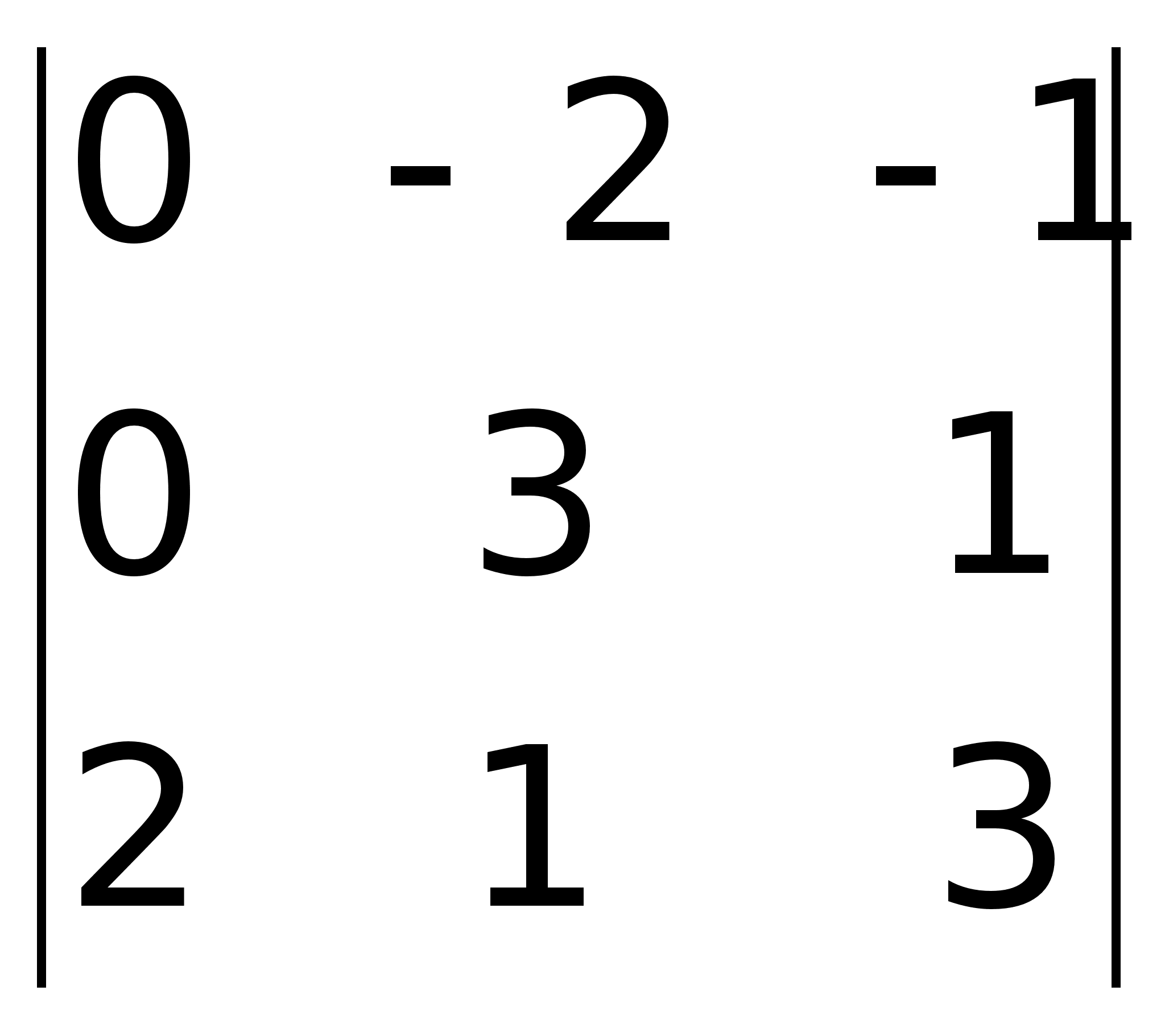 =
2(0 – 2) – 1(0 – 6) = 2.
=
2(0 – 2) – 1(0 – 6) = 2.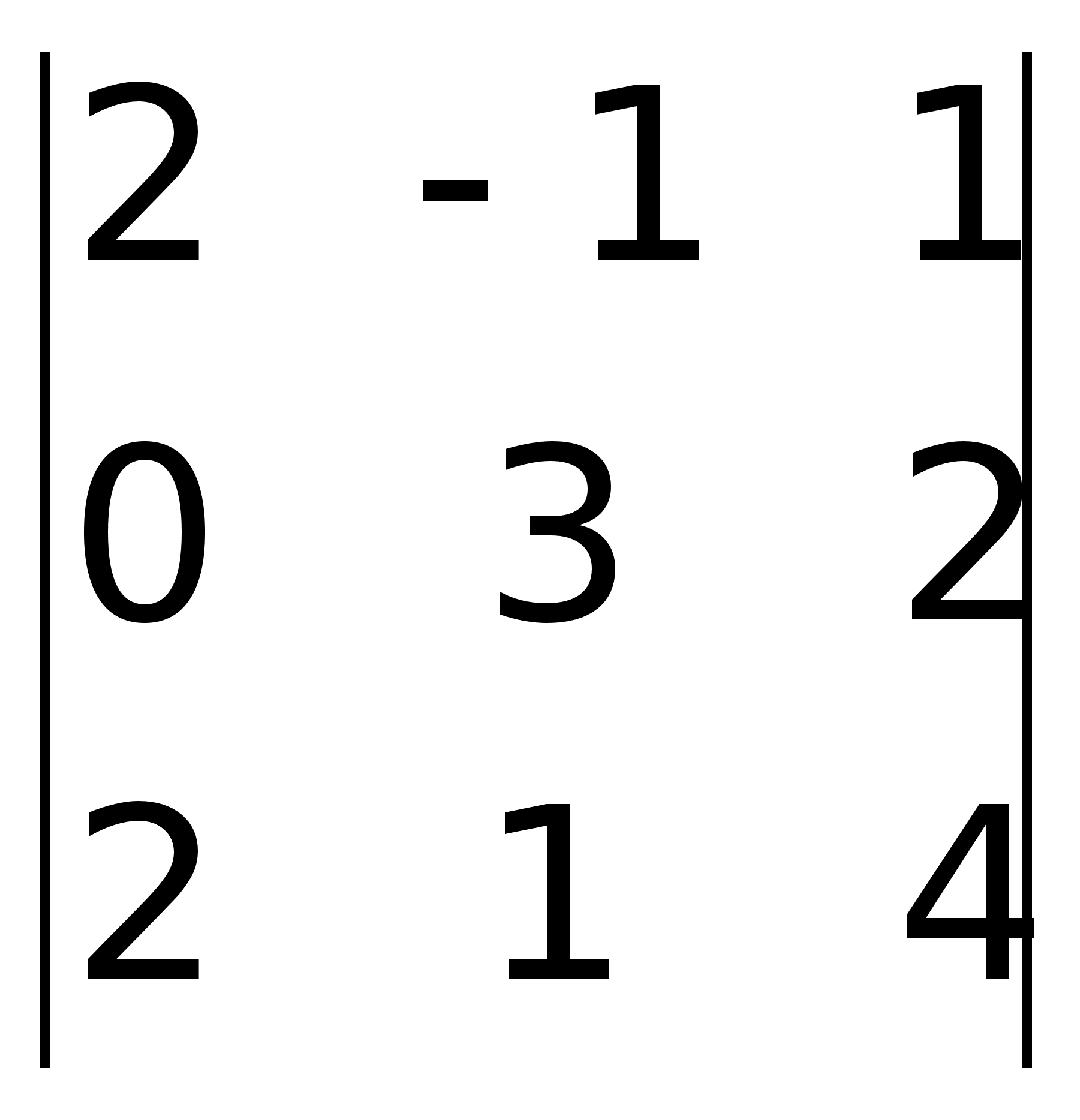 =
=
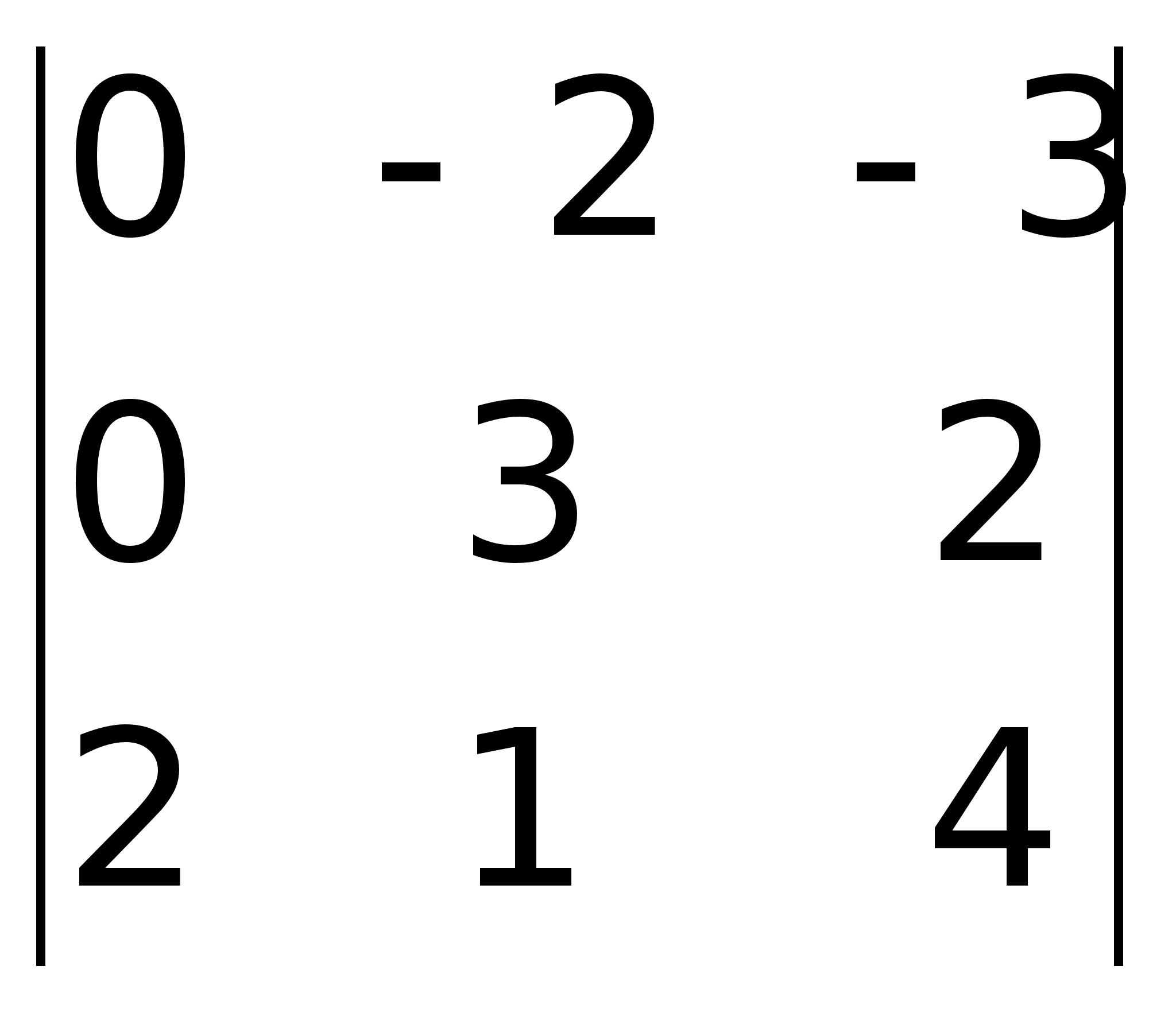 = 2(-4) – 3(-6) = -8 + 18 = 10.Значение
определителя:
-10 + 6 – 40 = -44.
= 2(-4) – 3(-6) = -8 + 18 = 10.Значение
определителя:
-10 + 6 – 40 = -44.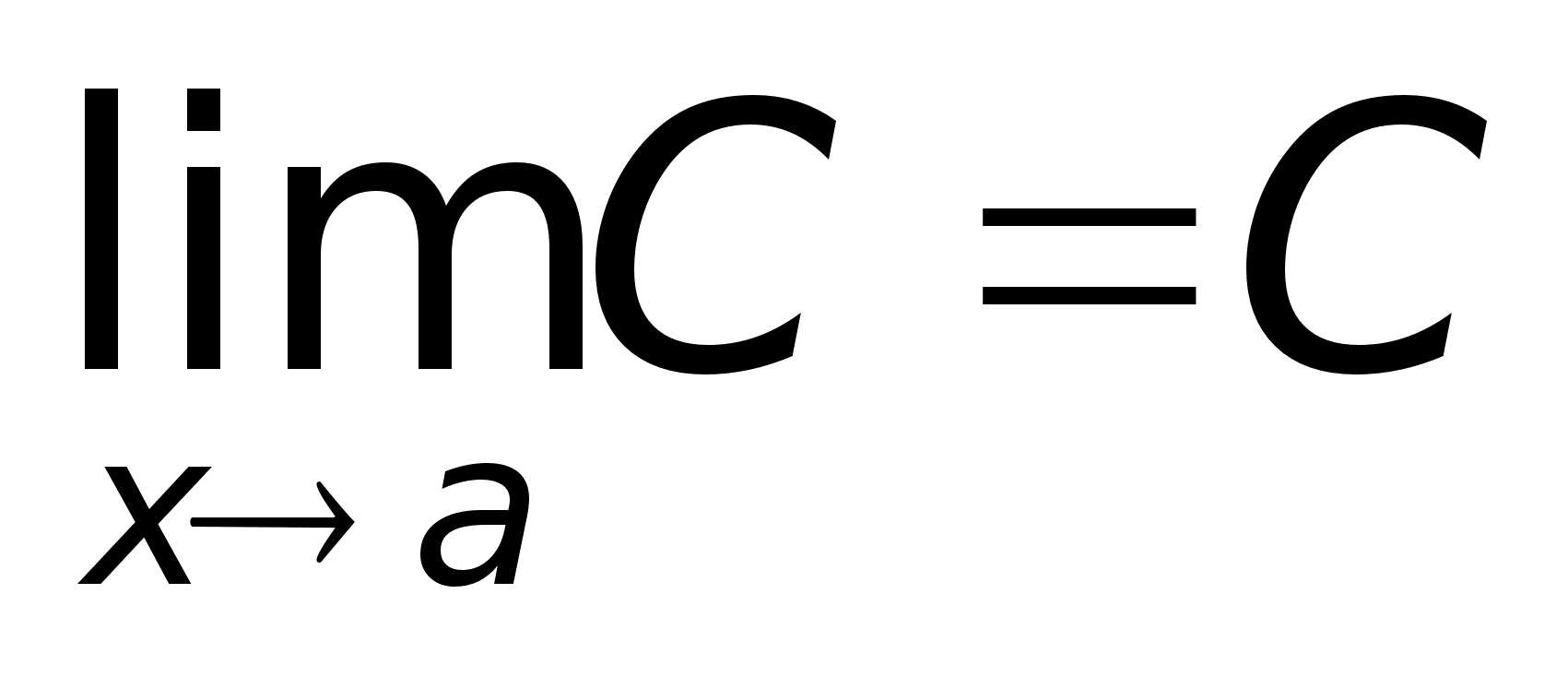 ,
где С = const.Следующие
теоремы справедливы
при предположении,
что функции
f(x)
и g(x)
имеют конечные
пределы при
х
,
где С = const.Следующие
теоремы справедливы
при предположении,
что функции
f(x)
и g(x)
имеют конечные
пределы при
х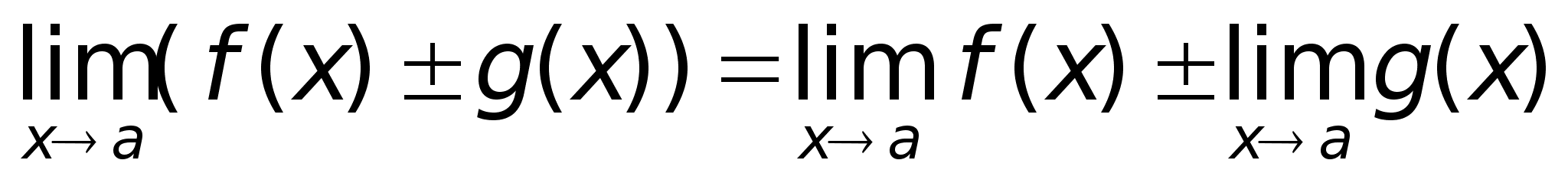 Доказательство
этой теоремы
будет приведено
ниже.Теорема
3.
Доказательство
этой теоремы
будет приведено
ниже.Теорема
3.
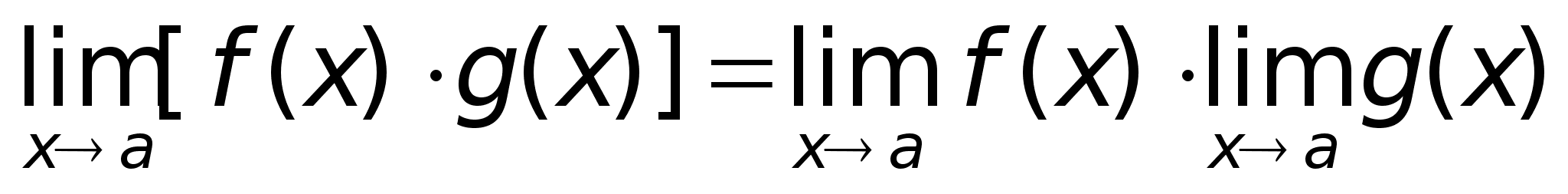 Следствие.
Следствие.
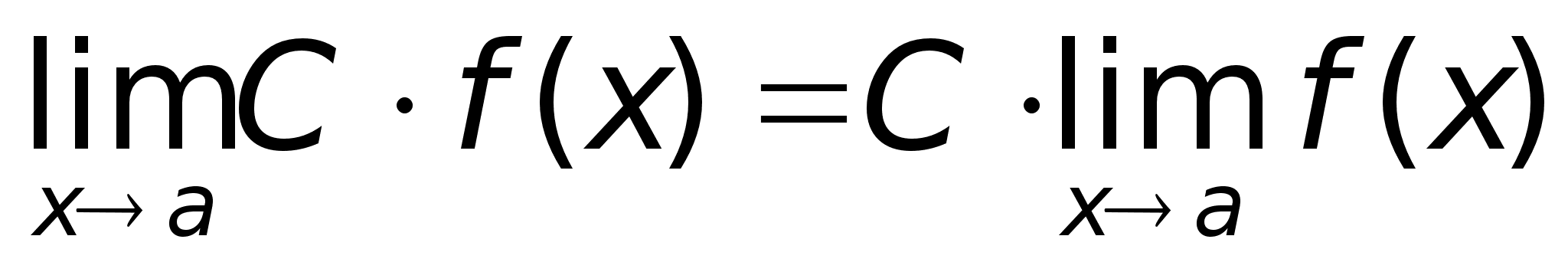 Теорема
4.
Теорема
4.
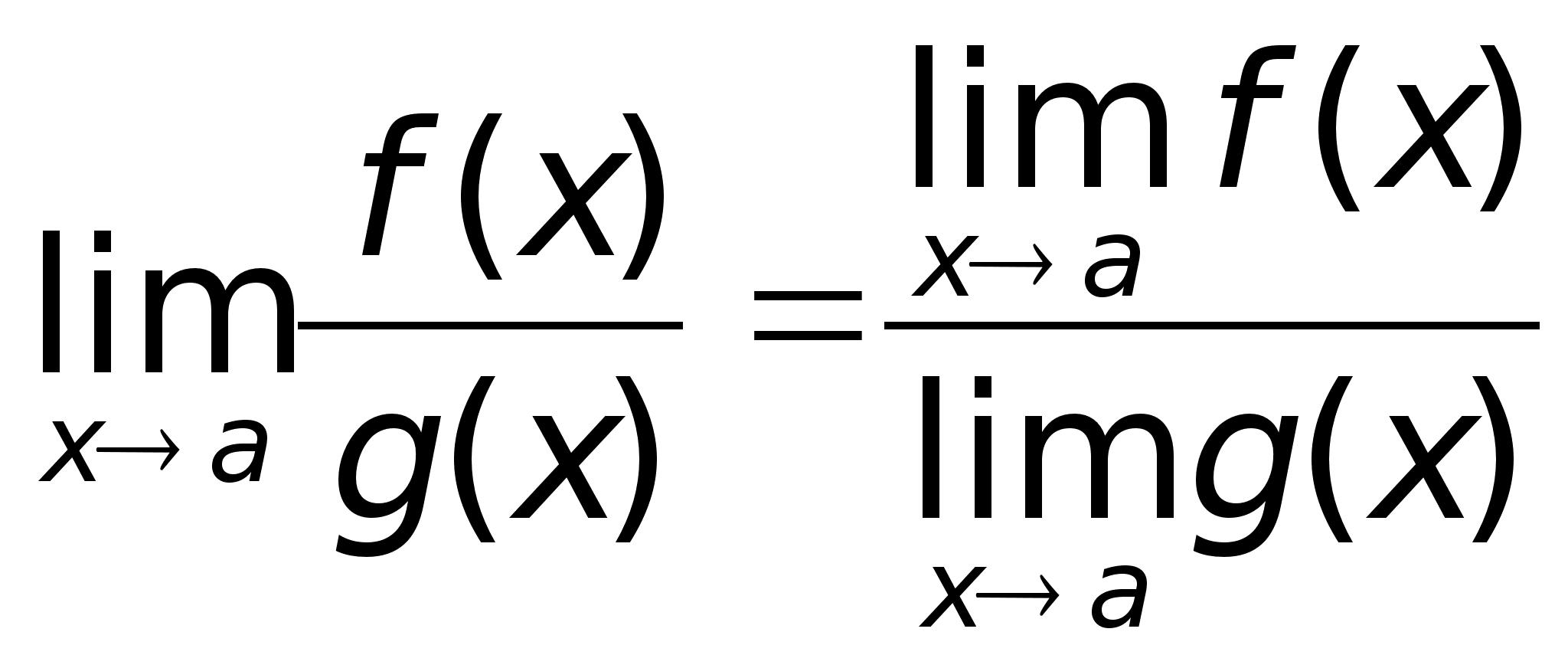 при
при
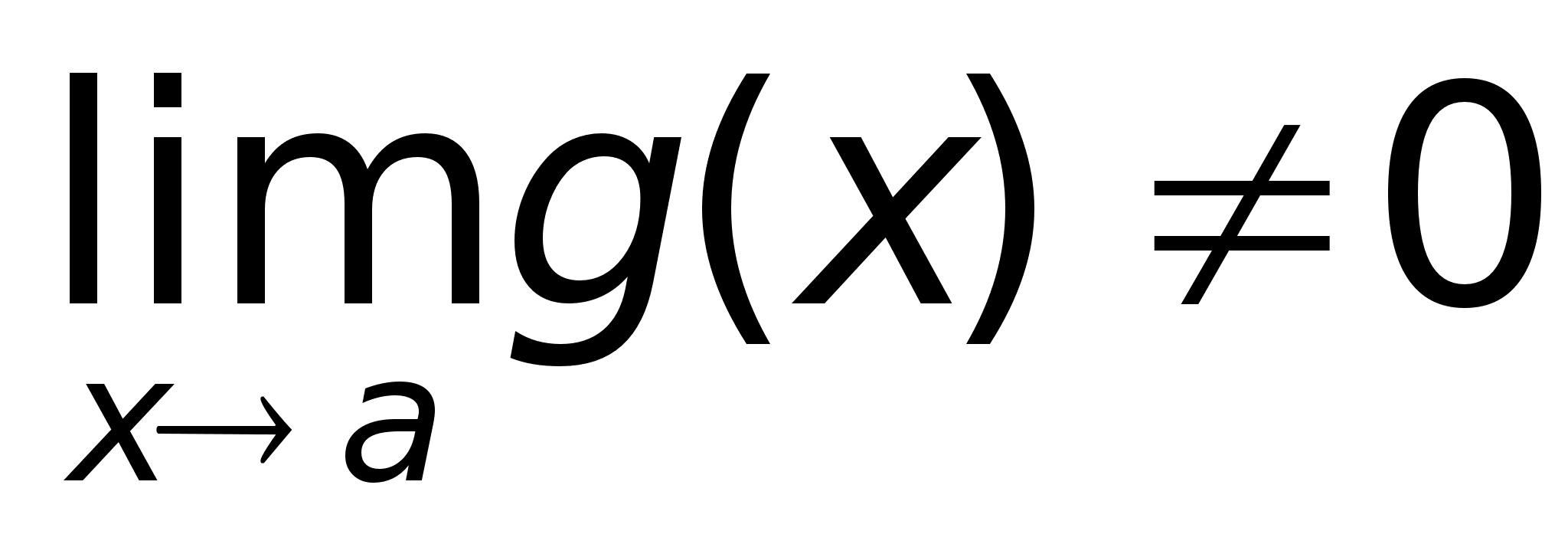 Теорема
5. Если
f(x)>0
вблизи точки
х = а и
Теорема
5. Если
f(x)>0
вблизи точки
х = а и
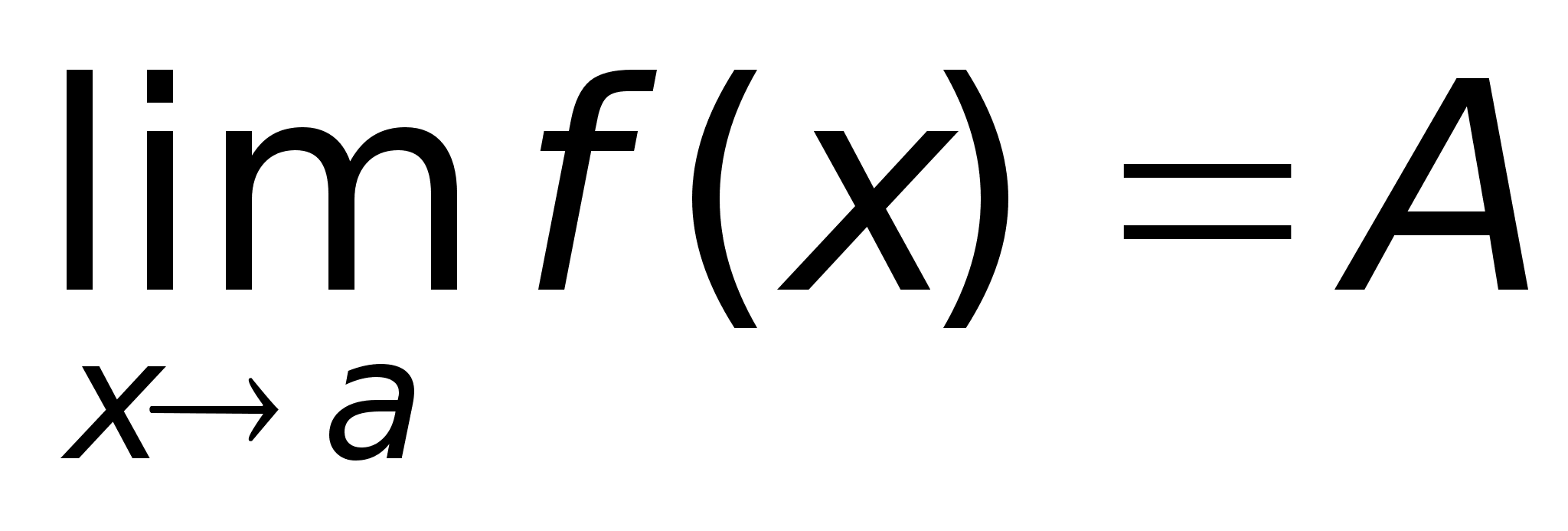 ,
то А>0.Аналогично
определяется
знак предела
при f(x)
< 0, f(x)
,
то А>0.Аналогично
определяется
знак предела
при f(x)
< 0, f(x)
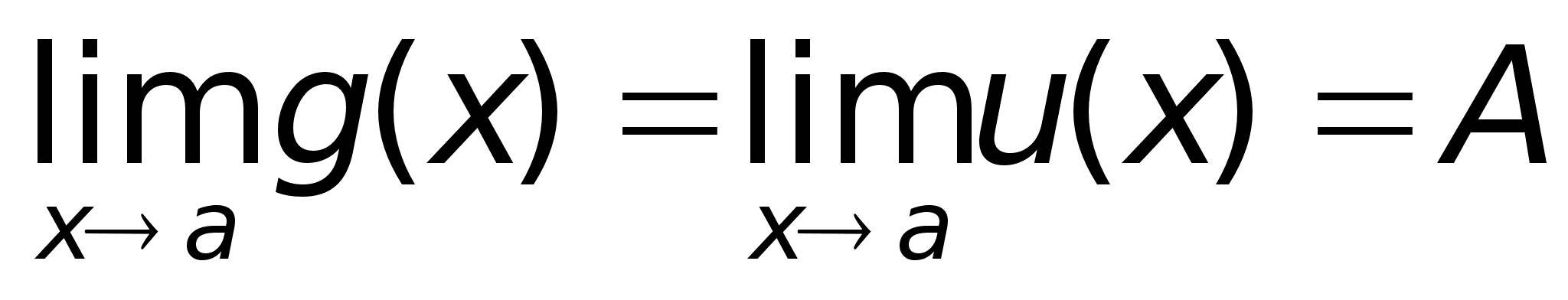 ,
то и
,
то и
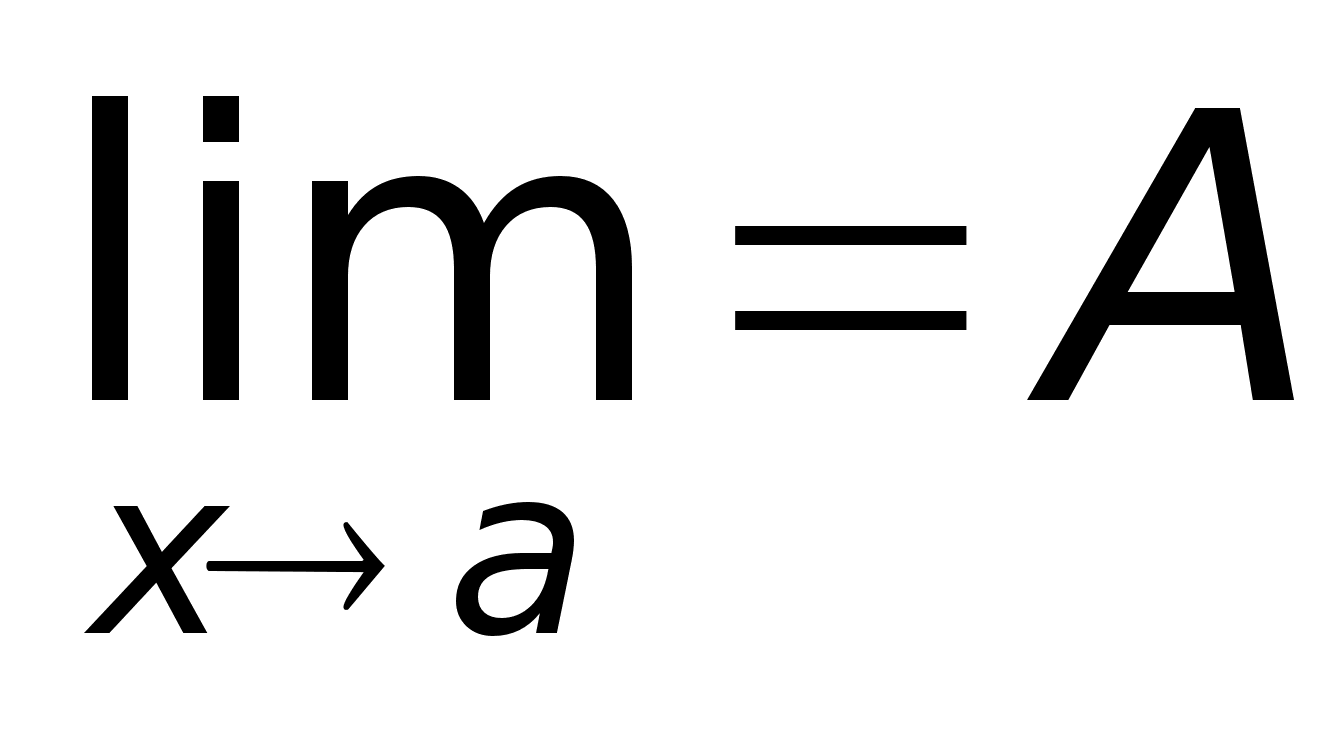 .
.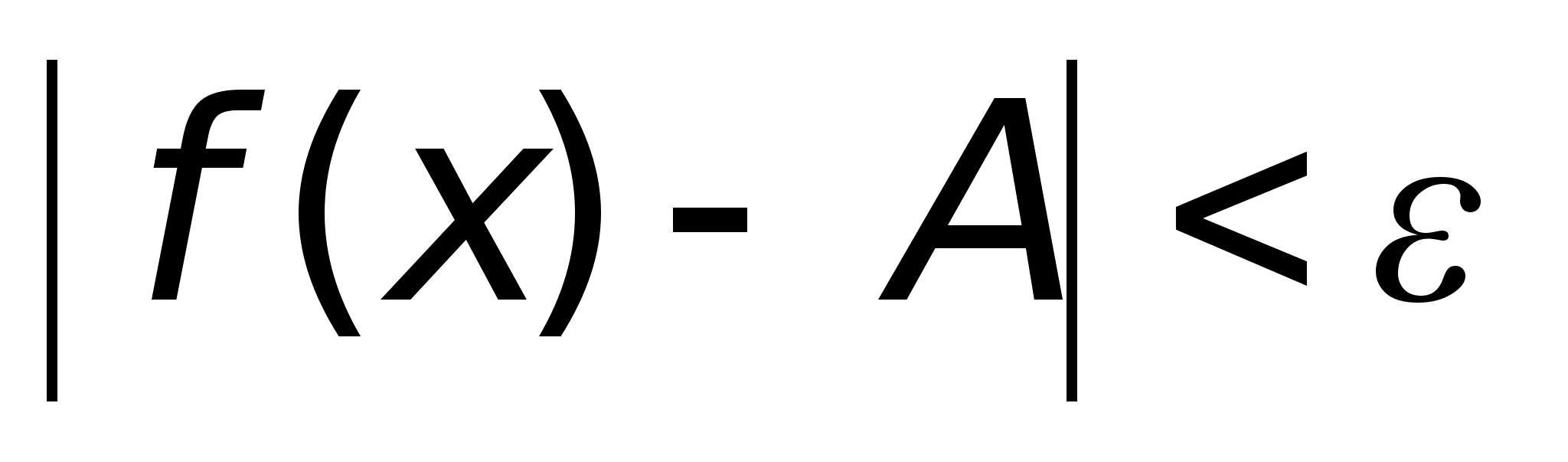 ,
тогда
,
тогда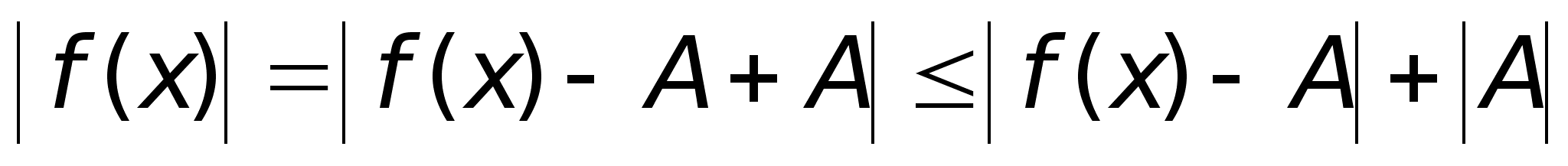 или
или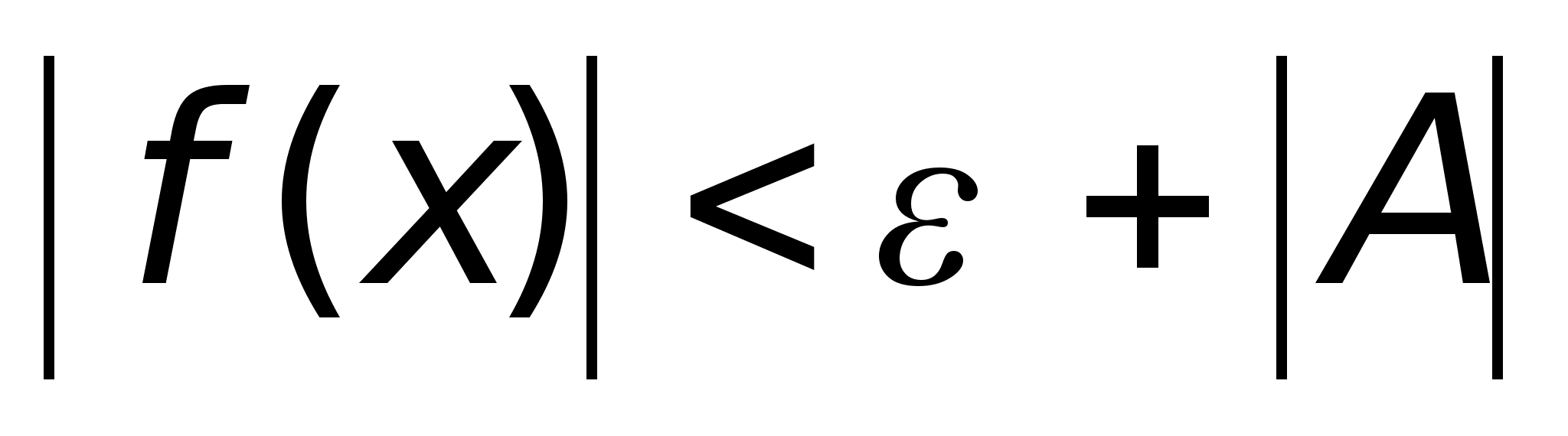 ,
.е.
,
.е.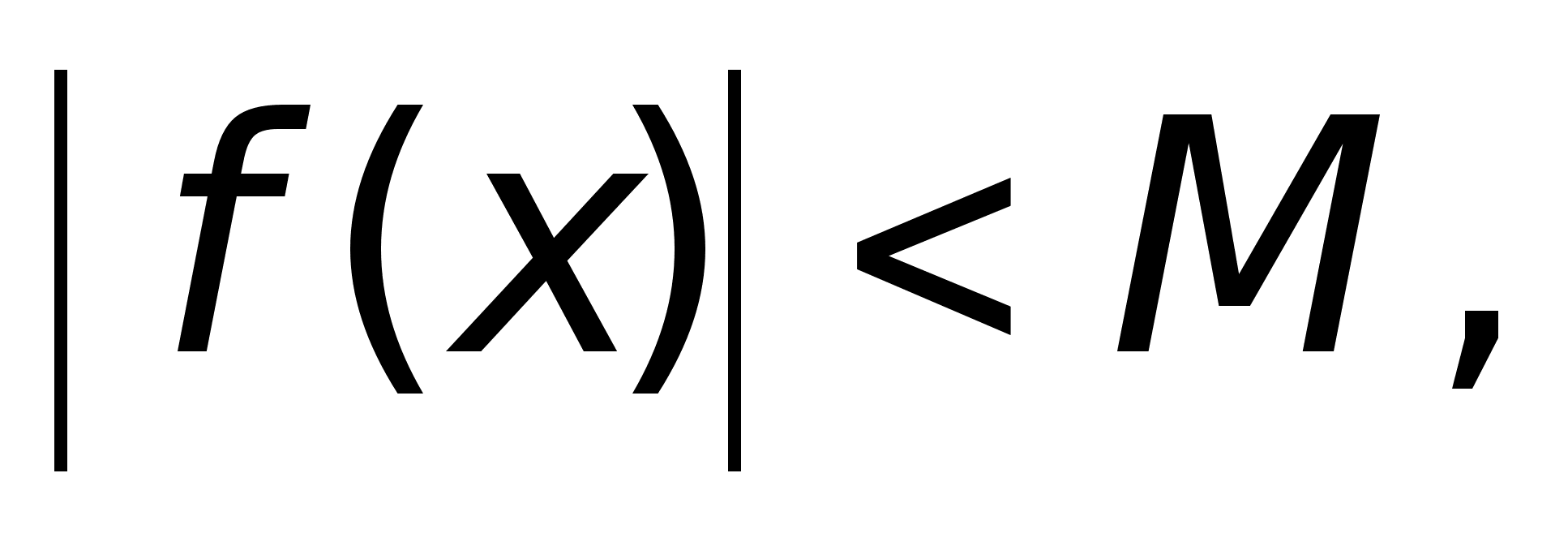 где
М =
где
М = 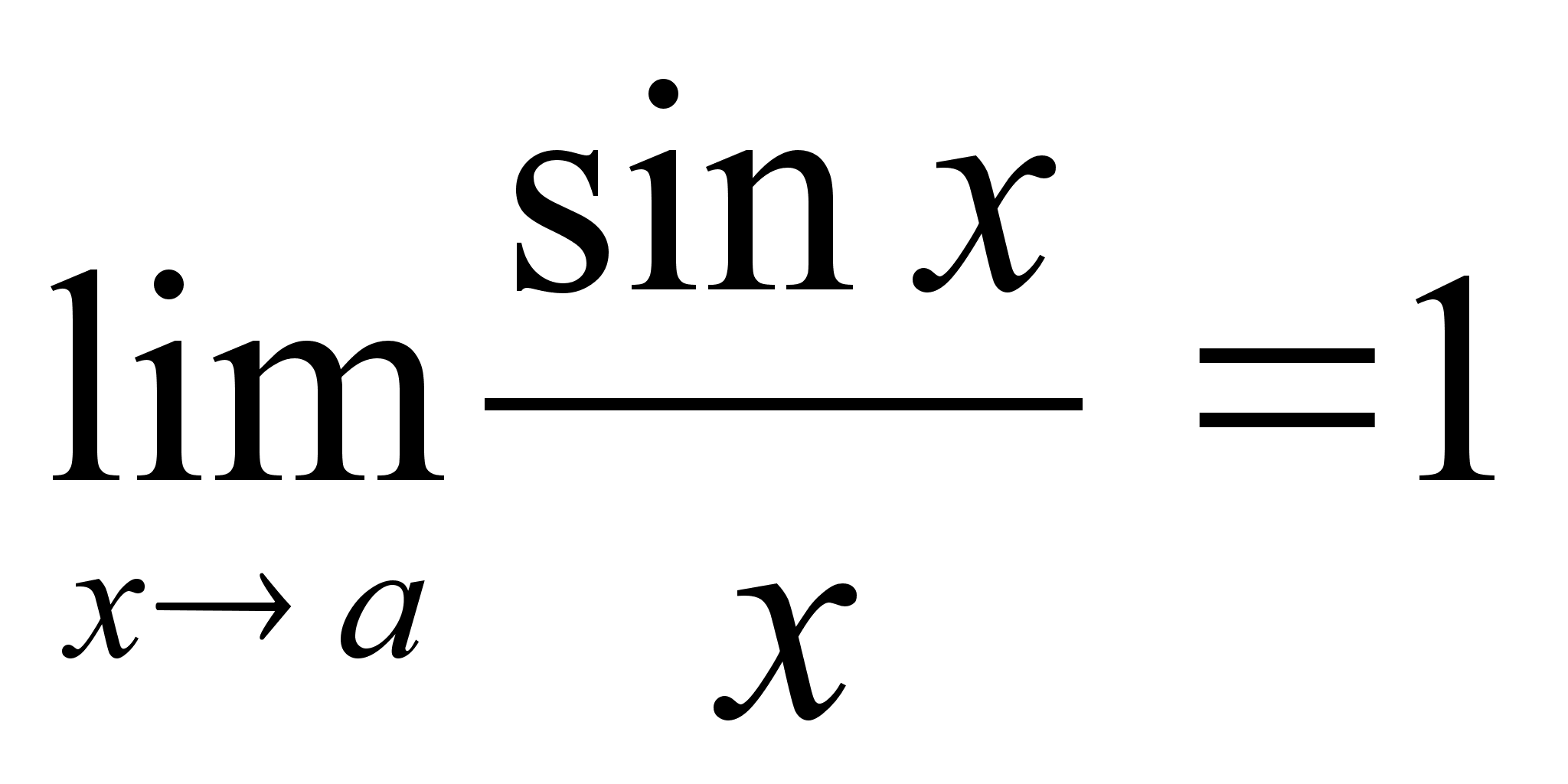 Доказательство:
докажем для
Доказательство:
докажем для
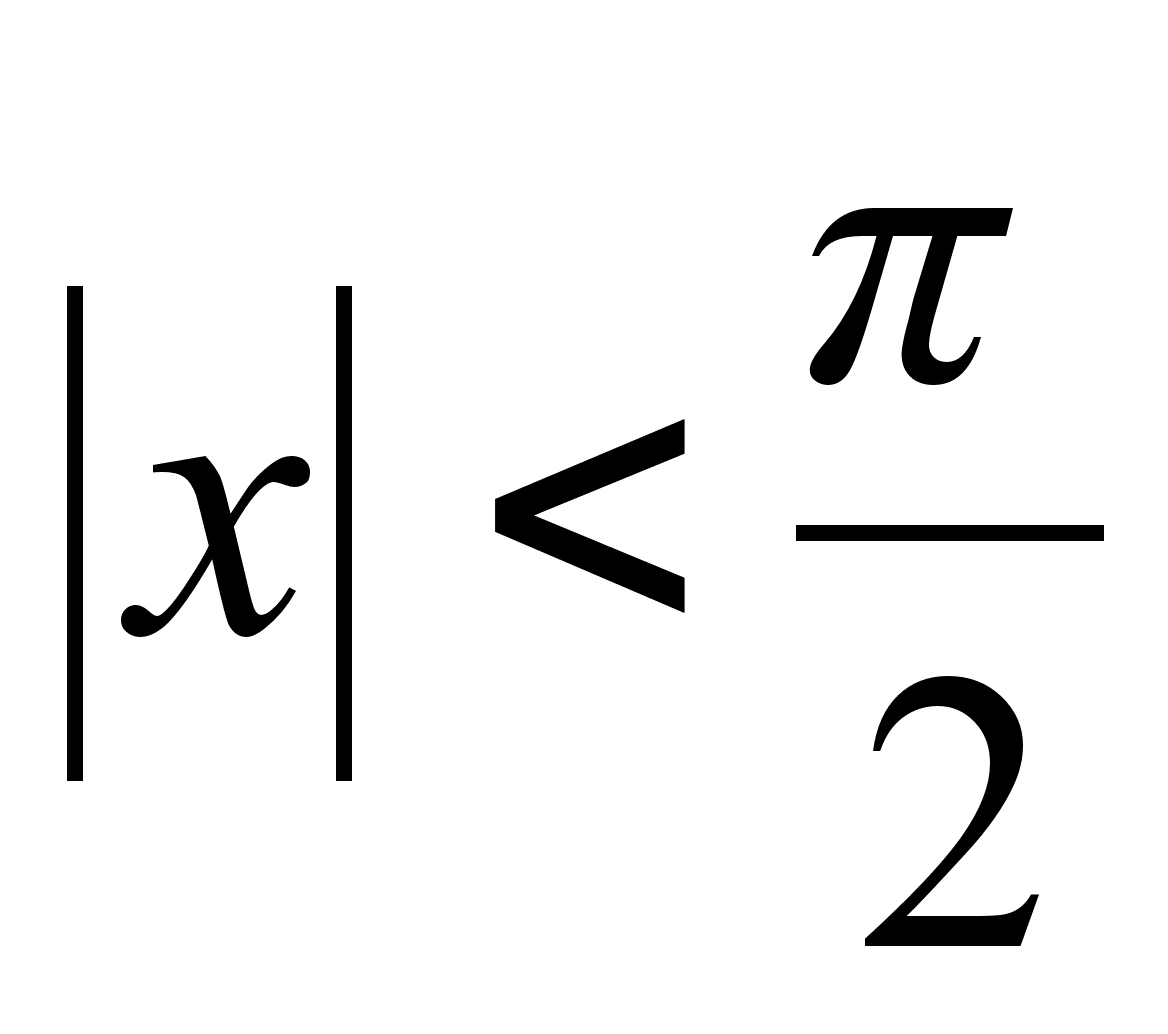 справедливость
неравенства
справедливость
неравенства
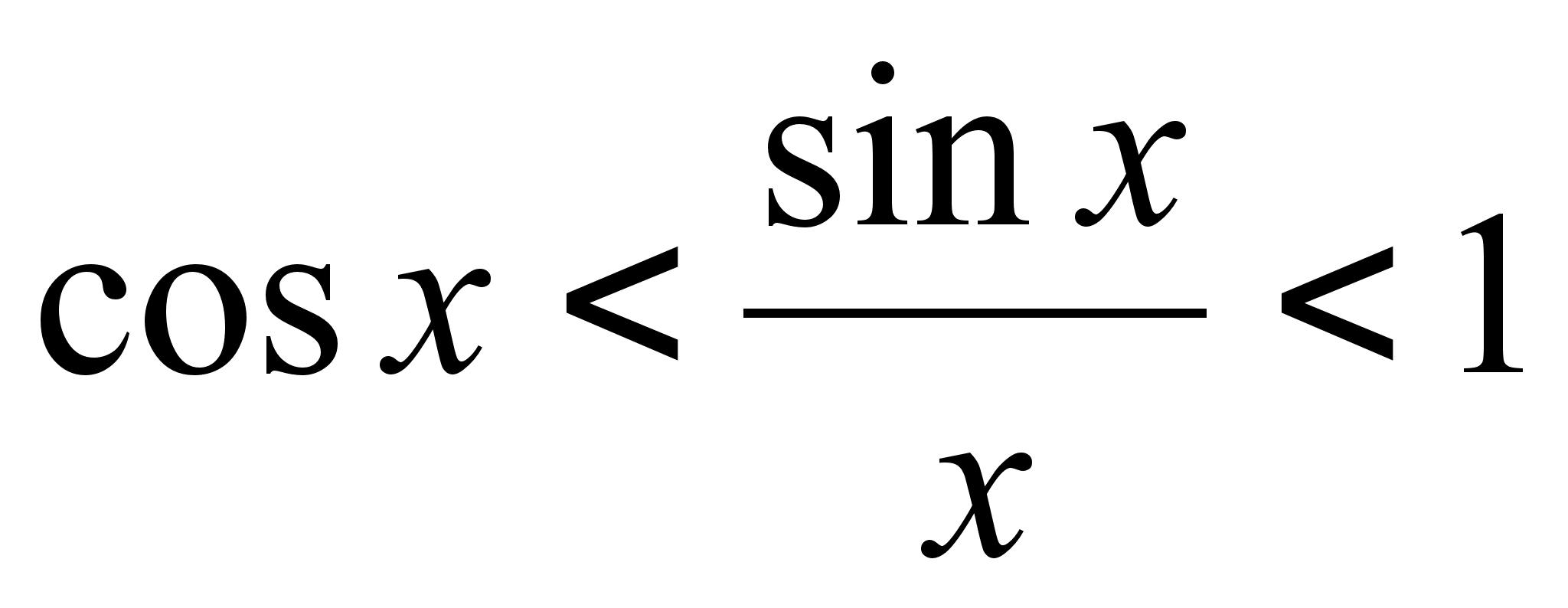
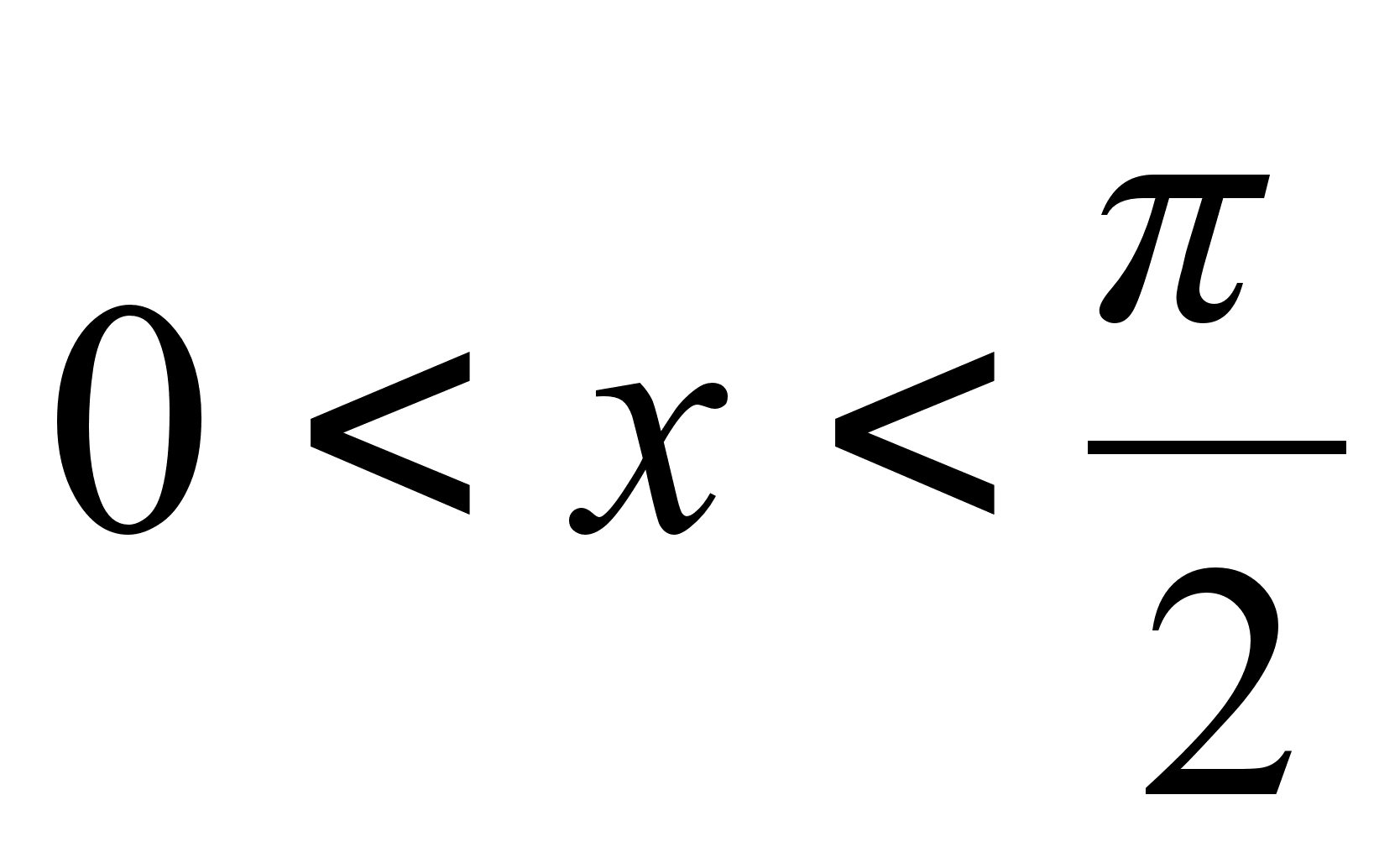 Из рисунка
видно, что площадь
кругового
сектора
Из рисунка
видно, что площадь
кругового
сектора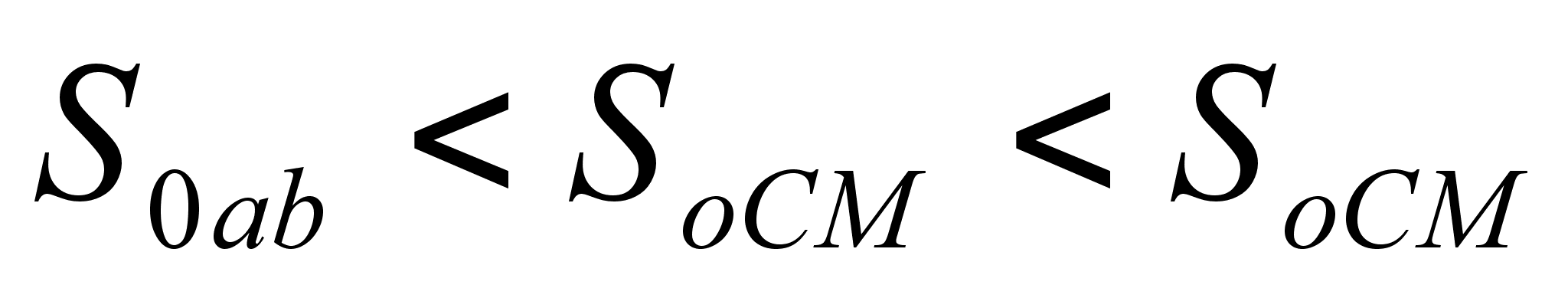
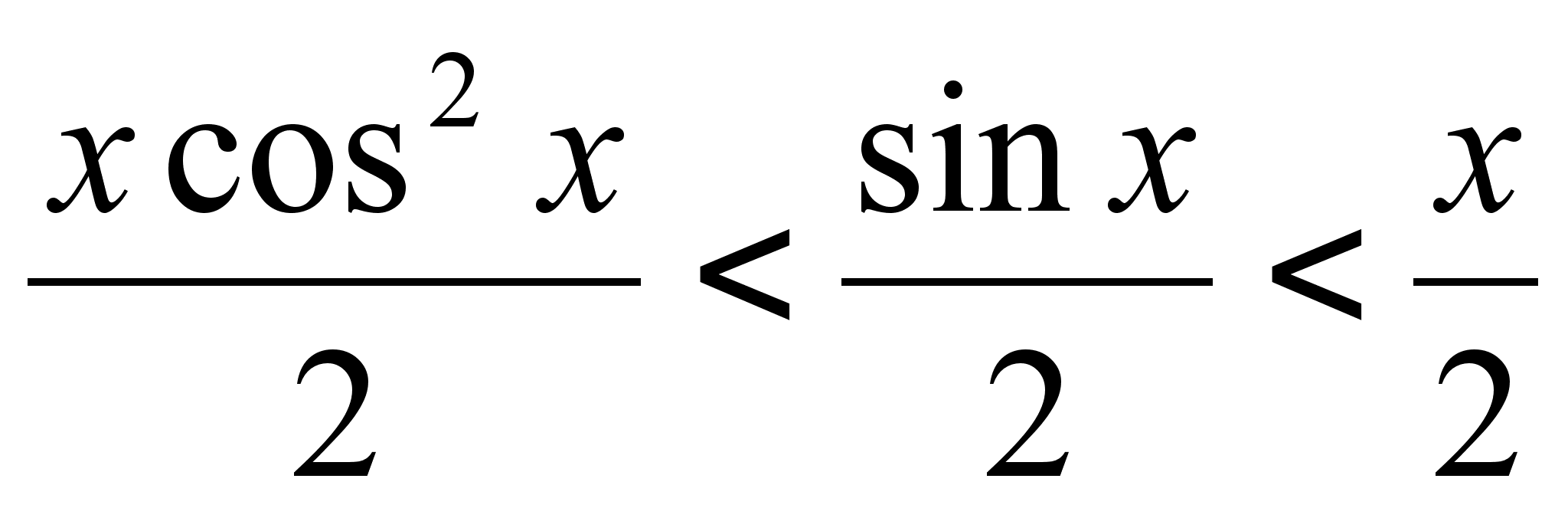 ,
так как х>0,
то
,
так как х>0,
то
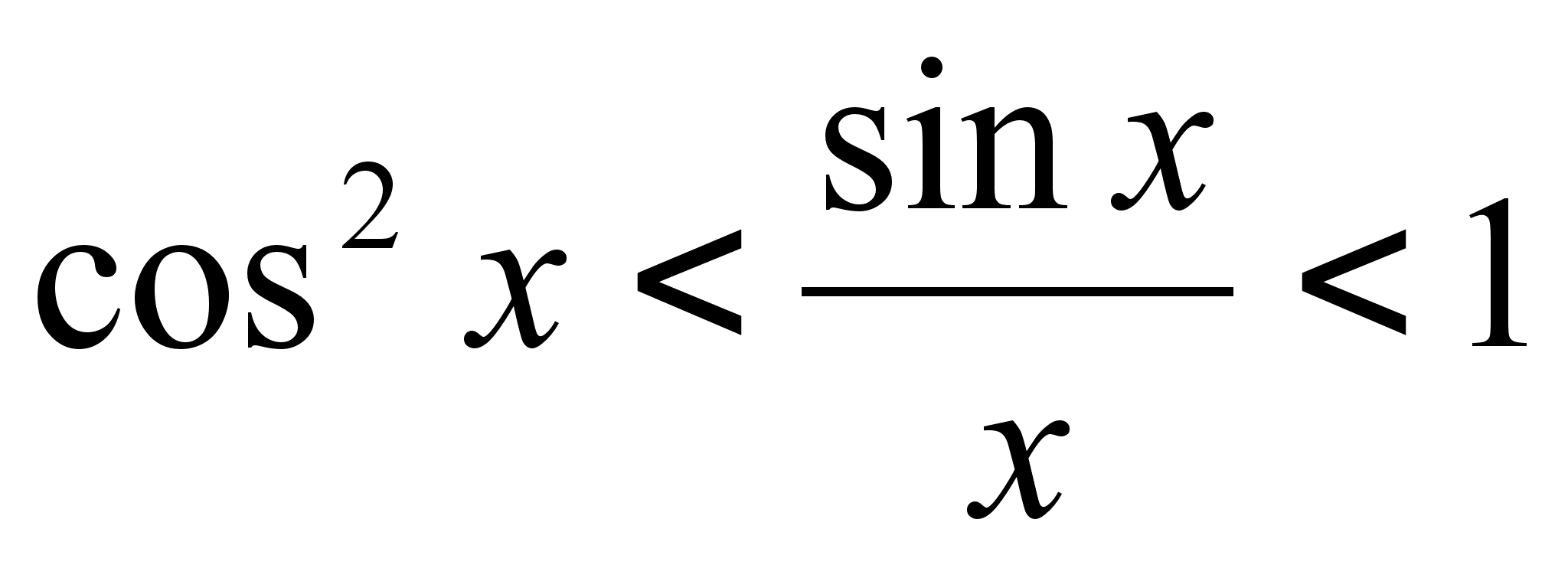 ,
,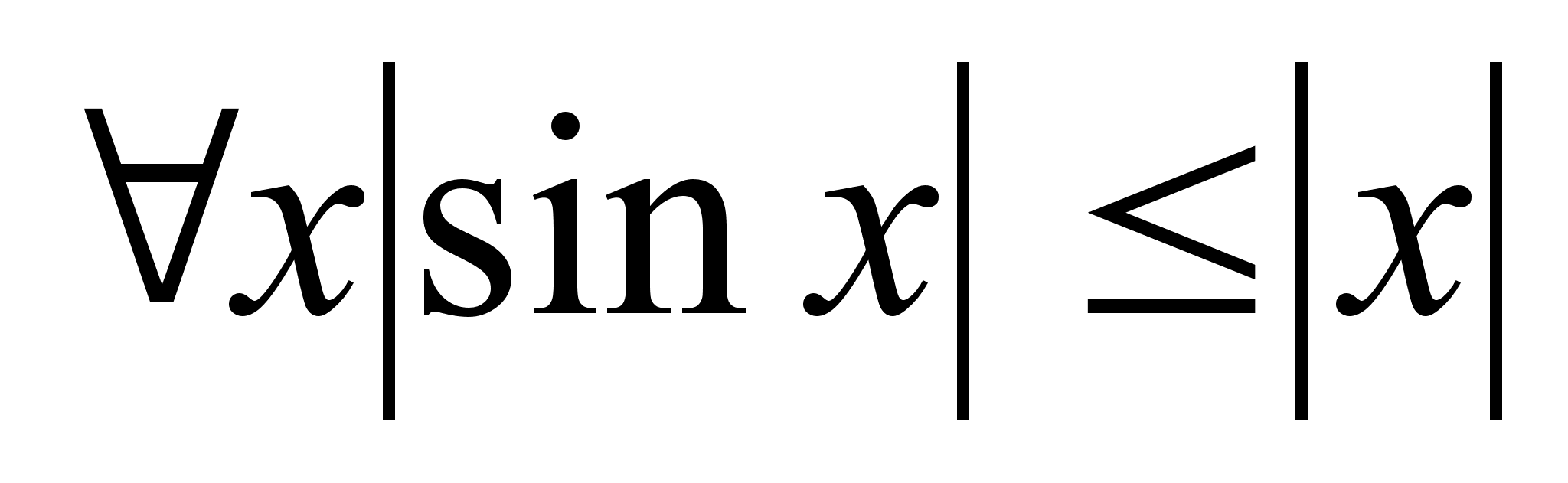
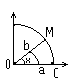
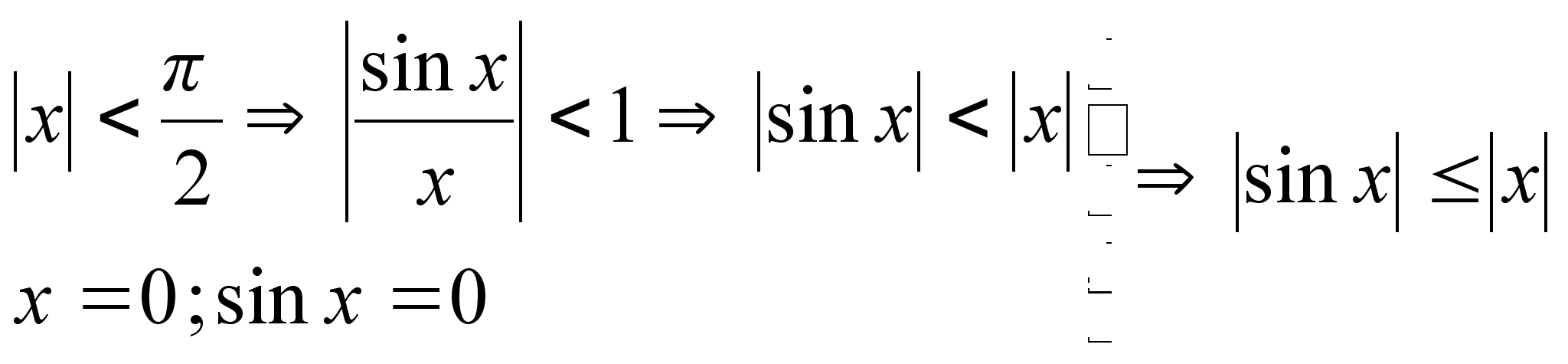
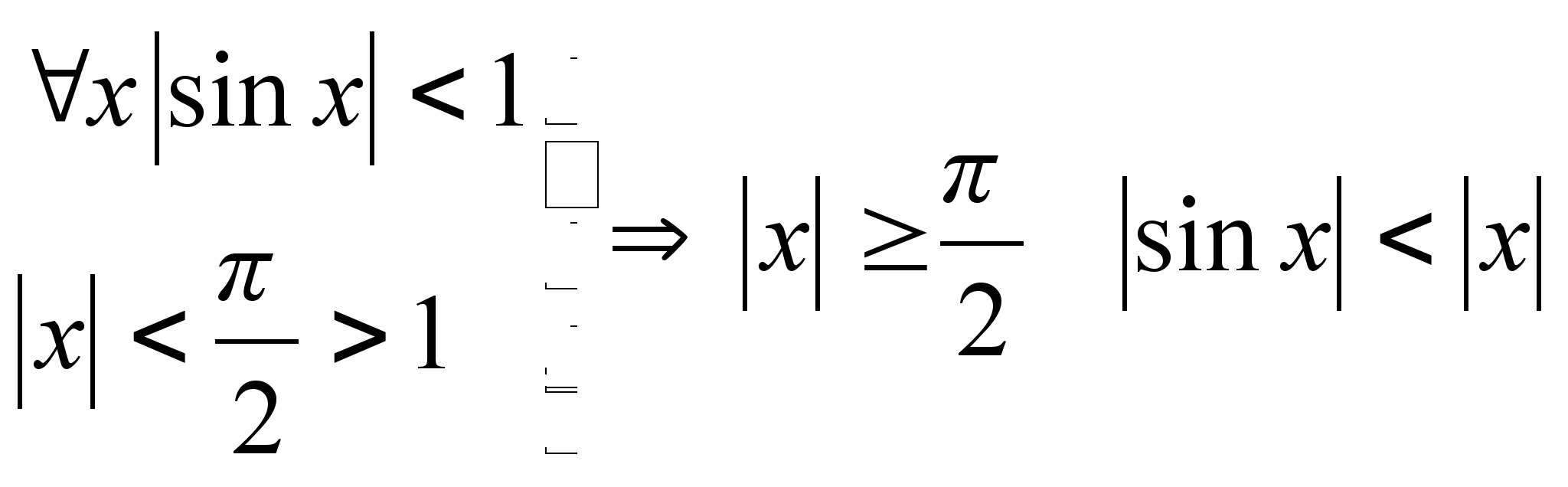
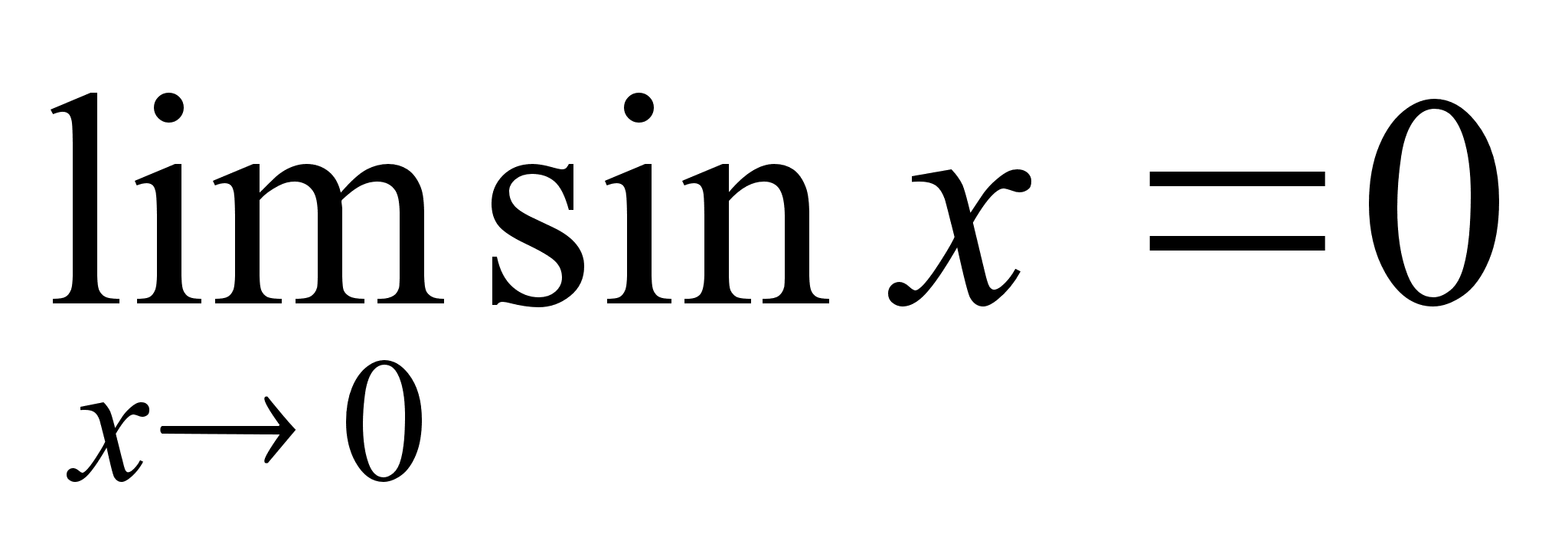
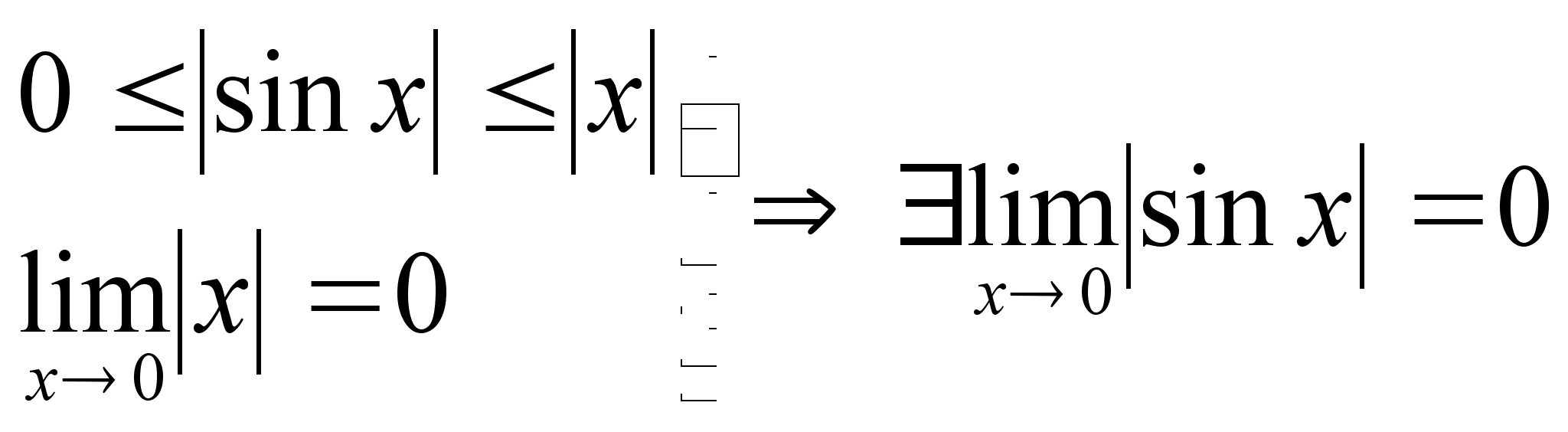
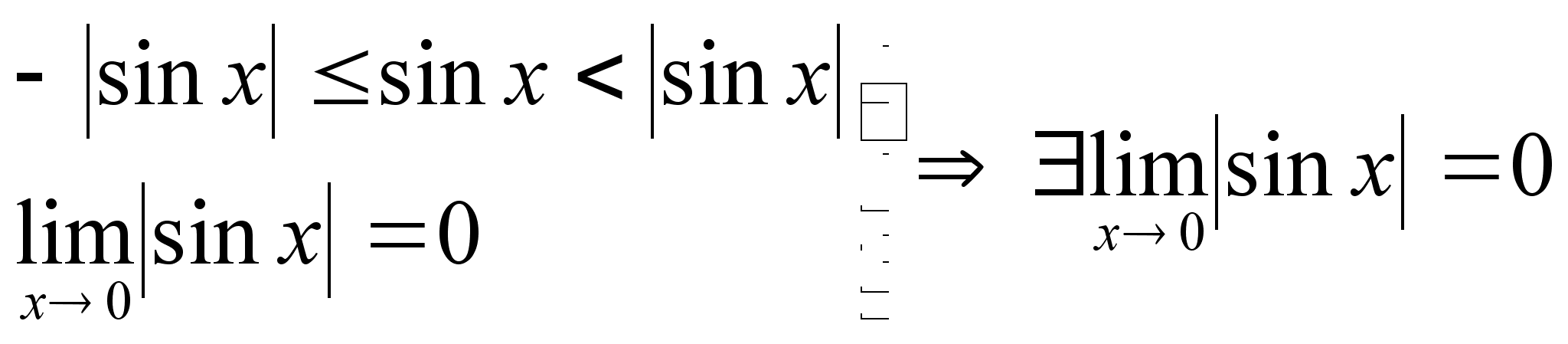
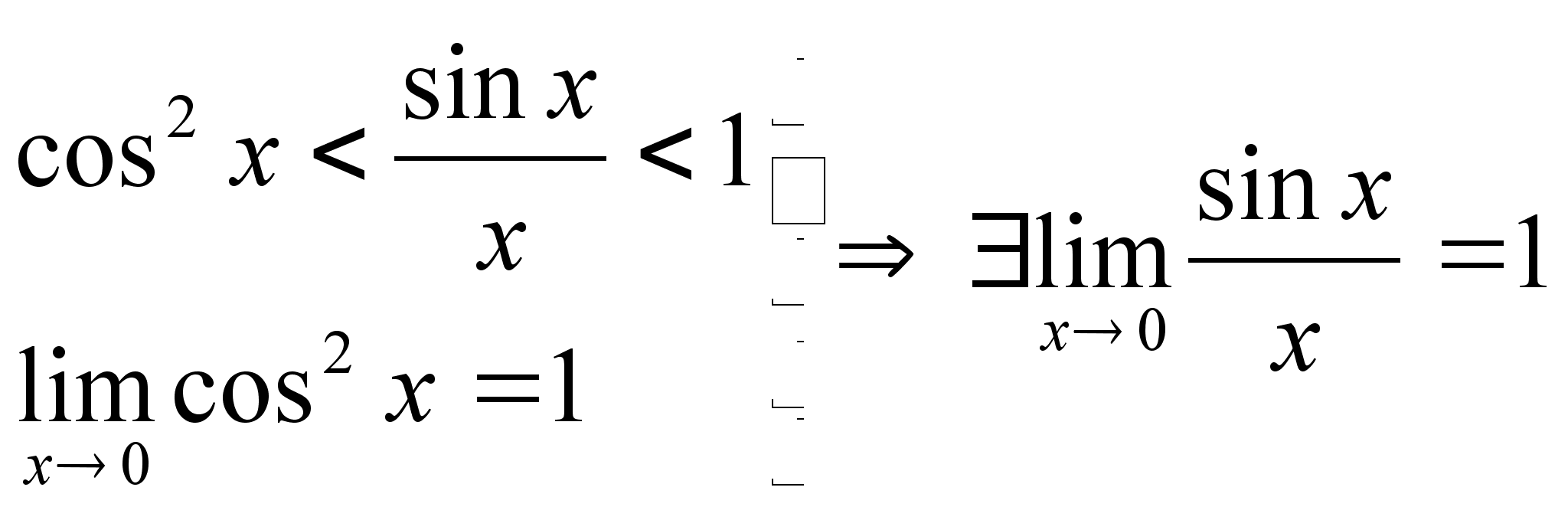
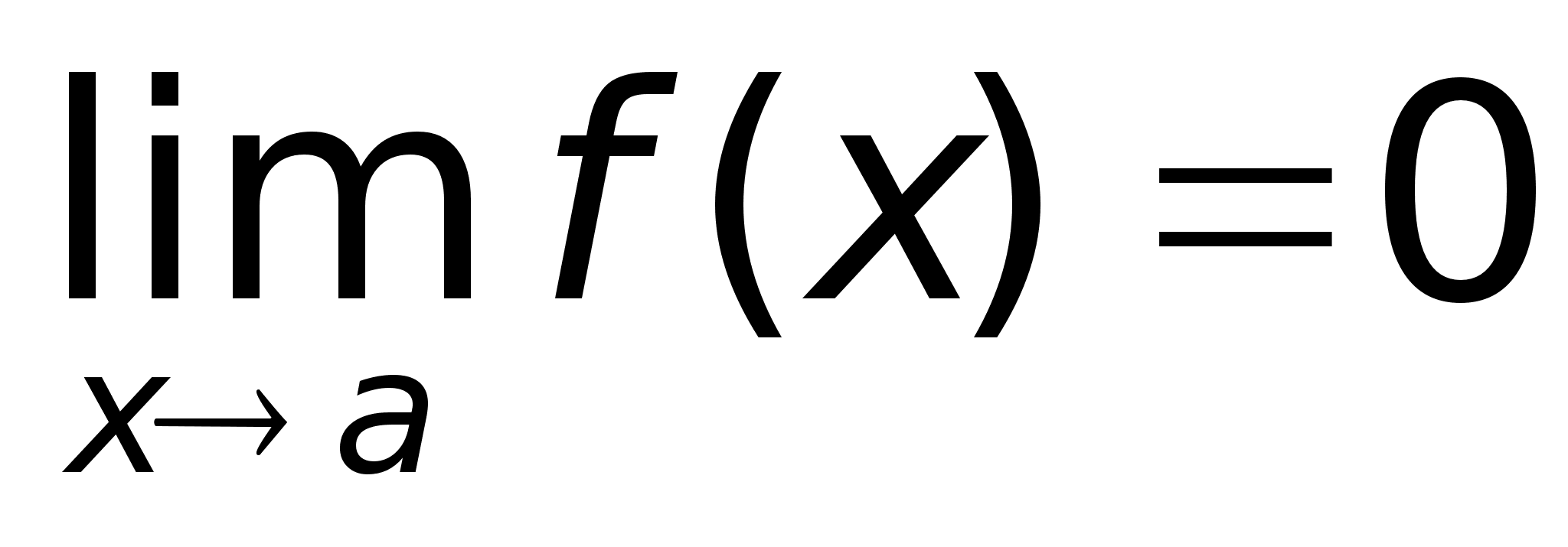 .Бесконечно
малой функция
может быть
только если
указать к какому
числу стремится
аргумент х.
При различных
значениях а
функция может
быть бесконечно
малой или
нет.Пример.
Функция f(x)
= xn
является
бесконечно
малой при х
.Бесконечно
малой функция
может быть
только если
указать к какому
числу стремится
аргумент х.
При различных
значениях а
функция может
быть бесконечно
малой или
нет.Пример.
Функция f(x)
= xn
является
бесконечно
малой при х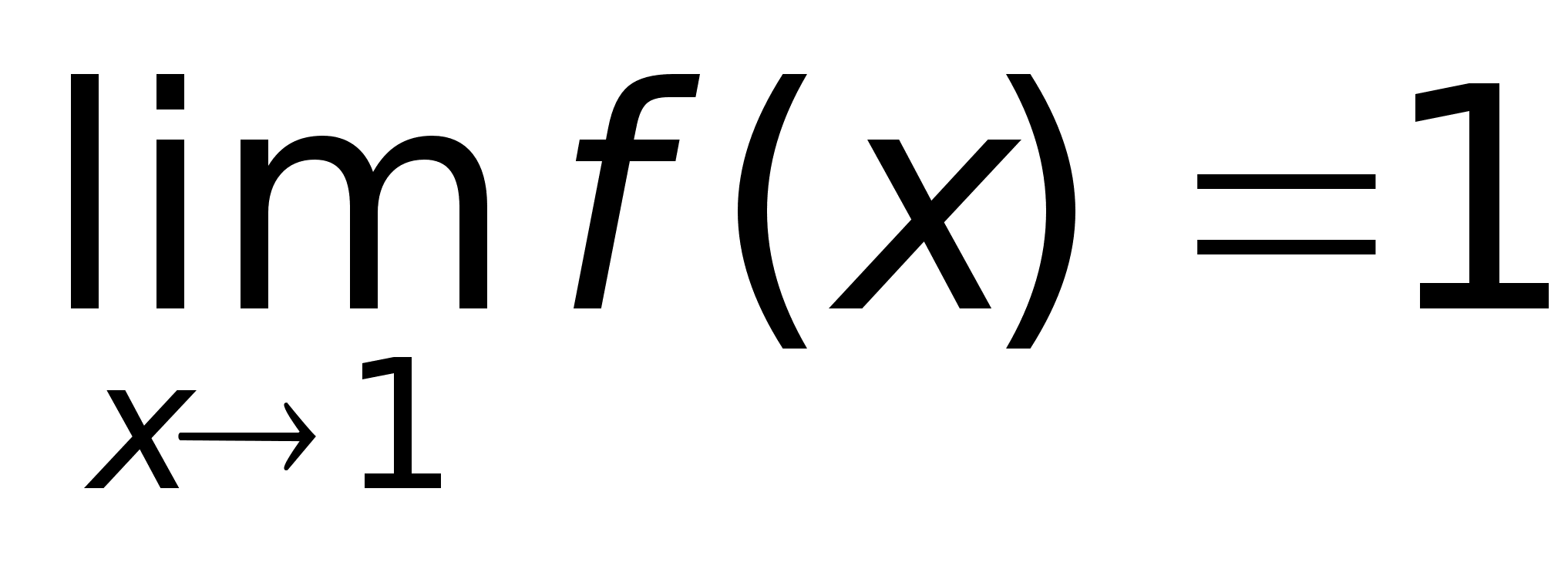 .Теорема.
Для
того, чтобы
функция f(x)
при ха
имела предел,
равный А, необходимо
и достаточно,
чтобы вблизи
точки х = а выполнялось
условие f(x)
= A
+ (x),где
(х)
– бесконечно
малая при х
а ((х)0
при х
а). Свойства
бесконечно
малых функций:
.Теорема.
Для
того, чтобы
функция f(x)
при ха
имела предел,
равный А, необходимо
и достаточно,
чтобы вблизи
точки х = а выполнялось
условие f(x)
= A
+ (x),где
(х)
– бесконечно
малая при х
а ((х)0
при х
а). Свойства
бесконечно
малых функций: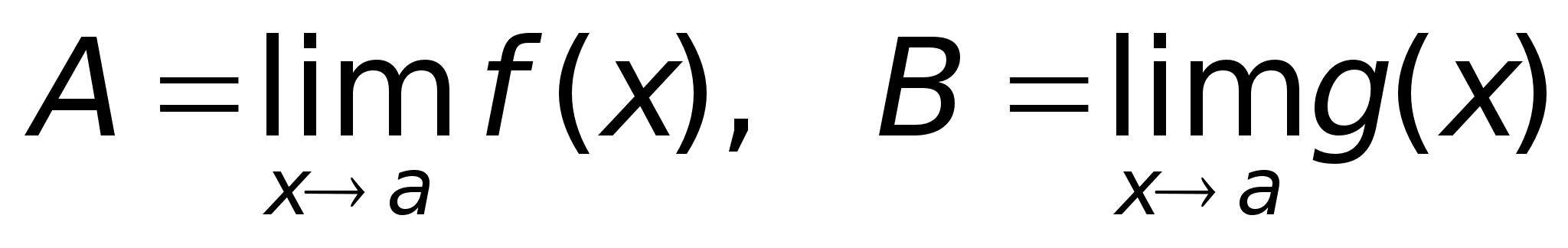 ,
тогдаf(x)
,
тогдаf(x)
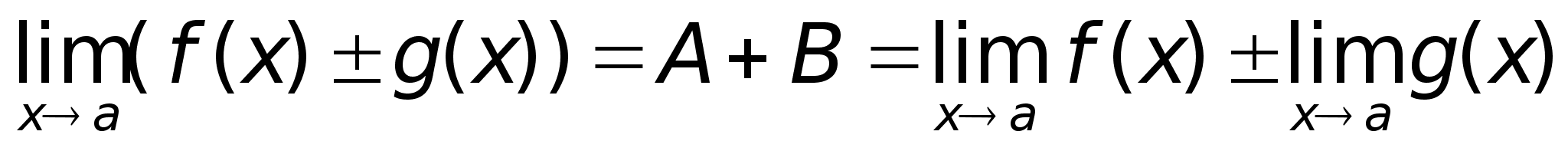
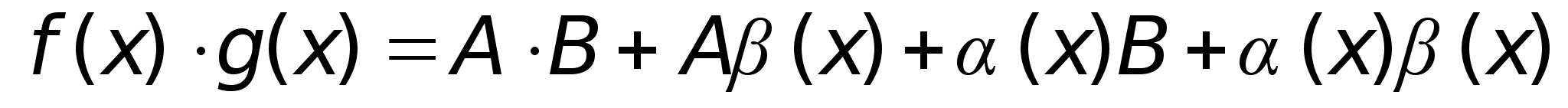
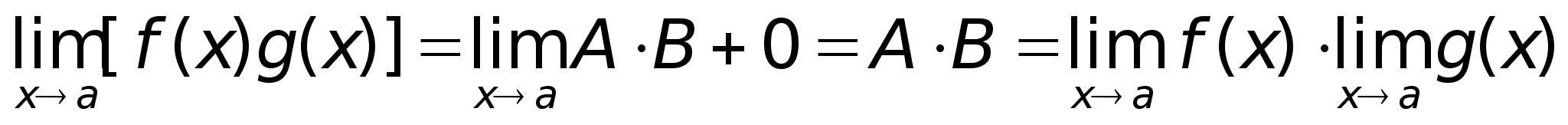 Теорема
доказана.
Теорема
доказана.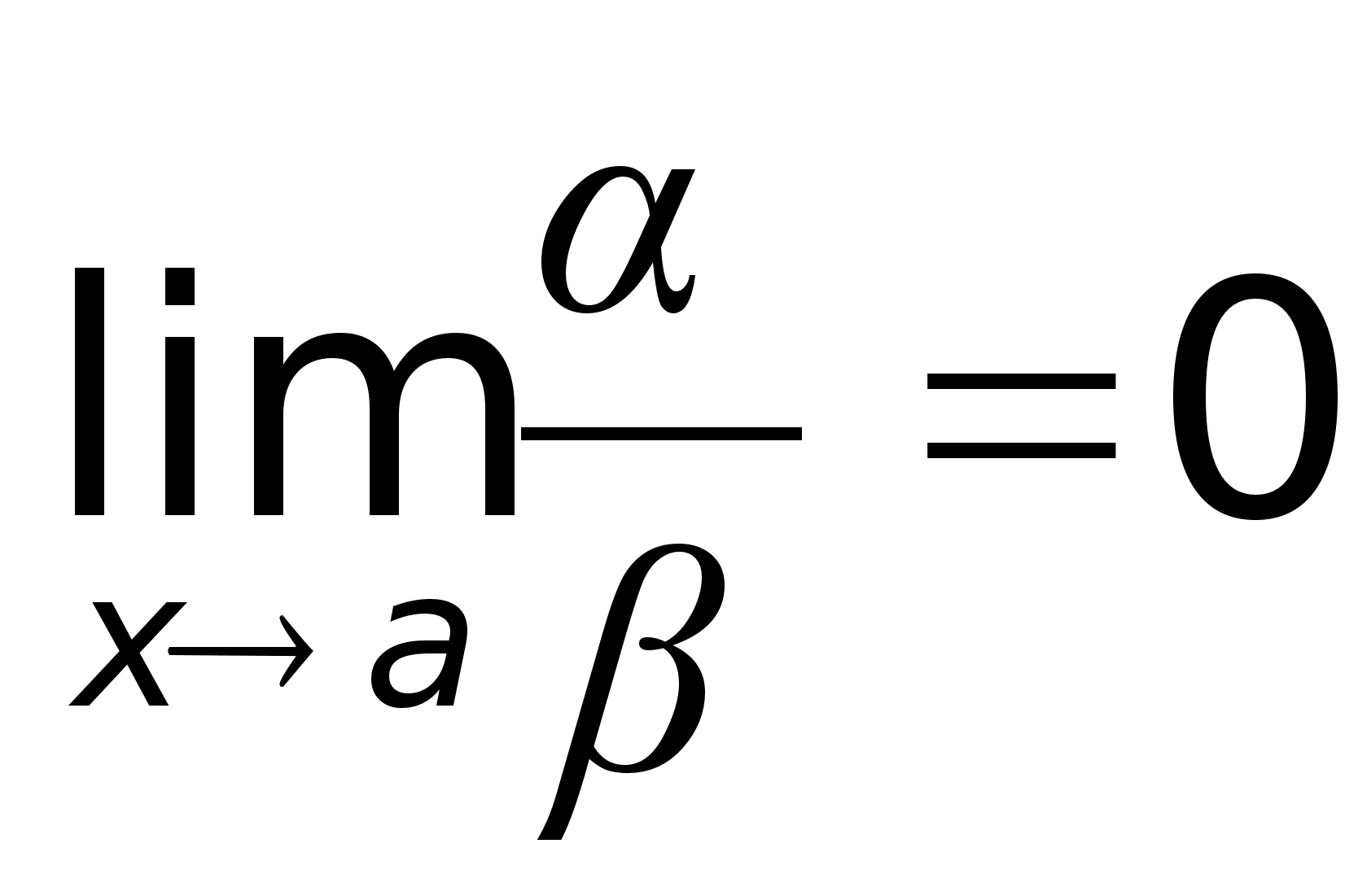 ,
то функция
,
то функция 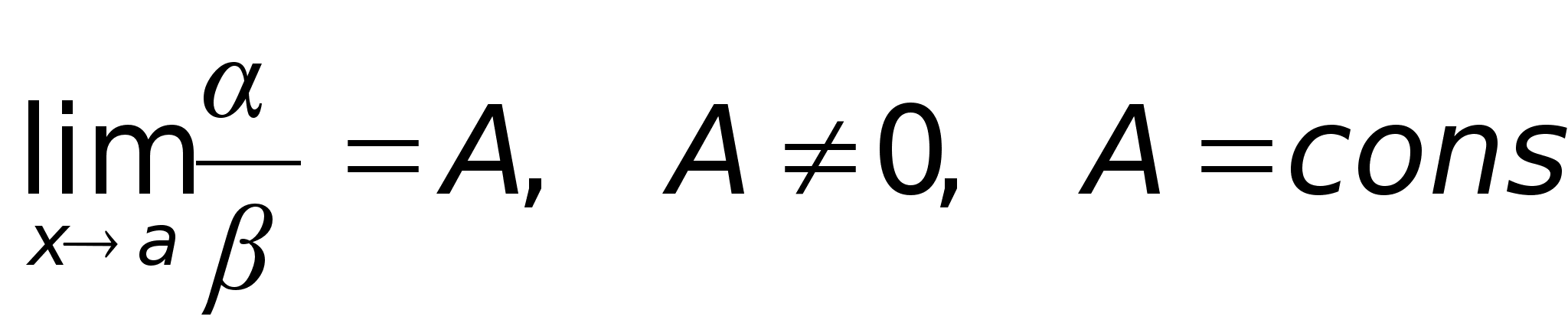 ,
то
,
то 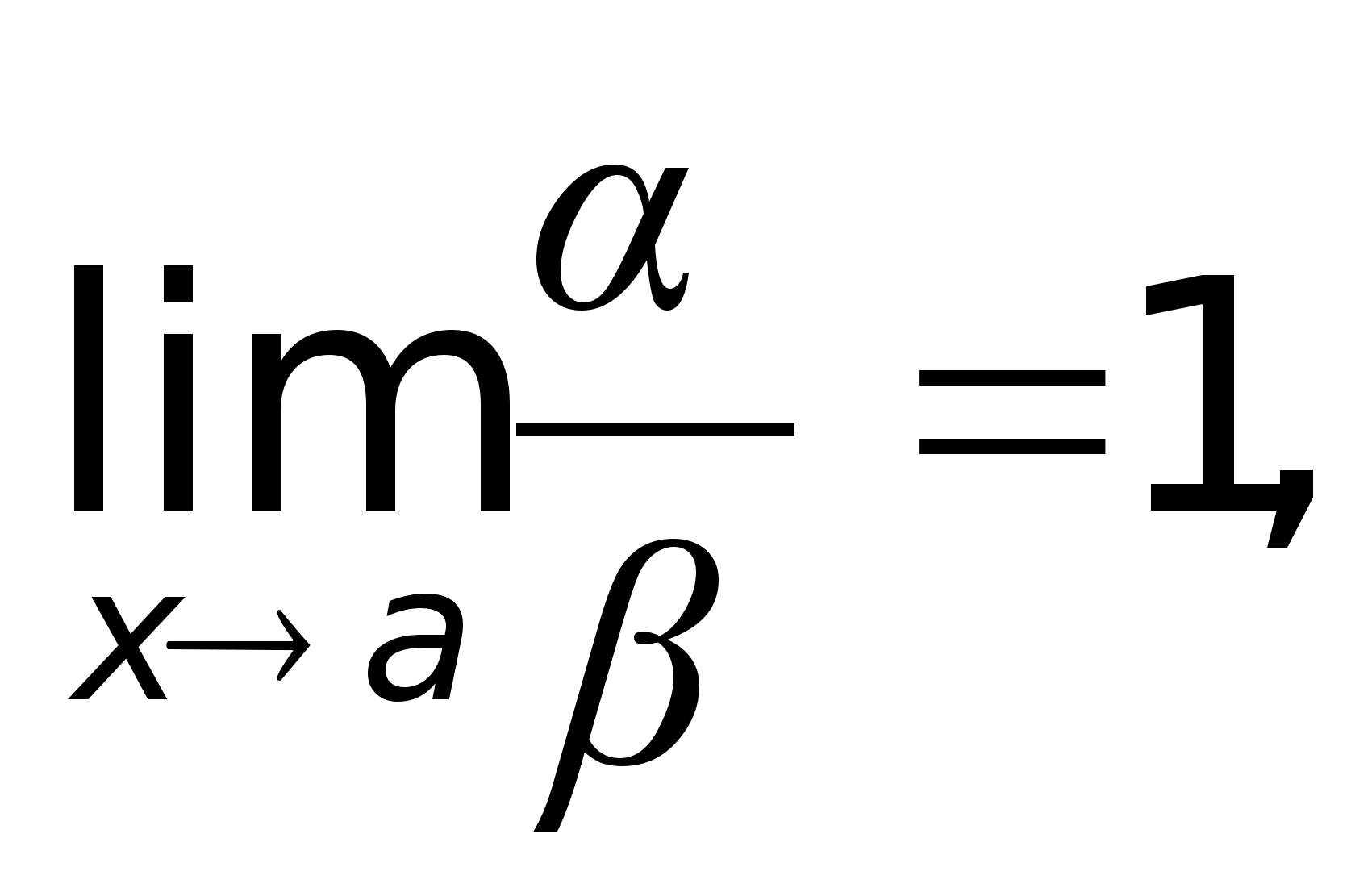 то
функции
то
функции 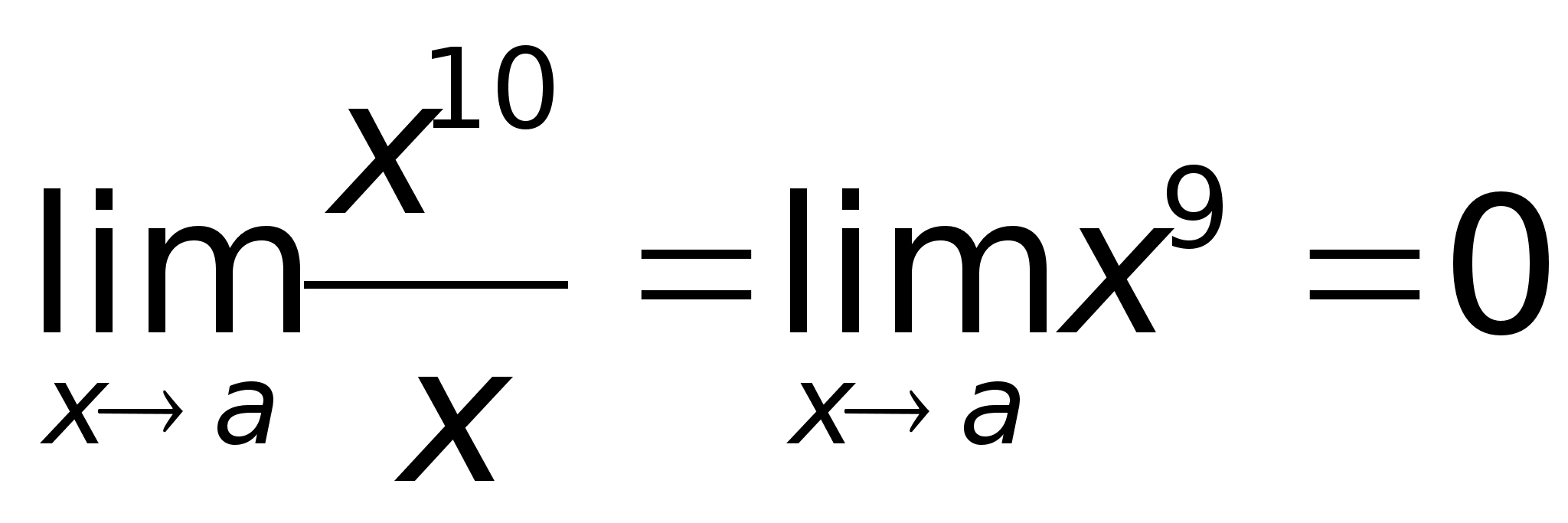 т.е.
функция f(x)
= x10
– бесконечно
малая более
высокого порядка,
чем f(x)
= x.
Определение.
Бесконечно
малая функция
т.е.
функция f(x)
= x10
– бесконечно
малая более
высокого порядка,
чем f(x)
= x.
Определение.
Бесконечно
малая функция
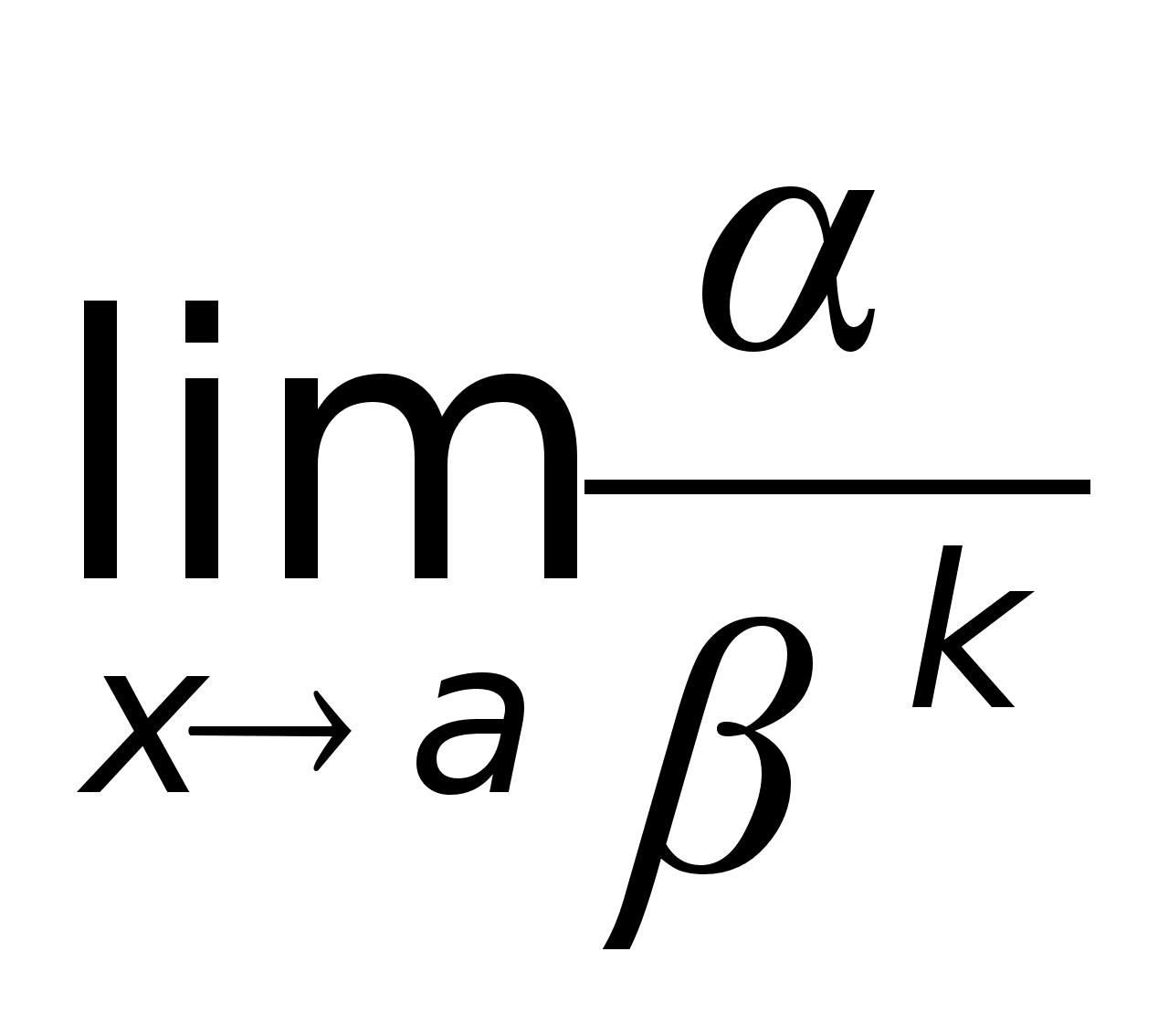 конечен и отличен
от нуля. Однако
следует отметить,
что не все
бесконечно
малые функции
можно сравнивать
между собой.
Например, если
отношение
конечен и отличен
от нуля. Однако
следует отметить,
что не все
бесконечно
малые функции
можно сравнивать
между собой.
Например, если
отношение
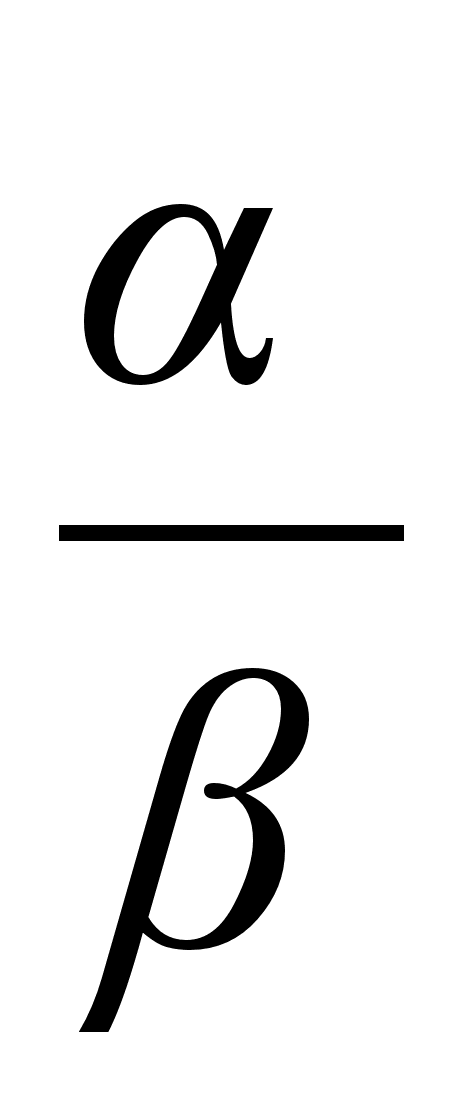 не имеет предела,
то функции
несравнимы.
Пример.
Если
не имеет предела,
то функции
несравнимы.
Пример.
Если
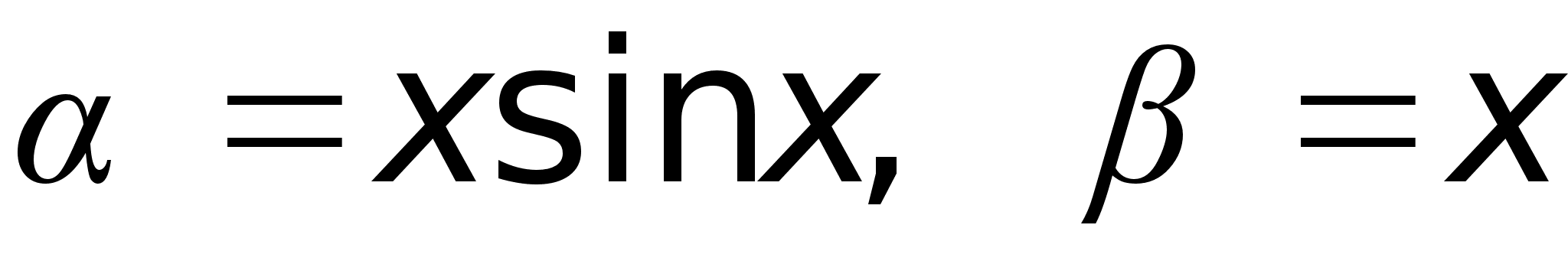 ,
то при х
,
то при х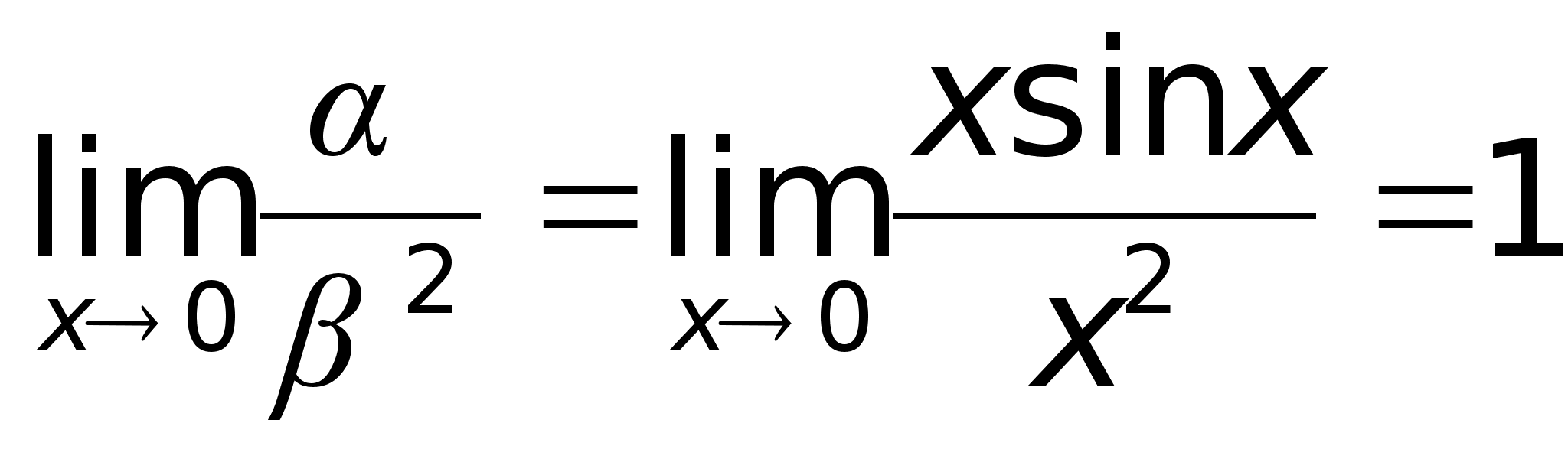 ,
т.е. функция
,
т.е. функция
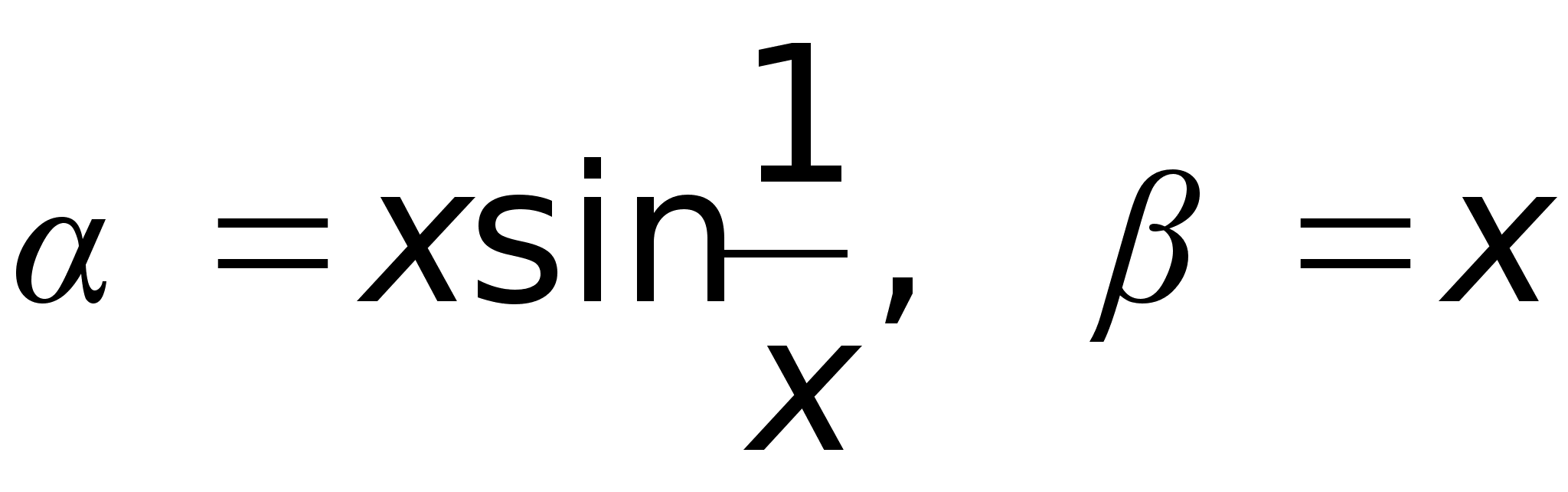 ,
то при х
,
то при х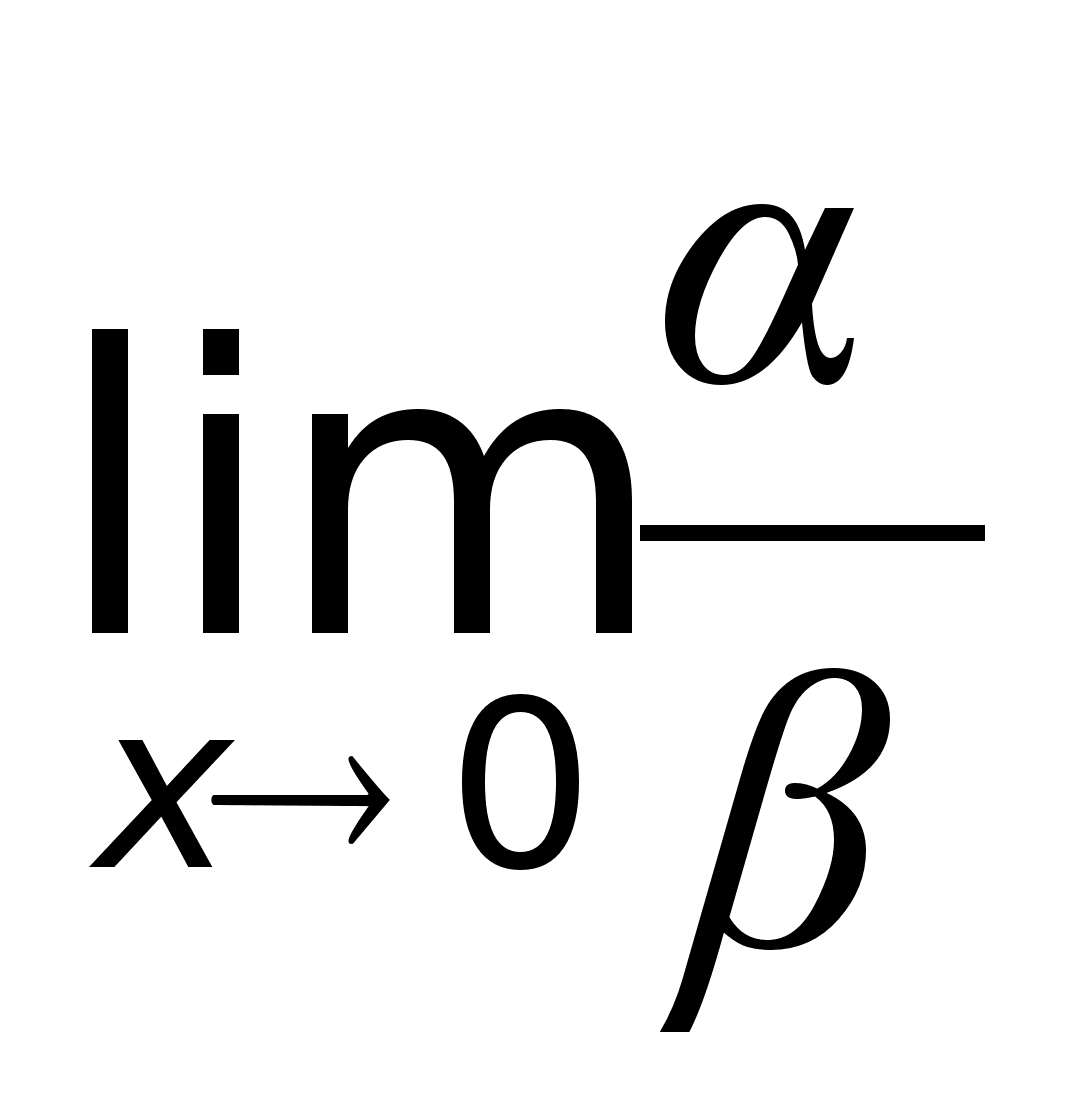 не существует,
т.е. функция
не существует,
т.е. функция
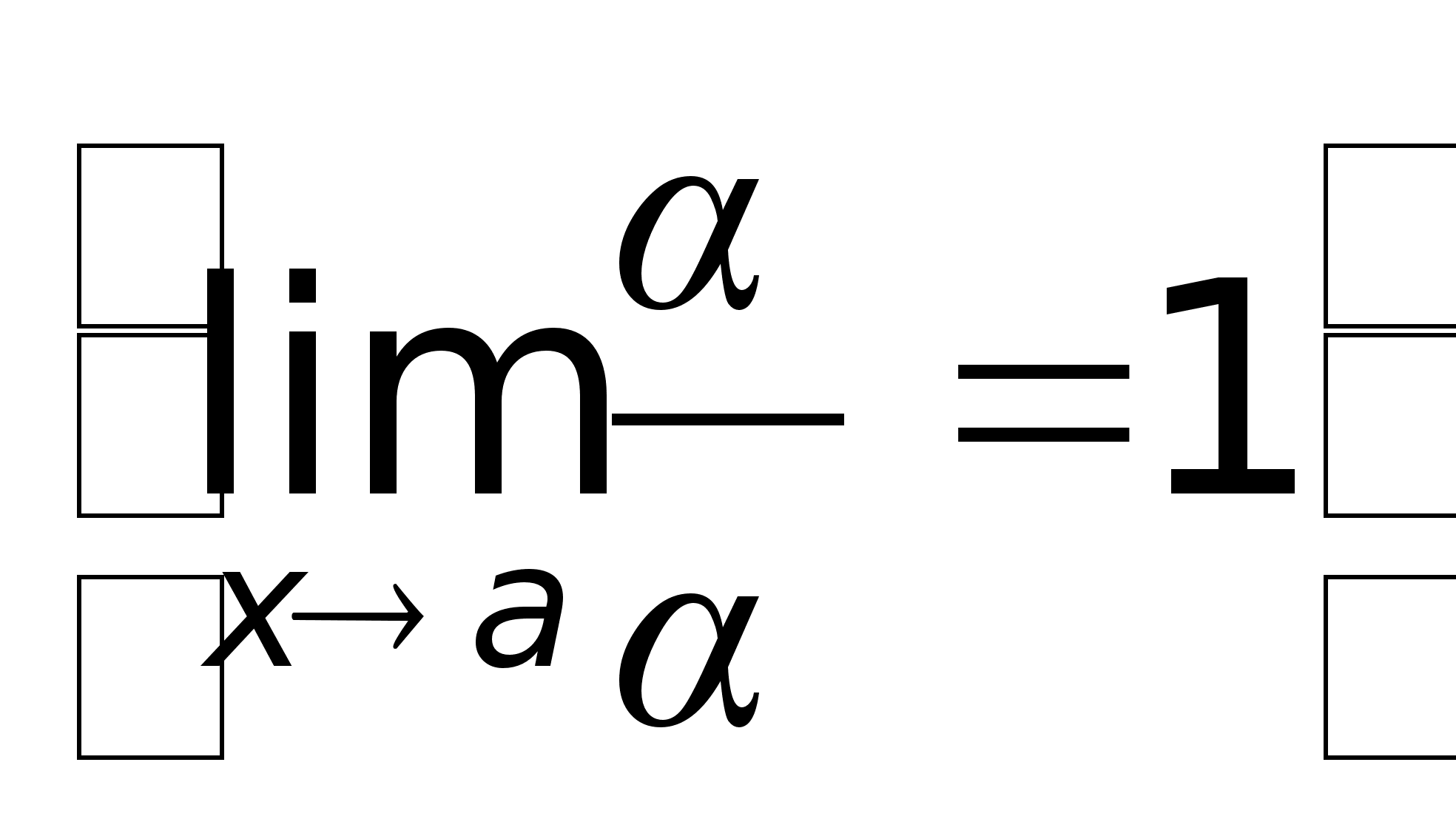 2)
Если
2)
Если 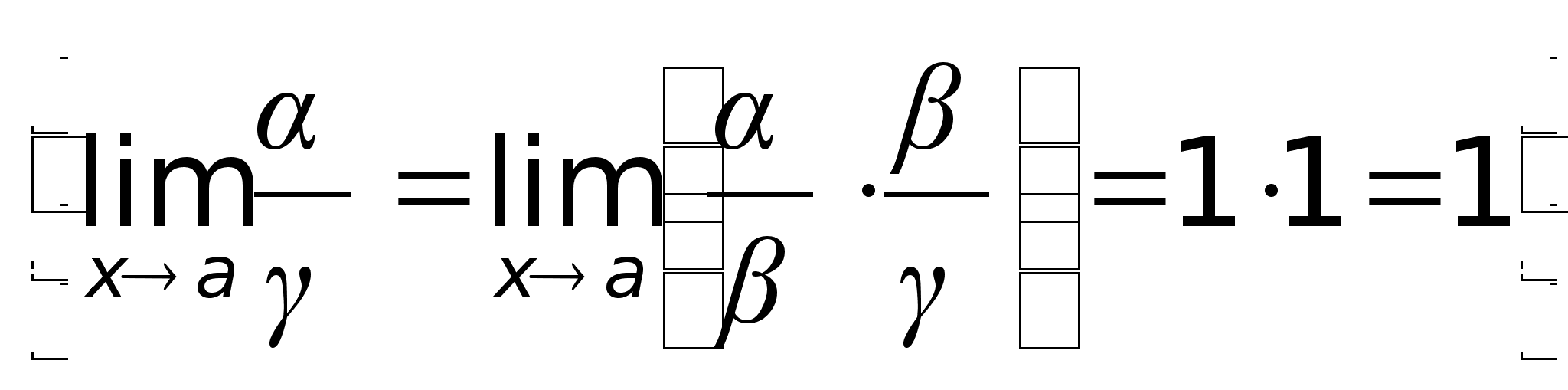 3)
Если
3)
Если 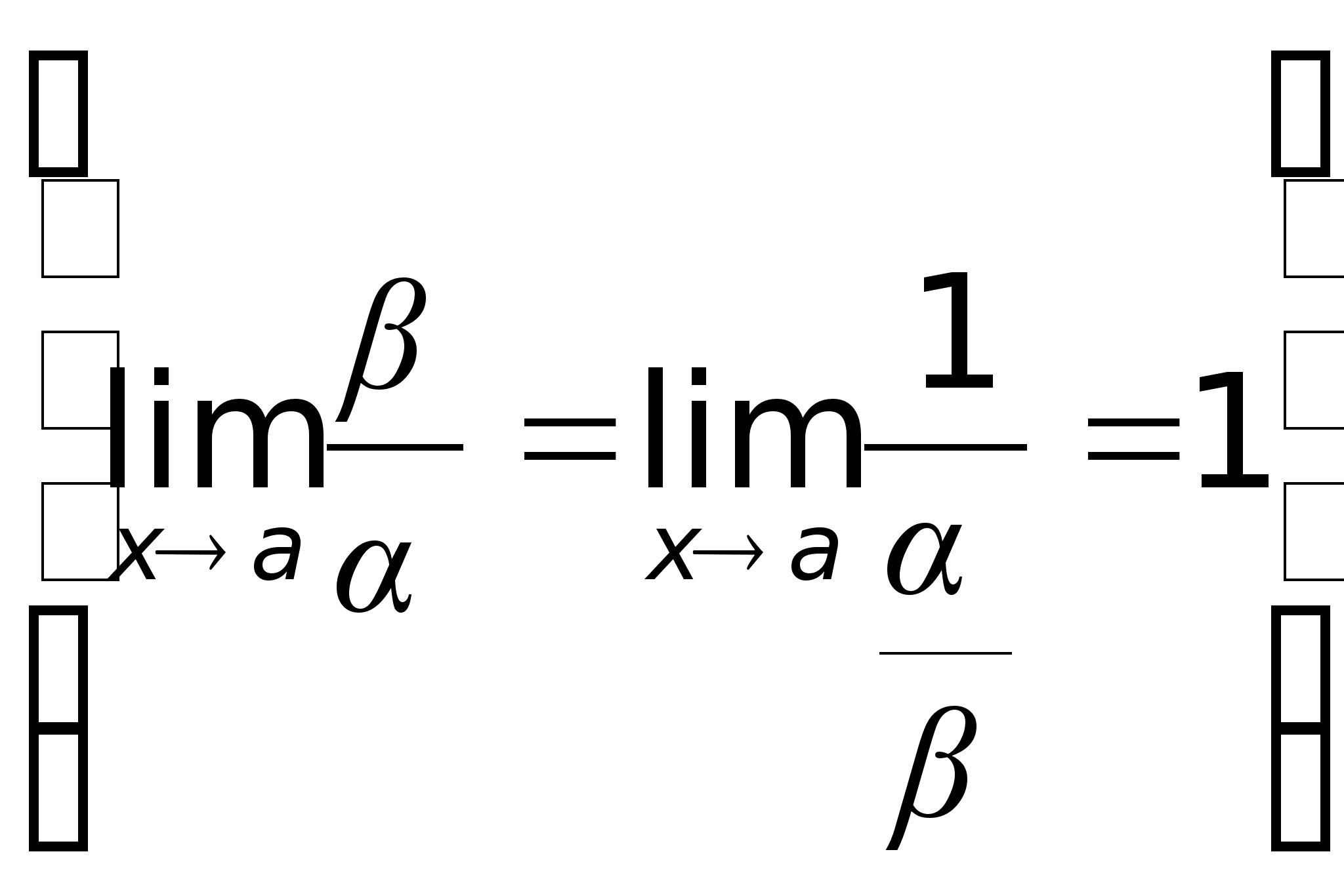 4) Если
4) Если 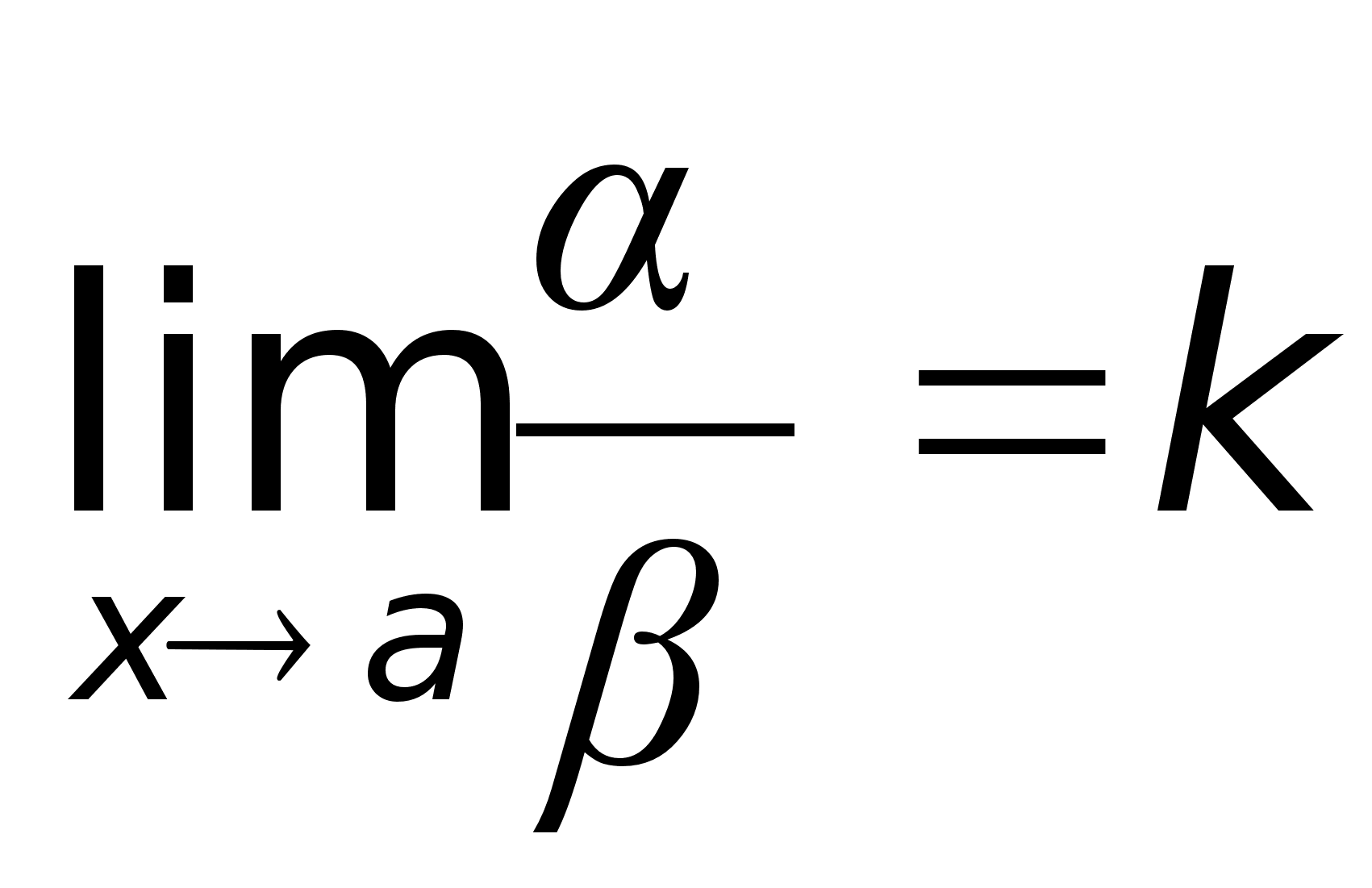 ,
то и
,
то и
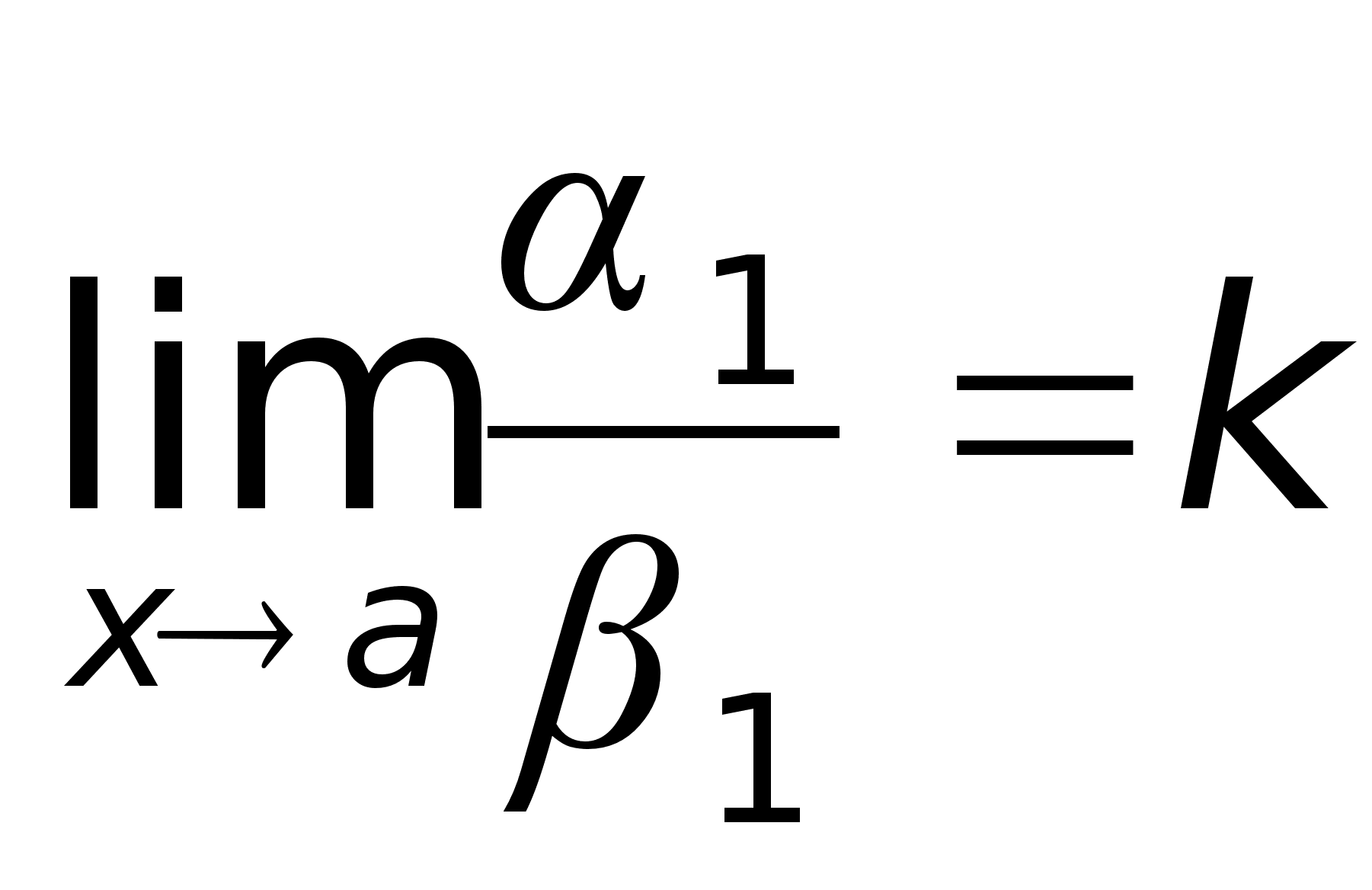 или
или
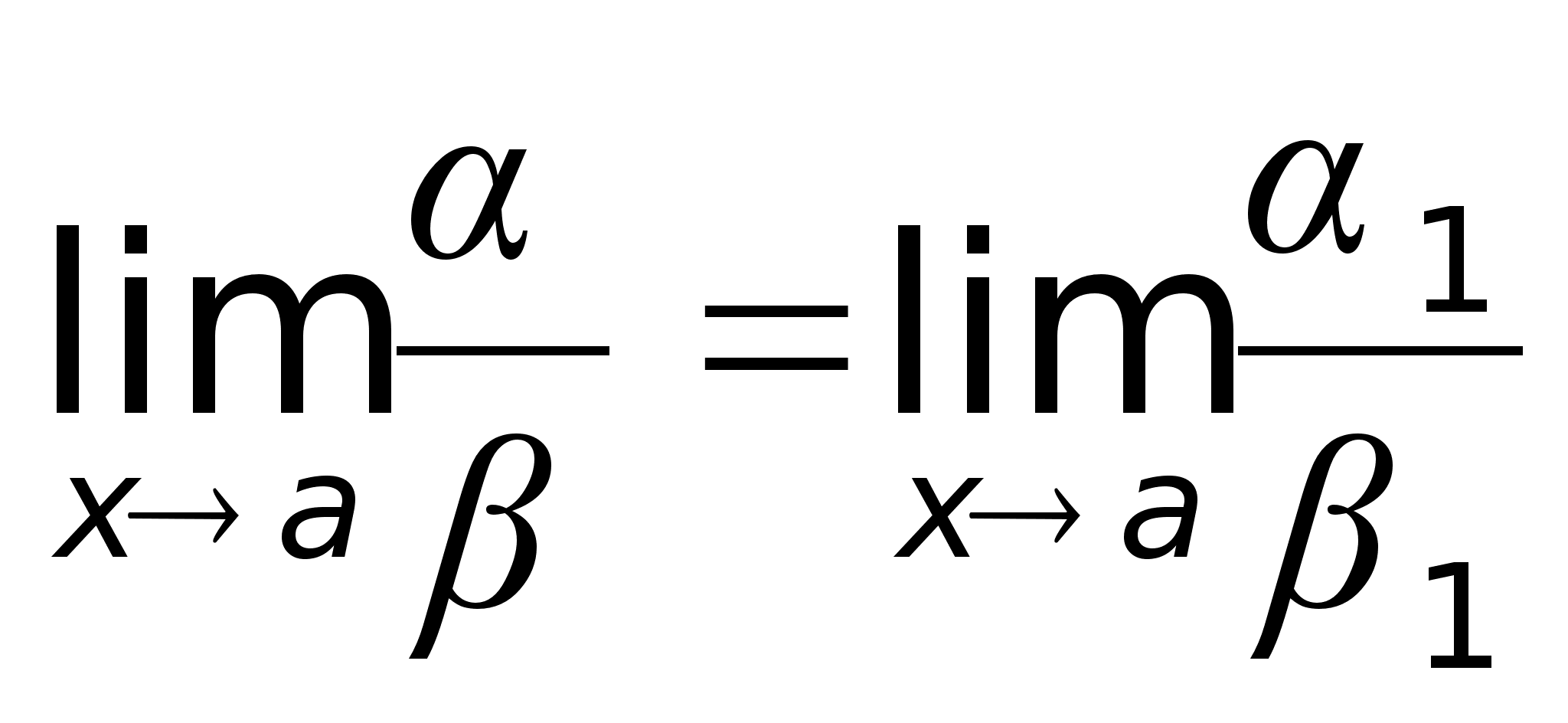 .Следствие:
а) если
.Следствие:
а) если 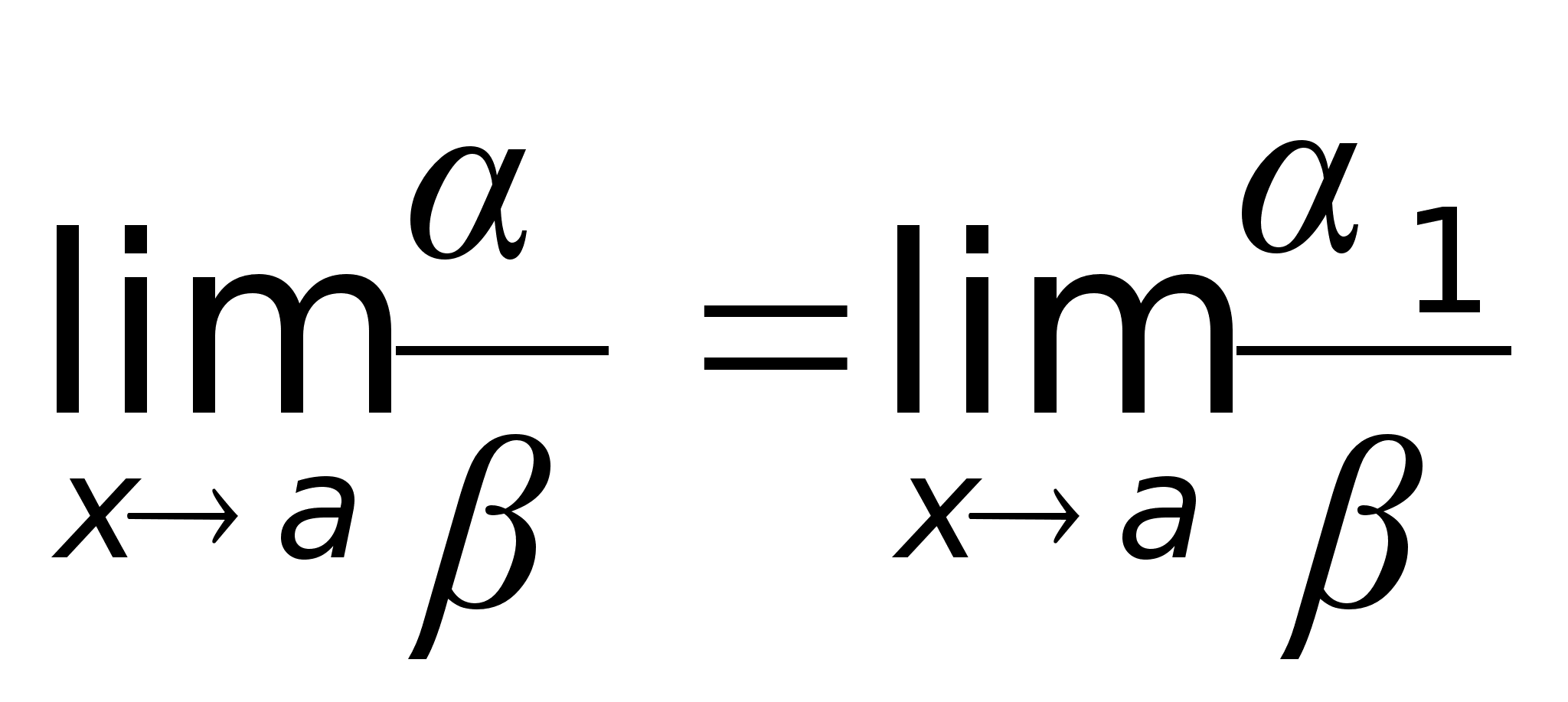 б) если
б) если 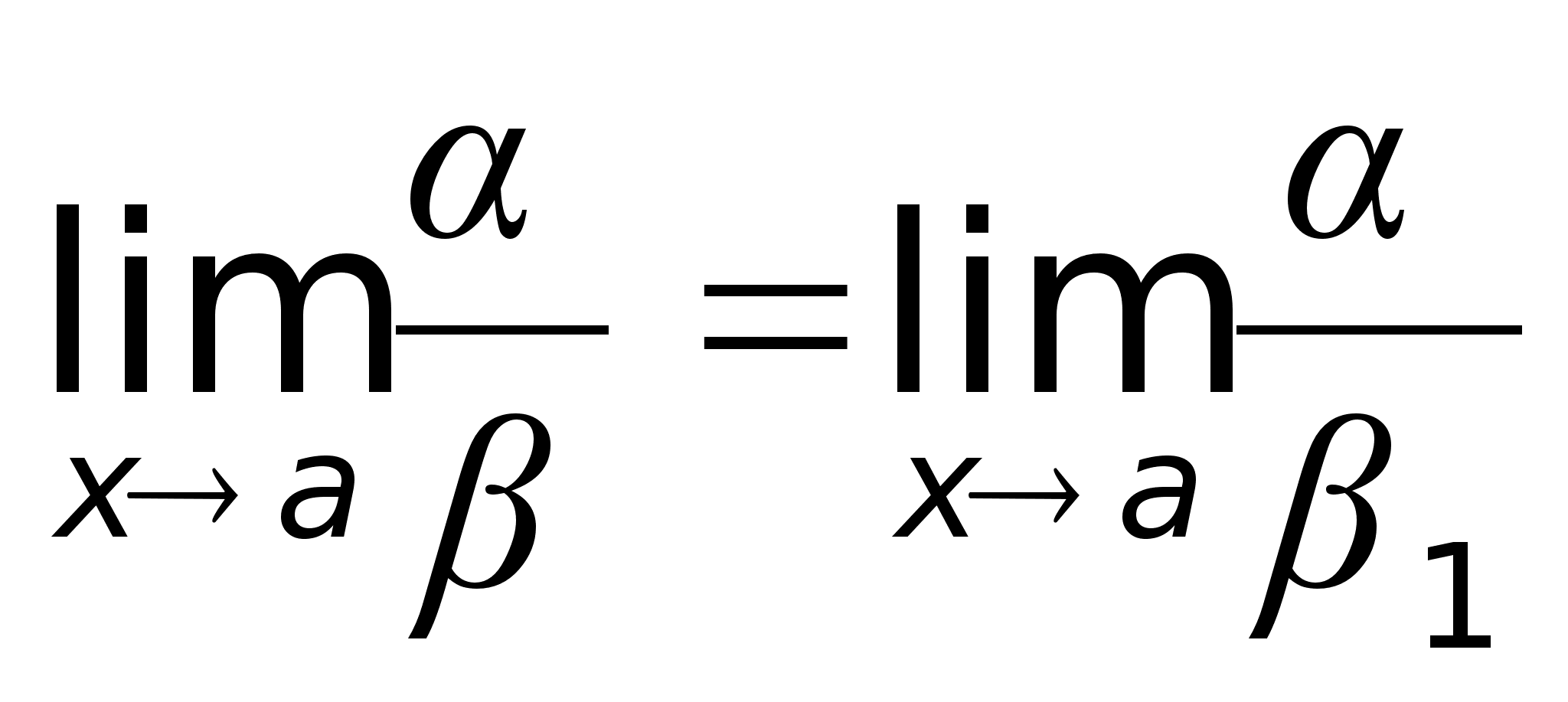 Свойство
4 особенно важно
на практике,
т.к. оно фактически
означает, что
предел отношения
бесконечно
малых не меняется
при замене
их на эквивалентные
бесконечно
малые. Этот
факт дает
возможность
при нахождении
пределов заменять
бесконечно
малые на эквивалентные
им функции,
что может сильно
упростить
вычисление
пределов.Пример.
Найти предел
Свойство
4 особенно важно
на практике,
т.к. оно фактически
означает, что
предел отношения
бесконечно
малых не меняется
при замене
их на эквивалентные
бесконечно
малые. Этот
факт дает
возможность
при нахождении
пределов заменять
бесконечно
малые на эквивалентные
им функции,
что может сильно
упростить
вычисление
пределов.Пример.
Найти предел
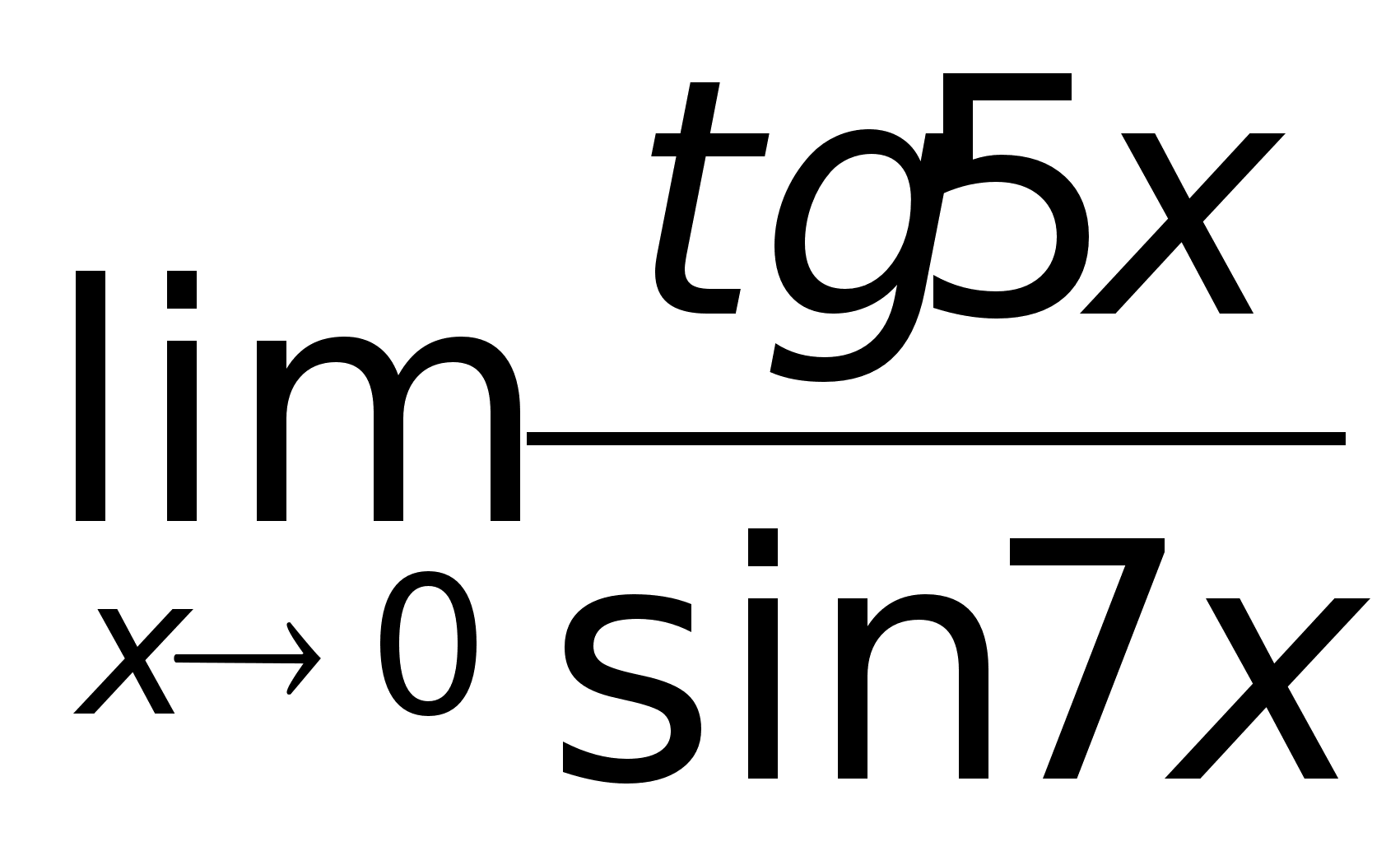
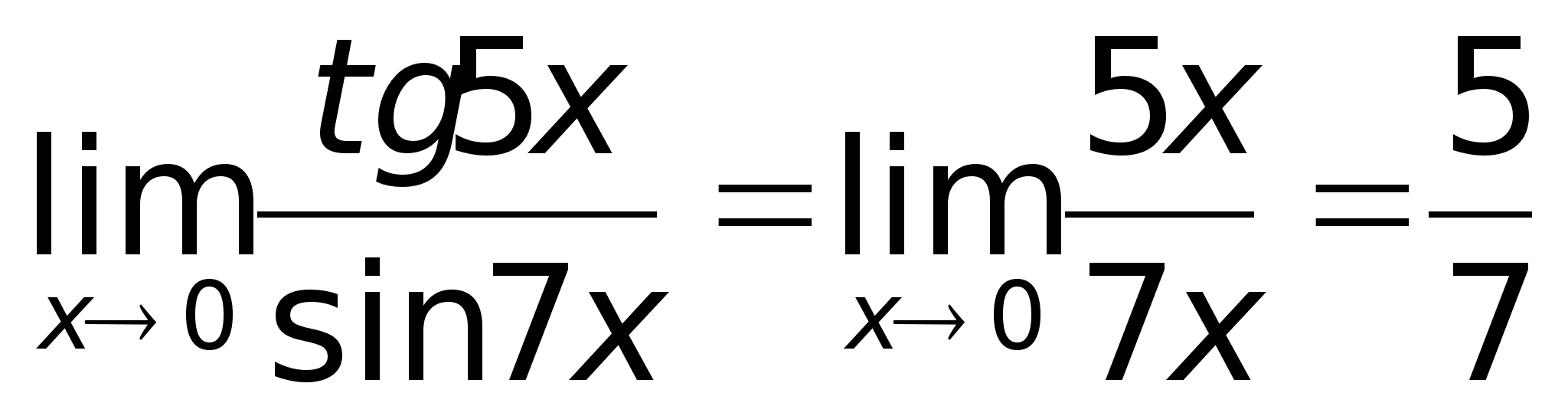 Пример.
Найти предел
Пример.
Найти предел
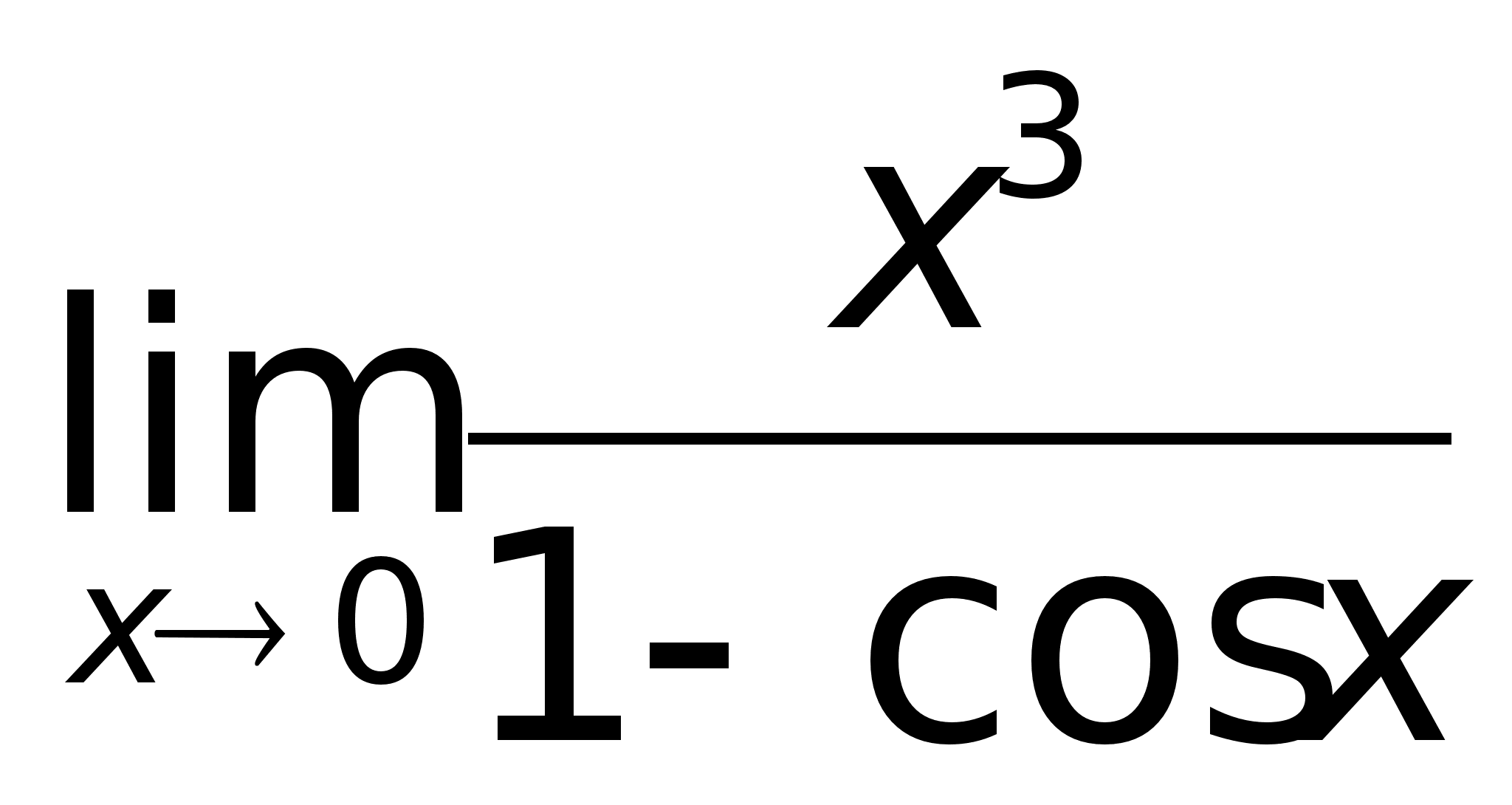 .Так
как 1 – cosx
=
.Так
как 1 – cosx
=
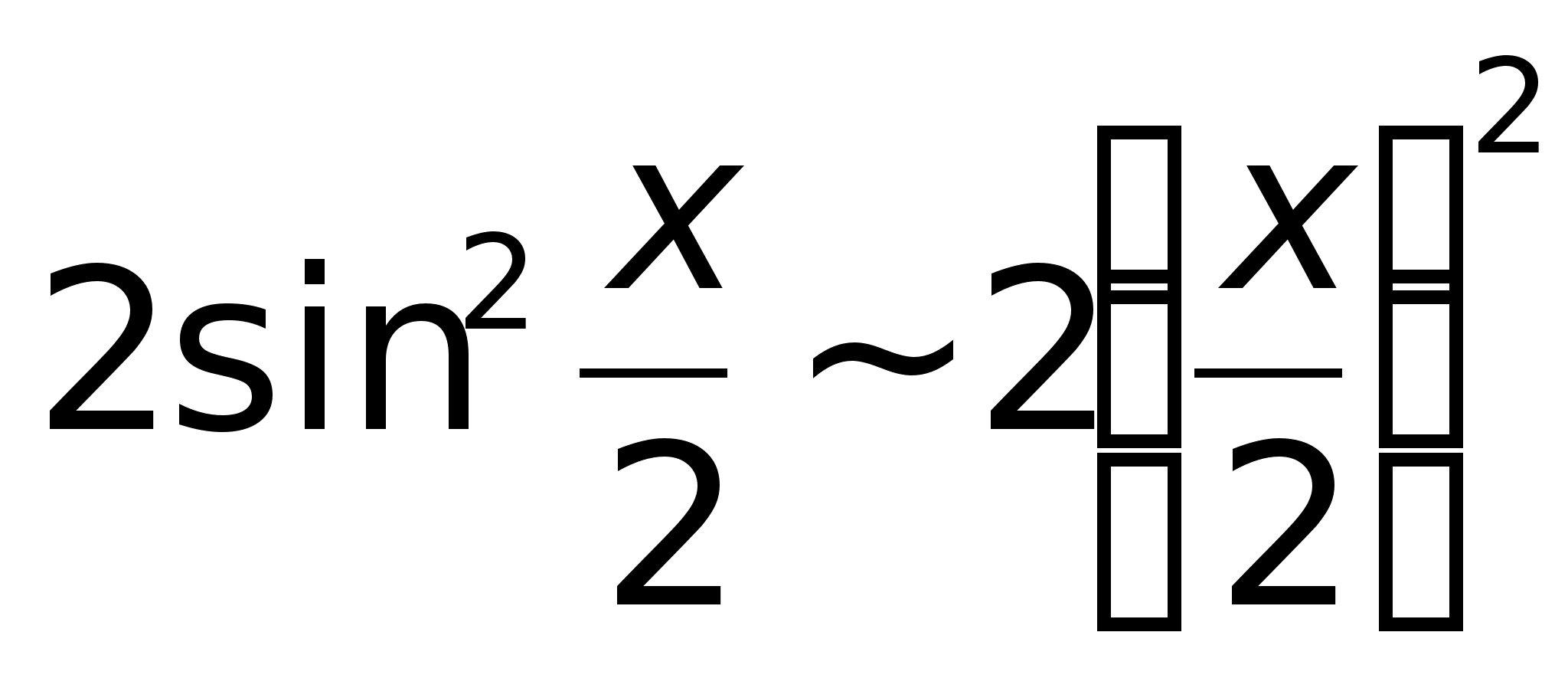 при х
при х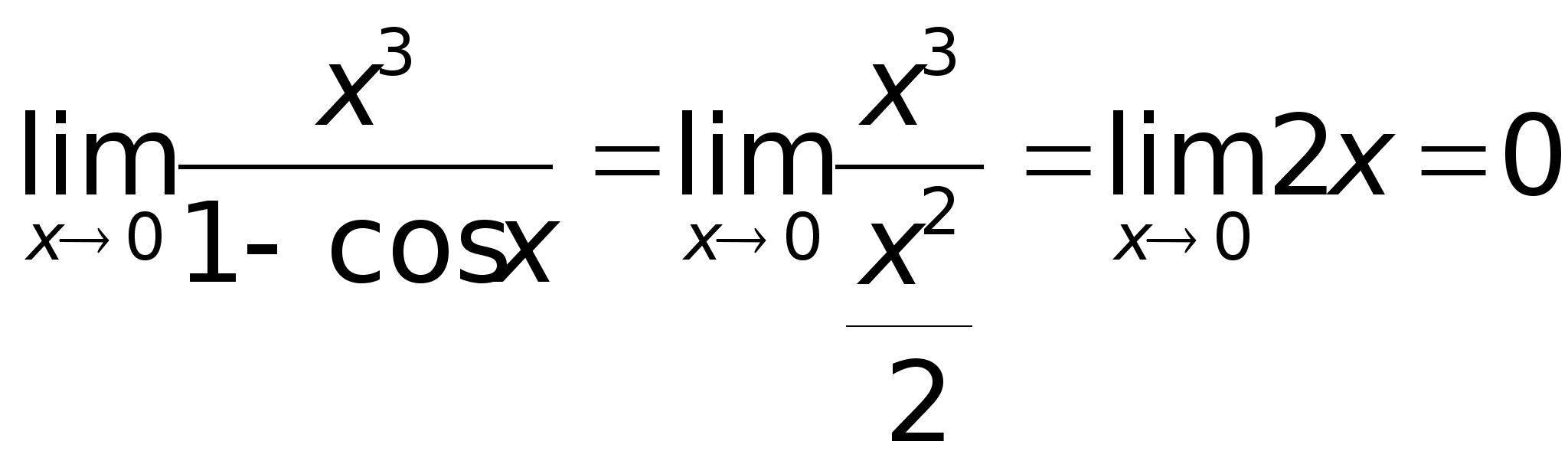 . Пример.
Найти предел
. Пример.
Найти предел
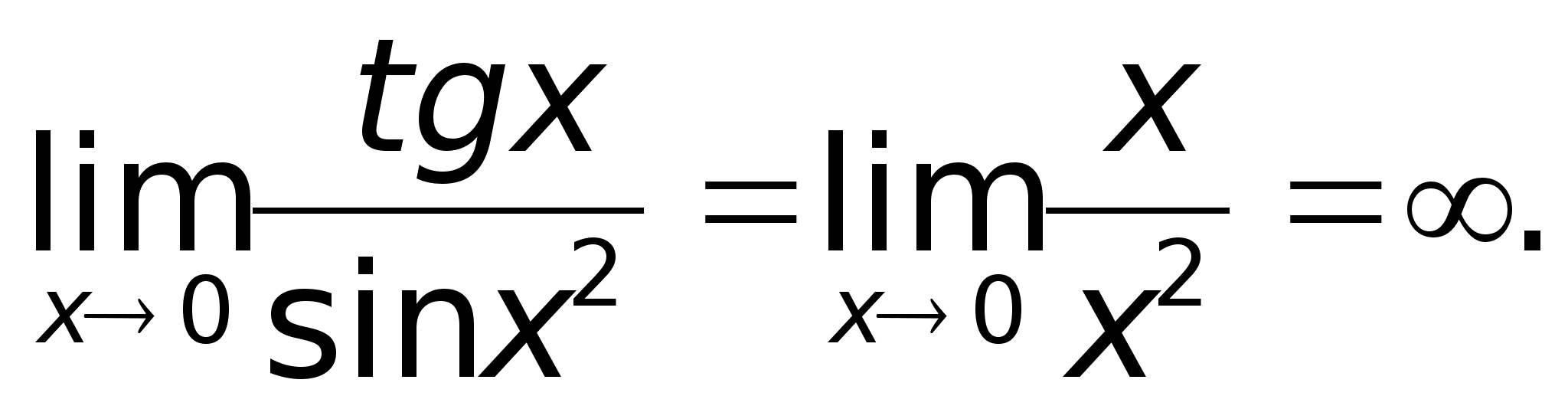 Если
Если
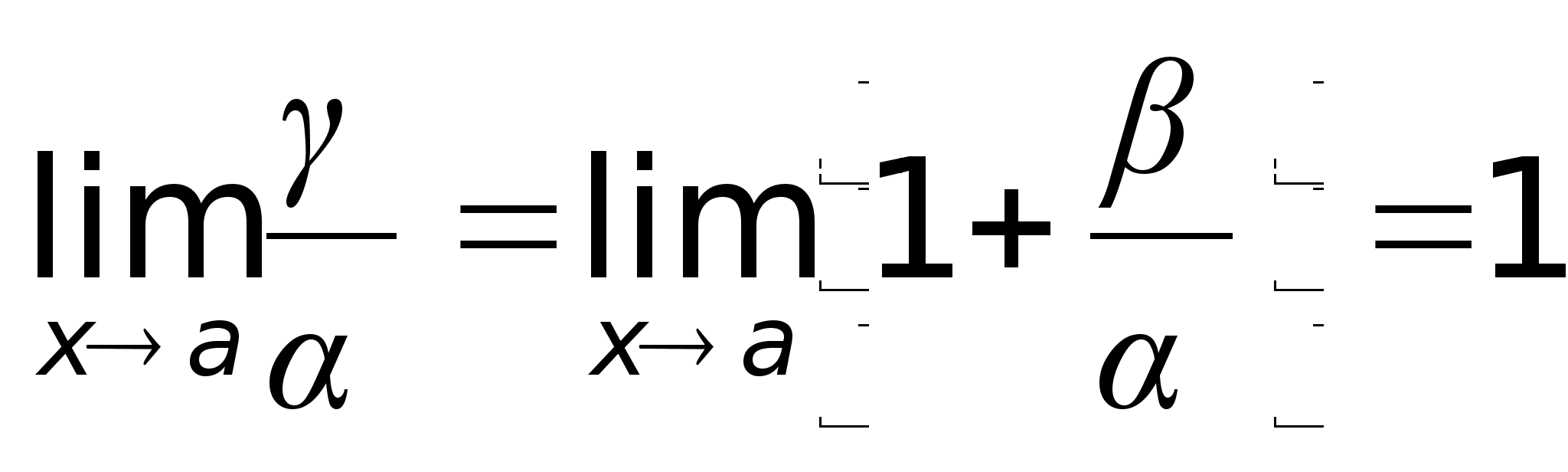 .Тогда
говорят, что
.Тогда
говорят, что
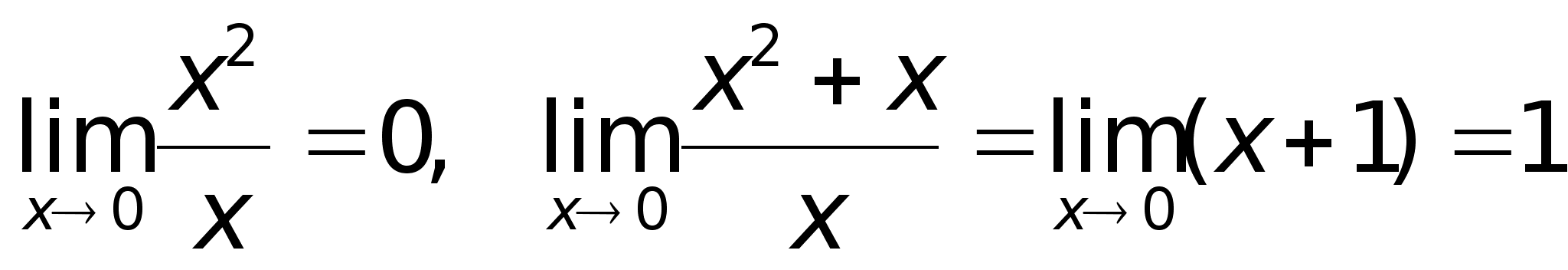 .
.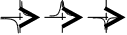 5)Связь
м\ж бесконечно
малыми и бесконечно
большими
ф-миОпределение.
Предел функции
f(x)
при х
5)Связь
м\ж бесконечно
малыми и бесконечно
большими
ф-миОпределение.
Предел функции
f(x)
при х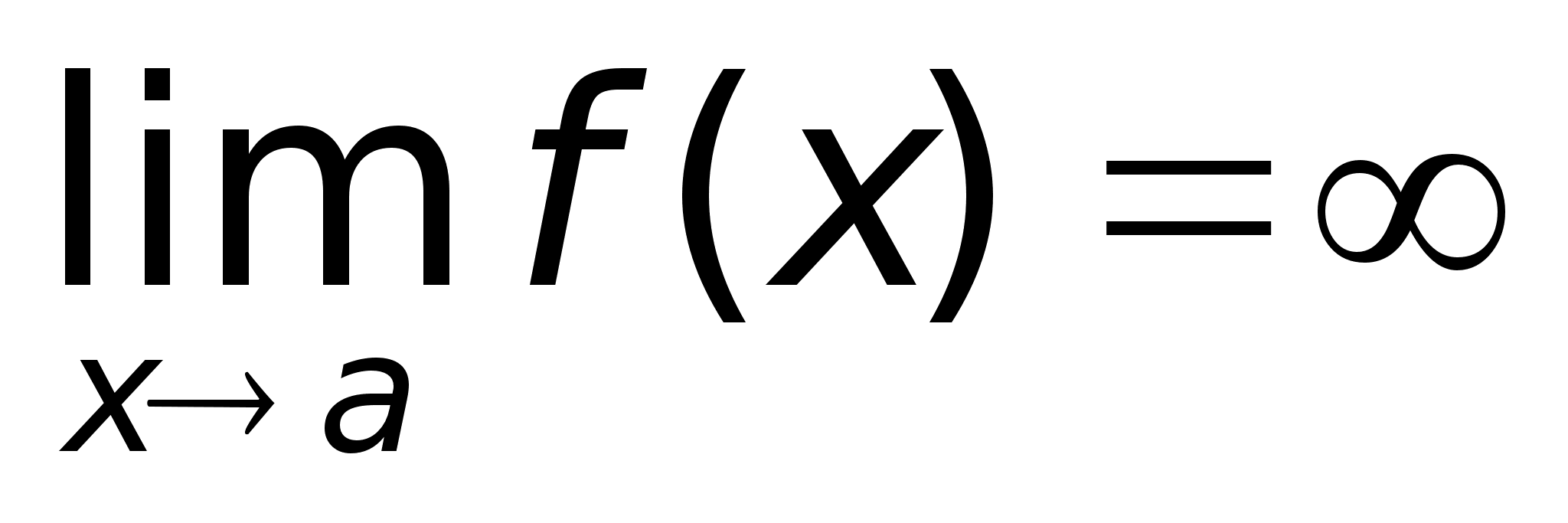 .
Собственно,
если в приведенном
выше определении
заменить условие
.
Собственно,
если в приведенном
выше определении
заменить условие
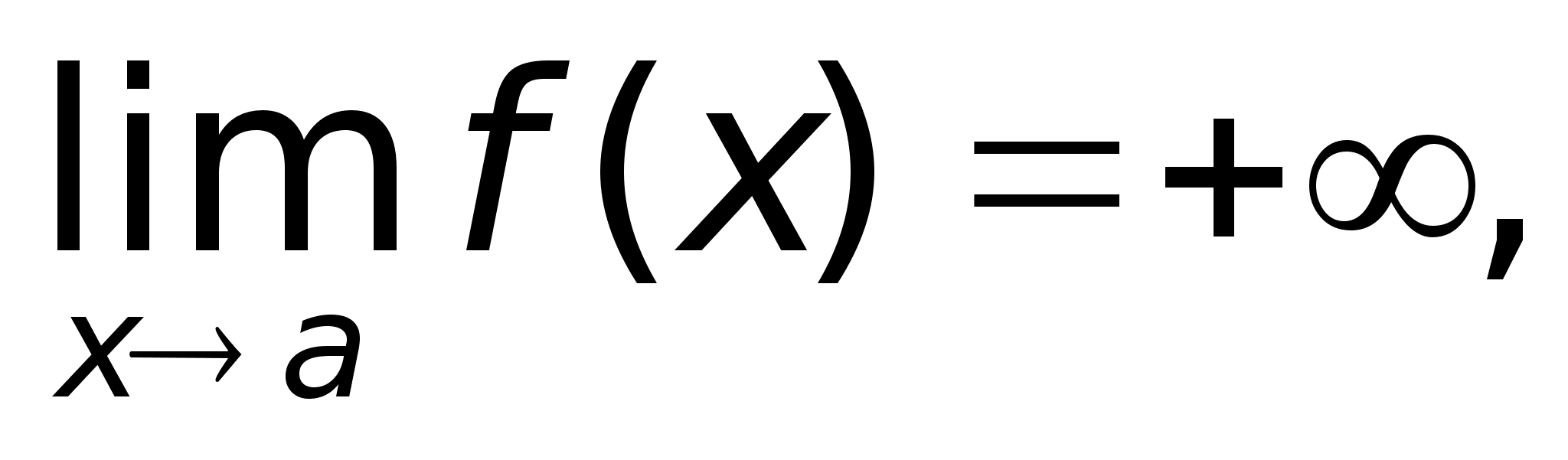 а если заменить
на f(x)
а если заменить
на f(x)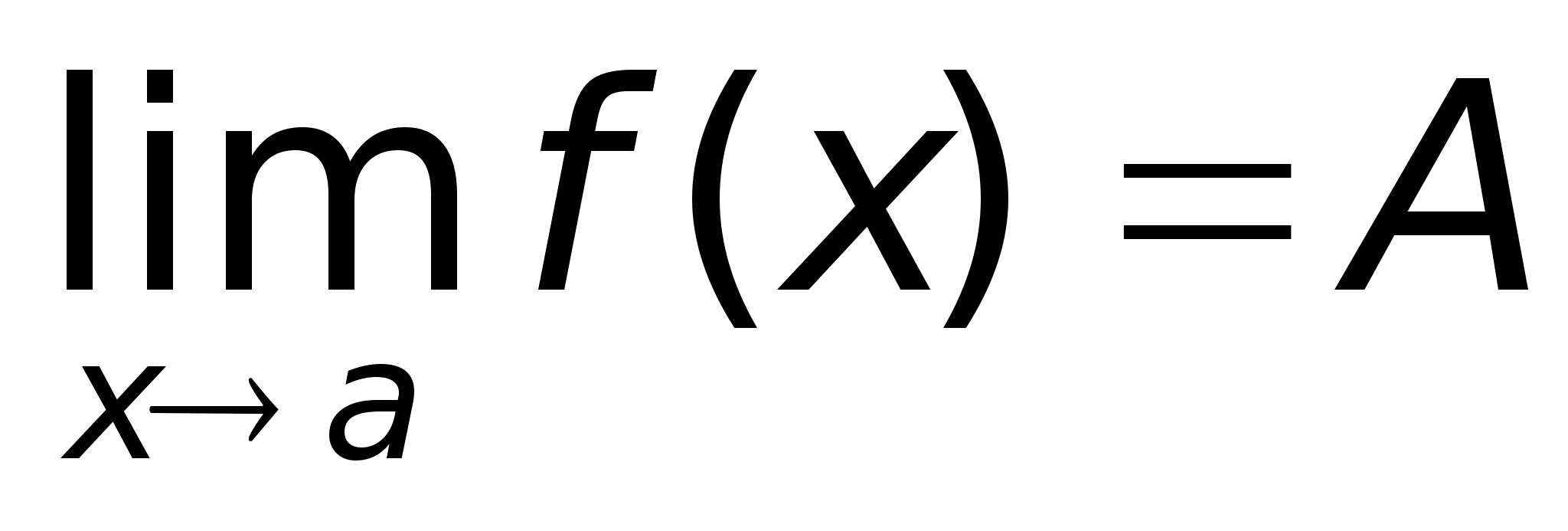 ,
где А – число
или одна из
величин
,
где А – число
или одна из
величин 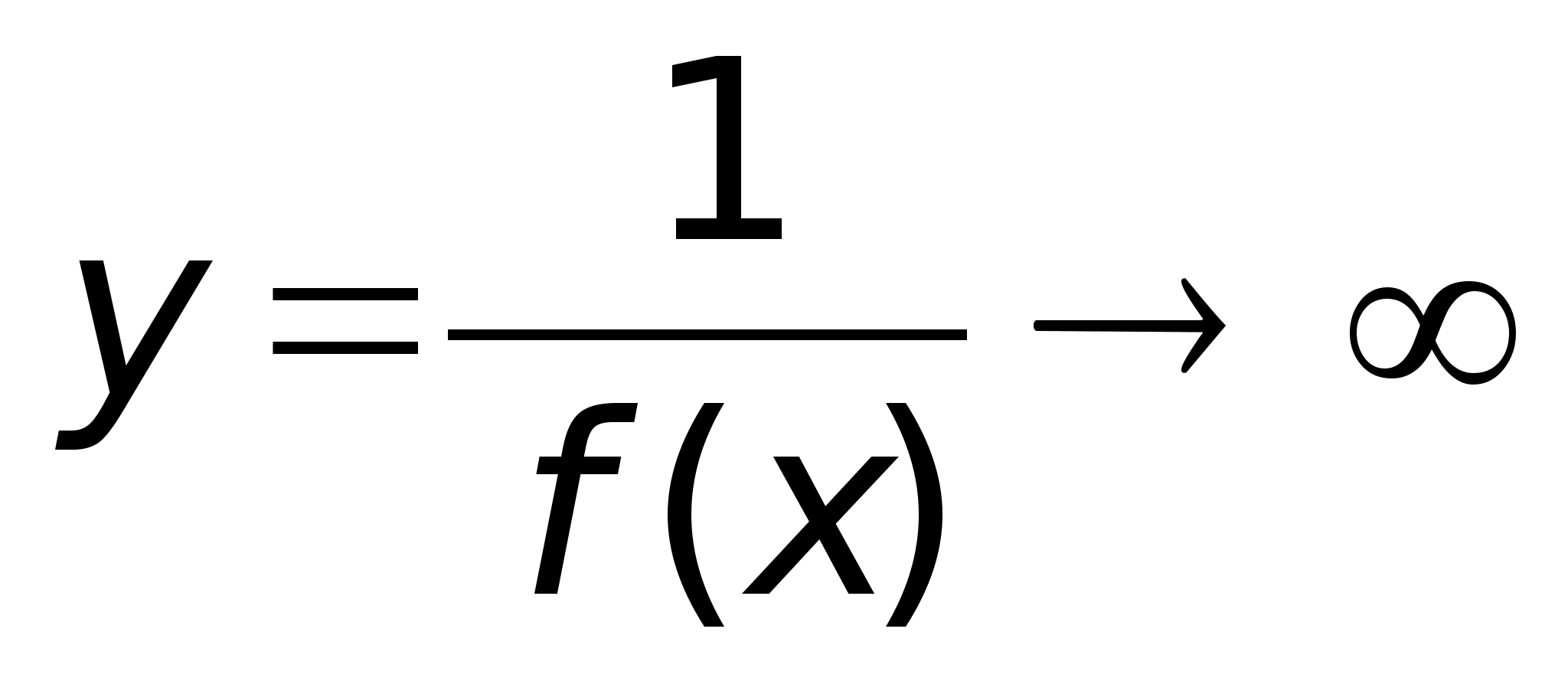
 6)Непрерывность
ф-ииОпределение.
Функция f(x),
определенная
в окрестности
некоторой
точки х0,
называется
непрерывной
в точке х0,
если предел
функции и ее
значение в
этой точке
равны, т.е.
6)Непрерывность
ф-ииОпределение.
Функция f(x),
определенная
в окрестности
некоторой
точки х0,
называется
непрерывной
в точке х0,
если предел
функции и ее
значение в
этой точке
равны, т.е.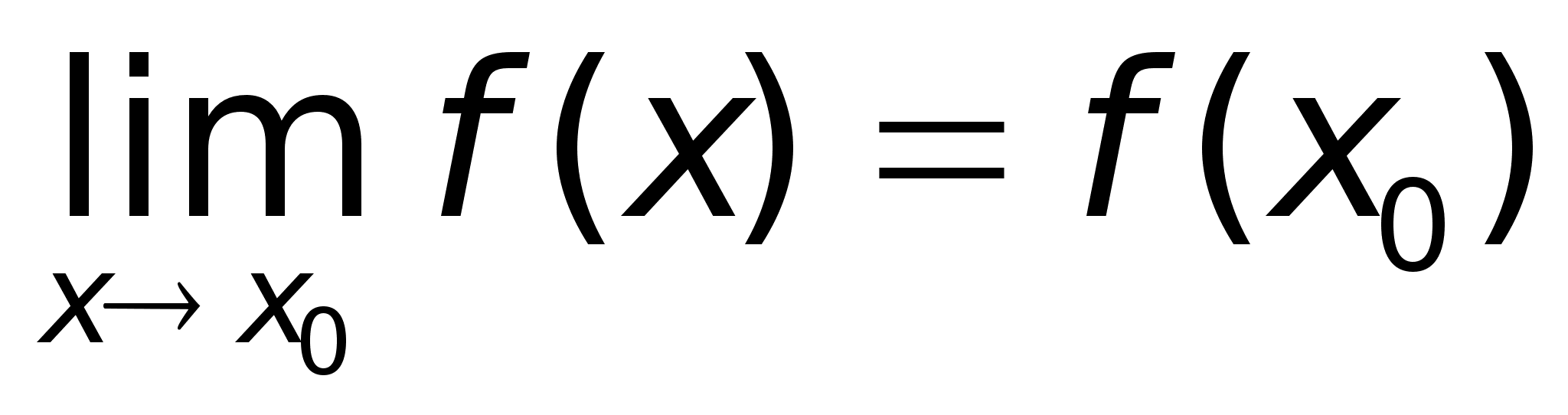 Тот
же факт можно
записать иначе:
Тот
же факт можно
записать иначе:
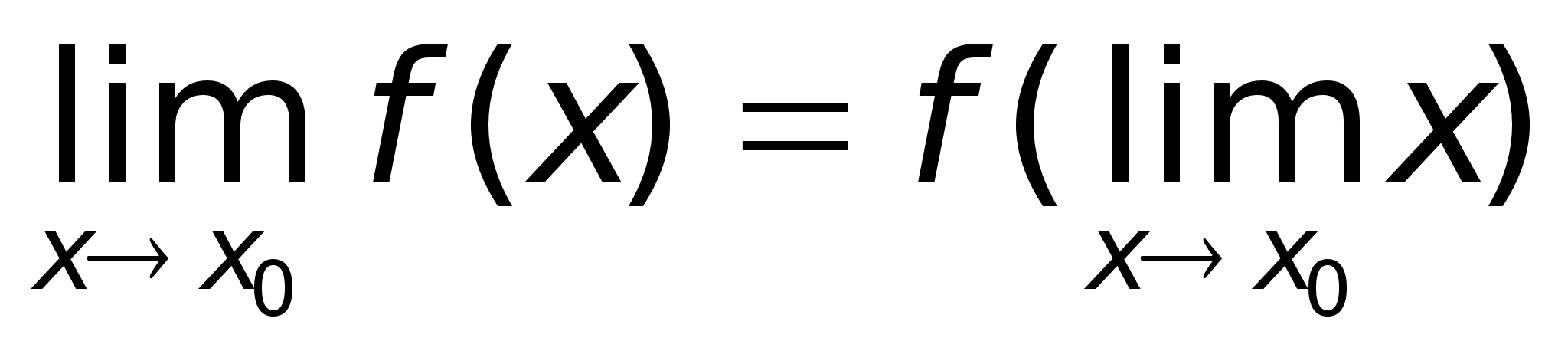 Определение.
Если функция
f(x)
определена
в некоторой
окрестности
точки х0,
но не является
непрерывной
в самой точке
х0,
то она называется
разрывной
функцией, а
точка х0
– точкой разрыва.Пример
непрерывной
функции:
Определение.
Если функция
f(x)
определена
в некоторой
окрестности
точки х0,
но не является
непрерывной
в самой точке
х0,
то она называется
разрывной
функцией, а
точка х0
– точкой разрыва.Пример
непрерывной
функции:
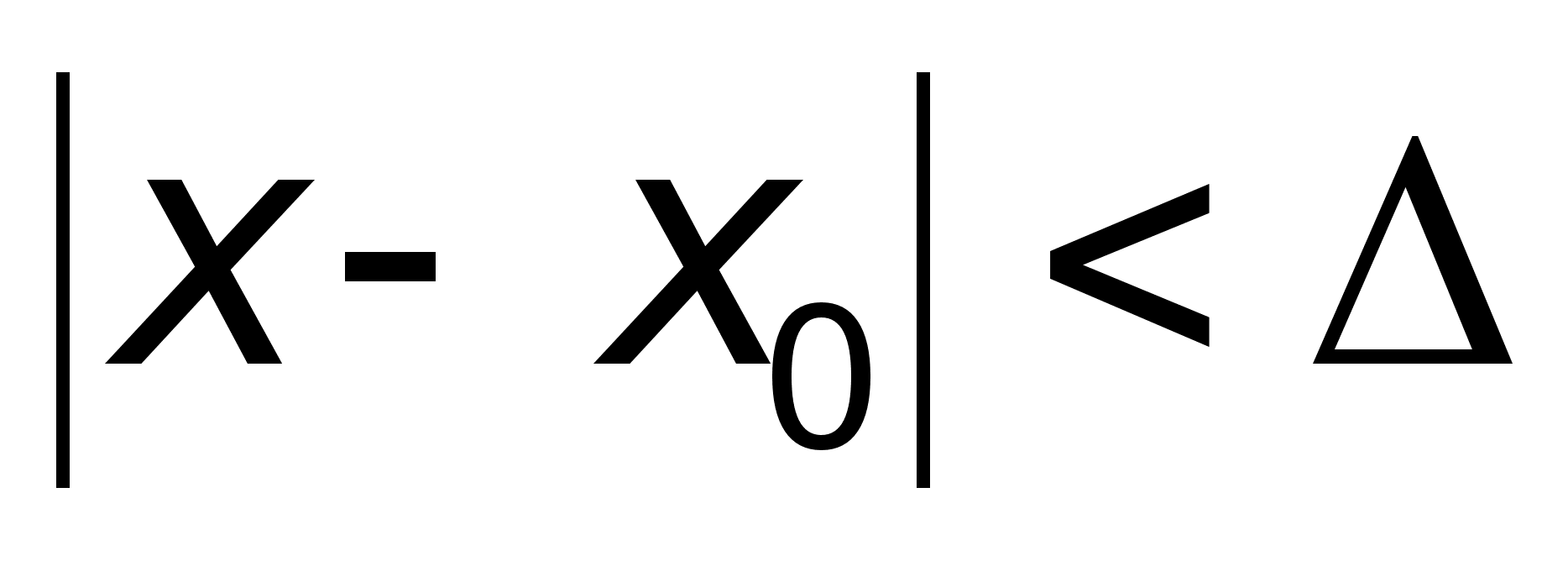 верно
неравенство
верно
неравенство
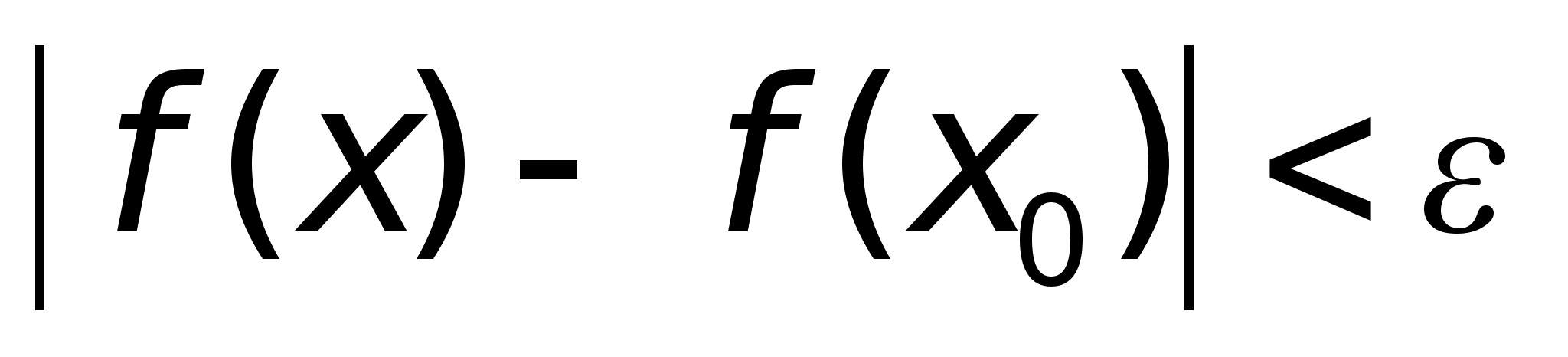 .Определение.
Функция f(x)
называется
непрерывной
в точке х = х0,
если приращение
функции в точке
х0
является
бесконечно
малой величиной.f(x)
= f(x0)
+
.Определение.
Функция f(x)
называется
непрерывной
в точке х = х0,
если приращение
функции в точке
х0
является
бесконечно
малой величиной.f(x)
= f(x0)
+ 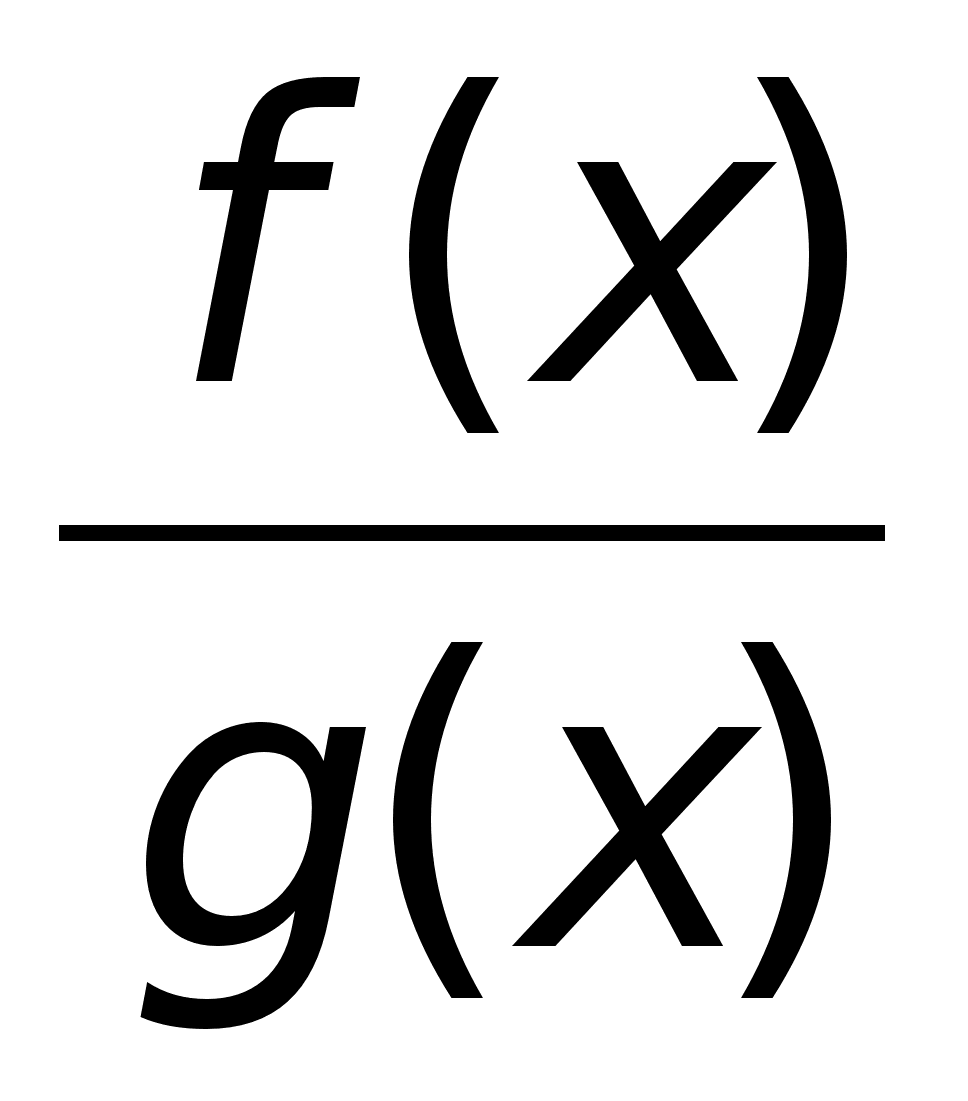 –
есть непрерывная
функция при
условии, что
g(x)
не равна нулю
в точке х0.3)
Суперпозиция
непрерывных
функций – есть
непрерывная
функция.Это
свойство может
быть записано
следующим
образом:Если
u
= f(x),
v
= g(x)
– непрерывные
функции в точке
х = х0,
то функция v
= g(f(x))
– тоже непрерывнаяфункция
в этой точке.Справедливость
приведенных
выше свойств
можно легко
доказать,
используя
теоремы о
пределах.
–
есть непрерывная
функция при
условии, что
g(x)
не равна нулю
в точке х0.3)
Суперпозиция
непрерывных
функций – есть
непрерывная
функция.Это
свойство может
быть записано
следующим
образом:Если
u
= f(x),
v
= g(x)
– непрерывные
функции в точке
х = х0,
то функция v
= g(f(x))
– тоже непрерывнаяфункция
в этой точке.Справедливость
приведенных
выше свойств
можно легко
доказать,
используя
теоремы о
пределах.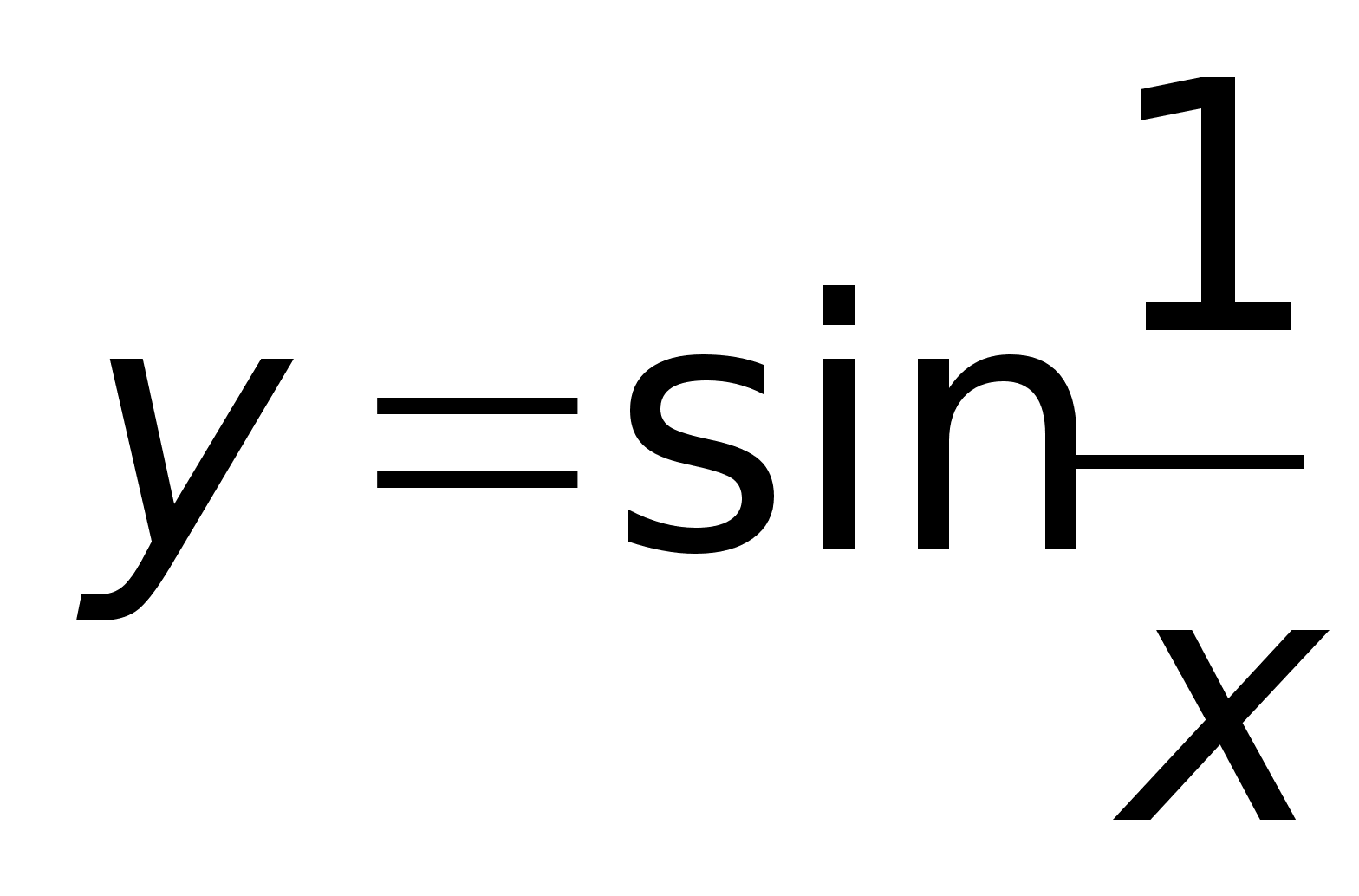

 ункция
ункция

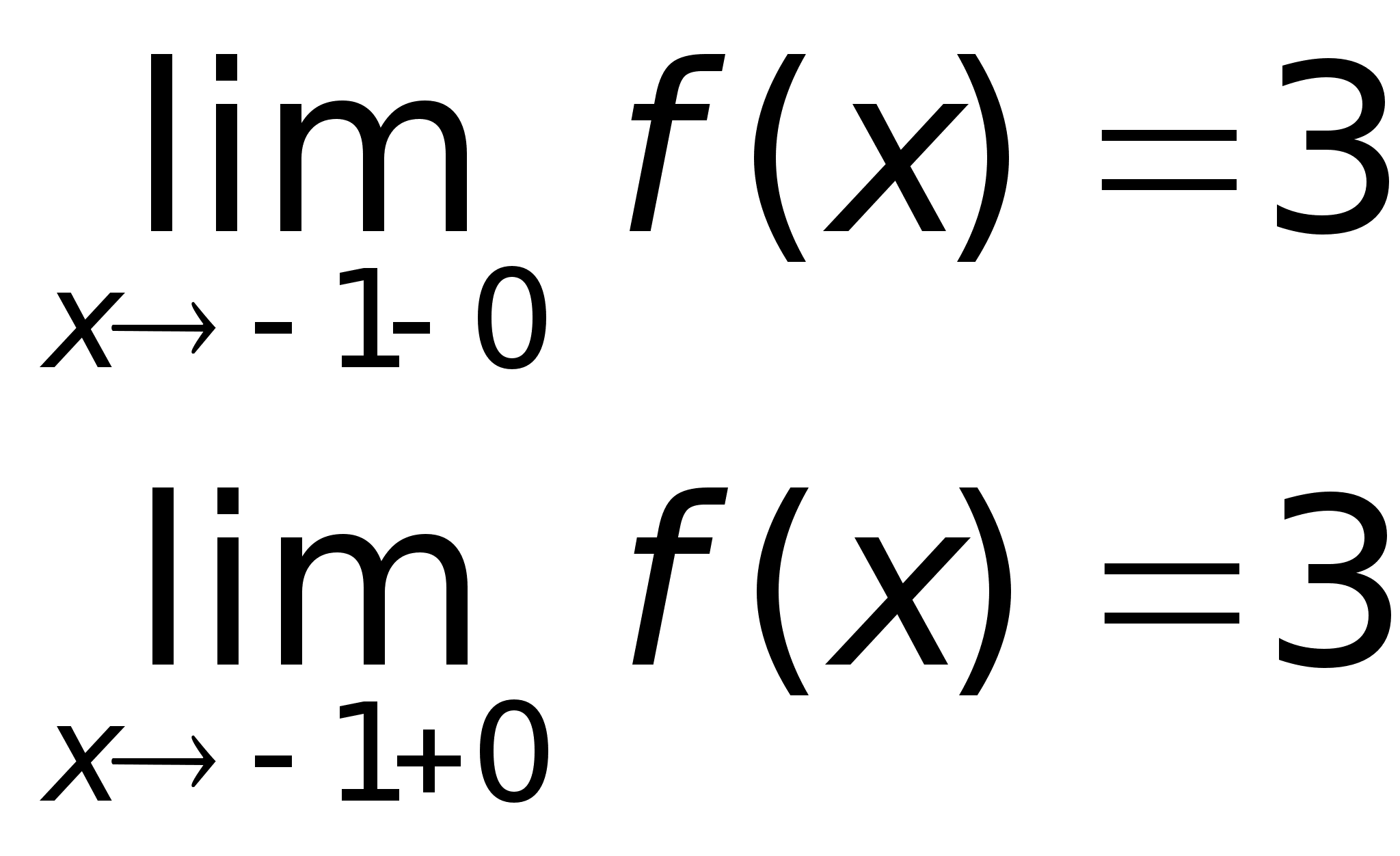
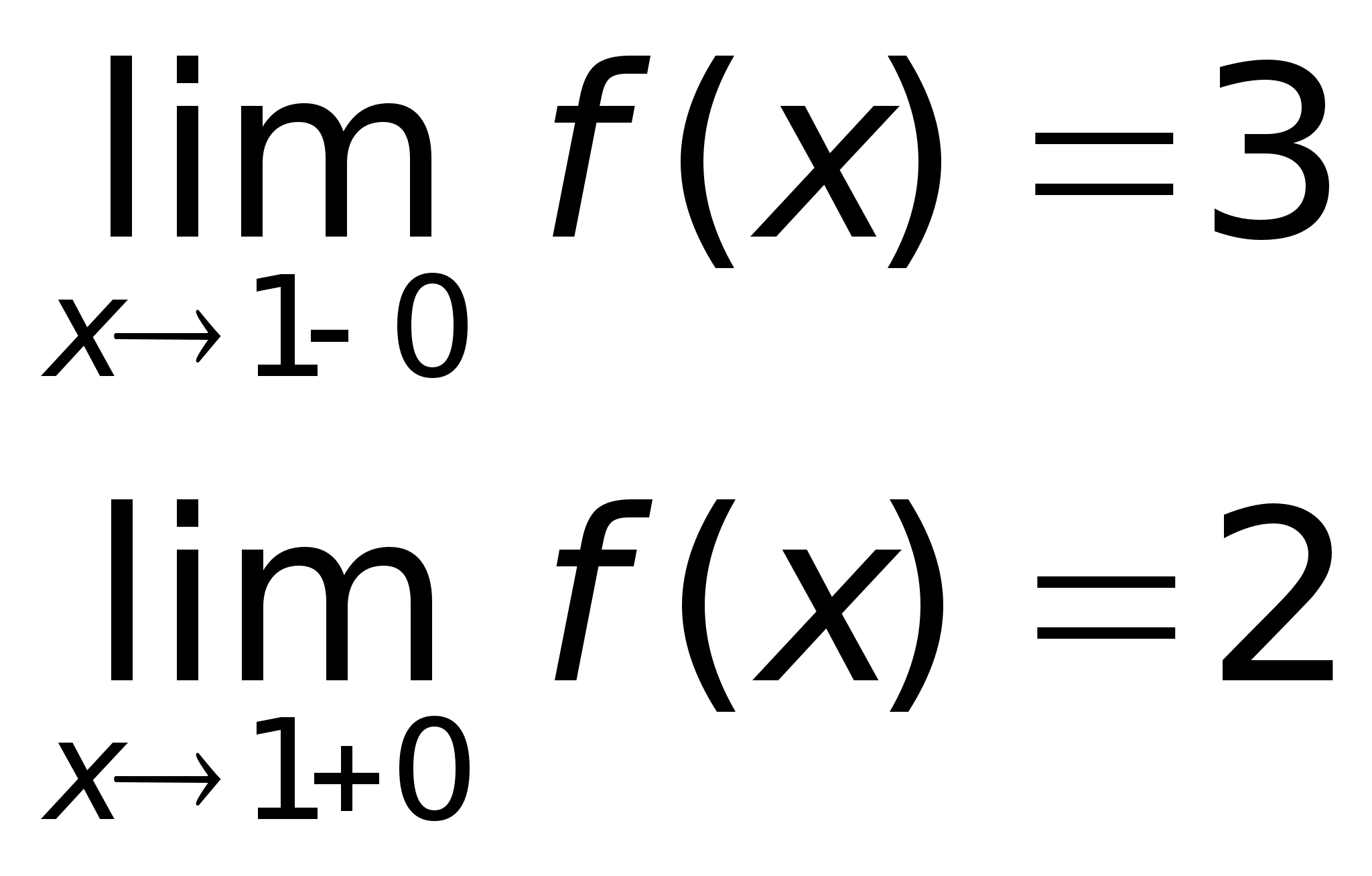 в
точке х = -1 функция
непрерывна
в точке х =
1 точка разрыва
1 – го рода
в
точке х = -1 функция
непрерывна
в точке х =
1 точка разрыва
1 – го рода
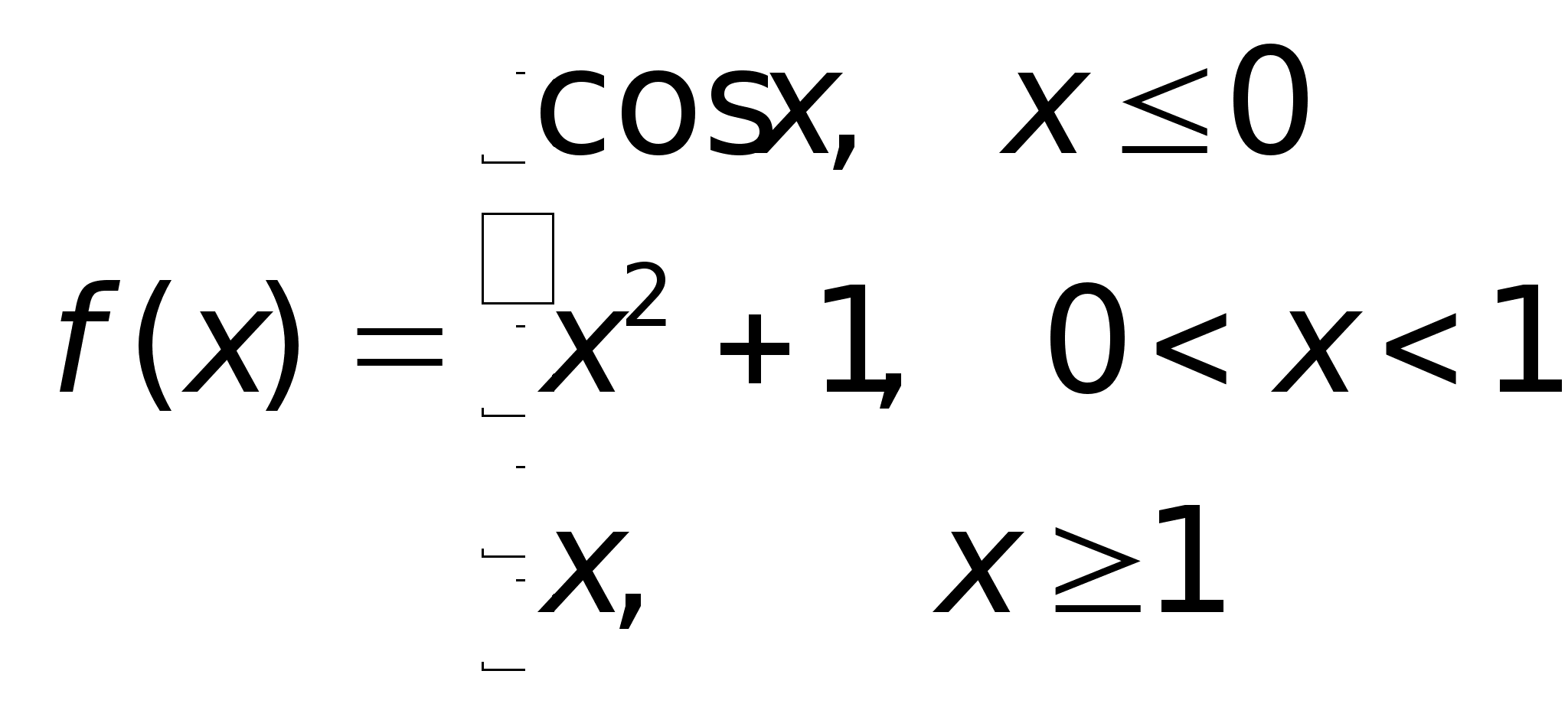
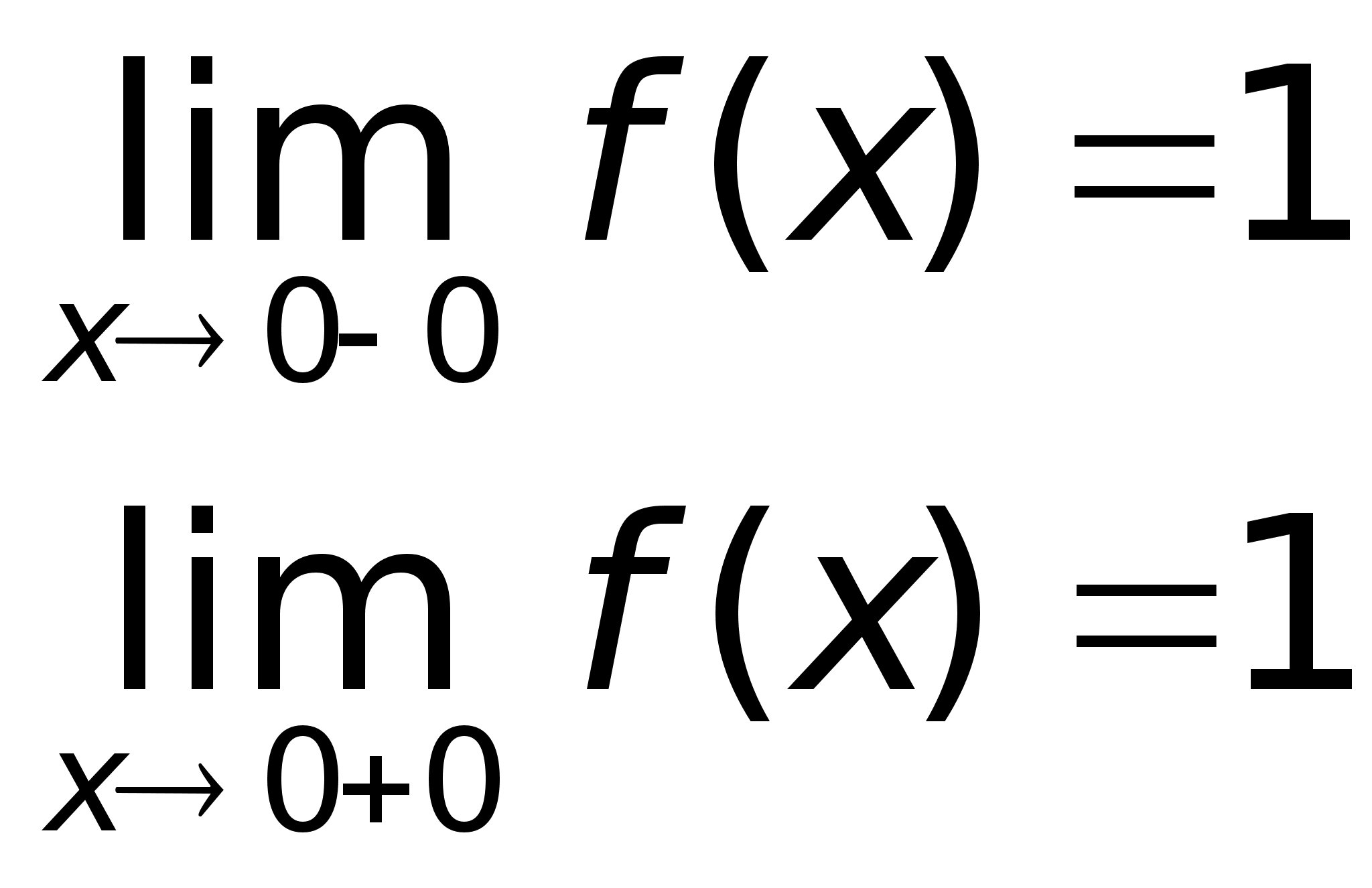
 в
точке х = 0 функция
непрерывна
в точке х =
1 точка разрыва
1 – го рода
в
точке х = 0 функция
непрерывна
в точке х =
1 точка разрыва
1 – го рода
 8)
Производная
ф-ииОпределение.
Производной
функции f(x)
в точке х = х0
называется
предел отношения
приращения
функции в этой
точке к приращению
аргумента,
если он существует.
8)
Производная
ф-ииОпределение.
Производной
функции f(x)
в точке х = х0
называется
предел отношения
приращения
функции в этой
точке к приращению
аргумента,
если он существует.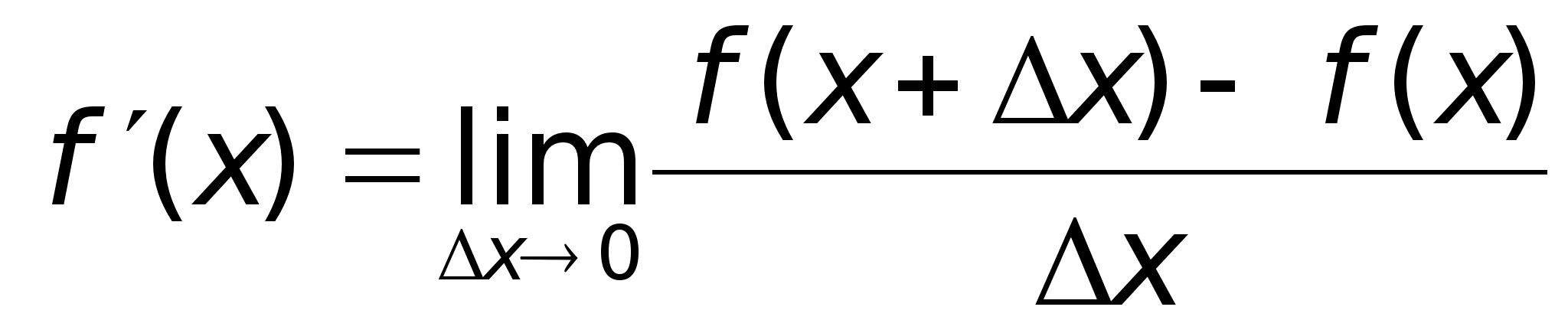 f(x)
f(x)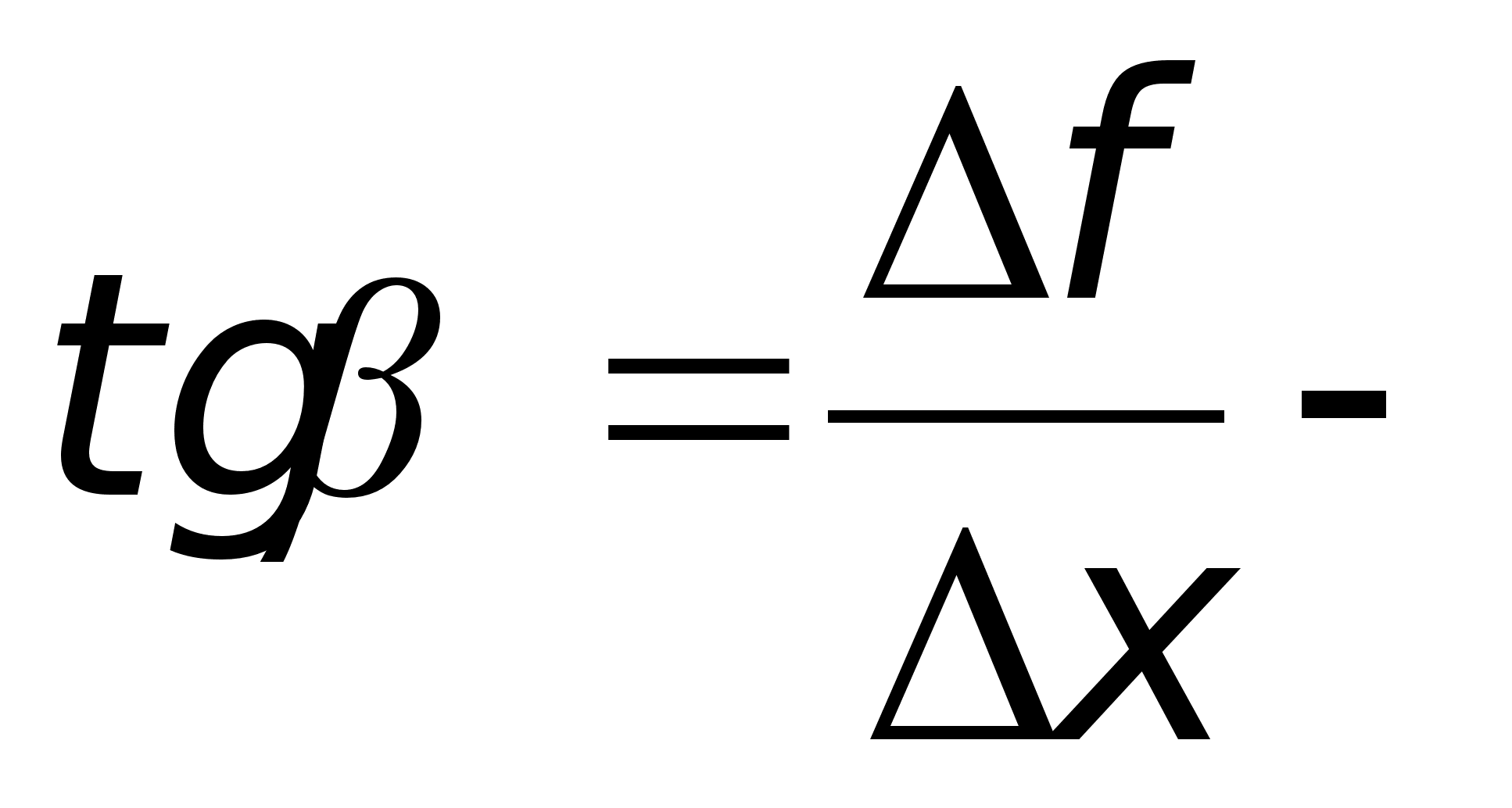 тангенс угла
наклона секущей
МР к графику
функции.
тангенс угла
наклона секущей
МР к графику
функции.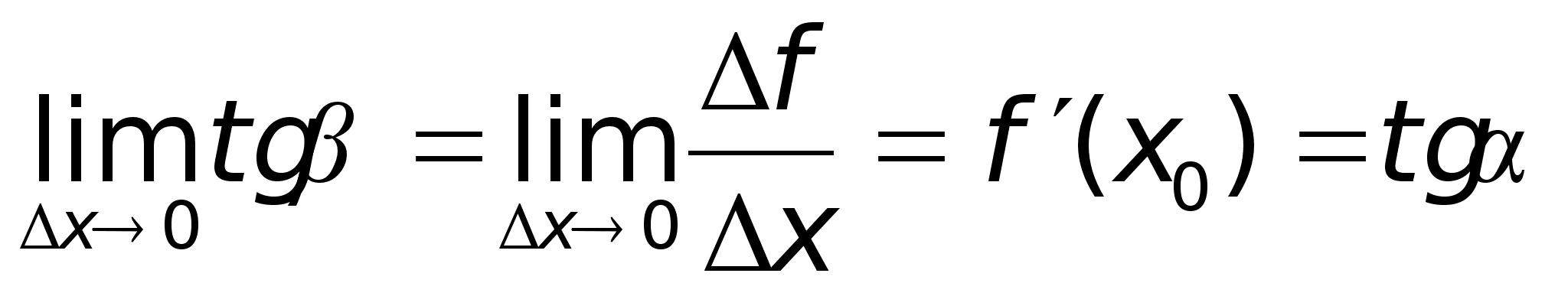 ,где
,где
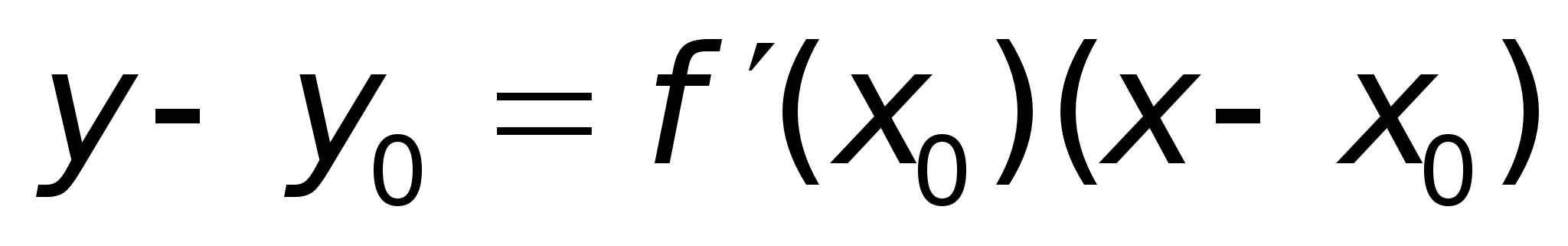 Уравнение
нормали к кривой:
Уравнение
нормали к кривой:
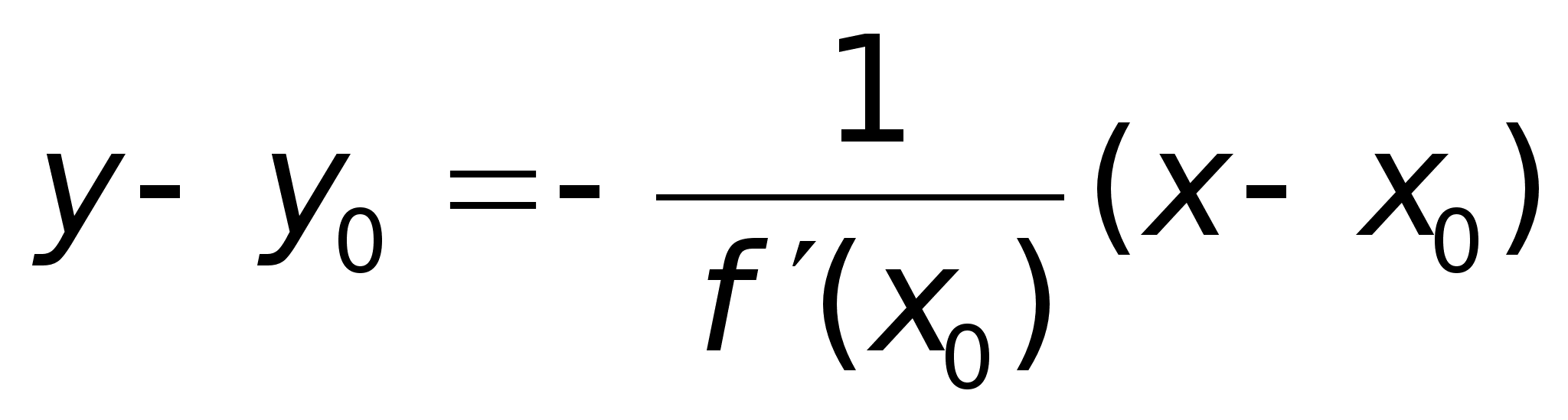 .Фактически
производная
функции показывает
как бы скорость
изменения
функции, как
изменяется
функция при
изменении
переменной.
.Фактически
производная
функции показывает
как бы скорость
изменения
функции, как
изменяется
функция при
изменении
переменной.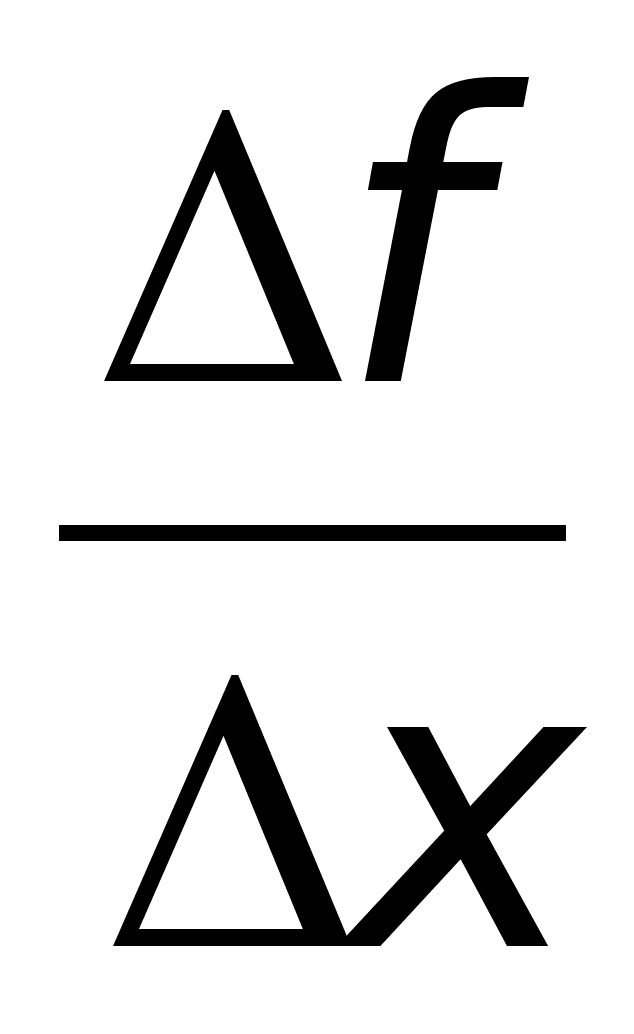 при условии,
что это отношение
существует.
при условии,
что это отношение
существует.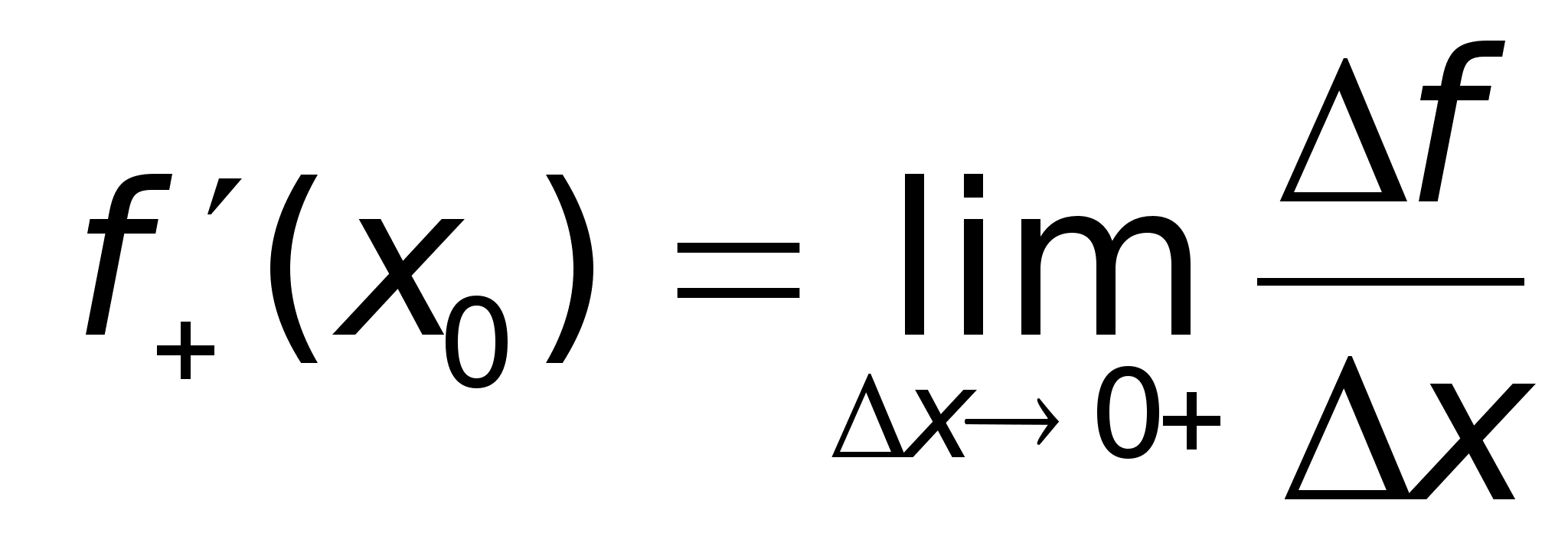
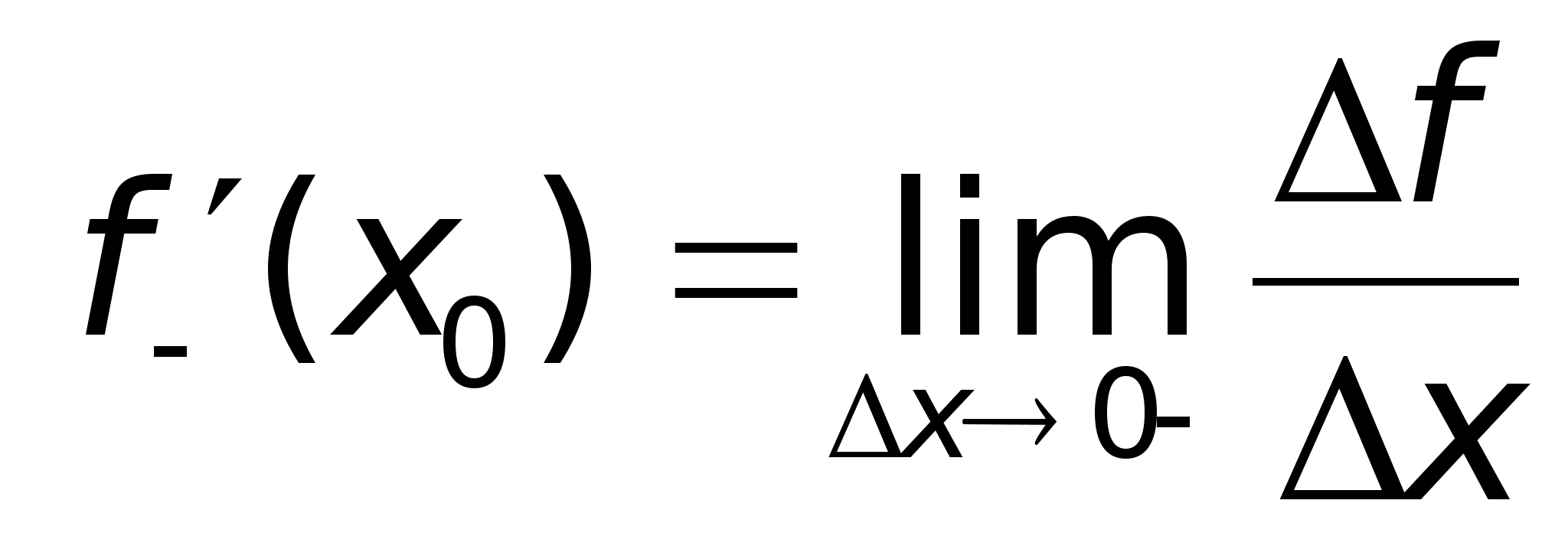
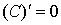 ,
C=const. 2.
,
C=const. 2. 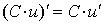 .
3.
.
3. 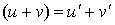 .
4.
.
4.
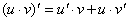 .
5.
.
5. 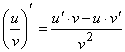 .
6.
.
6.
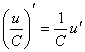 .
7.
.
7.
 .
8.
.
8.
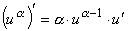 ,
a О R. 9.
,
a О R. 9.

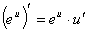 .
10.
.
10. 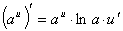 ,
где
а
ОR+. 11.
,
где
а
ОR+. 11.
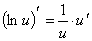 .
12.
.
12.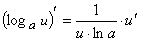 ,
a О R, a № 1. 13.
,
a О R, a № 1. 13.
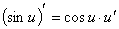 .
14.
.
14.
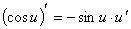 .
15.
.
15.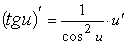 .
16.
.
16.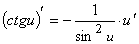 .
17.
.
17.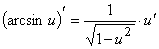 .
18.
.
18.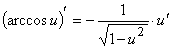 .
19.
.
19.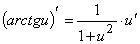 .
20.
.
20.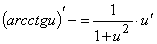 .
21.
.
21.
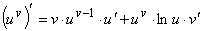 .
22.
.
22.
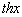 =
=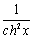 23.
23.
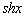 =
=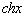 24.
24.
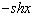 25.
25.
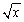 =
=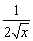 26.
26.
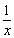 =
=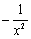 Доказательство.Докажем
формулу
Доказательство.Докажем
формулу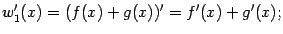 .Пусть аргументу
x
дано приращение
h;
при этом функция
.Пусть аргументу
x
дано приращение
h;
при этом функция
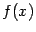 получает
приращение
получает
приращение
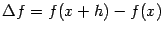 ,
а функция
,
а функция
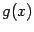 --
приращение
--
приращение
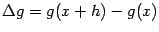 .
Их сумма
.
Их сумма
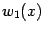 получит
тогда приращение
получит
тогда приращение
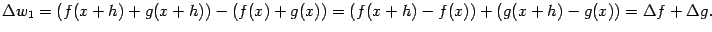
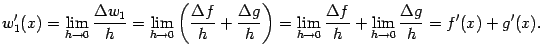 Совершенно
аналогично
доказывается
формула
Совершенно
аналогично
доказывается
формула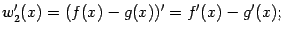 . Докажем теперь
формулу
. Докажем теперь
формулу
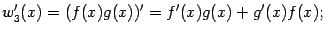 .
Пусть снова
.
Пусть снова
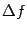 и
и
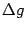 --
приращения
функций, соответствующие
приращению
--
приращения
функций, соответствующие
приращению
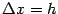 аргумента
аргумента
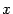 .
Тогда
.
Тогда
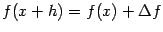 ,
,
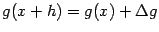 и
приращением
произведения
будет
и
приращением
произведения
будет
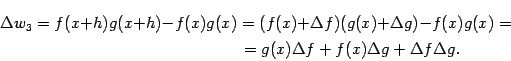
 При
этом мы вынесли
множители
При
этом мы вынесли
множители
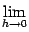 как
постоянные,
не зависящие
от переменного
как
постоянные,
не зависящие
от переменного
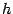 ,
к которому
относится
база предела.
,
к которому
относится
база предела.
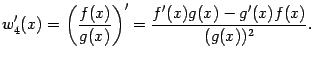 .
Заметим, что
.
Заметим, что
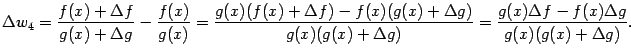 Поэтому,
согласно правилам
вычисления
пределов,
Поэтому,
согласно правилам
вычисления
пределов,
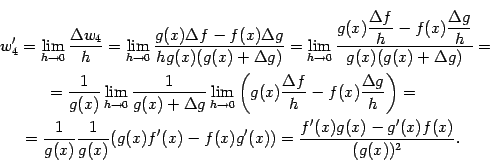
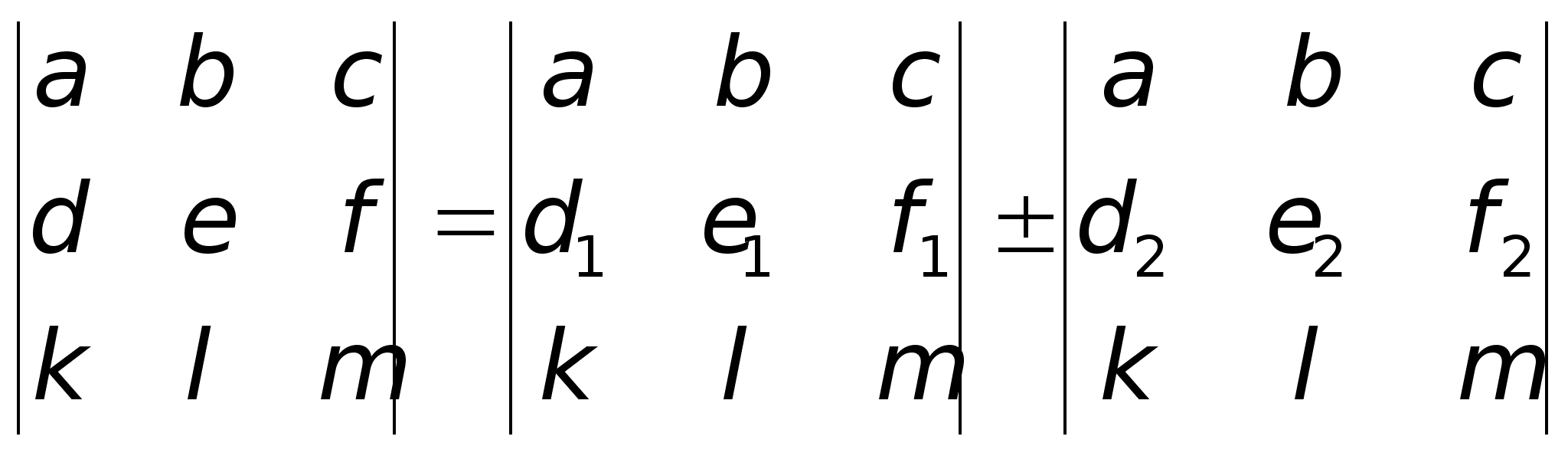
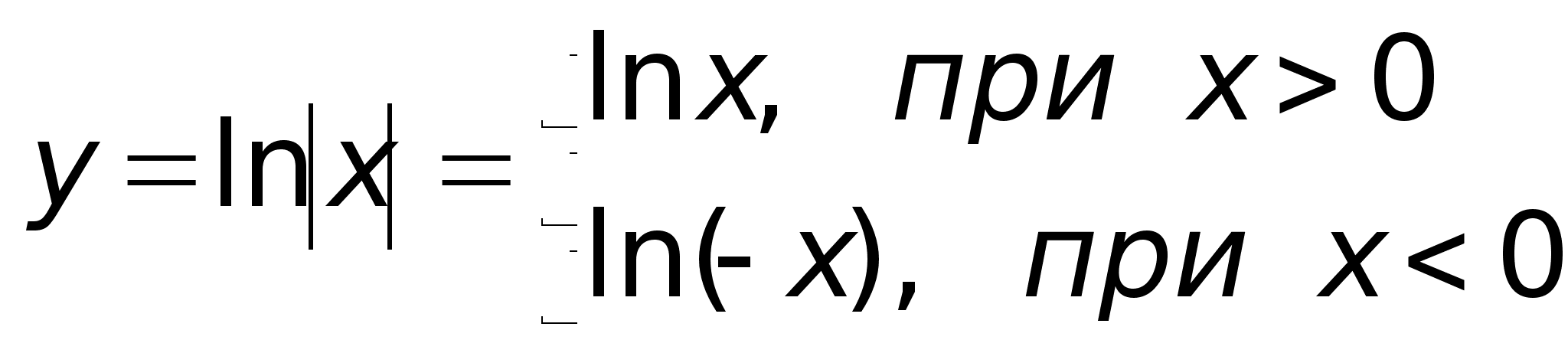 .Тогда
(ln
.Тогда
(ln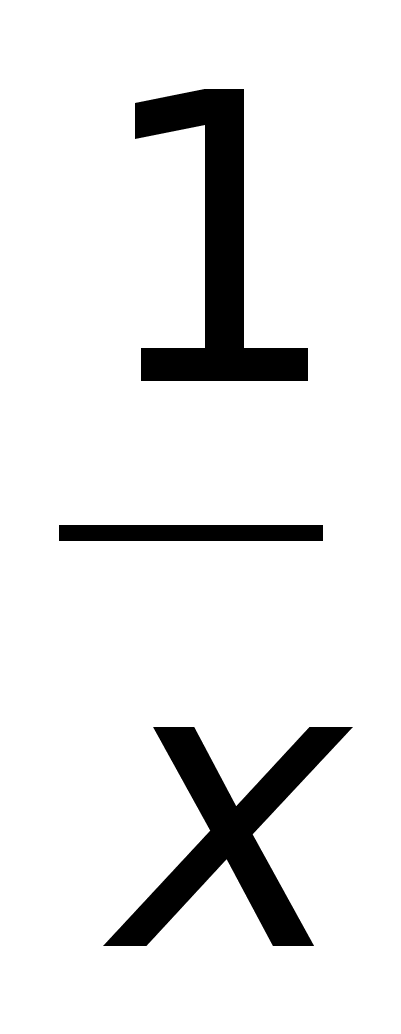 ,
т.к.
,
т.к.
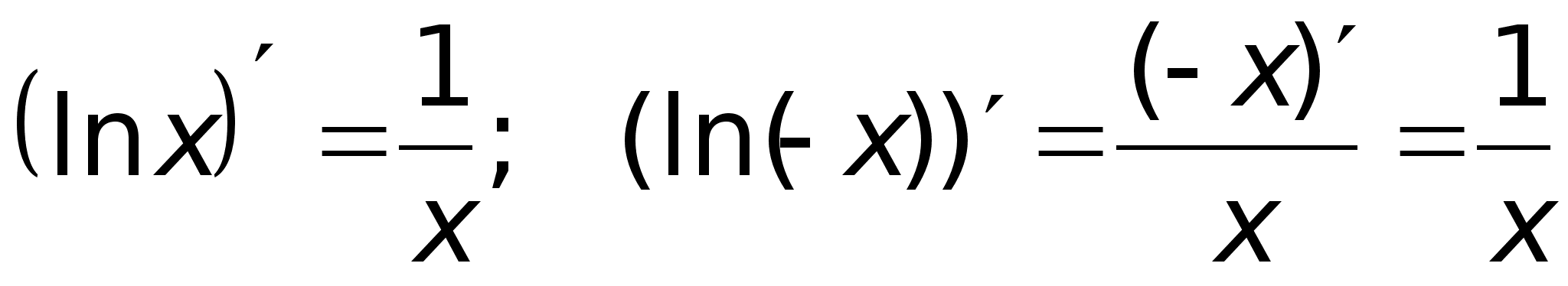 .Учитывая
полученный
результат,
можно записать
.Учитывая
полученный
результат,
можно записать
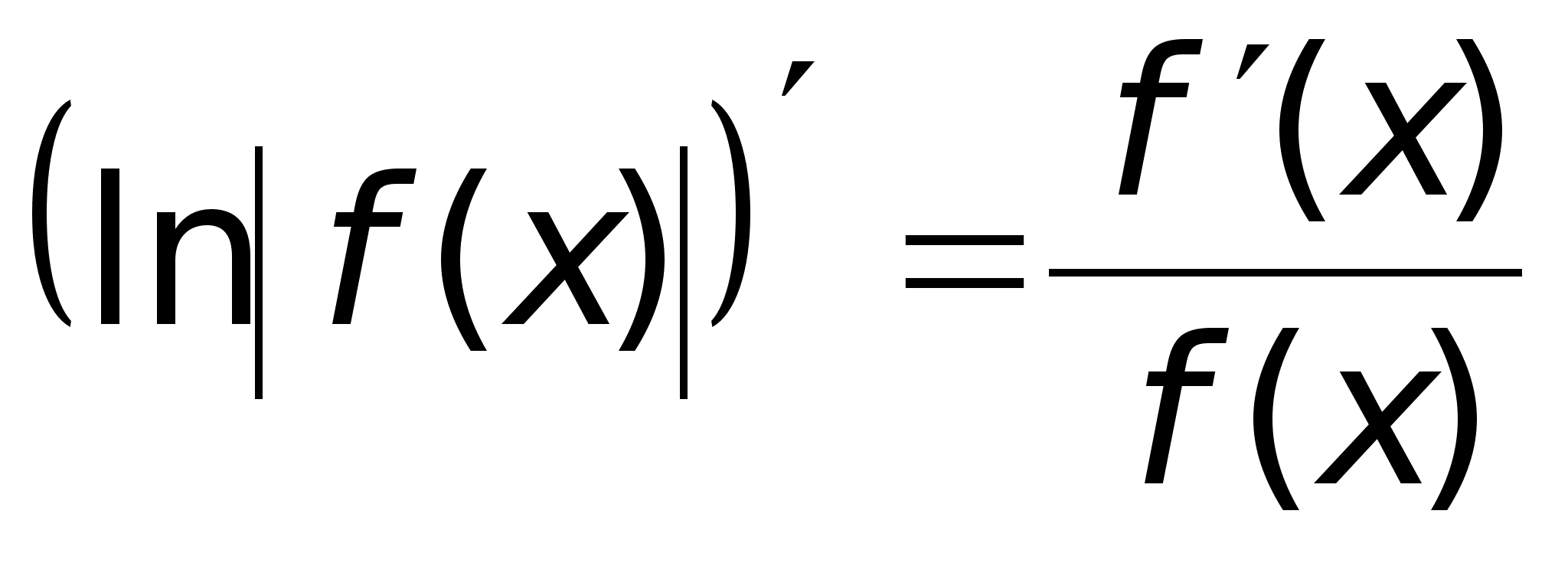 .Отношение
.Отношение
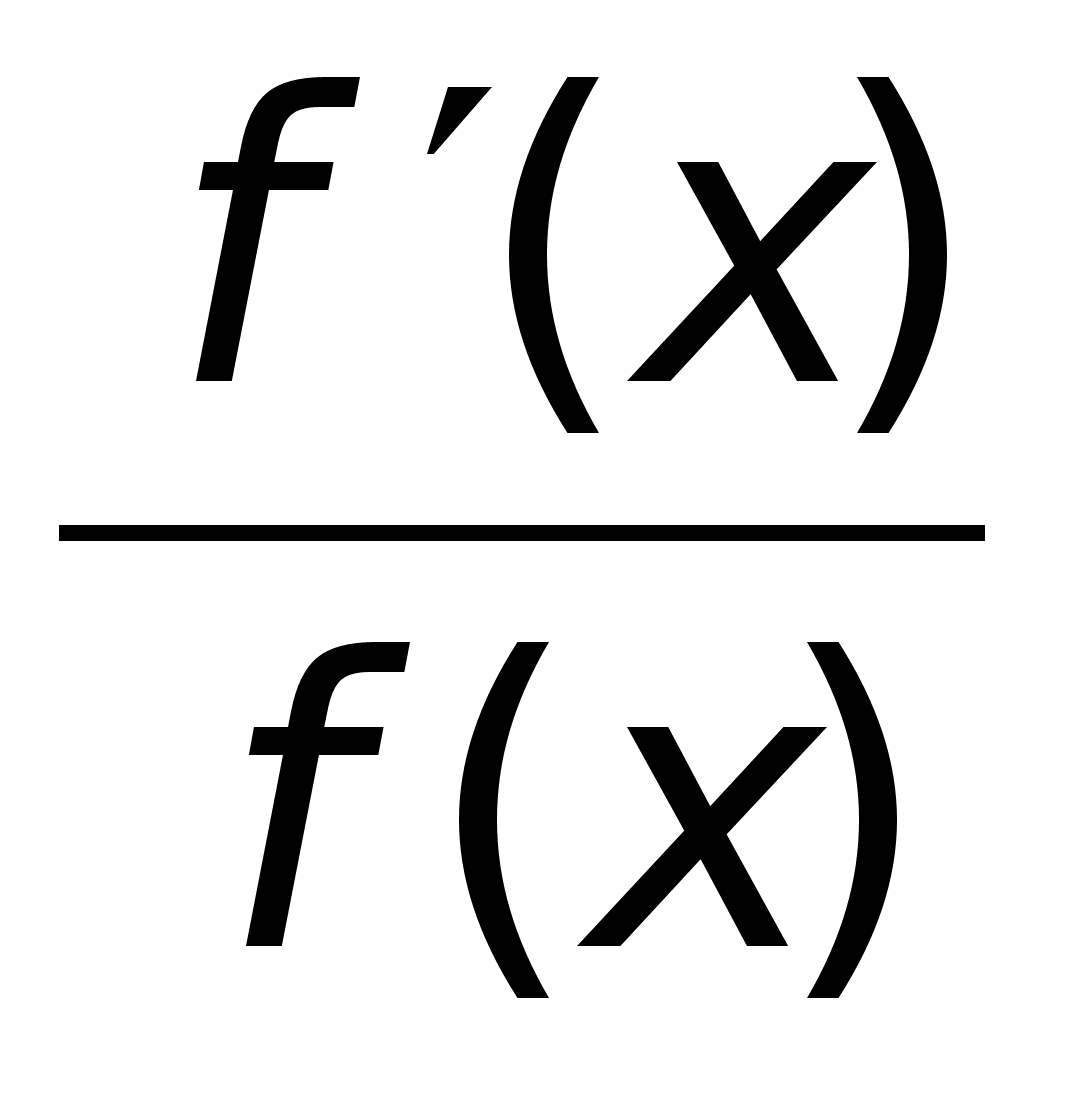 называется
логарифмической
производной
функции f(x).Способ
логарифмического
дифференцирования
состоит
в том, что сначала
находят логарифмическую
производную
функции, а затем
производную
самой функции
по формуле
называется
логарифмической
производной
функции f(x).Способ
логарифмического
дифференцирования
состоит
в том, что сначала
находят логарифмическую
производную
функции, а затем
производную
самой функции
по формуле
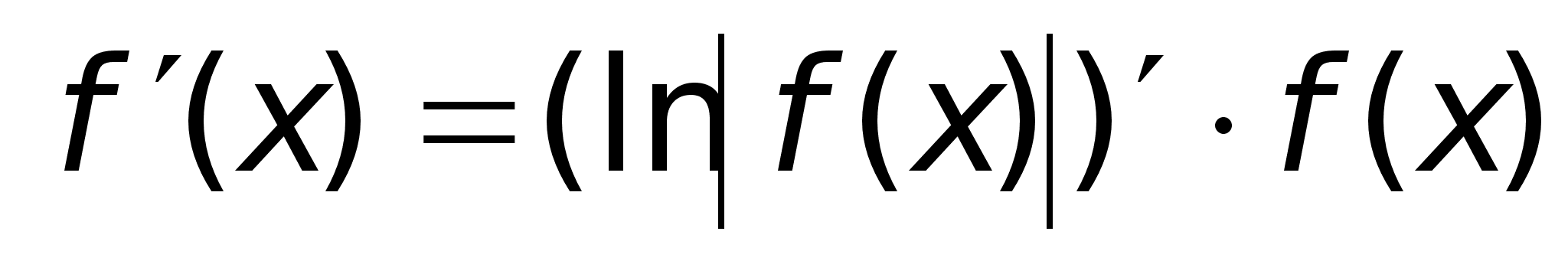 Способ
логарифмического
дифференцирования
удобно применять
для нахождения
производных
сложных, особенно
показательных
функций, для
которых непосредственное
вычисление
производной
с использованием
правил дифференцирования
представляется
трудоемким.Производная
показательно-
степенной
функции.Функция
называется
показательной,
если независимая
переменная
входит в показатель
степени, и
степенной,
если переменная
является
основанием.
Если же и основание
и показатель
степени зависят
от переменной,
то такая функция
будет показательно
– степенной.Пусть
u
= f(x)
и v
= g(x)
– функции, имеющие
производные
в точке х, f(x)>0.Найдем
производную
функции y
= uv.
Логарифмируя,
получим:lny
= vlnu
Способ
логарифмического
дифференцирования
удобно применять
для нахождения
производных
сложных, особенно
показательных
функций, для
которых непосредственное
вычисление
производной
с использованием
правил дифференцирования
представляется
трудоемким.Производная
показательно-
степенной
функции.Функция
называется
показательной,
если независимая
переменная
входит в показатель
степени, и
степенной,
если переменная
является
основанием.
Если же и основание
и показатель
степени зависят
от переменной,
то такая функция
будет показательно
– степенной.Пусть
u
= f(x)
и v
= g(x)
– функции, имеющие
производные
в точке х, f(x)>0.Найдем
производную
функции y
= uv.
Логарифмируя,
получим:lny
= vlnu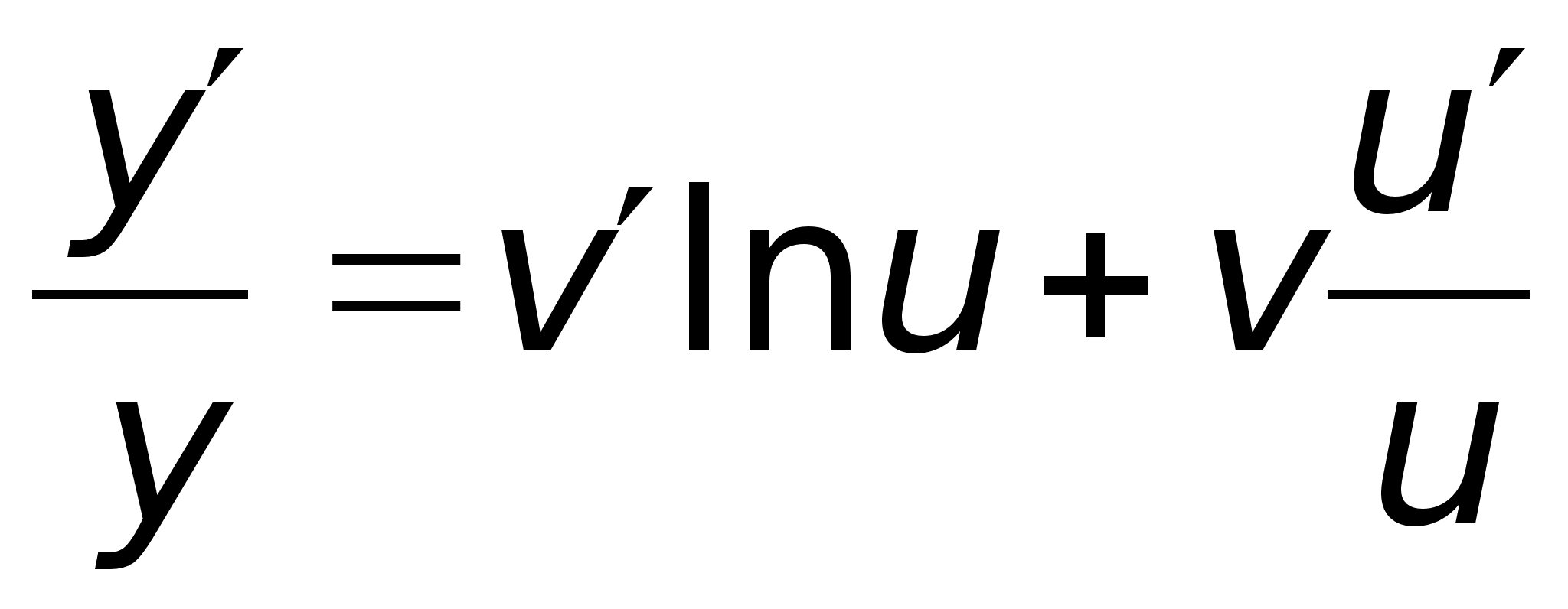
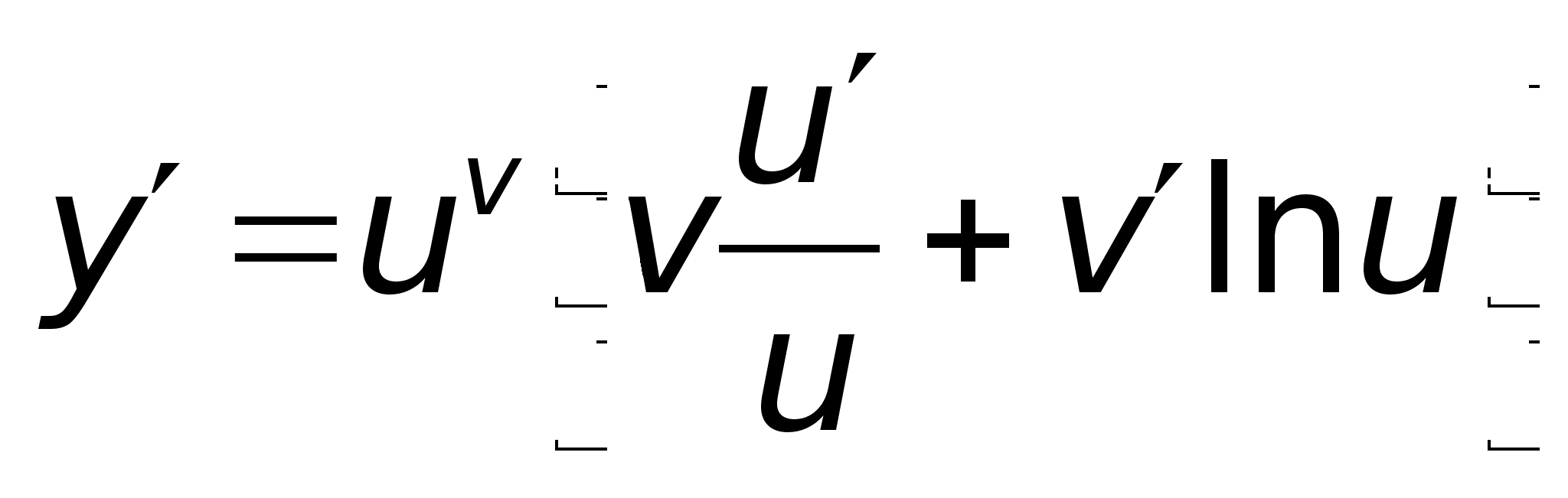
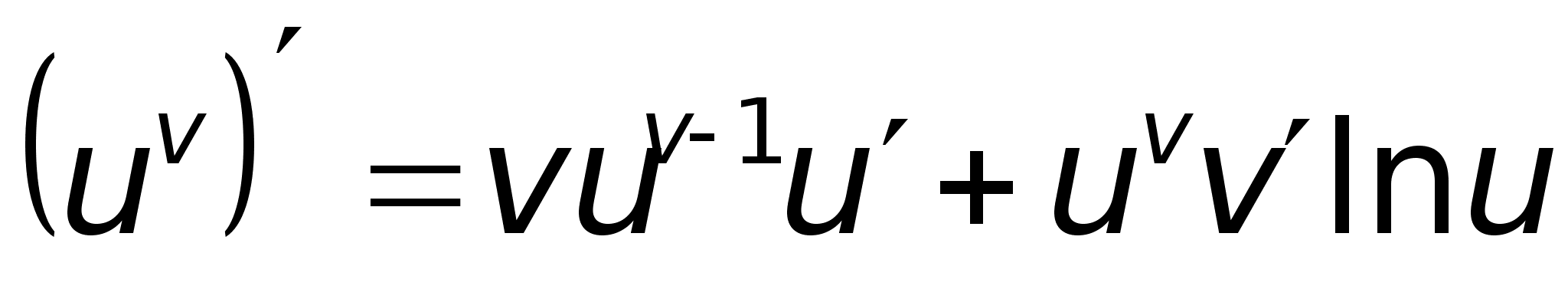 Пример.
Найти производную
функции
Пример.
Найти производную
функции
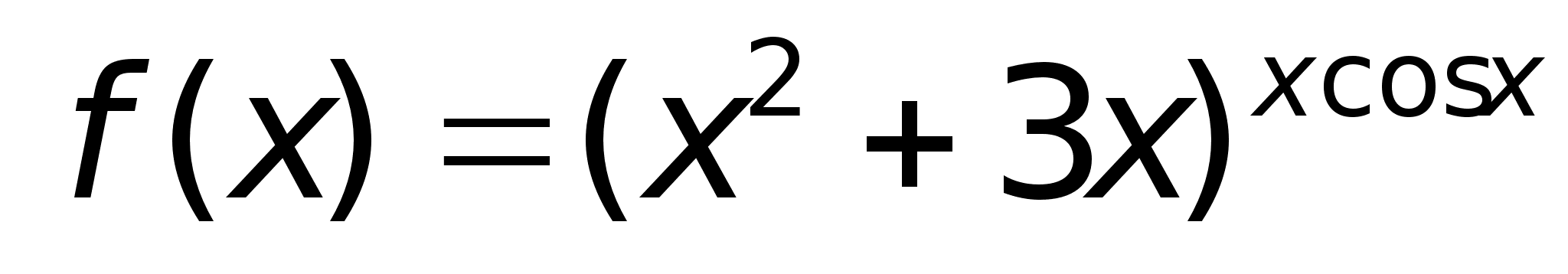 .По
полученной
выше формуле
получаем:
.По
полученной
выше формуле
получаем:
 Производные
этих функций:
Производные
этих функций:
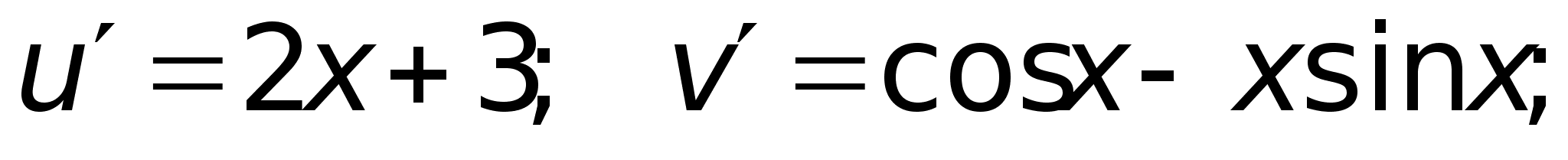 Окончательно:
Окончательно:
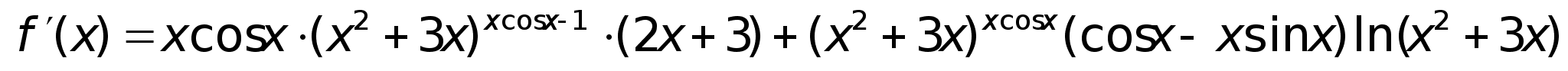
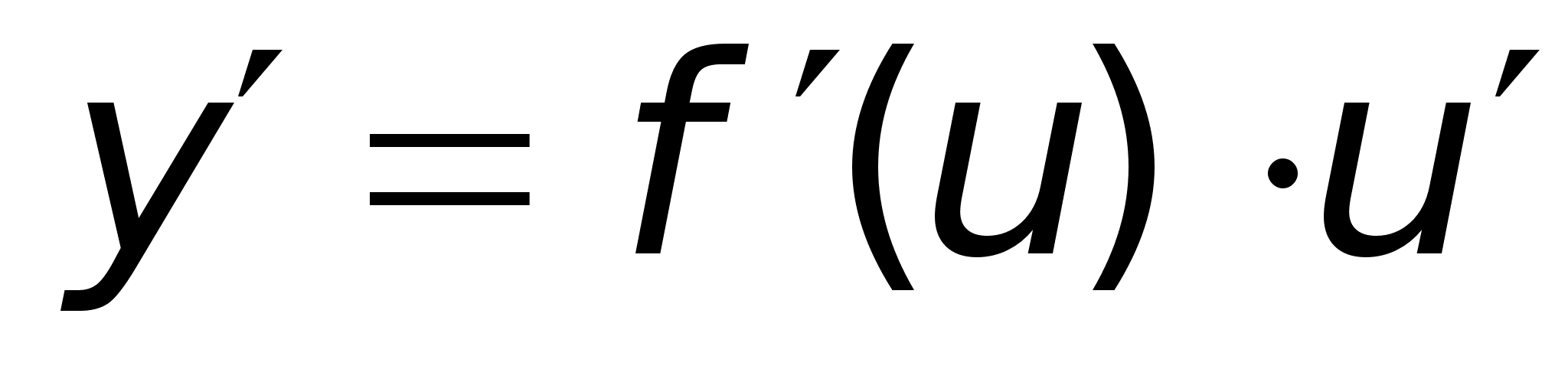 Доказательство.
Доказательство.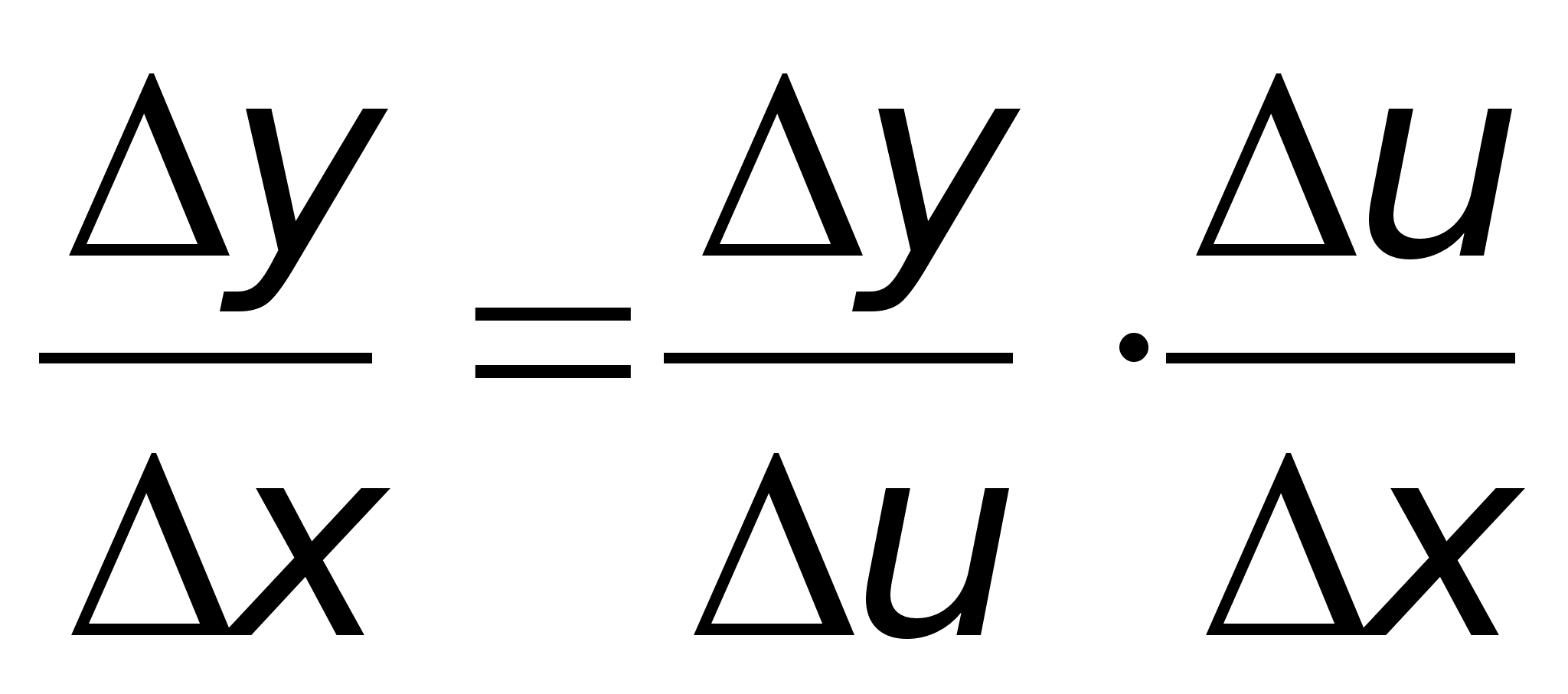
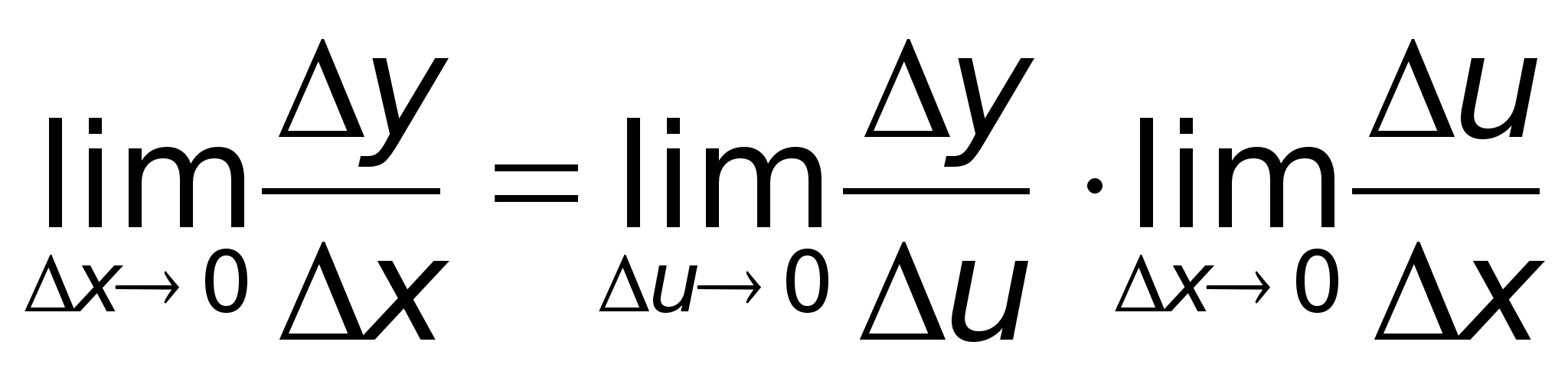
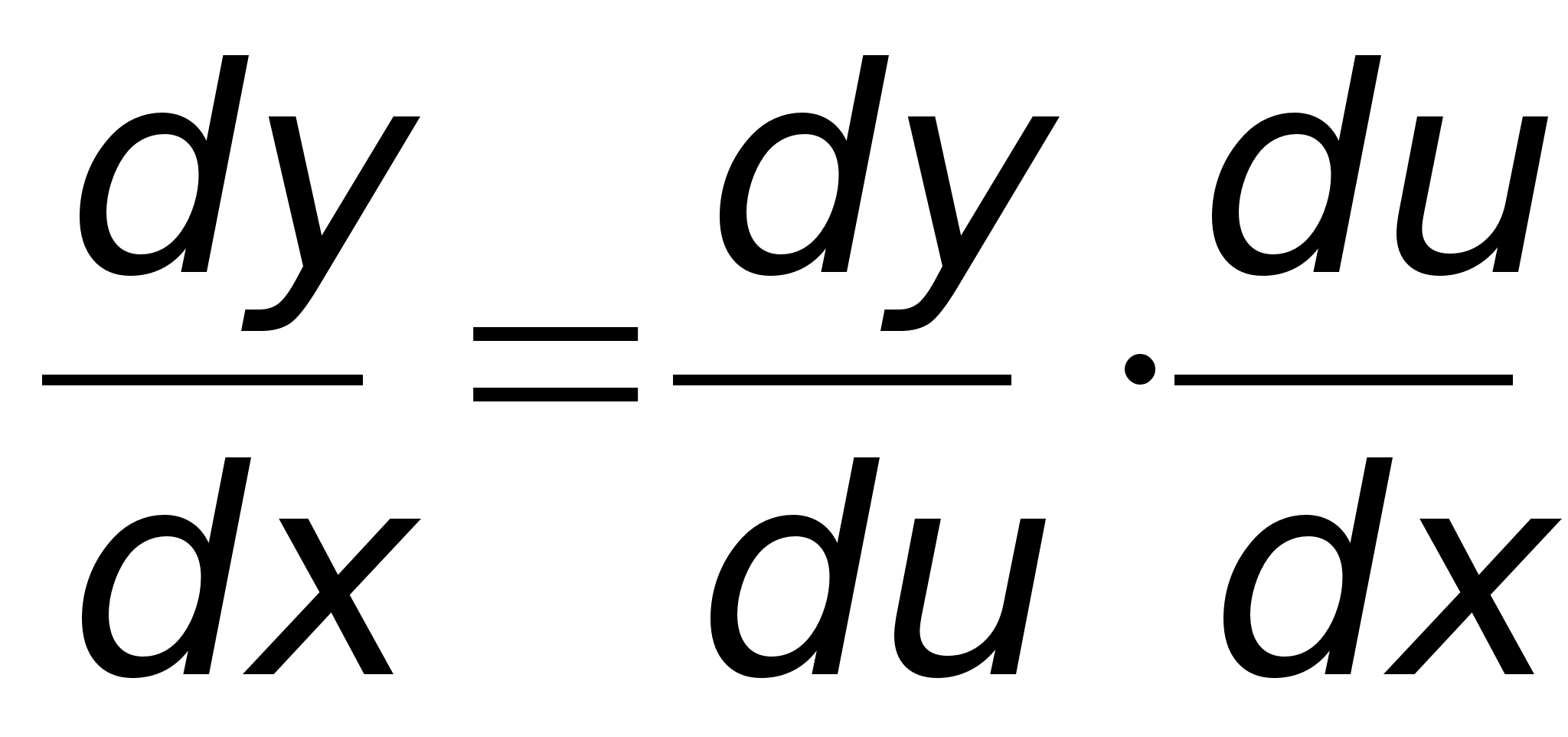
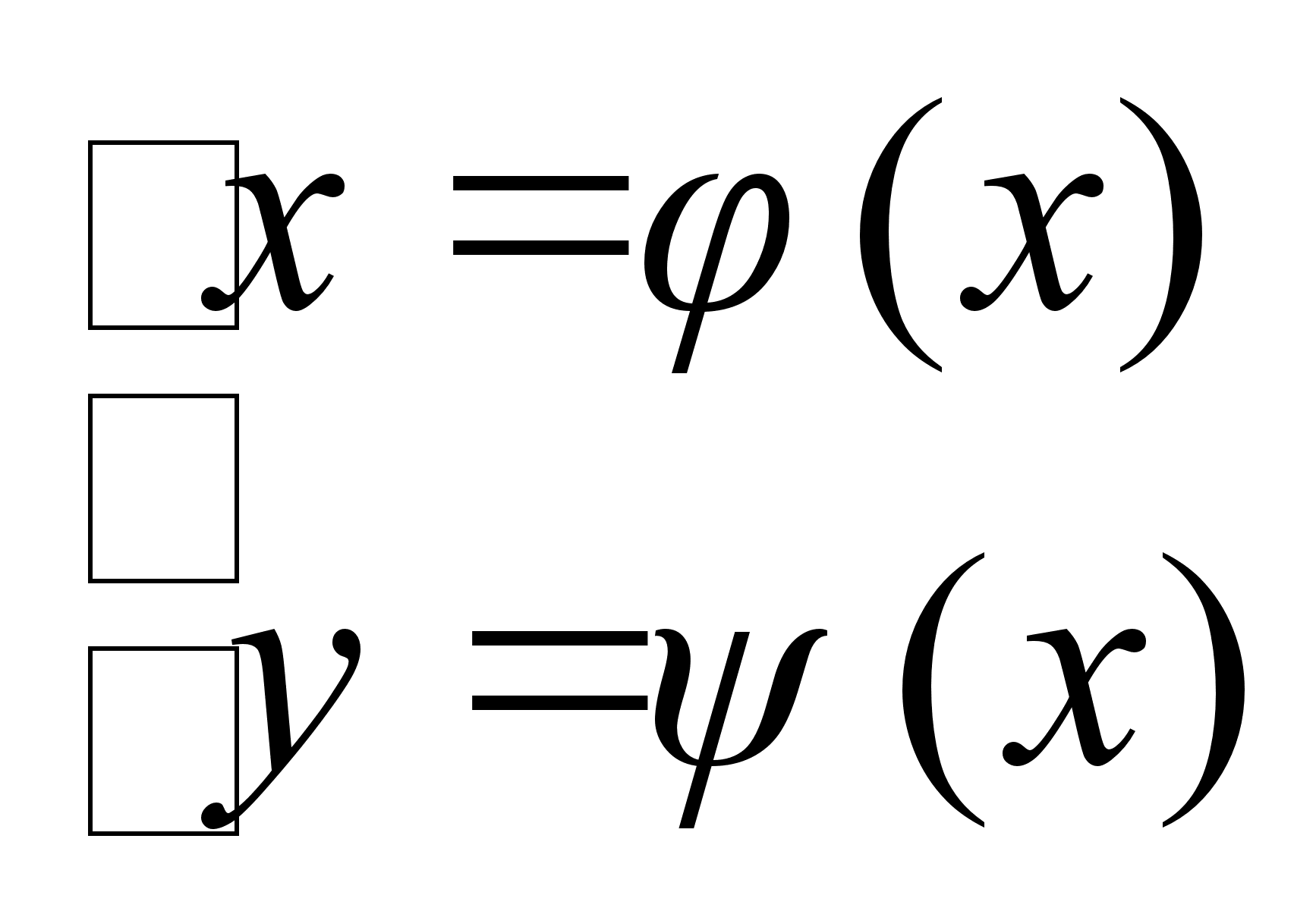 по
определению
производной
имеем
по
определению
производной
имеем
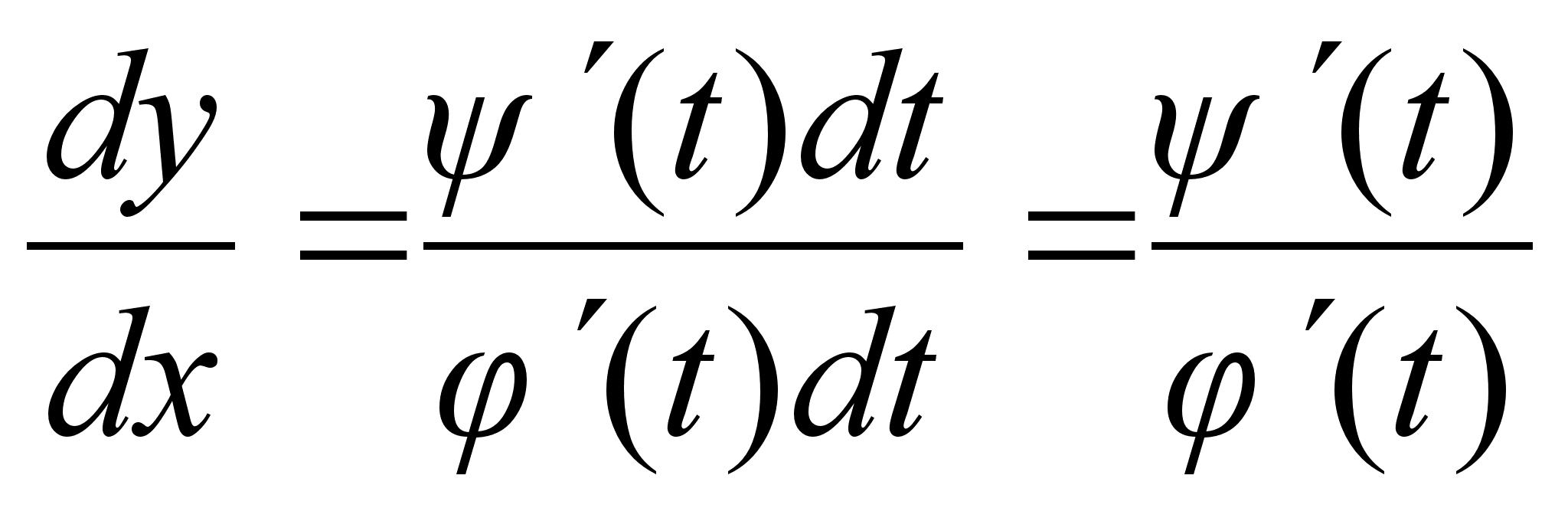 Производная
параметрически
заданной
функции.Пример:
Производная
параметрически
заданной
функции.Пример: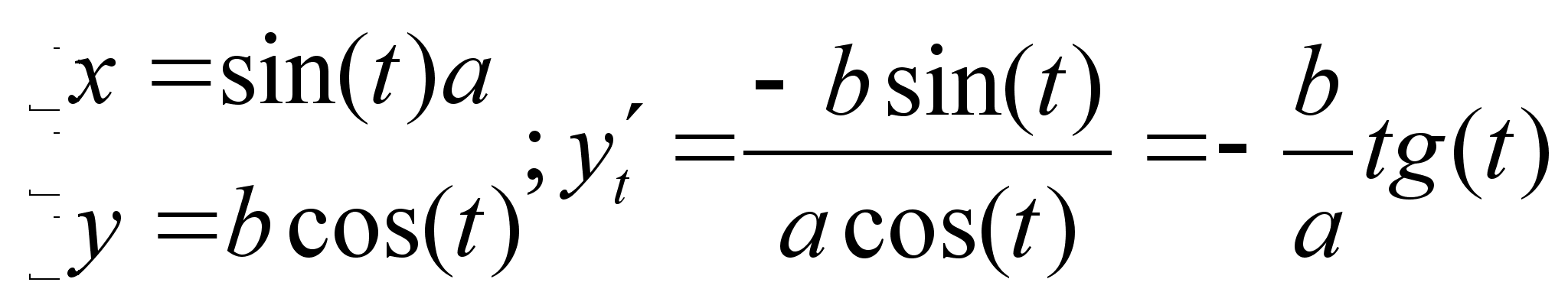 Логарифмическое
дифференцирование
Если дифференцируемая
функция имеет
сложный вид,
а именно содержит
степени, произведения,
частное, то
перед дифференцированием
её целесообразно
прологарифмировать,
при этом функция
примет линейный
или более простой
вид, дифференцирование
которой намного
проще. Дифференцирование
степенно-показательных
функций проводится
только после
предварительного
логарифмирования.Пример:
y=xx
ln(y)=xlnx
y`=xx(lnx+1)
Логарифмическое
дифференцирование
Если дифференцируемая
функция имеет
сложный вид,
а именно содержит
степени, произведения,
частное, то
перед дифференцированием
её целесообразно
прологарифмировать,
при этом функция
примет линейный
или более простой
вид, дифференцирование
которой намного
проще. Дифференцирование
степенно-показательных
функций проводится
только после
предварительного
логарифмирования.Пример:
y=xx
ln(y)=xlnx
y`=xx(lnx+1)
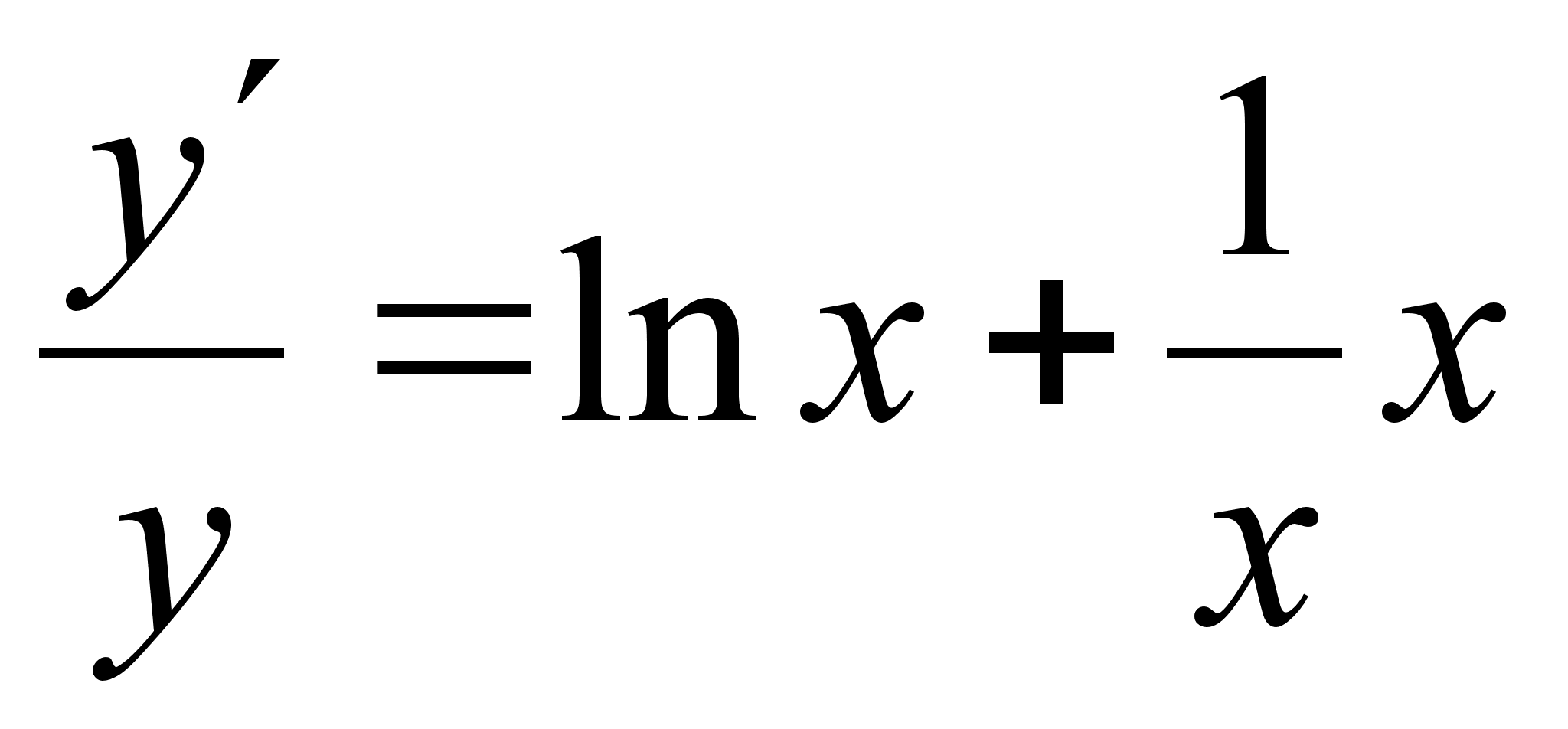
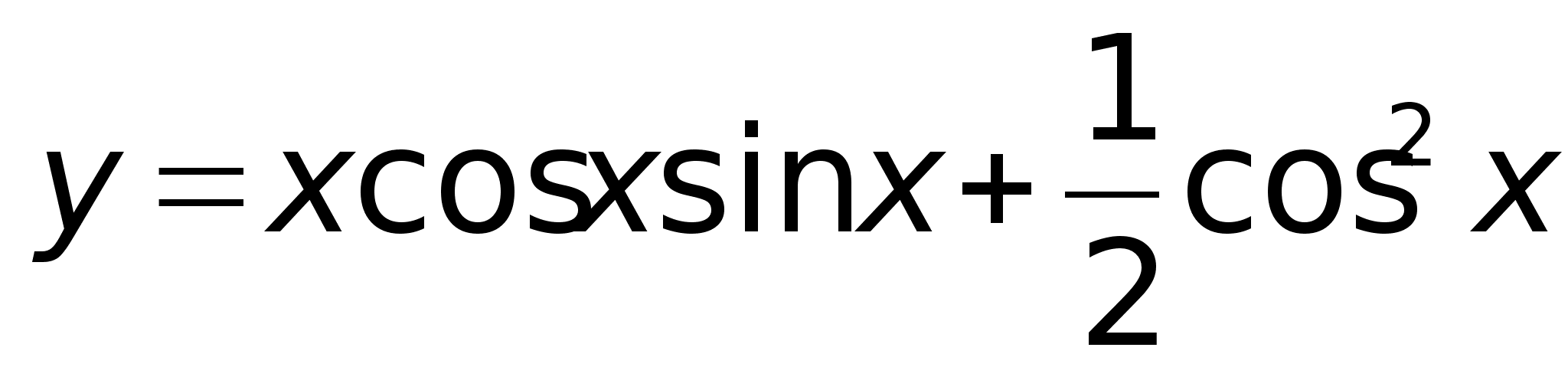 .Сначала
преобразуем
данную функцию:
.Сначала
преобразуем
данную функцию:
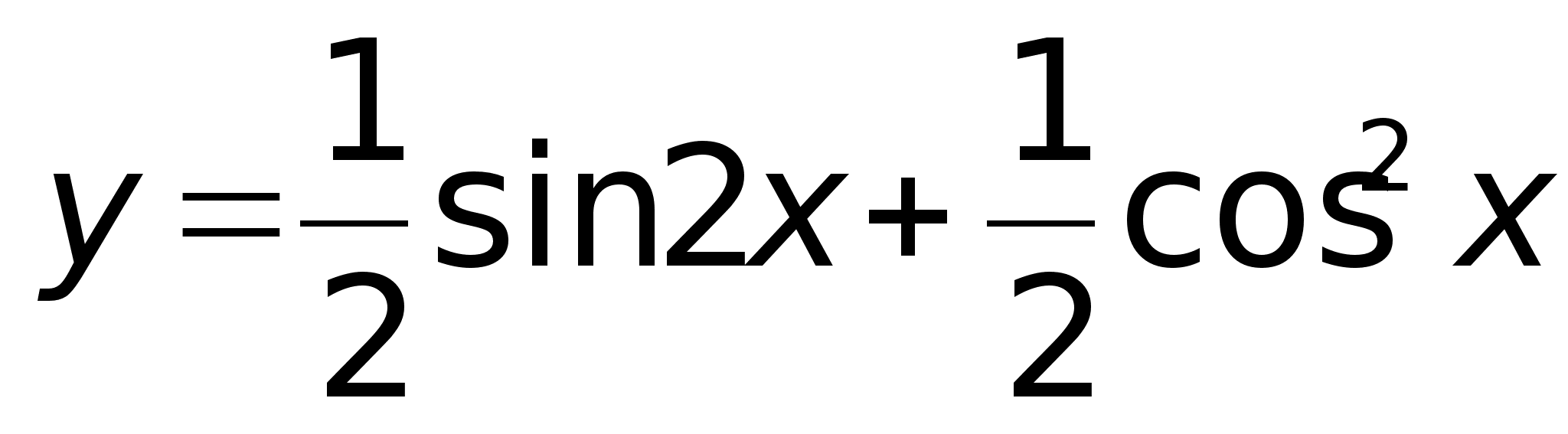
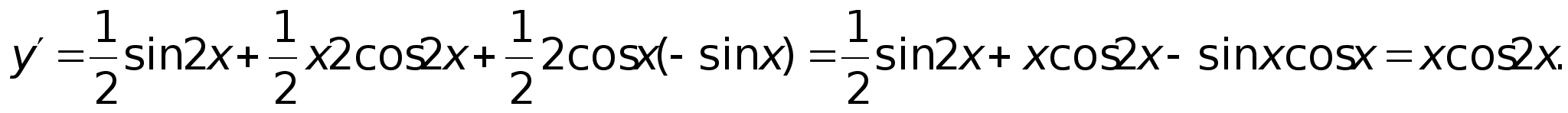 Пример.
Найти производную
функции
Пример.
Найти производную
функции
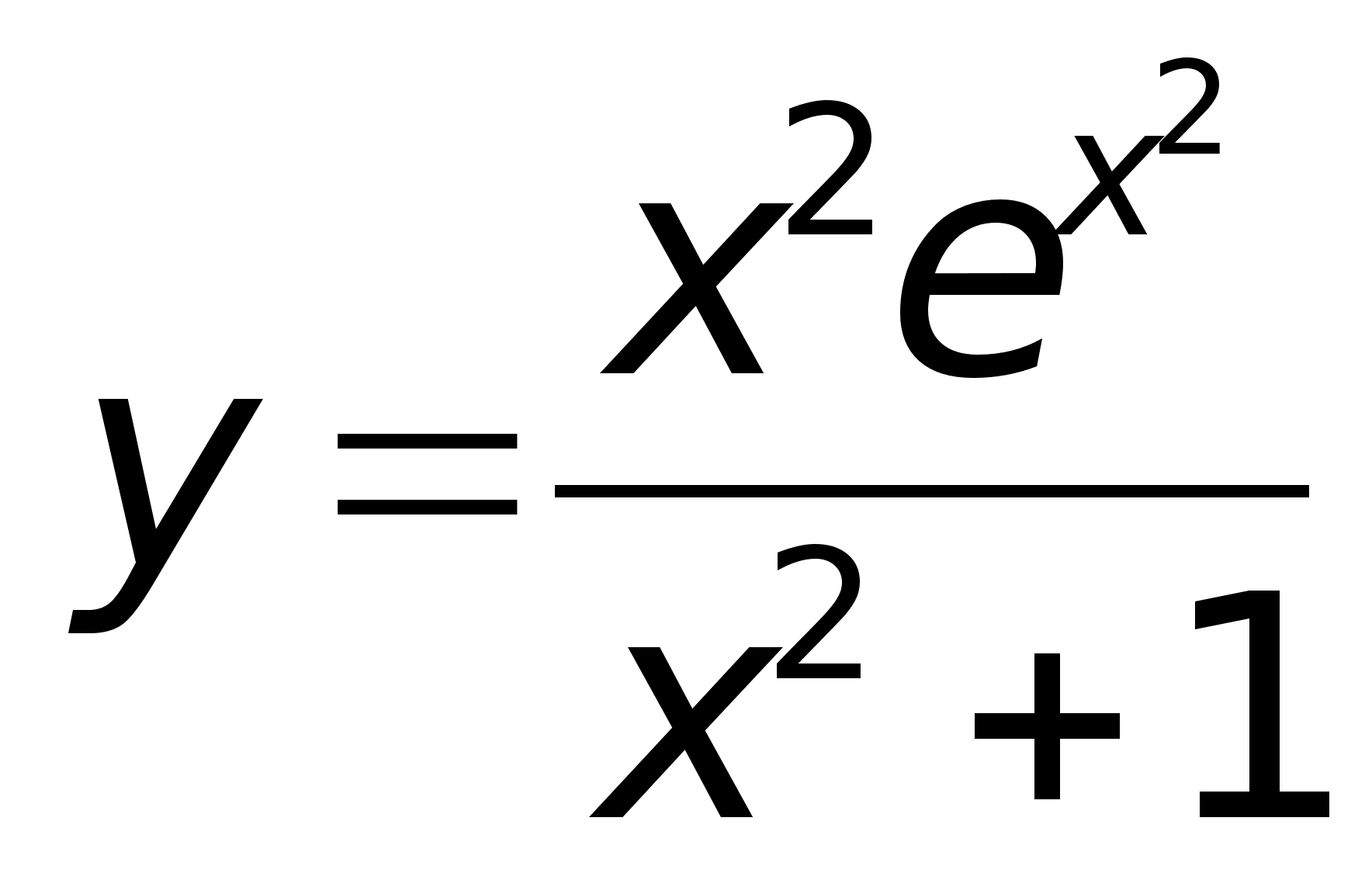 .
.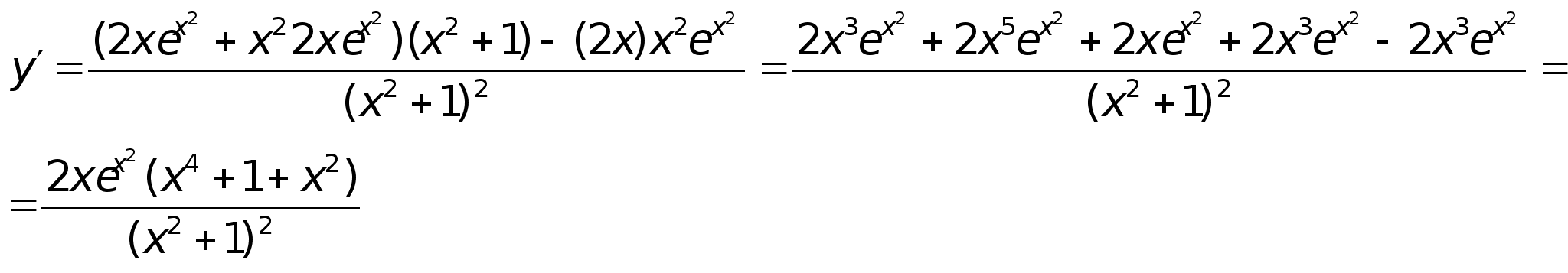 Пример.
Найти производную
функции
Пример.
Найти производную
функции
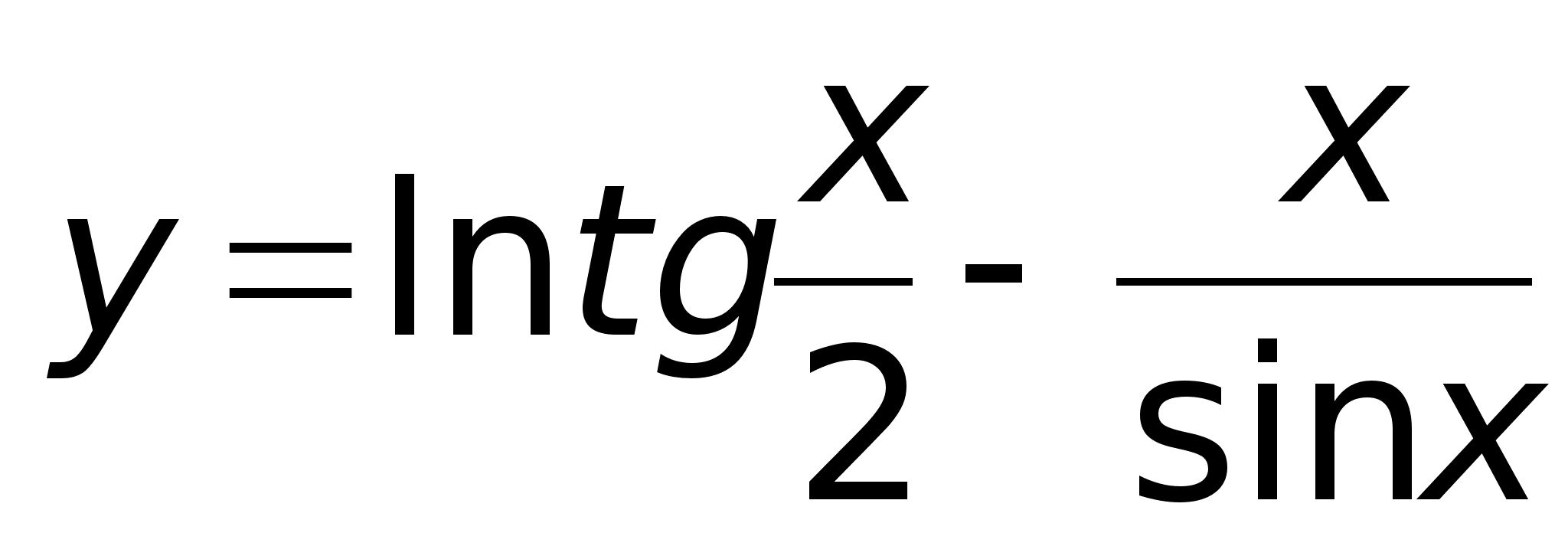
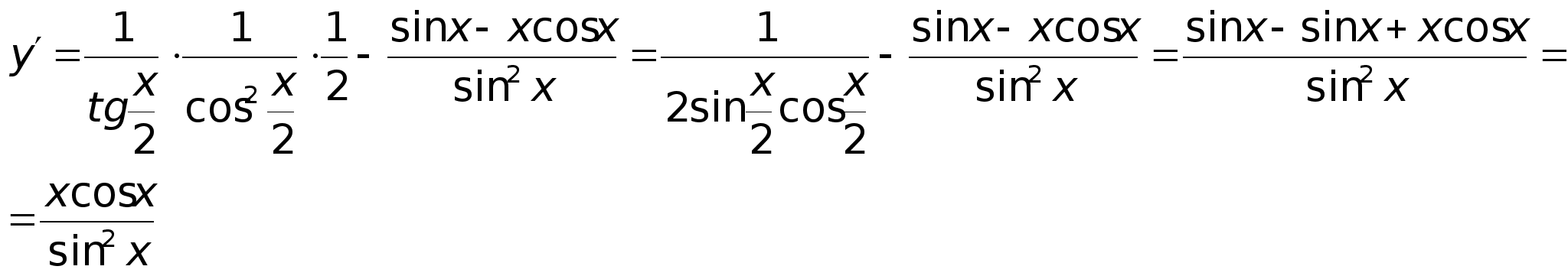 Пример.
Найти производную
функции
Пример.
Найти производную
функции
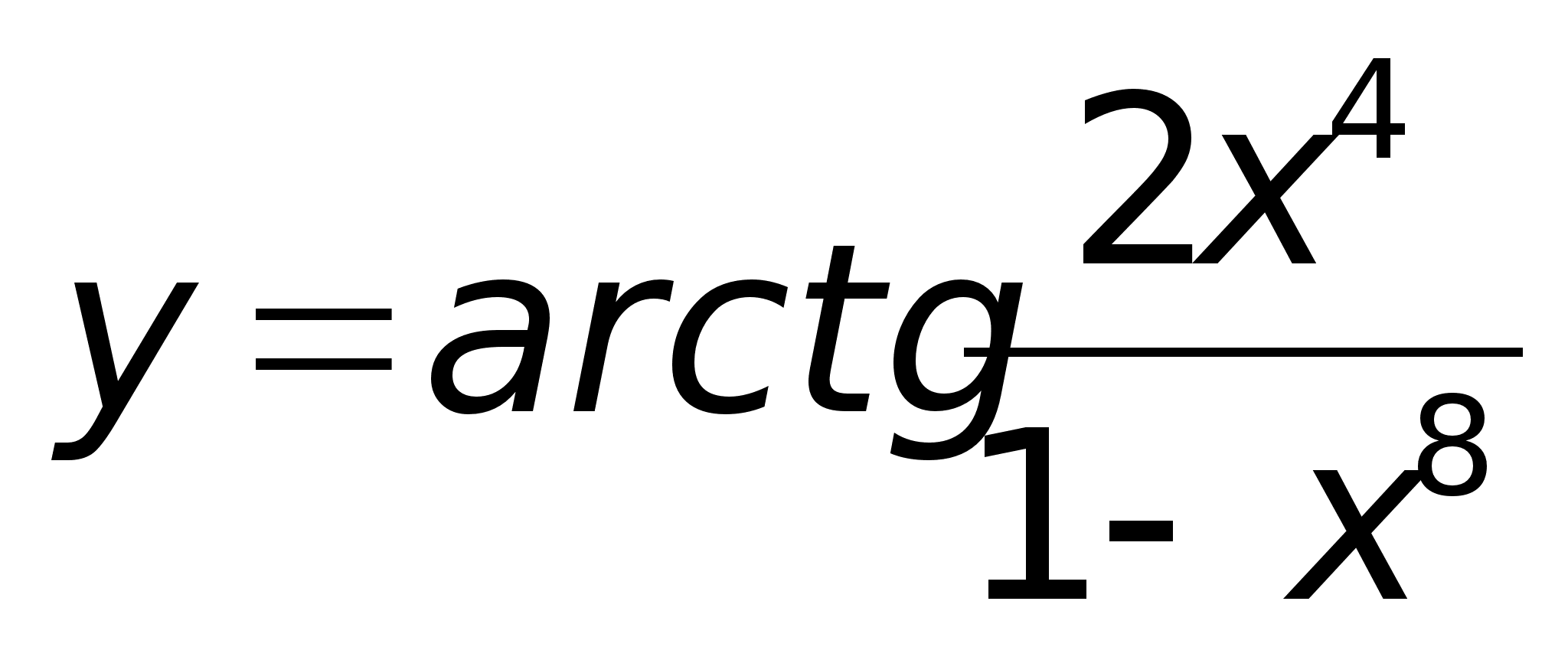
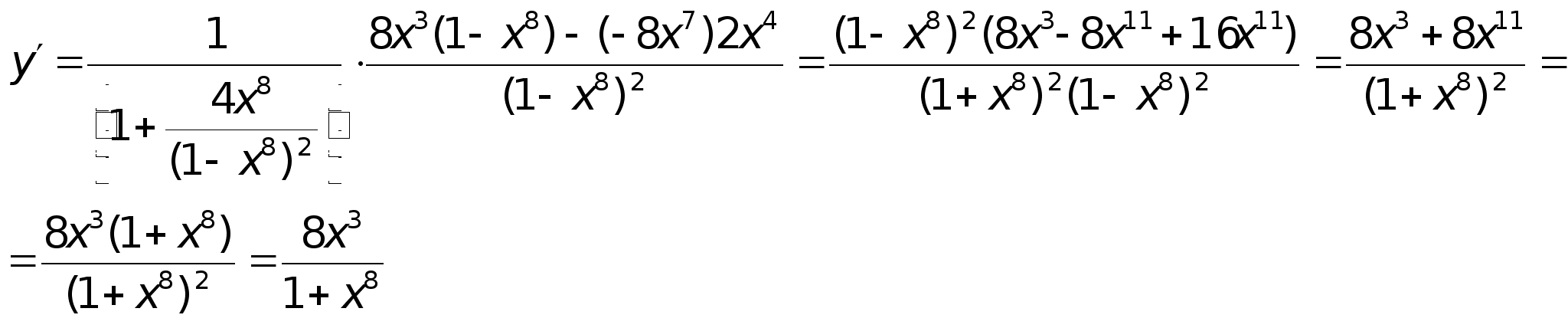 Пример.
Найти производную
функции
Пример.
Найти производную
функции
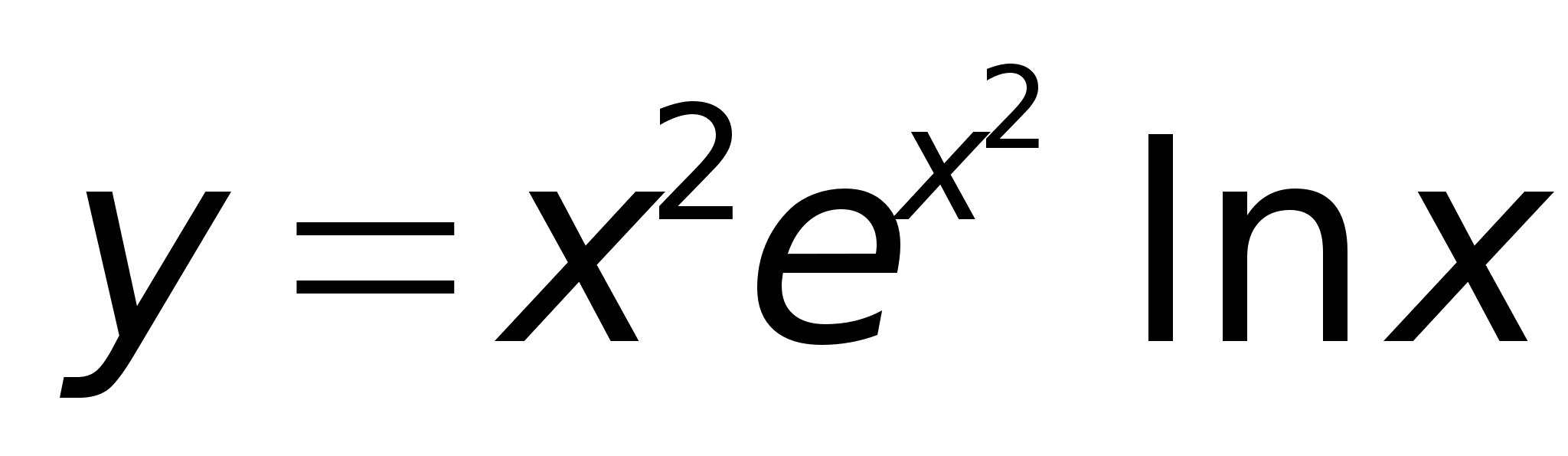
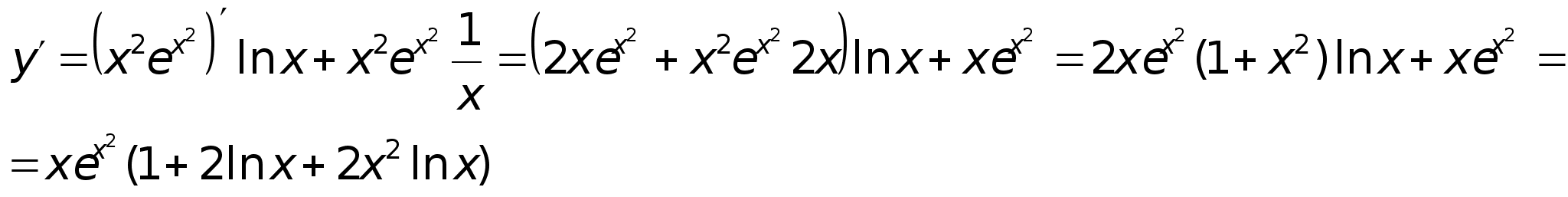
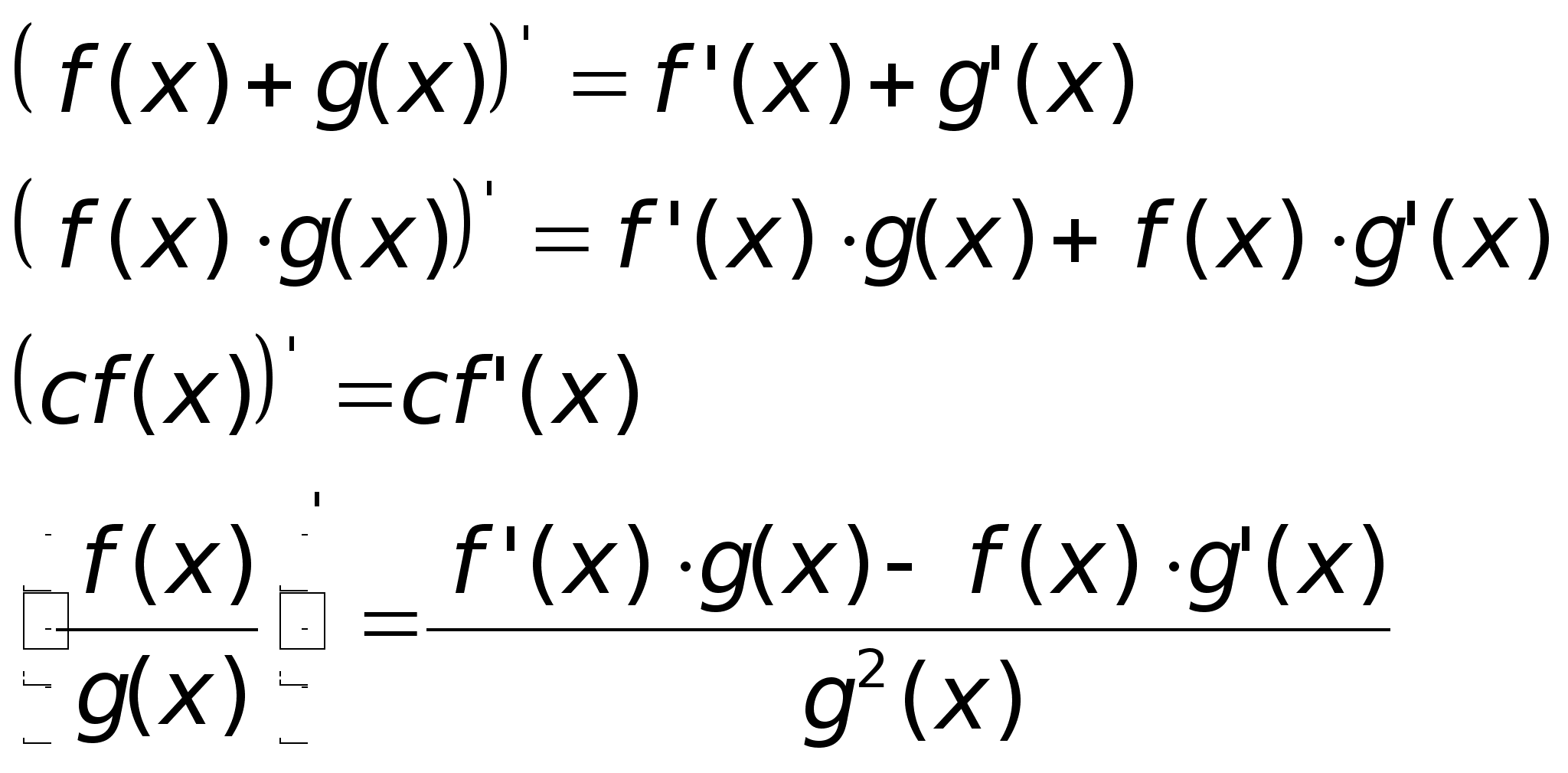
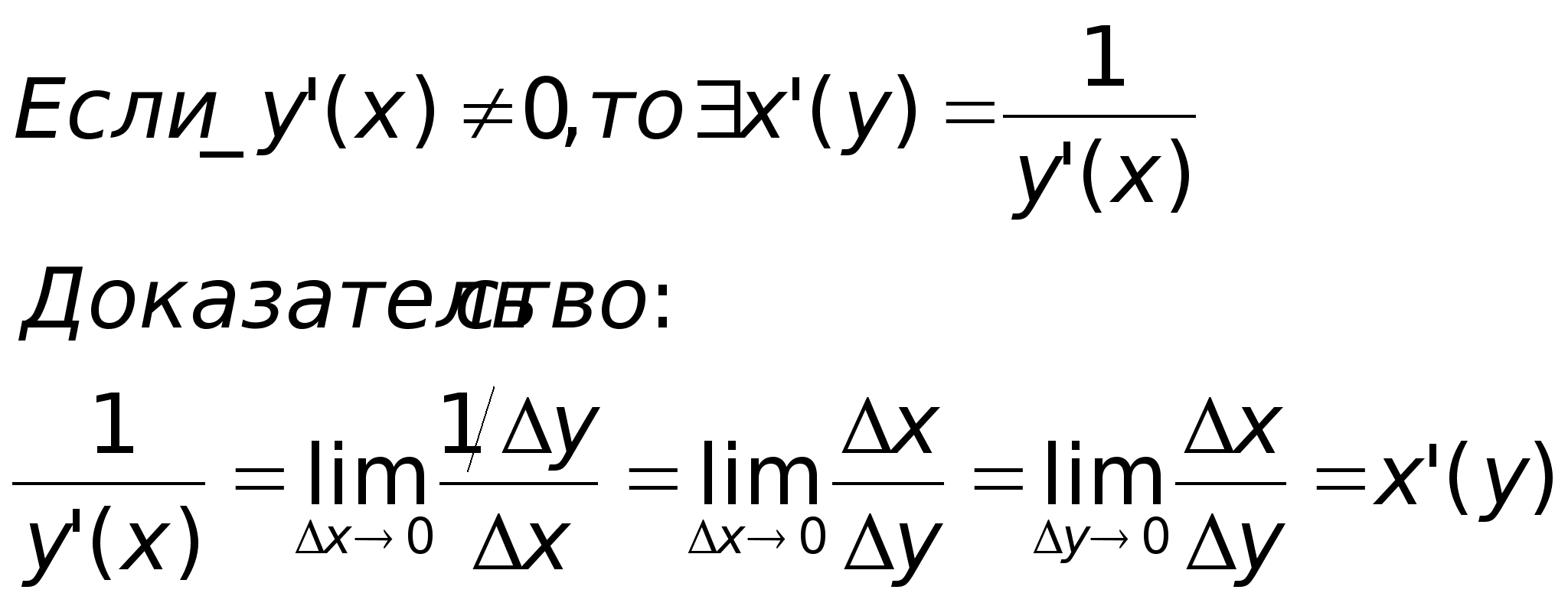 Таблица
производных:
Таблица
производных:
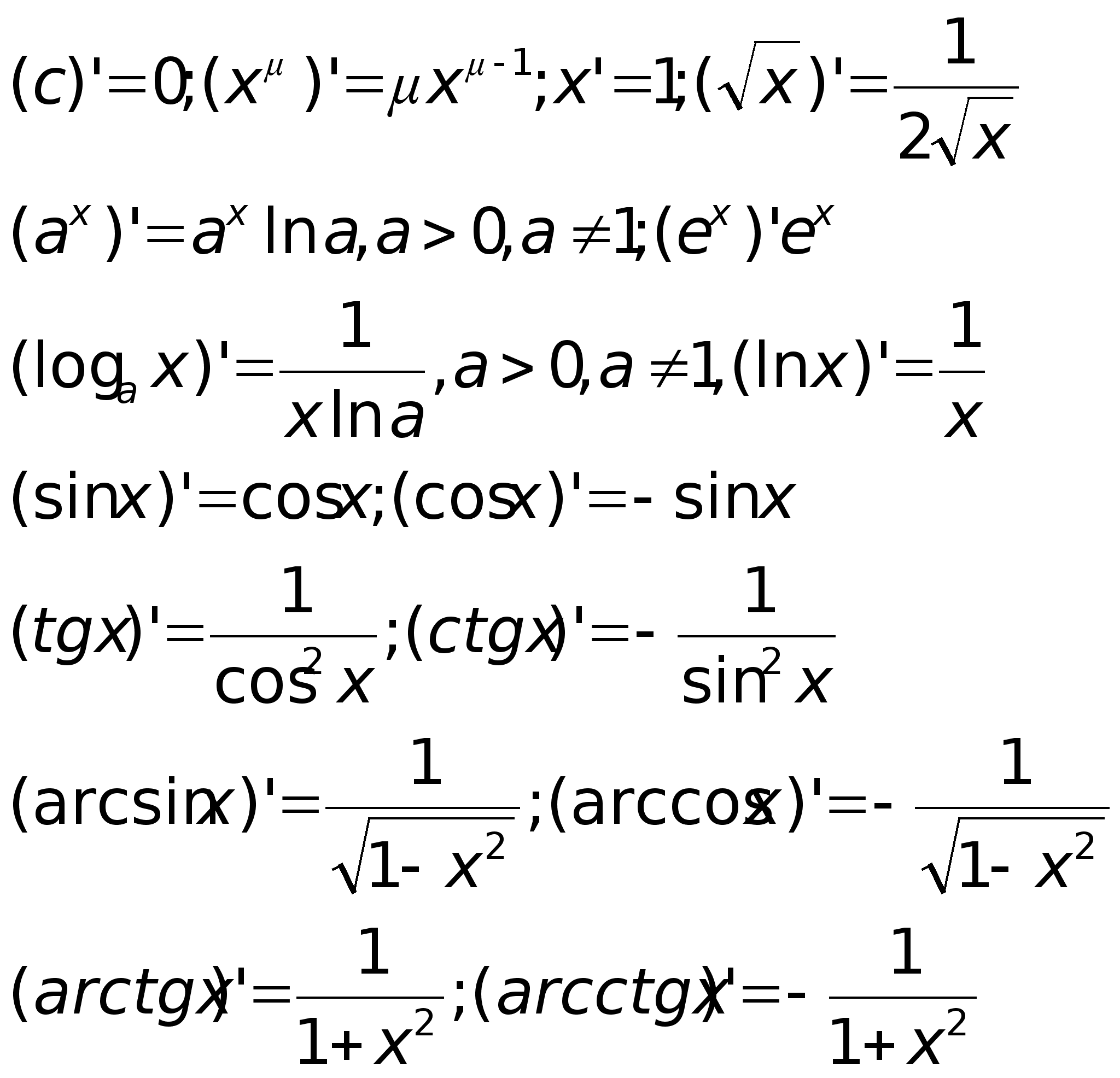
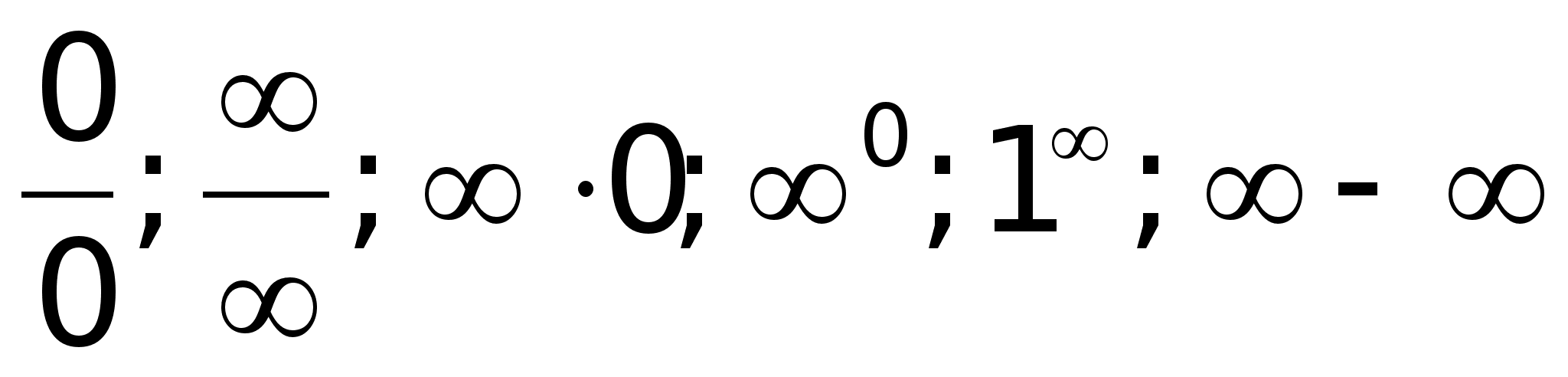 Теорема
(правило Лопиталя).
Если
функции f(x)
и g(x)
дифференцируемы
в вблизи точки
а, непрерывны
в точке а, g(x)
отлична от
нуля вблизи
а и f(a)
= g(a)
= 0, то предел
отношения
функций при
ха
равен пределу
отношения их
производных,
если этот предел
(конечный или
бесконечный)
существует.
Теорема
(правило Лопиталя).
Если
функции f(x)
и g(x)
дифференцируемы
в вблизи точки
а, непрерывны
в точке а, g(x)
отлична от
нуля вблизи
а и f(a)
= g(a)
= 0, то предел
отношения
функций при
ха
равен пределу
отношения их
производных,
если этот предел
(конечный или
бесконечный)
существует.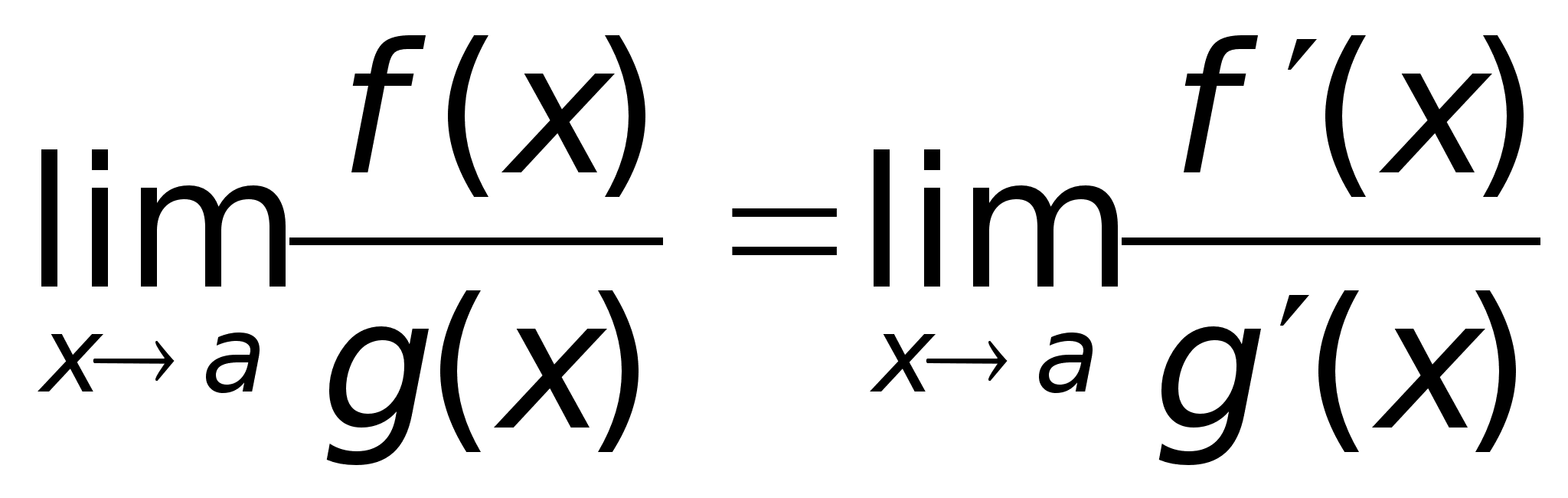 Доказательство.
Применив формулу
Коши, получим:
Доказательство.
Применив формулу
Коши, получим: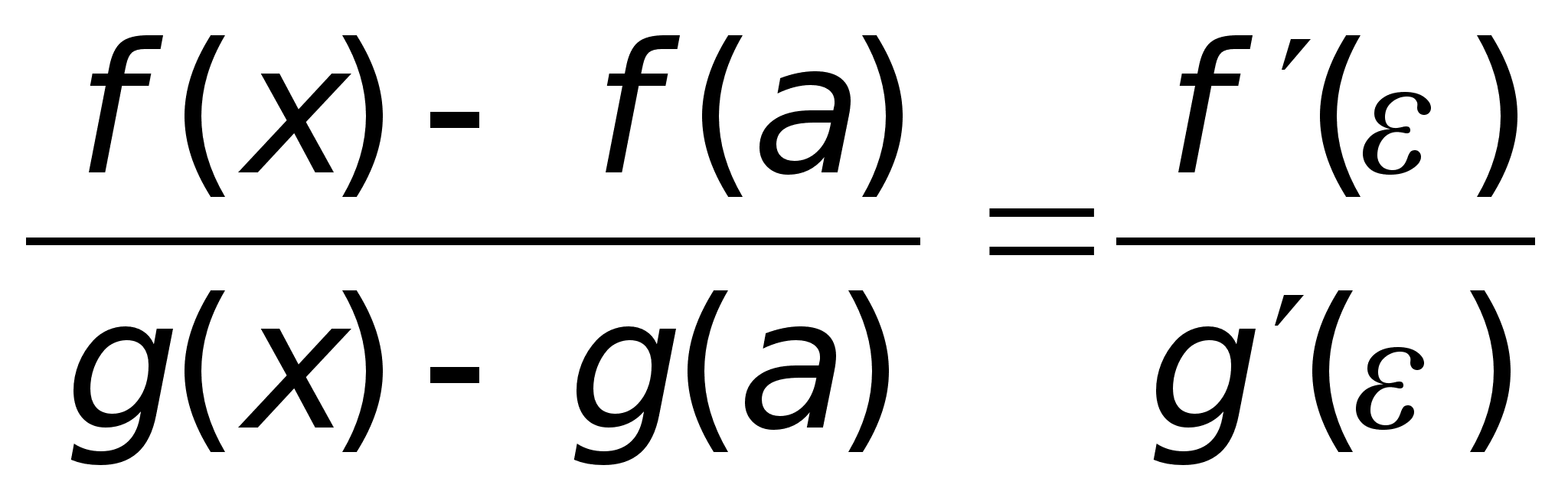
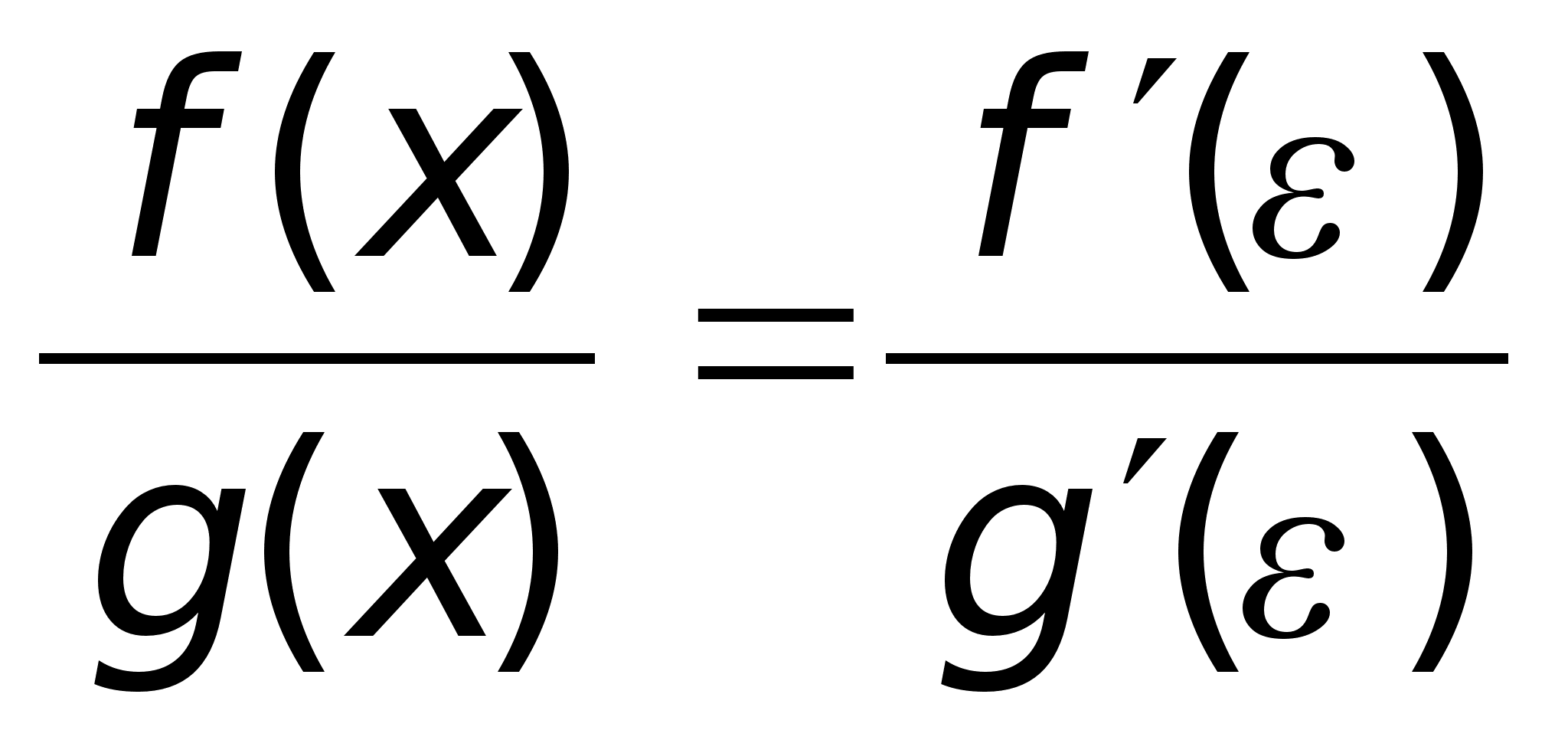 Пусть
при х
Пусть
при х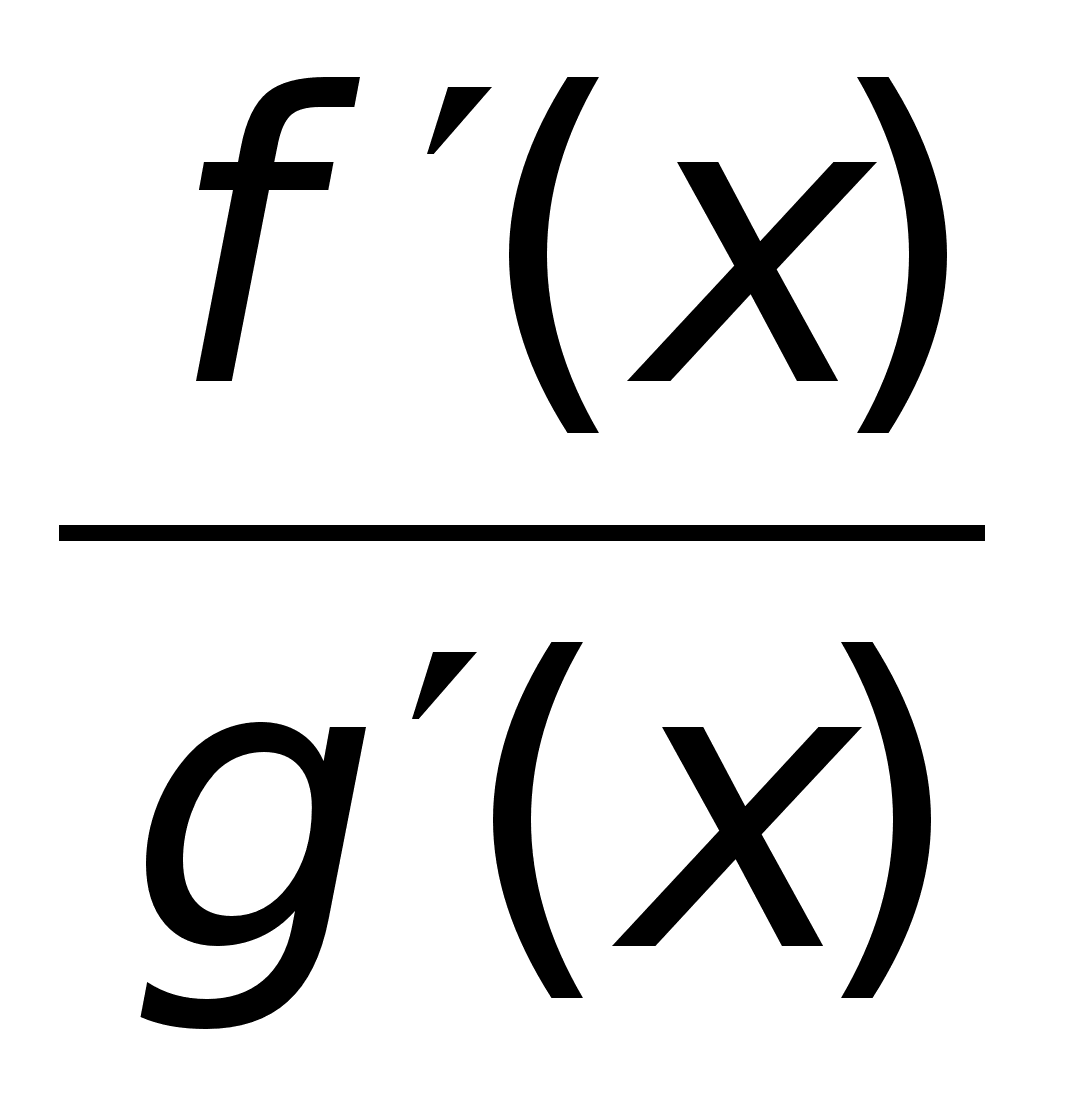 стремится к
некоторому
пределу. Т.к.
точка
стремится к
некоторому
пределу. Т.к.
точка 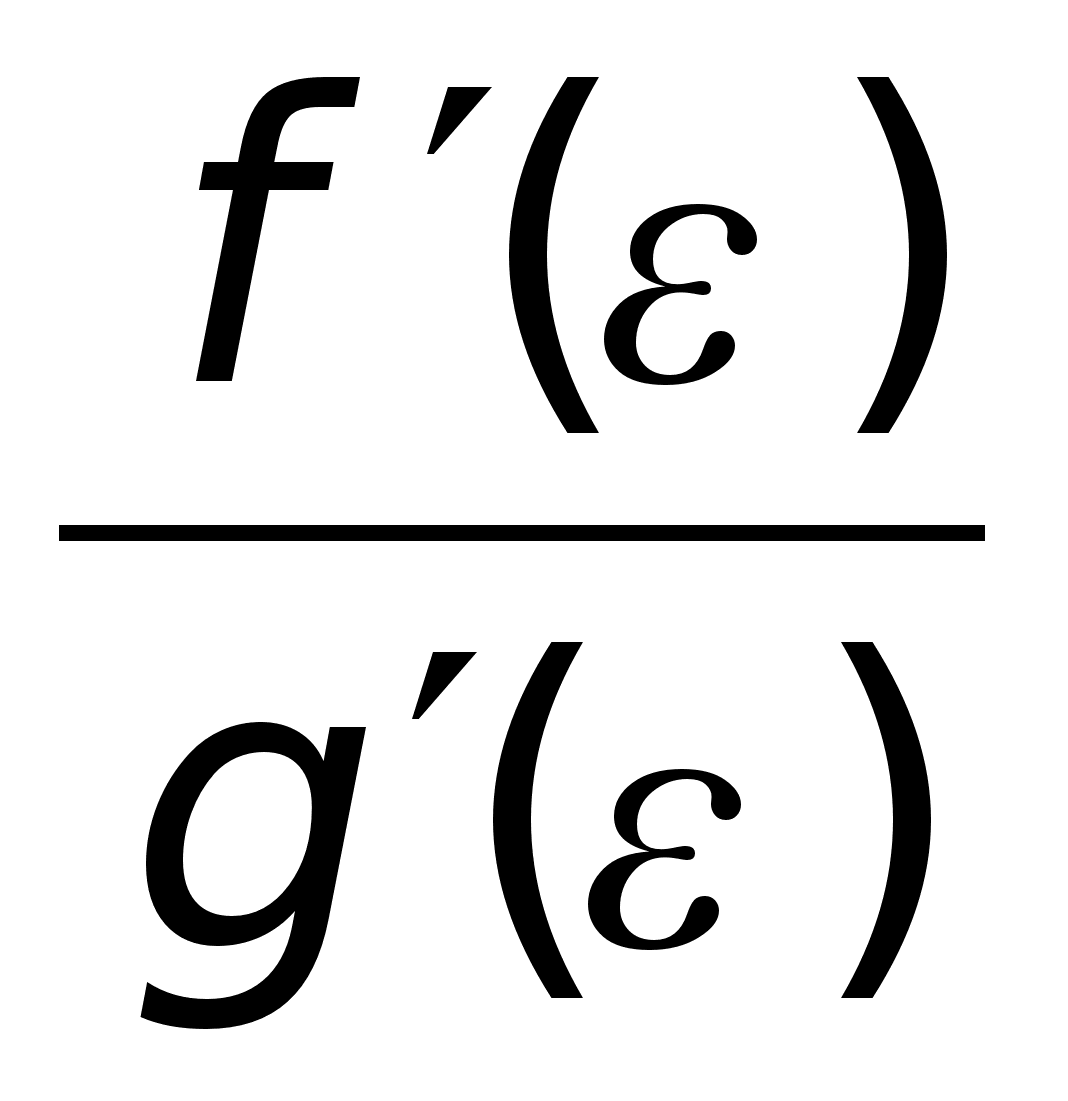 стремится к
тому же пределу.
Таким образом,
можно записать:
стремится к
тому же пределу.
Таким образом,
можно записать: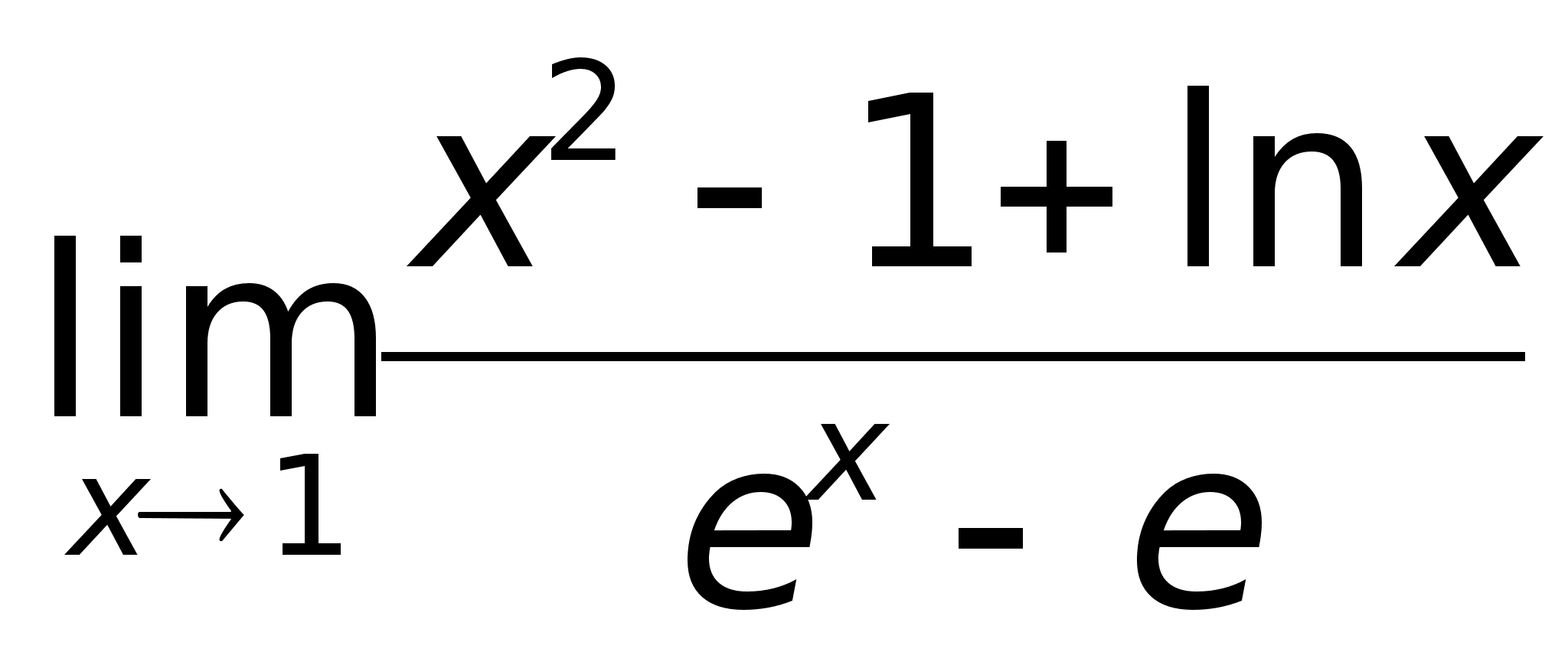 .Как
видно, при попытке
непосредственного
вычисления
предела получается
неопределенность
вида
.Как
видно, при попытке
непосредственного
вычисления
предела получается
неопределенность
вида
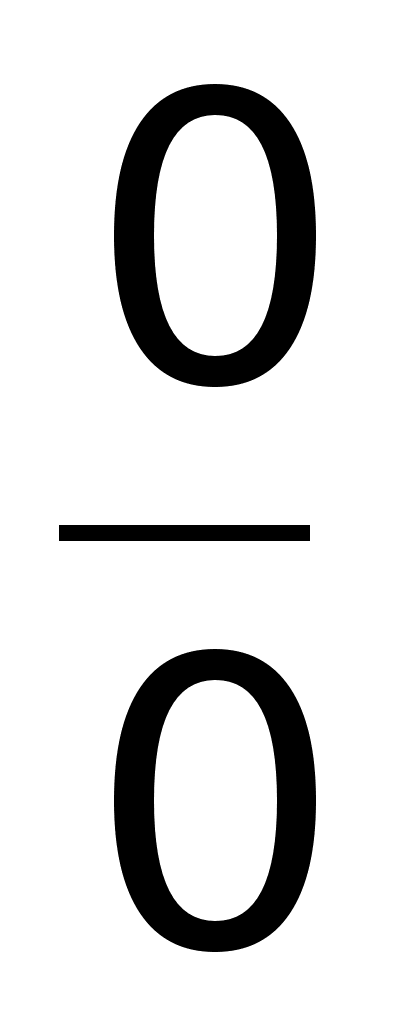 .
Функции, входящие
в числитель
и знаменатель
дроби удовлетворяют
требованиям
теоремы Лопиталя.f
.
Функции, входящие
в числитель
и знаменатель
дроби удовлетворяют
требованиям
теоремы Лопиталя.f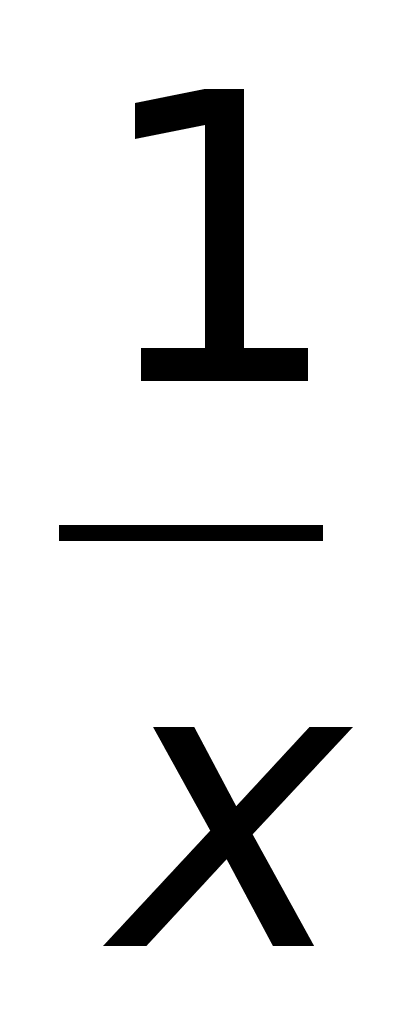 ;
g
;
g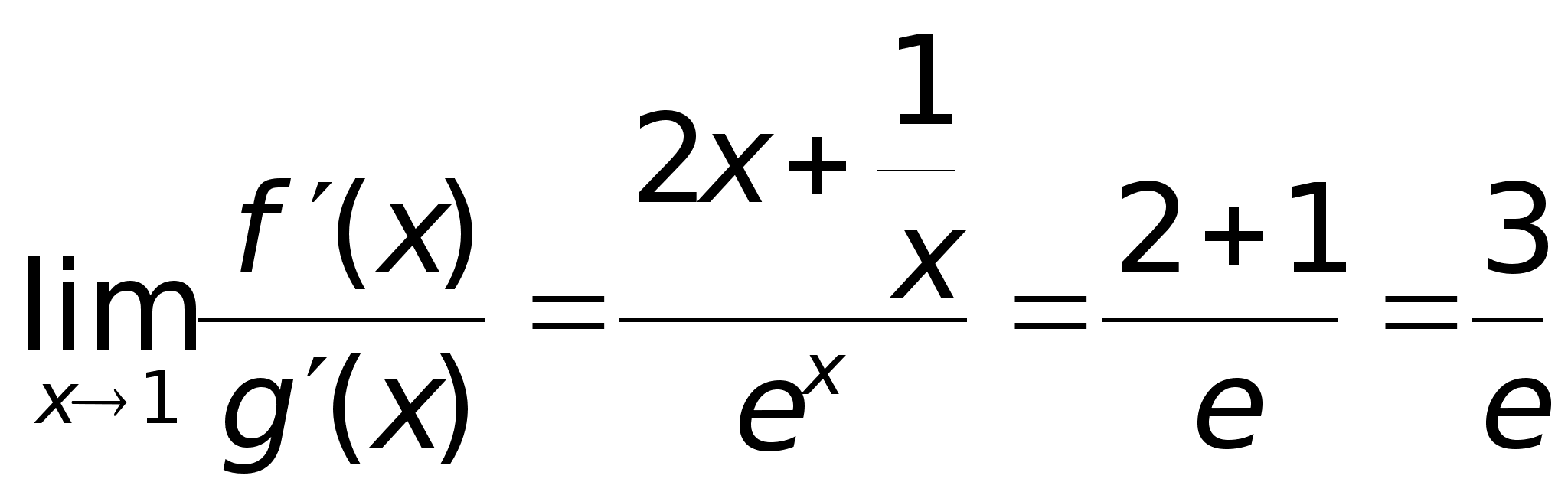 ;
;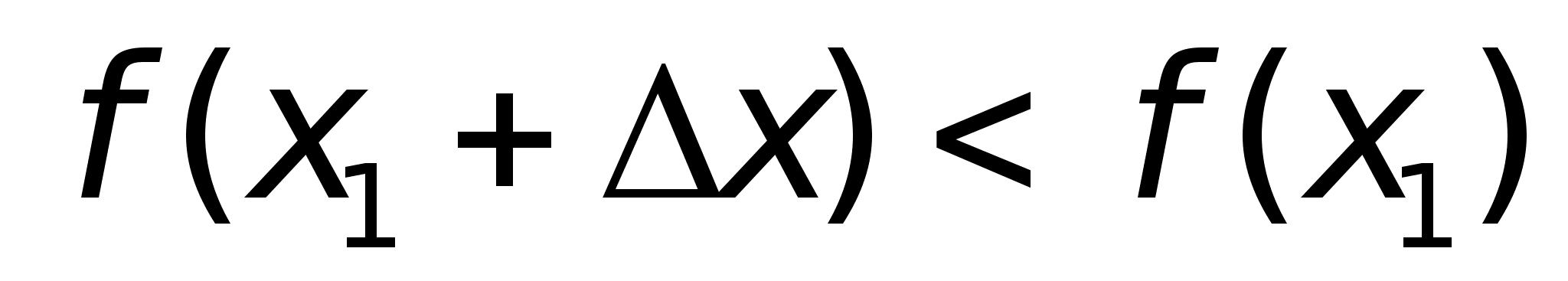 ,
т.е.
,
т.е.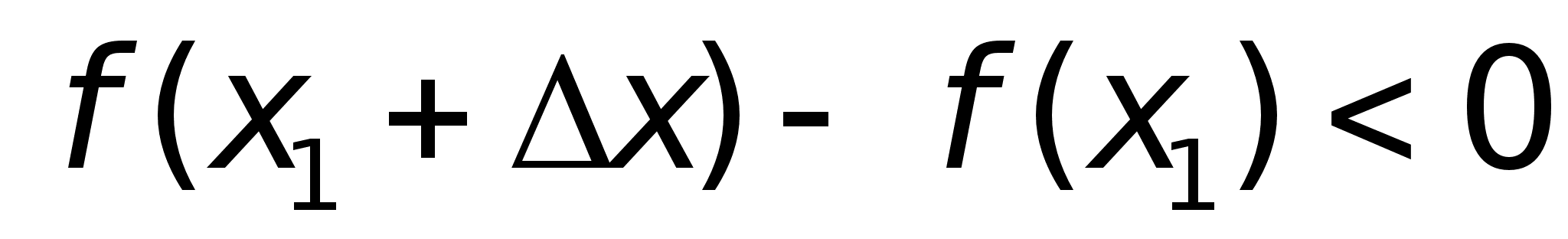 Тогда
Тогда
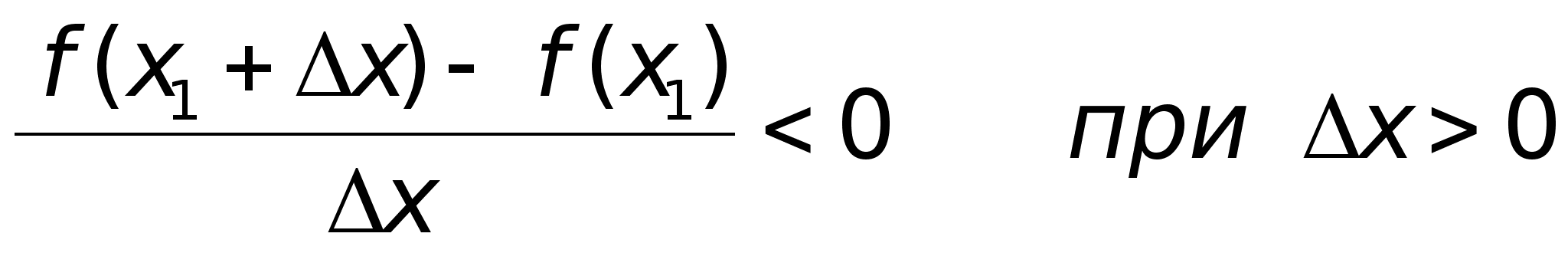 По
определению:
По
определению: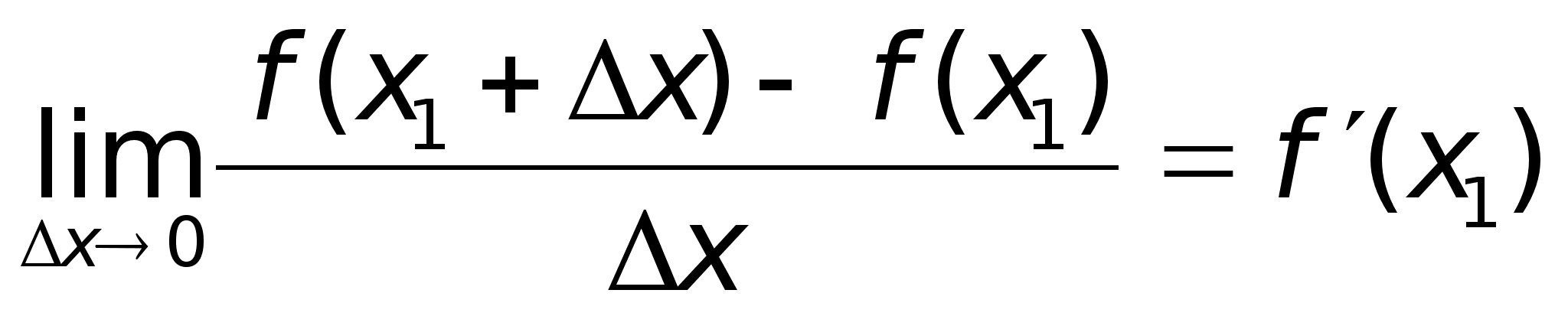
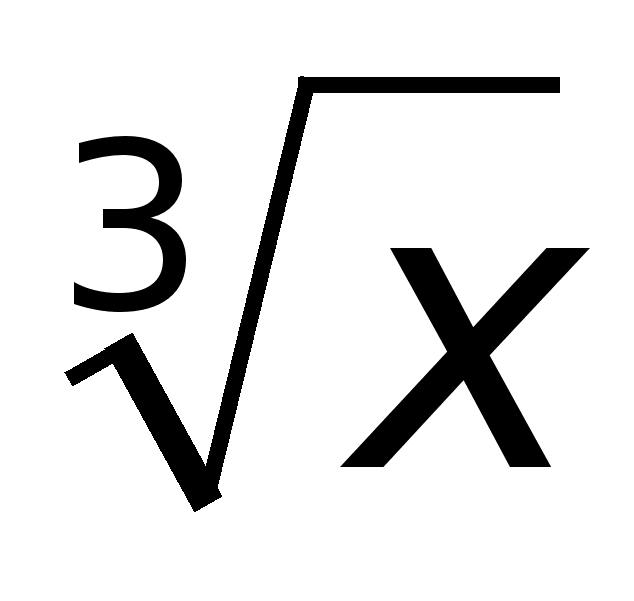
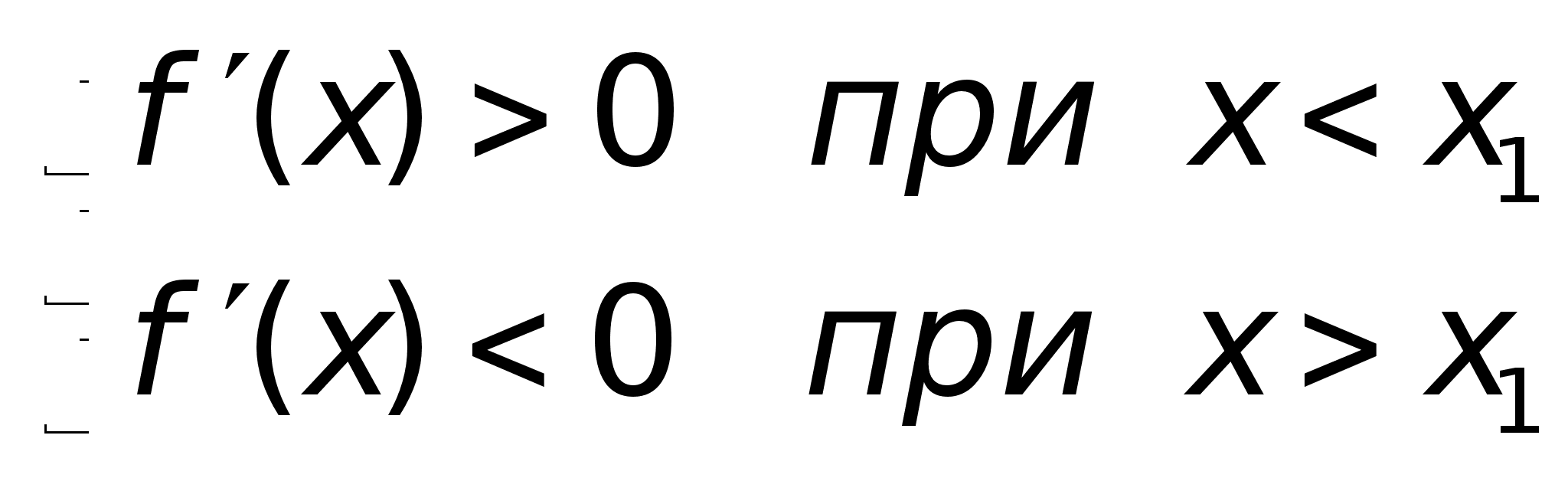 По
теореме Лагранжа:
f(x)
– f(x1)
= f()(x
– x1),
где x
<
По
теореме Лагранжа:
f(x)
– f(x1)
= f()(x
– x1),
где x
<  8)Точки
перегиба граф
ф-ии.ПримерОпределение.
Кривая обращена
выпуклостью
вверх
на интервале
(а, b),
если все ее
точки лежат
ниже любой
ее касательной
на этом интервале.
Кривая, обращенная
выпуклостью
вверх, называется
выпуклой,
а кривая, обращенная
выпуклостью
вниз – называется
вогнутой.
8)Точки
перегиба граф
ф-ии.ПримерОпределение.
Кривая обращена
выпуклостью
вверх
на интервале
(а, b),
если все ее
точки лежат
ниже любой
ее касательной
на этом интервале.
Кривая, обращенная
выпуклостью
вверх, называется
выпуклой,
а кривая, обращенная
выпуклостью
вниз – называется
вогнутой.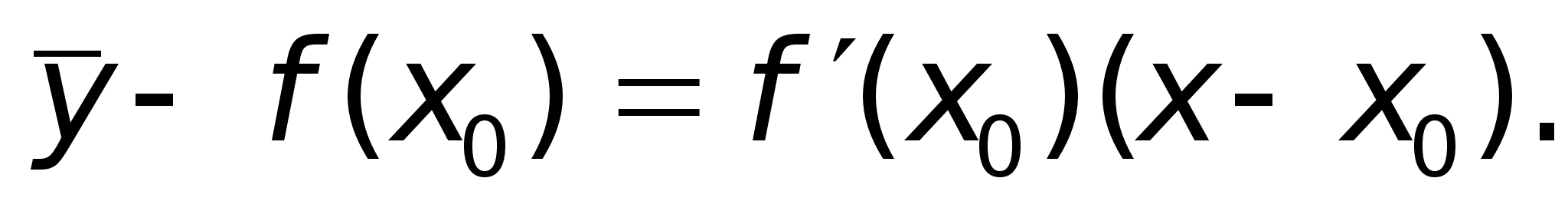 Следует
доказать, что
Следует
доказать, что
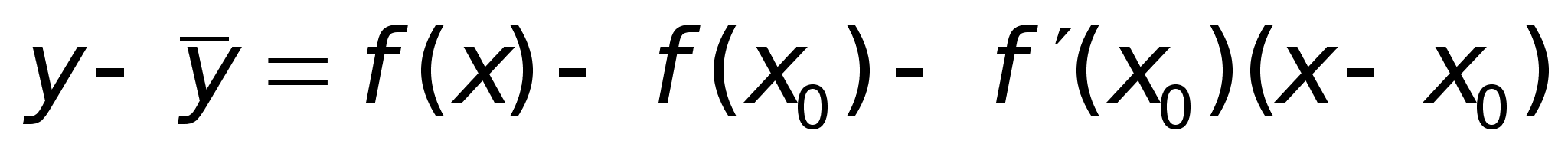 .По
теореме Лагранжа
для f(x)
– f(x0):
.По
теореме Лагранжа
для f(x)
– f(x0):
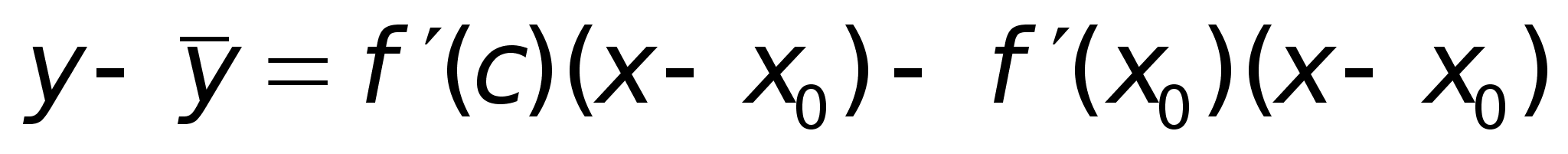 ,
x0
< c
< x.
,
x0
< c
< x. По
теореме Лагранжа
для
По
теореме Лагранжа
для
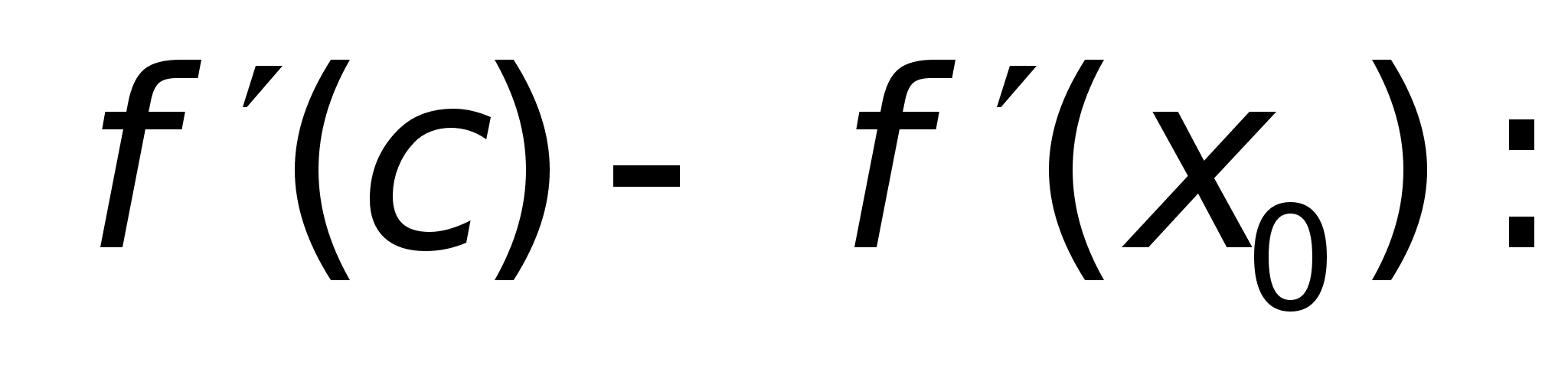
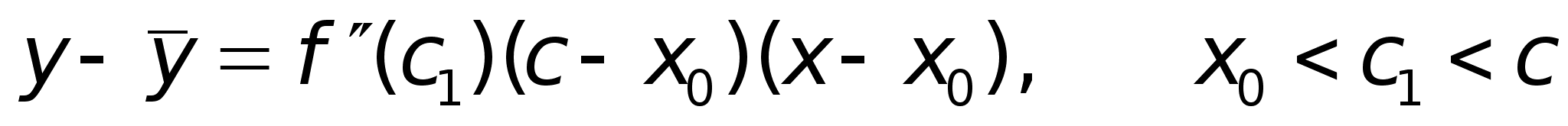 Пусть
х > x0
тогда x0
< c1
< c
< x.
Т.к. x
– x0
> 0 и c
– x0
> 0, и кроме того
по условию
Пусть
х > x0
тогда x0
< c1
< c
< x.
Т.к. x
– x0
> 0 и c
– x0
> 0, и кроме того
по условию
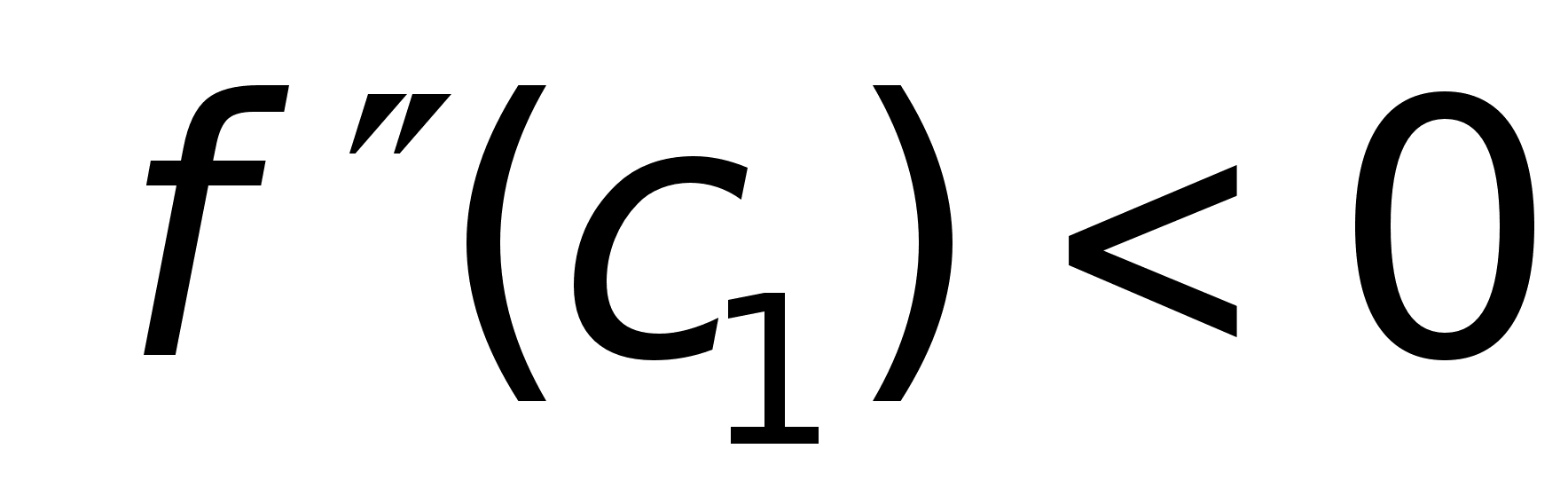 ,
следовательно,
,
следовательно,
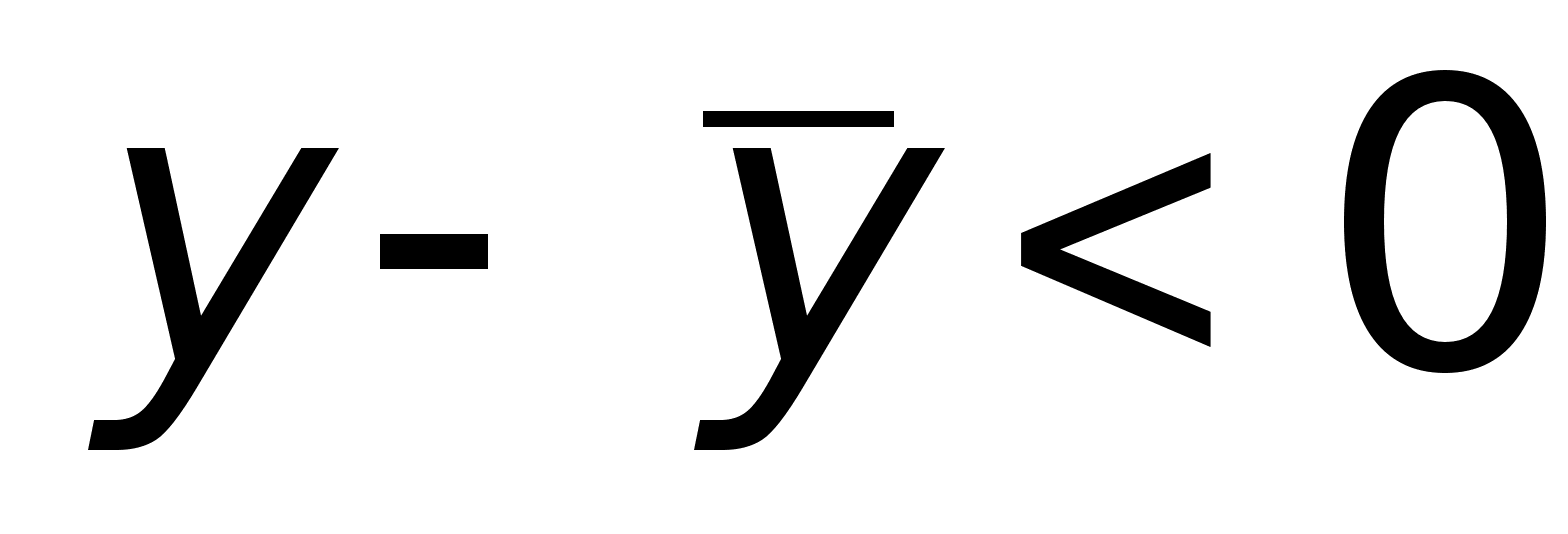 .Пусть
x
< x0
тогда x
< c
< c1
< x0
и x
– x0
< 0, c
– x0
.Пусть
x
< x0
тогда x
< c
< c1
< x0
и x
– x0
< 0, c
– x0
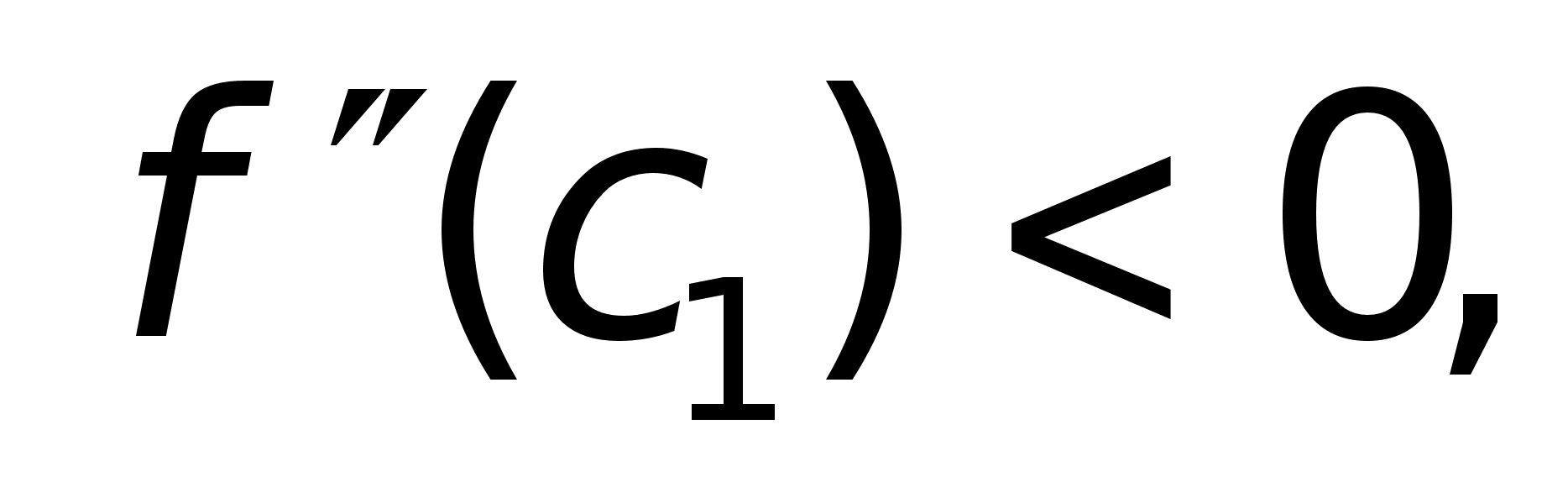 то
то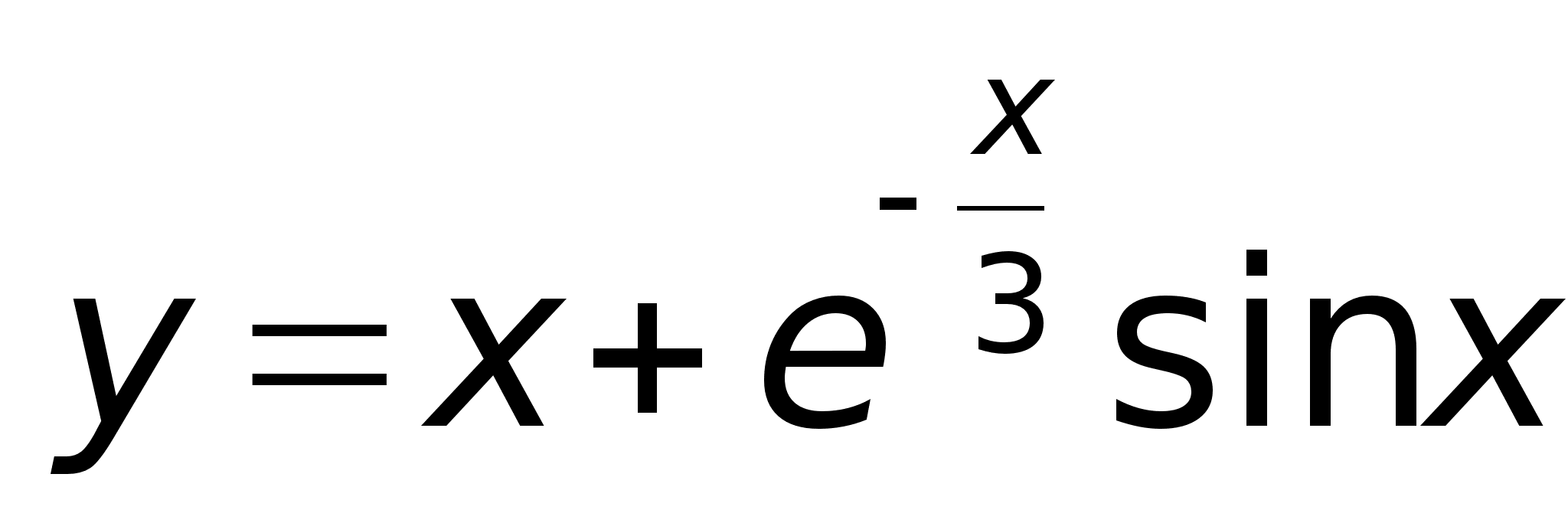 .
Ее наклонная
асимптота у
= х.
.
Ее наклонная
асимптота у
= х.
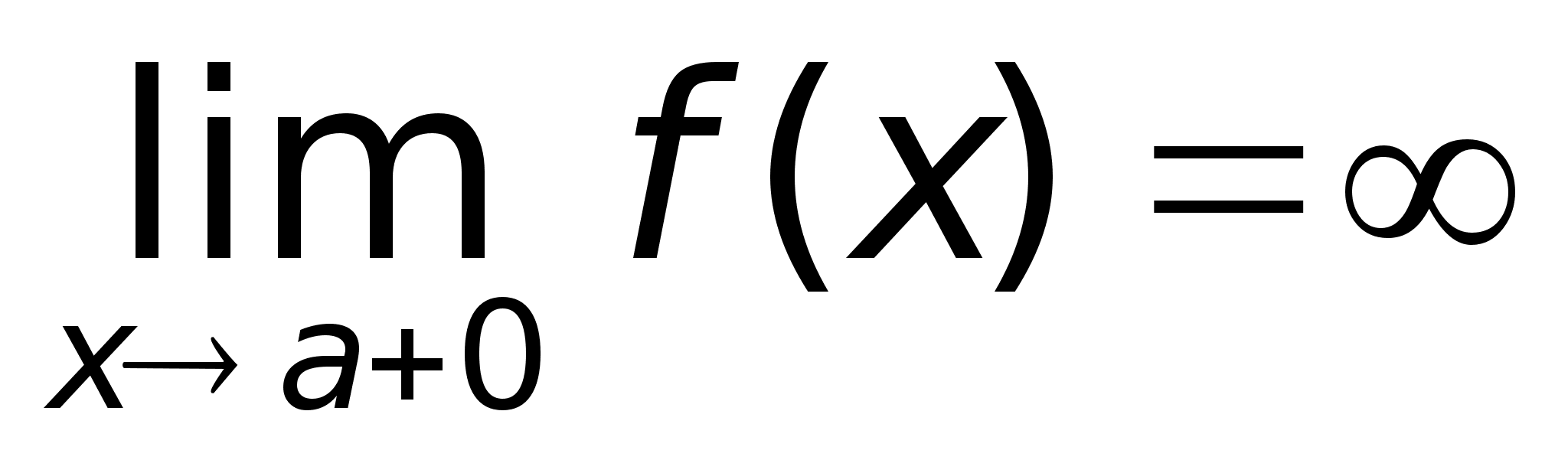 или
или
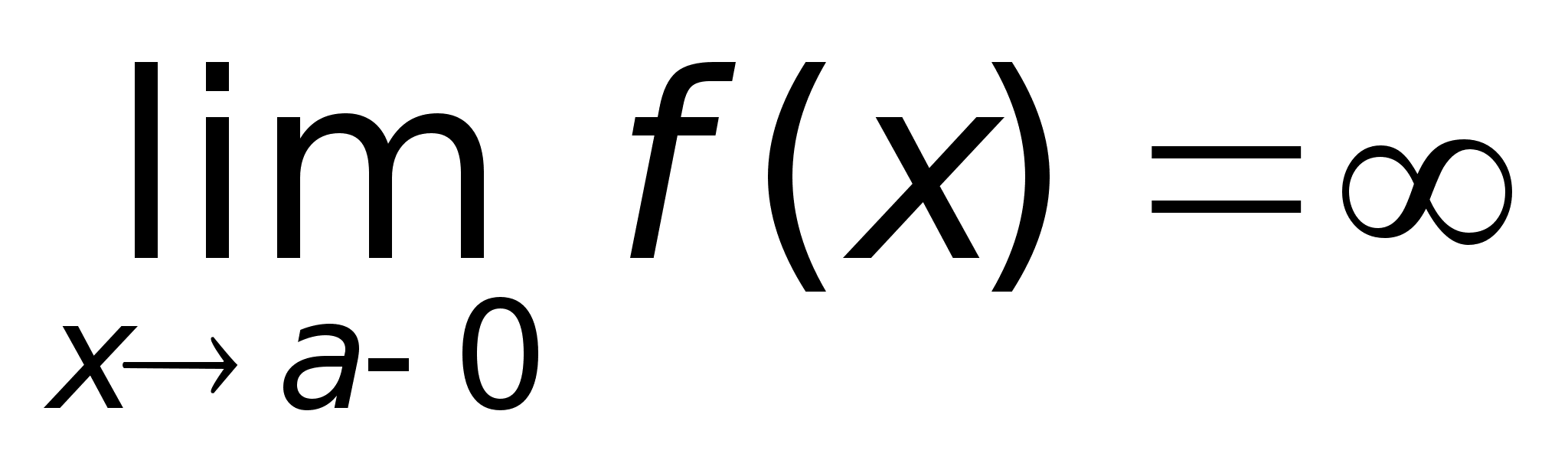 или
или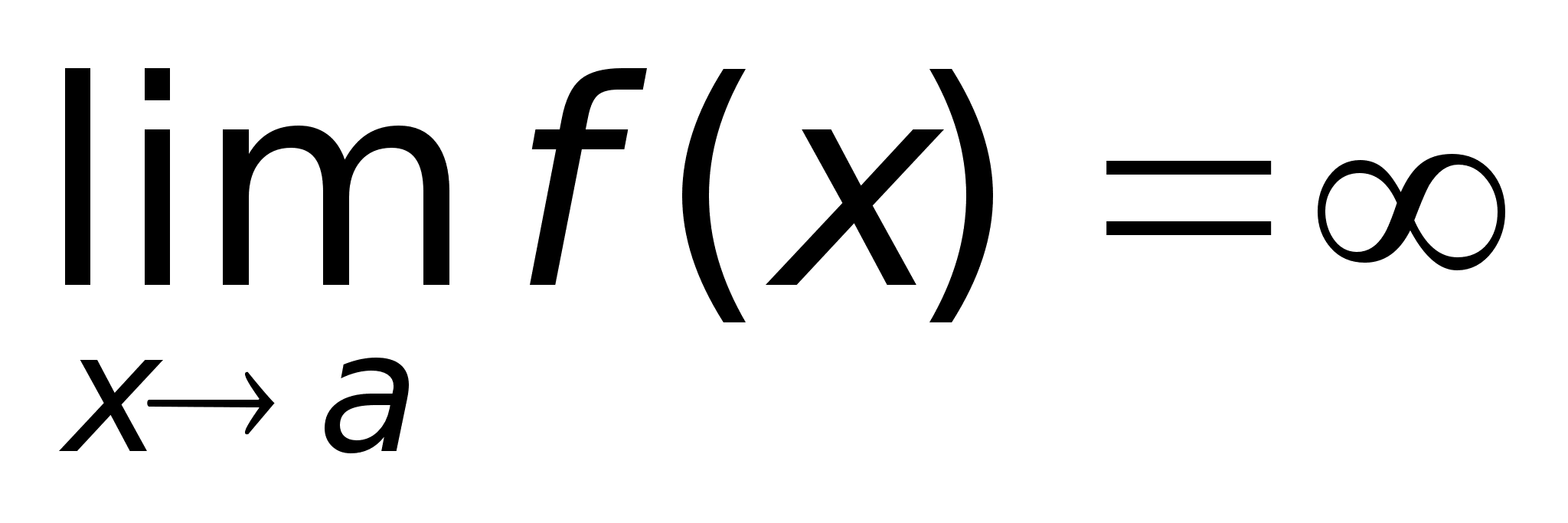 ,
то прямая х
= а – асимптота
кривой y
= f(x).Например,
для функции
,
то прямая х
= а – асимптота
кривой y
= f(x).Например,
для функции
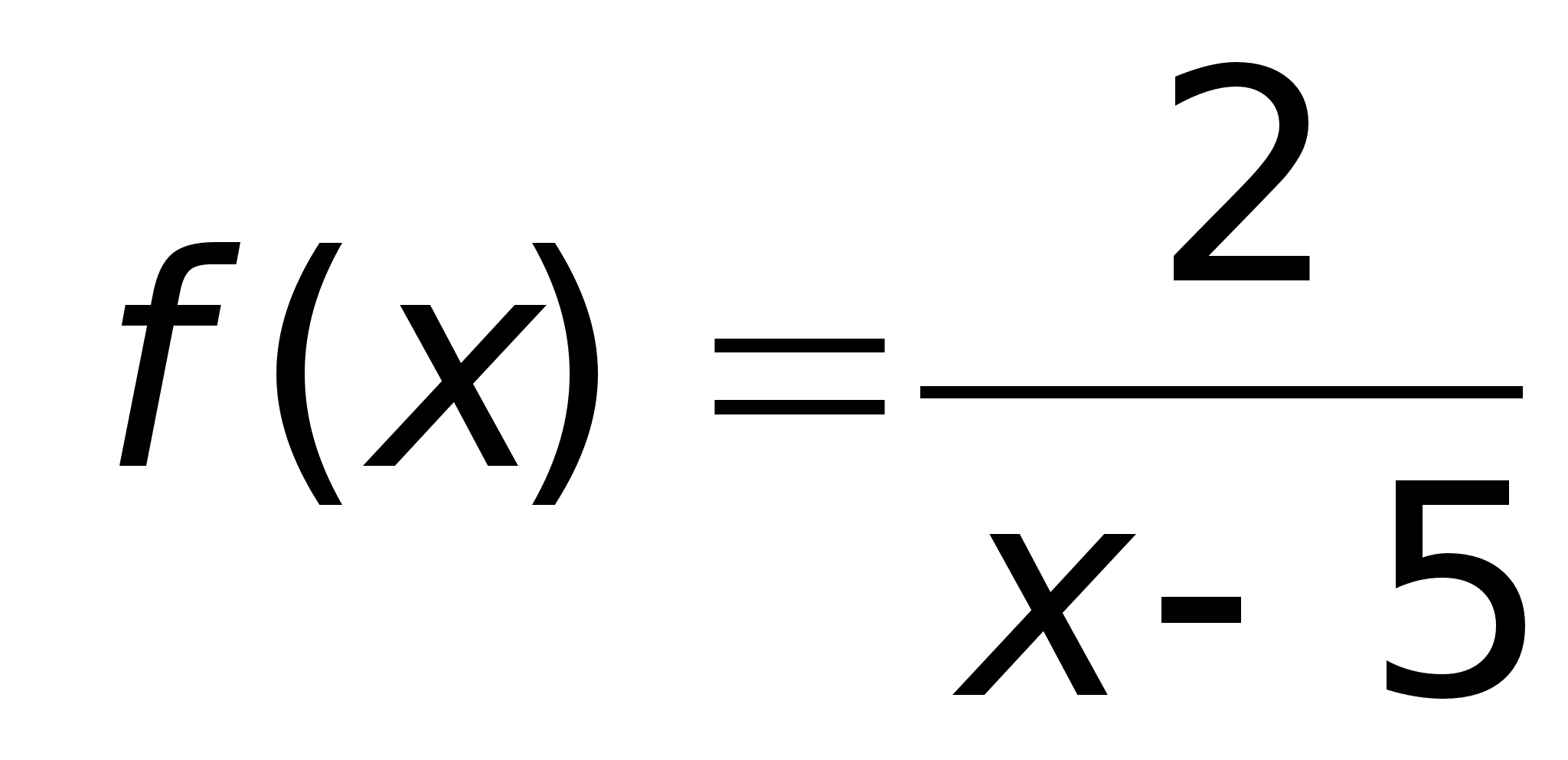 прямая х = 5 является
вертикальной
асимптотой.Наклонные
асимптоты.Предположим,
что кривая y
= f(x)
имеет наклонную
асимптоту y
= kx
+ b.
прямая х = 5 является
вертикальной
асимптотой.Наклонные
асимптоты.Предположим,
что кривая y
= f(x)
имеет наклонную
асимптоту y
= kx
+ b.
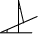
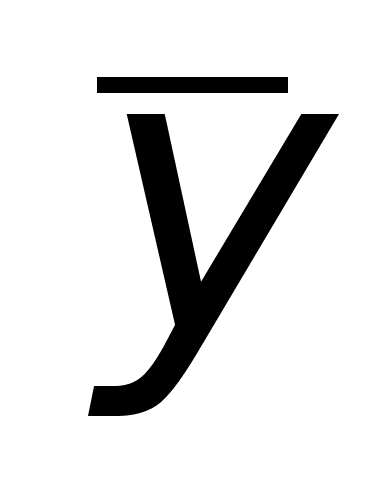 - ордината точки
N на асимптоте.По
условию:
- ордината точки
N на асимптоте.По
условию:
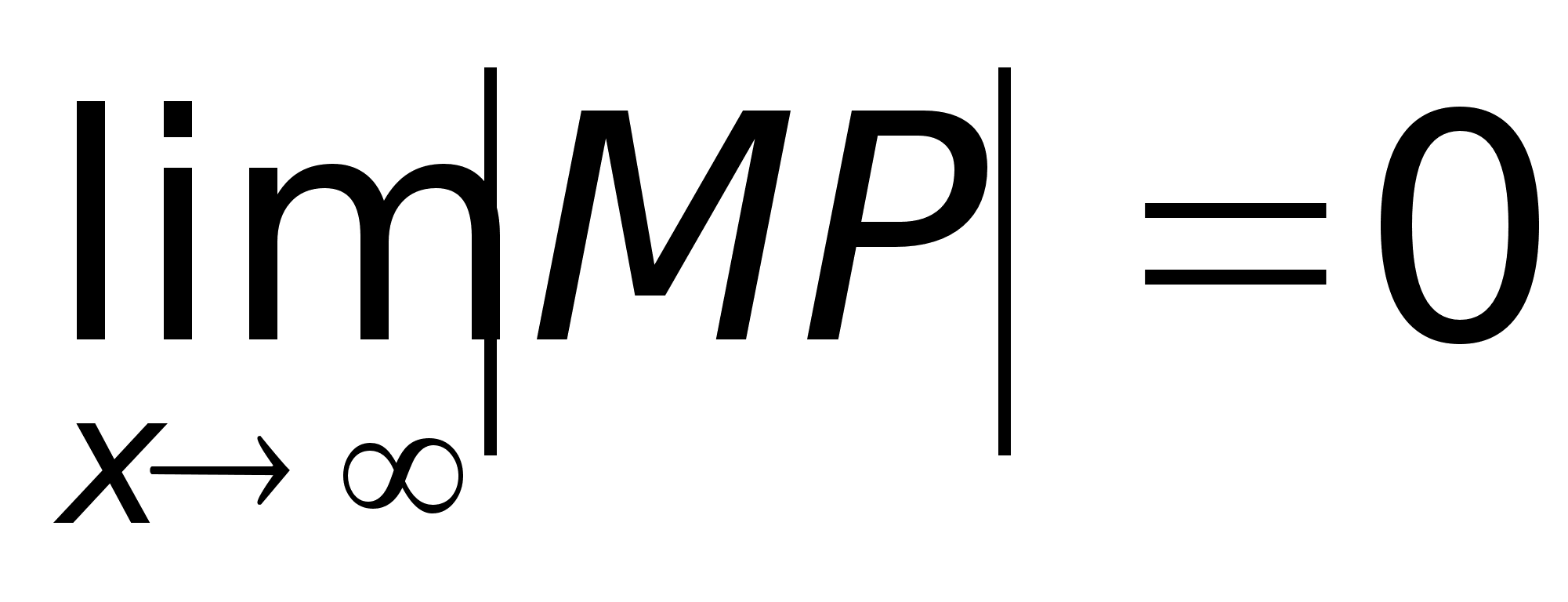 ,
,
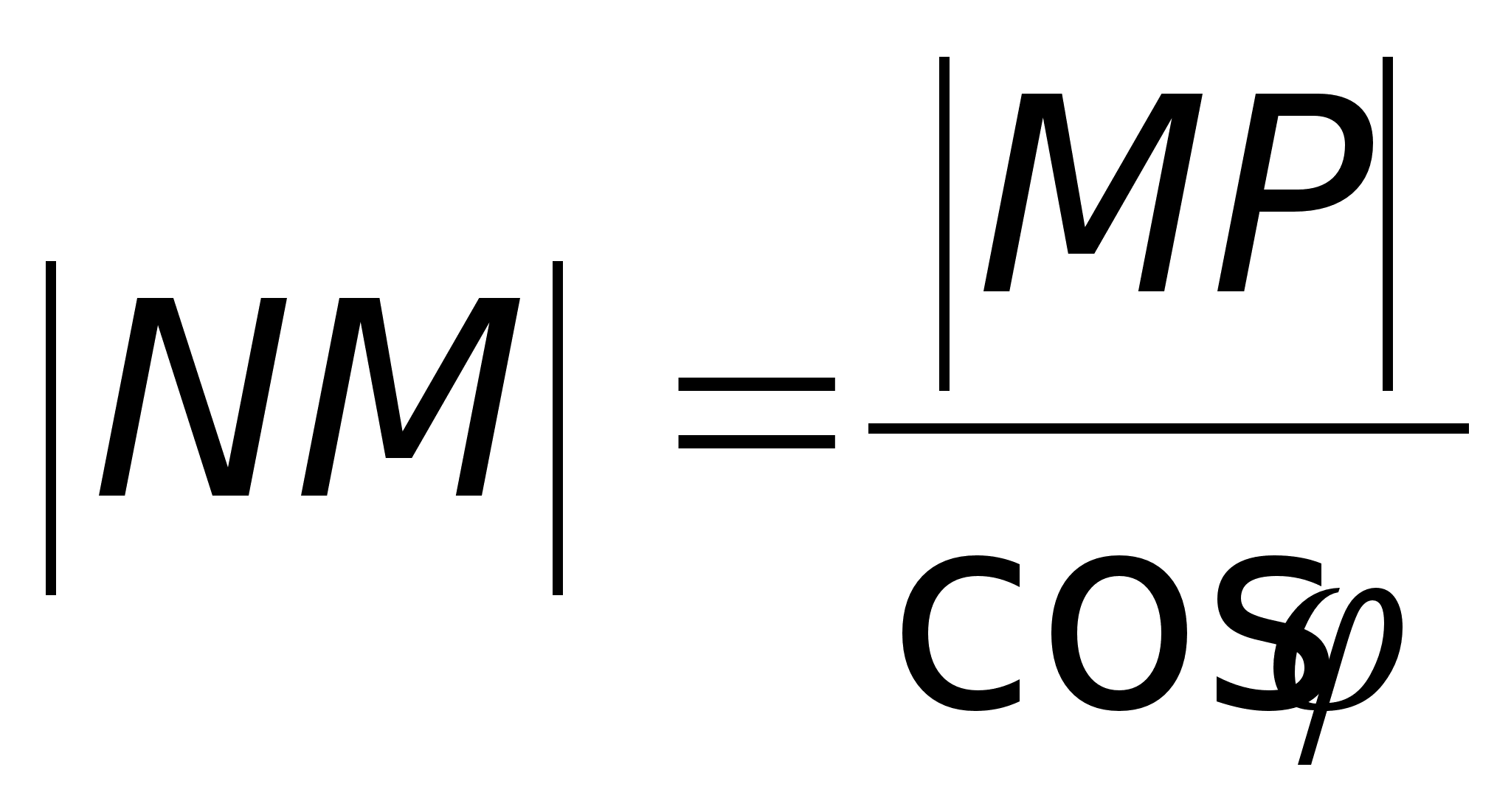 .
.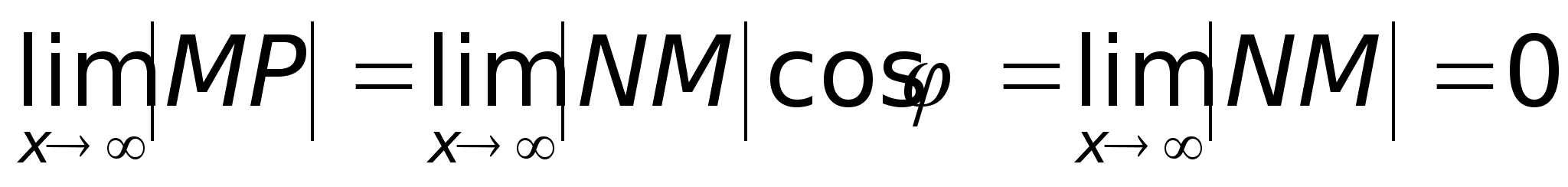
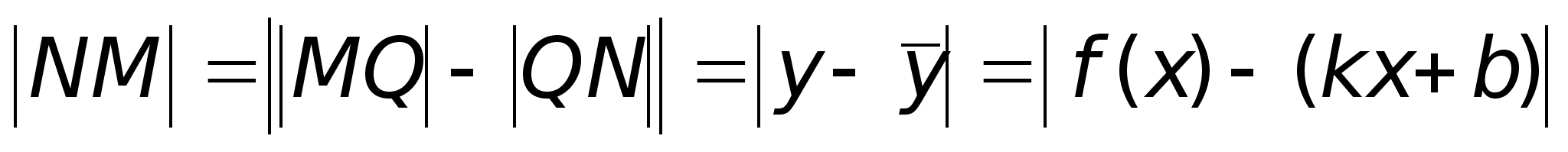
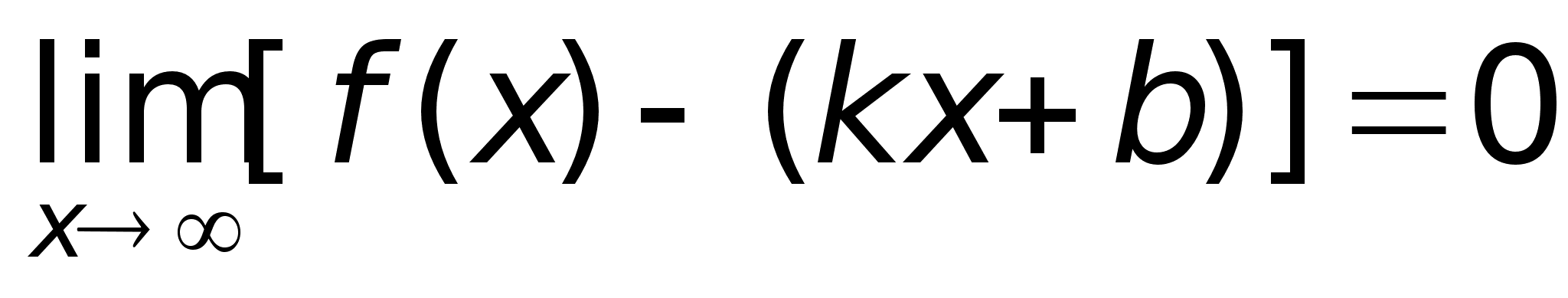 .Итак,
прямая y
= kx
+ b
– асимптота
кривой. Для
точного определения
этой прямой
необходимо
найти способ
вычисления
коэффициентов
k
и b. В
полученном
выражении
выносим за
скобки х:
.Итак,
прямая y
= kx
+ b
– асимптота
кривой. Для
точного определения
этой прямой
необходимо
найти способ
вычисления
коэффициентов
k
и b. В
полученном
выражении
выносим за
скобки х:
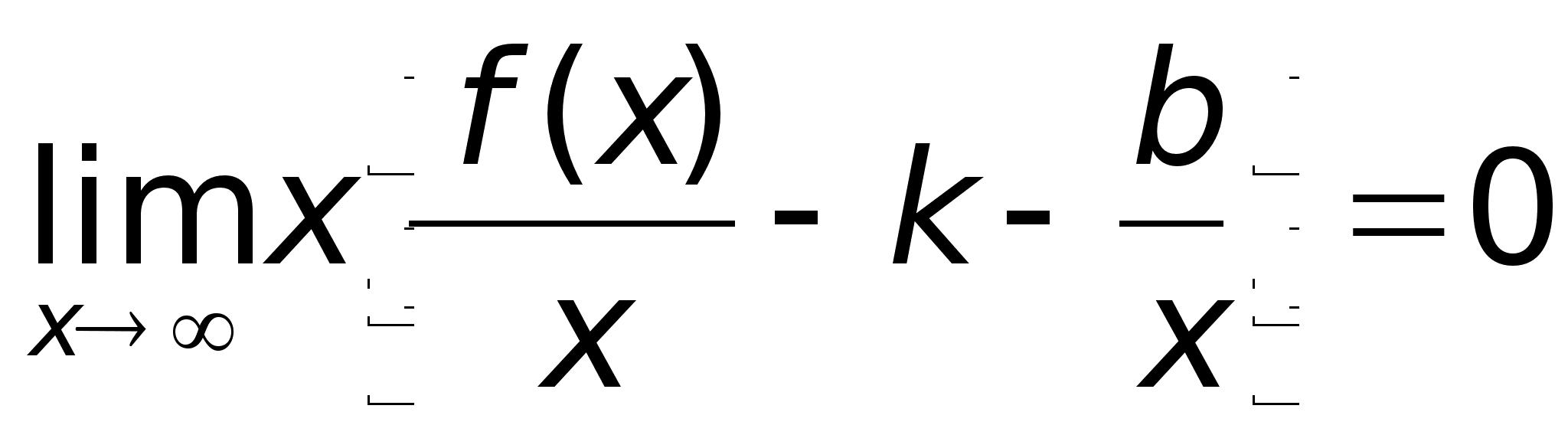
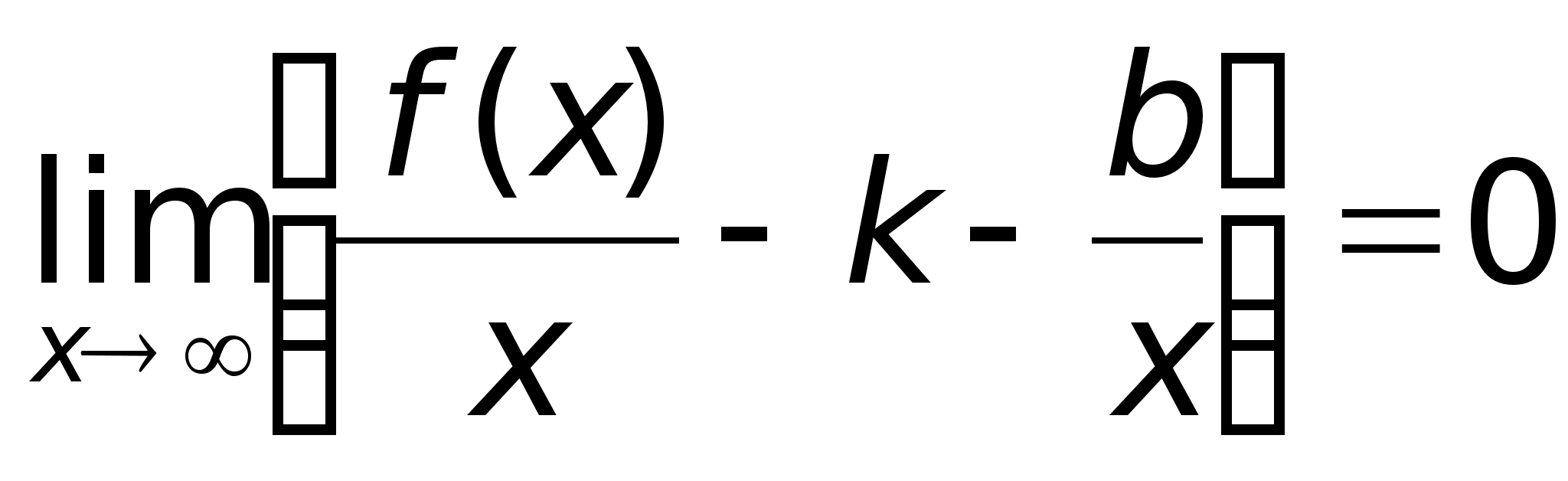 ,
т.к. b
= const,
то
,
т.к. b
= const,
то
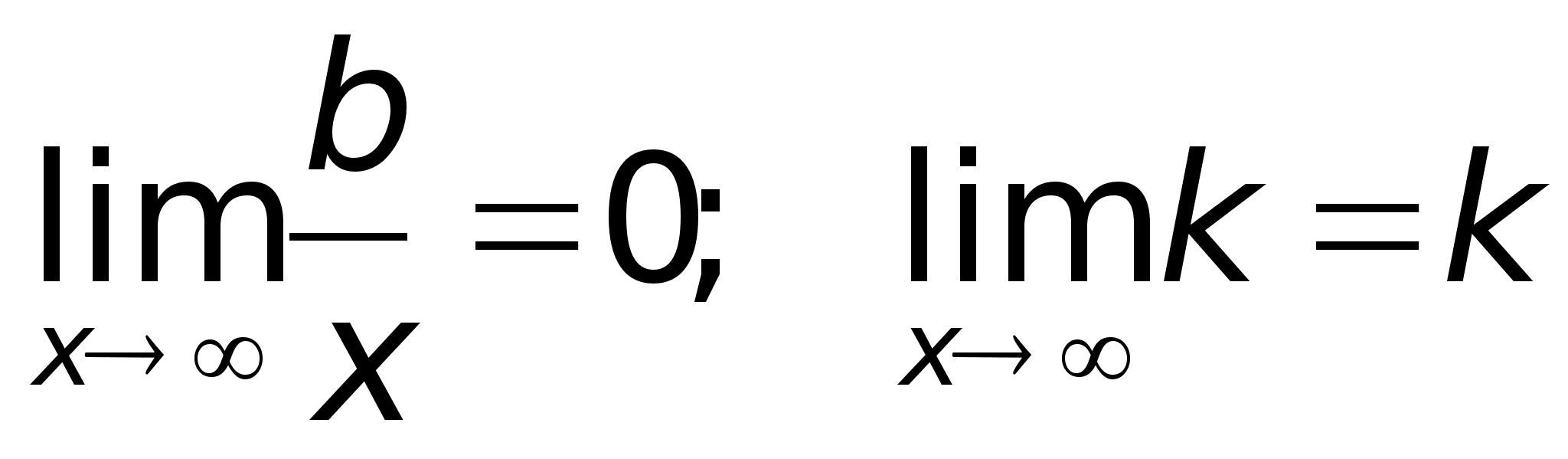 .Тогда
.Тогда
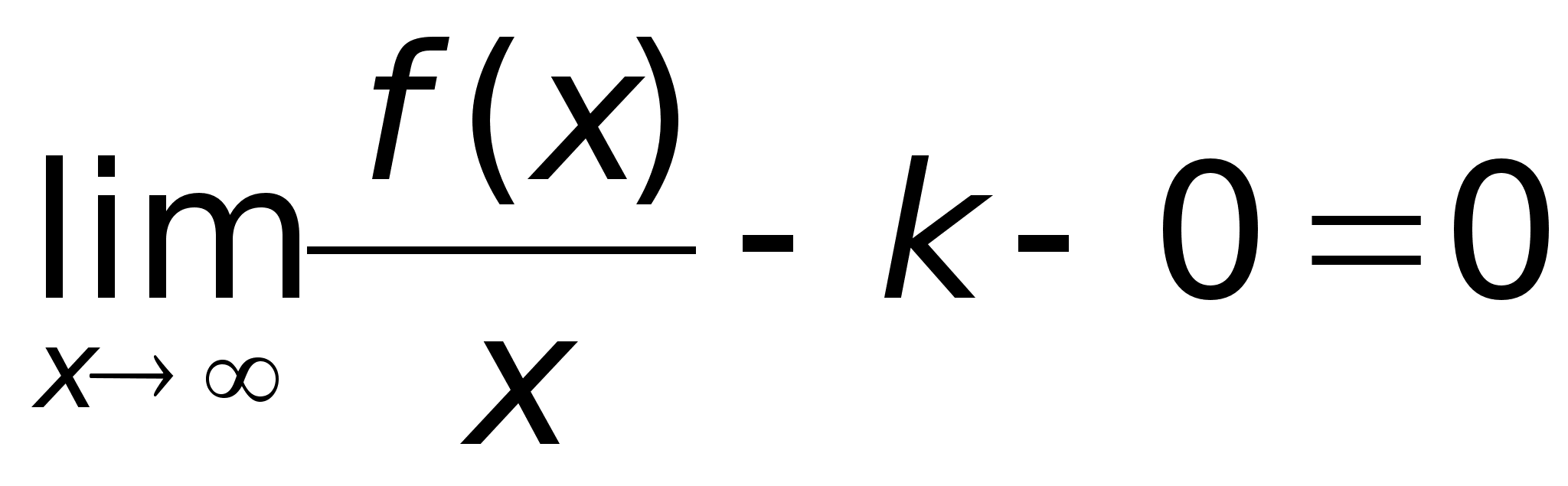 ,
следовательно,
,
следовательно,
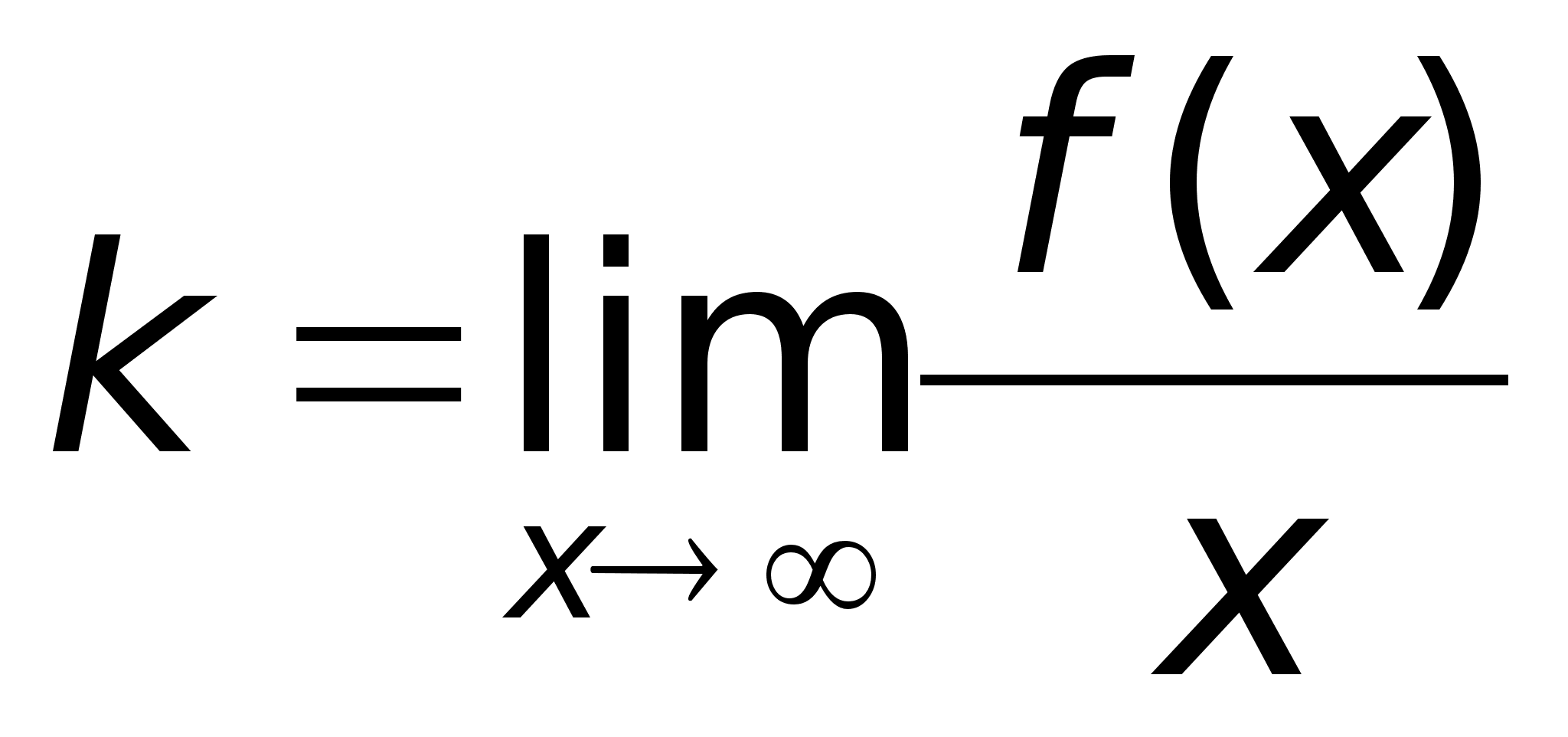 .Т.к.
.Т.к.
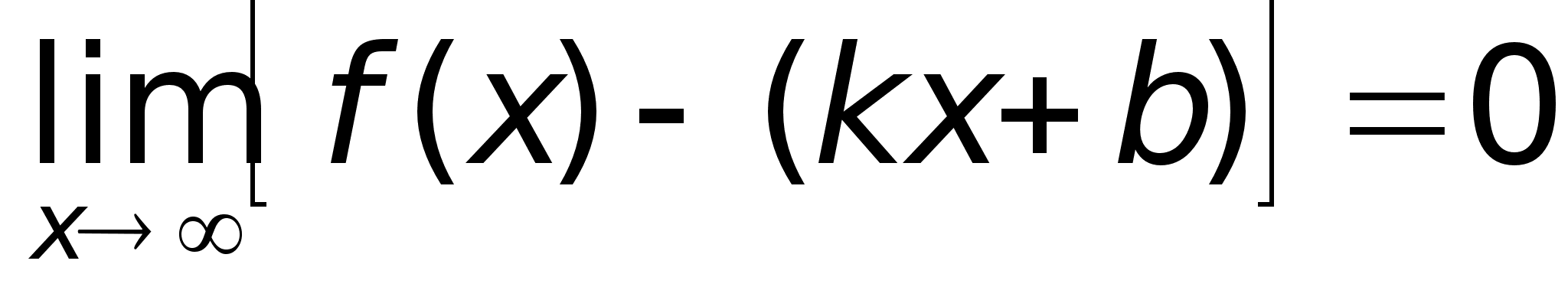 ,
то
,
то
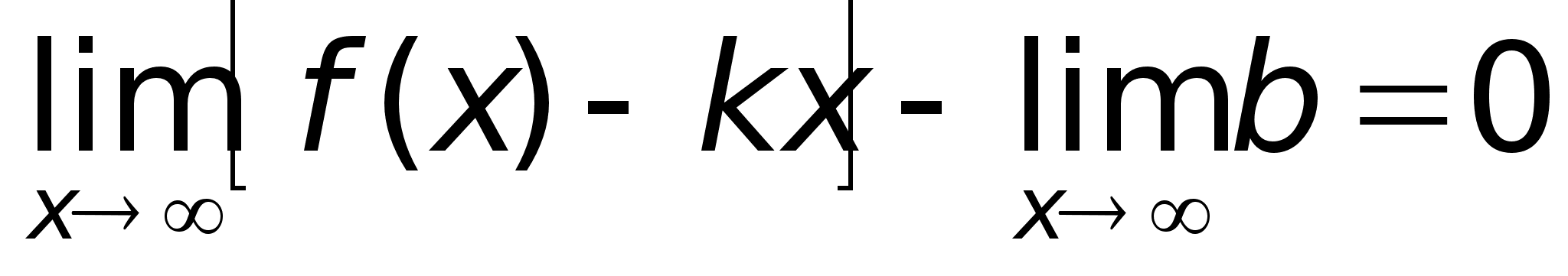 ,
следовательно,
,
следовательно,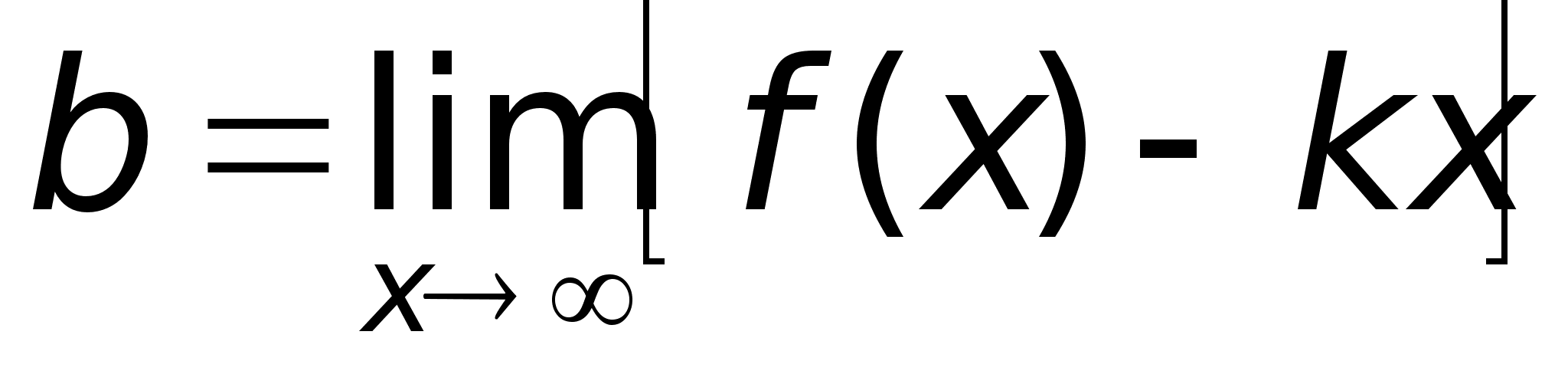 Отметим,
что горизонтальные
асимптоты
являются частным
случаем наклонных
асимптот при
k
=0. Пример.
Найти асимптоты
и построить
график функции
Отметим,
что горизонтальные
асимптоты
являются частным
случаем наклонных
асимптот при
k
=0. Пример.
Найти асимптоты
и построить
график функции
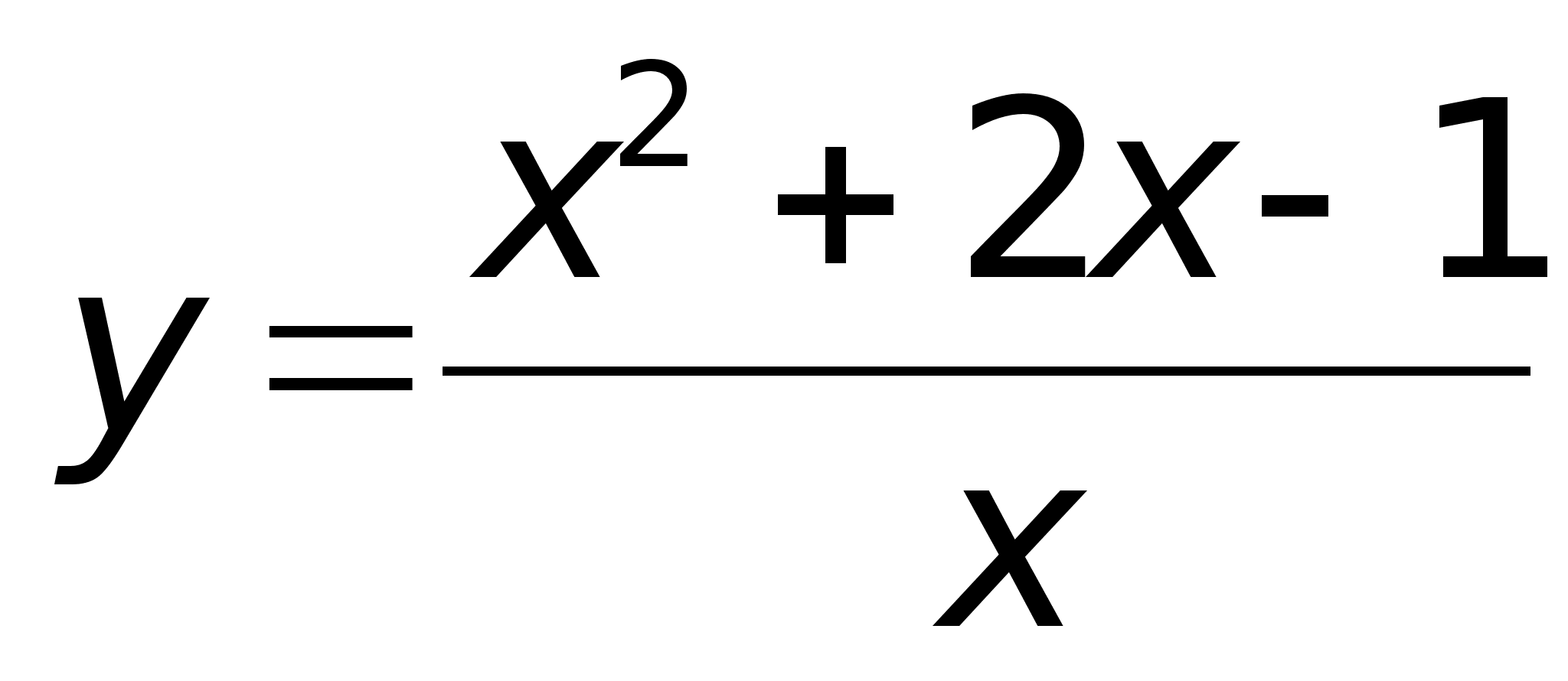 .1)
Вертикальные
асимптоты:
y
.1)
Вертикальные
асимптоты:
y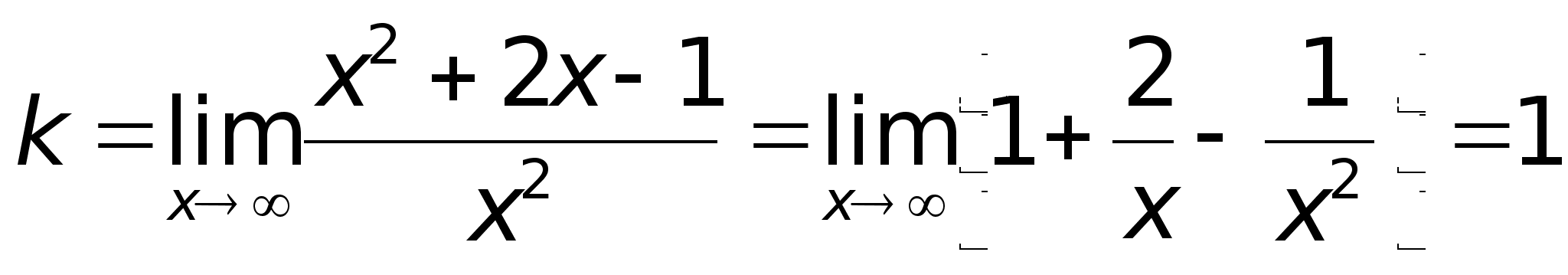
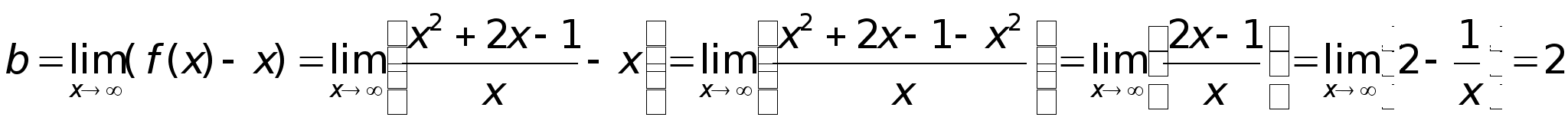
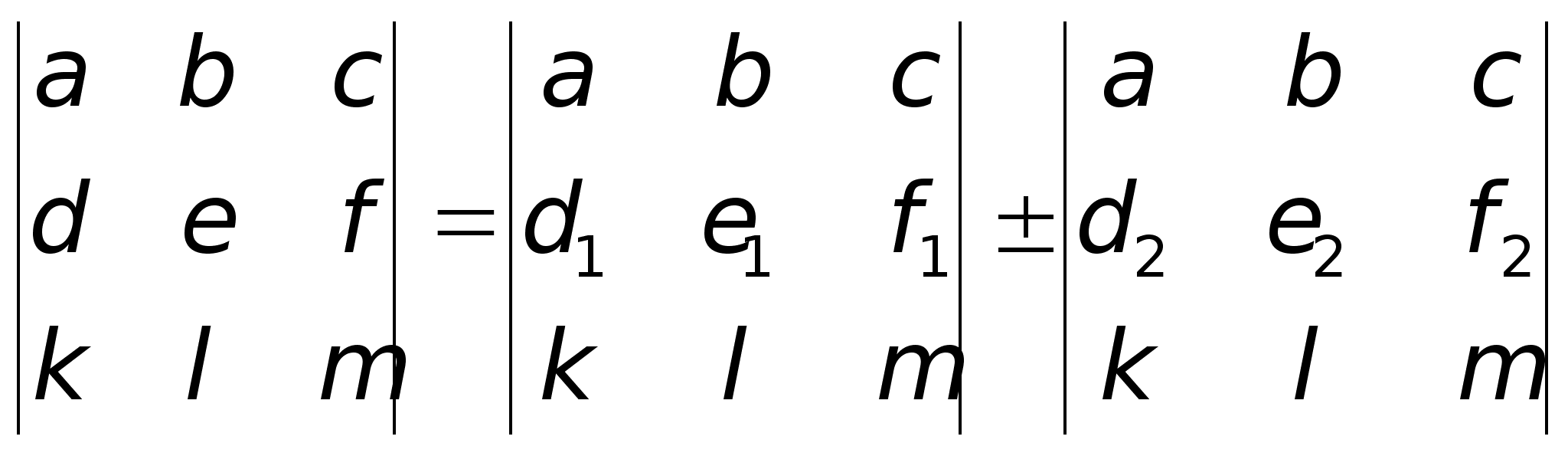
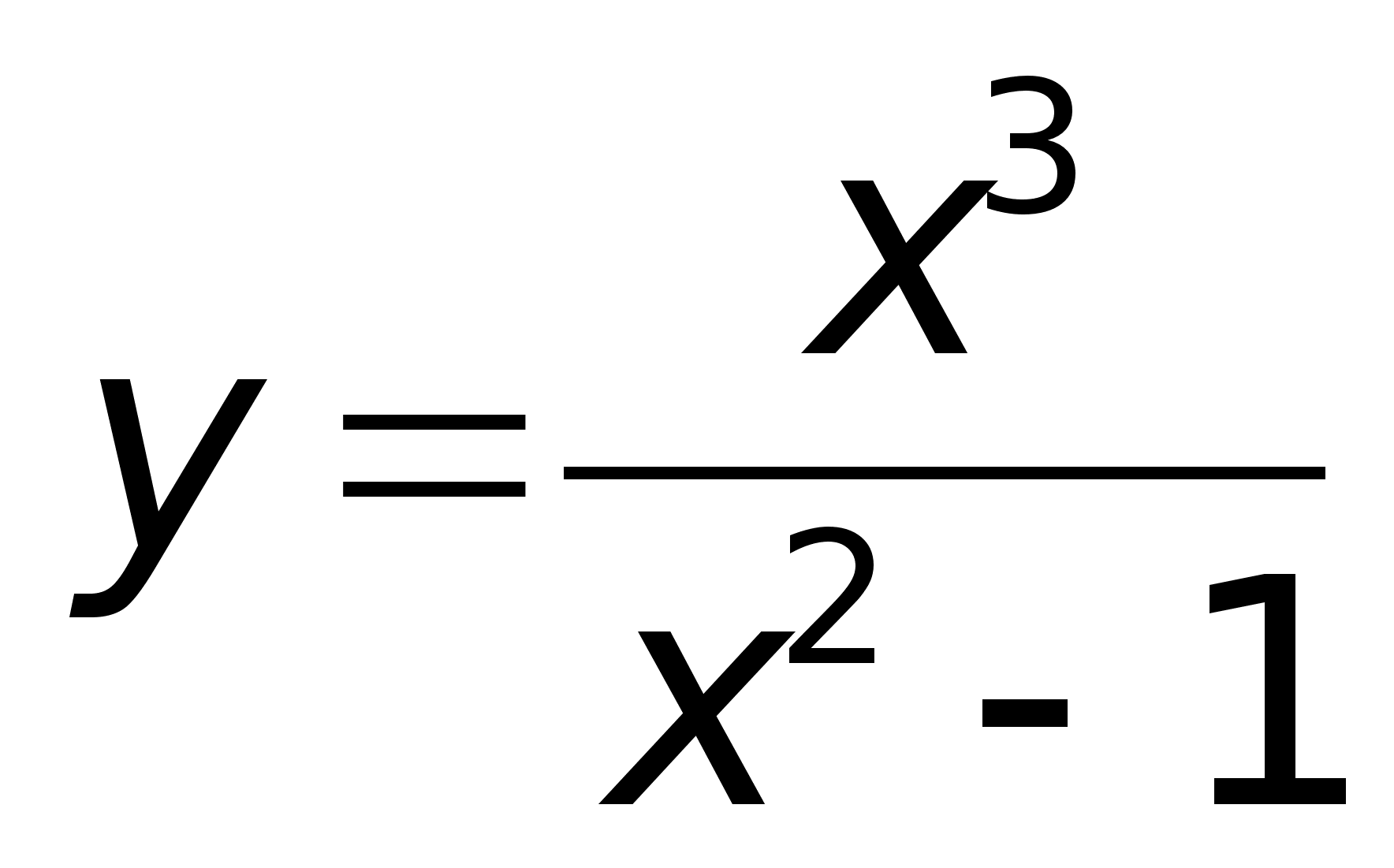 и
построить ее
график.Находим
область существования
функции. Очевидно,
что областью
определения
функции является
область (-
и
построить ее
график.Находим
область существования
функции. Очевидно,
что областью
определения
функции является
область (-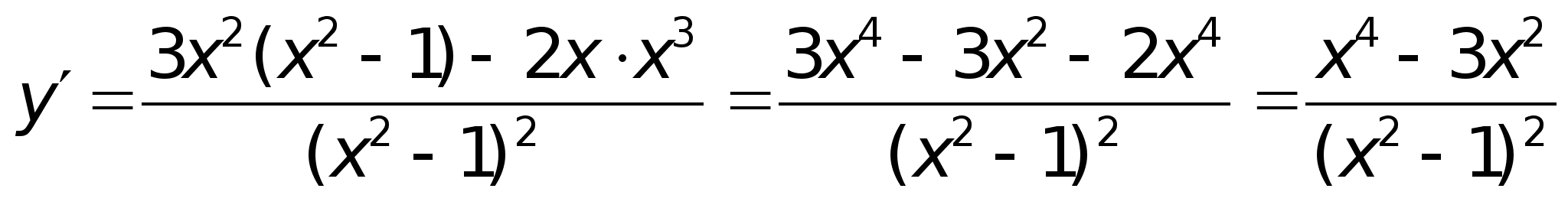 Критические
точки: x
= 0; x
= -
Критические
точки: x
= 0; x
= -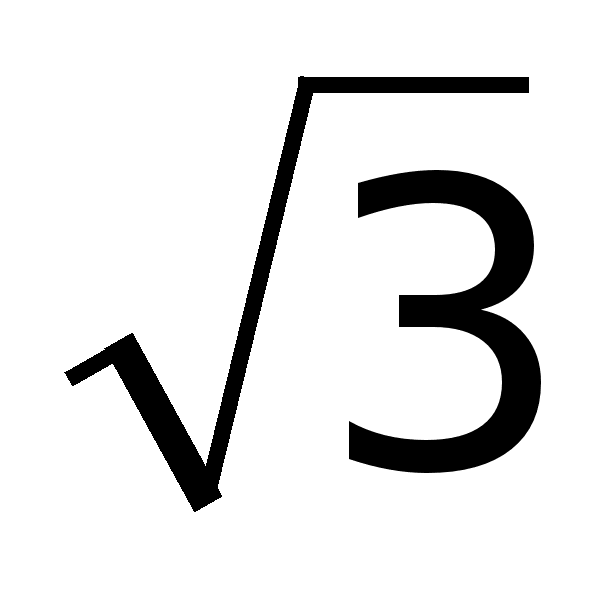 ;
x
=
;
x
=
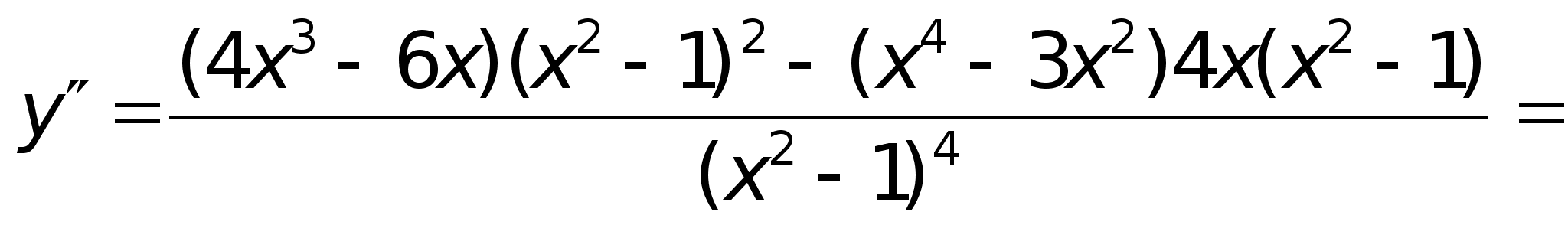
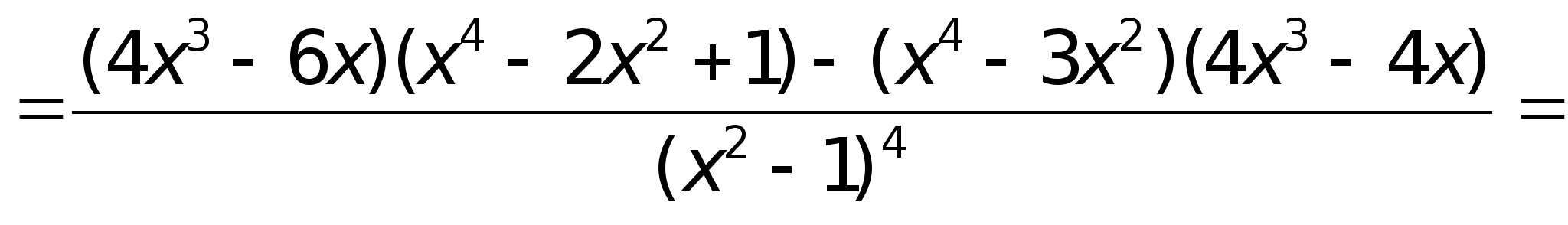
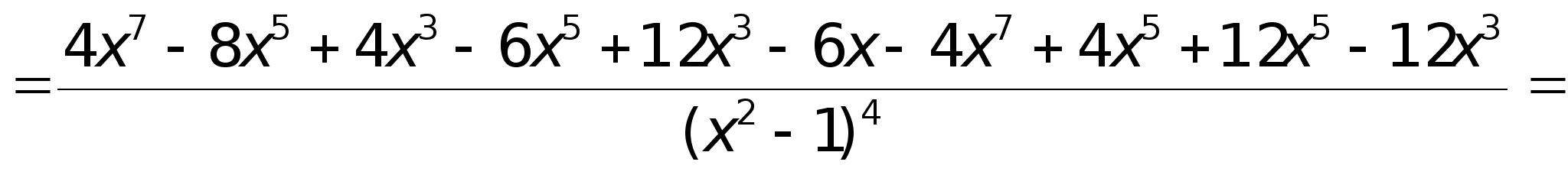
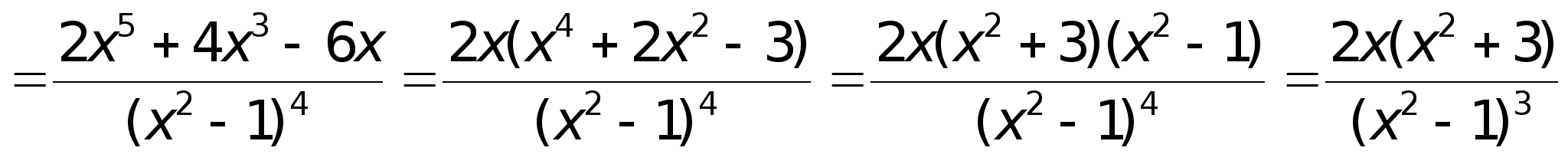
 .
Определим
выпуклость
и вогнутость
кривой на
промежутках.
-
.
Определим
выпуклость
и вогнутость
кривой на
промежутках.
- ,
y
,
y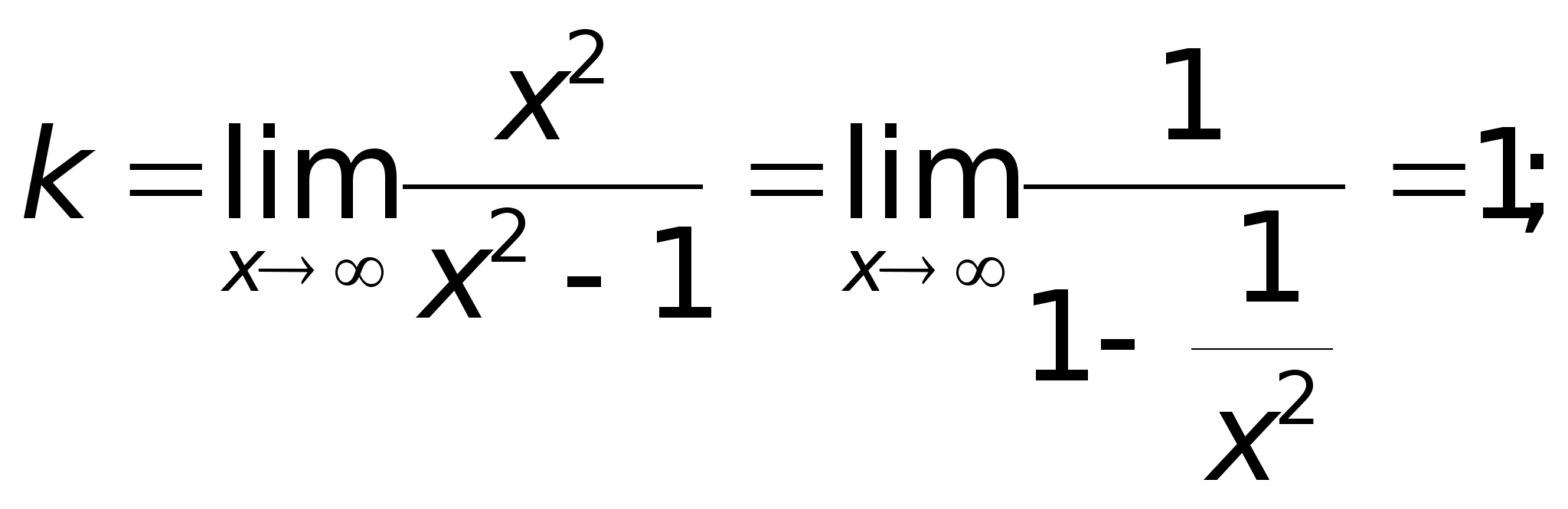
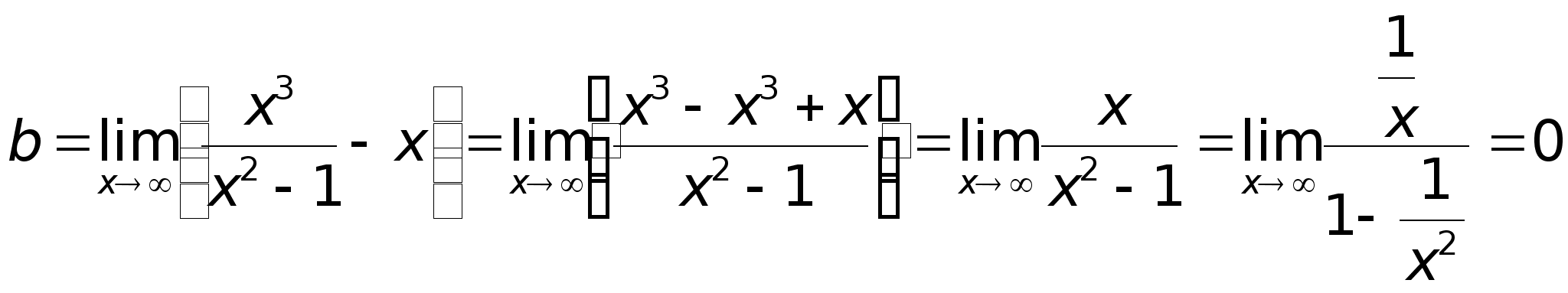 Итого,
уравнение
наклоннойасимптоты
– y
= x.
Построим график
функции:
Итого,
уравнение
наклоннойасимптоты
– y
= x.
Построим график
функции: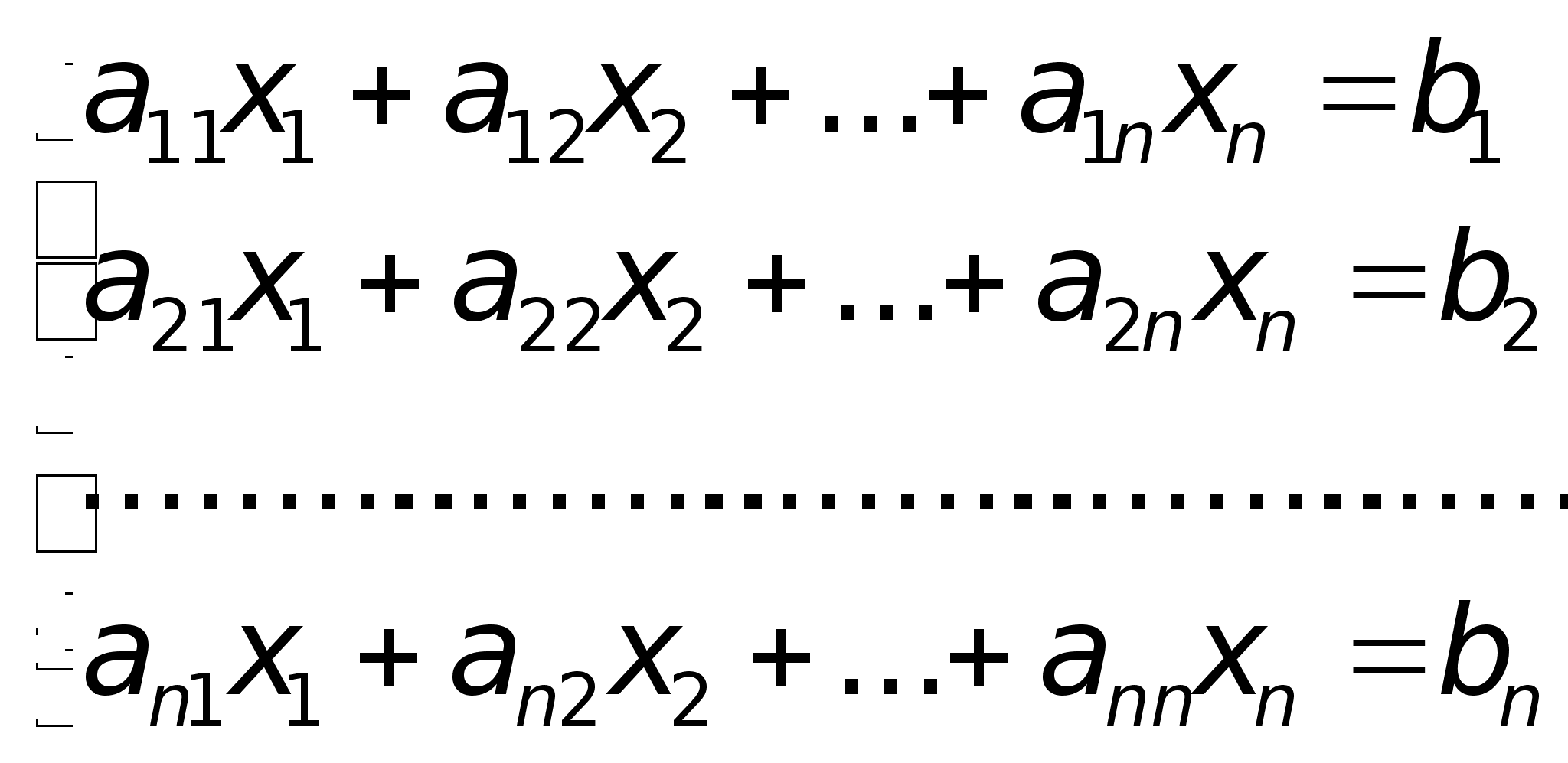 в
случае, если
определитель
матрицы системы
не равен нулю,
имеет единственное
решение и это
решение находится
по формулам:xi
=
в
случае, если
определитель
матрицы системы
не равен нулю,
имеет единственное
решение и это
решение находится
по формулам:xi
= 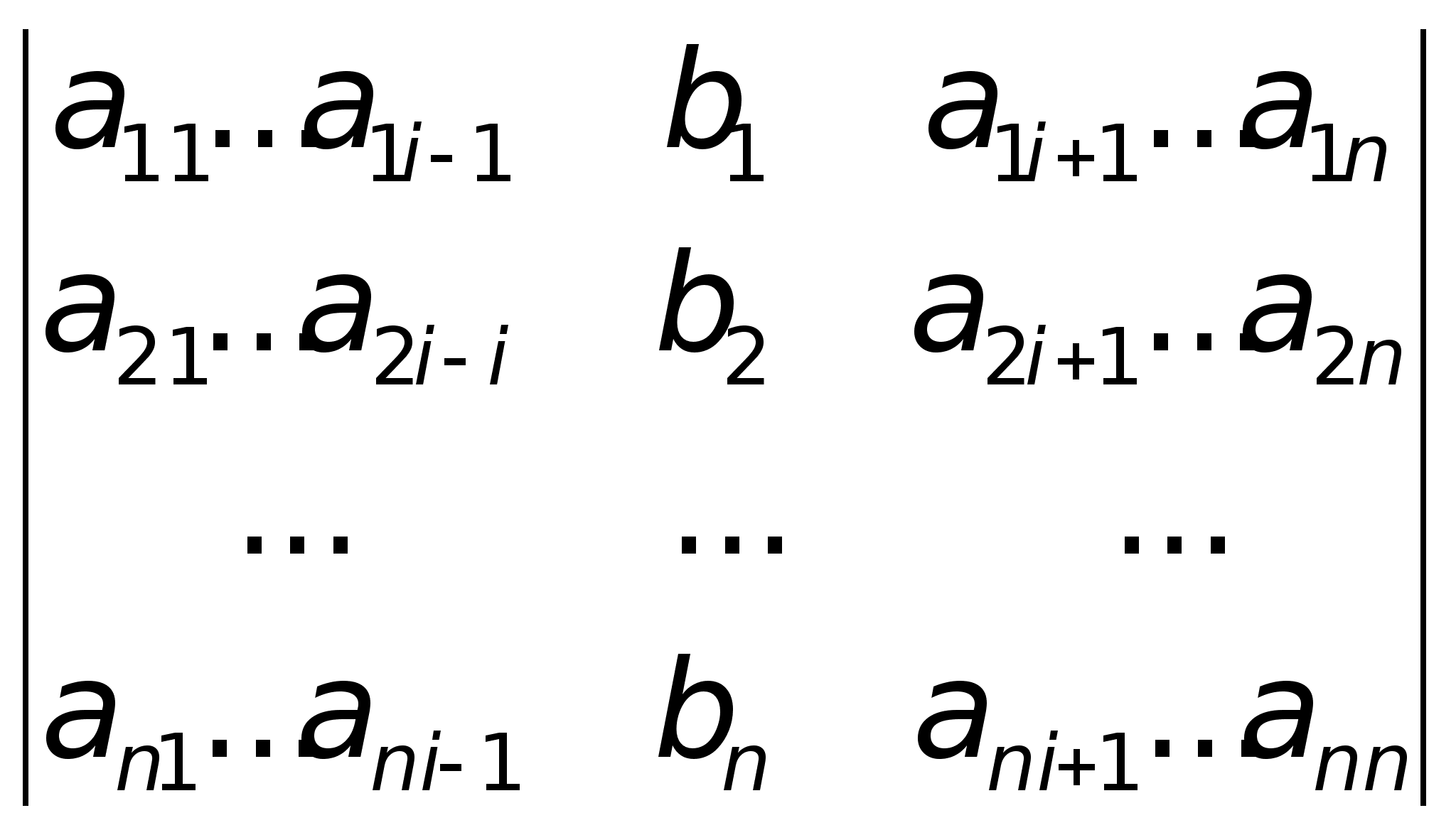 Пример.
Пример.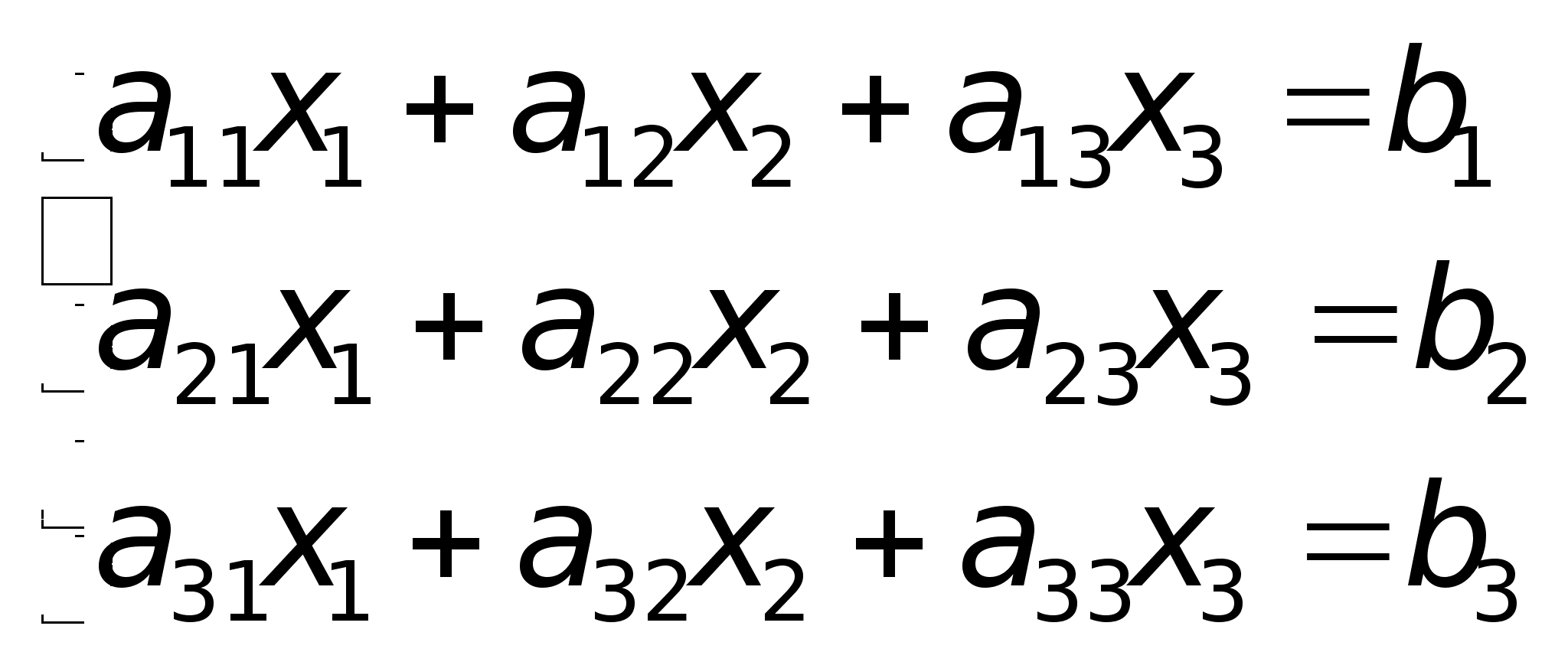 A
=
A
=
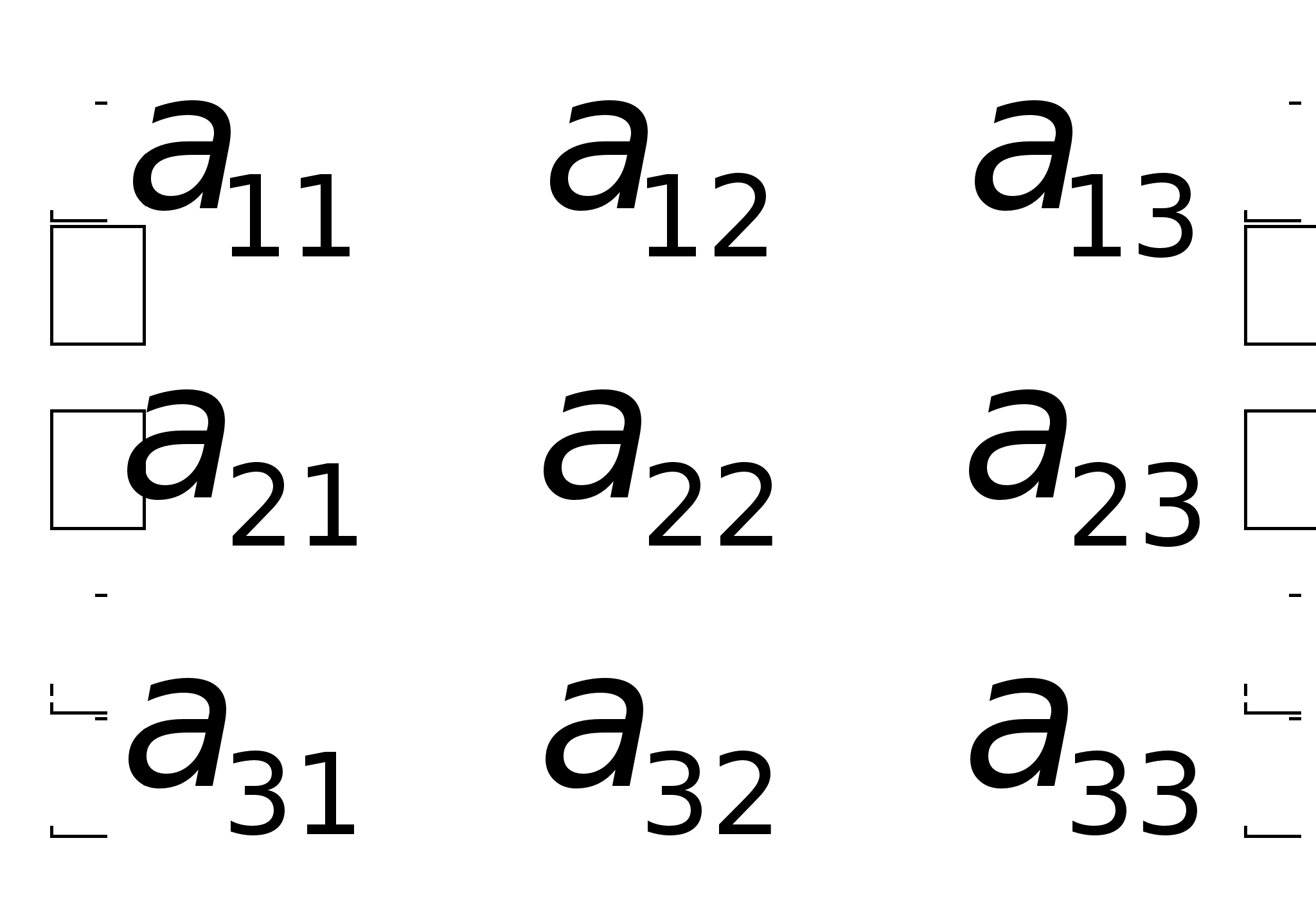 ;
;
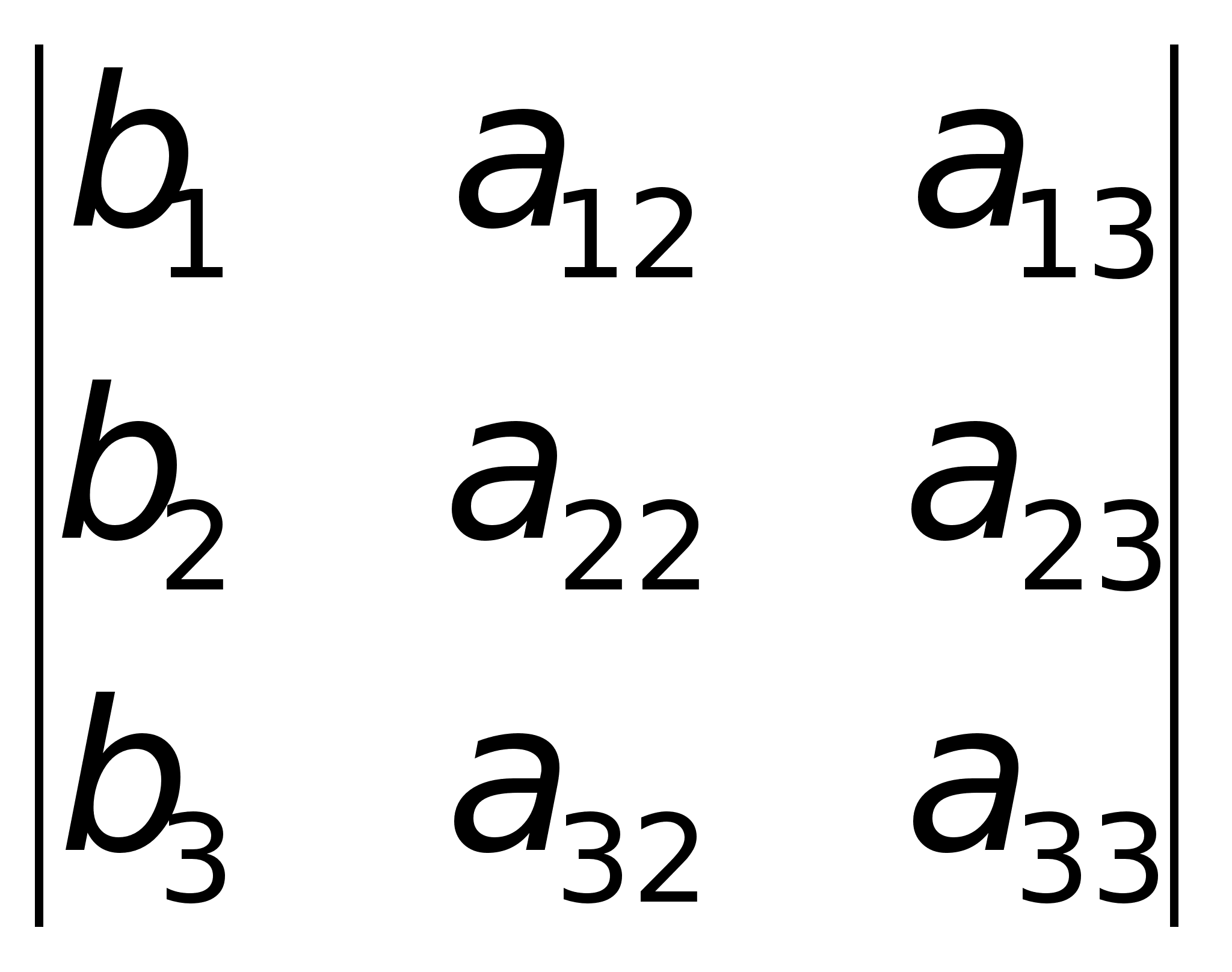 ;
;
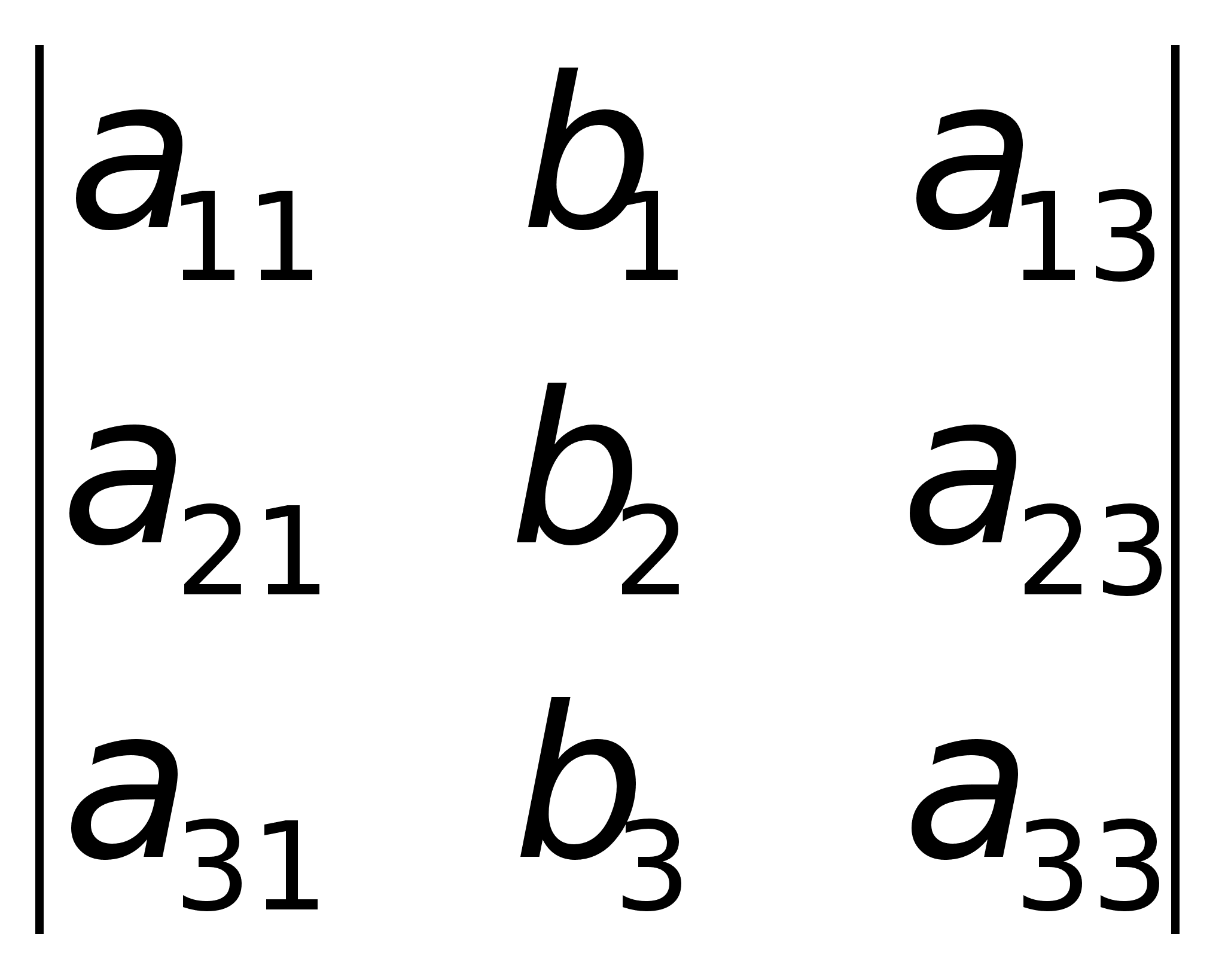 ;
;
 ;x1
=
;x1
= 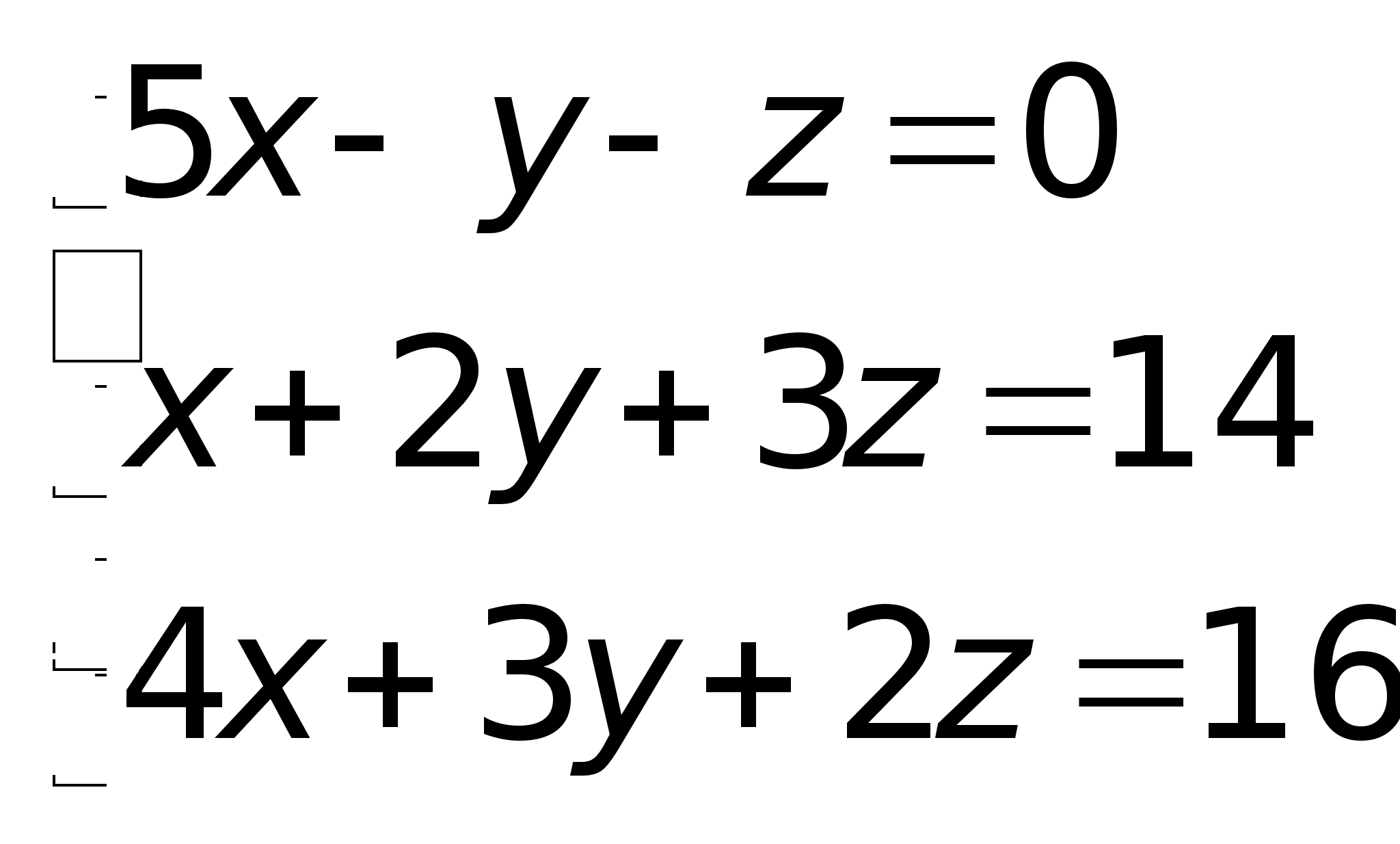
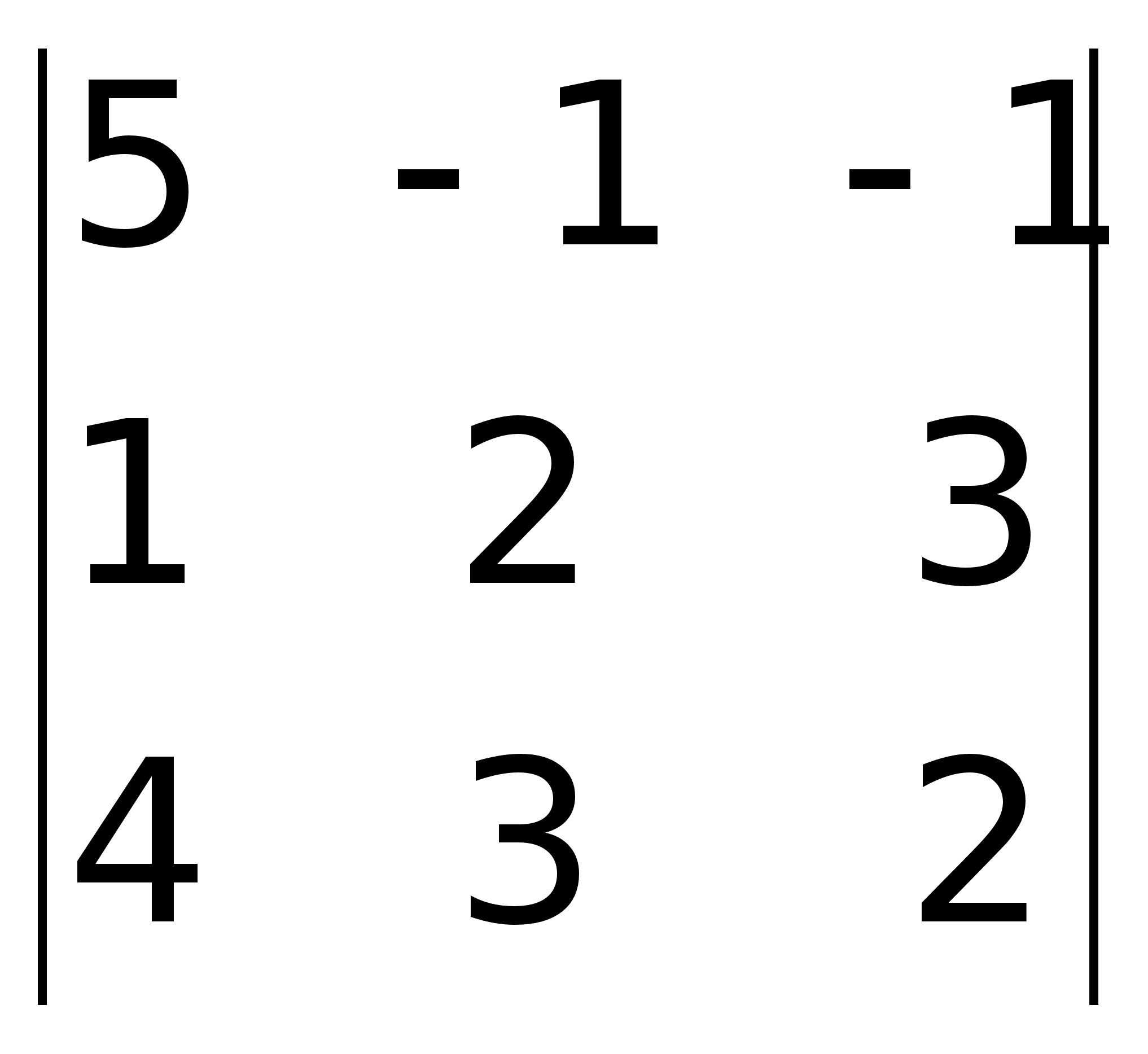 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 –
10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 –
10 + 5 = -30;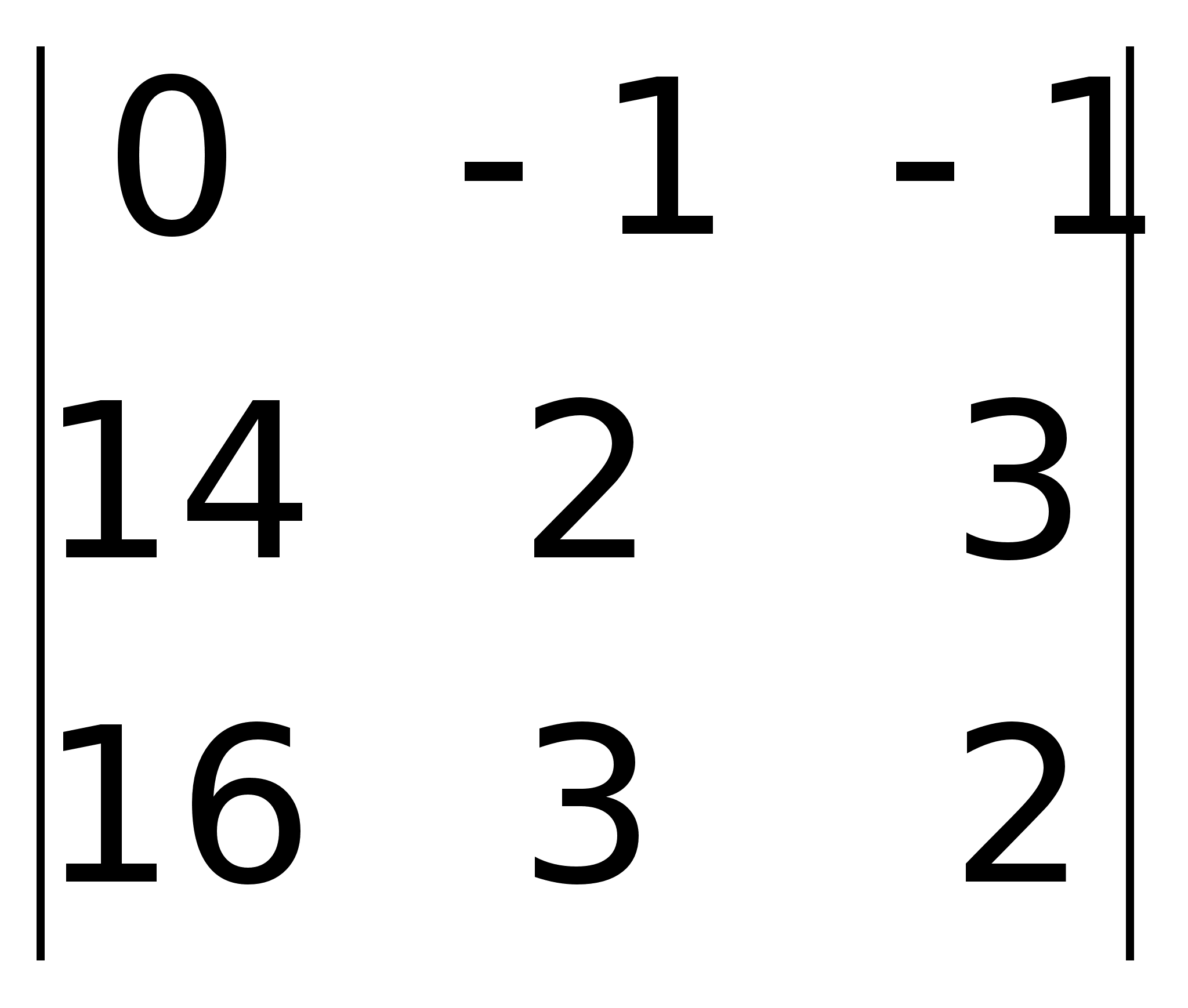 28
– 48) – (42 – 32) = -20 – 10 = -30. x1
=
28
– 48) – (42 – 32) = -20 – 10 = -30. x1
= 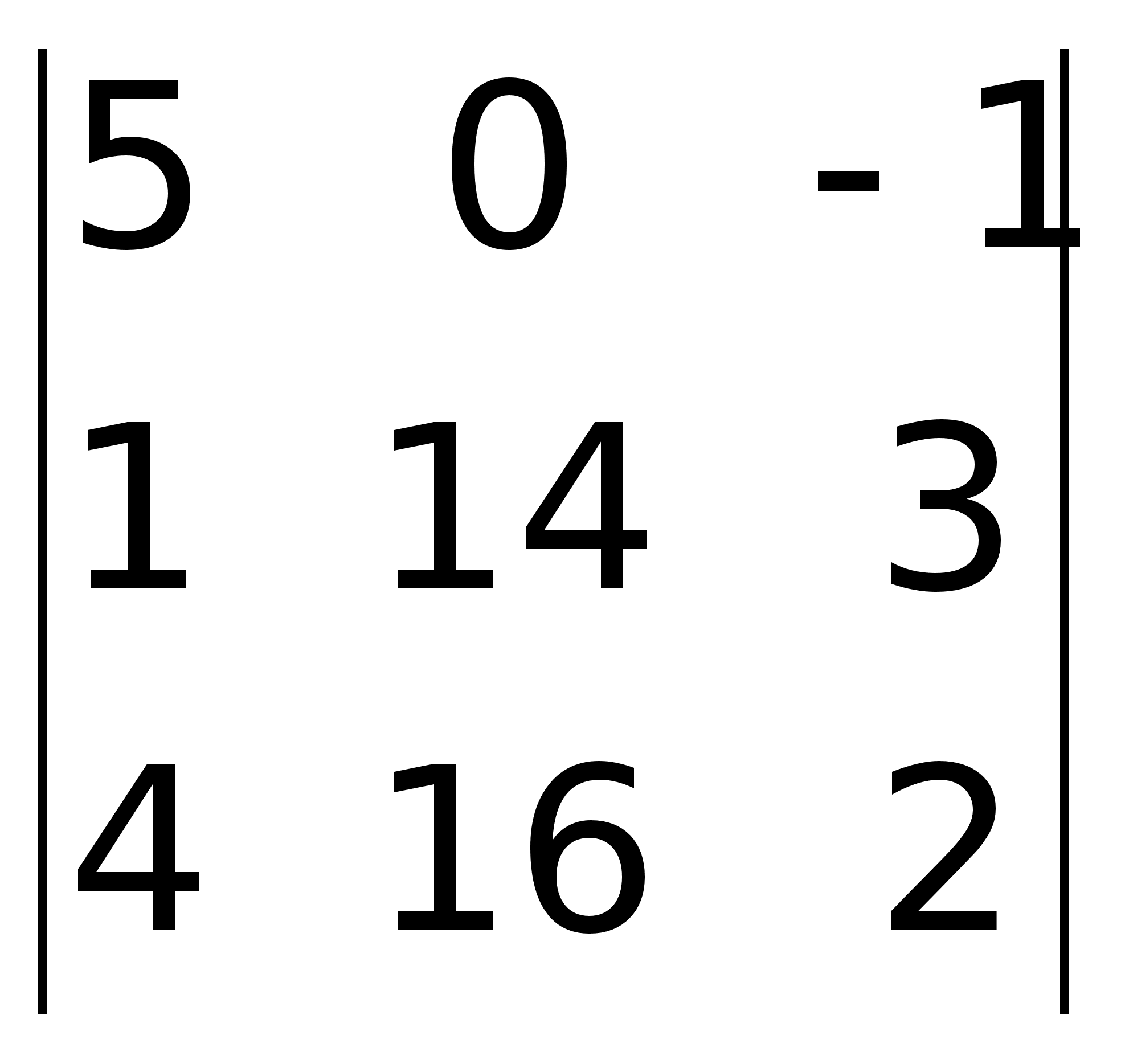 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.x2
=
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.x2
=  = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.x3
=
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.x3
= 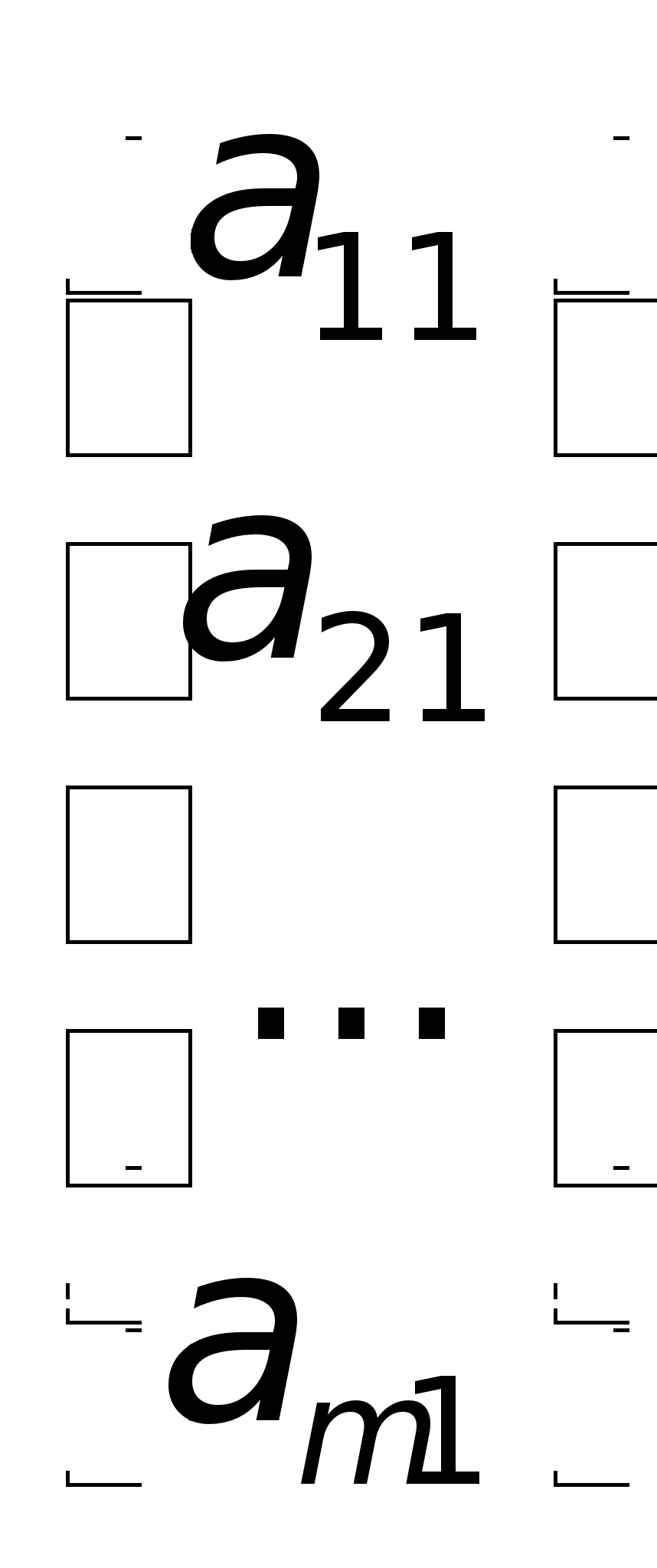 + x2
+ x2
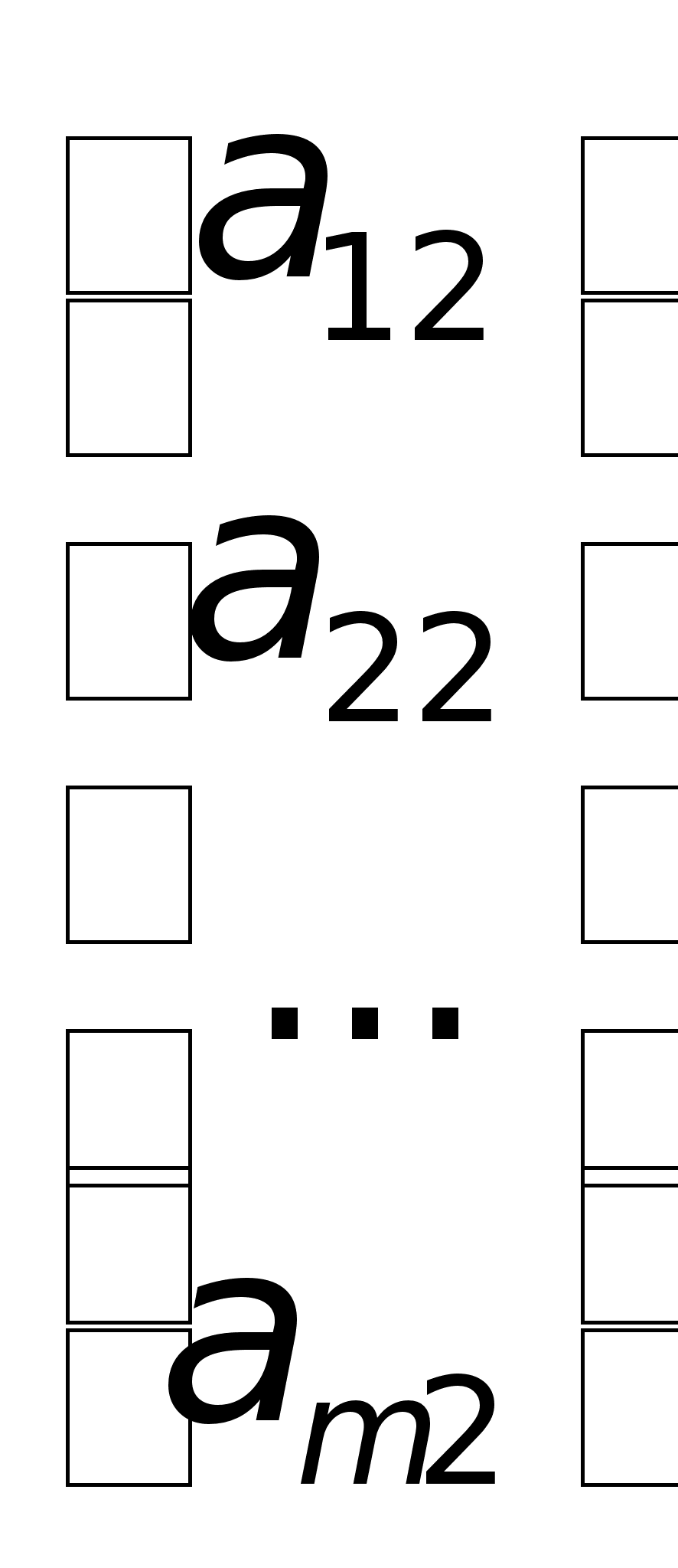 +
… + xn
+
… + xn
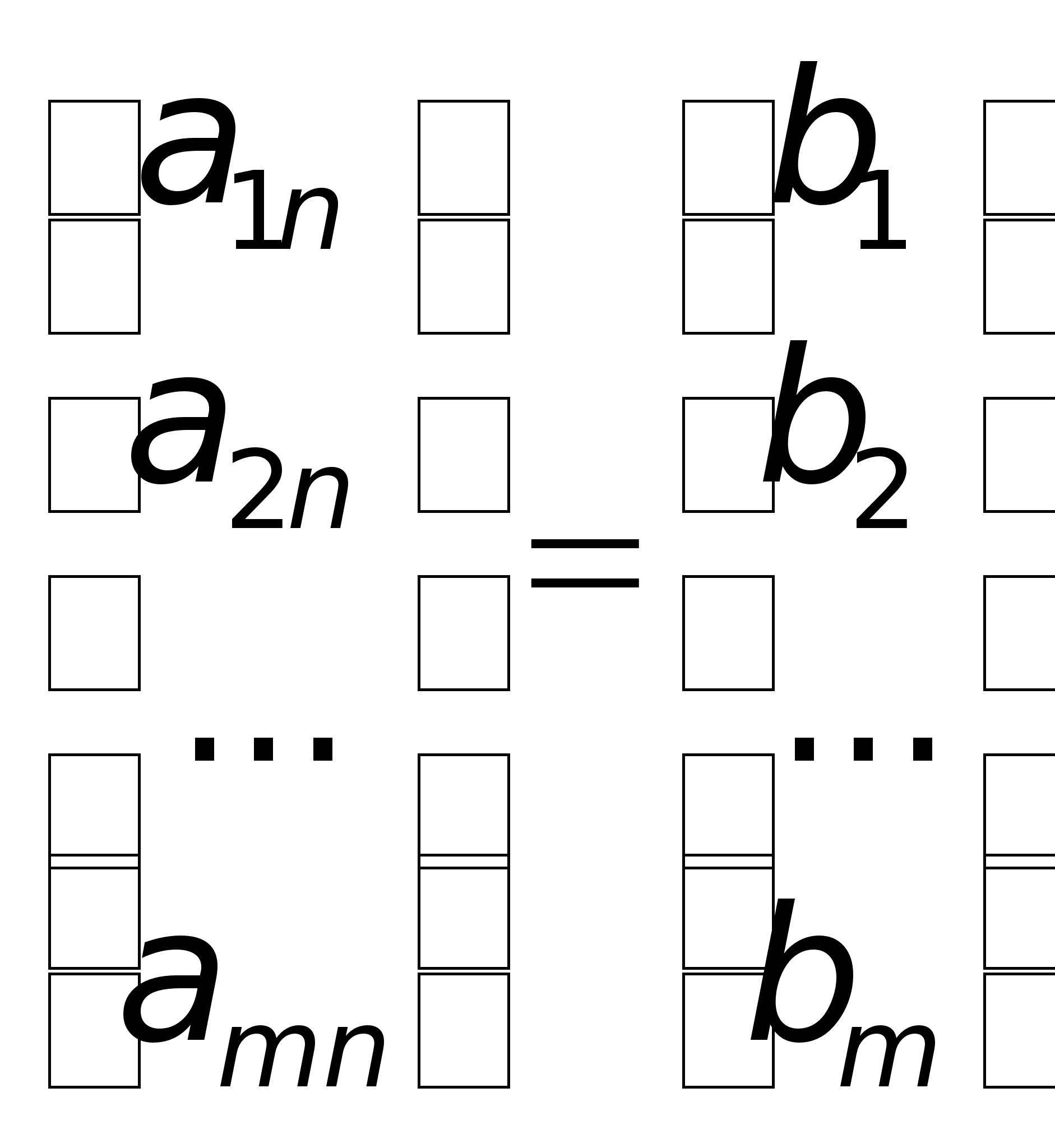 Доказательство.1)
Если решение
существует,
то столбец
свободных
членов есть
линейная
комбинация
толбцов матрицы
А, а значит
добавление
этого столбца
в матрицу, т.е.
переход А
Доказательство.1)
Если решение
существует,
то столбец
свободных
членов есть
линейная
комбинация
толбцов матрицы
А, а значит
добавление
этого столбца
в матрицу, т.е.
переход А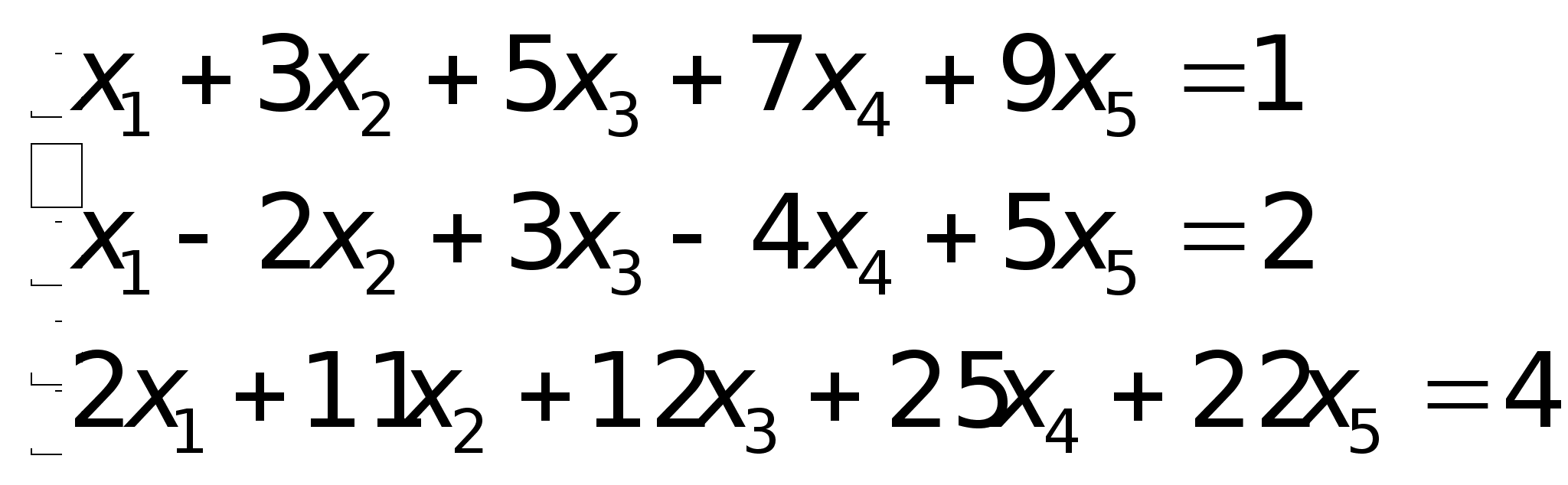 A
=
A
=
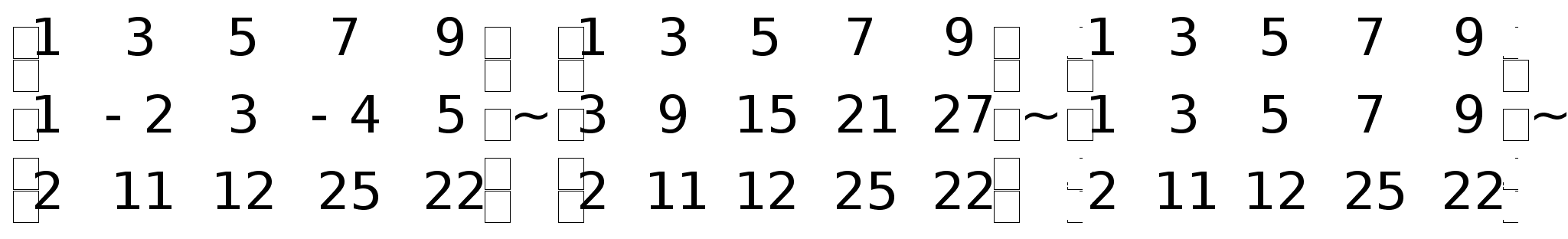 ~
~
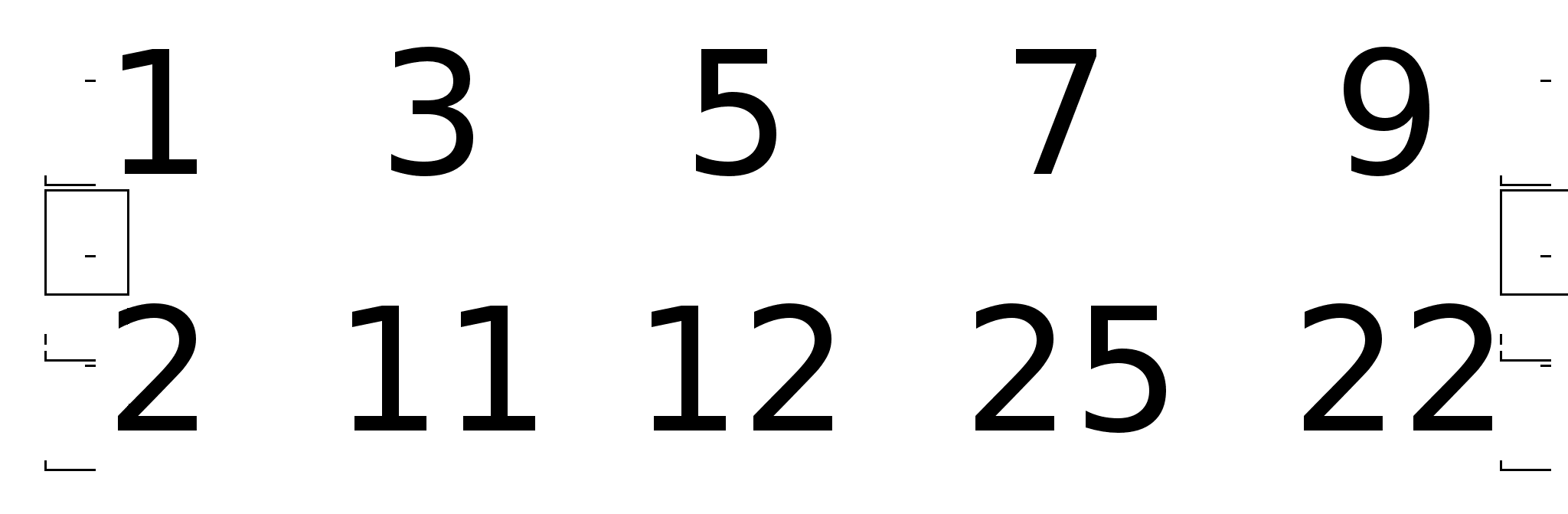 .
.
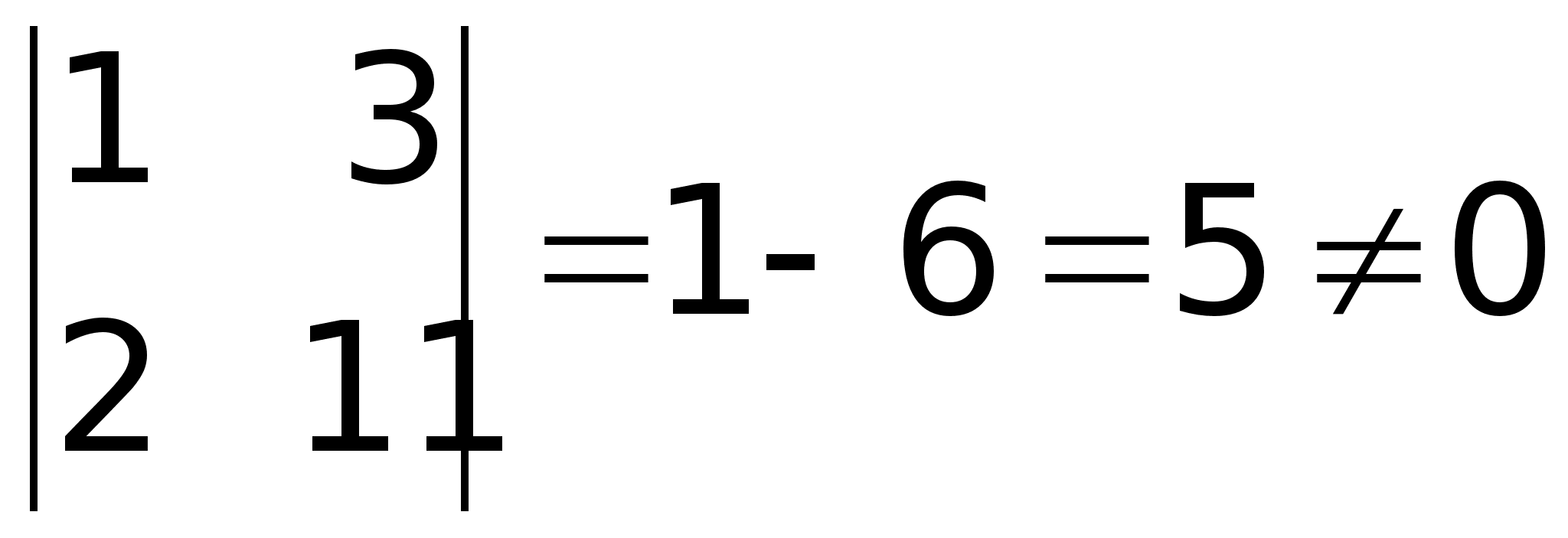 RgA
= 2.A*
=
RgA
= 2.A*
=
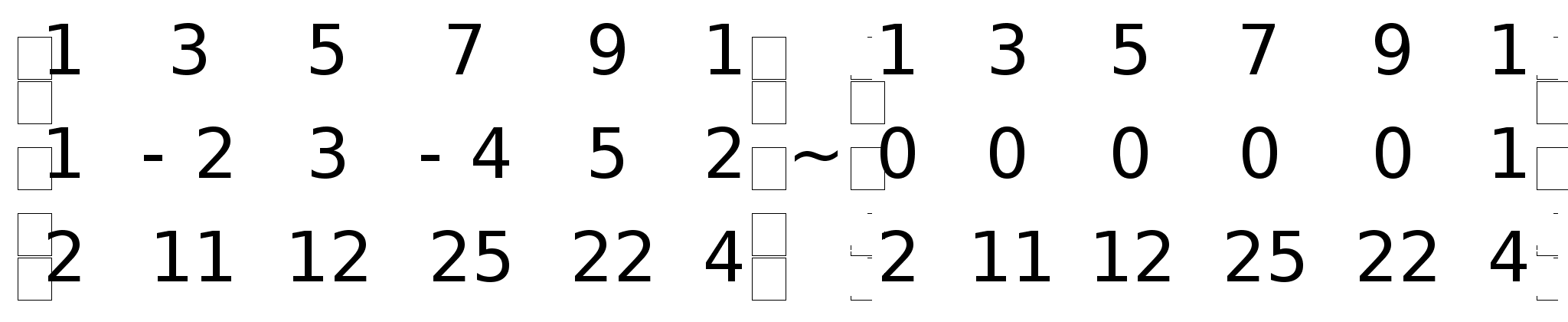 RgA*
= 3.Система
несовместна.Пример.
Определить
RgA*
= 3.Система
несовместна.Пример.
Определить
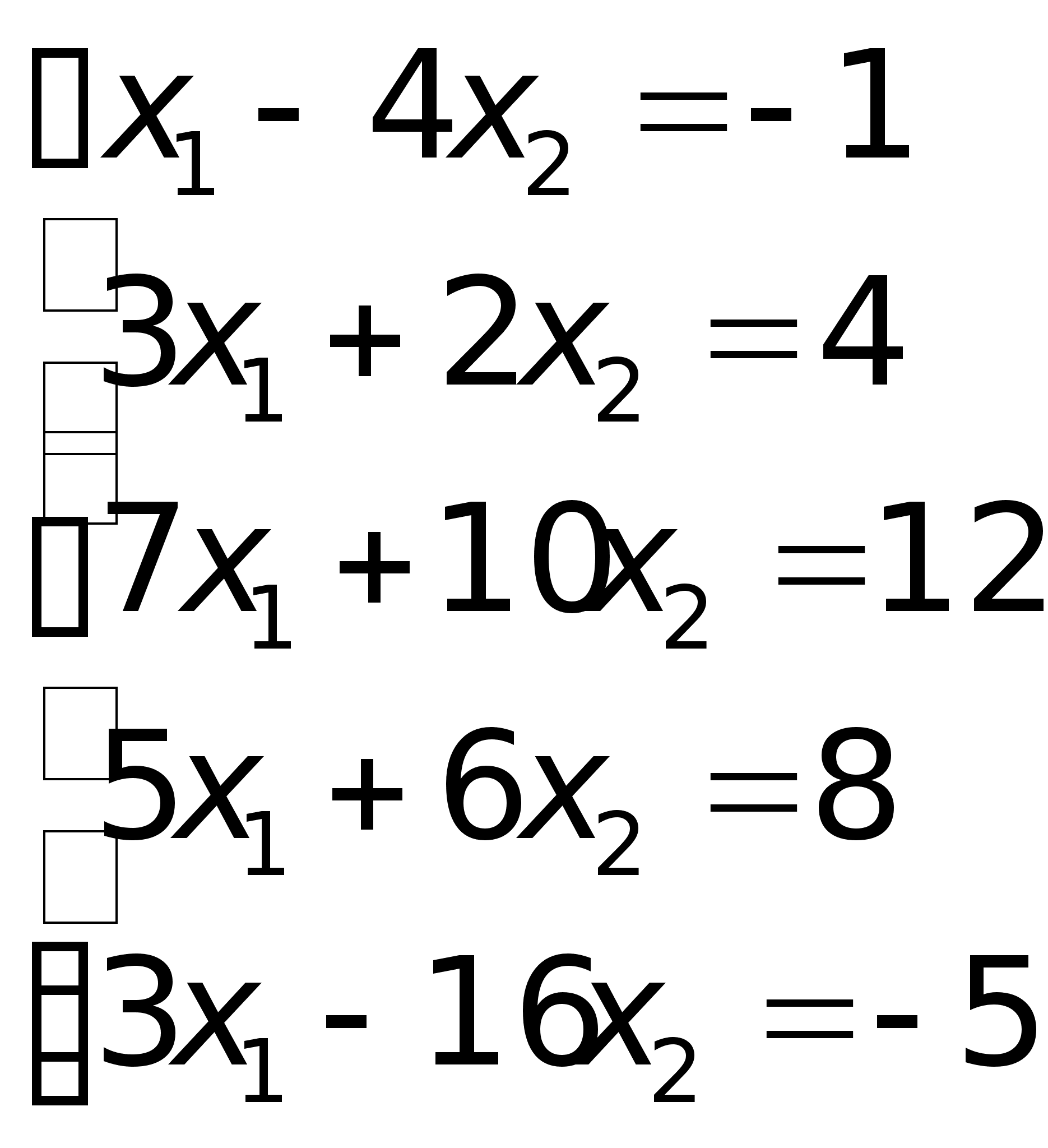 А =
А =
 ;
;
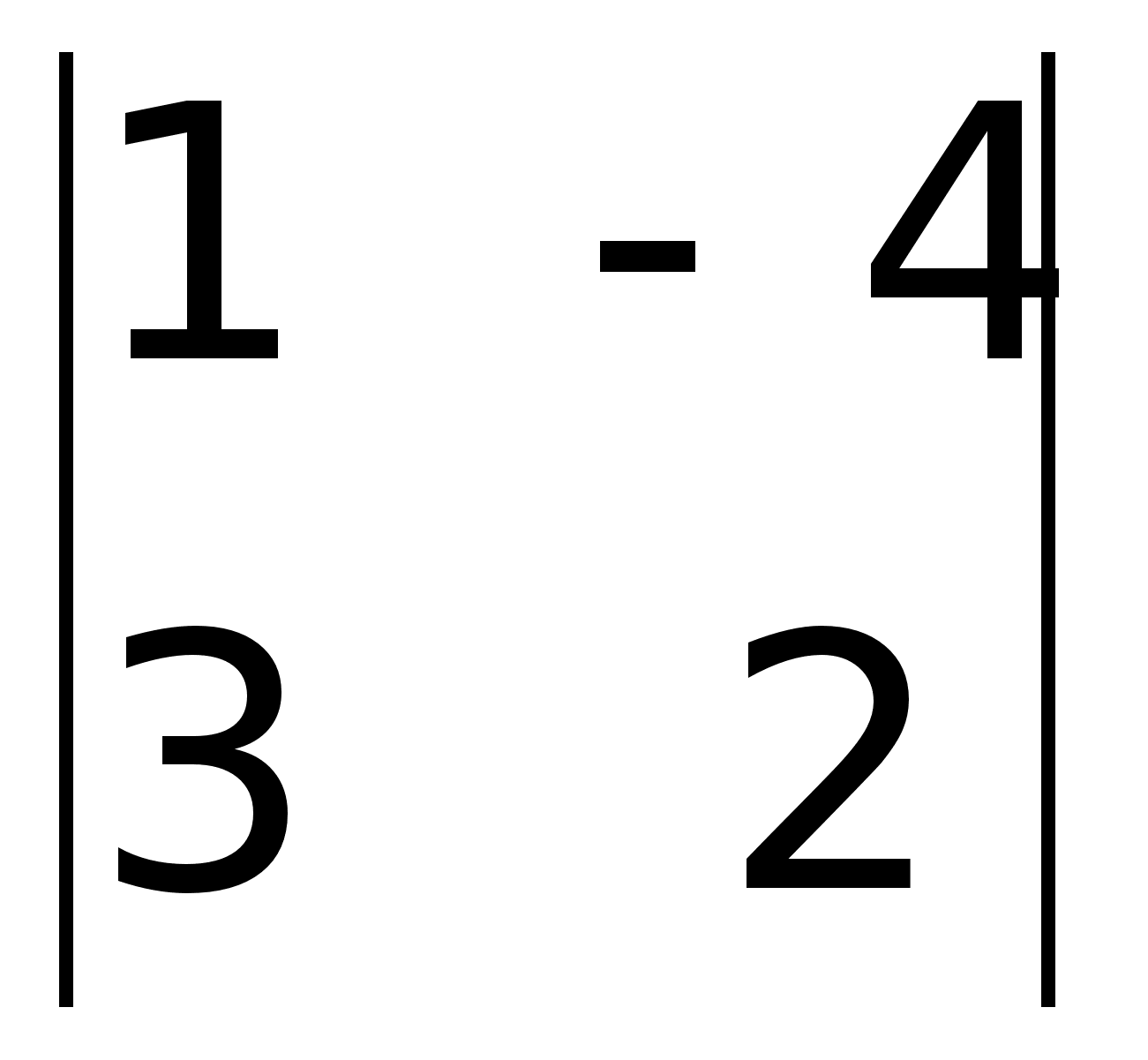 = 2 +
= 2 +
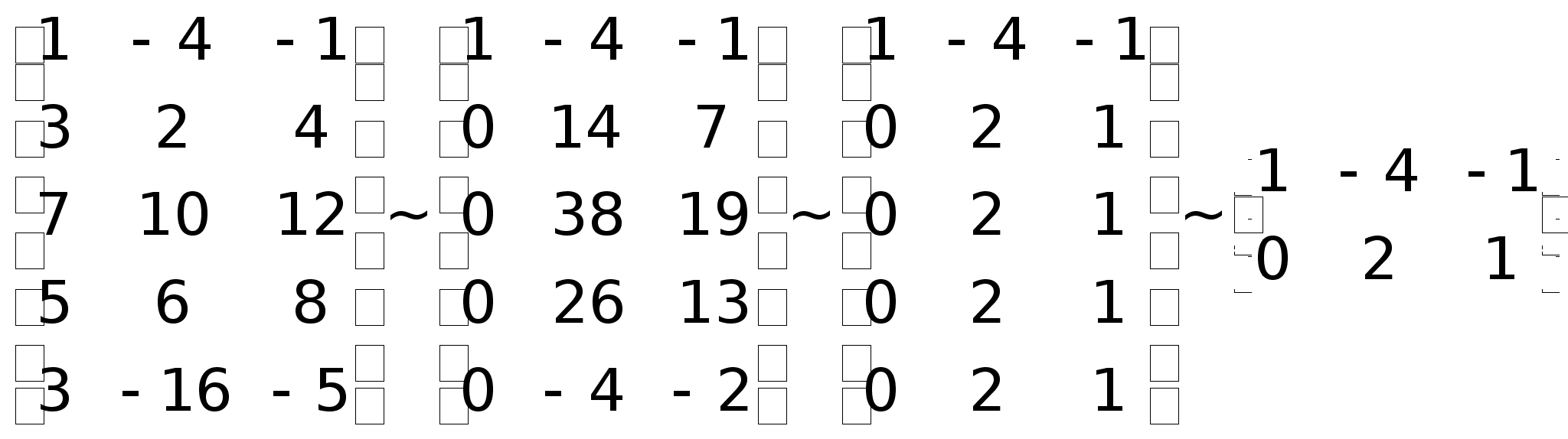
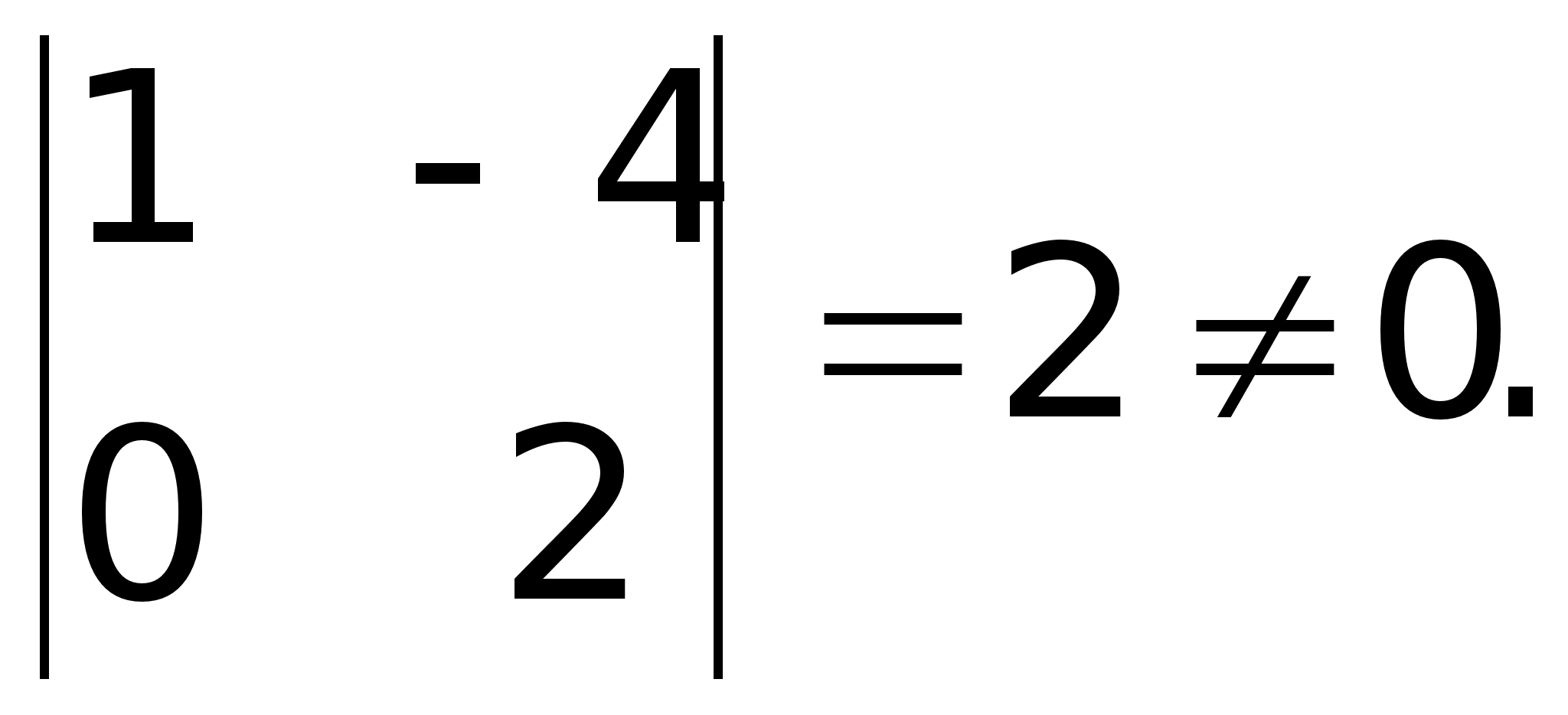 RgA*
= 2.Система совместна.
Решения: x1
= 1; x2
=1/2.
RgA*
= 2.Система совместна.
Решения: x1
= 1; x2
=1/2.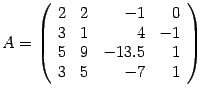 .
Решение.
Первую строку
оставляем
без изменений.
Чтобы избежать
появления
дробей, умножим
вторую, третью
и четвертую
строки на 2:
.
Решение.
Первую строку
оставляем
без изменений.
Чтобы избежать
появления
дробей, умножим
вторую, третью
и четвертую
строки на 2:
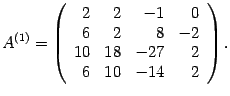 Первую
строку умножим
на
Первую
строку умножим
на
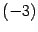 и
прибавим ко
второй. Получим
строку
и
прибавим ко
второй. Получим
строку
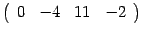 .
Первую строку
умножим на
.
Первую строку
умножим на
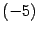 и
прибавим к
третьей. Получим
строку
и
прибавим к
третьей. Получим
строку
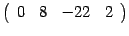 .
Первую строку
умножим на
.
Первую строку
умножим на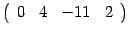 .В
итоге имеем
матрицу
.В
итоге имеем
матрицу
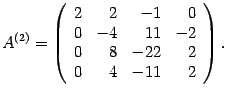 Вторую
строку оставляем
без изменений.
К третьей строке
прибавляем
вторую, умноженную
на 2. Получим
строку
Вторую
строку оставляем
без изменений.
К третьей строке
прибавляем
вторую, умноженную
на 2. Получим
строку
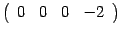 К
четвертой
строке прибавляем
вторую. Получим
нулевую строку.
Преобразованная
матрица имеет
вид
К
четвертой
строке прибавляем
вторую. Получим
нулевую строку.
Преобразованная
матрица имеет
вид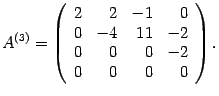 Поменяем
местами третий
и четвертый
столбцы:
Поменяем
местами третий
и четвертый
столбцы: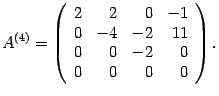 Базисный
минор матрицы
Базисный
минор матрицы
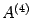 стоит
в первых трех
столбцах и
первых трех
строках,
стоит
в первых трех
столбцах и
первых трех
строках,
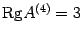 .
Следовательно,
.
Следовательно,
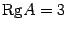
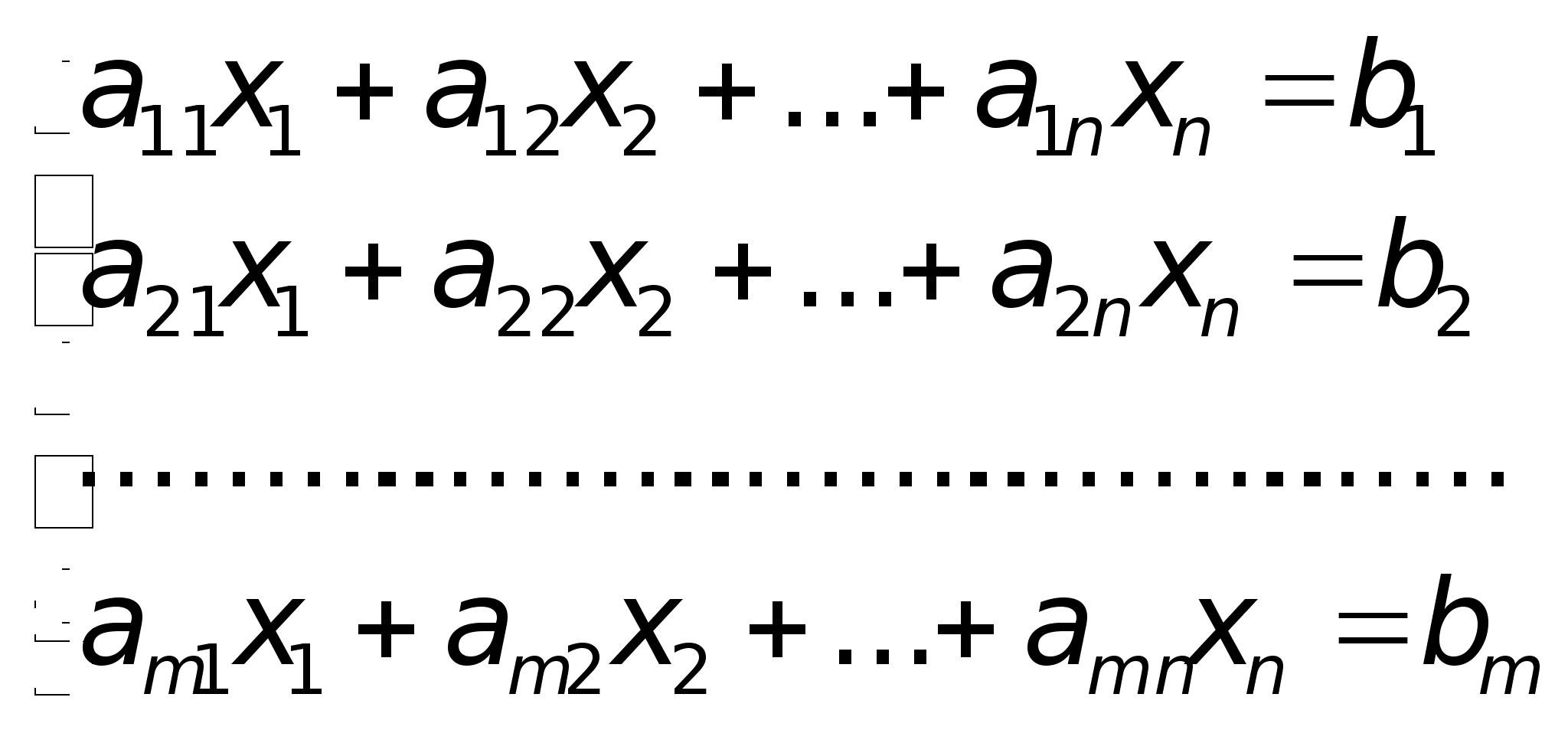 ,
,
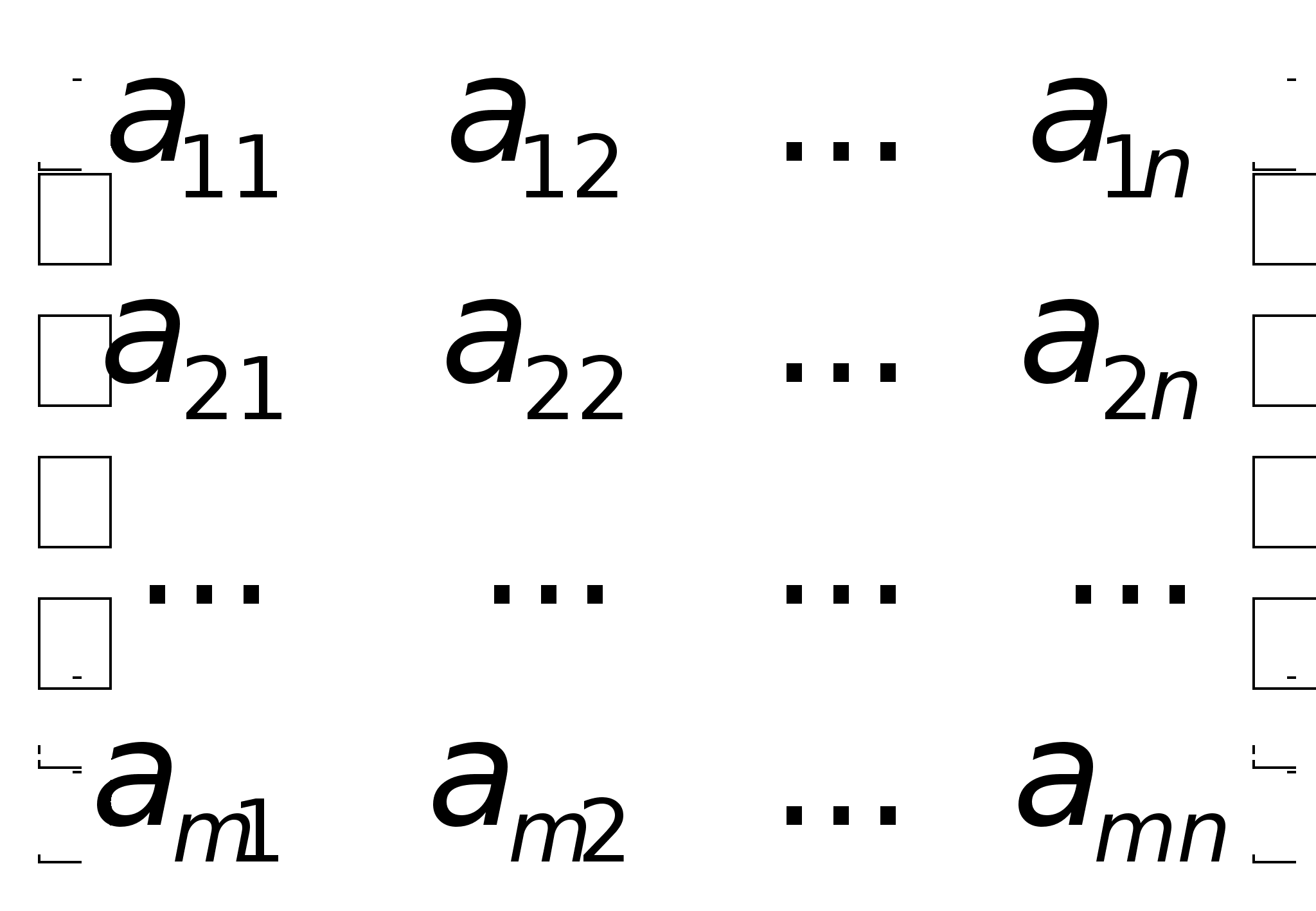 называется
матрицей системы,
а матрицаА*=
называется
матрицей системы,
а матрицаА*=
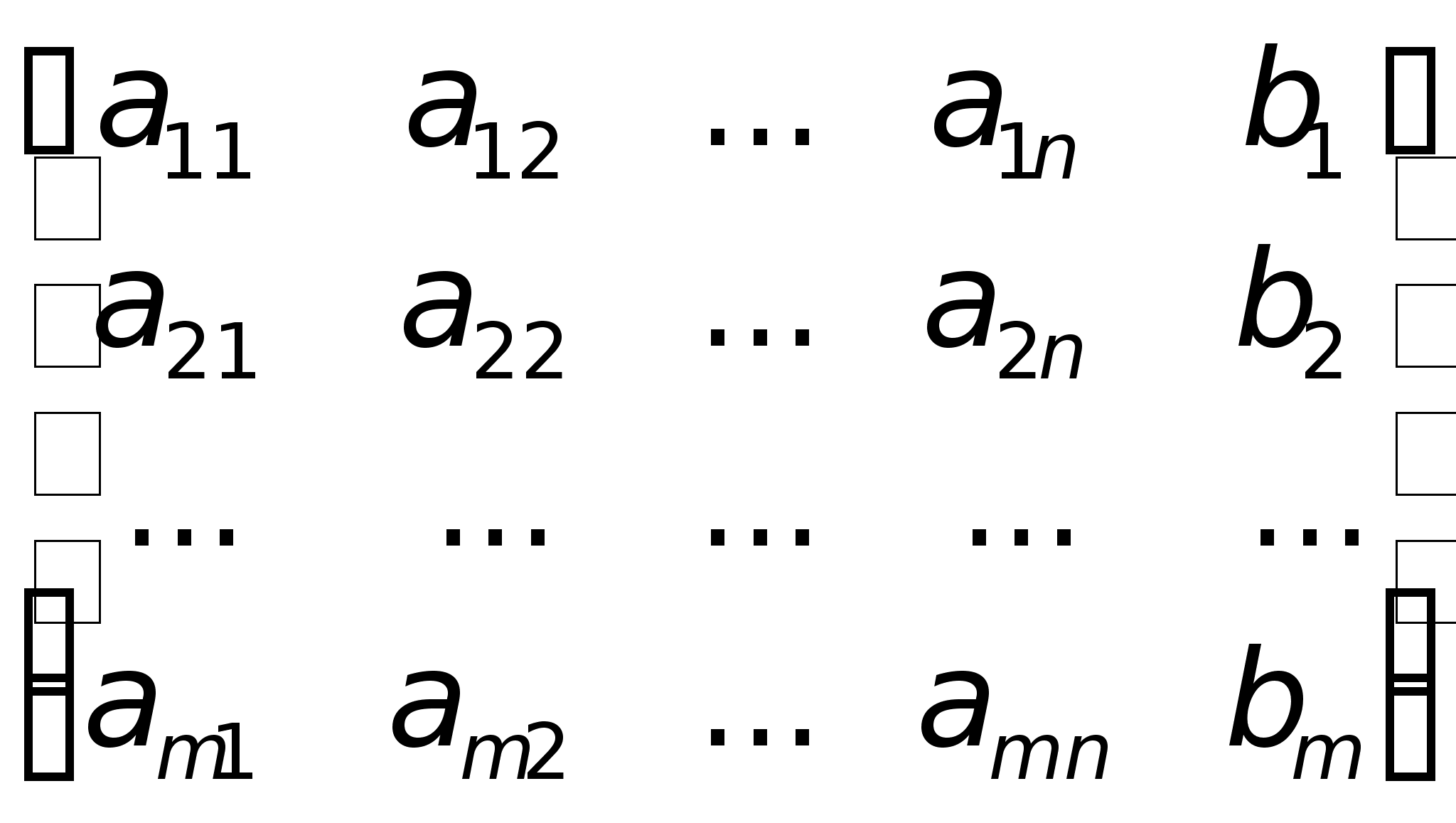 называется
расширенной
матрицей
системыОпределение.
Если b1,
b2,
…,bm
= 0, то система
называется
однородной.
однородная
система всегда
совместна,
т.к. всегда имеет
нулевое решение.
называется
расширенной
матрицей
системыОпределение.
Если b1,
b2,
…,bm
= 0, то система
называется
однородной.
однородная
система всегда
совместна,
т.к. всегда имеет
нулевое решение.