Курсовая работа: Проверка гипотезы о законе распределения генеральной совокупности X по критерию Пирсона
Федеральное агентство по образованию РФ
Сибирская государственная автомобильно-дорожная академия (СибАДИ)
Кафедра: «Высшая математика»
Хасянова А.Ф.
Проверил: Матвеева С.В
Дата_______________
Оценка_____________
Омск-2010
Содержание
1. Введение. Исходные данные
2. Вариационный ряд
3. Интервальный вариационный ряд
4. Построение гистограммы плотности относительных частот. Выдвижение гипотезы о законе распределения генеральной совокупности Х
5. Оценки числовых характеристик и параметров выдвинутого закона
6. Теоретическая функция плотности рассматриваемого закона распределения «Построение ее на гистограмме»
7. Проверка критерия Пирсона
Вывод
1. Исходные данные варианта №20
Дана выборка из генеральной совокупности случайной величины Х. Данные представлены в таблице 1.
Таблица 1
| 79,02 | 79,70 | 74,68 | 20,47 | 11,70 | 44,64 | 40,75 | 8,59 | 96,42 | 6,17 |
| 91,75 | 93,29 | 77,57 | 81,25 | 76,59 | 51,84 | 6,17 | 42,79 | 80,87 | 92,81 |
| 48,04 | 14,70 | 100,64 | 69,83 | 94,56 | 70,42 | 47,93 | 47,48 | 66,79 | 42,12 |
| 20,27 | 51,36 | 62,51 | 66,86 | 87,99 | 99,29 | 5,96 | 60,38 | 62,53 | 75,50 |
| 46,55 | 83,53 | 55,65 | 59,26 | 77,05 | 101,10 | 29,93 | 102,21 | 86,11 | 45,92 |
| 90,93 | 24,30 | 9,76 | 90,25 | 36,72 | 84,96 | 20,50 | 81,99 | 56,29 | 31,75 |
| 43,61 | 68,70 | 80,47 | 100,66 | 29,98 | 48,88 | 40,37 | 67,46 | 91,46 | 59,11 |
| 90,75 | 4,64 | 36,53 | 32,39 | 6,99 | 8,41 | 30,85 | 37,30 | 64,44 | 25,60 |
| 18,00 | 84,27 | 98,88 | 36,39 | 34,64 | 49,49 | 10,53 | 50,97 | 39,40 | 3,59 |
| 100,39 | 18,57 | 9,27 | 10,89 | 65,91 | 35,62 | 75,45 | 37,86 | 89,74 | 4,57 |
Выборка содержит 100 наблюдаемых значений, поэтому выборка имеет объем n=100.
2. Построение вариационного ряда
Операция расположения значений случайной величины по не убыванию называется ранжированием. Последовательность элементов х(1) ≤ х(2) ≤…≤ х(k) называется вариационным рядом, элементы которого называют вариантами.
Проранжировав статистические данные, получаем вариационный ряд (табл. 2).
Таблица 2
| 3,59 | 9,76 | 24,30 | 36,53 | 44,64 | 51,84 | 66,68 | 77,05 | 84,96 | 93,29 |
| 4,57 | 10,53 | 25,60 | 36,72 | 45,92 | 55,65 | 66,79 | 77,75 | 86,11 | 94,56 |
| 4,64 | 10,89 | 29,93 | 37,30 | 46,55 | 56,29 | 67,46 | 79,02 | 87,99 | 96,42 |
| 5,96 | 11,70 | 29,98 | 37,86 | 47,48 | 59,11 | 68,78 | 79,70 | 89,74 | 98,88 |
| 6,17 | 14,70 | 30,85 | 39,40 | 47,93 | 59,26 | 69,83 | 80,47 | 90,25 | 99,29 |
| 6,17 | 18,00 | 31,75 | 40,37 | 48,04 | 60,38 | 70,42 | 80,87 | 90,75 | 100,39 |
| 6,99 | 18,57 | 32,39 | 40,75 | 48,88 | 62,51 | 74,68 | 81,25 | 90,93 | 100,46 |
| 8,41 | 20,27 | 34,64 | 42,12 | 49,49 | 62,53 | 75,45 | 81,99 | 91,46 | 100,66 |
| 8,59 | 20,47 | 35,62 | 42,79 | 50,97 | 64,44 | 75,50 | 83,53 | 91,75 | 101,10 |
| 9,27 | 20,50 | 36,39 | 43,61 | 51,36 | 65,71 | 76,59 | 84,27 | 92,81 | 102,21 |
3. Построение интервального вариационного ряда
Опытные данные объединяем в группы так, чтобы в каждой отдельной группе значения вариант будут одинаковы, и тогда можно определить число, показывающее, сколько раз встречается соответствующая варианта в определенной (соответствующей) группе.
Численность отдельной
группы сгруппированного ряда опытных данных называется выборочной частотой
соответствующей варианты x(i) и обозначается mi; при этом 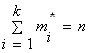 , где n – объем выборки.
, где n – объем выборки.
Отношение выборочной частоты данной варианты к объему выборки называется относительной выборочной частотой и обозначается Pi*,
т.е. 
![]() – число (частота) попаданий
значений X в i-й разряд,
– число (частота) попаданий
значений X в i-й разряд, ![]() n – объем выборки.
n – объем выборки.
Т.к. согласно теореме
Бернулли имеем, что ![]() т.е. выборочная относительная
частота сходится по вероятности соответствующей вероятности, тогда из условия:
т.е. выборочная относительная
частота сходится по вероятности соответствующей вероятности, тогда из условия: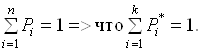
Интервальным вариационным рядом распределения называется упорядоченная совокупность частичных интервалов значений С.В. с соответствующими им частотами или относительными частотами.
Для построения интервального вариационного ряда выполняем следующие действия.
1. Находим размах выборки R = xmax – xmin. Имеем R = 102,21-3,59=98,62 .
2.
Определяем длину
частичного интервала ∆ – шаг разбиения по формуле Стерджеса: 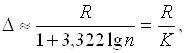 где n – объем выборки, К– число частичных
интервалов .
где n – объем выборки, К– число частичных
интервалов . ![]() ,
,
3.
∆=![]()
![]() 10
10
4.
Определяем начало
первого частичного интервала ![]()
После разбиения на частичные интервалы просматриваем ранжированную выборку и определяем, сколько значений признака попало в каждый частичный интервал, включая в него те значения, которые ≥ нижней границы и меньше верхней границы. Строим интервальный вариационный ряд (табл. 3).
Таблица 3
|
Разряды
|
mi |
|
|
|
|
| 1 | [3.5-13.5) | 14 | 0.14 | 0.014 | 8.5 |
| 2 | [13.5-23.5) | 6 | 0.06 | 0.006 | 18.5 |
| 3 | [23.5-33.5) | 7 | 0.07 | 0.007 | 28.5 |
| 4 | [33.5-43.5) | 12 | 0.12 | 0.012 | 38.5 |
| 5 | [43.5-53.5) | 12 | 0.12 | 0.012 | 48.5 |
| 6 | [53.5-63.5) | 7 | 0.07 | 0.007 | 58.5 |
| 7 | [63.5-73.5) | 8 | 0.08 | 0.008 | 68.5 |
| 8 | [73.5-83.5) | 12 | 0.12 | 0.012 | 78.5 |
| 9 | [83.5-93.5) | 13 | 0.13 | 0.013 | 88.5 |
| 10 | [93.5-103.5) | 9 | 0.09 | 0.009 | 98.5 |
| Контроль |
|
|
Где ![]() -плотность относительной
частоты
-плотность относительной
частоты
![]() -середина частичных интервалов
-середина частичных интервалов
4. Построение гистограммы
Гистограммой частот называют
ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат
частичные интервалы длины ![]() , а высоты равны отношению
, а высоты равны отношению ![]() – плотность
частоты (или
– плотность
частоты (или ![]() – плотность частности).
– плотность частности).
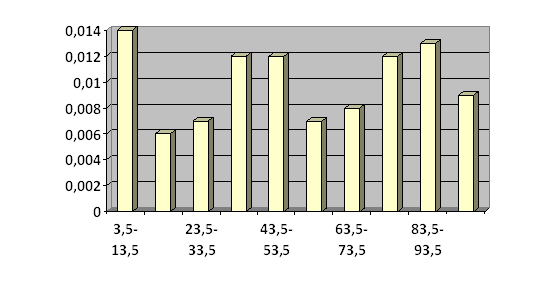
По данным таблицы 4 строим гистограмму (рис. 1).
Гистограмма частот является статистическим аналогом
дифференциальной функции распределения (плотности) 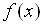 случайной величины Х. Площадь
гистограммы равна единице.
случайной величины Х. Площадь
гистограммы равна единице.
Выдвижение гипотезы о законе распределения генеральной совокупности
По данным наблюдений
статистическое среднее ![]() и выборочное среднее
квадратическое отклонение у* по значению почти совпадают. Учитывая данный факт,
а также вид гистограммы можно предположить, что случайная величина имеет
равномерное распределение.
и выборочное среднее
квадратическое отклонение у* по значению почти совпадают. Учитывая данный факт,
а также вид гистограммы можно предположить, что случайная величина имеет
равномерное распределение.
По виду гистограммы выдвигаем гипотезу о равномерном законе распределения генеральной совокупности Х.
5. Оценка числовых характеристик и параметров закона распределения
Оценками математической статистики называют приближенные значения числовых характеристик или параметров законов распределения генеральной совокупности Х вычисленные на основе выборки.
Оценка называется точечной, если она определяется числом или точкой на числовой оси.
Оценка (как точечная, так и интервальная) является случайной величиной, так как она вычисляется на основе экспериментальных данных и является функцией выборки.
При вычислении точечных оценок для удобства берут не сами элементы выборки, а середины частичных интервалов из интервального вариационного ряда (табл. 1) и применяют формулы:
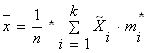
где n - объем выборки, ![]() – i-й элемент выборки
– i-й элемент выборки
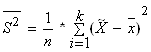
Составим таблицу для
нахождения ![]() и
и
![]()


Таблица 4
| i |
|
|
| 1 |
|
8.5*14=119 |
| 2 |
|
18.5*6=111 |
| 3 |
|
28.5*7=199.5 |
| 4 |
|
38.5*12=462 |
| 5 |
|
48.5*12=582 |
| 6 |
|
58.5*7=409.5 |
| 7 |
|
68.5*8=548 |
| 8 |
|
78.5*12=942 |
| 9 |
|
88.5*13=1150.5 |
| 10 |
|
98.5*9=886.5 |
|
|
|
6. Равномерный закон
интервальный вариационный генеральный совокупность
Выдвинута гипотеза о распределении генеральной совокупности Х по равномерному закону
найдем функцию плотности
равномерного закона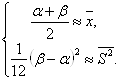 вычислив оценки параметров
вычислив оценки параметров ![]() и
и ![]()

![]() ,
, ![]()
Т.к М(x)= ![]() ,
, ![]() , D(x)=
, D(x)=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таблица 5
| i |
|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
|
|
После того, как найдены значения функции плотности для каждого разряда, нанесем их прямо на гистограмму, получая тем самым кривую функции плотности
7 Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона
В качестве меры расхождения между статистическим и гипотетическим (теоретическим) распределениями возьмем критерий Пирсона К = ч2.
Пирсон
доказал, что значение статистического критерия не зависит от функции ![]() и от числа
опытов n, а зависит от числа частичных интервалов
и от числа
опытов n, а зависит от числа частичных интервалов ![]() интервального
вариационного ряда. При увеличении ч2, и находится по формуле:
интервального
вариационного ряда. При увеличении ч2, и находится по формуле:
К =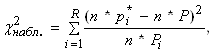 или К =
или К =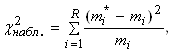
Дальнейшие
вычисления, необходимые для определения расчетного значения выборочной
статистики ![]() ,
проведем в таблице 5.
,
проведем в таблице 5.
Таблица 6
| i |
|
|
|
|
|
|
| 1 | 0.14 | 14 | 0.1029 | 10.29 |
|
13.76/10.37=1.33 |
| 2 | 0.06 | 6 | 0.1 | 10 |
|
16/10=1.6 |
| 3 | 0.07 | 7 | 0.1 | 10 |
|
16/10=1.6 |
| 4 | 0.12 | 12 | 0.1 | 10 |
|
16/10=1.6 |
| 5 | 0.12 | 12 | 0.1 | 10 |
|
16/10=1.6 |
| 6 | 0.07 | 7 | 0.1 | 10 |
|
16/10=1.6 |
| 7 | 0.08 | 8 | 0.1 | 10 |
|
16/10=1.6 |
| 8 | 0.12 | 12 | 0.1 | 10 |
|
16/10=1.6 |
| 9 | 0.13 | 13 | 0.1 | 10 |
|
16/10=1.6 |
| 10 | 0.09 | 9 | 0.1149 | 11.49 |
|
6.3/11.49=0.548 |
|
|
|
|
|
Чтобы найти значение ![]() надо
воспользоваться табличными распределениями
надо
воспользоваться табличными распределениями ![]() в которых значение сл. величины находят по заданному
уровню значимости
в которых значение сл. величины находят по заданному
уровню значимости ![]() и вычисленному числу степеней
свободы
и вычисленному числу степеней
свободы ![]()
![]()
R- число частичных интервалов в
таблице 1 но если в некоторых из интервалов значения ![]() то надо объединить расположенные
рядом интервалы так, чтобы
то надо объединить расположенные
рядом интервалы так, чтобы ![]() тогда число
тогда число
R-это число из необъединенных интервалов
i- число неизвестных параметров
В
рассматриваемом эмпирическом распределении не имеются частоты, меньшие 5. Случайная
величина ч2 (мера расхождения) независимо от вида закона распределения
генеральной совокупности при (n ≥
50) имеет распределение ч2 с числом степеней свободы ![]()
1) К =
![]()
уровень
значимости б =1–![]() =0,05
=0,05
![]() ,
, ![]()
найдем по
таблице значений ![]() критическое значение для б = 0,05
и
критическое значение для б = 0,05
и ![]() =9
=9
Имеем ![]() =16.9. Так как
=16.9. Так как ![]()
![]() то предполагаемая
гипотеза о показательном законе распределения генеральной совокупности не
противоречит опытным данным и принимается на уровне значимости б.
то предполагаемая
гипотеза о показательном законе распределения генеральной совокупности не
противоречит опытным данным и принимается на уровне значимости б.
2)![]() =
=![]() ,
,
![]()
![]() =
=![]()
3) M(x)= ![]() ,
,
M(x)= ![]()
4) D(x)=![]()
![]()
![]()
D(x.1)= ![]()
5) Таким
образом, критическая область для гипотезы задается неравенством ![]() ; P(
; P(![]() )=
)=![]() Это означает,
что нулевую гипотезу можно считать правдоподобной и гипотеза Но принимается
Это означает,
что нулевую гипотезу можно считать правдоподобной и гипотеза Но принимается
Вывод: В ходе расчетно-графической работы мы установили, что генеральная совокупность X распределена по равномерному закону, проверив это по критерию Пирсона. Определили параметры и числовые характеристики закона и построили для них доверительные интервалы.
| Серьёзные лекции по высшей экономической математике | |
|
Комбинаторные задачи. 1.Сколькими способами колода в 52 карты может быть роздана 13-ти игрокам так, чтобы каждый игрок получил по одной карте каждой ... Если промежуток между наименьшим и наибольшим значениями признака в выборке разбить на несколько интервалов одинаковой длины, каждому интервалу поставить в соответствие число ... Для доказательства несмещённости некоторых точечных оценок будем рассматривать выборку объема n как систему n независимых случайных величин x1, x2,... xn , каждая из которых имеет ... |
Раздел: Рефераты по математике Тип: реферат |
| Основные понятия статистики | |
|
ТЕМА 1.4. Законы распределения случайных величин, наиболее часто используемые в экономических приложениях, и их числовые характеристики 1. Основные ... Графическое представление интервального вариационного ряда в виде прямоугольников, с основаниями, равными длине интервалов и с высотой, равной соответствующей относительной частоте ... В качестве критической области примем интервал .Определив по данным выборки, мы получим одно из двух: или (т.е. выборочное значение критерия попадает в критическую область и тогда ... |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Трансформации социально-экономических систем в КНР и Венгрии | |
|
Санкт-Петербургский государственный политехнический университет Институт интеллектуальных систем и технологий Кафедра Мировой экономики Курсовой ... определяется вероятность, которую примет статистика критерия (см. этап b) при выполнении нулевой гипотезы, а для альтернативной гипотезы определяется критическое значение ... Все значения данного показателя принадлежат отрезку [-4422,6, 58893,5]. Разобьем отрезок [-4422,6, 58893,5] на семь интервалов [(-4422,6 - 4622,58); (4622,59 - 13667,7); (13667,8 ... |
Раздел: Рефераты по международным отношениям Тип: реферат |
| Комплексная статистическая обработка экспериментальных данных | |
|
Министерство образования и науки Украины Пояснительная записка к курсовой работе по дисциплине Статистика Комплексная статистическая обработка ... г) вычислить и проанализировать точечные оценки и для простого и интервального рядов; построить и проанализировать зависимость величины точечной оценки от объема выборки и от ... и) по виду гистограмм выдвинуть гипотезу о предполагаемых законах распределений исследуемых случайных величин, определить оценки параметров предполагаемых распределений (метод ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Анализ и обобщение статистических данных экономики Республики Калмыкия | |
|
СОДЕРЖАНИЕ СОДЕРЖАНИЕ 1. ИСХОДНЫЕ ДАННЫЕ 2. КРАТКАЯ ХАРАКТЕРИСТИКА РЕСПУБЛИКИ КАЛМЫКИЯ 3. ПОСТРОЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ 3.1 ПОСТРОЕНИЕ С ПОМОЩЬЮ ... Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
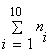 =100
=100