Курсовая работа: Исследование точности численного дифференцирования
Курсовая работа
"Исследование точности численного дифференцирования"
Екатеринбург 2009 г.
1. Подробное описание задачи и метод ее решения
Исследуйте два метода численного дифференцирования:
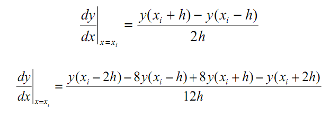
где xi – узел равномерной сетки с шагом h.
Предполагается, что отрезок дифференцирования [a, b] разбит на n равных частей системой точек (сеткой)
![]()
Исследование проведите на примерах:
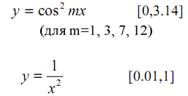
Относительную погрешность определяйте относительно максимального значения функции на интервале, абсолютную погрешность рассчитайте относительно значений аналитически вычисленной производной.
Численное дифференцирование применяется, если функцию y(x) трудно или невозможно продифференцировать аналитически – например, если она задана таблицей. Оно нужно также при решении дифференциальных уравнений при помощи разностных методов.
При численном дифференцировании функцию y(x) аппроксимируют легко вычисляемой функцией. При этом можно использовать различные способы аппроксимации. Задание требует исследовать 2 метода. Оба метода можно применять для всех функций, приведенных в задании, исходя из области определения этих функций.
На самом деле, метод решения данной задачи довольно тривиален, так как все формулы приведены в условии задачи.
Входные данные: номер функции, номер метода, точность (шаг), левое значение, правое значение. Для функции у=cos2mx нужно выбрать параметр m из предложенных.
Выходные данные: аргумент, значение функции при заданном параметре, значение первой производной, абсолютная погрешность, относительная погрешность.
1) y=cos2mx, для m=1 [0, 3.14]
выберем шаг=0,3 и интервал [0,3.14]
Метод 1
| параметр | значение функции |
значение производной |
абсолютная погрешность | относительная погрешность |
| 0 | 1 | 0 | 0 | 0 |
| 0,3 | 0,912668 | -0,531369 | 0,0596719 | 0,59104 |
| 0,6 | 0,681179 | -0,877115 | 0,25217 | 1,12928 |
| 0,9 | 0,386399 | -0,91646 | 0,650194 | 1,56665 |
| 1,2 | 0,131303 | -0,635659 | 1,22842 | 1,86408 |
| 1,5 | 0,00500375 | -0,132804 | 1,86219 | 1,99499 |
| 1,8 | 0,0516208 | 0,416443 | 2,36414 | 1,9477 |
| 2,1 | 0,25487 | 0,820214 | 2,54663 | 1,72642 |
| 2,4 | 0,543749 | 0,937461 | 2,28839 | 1,35093 |
| 2,7 | 0,817346 | 0,727226 | 1,58199 | 0,85476 |
| 3 | 0,980085 | 0,26295 | 0,54519 | 0,28224 |
Метод 2
| параметр | значение функции |
значение производной |
абсолютная погрешность | относительная погрешность |
| 0 | 1 | 0 | 0 | 0 |
| 0,3 | 0,912668 | -0,562306 | 0,0287348 | 0,59104 |
| 0,6 | 0,681179 | -0,928182 | 0,201103 | 1,12928 |
| 0,9 | 0,386399 | -0,969817 | 0,596837 | 1,56665 |
| 1,2 | 0,131303 | -0,672668 | 1,19141 | 1,86408 |
| 1,5 | 0,00500375 | -0,140536 | 1,85445 | 1,99499 |
| 1,8 | 0,0516208 | 0,440689 | 2,38838 | 1,9477 |
| 2,1 | 0,25487 | 0,867969 | 2,59439 | 1,72642 |
| 2,4 | 0,543749 | 0,992042 | 2,34297 | 1,35093 |
| 2,7 | 0,817346 | 0,769566 | 1,62433 | 0,85476 |
| 3 | 0,980085 | 0,278259 | 0,560499 | 0,28224 |
Графики
Для первого графика выберем шаг = 0,05, для большей точности построения
численный дифференцирование абсолютный погрешность
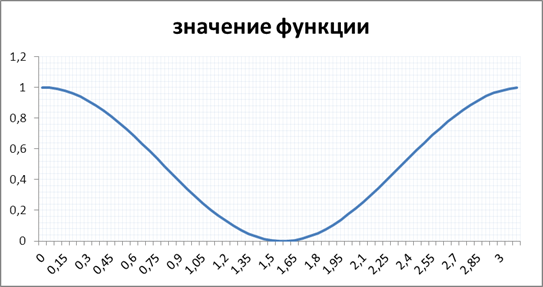
Рисунок 1. Значение функции y=cos2mx при m=1
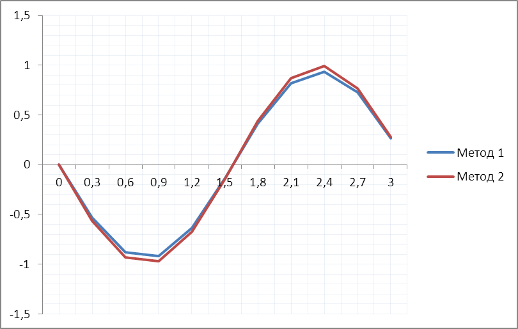
Рисунок 2. Значение первой производной функции y=cos2mx при m=1
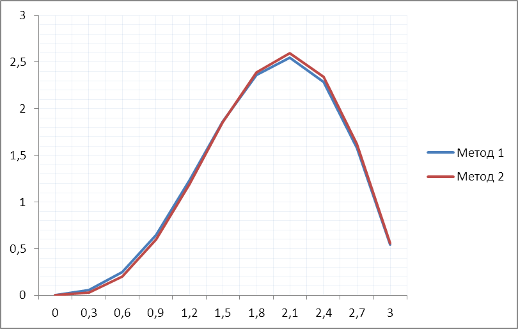
Рисунок 3. Абсолютная погрешность функции y=cos2mx при m=1
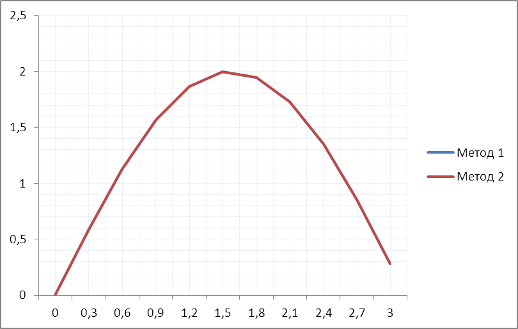
Рисунок 4. Относительная погрешность функции y=cos2mx при m=1
2) y=cos2mx, для m=12 [0, 3.14]
выберем шаг=0,3 и интервал [0,3.14]
Метод 1
| параметр | значение функции |
значение производной |
абсолютная погрешность | относительная погрешность |
| 0 | 1 | 0 | 0 | 0 |
| 0,3 | 0,804176 | -1,04985 | 1,93489 | 0,885041 |
| 0,6 | 0,370091 | -1,27735 | 0,309983 | 1,58734 |
| 0,9 | 0,037764 | -0,50431 | 2,46618 | 1,96187 |
| 1,2 | 0,067505 | 0,663757 | 2,59507 | 1,93132 |
| 1,5 | 0,436018 | 1,31191 | 0,190069 | 1,50197 |
| 1,8 | 0,854648 | 0,932442 | 1,69494 | 0,762501 |
| 2,1 | 0,995483 | -0,177401 | 0,0429848 | 0,134416 |
| 2,4 | 0,748207 | -1,14829 | 2,15186 | 1,00358 |
| 2,7 | 0,306512 | -1,21972 | 0,445798 | 1,66552 |
| 3 | 0,016375 | -0,335752 | 2,31931 | 1,98356 |
Метод 2
| параметр | значение функции |
значение производной |
абсолютная погрешность | относительная погрешность |
| 0 | 1 | 0 | 0 | 0 |
| 0,3 | 0,804176 | -1,04985 | 1,93489 | 0,885041 |
| 0,6 | 0,370091 | -1,27735 | 0,309983 | 1,58734 |
| 0,9 | 0,037764 | -0,50431 | 2,46618 | 1,96187 |
| 1,2 | 0,067505 | 0,663757 | 2,59507 | 1,93132 |
| 1,5 | 0,436018 | 1,31191 | 0,190069 | 1,50197 |
| 1,8 | 0,854648 | 0,932442 | 1,69494 | 0,762501 |
| 2,1 | 0,995483 | -0,177401 | 0,0429848 | 0,134416 |
| 2,4 | 0,748207 | -1,14829 | 2,15186 | 1,00358 |
| 2,7 | 0,306512 | -1,21972 | 0,445798 | 1,66552 |
| 3 | 0,016375 | -0,335752 | 2,31931 | 1,98356 |
Графики
Для первых двух графиков выберем шаг = 0,05
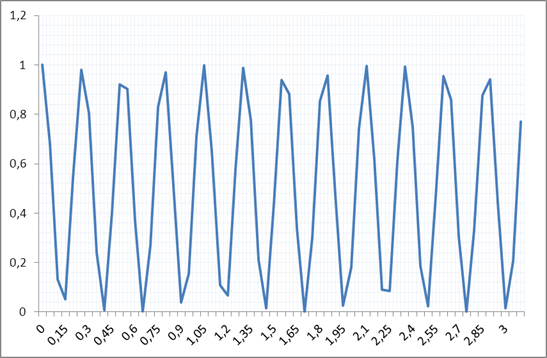
Рисунок 5. Значение функции y=cos2mx при m=12
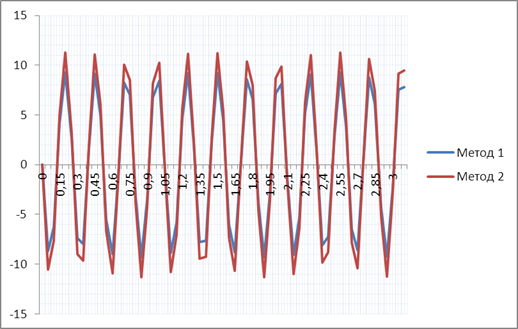
Рисунок 6. Значение первой производной функции y=cos2mx при m=12
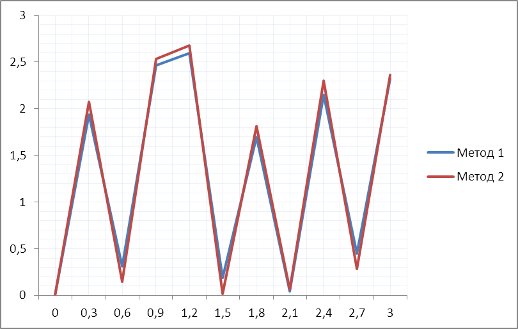
Рисунок 7. Абсолютная погрешность функции y=cos2mx при m=12
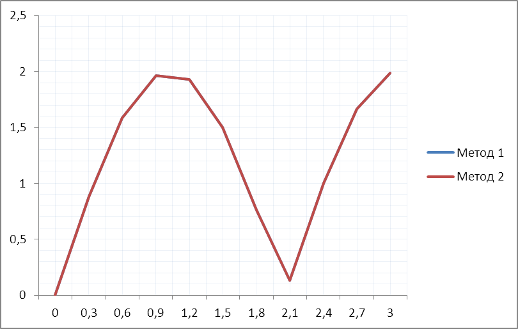
Рисунок 8. Относительная погрешность функции y=cos2mx при m=12
3)
y=![]() [0.
01,1]
[0.
01,1]
выберем шаг=0,05 на интервале [0. 5,1], графики при этих данных наиболее наглядные данные.
Метод 1
| параметр | значение функции |
значение производной |
абсолютная погрешность | относительная погрешность |
| 0,5 | 4 | -16,3249 | 0,324865 | 4 |
| 0,55 | 3,30579 | -12,2222 | 0,201185 | 3,00526 |
| 0,6 | 2,77778 | -9,38921 | 0,129953 | 2,31481 |
| 0,65 | 2,36686 | -7,36961 | 0,0869563 | 1,82066 |
| 0,7 | 2,04082 | -5,89086 | 0,0599575 | 1,45773 |
| 0,75 | 1,77778 | -4,78316 | 0,0424225 | 1,18519 |
| 0,8 | 1360531 | -3,93695 | 0,0306973 | 0,976562 |
| 0,85 | 1,38408 | -3,27932 | 0,022655 | 0,814166 |
| 0,9 | 1,23457 | -2,7605 | 0,0170138 | 0,685871 |
| 0,95 | 1,10803 | -2,34568 | 0,0129775 | 0,583175 |
| 1 | 1 | -2,01004 | 0,0100376 | 0,5 |
Метод 2
| параметр | значение функции | производная | абсолютная | относительная |
| 0,5 | 4 | -15,9794 | 0,0205506 | 4 |
| 0,55 | 3,30579 | -12,0106 | 0,01042 | 3,00526 |
| 0,6 | 2,77778 | -9,25364 | 0,0056158 | 2,31481 |
| 0,65 | 2,36686 | -7,27947 | 0,0031844 | 1,82066 |
| 0,7 | 2,04082 | -5,82902 | 0,00188505 | 1,45773 |
| 0,75 | 1,77778 | -4,73958 | 0,00115782 | 1,18519 |
| 0,8 | 1360531 | -3,90552 | 0,000734272 | 0,976562 |
| 0,85 | 1,38408 | -3,25619 | 0,000478899 | 0,814166 |
| 0,9 | 1,23457 | -2,74316 | 0,000320172 | 0,685871 |
| 0,95 | 1,10803 | -2,33248 | 0,000218821 | 0,583175 |
| 1 | 1 | -1,99985 | 0,000152533 | 0,5 |
В конце работы программы получен текстовый файл, содержащий аргумент функции, значение функции, значение первой производной, абсолютную и относительную погрешность. По этим данным построены графики зависимости аргумента от значения функции, производной, абсолютной и относительной погрешности. Каждый график содержит кривые, полученные вычислениями двумя различными методами, графики примерно совпадают, но все же есть некоторые погрешности.
Приложение
Описание применения
Техническое задание
Исследуйте два метода численного дифференцирования:
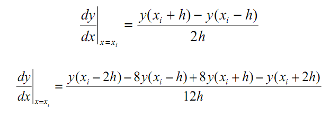
где xi – узел равномерной сетки с шагом h.
Предполагается, что отрезок дифференцирования [a, b] разбит на n равных частей системой точек (сеткой)
![]()
Исследование проведите на примерах:
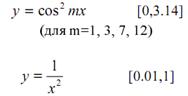
Относительную погрешность определяйте относительно максимального значения функции на интервале, абсолютную погрешность рассчитайте относительно значений аналитически вычисленной производной. Данная программа предназначена для исследования метода численного дифференцирования двумя способами.
Программа была отлажена и проверена на вычислительной установке PC c процессором AMD Turion(tm) X2 Dual Core Mobile RM-76 2.30 Гц, работающей под управлением операционной системы Windows 7 Ultimate, ОЗУ 4 Гб. На других вычислительных установках программа не проверялась.
Для выполнения программы выбрана вычислительная установка типа PC с процессором Pentium III (или быстрее) и 256 Мбайт оперативной памяти, оснащенной любой из следующих операционных систем: Windows NT и выше.
Для компиляции исходного кода в исполняемый файл необходим компилятор MS Visual Studio версии 2005 и выше, совместимость с другими компиляторами не гарантируется.
Программа derivation предназначена для исследования метода численного дифференцирования двумя способами.
Данная программа написана на языке С++, реализована в компиляторе Microsoft Visual Studio 2005.
Для выполнения программы достаточно вычислительной установки типа PC с процессором Pentium III (или быстрее) и 256 Мбайт оперативной памяти, оснащенной любой из следующих операционных систем: Windows NT и выше.
Программа derivation предназначена для исследования метода численного дифференцирования двумя способами.
Численное дифференцирование применяется, если функцию y(x) трудно или невозможно продифференцировать аналитически – например, если она задана таблицей. Оно нужно также при решении дифференциальных уравнений при помощи разностных методов.
Программа состоит из нескольких функций, рассмотрим их подробнее.
Описание функции first_function
Данная функция вычисляет значение y=cos2mx и возвращает.
Описание функции first_derivation_real
Данная функция вычисляет аналитическое значение производной первой функции.
Описание функции Rus
Данная функция предназначена для русификации программы
Описание функции second_function
Данная функция вычисляет значение y=![]()
Описание функции second_derivation_real
Данная функция вычисляет аналитическое значение производной второй функции.
Описание функции first_derivation
Данная функция производит дифференцирование первым способом
Описание функции second_derivation
Данная функция производит дифференцирование вторым способом
pFunc func – указатель на функци., которую надо продифферинцировать
Описание функции WriteToFile
Данная функция записывает полученные значения в файл и вывод в консоли
Описание функции compute_derivation
Данная функция вычисляет производную
Описание функции _finite
Данная функция проверяет на конечность число.
Описание функции main
Данная функция служит для ввода исходных данных, объединения всех предыдущих функций, вычисления абсолютных и относительных погрешностей.
Используемые технические средства
Для выполнения программы достаточно вычислительной установки типа PC с процессором Pentium III (или быстрее) и 256 Мбайт оперативной памяти, оснащенной любой из следующих операционных систем: Windows NT и выше.
Вызов и загрузка
Для запуска программы derivation необходимо открыть директорию, в которой находится программа, и использовать (двойной или одиночный клик, в зависимости от настроек ОС) для запуска файл derivation.exe. После чего должна запуститься данная программа.
Текст программы#include «main.h»
using namespace std;
char bufRus[256];
// файл для записи
ofstream *_out;
// Перевод в юникод
char* Rus (const char* text)
{
CharToOem (text, bufRus);
return bufRus;
}
// параметр m для первой функции
int param4func = 1;
// первая функция
double first_function (double x)
{
//cos^2 (m*x)
return cos (param4func*x)*cos (param4func*x);
}
// аналитическое значение производной первой функции
double first_derivation_real (double x)
{ // -2 * sin (m*x)
return -2 * sin (param4func*x);
}
// вторая функция
double second_function (double x)
{
// 1/x^2
return 1/(x*x);
}
// аналитическое значение производной второй функции
double second_derivation_real (double x)
{ // -2 * 1/x^3
return -2 * 1/(x*x*x);
}
| Кинематический анализ механизма транспортирования ткани | |
|
Кинематический анализ механизма верхней и нижней реек швейной машины 131-42+3 класса. Реферат Отчет с., 1 ч., 46 рис., 3 табл., 88 источников, 1 прил ... ... задачи решаются для каждой рейки в отдельности и, кроме того, определяются: степень дифференцирования подачи m (отношение шага транспортирования дополнительной рейки к шагу ... В ходе кинематического анализа указанных кинематических цепей необходимо определить угол координаты , i= 1.2, определить координаты x , y , x ,y , x , y точек E, M и Q ... |
Раздел: Рефераты по технологии Тип: реферат |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Вычислить производную функции y=(3x3-2x+1)=sin x. По правилу дифференцирования сложной функции, получим: y'x =y 'u u'x =()'u(x4 +1)'x =(2u + |
Раздел: Рефераты по математике Тип: дипломная работа |
| Производная и ее применение в алгебре, геометрии, физике | |
|
Гимназия №1 города Полярные Зори Алгебра, геометрия, физика. Научная работа ТЕМА "ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ В АЛГЕБРЕ, ГЕОМЕТРИИ, ФИЗИКЕ ... Для функции у=x2 при изменении х от 3 до 3,1 приращение =y = 2x*=x + + =x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy = 2х *=x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное ... Задача 4. Какая наименьшая плоскость может быть у треугольника OAB, если его стороны OA и OB лежат на графике функции y = (|x|-x)/2, а прямая AB проходит через точку M(0;1). |
Раздел: Рефераты по математике Тип: реферат |
| Вычислительная математика | |
|
Содержание Введение Тема 1. Решение задач вычислительными методами. Основные понятия 1.1 Погрешность 1.2 Корректность 1.3 Вычислительные методы Тема 2 ... Возьмем, например, f*(x) = f(x) + a sin(x/a2), где 0 < a < 1. Тогда, u*(x) = u(x) + a-1cos(x/a2), D(u*) = a-1, т. е. погрешность задания функции равна a, а погрешность производной ... Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции f(t, y(t)). Грубую оценку погрешности дает правило Рунге (правило ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... Пусть X,Y,Z-линеиные пространства размерностью m, r, n и пусть у=Вх, z=Ау - линейные преобразования пространства Х в пространство Y, и пространства Y в пространство Z, где В=[вkj ... где x(n)(t) и x(m)(t)- соответственно n-я и m-я производные в среднем квадратичном случайной функции Х(t). |
Раздел: Рефераты по математике Тип: реферат |