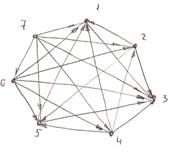
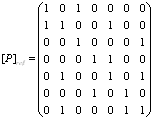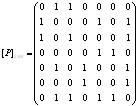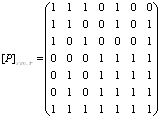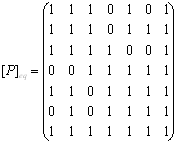Контрольная работа: Булевы функции и теория графов
Задание
Дано:
·
Универсум ![]()
·
Множества ![]() ,
, ![]() ,
, ![]()
· Бинарные отношения
·
Функция ![]()
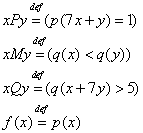
Требуется:
1. Найти
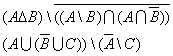
2. Решить уравнение ![]()
3. Построить графы и матрицы отношений P и Q, указать ![]() ,
, ![]() ,
, ![]()
4. Исследовать отношение Р на наличие стандартных свойств (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность).
5. Построить граф и матрицу отношения ![]() ,
указать
,
указать ![]() ,
, ![]() .
.
6. Построить граф и матрицу отношения ![]() ,
указать
,
указать ![]() ,
, ![]() .
.
7. Построить графы и матрицы замыканий отношения Р:
![]() . Для каждого из замыканий
указать
. Для каждого из замыканий
указать ![]() и
и![]() .
.
8. Найти![]() , построить
естественную проекцию
, построить
естественную проекцию ![]() :
:![]() .
.
9. Построить таблицу значений, граф и матрицу функции f. Указать ![]() .
.
10. Построить граф и матрицу отношения ![]() .
.
11. Найти ![]() , построить
индуцированное отображение
, построить
индуцированное отображение ![]() :
: ![]() .
.
12. Построить граф и матрицу отношения М. Указать ![]() ,
, ![]() .
.
13. Доказать, что отношение М есть отношение строгого порядка в А.
14. Исследовать М на линейность (полноту).
15. Интерпретируя отношение М как «меньше», найти в множестве А относительно М минимальные и максимальные, наименьшие и наибольшие элементы (если таковые существуют).
Решение
1. Найти
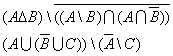


2. Решить уравнение ![]()
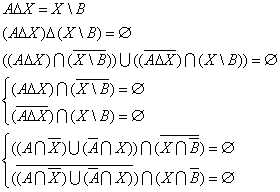

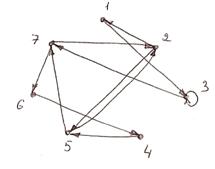
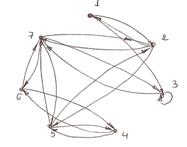
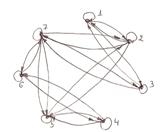
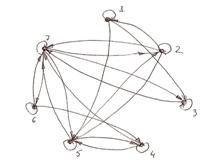
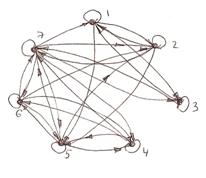
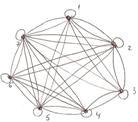
3. Построить графы и матрицы отношений P и Q, указать ![]() ,
, ![]() ,
, ![]()
рефлексивность симметричность граф матрица
|
|
|
|
|
|

4. Исследовать отношение Р на наличие стандартных свойств (рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность).
По матрице отношения Р определяем его свойства:
1. Не рефлексивно, т.к. на главной диагонали имеются нули.
2. Не антисимметрично, т.к. на главной диагонали имеются единицы.
3. Не симметрично
4. Не антисимметрично
5. Для определения является ли отношение транзитивным, возведем его матрицу в квадрат:

По полученной матрице видно, что отношение Р не транзитивно.
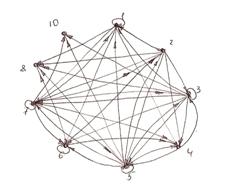
5. Построить граф и матрицу отношения ![]() ,
указать
,
указать ![]() ,
, ![]() .
.

![]()
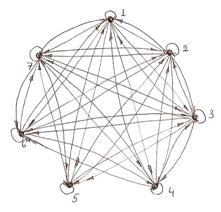
6. Построить граф и матрицу отношения ![]() ,
указать
,
указать ![]() ,
, ![]() .
.

![]()
7. Построить графы и матрицы замыканий отношения Р: ![]() . Для каждого из замыканий
указать
. Для каждого из замыканий
указать ![]() и
и![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Найти![]() , построить
естественную проекцию
, построить
естественную проекцию ![]() :
:![]() .
.
![]()

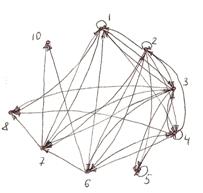
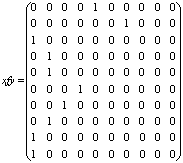
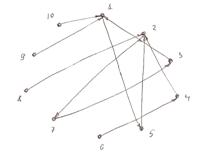
9. Построить таблицу значений, граф и матрицу функции f. Указать ![]() .
.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f(x) | 5 | 7 | 1 | 2 | 2 | 4 | 3 | 2 | 1 | 1 |
|
|
|
![]()
10. Построить граф и матрицу отношения ![]() .
.
![]() или в матричной форме
или в матричной форме ![]()
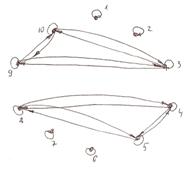

11. Найти ![]() , построить
индуцированное отображение
, построить
индуцированное отображение ![]() :
: ![]() .
.
![]()
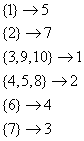
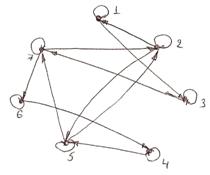
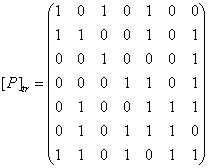
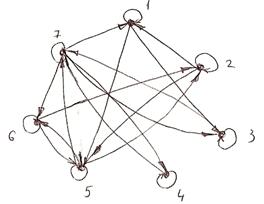
12. Построить граф и матрицу отношения М. Указать ![]() ,
, ![]() .
.
|
|
|
![]()
13. Доказать, что отношение М есть отношение строгого порядка в А.
Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно. По матрице отношении М:
1. Отношение антирефлексивно, т.к. на главной диагонали нет 1.
2. Отношение антисимметрично, т. к. при aRb и bRa a=b.
3. Для проверки на транзитивность возведем матрицу отношения в квадрат:
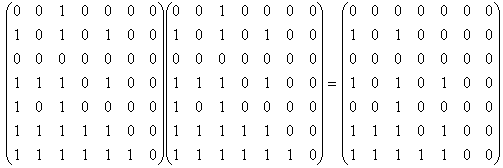
Сравнивая полученную матрицу с исходной видим, что отношение транзитивно.
Следовательно, отношение М является отношением строгого порядка.
14. Исследовать М на линейность (полноту).
Рассмотрим отношения связности:

На основе этого строим ранжированный граф:
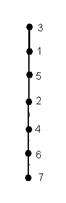
Граф представляет собой прямую линию, т.е. в нем нет параллельных вершин, следовательно, отношение М линейно.
15. Интерпретируя отношение М как «меньше», найти в множестве А относительно М минимальные и максимальные, наименьшие и наибольшие элементы (если таковые существуют).
Рассмотрим ранжированный граф.
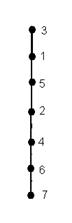
В графе нет параллельных вершин, поэтому минимальный элемент является наименьшим, а максимальный – наибольшим. Наименьший элемент – 3, наибольший элемент – 7.
| Эйлеровы и гамильтоновы графы | |
|
Министерство народного образования Республики Дагестан Дагестанский Государственный Университет Курсовая работа Программирование задач на графах ... 8. В эту матрицу нужно поставить запрет в клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е. [3,1,2] и нужно запретить преждевременное замыкание (2,3 ... В матрицу надо добавить запрет в клетку (5,3), ибо уже построен фрагмент тура [3,1,2,6,5] и надо запретить преждевременный возврат (5,3). Теперь, когда осталась матрица 2х2 с ... |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Нахождение кратчайшего пути | |
|
... заочного и послевузовского обучения Курсовой проект По дисциплине: "Технология программирования" Тема: "Определение кратчайшего пути в графе" Воронеж ... Например, наименьшее число вершин, разделяющих две несмежные вершины графа, равно наибольшему числу непересекающихся (по вершинам) простых цепей, соединяющих эту пару вершин. Найдены критерии и построены эффективные алгоритмы установления меры связности графа (наименьшего числа вершин или ребер, удаление которых нарушает связность графа). |
Раздел: Рефераты по информатике, программированию Тип: реферат |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Матрица размера m`n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной ... Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Графы. Решение практических задач с использованием графов (С++ | |
|
Курсовая работа Выполнил: студент 1-го курса факультета КНиИТ, группа № 121, Жучков Андрей Сергеевич Саратовский государственный университет им. Н.Г ... Радиусом графа G называется наименьший из эксцентриситетов вершин. Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю (или нижнюю) треугольную матрицу. |
Раздел: Рефераты по математике Тип: реферат |
| СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ | |
|
... факультет Кафедра прикладной математики ДИПЛОМНЫЙ ПРОЕКТ сингулярное разложение в линейной задаче метода наименьших квадратов Заведующий ... Требуется найти симметричную матрицу Т, размерности pxp, с неотрицательными собственным значениями заданного ранга k, k, являющуюся наилучшей аппроксимацией матрицы S в смысле ... Существует ортогональная m m-матрица Q такая, что в матрице QA=R под главной диагональю стоят только нулевые элементы. |
Раздел: Рефераты по математике Тип: реферат |