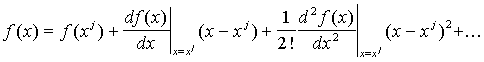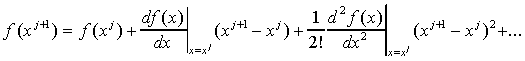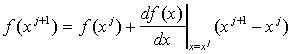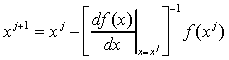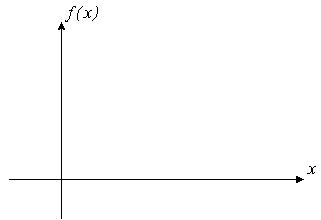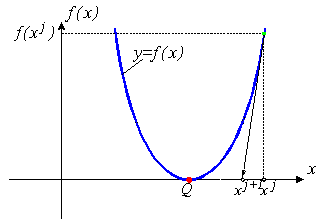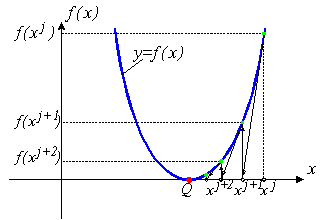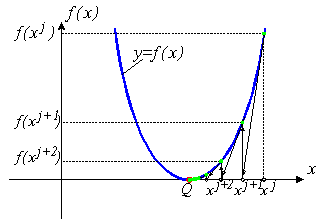Доклад: Метод решения уравнений Ньютона - Рафсона
Метод Ньютона-Рафсона, также известный как Метод Ньютона, представляет собой обобщенный метод поиска корня уравнения
|
|
(1) |
Примем x = xj в качестве j-го приближения к
корню уравнения (1). Предположим, что xj не является решением.
Следовательно,
. Предположим также, что мы получили разложение в ряд Тейлора для уравнения (1)
относительно точки x = xj:
|
|
(2) |
Если примем в качестве следующего члена x = xj+1, то уравнение (2) будет иметь вид:
|
|
(3) |
Теперь предположим, что справедливо необязательное допущение того, что предыдущее приближение xj было удовлетворительным, так что xj+1 - xj мало. Если это предположение верно, мы можем пренебречь членами более высокого порядка в уравнении (3), так как n-я степень малой величины значительно меньше, чем малая величина для n>=2. В этом случае уравнение (3) может быть аппроксимировано следующим образом:
|
|
(4) |
Нашей целью является выбор такого xj+1,
чтобы оно стало решением уравнения (1). Следовательно, если наше предыдущее
предположение справедливо, xj+1 должно быть выбрано таким, что
. Приравняв
уравнение (4) к нулю и решив относительно xj+1, получим:
|
|
(5) |
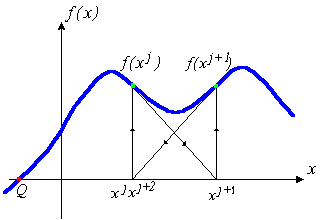
Уравнение (5) называется уравнением Ньютона - Рафсона. Если наше предположение, приведшее к выводу уравнения (5), справедливо, этот алгоритм будет сходящимся, но только в том случае, если точка начального приближения достаточно близка к точке решения. Геометрическая интерпретация сходящегося метода Ньютона - Рафсона приведена на рис. 1а.
|
|
|
| а) метод сходится | б) метод не сходится |
Рис.1. Геометрическая интерпретация метода Ньютона - Рафсона
Однако, если точка начального приближения далека от точки решения, то метод Ньютона - Рафсона может не сходиться совсем. Геометрическая интерпретация не сходящегося метода Ньютона - Рафсона приведена на рис. 1б.
Алгоритм
Назначение: поиск решения уравнения (1)
Вход:
Начальное приближение x0
Точность (число итераций I)
Выход:
xI - решение уравнения (1)
Инициализация:
calculate f’(x0)
Шаги:
1. repeat:
2. calculate xi using (5)
3. let i=i+1
4. if i>I then break the cycle
end of repeat
Модификация алгоритма Ньютона для решения системы нескольких уравнений заключается в линеаризации соответствующих функций многих переменных, т. е. аппроксимации их линейной зависимостью с помощью частных производных. Например, для нулевой итерации в случае системы двух уравнений:
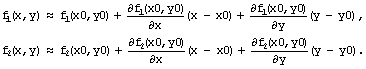
Чтобы отыскать точку, соответствующую каждой новой итерации, требуется приравнять оба равенства нулю, т.е. решить на каждом шаге полученную систему линейных уравнений.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.xaoc.ru/
| Основы проектирования и конструирования | |
|
Основы проектирования и конструирования Конспект лекций для студентов специальности 060800 "Экономика и управление на предприятии" Составитель ... Эти дополнительные уравнения отражают особенности геометрических связей, наложенных на деформируемые системы, и называются уравнениями перемещений. Традиционные (конструктивные) модели - такие как дифференциальные и интегральные уравнения, модели массового обслуживания и т.д. представляют собой алгоритм вычисления значения ... |
Раздел: Промышленность, производство Тип: учебное пособие |
| Высшая математика для менеджеров | |
|
ПРЕДИСЛОВИЕ Учебное пособие "Высшая математика для менеджеров" включает такие разделы высшей математики, изучение которых дает математический аппарат ... Наподобие того, как функция y = f(x) геометрически иллюстрируется своим графиком, можно геометрически истолковать и уравнение z = f(x, y). Возьмем в пространстве R3 прямоугольную ... ... трех переменных является множество точек пространства R3, но непосредственной геометрической интерпретации для функций с числом аргументов больше двух не существует, однако для них ... |
Раздел: Рефераты по математике Тип: дипломная работа |
| Экзаменационные билеты по численным методам за первый семестр 2001 ... | |
|
примерный перечень экзаменационных вопросов ЧИСЛЕННЫЕ МЕТОДЫ Математическая модель и ее погрешности. Представление чисел в ЭВМ. Работа компьютера с ... Приведите неравенство, связывающее погрешности на двух последовательных итерациях метода Ньютона нахождения корня нелинейного уравнения. Приведите геометрическую интерпретацию метода Ньютона для решения нелинейного уравнения F(x) = 0. |
Раздел: Остальные рефераты Тип: реферат |
| Дифференциальные уравнения I и II порядка | |
|
Введение. Исследование поведения различных систем (технические, экономические, экологические и др.) часто приводит к анализу и решению уравнений ... Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую ... Геометрическое представление решения дифференциального уравнения рассмотрим на примере уравнения 1-го порядка вида . |
Раздел: Рефераты по математике Тип: реферат |
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... Система Ф, определенная уравнением (1) называется управляемой в том и только том случае, если для всех х0=EN при начальном состоянии x0 системы в момент t=0 и некотором конечном T ... В тех случаях, когда поверхность отклика достаточно хорошо описывается уравнением второго порядка, резкое уменьшение числа шагов можно получить, если воспользоваться алгоритмом ... |
Раздел: Рефераты по математике Тип: реферат |