Лабораторная работа: Корреляционно-регрессионный анализ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Имени ЯРОСЛАВА МУДРОГО
ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ
Кафедра: Статистики и экономико-математических методов
Отчет
По дисциплине статистика
Лабораторная работа по теме:
«Корреляционно регрессионный анализ»
Вариант 2
Выполнила студентка гр.8431
Гарбузова Ю.
Егарева Т. Н
Ерошенко Н.Н
Проверила
Фетисова Г.В
Великий Новгород
2010
Корреляционный анализ изучает стохастические связи между случайными величинами в экономике. Метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выявить зависимость между результатом и факторами в том случае, если посторонние факторы не изменялись и не искажали основную зависимость. При этом число наблюдений должно быть достаточно велико, так как малое число наблюдений не позволяет обнаружить закономерность связи. Укрупненно можно рекомендовать: число наблюдений равно восьмикратному числу факторов, включенных в модель.
Задание:
1.) Построить корреляционное поле зависимости между y и x1. Сделать вывод относительно формы и направления связи.
2.)
Построить уравнение регрессии между у и х1 (линейная, степенная,
логарифмическая). Оценить каждую функцию через F-критерий, ![]() , ошибку аппроксимации.
, ошибку аппроксимации.
3.) Построить корреляционное поле зависимости между y и x2. Сделать вывод относительно формы и направления связи.
4.) Построить двухфакторное уравнение регрессии между y, x1,x2. Оценить показатели тесноты связи.
5.) Оценить модель через F-критерий Фишера.
6.) Оценить параметры через t-критерий Стьюдента.
Исходные данные :
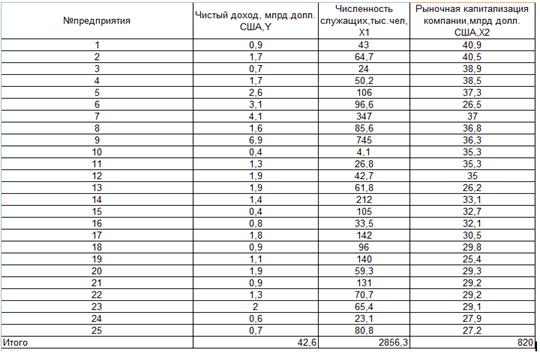
Уравнение регрессии между у и х1 (линейная):
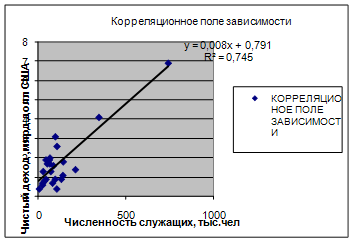
F расч = (0,7451/(1-0,7451))*((25-1-1)/1) = 67,232
Уравнение регрессии между у и х1 (логарифмическая):
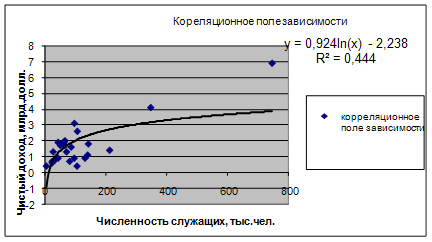
F расч = (0,4445/(1-0,4445))*((25-1-1)/1) = 18,404
Уравнение регрессии между у и х1 (степенная):
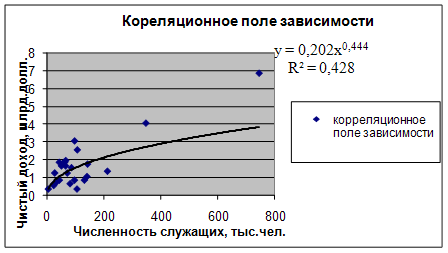
F расч = (0,4284/(1-0,4284))*((25-1-1)/1) = 0,019
| линейная | F расч | 67,23146332 |
| логарифмическая | F расч | 18,40414041 |
| степенная | F расч | 0,019459742 |
| Е1 | 53,9 |
| Е2 | 72,5 |
| Е3 | 48,2 |
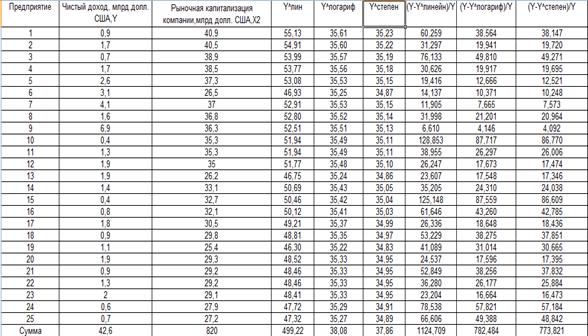
Уравнение регрессии между у и х2 (линейная):
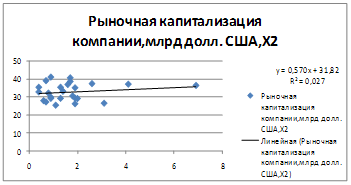
Уравнение регрессии между у и х2(логарифмическая):
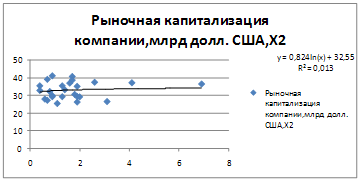
Уравнение регрессии между у и х2(степенная):
| E1 | 2171 |
| E2 | 166 |
| E3 | 165 |
С помощью пакета анализа
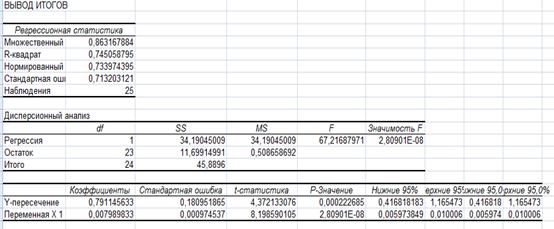
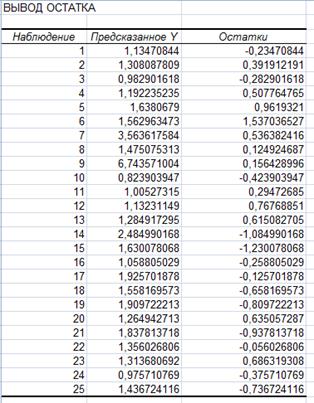
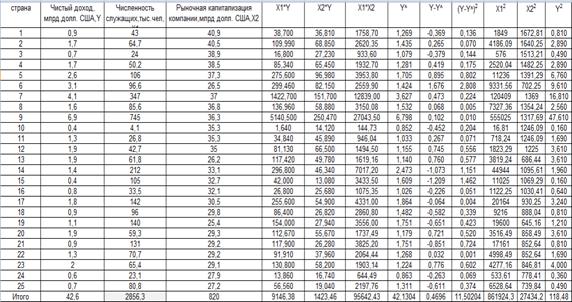
![]()
| Y=0,148+0,008*x1+0,019*x2 |
| r yx1 | 0,863 |
| ryx2 | 0,005 |
| rx1x2 | 0,395 |
| r yx1x2 | 0,937 |
| ryx2x1 | -0,723 |
| rx1x2y | 0,772 |
| R yx1x2 | 0,937 |
| R^2 yx1x2 | 0,878 |
| сигма ост | 0,003 |
| Fрасч | 72,08 |
| Fтабл | 2,086 |
| стьюдента | 34,40 |
Линейный коэффициент корреляции может быть определен по формуле:
![]()
Или
![]()
 .
.
Он изменяется в диапазоне от -1 до +1. положительный коэффициент характеризует прямую связь, отрицательный – обратную. Связь между факторным и результативным признаком можно признать тесной, если r>0,7.
Индекс корреляции может рассчитываться по формуле:
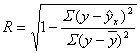 ,
,
Индекс корреляции изменяется от 0 до 1.
оценка существенности связи на основе t – критерия Стьюдента (при оценке параметров) или F – критерия Фишера (при оценке уравнения регрессии).
![]() для линейной
формы связи,
для линейной
формы связи,
![]() для
криволинейной формы связи,
для
криволинейной формы связи,
где k – число параметров.
Нахождение аппроксимирующего уравнения, для чего определяется средняя ошибка аппроксимации
![]() .
.
F-критерия Фишера:
![]()
| Математические основы теории систем | |
|
ОГЛАВЛЕНИЕ Оглавление 1 Введение 3 Объект и устройство 3 Задачи управления 4 Матричный формализм в теории систем 6 Линейные операторы 6 Инвариантное ... Пусть Х n - мерное линейное пространство и у=Ах -линейное преобразование на пространстве Х. Пусть X1=X является некоторым подпространством Х, обладающим однако, тем свойством, что ... Пусть f(х) - некоторая функция, заданная на выпуклом множестве Х, ах1, x2 - две произвольные точки из х, х=鋏х1+(1-鋏)х2; 0=1=1; - произвольная точка отрезка, соединяющая х1 и х2. |
Раздел: Рефераты по математике Тип: реферат |
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... В силу совпад-я рага: найдутся такие числа х1=ѭ1, х2=ѭ2, .хn=ѭn, что столбец своб-х чл-в будет выраж-ся через первые r столб-в => и через всю с-у столб-в матницы A, т.е. справед-о ... Точкой будема называть любую упорядоченную пару вещ. чисел(х,у). Прямой назовем множество всех точек координаты которых удавлетворяют линейному уравнению ах+by+c=0, (1) a,b R a2+b2 ... |
Раздел: Рефераты по математике Тип: реферат |
| Шпаргалки на экзамен в ВУЗе (1 семестр, математика) | |
|
1) Основные понятия линейной алгебры. Задачи о перевозках. Элементы линейной алгебры. Задачи о перевозках. На 2-х складах А1 и А2 сосредоточено а1, а2 ... отрезке [a, b], принимает на нем наибольшее и наименьшее значения.Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем m f(x) M Отметим эти наибольшие и ... ... функции, а затем производную самой функции по формуле Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, ... |
Раздел: Рефераты по математике Тип: реферат |
| Расчет коэффициента корреляции между притоком прямых иностранных ... | |
|
Министерство иностранных дел Дипломатическая академия КУРСОВАЯ РАБОТА "Расчет коэффициента корреляции между притоком прямых иностранных инвестиций ... Основная задача корреляционного анализа (являющаяся основной и в регрессионном анализе) состоит в оценке уравнения регрессии. . Т.к. r = ѭ, то будем считать, что линейная форма связи между х1 и х2, выбрана верно. |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Построение и анализ однофакторной эконометрической модели | |
|
Задача 1. Построение и анализ однофакторной эконометрической модели Однофакторная производственная функция накладных расходов в шахтном строительстве ... Для оценки тесноты связи между показателем Y и факторами Х1 и Х2, а также между факторами вычисляем парные коэффициенты корреляции, а потом составляем корреляционную матрицу ... С помощью полученных корреляционной матрицы и коэффициентов частичной корреляции можно сделать выводы о значимости факторов и проверить факторы на мультиколлинеарность - линейную ... |
Раздел: Рефераты по экономико-математическому моделированию Тип: контрольная работа |